Контрольная работа 8 по математике: ГБОУ Школа № 1191, Москва

Содержание

Итоговая контрольная работа по математике 8 класс

Пояснительная записка к аттестационному материалу для промежуточной аттестации по математике учащихся 8 класса

 

Промежуточная аттестация по математике в 8 классе  проводится в соответствии с :

  • Федеральным законом РФ от 29.12.12г № 273-ФЗ «Об образовании в Российской Федерации»;
  • Уставом МБОУ «СОШ №  »;
  • Учебным планом на 2020/2021 учебный год;

 

Содержание и структура  работы для промежуточной аттестации по математике разработаны на основе следующих документов:

  • Федерального государственного образовательного стандарта основного общего образования по математике
  •  Примерной программы (Математика.
    5-9 классы: проет.- 3-е изд. перераб. –М.: Просвещение, 2011.-64с.- (Стандарты второго поколения)
  • Алгебра-8: учебник для общеобразовательных учреждений А.Г.Мерзляк, В.Б.Полонский, М.С. Якир, Москва , «Вентана-Граф», 2020г .
  • Дидактические материалы по алгебре для 8 класса / А.Г.Мерзляк, В.Б. Полонский, Е.М. Рабинович — М.: Вентана-Граф, 2021.
  • Алгебра. Тематические тесты. 8 класс /  Ю.П.Дудницын, В.Л.Кронгауз. — М.: Просвещение, 2020.
  • Учебник. Геометрия 8 кл. / А.Г.Мерзляк, В.Б.Полонский, М.С.Якир, Москва, «Вентана-Граф», 2018
  • reshuoge.ru
  • www. fipi.ru

 

 

Цель: оценить уровень общеобразовательной подготовки по математике учащихся 8-х классов, обеспечить подготовку к государственной (итоговой) аттестации за курс основной школы.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Структура и содержание работы 

 

Тестовая контрольная работа по математике за курс 8 класса составлена в форме Основного государственного экзамена, содержит 2 модуля: «Алгебра», «Геометрия». Контрольная работа состоит из двух частей.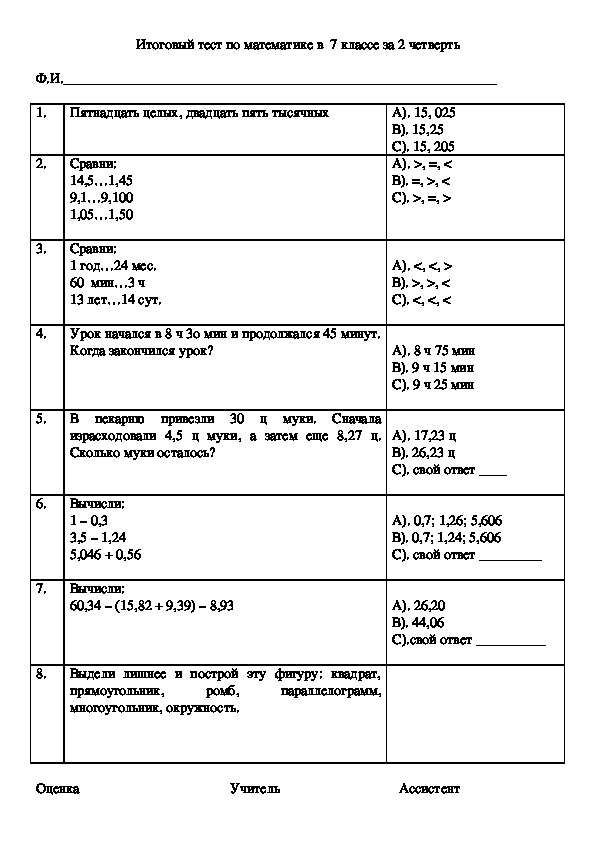

1 часть – 13 заданий, 2 часть – 5 задания. Контрольная работа рассчитана на 90 минут.

Характеристика структуры и содержания экзаменационной работы

Аттестационная  работа состоит из двух частей.

Часть 1 содержит 12 заданий базового уровня сложности. Задание 3-5,8 предусматривает выбор верных ответов из четырех предложенных. Задание считается выполненным правильно, если учащийся указал правильные варианты ответа. Учащийся не должен приводить какие-либо рассуждения, поясняющие его выбор. Задания 1,2,6,7, 9-12 со свободным ответом. Каждое задание этой части считается выполненным правильно, если учащийся записал правильный ответ. Все необходимые вычисления, преобразования и т.д. учащиеся выполняют на черновиках.

Правильный ответ на каждое из заданий первой части оценивается одним баллом.

С помощью заданий первой части проверяется знание и понимание важных элементов содержания (понятия, их свойства, приемы решения задач и т.

д.), владение основными алгоритмами, умение применить знания к решению математических задач, не сводящихся к прямому применению алгоритма, а также применение знаний в простейших практических ситуациях.

Часть 2 содержит 5 заданий повышенного уровня сложности, требующих развернутого ответа с записью решения. Задания этой части считаются выполненными правильно, если учащийся привел развернутую запись решения задания и дал правильный ответ. Правильное решение каждого из заданий второй части оценивается двумя баллами.

При выполнении второй части работы учащиеся должны продемонстрировать умение математически грамотно записать решение, приводя при этом необходимые пояснения и обоснования.

 

Время выполнения работы

На проведение экзамена отводится 120 минут.

 

Условия проведения экзамена и проверки работ

В начале экзамена учащемуся выдается полный текст работы.

Формулировки заданий не переписываются, рисунки Части 1 не перечерчиваются.

После решения задачи записывается ответ. При записи ответа учитывается следующее:

  • в заданиях с выбором ответа указываются номера верных ответов;
  • в заданиях с кратким ответом указывается число (целое число или десятичная дробь), получившееся в результате решения.

Все необходимые вычисления, преобразования производятся в черновике. Черновики не проверяются и не учитываются при выставлении отметки.

 

Дополнительные материалы и оборудование

Линейка, карандаш и циркуль. Справочная литература, калькуляторы, мобильные телефоны на экзамене не используются.

 

 

 

Оценка выполнения отдельных заданий и работы в целом

Общий балл формируется путем суммирования баллов, полученных за выполнение первой и второй частей работы.

Таблица 1

Схема формирования общего балла

Задания

Максимальное количество баллов за выполнение заданий части 1

Максимальное количество баллов за выполнение заданий части 2

Общий балл

Задания 1-12

Задания 13-17

12

13

14

15

16

 

Баллы

12

2

2

3

2

2

22

 

Таблица 2

Шкала перевода общего балла в школьную отметку

Отметка по пятибалльной шкале

«2»

«3»

«4»

«5»

Общий балл

0-5 балла

6-14 баллов

15-19 баллов

20-22 балла

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Вариант 1

Часть 1

Модуль «Алгебра»

  1. Вычислите:  — .

 

Ответ:____________

  1. Найдите значение выражения   

 

Ответ:____________

 

 

3.  На координатной прямой отмечены точки A, B, C, D. Одна из них соответствует числу .
 Какая это точка?

 

В ответе укажите номер правильного варианта.

 

1) точка A

2) точка B

3) точка C

4) точка D

 

 

 4. Решите уравнение: 

1) 6         2) 6,6      3) 3      4)  18

Ответ:_________

 

5. Какое  из  данных уравнений    не имеет корней?

1)       2)            3) 4)    

Ответ:_________

6. Сократите дробь    и найдите ее значение  при х = — 4

Ответ:_________

7.  Найдите значение выражения при a = 4.

Ответ:_________

 

8. Установите соответствие между графиками и формулами, которые их задают:

 

 

 

 

 

Графики

Формулы

Ответ:         

 

 

 

9.  В каждой десятой банке кофе согласно условиям акции есть приз.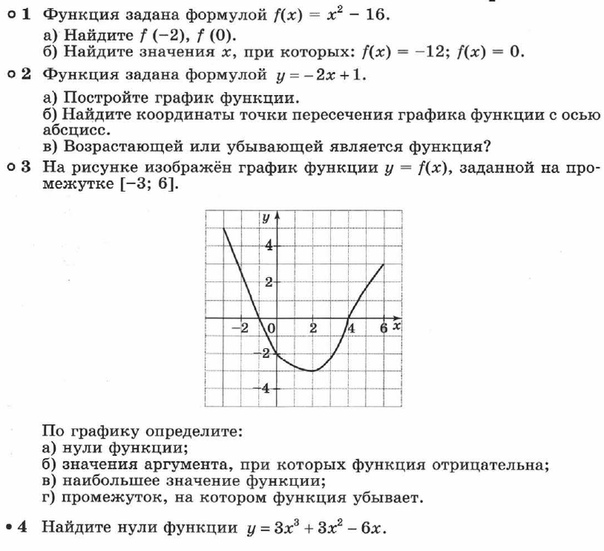 Призы распределены по банкам случайно. Варя покупает банку кофе в надежде выиграть приз. Найдите вероятность того, что Варя не найдет приз в своей банке.

 

 

Модуль «Геометрия»

10. Катеты прямоугольного треугольника равны 15 и 20. Найдите гипотенузу.

Ответ:_________

11.  Укажите номера неверных утверждений:

1) Диагонали трапеции пересекаются и делятся точкой пересечения пополам.

2) Противоположные углы параллелограмма равны.

3) Отношение периметров подобных треугольников равно квадрату коэффициенту подобия.             

Ответ:___________

 

12.На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,8 м, если  длина его тени равна 9 м,  а высота фонаря 4 м?

Ответ:____________

 

 

 

 

 

 

Часть 2

Модуль «Алгебра»

 

 13.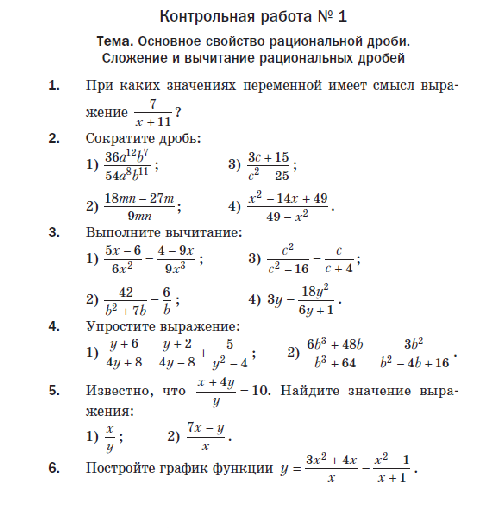 (2 балла) Решите уравнение: — 5х + 6= 0.

Ответ:____________

14. (2 балла) Решите уравнение:

Ответ:____________

15. (3 балла) 

Моторная лодка прошла 36 км по течению реки и вернулась обратно, потратив на весь путь 5 часов. Скорость течения реки равна 3 км/ч. Найдите скорость лодки в неподвижной воде.

                                                                          Модуль «Геометрия»

16. (2 балла) В равнобедренной трапеции   один из углов равен  , а высота, проведенная из вершины  тупого угла, делит большее основание на отрезки 4 см и 12 см. Найдите площадь трапеции.

Ответ:____________

 17. (2 балла) Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке, лежащей на стороне BC. Найдите AB, если BC = 34.

.

Ответ:____________

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Вариант 2

Часть 1

Модуль «Алгебра»                                                          

  1. Вычислите:  — .

 

Ответ:____________

2. Найдите значение выражения    

 

Ответ:___________

 

3. На  координатной прямой отмечены точки A, B, C и D. Одна из них соответствует числу  . Какая это точка?

 

 

4. Решите уравнение: 

1) -8         2) 32     3) 16      4)  -32

Ответ:_________

 

5. Какое  из  данных уравнений    имеет единственный корень?

1)       2)        3)        4) 4=0

Ответ:_________

6. Сократите дробь  и найдите ее значение при х= -3

Ответ:_________

7.Найдите значение выражения при a = 2.

Ответ:_________

 

8. Установите соответствие между графиками и формулами, которые их задают:

Графики

 

 

Формулы

Ответ

 

9. Телевизор у Маши сломался и показывает только один случайный канал. Маша включает телевизор. В это время по трем каналам из двадцати показывают кинокомедии. Найдите вероятность того, что Маша попадет на канал, где комедия не идет.

 

 

Модуль «Геометрия»

10. Катеты прямоугольного треугольника 30 и 40. Найдите гипотенузу.

Ответ:___________

11. Укажите номера верных утверждений:

1) Площадь параллелограмма равна произведению его основания на высоту.

2) Диагонали прямоугольника перпендикулярны.

3) Отношение площадей подобных треугольников равно коэффициенту подобия.

Ответ:___________

                                                      

12. На каком расстоянии (в метрах) от фонаря стоит человек ростом 2 м, если длина его тени равна 1 м, высота фонаря 9 м?

Ответ:____________

 

 

 

 

 

 

 

 

 

Часть 2

                                                            Модуль «Алгебра»

13. (2 балла) Решить уравнение: + 6x + 8 = 0.

Ответ:____________

14. (2 балла) Решите уравнение:

Ответ:____________

 

15. (3 балла) Моторная лодка прошла против течения реки 77 км и вернулась в пункт отправления, затратив на обратный путь на 2 часа меньше, чем на путь против течения. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 4 км/ч.

Модуль «Геометрия»

 

16. (2 балла) В прямоугольной трапеции  основания равны  6 см и 12 см,  а один из углов равен  .  Найдите площадь трапеции.

Ответ:____________

 

17. (2 балла)  Вы­со­та BH па­рал­ле­ло­грам­ма ABCD делит его сто­ро­ну AD на от­рез­ки AH=3 и HD=24. Диа­го­наль па­рал­ле­ло­грам­ма BD равна 51. Най­ди­те пло­щадь па­рал­ле­ло­грам­ма.

Ответ:____________

 

 

 

 

 

 

 

 

 

 

 

 

 

 

     Математика.8 класс. Вариант 3                                                                                                     

Часть 1

Модуль «Алгебра»

  1.  Вычислите: — + .

 

Ответ:____________

  1. Найдите значение выражения .
  2.  

Ответ:____________

3. Одна из точек, отмеченных на координатной прямой, соответствует числу 

 

Какая это точка?

В ответе укажите номер правильного варианта.

 

1) точка A

2) точка B

3) точка C

4) точка D

 

 

 4. Решите уравнение: 

1) 2         2) 6,6      3) 18   4)  -18

Ответ:_________

 

5. Какое  из  данных уравнений    не имеет корней?

1)       2)            3) 4)    

Ответ:_________

6. Сократите дробь    и найдите ее значение  при х = — 4

Ответ:_________

7.  Найдите значение выражения при a = 4.

Ответ:_________

 

8. Установите соответствие между графиками и формулами, которые их задают:

Графики

 

 

 

 

 

 

Формулы

Ответ:         

 

 

9. В фирме такси в данный момент свободно 20 машин: 9 черных, 4 желтых и 7 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет желтое такси.

 

 

 

Модуль «Геометрия»

10. Катеты прямоугольного треугольника равны 9 и 12. Найдите гипотенузу.

Ответ:_________

11.  Укажите номера неверных утверждений:

1) Диагонали трапеции пересекаются и делятся точкой пересечения пополам.

2) Площадь прямоугольного треугольника равна половине произведения его катетов.

3) Отношение периметров подобных треугольников равно квадрату коэффициенту подобия.             

Ответ:___________

12.На каком расстоянии (в метрах) от фонаря стоит человек

      ростом 1,8 м, если  длина его тени равна 9 м,   

      а высота фонаря 4 м?

Ответ:____________

 

 

 

 

Часть 2

Модуль «Алгебра»

 

 13. (2 балла) Решите уравнение + 4x — 5 = 0.

Ответ:____________

14. (2 балла) Решите уравнение:

Ответ:____________

15. (3 балла)  Моторная лодка прошла против течения реки 210 км и вернулась в пункт отправления, затратив на обратный путь на 4 часа меньше, чем на путь против течения. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 3 км/ч.

 

 

Модуль «Геометрия»

16. (2 балла) В равнобедренной трапеции   один из углов равен  , а высота, проведенная из вершины  тупого угла, делит большее основание на отрезки 5 см и 15см. Найдите площадь трапеции.

Ответ:____________

 17. (2 балла) Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке, лежащей на стороне BC. Найдите AB, если BC = 34.

 

Ответ:____________

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Математика.8 класс. Вариант 4                                                                                                    

Часть 1

Модуль «Алгебра»

  1. Вычислите: — + .

 

Ответ:____________

2. Найдите значение выражения  

 

Ответ:___________

 

3. На координатной прямой отмечена точка А.

 

Известно, что она соответствует одному из четырех указанных ниже чисел. Какому из чисел соответствует точка А?

 

1) 

2) 

3) 0,6

4) 4

 

4. Решите уравнение:   

 

1) 0.6         2) -6      3)       4)  6

Ответ:_________

 

5. Какое  из  данных уравнений    имеет единственный корень?

1)       2)        3)        4) 4=0

Ответ:_________

 

6. Сократите дробь  и найдите ее значение при х= -3

Ответ:_________

7.Найдите значение выражения при a = 5.

Ответ:_________

 

8.Установите соответствие между графиками и формулами, которые их задают:

Графики

Формулы

Ответ

 

9.  Родительский комитет закупил 25 пазлов для подарков детям на окончание года, из них 15 с машинами и 10 с видами городов. Подарки распределяются случайным образом. Найдите вероятность того, что Толе достанется пазл с машиной.   

             Ответ:___________

 

Модуль «Геометрия»

10. Катеты прямоугольного треугольника 6 и 8. Найдите гипотенузу.

Ответ:___________

11. Укажите номера верных утверждений:

1) Площадь треугольника равна половине произведению его основания на высоту.

2) Диагонали прямоугольника перпендикулярны.

3) Отношение площадей подобных треугольников равно коэффициенту подобия.

Ответ:___________

                                                      

12. На каком расстоянии (в метрах) от фонаря стоит человек ростом 2 м, если длина его тени равна 1 м, высота фонаря 9 м?

Ответ:____________

 

 

 

 

 

 

Часть 2

                                                            Модуль «Алгебра»

13. (2 балла) Решить уравнение: + 8x + 7 = 0.

Ответ:____________

14. (2 балла) Решите уравнение:

 

Ответ:____________

 

15. (3 балла) Моторная лодка прошла против течения реки 72 км и вернулась в пункт отправления, затратив на обратный путь на 2 часа меньше, чем на путь против течения. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 3 км/ч.

Модуль «Геометрия»

 

16. (2 балла) В прямоугольной трапеции  основания равны  8 см и 10 см,  а один из углов равен  .  Найдите площадь трапеции.

Ответ:____________

 

17. (2 балла)  Высота AH ромба ABCD делит сторону CD на отрезки DH = 12 и CH = 1. Найдите высоту ромба.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Ответы

№

 

1 вариант

2 вариант

3 вариант

4 вариант

1

 -0,05

0,55

0,05

-0,55

2

       -2

7

-2

3

1

1

4

2

4

1

4

3

2

5

3

4

3

4

6

— 8

-4

-8

-4

7

1/16

0,25

4

8

132

132

132

132

9

0,9

0,85

0,2

0,6

10

25

50

15

10

11

2

1

2

1

12

11

3,5

11

3,5

13

3;2

— 2; — 4

— 5; 1

-1; — 7

14

-1;1

2;-2

2;-2

0,3

15

15

18

18

15

16

48

54

75

18

17

68

1215

17

5

 

Итоговая контрольная работа по математике 8 класс

Итоговая контрольная работа по математике за 8 класс Вариант №1 Часть 1 Модуль «Алгебра» А1  Укажите выражение, значение которого является наименьшим. )1 4 3  5 6 ; )2  4 3 5 6 ; )3 4 1,0 ; 1,04)4  А2     Расположите в порядке возрастания числа:   √30 ; 3  √3  ; 5,5. 1. √30 ; 3√3  ; 5,5  2. 3. 5,5; 3√3;√30 4. 3√3 ; 5,5; √30 3√3;√30 ; 5,5 А3   Разложить квадратный трехчлен на множители: 3х2 + 15х + 12 А4   Решите неравенство х+4≥4х­5 и укажите, на каком рисунке изображено множество его  решений. А5  В прямоугольном треугольнике ВС = 8,  соs∟В = 0,8       Найти АВ. Модуль «Геометрия» А6 В прямоугольном треугольнике один из катетов равен 10 см, а угол, лежащий напротив него,  равен  . Найдите площадь треугольника. А7  Укажите номера верных утверждений: 1 Сумма двух противоположных углов параллелограмма равна 180°. 2 Если в четырехугольник можно вписать окружность и сумма длин двух его  противоположных , сторон равна 200, а длина третьей стороны равна 60, то длина  оставшийся стороны равна 140. 3 Около любого четырёхугольника можно описать окружность. А8   Угол АОВ  равен  63°. Найдите величину  угла АСВ. Часть 2 Модуль «Алгебра» В1. Решите уравнение  . х  х  2 7  х 2  8 2  х 4 В2. Упростить выражение:  2 20  2 45     180 1 4 В3. Решите неравенство:     5 2 х  х 8 В4. Решите задачу:  4 .0 Катер прошел 40 км по течению реки и 6 км против течения, затратив на весь путь 3 ч. Найдите  скорость катера в стоячей воде, если известно, что скорость течения равна 2 км/ч. Часть 2 Модуль «Геометрия» В5 В6.  Найдите площадь ромба, сторона которого 25 см, а   меньшая диагональ 14 см. В7. Дан  ABCD  ­ параллелограмм. На его сторонах отмечены точки  P, K, M и N так, что BK=ND,  BP=MD,  . Докажите, что четырехугольник  PKMN – параллелограмм В Итоговая контрольная работа по математике за 8 класс Вариант №2  Часть 1 Модуль «Алгебра» А1  Укажите выражение, значение которого является наименьшим. 1. 1 0,1 2. 5 + 2 3 5 3. 4. 1∙ 0,1 5− 2 3 5 А2   Расположите в порядке убывания числа:    √30;3√3 ; 5,5. 1. 2. 3. √30;3√3; 5 ,5  5,5; √30;3√3 4. 3√3 ; 5,5; √30 3√3;√30 ; 5,5 А3   Разложите на множители квадратный трехчлен:    8х2 + 16х ­ 64   А4  Решите неравенство 3х+5≥7х­3 и укажите, на каком рисунке изображено множество его  решений. А5  Найдите тангенс угла С Модуль «Геометрия» А6  В прямоугольном треугольнике гипотенуза равна  10, один из катетов равен 6. Найдите  площадь треугольника А7   .Укажите в ответе номера верных утверждений: 1 Центром окружности, вписанной в правильный треугольник, является точка пересечения  серединных перпендикуляров к его сторонам. 2 В любой прямоугольный треугольник можно вписать окружность. 3 Центр окружности, описанной около прямоугольного треугольника, находится на катете  этого треугольника. А8   Найдите величину угла ВОС, если    угол  ВАС равен 70° Часть 2 Модуль «Алгебра В1. Решите уравнение  4  2 х  9 х х   1 3 .  1 В2. Упростите выражение:  3 48  75  1 7 147 В3. Решите неравенств:     8 2 х  х 5  4 .0 В4. Решите задачу: Катер прошел 12 км против течения реки и 5 км по течению. При этом он затратил на весь путь 40 минут. Какова собственная скорость катера, если известно, что скорость течения реки равна 3  км/ч Часть 2 В5. Модуль «Геометрия В6. В ромбе АВСD одна из его диагоналей равна 8 см, а его площадь 24 см2.  Найдите длину  стороны ромба. В7. Дан   ABCD  ­ параллелограмм. На его сторонах отмечены точки  P, K, M и N так, что . Докажите, что четырехугольник  PKM N – параллелограмм. KC AN ,   BP  MD

Контрольная работа по математике в 8 классе

Центр образования № 1840

2008 – 2009 учебный год

Переводная (итоговая) контрольная работа по математике в 8 классе

Вариант № 1

1. Упростить выражения: а) ;

б) ; в) при .

2. Решить уравнение: а) ;б) ; в) ; г) .

3. Вычислить: .

4. Построить графики функций: а) ; б) .

5. При каких x определено выражение ?

6. При каких значениях выражение будет целым числом?

7. Абрикосы подешевели на 20 %. Сколько килограммов абрикосов можно купить теперь на деньги, на которые прежде продавали 56 кг?

8. Функция спроса на билеты в кинотеатр является линейной функцией, причем спрос равен 46 билетов при цене 2 у.е. за билет и равен 4 билета при цене 8 у.е. за билет. Сколько билетов будет куплено при цене 6 у.е. за билет?

Центр образования № 1840

2008 – 2009 учебный год

Переводная (итоговая) контрольная работа по математике в 8 классе

Вариант № 2

1. Упростить выражения: а) ;

б) ; в) при .

2. Решить уравнения: а) ;б) ; в) ; г) .

3. Вычислить: .

4. Построить графики функций: а) ; б) .

5. При каких x определено выражение ?

6. При каких значениях выражение будет целым числом?

7. Производительность труда возросла на 25 % поэтому, работа была выполнена на 6 дней быстрее плана. За сколько дней была выполнена работа?

8. Функция спроса на пирожки является линейной функцией, причем спрос равен 31 пирожок при цене 6 у.е. за пирожок и равен 13 пирожков при цене 12 у.е. за пирожок. Сколько пирожков будет куплено при цене 11 у.е. за штуку?

Центр образования № 1840

2008 – 2009 учебный год

Вступительная экзаменационная работа по математике в 9 класс

Вариант № 1

1. Упростить выражения:

а) ; б) .

2. Решить уравнения: а) ;

б) ; в) .

3. Вычислить: .

4. Построить графики функций: а) ; б).

5. При каких значениях переменной x определено выражение ?

6. Гарри Поттер и Гермиона решили встретиться, чтобы пойти в кино. До места встречи каждому надо было пройти по 5 километров. Гарри очень торопился и шел со скоростью на 1 км/ч большей, чем скорость Геомионы, поэтому он ждал Гермиону ещё 10 минут. Найдите скорость Гарри, если они вышли одновременно.

7. Сумма корней квадратного уравнения равна 5, а их произведение равно 4. Составить уравнение и найти его корни, если свободный член равен 8.

8. Найдите сумму квадратов корней уравнения и установите, при каких значениях a она будет наименьшей.

Центр образования № 1840

2008 – 2009 учебный год

Вступительная экзаменационная работа по математике в 9 класс

Вариант № 2

1. Упростить выражения:

а) ; б) .

2. Решить уравнения: а) ;

б) ; в) .

3. Вычислить: .

4. Построить графики функций: а) ; б) .

5. При каких значениях переменной x определено выражение ?

6. Гарри Поттер и Рон решили встретиться, чтобы потренироваться в игре в квиддич. До места встречи каждому надо было пролететь по 15 километров. Рон очень торопился и летел со скоростью на 5 км/ч большей, чем скорость Гарри, поэтому он ждал друга ещё 15 минут. Найдите скорость Рона, если они вылетели одновременно.

7. Сумма корней квадратного уравнения равна 5, а их произведение равно 6. Составить уравнение и найти его корни, если свободный член равен 12.

8. Найдите сумму квадратов корней уравнения и установите, при каких значениях p она будет наибольшей.

Контрольная работа по математике. Умножение и деление. 2 класс. Вариант 1

Контрольная работа по математике. 2 класс.

Умножение и деление.

Вариант 1

1.  Решите задачу.

У котёнка 4 лапы. Сколько лап у 3 котят?

2. Решите задачу.

12 ребят поделили на 2 команды поровну. Сколько ребят в каждой команде?

3. Замените умножение сложением, а сложение умножением и вычислите.

5 х 3         8+8+8+8

8 х 4         12+12+12

4. Найдите значения выражений.

8 х 2 + 60                      74 – 18 : 2

80 – 6 х 2                      38 + 16 : 2

14 : 7 х 5                        (16 + 34) : 10

5. Сравните числовые выражения.

5 х 9  и  9 х 5                             7 х 4  и  7 х 3 – 4

10 х 0  и  0 х 5                           70 : 10  и  70 : 7

6. Начертите квадрат со стороной 5 см. Найдите периметр этого квадрата.

7.* Сумма трёх чисел равна 16. Сумма первого и второго слагаемых равна 11, а сумма второго и третьего – 8. Найдите, чему равны все эти три числа.

 

Вариант 2

1.  Решите задачу.

В коробке 8 карандашей. Сколько карандашей в 2 таких коробках?

2. Решите задачу.

Кроликам дали 14 морковок по 2 морковки каждому. Сколько кроликов получили морковку?

3. Замените умножение сложением, а сложение умножением и вычислите.

5 х 7         6+6+6+6

8 х 3         13+13+13

4. Найдите значения выражений.

7 х 2 + 50                      65 – 16 : 2

70 – 6 х 2                      53 + 14 : 2

18 : 9 х 5                        (25 + 45) : 10

5. Сравните числовые выражения.

4 х 8  и  8 х 4                           8 х 5  и  8 х 3 – 8

12 х 0  и  0 х 3                          90 : 10  и  90 : 9

6. Начертите квадрат со стороной 6 см. Найдите периметр этого квадрата.

7.* Сумма трёх чисел равна 11. Сумма первого и второго слагаемых равна 6, а сумма второго и третьего – 9. Найдите, чему равны все эти три числа.

Контрольные работы по математике за 5 класс, УМК Виленкин (с ответами по паролю)

Виленкин — один из старых, известных многим, авторов учебников математики. Учебники довольно логично построены, материал не поверхностный, но и не слишком углубленный, то что нужно в пятом классе и ничего более. А чтобы проверить усвоенные учениками знания, обязательно нужно проводить самостоятельные и контрольные работы по математике. Вот такие работы к учебнику Виленкина за пятый класс мы и предлагаем вашему вниманию.

Контрольная работа №1 за 5 класс (Виленкин)

Вариант 1

1. Найдите сумму:
а) 3000000+5000+7
б) 654+765

2. Выполните действия:
(60+40):2 – 30:5

3. Сравните числа и поставьте вместо звездочки знак < или >
а) 63001 * 63002
б) 41527 * 42326

4. Задача. От туристского лагеря до города 84 км. Турист ехал на велосипеде из лагеря в город со скоростью 12 км/ч., а возвращался по той же дороге со скоростью 14 км/ч. На какой путь турист затратил больше времени и на сколько часов.

Вариант 2

1. Найдите сумму:
а) 2000000+7000+300+2
б) 763+448

2. Выполните действия:
(70-50)∙5:20+55

3. Сравните числа и поставьте вместо звездочки знак < или >
а) 20850 * 20860
б) 31255 * 32254

4. Задача. Игорь живет на расстоянии 48 км от районного центра. Путь от дома до райцентра он проехал на велосипеде со скоростью 16 км/ч, а обратный путь по той же дороге он проехал со скоростью 12 км/ч. На какой путь Игорь затратил меньше времени и насколько часов.

Контрольная работа №1 за 5 класс (Виленкин)

Вариант 1

1. Найдите сумму: а) 3000000+5000+7=3005004 б) 654+765=1419

2. Выполните действия: (60+40):2 – 30:5=100:2-6 = 50-6 = 44

3. Сравните числа и поставьте вместо звездочки знак < или > а) 63001 < 63002 б) 41527 < 42326

4. Задача. От туристского лагеря до города 84 км. Турист ехал на велосипеде из лагеря в город со скоростью 12 км/ч., а возвращался по той же дороге со скоростью 14 км/ч. На какой путь турист затратил больше времени и на сколько часов.

1) 84:12=7 (ч.) ехал из лагеря в город.
2) 84:14=6 (ч.) ехал из города в лагерь.
3) 7-6=1 (ч.) на 1 час дольше ехал из лагеря в город.
Ответ: на 1 час дольше ехал из лагеря в город.

Вариант 2

1. Найдите сумму: а) 2000000+7000+300+2=2007300 б) 763+448=1211

2. Выполните действия: (70-50)∙5:20+55=20*5:20+55=5+55=60

3. Сравните числа и поставьте вместо звездочки знак < или > а) 20850 < 20860 б) 31255 < 32254

4. Задача. Игорь живет на расстоянии 48 км от районного центра. Путь от дома до райцентра он проехал на велосипеде со скоростью 16 км/ч, а обратный путь по той же дороге он проехал со скоростью 12 км/ч. На какой путь Игорь затратил меньше времени и насколько часов.

1) 48:16=3 (ч.) ехал дома до райцентра.
2) 48:12=4 (ч.) ехал от райцентра до дома.
3) 4-3=1 (ч.) на 1 час дольше ехал от райцентра до дома.
Ответ: на 1 час дольше ехал от райцентра до дома.

Контрольная работа №2 за 5 класс (Виленкин)

Вариант 1

1. Выполнить действия:
а) (829-239)*75
б) 8991:111:3

2. Задача. Периметр треугольника 36 см, а периметр прямоугольника в 3 раза меньше. На сколько сантиметров периметр треугольника больше периметра прямоугольника?

3. Вычислить:
4 кг – 80 гр

4. 
а) На сколько число 59345 больше числа 53568?
б) На сколько число 59345 меньше числа 69965?

5. Задача. Вдоль аллеи (по прямой) высадили 15 кустов. Расстояние между любыми двумя соседними кустами одинаковое. Найдите это расстояние, если между крайними кустами 210 дм.

Вариант 2

1. Выполнить действия:
а) 2000 – (859+1085):243
б) 3969:(305 – 158)

2. Задача. Туристы в первый день ехали на велосипедах 6 часов со скоростью 12 км/ч, во — второй день они проехали с одинаковой скоростью такой же путь за 4 часа. С какой же скоростью ехали туристы во – второй день?

3. Вычислить:
2 кг – 60 гр

4. 
а) на сколько число 38954 больше числа 22359
б) На сколько число 38954 меньше числа 48234.

5. Задача. Вдоль шоссе (по прямой) высадили 20 деревьев. Расстояние между любыми двумя соседними деревьями одинаковое. Найдите это расстояние, если между крайними деревьями 380 м.

Контрольная работа №2 за 5 класс (Виленкин)

Вариант 1

1. Выполнить действия: а) (829-239)*75=590*75=44250

  *590
      75
+ 2950
 4130
 44250

б) 8991:111:3=81:3=27

2. Задача. Периметр треугольника 36 см, а периметр прямоугольника в 3 раза меньше. На сколько сантиметров периметр треугольника больше периметра прямоугольника?

1) 36:3=12 (см) периметр прямоугольника.
2) 36-12=24 (см) на столько периметр треугольника больше периметра прямоугольника.
Ответ: на 24 см периметр треугольника больше периметра прямоугольника.

3. Вычислить: 4кг – 80г = 3 кг 920 г

4. а) На сколько число 59345 больше числа 53568?

-59345
 53568
   5777

 б) На сколько число 59345 меньше числа 69965?

-69965
 59345
 10620

5. Задача. Вдоль аллеи (по прямой) высадили 15 кустов. Расстояние между любыми двумя соседними кустами одинаковое. Найдите это расстояние, если между крайними кустами 2100 дм.

2100 дм = 21000 см = 21м

1) 21:14=1,5 (м) между соседними кустами
Ответ: 1,5 метра между соседними кустами.

Вариант 2

1. Выполнить действия: а) 2000 – (859+1085):243=2000-1944:243=2000-8=1992 б) 3969:(305 – 158)=3969:147=27

2. Задача. Туристы в первый день ехали на велосипедах 6 часов со скоростью 12 км/ч, во — второй день они проехали с одинаковой скоростью такой же путь за 4 часа. С какой же скоростью ехали туристы во – второй день?

1) 6*12=72 (км) проехали туристы в 1 день.
2) 72:4=18 (км/ч) скорость туристов во второй день.
Ответ: 18 км/ч скорость туристов во второй день.

3. Вычислить: 2кг – 60г = 1 кг 940г

4.  а) на сколько число 38954 больше числа 22359.

— 38954
  22359
  16595
 

б) На сколько число 38954 меньше числа 48234.

-48234
 38954
  9280

5. Задача. Вдоль шоссе (по прямой) высадили 20 деревьев. Расстояние между любыми двумя соседними деревьями одинаковое. Найдите это расстояние, если между крайними деревьями 380 м.

380:19=20 (м) между соседними деревьями.
Ответ: 20 метров.

Контрольная работа №3 за 5 класс (Виленкин)

Вариант 1

1. Решите уравнение:
а) 21+х=56
б) у-89=90

2. Найти значение выражения:
260+в – 160, если в=93

3. Вычислите, выбирая удобный порядок действий
а) 5+1977+1515
б) 863 – (163+387)

4. Решить задачу с помощью уравнения.
В автобусе было 78 пассажиров. После того, как на остановке из него несколько человек вышли, в автобусе осталось 59 пассажиров. Сколько человек вышли из автобуса на остановке.

5.
На отрезке MN =19, отметили точку К такую, что МК=15 и точку F такую, что FN=13. Найти длину отрезка KF.

Вариант 2

1. Решите уравнение:
а) х+32=68
б) 76 – у=24

2. Найти значение выражения:
340+к – 240, если к=87

3. Вычислите, выбирая удобный порядок действий
а) 7231+1437+563
б) (964+479) – 264

4. Решить задачу с помощью уравнения.
В санатории было 97 отдыхающих. После того, как несколько человек уехали на экскурсию, в санатории осталось 78 отдыхающих. Сколько отдыхающих уехали на экскурсию.

5.
На отрезке DE=25 отметили точку L такую, что DL=19, и точку Р такую, что РЕ=17. Найдите длину отрезка LP.

Контрольная работа №3 за 5 класс (Виленкин)

Вариант 1

1. Решите уравнение:

а) 21+х=56
х=56-21
х=35

 

б) у-89=90
у=90+89
у=179

2. Найти значение выражения: 260+ в – 160, если в = 93
260+93-160=193

3. Вычислите, выбирая удобный порядок действий а) 5 + 1977 + 1515 = 1520 + 1977 = 34197 б) 863 – (163 + 387) = 700 + 387 = 1087

4. Решить задачу с помощью уравнения. В автобусе было 78 пассажиров. После того, как на остановке из него несколько человек вышли, в автобусе осталось 59 пассажиров. Сколько человек вышли из автобуса на остановке.

78 — х = 59
78 — 59 = х
х = 19

Ответ: 19 человек
 

5. На отрезке MN = 19 мм, отметили точку К такую, что МК=15 мм и точку F такую, что FN=13 мм. Найти длину отрезка KF.

1) 19 — 15 = 4 (мм) длина отрезка KN.
2) 19 — 13 = 6 (мм) длина отрезка MF
3) 19 — (4 + 6) = 10 (мм) длина отрезка KF.
Ответ: 10 мм.

 

Вариант 2

1. Решите уравнение: а) х+32=68
х=68-32
х = 36

б) 76 – у = 24
76 — 24 = y
y = 52

2. Найти значение выражения:

340 + к – 240, если к = 87

340 + 87 — 240 = 187

3. Вычислите, выбирая удобный порядок действий

а) 7231 + 1437 + 563 = 7231 + 2000 = 9 231

б) (964 + 479) – 264 = 964 — 264 + 479 = 700 + 469 = 1 169

4. Решить задачу с помощью уравнения. В санатории было 97 отдыхающих. После того, как несколько человек уехали на экскурсию, в санатории осталось 78 отдыхающих. Сколько отдыхающих уехали на экскурсию.

97 — x = 78
x = 97 — 78
x = 19

Ответ: 19 человек.

5. На отрезке DE = 25 мм отметили точку L такую, что DL = 19 мм, и точку Р такую, что РЕ = 17 мм. Найдите длину отрезка LP.

1) 25 — 19 = 6 (мм) длина LE.
2) 25 — 17 = 8 (мм) длина DP.
3) 25 — (6+8) = 9 (мм) длина LP
Ответ: 9 мм

Контрольная работа №4 за 5 класс (Виленкин)

Вариант 1

1. Найдите значение выражения:
а) 58∙196
б) 405∙208
в) 36490:178

2. Решите уравнение
а) х∙14=112
б) 133:у=19
в) m:15=90

3. Вычислите, выбирая удобный порядок действий.
а) 4∙289∙25
б) 50∙97∙20

4. Задача. Коля задумал число, умножил его на 3 и от произведения отнял 8. Он получил 50. Какое число задумал Коля?

5. Вычислите корень уравнения и сделайте проверку:
х+х – 20=х+5

Вариант 2

1. Найдите значение выражения:
а) 67∙189
б) 306∙805
в) 38130:186

2. Решите уравнение
а) х∙13=182
б) 187:у=17
в) n:14=98

3. Вычислите, выбирая удобный порядок действий.
а) 25∙197∙4
б) 50∙23∙40

4. Задача. Света задумала число, умножила его на 4 и к произведению прибавила 8. Получила 60. Какое число задумала Света?

5. Угадайте корень уравнения и сделайте проверку:
у+у – 25=у+10

Контрольная работа №4 за 5 класс (Виленкин)

Вариант 1

1. Найдите значение выражения: а) 58∙196

  * 196
      58
+ 1568
   980 
 11368

б) 405∙208

  *405
    208
+3240
810
84240

в) 36490:178

-36490|178
 356    |205
   -890
    890
       0

2. Решите уравнение а) х∙14=112

х = 112 : 14
х= 8

 

б) 133:у=19

у = 133 * 19
у = 2527

в) m:15=90

m = 90 * 15
m = 1350

3. Вычислите, выбирая удобный порядок действий.

а) 4∙289∙25 = 289 * 100 = 28 900

б) 50∙97∙20 = 97 * 1000 = 97 000

 

4. Задача. Коля задумал число, умножил его на 3 и от произведения отнял 8. Он получил 50. Какое число задумал Коля?

х — задуманное число.

х * 3 — 8 = 50
х * 3 = 50 — 8
х = 42 : 3
х = 14

5. Вычислите корень уравнения и сделайте проверку: х + х – 20 = х + 5

х + х — х = 20 + 5
х = 25

Вариант 2

1. Найдите значение выражения: а) 67∙189

  *189
     67
+1323
1134
12663

б) 306∙805

  *306
    805
 +1530
2448
246330
 в) 38130:186

-38130|186
 372   |205
   -930
    930
       0

2. Решите уравнение а) х∙13=182
х = 182 : 13
х = 14

 

б) 187:у=17

у = 187 : 17
у = 11

в) n:14=98

n = 98 * 14
n = 1372

3. Вычислите, выбирая удобный порядок действий.

а) 25∙197∙4 = 197 *100 = 19 700

б) 50∙23∙40 = 2000 * 23 = 46 000

4. Задача. Света задумала число, умножила его на 4 и к произведению прибавила 8. Получила 60. Какое число задумала Света?

х — задуманное число

х * 4 + 8 = 60
х * 4 = 60 — 8
х = 52 : 4
х = 13

5. Вычислите корень уравнения и сделайте проверку: у + у – 25 = у + 10

у + у — у = 25 + 10
у = 35

Контрольная работа №5 за 5 класс (Виленкин)

Вариант 1

1. Найдите значение выражения:
а) 684∙397 — 584∙397
б) 39∙58 – 9720:27+33
в) 23 + 32

2. Решите уравнение:
а) 7у – 39=717
б) х+3х=76

3. Упростите выражение:
а) 24а+16+13а
б) 25∙m∙16

4. Задача. В книге напечатаны 2 сказки. Первая занимает в 4 раза больше страниц, чем вторая, а обе они занимают 30 стр. Сколько страниц занимает каждая сказка?

5. Имеет ли корни уравнение:
    х2=х:х

Вариант 2

1. Найдите значение выражения:
а) 798∙349-798∙249
б) 57∙38-8640:24+66
в) 52+33

2. Решите уравнение:
а) 8х+14=870
б) 5у-у=68

3. Упростите выражение:
а) 37к+13+22к
б) 50∙n∙12

4. Задача. В двух корзинах 98 яблок. В первой яблок в шесть раз меньше, чем во второй. Сколько яблок в каждой корзине?

5. Имеет ли корни уравнение:
   у3=у∙у

 

Вариант 1

1. Найдите значение выражения:
а) 684∙397 — 584∙397 = (684 — 584 ) * 397 = 39 700

б) 39 ∙ 58 – 9720 : 27 + 33 = 1935

1) 39 * 58 = 2262
2) 9720 : 27 = 360
3) 2262 — 360 = 1902
4) 1902 + 33 = 1935

в) 23 + 32 = 55

2. Решите уравнение:
а) 7у – 39 = 717
7у = 717 + 39
7у = 756
у = 108

б) х + 3х = 76
4 * х = 76
х = 76 : 4
х = 19

3. Упростите выражение:

а) 24а + 16 + 13а = 37а + 16

б) 25∙m∙16 = 400m

4. Задача. В книге напечатаны 2 сказки. Первая занимает в 4 раза больше страниц, чем вторая, а обе они занимают 30 стр. Сколько страниц занимает каждая сказка?

Решение:

х — страниц перва сказка.
4х — вторая сказка

Составляем уравнение

х + 4 х = 30
х = 30 : 5
х = 6

5. Имеет ли корни уравнение:

х2=х:х
Имеет при х = 0 или 1.

Вариант 2

1. Найдите значение выражения:

а) 798∙349-798∙249 = 798 (349 — 249) = 79 800

б) 57∙38-8640:24+66 = 1872

1) 57 * 38 = 2166
2) 8640 : 24 = 360
3) 2166 — 360 = 1806
4) 1806 + 66 = 1872

в) 52 + 33 = 85

2. Решите уравнение:

а) 8х+14=870
8х = 870 — 14
х = 856 : 8
х = 107

б) 5у-у=68
4у = 68
у = 68 : 4
у = 22

3. Упростите выражение:

а) 37к+13+22к = 59к + 13

б) 50∙n∙12 = 62n

4. Задача. В двух корзинах 98 яблок. В первой яблок в шесть раз меньше, чем во второй. Сколько яблок в каждой корзине?

x — в первой корзине
6х — во второй корзине

х + 6х = 98
7х = 98
х = 14

5. Имеет ли корни уравнение:
у3=у∙у
Имеет при у = 0 или 1.

Контрольная работа №6 за 5 класс (Виленкин)

Вариант 1

1. Вычислите:
а) (53+132):21
б) 180∙94-47700:45+4946

2. Задача. Длина прямоугольного участка земли 125 м, а ширина 96 м. Найдите площадь поля и выразите её в арах.

3. Задача. Найдите объем прямоугольного параллелепипеда, измерения которого равны 4 м, 3 м и 5 дм.

4. Используя формулу пути s=v∙t, найдите:
а) путь, пройденный автомашиной за 3 ч, если её скорость 80 км/ч,
б) время движения катера, прошедшего 90 км со скоростью 15 км/ч

5. Задача. Найдите площадь поверхности и объем куба, ребро которого равно 6 дм. Во сколько раз уменьшится площадь поверхности и во сколько раз – объем куба, если ребро уменьшить вдвое?

Вариант 2

1. Вычислите:
а) (63+122):15
б) 86∙170-5793+72800:35

2. Задача. Ширина прямоугольного поля 375 м, а длина 1600 м. Найдите площадь поля и выразите её в гектарах.

3. Задача. Найдите объем прямоугольного параллелепипеда, измерения которого равны 2 дм, 6 дм и 5 см.

4. Используя формулу пути s=v∙t, найдите:
а) путь, пройденный моторной лодкой за 2 часа, если её скорость 18 км/ч
б) скорость движения автомобиля, за 3 ч прошедшего 150 км.

5. Задача. Ребро куба равно 5 см. Найдите площадь поверхности и объем этого куба. Во сколько раз увеличится площадь поверхности и во сколько раз – объем куба, если его ребро увеличить вдвое?

В РАБОТЕ

Контрольная работа №7 за 5 класс (Виленкин)

Вариант 1

1. Примите за единичный отрезок длину 8 клеток тетради и отметьте на координатном луче точки А( 3/8 ), М( 1/2 ), К( 7/8 ), Т( 1/4 ), Р ( 11/8 )

2. Сравните числа:
а) 5/13 и 7/13, б) 11/15 и 8/15, в) 1 и 7/6, г) 8/9 и 5/4

3. Сложите 3/5 числа 30 и 2/7 числа 14.

4. Какую часть составляют:
а) 9 см2 от квадратного дециметра,
б) 17 дм3 от кубического метра,
в) 13 кг от 2 ц?

5. Задача. Ширина прямоугольника 48 см, что составляет 3/16 его периметра. Найдите длину этого прямоугольника.

Вариант 2

1. Примите за единичный отрезок длину 12 клеток тетради и отметьте на координатном луче точки В( 5/12 ), С( 1/2 ), Е( 1/3 ), О( 3/4 ), Н( 17/12 )

2. Сравните числа:
а) 6/11 и 3/11, б) 11/17 и 12/17, в) 1 и 3/8, г) 6/7 и 5/3

3. Сложите 2/9 числа 18 и 2/5 числа 40.

4. Какую часть составляют:
а) 7 дм2 от квадратного метра,
б) 19 см3 от кубического дециметра,
в) 9 ц от 4 т?

5. Задача. Длина прямоугольника составляет 5/16 его периметра. Найдите ширину этого прямоугольника, если его длина равна 80 см.

В РАБОТЕ

Контрольная работа №8 за 5 класс (Виленкин)

Вариант 1

1. Выполните действия:
а) 10/11 — 4/11 + 3/11    б) 4 5/9 + 3 8/9
в) 6 — 2 3/8                    г) 5 6/13 — 1 11/13

2. Задача. Турист шел с постоянной скоростью и за 3 часа прошел 14 км. С какой скоростью он шел?

3. Задача. В гараже 45 автомобилей. Из них 5/9 — легковые. Сколько легковых автомобилей в гараже.

4. Решите уравнение:
а) 5 6/7 — х = 3 2/7         б) у + 4 8/11 = 10 7/11

5. Какое число надо разделить на 8, чтобы частное равнялось 5 7/8?

Вариант 2

1. Выполните действия:
а) 12/13 — 5/13 + 4/13        б)  5 — 2 3/8 
в) 5 7/11 + 1 9/11              г) 6 5/11 — 4 9/11

2. Задача. Автомобиль, двигаясь с постоянной скоростью, прошел 14 км за 9 мин. Какова скорость автомобиля?

3. Задача. В классе 40 учеников. Из них 5/8 занимаются в спортивных секциях. Сколько учеников класса занимаются спортом?

4. Решите уравнение:
а) х + 2 5/13 = 4 11/13        б) 6 3/7 — у = 3 5/7

5. Какое число надо разделить на 6, чтобы частное равнялось 8 5/6?

В РАБОТЕ

Контрольная работа №9 за 5 класс (Виленкин)

Вариант 1

1. Сравните числа: 7,195 и 12,1; 8,276 и 8,3; 0,76 и 0,7598

2. Выполните действия:
а) 12,3 + 5,26   в) 79,1-6,08
б) 0,48 + 0,057  г) 5-1,63

3. Округлите:
а) 3,18; 30,625; 257,51; 0,28 до единиц
б) 0,531; 12,467; 8,5452 и 0,009 до сотых

4. Задача. Собственная скорость лодки 3,4 км/ч. Скорость лодки против течения реки 0,8 км/ч. Найдите скорость лодки по течению.

5. Запишите четыре значения m, при которых верно неравенство 0,71<m<0,74.

Вариант 2

1. Сравните числа: 8,2 и 6,984; 7,6 и 7,596; 0,6387 и 0,64

2. Выполните действия:
а) 15,4+3,18   в) 86,3 – 5,07
в) 0,068+0,39 г) 7 – 2,78

3. Округлите:
а) 8,72; 40,198; 164,53 и 0,61 до единиц
б) 0,834; 19,471; 6,352 и 0,08 до десятых.

4. Задача. Собственная скорость катера 32,8 км/ч. Скорость катера по течению реки 34,2 км/ч. Найдите скорость катера против течения.

5. Запишите четыре значения n, при которых верно неравенство 0,65<n<0,68.

В РАБОТЕ

Контрольная работа №10 за 5 класс (Виленкин)

Вариант 1

1. Вычислите:
а) 4,35∙18       г) 53,3:26
б) 6,25∙108     д) 6:24
в) 126,385∙10  е) 126,385:100

2. Решить уравнение:
7у+2,6=27,8

3. Найдите значение выражения
90-16,2:9+0,08

4. Задача. На автомобиль погрузили 6 контейнеров и 8 одинаковых ящиков по 0,28т каждый. Какова масса одного ящика, если масса всего груза 2,4т?

5. Задача. Как изменится произведение двух десятичных дробей, если в одном множителе перенести запятую вправо через две цифры, а в другом – влево через четыре цифры?

Вариант 2

1. Вычислите:
а) 3,85∙24;        г) 35,7:34
б) 4,75∙116;     д) 7:28
в) 234,166∙100 е) 234,166:10

2. Решить уравнение:
6х+3,8=20,6

3. Найдите значение выражения
40-23,2:8+0,07

4. Задача. Из 7,7 м ткани сшили 7 платьев для кукол и 9 одинаковых полотенец. Сколько ткани пошло на одно полотенце, если на каждое платье потребовалось 0,65 м ткани?

5. Задача. Как изменится произведение двух десятичных дробей, если в одном множителе перенести запятую влево через четыре цифры, а в другом — вправо через две цифры?

В РАБОТЕ

Контрольная работа №11 за 5 класс (Виленкин)

Вариант 1

1. Выполните действия:
а) 0,872∙6,3 г) 30,42:7,8
б) 1,6∙7,625 д) 0,702:0,065
в) 0,045∙0,1 е) 0,026:0,01

2. Найдите среднее арифметическое чисел 32,4; 41; 27,95; 46,9; 55,75.

3. Найдите значение выражения 296,2 – 2,7∙6,6 + 6:0,15.

4. Задача. Поезд 3 ч шел со скоростью 63,2 км/ч и 4 ч со скоростью 76,5 км/ч. Найдите среднюю скорость поезда на всем пути.

5. Задача. Сумма трех чисел 10,23, а среднее арифметическое шести других чисел 2,9. Найти среднее арифметическое всех этих девяти чисел.

Вариант 2

1. Выполните действия:
а) 0,964∙7,4 г) 25,23:8,7
б) 2,4∙7,375 д) 0,0918:0,0085
в) 0,72∙0,01 е) 0,39:0,1

2. Найдите среднее арифметическое чисел 63; 40,63; 70,4; 67,97

3. Найдите значение выражения 398,6 – 3,8∙7,7 + 3:0,06

4. Задача. Легковой автомобиль шел 2 ч со скоростью 55,4 км/ч и ещё 4 ч со скоростью 63,5 км/ч. Найдите среднюю скорость автомобиля на всем пути.

5. Задача. Среднее арифметическое пяти чисел 4,7, а сумма других трех чисел 25,14. Найдите среднее арифметическое всех этих восьми чисел.

В РАБОТЕ

Контрольная работа №12 за 5 класс (Виленкин)

Вариант 1

1. Задача. Площадь поля 260 га. Горохом засеяно 35% поля. Какую площадь занимают посевы гороха?

2. Найдите значение выражения 201 – (176,4:16,8+9,68)∙2,5.

3. Задача. В библиотеке 12% всех книг – словари. Сколько книг в библиотеке, если словарей в ней 900?

4. Решите уравнение 12+8,3х+1,5х = 95,3

5. Задача. От мотка провода отрезали сначала 30%, а затем ещё 60% остатка. После этого в мотке осталось 42 м провода. Сколько метров провода было в мотке первоначально?

Вариант 2

1. Задача. В железной руде содержится 45% железа. Сколько тонн железа содержится в 380 т руды?

2. Найдите значение выражения (299,3:14,6 – 9,62)∙3,5+72,2

3. Задача. За день вспахали 18% поля. Какова площадь всего поля, если вспахали 1170 га?

4. Решите уравнение 6,7у+13+3,1у=86,5

5. Задача. Израсходовали сначала 40% имевшихся денег, а затем ещё 30% оставшихся. После этого осталось 105р. Сколько было денег первоначально?

В РАБОТЕ

Контрольная работа №13 за 5 класс (Виленкин)

Вариант 1

1. Постройте углы, если:
а) <ВМЕ = 68° б) <СКР = 115°

2. Начертите треугольник AKN такой, чтобы <A = 120°. Измерьте и запишите градусные меры остальных углов треугольника.

3. Луч ОК делит прямой угол DOS на два угла так, что угол DOK составляет 0,7 угла DOS. Найдите градусную меру угла KOS.

4. Развернутый угол AMF разделен лучом МС на два угла АМС и CMF. Найдите градусные меры этих углов, если угол АМС вдвое больше угла CMF.

5. Из вершины развернутого угла DKP проведены его биссектриса КВ и луч КМ так, что <ВКМ =38°. Какой может быть градусная мера угла DKM?

Вариант 2

1. Постройте углы, если:
а) <ADF = 110° б) <HON = 73°

2. Начертите треугольник BCF такой, чтобы <В = 105°. Измерьте и запишите градусные меры остальных углов треугольника.

3. Луч АР делит прямой угол CAN на два угла так, что угол NAP составляет 0,3 угла CAN. Найдите градусную меру угла РАС.

4. Развернутый угол ВОЕ разделен лучом ОТ на два угла ВОТ и ТОЕ. Найдите градусные меры этих углов, если угол ВОТ втрое меньше угла ТОЕ.

5. Из вершины развернутого угла MNR проведены его биссектриса NB и луч NP так, что <BNP = 26°. Какой может быть градусная мера угла MNP?

В РАБОТЕ

Контрольная работа №14 за 5 класс (Виленкин)

Вариант 1

1. Вычислите: 2,66:3,8 – 0,81∙0,12 + 0,0372

2. В магазине 240 кг фруктов. За день продали 65% фруктов. Сколько килограммов фруктов осталось.

3. Найдите высоту прямоугольного параллелепипеда, объем которого равен 25,2 дм3, длина 3,5 дм и ширина 16 см.

4. Собственная скорость теплохода 24,5 км/ч, скорость течения реки 1,3 км/ч. Сначала теплоход 0,4 ч плыл по озеру, а затем 3,5 ч по реке против течения. Какой путь прошел теплоход за все это время?

5. Постройте углы МОК и КОС, если <МОК = 110°, <КОС = 46°. Какой может быть градусная мера угла СОМ?

Вариант 2

1. Вычислите: 7,8∙0,26 – 2,32:2,9 + 0,672.

2. В цистерне 850 л молока. 48% молока разлили в бидоны. Сколько литров молока осталось в цистерне?

3. Объем прямоугольного параллелепипеда равен 1,35 м3, высота 2,25 м и длина 8 дм. Найдите его ширину.

4. Катер плыл 3,5 ч по течению реки и 0,6 ч по озеру. Найдите путь, пройденный катером за все это время, если собственная скорость катера 16,5 км/ч, а скорость течения реки 2,1 км/ч.

5. Постройте углы AND и NDB, если <ADN = 34°, <NDB = 120°. Какой может быть градусная мера угла ADB?

Вариант 1

1. Вычислите: 2,66 : 3,8 – 0,81 ∙ 0,12 + 0,0372 = 0,6628
1) 2,66 : 3,8 = 0,7
2) 0,81 * 0,12 = 0,0972
3) 0,7 — 0,0972 = 0,6028
4) 0,6028 + 0,0372 = 0,6628

2. В магазине 240 кг фруктов. За день продали 65% фруктов. Сколько килограммов фруктов осталось.

1) 240 : 100 = 2,4 (кг) фруктов это 1 процент от всех фруктов.
2) 2,4 * 65 = 156 (кг) фруктов продали.
3) 240 — 156 = 84 (кг) осталось.
Ответ: 84 кг

3. Найдите высоту прямоугольного параллелепипеда, объем которого равен 25,2 дм3, длина 3,5 дм и ширина 16 см.

1) 3,5 * 1.6 = 5,6 (дм2) площадь одной стороны.
2) 25,2 : 5,6 = 4,5 (дм) высота прямоугольного параллелепипеда.
Ответ: 4,5 дм.

4. Собственная скорость теплохода 24,5 км/ч, скорость течения реки 1,3 км/ч. Сначала теплоход 0,4 ч плыл по озеру, а затем 3,5 ч по реке против течения. Какой путь прошел теплоход за все это время?

1) 24,5 * 0,4 = 9,8 (км) проплыл теплоход по озеру.
2) 24,5 — 1,3 = 23,2 (км/ч) скорость теплохода по реке, против течения реки.
3) 23,2 * 3,5 = 81,2 (км) проплыл теплоход по реке, против течения реки.
4) 81,2 + 9,8 = 91 (км) проплыл параход.
Ответ: 91 км.

5. Постройте углы МОК и КОС, если <МОК = 110°, <КОС = 46°. Какой может быть градусная мера угла СОМ?

Строим в тетради с помощью транспортира. COM может быть: 110° — 46° = 64° или 180° — 110° — 46° = 24°

Вариант 2

1. Вычислите: 7,8 ∙ 0,26 – 2,32 : 2,9 + 0,672 = 1,9
1) 7,8 ∙ 0,26 = 2.028
2) 2,32 : 2,9 = 0,8
3) 2,028 — 0,8 = 1.228
4) 1,228 + 0,672 = 1,9

2. В цистерне 850 л молока. 48% молока разлили в бидоны. Сколько литров молока осталось в цистерне?

1) 850 : 100 = 8,5 (л) 1 процент от 850 литров.
2) 8,5 * 48 = 408 (л) разлили в бидоны.
3) 850 — 408 = 442 (л)молока осталось в цистерне.
Ответ: 442 л

3. Объем прямоугольного параллелепипеда равен 1,35 м3, высота 2,25 м и длина 8 дм. Найдите его ширину.

1) 2.25 * 0.8 = 1,8 (м2) площадь одной из сторон прямоугольного параллелепипеда.
2) 1,35 : 1,8 = 0,75 (м) высота прямоугольного параллелепипеда.
Ответ: 0,75 м.

4. Катер плыл 3,5 ч по течению реки и 0,6 ч по озеру. Найдите путь, пройденный катером за все это время, если собственная скорость катера 16,5 км/ч, а скорость течения реки 2,1 км/ч.

1) 16.5 + 2,1 = 18.6 (км/ч) скорость по течению реки.
2) 18,6 * 3,5 = 65.1 (км) проплыл по течению реки.
3) 16.5 * 0,6 = 9,9 (км) проплыл по озеру.
4) 9,9 + 65,1 = 75 (км) проплыл катер.
Ответ: 75 км.

5. Постройте углы AND и NDB, если <ADN = 34°, <NDB = 120°. Какой может быть градусная мера угла ADB?

Строим в тетради с помощью транспортира. ADB может быть: 120° — 34° = 86° или 180° — 120° — 34° = 26°

Итоговая контрольная работа за 5 класс (Виленкин)

Вариант 1

1. Вычислите: 8,45 + (346 – 83,6):12,8

2. Вычислите площадь прямоугольника, если его ширина 1,9 дм, а длина вдвое больше.

3. Катер шел 3ч против течения реки и 2ч по течению. Какой путь прошел катер за эти 5 ч, если собственная скорость катера 18,6 км/ч, а скорость течения реки 1,3 км/ч?

4. Начертите треугольник АОВ, в котором угол АОВ равен 75°.

5. В классе 30 учеников. Оценку «5» на экзамене получили 30% учеников. Сколько учеников получили на экзамене пятерки?

Вариант 2

1. Вычислите 6,35 + (359 – 63,8):14,4.

2. Длина прямоугольника 12,6 см, а ширина втрое меньше. Найдите площадь этого прямоугольника.

3. Собственная скорость моторной лодки 6,7 км/ч. Скорость течения реки 1,2 км/ч. Лодка шла 2ч против течения и 2ч по течению реки. Какой путь прошла моторная лодка за эти 4 ч?

4. Начертите треугольник ВСК, в котором угол ВСК равен 110°.

5. Площадь поля 120 га. Тракторист вспахал 70% поля. Сколько гектаров земли вспахал тракторист?

 

Вариант 1

1. Вычислите: 8,45 + (346 – 83,6):12,8 = 20.45
1) 346 — 83.6 = 262.4
2) 262.4 : 12.8 = 20,5
3) 8.45 + 20.5 = 28.45

2. Вычислите площадь прямоугольника, если его ширина 1,9 дм, а длина вдвое больше.

1) 1,9 * 2 = 3,8 (дм) длина прямоугольника.
2) 1,9 * 3,8 = 4,142 (дм2) площадь.
Ответ: 4.142 дм2

3. Катер шел 3ч против течения реки и 2 ч по течению. Какой путь прошел катер за эти 5 ч, если собственная скорость катера 18,6 км/ч, а скорость течения реки 1,3 км/ч?

Решение:

каждый час туда и обратно можно представить как выражение:

а + b — (b — a) = 2a, где
а — скорость реки;
b — скорость катера.

В итоге у нас остается один час против течения реки, к которому надо прибавить два значения скорости реки.

1) 18.6 — 1.3 = 17.3 (км) прошел катер за 1 час против течения.
2) 17.3 + 1,3 * 2 = 19.9 (км) катер прошел за 5 часов.
Ответ: 19.9 км

4. Начертите треугольник АОВ, в котором угол АОВ равен 75°.

Самостоятельно. Первым чертим угол именно 75 градусов, а дальше продолжаем построение треугольника!

5. В классе 30 учеников. Оценку «5» на экзамене получили 30% учеников. Сколько учеников получили на экзамене пятерки?

1) 30 : 100 * 30 = 0,3 * 30 = 9 (уч.) получили 5.
Ответ: 9 учеников.

Вариант 2

1. Вычислите 6,35 + (359 – 63,8) : 14,4 = 26.85

1) 359 – 63,8 = 295.2
2) 295.2 : 14.4 = 20.5
3) 6.35 + 20.5 = 26.85

2. Длина прямоугольника 12,6 см, а ширина втрое меньше. Найдите площадь этого прямоугольника.

1) 12.6 : 3 = 4.2 (см) ширина прямоугольника.
2) 12.6 * 4,2 = 52.92 (см2) площадь прямоугольника.
Ответ: 52.92 см2

3. Собственная скорость моторной лодки 6,7 км/ч. Скорость течения реки 1,2 км/ч. Лодка шла 2ч против течения и 2ч по течению реки. Какой путь прошла моторная лодка за эти 4 ч?

Решение:

каждый час туда и обратно можно представить как выражение:

а + b — (b — a) = 2a, где
а — скорость реки;
b — скорость лодки.

В итоге у нас остается два значения скорости реки умноженное на количество часов.

2 * 1,2 * 2 = 4.8 (км) прошла лодка.
Ответ: 4,8 км.

4. Начертите треугольник ВСК, в котором угол ВСК равен 110°.

Самостоятельно. Первым чертим угол именно 110 градусов, а дальше продолжаем построение треугольника!

5. Площадь поля 120 га. Тракторист вспахал 70% поля. Сколько гектаров земли вспахал тракторист?

120 : 100 * 70 = 1.2 * 70 = 84 (га) вспахал тракторист.
Ответ: 84 га.

Лицей №7

В преддверие 76-летия Победы советского народа в Великой Отечественной войне, учащиеся Лицея №7 приняли участие в «Марафоне Победы», который включал в себя Конкурсы рисунков, плакатов, праздничных открыток «Победный май», Фестиваль военной песни, конкурсы стихов, Музейные уроки и др. Заключительным этапом Марафона Победы стали торжественные линейки, на которых учащиеся возложили цветы… Читать далее

Онлайн-школа «Фоксфорд» реализует «Бесплатный доступ к пробникам ЕГЭ-2021». С 1 марта по 30 апреля доступ к пробникам по 10 (десяти) предметам: математика, физика, русский язык, информатика, обществознание, английский язык, химия, биология, история, литература — будет бесплатным. Преподаватели «Фоксфорда» с большим стажем подготовки к ЕГЭ оценивают вторую часть и дают обратную… Читать далее

«Счастье – это когда утром с радостью идёшь на работу, а вечером с радостью возвращаешься домой». Значит, одной из составляющих счастья является правильный выбор работы, на которую будешь идти с радостью. Сейчас выпускники находятся в том возрасте, когда они должны сделать самый главный выбор в своей жизни – выбор профессии.… Читать далее

Министерство образования и науки Республики Хакасия (далее — Министерство) информирует, что в целях мониторинга ситуации по организации горячего питания в общеобразовательных учреждениях республики, разработана и согласована с Управлением Роспотребнадзора по Республике Хакасия форма чек- листа родительского контроля, которая предоставляет родителям (законным представителям) обучающихся возможность направить предложения по улучшению качества питания… Читать далее

Дорогие ученики! В марте – апреле 2021 года вы будете принимать участие в ВПР. ВПР – это итоговые контрольные работы по различным предметам, проводимые по единым заданиям и оцениваемые по единым критериям, разработанным для всей страны. Мы знаем, как вы старательно учились весь год. Главное не волнуйтесь, ведь день проведения… Читать далее

С 1 сентября 2021-го в республике Хакасия вводится система персонифицированного финансирования дополнительного образования детей в рамках реализации федерального проекта «Успех каждого ребенка» нацпроекта «Образование». Теперь, заниматься в кружках и спортивных секциях сможет каждый ребенок, независимо от финансового положения семьи. Для этого нужно: зайти на сайт Навигатора дополнительного образования https://xn--19-kmc.xn--80aafey1amqq.xn--d1acj3b/  Выбрать… Читать далее

Онлайн-встречи с родителями выпускников продолжила заместитель председателя предметной комиссии по математике Подготовка к государственной итоговой аттестации предстоящей в конце учебного года в Республике Хакасия идёт полным ходом. К единому государственному экзамену готовятся не только выпускники, но и их родители. С целью снизить эмоциональное напряжение, рассказать о структуре контрольно-измерительных материалов, ходе… Читать далее

Учителя Хакасии продолжают готовить выпускников к предстоящей государственной итоговой аттестации. Чтобы разъяснить родителям выпускников и самим старшеклассникам порядок предстоящих экзаменов, дать полезные советы, рассказать о структуре контрольно-измерительных материалов по тем или иным предметам, разъяснить порядок подготовки и подачи заявления на ЕГЭ, Министерство образования и науки Хакасии запустило цикл онлайн-встреч с… Читать далее

Напоминаем, отмена учебных занятий и массовых мероприятий с обучающимися осуществляется в соответствии со следующими температурными параметрами наружного воздуха: — при температуре «минус 30 градусов» и ниже – для учащихся 1-4 классов ОО — при температуре «минус 35 градусов» и ниже – для учащихся 1-9 классов ОО — при температуре «минус 40… Читать далее

Школа №124 |

ВНИМАНИЕ! 

26 мая в 18.00 в актовом зале Школы состоится родительское собрание для желающих  записать ребенка в «Школу дошкольника». 

 

 

НОВЫЕ Банковские реквизиты

МБОУ школы № 124 г.о. Самара, действующие с

01.01.2021 года

Банк получателя:

ОТДЕЛЕНИЕ САМАРА БАНКА РОССИИ (УФК

ПО САМАРСКОЙ ОБЛАСТИ Г. САМАРА)

БИК банка получателя средств (БИК ТОФК): 013601205

Номер счета банка получателя средств:

40 102 810 545 370 000 036

Номер счета получателя средств — казначейский счет:

03234643367010004200

л/с МБОУ Школы № 124 г.о. Самара: 206.08.041.0

 

 

 

 

 

Директор Железникова Татьяна Петровна

 

 

 

Сотрудничество с СамГТУ

Постановление губернатора Самарской области о выплате выпускникам 11 классов

 

 

Free Time online

«Осенняя профильная смена

«Умные каникулы УмКа»

Проект #ПРОкачайЗиму

 

Навигатор детства

Навигатор дополнительного образования

Дистанционное обучение  

 

 

 

 

 

Детский телефон доверия

Телефоны горячей линии

Анкетирование о независимой оценке качества образовательной деятельности общеобразовательными организациями

Грипп — это опасно

ПРАВИЛА ПРОФИЛАКТИКИ КОРОНАВИРУСНОЙ ИНФЕКЦИИ

Информация о реализации национальных проектов «Образование » и «Демография»

Сведения о качестве условий образовательной деятельности организаций, осуществляющих образовательную деятельность, расположенных на территории Самарской области, размещаются на официальном сайте http://bus.gov.ru

Инструкция о размещении гражданами отзывов по результатам ознакомления с представленной на сайте bus.gov.ru информацией

 

Родительское собрание профориентационного проекта «Билет в будущее»;

Федеральный институт педагогических измерений проводит

видеоконсультации для выпускников 11 классов, их родителей и педагогов посвященные изменениям в контрольных измерительных материалах единого государственного экзамена 2021 года.

Видеоконсультации пройдут в прямом эфире в официальном

сообществе Рособрнадзора в социальной сети «Вконтакте» и канале

Рособрнадзора на Youtube по следующим ссылкам:

https :// vk . com / rosobrnadzor ;

https:// www . youtube . com / user / RosObrNadzor /.

По окончании трансляции видеозаписи консультаций будут доступны

на вышеуказанных ресурсах и размещены на официальном сайте

График консультаций

 

Управление МВД России по г. Самаре объявляет набор в образовательные учреждения МВД России

в 2021-2022 годах

Казанский юридический институт МВД России

Подготовка специалистов с высшим образованием по специальностям:

40.05.02 «Правоохранительная деятельность»

40.05.01 «Правовое обеспечение национальной безопасности»

Нижегородская академия МВД России

40.05.02 «Правоохранительная деятельность»

40.05.01 «Правовое обеспечение национальной безопасности»

38.05.01 «Экономическая безопасность»

Волгоградская академия МВД России

40.05.03 «Судебная экспертиза»

40.05.01 «Правовое обеспечение национальной безопасности»

Уфимский юридический институт МВД России

40.05.02 «Правоохранительная деятельность»

Белгородский юридический университет МВД России им. И.Д. Путилина

40.05.02 «Правоохранительная деятельность»

40.05.01 «Правовое обеспечение национальной безопасности»

Орловский юридический институт МВД России имени В.В. Лукьянова

40.05.02 «Правоохранительная деятельность»

Порядок и условия поступления

          Юноши и девушки в возрасте до 25 лет, имеющие среднее (полное) общее образование, изъявившие желание поступать в институт, подают заявление установленной формы в Управление МВД России по г. Самаре              (г. Самара, ул. Мориса Тореза д.12, каб. 508).

          Все кандидаты сдают ЕГЭ по русскому языку, обществознанию и математике.

          Срок обучения на очном отделении 5 лет, предоставляется бесплатное проживание в благоустроенном общежитии, ежемесячно выплачивается заработная плата курсанта, предоставляется два оплачиваемых отпуска в год, по окончании учебного заведения присваивается специальное звание лейтенант полиции, период обучения учитывается в стаж службы, льготная пенсия.

 

По вопросу поступления обращаться по адресу: г. Самара, ул. М. Тореза, 12,

 

тел. 373-76-30, 373-77-56

Для испытуемых: Пенсильвания, 4–8 классы Концентрация по предметам: математика

Для просмотра материалов по другой теме используйте следующее поле со списком.

—Выберите тест Praxis по названию — — — — — — — — — — -Основные академические навыки преподавателей: математика (5732) Основные академические навыки преподавателей: математика (5733) Основные академические навыки преподавателей: чтение ( 5712) Основные академические навыки преподавателей: чтение (5713) Основные академические навыки преподавателей: письмо (5722) Основные академические навыки преподавателей: письмо (5723) — — — — — — — — — — — Сельское хозяйство (5701) Алгебра I ( 5162) Искусство: содержание и анализ (5135) Искусство: знание содержания (5134) Аудиология (5342) Аудиология (5343) Биология: знание содержания (5235) Знание шрифта Брайля (0633) Бизнес-образование: знание содержания (5101) Химия: знание содержания ( 5245) Китайский (мандаринский диалект): мировой язык (5665) Гражданское образование: знание содержания (5087) Коммуникация и грамотность: чтение (5714) Общение и грамотность: письмо (5724) Информатика (5652) Оценка детей младшего возраста (5026; субтесты 5027 и 5028) Оценка начального образования (5006; субтесты 5007 и 5008) Дошкольное образование (5025) Науки о Земле и космосе: предметные знания (5571) Экономика (5911) Образование детей младшего возраста (5024) Образовательное лидерство: администрация и надзор (5412) Начальное образование: пакет — математика, обществознание и естественные науки (5901) Начальное образование: предметные знания ( 5018) Начальное образование: содержание знаний для преподавания (7811) Начальное образование: учебная программа, обучение и оценка (5017) Начальное образование: несколько предметов (5001) Искусство английского языка: содержание и анализ (5039) Искусство английского языка: знание содержания (5038 ) Английский для носителей других языков (5362) Семейные и потребительские науки (5122) Французский: Мировой язык (5174) Фундаментальные предметы: Знание содержания (5511) Общие науки: Знание содержания (5435) География (5921) Геометрия (5163) Немецкий: Мировой язык (5183) Образование для одаренных детей (5358) Государство / Политология (5931) Здоровье и физическое воспитание: предметные знания (5857) Медицинское просвещение (5551) Междисциплинарное дошкольное образование (5023) Япония se: Мировой язык (5661) Журналистика (5224) Латинский (5601) Специалист по библиотечным СМИ (5311) Маркетинговое образование (5561) Математика (5165) Математика: знание содержания (5161) Средняя школа: знание содержания (5146) Искусство английского языка в средней школе (5047) Математика в средней школе (5164) Математика в средней школе (5169) Наука в средней школе (5440) Наука в средней школе (5442) Социальные науки в средней школе (5089) Музыка: содержание и обучение (5114) Музыка: знание содержания (5113) Музыка : Инструментальные и общие знания (5115) Музыка: вокал и общие знания (5116) PA 4-8 классы Основная оценка (5152) PA 4-8 классы Основная оценка: педагогика (5153) PA 4-8 классы Основная оценка: искусство английского языка и социальные науки (5154) PA 4-8 классы Математика и естественные науки (5155) PA 4-8 классы Концентрация предмета: английский язык (5156) PA 4-8 классы Концентрация предмета: математика (5158) PA 4-8 классы Концентрация предмета : Естественные науки (5159) PA 4-8 классы Концентрация на предметах: Общественные науки (5157) Физические науки Образование: содержание и дизайн (5095) Физическое воспитание: содержание знаний (5091) Физические науки (5485) Физика: содержание знаний (5265) Дошкольное образование (5531) Принципы обучения и преподавания: дошкольное образование (5621) Принципы обучения и Преподавание: классы K-6 (5622) Принципы обучения и преподавания: 5–9 классы (5623) Принципы обучения и преподавания: 7–12 классы (5624) Принципы обучения и преподавания: Консультант профессиональной школы PreK – 12 (5625) (5421) Психология (5391) Чтение для педагогов Вирджинии: начальное и специальное образование (5306) Чтение для педагогов Вирджинии: специалист по чтению (5304) Специалист по чтению (5301) Специалист по чтению (5302) Школьный психолог (5402) Социальные исследования: содержание и интерпретация (5086) Социальные исследования: контентные знания (5081) Социология (5952) Испанский: мировой язык (5195) Специальный редактор: основные знания и приложения (5354) Специальный редактор: базовые знания и умеренные и умеренные приложения (5543) Специальный редактор: основные знания и от серьезного до глубокого d Приложения (5545) Специальное издание: Дошкольное / раннее детство (5691) Специальное издание: Обучение глухих и слабослышащих учащихся (5272) Специальное издание: Обучение речи студентов с языковыми нарушениями (5881) Специальное издание: Обучение студентов с нарушением слуха Behav.Расстройства / Эмот. Нарушения (5372) Специальное издание: обучение студентов с нарушениями обучаемости (5383) Специальное издание: обучение студентов с нарушениями интеллекта (5322) Специальное издание: обучение студентов с нарушениями зрения (5282) Речевая коммуникация: знание содержания (5221) Речь- Языковая патология (5331) Обучение чтению (5204) Обучение чтению: элементарное (5205) Обучение чтению: начальное образование (5203) Обучение чтению: K – 12 (5206) Техническое образование (5051) Театр (5641) История мира и США: знание содержания (5941) Педагогика мировых языков (5841)

Пенсильвания, 4–8 классы Концентрация на предметах: математика (5158)

Видео о подготовке к экзамену

Наши ознакомительные видеоролики с тестами содержат важную информацию, которую вы должны знать, когда собираетесь к тесту.Чтобы узнать, чего ожидать в день вашего теста, как пройти через тест Praxis ® и многое другое, посетите видео библиотеку.

Стоимость подготовки к экзамену

  • Интерактивный практический тест

    Пенсильвания, 4–8 классы Концентрация предмета: математика, интерактивный практический тест
    Используйте этот интерактивный практический тест, чтобы подготовиться к Пенсильвании для 4–8 классов Концентрация предмета: математический тест (5158). Этот полноценный практический тест позволяет вам попрактиковаться в ответах на один набор аутентичных тестовых вопросов в среде, имитирующей компьютерный тест.Практический тест рассчитан так же, как и настоящий тест, и позволяет вам легко переходить от вопроса к вопросу, чтобы смоделировать то, что вы испытаете в день теста. После завершения теста вы также можете увидеть правильные ответы и объяснения для каждого правильного ответа и просмотреть свои результаты по категориям контента.

    Примечание. Для каждого названия теста доступна только одна версия, поэтому каждый раз, когда вы проходите практический тест, вы отвечаете на одни и те же вопросы в одном и том же порядке. Повторная или повторная покупка одного и того же практического теста более одного раза не приведет к появлению различных практических вопросов и не изменит порядок их доставки.

Государственные требования — Выберите — Показать AllAlabamaAlaskaAmerican SamoaArkansasCaliforniaColoradoConnecticutDelawareDistrict из ColumbiaGeorgiaGuamHawaiiIdahoIndianaIowaKansasKentuckyLouisianaMaineMarylandMinnesotaMississippiMissouriMontanaNebraskaNevadaNew HampshireNew JerseyNew MexicoNew YorkNorth CarolinaNorth DakotaNorthern Mariana IslandsOhioOklahomaOregonPennsylvaniaRhode IslandSouth CarolinaSouth DakotaTennesseeTexasUS Virgin IslandsUtahVermontVirginiaWashingtonWest VirginiaWisconsinWyomingACSLPAASHACSHBCDODEANASP

Дизайн теста по математике

— Новый меридиан

Суммативные экзамены по математике доступны в 3–8 классах и в старших классах.Учащиеся решают многоступенчатые математические задачи, которые требуют рассуждений и обращаются к реальным ситуациям. Это требует от учащихся математических рассуждений, понимания величин и их взаимосвязей для решения реальных задач и демонстрации своего понимания. Многие предыдущие оценки были сосредоточены в основном только на механической процедуре.

Существуют документы со спецификациями тестов, включая схемы оценок высокого уровня и таблицы доказательств, чтобы помочь преподавателям и широкой общественности лучше понять структуру итоговых оценок штата.Экзамены включают как полную, так и краткую формы New Meridian.

Дескрипторы уровня успеваемости описывают, что типичный учащийся на каждом уровне должен уметь продемонстрировать на основе его / ее владения стандартами на уровне своего класса.

Схема высокого уровня математики определяет общее количество задач и / или элементов для любой данной оценки / оценки курса, типы элементов и значения баллов для каждого.

Структура блока аттестации по математике определяет структуру экзаменов по математике, включая количество единиц, время и назначение калькулятора для каждой единицы.

Документ о структуре требований определяет основное утверждение оценок по математике, а также четыре дополнительных утверждения, в которых будут измеряться достижения учащихся.

Таблицы доказательств

и утверждения доказательств описывают знания и навыки, которые элемент оценивания или задача извлекает у учащихся. Они согласованы непосредственно с Общими основными государственными стандартами и подчеркивают их достижения, особенно в отношении согласованного характера стандартов.

Доказательства

включают информацию о «Разъяснениях, пределах и акцентах», связанных «Математических методах» и «Обозначениях калькулятора.”

Свидетельские показания документов

Дескрипторы успеваемости по математике — 3–11 классы

Результаты представлены в соответствии с пятью уровнями успеваемости, которые определяют знания, навыки и практические навыки, которые учащиеся могут продемонстрировать:

  • Уровень 1: Еще не оправдал ожиданий
  • Уровень 2: Частично оправдал ожидания
  • Уровень 3: Соответствие ожиданиям
  • Уровень 4: оправдал ожидания
  • Уровень 5: Превышение ожиданий

Дескрипторы уровня успеваемости (PLD) указывают, что типичный учащийся на каждом уровне должен уметь продемонстрировать на основе его / ее владения стандартами уровня своего класса.По математике уровни успеваемости на каждом уровне обучения записываются для каждого из четырех оценочных утверждений:

  • Основное содержание
  • Дополнительный и вспомогательный контент
  • Рассуждения
  • Моделирование

Уровни производительности в каждой области требований различаются по ряду факторов, согласующихся с включением в Common Core стандартов как для математического содержания, так и для математических практик, а также для Cognitive Complexity Framework for Mathematics.

Дескрипторы уровня успеваемости по шкале оценок

AMC 8 | Математическая ассоциация Америки

Что такое AMC 8?

AMC 8 — это 40-минутный экзамен с несколькими вариантами ответов по математике в средней школе, состоящий из 25 вопросов, предназначенный для развития навыков решения проблем. AMC 8 дает ученикам средней школы возможность развить позитивное отношение к аналитическому мышлению и математике, которые могут помочь в будущей карьере.Студенты применяют классные навыки для решения уникальных задач в спокойной и дружелюбной обстановке.

Материал, охватываемый AMC 8, включает темы из типовой учебной программы по математике в средней школе. Возможные темы включают, но не ограничиваются: подсчет и вероятность, оценка, пропорциональные рассуждения, элементарная геометрия, включая теорему Пифагора, пространственную визуализацию, повседневные приложения, а также чтение и интерпретацию графиков и таблиц. Кроме того, некоторые из последующих вопросов могут включать линейные или квадратичные функции и уравнения, координатную геометрию и другие темы, традиционно рассматриваемые в начальном курсе алгебры.

AMC 8 также доступен на французском, испанском, крупным шрифтом и шрифтом Брайля только для управления печатью.

Сроки регистрации и дата конкурса

  • Срок ранней регистрации: 31 октября 2021 г.
  • Крайний срок обычной регистрации: 5 декабря 2021 г.
  • Крайний срок поздней регистрации: 10 декабря 2021 г. *
  • Дата соревнования: 18 января 2022 г. с 8:00 по восточноевропейскому времени по 24 января 2022 г., в 23:59 по восточноевропейскому времени

* Этот вариант доступен только для школ, расположенных в континентальной части США.

Ресурсы для размещения AMC 8

Сначала загрузите и прочтите Пособие для учителя AMC 8 2021-2022, чтобы получить более подробную информацию о том, как проводить соревнования AMC 8.

2021-2022 AMC 8 Пособие для учителя (онлайн)

2021-2022 AMC 8 Пособие для учителя (печатное)

Менеджеры соревнований могут найти все необходимые дополнительные формы ниже или на amc-reg.maa.org.

Подготовка студентов к AMC 8

Эти ресурсы помогут вам подготовить учащихся к ответам на вопросы, которые можно найти на экзамене AMC 8.

После ознакомления с Руководством для учителя и указанными выше ресурсами, если у вас все еще есть вопросы, просмотрите наши Часто задаваемые вопросы ниже.

Часто задаваемые вопросы по AMC 8

  1. В. Что входит в AMC 8?

    A. Материал, охватываемый AMC 8, включает темы из типовой учебной программы по математике в средней школе. Возможные темы включают, но не ограничиваются: подсчет и вероятность, оценка, пропорциональные рассуждения, элементарная геометрия, включая теорему Пифагора, пространственную визуализацию, повседневные приложения, а также чтение и интерпретацию графиков и таблиц.Кроме того, некоторые из последующих вопросов могут включать линейные или квадратичные функции и уравнения, координатную геометрию и другие темы, традиционно рассматриваемые в начальном курсе алгебры.

  2. В. Кто имеет право участвовать в конкурсе ?

    A. Учащиеся, увлеченные решением проблем, которые находятся в классе 8 или ниже и младше 14,5 лет на день конкурса, имеют право участвовать в AMC 8.

  3. Q. Кто может контролировать соревнование?

    A. Разрешен только контроль со стороны менеджера соревнований. Учащиеся будут находиться под личным наблюдением их менеджера соревнований по усмотрению менеджера соревнований и протоколов безопасности школы / учреждения. Если есть какие-либо подозрения в мошенничестве или использовании неутвержденных ресурсов, мы свяжемся с Менеджерами по конкуренции. Ознакомьтесь с политикой дисквалификации и мошенничества здесь. С дополнительными вопросами о политике прокторинга AMC 8 обращайтесь в AMC AMC по адресу amcinfo @ maa.org

  4. Q. Когда мы получим официальные результаты и отчеты по AMC 8?

    A. Офис MAA AMC начнет рассылать по электронной почте официальные результаты и отчеты в начале — конце февраля после AMC 8 в январе. Отчеты по электронной почте отправляются примерно в том порядке, в котором мы обрабатываем формы ответов, отправленные из школ. Обработка и отчетность от начала до конца занимают от 3 до 4 недель.

  5. Q. Как мне сделать запрос на повторную оценку моих форм ответов?

    А. Используйте форму запроса AMC 8 Rescore. За каждую переоцененную форму ответа студента взимается плата в размере 35 долларов США. Официальными ответами будут те, которые затемнены в форме ответа. Все формы ответов учащихся, возвращенные для выставления оценок, будут переработаны через 80 дней после даты конкурса AMC 8.

  6. Q. Я уже зарегистрировался в AMC 8, но я хотел бы заказать больше наборов, чем было указано в моем первоначальном заказе, можно?

    A. Да, вы можете использовать форму заказа дополнительных комплектов, чтобы заказать больше.Заказы на дополнительные пакеты будут приниматься до 10 декабря 2021 г. для участвующих учреждений, расположенных на континентальной части США. Крайний срок для заказов дополнительных пакетов для учреждений, расположенных в Канаде, Аляске, Пуэрто-Рико, Гавайях, Гуаме и Северных Марианских островах, — 3 декабря 2021 г.

Поисковик тестов и оценок — от математики до профессионального развития

{{#IsMagProduct WebSiteDeltaID SubTypeID}} {{> MagProduct}} {{/ IsMagProduct}} {{#IsBookProduct WebSiteDeltaID}} {{#if IsAssessmentPlusProduct}} {{> AssessmentPlusProduct}} {{еще}} {{#if IsDigitalDownload}} {{> DigitalDownload}} {{еще}} {{> BookProduct}} {{/если}} {{/если}} {{/ IsBookProduct}} {{#IsMarkCreditProduct SubTypeID}} {{> BookProduct}} {{/ IsMarkCreditProduct}} {{#IsSingaporeBookProduct WebSiteDeltaID}} {{> SingaporeBookProduct}} {{/ IsSingaporeBookProduct}} {{#if IsDLProduct}} {{> DLProduct}} {{/если}} {{#if IsRisingStarsAchieveProduct}} {{> DLProduct}} {{/если}} {{#IsSNAPProduct SubTypeID}} {{> DLProduct}} {{/ IsSNAPProduct}} {{#IsAutoMathsProduct SubTypeID}} {{> DLProduct}} {{/ IsAutoMathsProduct}} {{#IsWellbeingProduct SubTypeID}} {{> DLProduct}} {{/ IsWellbeingProduct}} {{#if IsDigitalAssessmentBankProduct}} {{> DigitalAssessmentBankProduct}} {{/если}} {{#IsQuestionBankProduct SubTypeID}} {{> DigitalAssessmentBankProduct}} {{/ IsQuestionBankProduct}} {{#if IsGaloreParkProduct}} {{> GaloreParkProduct}} {{/если}} {{#IsRisingStarsProduct WebSiteDeltaID}} {{#if IsAssessmentPlusProduct}} {{> AssessmentPlusProduct}} {{еще}} {{#IsRisingStarsPhysicalProduct SubTypeID}} {{> BookProduct}} {{/ IsRisingStarsPhysicalProduct}} {{/если}} {{/ IsRisingStarsProduct}}

{{#if IsPackage}} Сводка пакета {{еще}} Резюме {{/если}}

{{{WebDescription}}}

{{> PackageContents}}

Бесплатная онлайн-практика и советы по тестированию STAAR

Время экзамена сопряжено с большим давлением, и оно может ухудшиться, если вы не будете хорошо подготовлены.Тем не менее, тест STAAR не обязательно должен вызывать стресс, если учащиеся прошли надлежащую онлайн-практику. При достаточной онлайн-практике студенты получают возможность задавать вопросы теста, что дает им лучшее понимание того, как решать вопросы во время основного оценивания.

Что такое тест STAAR?

STAAR — это аббревиатура от «Оценка академической готовности штата Техас». STAAR — это государственная программа тестирования, которая была запущена весной 2012 года для замены TAKS (Техасская оценка знаний и навыков), которая использовалась в течение нескольких лет.Основные предметы, протестированные в STAAR, включают письмо, чтение, математику, общественные науки и естественные науки. Учащиеся 3–12 классов в государственных школах Техаса сдают тесты STAAR, разработанные TEA (Техасское образовательное агентство) в сотрудничестве с преподавателями Техаса и THECB (Координационный совет по высшему образованию Техаса).

Ключевая информация о тестировании STAAR

Это стандартизированные тесты, которые проводятся как в государственных, так и в средних школах для оценки достижений учащихся.Цель теста STAAR — измерить, чему студенты научились и как они могут применить свои навыки и знания, как указано в TEKS (Texas Essential, стандарт учебной программы штата Техас. Каждый вопрос, проверяемый в STAAR, согласован со стандартами TEKS для каждого предмет и оценка.

Достигнув третьего класса, ребенок начинает сдавать различные тесты STAAR в зависимости от класса. В младших классах тесты и оценки STAAR в основном сосредоточены на письме, чтении и математике.В пятом классе экзамены в Техасе включают письмо, естественные науки и общественные науки. На уровне старшей школы учащиеся сдают экзамены EOC (в конце курса), которые охватывают пять предметов: английский I, английский II, биология, алгебра I и история США. Студенты должны сдать пять тестов, чтобы получить допуск к выпуску.

Задания STAAR подразделяются на бумажные тесты и компьютерные тесты, предлагаемые онлайн. Существует бумажный тест STAAR Grade 3–8 и онлайн-версия этого же экзамена.Техасский звездный тест помогает студентам привыкнуть к среде онлайн-тестирования и задействованным технологиям. STAAR A — это специализированный онлайн-тест, который позволяет учащимся с ограниченными возможностями сдавать свои тесты онлайн. STAAR Alternate 2 разработан для детей с когнитивными нарушениями, обучающихся по программам специального образования. STAAR L — это модифицированная версия для изучающих английский язык, чьи тестовые вопросы упрощены, чтобы кандидатам было легче читать.

Сроки, сроки и структура тестов STAAR

В отличие от TAKS, где оценивание занимало целый день и студентам разрешалось делать перерывы, тесты STAAR занимают около 4-5 часов, в зависимости от типа теста и предмета.Например, учащимся 3-5 классов требуется около двух часов на выполнение тестов, а учащимся 6-8 классов — около трех часов. В некоторых случаях тесты длятся от 4 до 5 часов. Итоговые курсы STAAR занимают 4 часа, за исключением английского I, английского II и английского III, которые длятся по 5 часов.

В 3 классе учащиеся проходят тестирование по чтению и математике, а четвероклассники сдают тесты по чтению, письму и математике. В пятом классе тестируются предметы по математике, естественным наукам и чтению.Особое внимание уделяется математике и тестам по чтению, поскольку они определяют, могут ли учащиеся перейти в следующий класс.

Поскольку существует множество типов тестов STAAR, даты экзаменов зависят от оценки и предмета. Например, большинство тестов STAAR в конце курса проводится в декабре и июне, а другие тесты — в период с апреля по май.

В 6-м классе проходят тесты по математике и чтению, а учащиеся 7-го класса сдают тесты по чтению, письму и математике.Тесты 8-го класса включают больше предметов: математику, чтение, естественные науки и общественные науки. После прохождения теста STAAR 8-го класса ученик может перейти в 9-й класс. Старшеклассники изучают английский I, английский II, биологию и историю США. Тесты STAAR для старших классов проводятся весной, но неуспешные ученики получают еще один шанс пересдать тесты летом.

Как Edulastic готовит студентов к тестам STAAR

Edulastic предоставляет студентам идеальную платформу, которая позволяет им подготовиться к тестам STAAR.В удобное для них время студенты могут прийти на платформу и пройти практические тесты, чтобы подготовиться к экзаменам. В Интернете есть множество ресурсов, которые помогут студентам практиковаться и взаимодействовать с вопросами и форматами, которые появятся на реальном экзамене.

Некоторые из ключевых навыков, которые студенты могут усвоить на стартовом тесте, включают совершенствование навыков клавиатуры. Это очень важно, потому что онлайн-тесты требуют глубоких знаний клавиатурных команд для выполнения различных задач, таких как перетаскивание и заполнение информации в таблицах.Понимание команд клавиатуры и практика помогут развить эти навыки.

Онлайн-тесты состоят из вопросов с усовершенствованными технологиями, которые требуют специальных навыков навигации. Например, учащимся необходимо попрактиковаться в онлайн-вычислениях и создании уравнений и числовых ответов с помощью поля ввода на клавиатуре.

Компьютерный тест STAAR проводится с помощью различных технических устройств, таких как компьютеры, iPad и планшеты.При подготовке к основному экзамену студенты должны иметь как можно больше времени для выполнения практических тестов с использованием того же устройства, которое будет использоваться на экзамене. Это позволит им привыкнуть к гаджетам и понять основные навыки устранения неполадок.

Ресурсы Edulastic и оценки для теста STAAR определенно повышают уровень уверенности учащихся, готовящихся к выполнению различных тестов STAAR в разных классах.

Инструкции по подготовке к тесту STAAR

Есть несколько тем, которые необходимо осветить в течение года.Однако общие для английского языка включают базовое чтение и письмо. Для математики предметные области включают алгебраические отношения, коэффициенты пересчета, формулы, анализ данных. Темами социальных исследований являются география Северной Америки, правительство и гражданство США, гражданская война и основные экономические принципы.

Для старшеклассников математические темы включают экспоненциальные функции, линейные и квадратичные функции. Предметные области биологии включают генетические принципы, отношения между живыми организмами и окружающей средой и теорию эволюции.

No related posts.

Leave a Reply

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *