Контрольная работа 10 класс векторы: Контрольная работа «Координаты и векторы в пространстве» 10 класс скачать

Содержание

Контрольная работа по математике (геометрия) 10 класс по теме «Векторы» | План-конспект урока по математике (10 класс) на тему:

                         

                                Контрольная работа по геометрии 10 класс  «Векторы»

                                                             Вариант №1

1.  Даны точки А(2;0;-1), В(3;1;-2), С(4;-7;2), Д(1;4;-5). Найти:   а) координаты векторов АВ и СД.

 Б) 2 –             в) косинус угла между векторами АВ и СД.

2. При каком значении п векторы  и  будут перпендикулярны, если А(1;0;1), В(-2;3;0), С(4;6;п), Д(п;6;-8).

3. Даны точки с координатами  Р(4;-1;2), К(3;0;-1), М(1;-6;8). Найдите координаты точки С, чтобы вектора РК и МС были равны.

                                Контрольная работа по геометрии 10 класс  «Векторы»

                                                             Вариант №2

1.  Даны точки А(3;0;-2), В(4;2;-2), С(5;-6;3), Д(2;5;-4). Найти:   а) координаты векторов АВ и СД.

 Б) 5 –             в) косинус угла между векторами АВ и СД.

2. При каком значении п векторы  и  будут перпендикулярны, если А(2;0;2), В(-3;4;0), С(5;7;п), Д(п;4;-3).

3. Даны точки с координатами  Р(5;-2;3), К(4;1;-2), М(2;-5;7). Найдите координаты точки С, чтобы вектора РК и МС были равны.

 

                                Контрольная работа по геометрии 10 класс  «Векторы»

                                                             Вариант №1

1.  Даны точки А(2;0;-1), В(3;1;-2), С(4;-7;2), Д(1;4;-5). Найти:   а) координаты векторов АВ и СД.

 Б) 2 –             в) косинус угла между векторами АВ и СД.

2. При каком значении п векторы  и  будут перпендикулярны, если А(1;0;1), В(-2;3;0), С(4;6;п), Д(п;6;-8).

3. Даны точки с координатами  Р(4;-1;2), К(3;0;-1), М(1;-6;8). Найдите координаты точки С, чтобы вектора РК и МС были равны.

                                Контрольная работа по геометрии 10 класс  «Векторы»

                                                             Вариант №2

1.  Даны точки А(3;0;-2), В(4;2;-2), С(5;-6;3), Д(2;5;-4). Найти:   а) координаты векторов АВ и СД.

 Б) 5 –             в) косинус угла между векторами АВ и СД.

2. При каком значении п векторы  и  будут перпендикулярны, если А(2;0;2), В(-3;4;0), С(5;7;п), Д(п;4;-3).

3. Даны точки с координатами  Р(5;-2;3), К(4;1;-2), М(2;-5;7). Найдите координаты точки С, чтобы вектора РК и МС были равны.

                                Контрольная работа по геометрии 10 класс  «Векторы»

                                                             Вариант №1

1.  Даны точки А(2;0;-1), В(3;1;-2), С(4;-7;2), Д(1;4;-5). Найти:   а) координаты векторов АВ и СД.

 Б) 2 –             в) косинус угла между векторами АВ и СД.

2. При каком значении п векторы  и  будут перпендикулярны, если А(1;0;1), В(-2;3;0), С(4;6;п), Д(п;6;-8).

3. Даны точки с координатами  Р(4;-1;2), К(3;0;-1), М(1;-6;8). Найдите координаты точки С, чтобы вектора РК и МС были равны.

                                Контрольная работа по геометрии 10 класс  «Векторы»

                                                             Вариант №2

1.  Даны точки А(3;0;-2), В(4;2;-2), С(5;-6;3), Д(2;5;-4). Найти:   а) координаты векторов АВ и СД.

 Б) 5 –             в) косинус угла между векторами АВ и СД.

2. При каком значении п векторы  и  будут перпендикулярны, если А(2;0;2), В(-3;4;0), С(5;7;п), Д(п;4;-3).

3. Даны точки с координатами  Р(5;-2;3), К(4;1;-2), М(2;-5;7). Найдите координаты точки С, чтобы вектора РК и МС были равны.

Тесты по геометрии «Векторы» (10 класс) | Тест по геометрии (10 класс) на тему:

Вариант 1

  1. Какое утверждение неверное?  1) Любые два противоположно направленных вектора коллинеарны.  2) Любые два коллинеарных вектора сонаправлены.  3) Любые два равных вектора коллинеарны.
  2. DABC – тетраэдр. . Тогда = …  1) ;  2) ;       3) .
  3. ABCDA1B1C1D1 – параллелепипед. Компланарными являются векторы … 1);  2) ;  3) .
  4. ABCDA1B1C1D1 – параллелепипед. Найдите .
  5. ABCDA1B1C1D1 – параллелепипед. , . . Найдите коэффициенты разложения

Вариант 2

  1. Какое утверждение верное?  1) Любые два сонаправленных вектора коллинеарны.  2) Любые два коллинеарных вектора противоположно направлены.  3) Любые два коллинеарных вектора равны.
  2. DABC – тетраэдр. . Тогда = …  1) ;  2) ;       3) .
  3. ABCDA1B1C1D1 – параллелепипед. Не являются компланарными векторы … 1);  2) ;  3) .
  4. ABCDA1B1C1D1 – параллелепипед. Найдите .
  5. ABCDA1B1C1D1 – параллелепипед. , . . Найдите коэффициенты разложения

Вариант 1

  1. Какое утверждение неверное?  1) Любые два противоположно направленных вектора коллинеарны.  2) Любые два коллинеарных вектора сонаправлены.  3) Любые два равных вектора коллинеарны.
  2. DABC – тетраэдр. . Тогда = …  1) ;  2) ;       3) .
  3. ABCDA1B1C1D1 – параллелепипед. Компланарными являются векторы … 1);  2) ;  3) .
  4. ABCDA1B1C1D1 – параллелепипед. Найдите .
  5. ABCDA1B1C1D1 – параллелепипед. , . . Найдите коэффициенты разложения

Вариант 2

  1. Какое утверждение верное?  1) Любые два сонаправленных вектора коллинеарны.  2) Любые два коллинеарных вектора противоположно направлены.  3) Любые два коллинеарных вектора равны.
  2. DABC – тетраэдр. . Тогда = …  1) ;  2) ;       3) .
  3. ABCDA1B1C1D1 – параллелепипед. Не являются компланарными векторы … 1);  2) ;  3) .
  4. ABCDA1B1C1D1 – параллелепипед. Найдите .
  5. ABCDA1B1C1D1 – параллелепипед. , . . Найдите коэффициенты разложения

Вариант 1

  1. Какое утверждение неверное?  1) Любые два противоположно направленных вектора коллинеарны.  2) Любые два коллинеарных вектора сонаправлены.  3) Любые два равных вектора коллинеарны.
  2. DABC – тетраэдр. . Тогда = …  1) ;  2) ;       3) .
  3. ABCDA1B1C1D1 – параллелепипед. Компланарными являются векторы … 1);  2) ;  3) .
  4. ABCDA1B1C1D1 – параллелепипед. Найдите .
  5. ABCDA1B1C1D1 – параллелепипед. , . . Найдите коэффициенты разложения

Вариант 2

  1. Какое утверждение верное?  1) Любые два сонаправленных вектора коллинеарны.  2) Любые два коллинеарных вектора противоположно направлены.  3) Любые два коллинеарных вектора равны.
  2. DABC – тетраэдр. . Тогда = …  1) ;  2) ;       3) .
  3. ABCDA1B1C1D1 – параллелепипед. Не являются компланарными векторы … 1);  2) ;  3) .
  4. ABCDA1B1C1D1 – параллелепипед. Найдите .
  5. ABCDA1B1C1D1 – параллелепипед. , . . Найдите коэффициенты разложения

Контрольная работа № 1 по теме «Координаты и векторы в пространстве» (11 класс, Мерзляк А.Г. и др.)

Контрольная работа № 1 по теме «Координаты и векторы в пространстве»

Вариант 1

1. Точка A — середина отрезка MK. Найдите координаты точки A и длину отрезка MK, если M (5; −2; 1), K (3; 4; −3).

2. Точки A и B симметричны относительно точки C. Найдите координаты точки B, если A (−3; 5; −7), C (6; 2; −1).

3. Даны векторы (3; −2; −1) и (1; 2; 4). Найдите:

1) координаты вектора ;

2) косинус угла между векторами и .

4. Даны векторы (2; −6; 8) и (−1; k; −4). При каком значении k векторы и :

1) коллинеарны;

2) перпендикулярны?

5. Составьте уравнение плоскости, проходящей через точку A и перпендикулярной прямой AB, если A (1; 2; −3), B (4; 8; −6).

6. Дан куб ABCDA1B1C1D1, ребро которого равно 1 см. На диагонали C1D его грани отметили точку M так, что DM : MC1 = 5 : 3.

1) Выразите вектор через векторы , и .

2) Найдите модуль вектора .

Вариант 2

1. Точка M — середина отрезка AB. Найдите координаты точки M и длину отрезка AB, если A (6; −5; 2), B (−4; 3; 10).

2. Точки M и K симметричны относительно точки D. Найдите координаты точки K, если M (4; −6; 3), D (−2; 1; 5).

3. Даны векторы (2; −1; 3) и (−1; 2; 5). Найдите:

1) координаты вектора ;

2) косинус угла между векторами и .

4. Даны векторы (5; −4; 6) и (15; −12; p). При каком значении p векторы и :

1) коллинеарны;

2) перпендикулярны?

5. Составьте уравнение плоскости, проходящей через точку B и перпендикулярной прямой BC, если B (3; −2; 4), C (−2; 8; 19).

6. Дан куб ABCDA1B1C1D1, ребро которого равно 1 см. На диагонали AD1 его грани отметили точку E так, что AE : ED

1 = 2 : 7.

1) Выразите вектор через векторы , и .

2) Найдите модуль вектора .

Вариант 3

1. Точка K — середина отрезка CD. Найдите координаты точки K и длину отрезка CD, если C (−3; 4; −1), D (1; −2; 3).

2. Точки E и F симметричны относительно точки P. Найдите координаты точки F, если E (0; −8; 4), P (−4; 2; 2).

3. Даны векторы (2; 0; −3) и (1; −2; −1). Найдите:

1) координаты вектора ;

2) косинус угла между векторами и .

4. Даны векторы (−20; 10; −15) и (a; −2; 3). При каком значении a векторы и :

1) коллинеарны;

2) перпендикулярны?

5. Составьте уравнение плоскости, проходящей через точку C и перпендикулярной прямой CD, если C (4; 1; −1), D (7; −2; 5).

6. Дан куб ABCDA1B1C1D1, ребро которого равно 1 см. На диагонали A1B его грани отметили точку K так, что A1K : KB = 4 : 3.

1) Выразите вектор через векторы , и .

2) Найдите модуль вектора .

Вариант 4

1. Точка D — середина отрезка FK. Найдите координаты точки D и длину отрезка FK, если F (6; −3; 2), K (4; 1; 4).

2. Точки B и C симметричны относительно точки M. Найдите координаты точки B, если C (9; −5; 6), M (3; 0; −2).

3. Даны векторы (4; −1; 2) и (−2; 1; 0). Найдите:

1) координаты вектора ;

2) косинус угла между векторами и .

4. Даны векторы (1; −2; 3) и (7; m; 21). При каком значении m векторы и :

1) коллинеарны;

2) перпендикулярны?

5. Составьте уравнение плоскости, проходящей через точку D и перпендикулярной прямой DM, если D (−3; 20; −4), M (9; 24; 16).

6. Дан куб ABCDA1B1C1D1, ребро которого равно 1 см. На диагонали AC его грани отметили точку F так, что AF : FC = 3 : 7.

1) Выразите вектор через векторы , и .

2) Найдите модуль вектора .

Контрольная работа по теме Векторы в пространстве

I вариант

Даны точки А(1;6;-4), В(0;-1;2), С(-1;-2;7) и D(0;5;1). Указать среди векторов равные векторы.

При каких значениях m и n векторы коллинеарны:

При каком значении n данные векторы перпендикулярны:

Даны векторы: (-4;-2;1),(3;0;5),(4;-3;6). Найдите координаты вектора 1) 2 ; 2) — + 3 ; 3) + —

Даны точки А(2;3;-1), В(1;-1;2), С(2;3;0), D(4;-2;1). Найдите косинус угла между векторами и .

Найдите координаты вектора, если ; ; .

II вариант

Даны точки А(4;9;-1), В(3;2;5), С(-4;-5;4) и D(-3;2;-2). Указать среди векторов равные векторы.

При каких значениях m и n векторы коллинеарны:

При каком значении n данные векторы перпендикулярны:

Даны векторы: (-4;-2;4),(3;9;5),(4;-3;6).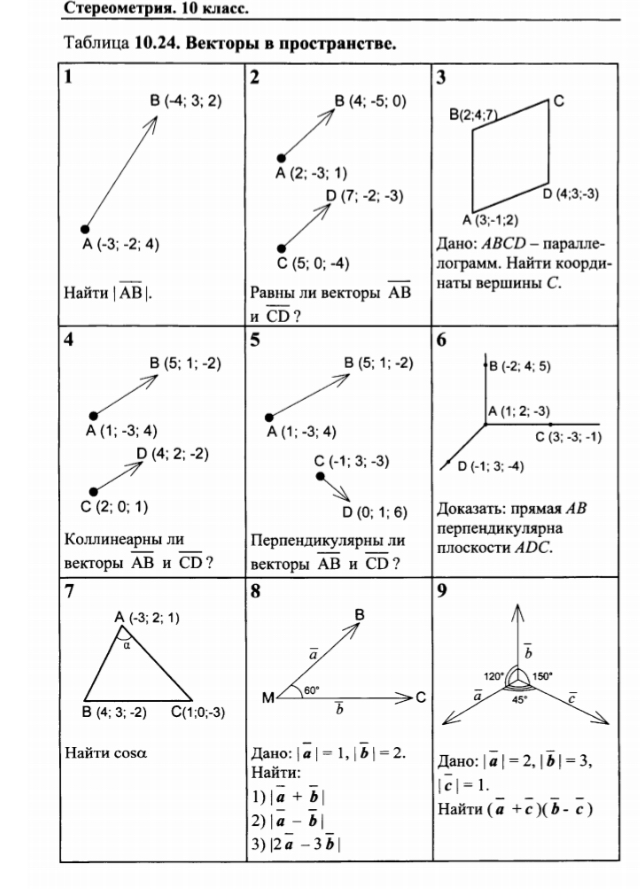 Найдите координаты вектора 1) 2 ; 2) — + 3 ; 3) 2 + —

Даны точки А(5;4;-2), В(2;-2;3), С(4;2;0), D(3;-2;2). Найдите косинус угла между векторами и .

Найдите координаты вектора, если ; ; .

III вариант

Даны точки А(-2;3;-7), В(-3;-4;1), С(-1;-2;7) и D(0;5;1). Указать среди векторов равные векторы.

При каких значениях m и n векторы коллинеарны:

При каком значении n данные векторы перпендикулярны:

Даны векторы: (-3;-1;2),(4;-3;0),(5;-2;6). Найдите координаты вектора 1) 2 ; 2) — + 3 ; 3) 2 + —

Даны точки А(4;7;-2), В(2;-3;0), С(2;1;0), D(4;-5;1). Найдите косинус угла между векторами и .

Найдите координаты вектора, если ; ; .

IV вариант

Даны точки А(7;12;2), В(6;5;8), С(-5;-6;3) и D(-4;1;-3). Указать среди векторов равные векторы.

При каких значениях m и n векторы коллинеарны:

При каком значении n данные векторы перпендикулярны:

Даны векторы: (-4;-3;5),(6;0;-3),(4;-1;2). Найдите координаты вектора 1) 2 ; 2) — + 3 ; 3) + —

Даны точки А(4;-5;-1), В(-3;-2;0), С(4;-7;-2), D(3;2;8). Найдите косинус угла между векторами и .

Найдите координаты вектора, если ; ; .

Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/301691-kontrolnaja-rabota-po-teme-vektory-v-prostran

Векторы в пространстве. Действия с векторами. Геометрия, 10 класс: уроки, тесты, задания.

Вход
Вход Регистрация Начало Новости ТОПы Учебные заведения Предметы Проверочные работы Обновления Переменка Поиск по сайту Отправить отзыв
    org/BreadcrumbList»>
  • Предметы
  • Геометрия
  • 10 класс

  1. Определение и физический смысл вектора в пространстве

  2. Как складывать векторы и умножать вектор на число

  3. Разложение вектора.

    Понятие компланарности
Отправить отзыв Нашёл ошибку? Сообщи нам! Copyright © 2021 ООО ЯКласс Контакты Пользовательское соглашение

ГДЗ самостоятельные и контрольные работы по геометрии за 10 класс Ершова, Голобородько

Десятиклассники переживают непростой период, так как им остается всего два года до сдачи экзаменов. Лишь на первый взгляд кажется, что это много, ведь время всегда летит незаметно, а к выпускному надо сделать еще много всего (покупка одежды, задумка номера). К тому же, например, в математику входит много правил из различных отраслей этой науки и очень сложно их выучить все. Однако это нужно для того, чтобы подготовиться качественно и получить в результате высокий балл. Потом предстоит поступать в университет, там эти же предметы изучаются на гораздо более высоком уровне сложности. Поэтому учить все надо сейчас, чтобы потом не возникало проблем.

А геометрия вообще доставляет школьникам больше всего сложностей, так как для успешного ее изучения нужно заучивать огромное количество формул, алгоритмов, постулатов и аксиом. Зато она благотворно влияет на интеллект человека: развивает вычислительные навыки, способности доказывать и делать выводы. Как сделать обучения более эффективным и быстрым? Этому поспособствует эвристический метод. Он состоит в том, что ребенок сам усваивает материал, с помощью средства-помощника, таким будет онлайн-решебник. Вашему вниманию предлагается отличный сборник, который долгое время со старанием разрабатывали и составляли опытные и профессиональные методисты, и выпустило издательство «Илекса» в 2014 году.

По каким причинам пользователи выбирают учебно-методическицй комплекс по геометрии за 10 класс для самостоятельных и контрольных работ (авторы: Ершова А.П., Голобородько В.В.)

Этот справочник поможет не только учащимся. Отстающий сможет сам проходить разделы и усваивать темы, а отличник будет делать заранее перед уроками для того, чтобы в школе быть более уверенным. Родители смогут контролировать учебный процесс ребенка, а учителя- составлять классные задания. К тому же, все подано в интересной форме специально для детей. Другие преимущества:

  • Можно научиться независимой работе, синтезу и анализу. Хотя, в этом возрасте, получение данного навыка достаточно тяжело дается детям. Поэтому если использовать решебник регулярно, обучающийся сможет научиться навыкам самоконтроля гораздо быстрее;
  • самостоятельно рассматривать новый материал;
  • закреплять пройденные на уроке темы;
  • учтены европейские стандарты преподавания;
  • исключительно правильные ответы;
  • больше не потребуется ждать, когда мамы и папы вернутся с работы или учитель наконец-то освободится для того, чтобы объяснить вам принцип решения очередного примера.

Содержание решебника с ГДЗ по геометрии для 10 класса от Ершовой

Книга включает все главы, рекомендованные к изучению:

  • планиметрия;
  • стереометрия;
  • многогранники.

Контрольная работа координаты и векторы

Контрольная работа №3.

Тема: «Координаты и векторы»

Вариант 1.

  1. Если то .

  2. Каждая координата суммы двух векторов равна ___________________

  3. Как вычисляется скалярное произведение двух векторов, если дан угол?

  4. По какой формуле вычисляется уравнение сферы?

  5. Если .

  6. Векторы называются компланарными, если ______________________

  7. Если .

  8. Если Запиши подробно решение.

  9. Коллинеарны ли векторы ? Ответ объясни.

  10. Для векторов и , вычислить:

  1. Модуль вектора и ;

  2. Скалярное произведение векторов;

  3. Угол между векторами.

Контрольная работа №3.

Тема: «Координаты и векторы»

Вариант 2.

  1. Если то .

  2. Каждая координата разности двух векторов равна ___________________

  3. Как вычисляется угол между двумя векторами?

  4. По какой формуле вычисляется уравнение сферы, с центром в начале координат?

  5. Если .

  6. Векторы называются коллинеарными, если _________________________

  7. Если .

  8. Если Запиши подробно решение.

  9. Коллинеарны ли векторы ? Ответ объясни.

  10. Для векторов и , вычислить:

  1. Модуль вектора и ;

  2. Скалярное произведение векторов;

  3. Угол между векторами.

Введение в векторы и скаляры | Векторы и скаляры

20.1 Введение в векторы и скаляры (ESAGH)

Мы ежедневно соприкасаемся со многими физическими величинами в мире природы. Например, такие вещи, как время, масса, вес, сила и электрический заряд, являются физическими величинами, с которыми мы все знакомы. Мы знаем, что время идет и физические объекты обладают массой. Вещи имеют вес из-за силы тяжести. Мы прикладываем силу, когда открываем двери, идем по улице и пинаем мячи.Мы испытываем электрический заряд напрямую от статического электричества зимой и от всего, что работает на электричестве.

В природе существует множество физических величин, и мы можем разделить их на две большие группы, называемые векторами и скалярами .

Скаляры и векторы (ESAGI)

Скаляры — это физические величины, которые имеют только числовое значение или размер (величину). Скаляр говорит вам , сколько там чего-то.

Скалярная

Скаляр — это физическая величина, имеющая только величину (размер).

Например, человек покупает кадку с маргарином, на которой указана масса \ (\ text {500} \) \ (\ text {g} \). Масса кадки маргарина — величина скалярная. Для его описания требуется только одно число, в данном случае \ (\ text {500} \) \ (\ text {g} \).

Векторы отличаются, потому что это физические величины, имеющие размер и направление a. Вектор говорит вам , сколько чего-то есть и , в каком направлении он находится.{-1} $} \) (это величина), и мы знаем, куда он идет — на восток (это направление). Эти две величины, скорость и направление автомобиля (величина и направление) вместе образуют вектор, который мы называем скоростью.

Примеры скалярных величин:

  • масса имеет только значение, без направления

  • электрический заряд имеет только значение, без направления

Примеры векторных величин:

  • сила имеет значение и направление.Вы толкаете или тянете что-то с некоторой силой (величиной) в определенном направлении

  • вес имеет значение и направление. Ваш вес пропорционален вашей массе (величине) и всегда направлен к центру Земли.

Практика Сиявула дает вам доступ к неограниченному количеству вопросов с ответами, которые помогут вам в обучении. Тренируйтесь где угодно, когда угодно и на любом устройстве!

Зарегистрируйтесь, чтобы попрактиковаться

Векторы и скаляры

Упражнение 20.1

Классифицируйте следующие элементы как векторы или скаляры

  1. длина

  2. сила

  3. направление

  4. высота

  5. время

  6. скорость

  7. температура

  1. скаляр

  2. вектор

  3. скаляр

  4. скаляр

  5. скаляр

  6. скаляр

  7. скаляр

Векторное представление (ESAGJ)

Векторы отличаются от скаляров и должны иметь свои собственные обозначения.Есть много способов записать символ вектора. В этой книге векторы будут обозначаться символами со стрелкой, указывающей вправо над ней. Например, \ (\ vec {F} \), \ (\ vec {W} \) и \ (\ vec {v} \) представляют векторов силы, веса и скорости, что означает, что оба они имеют величину и направление.

Иногда нужна просто величина вектора. В этом случае стрелка опускается. Для случая вектора силы:

Скаляров и векторов

Физика — математическая наука.Основные концепции и принципы имеют математическую основу. В ходе изучения физики мы будем сталкиваться с множеством концепций, связанных с математической базой. Хотя мы часто делаем упор на концептуальную природу физики, мы будем уделять значительное и постоянное внимание ее математическому аспекту.

Движение предметов можно описать словами. Даже у человека без образования в области физики есть набор слов, которые можно использовать для описания движущихся объектов.Слова и фразы, такие как , идет быстро, , , остановился, , , замедляется, , , ускоряется, и , поворачивает, обеспечивают достаточный словарный запас для описания движения объектов. В физике мы используем эти и многие другие слова. Мы будем расширять этот словарный список такими словами, как расстояние , смещение , скорость , скорость и ускорение . Как мы вскоре увидим, эти слова связаны с математическими величинами, имеющими строгие определения.Математические величины, которые используются для описания движения объектов, можно разделить на две категории. Величина может быть векторной или скалярной. Эти две категории можно отличить друг от друга по их различным определениям:

  • Скаляры — это величины, которые полностью описываются только величиной (или числовым значением).
  • Векторы — это величины, которые полностью описываются величиной и направлением.

Остальная часть этого урока будет посвящена нескольким примерам векторных и скалярных величин (расстояние, смещение, скорость, скорость и ускорение).По мере прохождения урока обращайте особое внимание на векторную и скалярную природу каждой величины. По мере того, как мы переходим к другим разделам Учебного пособия по физике и знакомимся с новыми математическими величинами, обсуждение часто начинается с определения новой величины как вектора или скаляра.

Проверьте свое понимание

1. Чтобы проверить ваше понимание этого различия, примите во внимание следующие величины, перечисленные ниже.Классифицируйте каждую величину как вектор или скаляр. Нажмите кнопку, чтобы увидеть ответ.

Кол-во Категория
а. 5 м
б. 30 м / сек, Восток
г. 5 миль, север
г. 20 градусов Цельсия
e.256 байт
ф. 4000 калорий

Gr10_Term3_ResourcePack.indb

% PDF-1.3 % 1 0 объект >] / Pages 3 0 R / Type / Catalog / ViewerPreferences >>> эндобдж 2 0 obj > поток 2019-05-31T12: 27: 51 + 02: 002019-05-31T12: 32: 52 + 02: 002019-05-31T12: 32: 52 + 02: 00Adobe InDesign CC 13.1 (Windows) uuid: fbf44e60-1eef-47d4-97e7-70194e9f1533xmp.did: 31aa2a1e-1766-ee44-9dfc-04562ffe8ddbxmp.id: ec4c22df-adca-7643-b057-ec281277af5f41fproof-pdf1 a93a-b1255ed1f366xmp.did: dacfbfc0-aeb6-e149-9ef4-59eebdb86e7bxmp.did: 31aa2a1e-1766-ee44-9dfc-04562ffe8ddbdefault

  • преобразовано из приложения / x-indfAign в приложение / x-indfAdo 13.1 для Windows : 27: 51 + 02: 00
    • application / pdf
  • Gr10_Term3_ResourcePack.indb
    • Библиотека Adobe PDF 15.0FalsePDF / X-1: 2001PDF / X-1: 2001PDF / X-1a: 2001 конечный поток эндобдж 3 0 obj > эндобдж 15 0 объект > эндобдж 16 0 объект > эндобдж 17 0 объект > эндобдж 18 0 объект > эндобдж 34 0 объект > эндобдж 35 0 объект > эндобдж 36 0 объект > эндобдж 37 0 объект > эндобдж 38 0 объект > эндобдж 59 0 объект > / ExtGState> / Font> / ProcSet [/ PDF / Text] / Properties> / Shading> / XObject >>> / TrimBox [35.1732 35.1732 630.449 877.063] / Тип / Страница >> эндобдж 60 0 объект > / ExtGState> / Font> / ProcSet [/ PDF / Text] / XObject >>> / TrimBox [35.1732 35.1732 630.449 877.063] / Type / Page >> эндобдж 61 0 объект > / ExtGState> / Font> / ProcSet [/ PDF / Text] / Properties> / XObject >>> / TrimBox [35.1732 35.1732 630.449 877.063] / Type / Page >> эндобдж 62 0 объект > / ExtGState> / Font> / ProcSet [/ PDF / Text / ImageC] / Properties> / XObject >>> / TrimBox [35.1732 35.1732 630.449 877.063] / Тип / Страница >> эндобдж 63 0 объект > / ExtGState> / Font> / ProcSet [/ PDF / Text] / XObject >>> / TrimBox [35.1732 35.1732 630.449 877.063] / Type / Page >> эндобдж 64 0 объект > / ExtGState> / Font> / ProcSet [/ PDF / Text] / XObject >>> / TrimBox [35.1732 35.1732 630.449 877.063] / Type / Page >> эндобдж 65 0 объект > / ExtGState> / Font> / ProcSet [/ PDF / Text] / Properties> / XObject >>> / TrimBox [35.1732 35.1732 630.449 877.063] / Type / Page >> эндобдж 176 0 объект > поток HW [s} 8SBX ܑ9 && 1> ؙ L1Q -}} HIv] Mxdwo &? OϱIo | tY «/ HyL2» + 5F ד_ N ￜ 0 {XW ե ߅5 ժ) «| V @» {J [~ _k Da> 1NX̓ * I ~ O.\ LqAJuu-v «VZeC 0C ՘ WXEyȇrhˌPL {㹬 WuhAh) TeH п L L6zr $ HE6

    Вопросы и решения по математике для 10 класса

    Консорциум Smarter Balanced Assessment Consortium (SBAC) — это стандартизированный тест, который включает в себя множество вопросов, усовершенствованных с помощью новых технологий.

    Некоторые из них: Множественный выбор — один правильный ответ, Множественный выбор — несколько правильных ответов, Таблицы соответствия, Перетаскивание, Горячий текст, Заполнение таблицы, Графики, Уравнение / числовое значение, Расширенный составной ответ, Короткий ответ и многие другие.

    Эта страница содержит несколько примеров вопросов вместе со ссылками на практические тесты по математике для 10 класса, которые дают вам представление о вопросах, которые ваши ученики, вероятно, увидят на тесте. После каждого типового вопроса следует объяснение ответа. Объяснение включает в себя важные аспекты задачи, которые вам, возможно, придется учитывать в отношении навыков, процессов и информации, которые должны знать ваши ученики.

    Домен: оценка 10 >> Число и количество — система вещественных чисел

    Пример вопроса: Оценить 9 150/300

    1. 18
    2. 9
    3. 3
    4. 81

    Ответ Объяснение: 9 150/300 = 9 1/2 = квадратный корень из 9 = 3.В задаче с рациональным показателем числитель указывает степень, а знаменатель — корень. Однако в этой задаче показатель степени может быть уменьшен, поэтому сначала мы должны уменьшить его. Показатель 150/300 = 1/2. Таким образом, проблема становится 9 в степени 1/2. Знаменатель равен 2, поэтому мы извлекаем квадратный корень из 9, который равен 3. Числитель равен 1, поэтому мы возводим 3 в 1-ю степень и получаем ответ 3.

    Стандарты: HSN.RN.A.1

    Нажмите здесь, чтобы попрактиковаться: Число и количество — система действительных чисел Вопросы по математике 10-го класса

    Домен: Оценка 10 >> Количество и количество — Количество

    Пример вопроса: Перепишите x 1/2 в радикальной форме.

    1. √x
    2. √x 2
    3. 1 / √x
    4. -√x

    Ответ Объяснение: В задаче с рациональным показателем числитель указывает степень, а знаменатель — корень. Поскольку проблема в том, что x 1/2 , знаменатель равен 2, что означает, что мы должны извлечь квадратный корень, а числитель равен 1, поэтому мы возведем его в первую степень, иначе экспоненты не будет, поскольку показатель степени 1 редко бывает использовал. Это делает ответ квадратным корнем из x, записанным как √x.

    Стандарты: HSN.RN.A.1

    Нажмите здесь, чтобы попрактиковаться: Число и количество 10-го класса — вопросы о количестве

    Область: уровень 10 >> Число и количество — комплексная система счисления

    Пример вопроса: Полное упрощение i (7 − i)

    1. 7i − i 2
    2. 1 + 7i
    3. 6i
    4. −1 + 7i

    Объяснение ответа: i (7 − i) = i * 7 − i * i = 7i − i 2 = 7i — (- 1) = 7i + 1 = 1 + 7i

    Начните с использования распределительного метода.Теперь упростим −i 2 = 1 по определению. Теперь переставьте и поместите реальную часть первой, а воображаемую — последней, чтобы она выглядела так: a + bi.

    Стандарты: HSN.CN.A.2

    Нажмите здесь, чтобы попрактиковаться: Математические числа и количество для 10 класса — вопросы по комплексной системе счисления

    Домен: Оценка 10 >> Число и количество — векторные и матричные количества

    Пример вопроса: Вектор в стандартной форме имеет компоненты.Какая начальная точка?

    1. (0, 0)
    2. (3, 10)
    3. (6, 20)
    4. Недостаточно информации

    Объяснение ответа: Поскольку вектор находится в стандартном положении, мы знаем, что начальная точка — это (0, 0) или начало координат.

    Стандарты: HSN.VM.A.2

    Нажмите здесь, чтобы попрактиковаться: Число и количество — Вопросы о векторных и матричных величинах для 10-го класса по математике

    Область: 10 класс >> Алгебра — видение структуры в выражениях

    Пример вопроса: Какое выражение эквивалентно 9x 2 — 16y 2 ?

    1. (3x — 4 года) (3x — 4 года)
    2. (3x + 4 года) (3x + 4 года)
    3. (3x + 4 года) (3x — 4 года)
    4. (3–4 года) 2

    Ответ Объяснение: Студент должен понять, что выражение — это разница двух полных квадратов

    Стандарты: HSA.SSE.A.2

    Щелкните здесь, чтобы попрактиковаться: Алгебра — определение структуры выражений Вопросы для 10 класса по математике

    Область: 10 класс >> Алгебра — арифметика с многочленами и рациональными выражениями

    Пример вопроса: Вычислить f (x) = — a 3 + 6a − 7 при a = — 1 и сформулировать остаток.

    1. -14
    2. -12
    3. 14
    4. 12

    Объяснение ответа: Студент должен подставить — 1 в функцию следующим образом — (- 1) 3 +6 (−1) −7 = −12 и найти значение, чтобы получить остаток

    Стандарты: HSA.APR.B.2

    Щелкните здесь, чтобы попрактиковаться: Алгебра — Арифметика с многочленами и рациональными выражениями Вопросы для 10 класса по математике

    Область: 10 класс >> Алгебра — Создание уравнений

    Пример вопроса: Соотношение персонала и гостей на гала-вечере было 3: 5. Всего в бальном зале присутствовало 576 человек. Сколько гостей было на гала-вечере?

    1. 276
    2. 300
    3. 360
    4. 216

    Объяснение ответа: Установите соотношение гостей к общему количеству людей, 8/5 = x / 576.Решить крестным умножением. 8x = 2880. Разделите обе части на 8. Итак, x = 360.

    Стандарты: HSA.CED.A.3

    Щелкните здесь, чтобы попрактиковаться: Алгебра — Создание уравнений Вопросы для 10 класса по математике

    Область: 10 класс >> Алгебра — Рассуждение с помощью уравнений и неравенств

    Пример вопроса: Решите квадратичный x 2 + 10x = −25.

    1. -10
    2. 10
    3. 5
    4. -5

    Ответ Объяснение: Эту проблему можно легко решить, переставив уравнение так, чтобы оно решалось для нуля, а затем разложив на множители, как показано:

    х 2 + 10х = -25

    x 2 + 10x + 25 = 0

    (х + 5) (х + 5) = 0

    Поскольку оба фактора абсолютно одинаковы, у вас будет только одно решение этой проблемы.

    х + 5 = 0

    х = −5

    Стандарты: HSA.REI.B.4

    Щелкните здесь, чтобы попрактиковаться: Алгебра — Рассуждение с помощью уравнений и неравенств Вопросы для 10 класса по математике

    Домен: Уровень 10 >> Функции — Функции интерпретации

    Пример вопроса: Какой график может представлять график f (x) = sin (x)?

    Ответ Пояснение: График функции sin всегда выглядит как волна.Единственная функция, которая может быть функцией sin, — это D.

    .

    Стандарты: HSF.IF.C.7

    Нажмите здесь, чтобы попрактиковаться: Функции — вопросы по интерпретации функций для 10-го класса по математике

    Домен: Уровень 10 >> Функции — Функции построения

    Пример вопроса: Опишите, как можно получить график g (x) = x 3 — 5 путем сдвига f (x) = x 3 + 2.

    1. Сдвиг вправо 7 шт.
    2. Сдвиг влево 7 шт.
    3. Сдвиг на 7 единиц
    4. Сдвиг вниз на 7 единиц

    Объяснение ответа: Единственное, что изменилось в двух уравнениях, — это точка пересечения по оси Y, которая управляет вертикальным смещением (вверх или вниз).Чтобы получить график g (x) путем сдвига графика f (x), вы должны сдвинуть f (x) вниз на 7 единиц, чтобы изменить значение от +2 до -5.

    Стандарты: HSF.BF.B.3

    Нажмите здесь, чтобы попрактиковаться: Функции — вопросы построения функций для 10-го класса по математике

    Домен: Уровень 10 >> Функции — Функции интерпретации

    Пример вопроса: Решите 3 x = 12, используя логарифмическую форму.

    1. x = ln12 / ln3
    2. x = ln (4)
    3. x = ln (9)
    4. Ни один из этих

    Ответ Объяснение:
    Решите, используя журналы следующим образом:
    3 x = 12
    x = log (основание 3) 12
    x = ln12 / ln3

    Стандарты: HSF.LE.A.4

    Нажмите здесь, чтобы попрактиковаться: Функции — вопросы по интерпретации функций для 10-го класса по математике

    Домен: Уровень 10 >> Функции — тригонометрические функции

    Пример вопроса: На единичном круге видно, что tan (5π / 4) = 1. Какое значение cos (5π / 4)?

    1. −√2 / 2
    2. undefined
    3. √2 / 2
    4. -1

    Ответ Пояснение:
    Тригонометрическое отношение косинуса — это отношение длины соседней стороны к длине гипотенузы.Длина соседней стороны — это значение x в точке на единичной окружности. Гипотенуза — это радиус единичной окружности, поэтому гипотенуза равна 1. Таким образом, значение отношения косинуса любого угла в единичной окружности — это значение x точки на единичной окружности, которая соответствует этому углу. Тригонометрическое отношение касательной — это длина противоположной стороны, деленная на длину соседней стороны. Длина противоположной стороны — это значение y в точке на единичной окружности, а длина соседней стороны — это значение x в точке на единичной окружности.Гипотенуза — это радиус единичной окружности, поэтому гипотенуза равна 1. Таким образом, значение тангенциального отношения любого угла в единичной окружности — это отношение yx от точки на единичной окружности, которая соответствует этому углу. В этом вопросе tan (5π / 4) = 1. Это отношение берется из точки (−2 / √2, −2 / √2), которая соответствует углу с мерой 5π / 4 радиан. Таким образом, используя информацию выше, значение cos (5π4) совпадает со значением x в точке (−2 / √2, −2 / √2). Следовательно, значение cos (5π / 4) = −2 / √2.

    Стандарты: HSF.TF.A.2

    Нажмите здесь, чтобы попрактиковаться: Функции — Вопросы по тригонометрическим функциям для 10-го класса по математике

    Домен: оценка 10 >> Геометрия — сравнение

    Пример вопроса: Какими будут координаты точки S после применения следующего правила: (x + 3, y -2)?

    1. (1, -4)
    2. (-2, -2)
    3. (2, -2)
    4. (3, -2)

    Ответ Объяснение: Ответ: B
    Объяснение: Данное правило преобразования состоит в том, чтобы перевести точку на 3 единицы вправо и на 2 единицы вниз, как показано на следующей диаграмме:

    Стандарты:

    Щелкните здесь, чтобы попрактиковаться: Геометрия — вопросы на соответствие для 10 класса по математике

    Область: уровень 10 >> Геометрия — подобие, прямоугольные треугольники и тригонометрия

    Пример вопроса: По какому свойству углы BAX и TSX могут быть сочтены совпадающими?

    1. Соответствующие углы
    2. Вертикальные углы
    3. Альтернативные внутренние углы
    4. Конгруэнтные углы

    Ответ Объяснение: Ответ: A

    Хотя это равные углы, вопрос задает свойство.Так как они находятся в соответствующих местах с поперечиной (AX), правильный ответ — A

    .

    Стандарты: HSG.SRT.A.3

    Щелкните здесь, чтобы попрактиковаться: вопросы по геометрии — подобию, прямоугольным треугольникам и тригонометрии для 10-го класса по математике

    Домен: уровень 10 >> Геометрия — круги

    Пример вопроса: Что такое правило перевода и масштабный коэффициент расширения как Окружность F → Окружность F ‘?

    1. (х, у) → 1/4 (х, у + 10)
    2. (х, у) → 4 (х, у + 10)
    3. (х, у) → 1/4 (х + 10, у)
    4. (х, у) → 1/4 (х, у-10)

    Ответ Пояснение: Исходная окружность F имеет центр в точке (−5, −6) с радиусом 4 единицы.Смещенный / расширенный круг F ’имеет центр в точке (-5,4) с радиусом 1 единицы. Это означает, что центр был переведен на 10 единиц. В качестве преобразования этот перевод записывается как (x, y) → (x, y + 10). Круг F также был расширен в 1/4 раза, потому что радиус был уменьшен с 4 единиц до 1 единицы. В качестве преобразования это расширение записывается как (x, y) → 1/4 (x, y). Объединяя перенос и расширение, получаем правило (x, y) → 1/4 (x, y + 10).

    Стандарты:

    Щелкните здесь, чтобы попрактиковаться: Геометрия — Круги Вопросы для 10 класса по математике

    Область: Уровень 10 >> Геометрия — Выражение геометрических свойств с помощью уравнений

    Пример вопроса: Какое значение на числовой прямой на рисунке ниже делит сегмент EF на две части с соотношением их длин 3: 1?

    1. -5
    2. -3
    3. -2
    4. -1

    Объяснение ответа: Точка E находится в -7 на числовой прямой на рисунке, а точка F находится в 1.Таким образом, длина сегмента EF равна 8. Чтобы разделить сегмент на две части с соотношением их длин 3: 1, измените соотношение на 3x: 1x, чтобы разрешить изменение положения на числовой прямой. Затем установите сумму двух частей равной 8 и решите относительно x. 3x + 1x = 8; 4x = 8; x = 2. Теперь, когда вы знаете, что x = 2, найдите 3x, что равно 6. Найдите значение на числовой прямой, добавив 6 к положению точки E. −7 + 6 = -1. Значение на числовой прямой, которая делит сегмент EF в соотношении 3: 1, равно -1.

    Стандарты: HSG.GPE.B.6

    Щелкните здесь, чтобы попрактиковаться: Геометрия — Выражение геометрических свойств с помощью уравнений Вопросы для 10 класса по математике

    Область: уровень 10 >> Геометрия — геометрические измерения и размеры

    Пример вопроса: Каков объем призмы, показанной ниже?

    1. 1350 см 3
    2. 1350 см
    3. 675 см 3
    4. 675 см

    Ответ Пояснение: Используйте формулу для объема пирамиды:

    В = 1/2.a.c.h

    В данном случае длина 15 см, длина основания 10 см, а высота 9 см. Следовательно:

    V = 1 / 2.15.10.9 = 675 см 3

    Стандарты: HSG.GMD.A.3

    Нажмите здесь, чтобы попрактиковаться: Геометрия — геометрические измерения и вопросы о размерах для 10 класса по математике

    Область: Уровень 10 >> Геометрия — Моделирование с помощью геометрии

    Пример вопроса: Компания отправляет сферические пресс-папье в кубических ящиках.Окружность пресс-папье составляет 9π см. Если коробка подходит к сфере точно так, чтобы стороны сферы касались коробки, каков объем самой маленькой коробки, которую компания может использовать для доставки.

    1. 81 см 3
    2. 81 π см 3
    3. 729 см 3
    4. 1009 π см 3

    Ответ Объяснение:

    Обратите внимание, что диаметр сферы будет таким же, как и сторона кубической коробки.Используя значение окружности, можно определить диаметр пресс-папье.
    C = πd9π
    см = πd9
    см = d
    Так как диаметр равен по мере сторонам {\ dots}
    V = s 3
    V = (9 см) 3
    V = 729 см 3

    Стандарты: HSG.MG.A.3

    Щелкните здесь, чтобы попрактиковаться: Геометрия — моделирование с помощью вопросов по геометрии для 10-го класса по математике

    Область: 10 класс >> Статистика и вероятность — интерпретация категориальных и количественных данных

    Пример вопроса: Учитывая приведенный ниже график разброса, какой тип функции выражает корреляцию между двумя переменными?

    1. Линейный
    2. Экспоненциальная
    3. Квадратичная
    4. Полярный

    Объяснение ответа: Обратите внимание, что тренд графика (красный) между точками данных образует линию.

    Стандарты: HSS.ID.A.4

    Нажмите здесь, чтобы попрактиковаться: Статистика и вероятности — Интерпретация категориальных и количественных данных Вопросы для 10 класса по математике

    Область: 10 класс >> Статистика и вероятность — делать выводы и обосновывать выводы

    Пример вопроса: В рамках исследовательского проекта о поведении домашних животных была выбрана случайная выборка из 400 кошек. Исследование показало, что 60% кошек предпочитают спать в доме.Курица была любимой едой 35% этих кошек. Исследование также показало, что 85% кошек, которые предпочитали спать вне дома, имели другое любимое блюдо. Сколько кошек в выборке больше всего любили курицу и предпочитали спать внутри?

    1. 84
    2. 56
    3. 160
    4. 156

    Объяснение ответа: Если в выборке 400 кошек и 60% кошек предпочли спать в помещении, то 400,0,60 = 240 кошек предпочли спать в помещении и 160 кошек предпочли спать на улице.Далее, если любимым блюдом 35% кошек, которые предпочитали спать внутри, была курица, то 240.0.35 = 84 кошки в выборке предпочли спать внутри и выбрали курицу в качестве своего любимого блюда.

    Стандарты: HSS.IC.B.6

    Нажмите здесь, чтобы попрактиковаться: Статистика и вероятность — делать выводы и обосновывать выводы Вопросы для 10-го класса по математике

    Область: оценка 10 >> Статистика и вероятность — условная вероятность и правила вероятности

    Пример вопроса: В студенческом совете есть одна предстоящая вакансия.В школе проводятся выборы, и у нее есть восемь равновероятных кандидатов. Класс AP Statistics хочет смоделировать результаты выборов, поэтому учащиеся должны выбрать подходящий метод моделирования. Они намерены провести испытания с симуляцией. Какой из этих методов будет наиболее подходящим?

    1. Покрутите колесо с восемью равными промежутками
    2. Подбросить монету восемь раз за каждые выборы
    3. Бросьте кости
    4. Бросить четыре кубика

    Объяснение ответа: В вопросе указано, что существует восемь равновероятных кандидатов.Это означает, что каждый кандидат имеет одинаковые шансы на победу на выборах. Только вращающееся колесо с восемью равными ячейками могло имитировать эту ситуацию, потому что колесо имеет равные шансы приземлиться на каждую ячейку.

    Стандарты: HSS.IC.A.1

    Нажмите здесь, чтобы попрактиковаться: Статистика и вероятность — условная вероятность и правила вероятностных вопросов для 10-го класса по математике

    Область: оценка 10 >> Статистика и вероятность — использование вероятности для принятия решений

    Пример вопроса:

    Используя приведенную выше диаграмму Венна, найдите P (C или E).

    1. 1/3
    2. 7/24
    3. 5/24
    4. Ни один из этих

    Объяснение ответа: Просто посчитайте точки данных в кругах C и E. Их 8 из 24 общих точек данных, и, уменьшив, мы получим 8/24 = 1/3.

    Стандарты: HSS.CP.B.7

    Щелкните здесь, чтобы попрактиковаться: Статистика и вероятность — использование вероятности для принятия решений Вопросы по математике для 10 класса

    Область: оценка 10 >> Статистика и вероятность — использование вероятности для принятия решений

    Пример вопроса: Статистик работает в Sweet Shop USA, и ему было поручено выяснить, какова вероятность того, что сбои в работе автомата по приготовлению фаджа испортят всю партию помадки в процессе.Каждая неисправность машины обходится компании в 250 долларов. Статистик рассчитывает вероятность того, что 1 из 20 партий фаджа будет потеряна из-за неисправности машины. Какова ожидаемая стоимость этих потерь за один месяц, если компания производит 20 партий помадки каждый день?

    1. $ 3750
    2. 150 000 долл. США
    3. $ 7500
    4. $ 375

    Объяснение ответа: Поскольку в большинстве месяцев 30 дней, мы предположим, что в месяце 30 дней. Мы можем использовать E (x) = x1p1 + x2p2 +… + xipi или просто вычислить следующим образом
    E (X) =.05 * 250 * 30 = 375

    долларов США

    Стандарты: HSS.MD.A.4

    Щелкните здесь, чтобы попрактиковаться: Статистика и вероятность — использование вероятности для принятия решений Вопросы по математике для 10 класса

    Общие сведения о скалярных и векторных величинах

    Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

    Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.

    Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

    Чтобы отправить уведомление, выполните следующие действия:

    Вы должны включить следующее:

    Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

    Отправьте жалобу нашему уполномоченному агенту по адресу:

    Чарльз Кон Varsity Tutors LLC
    101 S. Hanley Rd, Suite 300
    St. Louis, MO 63105

    Или заполните форму ниже:

    Математика средней школы (10, 11 и 12 классы)

    Математика средней школы для 10, 11 и 12 классов представлены математические вопросы и задачи для проверки глубокого понимания математических концепций и вычислительных процедур.Предоставляются подробные решения и ответы на вопросы.

    Оценка 12

    11 класс

    10 класс

    Онлайн-калькуляторы

    • Онлайн-математические калькуляторы и решатели
    • Онлайн-калькуляторы и решатели геометрии
    • Калькулятор проверки делимости. Онлайн-калькулятор, который проверяет целые числа на видимость 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 и 13.
    • Калькуляторы сложения, вычитания и умножения целых чисел.Три отдельных онлайн-калькулятора для сложения, вычитания и умножения целых чисел.
    • Калькулятор частных и остатков. Онлайн-калькулятор, вычисляющий частное и остаток от деления двух целых чисел.
    • Калькулятор наименьшего общего кратного (lcm). Вычислите наименьшее общее кратное двух натуральных чисел.
    • Калькулятор наибольшего общего коэффициента (GCF). Вычислите наибольший общий делитель двух натуральных чисел.
    • Калькулятор основных факторов.Разложите положительное целое число на простые множители.
    • Калькулятор сложения дробей. Добавьте 2 или 3 дроби и уменьшите окончательный ответ.
    • Калькулятор умножения дробей. Умножьте 2 дроби и уменьшите ответ.
    • Калькулятор деления дробей. Разделите 2 дроби и уменьшите ответ.
    • Калькулятор сокращения дробей. Перепишите дроби в уменьшенном виде.
    Больше математики в средней школе (6, 7, 8, 9 классы) — бесплатные вопросы и задачи с ответами
    Больше математики для начальной школы (4 и 5 классы) с бесплатными вопросами и задачи с ответами Домашняя страница
    Автор — сообщить об этом объявлении по электронной почте

    Изучение использования множественных представлений для обучения векторов в 10 классе по физическим наукам

    Аннотация

    Целью данной статьи было изучить использование множественного представления подход в качестве стратегии обучения для улучшения понимания учащимися векторов в 10 класс Физические науки.Исследование также хотело рассмотреть подход MR. через призму учащихся. Выборка, состоящая из 45 учеников 10 класса из Всего в исследовании приняли участие 160 учащихся 10-х классов физических наук. Оба количественные и качественные данные были собраны и проанализированы. Учащиеся были первыми прошли предварительный тест для установления их первоначального понимания векторов. Этот предварительный тест был с последующим вмешательством в форме урока. Урок проводился по порядку познакомить учащихся с обучением через множественные представления.Затем был проведен посттест вводится для определения воздействия вмешательства. Чтобы собрать и количественно оценить восприятие учащимися использования множественных представлений в преподавании и обучении векторов в 10-х классах учащихся физических наук раздали анкеты полный. Последним шагом было собеседование с учащимися для триангуляции результатов три инструмента. Исследование показало, что учащиеся боролись с понимание векторов в их традиционных уроках разговорной речи и их восприятие векторов было отрицательным.Исследование также показало, что множественные Представления могут улучшить понимание и развить позитивное восприятие учащихся к преподаванию и изучению векторов. Это улучшение происходит только если несколько представлений используются правильно. Исследование также выяснило, что когда Множественные представления используются неправильно, это ограничивает более глубокое понимание учащиеся.

    No related posts.

    Leave a Reply

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *