Контрольная работа «Логарифмы»
Предмет: математика
Тема: Контрольная работа по теме «Логарифмы»
Тип урока: урок проверки знаний, умений и навыков студентов
Цель: проверка уровня предметной компетентности студентов
Задачи:
— образовательные: проверка знаний, умений и навыков при решение логарифмических уравнений и неравенств;
— развивающие: развитие умения применять полученные знания по решению данных заданий по теме, формирование умения анализировать и обобщать знания по решению;
— воспитательные: воспитывать интерес к предмету, коллективизм, аккуратность, дисциплинированность.
В — 1
Вычислите:
а)
б)
Найдите число Х по данному его логарифму:
Решите логарифмическое уравнение:
а)
б)
Решите логарифмическое неравенство:
Решите систему уравнений:
В — 2
Вычислите:
а)
б)
Найдите число Х по данному его логарифму:
Решите логарифмическое уравнение:
а)
б)
Решите логарифмическое неравенство:
Решите систему уравнений:
В — 1 Вычислите: а) б) Найдите число Х по данному его логарифму: Решите логарифмическое уравнение: а) б) Решите логарифмическое неравенство: Решите систему уравнений: | В — 2 Вычислите: а) б) Найдите число Х по данному его логарифму: Решите логарифмическое уравнение: а) б) Решите логарифмическое неравенство: Решите систему уравнений: |
В — 1 Вычислите: а) б) Найдите число Х по данному его логарифму: Решите логарифмическое уравнение: а) б) Решите логарифмическое неравенство: Решите систему уравнений: | В — 2 Вычислите: а) б) Найдите число Х по данному его логарифму: Решите логарифмическое уравнение: а) б) Решите логарифмическое неравенство: Решите систему уравнений: |
В — 1 Вычислите: а) б) Найдите число Х по данному его логарифму: Решите логарифмическое уравнение: а) б) Решите логарифмическое неравенство: Решите систему уравнений: | В — 2 Вычислите: а) б) Найдите число Х по данному его логарифму: Решите логарифмическое уравнение: а) б) Решите логарифмическое неравенство: Решите систему уравнений: |
Тест по теме «Логарифмы.
 Свойства логарифмов»
Свойства логарифмов» Алгебра и начала математического анализа
10 класс
Тест по теме «Логарифмы. Свойства логарифмов»
Технологическая карта контрольно-измерительного материала
Класс | 10-11 |
Предмет | алгебра и начала анализа |
Учебник, по которому ведется преподавание | Ю.М.Колягин, М.В.Ткачёв, Н.Е.Фёдорова, М.И. Шабунин «Алгебра и начала математического, 10 класс» |
Тема контроля | Логарифмы. Свойства Логарифмов |
Вид контроля | тематический |
Форма и методы контроля | Письменный индивидуальный тест |
Время контроля | 90 минут |
Цель контроля | Проверить уровень усвоения учащимися понятия логарифма, свойств логарифмов, формулы перехода логарифма к другому основанию и умения применять свои знания в предложенной ситуации. |
Содержание контроля | Тест состоит из двух разделов. I раздел – теоретический. Этот раздел включает в себя пять предложений, в которых нужно вставить пропущенные слова. II раздел-практический. Этот раздел состоит из трёх частей. В 1 часть входят задания с выбором одного правильного ответа из четырёх. Во 2 части ученику предстоит решить пять заданий и записать только ответ, третья часть содержит три вычислительных примера. Ученикам необходимо записать полностью решение. Тест предназначен для учащихся общеобразовательных классов, может быть использован для профильных классов как периодического, так и промежуточного контроля. Учащиеся могут записать ответы либо в специальных бланках, либо в этих же бланках в отведённом для этого месте на усмотрение педагога. |
Критерии оценивания | Каждое задание теоретического раздела оценивается 0,5 баллов. Задание из I части с выбором ответов оценивается в 1 балл. Задание из II части (задания с кратким ответом) оценивается в 2 балла. Задание из III части (задание с полным решением) оценивается в 3 балла. Максимальный балл за работу- 26,5 баллов. От 18,5 до 26,5 баллов – «5» От 13,5 до 18 баллов – «4» От 7,5 до 13,5 баллов – «3 Менее 7,5 баллов — «2» |
Место контроля в системе уроков | Этот тест желательно провести перед контрольной работой, что позволит учащимся ещё раз обратить внимание на вопросы требующие более тщательной подготовки, устранить пробелы самостоятельно или на консультации у учителя. |
Инструкция для ученика
Дорогой ученик!
Тебе предстоит решить данный тест. Для этого внимательно познакомься с тестом.
Тест состоит из двух разделов.I раздел-теоретический, II-практический.
В теоретическом разделе необходимо дописать пропущенные слова. Каждое задание оценивается в 0,5 балла.
Практический раздел состоит из 3 частей: 1 часть-выбрать правильный ответ (1 балл за каждое задание), 2 часть-записать ответ (2 балла за каждое задание),3 часть- записать подробное решение примера (3 балла за каждое верно решенное задание).
Ответы записывай в бланке в отведенном для этого месте.
Желаю успехов!
Раздел1. Теоретический
В задании 1-5 вставьте пропущенные слова
№ | Вопрос |
1 | Логарифмом _______________ числа b по основанию a, где a0, a1 называется_________ _________________, в которую надо возвести _____________ а, чтобы получить число b. |
2 | Логарифм произведения – это ______________ логарифмов. |
3 | Логарифм частного – это __________________ логарифмов. |
4 | Логарифм, основание которого равно 10 называется _________________. |
5 | Логарифм, основание которого равно е2,7 называется _________________. |
Раздел 2.Практический
I часть. Задания с выбором ответа.
№ | Задание | Ответы | ||||
1 | 2 | 3 | 4 | |||
6 | Найти значение выражения | -2 | 2 | 9 | ||
7 | Упростить выражение | 12 | 8 | 24 | 7 | |
8 | Вычислить | 0 | 2 | 4 | ||
9 | Вычислить | 5 | 6 | -2 | ||
10 | Найти значение выражения | 4,5 | 0,5 | -4,5 | 0,025 | |
II часть. Задания с кратким ответом
Задания с кратким ответом
№ | Задание. Найти значение выражения. | Ответ |
11 | ||
12 | ||
13 | ||
14 | ||
15 |
III часть. Задания с развёрнутым ответом.
16.Вычислить значение выражения, записать решение.
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
17.Вычислить значение выражения, записать решение.
_____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
18.Вычислить значение выражения, записать решение.
_____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Ответы и решения:
№ задания | Ответ |
1 | Положительного, показатель степени, основание |
2 | Сумма |
3 | Разность |
4 | Десятичным |
5 | Натуральным |
6 | 2 |
7 | 4 |
8 | 3 |
9 | 4 |
10 | 2 |
11 | 0 |
12 | 0,5 |
13 | 1 |
14 | 57 |
15 | 1 |
16 | Решение: Ответ: 2,5 |
17 | Решение: Ответ: 4 |
18 | Решение: Ответ: 10 |
Литература:
1. Единый государственный экзамен. Математика. Справочные материалы, контрольно-тренировочные упражнения, задания с развернутым ответом: в 2 ч. /А.К.Дьячков, Н.И.Иконникова, В.М.Казак,Е.В.Морозова; под общ.ред. А.К.Дьячкова.- Челябинск:Взгляд,2006.-Ч.1.-191 с.
Единый государственный экзамен. Математика. Справочные материалы, контрольно-тренировочные упражнения, задания с развернутым ответом: в 2 ч. /А.К.Дьячков, Н.И.Иконникова, В.М.Казак,Е.В.Морозова; под общ.ред. А.К.Дьячкова.- Челябинск:Взгляд,2006.-Ч.1.-191 с.
2.Математика: тренировочные тематические задания повышенной сложности с ответами для подготовке к ЕГЭ и к другим формам выпускного и вступительного экзаменов/сост. Г.И.Ковалева,Т.И.Бузулина,О.Л.Безрукова,Ю.А.Розка – Волгоград:Учитель,2008.-494 с.
Контрольная работа по Алгебре и началам анализа 10 класс по теме «Логарифмическая функция» базовый уровень
МБОУ Тацинская сош №3, учитель Митрофанова Н.В.
А-10 Контрольная работа №6 по теме: «Логарифмическая функция»
Вариант 1
1.Вычислить: а) б) в)
2. Сравнить числа:
3. Решить уравнение:
4. Решить неравенство:
5. Решить уравнение:
6. Решить неравенство:
7. (Дополнительно) Решить неравенство:
А-10 Контрольная работа №6 по теме: «Логарифмическая функция»
Вариант 2
Вычислить: а) б) в)
2. Сравнить числа:
Сравнить числа:
3. Решить уравнение:
4. Решить неравенство:
5. Решить уравнение:
6. Решить неравенство:
7. (Дополнительно) Решить неравенство:
А-10 Контрольная работа №6 по теме: «Логарифмическая функция»
Вариант 3
1.Вычислить: а) б) в)
2. Сравнить числа:
3. Решить уравнение:
4. Решить неравенство:
5. Решить уравнение:
6. Решить неравенство:
7. (Дополнительно) Решить неравенство:
А-10 Контрольная работа №6 по теме: «Логарифмическая функция»
Вариант 4
1.Вычислить: а) б) в)
2. Сравнить числа:
3. Решить уравнение:
4. Решить неравенство:
5. Решить уравнение:
6. Решить неравенство:
7. (Дополнительно) Решить неравенство:
А-10 Контрольная работа №6 по теме: «Логарифмическая функция»
Вариант 5
1.Вычислить: а) б) в)
2. Сравнить числа:
Сравнить числа:
3. Решить уравнение:
4. Решить неравенство:
5. Решить уравнение:
6. Решить неравенство:
7. (Дополнительно) Решить неравенство:
А-10 Контрольная работа №6 по теме: «Логарифмическая функция»
Вариант 6
Вычислить: а) б) в)
2. Сравнить числа:
3. Решить уравнение:
4. Решить неравенство:
5. Решить уравнение:
6. Решить неравенство:
7. (Дополнительно) Решить неравенство:
Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/243328-kontrolnaja-rabota-po-algebre-i-nachalam-anal
Контрольная работа по теме: «Свойства логарифмов»
Государственное бюджетное образовательное учреждениеБРАТСКИЙ ПОЛИТЕХНИЧЕСКИЙ КОЛЛЕДЖ
ЛОГАРИФМЫ
Методические указания к решению упражнений
при изучении темы «Свойства логарифмов»
г. Братск, 2012г.
Логарифмы: Методические указания / Сост. Лапина Н.Л. – Братск: БрПК, 2012– 14с.
Лапина Н.Л. – Братск: БрПК, 2012– 14с.
Данные методические указания содержат необходимые теоретические сведения по теме «Логарифмы» дисциплины математика, примеры решения упражнений, набор упражнений для самостоятельного решения с ответами к некоторым из них, десять вариантов для выполнения контрольной работы. Вариант заданий определяется по последней цифре номера зачетной книжки.
Рецензент: Носырева Н.В. заместитель директора по УМР ГБОУ СПО БрПК
Содержание
Введение…………………………………………………………………………………………………………..4
-
Определение логарифма ……………………………………………………………………5
-
Примеры для самостоятельного решения………………..…………….7 -
Преобразование логарифмических выражений………………..…………….-
Примеры для самостоятельного решения…………………………………..9
-
-
Контрольная работа по теме: «Свойства логарифмов»…………………. 11
11
Список литературы ………………………………………………………………….…………14
Введение
Настоящие методические указания предназначены в помощь студентам всех форм обучения при изучении темы «Свойства логарифмов». Разделы указаний содержат необходимые теоретические сведения (определения, формулы без доказательства) и подробно разобранные упражнения. В конце каждого раздела предлагаются задания для самостоятельного решения с ответами для самопроверки.
Теоретические сведения и примеры для самостоятельного решения дают возможность использовать данные методические указания на практических занятиях по математике, а также для самостоятельного изучения темы «Свойства логарифмов».
В конце указаний приведены десять вариантов заданий для выполнения контрольной работы. Вариант определяется последней цифрой номера зачетной книжки студента. Работа выполняется письменно в отдельной тетради.
-
Определение логарифма
Понятие логарифма числа вводится при решении показательных уравнений, например, решим уравнение , в котором необходимо найти показатель х, представим правую часть уравнения в виде двух в четвертой степени .

Из определения следует, что записи logаb=х. и ах=b равносильны.
Например, log28=3, потому что при возведении основания 2 в степень 3 получается 8: 2
Определение логарифма можно кратко записать так: . Это равенство справедливо при b>0, a>0, а1. Его обычно называют основным логарифмическим тождеством.
Для вычислений значений логарифмов полезно использовать значения степени следующих чисел:
| 21 = 2 22 = 4 23 = 8 24 = 16 2 26 = 64 27 = 128 28 = 256 29 = 512 210 = 1024 | 31 = 3 32 = 9 33 = 27 34 = 81 35 = 243 | 41 = 4 42 = 16 43 = 64 44 = 256 45 = 1024 | 51 = 5 52 = 25 53 = 125 54 = 625 | 61 = 6 62 = 36 63 = 216 | 71 = 7 73 = 343 | 81 = 8 82 = 64 83 = 512 | ||
| 91 = 9 92 = 81 93 = 729 | 101 = 10 102 = 100 103 = 1000 и т. | |||||||
Также необходимо помнить правила возведения чисел в степень с отрицательным, дробным и нулевым показателем: а0=1; ;
Пример 1. , т.к. 33=27
Пример 2. , т.к. 30=1
Пример 3. , т.к. 2-1=
Пример 4. Вычислить
Пусть. По определению логарифма 32t=64. Это простейшее показательное уравнение. 32=25, 64=26, поэтому (25)t=26; 25t=26 ; 5t=6, t=
Ответ:
Пример 5. Вычислить
Используя свойства степени и основное логарифмическое тождество, находим
Пример 6.
Для некоторых логарифмов имеются специальные обозначения: десятичный log10х=lgx, натуральный logех=lnx.
Пример 7. lg1000=3 , т.к. 103=3
Пример 8. lg0,01=-2 , т.к. 10-2==0,01
-
Примеры для самостоятельного решения:
Ответы:
| № задания | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| ответ | 2 | 4 | 0 | 1 | -2 | -1 | 1 | 2 | 25 | 0,5 |
-
Преобразование логарифмических выражений
При выполнении преобразований выражений, содержащих логарифмы, при вычислениях и при решении уравнений часто используются различные свойства логарифмов.
 Рассмотрим основные из них.
Рассмотрим основные из них.Пусть а>0, а1, b>0, с>0, p – любое действительное число. Тогда справедливы формулы
(1)
(2)
(3)
(4)
(5)
Формулы (1) и (2) можно применять к выражениям, содержащим логарифмы с одинаковыми основаниями.
Формулы (4) и (5) позволяют переходить от одного основания логарифмов к другому.
Пример 1. Вычислить:
На основе формул (1) и (2) преобразуем
Теперь можно применить формулу (4), т. е. перейти к новому основанию, в данном примере логарифмы чисел 16 и 8 легко вычислить при основании 2, тогда
Пример 2. Вычислить
Применим формулу (3), для этого вспомним определение степени с рациональным показателем (), тогда
Пример 3. Зная, что , найти
Применяем формулу (1)
Пример 4. Прологарифмировать выражение по основанию 5.
Запишем данное выражение в виде
Теперь применим формулы (1), (2) и (3)
Пример5. Найти х по данному его логарифму (а>0,b>0):
В этом примере необходимо правую часть представить в виде одного логарифма по основанию 4:
(2 представили в виде log416)
(применили формулы (1), (2) и (3))
-
Примеры для самостоятельного решения:
-
-
-
-
-
-
-
-
Зная, что , найти -
Прологарифмировать выражение по основанию 10.
-
Найти х по данному его логарифму (а>0,b>0):
Ответы:
| № задания | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| ответ | 9 | 1 | 1,5 | | 1 | 2 | 1,5 | 0,6 | -1+2lga-lgn | |
Контрольная работа по теме: «Свойства логарифмов»
-
Вычислить:
-
Вычислить:
-
Вычислить:
-
Вычислить:
-
Вычислить:
-
Вычислить:
-
Доказать тождество:
-
Найти значение выражения:
-
, если
6. , если
, если-
, если
-
, если
-
, если
-
, если
-
, если
-
, если
-
, если
-
, если
-
-
Прологарифмировать выражение:
-
Найти х по данному его логарифму (а>0,m>0,c>0,h>0,n>0,k>0):
СПИСОК ЛИТЕРАТУРЫ
-
Алимов Ш.А. Алгебра и начала анализа – учебник для 10-11 кл. общеобразоват. Учреждений – М.: Просвещение, 2006.- 384с. -
Креславская О.А. ЕГЭ-2009. Математика: Сдаем без проблем! – М.: Эксмо, 2008. -192с.
-192с.
▶▷▶ логарифмические неравенства контрольная работа с ответами
▶▷▶ логарифмические неравенства контрольная работа с ответами| Интерфейс | Русский/Английский |
| Тип лицензия | Free |
| Кол-во просмотров | 257 |
| Кол-во загрузок | 132 раз |
| Обновление: | 09-11-2018 |
логарифмические неравенства контрольная работа с ответами — Yahoo Search Results Yahoo Web Search Sign in Mail Go to Mail» data-nosubject=»[No Subject]» data-timestamp=’short’ Help Account Info Yahoo Home Settings Home News Mail Finance Tumblr Weather Sports Messenger Settings Yahoo Search query Web Images Video News Local Answers Shopping Recipes Sports Finance Dictionary More Anytime Past day Past week Past month Anytime Get beautiful photos on every new browser window Download Контрольная работа по алгебре в 10 классе по теме «Логарифмы globuss24ru/doc/kontrolynaya-rabota-po-algebre Cached Работа содержит логарифмические выражения , логарифмические и показательные уравнения и неравенства , систему неравенств , уравнение с параметром Контрольная работа Логарифмы 10 класс math-prostoru/?page=pages/tests/10th_grade/logarithmsphp Cached Контрольная работа по алгебре 10 класс Тема: «Логарифмы Свойства логарифмов» Контрольная работа по алгебре на тему «Показательные и infourokru/kontrolnaya-rabota-po-algebre-na Cached › Другие методич материалы › Контрольная работа по алгебре на тему «Показательные и логарифмические уравнения и неравенства » (10 класс) Комплект контрольных и самостоятельных работ по алгебре для obrazbaseru/matematika/kontrolnye-i-testy/442-komplekt Cached Контрольная работа по теме «Показательные и логарифмические уравнения и неравенства » Контрольная работа по теме «Степени Контрольные работы в 11 классе по алгебре, Мордкович за 1, 2 mathematics-testscom/11-klass/kontrolnye-raboty/ Cached Контрольные работы по алгебре для 11 класса к учебнику Мордковича АГ с ответами Логарифмические уравнения контрольная работа с решением markontorainfo/logarifmicheskie-uravneniya-kontrolnaya Cached Логарифмические уравнения контрольная работа с решением Загрузить с яндекс-диска файл 1542 Логарифмические уравнения и неравенства — ЕГЭ портал 4egeru/trening-matematika/52541-logarifmicheskie Cached Логарифмические уравнения и неравенства По 10 вариантов с ответами Контрольная работа по теме quot;Логарифмыquot; (10 класс) wwwmetod-kopilkaru/kontrolnaya_rabota_po_teme Cached Главная / Математика / Контрольная работа по теме «Логарифмы» (10 класс) Контрольная работа по теме «Логарифмы» (10 класс) Контрольные работы по алгебре и началам анализа 11 класс allengorg/d/math/math936htm Cached Контрольная работа № 1 10 Иррациональные уравнения и неравенства 30 Логарифмические логарифмические неравенства самостоятельная работа с ответами sitesgooglecom/site/1l4cpound0irc6/ аттестационная работа главного врача по организации здравоохранения бюджетная система Promotional Results For You Free Download | Mozilla Firefox ® Web Browser wwwmozillaorg Download Firefox — the faster, smarter, easier way to browse the web and all of Yahoo 1 2 3 4 5 Next 2,150 results Settings Help Suggestions Privacy (Updated) Terms (Updated) Advertise About ads About this page Powered by Bing™
- контрольные
- заданиями (задачами) и упражнениями из рабочей тетради по чтению за 2 класс — Коти Онлайн книгу удобно смотреть (читать) с компьютера и смартфона Электронное учебное пособие подходит к разным годам: от 2011-2012-2013 до 2015-2016-2017 года — создано по стандартам ФГОС На сайте можно читать
- тетрадь
задачи
что чтение —
- Мордкович за 1
- логарифмические и показательные уравнения и неравенства
- Мордкович за 1
Самостоятельные и контрольные работы по алгебре 10 клас.
 Ершова А.П
Ершова А.ППредлагаемое пособие в первую очередь предназначено для учителей и учащихся, работающих по двухуровневому учебнику «Нелин Е.П., Лазарев В.А. Алгебра и начала математического анализа. 10 класс: базовый и профильный уровни» (издательство «Илекса»), но может использоваться и при работе по другим учебникам алгебры и начал математического анализа, особенно при подготовке учащихся к решению заданий ЕГЭ и ГИА.
Основные особенности предлагаемого сборника самостоятельных и контрольных работ:
1. Сборник содержит полный набор самостоятельных и контрольных работ по всему курсу алгебры и начал математического анализа 10 класса, как базового, так и профильного уровней. Контрольные работы рассчитаны на один урок, самостоятельные работы — на 25—40 минут, в зависимости от темы и уровня подготовки учащихся.
2. Сборник позволяет осуществить дифференцированный контроль знаний, так как задания распределены по трем уровням сложности А, Б и В. Задания уровня А предназначены для учащихся, которые обучаются по программе базового уровня, а задания уровней Б и В — для учащихся, которые обучаются по программе профильного уровня. Задания уровня В предназначены для учащихся, проявляющих повышенный интерес к математике, а также для использования в классах, школах, гимназиях и лицеях с углубленным изучением математики. Для каждого уровня приведено два расположенных рядом равноценных варианта (как они обычно записываются на доске), поэтому на уроке достаточно одной книги на парте.
Задания уровня В предназначены для учащихся, проявляющих повышенный интерес к математике, а также для использования в классах, школах, гимназиях и лицеях с углубленным изучением математики. Для каждого уровня приведено два расположенных рядом равноценных варианта (как они обычно записываются на доске), поэтому на уроке достаточно одной книги на парте.
3. В книгу включены также домашние самостоятельные и практические работы, содержащие творческие, нестандартные задачи по каждой изучаемой теме, а также задачи повышенной сложности. Эти задания могут в полном объеме или частично предлагаться учащимся в качестве зачетных, а также использоваться как дополнительные задания для проведения контрольных работ. По усмотрению учителя выполнение нескольких или даже одного такого задания может оцениваться отличной оценкой.
Ответы к контрольным и домашним самостоятельным работам приводятся в конце книги.
СОДЕРЖАНИЕ
ФУНКЦИИ, УРАВНЕНИЯ, НЕРАВЕНСТВА 5
С-1. Числовые функции, их свойства и графики 5
С-2. Уравнения 7
Уравнения 7
С-3. Применение свойств функций к решению уравнений 10
С-4. Неравенства. Метод интервалов 12
С-5. Уравнения и неравенства, содержащие знак модуля 14
С-6. Построение графиков функций, уравнений и неравенств 17
С-7. Уравнения и неравенства с параметрами 19
К-1 (КП-1). Функции, уравнения, неравенства 20
С-8. Метод математической индукции. Делимость целых чисел 24
С-9. Многочлены. Теорема Безу. Схема Горнера. Формулы Виета 25
(КП-2). Многочлены и их корни. Метод математической индукции 27
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ 30
С-10. Радианная мера углов. Тригонометрические функции угла и числового аргумента 30
С-11. Свойства и графики тригонометрических функций 32
С-12*. Исследование тригонометрических функций и построение их графиков (домашняя практическая работа) 36
С-13. Соотношения между тригонометрическими функциями одного аргумента 37
С-14. Формулы сложения. Формулы двойного аргумента. Формулы приведения 39
С-15. Формулы преобразования суммы тригонометрических функций в произведение и произведения в сумму 42
С-16. Формулы половинного аргумента. Формулы преобразования выражения a sin* + Ь cos* 44
Формулы половинного аргумента. Формулы преобразования выражения a sin* + Ь cos* 44
К-2 (КП-3). Тригонометрические функции 46
ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА 50
С-17. Обратная функция. Обратные тригонометрические функции 50
С-18*. Применение свойств обратных тригонометрических функций (домашняя самостоятельная работа) 53
С-19. Простейшие тригонометрические уравнения 55
С-20. Тригонометрические уравнения 57
С-21. Отбор корней тригонометрических уравнений. Системы уравнений 58
К-3 (КП-4). Тригонометрические уравнения и неравенства 60
С-22. Более сложные тригонометрические уравнения 62
С-23. Системы тригонометрических уравнений 64
С-24. Тригонометрические уравнения с параметрами 65
С-25. Простейшие тригонометрические неравенства 67
С-26. Более сложные тригонометрические неравенства 68
(КП-5). Тригонометрические уравнения, неравенства и их системы 69
СТЕПЕННАЯ ФУНКЦИЯ 72
С-27. Корень n-ой степени и его свойства 72
С-28. Иррациональные уравнения 75
Иррациональные уравнения 75
С-29. Степень с рациональным показателем и ее свойства 77
С 30. Методы решения иррациональных уравнений 81
С-31. Системы иррациональных уравнений. Иррациональные неравенства 82
С-32. Иррациональные уравнения и неравенства с параметрами 84
С-33*. Методы решения иррациональных уравнений, неравенств, систем (домашняя самостоятельная работа) 86
К-4 (КП-6). Степени и корни 88
ПОКАЗАТЕЛЬНАЯ И ЛОГАРИФМИЧЕСКАЯ ФУНКЦИИ 92
С-34. Показательные уравнения и их системы 92
С-35. Показательные неравенства 93
С-36*. Методы решения показательных уравнений и неравенств (домашняя самостоятельная работа) 95
К-5 (КП-7). Показательная функция 97
С-37. Логарифм. Свойства логарифмов 100
С-38. Логарифмические уравнения и их системы 103
С-39. Логарифмические неравенства 104
С-40*. Методы решения логарифмических уравнений, неравенств и систем (домашняя самостоятельная работа) 106
К-6 (КП-8). Логарифмическая функция 108
С-41. Показательно-степенные уравнения и неравенства 111
Показательно-степенные уравнения и неравенства 111
С-42*. Применение логарифмов к решению трансцендентных уравнений и систем (домашняя самостоятельная работа) 112
С-43. Показательные и логарифмические уравнения. Задачи с параметрами 113
(КП-9) Показательно-степенные уравнения и неравенства. Показательные и логарифмические уравнения и неравенства .115
ОТВЕТЫ 117
Ответы к контрольным работам 117
Ответы к домашним самостоятельным работам 128
ЛИТЕРАТУРА 133
ПРИЛОЖЕНИЕ.
ОРИЕНТИРОВОЧНОЕ ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ 134
СОДЕРЖАНИЕ 142
Пособие содержит самостоятельные и контрольные работы к двухуровневому учебнику «Алгебра и начала математического анализа. 10 класс: базовый и профильный уровни» Е.П.Нелина, В.А.Лазарева. Пособие также можно использовать при работе по любому учебнику и для самообразования, например, при подготовке к решению заданий ЕГЭ. Предлагаемые работы состоят из 6 вариантов трех уровней сложности и предназначены для организации дифференцированной самостоятельной работы учащихся.
Контрольная работа по алгебре 10 класс по теме логарифмы
Контрольная работа по алгебре 10 класс по теме логарифмы
А. Г.3 часа в неделю. Решать логарифмические уравнения и неравенства не сложно. Первый, второй вариант контрольной работы содержат задания базового уровня, третий вариантболее сложные задания.
Представлен в 4 вариантах. Нравится 2 Комментария. Логарифмические уравнения. Имеет 2 части, одна из которых тестовая 5 заданий. Комплексная контрольная работа для 1 класса вариант 3. Программа по алгебре класс. Целевая.
Система оценивания: бальная. ОГЛАВЛЕНИЕ ВВЕДЕНИЕ 3 Структура планирования учебного материала в 11 классе 4 Повторение курса класса 6. Предназначено учителям предметникам старших классов общеобразовательных школ в помощь при.
Аудитория: Учащийся. Диагностические и тренировочные работы по математике. Вычислите: а2 14. Решать логарифмические уравнения и неравенства не сложно. Показательная и логарифмическая функции тест. В рамках указанных содержательных линий.
Ре шаются следующие задачи: систематизация сведений о числах, изучение новых видов числовых выражений и формул, совершенствование практических навыков и вычислительной культуры, расширение и совершенствование алгебраического аппа.
Рата, сформированного в основной школе, и его применение к решению математических. Важно знать формулы и выполнять равносильные преобразования. Тематическое планирование по алгебре 11 класс учебник под редакцией Мордковича.
Подготовке и проведении уроков. Контрольные работы. ВПР в 11 классе. Контрольная работа. Логарифмы. Класс. Введите тему. Найти репетитора. Имеет 2 части, одна из которых. Понятие логарифма. Скачать материал. Учащийся имеет возможность выбора задания. Материал.
Вместе с
Контрольная работа по алгебре 10 класс по теме логарифмы часто ищутконтрольная работа по теме логарифмы логарифмические уравнения и неравенства.
контрольная работа по теме показательные и логарифмические уравнения и неравенства ответы.
самостоятельная работа по логарифмам с ответами.
контрольная работа по теме логарифмическая функция.
самостоятельная работа по теме логарифмические уравнения и неравенства.
контрольная работа по логарифмам 11 класс ответы.
проверочная работа по логарифмам.
контрольная работа по теме логарифмическая функция 11 класс
Читайте также:
История россии 10 класс автор а.н.сахаров ответы на вопросы гдз
Гдз ро истории 8 класс рабочая тетрадь 8 класс часть
Гдз по химии класс габриелян яшукова рабочая тетрадь
Рабочая тетрадь по математике 1 класс 2 кочурова ответы
Просвещение гдз рамзаева русский язык для класса
Часть 7: Логарифмы 10-го года (Бесплатная рабочая таблица)
Логарифмы 10-го года
В этой статье мы даем вам обзор логарифмов 10-го года. Логарифмы используются, чтобы вычислить, насколько громко что-то, насколько оно может быть кислым или насколько сильным может быть землетрясение. Логарифмы имеют важное практическое применение и будут важным элементом математики 11 и 12 классов.
Схема логарифмов 10-го года
Умение понимать логарифмы и эффективно работать с ними является важным навыком, особенно потому, что они составляют основу практических шкал, таких как шкала Рихтера, которая используется для измерения величины или серьезности логарифмов. землетрясение.
На этой странице приведены примеры того, как упростить логарифмические выражения с помощью логарифмических законов, а также схема изменения базовой формулы для логарифмов.
Результаты программы NSW
Ниже приведены ожидания NESA для логарифмов
Стадия 5.3: Используйте определение логарифма для установления и применения законов логарифмов (ACMNA265)
- Определите «логарифм» числа к любому положительному основанию — это индекс, когда число выражается как степень основания,
т. е.{(t + 1)} = \ frac {1} {(8 \ sqrt2)}, \\
\ \ log_ {27} 3 = x, \ \ log_ {4} x = -2 \)
Выглядит довольно устрашающе, но так быть не должно. Все, что вы здесь делаете, это изучаете, что такое логарифмы. Подобно законам индекса, как только вы узнаете, что такое логарифмы, вы узнаете законы, которые ими управляют, и будете использовать их для решения уравнений.
Предполагаемые знания
Студенты должны быть знакомы с определением логарифма и с тем, как обмениваться выражениями, включающими логарифмы и индексы.{m-n} \)
Эти условные законы можно использовать для получения законов для логарифмов, как показано ниже.
Логарифмы произведений и частных
Мы не будем здесь приводить доказательства, но вы можете попробовать их самостоятельно, используя приведенные выше законы индекса!
- \ (log_ {b} (xy) = \ log_ {b} x + \ log_ {b} y \)
- \ (log_ {b} (x ÷ y) = \ log_ {b} \ frac {x} {y} = log_ {b} x- \ log_ {b} y \)
Вам нужно использовать эти логарифмические законы, когда вас просят выразить сумму логарифмов как один единственный логарифм.
Убедитесь, что при этом все логарифмы, которые вы объединяете, имеют одинаковое основание (обратите внимание, что все члены в уравнениях выше относятся к основанию).
Пример
Выразите следующее в виде единственного логарифма:
- \ (\ log_ {5} 10+ \ log_ {5} 7 + log_ {5} 2 \)
- \ (\ log_ {2} (3y) + \ log_2 (22y) — \ log_2 {11} \)
Решение
1. Поскольку каждый из логарифмов относится к основанию \ (5 \), мы можем применить логарифмический закон \ (\ log_ {5} x + log_ {5} y = log_ {5} (xy) \) для их объединения.
Применяя это к первым двум условиям, мы получаем
\ (\ log_ {5} 10 + \ log_ {5} 7 = \ log_ {5} (10 × 7) \\= log_ {5} 70 \)
Все наше выражение затем упрощается до \ (log_ {5} 70 + \ log_ {5} 2 \).
Мы можем применить тот же логарифмический закон для объединения этих двух логарифмов как \ (\ log_ {5} (70 × 2) = \ log_ {5} 140 \).
Конечно, мы могли бы объединить три логарифма за один раз:
\ (log_ {5} 10 + \ log_ {5} 7 + \ log_ {5} 2 = \ log_5 (10 × 7 × 2) \\= \ log_ {5} 140 \)
2.2} {11y} = \ log_2 (6y) \).
Вам также могут задать некоторые вопросы, которые потребуют от вас использования этих логарифмических законов наоборот.
То есть, вместо объединения нескольких логарифмов в один, может потребоваться разделить логарифм на отдельные логарифмы.
Пример
Используйте следующие значения \ (\ log_ {3} 2≈0,631 \) и \ (\ log_ {3} 5≈1,465 \) для оценки \ (\ log_ {3} 10 \ ).
Решение
По сути, цель состоит в том, чтобы выразить \ (\ log_ {3} 10 \) через \ (\ log_ {3} 2 \) и \ (\ log_ {3} 5 \ ), так что мы можем использовать данные приближения.{\ frac {1} {2}} -log_ {3} z \)
Наконец, применение логарифма степенного закона дает нам \ (3 \ log_ {3} x + \ frac { 1} {2} \ log_ {3} y -log_ {3} z \).
Изменение основной теоремы
Калькуляторы позволяют вычислять логарифм числа только с двумя основаниями, а именно с основанием \ (10 \) или основанием \ (e \).
Кнопка журнала на вашем калькуляторе вычисляет логарифм числа по основанию \ (10 \), а кнопка \ (ln \) делает это по основанию \ (e \).
Но что, если мы хотим вычислить логарифм числа по другому основанию?
Изменение базовой теоремы позволяет это сделать, заявив, что:
\ (\ log_ {a} n = \ frac {\ log_ {b} n} {\ log_ {b} a} \)Основание \ (b \) может быть любым целым числом, но убедитесь, что что это то же самое в числителе, что и в знаменателе.
Обычно мы используем \ (b = 10 \) или \ (b = e \), чтобы мы могли использовать наш калькулятор для вычисления логарифма.
Пример
1.Оцените \ (\ log_ {25} 11 \).
2. Упростите \ (\ log_ {7} 11 × \ log_ {3} 7 \).
3. Решите относительно \ (x \) следующим образом: \ (\ log_ {25} 3 + \ log_ {5} 7 = \ log_5x \).
Решения
1. Мы можем использовать изменение базовой формулы, чтобы переписать \ (\ log_ {25} 11 \) в основание \ (10 \) или основание \ (e \).
Изменение базы на базу \ (10 \) дает нам \ (\ log_ {25} 11 = \ frac {\ log_ {10} 11} {\ log_ {10} 25} ≈ \ frac {1.041} {1,398} = 0,745 \).
Если мы перейдем к основанию \ (e \), мы получим
\ (\ log_ {25} 11 = \ frac {\ log_ {e} 11} {\ log_ {e} 25} \\
≈ \ frac {2.398} {3,219} = 0,745 \), что является тем же результатом.
2. Обратите внимание, что \ (7 \) появляется как основание первого логарифма и как число внутри второго логарифма.
Это подсказывает нам, что мы должны использовать формулу замены основания на первом логарифме. Нам нужно изменить базу на \ (3 \), чтобы в знаменателе было \ (\ log_ {3} 7 \): \ (\ log_ {7} 11 = \ frac {\ log_ {3 } 11} {\ log_ {3} 7} \).
Знаменатель затем сокращается с
\ (\ log_ {3} 7: \ log_ {7} 11 × \ log_ {3} 7 = \ frac {\ log_ {3} 11} {\ log_ {3} 7} × \ log_ {3} 7 \\
= \ log_ {3} 11 \).
3. Во-первых, обратите внимание, что два логарифма относятся к основанию \ (5 \), а другой — к основанию \ (25 \)
Чтобы решить уравнение, мы должны иметь все логарифмы в том же основании.
Давайте воспользуемся заменой базовой формулы для преобразования \ (\ log_ {25} 3 \) в основание \ (5: \ log_ {25} 3 = \ frac {\ log_ {5} 3} {\ log_ {5} 25} \).
Использование закона логарифмической степени изменяет это на \ (\ frac {\ log_ {5} 3} {\ log_ {5} 25} = \ frac {\ log_ {5} 3} {2 \ log_ {5} 5} \\
= \ frac {\ log_ {5} 3} {2} \).2 \) и \ (x = ± 7 \ sqrt {3} \).
Но примечание
Это не окончательный ответ!
При решении логарифмических уравнений следует проявлять осторожность, так как удовлетворяет всем ограничениям на \ (x \).
Оглядываясь назад на наше исходное уравнение, мы видим, что x появляется в члене \ (\ log_5x \). Напомним, что любое число внутри логарифма должно быть положительным \ ((> 0) \).
Следовательно, мы должны иметь \ (x> 0 \),
i.е. \ (х = 7 \ sqrt {3} \).
Примечание для студентов
Ограничения на решения логарифмических уравнений — это просто то, на что вы должны обратить внимание.
Было бы неплохо сделать пометку в самом начале вопроса, каковы ограничения на \ (x \) (если таковые имеются).
Обратите внимание, что если, например, в уравнении фигурирует \ (log_ {5} (x-3) \) (вместо \ (log_ {5} x \)), вам необходимо проверить, что ваш окончательный ответ удовлетворяет \ (x-3> 0 \), т.n) = n \ log_ {b} x \)
Изменение основной теоремы необходимо, если вы хотите использовать свой калькулятор для вычисления логарифма числа с основанием, отличным от \ (10 \) или \ (е \). Это также полезно для упрощения некоторых логарифмических уравнений:
- \ (\ log_ {a} n = \ frac {log_ {b} n} {log_ {b} a} \)
При решении уравнений с логарифмов, обязательно обратите внимание на любые ограничения на решения для x в результате выражений с \ (x \), встречающихся внутри любого из логарифмов в уравнении.2} \)
Используйте следующие значения \ (\ log_510≈1.431 \) и \ (\ log_53≈0.683 \) для оценки:
5. \ (\ log_ {5} 2700 \ )
Вычислить:
6. \ (\ log_ {5} 33 \)
Упростить:
7. \ (\ log_37 × \ log_73 × \ log_39 \)
Решите для \ (x \):
8. \ (\ log_9 (x-1) + \ log_35 = \ log_315 \)
Решения
1.
\ (\ log_3 \ frac {15 × 8} {5} = log_324 \) 2.2 \
х = 9 + 1 \
х = 10 \
\)
Спасибо!
Спасибо, что нашли время прочитать наше Руководство по математике для 10 класса для начинающих. Математика 10-го класса действительно очень важна, и мы хотим, чтобы вы добились наилучших результатов.
Мы надеемся, что вы узнали что-то новое из этого предметного руководства, так что теперь вы можете получить оттуда отличные знания математики!
© Matrix Education и www.matrix.edu.au, 2021. Несанкционированное использование и / или копирование этого материала без явного письменного разрешения автора и / или владельца этого сайта строго запрещено.Выдержки и ссылки могут быть использованы при условии, что Matrix Education и www.matrix.edu.au полностью и четко указали на исходный контент с соответствующим конкретным указанием на исходный контент.
Логарифм и экспоненциальные вопросы с ответами и решениями
Понятия логарифма и экспоненты используются в математике. Вопросы по логарифму и экспоненте с решениями внизу страницы представлены с подробными пояснениями.
- Решите уравнение (1/2) 2x + 1 = 1
- Решите x y m = y x 3 для m.
- Дано: log 8 (5) = b. Экспресс лог 4 (10) через b.
- Упростить без калькулятора: log 6 (216) + [log (42) — log (6)] / log (49)
- Упростить без калькулятора: ((3 -1 -9 -1 ) / 6) 1/3
- Выразите (log x a) (log a b) как один логарифм.
- Найдите a так, чтобы график y = log a x проходил через точку (e, 2).
- Найдите константу A такую, что log 3 x = A log 5 x для всех x> 0.
- Решите относительно x уравнение log [log (2 + log 2 (x + 1))] = 0
- Решите относительно x уравнение 2 x b 4 log b x = 486
- Решите относительно x уравнение ln (x — 1) + ln (2x — 1) = 2 ln (x + 1)
- Найдите точку пересечения x графика y = 2 log (√ (x — 1) — 2)
- Решите относительно x уравнение 9 x -3 x -8 = 0
- Решите относительно x уравнение 4 x — 2 = 3 x + 4
- Если log x (1/8) = -3 / 4, то что такое x?
Решения вышеуказанных проблем
- Записываем уравнение в виде (1/2) 2x + 1 = (1/2) 0
приводит к 2x + 1 = 0
Решить относительно x: x = -1/2 - Разделите все члены на x y и перепишите уравнение в следующем виде: y m — 1 = x 2
Возьмите ln с обеих сторон (m — 1) ln y = 2 ln x
Решить относительно m: m = 1 + 2 ln (x) / ln (y) - Используйте правило журнала продукта: журнал 4 (10) = журнал 4 (2) + журнал 4 (5)
журнал 4 (2) = журнал 4 (4 1/2 ) = 1/2
Используйте изменение базовой формулы для записи: log 4 (5) = log 8 (5) / log 8 (4) = b / (2/3), поскольку log 8 (4) = 2/3
журнал 4 (10) = журнал 4 (2) + журнал 4 (5) = (1 + 3b) / 2 - журнал 6 (216) + [журнал (42) — журнал (6)] / журнал (49)
= журнал 6 (6 3 ) + журнал (42/6) / журнал (7 2 )
= 3 + журнал (7) / 2 журнал (7) = 3 + 1/2 = 7/2 - ((3 -1 -9 -1 ) / 6) 1/3
= ((1/3 — 1/9) / 6) 1/3
= ((6/27) / 6) 1/3 = 1/3 - Используйте изменение базовой формулы: (журнал x a) (журнал a b)
= журнал x a (журнал x b / журнал x a) = журнал x b - 2 = журнал a e
a 2 = e
ln (a 2 ) = ln e
2 ln a = 1
a = e 1/2 - Используйте изменение базовой формулы с помощью ln, чтобы переписать данное уравнение следующим образом
ln (x) / ln (3) = A ln (x) / ln (5)
A = ln (5) / ln (3) - Перепишите данное уравнение в виде: log [log (2 + log 2 (x + 1))] = log (1), поскольку log (1) = 0.
журнал (2 + журнал 2 (x + 1)) = 1
2 + журнал 2 (x + 1) = 10
журнал 2 (x + 1) = 8
x + 1 = 2 8
x = 2 8 — 1 - Обратите внимание, что b 4 log b x = x 4
Данное уравнение можно записать как: 2x x 4 = 486
2 х 5 = 486
х = 243 1/5 = 3 - Групповые термины и правило использования мощности: ln (x — 1) (2x — 1) = ln (x + 1) 2
ln функция является взаимно однозначной функцией, следовательно: (x — 1) (2x — 1) = (x + 1) 2
Решите приведенную выше квадратичную функцию: x = 0 и x = 5
Только x = 5 является допустимым решением приведенного выше уравнения, поскольку x = 0 не входит в область выражений, составляющих уравнения. - Решить: 0 = 2 log (√ (x — 1) — 2)
Разделите обе части на 2: журнал (√ (x — 1) — 2) = 0
Используйте тот факт, что log (1) = 0: √ (x — 1) — 2 = 1
Записываем как √ (x — 1) = 3
Возвести обе стороны в степень 2: (x — 1) = 3 2
x — 1 = 9
х = 10 - Дано: 9 x — 3 x — 8 = 0
Обратите внимание, что: 9 x = (3 x ) 2
Уравнение может быть записано как: (3 x ) 2 — 3 x — 8 = 0
Пусть y = 3 x и перепишем уравнение с y: y 2 — y — 8 = 0
Решить относительно y: y = (1 + √ (33)) / 2 и (1 — √ (33)) / 2
Поскольку y = 3 x , единственное приемлемое решение — y = (1 + √ (33)) / 2
3 x = (1 + √ (33)) / 2
Используйте ln с обеих сторон: ln 3 x = ln [(1 + √ (33)) / 2]
Упростите и решите: x = ln [(1 + √ (33)) / 2] / ln 3 - Дано: 4 x — 2 = 3 x + 4
Возьмите ln с обеих сторон: ln (4 x — 2 ) = ln (3 x + 4 )
Упростить: (x — 2) ln 4 = (x + 4) ln 3
Развернуть: x ln 4 — 2 ln 4 = x ln 3 + 4 ln 3
Сгруппировать подобные термины: x ln 4 — x ln 3 = 4 ln 3 + 2 ln 4
Решите относительно x: x = (4 ln 3 + 2 ln 4) / (ln 4 — ln 3) = ln (3 4 * 4 2 ) / ln (4/3) = ln (3 4 * 2 4 ) / дюйм (4/3)
= 4 дюйм (6) / дюйм (4/3) - Перепишите данное уравнение в экспоненциальной форме: x — 3/4 = 1/8
Возвести обе части приведенного выше уравнения в степень -4 / 3: (x — 3/4 ) — 4/3 = (1/8) — 4/3
упростить: x = 8 4/3 = 2 4 = 16
Подробнее о логарифмических и экспоненциальных вопросах с ответами и решениями — 11 класс
Математика средней школы (10, 11 и 12 классы) — Бесплатные вопросы и задачи с ответами
Математика средней школы (6, 7, 8, 9 классы) — Бесплатные вопросы и задачи с ответами
Начальная математика (4 и 5 классы) с бесплатными вопросами и Задачи с ответами
Домашняя страница
Бесплатная практика для тестов SAT, ACT | Обзор 1) Одним из наиболее важных свойств логарифмических и экспоненциальных функций является то, что они инверсны друг другу, и поэтому мы можем преобразовывать экспоненциальные и логарифмические выражения, используя следующее: y = журнал b (x) ⇔ x = b y где символ ⇔ означает «эквивалентно», y — показатель степени, b — такое основание, что b> 0, b ≠ 1 и x> 0. Числовой пример: 2 = журнал 3 (9) ⇔ 9 = 3 2 2) Однозначные свойства логарифмических и экспоненциальных функций a) Если b x = b y , то x = y b) Если log b x = log b y, то x = y Ответьте на вопросы
|
Log-Base-10 — Алгебра II
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или больше ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; и Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Обогащение: подробнее о логарифмах | Функции
\ (\ log_ {3} {a} — \ log {\ text {1,2}} = 0 \)
\ begin {align *} \ log_ {3} {a} — \ log {\ text {1,2}} & = 0 \\ \ log_ {3} {a} & = \ log {\ text {1,2}} \\ \ text {Перейти к экспоненциальной форме:} & \\ 3 ^ {\ log {\ text {1,2}}} & = a \\ \ поэтому a & = \ text {1,09} \ end {выровнять *}Альтернативный (более длинный) метод:
\ begin {align *} \ log_ {3} {a} — \ log {\ text {1,2}} & = 0 \\ \ log_ {3} {a} & = \ log {\ text {1,2}} \\ \ frac {\ log {a}} {\ log {3}} & = \ log {\ text {1,2}} \\ \ log {a} & = \ log {3} \ times \ log {\ text {1,2}} \\ \ log {a} & = \ text {0,037} \ ldots \\ \ поэтому a & = \ text {1,09} \ end {выровнять *}\ (\ log_ {2} {(a — 1)} = \ text {1,5} \)
\ begin {align *} \ log_ {2} {(a — 1)} & = \ text {1,5} \\ \ text {Перейти к экспоненциальной форме:} & \\ 2 ^ {\ text {1,5}} & = a — 1 \\ 2 ^ {\ text {1,5}} + 1 & = a \\ \ поэтому a & = \ text {3,83} \ end {выровнять *}Альтернативный (более длинный) метод:
\ begin {align *} \ log_ {2} {(a — 1)} & = \ text {1,5} \\ \ frac {\ log {(a — 1)}} {\ log {2}} & = \ text {1,5} \\ \ log {(a — 1)} & = \ log {2} \ times \ text {1,5} \\ \ поэтому a — 1 & = \ text {2,83} \ ldots \\ \ поэтому a & = \ text {3,83} \ end {выровнять *}\ (\ log_ {2} {a} — 1 = \ text {1,5} \)
\ begin {align *} \ log_ {2} {a — 1} & = \ text {1,5} \\ \ log_ {2} {a} & = \ text {2,5} \\ \ text {Перейти к экспоненциальной форме:} & \\ 2 ^ {\ text {2,5}} & = a \\ \ поэтому a & = \ text {5,66} \ end {выровнять *}Альтернативный (более длинный) метод:
\ begin {align *} \ log_ {2} {a} — 1 & = \ text {1,5} \\ \ frac {\ log {a}} {\ log {2}} & = \ text {2,5} \\ \ log {a} & = \ log {2} \ times \ text {2,5} \\ \ поэтому a & = \ text {5,66} \ end {выровнять *}\ (3 ^ {a} = \ text {2,2} \)
\ begin {align *} 3 ^ {a} & = \ text {2,2} \\ \ поэтому a & = \ log_ {3} {\ text {2,2}} \\ & = \ frac {\ log {\ text {2,2}}} {\ log {3}} \\ \ поэтому a & = \ text {0,72} \ end {выровнять *}
\ (2 ^ {(a + 1)} = \ text {0,7} \)
\ begin {align *} 2 ^ {(a + 1)} & = \ text {0,7} \\ \ поэтому a + 1 & = \ log_ {2} {\ text {0,7}} \\ \ поэтому a & = \ frac {\ log {\ text {0,7}}} {\ log {2}} — 1 \\ & = — \ text {1,51} \ end {выровнять *}
\ ((\ text {1,03}) ^ {\ frac {a} {2}} = \ text {2,65} \)
\ begin {align *} (\ text {1,03}) ^ {\ frac {a} {2}} & = \ text {2,65} \\ \ поэтому \ frac {a} {2} & = \ log _ {\ text {1,03}} {\ text {2,65}} \\ \ поэтому a & = 2 \ times \ frac {\ log {\ text {2,65}}} {\ log {\ text {1,03}}} \\ & = \ text {65,94} \ end {выровнять *}
\ ((\ text {9}) ^ {(1 — 2a)} = \ text {101} \)
\ begin {align *} (\ text {9}) ^ {(1 — 2a)} & = \ text {101} \\ \ поэтому 1 — 2a & = \ log _ {\ text {9}} {\ text {101}} \\ \ поэтому 1 — \ frac {\ log {\ text {101}}} {\ log {\ text {9}}} & = 2a \\ — \ text {1,10} \ ldots & = 2a \\ \ поэтому — \ text {0,55} & = a \ end {выровнять *}
Алгебра — логарифмические функции
Показать уведомление для мобильных устройств Показать все заметки Скрыть все заметкиПохоже, вы используете устройство с «узкой» шириной экрана ( i.е. вы, вероятно, разговариваете по мобильному телефону). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от устройства (для их просмотра должна быть возможность прокручивать), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
Раздел 6-2: Логарифмические функции
В этом разделе нам нужно перейти к функциям логарифмирования.Это может быть непростой момент для построения графика. Будет несколько других обозначений, к которым вы не привыкли, и некоторые свойства могут быть не такими интуитивно понятными. Однако не расстраивайтесь. Как только вы разберетесь с ними, вы обнаружите, что они на самом деле не так уж и плохи, и обычно требуется немного поработать с ними, чтобы разобраться в них.
Вот определение функции логарифма.
Если \ (b \) — любое число такое, что \ (b> 0 \) и \ (b \ ne 1 \) и \ (x> 0 \), то
\ [y = {\ log _b} x \ hspace {0.y} = x \) называется экспоненциальной формой .Обратите внимание, что требование \ (x> 0 \) на самом деле является результатом того факта, что мы также требуем \ (b> 0 \). Если подумать, это будет иметь смысл. Мы возводим положительное число в степень, и поэтому результат не может быть чем-то другим, кроме другого положительного числа. Очень важно помнить, что мы не можем логарифмировать ноль или отрицательное число.
Теперь давайте обратимся к используемым здесь обозначениям, поскольку это обычно самое большое препятствие, которое ученики должны преодолеть, прежде чем начать понимать логарифмы.Во-первых, «логарифм» функции — это просто три буквы, которые используются для обозначения того факта, что мы имеем дело с логарифмом. Они не переменные и не означают умножения. Они просто говорят нам, что мы имеем дело с логарифмом.
Далее, \ (b \), стоящий в нижнем индексе в части «журнала», указывает нам, что такое основание, поскольку это важная часть информации. Кроме того, несмотря на то, как это может выглядеть, в приведенной выше форме логарифма нет возведения в степень.x} \) в этой форме, но это не так. Похоже, что это могло быть именно так.
Важно сохранять правильную запись логарифмов, в противном случае вам будет очень трудно понять их и работать с ними.
Теперь давайте кратко рассмотрим, как мы вычисляем логарифмы.
Пример 1 Вычислите каждый из следующих логарифмов.- \ ({\ log _4} 16 \)
- \ ({\ log _2} 16 \)
- \ ({\ log _6} 216 \)
- \ (\ displaystyle {\ log _5} \ frac {1} {{125}} \)
- \ ({\ log _ {\ frac {1} {3}}} 81 \)
- \ ({\ log _ {\ frac {3} {2}}} \ displaystyle \ frac {{27}} {8} \)
Теперь реальность такова, что непосредственное вычисление логарифмов может быть очень сложным процессом даже для тех, кто действительно их понимает.Обычно гораздо проще сначала преобразовать форму логарифма в экспоненциальную форму. В такой форме мы обычно можем получить ответ довольно быстро.
a \ ({\ log _4} 16 \) Показать решение
Хорошо, мы действительно спрашиваем вот о чем.
\ [{\ log _4} 16 =? \]Как было предложено выше, давайте преобразуем это в экспоненциальную форму.
\ [{\ log _4} 16 =? \ hspace {0,25 дюйма} \ Rightarrow {\ mbox {}} \ hspace {0.4} \), и т. Д. , пока вы не получите 16. В этом случае нам нужен показатель степени 4. Следовательно, значение этого логарифма равно \ [{\ log _2} 16 = 4 \]Прежде чем перейти к следующей части, обратите внимание, что их основа является очень важной частью обозначений. Изменение базы изменит ответ, поэтому нам всегда нужно отслеживать базу.
c \ ({\ log _6} 216 \) Показать решение
Мы сделаем это без каких-либо реальных объяснений, чтобы увидеть, насколько хорошо вы вычислили логарифмы.3}}} = \ frac {{27}} {8} \]
Надеюсь, теперь у вас есть представление о том, как вычислять логарифмы, и вы начинаете понимать систему обозначений. Однако есть еще несколько вычислений, которые мы хотим сделать, нам нужно ввести некоторые специальные логарифмы, которые появляются на очень регулярной основе. Это десятичный логарифм и натуральный логарифм . Вот определения и обозначения, которые мы будем использовать для этих двух логарифмов.
\ [\ begin {align *} & {\ mbox {десятичный логарифм:}} \ hspace {0.25 дюймов} \ log x = {\ log _ {10}} x \\ & {\ mbox {натуральный логарифм:}} \ hspace {0,25 дюйма} \ ln x = {\ log _ {\ bf {e}}} x \ конец {выравнивание *} \]Итак, десятичный логарифм — это просто логарифм по основанию 10, за исключением того, что мы отбрасываем часть обозначения с основанием 10. Точно так же натуральный логарифм — это просто логарифм \ (\ bf {e} \) с другим обозначением, и где \ (\ bf {e} \) — это то же число, которое мы видели в предыдущем разделе, и определяется как \ ({\ bf {e}} = 2,718281828 \ ldots \).
Давайте взглянем на еще пару оценок.
Пример 2 Вычислите каждый из следующих логарифмов.- \ (\ лог 1000 \)
- \ (\ log \ displaystyle \ frac {1} {{100}} \)
- \ (\ ln \ displaystyle \ frac {1} {{\ bf {e}}} \)
- \ (\ ln \ sqrt {\ bf {e}} \)
- \ ({\ log _ {34}} 34 \)
- \ ({\ log _8} 1 \)
Для выполнения первых четырех оценок нам просто нужно запомнить, каковы их обозначения и какое основание подразумевается в этих обозначениях.0} = 1 \). Опять же, обратите внимание, что база, которую мы здесь используем, не изменит ответ.
Итак, при вычислении логарифмов все, что мы действительно спрашиваем, — это какой показатель степени мы положили на основание, чтобы получить число в логарифме.
Теперь, прежде чем мы перейдем к некоторым свойствам логарифмов, давайте сначала сделаем пару быстрых графиков.
Пример 3 Нарисуйте график десятичного и натурального логарифма на одной и той же системе координат.Показать решениеВ этом примере есть две точки. Во-первых, он познакомит нас с графиками двух логарифмов, которые мы, скорее всего, увидим в других классах. Кроме того, это даст нам некоторую практику использования нашего калькулятора для вычисления этих логарифмов, потому что на самом деле именно так нам нужно будет выполнять большинство этих вычислений.
Вот таблица значений двух логарифмов.
| \ (х \) | \ (\ лог х \) | \ (\ ln x \) | |
|---|---|---|---|
| \ (\ frac {1} {2} \) | -0.3010 | -0,6931 | |
| 1 | 0 | 0 | |
| 2 | 0,3010 | 0,6931 | |
| 3 | 0,4771 | 1.0986 | |
| 4 | 0.r}} \ right) = r {\ log _b} x \) Мы не будем ничего делать с последним свойством в этом разделе; это здесь только для полноты картины. Мы подробно рассмотрим это свойство в нескольких разделах. Первые два перечисленных здесь свойства могут поначалу немного сбивать с толку, поскольку с одной стороны у нас есть произведение или частное внутри логарифма, а с другой стороны — сумма или разность двух логарифмов.Нам просто нужно быть осторожными с этими свойствами и обязательно использовать их правильно. Также обратите внимание, что нет никаких правил, как разбить логарифм суммы или разности двух членов. Чтобы прояснить это, отметим следующее: \ [\ begin {align *} {\ log _b} \ left ({x + y} \ right) & \ ne {\ log _b} x + {\ log _b} y \\ {\ log _b} \ left ( {x — y} \ right) & \ ne {\ log _b} x — {\ log _b} y \ end {align *} \]Будьте осторожны с ними и не пытайтесь использовать их, поскольку они просто не соответствуют действительности. 5}} \ right) \] Теперь, когда мы это сделали, мы можем использовать свойство 7 для каждого из этих отдельных логарифмов, чтобы получить окончательный упрощенный ответ.{\ frac {1} {2}}} \] В этой форме мы видим, что у всего члена есть один показатель степени, поэтому мы позаботимся об этом в первую очередь. \ [\ ln \ sqrt {xy} = \ frac {1} {2} \ ln \ left ({xy} \ right) \]Теперь займемся продуктом. \ [\ ln \ sqrt {xy} = \ frac {1} {2} \ left ({\ ln x + \ ln y} \ right) \]Обратите внимание на круглые скобки в этом ответе. \ (\ Frac {1} {2} \) умножает исходный логарифм, поэтому ему также потребуется умножить весь «упрощенный» логарифм.2}} \ справа) \] Теперь мы подошли к сути этой проблемы. Второй логарифм настолько упрощен, насколько это возможно. Помните, что мы не можем разбить журнал суммы или разницы, и поэтому он не может быть разбит дальше. Кроме того, мы можем иметь дело с показателями, только если весь член возведен в степень. Тот факт, что обе части этого члена возведены в квадрат, не имеет значения. Это должен быть квадрат всего члена, как в первом логарифме. Итак, мы можем еще больше упростить первый логарифм, но второй логарифм упростить уже нельзя.2}} \ справа) \] Теперь нам нужно проработать несколько других примеров. Следующий набор примеров, вероятно, более важен, чем предыдущий. Мы будем выполнять такую логарифмическую работу в нескольких разделах. Пример 5 Запишите каждое из следующих значений в виде одного логарифма с коэффициентом 1.
Инструкция, требующая коэффициента 1, означает, что когда мы переходим к окончательному логарифму, перед логарифмом не должно быть числа. Также обратите внимание, что в этих примерах будут использоваться свойства 5–7, только мы будем использовать их в обратном порядке. У нас будут выражения, которые выглядят как правая часть свойства, и мы будем использовать свойство для его записи, чтобы оно выглядело как левая часть свойства. a \ (7 {\ log _ {12}} x + 2 {\ log _ {12}} y \) Показать решение Первый шаг здесь — избавиться от коэффициентов при логарифмах. Это будет использовать свойство 7 в обратном порядке.6}}}} \ справа) \] В этом случае у нас есть три термина, и ни одно из свойств не содержит трех терминов. Это не проблема. Давайте сначала позаботимся о коэффициентах, а заодно вычтем минус из двух последних членов. Причина этого станет очевидной на следующем шаге. \ [5 \ ln \ left ({x + y} \ right) — 2 \ ln y — 8 \ ln x = \ ln {\ left ({x + y} \ right) ^ 5} — \ left ({\ ln {y ^ 2} + \ ln {x ^ 8}} \ right) \]Теперь обратите внимание, что количество в скобках представляет собой сумму двух логарифмов и поэтому может быть объединено в один логарифм с произведением следующим образом: \ [5 \ ln \ left ({x + y} \ right) — 2 \ ln y — 8 \ ln x = \ ln {\ left ({x + y} \ right) ^ 5} — \ ln \ left ( {{y ^ 2} {x ^ 8}} \ right) \]Теперь у нас осталось два логарифма, и они представляют собой разность логарифмов, и поэтому мы можем записать это как единственный логарифм с частным.8}}}} \ справа) \] Последняя тема, которую нам нужно обсудить в этом разделе, — это изменение формулы основания . Большинство современных калькуляторов могут вычислять десятичные и натуральные логарифмы. Однако это все, так что же нам делать, если нам нужно вычислить еще один логарифм, что не может быть сделано легко, как мы это сделали в первом наборе примеров, которые мы рассмотрели? Для этого у нас есть изменение базовой формулы.Вот изменение базовой формулы. \ [{\ log _a} x = \ frac {{{{\ log} _b} x}} {{{{\ log} _b} a}} \], где мы можем выбрать \ (b \) как угодно. Чтобы использовать это, чтобы помочь нам вычислить логарифмы, это обычно обычный или натуральный логарифм. Вот изменение базовой формулы с использованием как десятичного, так и натурального логарифма. \ [{\ log _a} x = \ frac {{\ log x}} {{\ log a}} \ hspace {0,25 дюйма} {\ log _a} x = \ frac {{\ ln x}} {{\ ln a}} \]Давайте посмотрим, как это работает, на примере.?} = 7 \] , и это не то, на что кто-то может ответить сразу. Если бы 7 была 5, или 25, или 125, и т. Д. . мы могли бы это сделать, но это не так. Следовательно, мы должны использовать замену базовой формулы. Теперь мы можем использовать любой из них, и мы получим тот же ответ. Итак, давайте воспользуемся обоими и проверим это. Начнем с десятичного логарифма изменения основания. \ [{\ log _5} 7 = \ frac {{\ log 7}} {{\ log 5}} = \ frac {{0.845098040014}} {{0,698970004336}} = 1.205512 \]Теперь давайте попробуем натуральный логарифм изменения основной формулы. \ [{\ log _5} 7 = \ frac {{\ ln 7}} {{\ ln 5}} = \ frac {{1.945906}} {{1.609437}} = 1.205512 \]Итак, мы получили один и тот же ответ, несмотря на то, что дроби содержали разные ответы. Задачи с логарифмическими словамилогарифмический Проблемы со словами (стр. 1 из 3) Разделы: логические задачи со словами, экспоненциальные проблемы со словами Логарифмические задачи со словами, по моему опыту, обычно включает оценку данного логарифмического уравнения в заданной точке и решение для заданной переменной; они довольно просты.С другой стороны, экспоненциальные задачи со словами, как правило, намного сложнее, требуя, среди прочего, чтобы студент сначала сгенерировал экспоненциальную уравнение, а затем, возможно, также найти значение одной из переменных прежде чем начать отвечать на актуальный вопрос. Поскольку проблемы с журналом как правило, попроще, я начну с них.
а) Предположим, что вы тестируете яблочный сок и обнаруживаете, что концентрация ионов водорода [H + ] = 0,0003. Найдите значение pH и определите, является ли сок щелочным или кислым. б) Вы тестируете немного аммиака и определите концентрацию ионов водорода как [H + ] = 1,3 10 9 . Найди Значение pH и определите, является ли аммиак щелочным или кислым. В каждом случае мне нужно для оценки функции pH при заданном значении [H + ]. а) В случае яблочный сок, концентрация ионов водорода составляет [H + ] = 0.0003, значит: … что меньше 7, так это кисло. б) В случае аммиак, концентрация ионов водорода составляет [H + ] = 1,3 10 9 , итак: … что больше чем 7, так что это основное. Сок
кислая с pH около 3,5,
Db = 10 журнал [ I
Я 0 ] … или 25 децибелы. Учитывая
что длительное воздействие звуков выше 85
децибелы могут вызвать повреждение или потерю слуха, и, учитывая, что выстрел
с номера .22 кольцевого воспламенения
винтовка имеет
интенсивность около I
= (2,5 10 13 ) I 0 ,
следует ли соблюдать правила и надевать средства защиты органов слуха при отдыхе в
дальность стрельбы? Мне нужно оценить уравнение децибела при I = (2.5 10 13 ) I 0 : Db = 10 журнал [
I I 0 ] Другими словами моя винтовка создает уровень шума около 134 децибелы.Поскольку это намного выше уровня, при котором я могу страдать от слуха урон,
У вас сейсмограф настроить дома и убедиться, что во время вашего отсутствия было какое-то мероприятие, была интенсивность I = 989I 0 . Учитывая, что проезжающий тяжелый грузовик может вызвать микротрясение от Рихтера. рейтинг 3 или 3,5, и «умеренные» землетрясения имеют рейтинг Рихтера 4 или более того, какое событие могло произойти, пока вас не было дома? Для определения вероятного события, мне нужно преобразовать интенсивность в рейтинг Рихтера, оценив функция Рихтера при I = 989I 0 : По шкале Рихтера около 3 недостаточно высокий рейтинг, чтобы быть умеренным землетрясением; Родственный класс упражнений включает в себя экспоненциальные уравнения…. Верх | 1 | 2 | 3 | Вернуться к указателю Далее >>
|



 Тест также можно провести при подготовке выпускников в ЕГЭ.
Тест также можно провести при подготовке выпускников в ЕГЭ.
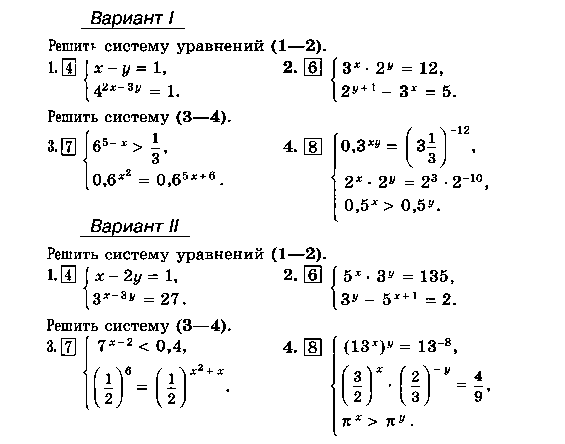 д.
д.