Геометрия 10 класс Контрольная № 5 с ответами
Контрольная работа по геометрии в 10 классе «Векторы в пространстве» в форме зачета с ответами и решениями (2 уровня сложности по 2 варианта). УМК Атанасян и др. (Просвещение). Поурочное планирование по геометрии для 10 класса (В.А. Яровенко, ВАКО). Урок 62. Геометрия 10 класс Контрольная № 5 «Векторы в пространстве».
Смотреть Список всех контрольных по геометрии в 10 классе (Атанасян)
Контрольная работа № 5 (зачет)
«Векторы в пространстве»
Цель: проверить знания, умения и навыки учащихся по теме.
Тип урока: урок контроля, оценки и коррекции знаний.
ХОД УРОКА
1. Организационный момент
Мотивация к учебной деятельности. Учитель сообщает тему урока, формулирует цели урока.
2. Контрольная работа
Задания I уровня сложности
Вариант 1
- Вопрос.

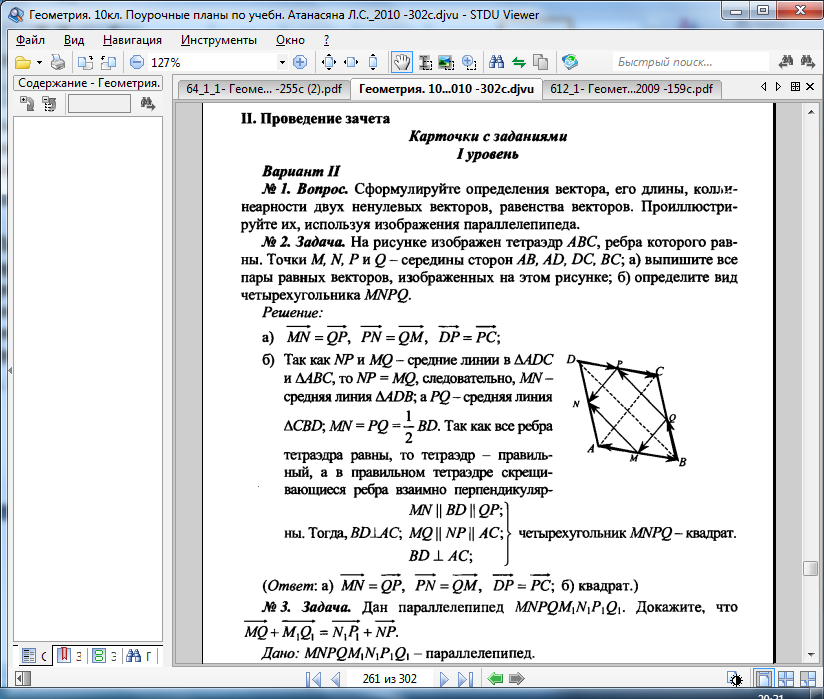
- Задача. На рисунке изображен тетраэдр АВС, ребра которого равны. Точки М, N, P и Q — середины сторон АВ, AD, DC, ВС;
а) выпишите все пары равных векторов, изображенных на этом рисунке;
б) определите вид четырехугольника MNPQ. - Задача. Дан параллелепипед MNPQM1N1P1Q1. Докажите, что .
Вариант 2
- Вопрос. Расскажите о правиле треугольника сложения двух векторов. Проиллюстрируйте эти правила на рисунке.
- Задача. Упростите выражение: .
- Задача. Дан параллелепипед MNPQM1N1P1Q1. Докажите, что
Задания II уровня сложности
Вариант 1
- Вопрос.
 Расскажите о правиле параллелограмма сложения двух векторов. Проиллюстрируйте это правило на рисунке.
Расскажите о правиле параллелограмма сложения двух векторов. Проиллюстрируйте это правило на рисунке. - Задача. Дана треугольная призма АВСА1В1С1. Укажите вектор
- Задача. Основанием пирамиды с вершиной О является параллелограмм ABCD, диагонали которого пересекаются в точке М. Разложите векторы по векторам .
Вариант 2
- Вопрос. Расскажите о правиле многоугольника сложения нескольких векторов. Проиллюстрируйте его на рисунке.
- Задача. Дана треугольная призма АВСА1В1С1. Укажите вектор х, начало и конец которого являются вершинами призмы, такой, что .
- Задача. Точка К — середина ребра В1С1 куба ABCDA1B1C1D.
 Разложите вектор по векторам и найдите длину этого вектора, если ребро куба равно m.
Разложите вектор по векторам и найдите длину этого вектора, если ребро куба равно m.
Задания III уровня сложности
Вариант 1
- Вопрос. Сформулируйте определение произведения вектора а на число k, сочетательный, первый и второй распределительные законы умножения вектора на число. Проиллюстрируйте их на примерах.
- Задача. На рисунке изображен правильный октаэдр. Докажите, что .
- Задача. Точки А1, В1, С1 — середины сторон ВС, АС, АВ треугольника АВС, точка О — произвольная точка пространства. Докажите, что .
Вариант 2
- Вопрос. Сформулируйте определение компланарных векторов. Приведите примеры компланарных и некомпланарных векторов, используя изображение параллелепипеда.
- Задача.
 Дан параллелепипед
Дан параллелепипед - Задача. В тетраэдре ABCD точка К — середина медианы ВВ1 грани BCD. Разложите вектор по векторам .
3. Рефлексия учебной деятельности (Решения и Ответы)
В конце урока учитель раздает на каждую парту краткую запись решения задач контрольной работы.
Домашнее задание: решить задачи, с которыми ученик не справился.
Решение задач I уровня сложности.
Вариант 1
Решение задач I уровня сложности.
Вариант 2
Решение задач II уровня сложности.
Вариант 1
Решение задач II уровня сложности.
Вариант 2
Решение задач III уровня сложности.
Вариант 1
Решение задач III уровня сложности.
Вариант 2
Вы смотрели: Геометрия 10 класс Контрольная № 5. Поурочное планирование по геометрии для 10 класса. УМК Атанасян (Просвещение). Урок 62. Контрольная работа по геометрии «Векторы в пространстве» + ОТВЕТЫ.
Смотреть Список всех контрольных по геометрии в 10 классе по УМК Атанасян.
Контрольная работа по геометрии «Векторы в пространстве»
Вариант №1
1. В параллелепипеде ABCD A1B1C1D1 укажите векторы, противоположно направленные вектору и имеющие такую же длину. 1) и 2) и 3) и 4) и
2. Дан параллелепипед ABCD A1B1C1D1 .
3. Вектор разложен по трем некомпланарным векторам Найдите разложение вектора по векторам и. 1) 2) 3) 4)
1) 2) 3) 4)
4. В пирамиде SАВС все ребра равны, апофема равна 18 Точка Е и АЕ:ЕS = 2:1, точка FAB и BF : FA = 1:2. Найдите ||. 1)22 2)16 3)8 4)24
5. Дан куб ABCD A1B1C1D1 с ребром, равным a. Точка Е и АЕ:Е = 1: 2, точка F C1 и CF : FC1 = 2 : 3. Разложите вектор по векторам и и найдите его длину.
Вариант №2
2. В тетраэдре АВСD: =8. Найдите величину . 1) 1; 2) 2; 3)8; 4)11
3. Упростите выражение: 3(2 3) + 5( ) 2()
4. В пирамиде SАВС все ребра равны, апофема равна 18 Точка Е и АЕ:ЕS = 2:1, точка FAB и BF : FA = 1:2. Найдите ||.
5. Ребро куба ABCD A1B1C1D1 равно 3. Найдите величины: +| и
Вариант №3
1. В параллелепипеде ABCD A1B1C1D1 укажите векторы, coнаправленные вектору и имеющие такую же длину.
2. В тетраэдре АВСD: =5. Найдите величину . 1) 12; 2) 2; 3)3; 4)4
3. Дан куб ABCD A1B1C1D1 с ребром, равным a. Вычислите. 1) 3 a; 2) 2 a; 3) a; 4) a
4. Вектор разложен по трем некомпланарным векторам Найдите разложение вектора по векторам и. 1) 2) 3) 4)
5. Векторы и некомпланарны, точка К лежит в плоскости треугольника АВС. Найдите значение числа х, если .
Вариант №4
2. Дан параллелепипед ABCD A1B1C1D1 . Упростите сумму . Укажите полученный вектор. 1) ; 2) 3) 4)
1. В параллелепипеде ABCD A1B1C1D1 укажите векторы, coнаправленные вектору и имеющие такую же длину. 1) и 2) и 3) и 4) и
3. Дан куб ABCD A1B1C1D1 с ребром, равным b. Вычислите. 1) 3b; 2) 2 b; 3) b; 4) b
4. В пирамиде SАВС все ребра равны, апофема равна 18 Точка Е и АЕ:ЕS = 2:1, точка FAB и BF : FA = 1:2. Найдите |EF|.
В пирамиде SАВС все ребра равны, апофема равна 18 Точка Е и АЕ:ЕS = 2:1, точка FAB и BF : FA = 1:2. Найдите |EF|.
5. Дан куб ABCD A1B1C1D
Векторы в пространстве. Геометрия, 10 класс: уроки, тесты, задания.
Вход- org/BreadcrumbList»>
- Предметы
- Геометрия
- 10 класс
-
Понятие вектора в пространстве
-
Сложение и вычитание векторов.
 Умножение вектора на число
Умножение вектора на число
-
Компланарные векторы
Контрольная работа по геометрии 9 класс «Векторы»
Нужно рассматривать векторы с привязкой к координатам, выйдите немного за пределы программы. Кому, кроме школы нужна терминология? Нужны знания, востребованные жизнью и инженерной практикой. А в учебнике этих знаний нет. Постройте хоть один вектор по координатам, это гораздо важнее всех определений. Покажите, как измерять расстояние между точками на плоскости, как применить это для решения реальных задач. Покажите связь с формулой прямой линии, как с помощью формулы y = kx + b найти точку пересечения отрезков, векторов на плоскости. Это пригодится в век 3D технологий, а определения из «мертвого» учебника никому в жизни не нужны. Пусть попробуют доказать теорему Пифагора через использование координат, от этого хоть толк будет, так как здесь нужны знания, которые можно использовать в жизни. Именно координаты связывают геометрию с алгеброй, физикой, черчением, технологией. Не изучают в приведенных науках за ненадобностью коллинеарность и сонаправленность. Надо изучать не математику ради математики, а ее связь с другими науками. Векторы это важная тема, это шаг к матрицам, которые состоят из векторов.
Кому, кроме школы нужна терминология? Нужны знания, востребованные жизнью и инженерной практикой. А в учебнике этих знаний нет. Постройте хоть один вектор по координатам, это гораздо важнее всех определений. Покажите, как измерять расстояние между точками на плоскости, как применить это для решения реальных задач. Покажите связь с формулой прямой линии, как с помощью формулы y = kx + b найти точку пересечения отрезков, векторов на плоскости. Это пригодится в век 3D технологий, а определения из «мертвого» учебника никому в жизни не нужны. Пусть попробуют доказать теорему Пифагора через использование координат, от этого хоть толк будет, так как здесь нужны знания, которые можно использовать в жизни. Именно координаты связывают геометрию с алгеброй, физикой, черчением, технологией. Не изучают в приведенных науках за ненадобностью коллинеарность и сонаправленность. Надо изучать не математику ради математики, а ее связь с другими науками. Векторы это важная тема, это шаг к матрицам, которые состоят из векторов. А без использования матриц сегодня нельзя представить ни одну науку, включая гуманитарные направления. С помощью координат многие даже олимпиадные задачи по геометрии решаются проще. Когда даете методы по теме «Векторы» из учебника, то говорите, что метод параллелограмма это ЭКВИВАЛЕНТНЫЙ метод, так как в жизни никто вектора не переносит в любую точку пространства, иначе может оказаться, что сила может быть приложена к другому объекту в пространстве, а это абсурд. Правильно говорить только о проекции векторов, все остальное с точки зрения физики приложения сил, скоростей, ускорений к объекту в пространстве смысла не имеет(не может сила одного объекта приложена к другому объекту в пространстве, если они лежат, например, на разных поверхностях). А по учебнику геометрии может — фантастика это уже другой предмет, другая область знаний.
А без использования матриц сегодня нельзя представить ни одну науку, включая гуманитарные направления. С помощью координат многие даже олимпиадные задачи по геометрии решаются проще. Когда даете методы по теме «Векторы» из учебника, то говорите, что метод параллелограмма это ЭКВИВАЛЕНТНЫЙ метод, так как в жизни никто вектора не переносит в любую точку пространства, иначе может оказаться, что сила может быть приложена к другому объекту в пространстве, а это абсурд. Правильно говорить только о проекции векторов, все остальное с точки зрения физики приложения сил, скоростей, ускорений к объекту в пространстве смысла не имеет(не может сила одного объекта приложена к другому объекту в пространстве, если они лежат, например, на разных поверхностях). А по учебнику геометрии может — фантастика это уже другой предмет, другая область знаний.
В целом хорошо подготовленная работа.
1. |
2. Как называется вторая по величине планета в нашей солнечной системе? |
3. Какая планета в нашей солнечной системе самая горячая? |
4. Какая планета известна своим большим красным пятном на ней? |
5.Какая планета славится окружающими ее красивыми кольцами? |
6. Могут ли люди нормально дышать в космосе, как на Земле? |
7. Солнце — звезда или планета? |
8. Кто был первым человеком, ступившим на Луну? |
9. Какая планета известна как красная планета? |
10.Как называется сила, удерживающая нас на Земле? |
11. |
12. Как называется место, в котором для исследования космоса и астрономии используются телескопы и другое научное оборудование? |
13. Как называется самый известный космический телескоп НАСА? |
14.В какой галактике находится Земля? |
15. Как называется первый спутник, отправленный в космос? |
16. Ганимед является спутником какой планеты? |
17. Как называется самый большой спутник Сатурна? |
18. На какой планете гора Олимп — большая вулканическая гора? |
19.Солнце вращается вокруг Земли? |
20. |
Компания Vector Space осуществила первый испытательный запуск малой ракеты-спутника
Небольшая ракета, предназначенная для доставки в космос особо небольших грузов, совершила свой первый испытательный полет сегодня (3 мая) из Мохаве, штат Калифорния.
Поставщик коммерческих запусков Vector Space Systems успешно запустил инженерный образец ракеты-носителя Vector-R компании вскоре после 12:00.м. PDT (15:00 по восточноевропейскому времени / 19:00 по Гринвичу) с сайта Друзья любительской ракетной техники (FAR) в Мохаве, Калифорния. Модель состояла из двигателя первой ступени Vector-R и напечатанного на 3D-принтере инжектора. Ракета должна была достичь высоты 4500 футов (1370 метров).
Ракета Vector-R предназначена для полета с полезной нагрузкой до 130 фунтов. (60 кг) на низкую околоземную орбиту, что делает этот аппарат идеальным для запуска «микроспутников», подкласса малых спутников, которые весят от 22 до 220 фунтов. (10 и 100 кг), по данным НАСА. Компания планирует начать коммерческие запуски в 2018 году, а этим летом планирует провести дополнительный испытательный полет. [Вектор космических испытаний ракетных технологий для запусков микроспутников | Видео]
(10 и 100 кг), по данным НАСА. Компания планирует начать коммерческие запуски в 2018 году, а этим летом планирует провести дополнительный испытательный полет. [Вектор космических испытаний ракетных технологий для запусков микроспутников | Видео]
«2017 год уже стал новаторским для Vector, поскольку мы продолжаем испытания полномасштабных инженерных моделей транспортных средств, чтобы продемонстрировать функциональность и летные операции», — сказал Джим Кантрелл, соучредитель и генеральный директор Vector в пресс-релизе компании. . «Успех этого испытания не только устанавливает стандарт для быстрой мобильной разработки наших ракет-носителей, но также способствует нашей миссии по революционному преобразованию космической индустрии и увеличению скорости выхода на орбиту.»
Микроспутниковая ракета Vector Space Systems Vector-R, показанная здесь перед испытательным запуском в Мохаве, Калифорния. (Изображение предоставлено Vector Space Systems)Малые спутники
Возможности малых спутников, таких как кубесаты, некоторые из размером с коробку для завтрака — быстро увеличивается, поскольку компании и космические агентства заинтересованы в использовании космических аппаратов для таких приложений, как получение изображений Земли и связь. Но эти небольшие спутники обычно попадают в космос, «совмещая» большие полезные нагрузки, отправляемые в космос массивными ракетами.Такие компании, как Vector, хотят, чтобы операторы малых спутников могли отправлять эти полезные нагрузки в космос чаще и независимо от более крупных.
Но эти небольшие спутники обычно попадают в космос, «совмещая» большие полезные нагрузки, отправляемые в космос массивными ракетами.Такие компании, как Vector, хотят, чтобы операторы малых спутников могли отправлять эти полезные нагрузки в космос чаще и независимо от более крупных.
«Вектор — первая ракета-носитель, созданная исключительно для рынка микроспутников», — говорится на сайте компании. «Этот аппарат« подходящего размера »для нового поколения микроспутников и обеспечивает надежный и частый выход на орбиту».
Компания планирует произвести 12 коммерческих запусков с Vector-R в 2019 г. и до 100 запусков в год на полной пусковой мощности.Vector также работает над ракетой Vector-H (Vector Heavy), которая будет нести полезную нагрузку до 275 фунтов. (125 кг) на околоземную орбиту. Vector недавно объявила о своих планах запустить Vector-R со стартового комплекса 46 (LC 46) на авиабазе Кейп-Канаверал во Флориде, который находится в ведении агентства экономического развития Space Florida, поддерживаемого государством.
Детали, напечатанные на 3D-принтере
Компания Vector разработала напечатанный на 3D-принтере инжектор двигателя с помощью НАСА. Согласно сообщению Vector, компания выиграла грант в рамках программы полетных возможностей Управления науки, технологий и миссий НАСА (STMD), которая «расширяет исследовательские лаборатории [НАСА] на космическую среду за счет партнерства с небольшими компаниями по запуску спутников».
Грант позволил компании Vector разработать и протестировать моноблочный инжектор, созданный с использованием технологии, называемой аддитивным производством (также известной как 3D-печать). Вместо того, чтобы производить различные части инжектора и затем прикреплять их к готовому инструменту, подход аддитивного производства позволяет производить инжектор как единое оборудование.
«Благодаря этой успешной эксплуатации аддитивного инжектора в полете мы перешли на новый уровень развития этой технологии для малых ракет-носителей», — сказал Джон Пежо, руководитель проекта по аддитивному производству 3D (AM), работает с Vector над его форсункой, говорится в пресс-релизе, касающемся сегодняшнего испытательного полета. «Это представляет собой важный шаг в продвижении оборудования AM за пределы лабораторных испытаний и его квалификации для реальных приложений».
«Это представляет собой важный шаг в продвижении оборудования AM за пределы лабораторных испытаний и его квалификации для реальных приложений».
Следуйте за Каллой Кофилд @callacofield. Следуйте за нами @Spacedotcom, Facebook и Google+. Оригинальная статья на Space.com.
Определение того, является ли набор векторным пространством
Мы рассмотрели множество различных векторных пространств, в том числе:
Теперь мы рассмотрим некоторые надуманные примеры множеств при определенных операциях сложения и скалярного умножения и определим, являются ли они векторными пространствами.2 $, и пусть $ u, v \ in \ mathbb {V} $ такие, что $ u = (u_1, u_2) $ и $ v = (v_1, v_2) $. Определите компонентное сложение, то есть $ u + v = (u_1 + v_1, u_2 + v_2) $, и определите скалярное умножение на $ a \ in \ mathbb {F} $ как $ au = (au_1, 0) $. Определите, является ли этот набор при этих операциях векторным пространством.
Сначала отметим, что сложение векторов $ u + v $ определяется как стандартное сложение, однако умножение стандартно не определяется. Пусть $ u $ — вектор, вторая компонента которого отлична от нуля, то есть $ u_2 \ neq 0 $, и рассмотрим существование мультипликативного тождества $ 1 $, такого что $ 1 u = u $.2 $, и пусть $ u, v, w \ in \ mathbb {V} $ такие, что $ u = (u_1, u_2) $ и $ v = (v_1, v_2) $. Определите сложение как $ u + v = (u_1v_1, u_2v_2) $ и определите скалярное умножение на $ a \ in \ mathbb {F} $ как $ au = (au_1, au_2 + 1) $. Определите, является ли этот набор при этих операциях векторным пространством.
Пусть $ u $ — вектор, вторая компонента которого отлична от нуля, то есть $ u_2 \ neq 0 $, и рассмотрим существование мультипликативного тождества $ 1 $, такого что $ 1 u = u $.2 $, и пусть $ u, v, w \ in \ mathbb {V} $ такие, что $ u = (u_1, u_2) $ и $ v = (v_1, v_2) $. Определите сложение как $ u + v = (u_1v_1, u_2v_2) $ и определите скалярное умножение на $ a \ in \ mathbb {F} $ как $ au = (au_1, au_2 + 1) $. Определите, является ли этот набор при этих операциях векторным пространством.
В этом примере и сложение, и скалярное умножение не являются стандартными. Мы попытаемся проверить, что все десять аксиом верны, и перестанем проверять, если одна аксиома не работает.
- 1. $ u + v = (u_1v_1, u_2v_2) = (v_1u_1, v_2u_2) = v + u $.
- 2. $ u + (v + w) = (u_1 [v_1w_1], u_2 [v_2w_2]) = (u_1v_1w_1, u_2v_2w_2) = ([u_1v_1] w_1, [u_2v_2] w_2) = (u + v ) + w $.
- 3. Нулевой вектор равен $ 1 = (1, 1) $, то есть $ 1 + u = (1u_1, 1u_2) = (u_1, u_2) = u $.

- 4. Здесь происходит сбой $ V $ при указанных операциях. Обратите внимание, что для любого вектора $ u $ эта аддитивная обратная величина должна быть $ -u = \ left (\ frac {1} {u_1}, \ frac {1} {u_2} \ right) $.2} \ right) $. Но этот нулевой вектор справедлив только для $ u $. Если $ u \ neq v $, то $ v $ имеет другой нулевой вектор.
Международная космическая станция | IGCSE ESL Listening Exam Exercise 4
Вы услышите интервью с астронавтом по имени Фред Лукатони, который недавно прожил шесть месяцев на Международной космической станции. Послушайте интервью и посмотрите вопросы. Для каждого вопроса выберите правильный ответ: A, B или C.
F: Добро пожаловать в сегодняшнюю программу — третью в нашей серии о жизни в космосе.Я рад, что со мной в студии был Фред Лукатони, который недавно полгода жил на Международной космической станции. Фред, можешь рассказать нам, на что это было похоже?
М: Конечно. Что ж, международная космическая станция — потрясающее место. На самом деле он довольно большой: здесь больше жилого пространства, чем в доме с шестью спальнями, он равен длине футбольного поля и по объему равен самолету Боинг 747. Это дает вам представление?
Что ж, международная космическая станция — потрясающее место. На самом деле он довольно большой: здесь больше жилого пространства, чем в доме с шестью спальнями, он равен длине футбольного поля и по объему равен самолету Боинг 747. Это дает вам представление?
F: Есть. А теперь, когда вы вернулись на Землю, чего вам не хватает в космической станции?
М: Ну, конечно, смотреть на Землю сверху — это невероятно — это так красиво.И это очень весело, когда ты двигаешься, паря в воздухе. Мне это никогда не надоест! Но вы не поверите, когда я скажу, что никогда не спал лучше, чем там, — я бы хотел, чтобы на Земле было так же!
F: Интересно! Было ли что-нибудь, с чем было трудно мириться?
М: Вообще-то, предварительная подготовка настолько тщательная, что ничего удивительного. Я знал, что мы все будем жить на небольшом участке, все время очень близко друг к другу, и, конечно же, все знают о тебе все, пока ты там.Это не было проблемой. Я полагаю, что иногда я немного устал от необходимости тратить два часа на тренировку каждый день, но это просто то, что вам нужно делать.
F: Чтобы ваши мышцы и кости не ослабели?
М: Верно. И вы должны быть осторожны с тем, что вы едите, чтобы убедиться, что получаете все необходимые витамины и так далее. Мы все сами выбираем себе еду перед тем, как отправиться на космическую станцию, поэтому у каждого из нас есть личные запасы — есть удивительно широкий выбор вещей, которые вы можете там съесть! И готовить еду не так уж и долго, и это хорошо.
F: На космической станции довольно много людей, не так ли?
М: Да. Одна из вещей, которыми мы довольно много занимались, — это проводили эксперименты. Никогда не забуду того, что мне приходилось делать с живыми муравьями — наблюдать, как они пытаются передвигаться, было довольно интересно, потому что, как и мы, они не могут контролировать свои движения в пространстве. Я не был уверен, для чего был проведен эксперимент — иногда они бывают довольно странными, если честно, но вы просто выполняете инструкции и надеетесь, что это будет полезно для тех, кто их просил.
F: Вам когда-нибудь было одиноко, когда вы были там?
М: Одиноко? Не за что.Нас было трое, плюс, конечно, огромная команда на земле.
F: Не кажется ли вам, что за вами все время следят?
М: Ну они есть! Но вы скоро забываете об этом. На самом деле приятно осознавать, что вы можете обратиться к ним в любое время. Они следят за каждым аспектом экспедиции и постоянно получают от нас обратную связь — мы должны ежедневно присылать им всевозможную информацию, заполнять формы на компьютере и так далее.
Ж: Было ли шесть месяцев долгим отсутствием дома?
М: Не слишком долго, нет.Но вы начинаете мечтать о том, чтобы иметь возможность делать определенные вещи на Земле, например, кататься на своей машине — это то, что мой коллега отчаянно пытался сделать! Мне, конечно, не терпелось принять нормальный душ — там нет водопровода. И, наверное, в какой-то степени я тоже думал о возможности дышать прекрасным свежим воздухом.
Ф: О да, я бы это пропустил . .. В любом случае, последний вопрос. Как вы думаете, что делает космонавта хорошим?
.. В любом случае, последний вопрос. Как вы думаете, что делает космонавта хорошим?
M: Ну что ж, тот, кто не паникует, но тогда вас учат справляться со всем.Я бы сказал, больше всего на свете вам нужно хорошо работать в команде — в конце концов, оказавшись там наверху, вы не сможете очень легко избегать друг друга! Но также важно уметь хорошо общаться — и, конечно же, следовать командам других.
Ф: Фред, было действительно интересно поговорить с тобой. Спасибо за ваше время.
М: Спасибо.
Векторное пространство и пространства со скалярным произведением
Абстрактное вещественное векторное пространство — это коммутативная группа с
одна дополнительная операция: его элементы могут быть умножены на действительные числа (скаляры).Это ни в коем случае не
групповая операция (кроме случая, когда мы рассматриваем множество действительных чисел R как реальное векторное пространство)
потому что в групповых операциях оба операнда должны происходить из одного и того же набора. Умножение на скаляр
требуется для выполнения трех дополнительных законов: для u, v∈ и
векторы a и b ,
Умножение на скаляр
требуется для выполнения трех дополнительных законов: для u, v∈ и
векторы a и b ,
- (распределенность): (u + v) a = u a + v a
- (ассоциативность): u (v a ) = (uv) a
- (распределенность): u ( a + b ) = u a + u b
Это варианты распределительных и ассоциативных законов.Как, например, для пространств из n элементов умножение на скаляр определяется покомпонентно:
| u (a 1 , a 2 , a 3 ) = (ua 1 , ua 2 , ua 2 ) |
С этим определением и сложением определено также покомпонентно множество
из трех кортежей становится векторным пространством . Важно понимать, что кортеж из n
только тогда рассматривается как вектор, когда он рассматривается как элемент набора, в котором две операции
(сложение и умножение на скаляр) определены. Таким образом, вектора и векторных пространств рождаются одновременно.
Таким образом, вектора и векторных пространств рождаются одновременно.
Пространства со скалярным произведением
Для некоторых векторных пространств можно определить другое умножение — скалярное произведение (или внутреннее , или точка ). Скалярное произведение определяется для двух векторных операндов, в результате чего получается скаляр. Следовательно, скалярное произведение тоже это не групповая операция. Скалярное произведение двух векторов a и b обозначается a . b или ( a , b ) и имеет следующие свойства:
- (коммутативность): a . b = b . a
- (распределенность): a . ( b + c ) = a . б + а . c
В качестве примера скалярное произведение для кортежей из трех элементов определяется следующим образом:
( 1 , 2 , 3 ). (b 1 , b 2 , b 3 ) = a 1 b 1 + a 2 b 2 + a 3 b 3 (b 1 , b 2 , b 3 ) = a 1 b 1 + a 2 b 2 + a 3 b 3 |
Как приложение этих законов, давайте докажем простое, но интересное тождество.
| (*) |
|
Два вектора, скалярное произведение которых равно нулю, называются ортогональными или перпендикулярными . Например, следующие пары троек ортогональны: a и (0, 1, 0), (1, 0, 1) и (2, 1, -2). Для ортогональных векторов имеем следующее обобщение теоремы Пифагора:
( a + b ).( a + b ) = a . а + б . b а + б . b |
Если мы введем длину (также называемую нормой ) вектора a как || a || 2 = a . a , то теорема Пифагора допускает более традиционный вид:
| || a — b || 2 = || a || 2 + || b || 2 . |
Идентификатор (*) является обобщением закона косинуса . Фактически (*) является одной из причин того, что угол между двумя векторами определяется как:
| cos (α) = a . b / || a || || b ||. |
Что можно умножить?
| Контакты | | Первая страница | | Содержание | | Вверх |
Copyright © 1996-2018 Александр Богомольный«Вектор» испытал прототип малой ракеты-носителя
Обновлено 5 мая.
ВАШИНГТОН — Vector, одна из нескольких компаний, которые в настоящее время разрабатывают малые ракеты-носители, заявила, что успешно провела испытательный полет на малой высоте на прототипе своей машины 3 мая.
Компания, ранее известная как Vector Space Systems, сообщила, что инженерная модель ее ракеты Vector-R, получившая обозначение P-19H, взлетела с площадки в пустыне Мохаве в Калифорнии около 15:00. Восточное 3 мая. Тест проводился после того, как компьютеры прервали предыдущую попытку 6 апреля из-за неустановленной проблемы в последние секунды.
Компания в своем заявлении объявила запуск успешным, но предоставила несколько технических деталей полета. Представитель компании Сара Никелл заявила, что запланированная максимальная высота для ракеты при этом запуске составляла 1370 метров, но позже сообщила, что компания не будет раскрывать фактическую пиковую высоту полета.
Автомобиль Vector-R, разрабатываемый компанией, будет иметь три двигателя мощностью 5 000 фунтов на первой ступени ракеты и один двигатель меньшей мощности на второй ступени.Он предназначен для вывода на низкую околоземную орбиту до 60 кг.
У ракеты, запущенной из Мохаве, был только один двигатель, и фотографии ракеты, опубликованные компанией в социальных сетях ранее в этом году, предполагали, что у ракеты были только очень маленькие топливные баки. Обозначение P-19H, по-видимому, осталось от компании Garvey Spacecraft Corporation, которая в 2014 году испытала небольшую суборбитальную ракету под названием P-19. Компания Vector официально приобрела Garvey в середине 2016 года.
Обозначение P-19H, по-видимому, осталось от компании Garvey Spacecraft Corporation, которая в 2014 году испытала небольшую суборбитальную ракету под названием P-19. Компания Vector официально приобрела Garvey в середине 2016 года.
Такой дизайн для этого прототипа был преднамеренным выбором для поэтапных испытаний транспортного средства, Джеймс Кантрелл, исполнительный директор Vector, в телефонном интервью 4 мая.«Это поэтапный подход к разработке, который постепенно добавляет машине все больше и больше сложности и производительности», — сказал он. Он пояснил, что использование небольших топливных баллонов ограничивало летные характеристики машины в этом полете и позволяло им соответствовать правилам Федерального управления гражданской авиации об отказе от лицензии на коммерческий запуск.
Он противопоставил это подходу, принятому многими другими разработчиками ракет-носителей, которые впервые запускают свою ракету на полную орбиту.«По моему опыту, люди поступают так, потому что видят в этом самый короткий и недорогой путь к достижению этой точки», — сказал он. «Моя теория заключается в том, что на самом деле это не так».
«Моя теория заключается в том, что на самом деле это не так».
Второй испытательный полет планируется провести примерно через два месяца, сказал Кантрелл, и в нем будут установлены топливные баки большего размера, чтобы аппарат мог летать на сверхзвуке. Через два месяца после этого состоится третий испытательный полет, цель которого — продемонстрировать систему управления вектором тяги. Он сказал, что планирует провести от пяти до шести испытательных полетов прототипов Vector-R, которые завершатся испытательным орбитальным полетом.
В апреле компания сообщила, что привлекла «промежуточный раунд» в размере 4,5 млн долларов для поддержки операций компании до тех пор, пока она не сможет закрыть более крупный раунд серии A в конце этого года. Компания также планирует построить новую штаб-квартиру и автомобильный завод в Тусоне, штат Аризона, где она базируется.
В прошлом месяце компания представила модель своей ракеты Vector-R в комплексе для посетителей Космического центра Кеннеди во Флориде.

 Какая планета ближайшая к Солнцу?
Какая планета ближайшая к Солнцу? Ступали ли когда-нибудь люди на Марс?
Ступали ли когда-нибудь люди на Марс? Планета Нептун больше Земли?
Планета Нептун больше Земли?