ГДЗ контрольная работа / КР-1 / вариант 1 9 алгебра 8 класс Задачник Мордкович, Александрова
 Решение есть!
Решение есть!- 1 класс
- Математика
- Английский язык
- Русский язык
- Литература
- Окружающий мир
- 2 класс
- Математика
- Английский язык
- Русский язык
- Информатика
- Музыка
- Литература
- Окружающий мир
- Технология
- 3 класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Информатика
- Музыка
- Литература
- Казахский язык
- 4 класс
- Математика
- Русский язык
- Немецкий язык
- Музыка
- Литература
- Окружающий мир
- Казахский язык
- 5 класс
- Математика
- Английский язык
- Русский язык
- Физика
- Немецкий язык
- Украинский язык
Алгебра Мордкович. Контрольная работа 4
ГДЗ Алгебра 9 класс Мордкович. Решения и ответы на Контрольную работу № 4 (4 варианта). Цитаты из пособия указаны в учебных целях. Ответы на контрольные работы адресованы родителям.
Алгебра 9 Мордкович.
Контрольная работа 4 (образец)
Ответы на контрольную работу № 4
РЕШЕНИЯ и ОТВЕТЫ на Вариант 1
Смотреть Вариант 1

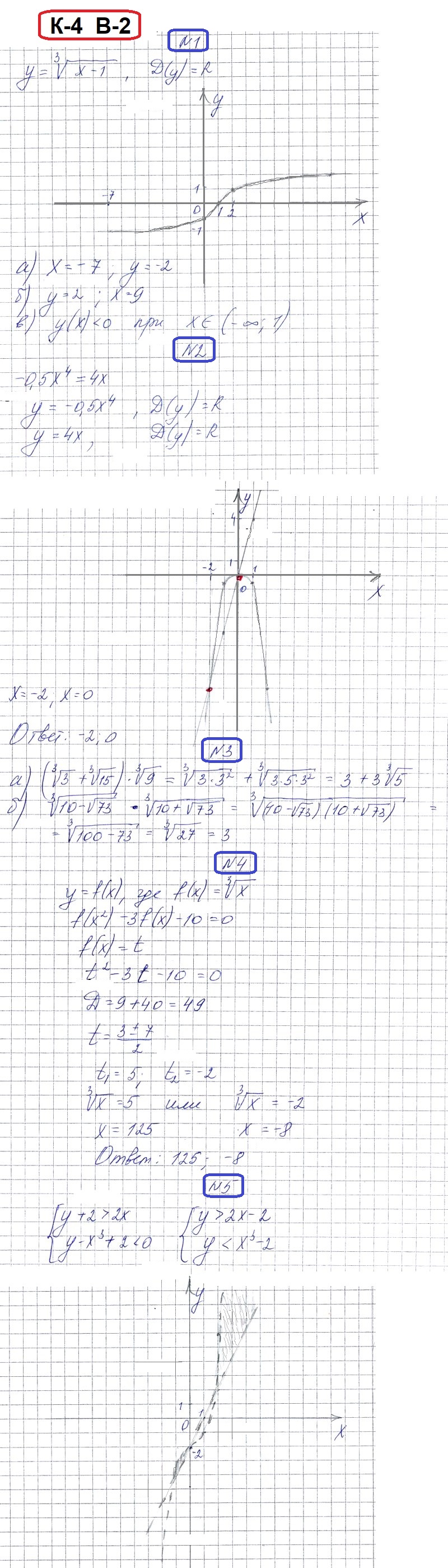
РЕШЕНИЯ и ОТВЕТЫ на Вариант 2
Смотреть Вариант 2
РЕШЕНИЯ и ОТВЕТЫ на Вариант 3
Смотреть Вариант 3

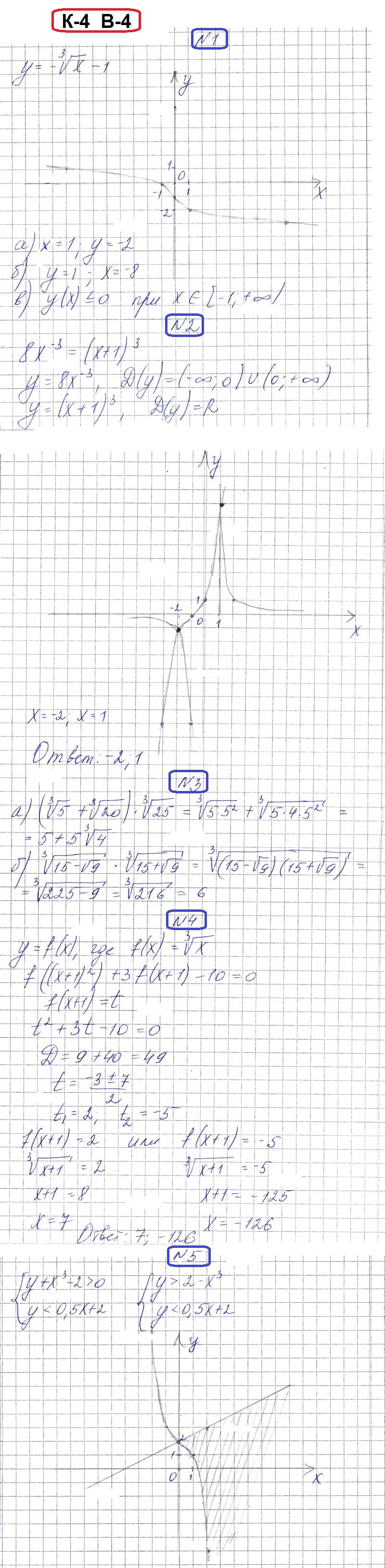
РЕШЕНИЯ и ОТВЕТЫ на Вариант 4
Смотреть Вариант 4
ГДЗ Алгебра 9 класс Мордкович. Решения и ответы на Контрольную работу № 4. Цитаты из пособия указаны в учебных целях. Ответы на контрольные работы адресованы родителям.
Вернуться к списку контрольных работ по алгебре УМК Мордкович
Мордкович Алгебра 8 ДКР-1 | КОНТРОЛЬНЫЕ РАБОТЫ
Мордкович Алгебра 8 ДКР-1
Мордкович Алгебра 8 ДКР-1 — РЕШЕНИЯ и ОТВЕТЫ на домашнюю контрольную работу № 1 «Алгебраические дроби» из учебного пособия: «Алгебра 8 класс в 2 частях. Часть 2. Задачник для учащихся общеобразовательных учреждений / А.Г. Мордкович и др. — М.: Мнемозина, 2014». Представленные ниже 2 варианта контрольной работы по алгебре 8 класса и ответы на нее ориентированы на задачник «Алгебра 8 класс» авторов А.Г. Мордкович и др.
Ответы на контрольную работу по алгебре адресованы учителям и родителям, которые смогут проконтролировать правильность выполнения задания.
Контрольная работа № 1. Вариант 1

Контрольная работа № 1. Вариант 2

Ответы на контрольную «Алгебраические дроби»
Вариант 1.


Ответы на контрольную № 1 по алгебре (Мордкович)
Вариант 2


Вы смотрели «Мордкович Алгебра 8 ДКР-1» — ГДЗ на контрольную работу № 1 «Алгебраические дроби» из учебного пособия: «Алгебра 8 класс в 2 частях. Часть 2. Задачник для учащихся общеобразовательных учреждений / А.Г. Мордкович и др. — М.: Мнемозина, 2014». Представленные ниже 2 варианта контрольной работы по алгебре 8 класса и ответы на нее ориентированы на задачник «Алгебра 8 класс» авторов А.Г. Мордкович и др.
Вернуться к Списку самостоятельных работ по алгебре 8 класс (УМК Мордкович и др.)
Контрольные работы КР-1. вариант — 1 гдз по алгебре 9 класс Мордкович, Семенов учебник и задачник (2018)
Решебники, ГДЗ
- 1 Класс
- Математика
- Русский язык
- Английский язык
- Информатика
- Немецкий язык
- Литература
- Человек и мир
- Природоведение
- Основы здоровья
- Музыка
- Окружающий мир
- Технология
- 2 Класс
- Математика
- Русский язык
- Белорусский язык
- Английский язык
- Информатика
- Украинский язык
- Французский язык
- Немецкий язык
- Литература
- Человек и мир
- Природоведение
- Основы здоровья
- Музыка
- Окружающий мир
- Технология
- Испанский язык
- 3 Класс
- Математика
- Русский язык
- Белорусский язык
- Английский язык
- Информатика
- Украинский язык
- Французский язык
- Немецкий язык
- Литература
- Человек и мир
ГДЗ решебник по алгебре 7 класс Попов, Мордкович тетрадь для к/р и с/р Экзамен

Алгебра 7 класс
Тип пособия: Тетрадь для к/р и с/р
Авторы: Попов, Мордкович
Издательство: «Экзамен»
К изучению алгебраической науки ученик седьмого класса должен отнестись со всей серьёзностью. Предмет очень сложный и малейшее недопонимание ведёт в негативным последствиям в виде неудовлетворительных оценок и низкой успеваемости. Поможет в такой ситуации «ГДЗ по Алгебре 7 класс Тетрадь для самостоятельных и контрольных работ Попов, Мордкович (Экзамен)».
Неоценимая помощь сборника
Решебник даст возможность разобрать и понять в деталях сложный материал, а также:
- выявить допущенные ошибки в домашней работе и поработать над ними;
- качественно подготовиться к предстоящему уроку;
- сэкономить время и силы.
Структура ГДЗ позволяет найти нужный ответ легко и быстро по номеру задания, а удобство и доступность использования обеспечивает электронный формат, онлайн. Систематическое применение сборника только положительно отразится на учёбе, к тому же ученик всегда будет во всеоружии перед любой проверкой знаний.
Описание тетради
Отследить предметные успехи и уровень усвояемости материала поможет тетрадь для самостоятельных и контрольных работ по алгебре за 7 класс авторы Попов, Мордкович. Работы рассчитаны как на текущий, так и на итоговый контроль навыков и умений школьника по всему курсу. По результатам проверки учитель отследит пробелы и недочёты в понимании дисциплины и своевременно проведёт коррекционную работу.
ГДЗ за 7‐9 класс по Алгебре Мордкович А.Г. контрольные работы Углубленный уровень
gdz-bot.ru НайтиНавигация по гдз
1 класс Русский язык Математика Английский язык Окружающий мир Литература Информатика Музыка Человек и мир 2 класс Русский язык Математика Английский язык Немецкий язык Окружающий мир Литература Информатика Музыка Технология Человек и мир 3 класс Русский язык Математика Английский язык Немецкий язык Окружающий мир Литература Информатика Музыка 4 класс Русский язык Математика Английский язык Немецкий язык Окружающий мир Литература Информатика Музыка Белорусский язык 5 класс Русский язык Математика Английский язык Немецкий язык История География Биология Обществознание Физика Литература Информатика Музыка Технология ОБЖ Природоведение Естествознание Человек и мир Белорусский язык Украинский языкTest (algebra) — Wikipédia
Az algebrában a test egy olyan F = (T; +, ⋅) {\ displaystyle F = (T; +, \ cdot)} kétműveletes algebrai structúrát jelöl, ahol T {\ displaystyle jelöl, ahol T {\ displaystyle F = (T; +, \ cdot)} T} kommutatív csoportot alkot a + {\ displaystyle +} («összeadás») műveletre nézve, a ⋅ {\ displaystyle \ cdot} («szorzás») kommutatív, asszociatív, minden nem nerze alemnek { } műveletre nézve, továbbá a ⋅ {\ displaystyle \ cdot} művelet disztributív a + {\ displaystyle +} műveletre.
Egyes szerzők testnek nevezik az olyan algebrai Struktúrákat is, amelyekben a szorzás nem feelétlenül kommutatív, де a fenti tulajdonságok egyébként teljesülnek. E cikkben az ilyenstruktúrákat ferdetestnek nevezzük, és testen mindig kommutatív ferdetestet értünk.
A test nagyon fontos fogalom az algebrán belül, nem utolsósorban amiatt, mivel rendkívül sok, az elemi matematikából is ismert számcsoport közös általánosítújtását ny. racionális, valós — это komplex számokét.Тест на математику над соком más területén — это felhasználhatóak (ld. «A testelmélet alkalmazásai»).
Тест [szerkesztés]
- R (x) знак равно {p (x) q (x) | p (x), q (x) ∈R [x], q (x) ≢0} {\ displaystyle \ mathbb {R} ( x) = {\ biggl \ {} {\ frac {p (x)} {q (x)}} \, {\ biggl |} \, p (x), q (x) \ in \ mathbb {R} [x], \ q (x) \ not \ Equiv 0 {\ biggl \}}}
- a racionális számok kibővítve t {\ displaystyle {\ sqrt {t}}} — vel (t∈Q { \ displaystyle t \ in \ mathbb {Q}})
- Q (t) = {a + bt | a, b∈Q} {\ displaystyle \ mathbb {Q} ({\ sqrt {t}} ) = {\ big \ {} a + b {\ sqrt {t}} \, {\ big |} \, a, b \ in \ mathbb {Q} {\ big \}}}
Ferdetest [szerkesztés]
- {a + bi + cj + dk | a, b, c, d∈R} {\ displaystyle \ {a + bi + cj + dk \, | \, a, b, c, d \ in \ mathbb {R} \}}
A testaxiómák és egyszerű következményeik [szerkesztés]
A testaxiómák:
- ∀a, b, c∈F: a + (b + c) = (a + b) + c, a ∗ (b ∗ c) = (a ∗ b) ∗ c {\ displaystyle \ forall a, b, c \ in F: \ quad a + (b + c) = (a + b) + c, a * (b * c) = (a * b) * c}
- ∀a , b∈F: a + b = b + a, a ∗ b = b ∗ a {\ displaystyle \ forall a, b \ in F: \ quad a + b = b + a, a * b = b * a}
- ∀a, b∈F: a ∗ (b + c) = (a ∗ b) + (a ∗ c) {\ displaystyle \ forall a, b \ in F: \ quad a * (b + c) = (a * b) + (a * c)}
- Létezik nullelem (additív semleges elem), azaz olyan 0-val jelölt elem, hogy
- ∃ 0∈F: ∀a∈F: a + 0 = a {\ displaystyle \ exists 0 \ in F: \ quad \ forall a \ in F: \ quad a + 0 = a}
- Létezik egységelem (multiplikatív semleges elem), azaz olyan 1-gyel jelölt elem, hogy
- ∃1 (≠ 0) ∈F: ∀a∈F: a ∗ 1 = a {\ displaystyle \ exists 1 (\ neq 0) \ in F: \ quad \ forall a \ in F: \ quad a * 1 = a}
- ∀a∈F: ∃ − a ∈F: a + (- a) = 0 {\ displaystyle \ forall a \ in F: \ quad \ exists -a \ in F: \ quad a + (- a) = 0}
- Léteznek multiplikatív Inverz Elemek vagy reciprokok (родословная 0-hoz az előbbiekből bizonyítóan biztosan nincs):
- ∀a ≠ 0∈F: ∃a − 1∈F: a ∗ a − 1 = 1 {\ displaystyle \ forall a \ neq 0 \ in F: \ quad \ существует ^ {- 1} \ in F: \ quad a * a ^ {- 1} = 1}
Általában ki szokták kötni, hogy a test legalább két elemet tartalmazzon, ezt a fentiekben az 1 ≠ 0 követelmény biztosítja.Tehát egyelem (se üres) испытание нинков.
Bizonyítható, hogy nullelem és egységelem pontosan egy van, azonkívül minden elemnek pontosan egy ellentettje és pontosan egy reciproka van.
Mivel a * műveletre minden nem nulla elemnek van converze, minden nem nulla elem egység (nem összekeverendő az 1 egységelemmel), vagyis minden nem nulla elem minden elemnek osztója:
- ∀a ≠ 0, b∈F: a | b {\ displaystyle \ forall a \ neq 0, b \ in F: \ quad a | b}
hiszen
- a ∗ (a − 1 ∗ b) = (a ∗ a − 1) ∗ b = 1 ∗ b = b {\ displaystyle a * (a ^ {- 1} * b) = (a * a ^ {- 1}) * b = 1 * b = b \,}
Fontosabb azonosságok testekben [szerkesztés]
- (a ∗ b) −1 = b − 1 ∗ a − 1 = a − 1 ∗ b − 1 {\ displaystyle (a * b) ^ {- 1} = b ^ {- 1} * a ^ {- 1} = a ^ {- 1} * b ^ {- 1}}
га a és b nem nulla;
- −a = (- 1) ∗ a {\ displaystyle -a = (- 1) * a}
- sőt — (a ∗ b) = (- a) ∗ b = a ∗ (- b) {\ displaystyle — (a * b) = (- a) * b = a * (- b)}
- továbbá a * 0 = 0 {\ displaystyle a * 0 = 0};
Testben érvényesek Az alapműveletekkel kapcsolatban a racionális vagy a valós számok között megszokott azonosságok (például a törtekkel való műveletegysek elvállás), когда вы + 1 тестируете, когда хотите ответить.
Ha van olyan n pozitív egész szám, hogy a test valamelyik elemét n -szer önmagához adva 0-t kapunk, akkor n többszörösei is ilyáúgakakd. A legkisebb ilyen n -t a test karakterisztikájának nevezzük; ennek gyakori jelölése char F. Ez könnyen láthatóan ugyanaz minden elemre és prímszám. Ha ilyen szám nincs, akkor azt mondjuk, hogy a test karakterisztikája 0 (ritkábban: végtelen).
Résztest, testbővítés [szerkesztés]
Ha az elemek egy T ‘ részhalmaza maga is testet alkot az F -beli műveletekkel (ebbe beleértjük, hogy tartalmazza a testbeli 0-t és az 1-et), akhetkün elemek a testbeli 0-t és az 1-et. résztestről ; ezt például K ⊂ F -fel jelölhetjük.Gyakran lenyeglátóbb az a nézőpont, mikor a nagyobb testet a kisebb bővítésének mondjuk; ennek gyakori jelölése F | K vagy F / K.
Egypt F test tetszőleges számú résztestének metszete is résztest, így defiálható T egy A részhalmazának general részteste. Ez jellemezhető „kívülről”: az összes A -t tartalmazó résztest metszete; s „belülről”: A -ból, a 0-ból és az 1-ből a testműveletekkel megkapható összes F -beli elem által alkotott részhalmaz, ami történetesen részhalmaz.
Test és résztestének karakterisztikája egyenlő. Bővebb F тестирует K fölött lineáris teret (sőt, algebrát) alkot a testműveletekkel; a testbővítés fokának nevezzük e vektortér dimenzióját.
Az F bővebb test egy eleme algebrai K fölött, ha gyöke egy nem konstans nulla K -beli együtthatós polinomnak; egyébként transzcendens . Például π szám transzcendens a racionális számok teste felett.Algebrai elemmel bővítve algebrai, transzcendens elemmel bővítve transzcendens bővítéshez jutunk. Ha egy bővítés foka véges, akkor algebrai bővítésről van szó. Véges sok algebrai elemmel való bővítés helyettestő egy algebrai elemmel való bővítéssel; ekkor a testbővítés foka megegyezik az adott algebrai elem minimálpolinomjának a fokával, amit az adott elem fokának is neveznek.
Egypt testbővítés normális , ha azok a kisebb test fölötti felbonthatatlan polinomok, amiknek van gyökük a bővebb testben, elsőfokú tényezők szorzatára fvebbö test a bomble.Megmutatható, hogy egy bővítés akkor és csak akkor ilyen, имеет тест bővebb, egy polinomhalmaz felbontási teste , vagyis olyan bővítésről van szó, amibérazaféské elekomúraz Minden polinomhalmaznak van felbontási teste, és az izomorfia erejéig egyértelmű. Ha egy test fölötti összes polinom felbontási testét vesszük, akkor az adott test algebrai lezártját kapjuk.
Egypt K fölötti polinom szeparábilis , ha K egy bővítésében sincsenek többszörös gyökei.Ha egy algebrai elem főpolinomja szeparábilis, akkor az az elem szeparábilis, és a vele való bővítés is szeparábilis. Ha egy K test minden algebrai bővítése szeparábilis, akkor K tökéletes test . Az összes nulla karakterisztikájú test tökéletes, és a véges testek is azok.
A nevezetes Galois-elmélet olyan bővítésekkel foglalkozik, amik véges fokúak, normálisak, és szeparábilisek. Galois-elmélet nevezetes alkalmazásai a szerkeszthetőségi feladatok, és az algebrai egyenletek megoldása gyökjelekkel.Így lehet bebizonyítani, hogy például mely szabályos sokszögek szerkeszthetők, és hogy a három klasszikus probléma: a kockakettőzés, a szögharmadolás, ézöszörnétglan. Továbbá a Galois-elmélettel belátható, hogy csak az első-, a másod-, harad- és a negyedfokú egyenleteket lehet mindig megoldani gyökvonások segítségével; csak ezekre létezik megoldóképlet.
A fentiek alapján bármely testnek van minimális részteste, ezt nevezzük a test prímtestének .Ezt izomorfizmustól eltekintve egyértelműen meghatározza a test karakterisztikája: véges p karakterisztika esetén a prímtest az Fp {\ displaystyle F_ {p}} p elemű vézézigás display, pététélé ém vézézézé é testével. Tehát Q {\ displaystyle \ mathbb {Q}} -nál szűkebb végtelen test nincs.
Тест Minden véges ferdetest. (Веддерберн-тетель.)
Könnyen elérhető példát устанавливает Veges testekre по модулю р maradékosztályok rendszere, ahol р prímszám: а szorzás invertálhatóságát kivéve Minden testaxióma következik аз egész számok és kongruencia megfelelő tulajdonságából, AZT pedig элого számelmélettel мек Lehet mutatni.{q} -x} polinom felbontási teste. E test multiplikatív csoportja ciklikus. q elemű testet — это Fq {\ displaystyle F_ {q}} — val, vagy GF (q) {\ displaystyle GF (q)} — val jelöljük; ezek igen fontos szerepet töltenek быть számítástudományi alkalmazásokban, különösen a kódelméletben.
Kapcsolódó szócikkek [szerkesztés]
- Поцелуй Эмиля: Bevezetés az algebrába
- Пеликан Йожеф: Алгебра (PDF / Postscript). Összeállította Gröller Ákos .ЭЛТЕ ТТК
- Редей Ласло: Алгебра I. kötet , Akadémiai Kiadó, Bp (1954)
- Szendrei Ágnes: Diszkrét matematika , Polygon, JATE Bolyai Intézet, Szeged (1994)
- И. Р. Шафаревич: Алгебра , Typotex Kiadó, Bp (2000) ISBN 963-9132-53-5
уроков алгебры — School Yourself
1. Сложение и вычитание.
2. Умножение и деление
Умножение положительных чисел в любом порядке
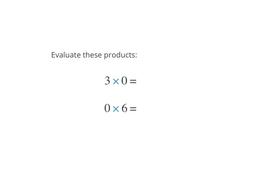
Узнайте, что происходит при умножении на 1 и 0

Деление положительных чисел и способы осмысления этого

Операция, которую вы просто не можете выполнить…

Есть более одного способа оценить выражение?

Избавление от скобок при сложении и умножении
Что произойдет, если умножить негативы вместе?

Что происходит при делении отрицательных чисел?
Раздача негативных знаков
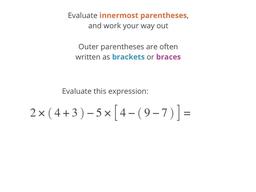
Что делать, если у вас слишком много скобок!
Узнайте, как найти «среднее» чисел
3.Факторинг
При делении на коэффициент всегда получается целое число
Их единственные факторы — 1 и сами
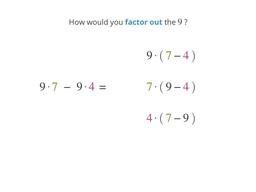
Выделение общих множителей с помощью закона распределения
Переверните знаки, когда вы выносите отрицательные числа
Самый большой общий фактор чисел
Когда два числа не имеют общих делителей

Способ расчета GCF
, существующий уже 2000 лет
Что вы получите, если умножить числа на целые

Общее наименьшее кратное число
4.Фракции
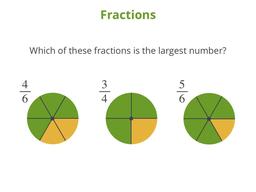
Нарисуйте и сравните дроби и преобразуйте в десятичные числа

Сколько 1/2 умножить на 3/5? Узнайте трюк на этом уроке!

Как узнать, когда дроби равны, а какая больше

Упрощение дробей путем удаления общих множителей

Сложить и вычесть дроби, используя общие знаменатели

Деление на дробь — это действительно умножение на обратную величину!

Множитель обратного числа равен 1 над числом
.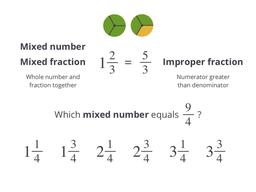
Переключение между смешанной и неправильной дробью

Закон распределения работает как для умножения, так и для деления

Вычисление дробей чисел (например, 5/7 из 210)
|

