Геометрия 9 класс Контрольная № 1 с ответами
Контрольная работа № 1 по геометрии в 9 классе «Векторы» с ответами и решениями (3 уровня сложности по 2 варианта). УМК Атанасян и др. (Просвещение). Поурочное планирование по геометрии для 7 класса (Н.Ф. Гаврилова, ВАКО). Урок 14. Геометрия 9 класс Контрольная № 1 «Векторы».
Смотреть Список всех контрольных по геометрии в 9 классе (УМК Атанасян)
Контрольная работа № 1
«Векторы»
Цель: проверить знания, умения и навыки учащихся по теме.
Тип урока: урок контроля, оценки и коррекции знаний.
ХОД УРОКА
1. Организационный момент
Мотивация к учебной деятельности. Учитель сообщает тему урока, формулирует цели урока.
2. Контрольная работа
I уровень сложности
Вариант 1
- Начертите два неколлинеарных вектора a и b.

- На стороне ВС ромба ABCD лежит точка К так, что ВК = КС, О — точка пересечения диагоналей. Выразите векторы АО, АК, KD через векторы a = АВ и b = AD.
- В равнобедренной трапеции высота делит большее основание на отрезки, равные 5 см и 12 см. Найдите среднюю линию трапеции.
- * В треугольнике АВС точка О — точка пересечения медиан. Выразите вектор АО через векторы а = АВ и b = АС.
Вариант 2
- Начертите два неколлинеарных вектора m и n. Постройте векторы, равные: а) —m/3 + 2n; б) 3n – m.
- На стороне CD квадрата ABCD лежит точка Р так, что СР = PD, О – точка пересечения диагоналей. Выразите векторы ВО, ВР, РА через векторы х = ВА и у = ВС.
- В равнобедренной трапеции один из углов равен 60°, боковая сторона равна 8 см, а меньшее основание — 7 см.
 Найдите среднюю линию трапеции.
Найдите среднюю линию трапеции. - * В треугольнике MNK точка О — точка пересечения медиан, MN = а, МК = у, МО = k (х + у). Найдите число k.
II уровень сложности
III уровень сложности
3. Рефлексия учебной деятельности
В конце урока учитель раздает на каждую парту краткую запись решения задач контрольной работы.
Ответы на контрольную I уровня сложности
Ответы на контрольную II уровня сложности
Ответы на контрольную III уровня сложности
Вы смотрели: Геометрия 9 класс Контрольная № 1. Поурочное планирование по геометрии для 9 класса. УМК Атанасян (Просвещение). Урок 14. Контрольная работа по геометрии «Векторы» + ОТВЕТЫ.
Урок 14. Контрольная работа по геометрии «Векторы» + ОТВЕТЫ.
Смотреть Список всех контрольных по геометрии в 9 классе по УМК Атанасян.
Вернуться к Списку уроков Тематического планирования в 9 классе.
Методическая разработка по геометрии (9 класс) на тему: 9 класс. Контрольная работа № 1. «Векторы».
Контрольная работа № 1 по геометрии для 9 класса
по теме «Векторы»
1 вариант.
1. Вектором называется направленный …. (закончить предложение)
2. Начертите два неколлинеарных вектора и . Постройте векторы, равные
а) б) 2
3. На стороне ВС ромба АВСD лежит точка К так, что ВК = КС, О – точка пересечения диагоналей. Выразите векторы , , через векторы .
4. В равнобедренной трапеции высота делит большее основание на отрезки, равные 5 см и 12 см. Найдите среднюю линию трапеции.
5. Расстояния от концов диаметра окружности до некоторой касательной равны a и b. Найдите радиус окружности.
Найдите радиус окружности.
Контрольная работа № 1 по геометрии для 9 класса
по теме «Векторы»
2 вариант.
1. От любой точки М можно отложить вектор, равный данному вектору, и притом только… (закончить предложение).
2. Начертите два неколлинеарных вектора . Постройте векторы, равные
а) б) .
3. На стороне CD квадрата ABCD лежит точка Р так, что CP=PD, O- точка пересечения диагоналей. Выразите векторы через векторы .
4. В равнобедренной трапеции один из углов равен 60о, боковая сторона равна 8см, а меньшее основание 7см. Найдите среднюю линию трапеции.
5. Найдите площадь трапеции ABCD с боковой стороной BC = 5, если расстояния от вершин A и D до прямой BC равны 3 и 7 соответственно.
Контрольная работа № 1 по геометрии для 9 класса
по теме «Векторы»
1 вариант.
1. Вектором называется направленный …. (закончить предложение)
2. Начертите два неколлинеарных вектора и . Постройте векторы, равные
а) б) 2
3. На стороне ВС ромба АВСD лежит точка К так, что ВК = КС, О – точка пересечения диагоналей. Выразите векторы , , через векторы .
На стороне ВС ромба АВСD лежит точка К так, что ВК = КС, О – точка пересечения диагоналей. Выразите векторы , , через векторы .
4. В равнобедренной трапеции высота делит большее основание на отрезки, равные 5 см и 12 см. Найдите среднюю линию трапеции.
5. Расстояния от концов диаметра окружности до некоторой касательной равны a и b. Найдите радиус окружности.
Контрольная работа № 1 по геометрии для 9 класса
по теме «Векторы»
2 вариант.
1. От любой точки М можно отложить вектор, равный данному вектору, и притом только… (закончить предложение).
2. Начертите два неколлинеарных вектора . Постройте векторы, равные
а) б) .
3. На стороне CD квадрата ABCD лежит точка Р так, что CP=PD, O- точка пересечения диагоналей. Выразите векторы через векторы .
4. В равнобедренной трапеции один из углов равен 60о, боковая сторона равна 8см, а меньшее основание 7см. Найдите среднюю линию трапеции.
5. Найдите площадь трапеции ABCD с боковой стороной BC = 5, если расстояния от вершин A и D до прямой BC равны 3 и 7 соответственно.
Материал по геометрии (9 класс) по теме: Контрольные работы по геометрии (9 кл.)
К — 3
Вариант 1
• 1. В АВС, А = 45, В = 60, ВС = 3.
Найдите АС.
2. Две стороны треугольника равны 7 см и 8 см, а
угол между ними равен 120. Найдите третью
сторону треугольника.
3. В АВС, АВ = ВС, САВ = 30, АЕ – биссектриса,
ВЕ = 8 см. Найдите площадь треугольника АВС.
К — 3
Вариант 1
• 1. В АВС, А = 45, В = 60, ВС = 3.
Найдите АС.
2. Две стороны треугольника равны 7 см и 8 см, а
угол между ними равен 120. Найдите третью
сторону треугольника.
3. В АВС, АВ = ВС, САВ = 30, АЕ – биссектриса,
ВЕ = 8 см. Найдите площадь треугольника АВС.
К — 3
Вариант 1
• 1. В АВС, А = 45, В = 60, ВС = 3.
Найдите АС.
2. Две стороны треугольника равны 7 см и 8 см, а
угол между ними равен 120.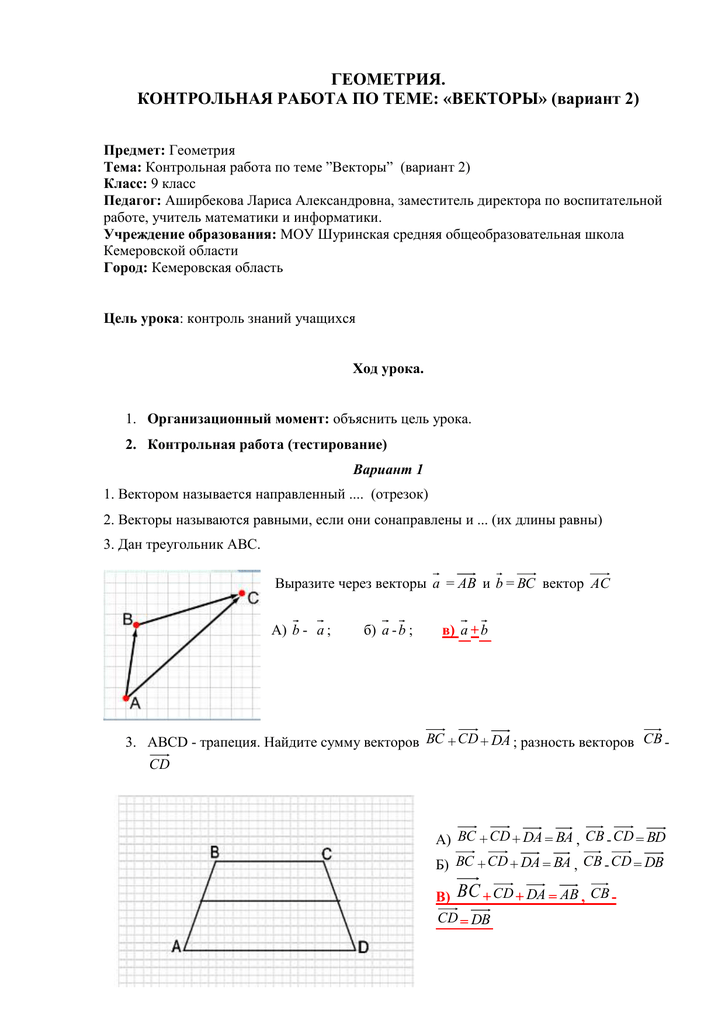 Найдите третью
Найдите третью
сторону треугольника.
3. В АВС, АВ = ВС, САВ = 30, АЕ – биссектриса,
ВЕ = 8 см. Найдите площадь треугольника АВС.
К — 3
Вариант 1
• 1. В АВС, А = 45, В = 60, ВС = 3.
Найдите АС.
2. Две стороны треугольника равны 7 см и 8 см, а
угол между ними равен 120. Найдите третью
сторону треугольника.
3. В АВС, АВ = ВС, САВ = 30, АЕ – биссектриса,
ВЕ = 8 см. Найдите площадь треугольника АВС.
К — 3
Вариант 1
• 1. В АВС, А = 45, В = 60, ВС = 3.
Найдите АС.
2. Две стороны треугольника равны 7 см и 8 см, а
угол между ними равен 120. Найдите третью
сторону треугольника.
3. В АВС, АВ = ВС, САВ = 30, АЕ – биссектриса,
ВЕ = 8 см. Найдите площадь треугольника АВС.
К – 3
Вариант 2
• 1. В СДЕ, С = 30, Д = 45, СЕ = 5.
Найдите ДЕ.
2. Две стороны треугольника равны 5 см и 7 см, а
угол между ними равен 60. Найдите третью
Найдите третью
сторону треугольника.
3. В ромбе АВСД, АК – биссектрису угла САВ,
ВАД = 60, ВК = 12 см. Найдите площадь ромба.
К – 3
Вариант 2
• 1. В СДЕ, С = 30, Д = 45, СЕ = 5.
Найдите ДЕ.
2. Две стороны треугольника равны 5 см и 7 см, а
угол между ними равен 60. Найдите третью
сторону треугольника.
3. В ромбе АВСД, АК – биссектрису угла САВ,
ВАД = 60, ВК = 12 см. Найдите площадь ромба.
К – 3
Вариант 2
• 1. В СДЕ, С = 30, Д = 45, СЕ = 5.
Найдите ДЕ.
2. Две стороны треугольника равны 5 см и 7 см, а
угол между ними равен 60. Найдите третью
сторону треугольника.
3. В ромбе АВСД, АК – биссектрису угла САВ,
ВАД = 60, ВК = 12 см. Найдите площадь ромба.
К – 3
Вариант 2
• 1. В СДЕ, С = 30, Д = 45, СЕ = 5.
Найдите ДЕ.
2. Две стороны треугольника равны 5 см и 7 см, а
угол между ними равен 60.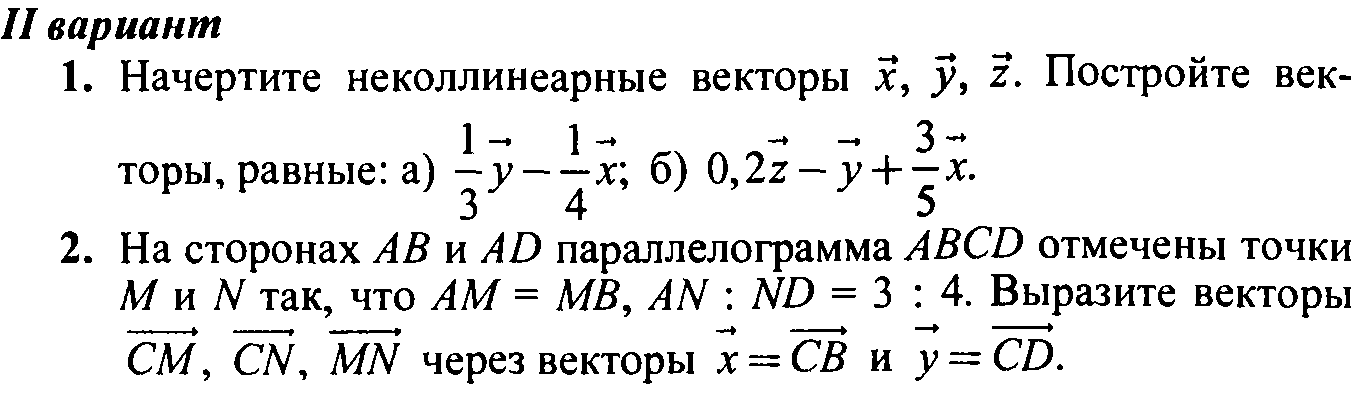 Найдите третью
Найдите третью
сторону треугольника.
3. В ромбе АВСД, АК – биссектрису угла САВ,
ВАД = 60, ВК = 12 см. Найдите площадь ромба.
К – 3
Вариант 2
• 1. В СДЕ, С = 30, Д = 45, СЕ = 5.
Найдите ДЕ.
2. Две стороны треугольника равны 5 см и 7 см, а
угол между ними равен 60. Найдите третью
сторону треугольника.
3. В ромбе АВСД, АК – биссектрису угла САВ,
ВАД = 60, ВК = 12 см. Найдите площадь ромба.
Контрольная работа № 1. Векторы | |
1 вариант. 1. Начертите два неколлинеарных вектора и . Постройте векторы, равные: а) ; б) 2. На стороне ВС ромба АВСD лежит точкаК такая, что ВК = КС, О – точка пересечения диагоналей. Выразите векторы через векторы и . 3. В равнобедренной трапеции высота делит большее основание на отрезки, равные 5 и 12 см. Найдите среднюю линию трапеции. 4.* В треугольнике АВС О – точка пересечения медиан. Выразите вектор через векторы и . | 2 вариант 1. Начертите два неколлинеарных вектора и . Постройте векторы, равные: а) ; б) 2. На стороне СD квадрата АВСD лежит точка Р такая, что СР = РD , О – точка пересечения диагоналей. Выразите векторы через векторы и 3. В равнобедренной трапеции один из углов равен 600, боковая сторона равна 8 см, а меньшее основание 7 см. Найдите среднюю линию трапеции. 4. * В треугольнике МNK О – точка пересечения медиан, . Найдите число k. |
Контрольная работа № 2. Метод координат. | |
1 вариант. 1. Найдите координаты и длину вектора , если . 2. Напишите уравнение окружности с центром в точкеА (- 3;2), проходящей через точку В (0; — 2). 3. Треугольник МNK задан координатами своих вершин: М (- 6; 1), N (2; 4), К (2; — 2). а) Докажите, что Δ- равнобедренный; б) Найдите высоту, проведённую из вершины М. 4. * Найдите координаты точки N, лежащей на оси абсцисс и равноудалённой от точек Р и К, если Р( — 1; 3 ) и К( 0; 2 ). | 2 вариант. 1). Найдите координаты и длину вектора , если . 2). Напишите уравнение окружности с центром в точке С ( 2; 1 ), проходящей через точку D ( 5; 5 ). 3). Треугольник СDЕ задан координатами своих вершин: С (2; 2), D (6; 5), Е (5; — 2). а) Докажите, что Δ- равнобедренный; б) Найдите биссектрису, проведённую из вершины С. 4. * Найдите координаты точки А, лежащей на оси ординат и равноудалённой от точек В и С, если В( 1; — 3 ) и С( 2; 0 ). |
Контрольная работа № 3. Соотношения между сторонами и углами треугольника. | |
1 вариант
В = 600, ВС = Найдите АС.
7 см и 8 см, а угол между ними равен 1200. Найдите третью сторону треугольника.
А ( 3;9 ), В ( 0; 6 ), С ( 4; 2 ).
| 2 вариант
D = 450, СЕ =Найдите DE.
5 см и 7 см, а угол между ними равен 600. Найдите третью сторону треугольника.
А ( 3;9 ), В ( 0; 6 ), С ( 4; 2 ).
|
Контрольная работа № 4. Длина окружности и площадь круга. | |
1 вариант 1. 2. Вычислите длину дуги окружности с радиусом 4 см, если её градусная мера равна 1200. Чему равна площадь соответствующего данной дуге кругового сектора? 3. Периметр правильного треугольника, вписанного в окружность, равен Найдите периметр правильного шестиугольника, описанного около той же окружности. | 2 вариант 1. Найдите площадь круга и длину ограничивающей его окружности, если сторона квадрата, описанного около него, равна 6 см. 2. Вычислите длину дуги окружности с радиусом 10 см, если её градусная мера равна 1500. Чему равна площадь соответствующего данной дуге кругового сектора? 3. Периметр квадрата, описанного около окружности, равен 16 дм. Найдите периметр правильного пятиугольника, вписанного в эту же окружность. |
Контрольная работа № 5. Движения. | |
1 вариант 1. Начертите ромб АВСD. Постройте образ этого ромба: а) при симметрии относительно точки С; б) при симметрии относительно прямой АВ; в) при параллельном переносе на вектор ; г) при повороте вокруг точки D на 600 по часовой стрелке. 2. Докажите, что прямая, содержащая середины двух параллельных хорд окружности, проходит через её центр. 3. * Начертите два параллельных отрезка, длины которых равны.начертите точку, являющуюся центром симметрии, при котором один отрезок отображается на другой. | 2 вариант 1. Начертите параллелограмм АВСD. Постройте образ этого параллелограмма: а) при симметрии относительно точки D; б) при симметрии относительно прямой CD; в) при параллельном переносе на вектор ; г) при повороте вокруг точки А на 450 против часовой стрелки. 2. Докажите, что прямая, содержащая середины противоположных сторон параллелограмма, проходит через точку пересечения его диагоналей. 3.* Начертите два параллельных отрезка, длины которых равны. Постройте центр поворота, при котором один отрезок отображается на другой. |
Контрольная работа по геометрии №1 (9 класс) Вариант I 1. В параллелограмме ABCD точка M – середина стороны CD; N – точка на стороне AD, такая, что AN : ND = 3 : 4. Выразите векторы и , через векторы и . 2. Упростите выражение: а) б) в) г) д) 3. Высота, проведенная из вершины тупого угла равнобедренной трапеции, делит среднюю линию трапеции на отрезки, равные 2 см и 6 см. Найдите основания трапеции 4* В прямоугольной трапеции один из углов равен 120°. Найдите ее среднюю линию, если меньшая диагональ и большая боковая сторона трапеции равна b. | Контрольная работа по геометрии №1 (9 класс) Вариант II 1. Четырехугольник KMNP – параллелограмм. Выразите через векторы и векторы , , где А – точка на стороне PN, такая, что PA : AN = 2 : 5, B – середина отрезка MN. 2. Упростите выражение: а) б) в) г) д) 3. Высота, проведенная из вершины тупого угла равнобедренной трапеции, делит большее основание трапеции на два отрезка, меньший из которых равен 2 см. Найдите большее основание трапеции, если ее средняя линия равна 8 см. 4* В прямоугольной трапеции один из углов равен 120°. Найдите ее среднюю линию, если меньшая диагональ и большая боковая сторона трапеции равна b. | Контрольная работа по геометрии №1 (9 класс) Вариант I 1. 2. Упростите выражение: а) б) в) г) д) 3. Высота, проведенная из вершины тупого угла равнобедренной трапеции, делит среднюю линию трапеции на отрезки, равные 2 см и 6 см. Найдите основания трапеции 4* В прямоугольной трапеции один из углов равен 120°. Найдите ее среднюю линию, если меньшая диагональ и большая боковая сторона трапеции равна b. | Контрольная работа по геометрии №1 (9 класс) Вариант II 1. Четырехугольник KMNP – параллелограмм. Выразите через векторы и векторы , , где А – точка на стороне PN, такая, что PA : AN = 2 : 5, B – середина отрезка MN. 2. Упростите выражение: а) б) в) г) д) 3. Высота, проведенная из вершины тупого угла равнобедренной трапеции, делит большее основание трапеции на два отрезка, меньший из которых равен 2 см. Найдите большее основание трапеции, если ее средняя линия равна 8 см. 4* В прямоугольной трапеции один из углов равен 120°. Найдите ее среднюю линию, если меньшая диагональ и большая боковая сторона трапеции равна b. |
Контрольная работа для 9 класса по геометрии на тему «Координаты и Векторы»
Контрольная работа составлена для классов с базовым изучением математики. Содержит 2 варианта. Рассчитана на 2 урока.
Каждый вариант — готовый бланк с чертежами и места для рисунков (размещается с двух сторон листа А4). Удобны при проверке и оценивании работы: каждый вариант содержит таблицу для результатов.
Проверяет следующие знания и умения:
- Найти длину векторов (по рисунку на клетчатой бумаге)
- Изобразить линейную комбинацию изображенных векторов
- Найти координаты вектора по рисунку
- Отложить вектор от заданной точки
- Найти середину отрезка
- Найти площадь треугольника по координатам вершин
- Задача на доказательство (в координатах)
Просмотр содержимого документа
«Контрольная работа для 9 класса по геометрии на тему «Координаты и Векторы» »
Контрольная работа №1 по теме «Координаты и Векторы»
Выполнил ученик 9 класс ___________________________
Вариант I
1а | 1б | 2а | 2б | 2в | 3а | 3б | 4 | 5 | ⅀ | оц |
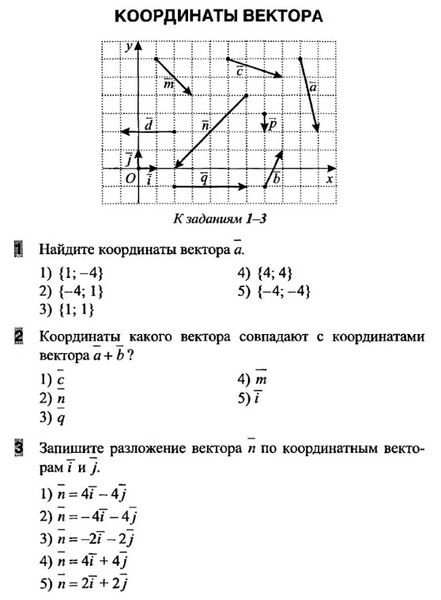
№1 а) Найти длину векторов данных векторов
б) Изобразить вектора: и
№2 на плоскости даны вектора a, b, c.
а) Найти координаты этих векторов и их длины
б) Координаты векторов и
№3 Вектор а)отложить его от точки (-8;7) и найти середину отрезка, соответствующего вектору на рисунке
№4 Найти площадь треугольника АВС, где А(-2;-4), B(6;8), C(-1;4)
№5 Доказать, что четырехугольник ABCD является ромбом и найти его площадь.
A(2;0), B(3;7), C(-2;-2), D(-3;5)
Контрольная работа №1 по теме «Координаты и Векторы»
Выполнил ученик 9 класс ___________________________
|
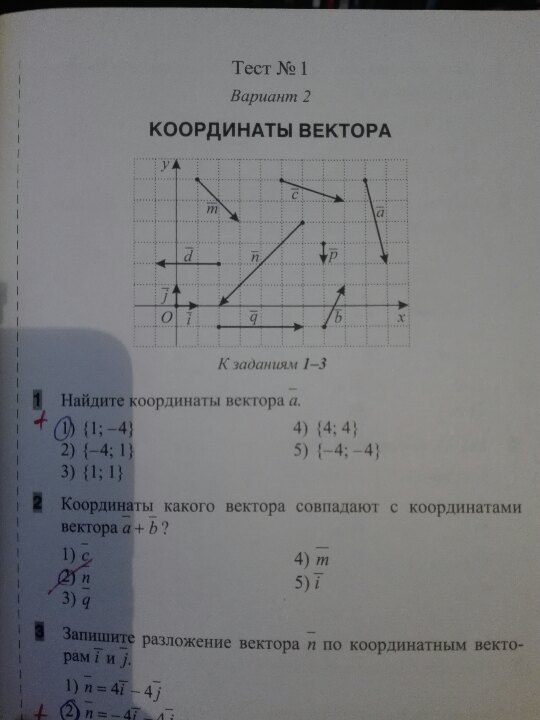
№1 а) Найти длину векторов данных векторов
б) Изобразить вектора: и
№2 на плоскости даны вектора a, b, c.
а) Найти координаты этих векторов и их длины
б) Координаты векторов и
№3 Вектор а)отложить его от точки (6;5) и найти середину отрезка, соответствующего вектору на рисунке
№4 Найти площадь треугольника АВС, где А(-4;5), B(4;1), C(4;6)
№5 Доказать, что четырехугольник ABCD является ромбом и найти его площадь.
A(1;-2), B(2;5), C(-5;4), D(-6;-3)
MCV4U — Исчисление и векторные изображения для 12-го класса — Примечания к экзамену— onstudynotes
12 класс — Исчисление и векторы
Тест на геометрические векторы
Векторы
- Вектор : величина, имеющая направление и величину
- Скаляр: — это величина, имеющая только величину
- Истинный пеленг: — это направленное измерение компаса, начиная с севера и вращаясь по часовой стрелке.

- Квадрантный пеленг: — измерение по компасу к востоку или западу от линии Север-Юг
- Эквивалентные векторы: равны по величине и направлению.
- Векторы могут быть переведены в любую точку одной плоскости и при этом будут эквивалентными
- Противоположные векторы: равны по величине, но противоположны по направлению
- Векторы могут быть
Сложение и вычитание векторов
- Поскольку векторы остаются эквивалентными независимо от того, куда они переводятся, их можно перемещать для построения диаграмм, более удобных для решения.
- Добавление векторов с использованием метода «хвост к голове» с использованием треугольника или «хвост к хвосту», метод с использованием параллелограмма.
- Результат — это вектор, соединяющий начало первого вектора с хвостом последнего вектора
- Если 2 вектора a и b параллельны в одном направлении, | a + b | = | а | + | b | и в том же направлении
- Если a и b имеют противоположные направления и | а | > | b |, то | а + б | = | а | — | б | и a + b находится в том же направлении, что и a.

- Вычесть векторы, добавив противоположный вектор
- Нулевой вектор: означает, что нет величины или направления. Сложение двух противоположных векторов
- Векторы соответствуют коммутативным, ассоциативным, и идентичности свойств
- Их можно складывать в любом порядке
- Упрощение векторных выражений аналогично упрощению целочисленных выражений
Скалярное умножение векторов
- Когда вектор умножается на скаляр, величина умножается на скаляр, и векторы параллельны.Направления остаются неизменными, если скаляр положительный, и становятся противоположными, если скаляр отрицательный.
- Умножение векторов подчиняется правилу распределения и ассоциативности
- Их можно расширить с помощью FOIL
- Их можно умножать в любом порядке
- Линейная комбинация векторов может быть сформирована путем добавления скалярных кратных 2 или более векторов.

Приложения геометрических векторов
- 2 Векторы, которые перпендикулярны друг другу и складываются, чтобы дать вектор v, называются компонентами прямоугольного вектора v.
- При решении результирующих вы можете использовать векторные операции, теорему Пифагора или тригонометрию.
- Equilibriant Vector : противоположность результирующего
12 класс — Исчисление и векторы
Тест декартовых векторов
Векторы
- Единичные векторы: i = [1, 0], j = [0,1] имеют величину 1 и хвосты в начале координат.
- Декартов вектор — это представление вектора на декартовой плоскости, где конечными точками являются точки на декартовой плоскости.
- Если вектор u транслируется так, что хвост находится в точке 0,0, то этот вектор называется вектором положения .
 Векторы положения представлены в квадратных скобках, где точки — [u1, u2].
Векторы положения представлены в квадратных скобках, где точки — [u1, u2]. - Величина u = [u1, u2] равна | u | = √ (u1 2 + u2 2 )
- Горизонтальные и вертикальные компоненты вектора u можно обозначить как [u1, 0] и [0, u1] соответственно
- Для векторов u = [u1, u2] и v = [v1, v2] и скаляра k,
- u + v = [u1 + v1, u2 + v2]
- u — v = [u1 — v1, u2 — v2]
- кв = [кв1, кв2]
- Декартов вектор между двумя точками P1 (x1, y1) и P2 (x2, y2) равен P1P2 = [x2 — x1, y2 — y1]
- Геометрические векторы также можно записать как:
- v = [| v | cosX, | v | sinX], где X — угол, составляющий v относительно положительной оси x
Точечный продукт
- Скалярное произведение определяется как a ∙ b = | a | | б | cos X, где X — угол между a и b.
- Точечное произведение дает скаляр.
- Для любых векторов u, v и w и скаляра k,
- u и v не могут быть нулевыми, перпендикулярны тогда и только тогда, когда u ∙ v = 0
- Коммутативная собственность
- Ассоциативное свойство
- Распределительная собственность
- u ∙ u = | u | 2
- ед ∙ 0 = 0
- Если u = [u1, u2] и v = [v1, v2], то u ∙ v = u1 * v1 + u2 * v2
Применения точечного произведения
- Для любых двух векторов u и v с углом X между ними проекция v на u является векторной составляющей v в направлении u.

- proj u v = | v | cos X (1 / | u | * | u |) или proj u v = (v ∙ u / u ∙ u) u
- | proj u v | = | v | cos X, если 0
- | proj u v | = — | v | cos X если 90
- | proj u v | = | u ∙ v / | u | |
- | proj u v | = — | v | cos X если 90
- На основании угла между u и v можно определить направление проекции.
Векторы в 3-м пространстве
- Те же свойства и формулы, что и у векторов в пространстве 2
- Ортогонально: Если два вектора ортогональны, угол между ними составляет 90 градусов.
Перекрестное произведение
- Перекрестное произведение двух векторов найдет вектор, перпендикулярный между ними обоими
- Используется для определения крутящего момента
- Направление определяется с помощью правила правой руки. Пальцы указывают на вектор r, затем наклоняются к вектору f, большой палец указывает в направлении векторного произведения
- a X b = (| a | | b | sin X) n где n — единичный вектор, ортогональный как a, так и b согласно правилу правой руки для направления, а X — угол между векторами.

- Для декартовых векторов:
- Если v = [v1, v2, v3] и u = [u1, u2, u3]
- u X v = [u2v3 — u3v1, u3v1 — u1v3, u1v2 — u2v1]
- | a X b | = | а | | б | грех X
- Это также вычисляет площадь параллелограмма
- Жилье
- u X v = — (v X u)
- Распределительная собственность
- ассоциативное свойство
- коммутативная собственность
- Если u! = 0 и v! = 0, u X v = 0 тогда и только тогда, когда u = mv, другими словами, они должны быть коллинеарны, чтобы это произошло.
Приложения перекрестного продукта
- Крутящий момент — это произведение длины гаечного ключа на прилагаемую силу
- Формулы для проекционных работ в 3D и 2D
- Тройное скалярное произведение: a * b X c
- Перекрестное произведение должно быть выполнено до того, как будет выполнено скалярное произведение
- Объем параллелограмма составляет: V = | w * u X v |
- Работа против силы тяжести — это скалярное произведение только с осью z для силы тяжести.

12 класс — Исчисление и векторы
Испытание линий и плоскостей
Уравнение линий с двумя и тремя пробелами
- В двухмерном пространстве линию можно определить четырьмя способами: наклонная форма пересечения оси y, векторное уравнение, параметрическая форма или скалярная форма.
- Наклон формы Y-пересечения: y = mx + b
- м — уклон
- b — точка пересечения по оси y
- Векторная форма: r = r 0 + tm
- или: [x, y] = [x 0 , y 0 ] + t [m 1 , m 2 ]
- [x, y] — вектор положения в любую точку на линии
- [x 0 , y 0 ] — вектор положения в любую точку на линии
- [m 1 , m 2 ] — вектор направления для линии
- Параметрическая форма:
- x = x o + tm 1 или x = x 0 + t [m 1 ]
- y = y 0 + tm 2 или y = y 0 + t [m 2 ]
- Те же определения, что и в векторной форме, полученные из векторной формы
- Скалярная форма: ax + by + c = 0
- n = [a, b] — вектор нормали к линии
- Если вектор направления d = [a, b], то вектор нормали n = [-b, a]
- Наклон формы Y-пересечения: y = mx + b
- В 3-пространстве линия может быть определена с помощью векторного уравнения или параметрического уравнения
- Векторная форма: r = r 0 + tm
- или: [x, y, z] = [x 0 , y 0, z 0 ] + t [m 1 , m 2 , м 3 ]
- [x, y, z] — вектор положения в любую точку на линии
- [x 0 , y 0, z 0 ] — вектор положения в любую точку на линии
- [m 1 , m 2, m 3 ] — вектор направления для линии
- Параметрическая форма:
- x = x o + tm 1 или x = x 0 + t [m 1 ]
- y = y 0 + tm 2 или y = y 0 + t [m 2 ]
- z = z 0 + tm 3 или y = z 0 + t [m 3 ]
- Те же определения, что и в векторной форме, полученные из векторной формы
- Векторная форма: r = r 0 + tm
- Вектор нормали — это линия, перпендикулярная этой линии
- Для определения линии необходимы 2 точки или точка и вектор направления
- Для линий в двухместном пространстве точка и вектор нормали также могут определять линию
Уравнения плоскостей
- В двухмерном пространстве скалярное уравнение определяет линию.
 В трехмерном пространстве скалярное уравнение определяет плоскость
В трехмерном пространстве скалярное уравнение определяет плоскость - В 3-пространстве плоскость может быть определена с помощью векторного уравнения, параметрического уравнения или скалярного уравнения.
- Векторная форма: r = r 0 + tm
- или: [x, y, z] = [x 0 , y 0, z 0 ] + t [a 1 , a 2 , a 3 ] + s [b 1 , b 2, b 3 ]
- [x, y, z] — вектор положения для любой точки на плоскости
- [x 0 , y 0, z 0 ] — вектор положения для любой точки на плоскости
- [a 1 , a 2, a 3 ] и [b 1 , b 2, b 3 ] должны быть непараллельными векторами на плоскости
- Параметрическая форма:
- x = x o + ta 1 + tb 1 или x = x 0 + t [a 1 ] + s [b 1 ]
- y = y 0 + ta 2 + tb 2 или y = y 0 + t [a 2 ] + s [b 2 ]
- z = z 0 + ta 3 + tb 3 или y = z 0 + t [a 3 ] + s [b 3 ]
- Те же определения, что и в векторной форме, полученные из векторной формы
- Скалярная форма: ax + by + cz + d = 0
- Где [a, b, c] — вектор, нормальный к плоскости
- Векторная форма: r = r 0 + tm
- Плоскость может быть определена 3 неколлинеарными точками или точкой и 2 непараллельными векторами направления
- Перехват самолета
- Пересечение плоскости по оси X находится путем задания y = z = 0 и решения относительно x
- Пересечения Y и Z одинаковы, если установить другие 2 переменные на ноль
Пересечение линий в 2-м и 3-м пространствах
- В 2-Space пересечение двух линий имеет 3 возможности.

- (1) Линии пересекаются ровно в одной точке
- (2) Линии совпадают, значит решений бесконечно много
- (3) Линии параллельны, решений нет
- В 3-пространстве пересечение двух линий может иметь 4 возможности
- (1) Они пересекаются в одной точке
- (2) Они совпадают
- (3) Они параллельны
- (4) Это перекошенных линий , где они не параллельны и не имеют решения
- Чтобы найти расстояние между двумя наклонными линиями, формула:
- d = | (P 1 P 2 точка n / n) |
- , где P 1 и P 2 — любые точки на каждой линии, а n = m 1 x m 2 .
- Чтобы найти пересечение, просто приравняйте каждую пару линий в параметрической форме и решите для X, Y и Z в каждом наборе.
Пересечение плоскостей и линий
- В 3-пространстве пересечение плоскостей и линий имеет 3 возможности
- (1) Прямая пересекает плоскость в одной точке
- (2) Прямая совпадает с плоскостью в бесконечном количестве точек
- (3) Линия параллельна и не касается плоскости, решений нет
- Расстояние между точкой P и плоскостью:
- d = | n точек PQ | / | n |
- где n — вектор нормали к плоскости, Q — любая точка на плоскости
- d = | n точек PQ | / | n |
- Чтобы найти пересечение, подставьте каждый X, Y и Z параметрического уравнения в уравнение плоскости.
 Затем после того, как t будет найдено, подставьте его обратно в строку, чтобы найти каждое значение X Y и Z.
Затем после того, как t будет найдено, подставьте его обратно в строку, чтобы найти каждое значение X Y и Z.
Пересечение плоскостей
- Есть 3 возможности пересечения 2-х плоскостей
- (1) Плоскости пересекаются по линии
- (2) Плоскости совпадают, решений бесконечно много
- (3) Плоскости параллельны, решений нет
- С 2 самолетами:
- 1) Проверить параллельность нормалей
- 2) Попробуйте решить на основе параллельности нормалей
- Если они параллельны, вы получите бесконечное количество решений или их отсутствие.
- Если они не параллельны, в качестве решения вы получите линию
- Есть 7 возможностей пересечения 3-х плоскостей:
- Если их нормали параллельны
- (1) Все 3 плоскости совпадают, если все нормали одинаковы
- (2) Все 3 плоскости параллельны, если все нормали различны
- (3) 2 плоскости совпадают и 1 параллельна, если 2 нормали различны
- (4) 1 плоскость пересекает 2 плоскости, совпадающие или параллельные, если 2 нормали совпадают
- Если их нормали не параллельны
- Если тройное скалярное произведение (n1 x n2) * n3 = 0
- (5) Треугольная призма сформирована без пересечения (0x + 0y = c)
- (6) «Вращающаяся дверь» образована пересечением линий (0x + 0y = 0)
- Если тройное скалярное произведение не равно 0
- (7) Все плоскости пересекаются в точке
- Если тройное скалярное произведение (n1 x n2) * n3 = 0
- Если их нормали параллельны
- Для пересечения карусельной двери и пересечения двух плоскостей на одной линии, параметр z = t должен использоваться для определения линии пересечения.

12 класс — Исчисление и векторы
Тест на скорость изменений
Темпы изменения и наклон кривой
- Средняя скорость изменения: означает скорость изменения функции за интервал. Он соответствует наклону секущей, соединяющей две конечные точки интервала .
- Мгновенная скорость изменения: относится к скорости изменения в определенной точке.Он соответствует наклону касательной, проходящей через единственную точку или точку касания на графике функции.
- Оценка мгновенной скорости изменения может быть получена путем вычисления средней скорости изменения на наименьшем интервале, для которого доступны данные.
- Его также можно определить, нарисовав касательную на графике
Темпы изменения с использованием уравнений
- Для заданной функции y = f (x) мгновенная скорость изменения при x = a оценивается путем вычисления наклона секущей на очень небольшом интервале, a <= x <= a + h, так что h очень маленькое число
- Выражение f (a + h) — f (a) / h, где h not = 0, называется коэффициентом разности
- Используется для вычисления наклона секущей между (a, f (a)) и (a + h, f (a + h)).
 Это позволит вам оценить наклон касательной при приближении h к 0.
Это позволит вам оценить наклон касательной при приближении h к 0.
- Используется для вычисления наклона секущей между (a, f (a)) и (a + h, f (a + h)).
Лимиты
- Последовательность — это функция, f (n) = t n , доменом которой является набор натуральных чисел N Предел
- , когда x приближается к a для f (x), существует, если выполняются следующие условия:
- существует предел, когда x приближается к a- для f (x) (существует левый предел)
- существует предел, когда x приближается к a + для f (x) (существует правый предел)
- правая граница и левая граница равны
- Если они не равны и критерии не соблюдаются, то ограничение не существует
- Пределы могут быть бесконечным действительным числом
- Функция продолжается со значением, если они верны:
- f (a) существует
- предел, когда x приближается к существует
- Предел, когда x приближается к a и f (a) одинаковы
Ограничения и непрерывность
- Предел функции при x = a может существовать, даже если функция является разрывной при x = a.

- Короче говоря, график прерывистой функции невозможно нарисовать, не подняв карандаш
- Есть 3 вида прерывания: прыжок, съемный и бесконечный
- Если прямая подстановка x = a приводит к неопределенному пределу 0/0, определите эквивалентную функцию, которая представляет f (x).
- Разрыв может быть устранен путем разложения на множители, рационализации числителя или знаменателя, расширения и упрощения.
Введение в производные инструменты
- Производные y = f (x) — это новая функция y = f ‘(x), которая представляет наклон касательной или мгновенную скорость изменения в любой точке кривой y = f (x) .
- Производная функция определяется определением первых принципов для производной, f ’(x) = lim h -> 0 f (x + h) — f (x) / h, если предел существует
- Различные обозначения для производной y = f (x) следующие: y = f ’(x), y’, dy / dx и d / dx f (x).
- Если производная не существует в точке кривой, функция недифференцируема в этом значении x.
 Это может произойти в точках, где функция является прерывистой, или в случаях, когда функция имеет резкое изменение, которое представлено острием или углом на графике.
Это может произойти в точках, где функция является прерывистой, или в случаях, когда функция имеет резкое изменение, которое представлено острием или углом на графике.
12 класс — Исчисление и векторы
Тест деривативов
Производные полиномиальной функции
- Правила производных упрощают процесс дифференцирования многочленов с использованием первых принципов
- При дифференцировании радикалов мы записываем радикалы в дробной форме
- Чтобы дифференцировать степень x, которая находится в знаменателе, сначала выразите ее как степень с отрицательной экспонентой
- Правило производной: x n = nx n-1
- Сумма производных: (f (x) + g (x)) ’= f’ (x) + g ’(x)
- Разница производных: (f (x) — g (x)) ’= f’ (x) — g ’(x)
Правило продукта
- Правило продукта: (f (x) * g (x)) = f ’(x) g (x) + f (x) g’ (x)
- Обозначение Лейбница: d / dx [f (x) g (x)] = d / dx [f (x)] g (x) + f (x) d / dx [g (x)]
Скорость, ускорение и секундные производные
- Вторая производная функции определяется путем дифференцирования первой производной функции
- Для заданной функции положения s (t) ее функция скорости равна v (t) или s ’(t), а ее ускорение равно a (t), v’ (t) или s ’’ (t)
- Когда v (t) = 0, объект покоится.
 Есть много случаев, когда объект временно находится в состоянии покоя при изменении направления.
Есть много случаев, когда объект временно находится в состоянии покоя при изменении направления. - Когда v (t)> 0, объект движется в положительном направлении
- Когда v (t) <0, объект движется в отрицательном направлении
- Когда a (t)> 0, скорость объекта увеличивается
- Когда a (t) <0, скорость объекта уменьшается
- Объект ускоряется, если a (t) x v (t)> 0, и замедляется, если v (t) x a (t) <0.
Правило цепочки
- Используется для различения составных функций, f = g o h.
- Для данной функции правило цепочки:
- (f (g (x))) ’= f’ (g (x) * g ’(x)
- В обозначениях Лейбница,
Правило частного
- Чтобы найти производную частного:
- q (x) = f ’(x) g (x) — f (x) g’ (x) / g 2 (x)
Скорость изменения проблем
- Функция спроса или цены p (x) — это цена, по которой может быть продано x единиц продукта или услуги
- Функция дохода R (x) — это общий доход от продажи x единиц продукта или услуги.
 R (х) = х * P (х)
R (х) = х * P (х) - Функция затрат C (x) — это общие затраты на производство x единиц продукта или услуги
- Функция прибыли, P (x) равно P (x) = R (x) — C (x)
- C ’(x) — функция предельных затрат
- R ’(x) — функция предельного дохода
- P ’(x) — функция предельной прибыли
12 класс — Исчисление и векторы
Тест построения эскиза кривой
Интервал увеличения и уменьшения
- Функция увеличивается, если наклон касательной положительный на всем интервале
- Функция уменьшается, если наклон касательной отрицателен на всем интервале
- Интервалы, в течение которых функция увеличивается или уменьшается, можно определить путем нахождения производной f ’(x) и решения неравенств f’ (x) <= 0 или f ’(x)> = 0.
Максимумы и минимумы
- Если f ’(x) изменяется с положительного на ноль на отрицательное, то всякий раз, когда он равен 0, будет точка локального максимума
- Если f ’(x) изменяется с отрицательного на ноль на положительный, то всякий раз, когда он равен 0, будет точка локального минимума
- Абсолютные максимальные и минимальные значения находятся в локальных экстремумах или в конечных точках интервала
- Критическое число — это число в области определения функции, где f ’(a) = 0 или f’ (a) существует
Тест на вогнутость и вторые производные
- Вторая производная — это производная от первой производной.
 Это скорость изменения наклона касательной
Это скорость изменения наклона касательной- Функция является вогнутой на интервале, если вторая производная положительна на этом интервале
- Функция вогнута вниз на интервале, если вторая производная отрицательна
- Функция имеет точку перегиба в точке, где вторая производная меняет знак, где f ’’ (x) = 0
- Критические точки можно классифицировать, используя вторую производную или исследуя график f ’’ (x)
- Если f ’(a) = 0 и f’ ’(a)> 0, существует локальный минимум в (a, f (a))
- Если f ’(a) = 0 и f’ ’(a) <0, существует локальный максимум в (a, f (a))
- Если f ’(a) = 0 и f’ ’(a) = 0, а f’ ’(x) меняет знак в x = a, то есть POI в (a, f (a))
Простые рациональные функции
- Вертикальные асимптоты — это значения x, при которых знаменатель равен нулю
- Учитывать ВА при поиске интервалов увеличения или уменьшения вогнутости
Эскиз кривой
- При рисовании кривой не забудьте включить область, асимптоты, точки пересечения, критические значения от первой производной, критические значения второй производной, локальные и абсолютные экстремумы, точки перегиба, интервалы увеличения и уменьшения и вогнутость.

Проблемы оптимизации
- Определите, в чем проблема
- Определите переменные и создайте диаграмму, если это помогает
- Определите количество, которое нужно оптимизировать, и напишите уравнение
- Определить независимую переменную
- Определить функцию
- Определение и ограничения функции
- Определите функции и классифицируйте критические точки
- Проверьте, соответствует ли решение заданному вопросу и соответствует ли оно вопросу
12 класс — Исчисление и векторы
Синусоидальные и логарифмические производные
Производные функции синуса и косинуса
- Производная y = sin x: y ’= cos x
- Производная y = cos x: y ’= -sin x
- Производная y = sin (f (x)): y ’= cos (f (x)) * f’ (x)
- Производная y = cos (f (x)): y ’= -sinx (f (x)) * f’ (x)
- Производная y = sin 2 (f (x)) равна y ’= 2 cos (f (x)) * f’ (x)
- Производная y = cos 2 (f (x)) равна y ’= -2 sin (f (x)) * f’ (x)
Простые задачи тригонометрических приложений с гармоническим движением
- 1-я производная, используемая для нахождения скоростей
- 2-я производная, используемая для определения ускорения, а также максимальной / минимальной скорости
- Чтобы найти период из его уравнения, это 360 / k или 2 Пи / k для радианов
Номер e
- Символ e определяется как предел, когда n -> бесконечность (1 + 1 / n) n .
 Значение ~ 2.71
Значение ~ 2.71 - Скорость изменения экспоненциальной функции также является экспоненциальной
- Производная y = e x равна y = e x (то же, что и исходная функция)
Натуральный логарифм
- Lnx = бревно e x
- Функции y = lnx и y = e x являются обратными
Производные от экспонент
- Производная y = b x : y ’= b x * lnx
- Производная y = b f (x) равна y ’= b f (x) * ln b * f’ (x)
- Производная y = e f (x) равна y ’= e f (x) * f’ (x)
- Вы решаете большинство логарифмов, применяя ln или записывая обе стороны и изолировав переменную.
MCV4U — Оценка 12 по исчислению и векторам — Тест по геометрическим векторам— onstudynotes
Векторы
- Вектор : величина, имеющая направление и величину
- Скаляр: — это величина, имеющая только величину .
- Истинный пеленг: — это направленное измерение компаса, начиная с севера и вращаясь по часовой стрелке.
- Квадрантный пеленг: — измерение по компасу к востоку или западу от линии Север-Юг
- Эквивалентные векторы: равны по величине и направлению.
- Векторы могут быть переведены в любую точку одной плоскости и при этом будут эквивалентными
- Противоположные векторы: равны по величине, но противоположны по направлению
- Векторы могут быть

Сложение и вычитание векторов
- Поскольку векторы остаются эквивалентными независимо от того, куда они переводятся, их можно перемещать для построения диаграмм, более удобных для решения.
- Добавление векторов с использованием метода «хвост к голове» с использованием треугольника или «хвост к хвосту», метод с использованием параллелограмма.

- Результат — это вектор, соединяющий начало первого вектора с хвостом последнего вектора
- Если 2 вектора a и b параллельны в одном направлении, | a + b | = | а | + | b | и в том же направлении
- Если a и b имеют противоположные направления и | а | > | b |, то | а + б | = | а | — | б | и a + b находится в том же направлении, что и a.
- Вычесть векторы, добавив противоположный вектор
- Нулевой вектор: означает, что нет величины или направления.Сложение двух противоположных векторов
- Векторы следуют коммутативным, ассоциативным, и идентичности свойств
- Их можно складывать в любом порядке
- Упрощение векторных выражений аналогично упрощению целочисленных выражений
Скалярное умножение векторов
- Когда вектор умножается на скаляр, величина умножается на скаляр, и векторы параллельны.
 Направления остаются неизменными, если скаляр положительный, и становятся противоположными, если скаляр отрицательный.
Направления остаются неизменными, если скаляр положительный, и становятся противоположными, если скаляр отрицательный. - Умножение векторов подчиняется правилу распределительного и ассоциативного
- Их можно расширить с помощью FOIL
- Их можно умножать в любом порядке
- Линейная комбинация векторов может быть сформирована путем добавления скалярных кратных 2 или более векторов.
Приложения геометрических векторов
- 2 Векторы, которые перпендикулярны друг другу и складываются, чтобы дать вектор v, называются компонентами прямоугольного вектора v.
- При решении результирующих вы можете использовать векторные операции, теорему Пифагора или тригонометрию.
- Equilibriant Vector : противоположность результирующего
MCV4U — Класс 12, Исчисление и векторы — Уравнения прямых и плоскостей — примечания к студентам
12 класс — Исчисление и векторы
Испытание линий и плоскостей
Уравнение линий 2-х и 3-х пространств
- В двухмерном пространстве линия может быть определена 4 способами: форма углового пересечения по оси Y, векторное уравнение, параметрическая форма или скалярная форма
- Угол наклона Y-образной формы: y = mx + b
- м — уклон
- b — точка пересечения по оси y
- Векторная форма: r = r 0 + tm
- или: [x, y] = [x 0 , y 0 ] + t [m 1 , m 2 ]
- [x, y] — вектор положения в любую точку на линии
- [x 0 , y 0 ] — вектор положения в любую точку на линии
- [m 1 , m 2 ] — вектор направления для линии
- Параметрическая форма:
- x = x o + tm 1 или x = x 0 + t [m 1 ]
- y = y 0 + tm 2 или y = y 0 + t [м 2 ]
- Те же определения, что и в векторной форме, полученные из векторной формы
- Скалярная форма: ax + by + c = 0
- n = [a, b] — вектор нормали к линии
- Если вектор направления d = [a, b], то вектор нормали n = [-b, a]
- В трехмерном пространстве линия может быть определена с помощью векторного уравнения или параметрического уравнения
- Векторная форма: r = r 0 + tm
- или: [x, y, z] = [x 0 , y 0, z 0 ] + t [m 1 , м 2, м 3 ]
- [x, y, z] — вектор положения в любую точку на линии
- [x 0 , y 0, z 0 ] — вектор положения в любую точку на линии
- [m 1 , m 2, m 3 ] — вектор направления для линии
- Параметрическая форма:
- x = x o + tm 1 или x = x 0 + t [m 1 ]
- y = y 0 + tm 2 или y = y 0 + t [m 2 ]
- z = z 0 + tm 3 или y = z 0 + t [m 3 ]
- Те же определения, что и в векторной форме, полученные из векторной формы
- Вектор нормали — это линия, перпендикулярная этой линии
- Для определения линии необходимы 2 точки или точка и вектор направления
- Для линий в двухместном пространстве точка и вектор нормали также могут определять линию
Уравнения плоскостей
- В двухмерном пространстве скалярное уравнение определяет линию.
 В трехмерном пространстве скалярное уравнение определяет плоскость
В трехмерном пространстве скалярное уравнение определяет плоскость - В трехмерном пространстве плоскость может быть определена с помощью векторного уравнения, параметрического уравнения или скалярного уравнения
- Векторная форма: r = r 0 + tm
- или: [x, y, z] = [x 0 , y 0, z 0 ] + t [a 1 , a 2, a 3 ] + s [b 1 , b 2, b 3 ]
- [x, y, z] — вектор положения для любой точки на плоскости
- [x 0 , y 0, z 0 ] — вектор положения для любой точки на плоскости
- [a 1 , a 2, a 3 ] и [b 1 , b 2, b 3 ] должны быть непараллельными векторами на плоскости
- Параметрическая форма:
- x = x o + ta 1 + tb 1 или x = x 0 + t [a 1 ] + s [b 1 ]
- y = y 0 + ta 2 + tb 2 или y = y 0 + t [a 2 ] + s [b 2 ]
- z = z 0 + ta 3 + tb 3 или y = z 0 + t [a 3 ] + s [b 3 ]
- Те же определения, что и в векторной форме, полученные из векторной формы
- Скалярная форма: ax + by + cz + d = 0
- Где [a, b, c] — вектор, нормальный к плоскости
- Плоскость может быть определена 3 неколлинеарными точками или точкой и 2 непараллельными векторами направления
- Перехват самолета
- Пересечение плоскости по оси X находится путем задания y = z = 0 и решения относительно x
- Пересечения Y и Z одинаковы, если установить другие 2 переменные на ноль
Пересечение линий в 2-х и 3-х пространствах
- В 2-Space пересечение двух линий имеет 3 возможности.
-reshenie-zadacha-413.jpg)
- (1) Линии пересекаются ровно в одной точке
- (2) Линии совпадают, значит решений бесконечно много
- (3) Линии параллельны, решений нет
- В 3-пространстве пересечение 2 линий может иметь 4 возможности
- (1) Они пересекаются в одной точке
- (2) Они совпадают
- (3) Они параллельны
- (4) Это перекошенных линий , где они не параллельны и не имеют решения
- Чтобы найти расстояние между двумя наклонными линиями, формула:
- d = | (P 1 P 2 точка н / п) |
- , где P 1 и P 2 — любые точки на каждой линии, а n = m 1 x m 2 .
- Чтобы найти пересечение, просто приравняйте каждую пару линий в параметрической форме и решите для X, Y и Z в каждом наборе.
Пересечение плоскостей и линий
- В 3-пространстве пересечение плоскостей и линий имеет 3 возможности
- (1) Прямая пересекает плоскость в одной точке
- (2) Прямая совпадает с плоскостью в бесконечном количестве точек
- (3) Линия параллельна и не касается плоскости, решений нет
- Расстояние между точкой P и плоскостью:
- d = | n точек PQ | / | n |
- где n — вектор нормали к плоскости, Q — любая точка на плоскости
- Чтобы найти пересечение, подставьте каждый X, Y и Z параметрического уравнения в уравнение плоскости.
 Затем после того, как t будет найдено, подставьте его обратно в строку, чтобы найти каждое значение X Y и Z.
Затем после того, как t будет найдено, подставьте его обратно в строку, чтобы найти каждое значение X Y и Z.
Пересечение плоскостей
- Есть 3 возможности пересечения 2-х плоскостей
- (1) Плоскости пересекаются по линии
- (2) Плоскости совпадают, решений бесконечно много
- (3) Плоскости параллельны, решений нет
- С 2-мя самолетами:
- 1) Проверить параллельность нормалей
- 2) Попробуйте решить на основе параллельности нормалей
- Если они параллельны, вы получите бесконечное количество решений или их отсутствие.
- Если они не параллельны, в качестве решения вы получите линию
- Есть 7 возможностей пересечения 3-х плоскостей:
- Если их нормали параллельны
- (1) Все 3 плоскости совпадают, если все нормали одинаковы
- (2) Все 3 плоскости параллельны, если все нормали различны
- (3) 2 плоскости совпадают и 1 параллельна, если 2 нормали различны
- (4) 1 плоскость пересекает 2 плоскости, совпадающие или параллельные, если 2 нормали совпадают
- Если их нормали не параллельны
- Если тройное скалярное произведение (n1 x n2) * n3 = 0
- (5) Треугольная призма сформирована без пересечения (0x + 0y = c)
- (6) «Вращающаяся дверь» образована пересечением линий (0x + 0y = 0)
- Если тройное скалярное произведение не равно 0
- (7) Все плоскости пересекаются в точке
- Для пересечения карусельной двери и пересечения двух плоскостей на одной линии следует использовать параметр z = t, чтобы найти линию пересечения.

БЕСПЛАТНЫХ видео и учебная страница в стиле учебника для 12 класса. Исчисление и векторы
. Исчисление и векторы для 12-го класса
Полный список БЕСПЛАТНЫХ видеоуроков по Исчислению и векторам для 12 класса в Канаде и Северной Америке
Исчисление было разработано немецким математиком и философом Готфридом Вильгельмом Лейбницем и английским математиком и физиком сэром Исааком Ньютоном (одновременно, но из разных частей мира).
Исчисление состоит из двух основных частей: производных и интегралов. Производные, компонент Исчисления, который преподается в Исчислении и Векторах, в основном помогают в решении проблем, связанных со скоростью изменений и построением кривых. Между тем, интеграция используется для поиска площадей и объемов, образованных самыми сложными кривыми и формами. Таким образом, Calculus наиболее полезен при решении задач, которые возникают в непрерывном состоянии.
В исчислении используется множество различных обозначений для обозначения производной функции. Лейбниц ввел обозначение df (x) / dx или dy / dx (читается как ‘d’ ‘y’ по ‘d’ ‘x’ или ‘производная от’ y ‘по отношению к’ x ‘), в то время как Ньютон придумал ‘точечная запись’
(ė или ë), который сейчас в основном используется для обозначения производных по времени. В нотации Леонарда Эйлера в качестве дифференциального оператора используется префикс «D», за которым следует функция «f (x)» (т.е. Df и D 2 f, D 3 f … D n f используется для высших порядок дифференциалов). Он также ввел обозначение D x f (x) или D x y, которое читается точно так же, как обозначение Лейбница выше.Самая популярная на сегодняшний день нотация принадлежит Джозефу Луи Лагранжу, так как он ввел «простую нотацию», такую как f ‘(x) (читается как «f» «простое число от« x ») и f’ ‘(x), f » ‘(x) … f n (x) для более высокого порядка дифференцирования.
Лейбниц ввел обозначение df (x) / dx или dy / dx (читается как ‘d’ ‘y’ по ‘d’ ‘x’ или ‘производная от’ y ‘по отношению к’ x ‘), в то время как Ньютон придумал ‘точечная запись’
(ė или ë), который сейчас в основном используется для обозначения производных по времени. В нотации Леонарда Эйлера в качестве дифференциального оператора используется префикс «D», за которым следует функция «f (x)» (т.е. Df и D 2 f, D 3 f … D n f используется для высших порядок дифференциалов). Он также ввел обозначение D x f (x) или D x y, которое читается точно так же, как обозначение Лейбница выше.Самая популярная на сегодняшний день нотация принадлежит Джозефу Луи Лагранжу, так как он ввел «простую нотацию», такую как f ‘(x) (читается как «f» «простое число от« x ») и f’ ‘(x), f » ‘(x) … f n (x) для более высокого порядка дифференцирования.
Пожалуйста, обратитесь к дереву предварительных требований по математике для старших классов, чтобы увидеть рекомендуемые курсы и материалы, с которыми следует ознакомиться, прежде чем приступить к изучению математики и векторов.
NB:
У каждой темы в разделе есть как минимум 3 разных докладчика.Это обеспечивает доступ к различным стратегиям обучения по любой одной теме. (Также обратите внимание, что темы не перечислены в каком-либо конкретном или рекомендуемом порядке). Мы советуем вам с осторожностью использовать наши скомпилированные источники. Это внешние источники. Если вы обнаружите ошибки или ошибки в видео, к которым вы обращаетесь, пожалуйста, сообщите нам через
статей для 9 класса
Гэльский — норвежский: курсы грамматики и языка
Оджибве — зарма: грамматика и языковые курсы
Около
FAQ: Вопросы о языке
Биографии и хроники известных людей
Как умер Брюс Ли?
Какие факты о Бараке Обаме?
Что Мартин Лютер Кинг сделал для продвижения движения за гражданские права?
Чем больше всего известна Глория Анзалдуа?
Каковы были достижения сэра Эдмунда Хиллари?
Почему Дарвин так долго ждал, чтобы опубликовать свою теорию?
Почему Шекспира называют бардом?
Хронология
Хронология Барака Обамы
Эдмунд Хиллари Хронология
Образовательные статьи и ресурсы
Какие бывают типы памяти?
Для студентов
Греческие и латинские коренные слова
Для учителей (и родителей)
Планы занятий и уроков
100 подсказок по творческому письму для средней школы
Грамматика 9 классов
Идеи плана урока по творческому письму
Дар волхвов Литературные термины
Урок грамматики для определения предметов
Английские литературные термины средней школы
Введение в слова перехода
План урока по написанию резюме фильма
Планы уроков по навыкам написания резюме
Планы уроков по написанию сценария
Планы уроков по написанию рассказов
План урока по литературным терминам
Планы уроков поэзии Звукоподражание
Советы по написанию светоотражающего дневника для студентов
Научи детей писать хайку
Обучение запутанным и незнакомым словам
Обучение написанию сочинений в средних школах
Обучение множественному владению
Преподавание орфографии в 9 классе
Какие простые стихотворения нужно запоминать?
Что такое план урока со словарным контекстом?
Написание одной минуты убедительной речи
Слова Dolch Sight
Действия с использованием слов Dolch
Советы и инструкции
Различные стили обучения
Эффективные инструкции по грамматике
Как оценивать словарный запас
Как улучшить свою память
Как научить новый словарный запас
Глоссарий по стратегиям преподавания
Советы по составлению планов уроков
Какие существуют форматы примерного плана урока?
Рабочие листы и печатные издания
Рабочий лист часто путаемых слов
Рабочие листы бесплатных глаголов
Таблица неправильных глаголов
Рабочий лист литературных терминов
Рабочие листы по глаголам прошедшего времени
Рабочие листы по глаголам настоящего времени
Правила грамматики английского языка и их использование
Помощь с домашним заданием
Прилагательные
Прилагательные к личным качествам
Атрибутивные прилагательные
Примеры личных прилагательных
Как упорядочить совокупные прилагательные в предложении
Используемые латинские прилагательные
Предикат Прилагательное
Рабочий лист предикатных прилагательных
Типы прилагательных
Что такое согласованные прилагательные?
Что такое сравнительное прилагательное?
Что такое демонстративное прилагательное?
Что такое причастное прилагательное?
Что такое подходящее прилагательное?
Что такое прилагательное дополнение?
Что такое прилагательное?
Наречия
Действия с наречиями
Наречия
Планы уроков наречия
Рабочий лист наречий
Наречия, начинающиеся с R
Конъюнктивное наречие
Список 100 наречий
Список наречий для улучшения вашего письма
Список конъюнктивных наречий
Относительные наречия
Типы наречий
Что такое наречие?
Капитализация
Игры с заглавной буквы
Использование заглавных букв в именах животных
Использование заглавных букв в названиях должностей
Капитализация сезонов
Использование заглавных букв в песнях
Капитализация состояний
Практика капитализации
Тесты капитализации
Рабочий лист без заглавных букв
Грамматические правила использования заглавных букв
Правила использования заглавных букв в заголовках статей
Правила использования заглавных существительных
Особые случаи капитализации
Обучающие заглавные буквы
Союзы
Условные соединения
Упражнения на соединение
Координационные союзы
Корреляционные Конъюнкции
Подчиненные союзы
Обучающие союзы
Типы союзов
Что такое соединение?
Грамматика
Список игровых слов для шарад
Списки слов в шарадах для детей
Рождественская схватка
Веселые языковые игры
Игры для изучения грамматики
Игры для изучения грамматики в средней школе
Как расшифровывать криптограммы
SAT Словарь Игры в слова
Поиск слова Scrabble
Игры в слова
Говори, как Шекспир
Словарные игры для групп
Программа для решения проблем со словами
Грамматические правила и советы по грамматике
11 правил грамматики
5 наиболее распространенных грамматических ошибок
7 правил грамматики, которые вы можете нарушить
Разве это не слово из четырех букв
Базовые слова и корневые слова — это одно и то же?
Определенные и неопределенные статьи
Правила грамматики английского языка для положительного множественного числа
Инструменты для обучения грамматике английского языка
Как официально записать дату
Неправильные существительные множественного числа
Правила для владельцев
Правила написания чисел
Что такое дополнение в грамматике?
Грамматический стиль и использование
100 наиболее часто неправильно произносимых слов и фраз на английском языке
Action vs. Слова бездействия
Слова бездействия
Эффект vs. эффект: выбор правильного слова
Антонимы, синонимы и омонимы
Соответствующие слова для обозначения серьезного заболевания
Соответствующие слова для некролога
Неси меня или обнажайся со мной: что правильно?
Изменить пассивный голос на активный
Утешительные слова во время смерти
Успокаивающие слова перед операцией
Утешительные слова для трудных времен
Слова, которые часто путают
Comprise vs.Составить
Описательные слова для мужчины
Описательные слова для обозначения еды
Описательные слова для музыки
Описательные слова для ароматов
Описательные слова, начинающиеся с буквы E
Описательные слова, начинающиеся с буквы Z
Двойная отрицательная проблема
Эффекты отрицательных слов
Ободряющие слова на 13-й день рождения
Ободряющие слова для друга с диагнозом рак
Ободряющие слова для солдата
Ободряющие слова для сотрудников
Ободряющие слова на все случаи жизни
Образный язык
В поисках противоположности слов
Бесплатная онлайн-проверка грамматики
Серый или Серый: какое правильное написание?
Как увеличить свой словарный запас
Как поставить точку в диалоге
Как выразить признательность словами
Как правильно использовать дополнение и комплимент
Как использовать i. е. и например
е. и например
Вдохновляющие слова на 60-летие
Ключевые слова и утверждения, которые можно использовать для описания себя
Любовь: слова
Оксфордская запятая: нужно ли ее использовать?
Персонификация против антропоморфизма
Положительные слова для оценки сотрудников
Правила для Там и их
Сентиментальные слова на день рождения папы
Сексистский язык
Там, их и они практикуют
Вдумчивые слова для благодарственной открытки
Советы по выбору правильных слов
10 лучших аргументационных тем для эссе
Беспристрастный язык
Словарные стратегии
Погода vs.Ли
Что такое жанр драматической биографии?
Что такое профессиональная биография?
Что такое тематическая биография?
Что входит в биографию?
В чем разница между наречием и наречием?
В чем разница между советом и советом?
В чем разница между всем и всем вместе?
В чем разница между коннотацией и обозначением?
В чем разница между и т. Д.и Et Al?
Д.и Et Al?
В чем разница между мисс, мисс и миссис?
В чем разница между «To» и «Too»?
Когда использовать принести, взять, принести и носить
Когда использовать хорошее, а когда —
Когда использовать Страхование, обеспечение и обеспечение
Когда использовать Lay или Lie
Когда использовать то или иное
Кто или Кого? Легкие способы запомнить
Слова на День Рождения
Слова поздравления с выходом на пенсию
Слова поздравления на свадьбу
Слова ободрения для того, кого любишь
Слова, начинающиеся на букву Н
слов, описывающих первое впечатление
Слова, описывающие хорошую дружбу
слов, описывающих торнадо
слов, описывающих черты личности
Слова на похоронах
слов благодарности учителю
Слова благодарности добровольцам
Слова пожелать вам счастливого Рождества
Междометия
Лист междометий
Список междометий для детей
Что такое междометие?
Существительные
Абстрактные существительные
Коллективное существительное
Существительные нарицательные и собственные
нарицательное существительное
Рабочий лист составного существительного
Сложные существительные
Конкретное существительное
Счетные и несчетные существительные
Примеры прилагательных существительных
Притяжательные существительные
Предикат Существительные
Имя собственное
Типы существительных
Что такое определитель?
Что такое существительное?
Предлоги
Правильное грамматическое использование At
Окончание приговора предлогом
Идиомы, начинающиеся с предлогов
Список общеупотребительных предлогов
Игры с предлогами
Рабочие листы для препозиций
Предлоги: правильное употребление In и On
Правила для предлогов
Местоимения
Тест на демонстративное местоимение
Рабочие листы с демонстративными местоимениями
Грамматические правила для него / нее
Неопределенное местоимение
Рабочие листы с неопределенным местоимением
Интенсивные местоимения
Вопросительное местоимение
Список личных местоимений
Местоимение именительного падежа
Местоимение объекта
Игры местоимений объекта
Использование местоимений множественного числа
Задания по притяжательному местоимению
Соглашение о местоимении
Игры местоимений
Местоимение Quiz
Возвратные местоимения
Родительное местоимение
Местоимение субъекта
Местоимения субъекта и объекта
Типы местоимений
Что такое демонстративное местоимение?
Что такое притяжательное местоимение?
Что такое местоимение единственного числа?
Что такое антецедент?
Почему у людей возникают проблемы с употреблением местоимений на английском языке?
Правила пунктуации
5 правил использования двоеточия
6 основных правил пунктуации
8 раз запятые были важными
Правила апострофа
Двоеточия, точка с запятой и тире
Использование запятой
Рабочие листы по грамматике для одинарных кавычек
Грамматика: использование фигурных скобок
Как использовать скобки в грамматике
Как использовать кавычки
Правила для дефисов
Практика использования кавычек
Правила подчеркивания
Правила использования одинарных кавычек
Использование курсива и кавычек в заголовках
Использование кавычек при цитировании информации
Какие 14 знаков препинания в грамматике английского языка?
Когда НЕ использовать апостроф
Когда выделять курсивом
Когда использовать эллипсы
Когда использовать восклицательные знаки
Где вы ставите кавычки при использовании зарегистрированной торговой марки?
Рифмы
Слова, рифмующиеся с другом
предложений
20 правил субъектно-глагольного соглашения
Прилагательное Прилагательное
Прилагательное
Предложения наречий
Сложные предложения
Сложные приговоры
Условные приговоры
Корректирующие модификаторы свисания
Исправление неуместных модификаторов
Исправление фрагментов предложения
Диаграмма предложений
Рабочий лист предложений для бесплатного построения диаграмм
Герундийские фразы
Грамматические статьи
Грамматические шаблоны для предложений
Как найти модификатор предложения наречия
Как использовать придаточное слово
Независимые и зависимые статьи
Инфинитивных фраз
Лист неуместных и свисающих модификаторов
Предложение существительного
Существительные фразы
Причастные фразы
Предложные фразы
Викторина в предметном глагольном соглашении
Правила сложения предложений
Дополнительные приговоры
Задания по объединению предложений
Предложения с использованием составных подлежащих и составных глаголов
Предметный глагол Соглашение
Рабочий лист согласования между субъектом и глаголом
Преподавание наречий и прилагательных
Обучающий приговор, объединяющий
Виды приговоров
Понимание субъектов, предикатов и объектов
Глагольная фраза
Каковы различные части приговора?
Что такое глаголы и словесные фразы?
Что такое предикат?
Что такое глагол относительного придаточного предложения?
Что такое абсолютная фраза?
Что является предметом приговора?
Написание сложных предложений
Сленг
Сленг 1930-х годов
Сленг 1940-х годов
Сленг 1950-х годов
Сленг 1960-х
Сленг 1980-х
Итальянский сленг XIX века
Словарь американского сленга
Баскетбольный сленг
Бит-сленг 1950-х
Определения британского сленга
Брамми vs. Кокни
Кокни
Канадский сленг по регионам
Карни-сленг
Оскорбления кокни
Переводчик кокни
Красочный байкерский сленг
Общие британские выражения
Классный сленг 1970-х
Смешные поговорки ковбоев
Глоссарий железнодорожной терминологии или сленга
Деревенский сленг
История американского сленга
Гомосексуальный сленг
Как сленг влияет на английский язык
Ирландские слова и фразы
Еврейский сленг
Военный сленг
Больше американского сленга
Морской сленг
Правильный английский и сленг
Сленговые слова деревенщины
Сленг русских иммигрантов
Сленговые слова для тюрьмы
Несколько сленговых слов для полиции
Текстовый сленг
Глаголы, начинающиеся с J
Глаголы, начинающиеся с U
Что такое сленг битников?
Орфография и орфография
100 слов с ошибками в английском написании чаще
100 слов с ошибками в написании слов на английском языке, которые часто ошибаются
13 выдающихся правил орфографии, которые необходимо знать
150 слов с ошибками, которые чаще всего пишутся с ошибками
Американское и британское написание слов
Отменено или отменено: какое правильное написание?
Проверить правописание слова
Распечатки со свободным правописанием
Правописание слов на уровне старшей школы
Как улучшить свое правописание
Как писать слова
Изобретенное правописание
Учимся с трудом произносить слова
Фонетический орфографический словарь
Практикуйте мое правописание
Орфографические упражнения
Проверка орфографии пчел
Правописание слов для изучения пчелы
Уроки по расширению правописания
Орфографические игры в слова
Списки орфографических слов
Изучение навыков для проверки орфографии
Обучение правописанию латинскими корнями
Преподавание исправительного правописания
Необычное написание английского языка
Глаголы
7 ошибок времени общего глагола
Глаголы действия
Категории времен английских глаголов
Конъюнктивный глагол
Глаголы будущего времени
Глагольные игры помощи
Глаголы помощи
Инфинитивный глагол
Непереходные глаголы
Таблица глаголов прошедшего времени
Глаголы прошедшего времени
Список фразовых глаголов
Правила спряжения глаголов
Таблица английских глаголов единственного и множественного числа
Сильные глаголы и слабые глаголы: в чем разница?
Переходные глаголы
Каковы времена английских глаголов?
Что такое сопряженный глагол?
Что такое глагол?
Что такое настроение в грамматике?
Какой главный глагол в предложении?
Списки слов
Прилагательные, начинающиеся на
Прилагательные, начинающиеся на букву В
Прилагательные, начинающиеся на букву С
Прилагательные, начинающиеся на D
Прилагательные, начинающиеся на E
Прилагательные, начинающиеся на F
Прилагательные, начинающиеся на G
Прилагательные, начинающиеся на H
Прилагательные, начинающиеся с I
Прилагательные, начинающиеся на J
Прилагательные, начинающиеся на L
Прилагательные, начинающиеся с Q
Прилагательные, начинающиеся с R
Прилагательные, начинающиеся на Т
Прилагательные, начинающиеся с U
Прилагательные, начинающиеся с V
Прилагательные, начинающиеся на W
Прилагательные, начинающиеся с X
Прилагательные, начинающиеся на Z
Смешные южные слова
Список из 228 распространенных прилагательных
Список прилагательных для описания тона, чувств и эмоций
Список собирательных существительных для людей
Список описательных прилагательных
Список слов, описывающих внешний вид
Список описательных слов: прилагательные, наречия и герундий
Список положительных прилагательных
Список коротких гласных слов
Список слов перехода
Список слов для описания цветов
Список слов для описания мест
Самые длинные слова в английском языке
Существительные, начинающиеся на
Существительные, начинающиеся на C
Существительные, начинающиеся на D
Существительные, начинающиеся на E
Существительные, начинающиеся на I
Существительные, начинающиеся на J
Существительные, начинающиеся на K
Существительные, начинающиеся на L
Существительные, начинающиеся на M
Существительные, начинающиеся на N
Существительные, начинающиеся с Q
Существительные, начинающиеся на R
Существительные, начинающиеся на S
Существительные, начинающиеся на T
Существительные, начинающиеся на U
Существительные, начинающиеся с V
Существительные, начинающиеся на W
Существительные, начинающиеся с X
Существительные, начинающиеся на
Существительные, начинающиеся на Z
положительных слов, начинающихся с
положительных слов, начинающихся на букву В
положительных слов, начинающихся с E
положительных слов, начинающихся с I
положительных слов, начинающихся с М
положительных слов, начинающихся с N
положительных слов, начинающихся с О
положительных слов, начинающихся с
руб.
положительных слов, начинающихся с Т
Жуткие слова Хэллоуина
Глаголы, начинающиеся с
Глаголы, начинающиеся с B
Глаголы, начинающиеся с C
Глаголы, начинающиеся с E
Глаголы, начинающиеся с F
Глаголы, начинающиеся с I
Глаголы, начинающиеся с K
Глаголы, начинающиеся с L
Глаголы, начинающиеся с M
Глаголы, начинающиеся с N
Глаголы, начинающиеся с O
Глаголы, начинающиеся с P
Глаголы, начинающиеся с Q
глаголов, начинающихся с R
Глаголы, начинающиеся с S
Глаголы, начинающиеся с T
Глаголы, начинающиеся с V
Глаголы, начинающиеся с W
Глаголы, начинающиеся с X, Y и Z
слов, рифмующихся с апельсином
слов с множеством значений
Письмо
10 советов по написанию четких и кратких предложений
5 преимуществ наброска эссе
5 шагов для написания информативной речи
5 шагов к написанию мотивационной речи
6 советов для хорошей речи
Академические навыки письма
Советы по активному письму
Схема аргументационного эссе
Советы по написанию аргументационного эссе
Преимущества написания эмоционального дневника
Креативные письменные упражнения
Определение академического письма
Определение творческого письма
Эффективное написание академического журнала
Формат для написания книжного отчета
Проявите творческий подход: как написать рассказ
Руководство по написанию рецензии на книгу
Помощь в написании литературного эссе по книге
Как включить в сочинение переходные слова?
Как идиомы могут сделать ваше письмо более интересным
Как создать гипотезу
Как найти достоверные источники
Как найти главную идею
Как использовать точку зрения в письме
Как написать библиографию
Как написать биографию
Как написать отчет о книге
Как написать пример
Как написать анализ характера
Как написать эссе для сравнения и сопоставления
Как написать вывод
Как написать отличный крючок
Как написать описание работы
Как написать письмо
Как написать письмо о заинтересованности
Как написать запоминающуюся речь
Как написать заявление о миссии
Как написать личное заявление
Как написать петицию
Как написать пресс-релиз
Как написать эссе по решению проблем
Как написать благодарственное письмо
Как написать письмо с извинениями
Как написать апелляционное письмо
Как написать эссе
Как писать вдохновляющие основные ценности
Техники индуктивного мышления в речевом письме
Интересные темы убедительной речи для старших классов
Голос персонажа отличается от голоса автора?
Отрицательных слов, которых следует избегать
Оригинальные информативные речевые темы
Passive Voice: когда его использовать
Легкое создание убедительного эссе
Первичный vs. Вторичные источники
Вторичные источники
Формат написания отчета
Правила написания хайку
Советы по написанию сатиры
Как написать убедительную речь
Истории для начала: идеи для творческого письма
Стратегии улучшения составления резюме
Советы по написанию личного повествовательного эссе
Советы по академическому письму
Советы по написанию речи
Советы по искусству закадрового текста
Советы по написанию биографического очерка
Советы по написанию брошюры
Советы по написанию хорошей статьи
Советы по написанию новостного сообщения
Советы по написанию редакции газеты
Советы по написанию отличного пояснительного эссе
Советы по написанию стихов
Советы по написанию первой главы и после
Переходные слова для студентов
Что такое тезис?
Что такое рефлексивное письмо?
Каких тем следует избегать при написании исследовательской работы?
Что вам нужно в выигравшем интервью резюме и сопроводительном письме
Когда цитировать, перефразировать или резюмировать
Написание речи о школьных выборах
Статьи и ресурсы ESL
О ESL
Деловые письма ESL
Деловое письмо ESL
ESL Философия образования
Оценка программы ESL
ESL vs. Двуязычное образование
Двуязычное образование
Как родители помогают своим детям с английским английским языком учить английский
Межъязычный китайский ESL
Изучение английского как второго языка
История ESL
Планы уроков ESL
Действия для прошедшего времени неправильных глаголов в ESL
Упражнения для простого прошедшего времени в ESL
Упражнения для обучения аналогичным грамматическим структурам
Животные ESL Quiz
Создание успешного плана урока ESL
Планы уроков по созданию словарного запаса для студентов ESL
Примеры из практики для учителей ESL
Сравнительная и превосходная суффиксная деятельность ESL
Культура в классах ESL
Деятельность по проектированию как для студентов, так и для студентов, не владеющих английским языком
Разработка эффективных учебных занятий по английскому языку для студентов колледжей и взрослых
Разработка эффективных классных занятий по ESL для старшеклассников
Разработка эффективных классных занятий по английскому языку для учащихся средних школ
Электронные портфолио для преподавания английского как второго языка
Социальные мероприятия ESL
ESL Класс и культурные особенности
Рабочий лист составного прилагательного ESL
Разговорная деятельность ESL
Темы для разговоров на ESL
ESL План урока «Описание людей»
Карточки ESL
Развлекательные мероприятия ESL для разговоров о свиданиях
ESL Игры и лингвистические результаты
ESL Gerund Games
ESL Знакомство с вами Планы уроков
Письменные упражнения среднего уровня ESL
ESL Узнайте о моей истории сообщества
Планы уроков ESL по отношениям и дружбе
Планы уроков ESL по суевериям и убеждениям
Методологии ESL
Прошедшее время ESL
ESL Pilgrim Unit
Практические занятия ESL для гендерных местоимений
ESL Произношение
Фонологические таблицы произношения ESL
Занятия по чтению на ESL
ESL Ресторанные беседы
Отделение социальных исследований ESL
Песен ESL
Дизайн учебной программы ESL
Методы обучения ESL
Предложения для теста ESL
Словарная деятельность ESL
Уроки эвфемизма
Оценка плана урока ESL
Планы уроков ESL по моде и внешнему виду
Еда ESL Quiz
Веселые мероприятия по устранению пробелов в информации для учащихся ESL
Going Places Планы уроков ESL
Уроки здоровья для студентов ESL
Как адаптировать материалы для ученика ESL
Как преподавать ESL в классе
Как научить читать ESL
Интересные темы для ESL
Урок собеседований
План урока об авариях
Планы уроков по частям тела
Карточки единичного теста на экологию 9 класса
Нам не удалось определить язык звукового сопровождения на ваших карточках. Пожалуйста, выберите правильный язык ниже.
Пожалуйста, выберите правильный язык ниже.
аудио еще не доступно для этого языка
Назад Китайский, PinyinChinese, SimplifiedChinese, TraditionalEnglishFrenchGermanItalianJapaneseJapanese, RomajiKoreanMath / SymbolsRussianSpanishAfrikaansAkanAkkadianAlbanianAmharicArabicArmenianAzerbaijaniBasqueBelarusianBengaliBihariBretonBulgarianBurmeseCatalanCebuanoChamorroChemistryCherokeeChinese, PinyinChinese, SimplifiedChinese, TraditionalChoctawCopticCorsicanCroatianCzechDanishDeneDhivehiDutchEnglishEsperantoEstonianFaroeseFilipinoFinnishFrenchFulaGaelicGalicianGeorgianGermanGreekGuaraniGujaratiHaidaHaitianHausaHawaiianHebrewHindiHungarianIcelandicIgboIndonesianInuktitutIrishItalianJapaneseJapanese, RomajiJavaneseKannadaKazakhKhmerKoreanKurdishKyrgyzLakotaLaoLatinLatvianLingalaLithuanianLuba-KasaiLuxembourgishMacedonianMalayMalayalamMalteseMaoriMarathiMarshalleseMath / SymbolsMongolianNepaliNorwegianOccitanOjibweOriyaOromoOther / UnknownPashtoPersianPolishPortuguesePunjabiPāliQuechuaRomanianRomanshRussianSanskritSerbianSindhiSinhaleseSlovakSlovenianSpanishSundaneseSwahiliSwedishTaga logTajikTamilTatarTeluguThaiTibetanTigrinyaTohono O’odhamТонгаТурецкийУйгурскийУкраинскийUrduUzbek
.



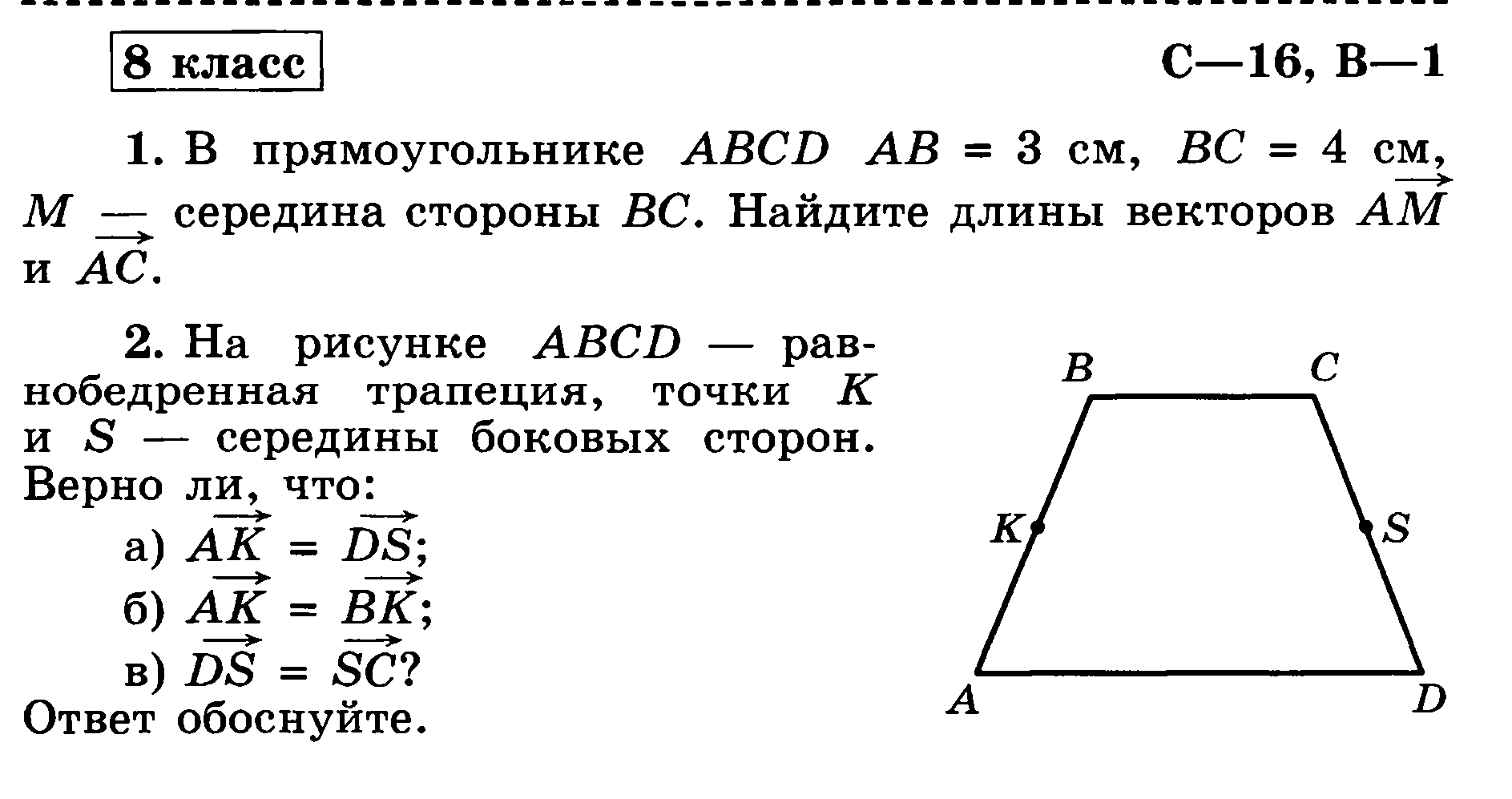
 Найдите площадь круга и длину ограничивающей его окружности, если сторона правильного треугольника, вписанного в него, равна
Найдите площадь круга и длину ограничивающей его окружности, если сторона правильного треугольника, вписанного в него, равна


 В параллелограмме ABCD точка M – середина стороны CD; N – точка на стороне AD, такая, что AN : ND = 3 : 4. Выразите векторы и , через векторы и .
В параллелограмме ABCD точка M – середина стороны CD; N – точка на стороне AD, такая, что AN : ND = 3 : 4. Выразите векторы и , через векторы и .