Контрольная по геометрии 8 класса: Геометрия 8 Бутузов Контрольные работы с ответами

Содержание

Геометрия 8 Контрольные Атанасян (Зив)

Геометрия 8 Контрольные Атанасян (Зив)
Контрольные работы + Ответы

Геометрия 8 Контрольные Атанасян (Зив) — это цитаты контрольных работ из пособия для учащихся «Геометрия. Дидактические материалы. 8 класс / Б.Г. Зив, В.М. Мейлер — М.: Просвещение», которое используется в комплекте с учебником «Геометрия. 7-9 классы» авторов: Л.С. Атанасяна, В.Ф. Бутузова, С.Б. Кадомцева, Э.Г. Позняка, И.И. Юдиной, а также ответы на контрольные работы.

Цитаты из пособия указаны в учебных и информационных целях. При постоянном использовании контрольных работ по геометрии в 8 классе рекомендуем купить книгу: Геометрия. Дидактические материалы. 8 класс / Б.Г. Зив, В.М. Мейлер — М.: Просвещение, в которой кроме контрольных работ есть еще 39 самостоятельных работ, математические диктанты и задачи повышенной трудности.

Для увеличения изображения — нажмите на картинку !
Чтобы скачать работу — нажмите на правую кнопку мыши и выберите «Сохранить изображение как …»

Контрольная работа № 1.
Четырехугольники

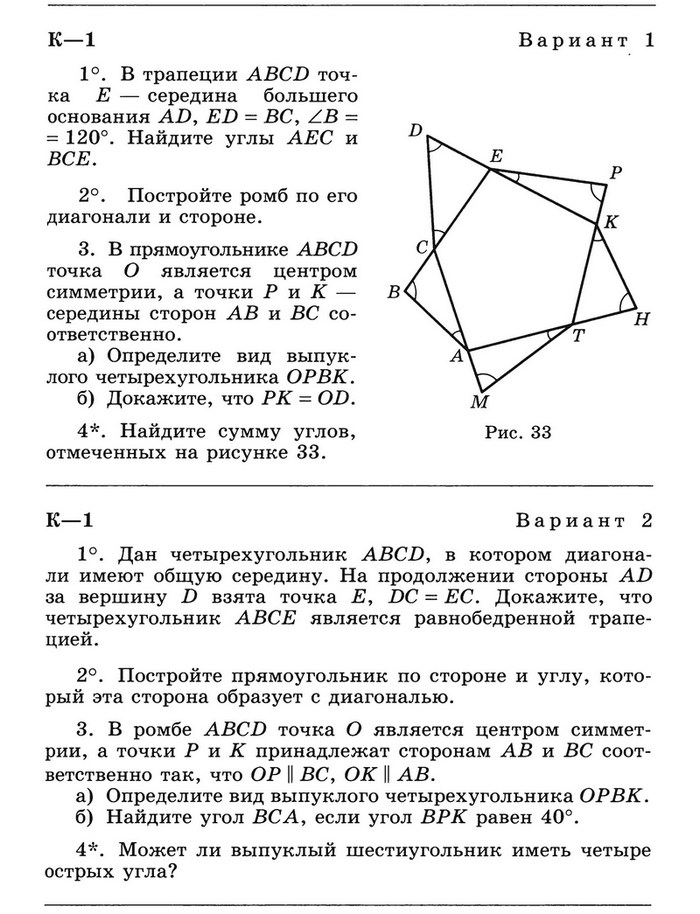
ОТВЕТЫ на Контрольную работу № 1

Контрольная работа № 2.
Площадь

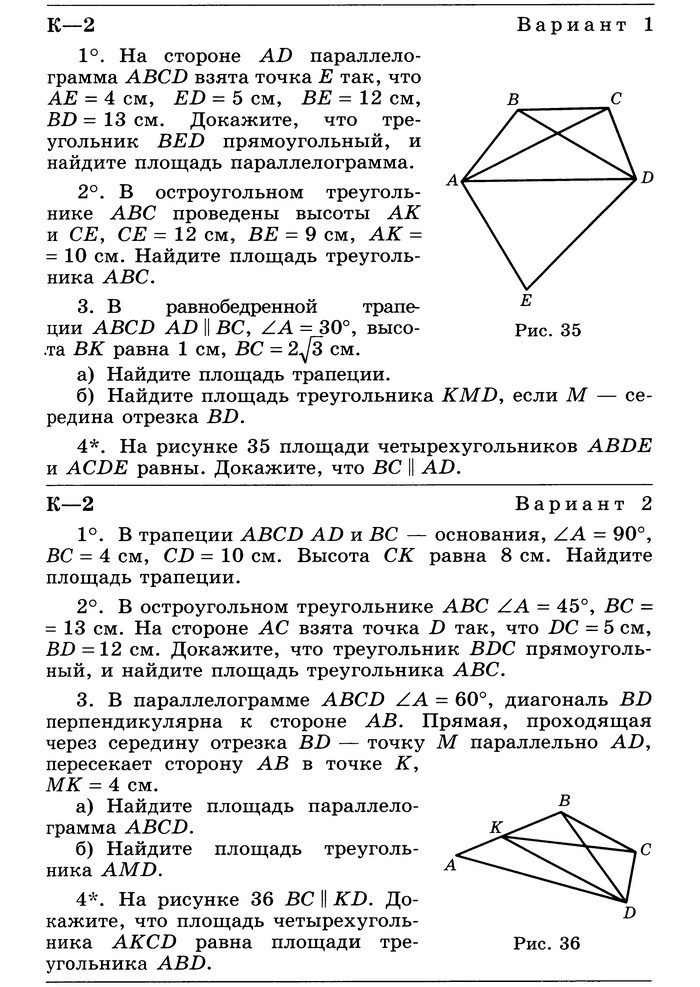
ОТВЕТЫ на Контрольную работу № 2

Контрольная работа № 3.
Подобные треугольники

ОТВЕТЫ на Контрольную работу № 3

Контрольная работа № 4.
Применение подобия, решение прямоугольных треугольников

ОТВЕТЫ на Контрольную работу № 4

Контрольная работа № 5.
Окружность

ОТВЕТЫ на Контрольную работу № 5

Контрольная работа № 6.
Векторы

ОТВЕТЫ на Контрольную работу № 6

Контрольная работа № 7.
Итоговая работа за 8 класс

ОТВЕТЫ на Контрольную работу № 7

Вы смотрели страницу «Геометрия 8 Контрольные Атанасян (Зив)» — Контрольные работы из пособия для учащихся «Геометрия. Дидактические материалы. 8 класс / Б.Г. Зив, В.М. Мейлер — М.: Просвещение», которое используется в комплекте с учебником «Геометрия. 7-9 классы» авторов: Л.С. Атанасяна, В.Ф. Бутузова, С.Б. Кадомцева, Э.Г. Позняка, И.И. Юдиной, а также ответы на контрольные работы.

Геометрия 8 класс . Тесты и Тренажеры

ГЕОМЕТРИЯ 8 класс. ТЕСТЫ И ТРЕНАЖЕРЫ

Геометрия 8. Свойства параллелограмма (на чертежах) — 8 заданий …

Геометрия 8. ПАРАЛЛЕЛОГРАММ (на чертежах) — 8 заданий …

Геометрия 8. Многоугольники (теория) — 15 вопросов …

Геометрия 8. Свойства и признаки параллелограмма — 15 вопросов …

Геометрия 8. Виды параллелограммов. Трапеция — 15 вопросов …

Геометрия 8. Средние линии треугольника и трапеции — 15 вопросов …

Геометрия 8. Площади многоугольников — 15 вопросов …

Геометрия 8. ТРАПЕЦИЯ (на чертежах) — 7 заданий …

Геометрия 8. Площадь прямоугольника (на чертежах) — 7 заданий …

Геометрия 8 класс. Площадь трапеции — 10 вопросов …

Геометрия 8 класс. Теорема Пифагора — 10 вопросов …

Геометрия 8 класс. Площади (теория) — 10 вопросов …

Геометрия 8. Площадь параллелограмма (на чертежах) — 7 заданий …

Геометрия 8. Площадь треугольника (на чертежах) — 7 заданий …

Геометрия 8. Площадь трапеции (на чертежах) — 7 заданий …

Геометрия 8. Теорема Пифагора (на чертежах) — 7 заданий …

Геометрия 8. Подобные треугольники (на чертежах) — 7 заданий …

Геометрия 8. Определение подобных треугольников — 10 вопросов …

Геометрия 8. Признаки подобия треугольников — 10 вопросов …

Геометрия 8. Применение признаков подобия — 10 вопросов …

Геометрия 8. Соотношения между сторонами и углами — 10 вопросов …

Геометрия 8. Подобные треугольники (теория) — 10 вопросов …

Геометрия 8. Касательная к окружности — 10 вопросов …

Геометрия 8. Центральные и вписанные углы — 10 вопросов …

Геометрия 8. Четыре замечательные точки окружности — 10 вопросов …

Геометрия 8. Вписанные и описанные окружности — 10 вопросов …

Геометрия 8. Окружность (теория) — 10 вопросов …

Геометрия 8. ИТОГОВЫЙ ТЕСТ за год — 16 вопросов …

ГЕОМЕТРИЯ 8 класс. КОНТРОЛЬНЫЕ РАБОТЫ

Рекомендуемые материалы для очного контроля знаний
по предмету «Геометрия 8 класс»:

Тесты по геометрии. 8 класс. К учебнику Атанасяна Л.С. и др. — Звавич Л.И., Потоскуев Е.В. (2013, 160с.)

Геометрия. 8 класс. Сборник заданий для тематического и итогового контроля знаний. Ершова А.П. (2013, 128с.)
Геометрия. 8 класс. Тематические тесты. Мищенко Т.М., Блинков А.Д. (2008, 128с.)
Геометрия 8 класс. Контрольные измерительные материалы. Рязановский А.Р., Мухин Д.Г. (2014, 96с.)
Геометрия. 8 класс. Тематические тесты. Мищенко Т.М. (2011, 176с.)
Геометрия. 8 класс. Итоговая аттестация. Типовые тестовые задания. Глазков Ю.А., Гаиашвили М.Я. (2015, 64с.)
Дидактические материалы по геометрии. 8 класс. К учебнику Атанасяна Л.С. — Мельникова Н.Б., Захарова Г.А. (2017, 144с.)

Геометрия. 8 класс. Контрольные работы. Мельникова Н.Б. (2016, 64с.)
Геометрия. 8 класс. Дидактические материалы. Зив Б.Г., Мейлер В.М. (2016, 159с.)
Геометрия 8 класс. Тренировочные задания. Дудницын Ю.П., Кронгауз В.А. (2018, 176с.)
Геометрия. 8 класс. Тематические тесты. Мищенко Т.М. (2010, 96с.)
Геометрия. Самостоятельные и контрольные работы: 7-9 классы. Иченская М.А. (2017, 144с.)
Геометрия. 8 класс. Дидактические материалы. Мерзляк А.Г., Полонский В.Б. и др. (2018, 112с.)

Программа обучения по геометрии в 8 классе (основные темы)

Глава I. Четырехугольники

Многоугольники. Параллелограмм и трапеция. Прямоугольник. Ромб. Квадрат. Решение задач

Глава II. Площадь

Площадь многоугольника. Площади параллелограмма, треугольника и трапеции. Теорема Пифагора. Решение задач

Глава III. Подобные треугольники

Определение подобных треугольников. Признаки подобия треугольников. Применение подобия к доказательству теорем и решению задач. Соотношения между сторонами и углами прямоугольного треугольника.

Глава IV. Окружность

Касательная к окружности. Центральные и вписанные углы. Четыре замечательные точки треугольника. Вписанная и описанная окружности. Решение задач

Вернуться

Контрольно- измерительные материалы по геометрии 8

МУНИЦИПАЛЬНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ

УЧРЕЖДЕНИЕ «СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ

ШКОЛА С.БЕРЕЗОВО ПУГАЧЕВСКОГО РАЙОНА

САРАТОВСКОЙ ОБЛАСТИ»

«Рассмотрено»

Руководитель МО

_____ /__________ /

ФИО

Протокол №____от

«__» ______ 20__г.

«Согласовано»

Заместитель директора по УВР МОУ СОШ с.Березово

_____ /_________/

ФИО

«__» ______ 20__г.

«Утверждено»

Директор МОУ СОШ с.Березово

_____ /________/

ФИО

Приказ №___ от

«___» ______ 20__г.

Контрольно-измерительный материал

по геометрии в 8 классе

на 2018-2019 учебный год

Рассмотрено на заседании

педагогического совета

протокол № __

« »_______20 г.

Примерные контрольные работы по геометрии по УМК Л.С. Атанасяна

Контрольные работы представлены в различных вариантах (отдельные варианты для более подготовленных учащихся )

оценка «5» — правильное выполнение двух задач; (3 задание на дополнительную оценку)

Оценка «4» — имеются вычислительные ошибки, с их учетом дальнейшее решение правильное;

Оценка «3» — решение двух задач неполное, есть вычислительные ошибки;

Оценка «2» — нет решения ни одной задачи.

Тематическое планирование учебного материала по геометрии в 8 классе

(2 часа в неделю, всего 68 часов)

№ п/п	ТЕМА	Контрольные работы
1	Четырехугольники	Контрольная работа №1 «Четырехугольники»
2	Площадь	Контрольная работа №2 «Площадь»
3	Подобные треугольники	Контрольная работа №3 «Подобные треугольники. Соотношения между сторонами и углами прямоугольного треугольника»
4	Окружность	Контрольная работа №4 «Окружность»
5	Повторение	Контрольная работа №5 «Итоговая контрольная работа за курс 7 класса»

КОНТРОЛЬНАЯ РАБОТА № 1

Цель: проверить знания, умения и навыки учащихся по усвоению и применению изученного материала.

Вариант I

1. Диагонали прямоугольника АВСD пересекаются в точке О. Найдите угол между диагоналями, если АВО = 30°.

2. В параллелограмме KМNP проведена биссектриса угла МKР, которая пересекает сторону MN в точке Е.

а) Докажите, что треугольник KМЕ равнобедренный.

б) Найдите сторону KР, если МЕ = 10 см, а периметр параллелограмма равен 52 см.

Вариант II

1. Диагонали ромба KМNP пересекаются в точке О. Найдите углы треугольника KОМ, если угол МNP равен 80°.

2. На стороне ВС параллелограмма АВСD взята точка М так, что АВ = ВМ.

а) Докажите, что АМ – биссектриса угла ВАD.

б) Найдите периметр параллелограмма, если СD = 8 см, СМ = 4 см.

Вариант III

1. Через вершину с прямоугольника АВСD проведена прямая, параллельная диагонали ВD и пересекающая прямую АВ в точке М. Через точку М проведена прямая, параллельная диагонали АС и пересекающая прямую ВС в точке N. Найдите периметр четырехугольника АСМN, если диагональ ВD равна 8 см.

2. Биссектрисы углов А и D параллелограмма АВСD пересекаются в точке М, лежащей на стороне ВС. Луч DМ пересекает прямую АВ в точке N. Найдите периметр параллелограмма АВСD, если АN = 10 см.

КОНТРОЛЬНАЯ РАБОТА № 2

Цель: проверить знания, умения и навыки учащихся решать задачи по теме «Площадь. Теорема Пифагора».

Вариант I

1. Смежные стороны параллелограмма равны 32 см и 26 см, а один из его углов равен 150°. Найдите площадь параллелограмма.

2. Площадь прямоугольной трапеции равна 120 см², а ее высота равна 8 см. Найдите все стороны трапеции, если одно из оснований больше другого на 6 см.

3. На стороне АС данного треугольника АВС постройте точку D так, чтобы площадь треугольника АВD составила одну треть площади треугольника АВС.

Вариант II

1. Одна из диагоналей параллелограмма является его высотой и равна 9 см. Найдите стороны этого параллелограмма, если его площадь равна 108 см².

2. Найдите площадь трапеции АВСD с основаниями АD и ВС, если АВ = 12 см, ВС = 14 см, АD = 30 см, В = 150°.

3. На продолжении стороны KN данного треугольника KМN постройте точку Р так, чтобы площадь треугольника NMP была в два раза меньше площади треугольника KМN.

Вариант III
(для более подготовленных учащихся)

1. Стороны параллелограмма равны 12 см и 8 см, а угол между высотами, проведенными из вершины тупого угла, равен 30°. Найдите площадь параллелограмма.

2. Середина М боковой стороны CD трапеции АВСD соединена отрезками с вершинами А и В. Докажите, что площадь треугольника АВМ в два раза меньше площади данной трапеции.

3. Точки А₁, В₁, С₁ лежат соответственно на сторонах ВС, АС, АВ треугольника АВС, причем АВ₁ = AC, CA₁ = CB, BC₁ = BA. Найдите площадь треугольника А₁В₁С₁, если площадь треугольника АВС равна 27 см².

КОНТРОЛЬНАЯ РАБОТА № 3

Цели: проверить знания, умения и навыки учащихся по усвоению и применению изученного материала.

Вариант I

1. На рисунке 1 АВ || СD. а) Докажите, что АО : ОС = ВО : ОD. б) Найдите АВ, если ОD = 15 см, ОВ = 9 см, СD = 25 см.

2. Найдите отношение площадей треугольников АВС и KMN, если АВ = 8 см, ВС = 12 см, АС = 16 см, KM = 10 cм, MN = 15 см, NK = 20 см.

Вариант II

1. На рисунке 2 MN || АС. а) Докажите, что АВ · BN = CВ · BM. б) Найдите MN, если AM = 6 см, ВM = 8 см, АС = 21 см.

2. Даны стороны треугольников PQR и АВС: PQ = 16 см, QR = 20 см, PR = 28 см и АВ = 12 cм, ВС = 15 см, АС = 21 см. Найдите отношение площадей этих треугольников.

Вариант III
(для более подготовленных учащихся)

1. Докажите, что прямая, проведенная через середины оснований трапеции, проходит через точку пересечения диагоналей трапеции и точку пересечения продолжения боковых сторон.

2. Даны отрезок АВ и параллельная ему прямая а. Воспользовавшись утверждением, доказанным в задаче 1, разделите отрезок АВ пополам при помощи одной линейки.

Рис. 1 Рис. 2

Контрольная работа № 4

Цель: проверить знания и умения учащихся в решении задач и применении изученного материала.

Вариант I

1. В прямоугольном треугольнике АВС А = 90°, АВ = 20 см; высота АD = 12 см. Найдите АС и cos C.

2. Диагональ ВD параллелограмма АВСD перпендикулярна к стороне АD. Найдите площадь параллелограмма АВСD, если АВ = 12 см,
А = 41°.

Вариант II

1. Высота ВD прямоугольного треугольника АВС равна 24 см и отсекает от гипотенузы АС отрезок DС, равный 18 см. Найдите АВ и соs A.

2. Диагональ АС прямоугольника АВСD равна 3 см и составляет со стороной АD угол 37°. Найдите площадь прямоугольника АВСD.

Вариант III
(для более подготовленных учащихся)

1. Диагональ АС равнобедренной трапеции АВСD перпендикулярна к боковой стороне СD. Найдите площадь трапеции, если ее основания равны 10 см и 8 см.

2. Найдите отношение высот BN и AM равнобедренного треугольника АВС, в котором угол при основании ВС равен α.

КОНТРОЛЬНАЯ РАБОТА № 5

Цель: выяснить степень усвоения учащимися изученного материала.

Вариант I

1. Через точку А окружности проведены диаметр АС и две хорды АВ и АD, равные радиусу этой окружности. Найдите углы четырехугольника АВСD и градусные меры дуг АВ, ВС, СD, АD.

2. Основание равнобедренного треугольника равно 18 см, а боковая сторона равна 15 см. Найдите радиусы вписанной в треугольник и описанной около треугольника окружностей.

Вариант II

1. Отрезок ВD – диаметр окружности с центром О. Хорда АС делит пополам радиус ОВ и перпендикулярна к нему. Найдите углы четырехугольника АВСD и градусные меры дуг АВ, ВС, СD, АD.

2. Высота, проведенная к основанию равнобедренного треугольника, равна 9 см, а само основание равно 24 см. Найдите радиусы вписанной в треугольник и описанной около треугольника окружностей.

Вариант III
(для более подготовленных учащихся)

1. МА и МВ – секущие, АС и ВД – хорды окружности с центром О. Докажите, что АОВ = АKВ + АМВ.

2. Площадь равнобедренной трапеции АВСD с основаниями ВС и АD, описанной около окружности с центром О и радиусом 3 см, равна 60 см². Найдите радиус окружности, описанной около треугольника ОСD.

9 класс
Контрольная работа № 1

Цели: проверить знания, умения и навыки учащихся по усвоению и применению изученного материала.

Вариант I

1. Точки E и F лежат соответственно на сторонах AD и BC параллелограмма ABCD; AE = ED, BF : FC = 4 : 3. Выразите вектор через векторы и .

2. Найдите координаты вектора , если , (3; –2),
( –6; 2).

3. Боковые стороны прямоугольной трапеции равны 15 см и 17 см, средняя линия равна 6 см. Найдите основания трапеции.

Вариант II

1. Точки K и M лежат соответственно на сторонах AB и CD параллелограмма ABCD; AK = KB, CM : MD = 2 : 5. Выразите вектор через векторы и .

2. Найдите координаты вектора , если , (–3; 6),
(2; –2).

3. Один из углов прямоугольной трапеции равен 120°, бóльшая боковая сторона равна 20 см, средняя линия равна 7 см. Найдите основания трапеции.

Вариант III

1. Точки P и O лежат соответственно на сторонах AD и BC параллелограмма ABCD; BP = PC, AO : OD = 3 : 2. Выразите вектор через векторы и .

2. Найдите координаты вектора , если , (6; –2),
(1; –2).

3. Основание и средняя линия прямоугольной трапеции равны соответственно 15 см и 12 см, а меньшая боковая сторона равна 8 см. Найдите вторую боковую сторону трапеции.

Вариант IV

1. Точки H и T лежат соответственно на сторонах AВ и CD параллелограмма ABCD; CT = TD, AH : HB = 5 : 3. Выразите вектор через векторы и .

2. Найдите координаты вектора , если , (2; 3), (9; –9).

3. Средняя линия прямоугольной трапеции равна 9 см, а бóльшая боковая сторона равна 24 см. Один из углов, прилежащих к боковой стороне, в два раза больше другого. Найдите основания трапеции.

Контрольная работа № 2

Цель: проверить знания, умения и навыки учащихся по теме «Соотношения между сторонами и углами треугольника. Скалярное произведение векторов».

Вариант I

1. Найдите угол между лучом ОА и положительной полуосью ОХ, если А (–1; 3).

2. Решите треугольник АВС, если угол В = 30°, угол С = 105°, ВС =
= 3см.

3. Найдите косинус угла М треугольника KLМ, если К (1; 7), L (–2; 4), М (2; 0). Найдите косинусы углов K и L.

Вариант II

1. Найдите угол между лучом ОВ и положительной полуосью ОХ, если В (3; 3).

2. Решите треугольник ВСD, если угол В = 45°; угол D = 60°, ВС =
=см.

3. Найдите косинусы углов А, В и С треугольника АВС, если А (3; 9), В (0; 6), С (4; 2).

Вариант III

1. Найдите угол между лучом ОС и положительной полуосью ОХ, если С (; 1).

2. Решите треугольник СDЕ, если угол С = 60°, СD = 8 дм, СЕ = 5 дм.

3. Найдите косинус угла между векторами и , если = 60°.

Вариант IV

1. Найдите угол между лучом ОD и положительной полуосью ОХ, если D (–2; 2).

2. Решите треугольник DЕF, если DЕ = 5 м, DF = 8 м и ЕF = 4 м.

3. Найдите косинус угла между векторами и , если = 60°.

Контрольная работа № 3

Цели: проверить умение учащихся решать задачи по изученной теме; выявить пробелы в знаниях учащихся для последующего их устранения.

Вариант I

1. Периметр правильного треугольника, вписанного в окружность, равен 45 см. Найдите сторону правильного восьмиугольника, вписанного в ту же окружность.

2. Найдите площадь круга, если площадь вписанного в ограничивающую его окружность квадрата равна 72 дм².

3. Найдите длину дуги окружности радиуса 3 см, если ее градусная мера равна 150°.

Вариант II

1. Периметр правильного шестиугольника, вписанного в окружность, равен 48 м. Найдите сторону квадрата, вписанного в ту же окружность.

2. Найдите длину окружности, если площадь вписанного в нее правильного шестиугольника равна 72 см².

3. Найдите площадь кругового сектора, если градусная мера его дуги равна 120°, а радиус круга равен 12 см.

вариант III

1. Периметр квадрата, вписанного в окружность, равен 48 см. найдите сторону правильного пятиугольника, вписанного в ту же окружность.

2. Найдите площадь кольца, ограниченного двумя окружностями с общим центром и радиусами 3 см и 7 см.

3. Найдите площадь фигуры, ограниченной дугой окружности и стягивающей ее хордой, если длина хорды равна 4 м, а градусная мера дуги равна 60°.

Вариант IV

1. Периметр правильного пятиугольника, вписанного в окружность, равен 6 дм. Найдите сторону правильного треугольника, вписанного в ту же окружность.

2. Площадь кольца, ограниченного двумя окружностями с общим центром, равна 45π м², а радиус меньшей окружности равен 3 м. Найдите радиус большей окружности.

3. Найдите площадь фигуры, ограниченной дугой окружности и стягивающей ее хордой, если длина хорды равна 2 см, а диаметр окружности равен 4 см.

Контрольная работа № 4

Цели: проверить знания, умения и навыки учащихся в решении задач по теме «Движения».

Вариант I

1. Дана трапеция АВСD. Постройте фигуру, на которую отображается эта трапеция при симметрии относительно прямой, содержащей боковую сторону АВ.

2. Две окружности с центрами О₁ и О₂, радиусы которых равны, пересекаются в точках М и N. Через точку М проведена прямая, параллельная О₁О₂ и пересекающая окружность с центром О₂ в точке D. используя параллельный перенос, докажите, что четырехугольник О₁МDО₂ является параллелограммом.

Вариант II

1. Дана трапеция АВСD. Постройте фигуру, на которую отображается эта трапеция при симметрии относительно точки, являющейся серединой боковой стороны СD.

2. Дан шестиугольник А₁А₂А₃А₄А₅А₆. Его стороны А₁А₂ и А₄А₅, А₂А₃ и А₅А₆, А₃А₄ и А₆А₁ попарно равны и параллельны. Используя центральную симметрию, докажите, что диагонали А₁А₄, А₂А₅, А₃А₆ данного шестиугольника пересекаются в одной точке.

Вариант III

1. Дана трапеция АВСD с основаниями АD и ВС. Постройте фигуру, на которую отображается эта трапеция при повороте вокруг точки А на угол, равный углу DАВ, по часовой стрелке.

2. На одной стороне угла ХОY отложены отрезки ОА и ОВ, а на другой стороне – отрезки ОМ и ОN так, что ОМ = ОА, ОN = ОВ. Используя осевую симметрию, докажите, что точка пересечения отрезков МВ и АN лежит на биссектрисе угла ХОY.

Вариант IV

1. Дана трапеция АВСD с основаниями АD и ВС. Постройте фигуру, на которую отображается эта трапеция при параллельном переносе на вектор .

2. На биссектрисе внешнего угла при вершине С треугольника АВС взята точка М. Используя осевую симметрию, докажите, что

АС + СВ < АМ + МВ.

Урок геометрии: контрольные работы. 8-й класс

Контрольная работа по геометрии №1

1 вариант

Периметр параллелограмма равен 122см. Одна из его сторон на 25см больше второй. Найдите стороны параллелограмма.

Диагональ ромба образует с одной из его сторон угол 40. Найдите углы ромба.

АВСD — прямоугольник, ВАС=30, АС=8. Найти ВС.

Контрольная работа по геометрии №1

2 вариант

Периметр прямоугольника равен 96см. Найдите его стороны, если они относятся как 1:3.

Найдите периметр ромба, если В= 60, АС=3см.

АВСD- прямоугольник, ВDА=30, АВ=3. Найти ВD.

Контрольная работа по геометрии №1

1 вариант

Диагональ ромба образует с одной из его сторон угол 40. Найдите углы ромба.

АВСD — прямоугольник, ВАС=30, АС=8. Найти ВС.

Контрольная работа по геометрии №1

2 вариант

Периметр прямоугольника равен 96см. Найдите его стороны, если они относятся как 1:3.

Найдите периметр ромба, если В= 60, АС=3см.

АВСD- прямоугольник, ВDА=30, АВ=3. Найти ВD.

ГДЗ 8 класс / контрольные работы / К-1. вариант 2 геометрия 7‐9 класс самостоятельные и контрольные работы Иченская

Решение есть!

1 класс Математика
Английский язык
Русский язык
Музыка
Литература
Окружающий мир

2 класс Математика
Английский язык
Русский язык
Немецкий язык
Информатика
Музыка
Литература
Окружающий мир
Технология

3 класс Математика
Английский язык
Русский язык
Немецкий язык
Информатика
Музыка
Литература
Окружающий мир
Казахский язык

4 класс Математика
Английский язык
Русский язык
Немецкий язык
Информатика
Музыка
Литература
Окружающий мир
Казахский язык

5 класс Математика
Английский язык
Русский язык
Физика
Немецкий язык
Украинский язык

Годовая контрольная работа по геометрии 8 класс

УТВЕРЖДАЮ:

Руководитель МО математики_______________

МБОУ «Лицей №2» г. Михайловск

«___» ____________ 2019 г.

ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА

по геометрии 2018-2019 уч.год 7 класс

Разработала:

Бережнова Н.Н.

учитель математики

Пояснительная записка

1.ВИД КОНТРОЛЯ– тестовая работа

2.СОДЕРЖАНИЕ КОНТРОЛЯ:

Проверяются следующие темы:

•Основные понятия планиметрии;

•площади многоугольников;

•касательные к окружности;

•центральные и вписанные углы;

•нахождение тригонометрических функций углов;

•подобные треугольники;

3. Цель: контроль освоения обучающимися образовательной программы, уровня сформированности следующих навыков по изученным темам: начальные геометрические сведения, треугольники, параллельные прямые, соотношения между сторонами и углами треугольника.

4. Работа ориен8класса.

5. Текст контрольной работы взят из учебно-методического пособия к учебнику Л.С.Атанасяна «Геометрия 7-9»: автор Н.Б. Мельникова «Контрольные работы по геометрии 8 класс».М.: «Экзамен», 2018.

Контрольная работа представлена в двух вариантах и содержит 7 заданий.

На выполнение работы отводится 40 минут.

6. Критерии оценивания

За верное выполнение каждого задания – 1 балл

Максимальное количество баллов –7.

Критерии выставления оценок

№Количество балловШкольная оценка

1.6-7 «5»

2.4-5 «4»

3.2-3 «3»

4.Менее 2-х «2»

Годовая контрольная работа по геометрии 8 класс. Вариант 1.

Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 28 и 100.

Найдите площадь трапеции, изображённой на рисунке.

Одна из сторон параллелограмма равна 12, а опущенная на нее высота равна 10. Найдите площадь параллелограмма.

Отрезок AB = 48 касается окружности радиуса 14 с центром O в точке B. Окружность пересекает отрезок AO в точке D. Найдите AD.

Точка О — центр окружности, ∠AOB = 84° (см. рисунок). Найдите величину угла ACB (в градусах).

Найдите тангенс угла B треугольникаABC, изображённого на рисунке.

Человек, рост которого равен 1,8 м, стоит на расстоянии 16 м от уличного фонаря. При этом длина тени человека равна 9 м. Определите высоту фонаря (в метрах).

Годовая контрольная работа по геометрии 8 класс. Вариант 2

1.Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 40 и 85.

2. Найдите площадь трапеции, изображённой на рисунке.

3. Одна из сторон параллелограмма равна 20, а опущенная на нее высота равна 23. Найдите площадь параллелограмма.

4. Отрезок AB = 40 касается окружности радиуса 75 с центром O в точке B. Окружность пересекает отрезок AO в точке D. Найдите AD.

5. Точка О — центр окружности, ∠ACB = 24° (см. рисунок). Найдите величину угла AOB (в градусах).

6.Найдите тангенс угла С треугольника ABC , изображённого на рисунке.

7. На каком расстоянии от фонаря находится человек?

GMAT Geometry & Solid Geometry практические вопросы

Вы можете получить от трех до пяти вопросов по геометрии и твердотельной геометрии в разделе GMAT Quantum — в обоих вариантах, а именно, решение проблем и достаточность данных. Проверенные концепции включают в себя линии, углы, треугольники, четырехугольники, круги, координатную геометрию, твердую геометрию, определение площади, периметра двухмерных геометрических форм и площади поверхности, объема, самую длинную диагностику твердых тел, включая конусы, цилиндры, куб, прямоугольный куб, сфера и полушарие.

Примеры практических вопросов GMAT от Geometry приведены ниже. Попробуйте ответить на эти вопросы и убедитесь, что вы получили правильный ответ. Если вы не смогли получить ответ, перейдите к пояснительному ответу или видеообъяснениям (где бы они ни были), чтобы узнать, как решить вопрос.

Вершины четырехугольника ABCD — это A (0, 0), B (4, 5), C (9, 9) и D (5, 4). Какой формы четырехугольник?
1. Квадрат
2. Прямоугольник, но не квадрат
3. Ромб
4. Параллелограмм, но не ромб
5. Воздушный змей
Какова площадь треугольника с тупым углом, две стороны которого равны 8 и 12, а угол между двумя сторонами равен 150 ^o?
1. 24 кв. Квартир
2. 48 кв. Единиц
5. Такого треугольника не существует
Какова мера радиуса круга, описывающего треугольник, стороны которого равны 9, 40 и 41?

Попробуйте эти вопросы в качестве бесплатного онлайн-теста по времени
Получите удобную аналитику | Сравнение с другими участниками GMAT | Определите щели в вашей броне

Если сумма внутренних углов правильного многоугольника составляет 1440 ^o, сколько сторон у многоугольника?
1. 10 сторон
2. 8 сторон
3. 12 сторон
4. 9 сторон
5. Ничего из этого
Каков радиус вписанной окружности треугольника, стороны которого равны 5, 12 и 13 единицам?
1. 2 шт.
2. 12 шт.
3. 6.5 шт.
4. 6 шт.
5. 7,5 шт.
Сколько диагоналей у 63-стороннего выпуклого многоугольника?
Если 10, 12 и ‘x’ — стороны остроугольного треугольника, сколько целых значений ‘x’ возможно?
Достаточность данных : Тупой угол треугольника ABC?
1. a ² + b ²> c ².
2. Центр окружности, описывающей треугольник, не лежит внутри треугольника.
Достаточность данных : Треугольник ABC со сторонами a, b и c остроугольным?
1. Треугольник со сторонами a ², b ², c ² имеет площадь 140 см2.
2. Медиана AD на сторону BC равна высоте AE на стороне BC.
Куб со стороной 5 см раскрашен со всей стороны. Если его разрезать на кубики размером 1 кубический сантиметр, у скольких кубиков размером 1 кубический сантиметр будет окрашена ровно одна сторона?
Колесо автомобиля радиусом 21 см вращается со скоростью 600 об / мин.Какая скорость автомобиля в км / час?
1. 79,2 км / ч
2. 47,52 км / ч
3. 7,92 км / ч
4. 39,6 км / ч
5. 3,96 км / ч
Площадь квадратного поля 24200 кв.м.Сколько времени потребуется женщине, чтобы пересечь поле по диагонали со скоростью 6,6 км / ч?
1. 3 минуты
2. 0,04 часа
3. 2 минуты
4. 2,4 минуты
5. 2 минуты 40 секунд
Женщина выращивает капусту в своем саду, имеющем форму квадрата.Каждая капуста занимает 1 квадратный фут в ее саду. В этом году она увеличила производство на 211 кочанов капусты по сравнению с прошлым годом. Форма площади, на которой выращивали капусту, оставалась квадратной в течение обоих этих лет. Сколько капусты она произвела в этом году?
1. 11236
2. 11025
3. 14400
4. 12696
5. Не определяется
Длина веревки, к которой привязана корова, увеличена с 19 м до 30 м.Сколько еще земли он сможет пасти? Предположите, что корова может двигаться со всех сторон с одинаковой легкостью. Используйте в расчетах π = \\ frac {22} {7} \\).
1. 1696 кв.м
2. 1694 кв.м
3. 1594 кв.м
4. 1756 кв.м
5. 1896 кв.м

Пояснение к видео

Grade 8 Geometry.Квадрат ABCD
Как найти площадь формы
9 Областей и периметров Это наш следующий ключевой блок геометрии. В нем мы резюмируем некоторые концепции, с которыми мы встречались раньше. Мы также начнем развивать более алгебраический подход к поиску площадей и периметров.
Дополнительная информация 5 класс по математике Содержание 1
5-й класс Математика Содержание 1 Число и операции: умножение и деление целых чисел В 5-м классе учащиеся укрепляют свое понимание вычислительных стратегий, которые они используют для умножения.
Дополнительная информация Бесплатный урок предалгебры 55! Страница 1
Бесплатный урок предалгебры 55! стр. 1 Урок 55 Проблемы периметра со связанными переменными Поднимите свои навыки решения текстовых задач на новый уровень в этом разделе.Все проблемы однотипные, так что можно
Дополнительная информация Задача строительных лесов: угловой клубок
Математический модуль для четвертого класса Задача по возведению строительных лесов: СТАНДАРТЫ ДЛЯ МАТЕМАТИЧЕСКОГО СОДЕРЖАНИЯ MCC4.MD.5. Распознавайте углы как геометрические фигуры, которые образуются там, где два луча имеют общую конечную точку,
Дополнительная информация Департамент образования Теннесси
Департамент образования штата Теннесси Задача: Задача по алгебре с патио у бассейна I Отель реконструирует свою территорию и планирует улучшить территорию вокруг прямоугольного бассейна размером 20 на 40 футов.Владелец хочет использовать
Дополнительная информация Окружность и площадь круга
Обзор Математические концепции Материалы Учащиеся узнают, как вычислить число пи (π) в виде отношения. Студенты также изучают окружность и площадь круга с помощью формул. числа и операции TI-30XS MultiView двумерный
Дополнительная информация Исследование области под кривой
Математика Исследование области под кривой Об этом уроке Этот урок представляет собой введение в области, ограниченные функциями и осью x на заданном интервале.Поскольку функции в начале
Дополнительная информация Образовательная программа CPM
Образовательная программа CPM A Калифорнийская некоммерческая корпорация Крис Миклес, национальный директор (888) 808-4276 e-mail: mikles @ cpm.org Курсы CPM и их основные направления Каждый курс построен на нескольких
Дополнительная информация Задача месяца: разрезание куба
Задача месяца: Задачи месяца (POM) используются по-разному, чтобы способствовать решению проблем и способствовать внедрению первого стандарта математической практики из Common Core State Standards:
Дополнительная информация Алгебра: задачи со словом
ССЫЛКА НА РАБОЧЕЕ МЕСТО: Нэнси работает в магазине одежды.Покупатель хочет знать первоначальную цену пары брюк, которые сейчас продаются со скидкой 40%. Цена продажи — 6,50 долларов. Нэнси знает, что 40% оригинального
Дополнительная информация 10,2 45-45-90 треугольников
Страница из 6 0. -0 Треугольников Цель Найдите стороны -0 треугольников со сторонами. Ключевые слова —0 треугольник равнобедренный треугольник p. 7 ножка прямоугольного треугольника п. гипотенуза p. Геодеятельность по равнобедренному краю
Дополнительная информация Распределительная собственность
Цели распределительного свойства Распознать общие шаблоны, используемые для написания распределительного свойства; и мысленно вычислять продукты, используя стратегии распределения.www.everydaymathonline.com
Дополнительная информация Примеры проблем. Проблемы с практикой
Конспект лекций Задачи о квадратичных словах стр. 1 Примеры задач 1. Сумма двух чисел равна 31, их разность равна 41. Найдите эти числа .. Произведение двух чисел равно 640. Их разность равна 1. Найдите эти
Дополнительная информация Вычислить алгебраическое выражение
1.5 Вычисление алгебраических выражений 1.5 ЗАДАЧИ 1. Вычислить алгебраические выражения при любом значении числа со знаком для переменных 2. Используйте калькулятор для вычисления алгебраических выражений 3. Найдите сумму
Дополнительная информация СЕРТИФИКАЦИЯ ДЛЯ НОУТБУКА MATH 60
СЕРТИФИКАЦИЯ НОУТБУКА MATH 60 Глава №1: Целые и действительные числа 1.1a 1.1b 1.2 1.3 1.4 1.8 Глава №2: Алгебраические выражения, линейные уравнения и приложения 2.1a 2.1b 2.1c 2.2 2.3a 2.3b 2.4 2.5
Дополнительная информация МНОЖЕНИЕ КВАДРАТИК 8.1.1 и 8.1.2
РАЗРАБОТКА КВАДРАТИК 8.1.1 и 8.1.2 Глава 8 знакомит студентов с квадратными уравнениями. Эти уравнения можно записать в виде y = ax 2 + bx + c, и при построении графика получается кривая, называемая параболой.
Дополнительная информация Свойства действительных чисел
16 Глава P Предварительные требования стр.2 Свойства действительных чисел Что вам следует изучить: Определить и использовать основные свойства действительных чисел Разработать и использовать дополнительные свойства действительных чисел Почему вам следует
Дополнительная информация Стандарты математики
Стандарты математики 6 класс Итоги успеваемости учащихся к концу 6 класса Обсуждение и решение задач Учащиеся представляют и интерпретируют рутинные и нестандартные математические задачи в диапазоне
Дополнительная информация Краткий обзор алгебры
1.Упрощение Epressions. Решение уравнений 3. Решение проблем 4. Неравенства 5. Абсолютные значения 6. Линейные уравнения 7. Системы уравнений 8. Законы компонентов 9. Квадраты 10. Рационалы 11. Радикалы
Дополнительная информация Геометрия и измерения
Учащийся сможет: Геометрия и измерение 1. Продемонстрировать понимание принципов геометрии, измерения и операций с использованием измерений. Использовать американскую систему измерения для
. Дополнительная информация Решение геометрических приложений
1.8 Решение геометрических приложений 1.8 ЗАДАЧИ 1. Найдите периметр 2. Решите приложения, которые включают периметр 3. Найдите площадь прямоугольной фигуры 4. Примените формулы площади 5. Примените формулы объема
Дополнительная информация Факторинг квадратичных трехчленов
Разложение квадратичных трехчленов на множители Фактор студента x x 3 10. Ответ: x 5 x Описание урока В этом уроке для разложения квадратичных трехчленов на множители используется модель умножения с площадью.Часть 1 урока состоит из
человек. Дополнительная информация Геометрия — 1206310 | CPALMS.org
Описание версии
Основная цель курса геометрии — формализовать и расширить геометрический опыт учащихся средних классов. Студенты исследуют более сложные геометрические ситуации и углубляют свои объяснения геометрических отношений, переходя к формальным математическим аргументам.Между этим курсом геометрии и историческим подходом, используемым в классах геометрии, существуют важные различия. Например, в начале этого курса делается упор на трансформации. Пристальное внимание следует уделить вводному содержанию концептуальной категории «Геометрия» в стандартах средней школы. Стандарты математической практики применяются на протяжении каждого курса и вместе со стандартами содержания предписывают студентам воспринимать математику как связный, полезный и логичный предмет, который использует их способность понимать проблемные ситуации.Ниже перечислены критические области, разделенные на пять блоков.
Раздел 1 — Сравнение, доказательство и построение: В предыдущих классах учащихся просили рисовать треугольники на основе заданных измерений. У них также есть предыдущий опыт работы с жесткими движениями: перемещениями, отражениями и вращениями, и они использовали их для развития представлений о том, что означает конгруэнтность двух объектов. В этом разделе учащиеся устанавливают критерии соответствия треугольника на основе анализа жестких движений и формальных конструкций.Они используют сравнение треугольников как привычную основу для разработки формального доказательства. Студенты доказывают теоремы, используя различные форматы, и решают задачи о треугольниках, четырехугольниках и других многоугольниках. Они применяют рассуждения для завершения геометрических построений и объясняют, почему они работают.
Раздел 2 — Сходство, доказательство и тригонометрия: Учащиеся применяют свой предыдущий опыт с расширением и пропорциональными рассуждениями, чтобы сформировать формальное понимание подобия. Они определяют критерии подобия треугольников, используют подобие для решения задач и применяют подобие в прямоугольных треугольниках для понимания тригонометрии прямоугольного треугольника, уделяя особое внимание специальным прямоугольным треугольникам и теореме Пифагора.Студенты разрабатывают законы синусов и косинусов, чтобы найти недостающие меры общих (не обязательно прямых) треугольников, основываясь на работе студентов с квадратными уравнениями, выполненной в первом курсе. Они могут различать, определяют ли три заданные меры (углы или стороны) 0, 1, 2 или бесконечное количество треугольников.
Раздел 3 — Расширение до трех измерений: Опыт учащихся с двумерными и трехмерными объектами расширен за счет неформальных объяснений формул окружности, площади и объема.Кроме того, учащиеся применяют свои знания о двумерных формах, чтобы рассмотреть формы поперечных сечений и результат вращения двухмерного объекта вокруг линии.
Раздел 4 — Соединение алгебры и геометрии через координаты: Основываясь на своей работе с теоремой Пифагора в 8-м классе для определения расстояний, учащиеся используют прямоугольную систему координат для проверки геометрических соотношений, включая свойства специальных треугольников и четырехугольников и наклоны параллельности и перпендикулярные линии, которые относятся к работе, выполненной в первом курсе.Студенты продолжают изучать квадратику, соединяя геометрическое и алгебраическое определения параболы.
Раздел 5-Круги с координатами и без них: В этом разделе студенты доказывают основные теоремы об окружностях, например, касательная линия перпендикулярна радиусу, теорема о вписанном угле и теоремы об хордах, секущих и касательных, касающихся длин отрезков. и угловые меры. Они изучают отношения между сегментами на аккордах, секущих и касательных как применение сходства.В декартовой системе координат учащиеся используют формулу расстояния, чтобы написать уравнение круга, когда заданы радиус и координаты его центра. Учитывая уравнение круга, они рисуют график в координатной плоскости и применяют методы решения квадратных уравнений, которые связаны с работой, выполненной в первом курсе, для определения пересечений между линиями и кругами или параболами и между двумя кругами.
уроков геометрии в 8 классе

Четырехугольник — замкнутая плоскость фигура ограничена четырьмя отрезками прямых.Например, цифра ABCD показана вот четырехугольник.
Отрезок, проведенный из одной вершины четырехугольник к противоположной вершине называется диагональю четырехугольник. Например, AC — это диагональ четырехугольник ABCD , а так же BD . четырехугольник ABCD-правильный При именовании четырехугольника его вершины должны быть в последовательный порядок (из расчета из рисунка выше)
Углы: (можно назвать одной буквой)
угол A / DAB
угол B / ABC
угол C / BCD
угол D / CDA
Типы четырехугольников
Есть особые виды четырехугольника:

Свойства четырехугольника
Четыре стороны (края)
Четыре вершины (углы)
Суммарные внутренние углы составляют 360 градусов :
Прямоугольник
означает «прямой угол»
а также показать равные стороны
Прямоугольник — это четырехсторонняя форма, каждый угол которой является прямым (90 °).
Также противоположные стороны параллельны и имеют одинаковую длину.
Ромб
Ромб — это четырехгранная форма, все стороны которой имеют одинаковую длину.
Также противоположные стороны параллельны и равны противоположные углы.
Еще один интересный момент: диагонали (пунктирные линии на втором рисунке) пересекаются посередине под прямым углом. Другими словами, они «рассекают» друг друга пополам под прямым углом.
Площадь
означает «прямой угол»
показать равные стороны
У квадрата равные стороны и каждый угол прямой (90 °)
Также противоположные стороны параллельны.
Квадрат также соответствует определению прямоугольника (все углы равны 90 °) и ромба (все стороны равной длины).
Параллелограмм
У параллелограмма противоположные стороны параллельны и равны по длине. Также равны противоположные углы (углы «а» одинаковы, а углы «b» одинаковы).
ПРИМЕЧАНИЕ: квадраты, прямоугольники и ромбы — это параллелограммы!
Пример:
Параллелограмм с:
все стороны равны и
углы «а» и «б» как прямые
это квадрат !
Трапеция (UK: Trapezium)
Трапеция
Равнобедренная трапеция
Трапеция (в Великобритании ее называют трапецией) имеет пару параллельных противоположных сторон.
Она называется равнобедренной трапецией , если стороны, которые не параллельны, равны по длине и оба угла, исходящие с параллельной стороны, равны, как показано.
А трапеция (UK: trapezoid) — это четырехугольник без параллельных сторон:
Трапеция Трапеция
США: пара параллельных сторон НЕТ параллельных сторон
Великобритания: НЕТ параллельных сторон 904 904 904 905 904 904 904 параллельных сторон Воздушный змей
Эй, похоже на воздушного змея.У него две пары сторон. Каждая пара состоит из смежных сторон равной длины. На стыке пар углы равны. Диагонали (пунктирные линии) пересекаются под прямым углом, и одна из диагоналей делит пополам (делит пополам) другую. Сумма внутренних углов
Сумма внутренних углов
Докажите, что сумма углов a четырехугольник равен 360º.

Следовательно, сумма углов четырехугольника равна 360º.
Применение свойств углов в четырехугольниках
Доказанные теоремы можно использовать для доказательства других теорем.Их также можно использовать, чтобы найти значения местоимений в задаче.

Найдите значение местоимения x в сопроводительная диаграмма. Обоснуйте свой ответ. Найдите значение каждого местоимения в кайт показан здесь. Обоснуйте свои ответы. Найдите значение каждого местоимения в сопроводительная диаграмма. Обоснуйте свои ответы.
Стандарты геометрии для 6-го класса по математике
Используйте упорядоченные пары для описания заданных точек в квадранте 1 системы координат.
6.3.2
AT
Billy Bug — Проведите Билли до координат, где прячется еда. координаты 0-10 | координаты 0-5
Создайте дом с привидениями … если осмелитесь! — Следуйте инструкциям, чтобы отточить свои навыки построения графиков, создать крутой дом с привидениями, а затем преобразовать его с помощью математики. Выражения, решение уравнений и построение графиков в координатной плоскости — дом с привидениями и многие другие практические задачи в координатной плоскости
Графический апплет — интерактивный сайт, который определяет упорядоченные пары точек, на которые студенты нажимают — Расширенная версия того же апплета
Викторина по графическим уравнениям и неравенствам
Графическое изображение упорядоченных пар — объяснение и интерактивная практика
Навыки построения графиков — в чем смысл? Найдите точку на сетке (выберите Легко для задач из квадранта 1)
Сетка График — определение и нанесение точек на сетку
Чтение сетки — Найдите Херкла за сеткой.Введите заказанные пары, чтобы найти его
Простая игра с координатами — учащиеся исследуют первый квадрант декартовой системы координат, определяя координаты точек или запрашивая построение конкретной точки.
Простая игра в лабиринт — учащиеся исследуют первый квадрант декартовой системы координат, направляя робота через минное поле, разложенное на плоскости.
.
No related posts.
Posted in Контрольная
Навигация по записям
Previous
Next
Leave a Reply
Добавить комментарий Отменить ответ
Ваш адрес email не будет опубликован. Обязательные поля помечены *
Комментарий *
Имя *
Email *
Сайт

Рубрики
Контрольная
Советы
2024 © Все права защищены. Карта сайта