Дан многочлен 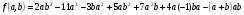 .
.
Контрольные работы по алгебре
Контрольная работа № 1
Вариант 1 (1 ч)
Дан многочлен 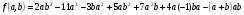 .
.
а) Приведите данный многочлен к стандартному виду.
б) Установите, является ли данный многочлен однородным.
в) Если данный многочлен является однородным, определите его
степень.
Разложите многочлен на множители: а) 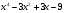 ;
;
б) 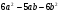 .
.
3. Решите уравнение 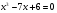 .
.
___________________________________________________________________
4. Докажите, что выражение 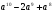 делится на
делится на 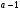 .
.
______________________________________
При каких значения параметров 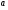 и
и 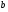 многочлен
многочлен
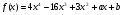 делится без остатка на многочлен
делится без остатка на многочлен
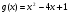 ?
?
Контрольная работа № 1
Вариант 2 (1 ч)
1. Дан многочлен
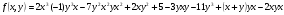 .
.
а) Приведите данный многочлен к стандартному виду.
б) Установите, является ли данный многочлен однородным.
в) Если данный многочлен является однородным, определите его
степень.
2. Разложите многочлен на множители: а) 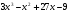 ;
;
б) 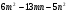 .
.
3. Решите уравнение 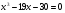 .
.
___________________________________________________________________
4. Докажите, что выражение 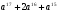 делится на
делится на 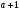 .
.
______________________________________
5. При каких значения параметров 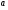 и
и 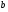 многочлен
многочлен
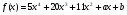 делится без остатка на многочлен
делится без остатка на многочлен
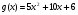 ?
?
Контрольная работа № 2
Вариант 1 (2 ч)
Вычислите: а) 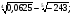 б)
б) 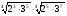 .
.
2. Решите уравнение: а) 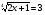 ; б)
; б) 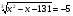 .
.
3. Постройте график функции 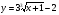 .
.
4. Найдите область определения функции 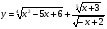 .
.
5. Упростите выражение 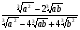 .
.
6. Расположите в порядке убывания следующие числа: 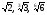 .
.
___________________________________________________________________
7. Найдите значение выражения 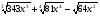 при
при 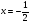 .
.
______________________________________
8. Решите неравенство 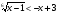 .
.
9. Решите уравнение 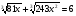 .
.
Контрольная работа № 2
Вариант 2 (2 ч)
1. Вычислите: а) 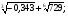 б)
б) 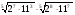 .
.
2. Решите уравнение: а) 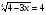 ; б)
; б) 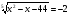 .
.
3. Постройте график функции 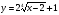 .
.
4. Найдите область определения функции 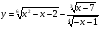 .
.
5. Упростите выражение 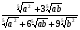 .
.
6. Расположите в порядке возрастания следующие числа: 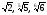 .
.
___________________________________________________________________
7. Найдите значение выражения 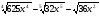 при
при 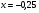 .
.
______________________________________
8. Решите неравенство 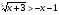 .
.
9. Решите уравнение 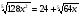 .
.
Контрольная работа № 3
Вариант 1 (1 ч)
Вычислите: а) 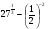 ; б)
; б) 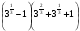 .
.
Упростите выражение 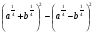 .
.
3. Решите уравнение 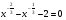 .
.
4. Составьте уравнение касательной к графику функции 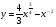
в точке 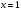 .
.
___________________________________________________________________
5. Решите неравенство 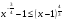 .
.
______________________________________
6. Решите уравнение 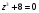 на множестве комплексных чисел.
на множестве комплексных чисел.
Контрольная работа № 3
Вариант 2 (1 ч)
1. Вычислите: а) 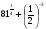 ; б)
; б) 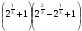 .
.
2. Упростите выражение 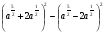 .
.
Решите уравнение 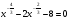 .
.
4. Составьте уравнение касательной к графику функции 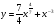
в точке 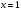 .
.
___________________________________________________________________
5. Решите неравенство 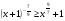 .
.
______________________________________
6. Решите уравнение 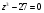 на множестве комплексных чисел.
на множестве комплексных чисел.
Контрольная работа № 4
Вариант 1 (2 ч)
1. Постройте график функции:
а) 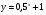 ; б)
; б) 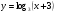 .
.
2. Решите уравнение: а) 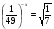 ; б)
; б) 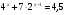 .
.
3. Решите неравенство 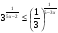 .
.
4. Вычислите 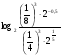 .
.
5. Сравните числа: а) 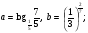 б)
б) 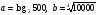 .
.
___________________________________________________________________
6. Решите неравенство 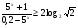 .
.
______________________________________
7. Решите неравенство 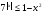 .
.
Контрольная работа № 4
Вариант 2 (2 ч)
1. Постройте график функции:
а) 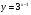 ; б)
; б) 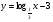 .
.
2. Решите уравнение: а) 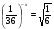 ; б)
; б) 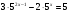 .
.
3. Решите неравенство 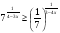 .
.
4. Вычислите 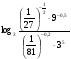 .
.
5. Сравните числа: а) 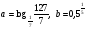 ; б)
; б) 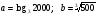 .
.
___________________________________________________________________
6. Решите неравенство 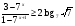 .
.
______________________________________
7. Решите неравенство 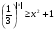 .
.
Контрольная работа № 5
Вариант 1 (2 ч)
1. Вычислите 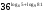 .
.
Решите уравнение:
а) 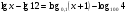 ;
;
б) 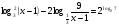 ;
;
в) 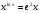 .
.
Решите неравенство:
а)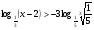 ; б)
; б) 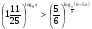 .
.
4. Исследуйте функцию 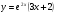 на монотонность и экстремумы.
на монотонность и экстремумы.
5. К графику функции 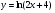 проведена касательная, параллельная прямой
проведена касательная, параллельная прямой 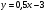 . Найдите точку пересечения этой касательной с осью x.
. Найдите точку пересечения этой касательной с осью x.
____________________________________________________________
6. Решите неравенство 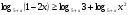 .
.
___________________________________
7. Решите систему уравнений 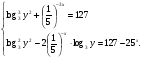
Контрольная работа № 5
Вариант 2 (2 ч)
1. Вычислите 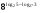 .
.
2. Решите уравнение:
а) 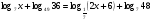 ;
;
б) 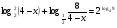 ;
;
в) 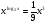 .
.
3. Решите неравенство:
а) 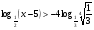 ; б)
; б) 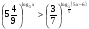 .
.
4. Исследуйте функцию 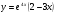 на монотонность и экстремумы.
на монотонность и экстремумы.
5. К графику функции 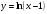 проведена касательная, параллельная биссектрисе первой координатной четверти. Найдите площадь треугольника, отсекаемого этой касательной от осей координат.
проведена касательная, параллельная биссектрисе первой координатной четверти. Найдите площадь треугольника, отсекаемого этой касательной от осей координат.
____________________________________________________________
6. Решите неравенство 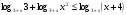 .
.
___________________________________
7. Решите систему уравнений 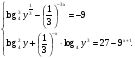
Контрольная работа № 6
Вариант 1 (1 ч)
1. Докажите, что функция 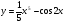 является первообразной для
является первообразной для
функции 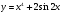 .
.
2. Для данной функции 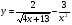 найдите ту первообразную, график
найдите ту первообразную, график
которой проходит через точку 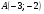 .
.
3. Вычислите определенный интеграл:
а)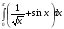 ; б)
; б) 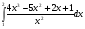 .
.
4. Найдите площадь фигуры, ограниченной графиком функции 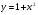
и прямой 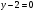 .
.
______________________________________________________________
5. Известно, что функция 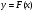 ─ первообразная для функции
─ первообразная для функции
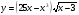 . Исследуйте функцию
. Исследуйте функцию 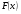 на монотонность
на монотонность
и экстремумы.
___________________________________
При каких значениях параметра 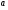 выполняется неравенство
выполняется неравенство
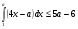 ?
?
Контрольная работа № 6
Вариант 2 (1 ч)
1. Докажите, что функция 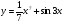 является первообразной для
является первообразной для
функции 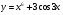 .
.
2. Для данной функции 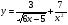 найдите ту первообразную, график
найдите ту первообразную, график
которой проходит через точку 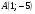 .
.
3. Вычислите определенный интеграл:
а) 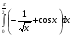 ; б)
; б) 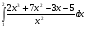 .
.
4. Найдите площадь фигуры, ограниченной графиком функции 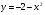
и прямой 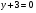 .
.
______________________________________________________________
5. Известно, что функция 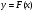 - первообразная для функции
- первообразная для функции
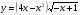 . Исследуйте функцию
. Исследуйте функцию 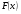 на монотонность
на монотонность
и экстремумы.
___________________________________
При каких значениях параметра 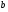 выполняется неравенство
выполняется неравенство
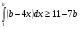 ?
?
Контрольная работа № 7
Вариант 1 (2 ч)
1. Решите уравнение:
а) 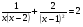 ;
;
б) 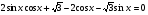 ;
;
в) 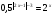 .
.
Решите неравенство:
а) 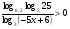 ; б)
; б) 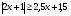 .
.
Решите уравнение 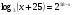 .
.
Решите уравнение 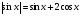 .
.
___________________________________________________________
Внутри равнобедренного прямоугольного треугольника случайным образом выбрана точка. Какова вероятность того, что она расположена ближе к вершине прямого угла, чем к вершинам двух его острых углов?
___________________________________
6. Решите уравнение 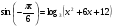 .
.
Контрольная работа № 7
Вариант 2 (2 ч)
1. Решите уравнение:
а) 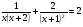 ;
;
б) 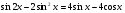 ;
;
в) 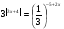 .
.
2. Решите неравенство:
а) 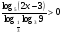 ; б)
; б) 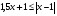 .
.
3. Решите уравнение 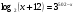 .
.
4. Решите уравнение 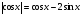 .
.
___________________________________________________________
5. Внутри квадрата случайным образом выбрана точка. Какова
вероятность того, что она расположена внутри вписанного в
него круга?
_________________________________
6. Решите уравнение 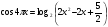 .
.
Контрольная работа № 8
Вариант 1 (2 ч)
1. Решите уравнение:
а) 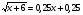 ; б)
; б) 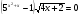 .
.
Решите неравенство 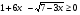 .
.
Решите систему уравнений: а) 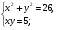 б)
б) 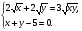
Найдите площадь фигуры, заданной системой неравенств
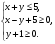
5. Докажите, что для любых неотрицательных чисел 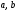 выполняется
выполняется
неравенство 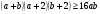 .
.
____________________________________________________________
6. Решите уравнение в целых числах: 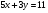 .
.
___________________________________
7. Три числа образуют арифметическую прогрессию. Если третий член
данной прогрессии уменьшить на 3, то полученные три числа
составят геометрическую прогрессию. Если второй член
геометрической прогрессии уменьшить на 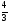 , то полученные три
, то полученные три
числа вновь составят геометрическую прогрессию. Найдите
первоначально заданные числа.
Контрольная работа № 8
Вариант 2 (2 ч)
1. Решите уравнение:
а) 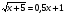 ; б)
; б) 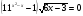 .
.
2. Решите неравенство 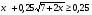 .
.
3. Решите систему уравнений: а) 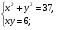 б)
б) 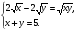
4. Найдите площадь фигуры, заданной системой неравенств
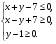
5. Докажите, что для любых неотрицательных чисел 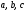
выполняется неравенство 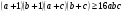 .
.
____________________________________________________________
6. Решите уравнение в целых числах: 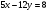 .
.
___________________________________
7. Три числа составляют геометрическую прогрессию. Если второй
член данной прогрессии увеличить на 2, то полученные числа
составят арифметическую прогрессию. Если третий член новой
прогрессии увеличить на 9, то полученные три числа составят
геометрическую прогрессию. Найдите первоначально заданные
infourok.ru
Контрольная работа № 1. Метод координат в пространстве в пространстве
1 вариант.
Найдите координаты вектора  , если А(5; -1; 3), В(2; -2; 4).
, если А(5; -1; 3), В(2; -2; 4).
Даны векторы  {3; 1; -2} и
{3; 1; -2} и  {1; 4; -3}. Найдите
{1; 4; -3}. Найдите  .
.
Изобразите систему координат Охуz и постройте точку А( 1; -2; -4). Найдите расстояние от этой точки до координатных плоскостей.
Вершины Δ АВС имеют координаты:
А( -2; 0; 1 ), В( -1; 2; 3 ), С( 8; -4; 9 ).
Найдите координаты вектора  , если ВМ – медиана ∆АВС.
, если ВМ – медиана ∆АВС.
2 вариант.
Найдите координаты вектора  , если
, если
А(6; 3; -2), В(2; 4; -5).
Даны векторы  {5; -1; 2} и
{5; -1; 2} и  {3; 2; -4}. Найдите
{3; 2; -4}. Найдите  .
.
Изобразите систему координат Охуz и постройте точку В( -2; -3; 4). Найдите расстояние от этой точки до координатных плоскостей.
Вершины ∆АВС имеют координаты:
А ( -1; 2; 3 ), В ( 1; 0; 4 ), С ( 3; -2; 1 ).
Найдите координаты вектора  , если АМ – медиана ∆АВС.
, если АМ – медиана ∆АВС.
26.12 Контрольная работа № 2. Цилиндр. Конус и шар
1 вариант
1. Радиус основания цилиндра равен 5 см, а высота цилиндра равна 6 см. Найдите площадь сечения, проведенного параллельно оси цилиндра на расстоянии 4 см от нее.
2. Радиус шара равен 17 см. Найдите площадь сечения шара, удаленного от его центра на 15 см.
3. Радиус основания конуса равен 3 м, а высота 4 м. Найдите образующую и площадь осевого сечения.
2 вариант
1. Высота цилиндра 8 дм, радиус основания 5 дм. Цилиндр пересечен плоскостью параллельно оси так, что в сечении получился квадрат. Найдите расстояние от этого сечения до оси цилиндра.
2. Радиус сферы равен 15 см. Найдите длину окружности сечения, удаленного от центра сферы на 12 см.
3. Образующая конуса l наклонена к плоскости основания под углом в 300. Найдите высоту конуса и площадь осевого сечения.
01.03 Контрольная работа № 3
Объемы тел. Объем призмы, цилиндра, конуса
1 вариант
1. Образующая конуса равна 60 см, высота 30 см. Найдите объём конуса.
2. Основание прямой призмы – прямоугольный треугольник с катетом 6 см и острым углом 450. Объем призмы равен 108 см3. Найдите площадь полной поверхности призмы.
3. Осевым сечением цилиндра является квадрат, диагональ которого равна  см. Найдите объем цилиндра.
см. Найдите объем цилиндра.
2 вариант
1. Образующая конуса, равная 12 см, наклонена к плоскости основания под углом 300. Найдите объём конуса.
2. Основанием прямой призмы является ромб со стороной 12 см и углом 600. Меньшее из диагональных сечений призмы является квадратом. Найдите объем призмы.
3. Осевым сечением цилиндра является квадрат, диагональ которого равна  см. Найдите объем цилиндра.
см. Найдите объем цилиндра.
26.04 Контрольная работа № . Итоговая контрольная работа
1 вариант
1. Диаметр шара равен высоте конуса, образующая которого составляет с плоскостью основания угол, равный 600. Найдите отношение объёмов конуса и шара.
2. Объём цилиндра равен 96π см3, площадь его осевого сечения 48см2. Найдите площадь сферы, описанной около цилиндра.
3. В конус вписана пирамида. Основанием пирамиды служит прямоугольный треугольник, катет которого равен 2р, а прилежащий угол равен  . Боковая грань пирамиды, проходящая через данный катет, составляет с плоскостью основания угол
. Боковая грань пирамиды, проходящая через данный катет, составляет с плоскостью основания угол  . Найдите объём конуса.
. Найдите объём конуса.
2 вариант
1. Диаметр шара равен высоте цилиндра, осевое сечение которого есть квадрат. Найдите отношение объёмов шара и цилиндра.
2. В конус, осевое сечение которого есть правильный треугольник, вписан шар. Найдите отношение площади сферы к площади боковой поверхности конуса.
3. В цилиндр вписана призма. Основанием призмы служит прямоугольный треугольник, катет которого равен 2р, а прилежащий угол равен  . Диагональ большей боковой грани призмы составляет с плоскостью её основания угол
. Диагональ большей боковой грани призмы составляет с плоскостью её основания угол  . Найдите объём цилиндра.
. Найдите объём цилиндра.
multiurok.ru
Контрольные работы
по геометрии
в 11 классе
по учебнику атанасян л.с.
Контрольная работа № 1
Тема: Векторы(на 20 мин)
Вариант 1
1. Найдите координаты вектора  , если А (5; –1; 3), В (2; –2; 4).
, если А (5; –1; 3), В (2; –2; 4).
2. Даны векторы  (3; 1; –2) и
(3; 1; –2) и  (1; 4; –3). Найдите
(1; 4; –3). Найдите  .
.
3. Изобразите систему координат Oxyz и постройте точку А (1; –2; –4). Найдите расстояния от этой точки до координатных плоскостей.
Контрольная работа № 1Тема: Векторы
(на 20 мин)
Вариант 2
1. Найдите координаты вектора  , если С (6; 3; – 2), D (2; 4; – 5).
, если С (6; 3; – 2), D (2; 4; – 5).
2. Даны вектора  (5; – 1; 2) и
(5; – 1; 2) и  (3; 2; – 4). Найдите
(3; 2; – 4). Найдите  .
.
3. Изобразите систему координат Oxyz и постройте точку В (– 2; – 3; 4). Найдите расстояние от этой точки до координатных плоскостей.
Контрольная работа № 2
Тема: Скалярное произведение векторов. Движения.
Вариант 1
1. Вычислите скалярное произведение векторов  и
и  , если
, если  ,
,  ,
,  = 2,
= 2,  = 3,
= 3,  = 60°,
= 60°,  ,
,  .
.
2. Дан куб ABCDA1B1C1D1. Найдите угол между прямыми AD1 и BM, где M – середина ребра DD1.
3. При движении прямая отображается на прямую b1, а плоскость β – на плоскость β1 и b || β1.
Контрольная работа № 2
Тема: Скалярное произведение векторов. Движения.
Вариант 2
1. Вычислите скалярное произведение векторов  и
и  , если
, если  ,
,  ,
,  = 3,
= 3,  = 2,
= 2,  = 60°,
= 60°,  ,
,  .
.
2. Дан куб ABCDA1B1C1D1. Найдите угол между прямыми AC и DC1.
3. При движении прямая a отображается на прямую a1, плоскость α – на плоскость α1, и . Докажите, что .
Контрольная работа № 3
Тема: Цилиндр, конус, шар.
Вариант 1
1. Осевое сечение цилиндра – квадрат, площадь основания цилиндра равна 16π см2. Найдите площадь поверхности цилиндра.
2. Высота конуса равна 6 см, угол при вершине осевого сечения равен 120°. Найдите:
а) площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми 30°;
б) площадь боковой поверхности конуса.
3. Диаметр шара равен 2m. Через конец диаметра проведена плоскость под углом 45° к нему. Найдите длину линии пересечения сферы с этой плоскостью.
Контрольная работа № 3
Тема: Цилиндр, конус, шар.
Вариант 2
1. Осевое сечение цилиндра – квадрат, диагональ которого 4 см. Найдите площадь поверхности цилиндра.
2. Радиус основания конуса равен 6 см, а образующая наклонена к плоскости основания под углом 30°. Найдите:
а) площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми 60°;
б) площадь боковой поверхности конуса.
3. Диаметр шара равен 4m. Через конец диаметра проведена плоскость под углом 30° к нему. Найдите площадь сечения шара этой плоскостью.
Контрольная работа № 4
Тема: Объемы тел.
Вариант 1
1. Апофема правильной треугольной пирамиды равна 4 см, а двугранный угол при основании равен 60°. Найдите объем пирамиды.
2. В цилиндр вписана призма. Основанием призмы служит прямоугольный треугольник, катет которого равен 2a, а прилежащий угол равен 30°. Диагональ большей боковой грани призмы составляет с плоскостью ее основания угол в 45°. Найдите объем цилиндра.
Контрольная работа № 4
Тема: Объемы тел.
Вариант 2
1. Боковое ребро правильной треугольной пирамиды равно 6 см и составляет с плоскостью основания угол в 60°. Найдите объем пирамиды.
2. В конус вписана пирамида. Основанием пирамиды служит прямоугольный треугольник, катет которого равен 2a, а прилежащий угол равен 30°. Боковая грань пирамиды, проходящая через данный катет, составляет с плоскостью основания угол в 45°. Найдите объем конуса.
Контрольная работа № 5
Тема: Объем шара и площадь сферы.
Вариант 1
1. Диаметр шара равен высоте конуса, образующая которого составляет с плоскостью основания угол в 60°. Найдите отношение объемов конуса и шара.
2. Объем цилиндра равен 96π см3, площадь его осевого сечения 48 см2. Найдите площадь сферы, описанной около цилиндра.
Контрольная работа № 5
Тема: Объем шара и площадь сферы.
Вариант 2
1. В конус, осевое сечение которого есть правильный треугольник, вписан шар. Найдите отношение площади сферы к площади боковой поверхности конуса.
2. Диаметр шара равен высоте цилиндра, осевое сечение которого есть квадрат. Найдите отношение объемов цилиндра и шара.
videouroki.net
Контрольная работа № 1. Метод координат в пространстве в пространстве
1 вариант.
Найдите координаты вектора  , если А(5; -1; 3), В(2; -2; 4).
, если А(5; -1; 3), В(2; -2; 4).
Даны векторы  {3; 1; -2} и
{3; 1; -2} и  {1; 4; -3}. Найдите
{1; 4; -3}. Найдите  .
.
Изобразите систему координат Охуz и постройте точку А( 1; -2; -4). Найдите расстояние от этой точки до координатных плоскостей.
Вершины Δ АВС имеют координаты:
А( -2; 0; 1 ), В( -1; 2; 3 ), С( 8; -4; 9 ).
Найдите координаты вектора  , если ВМ – медиана ∆АВС.
, если ВМ – медиана ∆АВС.
2 вариант.
Найдите координаты вектора  , если
, если
А(6; 3; -2), В(2; 4; -5).
Даны векторы  {5; -1; 2} и
{5; -1; 2} и  {3; 2; -4}. Найдите
{3; 2; -4}. Найдите  .
.
Изобразите систему координат Охуz и постройте точку В( -2; -3; 4). Найдите расстояние от этой точки до координатных плоскостей.
Вершины ∆АВС имеют координаты:
А ( -1; 2; 3 ), В ( 1; 0; 4 ), С ( 3; -2; 1 ).
Найдите координаты вектора  , если АМ – медиана ∆АВС.
, если АМ – медиана ∆АВС.
26.12 Контрольная работа № 2. Цилиндр. Конус и шар
1 вариант
1. Радиус основания цилиндра равен 5 см, а высота цилиндра равна 6 см. Найдите площадь сечения, проведенного параллельно оси цилиндра на расстоянии 4 см от нее.
2. Радиус шара равен 17 см. Найдите площадь сечения шара, удаленного от его центра на 15 см.
3. Радиус основания конуса равен 3 м, а высота 4 м. Найдите образующую и площадь осевого сечения.
2 вариант
1. Высота цилиндра 8 дм, радиус основания 5 дм. Цилиндр пересечен плоскостью параллельно оси так, что в сечении получился квадрат. Найдите расстояние от этого сечения до оси цилиндра.
2. Радиус сферы равен 15 см. Найдите длину окружности сечения, удаленного от центра сферы на 12 см.
3. Образующая конуса l наклонена к плоскости основания под углом в 300. Найдите высоту конуса и площадь осевого сечения.
01.03 Контрольная работа № 3
Объемы тел. Объем призмы, цилиндра, конуса
1 вариант
1. Образующая конуса равна 60 см, высота 30 см. Найдите объём конуса.
2. Основание прямой призмы – прямоугольный треугольник с катетом 6 см и острым углом 450. Объем призмы равен 108 см3. Найдите площадь полной поверхности призмы.
3. Осевым сечением цилиндра является квадрат, диагональ которого равна  см. Найдите объем цилиндра.
см. Найдите объем цилиндра.
2 вариант
1. Образующая конуса, равная 12 см, наклонена к плоскости основания под углом 300. Найдите объём конуса.
2. Основанием прямой призмы является ромб со стороной 12 см и углом 600. Меньшее из диагональных сечений призмы является квадратом. Найдите объем призмы.
3. Осевым сечением цилиндра является квадрат, диагональ которого равна  см. Найдите объем цилиндра.
см. Найдите объем цилиндра.
26.04 Контрольная работа № . Итоговая контрольная работа
1 вариант
1. Диаметр шара равен высоте конуса, образующая которого составляет с плоскостью основания угол, равный 600. Найдите отношение объёмов конуса и шара.
2. Объём цилиндра равен 96π см3, площадь его осевого сечения 48см2. Найдите площадь сферы, описанной около цилиндра.
3. В конус вписана пирамида. Основанием пирамиды служит прямоугольный треугольник, катет которого равен 2р, а прилежащий угол равен  . Боковая грань пирамиды, проходящая через данный катет, составляет с плоскостью основания угол
. Боковая грань пирамиды, проходящая через данный катет, составляет с плоскостью основания угол  . Найдите объём конуса.
. Найдите объём конуса.
2 вариант
1. Диаметр шара равен высоте цилиндра, осевое сечение которого есть квадрат. Найдите отношение объёмов шара и цилиндра.
2. В конус, осевое сечение которого есть правильный треугольник, вписан шар. Найдите отношение площади сферы к площади боковой поверхности конуса.
3. В цилиндр вписана призма. Основанием призмы служит прямоугольный треугольник, катет которого равен 2р, а прилежащий угол равен  . Диагональ большей боковой грани призмы составляет с плоскостью её основания угол
. Диагональ большей боковой грани призмы составляет с плоскостью её основания угол  . Найдите объём цилиндра.
. Найдите объём цилиндра.
multiurok.ru
Контрольная работа по геометрии №1 (11 класс).
Тема: «Многогранники». Погорелов А. В.
1 вариант
2 вариант
1.
В прямоугольном параллелепипеде стороны основания 12 дм и 15 дм, а высота параллелепипеда 11 дм.
Найти: а) площадь боковой поверхности параллелепипеда;
б) площадь полной поверхности параллелепипеда;
в) площадь диагонального сечения параллелепипеда;
г) диагональ.
1.
В прямоугольном параллелепипеде стороны основания 17 дм и 13 дм, а высота параллелепипеда 9 дм.
Найти: а) площадь боковой поверхности параллелепипеда;
б) площадь полной поверхности параллелепипеда;
в) площадь диагонального сечения параллелепипеда;
г) диагональ.
2.
Диагональ прямоугольного параллелепипеда равна 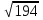 дм, а диагонали его боковых граней
дм, а диагонали его боковых граней 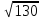 дм и
дм и 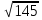 дм .
дм .
Определить полную поверхность параллелепипеда.
2.
Диагональ прямоугольного параллелепипеда равна 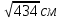 , а диагонали его боковых граней
, а диагонали его боковых граней 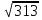 см и
см и 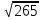 см.
см.
Определить полную поверхность параллелепипеда.
3.
Найти сторону основания и высоту правильной 4-х угольной призмы, если площадь ее поверхности равна 640 см, а боковая поверхность 440 см.
3.
Найти сторону основания и высоту правильной 4-х угольной призмы, если площадь ее поверхности равна 960 дм, а боковая поверхность 672 дм.
Контрольная работа по геометрии №2 (11 класс).
Тема: « Тела вращения». Погорелов А. В.
1 вариант
2 вариант
Постройте сечение треугольной пирамиды плоскостью, проходящей через сторону основания пирамиды и данную точку на противолежащем ребре.
Постройте сечение четырехугольной пирамиды плоскостью, проходящей через сторону основания пирамиды и точку на одном из боковых ребер.
У четырехугольной усеченной пирамиды стороны одного основания равны 15 м, 18 м, 12 м, 30м. А меньшая сторона другого основания равна 20 м. Найти остальные стороны этого основания.
У четырехугольной усеченной пирамиды стороны одного основания равны 16 м, 20 м, 32 м, 40 м. А большая сторона другого основания равна 60 м. Найти остальные стороны этого основания.
Боковое ребро треугольной пирамиды разделено на 5 равных частей и через точки деления проведены плоскости, параллельные основанию пирамиды. Площадь основания пирамиды равна 600 м2. Найти площади сечений.
Боковое ребро четырехугольной пирамиды разделено на 5 равных частей и через точки деления проведены плоскости, параллельные основанию пирамиды. Площадь основания пирамиды равна 800 м2. Найти площади сечений.
Контрольная работа по геометрии № 3 (11 класс).
Тема: «Объемы многогранников». Погорелов А. В.
1 вариант
вариант
В цилиндре с высотой 6 см проведено параллельно оси сечение, отстоящее от нее на расстоянии 4 см. Найти радиус цилиндра, если площадь указанного сечения равна 36 см2.
В цилиндре с радиусом 5см проведено параллельно оси сечение, отстоящее от нее на расстоянии 3 см. Найти радиус цилиндра, если площадь указанного сечения равна 64 см2.
Угол при вершине осевого сечения конуса с высотой 1 м равен 1200. Чему равна площадь сечения конуса, проведенного через две образующие, угол между которыми равен 600.
Угол при вершине осевого сечения конуса с высотой 1 м равен 600. Чему равна площадь сечения конуса, проведенного через две образующие, угол между которыми равен 450.
В усеченном конусе диагональ осевого сечения равна 10 см, радиусы оснований 2 см и 4 см. Найти высоту конуса.
В усеченном конусе диагональ осевого сечения равна 10 см, радиус меньшего основания 3 см, а высота 6 см. Найти радиус большего основания конуса.
Контрольная работа по геометрии №4 (11 класс).
Тема: « Объемы и поверхности тел вращения». Погорелов А. В.
1 вариант
2 вариант
1.
Чему равен объем прямоугольного параллелепипеда, диагонали граней которого равны 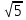 см.,
см., 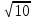 см.,
см., 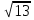 см.?
см.?
1.
Чему равен объем прямоугольного параллелепипеда, площади трех граней которого равны 12 см2, 15 см2 и 20 см2?
2.
Чему равен объем правильной шестиугольной призмы со стороной основания a и длиной большей диагонали b?
2.
Чему равен объем правильной треугольной призмы со стороной основания a и расстоянием от вершины одного основания до противолежащей стороны другого основания, равным b?
3.
Найти объем пирамиды, в основании которой лежит параллелограмм со сторонами 2 и 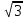 и углом между ними 300 , если высота пирамиды равна меньшей диагонали основания.
и углом между ними 300 , если высота пирамиды равна меньшей диагонали основания.
3.
Найти объем пирамиды, в основании которой лежит параллелограмм с диагоналями 4 и 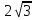 , если угол между ними 300 , а высота пирамиды равна меньшей стороне основания.
, если угол между ними 300 , а высота пирамиды равна меньшей стороне основания.
Контрольная работа по геометрии №5 (11 класс).
Тема: « Избранные вопросы планиметрии». Погорелов А. В.
1 ВАРИАНТ
2 ВАРИАНТ
1. В правильной треугольной пирамиде, объёмом 12 дм3, высоту увеличили в 3 раза, а сторону основания уменьшили в 9 раз. Чему равен объём получившейся пирамиды?
1. В правильной треугольной пирамиде, объёмом 35 дм3, высоту увеличили в 9 раз, а сторону основания уменьшили в 3 раза. Чему равен объём получившейся пирамиды?
2.Каким должен быть радиус основания цилиндра с квадратным осевым сечением, для того, чтобы его боковая поверхность была такая же, как поверхность шара с радиусом 4 м.?
2.Каким должен быть радиус основания цилиндра с квадратным осевым сечением, для того, чтобы его боковая поверхность была такая же, как поверхность шара с радиусом 6 м.?
3.Чему равна площадь сферы, вписанной в куб с ребром 2 м?
3.Чему равна площадь сферы, вписанной в куб с ребром 1 м?
4.Конусообразная палатка высотой 3,5 м с диаметром основания 4 м, покрыта парусиной. Сколько квадратных метров парусины пошло на палатку?
4. Чему равен объём шарового сектора, если радиус окружности его основания 60 см, а радиус шара 75 см?
infourok.ru
Годовая контрольная работа по геометрии.
11 класс
Цель: проверить уровень усвоение ГОСО
- умение изображать цилиндр, конус, шар, призму, пирамиду и их элементы;
- знание и применение формул нахождения площади боковой и полной поверхности многогранников, объемов многогранников и тел вращения;
- умения находить элементы многогранников и тел вращения;
Содержание работы:
1 вариант.
Найдите площадь полной поверхности и объем правильной треугольной призмы с ребром 3.
Осевое сечение цилиндра квадрат, площадь которого равна 16. Найдите площадь поверхности и объем цилиндра.
Диагональным сечением четырехугольной пирамиды служит правильный треугольник со стороной, равной 1. Найдите объем пирамиды.
На поверхности шара даны три точки. Расстояние между ними 6, 8, 10. Радиус шара 13. Найдите расстояние от центра шара до плоскости, проходящей через эти три точки.
Стороны оснований правильной четырехугольной усеченной пирамиды равны 4 и 4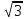 см, а боковая грань наклонена к плоскости большего основания угол 60
см, а боковая грань наклонена к плоскости большего основания угол 60 .Найдите площадь полной поверхности данной пирамиды.
.Найдите площадь полной поверхности данной пирамиды.
2 вариант.
Найдите площадь полной поверхности и объем правильной четырехугольной призмы с ребром равным 2.
Радиус основания конуса равен 1см. Осевое сечение конуса равносторонний треугольник. Найдите площадь поверхности и объем конуса.
В правильной четырехугольной призме площадь основания 144, а диагональ призмы 22. Найдите объем призмы.
Все стороны квадрата касаются сферы диаметром 50, сторона квадрата 14. Найдите расстояние от центра сферы до плоскости квадрата.
Стороны оснований правильной четырехугольной усеченной пирамиды относятся, как 3:2. Высота пирамиды равна 3. Боковое ребро составляет с плоскостью основания угол 60 . Найдите объем пирамиды.
. Найдите объем пирамиды.
Критерии оценивания
| № задания | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемого элемента | Балл за выполнение задания |
| 1 | Нахождение площади боковой и полной поверхности призмы, объемов призмы. | Знание формул площади боковой поверхности призмы | 1 | 4 |
| Знание формул площади полной поверхности призмы | 1 | |||
| Знание формул объема призмы | 1 | |||
| Вычисления | 1 | |||
| 2 | Нахождение элементов и объема цилиндра (конуса). | Выполнение чертежа | 1 | 4 |
| Понятие осевого сечения, связь с элементами цилиндра (конуса) | 1 | |||
| Знания формулы объема. | 1 | |||
| Вычисления | 1 | |||
| 3 | Нахождение объема пирамиды (призмы). | Выполнение чертежа | 1 | 5 |
| Знание формул | 1 | |||
| Нахождение элементов | 1 | |||
| Обоснования | 1 | |||
| Вычисления | 1 | |||
| 4 | Нахождение расстояния от центра шара до сечения и площади сечения. | Выполнение чертежа | 1 | 5 |
| Нахождение радиуса описанной окружности. | 2 | |||
| Нахождение расстояния | 1 | |||
| Вычисление площади сечения. | 1 | |||
| 5 | Усеченная пирамида | Выполнение чертежа | 1 | 5 |
| Нахождение необходимых элементов сечения | 1 | |||
| Решение треугольника | 1 | |||
| Обоснования | 1 | |||
| Нахождение поверхности (объема) | 1 |
Критерии оценки.
0-12 баллов – «2»
13-16 баллов – «3»
17-20 баллов – «4»
21-23 баллов – «5»
Распределение заданий по содержанию и видам деятельности.
| Содержательные линии | Воспроизведение знаний | Применение знаний | Интеграция знаний | Процентное Соотношение в тексте |
| Многогранники | № 1 | № 3 | №5 | 60% |
| Тела вращения | № 2 | № 4 | 40% | |
| Процентное Соотношение в тексте | 40% | 40% | 20% | 100% |
xn--j1ahfl.xn--p1ai
Диагностическая контрольная работа по геометрии 11 класс
Цель: проверить уровень усвоения ГОСО по темам «Параллельность прямых и плоскостей в пространстве», « «Перпендикулярность в пространстве», «Координаты вектора в пространстве»:
- знание взаимного расположения прямых и плоскостей в пространстве;
- знание и умение применять свойство параллельности прямых, параллельности прямой и плоскости;
- знание и умение применять свойство перпендикулярных прямой и плоскости;
- знание и умение применять при решении задач понятия перпендикуляр и наклонная, расстояние от точки до плоскости;
-знать и уметь применять признаки подобия треугольников и теорему Пифагора;
- умение находить расстояние между точками, заданными в координатной виде;
- умение находить угол между векторами.
Содержание контрольной работы
| Вариант 1 1.Длины сторон прямоугольника 8см и 6см.Через точку О пересечения его диагоналей проведена прямая ОК перпендикулярная его плоскости. Найдите расстояние от точки К до вершин прямоугольника, если ОК=12см. 2.Плоскость пересекает стороны АВ и ВС треугольника АВС в точках М и К соответственно и параллельна стороне АС. Найдите длину отрезка МК, если АС=12см, а ВМ АМ=3 1. 3. Даны точки: А(2; –8; 1), В(–7; 10; –8), С(–8; 0; –10), D( –9; 8; 7). Найдите: а) угол между векторами б) расстояние между серединами отрезков AB и CD. 4 .Из точки к плоскости проведены две наклонные, равные 17 см и 15 см. проекция одной из них на 4 см больше проекции другой. Найдите проекции наклонных. | Вариант 2 1. Длина стороны ромба ABCD1 0см.Длина диагонали BD равна 16 см. Через точку О пересечения его диагоналей проведена прямая ОК перпендикулярная его плоскости. Найдите расстояние от точки К до вершин ромба, если ОК= 6см. 2.Плоскость пересекает стороны DF и EF треугольника DEF в точках K и P соответственно и параллельна стороне DE. Найдите длину стороны DE треугольника, если DE-KP=4см, FK KD=2 1. 3. Даны точки: А(5; 0; 1), В(0; –1; 2), С(3; 0; 1), D(–2; –1; 2). Найдите: а) угол между векторами б) расстояние между серединами отрезков AB и CD. 4. Из точки к плоскости проведены две наклонные, одна из которых на 6 см длиннее другой. Проекции наклонных равны 17 см и 7 см. Найдите длины наклонных. |
Распределение заданий по содержанию и уровню сложности. Технологическая матрица.
| Содержательные линии | Воспроизведение | Применение | Интеграция | % |
| Перпендикулярность прямой и плоскости | №1 | 20% | ||
| Параллельность прямых и плоскостей в пространстве. | №2 | 20% | ||
| Метод координат в пространстве | №3 (а) №3 (б) | 40% | ||
| Перпендикуляр, наклонная и её проекция | №4 | 20% | ||
| 40% | 40% | 20% | 100% |
Критерии оценивания по проверяемым элементам.
| № задания | тема | Проверяемые элементы | Кол-во баллов | итого |
| 1 | Перпендикулярность прямой и плоскости | Построение чертежа по условию задачи Перпендикулярность прямой и плоскости Свойство диагоналей прямоугольника и ромба Теорема Пифагора Оформление решения задания | 1 1 1 1 1 | 5 |
| 2 | Параллельность прямых и плоскостей в пространстве. | Построение чертежа по условию задачи Признак подобия треугольников Оформление решения задания | 1 2 2 | 5 |
| 3 | Векторы в пространстве | Нахождение координат вектора по координатам его начала и конца Нахождение длины вектора по его координатам Нахождение угла между векторами Нахождение координат середины отрезка по координатам его концов Нахождение длины отрезка | 1 1 1 1 1 | 5 |
| 4 | Перпендикуляр, наклонная и её проекция | Понятие наклонная и её проекция Теорема Пифагора Составление уравнения по условию задачи Оформление решения задания | 1 1 2 1 | 5 |
Критерий оценивания
1-9 баллов – «2»
10-13 баллов – «3»
14-18 баллов – «4»
19-20 баллов – «5»
xn--j1ahfl.xn--p1ai