Учебно-методический материал по геометрии (11 класс): Контрольные работы по геометрии. 11 класс
КОНТРОЛЬНЫЕ РАБОТЫ по геометрии (11 класс)
Контрольная работа № 1 «Метод координат в пространстве»
Вариант №1.
10. Найдите координаты вектора , если А(5; -1; 3), В(2; -2; 4).
20. Даны векторы {3; 1; -2}, {1; 4; -3}. Найдите .
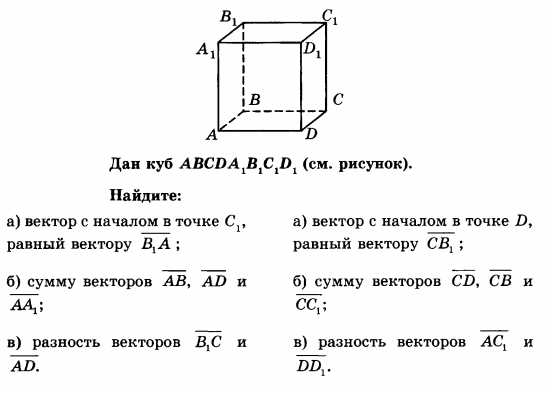
3. Дан куб АВСDА1В1С1D1. Найдите угол между прямыми АD1 и ВМ, где М – середина ребра DD1.
4. Вычислите скалярное произведение векторов и , если .
Вариант №2
10. Найдите координаты вектора , если А(6; 3; -2), В(2; 4; -5).
20. Даны векторы {5; -1; 2}, {3; 2; -4}. Найдите .
3. Дан куб АВСDА1В1С1D1. Найдите угол между прямыми АС и DС1.
4. Вычислите скалярное произведение векторов и , если .
Контрольная работа №2 «Цилиндр, конус и шар»
Вариант №1.
10. Осевое сечение цилиндра – квадрат. Площадь основания цилиндра равна. Найдите площадь полной поверхности цилиндра.
20. Высота конуса равна 6см. Угол при вершине осевого сечения равен .
а) Найти площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми равен .
б) Найти площадь боковой поверхности конуса.
3. Диаметр шара равен 2р. Через конец диаметра проведена плоскость под углом к нему. Найдите длину линии пересечения сферы этой плоскостью.
Вариант №2
10. Осевое сечение цилиндра – квадрат, диагональ которого равна 4см. Найдите площадь полной поверхности цилиндра.
20. Радиус основания конуса равен 6см, а образующая наклонена к плоскости основания под углом .
а) Найти площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми равен .
б) Найти площадь боковой поверхности конуса.
3. Диаметр шара равен 4р. Через конец диаметра проведена плоскость под углом к нему. Найдите площадь сечения шара этой плоскостью.
Контрольная работа № 3 «Объёмы тел»
Вариант №1.
10. Диаметр шара равен высоте конуса, образующая которого составляет с плоскостью основания угол . Найдите отношение объёмов конуса и шара.
Найдите отношение объёмов конуса и шара.
20. Объём цилиндра равен , площадь его осевого сечения . Найдите площадь сферы, описанной около цилиндра.
3. В конус вписана пирамида. Основанием пирамиды служит прямоугольный треугольник, катет которого равен 2р, а прилежащий угол равен . Боковая грань пирамиды, проходящая через данный катет, составляет с плоскостью основания угол . Найдите объём конуса.
Вариант №2.
10.В конус, осевое сечение которого есть правильный треугольник, вписан шар. Найдите отношение площади сферы к площади боковой поверхности конуса.
20. Диаметр шара равен высоте цилиндра, осевое сечение которого есть квадрат. Найдите отношение объёмов шара и цилиндра.
3. В цилиндр вписана призма. Основанием призмы служит прямоугольный треугольник, катет которого равен 2р, а прилежащий угол равен . Диагональ большей боковой грани призмы составляет с плоскостью её основания угол . Найдите объём цилиндра.
В каждой контрольной работе кружочком отмечены задания, соответствующие уровню обязательной подготовки.
Вариант 1 1. Дан параллелепипед ABCDA1B1C1D1. Укажите вектор с началом и концом в вершинах параллелепипеда, равный: 1) ; 2) . 2. DABC – тетраэдр. Точка М – середина ребра ВС, точка N – середина отрезка DМ. Выразите вектор через векторы , , . 3. Медианы ΔBDC пересекаются в точке Р, точка K – середина отрезка AP (точка А не лежит в плоскости BDC). Разложите вектор по векторам , , . 4. В параллелепипеде ABCDA1B1C1D1 М лежит на BB1, причем BМ : МB1 = 3 : 4, а Р лежит на B1D1, причем B1P : РD1 = 2 : 1. Разложите вектор по векторам , и . | Вариант 2 1. ABCDA1B1C1D1 – параллелепипед. Изобразите на рисунке векторы, равные: 1) ; 2) . 2. В тетраэдре DABC точка N – середина ребра AB, точка P – середина отрезка DN. Выразите вектор через векторы , , . 3. Медианы грани DBC тетраэдра DABC пересекаются в точке О, точка R – середина отрезка AO. Разложите вектор по векторам , , . 4. Дан параллелепипед ABCDA1B1C1D1. Точка М лежит на AB, причем AМ : МB = 5 : 2, а K ∈ AD1, причем AK : КD1 = 3 : 5. Разложите вектор по векторам , и . |
Вариант 3 1. ABCDA1B1C1D1 – параллелепипед. Изобразите на рисунке векторы, равные: 1) ; 2) . 2. Точка S – середина ребра AС тетраэдра DABC, точка N – середина отрезка DS. Выразите вектор через векторы , , . 3. В треугольнике KLM точка С – пересечение медиан, T – середина отрезка NС (N не лежит в плоскости KLM). Разложите по векторам , , . 4. В параллелепипеде ABCDA1B1C1D1 точка N делит CC1 так, что CN : NC1 = 1 : 3, а точка H делит A1С1 так, что А1Н : НС1 = | Вариант 4 1. Укажите вектор с началом и концом в вершинах параллелепипеда ABCDA1B1C1D1, равный: 1) ; 2) . 2. Дан тетраэдр DABC. Точка P – середина ребра AB, точка R – середина отрезка CP. Выразите вектор через векторы , , . 3. DABC – тетраэдр. Медианы грани DAB пересекаются в точке N, точка O – середина отрезка CN. Разложите вектор по векторам , , . 4. ABCDA1B1C1D1 – параллелепипед. Точка E лежит на ребре DC так, что DE : EC = 1 : 4, а F ∈ СB1, причем CF : FB1 = |
Вариант 5 1. ABCDA1B1C1D1 – параллелепипед. Изобразите на рисунке векторы, равные: 1) ; 2) . 2. На середине ребра ВС тетраэдра DABC лежит точка T, а на середине отрезка DT – точка H. Выразите вектор через векторы , , . 3. R – точка пересечения медиан треугольника SPQ, M – середина отрезка FR (точка F не лежит в плоскости SPQ). Разложите вектор по векторам , , . 4. Точка K лежит на ребре BB1 параллелепипеда ABCDA1B1C1D1 так, что BK : KB1 = 3 : 4, а N ∈ D1B1, причем D1N : NB1 = 1 : 2. | Вариант 6 1. Дан параллелепипед ABCDA1B1C1D1. Укажите вектор с началом и концом в вершинах параллелепипеда, равный: 1) ; 2) . 2. DABC – тетраэдр. На середине ребра AB лежит точка К, точка M – середина отрезка DK. Выразите вектор через векторы , , . 3. В тетраэдре ABCD медианы грани DBC пересекаются в точке E, на середине отрезка AE лежит точка N. Разложите вектор по векторам , , . 4. Точка S лежит на ребре BA, а точка Р лежит на диагонали AD1 параллелепипеда ABCDA1B1C1D1, BS : SA = 2 : 5, AP : РD1 = |
Вариант 7 1. Изобразите параллелепипед ABCDA1B1C1D1. Постройте на рисунке векторы, равные: 1) ; 2) . 2. В тетраэдре DABC на середине ребра AС лежит точка T, а на середине отрезка DT – точка K. Разложите вектор по векторам , , . 3. Дан ΔAMD, его медианы пересекаются в точке O, P – середина отрезка SO (точка S не лежит в плоскости AMD). Выразите через векторы , , . 4. ABCDA1B1C1D1 – параллелепипед. На C1A1 лежит точка N, причем C1N : NA1 = 2 : 5, а на C1C – М, причем C1М : МC = | Вариант 8 1. Дан параллелепипед ABCDA1B1C1D1. Укажите вектор с началом и концом в вершинах параллелепипеда, равный: 1) ; 2) . 2. Точка N – середина отрезка CK, соединяющего вершину С тетраэдра DABC с точкой K – серединой ребра AB. Разложите вектор по векторам , , . 3. Точка R – пересечение медиан грани DAB тетраэдра DABC, точка P – середина отрезка CR. Выразите вектор через векторы , , . 4. В параллелепипеде ABCDA1B1C1D1 точка T лежит на B1С так, что B1T : TС = 3 : 2, точка O делит CD так, что СО : ОD = |
ГДЗ контрольная работа / к-1 / вариант-1 2 геометрия 11 класс дидактические материалы Зив
Решение есть!- 1 класс
- Математика
- Английский язык
- Русский язык
- Литература
- Окружающий мир
- 2 класс
- Математика
- Английский язык
- Русский язык
- Информатика
- Музыка
- Окружающий мир
- Технология
- 3 класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Музыка
- Литература
- Казахский язык
- 4 класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Информатика
- Музыка
- Литература
- Окружающий мир
- 5 класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Украинский язык
- Биология
Контрольные работы по геометрии по теме Векторы в пространстве 11 класс
11 класс Контрольная работа по теме « Векторы в пространстве» вариант 1Часть 1
Какому из указанных векторов равен вектор 13 EMBED Equation.
 3 1415(1; 2;3)?
3 1415(1; 2;3)?А) 13 EMBED Equation.3 1415(2; 3; 1) Б) 13 EMBED Equation.3 1415(3;1;2) В) 13 EMBED Equation.3 1415(1;2;3) Г) 13 EMBED Equation.3 1415(1;3;2)13 EMBED Equation.3 1415
Найдите скалярное произведение векторов 13 EMBED Equation.3 1415 (-1; 3; -2) и 13 EMBED Equation.3 1415(0; -1; 5)
А) -14; Б) -13; В) 0; Г) 7; Д) 4.
А) ни при каких; Б) при n=-1; В) при n=1; Г) при n=13 EMBED Equation.3 14151.
Часть 2
Вычислите длину вектора 13 EMBED Equation.3 1415= 213 EMBED Equation.3 1415+ 313 EMBED Equation.3 1415, если 13 EMBED Equation.3 1415(1;1;-1), 13 EMBED Equation.3 1415(2; 0; 0).
При каком значении р векторы 13 EMBED Equation.3 1415(3; р; -1) и 13 EMBED Equation.3 1415(р; -2; 5) взаимно перпендикулярны?
Разложите вектор 13 EMBED Equation.3 1415(5; -17; 11) по векторам 13 EMBED Equation.
 3 1415(3; -2; 0), 13 EMBED Equation.3 1415(-2; 4; 1) и 13 EMBED Equation.3 1415(-1; -3; 4)
3 1415(3; -2; 0), 13 EMBED Equation.3 1415(-2; 4; 1) и 13 EMBED Equation.3 1415(-1; -3; 4) Часть 3
Найдите градусную меру угла
· между векторами 13 EMBED Equation.3 1415 = 313 EMBED Equation.3 1415+13 EMBED Equation.3 1415 и 13 EMBED Equation.3 1415= 13 EMBED Equation.3 1415+ 213 EMBED Equation.3 1415, где 13 EMBED Equation.3 1415 и 13 EMBED Equation.3 1415 — единичные и взаимно перпендикулярные векторы.
11 класс Контрольная работа по теме « Векторы в пространстве» вариант 2
Часть 1
1. Какому из указанных векторов равен вектор 13 EMBED Equation.3 1415(3; 1;2)?
А) 13 EMBED Equation.3 1415(2; 3; 1) Б) 13 EMBED Equation.3 1415(3;1;2) В) 13 EMBED Equation.3 1415(1;2;3) Г) 13 EMBED Equation.3 1415(1;3;2)
2. Найдите координаты вектора 13 EMBED Equation.3 1415, если А(-3;-2; -1), В(-1; 2; 3), С(0; -1; -2)
А) 13 EMBED Equation.3 1415(0; -5; -7) Б) 13 EMBED Equation.3 1415 (-2; 1; 3) В) 13 EMBED Equation.3 1415 (-3; 1; 2)
Г) 13 EMBED Equation. 3 1415 (2; -1; -3) Д) 13 EMBED Equation.3 1415(0; 5; 7)
3 1415 (2; -1; -3) Д) 13 EMBED Equation.3 1415(0; 5; 7)
3. При каких значениях n векторы 13 EMBED Equation.3 1415(2; 1; n) и 13 EMBED Equation.3 1415(n; 1; n) перпендикулярны?
А) ни при каких; Б) при n=-1; В) при n=1; Г) при n=13 EMBED Equation.3 14151.
Часть 2
При каких значениях n и m векторы 13 EMBED Equation.3 1415(-1; 4; -2) и 13 EMBED Equation.3 1415(-3; m; n) коллинеарны?
Дан треугольник АВС: А(0;1;-1), В(1;-1;2) и С(3;1;0). Найти косинус угла А треугольника АВС
Разложите вектор 13 EMBED Equation.3 1415(1; 4; 3) по векторам 13 EMBED Equation.3 1415(1; -1; 0), 13 EMBED Equation.3 1415(0; 1; 1) и
13 EMBED Equation.3 1415(1; 0; -1)
Часть 3
Вычислите длину вектора 13 EMBED Equation.3 1415= 13 EMBED Equation.3 1415- 213 EMBED Equation.3 1415, если 13 EMBED Equation.3 1415= 2, 13 EMBED Equation.3 1415=1, а угол между векторами 13 EMBED Equation.3 1415 и 13 EMBED Equation.3 1415 равен 600 .
11 класс. Векторы в пространстве вариант 3
Векторы в пространстве вариант 3
Часть 1
1. Вычислите координаты вектора 13 EMBED Equation.3 1415, если А(2;3;1), В(1;0;2)
А) 13 EMBED Equation.3 1415(1;3;-1) Б) 13 EMBED Equation
Тест Векторы в пространстве (11 класс) по геометрии
Сложность: знаток.Последний раз тест пройден 21 час назад.
Вопрос 1 из 10
Зная координаты точек A(-12, 7, -3) и B(-10, -2, -2) найдите значение вектора AB
- Правильный ответ
- Неправильный ответ
- Вы и еще 69% ответили правильно
- 69% ответили правильно на этот вопрос
В вопросе ошибка?
Следующий вопросОтветитьВопрос 2 из 10
При каком значении n векторы a(4;2n;-1), b(-1;1;n) перпендикулярны?
- Правильный ответ
- Неправильный ответ
- Вы и еще 63% ответили правильно
- 63% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 3 из 10
Векторы a, b, c единичной длины образуют попарно углы 60°.
 Найдите угол между векторами a и b-c
Найдите угол между векторами a и b-c- Правильный ответ
- Неправильный ответ
- Вы и еще 65% ответили правильно
- 65% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 4 из 10
Даны три точки A(1;0;1), B(-1;1;2), C(0;2;-1). Найдите на оси z такую точку D(0;0;c), чтобы векторы AB и CD были перпендикулярны
- Правильный ответ
- Неправильный ответ
- Вы и еще 72% ответили правильно
- 72% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 5 из 10
Найдите D(x,y,z), если сумма векторов AB и CD равна нулю. A(1;0;1), B(-1;1;2), C(0;2;-1)
- Правильный ответ
- Неправильный ответ
- Вы и еще 56% ответили правильно
- 56% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 6 из 10
При каком значении n векторы a(2;-1;3), b(1;3;n) перпендикулярны?
- Правильный ответ
- Неправильный ответ
- Вы и еще 64% ответили правильно
- 64% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 7 из 10
Дан вектор а(1;2;3), найдите коллинеарный ему вектор с началом в точке А(1;1;1) и В на плоскости xy
- Правильный ответ
- Неправильный ответ
- Вы ответили лучше 51% участников
- 49% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 8 из 10
Даны три точки A(1;0;1), B(-1;1;2), C(0;2;-1).
 Найдите точку D(x;y;z), если векторы AB и CD равны
Найдите точку D(x;y;z), если векторы AB и CD равны- Правильный ответ
- Неправильный ответ
- Вы и еще 60% ответили правильно
- 60% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 9 из 10
При каком значении n векторы a(n;-2;1), b(n;-n;1) перпендикулярны?
- Правильный ответ
- Неправильный ответ
- Вы и еще 67% ответили правильно
- 67% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 10 из 10
Заданы два вектора в пространстве a(0;1;1), b(-2;0;1). Найдите их векторное произведение
- Правильный ответ
- Неправильный ответ
- Вы ответили лучше 59% участников
- 41% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Доска почёта
Чтобы попасть сюда — пройдите тест.
Рейтинг теста
Средняя оценка: 3.5. Всего получено оценок: 192.
А какую оценку получите вы? Чтобы узнать — пройдите тест.
| 1. |
Скалярное произведение векторов, если дан угол
Сложность: лёгкое |
1 |
2.
|
Скалярное произведение векторов, данных в координатах
Сложность: лёгкое |
1 |
| 3. |
Скалярное произведение векторов
Сложность: среднее |
3 |
| 4. |
Перпендикулярные векторы
Сложность: среднее |
3 |
| 5. |
Перпендикулярность векторов
Сложность: среднее |
3 |
| 6. |
Угол между векторами
Сложность: среднее |
3 |
| 7. |
Косинус угла между векторами
Сложность: среднее |
4 |
| 8. |
Определение угла между векторами в кубе
Сложность: среднее |
4 |
| 9. |
Косинус угла треугольника
Сложность: среднее |
5 |
| 10. |
Угол между прямыми в кубе
Сложность: сложное |
5 |
| 11. |
Угол между прямой и плоскостью
Сложность: сложное |
5 |
Вычитание и умножение векторов | Примечания, видео, контроль качества и тесты | 11 класс> Физика> Скаляры и векторы
Вычитание и умножение векторов
Вычитание векторов
Вычитание вектора определяется как добавление одного вектора к отрицательному значению другого. Вычитание вектора \ (\ vec A \; \ text {from} \; \ vec B \) означает сложение вектора \ (- \ vec A \; \ text {with} \; \ vec B \). Мы можем проанализировать вычитание вектора, как показано на рисунке.{-1} (\ frac {B \ sin \ theta} {A — B \ cos \ theta}) $$
Вычитание векторов не подчиняется законам коммутативности и ассоциативности.
Разрешение векторов
Процесс разбиения одного вектора на множество компонентов называется разрешением векторов. Вектор может иметь несколько компонентных векторов.
Предположим, что вектор \ (\ vec A \) показан на рисунке. Компонента \ (\ vec A \) вдоль направления OX есть OQ.В POQ
$$ \ cos \ alpha = \ frac {OQ} {OP} = \ frac {OQ} {A} $$
$$ OQ = A \ cos \ alpha $$
Аналогично компонент вдоль OX’-направления есть \ (OT = A \ cos \ beta \), где \ (beta \) — угол, образованный с OX-направлением, а вдоль OX » — направление \ (OT = A \ cos \ alpha \ )
Прямоугольные компоненты вектора
Когда вектор разрешается \ (\ vec A \) на перпендикулярные направления, тогда составляющие векторы \ (\ vec A \) называются прямоугольными компонентами вектора. 2} $$
Делящее уравнение (i) и (ii) )
$$ \ tan \ theta = \ frac {A_x} {A_y} $$
Векторное умножение
Скалярное произведение: Оно определяется как произведение величины одного вектора на скалярную составляющую. другого вектора в направлении первого вектора.o (A \ neq 0, B = 0) \)
Векторное произведение: Если произведение двух векторов является векторной величиной, то такая операция называется векторным произведением.
Пусть два вектора \ (\ vec A и \ vec B \) наклонены под углом друг к другу, как показано на рисунке.
$$ \ vec A \ times \ vec B = AB \ sin \ theta \, \ widehat n $$
Где \ (\ widehat n \) — единичный вектор в направлении, перпендикулярном плоскости \ (\ vec A и \ vec B \), а крутящий момент, возникающий из-за силы, — это произведение силы и перпендикулярного расстояния.o = 0 \)
Геометрическая интерпретация Cross Product
Рассмотрим два вектора \ (\ vec A \, и \, \ vec B \), представленные по величине и направлению как \ (\ vec OZ \, и \, \ vec OX \). Завершим параллелограмм OXYZ и опустим перпендикуляр из X в точке N.
$$ \ vec A \ times \ vec B = AB \ sin \ theta $$
$$ \ text {Площадь параллелограмма OXYZ} = \ text {(основание)} \ times \ text {(расстояние по перпендикуляру)} $$
$$ = (OZ) \ times (XN) $$
$$ = (OZ) (OX \ sin \ theta) $$
$$ = (A) (B \ sin \ theta) $$
$$ = AB \ sin \ theta $$
То есть площадь параллелограмма равна величине векторного произведения двух векторов, которые представлены двумя смежными сторонами параллелограмма.
Вектор | Примечания, видео, контроль качества и тесты | 10 класс> Математика по выбору> Вектор
Вектор
Произведение векторов
Из-за того, что векторы встречаются в различных физических задачах по-разному, произведение двух векторов \ (\ overrightarrow {a} \) и \ (\ overrightarrow {b} \) определяется двумя следующими способами:
- скалярное произведение или скалярное произведение \ (\ overrightarrow a \). \ (\ overrightarrow b \) (читается как \ (\ overrightarrow a \) точка \ (\ overrightarrow b \))
- векторное произведение или перекрестное произведение \ (\ overrightarrow a \) × \ (\ overrightarrow b \) (читается как \ (\ overrightarrow a \) cross \ (\ overrightarrow b \)).
Скалярное произведение \ (\ overrightarrow a \). \ (\ overrightarrow b \) дает скалярный результат, а перекрестное произведение \ (\ overrightarrow a \) × \ (\ overrightarrow b \) дает векторный результат.
Скалярное произведение двух векторов
Скалярное произведение двух векторов \ (\ overrightarrow a \) и \ (\ overrightarrow b \) определяется как произведение величины двух векторов на косинус угла \ (\ theta \) между их направлениями. .
Таким образом, \ (\ overrightarrow a \).\ (\ overrightarrow b \) = | \ (\ overrightarrow a \) | | \ (\ overrightarrow b \) | соз \ (\ тета \) = ab соз \ (\ тета \)
где, | \ (\ overrightarrow a \) | = a и | \ (\ overrightarrow b \) | = б.
Сейчас,
Нарисуйте перпендикуляр BM от B до OA.
Здесь,
\ (\ overrightarrow {OA} \) = \ (\ overrightarrow a \) и \ (\ overrightarrow {OB} \) = \ (\ overrightarrow b \)
Сейчас,
\ (\ begin {align *} \ overrightarrow a. \ Overrightarrow b & = | \ overrightarrow a | | \ overrightarrow b | cos \ theta \\ & = ab cos \ theta \\ & = (OA) (OB) cos \ theta \\ & = OA (OB cos \ theta) \\ & = (OA) (OM) \\ & = (величина \; из \; \ overrightarrow a) (компонент \; of \; \ overrightarrow b \; в \; \; направлении \; из \; \ overrightarrow a) \\ \ end {align *} \)
Итак, очевидно, что скалярное произведение двух векторов эквивалентно произведению величины одного вектора на компонент другого вектора в направлении этого вектора.
Если мы напишем \ (\ overrightarrow a \). \ (\ overrightarrow b \), поворот \ (\ overrightarrow a \) в сторону \ (\ overrightarrow b \) осуществляется против часовой стрелки, а угол \ (\ theta \) считается положительным.
∴ \ (\ overrightarrow a \). \ (\ overrightarrow b \) = ab cos \ (\ theta \)
Если мы напишем \ (\ overrightarrow b \). \ (\ overrightarrow a \), поворот \ (\ overrightarrow b \) к \ (\ overrightarrow a \) осуществляется по часовой стрелке, а угол \ (\ theta \) считается отрицательным.
∴ \ (\ overrightarrow b \).\ (\ overrightarrow a \) = b a cos (- \ (\ theta \)) = ba cos \ (\ theta \)
Следовательно, \ (\ overrightarrow a \). \ (\ overrightarrow b \) = \ (\ overrightarrow b \). \ (\ overrightarrow a \)
Таким образом, скалярное произведение коммутативно.
Рассмотрим две точки A (a 1 , a 2 ) и B (b 1 , b 2 ) на плоскости. Затем
вектор положения A = \ (\ overrightarrow {OA} \) = \ (\ overrightarrow a \) = \ (\ begin {pmatrix} a_1 \\ a_2 \\ \ end {pmatrix} \)
вектор положения B = \ (\ overrightarrow {OB} \) = \ (\ overrightarrow b \) = \ (\ begin {pmatrix} b_1 \\ b_2 \\ \ end {pmatrix} \)
Величины \ (\ overrightarrow a \) и \ (\ overrightarrow b \) равны
.| \ (\ overrightarrow {OA} \) | = OA = a = | \ (\ overrightarrow a \) |
| \ (\ overrightarrow {OB} \) | = OB = b = | \ (\ overrightarrow b \) |
Пусть \ (\ angle \) XOA = β, \ (\ angle \) XOB = α и \ (\ angle \) AOB = θ.Тогда α-β = θ.
Нарисуйте перпендикуляры AM и BN от A и B к оси x. Затем
OM = a 1 , MA = a 2 , ON = b 1 и NB = b 2 .
Из прямоугольного треугольника OMA,
cosβ = \ (\ frac {OM} {OA} \) = \ (\ frac {a_1} a \) ∴ a 1 = a cosβ
sinβ = \ (\ frac {MA} {OA} \) = \ (\ frac {a_2} a \) ∴ a 2 = a sinβ
Аналогично
Из прямоугольного треугольника ОНБ,
b 1 = b cosα и b 2 = b sinα
Сейчас,
\ (\ begin {align *} a_1b_1 + a_2b_2 & = a cosβ b cosα + a sinβ sinα \\ & = ab cos (α — β) \\ & = | \ overrightarrow a | | \ overrightarrow b | cos \ theta ………………. (i) \\ \ end {align *} \)
Но,
По определению скалярного произведения двух векторов \ (\ overrightarrow a \) и \ (\ overrightarrow b \),
Сейчас,
Из (i) и (ii),
\ (\ overrightarrow a \). \ (\ overrightarrow b \) = a 1 b 1 + a 2 b 2 .
Этот результат заставляет нас по-другому определить скалярное произведение двух векторов.
Пусть \ (\ overrightarrow a \) = \ (\ begin {pmatrix} a_1 \\ a_2 \\ \ end {pmatrix} \) и \ (\ overrightarrow b \) = \ (\ begin {pmatrix} b_1 \\ b_2 \\ \ end {pmatrix} \) два вектора.Тогда скалярное произведение \ (\ overrightarrow a \) и \ (\ overrightarrow b \) обозначается \ (\ overrightarrow a \). \ (\ overrightarrow b \) и определяется как \ (\ overrightarrow a \). \ (\ overrightarrow b \) = \ (\ begin {pmatrix} a_1 \\ a_2 \\ \ end {pmatrix} \) и \ (\ overrightarrow b \). \ (\ begin {pmatrix} b_1 \\ b_2 \\ \ end {pmatrix} \) = a 1 b 1 + a 2 b 2 .
снова,
Из (i),
| \ (\ overrightarrow a \) | | \ (\ overrightarrow b \) | cos \ (\ theta \) = a 1 b 1 + a 2 b 2
или cos \ (\ theta \) = \ (\ frac {a_1b_1 + a_2b_2} {| \ overrightarrow a | | \ overrightarrow b |} \)
Этот результат дает нам угол между двумя векторами \ (\ overrightarrow a \) и \ (\ overrightarrow b \).
\ (\ theta \) = cos -1 \ (\ frac {a_1b_1 + a_2b_2} {| \ overrightarrow a | | \ overrightarrow b |} \)
Свойства скалярного произведения
Скалярное произведение векторов удовлетворяет следующим свойствам:
Пусть \ (\ overrightarrow a \), \ (\ overrightarrow b \) и \ (\ overrightarrow c \) — три вектора.
- Коммулятивная собственность: \ (\ overrightarrow a \). \ (\ overrightarrow b \) = \ (\ overrightarrow b \). \ (\ overrightarrow a \)
- Распределительная собственность: \ (\ overrightarrow a \).(\ (\ overrightarrow b \) + \ (\ overrightarrow c \)) = \ (\ overrightarrow a \). \ (\ overrightarrow b \) + \ (\ overrightarrow a \). \ (\ overrightarrow c \)
- Ассоциативное свойство: м \ (\ overrightarrow a \). п \ (\ overrightarrow b \) = mn (\ (\ overrightarrow a \). \ (\ overrightarrow b \))
Перпендикулярные векторы
Пусть \ (\ overrightarrow a \) = \ (\ begin {pmatrix} a_1 \\ a_2 \\ \ end {pmatrix} \) и \ (\ overrightarrow b \) = \ (\ begin {pmatrix} b_1 \\ b_2 \\ \ end {pmatrix} \) два вектора.Если \ (\ overrightarrow a \) и \ (\ overrightarrow b \) перпендикулярны друг другу, то угол между \ (\ overrightarrow a \) и \ (\ overrightarrow b \) равен \ (\ theta \) = — 90 °.
Сейчас,
\ (\ overrightarrow a \). \ (\ overrightarrow b \) = | \ (\ overrightarrow a \) | | \ (\ overrightarrow b \) | cos \ (\ theta \) = ab cos 90 ° = 0
И наоборот,
Пусть \ (\ overrightarrow a \). \ (\ overrightarrow b \) = 0
Затем,
| \ (\ overrightarrow a \) | | \ (\ overrightarrow b \) | соз \ (\ тета \) = 0
или, ab cos \ (\ theta \) = 0
или, cos \ (\ theta \) = 0
∴ \ (\ theta \) = 90 °
Таким образом, если два вектора перпендикулярны друг другу (или ортогональны), их скалярное произведение равно нулю.
Параллельный вектор
Пусть \ (\ overrightarrow a \) и \ (\ overrightarrow b \) — два вектора. Если \ (\ overrightarrow a \) и \ (\ overrightarrow b \) параллельны друг другу, то угол между ними равен 0 ° или 180 °.
Сейчас,
Если \ (\ theta \) = 0 °, \ (\ overrightarrow a \). \ (\ overrightarrow b \) = | \ (\ overrightarrow a \) | | \ (\ overrightarrow b \) | соз \ (\ тета \) = ab cos 0 ° = ab
Если \ (\ theta \) = 180 °, \ (\ overrightarrow a \). \ (\ overrightarrow b \) = | \ (\ overrightarrow a \) | | \ (\ overrightarrow b \) | cos \ (\ theta \) = ab cos 180 ° = -ab
Таким образом, два вектора \ (\ overrightarrow a \) и \ (\ overrightarrow b \) параллельны друг другу, если \ (\ overrightarrow a \).\ (\ overrightarrow b \) = ab или, \ (\ overrightarrow a \). \ (\ overrightarrow b \) = -ab.
Длина вектора (Модуль вектора)
Длина вектора (модуль вектора)Пусть \ (\ overrightarrow a \) = \ (\ begin {pmatrix} a_1 \\ a_2 \\ \ end {pmatrix} \) будет плоским вектором.
Затем \ (\ overrightarrow a \). \ (\ overrightarrow a \) = \ (\ begin {pmatrix} a_1 \\ a_2 \\ \ end {pmatrix} \). \ (\ begin {pmatrix} a_1 \\ a_2 \\ \ end {pmatrix} \) = a 1 a 1 + a 2 a 2 = a 1 2 + a 2 2 = 2
∴ a = \ (\ sqrt {\ overrightarrow a.2} \) + 2 \ (\ overrightarrow a \). \ (\ overrightarrow b \) + \ (\ overrightarrow {b} \) = a 2 + 2 \ (\ overrightarrow a \). \ (\ overrightarrow b \) + b 2
(\ (\ overrightarrow a \) + \ (\ overrightarrow b \)) = (\ (\ overrightarrow a \) + \ (\ overrightarrow b \)). ( \ (\ overrightarrow a \) + \ (\ overrightarrow b \)) = \ (\ overrightarrow a \). \ (\ overrightarrow a \) + \ (\ overrightarrow a \). \ (\ overrightarrow b \) + \ (\ overrightarrow b \). \ (\ overrightarrow a \) + \ (\ overrightarrow b \). \ (\ overrightarrow b \) = \ (\ overrightarrow a \) + 2 \ (\ overrightarrow a \).2} \) = a 2 — 2 \ (\ overrightarrow a \). \ (\ overrightarrow b \) + b 2
(\ (\ overrightarrow a \) — \ (\ overrightarrow b \)) 2 = (\ (\ overrightarrow a \) — \ (\ overrightarrow b \) ). (\ (\ overrightarrow a \) — \ (\ overrightarrow b \)) = \ (\ overrightarrow a \). \ (\ overrightarrow a \) — \ (\ overrightarrow a \). \ (\ overrightarrow b \) — \ (\ overrightarrow b \). \ (\ overrightarrow a \) + \ (\ overrightarrow b \). \ (\ overrightarrow b \) = \ (\ overrightarrow a \) — 2 \ (\ overrightarrow a \). \ (\ overrightarrow b \) + \ (\ overrightarrow b \) = a 2 — 2 \ (\ overrightarrow a \).2} \) — \ (\ overrightarrow b \) = a 2 — b 2
Взаимно перпендикулярный единичный вектор \ (\ overrightarrow i \) и \ (\ overrightarrow j \)
Пусть OX и OY — две взаимно перпендикулярные прямые. Тогда единичный вектор вдоль OX и OY, обозначенный \ (\ overrightarrow i \) и \ (\ overrightarrow j \), определяется как \ (\ overrightarrow i \) = \ (\ begin {pmatrix} 1 \\ 0 \\ \ end {pmatrix} \) и \ (\ overrightarrow j \) = \ (\ begin {pmatrix} 0 \\ 1 \\ \ end {pmatrix} \).
Сейчас,
\ (\ overrightarrow i \).2} \) = \ (\ begin {pmatrix} 0 \\ 1 \\ \ end {pmatrix} \). \ (\ begin {pmatrix} 0 \\ 1 \\ \ end {pmatrix} \) = 0 + 1 = 1
\ (\ overrightarrow i \). \ (\ overrightarrow j \) = \ (\ begin {pmatrix} 1 \\ 0 \\ \ end {pmatrix} \). \ (\ begin {pmatrix} 0 \\ 1 \\ \ end {pmatrix} \) = 0 + 0 = 0
\ (\ overrightarrow j \). \ (\ overrightarrow i \) = \ (\ begin {pmatrix} 0 \\ 1 \\ \ end {pmatrix} \). \ (\ begin {pmatrix} 1 \\ 0 \\ \ end {pmatrix} \) = 0 + 0 = 0
Значение скалярного произведения \ (\ overrightarrow i \) и \ (\ overrightarrow j \) можно запомнить из таблицы, приведенной рядом.
Представление вектора через единичные векторы
Пусть \ (\ overrightarrow a \) = \ (\ begin {pmatrix} x \\ y \\ \ end {pmatrix} \) будет вектором. Его можно записать как
\ (\ overrightarrow a \) = \ (\ begin {pmatrix} x \\ y \\ \ end {pmatrix} \) = \ (\ begin {pmatrix} x \\ 0 \\ \ end {pmatrix} \) = \ (\ begin {pmatrix} 0 \\ y \\ \ end {pmatrix} \) = x \ (\ begin {pmatrix} 1 \\ 0 \\ \ end {pmatrix} \) + y \ (\ begin { pmatrix} 0 \\ 1 \\ \ end {pmatrix} \) = x \ (\ overrightarrow i \) + y \ (\ overrightarrow j \).
Аналогично
Если \ (\ overrightarrow a \) = nx + y \ (\ overrightarrow j \), то:
\ (\ overrightarrow a \) = x \ (\ overrightarrow i \) + y \ (\ overrightarrow j \) = x \ (\ begin {pmatrix} 1 \\ 0 \\ \ end {pmatrix} \) + y \ (\ begin {pmatrix} 0 \\ 1 \\ \ end {pmatrix} \) = \ (\ begin {pmatrix} x \\ 0 \\ \ end {pmatrix} \) + \ (\ begin {pmatrix} 0 \\ y \\ \ end {pmatrix} \) = \ (\ begin {pmatrix} x \\ y \\ \ end {pmatrix} \)
Следовательно, любой вектор плоскости \ (\ begin {pmatrix} x \\ y \\ \ end {pmatrix} \) может быть представлен как x \ (\ overrightarrow i \) + y \ (\ overrightarrow j \) и наоборот.
Векторные операции в единицах векторов
Пусть \ (\ overrightarrow a \) = a 1 \ (\ overrightarrow i \) + a 2 \ (\ overrightarrow j \) и \ (\ overrightarrow b \) = b 1 \ (\ overrightarrow i \) + b 2 \ (\ overrightarrow j \)
- Сложение векторов:
\ (\ overrightarrow a \) + \ (\ overrightarrow b \) = a 1 \ (\ overrightarrow i \) + a 2 \ (\ overrightarrow j \) + b 1 \ (\ overrightarrow i \) + b 2 \ (\ overrightarrow j \) = (a 1 + b 1 ) \ (\ overrightarrow i \) + (a 2 + b 2 ) \ (\ overrightarrow j \) - Вычитание векторов:
\ (\ overrightarrow a \) — \ (\ overrightarrow b \) = a 1 \ (\ overrightarrow i \) + a 2 \ (\ overrightarrow j \) — (b 1 \ (\ overrightarrow i \) + b 2 \ (\ overrightarrow j \)) = a 1 \ (\ overrightarrow i \) + a 2 \ (\ overrightarrow j \) — b 1 \ (\ overrightarrow i \) — b 2 \ (\ overrightarrow j \) - Скалярное произведение векторов:
\ (\ overrightarrow a.\ overrightarrow b = (a_1 \ overrightarrow i + a_2 \ overrightarrow j). (b_1 \ overrightarrow i + b_2 \ overrightarrow j) = a_1b_1 \ overrightarrow i. \ overrightarrow i + a_1b_2 \ overrightarrow i. \ overrightarrow j + a_2b_1 \ overrightarrow j. \ overrightarrow i + a_2b_2 \ overrightarrow j. \ overrightarrow j = a_1b_1 + 0 + 0 + a + 2b_2 = a_1b_1 + a_2b_2 \)
Величина и направление вектора в единичных векторах
Пусть \ (\ overrightarrow a \) = x \ (\ overrightarrow i \) + y \ (\ overrightarrow j \) будет вектором.2}} \)
Векторная геометрия
Теорема 1: (Формула средней точки)
Если \ (\ overrightarrow a \) и \ (\ overrightarrow b \) — вектор положения двух точек A и B соответственно, а M — средняя точка отрезка AB, то вектор положения M равен \ (\ гидроразрыв 12 \) (\ (\ overrightarrow a \) + \ (\ overrightarrow b \)).
Проба:
Пусть AB — отрезок прямой, а O — начало координат.
Здесь,
Вектор положения A = \ (\ overrightarrow {OA} \) = \ (\ overrightarrow a \)
Вектор положения B = \ (\ overrightarrow {OB} \) = \ (\ overrightarrow b \)
Пусть M — средняя точка отрезка AB.
Затем,
\ (\ begin {align *} \ overrightarrow {OM} & = \ overrightarrow {OA} + \ overrightarrow {AM} \\ & = \ overrightarrow {OA} + \ frac 12 \ overrightarrow {AB} \\ & = \ overrightarrow {OA} + \ frac 12 (\ overrightarrow {OB} — \ overrightarrow {OA}) \\ & = \ overrightarrow a + \ frac 12 (\ overrightarrow b — \ overrightarrow a) \\ & = \ frac {2 \ overrightarrow a + \ overrightarrow b — \ overrightarrow a} {2} \\ & = \ frac 12 (\ overrightarrow a + \ overrightarrow b) \\ \ end {align *} \)
∴ Вектор положения M = \ (\ frac 12 \) (\ (\ overrightarrow a \) + \ (\ overrightarrow b \)) Доказано
Теорема 2: (Формула раздела для внутреннего деления)
Если \ (\ overrightarrow a \) и \ (\ overrightarrow b \) — вектор положения двух точек A и B соответственно, а точка M делит сегмент AB внутри в соотношении m: n, то вектор положения M — это \ (\ frac {m \ overrightarrow b + n \ overrightarrow a} {m + n} \).
Проба:
Пусть AB — отрезок прямой, а O — начало координат.
Здесь,
Вектор положения A = \ (\ overrightarrow {OA} \) = \ (\ overrightarrow a \)
Вектор положения B = \ (\ overrightarrow {OB} \) = \ (\ overrightarrow b \)
Пусть точка M делит AB внутри в соотношении m: n.
Затем,
\ (\ begin {align *} \ overrightarrow {OM} & = \ overrightarrow {OA} + \ overrightarrow {AM} \\ & = \ overrightarrow {OA} + \ frac {m} {m + n} \ overrightarrow { AB} \\ & = \ overrightarrow {OA} + \ frac m {m + n} (\ overrightarrow {OB} — \ overrightarrow {OA}) \\ & = \ overrightarrow a + \ frac m {m + n} ( — \ overrightarrow a) \\ & = \ frac {m \ overrightarrow a + n \ overrightarrow a + m \ overrightarrow b — m \ overrightarrow a} {m + n} \\ & = \ frac {m \ overrightarrow b + n \ overrightarrow a} {m + n} \\ \ end {align *} \)
∴ Вектор положения M = \ (\ frac {m \ overrightarrow b + n \ overrightarrow a} {m + n} \) Доказано
Теорема 3: (Формула раздела для внешнего деления)
Если \ (\ overrightarrow a \) и \ (\ overrightarrow b \) — вектор положения двух точек A и B соответственно, а точка P делит линейный сегмент AB снаружи в соотношении m: n, то вектор положения P — это \ (\ frac {m \ overrightarrow b — n \ overrightarrow a} {m — n} \).
Проба:
Пусть AB — отрезок прямой, а O — начало координат.
Здесь,
Вектор положения A = \ (\ overrightarrow {OA} \) = \ (\ overrightarrow a \)
Вектор положения B = \ (\ overrightarrow {OB} \) = \ (\ overrightarrow b \)
Пусть точка P делит AB внешне в соотношении m: n.
Затем,
\ (\ frac {AP} {BP} \) = \ (\ frac mn \)
∴ п \ (\ overrightarrow {AP} \) = m \ (\ overrightarrow {BP} \)
или, n (\ (\ overrightarrow {OP} \) — \ (\ overrightarrow {OA} \)) = m (\ (\ overrightarrow {OP} \) — \ (\ overrightarrow {OB} \))
или, n \ (\ overrightarrow {OP} \) — n \ (\ overrightarrow {OA} \) = m \ (\ overrightarrow {OP} \) — m \ (\ overrightarrow {OB} \)
или, m \ (\ overrightarrow {OB} \) — n \ (\ overrightarrow {OA} \) = m \ (\ overrightarrow {OP} \) — n \ (\ overrightarrow {OP} \)
или, m \ (\ overrightarrow b \) — n \ (\ overrightarrow a \) = (m — n) \ (\ overrightarrow {OP} \)
∴ \ (\ overrightarrow {OP} \) = \ (\ frac {m \ overrightarrow b — n \ overrightarrow a} {m — n} \)
Итак, вектор положения P = \ (\ frac {m \ overrightarrow b — n \ overrightarrow a} {m — n} \) Доказано
Теорема 4:
Отрезок, соединяющий середину двух сторон треугольника, параллелен третьей стороне и составляет половину ее.
Проба:
Пусть ABC — треугольник, а P и Q — середины сторон AB и AC соответственно.
Здесь,
\ (\ overrightarrow {PA} \) = \ (\ frac 12 \) \ (\ overrightarrow {BA} \)
\ (\ overrightarrow {AQ} \) = \ (\ frac 12 \) \ (\ overrightarrow {AC} \)
Затем,
\ (\ overrightarrow {PA} \) + \ (\ overrightarrow {AQ} \) = \ (\ frac 12 \) \ (\ overrightarrow {BA} \) + \ (\ frac 12 \) \ (\ overrightarrow { AC} \)
∴ \ (\ overrightarrow {PQ} \) = \ (\ frac 12 \) (\ (\ overrightarrow {BA} \) + \ (\ overrightarrow {AC} \))
и.е. \ (\ overrightarrow {PQ} \) = \ (\ frac 12 \) \ (\ overrightarrow {BC} \)
Очевидно, \ (\ overrightarrow {PQ} \) // \ (\ overrightarrow {BC} \) Доказано
Теорема 5:
Вектор положения центроида треугольника задается как \ (\ overrightarrow g \) = \ (\ frac 13 \) (\ (\ overrightarrow a \) + \ (\ overrightarrow b \) + \ (\ overrightarrow c \)), где \ (\ overrightarrow a \), \ (\ overrightarrow b \) и \ (\ overrightarrow c \) — векторы положения вершин, а \ (\ overrightarrow g \) — вектор положения центроида .
Проба:
Пусть ABC — треугольник, а O — начало координат.
Лет,
\ (\ overrightarrow {OA} \) = \ (\ overrightarrow a \)
\ (\ overrightarrow {OB} \) = \ (\ overrightarrow b \)
\ (\ overrightarrow {OC} \) = \ (\ overrightarrow c \)
Пусть D будет серединой AC.
По теореме о средней точке
\ (\ overrightarrow {OD} \) = \ (\ frac 12 \) (\ (\ overrightarrow a \) + \ (\ overrightarrow c \))
Пусть G — центр тяжести треугольника ABC.
Тогда G делит BD внутри в соотношении 2: 1.
Затем,
\ (\ begin {align *} \ overrightarrow {OG} & = \ frac {2 \ overrightarrow {OD} + 1 \ overrightarrow {OB}} {2 + 1} \\ & = \ frac {2 × \ frac 12 \ overrightarrow a + \ overrightarrow c + \ overrightarrow b} {3} \\ & = \ frac 13 (\ overrightarrow a + \ overrightarrow b + \ overrightarrow c) \\ \ end {align *} \)
∴ Вектор положения G (\ (\ overrightarrow g \)) = \ (\ frac 13 (\ overrightarrow a + \ overrightarrow b + \ overrightarrow c) \) Доказано
Теорема 6:
Медиана основания равнобедренного треугольника перпендикулярна основанию.
ABC — равнобедренный треугольник, где AB = AC, а AM — медиана основания BC. Проба:
Пусть \ (\ overrightarrow {AB} \) = \ (\ overrightarrow a \) и \ (\ overrightarrow {AC} \) = \ (\ overrightarrow b \)
Затем,
| \ (\ overrightarrow a \) | = | \ (\ overrightarrow b \) | или a = b
Сейчас,
\ (\ overrightarrow {AM} \) = \ (\ overrightarrow {AB} \) + \ (\ overrightarrow {BM} \) = \ (\ overrightarrow {AB} \) + \ (\ frac 12 \) \ ( \ overrightarrow {BC} \)
\ (\ overrightarrow {BC} \) = \ (\ overrightarrow {BA} \) + \ (\ overrightarrow {AC} \) = — \ (\ overrightarrow a \) + \ (\ overrightarrow b \)
\ (\ begin {align *} \ следовательно \ overrightarrow {AM} & = \ overrightarrow a + \ frac 12 (\ overrightarrow b — \ overrightarrow a) \\ & = \ frac {\ overrightarrow a + \ overrightarrow b — \ overrightarrow c} 2 \\ & = \ frac 12 (\ overrightarrow a + \ overrightarrow b) \\ \ end {align *} \)
Сейчас,
\ (\ begin {align *} \ overrightarrow {AM}.2) \\ & = 0 \\ \ end {align *} \)
∴ AM⊥ BC Доказано
Теорема 7:
Фигура, образованная соединением середин соседних сторон четырехугольника, представляет собой параллелограмм.
Проба:
Пусть ABCD — четырехугольник, а P, Q, R и S — середины AB, BC, CD и DA соответственно. Присоединяйтесь к BD.
Затем,
\ (\ overrightarrow {BA} \) + \ (\ overrightarrow {AD} \) = \ (\ overrightarrow {BD} \)
2 \ (\ overrightarrow {PA} \) + 2 \ (\ overrightarrow {AS} \) = \ (\ overrightarrow {BD} \)
\ (\ overrightarrow {PA} \) + \ (\ overrightarrow {AS} \) = \ (\ frac 12 \) \ (\ overrightarrow {BD} \)
∴ \ (\ overrightarrow {PS} \) = \ (\ frac 12 \) \ (\ overrightarrow {BD} \)
Очевидно, \ (\ overrightarrow {PS} \) // \ (\ overrightarrow {BD} \)
снова,
\ (\ overrightarrow {BC} \) + \ (\ overrightarrow {CD} \) = \ (\ overrightarrow {BD} \)
2 \ (\ overrightarrow {QC} \) + 2 \ (\ overrightarrow {CR} \) = \ (\ overrightarrow {BD} \)
\ (\ overrightarrow {QC} \) + \ (\ overrightarrow {CR} \) = \ (\ frac 12 \) \ (\ overrightarrow {BD} \)
∴ \ (\ overrightarrow {QC} \) = \ (\ frac 12 \) \ (\ overrightarrow {BD} \)
Очевидно, \ (\ overrightarrow {QR} \) // \ (\ overrightarrow {BD} \)
\ (\ overrightarrow {PS} \) = \ (\ overrightarrow {QR} \), \ (\ overrightarrow {PS} \) // \ (\ overrightarrow {QR} \)
Аналогично
\ (\ overrightarrow {PQ} \) = \ (\ overrightarrow {SR} \), \ (\ overrightarrow {PQ} \) // \ (\ overrightarrow {SR} \)
Следовательно, PQRS — параллелограмм.
Теорема 8:
Диагонали параллелограмма делят друг друга пополам.
Проба:
Пусть OACB — параллелограмм, а O — начало координат.
Пусть \ (\ overrightarrow {OA} \) = \ (\ overrightarrow a \) и \ (\ overrightarrow {OB} \) = \ (\ overrightarrow b \)
Пусть M — средняя точка AB.
Затем,
\ (\ overrightarrow {OM} \) = \ (\ frac 12 \) (\ (\ overrightarrow a \) + \ (\ overrightarrow b \))……………………………………… (i)
Также,
\ (\ overrightarrow {OC} \) = \ (\ overrightarrow a \) + \ (\ overrightarrow b \), параллелограммом сложения векторов.
Пусть N будет средней точкой OC.
Затем,
\ (\ overrightarrow {ON} \) = \ (\ frac 12 \) \ (\ overrightarrow {OC} \) = \ (\ frac 12 \) (\ (\ overrightarrow a \) + \ (\ overrightarrow b \ )) …………………………………….. (ii)
Из (i) и (ii), M и N имеют одинаковый вектор положения.Итак, M и N — одинаковые точки.
Следовательно, диагонали параллелограмма делят друг друга пополам.
Теорема 9:
Диагонали прямоугольника равны.
Проба:
Пусть ABCD — прямоугольник, а AC и BD — диагонали.
Затем,
\ (\ overrightarrow {AB} \) = \ (\ overrightarrow {DC} \), \ (\ overrightarrow {AD} \) = \ (\ overrightarrow {BC} \), \ (\ angle A \) = \ (\ угол B \) = \ (\ угол C \) = \ (\ угол D \) = 90 ° (\ (\ overrightarrow {AB} \).2 \)
BD 2 = BA 2 + 0 + AD 2
BD 2 = AB 2 + BC 2 …………………………….. … (i)
Из (i) и (ii),
AC 2 = BD 2
∴ AC = BD
Значит, диагонали прямоугольника равны.
Теорема 10:
Диагонали ромба пересекают друг друга под прямым углом.
Проба:
Пусть ABCD — ромб, а AC и BD — диагонали.
Очевидно,
\ (\ overrightarrow {AO} \) = \ (\ overrightarrow {OC} \) и \ (\ overrightarrow {BO} \) = \ (\ overrightarrow {OD} \)
Сейчас,
Докажем, что,
\ (\ overrightarrow {AO} \) ⊥ \ (\ overrightarrow {BO} \)
Пусть \ (\ overrightarrow {AB} \) = \ (\ overrightarrow a \) и \ (\ overrightarrow {AD} \) = \ (\ overrightarrow b \)
Затем,
\ (\ overrightarrow {AC} \) = \ (\ overrightarrow {AB} \) + \ (\ overrightarrow {BC} \) = \ (\ overrightarrow {AB} \) + \ (\ overrightarrow {AD} \) = \ (\ overrightarrow a \) + \ (\ overrightarrow b \)
\ (\ overrightarrow {AO} \) = \ (\ frac 12 \) \ (\ overrightarrow {AC} \) = \ (\ frac 12 \) (\ (\ overrightarrow a \) + \ (\ overrightarrow b \ ))………………………… (i)
снова,
\ (\ overrightarrow {BD} \) = \ (\ overrightarrow {BA} \) + \ (\ overrightarrow {AD} \) = — \ (\ overrightarrow a \) + \ (\ overrightarrow b \) = \ ( \ overrightarrow b \) — \ (\ overrightarrow a \)
\ (\ overrightarrow {BO} \) = \ (\ frac 12 \) \ (\ overrightarrow {BD} \) = \ (\ frac 12 \) (\ (\ overrightarrow b \) — \ (\ overrightarrow a \ )) ………………………… (ii)
Из (ii) и (ii),
\ (\ overrightarrow {AO} \). \ (\ Overrightarrow {BO} \) = \ (\ frac 12 \) (\ (\ overrightarrow a \) + \ (\ overrightarrow b \).2 \)) = \ (\ frac 14 \) (b 2 — a 2 ) = 0
Следовательно, диагонали ромба пересекают друг друга под прямым углом.
Теорема 11:
Угол в полукруге — это прямой угол.
Проба:
Пусть O — центр окружности, а AB — диаметр. \ (\ angle \) ACB — угол в полукруге. Присоединяйтесь к OC.
Сейчас,
\ (\ overrightarrow {AC} \) = \ (\ overrightarrow {AO} \) + \ (\ overrightarrow {OC} \)………………………… (i)
\ (\ overrightarrow {CB} \) = \ (\ overrightarrow {CO} \) + \ (\ overrightarrow {OB} \) = \ (\ overrightarrow {CO} \) + \ (\ overrightarrow {AO} \)
\ (\ overrightarrow {CB} \) = \ (\ overrightarrow {AO} — \ overrightarrow {OC} \) . 2 \) + 2 \ (\ overrightarrow {OA} \).2} 4 \)
∴ OM = \ (\ frac 12 \) AC
Также,
AM = MC = \ (\ frac 12 \) AC
∴ AM = MC =
OMСледовательно, середина гипотенузы прямоугольного треугольника равноудалена от его вершин.
векторов и векторной геометрии 12 класс Математика 7.2 | Решения
1.
(i)
Солн:
D — средняя точка BC.
Из ABD, $ \ overrightarrow {{\ rm {AB}}} $ = $ \ overrightarrow {{\ rm {AD}}} $ + $ \ overrightarrow {{\ rm {DB}}} $
Опять же, из треугольника ACD,
Или $ \ overrightarrow {{\ rm {AC}}} $ = $ \ overrightarrow {{\ rm {AD}}} $ + $ \ overrightarrow {{\ rm {DC}}} $
Добавление, $ \ overrightarrow {{\ rm {AB}}} $ + $ \ overrightarrow {{\ rm {AC}}} $ = 2 $ \ overrightarrow {{\ rm {AD}}} $ + ($ \ overrightarrow {{\ rm {DB}}} $ + $ \ overrightarrow {{\ rm {DC}}} $).
Поскольку, $ \ overrightarrow {{\ rm {DB}}} $ + $ \ overrightarrow {{\ rm {DC}}} $ равны по величине, но противоположны по направлению, поэтому
Или $ \ overrightarrow {{\ rm {DB}}} $ + $ \ overrightarrow {{\ rm {DC}}} $ = 0.
Итак, $ \ overrightarrow {{\ rm {AB}}} $ + $ \ overrightarrow {{\ rm {AC}}} $ = 2 $ \ overrightarrow {{\ rm {AD}}} $.
(ii)
Солн:
AC и BD — диагонали параллелограмма ABCD.
От, $ \ overrightarrow {{\ rm {AC}}} $ = $ \ overrightarrow {{\ rm {AB}}} $ + $ \ overrightarrow {{\ rm {BC}}} $
Или $ \ overrightarrow {{\ rm {AC}}} $ = $ \ overrightarrow {{\ rm {AB}}} $ + $ \ overrightarrow {{\ rm {BC}}} $
Или: $ \ overrightarrow {{\ rm {BD}}} $ = $ \ overrightarrow {{\ rm {BA}}} $ + $ \ overrightarrow {{\ rm {AD}}} $ = — $ \ overrightarrow { {\ rm {AB}}} $ + $ \ overrightarrow {{\ rm {BC}}}
долларов(AD = BC, AD // BC).
Теперь $ \ overrightarrow {{\ rm {AC}}} $ + $ \ overrightarrow {{\ rm {BD}}} $ = $ \ overrightarrow {{\ rm {AB}}} $ + $ \ overrightarrow {{ \ rm {BC}}} $ + (- $ \ overrightarrow {{\ rm {AB}}} $ + $ \ overrightarrow {{\ rm {BC}}} $) = 2 $ \ overrightarrow {{\ rm {BC }}} $.
$ \ overrightarrow {{\ rm {AC}}} $ — $ \ overrightarrow {{\ rm {BD}}} $ = $ \ overrightarrow {{\ rm {AB}}} $ + $ \ overrightarrow {{\ rm {BC}}} $ = (- $ \ overrightarrow {{\ rm {AB}}} $ + $ \ overrightarrow {{\ rm {BC}}} $) = 2 $ \ overrightarrow {{\ rm {AB}} } $.
2.
(i)
Солн:
Пусть в правильном шестиугольнике ABCDEF $ \ overrightarrow {{\ rm {AB}}} $ = $ {\ rm {\ vec a}} $ и $ \ overrightarrow {{\ rm {BC}}} $ = $ {\ rm {\ vec b}}
долларов СШАОт, $ \ overrightarrow {{\ rm {AC}}} $ = $ \ overrightarrow {{\ rm {AB}}} $ + $ \ overrightarrow {{\ rm {BC}}} $ = $ {\ rm { \ vec a}} $ + $ {\ rm {\ vec b}} $.
Или $ \ overrightarrow {{\ rm {AD}}} $ = 2. $ \ Overrightarrow {{\ rm {BC}}} $ = 2 $ {\ rm {\ vec b}} $.
Или $ \ overrightarrow {{\ rm {CD}}} $ = $ \ overrightarrow {{\ rm {CA}}} $ + $ \ overrightarrow {{\ rm {AD}}} $ = — $ \ overrightarrow { {\ rm {AC}}} $ + $ \ overrightarrow {{\ rm {AD}}}
долларов= $ — \ left ({{\ rm {\ vec a}} + {\ rm {\ vec b}}} \ right) + 2 {\ rm {\ vec b}} $ = $ {\ rm {\ vec b}} — {\ rm {\ vec a}} $.
Или: $ \ overrightarrow {{\ rm {DE}}} $ = $ \ overrightarrow {{\ rm {BA}}} $ = $ — \ overrightarrow {{\ rm {AB}}} $ = — $ {\ rm {\ vec a}}
долларов СШАИли, $ \ overrightarrow {{\ rm {EF}}} $ = $ \ frac {1} {2} $$ \ overrightarrow {{\ rm {DA}}} $ = $ \ frac {1} {2} $ (- 2 $ {\ rm {\ vec b}} $) = $ — {\ rm {\ vec b}} $.
Или $ \ overrightarrow {{\ rm {FA}}} $ = $ \ overrightarrow {{\ rm {DC}}} $ = $ — \ overrightarrow {{\ rm {CD}}} $ = $ — \ left ({{\ rm {\ vec b}} — {\ rm {\ vec a}}} \ right) $ = $ {\ rm {\ vec a}} — {\ rm {\ vec b}} $.
(ii)
Солн:
Или $ \ overrightarrow {{\ rm {AB}}} $ + $ \ overrightarrow {{\ rm {AC}}} $ + $ \ overrightarrow {{\ rm {AD}}} $ + $ \ overrightarrow {{ \ rm {AE}}} $ + $ \ overrightarrow {{\ rm {AF}}}
долларов= ($ \ overrightarrow {{\ rm {AB}}} $ + $ \ overrightarrow {{\ rm {AE}}} $) + ($ \ overrightarrow {{\ rm {AC}}} $ + $ \ overrightarrow {{\ rm {CD}}} $) + $ \ overrightarrow {{\ rm {AD}}} $.
= $ \ overrightarrow {{\ rm {AD}}} $ + $ \ overrightarrow {{\ rm {AD}}} $ + $ \ overrightarrow {{\ rm {AD}}} $
= 3 $ \ overrightarrow {{\ rm {AD}}} $ = 3 (2 $ \ overrightarrow {{\ rm {AO}}} $) = 6 $ \ overrightarrow {{\ rm {OA}}} $
3.
(i)
Солн:
В $ \ Delta $ ABC пусть $ \ overrightarrow {{\ rm {AB}}} {\ rm {\:}} $ = $ {\ rm {\ vec a}} $ и $ \ overrightarrow {{\ rm {AC}}} $ = $ {\ rm {\ vec b}} $.
Затем,
Или $ \ overrightarrow {{\ rm {BC}}} $ = $ \ overrightarrow {{\ rm {AC}}} — \ overrightarrow {{\ rm {AB}}} $ = $ {\ rm {\ vec b}} — {\ rm {\ vec a}} $.
Или: $ \ overrightarrow {{\ rm {AD}}} $ = $ \ overrightarrow {{\ rm {AB}}} $ + $ \ overrightarrow {{\ rm {BD}}} $ = $ \ overrightarrow {{ \ rm {AB}}} $ + $ \ frac {1} {2} \ overrightarrow {{\ rm {BC}}}
долларов= $ {\ rm {\ vec a}} $ + $ \ frac {1} {2} $ ($ {\ rm {\ vec b}} — {\ rm {\ vec a}} $) = $ \ frac {1} {2} $ ($ {\ rm {\ vec b}} + {\ rm {\ vec a}} $).
Или: $ \ overrightarrow {{\ rm {BE}}} $ = $ \ overrightarrow {{\ rm {BC}}} $ + $ \ overrightarrow {{\ rm {CE}}} $ = $ \ overrightarrow {{ \ rm {BC}}} $ + $ \ frac {1} {2} $$ \ overrightarrow {{\ rm {CA}}} $.
= $ {\ rm {\ vec b}} — {\ rm {\ vec a}} — \ frac {1} {2} {\ rm {\ vec b}} $ = $ \ frac {1} {2 } $$ {\ rm {\ vec b}} — {\ rm {\ vec a}} $.
Или $ \ overrightarrow {{\ rm {CF}}} $ = $ \ overrightarrow {{\ rm {CA}}} $ + $ \ overrightarrow {{\ rm {AF}}} $ = $ \ overrightarrow {{ \ rm {CA}}} $ + $ \ frac {1} {2} $$ \ overrightarrow {{\ rm {AB}}} $ = $ — {\ rm {\ vec b}} $ + $ \ frac { 1} {2} {\ rm {\ vec a}} $ = $ \ frac {1} {2} $$ {\ rm {\ vec a}} — {\ rm {\ vec b}} $.
Теперь $ \ overrightarrow {{\ rm {AD}}} $ + $ \ overrightarrow {{\ rm {BE}}} $ + $ \ overrightarrow {{\ rm {CF}}} $ = $ \ frac {1 } {2} $$ \ left ({{\ rm {\ vec b}} + {\ rm {\ vec a}}} \ right) $ + $ \ frac {1} {2} $$ {\ rm { \ vec b}} — {\ rm {\ vec a}} $ + $ \ frac {1} {2} $$ {\ rm {\ vec a}} $ — $ {\ rm {\ vec b}} $ = 0.
(ii)
Солн:
G — точка пересечения диагоналей AC и BD.
Итак, GA = GC, GB = GD,
От треугольника OAC,
Или $ \ overrightarrow {{\ rm {OA}}} $ + $ \ overrightarrow {{\ rm {OC}}} $ = 2 $ \ overrightarrow {{\ rm {OG}}} $. (G — средняя точка AC.)
Опять из треугольника OBD,
Или $ \ overrightarrow {{\ rm {OB}}} $ + $ \ overrightarrow {{\ rm {OD}}} $ = 2 $ \ overrightarrow {{\ rm {OG}}} $.
(G — средняя точка BD).
Добавление, $ \ overrightarrow {{\ rm {OA}}} + \ overrightarrow {{\ rm {OB}}} + \ overrightarrow {{\ rm {OC}}} + \ overrightarrow {{\ rm {OD}} } $ = 4. $ {\ Rm {\:}} \ overrightarrow {{\ rm {OG}}} $.
4.
(i)
Солн:
Пусть O будет началом. Тогда
Или, $ \ overrightarrow {{\ rm {OA}}} $ = (2, -1, -3), $ \ overrightarrow {{\ rm {OB}}} $ = (4,2,3) и $ \ overrightarrow {{\ rm {OC}}} $ = (6,3,4).
Или, $ \ overrightarrow {{\ rm {AB}}} $ = $ \ overrightarrow {{\ rm {OB}}} — \ overrightarrow {{\ rm {OA}}} $ = (4,2,3) — (2, -1, -3)
= (4 — 2,2 + 1,3 + 3) = (2,3,6).
Или, $ \ overrightarrow {{\ rm {AC}}} $ = $ \ overrightarrow {{\ rm {OC}}} — \ overrightarrow {{\ rm {OA}}} $ = (6,3,4) — (2, -1, -3)
= (6 — 2,3 + 1,4 + 3) = (4,4,7).
И, $ \ overrightarrow {{\ rm {BC}}} $ = $ \ overrightarrow {{\ rm {OC}}} — \ overrightarrow {{\ rm {OB}}} $ = (6,3,4) — (4,2,3) = (2,1,1).
AB = $ \ left | {\ overrightarrow {{\ rm {AB}}}} \ right | $ = | (2,3,6) | = $ \ sqrt {4 + 9 + 36} $ = 7.
AC = $ \ left | {\ overrightarrow {{\ rm {AC}}}} \ right | $ = | (4,4,7) | = $ \ sqrt {16 + 16 + 49} $ = 9.
г. до н.э. = $ \ left | {\ overrightarrow {{\ rm {BC}}}} \ right | $ = | (2,1,1) | = $ \ sqrt {4 + 1 + 1} $ = $ \ sqrt 6 $.
(ii)
Солн:
Пусть A, B и C — три точки с векторами позиций 7 $ {\ rm {\ vec j}} $ + 10 $ {\ rm {\ vec k}} $, $ — {\ rm {\ vec i}} $ + 6 $ {\ rm {\ vec j}} $ + 6 $ {\ rm {\ vec k}} $ и $ — 4 {\ rm {\ vec i}} $ + 9 $ {\ rm {\ vec j}} $ + 6 $ {\ rm {\ vec k}} $ соответственно.
Если O — начало отсчета, то
Или, $ \ overrightarrow {{\ rm {OA}}} $ = 7 $ {\ rm {\ vec j}} $ + 10 $ {\ rm {\ vec k}} $,
Или, $ \ overrightarrow {{\ rm {OB}}} $ = $ — {\ rm {\ vec i}} $ + 6 $ {\ rm {\ vec j}} $ + 6 $ {\ rm {\ vec k}} $
Или, $ \ overrightarrow {{\ rm {OC}}} = — 4 {\ rm {\ vec i}} $ + 9 $ {\ rm {\ vec j}} $ + 6 $ {\ rm {\ vec k}} $.
Или, $ \ overrightarrow {{\ rm {AB}}} $ = $ \ overrightarrow {{\ rm {OB}}} — \ overrightarrow {{\ rm {OA}}} $ = $ (- {\ rm { \ vec i}} $ + 6 $ {\ rm {\ vec j}} $ + 6 $ {\ rm {\ vec k}}) — \ left ({7 {\ rm {\ vec j}} + 10 { \ rm {\ vec k}}} \ right) $ = $ — {\ rm {\ vec i}} — {\ rm {\ vec j}} — 4 {\ rm {\ vec k}} $.
Или: $ \ overrightarrow {{\ rm {BC}}} $ = $ \ overrightarrow {{\ rm {OC}}} — \ overrightarrow {{\ rm {OB}}} $ = $ (- 4 {\ rm {\ vec i}} $ + 9 $ {\ rm {\ vec j}} $ + 6 $ {\ rm {\ vec k}}) — \ left ({- {\ rm {\ vec i}} + 6 {\ rm {\ vec j \:}} + 6 {\ rm {\ vec k}}} \ right) $ = $ — 3 {\ rm {\ vec i}} + 3 {\ rm {\ vec j} } $.
Или: $ \ overrightarrow {{\ rm {CA}}} $ = $ \ overrightarrow {{\ rm {OA}}} — \ overrightarrow {{\ rm {OC}}} $ = (7 $ {\ rm { \ vec j}} $ + 10 $ {\ rm {\ vec k}}) — \ left ({- 4 {\ rm {\ vec i}} + 9 {\ rm {\ vec j \:}} + 6 {\ rm {\ vec k}}} \ right) $ = $ — 4 {\ rm {\ vec i}} — 2 {\ rm {\ vec j}} $ + $ 4 {\ rm {\ vec k}} $.2} $ = 18 + 18 = 36 = (6) 2 = CA 2 .
Итак, ABC — прямоугольный треугольник.
Итак, A, B и C из вершин прямоугольного равнобедренного треугольника.
5.
а.
Солн:
Или $ \ overrightarrow {{\ rm {OP}}} $ = $ {\ rm {\ vec i}} + 3 {\ rm {\ vec j}} — 7 {\ rm {\ vec k}} $ и $ \ overrightarrow {{\ rm {OQ}}} $ = $ 5 {\ rm {\ vec i}} — 2 {\ rm {\ vec j}} + 4 {\ rm {\ vec k}} $
. 2}} $ = $ 9 \ sqrt 2 $.Или, $ \ widehat {{\ rm {PQ}}} $ = $ \ frac {{\ overrightarrow {{\ rm {PQ}}}}} {{\ left | {\ overrightarrow {{\ rm {PQ}}}} \ right |}} $ = $ \ frac {{4 {\ rm {\ vec i}} — 5 {\ rm {\ vec j}} + 11 {\ rm {\ vec k}}}} {{9 \ sqrt 2}} $ = $ \ frac {4} {{9 \ sqrt 2}} {\ rm {\ vec i}} $ — $ \ frac {5} {{9 \ sqrt 2}} {\ rm {\ vec j}} $ + $ \ frac {{11}} {{9 \ sqrt 2}} {\ rm {\ vec k}} $.
Таким образом, постоянными токами PQ являются $ \ frac {4} {{9 \ sqrt 2}}, — \ frac {5} {{9 \ sqrt 2}}, \ frac {{11}} {{9 \ sqrt 2}} $.
г.
Солн:
Или, $ {\ rm {\ vec b}} $ = (-2,4, -3).
Итак, 2 $ {\ rm {\ vec b}} $ = (-4,8, -6).
(i)
$ {\ rm {\ vec a}} — 2 {\ rm {\ vec b}} + {\ rm {\ vec c}} $ = (3, -1, -4) — (-4,8, -6) + (-5,7, -1).
= (3 + 4-5, — 1-8 + 7, — 4 + 6-1) = (2, -2,1).
(ii) $ \ left | {{\ rm {\ vec a}} — 2 {\ rm {\ vec b}} + {\ rm {\ vec c}}} \ right | $ = $ \ sqrt {4 + 4 + 1} $ = 3
(iii) Единичный вектор = $ \ frac {{2, — 2,1}} {3} $ = $ \ left ({\ frac {2} {3}, — \ frac {2} {3}, \ frac {1} {3}} \ right) $.
(iv) Требуемый d.c’s = $ \ frac {2} {3} $, $ — \ frac {2} {3} $, $ \ frac {1} {3} $.
6.
Солн:
Или, $ \ frac {{{\ rm {BD}}}} {{{\ rm {DC}}}} = \ frac {{\ rm {m}}} {{\ rm {n}}} $ .
Или n. $ \ Overrightarrow {{\ rm {BD}}} $ = m. $ \ Overrightarrow {{\ rm {DC}}} $.
Или, n ($ \ overrightarrow {- {\ rm {OB}}} + \ overrightarrow {{\ rm {OD}}} $) = m ($ \ overrightarrow {- {\ rm {OD}}} + \ overrightarrow {{\ rm {OC}}} $)
Или, $ — {\ rm {n}} $.$ \ overrightarrow {{\ rm {OB}}} $ + n. $ \ overrightarrow {{\ rm {OD}}} $ = -m. $ \ overrightarrow {{\ rm {OD}}} $ + m. $ \ overrightarrow {{\ rm {OC}}} $.
Или m. $ {\ Rm {\:}} \ overrightarrow {{\ rm {OD}}} $ + n. $ \ Overrightarrow {{\ rm {OD}}} $ = n. $ {\ Rm { \:}} \ overrightarrow {{\ rm {OB}}} $ + m. $ {\ rm {\:}} \ overrightarrow {{\ rm {OC}}} $
Или (m + n) $ {\ rm {\:}} \ overrightarrow {{\ rm {OD}}} $ = n. $ {\ Rm {\:}} \ overrightarrow {{\ rm {OB} }} $ + m. $ {\ rm {\:}} \ overrightarrow {{\ rm {OC}}} $.
Итак, $ \ overrightarrow {{\ rm {OD}}} $ = $ \ frac {{{\ rm {n}}.\ overrightarrow {{\ rm {OB}}} + {\ rm {m}}. \ overrightarrow {{\ rm {OC}}}}} {{{\ rm {m}} + {\ rm {n}} }} $.
7.
(i)
Солн:
Пусть $ \ overrightarrow {{\ rm {OA}}} $ = (1, -2,3), $ \ overrightarrow {{\ rm {OB}}} $ = (2,3, -4) и $ \ overrightarrow {{\ rm {OC}}} $ = (0, -7,10).
Или, $ \ overrightarrow {{\ rm {AB}}} $ = $ \ overrightarrow {{\ rm {OB}}} — \ overrightarrow {{\ rm {OA}}} $ = (2,3, -4 ) — (1, -2,3) = (1,5, -7).
Или, $ \ overrightarrow {{\ rm {BC}}} $ = $ \ overrightarrow {{\ rm {OC}}} — \ overrightarrow {{\ rm {OB}}} $ = (0, -7,10 ) — (2,3, -4) = (-2, -10,14).
Итак, $ \ overrightarrow {{\ rm {BC}}} $ = — 2 $ \ overrightarrow {{\ rm {AB}}} $.
Итак, BC и AB параллельны. Но B — общая точка, поэтому A, B и C лежат на одной прямой.
(ii)
Солн:
Пусть $ \ overrightarrow {{\ rm {OA}}} $ = $ {\ rm {\ vec i}} + 2 {\ rm {\ vec j}} + 4 {\ rm {\ vec k}} $, $ \ overrightarrow {{\ rm {OB}}} = $$ 2 {\ rm {\ vec i}} + 5 {\ rm {\ vec j}} — {\ rm {\ vec k}} $ = и $ \ overrightarrow {{\ rm {OC}}} $ = $ 3 {\ rm {\ vec i}} + 8 {\ rm {\ vec j}} — 6 {\ rm {\ vec k}} $
Или: $ \ overrightarrow {{\ rm {AB}}} $ = $ \ overrightarrow {{\ rm {OB}}} — \ overrightarrow {{\ rm {OA}}} $ = $ 2 {\ rm {\ vec i}} + 5 {\ rm {\ vec j}} — {\ rm {\ vec k}} — \ left ({{\ rm {\ vec i}} + 2 {\ rm {\ vec j}} + 4 {\ rm {\ vec k}}} \ right) $ = $ {\ rm {\ vec i}} + 3 {\ rm {\ vec j}} — 5 {\ rm {\ vec k}} $
Или, $ \ overrightarrow {{\ rm {BC}}} $ = $ \ overrightarrow {{\ rm {OC}}} — \ overrightarrow {{\ rm {OB}}} $ = $ 3 {\ rm {\ vec i}} + 8 {\ rm {\ vec j}} — 6 {\ rm {\ vec k}} — \ left ({2 {\ rm {\ vec i}} + 5 {\ rm {\ vec j}) } — {\ rm {\ vec k}}} \ right) $ = $ {\ rm {\ vec i}} + 3 {\ rm {\ vec j}} — 5 {\ rm {\ vec k}} $
Итак, $ \ overrightarrow {{\ rm {AB}}} $ = $ \ overrightarrow {{\ rm {BC}}} $.
Итак, A, B и C коллинеарны.
(б)
Солн:
Заданных векторов:
Или, $ {\ rm {\ vec a}} $ = 3 $ {\ rm {\ vec i}} $ + $ {\ rm {\ vec j}} $ — $ {\ rm {\ vec k}} $
А, $ {\ rm {\ vec b}} $ = λ $ {\ rm {\ vec i}} $ — 4 $ {\ rm {\ vec j}} $ + 4 $ {\ rm {\ vec k }} $
Так как $ {\ rm {\ vec a \:}} $ и $ {\ rm {\ vec b}} $ коллинеарны, поэтому
Или, $ {\ rm {\ vec a}} $ = l. $ {\ Rm {\: \ vec b}} $, где l — скаляр.
Или, 3 $ {\ rm {\ vec i}} $ + $ {\ rm {\ vec j}} $ — $ {\ rm {\ vec k}} $ = l (λ $ {\ rm {\ vec i}} $ — 4 $ {\ rm {\ vec j}} $ + 4 $ {\ rm {\ vec k}} $).
Приравнивая коэффициенты при одинаковых членах, получаем,
Или, 3 = l.λ… (i)
Или, 1 = — 4l… (ii)
А — 1 = 4л… (iii)
Итак, из (ii) и (iii) l = $ — \ frac {1} {4} $.
Таким образом, из (i) 3 = $ — \ frac {1} {4} $. λ à λ = — 12.
8.
(i)
Солн:
Пусть $ \ overrightarrow {{{\ rm {r}} _ 1}} $ = $ {\ rm {\ vec a}} $ — 2 $ {\ rm {\ vec b}} $ + 3 $ {\ rm { \ vec c}} $, $ \ overrightarrow {{{\ rm {r}} _ 2}} $ = $ — 2 {\ rm {\ vec a}} $ + 3 $ {\ rm {\ vec b}} $ — 4 $ {\ rm {\ vec c}} $ и $ \ overrightarrow {{{\ rm {r}} _ 3}} $ = $ — {\ rm {\ vec b}} $ + 2 $ {\ rm {\ vec c}}
долларов СШАЕсли три вектора копланарны,
Или $ \ overrightarrow {{{\ rm {r}} _ 3}} $ = x.$ {\ rm {\:}} \ overrightarrow {{{\ rm {r}} _ 1}} $ + y. $ {\ rm {\:}} \ overrightarrow {{{\ rm {r}} _ 2}} $. …. (I)
Где x и y — скаляры,
Или, $ — {\ rm {\ vec b}} $ + 2 $ {\ rm {\ vec c}} $ = x $ \ left ({{\ rm {\ vec a}} — 2 {\ rm { \ vec b}} + 3 {\ rm {\ vec c}}} \ right) $ + y $ \ left ({- 2 {\ rm {\ vec a}} + 3 {\ rm {\ vec b}} — 4 {\ rm {\ vec c}}} \ right) $
Или, $ — {\ rm {\ vec b}} $ + 2 $ {\ rm {\ vec c}} $ = (x — 2y) $ {\ rm {\ vec a}} $. + (-2x + 3y). $ {\ Rm {\ vec b}} $ + (3x — 4y). $ {\ Rm {\ vec c}} $.
Уравнение коэфф.подобных терминов,
Или, x — 2y = 0… (ii)
Или, — 2x + 3y = — 1… (iii)
Или, 3x — 4y = 2…. (Iv).
Решение (ii) и (iii), x = 2, y = 1.
Или, x = 2, y = 1 также удовлетворяют уравнению (iv).
От (i) $ \ overrightarrow {{{\ rm {r}} _ 3}} $ = 2. $ {\ Rm {\:}} \ overrightarrow {{{\ rm {r}} _ 1}} $ +. $ {\ rm {\:}} \ overrightarrow {{{\ rm {r}} _ 2}}
долларовСледовательно, данные векторы компланарны.
(ii)
Солн:
Пусть $ \ overrightarrow {{{\ rm {r}} _ 1}} $ = $ {\ rm {\ vec a}} $ — 3 $ {\ rm {\ vec b}} $ + 5 $ {\ rm { \ vec c}} $, $ \ overrightarrow {{{\ rm {r}} _ 2}} $ = $ {\ rm {\ vec a}} $ — 2 $ {\ rm {\ vec b}} $ + 3 $ {\ rm {\ vec c}} $ и $ \ overrightarrow {{{\ rm {r}} _ 3}} $ = $ — 2 {\ rm {\ vec a}} + 3 {\ rm {\ vec b}} $ — 4 $ {\ rm {\ vec c}}
$Если три вектора копланарны,
Или $ \ overrightarrow {{{\ rm {r}} _ 3}} $ = x.$ {\ rm {\:}} \ overrightarrow {{{\ rm {r}} _ 1}} $ + y. $ {\ rm {\:}} \ overrightarrow {{{\ rm {r}} _ 2}} $. …. (I)
Или, — 2 $ {\ rm {\ vec a}} $ + 3 $ {\ rm {\ vec b}} $ — 4 $ {\ rm {\ vec c}} $ = x ($ {\ rm { \ vec a}} $ — 3 $ {\ rm {\ vec b}} $ + 5 $ {\ rm {\ vec c}} $) + y ($ {\ rm {\ vec a}} $ — 2 $ {\ rm {\ vec b}} $ + 3 $ {\ rm {\ vec c}} $).
Или, — 2 $ {\ rm {\ vec a}} $ + 3 $ {\ rm {\ vec b}} $ — 4 $ {\ rm {\ vec c}} $ = (x + y). $ {\ rm {\: \ vec a}} $ + (- 3x — 2y). $ {\ rm {\: \ vec b}} $ + (5x + 3y). $ {\ rm {\: \ vec c }} $.
Или, x + y = — 2…. (Ii)
Или, -3x — 2y = 3… (iii)
Или, 5x + 3y = — 4….. (iv).
Решение (ii) amd (iii),
Или, x = 1, y = — 3.
Или, x = 1, y = — 3 также удовлетворяют уравнению (iv),
От (i), $ {\ rm {\:}} \ overrightarrow {{{\ rm {r}} _ 3}} $ = $ \ overrightarrow {{{\ rm {r}} _ 1}} — 3 \ overrightarrow {{{\ rm {r}} _ 2}} $.
Следовательно, векторы компланарны.
(iii).
Солн:
Пусть $ \ overrightarrow {{{\ rm {r}} _ 1}} $ = $ — {\ rm {\ vec a}} $ + 4 $ {\ rm {\ vec b}} $ + 3 $ {\ rm {\ vec c}} $, $ \ overrightarrow {{{\ rm {r}} _ 2}} $ = 2.$ {\ rm {\ vec a}} $ — 3 $ {\ rm {\ vec b}} $ — 5 $ {\ rm {\ vec c}} $ и $ \ overrightarrow {{{\ rm {r} } _3}} $ = $ 2 {\ rm {\ vec a}} + 7 {\ rm {\ vec b}} $ — 3 $ {\ rm {\ vec c}} $.
Если три вектора копланарны,
Или: $ \ overrightarrow {{{\ rm {r}} _ 3}} $ = x. $ {\ Rm {\:}} \ overrightarrow {{{\ rm {r}} _ 1}} $ + y. $ {\ rm {\:}} \ overrightarrow {{{\ rm {r}} _ 2}} $. …. (I)
Или 2 $ {\ rm {\ vec a}} $ + 7 $ {\ rm {\ vec b}} $ — 3 $ {\ rm {\ vec c}} $ = x ($ — {\ rm { \ vec a}} $ + 4 $ {\ rm {\ vec b}} $ + 3 $ {\ rm {\ vec c}} $) + y ($ 2 {\ rm {\ vec a}} $ — 3 $ {\ rm {\ vec b}} $ — 5 $ {\ rm {\ vec c}} $).
Или, (-x + 2y). $ {\ Rm {\: \ vec a}} $ + (4x — 3y) $ {\ rm {\: \ vec b}} $ + (3x — 5y). $ {\ rm {\: \ vec c}}
долларов СШАИли, — x + 2y = 2…. (Ii)
Или, 4x — 3y = y… (iii)
Или, 3x — 5y = — 3… .. (iv).
Решение (ii) amd (iii),
Или, x = 4, y = 3.
Или, x = 4, y = 3 также удовлетворяют уравнению (iv),
От (i), $ {\ rm {\:}} \ overrightarrow {{{\ rm {r}} _ 3}} $ = 4. $ \ Overrightarrow {{{\ rm {r}} _ 1}} + 3 \ overrightarrow {{{\ rm {r}} _ 2}} $.
Следовательно, векторы компланарны.
9.
а.
Солн:
Пусть, $ {\ rm {\ vec r}} $ = l. $ {\ Rm {\ vec a}} $ + m. $ {\ Rm {\ vec b}} $…. (I)
Или, (4,7) = l (5, -4) + m (-2,5)
Или, (4,7) = (5l — 2m, -4l + 5m).
Таким образом, 5l — 2m = 4…. (Ii)
А — 4л + 5м = 7… (iii)
Решая (ii) и (iii), получаем
l = 2, m = 3.
Таким образом, из (i) требуемого соотношения, $ {\ rm {\ vec r}} $ = 2 $ {\ rm {\ vec a}} $ + 3 $ {\ rm {\ vec b}} $.
г.
Солн:
Пусть, $ {\ rm {\ vec a}} $ = x. $ {\ Rm {\ vec b}} $ + y. $ {\ Rm {\ vec c}} $…. (I)
Или 2 $ {\ rm {\ vec i}} $ + $ {\ rm {\ vec j}} $ = x ($ {\ rm {\ vec i}} $ + $ {\ rm {\ vec j }} $) + y ($ {\ rm {\ vec i}} $ — $ {\ rm {\ vec j}} $).
Или 2 $ {\ rm {\ vec i}} $ + $ {\ rm {\ vec j}} $ = (x + y). $ {\ Rm {\ vec i}} $ + (x — y ). $ {\ rm {\: \ vec j}} $.
Приравнивая коэффициенты при одинаковых членах,
x + y = 2…. (I)
и x –y = 1… (i).
Решая (i) и (ii), получаем
x = $ \ frac {3} {2} $, y = $ \ frac {1} {2} $.
10.
а.
Солн:
Пусть $ {\ rm {\ vec a}} $ = $ {\ rm {\ vec i}} $ + $ {\ rm {\ vec k}} $ = (1,0,1), $ {\ rm {\ vec b}} $ = $ {\ rm {\ vec i}} $ + $ {\ rm {\ vec j}} $ = (1,1,0)
И $ {\ rm {\ vec c}} $ = — $ {\ rm {\ vec i}} $ — $ {\ rm {\ vec k}} $ = (-1,0, -1).
Пусть $ {\ rm {\ vec a}} $ = x. $ {\ Rm {\: \ vec b}} $ + y. $ {\ Rm {\: \ vec c}} $… .. (i ).
Или, (1,0,1) = x (1,1,0) + y (-1,0, -1) = (x — y, x, -y)
Итак, x — y — 1….(ii)
Или, x = 0…. (Iii)
А — y = 1…. (Iv)
Из (iii) и (iv) имеем,
Или, x = 0, y = — 1.
Эти значения x = 0, y = 1 также удовлетворяют,
x — y = 1, т.е. 0 — 1 = — 1, т.е. — 1 = — 1.
Поскольку, y = — 1 ≠ 0, значит, данные векторы линейно зависимы.
г.
Солн:
Пусть $ {\ rm {\ vec a}} $ = $ 2 {\ rm {\ vec i}} $ +3 $ {\ rm {\ vec j}} $$ + {\ rm {\:}} 4 { \ rm {\ vec k}} $ = (2,3,4), $ {\ rm {\ vec b}} $ = $ {\ rm {\ vec i}} $ — $ {\ rm {\ vec j }} $ + $ {\ rm {\:}} 2 {\ rm {\ vec k}} $ = (1, -1,2)
И $ {\ rm {\ vec c}} $ = 5 $ {\ rm {\ vec i}} $ + 6 $ {\ rm {\ vec j}} $ + $ {\ rm {\:}} 8 {\ rm {\ vec k}} $ = (5,6.8)
Пусть $ {\ rm {\ vec a}} $ = x. $ {\ Rm {\: \ vec b}} $ + y. $ {\ Rm {\: \ vec c}} $… .. (i ).
Или, (2,3,4) = x (1, -1,2) + y (5,6,8)
Итак, (2,3,4) = (x + 5y, — x + 6y, 2x + 8y).
Итак, x + 5y = 2… (ii)
Или, — x + 6y = 3…. (Iii)
Или, 2x + 8y = 4…. (Iv).
Решая (ii) и (iii), имеем y = $ \ frac {5} {{11}} $ и x = $ — \ frac {3} {{11}} $.
Эти значения x и y не удовлетворяют (iv),
Т.е. 2. $ \ left ({- \ frac {3} {{11}}} \ right) + 8 \ left ({\ frac {5} {{11}}} \ right) $ = 4.
то есть $ \ frac {{- 5 + 40}} {{11}} $ à 4 à 34 = 44, что неверно,
Следовательно, x и y не удовлетворяют (i), поэтому данные векторы независимы.
Векторы и векторная геометрия 12 класс Математика |
Векторная и векторная геометрия
Физические величины, характеризующиеся как величиной, так и направлением, называются векторными величинами.
Например, ускорение, импульс и т. 2}} $
Типы векторов
Нулевые векторы:
Если модуль вектора равен нулю и начальная точка вектора совпадает с конечной точкой.Обозначается он 0⃗. Направление такого вектора неопределенно.
Единичный вектор:
Вектор, имеющий величину единичной длины, называется единичным вектором. Предположим, что если OA⃗ — вектор, имеющий величину OA, тогда единичный вектор обозначен $ \ widehat {{\ rm {OA}}} $ в направлении вектора OA⃗ и имеет величину, равную 1.
Вектор положения:
Если O берется за начало отсчета, а A — любая произвольная точка в пространстве, то вектор OA⃗ называется вектором положения точки.Вектор положения обозначает положение точки в трехмерной декартовой системе относительно начала координат.
Совместные инициалы векторов:
Векторы, которые имеют одинаковую начальную точку, называются ко-начальными векторами.
Векторы AB⃗ и AC⃗ называются ко-начальными векторами, поскольку они имеют одну и ту же начальную точку A.
Как и отличия от векторов:
Векторы, имеющие одинаковое направление, называются одинаковыми векторами и векторами, имеющими противоположные направления w.r.t. друг друга называются непохожими векторами.
Копланарные векторы:
Три или более вектора, лежащих в одной плоскости или параллельно одной плоскости, называются копланарными векторами.
Коллинеарные векторы:
Известно, что векторы, лежащие на одних и тех же параллельных прямых, являются коллинеарными векторами.
Равные векторы:
Два или более вектора считаются равными векторами, если их величина и направление одинаковы.
Эти два вектора, как показано, являются равными векторами, поскольку они имеют одинаковое направление и величину.
Вектор смещения :
Если точка смещается из положения A в положение B, то смещение AB представляет собой вектор AB, который известен как вектор смещения.
Негатив вектора :
Если два вектора одинаковы по величине, но точно противоположны по направлению, то оба вектора отрицательны друг относительно друга.
Линейная комбинация векторов
Если r ⃗ — линейные комбинации наборов векторов a ⃗, b⃗, c⃗, то это можно записать как
r⃗ = xa⃗ + yb⃗ + zc⃗ + t⃗v, где x, y, z …… .t — скаляры
Линейно зависимые и независимые векторы
Если существует соотношение xa⃗ + yb⃗ + zc⃗ + t⃗v = 0 такое, что хотя бы один из скаляров не равен нулю, то набор векторов sa ⃗, b⃗, c⃗ называется линейно зависимыми векторами
Если существует соотношение xa⃗ + yb⃗ + zc⃗ + t⃗v = 0 такое, что все скаляры x, y, z …….равны нулю, то набор векторов sa ⃗, b⃗, c⃗ называется линейно независимыми векторами
Пример 1
Найдите $ {\ rm {\ vec a}} $ + $ {\ rm {\ vec b}} $, $ {\ rm {\ vec a}} $ — $ {\ rm {\ vec b}} $, $ — \ frac {1} {3} {\ rm {\ vec b}}
долларов СШАСолн:
(i)
$ {\ rm {\ vec a}} $ + $ {\ rm {\ vec b}} $ = (0,0) + (1,2) = (0 + 1,0 + 2) = (1, 2).
$ {\ rm {\ vec a}} $ — $ {\ rm {\ vec b}} $ = (0,0) — (1,2) = (0 — 1,0 — 2) = (-1 , -2).
2 $ {\ rm {\ vec a}} $ = 2 (0,0) = (0,0).
Или, $ — \ frac {1} {3} {\ rm {\ vec b}} $ = $ — \ frac {1} {3} $ (1,2) = $ \ left ({- \ frac { 1} {3}, — \ frac {2} {3}} \ right) $.
Пример 2
ABCD — это параллелограмм G — это точка пересечения диагоналей, и если O — любая точка, покажите, что
$ \ overrightarrow {{\ rm {OA}}} + \ overrightarrow {{\ rm {OB}}} + \ overrightarrow {{\ rm {OC}}} + \ overrightarrow {{\ rm {OD}}} $ = 4. $ {\ Rm {\:}} \ overrightarrow {{\ rm {OG}}} $.
Солн:
G — точка пересечения диагоналей AC и BD.
Итак, GA = GC, GB = GD,
От треугольника OAC,
Или $ \ overrightarrow {{\ rm {OA}}} $ + $ \ overrightarrow {{\ rm {OC}}} $ = 2 $ \ overrightarrow {{\ rm {OG}}} $. (G — это средняя точка AC.)
Опять из треугольника OBD,
Или $ \ overrightarrow {{\ rm {OB}}} $ + $ \ overrightarrow {{\ rm {OD}}} $ = 2 $ \ overrightarrow {{\ rm {OG}}} $.
(G — средняя точка BD).
Добавление, $ \ overrightarrow {{\ rm {OA}}} + \ overrightarrow {{\ rm {OB}}} + \ overrightarrow {{\ rm {OC}}} + \ overrightarrow {{\ rm {OD}} } $ = 4.$ {\ rm {\:}} \ overrightarrow {{\ rm {OG}}} $.
Пример 3
Проверить, являются ли векторы линейно зависимыми или независимыми
$ {\ rm {\ vec i}} $ + $ {\ rm {\ vec k}} $ и $ {\ rm {\ vec i}} $ + $ {\ rm {\ vec j}} $
Солн:
Пусть $ {\ rm {\ vec a}} $ = $ {\ rm {\ vec i}} $ + $ {\ rm {\ vec k}} $ = (1,0,1), $ {\ rm {\ vec b}} $ = $ {\ rm {\ vec i}} $ + $ {\ rm {\ vec j}} $ = (1,1,0)
И $ {\ rm {\ vec c}} $ = — $ {\ rm {\ vec i}} $ — $ {\ rm {\ vec k}} $ = (-1,0, -1).
Пусть $ {\ rm {\ vec a}} $ = x. $ {\ Rm {\: \ vec b}} $ + y. $ {\ Rm {\: \ vec c}} $… .. (i ).
Или, (1,0,1) = x (1,1,0) + y (-1,0, -1) = (x — y, x, -y)
Итак, x — y — 1…. (Ii)
Или, x = 0…. (Iii)
А — y = 1…. (Iv)
Из (iii) и (iv) имеем,
Или, x = 0, y = — 1.
Эти значения x = 0, y = 1 также удовлетворяют,
x — y = 1, т.е. 0 — 1 = — 1, т.е. — 1 = — 1.
Поскольку, y = — 1 ≠ 0, значит, данные векторы линейно зависимы.
г. $ 2 {\ rm {\ vec i}} $ +3 $ {\ rm {\ vec j}} $$ + {\ rm {\:}} 4 {\ rm {\ vec k}} $ и $ {\ rm {\ vec i}} $ — $ {\ rm {\ vec j}} $ + $ {\ rm {\:}} 2 {\ rm {\ vec k}}
долларовСолн:
Пусть $ {\ rm {\ vec a}} $ = $ 2 {\ rm {\ vec i}} $ +3 $ {\ rm {\ vec j}} $$ + {\ rm {\:}} 4 { \ rm {\ vec k}} $ = (2,3,4), $ {\ rm {\ vec b}} $ = $ {\ rm {\ vec i}} $ — $ {\ rm {\ vec j }} $ + $ {\ rm {\:}} 2 {\ rm {\ vec k}} $ = (1, -1,2)
И $ {\ rm {\ vec c}} $ = 5 $ {\ rm {\ vec i}} $ + 6 $ {\ rm {\ vec j}} $ + $ {\ rm {\:}} 8 {\ rm {\ vec k}} $ = (5,6.8)
Пусть $ {\ rm {\ vec a}} $ = x. $ {\ Rm {\: \ vec b}} $ + y. $ {\ Rm {\: \ vec c}} $… .. (i ).
Или, (2,3,4) = x (1, -1,2) + y (5,6,8)
Итак, (2,3,4) = (x + 5y, — x + 6y, 2x + 8y).
Итак, x + 5y = 2… (ii)
Или, — x + 6y = 3…. (Iii)
Или, 2x + 8y = 4…. (Iv).
Решая (ii) и (iii), имеем y = $ \ frac {5} {{11}} $ и x = $ — \ frac {3} {{11}} $.
Эти значения x и y не удовлетворяют (iv),
Т.е. 2. $ \ left ({- \ frac {3} {{11}}} \ right) + 8 \ left ({\ frac {5} {{11}}} \ right) $ = 4.
то есть $ \ frac {{- 5 + 40}} {{11}} $ à 4 à 34 = 44, что неверно,
Следовательно, x и y не удовлетворяют (i), поэтому данные векторы независимы.
Прямые, лучи и углы — бесплатный урок геометрии с упражнениями
На этом уроке геометрии для четвертого класса изучаются определения линии, луча, угла, острого угла, прямого угла и тупого угла. Мы также изучаем, как размер угла определяется ТОЛЬКО тем, насколько он «раскрылся» по сравнению со всем кругом.Урок содержит множество разнообразных упражнений для студентов.
| ||||||||||
Строка не имеет начальной или конечной точки. Представьте, что это продолжается
бесконечно в обоих направлениях. Мы можем назвать линию, используя две точки на ней.Это строка EF или строка
(обратите внимание на стрелки). | ||||||||||
| ||||||||||
Что такое
угол? Много людей
думаю, что угол — это какая-то наклонная линия Это
точка называется вершиной , а два луча называются стороны Чтобы назвать
угол, мы используем три точки, перечисляя вершину посередине. |
1. Напишите, является ли каждая фигура линией, лучом, отрезком или угол, и назовите его.
Решения NCERT для класса 12 по математике Глава 11 в формате PDF на 2020-2021 годы.
Решения NCERT для класса 12 по математике Глава 11
| Класс: | 12 |
| Тема: | Математика |
| Глава 11: | 11 Решения



 Разложите вектор по векторам , и .
Разложите вектор по векторам , и .