Контрольная 6 класс по дробям: Математика 6 Виленкин Контрольная 2 + ОТВЕТЫ

Математика 6 Виленкин Контрольная 2 + ОТВЕТЫ

Контрольная работа по математике 6 класс Виленкин с ответами «Основное свойство дроби. Сокращение дробей» (4 варианта). Цитаты из пособия «Дидактические материалы по математике 6 класс к учебнику Н.Я. Виленкина и др. «Математика 6 класс» ФГОС (к новому учебнику) / М.А. Попов — М.: Издательство «Экзамен», 2017» использованы в учебных целях. Математика 6 Виленкин Контрольная 2. Проверочные работы ориентированы на школьный учебник Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд «Математика 6 класс». Ответы на контрольные работы адресованы родителям, которые смогут проконтролировать правильность выполнения задания.

Математика 6 класс (Виленкин)

Контрольная работа № 2

Основное свойство дроби. Сокращение дробей. Приведение дробей к общему знаменателю. Сравнение, сложение и вычитание дробей с разными знаменателями. Сложение и вычитание смешанных чисел

КР-01. Вариант 1 (транскрипт)

1. Сократите дроби: 2/4; 5/15; 6/10 8n/14n.

2. Приведите к наименьшему общему знаменателю дроби: 2/7 и 5/8.
3. Сравните дроби: а) 5/7 и 2/3; б) 3/11 и 2/9.
4. Найдите значение выражения:
5. Решите уравнение:
6. Сколькими способами могут разместиться 3 пассажира в 6-местной лодке?

КР-01. Вариант 2 (транскрипт)

1. Сократите дроби: 3/6; 4/12; 5/20; 6n/18n.
2. Приведите к наименьшему общему знаменателю дроби: 4/9 и 5/12.
3. Сравните дроби: а) 2/11 и 3/14; б) 1/15 и 2/29.
4. Найдите значение выражения:
5. Решите уравнение:
6. Сколькими способами могут разместиться 4 пассажира в 6-местной лодке?

 

ОТВЕТЫ на контрольную работу

 

---

Вы смотрели: Контрольная работа по математике 6 класс Виленкин (2 варианта) «Основное свойство дроби. Сокращение дробей» с ответами (4 варианта).

 Цитаты из пособия «Дидактические материалы по математике 6 класс к учебнику Н.Я. Виленкина и др. «Математика 6 класс» (к новому учебнику) / М.А. Попов — М.: Издательство «Экзамен», 2017» использованы в учебных целях. Математика 6 Виленкин Контрольная 2. Проверочные работы ориентированы на школьный учебник Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд «Математика 6 класс».

Вернуться к Списку контрольных работ по математике в 6 классе по УМК Виленкин и др.

 

Контрольная работа 6 класс все действия с дробями

Фамилия и имя_____________________________________________________

I вариант

  В заданиях 1 – 7 вычислите и запишите ответы

        1. Представить неправильные дроби в виде смешанных чисел:

а) 29 б) 17 в) 40

6 8 7

2.Записать смешанные числа в виде неправильной дроби:

а) б) в)

3.Сократить дробь:

а) 9 б) 30 в) 5

12 42 90

4. Выполнить сложение дробей:

а) + б) + в) +

5. Найти разность дробей:

а) — б) — в) —

6. Выполнить умножение:

а) ∙ б) ∙ в) ∙

7. Найти частное от деления:

а) : б) : в) :

Выполняя задания 8, 9 и 10, запишите полное решение и ответ. 

 8. Решите задачу.
В первый день тракторист вспахал ²⁄₅ поля, размеры которого составляют 45 га. Во второй день он вспахал ещё ³⁄₅ поля. Сколько га он вспахал в первый и во второй дни? 
9. Решите задачу.

 Два велосипедиста выехали из одного пункта в противоположных направлениях. Скорость одного из них 15 км в час, а скорость другого в  2 раза меньше. Через сколько времени расстояние между ними будет равно 4 км?

 

Фамилия и имя_____________________________________________________

II вариант

  В заданиях 1 – 7 вычислите и запишите ответы

1. Представить неправильные дроби в виде смешанных чисел:

а) б) в)

2.Записать смешанные числа в виде неправильной дроби:

а) б) в)

3. Сократить дробь:

а) б) в)

4. Выполнить сложение дробей:

а) + б) + в) +

5. Найти разность дробей:

а) — б) — в) —

6. Выполнить умножение:

а) ∙ б) ∙ в) ∙

7. Найти частное от деления:

а) : б) : в) :

Выполняя задания 8, 9 и 10, запишите полное решение и ответ. 

8. Решите задачу.
Садовник должен посадить 56 яблонь. В первый день он посадил ³⁄₈ от всех яблонь, а во второй день посадил оставшиеся деревья. Сколько яблонь он посадил в первый и во второй дни?
9. Решите задачу.    
Два велосипедиста выехали навстречу друг другу. Скорость одного из них

18 км в час, а скорость другого в  4 раза меньше. Через сколько времени они встретятся, если расстояние между ними равно 6 км?

 

Контрольная работа по теме «Доли.

Обыкновенные дроби», 6 класс

Вариант 1 Контрольная работа по теме «Доли. Обыкновенные дроби»

1.Купили дыню массой 4 кг 800 г. Пете отрезали часть дыни, Оле — дыни. Чему равна масса каждого отрезанного куска? Сколько граммов дыни осталось?

2.Сколько молока в бидоне, если этого молока составляет 12 л?

3.В куске материи 165 метра. Для детского сада взяли этого куска, а для детских яслей куска. Для кого взяли больше материи – для детского сада или для яслей? На сколько метров?

4.Сравните значения выражений: а) одна пятая от 125 и три восьмых от 80

б) сумма двух пятых от 180 и одной десятой от 100

в) разность трёх одиннадцатых от 22 и двух десятых от 20.

5. На отрезке длиной в 10 см укажите часть, которая составляет две пятых от данного отрезка. Назовите полученный отрезок и укажите его длину.

6.На координатном луче отметьте точки с соответствующими координатами:

. За единичный отрезок примите длину 15 клеток тетради. Назовите полученные точки.

7. Сравните дроби: а) и ; б) ; в) и ; г) .

8. Среди предложенных дробей «шесть десятых», «восемь пятнадцатых», «десять четвёртых», «двадцать сотых», «четырнадцать четвёртых», «тридцать тридцатых», «сто пятых», «шесть восьмых», «десять десятых», «восемь двадцатых»

а) укажите правильные и неправильные дроби; б) запишите их; в) придумайте пять различных заданий с данными дробями.

Вариант 2 Контрольная работа по теме «Доли. Обыкновенные дроби»

1.Купили дыню массой 6 кг 800 г. Пете отрезали часть дыни, Оле — дыни. Чему равна масса каждого отрезанного куска? Сколько граммов дыни осталось?

2.Сколько молока в бидоне, если этого молока составляет 28 л?

3. В куске материи 176 метра. Для детского сада взяли этого куска, а для детских яслей куска. Для кого взяли больше материи – для детского сада или для яслей? На сколько метров?

4.Сравните значения выражений: а) одна пятая от 135 и три восьмых от 160

б) сумма двух пятых от 180 и одной десятой от 100

в) разность трёх одиннадцатых от 22 и двух десятых от 20.

5. На отрезке длиной в 15 см укажите часть, которая составляет две пятых от данного отрезка. Назовите полученный отрезок и укажите его длину.

6.На координатном луче отметьте точки с соответствующими координатами:

. За единичный отрезок примите длину 15 клеток тетради. Назовите полученные точки.

7. Сравните дроби: а) и ; б) ; в) и ; г) .

8. Среди предложенных дробей «шесть десятых», «восемь пятнадцатых», «десять четвёртых», «двадцать сотых», «четырнадцать четвёртых», «тридцать тридцатых», «сто пятых», «шесть восьмых», «десять десятых», «восемь двадцатых»

а) укажите правильные и неправильные дроби; б) запишите их; в) придумайте пять различных заданий с данными дробями.

Контрольная работа по математике Основное свойство дроби 6 класс

Контрольная работа по математике Основное свойство дроби. Сокращение дробей. Приведение дробей к общему знаменателю. Сравнение, сложение и вычитание дробей с разными знаменателями. Сложение и вычитание смешанных чисел 6 класс с ответами. Контрольная работа включает 4 варианта, в каждом по 6 заданий.

Вариант 1

1. Сократите дроби:

2/4; 5/15; 6/10; 8n/14n

2. Приведите к наименьшему общему знаменателю дроби.

2/7 и 5/8

3. Сравните дроби:

а) 5/7 и 2/3
б) 3/11 и 2/9

4. Найдите значение выражения:

(2³/₅ − 1⁷/₁₀) + (1¹/₂ − ⁷/₂₀)

5. Решите уравнение:

х + 2¹/₃ + 3¹/₉ − 1¹/₁₂ = 5⁷/₁₂

6.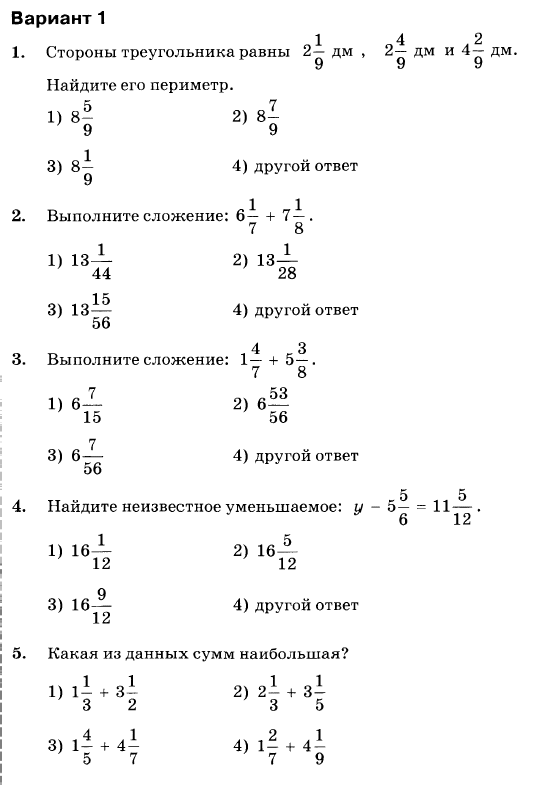 Сколькими способами могут разместиться 3 пассажи­ра в 6-местной лодке?

Вариант 2

1. Сократите дроби:

3/6; 4/12; 5/20; 6n/18n

2. Приведите к наименьшему общему знаменателю дроби.

4/9 и 5/12

3. Сравните дроби:

а) 2/11 и 3/14
б) 1/15 и 2/29

4. Найдите значение выражения:

(3¹/₇ − 2³/₁₄) + (2³/₄₂ − 1¹/₁₇)

5. Решите уравнение:

3¹/₅ + 2²/₅ − х = 3¹/₁₀ − 1¹/₅

6. Сколькими способами могут разместиться 4 пассажи­ра в 6-местной лодке?

Вариант 3

1. Сократите дроби:

14/21; 13/39; 24/36; 17n/51n

2. Приведите к наименьшему общему знаменателю дроби.

3/14 и 5/21

3. Сравните дроби:

а) 3/8 и 2/5
б) 4/13 и 2/7

4. Найдите значение выражения:

(4²/₇ − 3¹/₁₄) + (1¹/₂₈ − ³/₁₄)

5. Решите уравнение:

3²/₅ − х − 1¹/₄ = 1¹/₁₂

6. Сколькими способами могут разместиться 3 пассажи­ра в 5-местной лодке?

Вариант 4

1. Сократите дроби:

3/18; 4/16; 18/54; 13n/52n

2. Приведите к наименьшему общему знаменателю дроби.

5/11 и 1/6

3. Сравните дроби:

а) 3/7 и 1/3
б) 4/19 и 2/11

4. Найдите значение выражения:

(5¹/₈ − 2¹/₄) + (3⁷/₁₆ − ⁹/₈)

5. Решите уравнение:

х + 2⁶/₁₃ − 1¹/₃₉ = 2³/₁₃ + 3²/₁₃

6. Сколькими способами могут разместиться 4 пассажи­ра в 5-местной лодке?

Ответы на контрольную работу по математике Основное свойство дроби. Сокращение дробей. Приведение дробей к общему знаменателю. Сравнение, сложение и вычитание дробей с разными знаменателями. Сложение и вычитание смешанных чисел 6 класс
Вариант 1
1. 1/2; 1/3; 3/5; 4/7
2.
2/7 = 16/56
5/8 = 35/56
3.
а) 5/7 > 2/3
б) 3/11 > 2/9
4. 2¹/₂₀
5. 1²/₉
6. 120
Вариант 2
1. 1/2; 1/3; 2/3; 1/3
2.
4/9 = 16/36
5/12 = 15/36
3.
а) 2/11 < 3/14
б) 1/15 < 2/29
4. 1⁶/₇
5. 3⁷

/₁₀
6. 360
Вариант 3
1. 2/3; 1/3; 2/3; 1/3
2.
3/14 = 9/42
5/21 = 10/42
3.
а) 3/8 < 2/5
б) 4/13 > 2/7
4. 2¹/₂₈
5. 1¹/₁₅
6. 60
Вариант 4
1. 1/6; 1/4; 1/3; 1/4
2.
5/11 = 30/66
1/6 = 11/66
3.
а) 3/7 > 1/3
б) 4/19 > 2/11
4. 5³/₁₆
5. 3³⁷/₃₉
6. 120

Контрольная Работа Десятичные Дроби 6 Класс Бунимович – Telegraph

>>> ПОДРОБНЕЕ ЖМИТЕ ЗДЕСЬ <<<

Контрольная Работа Десятичные Дроби 6 Класс Бунимович
Контрольная работа «Десятичные дроби» 6 класс (по учебнику Е.А. Бунимович)
К/р № 1 Вариант 1 ( «3» — 3- 4 б. «4» — 5- 6 б. « 5» — 7- 8 б. «5» и «5» — 9 б. )
1. Выберите верные утверждения: (1 б.)
1. Е с ли у д в ух д е с ят и ч н ых д ро б е й ц е л ы е ч а ст и од и н а к о в ы , т о и з н и х т а
б о ль ш е , у к о т о р ой ци ф р п о сл е з а п я т о й бо л ь ш е .
можно представить в виде десятичной.
3. У дроби 46, 2071 в разряде тысячных стоит цифра 7.
2. Запишите в виде десятичной дроби число: а)
3. Представьте в виде десятичной дроби число: а) 
4. Выразите: а) массу, равну ю 640 г, в ки лограммах
б) расстояние, равное 1 км 80 м, в километрах. (1б.)
5. Сравните: а)    и    ; б)    и   (1 б.)
6. Найдите значение выражения : 2 – (
  ). (2б.)
7. Сократите дробь и представьте её в виде десятичной а) 
К/р № 1 Вариант 2 ( «3» — 3- 4 б. «4» — 5- 6 б. «5» — 7- 8 б. «5» и «5» — 9 б.)
1. Выберите верные утверждения: (1б. )
1. Е с ли в д е ся т и ч н о й д р о б и в ы ч е р кн ут ь н ул ь , с т о я щи й п о с л е з а п ят о й , т о
по луч и т с я д р о бь , р ав н а я и сх о д н о й
можно представить в виде десятичной.
3. У дроби 23, 80309 в разряде сотых стоит цифра 0.
2. Запишите в виде десятичной дроби число: а)
3. Представьте в виде десятичной дроби число: а) 
4. Выразите: а) расстояние, равное 280 м , в километрах;
б) массу, равну ю 3 кг 70 г, в ки лограммах; (1б.)
5. Сравните: а)    и    ; б)    и   (1б.)
6. Найдите значение выражения: 2 – (  
) (2б.)
7. Сократите дробь и представьте её в виде десятичной а)
Математика — еще материалы к урокам:
Copyright © 2013-2020 «Учителя. com» | Обратная связь: [email protected]

Контрольная работа » Десятичные дроби » 6 класс (по учебнику…)
Проверочная работа «Все действия с десятичными дробями …»
Контрольная работа по теме: «Действия с десятичными …»
Контрольная работа по теме: Десятичные дроби 6 класс
Контрольные работы по математике для 6 класса по учебнику…
Как Начать Сочинение Про Капитанскую Дочку
Направления Добро И Зло Сочинение
Сочинение Про Учителя Кратко
Сочинение На Тему Корабельная Роща Шишкина
Темы Рефератов По Метрологии И Стандартизации

Математика 6 класс Виленкин К-02

Контрольная работа по математике в 6 классе с ответами «Основное свойство дроби. Сокращение дробей» по УМК Виленкин и др. (4 варианта). Цитаты из пособия «Дидактические материалы по математике 6 класс к учебнику Н.Я. Виленкина и др. «Математика 6 класс» ФГОС / М.А. Попов — М.: Издательство Экзамен» использованы в учебных целях. Проверочные работы ориентированы на школьный учебник Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. Математика 6 класс Виленкин К-02. Ответы на контрольные работы адресованы родителям, которые смогут проконтролировать правильность выполнения задания.

 

Математика 6 класс (УМК Виленкин)

Контрольная работа № 2 (4 варианта)

Тема контрольной: Основное свойство дроби. Сокращение дробей. Приведение дробей к общему знаменателю. Сравнение, сложение и вычитание дробей с разными знаменателями. Сложение и вычитание смешанных чисел.

К-02. Вариант 1

1. Сократите дроби: 2/4; 5/15; 6/10; 8n/14n.
2. Приведите к наименьшему общему знаменателю дроби: 2/7 и 5/8.
3. Сравните дроби: а) 5/7 и 2/3; б) 3/11 и 2/9.
4. Найдите значение выражения: (2 ³/₅ – 1 ⁷/₁₀) + (1 ¹/₂ — 7/20)..
5. Решите уравнение: х + 2 ¹/₃ +3 ¹/₉ — 1 ¹/₁₂ = 5 ⁷/₁₂.
6. Сколькими способами могут разместиться 3 пассажира в 6-местной лодке?

К-02. Вариант 2

1. Сократите дроби: 3/6; 4/12; 5/20; 6n/18n.
2. Приведите к наименьшему общему знаменателю дроби: 4/9 и 5/12.
3. Сравните дроби: а) 2/11 и 3/14; б) 1/15 и 2/29.
4. Найдите значение выражения (3 ¹/₇ – 2 ³/₁₄) + (2 ³/₄₂ – 1 ¹/₇).
5. Решите уравнение: 3 ¹/₅ + 2 ²/₅ —х = 3 ¹/₁₀ — 1 ¹/₅.
6. Сколькими способами могут разместиться 4 пассажира в 6-местной лодке?

К-02. Вариант 3

1. Сократите дроби: 14/21; 13/39; 24/36; 27n/51n.
2. Приведите к наименьшему общему знаменателю дроби 3/14 и 5/21.
3. Сравните дроби: а) 3/8 и 2/5; б) 4/13 и 2/7.
4. Найдите значение выражения: (4 ²/₇ – 3 ¹/₁₄) + (1 ¹/₂₈ – ³/₁₄).
5. Решите уравнение: 3 ²/₅ – х – 1 ¹/₄ = 1 ¹/₁₂.
6. Сколькими способами могут разместиться 3 пассажира в 5-местной лодке?

К-02. Вариант 4

1. Сократите дроби: 3/18; 4/16; 18/54; 13n/52n.
2. Приведите к наименьшему общему знаменателю дроби 5/11 и 1/6.
3. Сравните дроби: а) 3/7 и 1/3; б) 4/19 и 2/11.
4. Найдите значение выражения: (5 ¹/₈ – 2 ¹/₄) + (3 ⁷/₁₆ – ⁹/₈).
5. Решите уравнение: х + 2 ⁶/₁₃ – 1 ¹/₃₉ = 2 ³/₁₃ + 3 ²/₁₃.
6. Сколькими способами могут разместиться 4 пассажира в 5-местной лодке?

 

ОТВЕТЫ на контрольную работу № 2.

 

---

Вы смотрели: Контрольная работа по математике в 6 классе с ответами «Основное свойство дроби. Сокращение дробей. Приведение дробей к общему знаменателю. Сравнение, сложение и вычитание дробей с разными знаменателями. Сложение и вычитание смешанных чисел» (4 варианта). Проверочные работы ориентированы на школьный учебник Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. Математика 6 класс Виленкин К-02. Ответы на контрольные работы адресованы родителям, которые смогут проконтролировать правильность выполнения задания.

Вернуться к Списку контрольных работ по математике в 6 классе (УМК Виленкин и др.)

 

Контрольна з математики 6 класс дроби

Скачать контрольна з математики 6 класс дроби txt

перевірка знань та вмінь учнів з темми «Звичайні дроби», контрольна на два варіанта.. Тест на урок Математика скачати. Математика 6 Виленкин — Жохов. Контрольные работы по математике 6 класс с ответами и решениями (авт. В. И. Жохов, Л. Б. Крайнева).  6 класс. Контрольные работы для учащихся общеобразовательных учреждений / В. И. Жохов, Л. Б. Крайнева. — М.: Мнемозина» использованы на сайте в незначительных объемах, исключительно в учебных и информационных целях (пп.

1 п. 1 ст. ГК РФ). Ответы адресованы родителям. При постоянном использовании контрольных работ по математике в 6 классе рекомендуем купить книгу: Математика. 6 класс. контрольной работе по математике по теме: «Дробные выражения. Нахождение числа по его дроби и дроби от числа».

для учащихся 6 классов. Контрольная работа предусматривает проверку знаний учеников по темам: сложение и вычитание, умножение и деление десятичных, обыкновенных. дробей и смешанных чисел, применение основного свойства дроби, решение. задач на нахождение дроби от числа и числа по его дроби, решение уравнений. Фактически контрольную работу можно использовать, как итоговую работу по.

изучению дробей или итоговую работу за первое полугодие 6 класса. (Преподавание предмета велась по учебни. ГДЗ: готовые решения по математике за 6 класс Дудницын, Кронгауз Задание: Вариант 3, онлайн ответы на Еуроки.   На данной странице представлено детальное решение задания Вариант 3 по математике для учеников 6 классa контрольные работы автор(ы) Дудницын, Кронгауз.

Add. «Предыдущий Следующий». Похожие решебники по математике 6 класс. Новыe решебники. © Copyright. Все права защищены.

Содержание: сокращение дробей; приведение дроби к данному знаменателю; приведение дробей к наименьшему общему знаменателю; сравнение, сложение и вычитание дробей с разными знаменателями. I ПОЛУГОДИЕ | Просмотров: | Загрузок: 0 | Добавил: admin | Дата: КОНТРОЛЬНАЯ РАБОТА №4.  Содержание: решение задач на нахождение числа по его дроби или процентам; дробные выражения и вычисление их значений.

I ПОЛУГОДИЕ | Просмотров: | Загрузок: 0 | Добавил: admin | Дата: КОНТРОЛЬНАЯ РАБОТА №8.

Математика — еще материалы к урокам: Контрольная работа «Алгебраическая сумма и ее свойства» 6 класс. Контрольная работа «Умножение и деление обыкновенных дробей, смешанных чисел» 5 класс.

Контрольная работа «Умножение и деление на натуральное число» 5 класс. Самостоятельная работа «Умножение и деление многозначных чисел без перехода через разряд» 5 класс. Тест «Сложение и вычитание натуральных чисел» 5 класс. Тест «Обыкновенные дроби» 5 класс. Предметы. Алгебра. Ещё документы из категории математика: Контрольная работа «Деление дробей» 6 класс (Виленкина). Контрольная работа «Умножение дробей» 6 класс (Виленкина). Контрольная работа «Сложение и вычитание смешанных чисел» 6 класс (Виленкина).

Контрольная работа «Сравнение, сложение и вычитание дробей» 6 класс (Виленкина). Контрольная работа «Разложение на множители» 6 класс (Виленкина). Урок математики 6 класс «Координатная плоскость». Внеклассное мероприятие Физика+Математика 7 класс «Математический поезд». X Код для использования на сайте. Сравнение, сложение и вычитание дробей с разными знаменателями. Сложение и вычитание смешанных чисел 6 класс с ответами.

Контрольная работа включает 4 варианта, в каждом по 6 заданий. Вариант 1. 1. Сократите дроби: 2/4; 5/15; 6/10; 8n/14n. 2. Приведите к наименьшему общему знаменателю дроби. 2/7 и 5/8.  Ответы на контрольную работу по математике Основное свойство дроби. Сокращение дробей. Приведение дробей к общему знаменателю.

Сравнение, сложение и вычитание дробей с разными знаменателями. Сложение и вычитание смешанных чисел 6 класс Вариант 1 1. 1/2; 1/3; 3/5; 4/7 2. 2/7 = 16/56 5/8 = 35/56 3. а) 5/7 > 2/3 б) 3/11 > 2/9 4. 21/20 5. 12/9 6. Вариант 2 1. 1/2; 1/3; 2/3; 1/3 2. 4/9 = 16/

rtf, doc, EPUB, PDF

Похожее:

Підручник українська мова 4 клас нова програма мовчун

План конспект уроку з англійської мови 6 клас подорожі

Презентація на тему михайло врубель

Контрольна робота математика 2 клас іі семестр

Гдз позакласне читання 4 клас бикова відповіді

Гдз збірник мерзляк 6 клас 2014 р

5 способов упростить обучение дробям

Каждый год примерно в это время я слышу один и тот же хор в коридорах: «Мои дети просто не понимают! Учить дроби так сложно! » Хотя дроби традиционно преподают в начальной и средней школе, я даже слышал от некоторых учителей старших классов, которые говорили, что их ученики с трудом понимают их.

На самом деле, ведущие математики, такие как доктор Том Дик, один из авторов программы Texas Instruments Building Concepts, сказали, что твердое понимание дробей является одной из основ, на которой строится успех в математике в средней школе.

Обучение дробям является неотъемлемой частью учебной программы по математике. Но почему детям так сложно понять дроби? Есть три важные вещи, которые чаще всего сбивают с толку детей.

1. Мы часто просим детей выполнить серию шагов, не понимая причин, по которым они выполняются. Иногда, когда они моложе, учащиеся даже не готовы к пониманию понятий.
2. У детей часто возникают неправильные представления обо всех сложных вопросах математики, включая дроби.Когда мы можем помочь детям противостоять этим заблуждениям, учиться легче.
3. Дети борются с дробями по той же причине, по которой дети борются с множеством новых концепций: им просто нужна практика.

Мы можем помочь детям преодолеть эти препятствия. Вот пять идей обучения дробям, чтобы добиться цели.

1. Возьмите в руки

Концепция «дроби» абстрактна, и визуализация части по сравнению с целым — это развивающий навык, который не полностью у некоторых детей до средней или старшей школы.Манипуляторы могут помочь концепциям стать более конкретными. Я люблю строить наборы дробей с моими детьми в начале каждой единицы дроби, которую я преподаю.

Совместная сборка набора дает детям визуальную концепцию, на которой они могут развить остальные свои знания, и мы используем наборы во всем нашем блоке фракций. Я буду прикреплять свой набор фракций к доске во всем отделении и обращаться к нему, когда нам нужно вместе решить проблему.

Мне нравится собирать комплекты со своими учениками, когда они моложе, но мои коллеги со старшими учениками часто держат под рукой несколько заранее приобретенных комплектов, чтобы дети могли обратиться к ним.

Бонус: Этот манипулятор с лапшой для бассейна, предназначенный для обучения дробям, дешево и весело.

2. Используйте визуальные эффекты

В любое время, когда я могу предоставить изображение, соответствующее концепции, которую я преподаю, я знаю, что буду в лучшей форме. Один из способов, которым я делаю это при обучении дробям, — это просить студентов создать наглядное пособие на бумаге. Это упражнение от Texas Instruments учит студентов, как они могут более наглядно представлять дроби.

Используя сеточную систему, учитель использует проектор или интерактивную доску, чтобы представить урок, в котором дроби (а также вычисления на основе дробей для более продвинутых учеников) представлены в виде фигур.После того, как дети увидят визуальное представление на экране, они могут сделать свои собственные изображения дробей на бесплатных печатных формах, которые прилагаются к заданиям.

3. Получите игры

Игры служат более чем одной цели. Во-первых, они делают то, что может быть сухой и скучной темой для ваших учеников, более увлекательной и интересной. Они также часто предоставляют тот визуальный компонент, который особенно полезен для некоторых студентов. Вот пара моих любимых:

Игра с отсутствующим числителем: В этой игре ученику необходимо определить недостающий числитель, чтобы определить, на сколько делений нужно продвинуться вперед.Иногда детям просто нужна практика, чтобы овладеть определенным навыком. Подобные игры могут сделать необходимую тренировку немного менее болезненной.

Domino Fraction Games: на сайте Upper Elementary Snapshots есть две забавные игры. Оба они включают в себя рисование домино, но с использованием двух противоположных сторон домино как дробей. Возможности здесь безграничны: сравнивайте дроби, складывайте дроби, сопоставляйте дроби. Выберите свой любимый и погрузитесь в мир вместе с детьми.

4.Обратитесь к Tech

Еще одна стратегия, которую я люблю использовать, чтобы помочь детям развить беглость с их навыками дроби, — это позволить им практиковаться в цифровом формате. Приложения и другие онлайн-ресурсы могут помочь укрепить концепции. Двумя приложениями, которые особенно нравятся моим детям, являются Squeebles Fractions и Fractions. Умные пираты. Но вы можете найти здесь огромный список веб-сайтов и приложений.

Оба приложения представляют дроби визуально и включают забавные игры, которые просят учащихся быть более гибкими в их мышлении о дробях, часто помогая исправить заблуждения, которые могут быть у детей.Например, это упражнение из Squeebles Fractions помогает студентам понять, что для подачи ⅓ торта может потребоваться не один, а два куска.

5. Будьте стратегичны в обучении фракций

Когда вы представляете новую концепцию, бесплатное исследование с помощью манипуляторов и игр может помочь учащимся подготовиться к обучению. Но я понял, что когда приходит время преподавать особенно сложную концепцию, мне всегда полезно наметить свои цели и задачи.

Пошаговое стратегическое обучение может решить все три более крупные проблемы, перечисленные выше, с которыми учащиеся сталкиваются, когда им сложно усвоить дроби: ограниченное понимание, неправильные представления и недостаток практики. Если вы чувствуете, что ваш учебный план по математике не предлагает достаточно рекомендаций, мне нравятся бесплатные ресурсы, доступные в рамках программы TI Building Concepts, которые обеспечивают структуру, которая помогает студентам разобраться в том, что может быть сложной концепцией.

10 способов освоить дроби для студентов

Обучение дробям очень важно, но их так плохо понимают даже многие взрослые.Если многие взрослые их не понимают, это означает, что наши ученики находятся в худшей форме. Дроби получили плохую репутацию и должны быть запутанными и сложными. Что касается меня, я люблю дроби и, честно говоря, мог бы заниматься ими целый день!

Между нами, учителями, действительно начался разрыв. Я знаю, что это не то, что вы хотели услышать сразу после того, как зашли на мой сайт, но это правда, и если вы продолжите, то поймете, почему. После обширных исследований по этому вопросу для моих модулей математического семинара я обнаружил много передовых методов, которые даже я «ломал», что добавляло учащимся замешательства.

К сожалению, ученики часто применяют целые числа к дробям, и немногие учителя исправляют это (подробнее об этом через минуту). Кроме того, большинство учителей больше рассказывают о процедурах и , а не о фактическом значении дробей или «смысле дроби». Чтобы помочь «исправить» это и устранить эти затруднения, я предлагаю вам лучшие практики или 10 способов, с помощью которых студенты могут овладеть дробями.

10 способов освоить дроби учащимися

1.) Следите за языком, который мы используем в классе. Иногда язык, который мы используем в классе, действительно может сбить с толку учащихся. Например, если мы говорим неправильную дробь (хотя я знаю, что в некоторых округах это требуется), это может сбивать с толку и показаться, что если они так пишут дробь, это неправильно. Вместо этого, возможно, назовите это дробью «больше единицы», что также можно использовать, когда вы используете термин смешанное число. (Я знаю, это кажется безумным, но это правда!) Другой пример — это когда мы используем термин «сокращение дробей.«Для студентов это звучит так, как будто дробь становится меньше, когда на самом деле мы не делаем более мелкие дроби — помните, они эквивалентны более крупным частям. Вы видите, как быстро ученик может начать думать, что 2/5 меньше, чем 4/10, потому что мы сказали, что уменьшили его? Нам не всегда кажется, что это сбивает нас с толку, потому что мы хорошо знаем материал.

2.) Помогите учащимся увидеть, что числитель и знаменатель дроби равны , одно единственное значение, — одно число. Часто учащиеся рассматривают их как два отдельных значения, потому что мы называем их «верхним числом» и «нижним числом». (видите, опять этот язык). Иногда мы также называем это «три из четырех» или «три из четырех». Вместо этого мы должны назвать это числом, три четверти. Если вы хотите подчеркнуть связь с делением, напомните учащимся, чтобы они видели знаменатель как делитель, а числитель как множитель. Это означает, что в 3 раза больше, чем вы получите, если разделите целое на 4 части, или 3 ÷ 4.Кроме того, вы можете помочь студентам понять, что дроби являются числами, постоянно используя числовую линию.

3.) Учащиеся должны понимать, что детали должны быть равными по размеру деталями . Я встречал много студентов за эти годы, которые считают, что 2/3 означают любые 2 части, а не части одинакового размера. В этом примере ниже, если бы вы спросили своих учеников, сколько затенения, они бы ответили 3/4 или 1/2?

Этому недоразумению способствует то, что иногда наши ученики рисуют модели областей.Поскольку учащимся начальной школы не хватает точности, они могут легко создавать неравные разделы и полагать, что части не обязательно должны быть равными. Один из способов борьбы с этим — создание контурных моделей, другой — показать контрпримеры неточно нарисованных моделей. Постоянное напоминание о том, что части должны быть равны, тоже важно.

4.) Нам нужно построить «чувство дроби». Это означает, что мы должны уделять больше внимания значению дробей. Фактически, учителям настоятельно рекомендуется подождать, чтобы научить «алгоритмам» или «процедурам» любых дробей, пока ученики полностью не изучат конкретные методы любых концепций дробей.Например, часто ученики бросаются к методу перекрестного умножения, когда дело доходит до сравнения дробей, умножения эквивалентных дробей или неправильных / смешанных чисел или алгоритма умножения и деления, даже не понимая почему. В своем посте «Преподавание математики, чтобы учащиеся ее усвоили» я объясняю, как студенты лучше всего усваивают математику.

5.) Помогите студентам действительно понять размер дробей. Часто студенты путаются, потому что думают целыми числами.Для целых чисел 5 меньше 10. Для дробей 1/5 на самом деле намного больше 1/10. Это сбивает детей с толку — если они не имеют ОЧЕНЬ много практики, глядя на ТОННУ наглядных материалов. Им нужно практиковаться, пока они не смогут сразу сказать вам, что 1/10 меньше, потому что в ней больше частей. Просто сказать ребенку, что чем больше знаменатель, тем меньше число, не поможет. Это особенно не поможет, когда они дойдут до таких задач, как 7/10 против 1/5. Попросите студентов попрактиковаться в этом и смотреть на это снова и снова, пока они не смогут визуализировать это! Это СООО критично!

6.) Используйте различные модели дробей и соедините эти модели с контекстами реального мира. Повторное использование этих физических инструментов может привести к использованию ментальных моделей и понимания. Иногда полезно выполнить одно и то же упражнение с двумя разными представлениями, чтобы помочь учащимся по-настоящему понять. Эти модели фракций будут:

• Сотовые модели — Обычно разделяют задачи, разрезают на более мелкие части. Это наиболее часто используемый. Примерами могут служить кусочки «пирога», прямоугольные области, геодоска, блоки с узорами, складывание бумаги, рисунки на бумаге с сеткой или точечная бумага.
• Длина или модели измерения — Они показывают непрерывную длину или сравниваются размеры. Это числовые линии или дробные полосы. Линии обычно делятся на части, хотя можно использовать и измерительный инструмент со шкалой (линейка, мерный стаканчик, термометр). Примерами могут служить дробные полоски, стержни Cuisenaire, сложенные бумажные полоски, линейка, числовая линия. ** Число на линии обозначает расстояние от идентифицированной точки до нуля, а не саму точку. **
• Набор моделей — Под целым понимается набор отдельных (дискретных) объектов и подмножеств целого. , составляя дробные части.Примером может быть набор из 12 объектов, а 3 объекта обведены пряжей, то есть 3/12 или 1/4. Может использоваться со счетчиками двух цветов.

7.) Поощряйте использование оценок и контрольных показателей. Оценка помогает учащимся узнать «о» величине определенной дроби, и учащиеся должны иметь возможность использовать ее для сравнения дробей, а затем снова для операций. Поскольку учащиеся обычно менее уверены в оценке, помогите им, используя контрольные показатели на числовой прямой.Я использую контрольные точки (контрольные точки) 0, 1/2 и 1. Если число больше единицы, я все равно использую те же контрольные точки, только с числами, между которыми находится смешанное число. Как и выше, тренируйтесь, пока ученики не смогут это реально визуализировать.

8.) Уделите много времени обучению эквивалентным дробям. Эквивалентные дроби — важная концепция, лежащая в основе всего, что связано с дробями — от операций до отношений и величины. Предоставьте студентам возможность попрактиковаться с эквивалентными дробями в различных моделях.Убедитесь, что они действительно это понимают и понимают, почему дроби равны. Даже не учите методу умножения, пока ученики не покажут вам, почему дроби эквивалентны. Затем предложите им начать замечать закономерность и перейти к методу умножения.

9.) Остерегайтесь использования правил операций, когда целые числа используются с дробями. Я уверен, что все мы видели, как ученики складывали даже дробные части, как если бы они складывали целые числа. Например, 1/2 + 1/2 = 2/4.Они складывают дроби, как если бы они были целыми числами, вместо того, чтобы думать о значении дробей. Это показывает, что они не понимают дробь и не визуализируют дробь. Мы можем предотвратить это, предоставив много практики дробным частям, чтобы они могли начать визуализировать это — даже если это всего лишь единичные дроби.

1 0.) Вводите дроби как можно чаще. Например, если у вас есть минутка во время урока, просто быстро спросите: «Какая часть класса сегодня носит свитера?» Проявите творческий подход.Поиск способов привнести дроби в свой распорядок дня поможет дать студентам регулярную ежедневную практику, сохранить ее в памяти и поможет им увидеть ее актуальность.

С помощью этих 10 передовых методов вы обязательно поможете своим ученикам освоить дроби — сложная концепция в классах элементарной математики во всем мире!

Хотите получать потрясающие подарки, участвовать в потрясающих рекламных акциях и получать доступ к советам по обучению, которые будут и дальше помогать вашим ученикам преуспевать? Присоединяйтесь к моему списку рассылки! Просто щелкните здесь!

Разделение фракций с помощью полосок фракций | Разобрался

Для многих студентов деление на дроби может быть непростой задачей.Трудно представить себе разделение фракции на группы из других фракций. Чтобы разделить дроби, многие студенты запоминают алгоритм «сохранить-изменить-перевернуть», не зная, почему он работает.

Без концептуального понимания деления дробей ученики, как правило, застревают, когда сталкиваются с проблемами (особенно с задачами со словами), когда им приходится делить на дроби, не являющиеся единицами, например 2/3 или 3/4, или задачи, в которых делитель равен больше, чем дивиденд.

К шестому классу, когда ученикам нужно разделить смешанные числа, они часто сильно полагаются на многоступенчатый метод «сохранить-изменить-перевернуть», который трудно запомнить и понять.

Вы можете помочь своим ученикам понять, как делить дроби, используя полоски дробей, которые они могут перемещать. Манипулятивные средства и визуальные представления — это основанные на фактах стратегии, поддерживающие изучение новых математических концепций. Полоски с дробями могут помочь учащимся не только понять концепцию деления дробей, но и буквально увидеть, как решить эти задачи, не выполняя никаких вычислений.

Прокрутите вниз, чтобы получить советы по адаптации этой стратегии для дистанционного обучения.

Поделиться Полосы фракции

• Facebook
• Твиттер
• Pinterest
• Электронное письмо
• Копировать ссылку
• Текстовое сообщение
• Скоро в Google Классе

Задача: Учащиеся будут использовать полосы с дробями, чтобы показать и решить деление двух дробей.

Уровни оценок (со стандартами):

• 5 (Common Core 5.NF.B.7: Применяйте и расширяйте предыдущие представления о делении для деления дробей на целые числа и целых чисел на дроби)

• 5 (Common Core 5.NF.B.7.B: Интерпретировать деление целого числа на единичную дробь и вычислить такие частные)

• 6 (Common Core 6.NS.A.1: Интерпретация и вычисление частных дробей, а также решение словесных задач, включающих деление дробей на дроби, например, с использованием визуальных моделей дробей и уравнений для представления проблемы)

• 5–6 (Common Core Math Practice MP1: разбираться в проблемах и упорно их решать; Common Core Math Practice MP5: стратегически использовать соответствующие инструменты)

Лучше всего использовать для обучения с:

• Весь класс

• Небольшие группы

• Физические лица

Собирайте и исследуйте материалы. Раздайте каждому ученику или паре учеников набор полосок с дробями. Попросите учащихся разрезать каждую полоску на единичные дроби (с числителем 1). Для учащихся, которые борются с мелкой моторикой, подумайте о том, чтобы уже вырезать несколько наборов. Вы также можете сделать несколько наборов из ламината или карточек для студентов.

После разрезания каждой полоски на части, попросите учащихся собрать каждую из полос, чтобы у них был полный набор, соответствующий тому, что указано в печатной форме. Раздайте учащимся копию печатной формы или спроецируйте изображение печатной формы, чтобы у них была визуальная модель, на которую можно ссылаться.

Когда учащиеся разложат все полоски, заново представьте себе концепцию целого. Напомните учащимся, что визуальное представление 1 и слова «целое» часто взаимозаменяемо, когда мы говорим о дробях. Скажите: «В верхней части нашего набора у нас есть 1 целая деталь». Затем спросите учащихся, что они замечают в полосках под всей фигурой. Смоделируйте пример. Вы могли бы сказать: «Я заметил, что каждый ряд полосок фракций одинакового размера». Предложите учащимся поделиться с партнером тем, что они замечают.Затем попросите нескольких студентов поделиться со всем классом. Напомните учащимся о предыдущих уроках, на которых они работали над делением целых чисел на дроби.

1. Проверьте деление целого числа на дробь. Попросите учащихся положить 1 полоску целиком на парту. Попросите учащихся разместить под этой полосой столько полосок 1/4, сколько необходимо, чтобы они совпадали по размеру с 1 целым. Напишите на доске уравнение 1 ÷ 1/4 = 4 и спросите учащихся, откуда они узнали, что это правда. Студенты должны обратиться к полосам перед ними, чтобы объяснить ответ.

Просмотрите все распространенные способы, которыми учащиеся могут объяснить свои ответы, представив следующие примеры как визуально, так и устно:

• «1/4 соответствует 1 целому 4 раза»

• «Есть 4 группы по 1/4 в 1 целом »

• « 1 разделить на группы по 1/4 равно 4 »

• « 4 умножить на 1/4 равно 1 »

2. Объясните, как использовать дробные полосы для деления дроби на дробь. Используйте модель «Я делаю, мы делаем, вы делаете» (также известную как модель обучения с постепенным выпуском), чтобы направлять учащихся в процессе использования полосок.

Делаю: Объясните и смоделируйте с помощью полосок. Скажите: «Теперь мы можем использовать аналогичную стратегию для решения задач деления с двумя дробями в них. Давайте посмотрим на 1/2 ÷ 1/6. Я начну с размещения полоски 1/2 наверху вот так. Затем я положу под ним столько полосок 1/6, сколько смогу, чтобы они совпадали с полосой 1/2. Мы видим, что требуется одна, две, три полоски 1/6, чтобы соответствовать полоске 1/2. Таким образом, я могу сделать вывод, что 1/2 ÷ 1/6 = 3, или 1/6 трижды умещается в 1/2 ».

Мы делаем: Помогите студентам попробовать это вместе с вами.Скажите: «А теперь давайте попробуем это вместе. Снова начните с 1/2. Я помещу 1/2 вверху. Ты делаешь тоже самое.» Модель размещает полоску 1/2 вверху. «На этот раз разделите 1/2 на 1/8. Давайте разместим столько полосок 1/8, сколько сможем, чтобы они совпадали с полосой 1/2 «. Смоделируйте его, а затем ходите вокруг, чтобы помочь студентам, которым может понадобиться поддержка. Для учащихся, которые могут правильно настроить его, предложите им записать задачу разделения с решением.

Когда все закончат, обсудите ответ всем классом. Напишите предложение с номером деления для учащихся, которые, возможно, не получили правильный ответ.Опишите решение несколькими способами.

Вам нужно: Выберите три задачи деления, используя единичные дроби как для делителя, так и для делимого. Скажите студентам, что они будут делать их самостоятельно. Скажите: «Попробуйте решить несколько следующих задач самостоятельно или со своим партнером. Обязательно напишите предложение о делении с вашим решением, как только вы настроите его с помощью полосок дробей ». При необходимости дайте рекомендации. При регистрации попросите учащихся объяснить свои решения, используя язык, обсуждаемый в начале урока, например: «____ группы ____ вписываются в ____.”

Совет для учителей: Многим учащимся, в том числе изучающим английский язык (ELL) и учащимся, испытывающим трудности с выразительной речью, полезно иметь рамки предложений на своих партах. Распечатайте набор рамок и положите их в карманы для сухого стирания, чтобы учащиеся могли каждый раз записывать свои ответы.

3. Переходите к решению более сложных задач. Снова следуйте модели «Я делаю, мы делаем, ты делаешь».

Да: Скажем, «Давайте попробуем несколько более сложных задач.На этот раз начните с 2/3 ». Модель для них. Учащимся следует положить две полоски 1/3 на верхнюю часть стола. «Я хочу, чтобы ты разделил 2/3 на 1/6». Продемонстрируйте, как выровнять 1/6 полоски ниже 2/3, пока вы не совместите все. Подсчитайте количество полосок, которые вы использовали, вслух, показывая на них. «Итак, 2/3 ÷ 1/6 = 4.»

Мы делаем: «А теперь давайте вместе займемся этим следующим. Давайте попробуем 3/4 ÷ 1/8. Я собираюсь показать 3/4 вверху, используя три полоски 1/4. Ты делаешь тоже самое.» Модель размещает 3/4 вверху.«На этот раз разделите 3/4 на 1/8. Давайте разместим столько полосок 1/8, сколько сможем, чтобы они совпадали с полосой 3/4 «. Смоделируйте его, а затем ходите вокруг, чтобы помочь студентам, которым может понадобиться поддержка. Для учащихся, которые могут правильно настроить его, предложите им записать задачу разделения с решением.

Когда все закончат, обсудите ответ всем классом. Напишите предложение с номером деления для учащихся, которые, возможно, не получили правильный ответ. Опишите решение несколькими способами.

Вы делаете: Предложите учащимся несколько практических задач, которые они могут попробовать самостоятельно.Проверьте, как учащиеся используют дробные полоски. Некоторые ученики к этому моменту могли понять, как решать задачи без использования полосок. Поговорите с этими студентами о том, какую процедуру они используют. Если вы чувствуете, что к концу урока класс готов, попросите этих учеников продемонстрировать алгоритм «сохранить-изменить-перевернуть». Это поможет начать переход к использованию алгоритма над полосами дробей.

4. Продолжайте практиковаться. Некоторые ученики могут начать решать без полосок с дробями.Другие будут продолжать их использовать. По мере того, как все тренируются, предложите ученикам, которые используют полоски, вместо этого нарисовать модели для каждой задачи деления. Они могут ссылаться на полосы как на образец, но рисование их собственных версий полосок поможет перейти от бетон полос к конспекту номеров .

Полоски с дробями (или столбцы с дробями, или плитки) помогают учащимся увидеть, что одно и то же «целое» можно разбить на разные части равного размера. Когда ученики перемещают полоски и кладут их рядом, они могут визуализировать дробные количества.Они также могут сравнивать дроби и выполнять сложение, вычитание, умножение и деление на дроби.

Учащиеся, испытывающие трудности с математикой, особенно с дробями, часто не могут связать значение с числами и символами в алгоритме. Полоски с дробями дают студентам концептуальное представление о проблеме. Они могут использовать полосы для создания и делимого, и делителя, чтобы они могли видеть и то, и другое как дробные части целого. Студенты также могут подсчитать количество групп (частное), образованных путем деления.

С этой стратегией вы используете явное указание в модели «Я делаю, мы делаем, ты делаешь». Показывая студентам, как использовать дробные полоски, а затем позволяя им практиковаться как с учителем, так и со сверстниками, эта стратегия предоставляет множество возможностей для обучения.

Использование этой стратегии перед тем, как перейти к делителям, которые не являются единичными дробями, поможет учащимся лучше понять , почему работает алгоритм , а не только , как он работает.

Когда учащиеся ознакомятся с тем, как использовать дробные полосы, отправьте домой новую страницу с дробными полосами или набор, который уже был вырезан. Семьи могут помочь подкрепить, используя дробные полоски дома, когда ученики работают над своим домашним заданием.

Если вы обнаружите, что домашнее задание сбивает семьи, рассмотрите возможность отправки этот ресурс чтобы помочь родителям и опекунам понять, почему сейчас математику преподают иначе, чем когда они были в школе.

• Сотрудничайте с семьями ваших студентов.Узнайте, какие ресурсы у них есть и что им может понадобиться для поддержки обучения дома.

• Проведите учащихся по этапам синхронного онлайн-класса или запишите видео для асинхронного обучения. Так или иначе, использовать UDL пока вы планируете урок.

• Попросите учащихся распечатать полоски с дробями или нарисовать свои собственные, скопировав их. Если у учащихся нет дома бумаги, они могут использовать инструмент цифровых дробей.

Бесплатные задания по математике

Вы здесь: На главную → Рабочие листы Здесь вы можете создавать распечатываемые математические рабочие листы по множеству тем: все основные операции, часы, деньги, измерения, дроби, десятичные дроби, проценты, пропорции, отношения, разложение на множители, уравнения, выражения, геометрия, квадратные корни и многое другое.Мы также предлагаем страницы со списком рабочих листов по классам (1, 2, 3, 4, 5, 6 и 7). Рабочие листы доступны как в формате PDF, так и в формате HTML. Они также очень настраиваемые : вы можете контролировать количество задач, размер шрифта, интервал, диапазон чисел и так далее. Рабочие листы генерируются случайным образом, поэтому каждый раз вы получаете разные. Все рабочие листы имеют ключ ответа на 2-й странице файла. НОВИНКА! Страница рабочих листов с квадратным корнем была обновлена ​​с большим количеством опций, включая рабочие листы в форматах PDF и html. Разрешение на копирование : вы можете свободно распечатывать и копировать неограниченное количество копий рабочих листов для использования в классе, дома, в учебном центре — в любом месте, где вы, возможно, преподаете. Если вы хотите разместить ссылки или рабочие листы на веб-сайте или в публикации, свяжитесь с нами. Ниже вы можете увидеть примеры разнообразия рабочих листов: По классам ГОТОВЫЕ рабочие листы по различным математическим темам для 4 класса.По-прежнему генерируется случайным образом, но все, что вам нужно сделать, это щелкнуть ссылки. Готовые рабочие листы по различным математическим темам для 5 класса. По-прежнему генерируется случайным образом, но все, что вам нужно сделать, это щелкнуть ссылки. Готовые рабочие листы по различным математическим темам для 6-го класса. По-прежнему генерируется случайным образом, но все, что вам нужно сделать, это щелкнуть ссылки. Готовые рабочие листы по различным математическим темам для 7-го класса.По-прежнему генерируется случайным образом, но все, что вам нужно сделать, это щелкнуть ссылки. Элементарная математика Сложение целых и целых чисел по горизонтали или по столбцам. Может иметь до 6 слагаемых. Отсутствуют проблемы с аддендом, вариант без переноски. Числовые связи — это пары чисел, которые в сумме дают заданное число. Найдите готовые рабочие листы для числовых связей от 8 до 15 и генератор, который вы можете использовать для других чисел.Доступен как в формате html, так и в формате PDF. Таблицы с числами для счета, пропуска, кратного. Выберите список или диаграмму с числами в квадратах. Выберите шаг подсчета и сколько заполняет студент. Основные операции с целыми числами и целыми числами, включая операции со столбцами, деление в столбцы и деление с остатком, проблемы с отсутствующим сложением / множителем. Легко контролировать диапазоны номеров. Для классов 3, 4 и 5.Включает подсчет пропусков, таблицы умножения, недостающие факторы, алгоритм умножения (длинное умножение) и факторинг. Заменить обычные числа на римские или наоборот. Или решите задачи на сложение и вычитание с римскими цифрами. Назовите время по аналоговым часам или начертите стрелки на часах, когда указано цифровое время. Вы можете выбрать размер изображения часов. Доступен как в формате PDF, так и в формате html.На странице есть как генератор, так и готовые рабочие листы для 1-3 классов. Практикуйтесь в преобразовании общепринятых единиц измерения. Доступен как в формате PDF, так и в формате html. На странице есть как генератор, так и готовые рабочие листы для 2-7 классов. Попрактикуйтесь в переводе метрических единиц измерения. Доступен как в формате PDF, так и в формате html. На странице есть как генератор, так и готовые рабочие листы для 2-7 классов. Особый … и образцы страниц из книг Math Mammoth, совершенно бесплатно! Они не созданы по сценариям, но содержат очень разные проблемы по множеству тем. Подсчет объектов, чет / нечет, сложение, вычитание, умножение, деление, валюта, сравнения, значения разряда, последовательности, игры. Деньги (разные валюты) Считайте обычные монеты или банкноты США. Вы можете выбрать, какие монеты / купюры будут использоваться, и сколько монет / купюр будет отображаться максимум. Считайте обычные канадские монеты или банкноты. Вы можете выбрать, какие монеты / купюры будут использоваться, и сколько монет / купюр будет отображаться максимум. Считайте обычные австралийские монеты и / или банкноты. Вы можете выбрать, какие монеты / купюры будут использоваться, и сколько монет / купюр будет отображаться максимум. Подсчитайте обычные южноафриканские монеты и / или банкноты. Вы можете выбрать, какие монеты / купюры будут использоваться, и сколько монет / купюр будет отображаться максимум. Считайте обычные британские монеты и / или банкноты. Вы можете выбрать, какие монеты / купюры будут использоваться, и сколько монет / купюр будет отображаться максимум. Считайте обычные монеты и / или банкноты евро. Вы можете выбрать, какие монеты / купюры будут использоваться, и сколько монет / купюр будет отображаться максимум. Дроби Генератор рабочих листов для сложения, вычитания, умножения и деления дробей и смешанных числа. Упрощение (сокращение) дробей, эквивалентных дробей, преобразование дробей в смешанные числа или наоборот. Вы можете контролировать диапазоны числителя, знаменателя и целой числовой части. Рабочие листы для сложения фракций, разделенные на разделы для классов 4, 5 и 6-7. Доступен как в формате PDF, так и в формате html. Рабочие листы для умножения дробей и смешанных чисел, сгруппированные по разделам для классов 4, 5 и 6-7.Доступен как в формате PDF, так и в формате html. Сравните или упорядочите дроби. Множество вариантов; вы даже можете добавить изображения пирогов, чтобы студенты раскрасили их! Пять различных типов задач, четыре из которых включают визуальные модели (круговые изображения). Доступен как в формате PDF, так и в формате html. На странице есть как генератор, так и готовые рабочие листы для 4-5 классов. Сложите, вычитайте, умножайте или делите дроби с помощью этого удобного калькулятора. Десятичные знаки Теория чисел Рабочие листы для округления целых чисел с различными вариантами. Рабочие листы для записи чисел в развернутой или нормальной форме или записи чисел в экспоненциальном представлении. Рабочие листы для экспонентов с множеством вариантов. Доступен в форматах PDF и html. Опции включают диапазон подкоренных выражений, ограничение подкоренных выражений до точных квадратов, использование целых или десятичных чисел, предоставление ответа в упрощенной форме или в виде десятичной дроби, а также другие операции (сложение, вычитание, умножение, деление и возведение в квадрат), помимо взятия квадрата. корень.Доступен в форматах PDF и html. Рабочие листы для разложения на простые множители. Легкий, средний или сложный уровни. Рабочие листы для определения наибольшего общего множителя и / или наименьшего общего кратного чисел. Соотношение, пропорции и проценты Создавайте рабочие листы пропорций с числовыми задачами или простыми задачами со словами (например, задачи скорости / расстояния или стоимости / количества).Варианты использования только целых чисел или чисел с определенным диапазоном или определенным количеством десятичных цифр. Простые словесные задачи с коэффициентами для 6–8 классов. Рабочие листы для изменения процентов на десятичные числа или десятичных чисел на проценты. Или выберите смешанный лист с обоими типами. Таблицы для определения процента от заданного числа в форматах PDF и html. Вы можете управлять диапазоном процентов и основного числа, а также десятичных цифр, чтобы создавать процентные задачи, которые вы можете решить в уме, или более сложные. Три различных основных типа задач: найти процент от заданного числа, найти фактический процент, когда даны число и часть, или найти базовое число, когда даны процент и часть. Вы можете выбрать формулировку задач и контролировать количество десятичных знаков, диапазон, размер шрифта и многое другое. Геометрия Определите различные типы треугольников.Классифицируйте треугольники по сторонам, углам или по обоим направлениям. Определите семь различных типов четырехугольников (квадрат, прямоугольник, ромб, параллелограмм, трапеция, воздушный змей и разносторонний четырехугольник). Задачи для площади и периметра прямоугольников / квадратов с изображениями, задачи со словами, напишите выражение для площади, используя свойство распределения, неправильные прямоугольные области и многое другое. Вычислить радиус, диаметр, длину окружности или площадь, если указан один из них. Найдите площадь треугольников, параллелограммов, других четырехугольников и многоугольников (пятиугольников / шестиугольников) в координатной сетке. Найдите объем и / или площадь поверхности прямоугольной призмы, в том числе с дробными длинами кромок. Вы также можете создать задачи, где указан объем или площадь поверхности вместе с некоторыми размерами, а затем вам нужно вычислить либо объем, либо площадь поверхности. Учащиеся рисуют точки, сообщают координаты точек, строят фигуры из точек, отражают фигуры по оси x или y или перемещают (переводят) их вверх, вниз, влево или вправо. Предалгебра Рабочие листы для написания простых выражений с переменными, когда выражения заданы словами. Для 6-8 классов, предалгебра и алгебра 1. Рабочие листы для оценки простых выражений с переменными, когда задано значение переменной (ей). Для 6-8 классов, предалгебра и алгебра 1. Для преалгебры и алгебры 1.Вы можете контролировать количество задач, уровень сложности, тип выражений, рабочее пространство и многое другое. Рабочие листы для линейных уравнений. Включает одношаговые, двухшаговые, многоступенчатые уравнения, переменные с обеих сторон и многое другое. Для 6-9 классов, предалгебра и алгебра 1. Для предалгебры и алгебры 1. Постройте линейные уравнения и определите наклон или уравнение прямой. Вы можете контролировать тип проблем, количество проблем, разрешен ли дробный уклон, рабочее пространство и многое другое. Для предалгебры и алгебры 1. Постройте заданное неравенство, запишите неравенство из графика или решите различные типы линейных неравенств с построением набора решений или без него. Задачи со словами, связанные с постоянной (или средней) скоростью, временем и расстоянием. Выберите одну из пяти операций и скобок. Вы можете выбрать используемый диапазон номеров, количество проблем и многое другое. Решайте уравнения, неравенства и системы уравнений, упрощайте или множите выражения и многое другое с помощью этого онлайн-решателя алгебры. Бесплатный онлайн-редактор формул для учителей. Создает изображение, которое вы можете сохранить. Рабочие листы для отработки отрицательных и нулевых показателей, доступные в форматах PDF и html. Список других веб-сайтов, предлагающих бесплатные рабочие листы по алгебре. Другие веб-сайты с математическими листами DadsWorksheets.com — тысячи бесплатных заданий по математике На этом сайте есть более 5000 различных заданий по математике от детского сада до предварительной алгебры и обучения. Math Maze Создайте лабиринт, выполняющий любую из четырех операций. Вы можете выбрать уровень сложности и размер лабиринта. 10 рабочих листов Quickies Интересные рабочие листы по математике … с 10 вопросами на страницу, но на каждой странице есть декорации, которые дети могут потом раскрасить. Доступно несколько бесплатных образцов.

Ретроспективный анализ лечения рака носоглотки с ускоренным фракционированием (6 фракций в неделю) по сравнению с традиционным фракционированием (5 фракций в неделю): отчет о 3-летнем контроле опухоли и токсичности для нормальных тканей

Предпосылки и цель: Оценить терапевтический эффект, достигаемый ускоренным фракционированием для некератинизирующей / недифференцированной карциномы носоглотки (NPC).

Материалы и методы: В период с января 1994 г. по октябрь 1997 г. 325 пациентов получили общую дозу 66 Гр в 33-37 фракциях: 167 (облученных до середины января 1996 г.) с 5 дневными фракциями (CF) и последующие 158 с 6 дневными фракциями (AF). в неделю. Среднее время лечения составляло 46 и 39 дней соответственно. Дополнительная стимуляция парафарингеального расширения была проведена 181 пациенту, а химиотерапия на основе цисплатина — 57 пациентам (24 пациента одновременно с лучевой терапией).

Полученные результаты: В группе ФП частота отсутствия прогрессирования заболевания была значительно выше, чем в группе МВ (74 против 63% через 3 года, P = 0,02 по логарифмическому критерию). Однако разница в выживаемости по конкретному заболеванию (86 против 80%, P = 0,39) и общей выживаемости (81 против 78%, P = 0,9) не достигла статистической значимости. Сильно значимое улучшение показателей локальной безотказности было достигнуто у пациентов с опухолями T3-4 (87 vs.62%, P <0,01). Многофакторный анализ показал, что фракционирование было независимым значимым фактором для общего прогрессирования: отношение рисков = 0,63, 95% доверительный интервал: 0,41–0,98, P = 0,04. Среди 268 пациентов, получавших только лучевую терапию, у тех, кого лечили ФП, частота острой реакции была значительно выше или = 3 (72 против 13%, P <0,01). Однако все пациенты получили запланированную дозу без чрезмерного продления, и не наблюдалось значительного увеличения поздних осложнений (20 vs.15% через 3 года, P = 0,19).

Выводы: Текущий анализ показал, что ускорение до 6 ежедневных фракций в неделю может значительно улучшить показатель отсутствия прогрессирования для NPC без чрезмерной поздней токсичности. Улучшение местного контроля было ограничено опухолями T3-4.

6 занятий для отработки эквивалентных дробей в третьем классе

Эквивалентные дроби очаровывают моих учеников! Наличие двух чисел, фактически представляющих ОДНОВУЮ сумму, отличается от всего, что они испытывали раньше! Обычно десять означает просто десять, а любое другое число означает нечто иное.Эквивалентные фракции могут быть УДИВИТЕЛЬНЫМИ!

Мне нравится позволять моим ученикам исследовать и практиковать эквивалентные дроби! Сегодня я делюсь 6 своими любимыми играми и упражнениями, которые использую, чтобы дать моим ученикам дополнительную практическую практику, пока я встречаюсь со своими небольшими группами.

Отображение эквивалентной фракции

Я люблю визуальные ссылки для студентов, поэтому неудивительно, что это одна из моих любимых. Мне также нравится, что это ничего не стоит и может быть целой группой, общим математическим опытом с эквивалентными дробями.

Все, что вам нужно, это разрезать бумагу на квадраты (бумага для наклеек или принтеров отлично работает, а картон может быть еще лучше для долговечности). В зависимости от группы перед вами решите, как вы хотите назначить, или попросите учащихся выбрать фракции, которые они создадут.

После того, как студенты создали свои наглядные пособия, я прошу их поместить их в числовую линию, которую мы создали вместе. Это можно сделать с помощью прищепок на веревке, прикрепить клейкой лентой к стене, положить на землю или прикрепить к доске объявлений.Что бы у вас ни было, это будет работать.

Учащиеся используют то, что они узнали о сравнении дробей и контрольных дробей, чтобы помочь им ориентироваться в нашей строке чисел дробей и соответствующим образом расставлять дроби. После этого мы помечаем дроби и составляем список в каждом месте числовой строки эквивалентных дробей, которые могут принадлежать этому месту.

Мне лично нравится печатать на стикерах, потому что их так легко перемещать по доске, когда мы создаем наш дисплей. Если вам нужен БЕСПЛАТНЫЙ набор шаблонов для заметок, вы можете скачать их ниже!

Бумажные стикеры со свободной фракцией

Ищете конкретный способ помочь вашим ученикам визуализировать дроби? Просто приклейте, распечатайте и позвольте вашим ученикам раскрасить свои фракции, чтобы создать полезные визуальные эффекты в вашем классе!

Бумажные стикеры со свободной фракцией

Ищете конкретный способ помочь вашим ученикам визуализировать дроби? Просто приклейте, распечатайте и позвольте вашим ученикам раскрасить свои фракции, чтобы создать полезные визуальные эффекты в вашем классе!

Когда мы закончим, у нас будет мощное визуальное отображение эквивалентных дробей, И оно включает их размещение на числовой прямой!

Доли прокатного эквивалента

Я пользуюсь любой возможностью позволить студентам составлять свои собственные эквивалентные дроби.В этом случае мне нравится, что ученики могут использовать одно изображение, чтобы помочь им создать другой!

Все, что вам нужно для этого упражнения, — это набор игральных костей (у меня также есть версия с домино, если вы, как я, любитель домино), цветной карандаш / фломастер и фотокопию упражнения.

Ученики бросают кости, чтобы составить свою дробь. Они используют левый квадрат для создания своей дроби. Затем они используют правый квадрат для создания эквивалентной дроби, добавляя / удаляя раздел.В конце они создают математическое предложение, показывающее их эквивалентность.

Другая версия этого упражнения посвящена этому способу отработки эквивалентных дробей, требующих только игральных костей или домино. Однако это упражнение было сосредоточено на разделении числовой прямой, а не на разделении фигур.

Если ваши ученики освоили формы разбиения, но борются с дробями на числовой прямой, это может быть отличным способом поддержать их!

Визуальные эффекты для видеокарт

БОЛЬШЕ ВИЗУАЛИЗАЦИИ, ПОЖАЛУЙСТА! Я люблю использовать клип-карты по нескольким причинам, но вот две мои лучшие:

1. Прищепки обеспечивают ОТЛИЧНУЮ практику мелкой моторики.
2. Наличие ответов на выбор может действительно помочь учащимся, которые уже раньше понимают концепцию.Это позволяет им рассуждать о трех возможных вариантах, вместо того, чтобы чувствовать себя перегруженными бесконечными возможными ответами.

Это действительно должна быть тройка лучших, потому что я могу быстро просмотреть карточки, чтобы увидеть их уровень понимания, И мы можем исправить любые ошибки на данный момент, не нуждаясь в ластике или вычеркивая вещи. Это может быть большим подспорьем для студентов, которые борются с самооценкой.

Эквивалентная фракция Bump

Если вы здесь какое-то время, то знаете, что мои ученики ЛЮБЯТ Bump! Как LOVEEEEEEEE Удар! Это такая простая и увлекательная игра для студентов, так почему бы не сделать версию Equivalent Fractions Bump, верно?

Для этой версии я использую счетчик, и в зависимости от того, какую дробь они вращают, они могут покрыть соответствующую эквивалентную дробь.Это еще один отличный способ помочь учащимся УВИДЕТЬ эквивалентные дроби, потому что визуальные эффекты встроены в саму игру!

Домино с эквивалентными дробями

Иногда действительно приятно иметь варианты! Домино с эквивалентными дробями хороши тем, что учащиеся могут сами создавать цепочки, работать с партнером или играть в полную игру с небольшой группой.

Я ценю то, что с помощью этого задания вы можете подготовить задание, но затем проверьте пульс своего класса в данный момент и посмотрите, какой вариант будет работать лучше всего в это время.Надо любить универсальность и то, как она поддерживает управление классом.

Логические головоломки Magic Square

Ищете увлекательный способ бросить вызов своим ученикам? Мне не хватает логических головоломок с магическим квадратом, потому что они побуждают студентов ПРИМЕНИТЬ то, что они понимают об эквивалентных дробях, вместо того, чтобы просто отвечать на вопросы на листе.

Обычно у меня есть пачка этих головоломок (разных тем), доступных в центре, чтобы мои ученики могли выбирать из них.Они могут работать над своей головоломкой самостоятельно или с партнером, а затем, когда они будут готовы, они могут начать новую.

Эти головоломки на самом деле доступны на трех разных уровнях и для нескольких концепций дроби, что упрощает различение!

ВСЕ эти действия можно найти в моем мегапакете фракций. Это чуть менее 400 страниц действий с дробями, включая дроби единиц, сравнение дробей, эквивалентные дроби, дроби в числовой строке, а также неправильные и смешанные дроби.Не зря он называется МЕГА-ПАКЕТ! Посмотрите ЗДЕСЬ!

Надеюсь, эти идеи были полезны, и вам и вашим ученикам они понравятся!

Задачи с разделением дробей на дроби 7-й класс pdf

Задачи на дроби со словами могут быть немного сложнее, чем задачи с простыми дробями, потому что они требуют, чтобы дети извлекали дроби из описанной ситуации, понимали, какую операцию использовать, а затем решали задачу о дробях. Тем не менее, при четком понимании дробей, проблемы с дробным словом и проблемы с дробным рассказом могут быть:..

математика раскраски 7 класс 03 | Математика | Pinterest | Math, Math … # 270229

Дробь a / b с a> 1 понимается как сумма дробей 1 / b. Соединяйте и разделяйте части, относящиеся к одному целому. Решайте задачи со словами, включающие сложение и вычитание дробей, относящихся к одному целому и имеющих одинаковые знаменатели. Решайте задачи со словами, связанные с умножением дроби на целое число.

Пример 1. Если для изготовления платья требуется 5/6 ярдов ткани, то сколько ярдов потребуется для изготовления 8 платьев? Анализ: Чтобы решить эту проблему, мы преобразуем целое число в неправильную дробь.Затем мы умножим две дроби. Решение: Ответ: Для изготовления 8 платьев потребуется 6 и 2/3 ярда ткани. Пример 2: у Рене была коробка кексов, из которых она дала

У нас есть бесплатные рабочие листы по математике, подходящие для 7-го класса. Умножение десятичных знаков, деление десятичных знаков, сложение, вычитание, умножение и деление целых чисел, вычисление экспонентов, дробей и смешанных чисел, Решайте задачи алгебры со словом, найдите последовательность и n-й член, наклон и пересечение линии, круги, объем, площадь поверхности, соотношение, процент, статистику, рабочие листы вероятностей, с видео-уроками, примерами и пошаговыми инструкциями…

Эта таблица задач на дробные слова подходит для 5-7 классов.

No related posts.