Алгебра 10 Рурукин Контрольная 1 . Задания и ответы
Контрольная работа № 1 по алгебре в 10 классе «Числовые функции» с ответами. Используется при работе по УМК Мордкович и УМК Колмогоров. Цитаты из пособия «Контрольно-измерительные материалы. Алгебра и начала анализа. 10 класс / А.Н. Рурукин — М.:ВАКО» использованы в учебных целях. Ответы адресованы родителям. Алгебра 10 Рурукин Контрольная 1 + ответы.
Алгебра и начала анализа. 10 класс
Контрольная работа № 1 «Числовые функции»
Алгебра 10 Рурукин Контрольная 1К-1. Вариант 1 (транскрипт)
- Найдите область определения функции f(x) = √(x2 + x – 2) / √(9 – x2).
- Определите область значений функции f(x) = 3 + √(4x – x2) и постройте ее график.
- Постройте график функции у = x2 – 3|х| + 2 и найдите промежутки монотонности.
- Найдите множество значений функции у = x2 – 3|х| +2 на промежутке х ∈ [–1; 2].
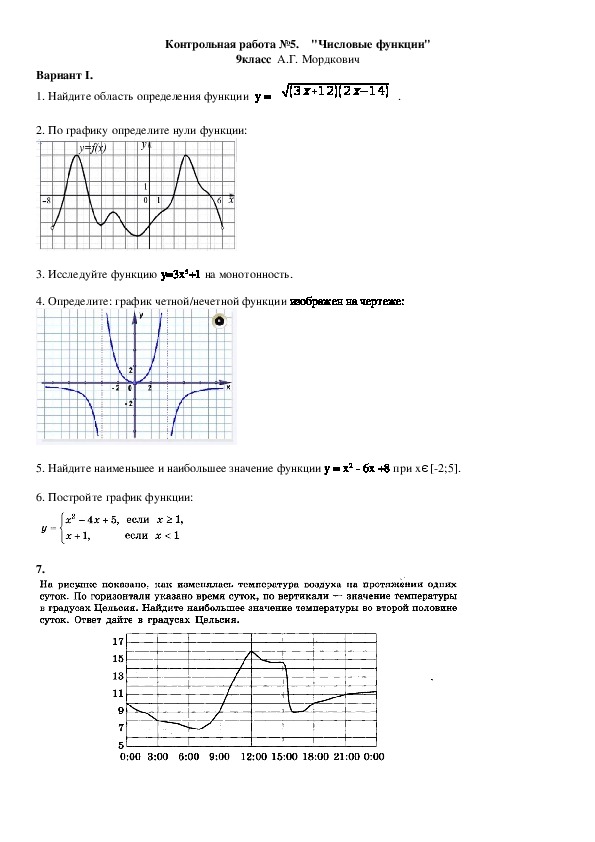
- Постройте график функции у = 2х + |х – 1|.
- Для функции f(х) = 3√(5x + 2) найдите обратную функцию.
К-1. Вариант 2 (транскрипт)
- Найдите область определения функции f(x) = √(16 – x2) / √(x2 – x – 6).
- Определите область значений функции f(x) = 2 – √(6x – x2) и постройте ее график.
- Постройте график функции у = x2 – 4|х| + 3 и найдите промежутки монотонности.
- Найдите множество значений функции у = x2 – 4|x| +3 на промежутке х ∈ [–2; 3].
- Постройте график функции у = 2х – |х + 3|.
- Для функции f(x) = 3√(4х – 7) найдите обратную функцию.
Ответы на контрольную работу
Вернуться к Списку контрольных работ по алгебре в 10 классе (Рурукин)
Вы смотрели: Алгебра и начала анализа. 10 класс. Контрольная работа «Числовые функции» с ответами. Используется при работе по УМК Мордкович и УМК Колмогоров. Цитаты из пособия А.Н. Рурукина использованы в учебных целях. Ответы адресованы родителям.
Цитаты из пособия А.Н. Рурукина использованы в учебных целях. Ответы адресованы родителям.
Алгебра 10 Рурукин Контрольная 1 + ответы.
Контрольная работа по алгебре 10 класс Мордкович числовые функции
- Исследуйте функцию на монотонность и экстремумы.
2. Постройте график функции
3. Найдите наименьшее и наибольшее значения функции
на отрезке .
- В равнобедренный треугольник с длинами сторон 15, 15 и 24 см. вписан параллелограмм так, что угол при основании у них общий. Определите длины сторон параллелограмма так, чтобы его площадь была наибольшей.
___________________________________________________________
5. Докажите, что при справедливо неравенство
.
___________________________________
6. При каких отличных от нуля значениях параметров и все
экстремумы функции положительны и максимум находится в точке ?
Контрольная работа № 9 (1 час)
Вариант 1
- Сколькими способами можно составить трехцветный
полосатый флаг, если имеется материал 5 различных цветов?
- Сколько четырехзначных чисел можно составить из цифр 1,2,3,4
при условии, что каждая цифра может содержаться в записи числа лишь нечетное число раз?
3..bmp) Решите уравнение .
Решите уравнение .
4. Из колоды в 36 карт вытаскивают две карты. Какова вероятность извлечь при этом 2 туза?
_____________________________________________________
- На прямой взяты 8 точек, а на параллельной ей прямой – 5 точек. Сколько существует треугольников, вершинами которых являются данные точки?
6. В разложении бинома коэффициент третьего члена на 44 больше коэффициента второго члена. Найдите член, не зависящий от .
Вариант 6
1. В классе 15 девочек и 17 мальчиков. Для дежурства на избирательном участке надо выделить трех девочек и двух мальчиков. Сколькими способами это можно сделать?
- Сколько четырехзначных чисел можно составить из цифр 1,2,0
при условии, что одна и только одна цифра содержится в записи числа четное число раз?
- Решите систему уравнений
- Из колоды в 36 карт наудачу вынимают 3 карты. Какова вероятность того, что среди них окажется хотя бы один туз?
________________________________________________________
5. На прямой взяты n точек, а на параллельной ей прямой – q точек. Сколько существует треугольников, вершинами которых являются данные точки?
На прямой взяты n точек, а на параллельной ей прямой – q точек. Сколько существует треугольников, вершинами которых являются данные точки?
6. Найдите число рациональных членов разложения , если известно, что сумма третьего от начала и третьего от конца биномиальных коэффициентов разложения равна 9900.
Контрольная работа по теме «Функции, их свойства и графики»
Контрольная работа по теме
«Функции, их свойства и графики»
Л. В.
Брова
В.
Брова
2019
Вариант 1.
1. Найдите область определения функции .
а) 4; ; в) ; 4 U 4; ;
2. Найдите область значений функции yx2 5x9.
а) 212;; в) ;314;
б) ;2
3;
г) 112;.
4
x 2sin x
3. Что можно сказать о функции f (x) 2 : 3cos x x
а) четная; в) ни четная, ни нечетная;
б) нечетная; г) периодическая?
x
4. Найдите «нули» функции f (x) 2
а) 0;8; б) 4;4 ; г) 2 2 ;2 2 .
5. При каких значениях x f (x) <0, если f (x) 3 2x ?
4x 1
3 1 1 2
а) ;
2
;
б) ;
4
U1,5;;
в) (0,25
;1,5) ;
г)
4
; 3 
6. Найдите промежуток (-тки) убывания функции f (x) 96x x2 .
а) 3; ; б) ; ; в) ;3; г) 3;3.
Вариант 2.
1. Найдите область определения функции y 3x .
а) ;12 ; в) 0;12 ;
б) 12; 12; г) 12 ;0 .
2. Найдите область значений функции yx2 3x1.
а) ;1,25 ; в) ; 1,5;
б) 1,5;
;
г)
3,25
;
.
x tgx
3.
Что можно сказать о функции f
(x)
:
x
3sin
а) четная; в) ни четная, ни нечетная;
б) нечетная; г) периодическая?
4. Найдите «нули» функции f (x) x 2 .
3 x
а) 6; б) 2,45 ; в) 0;6; г) 6 ; 6.
5. При каких значениях x f
а)
;2;
б)
2,5;
1
;
в)
2
; 1
;
г) ;2,5U1;.
5 3 5 3 3
6. Найдите промежуток (-тки) убывания функции f(x)
Контрольные работы по алгебре и началам математического анализа 10 класс
Контрольная работа 2. 1 вариант. 2 вариант. 1). Для функции f (х) = 3х 2 х Найти f (0), f (1), f (-3), f (5).
Контрольная работа 1 вариант 1) Для f (х) = х + х 1 Найти f (), f (1), f (-), f (5) 1) Для f (х) = х х + Найти f (), f (1), f (-), f (5) ) Найти D(у), если: у 5х 5 в) у х х 5х 6 г) 7х 1 у х х у х ) Найти
ПодробнееСОДЕРЖАНИЕ Сроки Упражнения для
Тематическое планирование по алгебре и началам анализа (заочное отделение) в 1 классе Учебник: А. Г. Мордкович и др. в двух частях, Мнемозина 1 г Самостоятельные работы. Л.А. Александрова. Алгебра и начала
Г. Мордкович и др. в двух частях, Мнемозина 1 г Самостоятельные работы. Л.А. Александрова. Алгебра и начала
Предлагаются задания в 20 вариантах.
Предлагаем 0 вариантов контрольной работы по математике. Годовая контрольная работа по алгебре и началам математического анализа в 11 классах, для тех, кто обучается по учебнику авторов: Ш.А. Алимов, Ю.М.
ПодробнееМатематика. Алгебра и начала анализа
А.В. Землянко Математика. Алгебра и начала анализа Воронеж СОДЕРЖАНИЕ ТЕМА 1. ОСНОВНЫЕ СВОЙСТВА ФУНКЦИИ… 6 1.1. Числовая функция… 6 1.2. График функции… 9 1.3. Преобразование графиков функции…
ПодробнееЗадание 7 Производная и первообразная
Задание 7 Производная и первообразная Физический смысл производной 1.Материальная точка движется прямолинейно по закону x(t)= 6t 2 48t + 17 (где x расстояние от точки отсчета в метрах, t время в секундах,
ПодробнееАлгебра и начала анализа, ХI
Алгебра и начала анализа, ХI АЛГЕБРА И НАЧАЛА АНАЛИЗА По Положению о государственной (итоговой) аттестации выпускников XI(XII) классов общеобразовательных учреждений Российской Федерации учащиеся сдают
ПодробнееПРОМЕЖУТКИ ВОЗРАСТАНИЯ
1) На рисунке изображён график дифференцируемой функции y = f (x). На оси абсцисс отмечены девять точек:. Среди этих точек найдите все точки, в которых производная функции f (x) отрицательна. В ответе
На оси абсцисс отмечены девять точек:. Среди этих точек найдите все точки, в которых производная функции f (x) отрицательна. В ответе
y и постройте еѐ график.
Вариант 1 1 Найдите производную функции y 1 в точке Найдите f (0), если sin 0 Составьте уравнение касательной к графику функции 1, в точке графика с абсциссой 0 Составьте уравнение касательной к графику
Подробнее4 урока в неделю (136 уроков за год)
Рабочая программа по алгебре 9 класс по учебнику А.Г.Мордковича «Алгебра,9». урока в неделю ( уроков за год) Номер п/п 7 8 9 0 7 8 9 0 Изучаемый материал Повторение курса 8 класса. Неравенства и системы
ПодробнееФункция y = cos x. Ее свойства и график
Функция y = cos x Ее свойства и график 1 Сегодня мы рассмотрим Построение графика функции y = cos x; Свойства функции y = cos x; Изменение графика функции y = cos x в зависимости от изменения функции и
ПодробнееПримерные практические задания:
Банк заданий по теме «ПРОИЗВОДНАЯ» МАТЕМАТИКА 11 класс (база) Учащиеся должны знать/понимать: Понятие производной. Определение производной. Теоремы и правила нахождения производных суммы, разности, произведения
Определение производной. Теоремы и правила нахождения производных суммы, разности, произведения
Набережные Челны 2013 год
Муниципальное бюджетное общеобразовательное учреждение «Открытая (сменная) общеобразовательная школа 65» город Набережные Челны Республика Татарстан МЕТОДИЧЕСКОЕ ПОСОБИЕ по подготовке учащихся вечерней
ПодробнееПояснительная записка по алгебре. 11 класс
Пояснительная записка по алгебре класс Программа по геометрии составлена на основе следующих документов:. Федеральный компонент государственного образовательного стандарта 00г.. Примерная программа основного
ПодробнееПовторение. Тема урока. урока
урока Дата проведения Вид контро ля Тема урока Использование ИКТ Повторение 3 четверть (40 часов) Глава 5. Производная (40 часов). 1 24 Числовые последовательности и их свойства. Прогрессии 2 24 Предел
Производная (40 часов). 1 24 Числовые последовательности и их свойства. Прогрессии 2 24 Предел
Контрольное тестирование по Математике «Функции и графики» 10 класс
Категории
- ЕГЭ
- Авиация, Космонавтика
- Административное право
- Алгебра
- Английский язык
- Арбитражный процесс
- Архитектура
- Астрология
- Астрономия
- Банковское дело
- БЖД
- Биография
- Биология
- Биржевое дело
- Ботаника, сельское хоз-во
- Бухгалтерский учет, аудит
- Валютные отношения
- Ветеринария
- Военная кафедра
- География
- Геодезия
- Геология
- Геометрия
- Геополитика
- Государство и право
- Гражданское право
- Делопроизводство
- Деньги и кредит
- Естествознание
- Журналистика
- Зоология
- Издательское дело
- ИЗО
- Инвестиции
- Информатика
- Исторические личности
- История
- Кибернетика
- Коммуникации, связь
- Косметология
- Краеведение, этнография
- Краткое содержание произведений
- Криминалистика
- Криминология
- Криптология
- Кулинария
- Литература
- Логика
- Логистика
- Маркетинг
- Математика
- Медицина, здоровье
- Международное право
- Международные отношения
- Менеджмент
- Металлургия
- Москвоведение
- Музыка
- Муниципальное право
- Налоги, налогообложение
- Наука, техника
- Начальная школа
- ОБЖ
- Обществознания
- Оккультизм, уфология
- Окружающий мир
- Педагогика
- Политология
- Право, юриспруденция
- Предпринимательство
- Природоведение
- Промышленность, производство
- Психология
- Радиоэлектроника
- Разное
- Реклама
- Религия
- Риторика
- Русский язык
- Социология
- Статистика
- Страхование
- Строительство
- Схемотехника
- Таможенная система
- Теория государства и права
- Теория организации
- Теплотехника
- Технология
- Товароведение
- Транспорт
- Трудовое право
- Туризм
- Уголовное право
- Управление
- Физика
- Физкультура
- Философия
- Финансы
- Фотография
- Химия
- Хозяйственное право
- Художественная культура
- Цифровые устройства
- Экологическое право
- Экология
- Экономика
- Экономико-математическое моделирование
- Экономическая география
- Экономическая теория
- Языкознание, филология
32333412353637383940414424344454647548496505152535455565758959106076162636465666768698707172117374757677781479808131171582162083848519868788308918902191929394959697989922100101102103104105232410610710826109131101112928112113114115
Расширенная численная оптимизация
CMSC764 / AMSC604 — Весна 2017 | Это подробный обзор оптимизации как с вычислительной, так и с теоретической точки зрения. Особое внимание будет уделено масштабируемым методам с приложениями в машинном обучении, подборе моделей и обработке изображений. Для этого курса нет формальных предпосылок, однако студенты должны хорошо разбираться в прикладной математике (особенно линейной алгебре) и компьютерном программировании. Особое внимание будет уделено масштабируемым методам с приложениями в машинном обучении, подборе моделей и обработке изображений. Для этого курса нет формальных предпосылок, однако студенты должны хорошо разбираться в прикладной математике (особенно линейной алгебре) и компьютерном программировании.Теоретические темы будут включать выпуклый анализ, двойственность, скорость сходимости и продвинутые темы по линейной алгебре. Вычислительные темы будут включать методы градиента, методы расщепления, методы внутренней точки, линейное программирование и методы для больших матриц. Домашние задания потребуют как математической работы на бумаге, так и реализации алгоритмов. |
Основы
| Когда: Вт 11:00 — 12:15 | Где: CSI 3120 |
| Инструктор: Том Голдштейн | Часы работы: Чт 13-13, AVW π 3141 |
| TA: Хао Ли | Часы работы: пн 10-12, AVW 4431 |
Заключительный экзамен: Сб, 13 мая в 8:00 (предварительно)
Курсовая работа и выставление оценок
Домашнее задание будет назначаться примерно раз в неделю. Домашние задания будут состоять как из упражнений по программированию, так и из теоретических наборов задач. Задания по программированию будут кумулятивными — вам понадобятся результаты ранних заданий для выполнения заданий, которые даются позже в курсе. Выполненные домашние задания, которые вы сдаете, должны представлять вашу собственную работу.
Домашние задания будут состоять как из упражнений по программированию, так и из теоретических наборов задач. Задания по программированию будут кумулятивными — вам понадобятся результаты ранних заданий для выполнения заданий, которые даются позже в курсе. Выполненные домашние задания, которые вы сдаете, должны представлять вашу собственную работу.
Вы можете выполнять свои задания в Matlab или Python 2.7. Другие языки (включая Python 3+) не будут разрешены. Когда даются задания по программированию, вам необходимо будет подготовить короткий документ в формате pdf, содержащий выходные данные вашего кода, и этот PDF-файл будет сдан вместе с вашим кодом.
Примерная разбивка по курсу будет
- 50% домашнее задание
- 25% промежуточный экзамен
- 25% финальный экзамен.
Примечание. Это квалификационный курс по информатике для получения докторской степени.
Домашнее задание
Домашнее задание будет сдано с использованием вязов / холста. Перейдите по этой ссылке
в Elms, а затем после входа в систему найдите страницу курса.
Я рекомендую сгенерировать ваш PDF-файл с помощью латекса. Взгляните на эти
примеры решений,
и соответствующий источник латекса.
Перейдите по этой ссылке
в Elms, а затем после входа в систему найдите страницу курса.
Я рекомендую сгенерировать ваш PDF-файл с помощью латекса. Взгляните на эти
примеры решений,
и соответствующий источник латекса.
Домашнее задание 1: основы линейной алгебры (срок сдачи 7 февраля)
Домашнее задание 2: задачи тестирования БПФ и оптимизации (срок сдачи 14 февраля)
Домашнее задание 3: градиенты (срок сдачи 22 февраля)
Домашнее задание 4: обратное распространение (срок сдачи 28 февраля)
Домашнее задание 5: числовая линейная алгебра (срок сдачи 8 марта)
Домашнее задание 6: выпуклые функции (до 14 марта)
Домашнее задание 7: градиентные методы (до 14 апреля)
Домашнее задание 8: двойственность (сдано 26 апреля)
Домашнее задание 9: методы прокси (до 3 мая)
Домашнее задание 10: ADMM (до 10 мая)
Слайды лекций
Обзор курса
Обзор линейной алгебры
Задачи оптимизации
ТВ, БПФ и исчисление
Квадратичные формы
Выпуклые функции
Градиентные методы
Квазиньютоновские методы
Двойственность
Проксимальные методы
Лагранжевые методы
Случайные темы | Пример кода MCMC
Книги и другие источники
Все материалы курса доступны бесплатно в Интернете. Предлагаемые материалы для чтения по различным темам включают:
Предлагаемые материалы для чтения по различным темам включают:
Тест численного мышления
Как работать над ответами
1) 83-17 = 56 +?
66 = 56 +?
? = 66 — 56 = 10
2) Продажи какой компании были наиболее стабильными в течение года?
Минимальный диапазон Frying Tonight равен 1 (т.е.грамм. Январь) максимум 3 (например, май): диапазон всего 2.
3) В каком месяце продажи Hole in Roof и Stones ‘Throw больше всего различались?
Продажи Hole in the Roof равны 2 в июль : продажи Stones ‘Throw в этом месяце равны 9: разница в 7, что является наибольшей разницей.
4) В каком месяце было наибольшее количество продаж для всех компаний вместе взятых?
Июнь: 3 + 6 + 6 + 7 + 8 = 30 продаж в Июнь
5) Каков процент увеличения продаж Hot House с июля по август?
Распродажа Hot House в июле = 5. Продажи в августе = 6
Продажи в августе = 6
а) Найдите разницу между двумя числами: 6-5 = 1
б) Возьмите эту разницу (1) и разделите на исходное число: 1/5 = 0,2
в). Наконец, умножьте это на 100: 0,2 x 100 = 20%
6) Как далеко в целом студент проходит?
Один км с 8.00 до 8.10 и еще один км с 8,25 до 8,35 = 2 км всего
7) Как далеко он от союза студентов вуза на 8.20 утра?
Студенческий союз находится в 6 км от дома.
В 8.20 студент находится в 3 км от дома. Следовательно, у него есть 3 км , которые нужно проехать в профсоюз.
8) Какая средняя скорость автобуса?
Студент садится в автобус в 8.15 утра в 1 км от дома.
Студент садится в автобус в 8. 25 в 5 км от дома.
25 в 5 км от дома.
Следовательно, автобус едет 4 км за 10 минут
Автобус проедет в шесть раз больше за час = 6 x 4 км за час = 24 км / ч
9) Какой недостающий номер? 56/7 =? — 5
56/7 = 8
Следовательно, 8 =? — 5
8 = 13 — 5
10) Какой недостающий номер? 20/0.8 =?
20 / 0,8 = 25 (НЕ 16: попробуйте на калькуляторе, если не верите. Деление на дробь всегда дает большее число)
11) Какая дробь является наибольшей: 3/4 7/8 4/5 7/9 7/10
3/4 = 0,75, 7/8 = 0,875 , 4/5 = 0,8, 7/9 = 0,777 …, 7/10 = 0,7
12) Если апельсины стоят 5 фунтов стерлингов за 75 пенсов, сколько вы можете купить за 2,70 фунта стерлингов? (Предполагая, что их можно купить по отдельности)
5 апельсинов стоят 75 пенсов, поэтому один апельсин стоит 75, разделенное на 5 = 15
пенсов. 2 фунта стерлингов.70 то же самое, что 270p.
2 фунта стерлингов.70 то же самое, что 270p.
Следовательно, количество апельсинов вы получите за 270 пенсов
= 270 разделить на стоимость одного апельсина
= 270 разделить на 15
= 18 апельсинов
13) Сарай имеет боковую стенку указанных размеров. Вычислите площадь стены в квадратных футах.
Площадь = площадь квадрата + площадь треугольника вверху
Площадь квадрата = длина x ширина = 6 x 4 = 24 квадратных фута
Площадь треугольника = основание x высота перпендикуляра / 2 = 6 x (6-4) / 2 = 6 квадратных футов
Общая площадь = 24 + 6 = 30 квадратных футов
Или вы можете использовать формулу для площади трапеции.
Площадь = среднее значение длины двух сторон x длина основания
= (6 + 4) / 2 х 6 = 5 х 6 = 30
14) Автомобиль выехал из Кентербери в 7. 12 и прибыл в Бирмингем, находящийся на расстоянии 180 миль, в 10.57. Какова его средняя скорость в милях в час?
12 и прибыл в Бирмингем, находящийся на расстоянии 180 миль, в 10.57. Какова его средняя скорость в милях в час?
Затраченное время = 3 часа 45 минут = 3,75 часа (15/4 часа, если вы предпочитаете дроби).
Скорость = расстояние / затраченное время = 180/3.75 = 48 миль / ч
15) Самолет пролетает 930 миль за 75 минут. Сколько миль он пролетает за 4 часа 45 минут при постоянной скорости?
75 минут = 75/60 часов = 1,25 часа (или 5/4 часа, если вы предпочитаете дроби)
Скорость самолета = 930 / 1,25 = 744 миль / ч
4 часа 45 м = 4,75 часа (или 19/4 часа в долях)
Таким образом, самолет будет летать 744 х 4.75 миль = 3534 миль
16) Вы получаете повышение заработной платы на 4% плюс дополнительные 5 фунтов стерлингов в неделю. Ваша нынешняя заработная плата составляет 250 фунтов стерлингов в неделю. Какой будет ваша новая зарплата?
Какой будет ваша новая зарплата?
Текущая заработная плата = 250
4% от 250 = 4 x 2,5 = 10
фунтов стерлингов
Следовательно, новая заработная плата = 250 + 10 + 5 = 265 фунтов стерлингов
17) Каков общий доход таксиста за год?
Средний тариф = 4 x 90 пенсов = 3 фунта стерлингов.60
Доход в неделю = 70 тарифов по 3,60 £ каждый = 70 x 3,60 = 252 £
Доход за 46 недель работы = 252 £ x 46 = £ 11592
18) Каковы ее общие расходы за год с точностью до фунта?
Автомобиль / Сервис / ТО / Ремонт / Страховка = 1250 £ в год
Расходы по ипотеке = 250 фунтов стерлингов в месяц = 250 x 12 в год = 3000 фунтов стерлингов в год
Прочие расходы = 125 £ в неделю = 125 £ x 52 в год = 6500 £ p. а.
а.
Стоимость дизельного топлива = 6 пенсов за милю.
Годовой пробег = 4 мили x 70 тарифов в неделю = 280 миль в неделю
= 280 x 46 рабочих недель каждый год = 12880 миль
Следовательно, стоимость дизельного топлива = 12880 x 0,06 фунта стерлингов = 772,8 фунта стерлингов
Следовательно, общие расходы = 1250 фунтов стерлингов + 3000 фунтов стерлингов + 6500 фунтов стерлингов + 772,8 фунтов стерлингов = 11522,8 фунтов стерлингов = фунтов стерлингов 11523 фунтов стерлингов с точностью до
19) Каково ее среднее превышение доходов над расходами в месяц до ближайшего фунта?
Доход p.а. = 11 592 £ Расходы в год = 11523 £ (ответы на два предыдущих вопроса)
Следовательно, превышение доходов над расходами = 69 фунтов стерлингов в год. = 69 фунтов стерлингов / 12 фунтов стерлингов в месяц = 5,75 фунтов стерлингов = фунтов стерлингов 6 фунтов стерлингов в месяц от до ближайшего фунта стерлингов
20) Куб имеет объем 8 кубических метров. Если каждую сторону увеличить вдвое, каков будет ее новый объем в кубических метрах?
Если каждую сторону увеличить вдвое, каков будет ее новый объем в кубических метрах?
Объем = длина x ширина x высота
8 = l x w x h, но l, w и h равны, так как это куб
Следовательно, l = w = h = 2m
Если каждая сторона удвоена по длине l = w = h = 4м
Следовательно, новый объем = 4 x 4 x 4 = 64 кубических метра
Или, если вы предпочитаете более быстрый метод.Если каждая сторона удвоена по длине, то новый объем должен быть 2 в степени 3 больше = 8 x 8 = 64
21) Водитель проезжает 8 км к югу, затем 6 км к западу и снова 2 км к югу. Затем она проезжает 3 км в. Д., Чтобы избежать пробки, и затем проезжает 6 км север.
Общее расстояние, пройденное на юг = 8 + 2-6 км = 4 км
Общее расстояние, пройденное на запад = 6 — 3 км = 3 км
Таким образом получается прямоугольный треугольник, где расстояние от начальной точки — гипотенуза.
Использование теоремы Пифагора: «В любом прямоугольном треугольнике площадь квадрата, сторона которого является гипотенузой (равна сумме площадей квадратов двух других сторон»
4 в квадрате + 3 в квадрате = квадрат гипотенузы
16 + 9 = 25 = квадрат гипотенузы
Следовательно, гипотенуза (расстояние от начальной точки) = квадратный корень из 25 = 5 км
Или более простой метод — увидеть, что расстояния составляют треугольник 3, 4, 5, поэтому расстояние от начала составляет 5 км.
22) Какое наибольшее количество студентов за любой год продолжили обучение?
В 2004 году наибольшее количество студентов поступило на обучение: 39% из 1500 студентов
39/100 x 1500 = 585 студентов в 2004 г.
23) Как уменьшилось количество выпускников, трудоустроенных с 2002 по 2004 год?
Количество выпускников, трудоустроенных в 2002 г. = 1700 х 40/100 = 680
= 1700 х 40/100 = 680
Количество выпускников, трудоустроенных в 2004 г. = 1500 x 37/100 = 555
Уменьшение = 680 — 555 = 125 выпускник с
24) Сколько студентов, изучающих общественные науки, были трудоустроены после окончания вуза в 2004 году?
Не могу сказать: недостаточно данных.
25) В каком месяце продажи ПК снизились больше всего по сравнению с предыдущим месяцем?
Падение составляет с 3,400 + 3,800 + 2,900 в апреле (всего 10,100) до 2,800 + 2,900 + 2,900 в мае (всего 8,600), снижение на 1,500.
26) Какой процент продаж производителя 2 пришелся на апрель (с точностью до процента)?
Продажи производителя 2: 4100 март 3800 апрель 2900 июнь 3100 июль 3500
Общий объем продаж = 17 400
Продажи в апреле = 3,800
Процент продаж в апреле = 3,800 / 17,400 х 100 = 21. 8% = 22% округлено до ближайшего процента
8% = 22% округлено до ближайшего процента
27) Если средняя прибыль, полученная от каждого ПК, проданного производителем 3 за все 5 месяцев, составила 78 фунтов стерлингов, какова была бы общая прибыль от всех продаж этого производителя за этот период?
Общий объем продаж производителя 3 = 2,800 + 2,900 + 2,900 + 3,200 + 3,300 = 15,100
Прибыль на ПК = 78 фунтов стерлингов, следовательно, общая прибыль = 15 100 x 78 фунтов стерлингов = 1177 800 фунтов стерлингов
числовые навыки Вопросы и ответы
На главную> Численные тесты> Числовые способности> Числовые способности Вопросы
Лодка может двигаться со скоростью 13 км / ч в стоячей воде.Если скорость потока составляет 4 км / час, найдите время, за которое лодка плывет на 68 км вниз по течению.
A. 2 часа
B. 3 часа
C. 4 часа
D. 5 часов
Ответ и объяснение:
Ответ: Вариант C
Пояснение: Скорость по течению = (13 + 4) км / час = 17 км / час.
Время прохождения 68 км вниз по течению = 68/17 часов = 4 часа.
Скорость человека по течению — 15 км / час, по течению — 2,5 км / час. Скорость человека против течения:
A. 8,5 км / час
B. 9 км / час
C. 10 км / час
D. 12,5 км / час
Ответ и объяснение:
Ответ: Вариант C
Пояснение: Скорость человека в стоячей воде = (15 — 2,5) км / час = 12.5 км / час.
Скорость человека против течения = (12,5 — 2,5) км / час = 10 км / час.
Лодке, идущей вверх по течению, требуется 8 часов 48 минут, чтобы преодолеть определенное расстояние, и 4 часа, чтобы преодолеть такое же расстояние, идущее вниз по течению. Какое соотношение между скоростью лодки и скоростью течения воды соответственно?
Какое соотношение между скоростью лодки и скоростью течения воды соответственно?
A. 2: 1
B. 3: 2
C. 8: 3
D. Не может быть определено
E.Ни один из этих
Ответ и объяснение:
Ответ: Вариант C
Пояснение: Пусть скорость человека вверх по течению будет x км / ч, а вниз по течению — y км / ч.
Затем расстояние, пройденное вверх по течению за 8 часов 48 минут = Расстояние, пройденное вниз по течению за 4 часа.
Моторная лодка, скорость которой в стоячей воде составляет 15 км / ч, проходит 30 км вниз по течению и возвращается в общей сложности за 4 часа 30 минут.Скорость ручья (км / час):
Ответ и объяснение:
Ответ: Вариант Б
Пояснение:
Пусть скорость потока будет x км / час. Затем
Затем
Скорость вниз по течению = (15 + x) км / час,
Скорость вверх по течению = (15 — x) км / час.
За один час лодка проходит 11 км / ч по течению и 5 км / ч против течения.Скорость лодки на стоячей воде (в км / час):
A. 3 км / час
B. 5 км / час
C. 8 км / час
D. 9 км / час
Ответ и объяснение:
Ответ: Вариант C
Пояснение: Скорость в стоячей воде = 1 / 2x (11 + 5) км / ч = 8 км / ч.
Страница 1 | Страница 2 | Page 3
Дополнительные обучающие и развлекательные тесты ниже.
Вопросы или комментарии? Пожалуйста, обсудите ниже.
Тест независимости хи-квадрат на языке R — Easy Guides — Wiki
Критерий независимости хи-квадрат используется для анализа таблицы частот (т. Е. Таблицы соответствия ), сформированной двумя категориальными переменными. Тест хи-квадрат оценивает, существует ли значимая связь между категориями двух переменных.В этой статье описываются основы теста хи-квадрат и приводятся практические примеры с использованием программного обеспечения R .
Е. Таблицы соответствия ), сформированной двумя категориальными переменными. Тест хи-квадрат оценивает, существует ли значимая связь между категориями двух переменных.В этой статье описываются основы теста хи-квадрат и приводятся практические примеры с использованием программного обеспечения R .
Формат данных: таблицы непредвиденных обстоятельств
Мы будем использовать домашних задач наборов данных из STHDA: http://www.sthda.com/sthda/RDoc/data/housetasks.txt.
# Импортировать данные
file_path Изображение данных показано ниже:
Анализ соответствия форматов данных
Данные представляют собой таблицу непредвиденных обстоятельств, содержащую 13 домашних задач и их распределение в паре:
- строки разные задачи Значения
- — частота выполняемых задач:
- от жены только
- или
- муж только
- или совместно
Графическое отображение таблиц соответствия
Таблицу непредвиденных обстоятельств можно визуализировать с помощью функции balloonplot () [в пакете gplots ]. Эта функция рисует графическую матрицу, где каждая ячейка содержит точку, размер которой отражает относительную величину соответствующего компонента.
Эта функция рисует графическую матрицу, где каждая ячейка содержит точку, размер которой отражает относительную величину соответствующего компонента.
Чтобы выполнить приведенный ниже код R, вы должны установить пакет gplots : install.packages («gplots») .
Библиотека (gplots)
# 1. преобразовать данные в таблицу
dt Тест независимости хи-квадрат в R
Обратите внимание, что суммы строк и столбцов по умолчанию печатаются на нижнем и правом полях соответственно.Эти значения можно скрыть с помощью аргумента show.margins = FALSE .
Также возможно визуализировать таблицу непредвиденных обстоятельств как мозаичный график . Это делается с помощью функции мозаики () из встроенного пакета R garphics :
библиотека («графика»)
мозаика (dt, тень = ИСТИНА, las = 2,
main = "housetasks") Тест независимости хи-квадрат в R
- Аргумент оттенок используется для раскрашивания графика
- Аргумент las = 2 производит вертикальные метки
Обратите внимание, что поверхность элемента мозаики отражает относительную величину его стоимости.
- Синий цвет указывает на то, что наблюдаемое значение выше ожидаемого значения, если данные были случайными
- Красный цвет указывает, что наблюдаемое значение ниже ожидаемого значения, если данные были случайными
Из этого мозаичного участка видно, что домашние задачи Стирка, Основное блюдо, Ужин и завтрак (синий цвет) в нашем примере в основном выполняются женой.
Существует еще один пакет с именем vcd , который можно использовать для создания мозаичного графика (функция mosaic ()) или ассоциативного графика (функция assoc ()).
# install.packages ("vcd")
библиотека ("vcd")
# построить только часть таблицы
assoc (head (dt, 5), shade = TRUE, las = 3) Тест независимости хи-квадрат в R
Основы теста хи-квадрат
Тест хи-квадрат проверяет, связаны ли строки и столбцы таблицы непредвиденных обстоятельств статистически значимо.
- Нулевая гипотеза (H0) : переменные строки и столбца таблицы непредвиденных обстоятельств независимы.2} {e}}
\]
- o — наблюдаемое значение
- e — математическое ожидание
Эта вычисленная статистика хи-квадрат сравнивается с критическим значением (полученным из статистических таблиц) с \ (df = (r — 1) (c — 1) \) степенями свободы и p = 0,05.
- r — количество строк в таблице непредвиденных обстоятельств
- c — номер столбца в таблице непредвиденных обстоятельств
Если вычисленная статистика хи-квадрат больше критического значения, то мы должны сделать вывод, что переменные строки и столбца не являются независимыми друг от друга.Это означает, что они существенно связаны.
Обратите внимание, что критерий хи-квадрат следует применять только тогда, когда ожидаемая частота любой ячейки составляет не менее 5.
Вычислить тест хи-квадрат в R
Статистику хи-квадратможно легко вычислить с помощью функции chisq.test () следующим образом:
чискКритерий хи-квадрат Пирсона данные: домашние задачи X-квадрат = 1944,5, df = 36, p-значениеВ нашем примере переменные строки и столбца статистически значимо связаны ( p-значение = 0).
Наблюдаемые и ожидаемые подсчеты можно извлечь из результата теста следующим образом:
# Наблюдаемые подсчеты chisq $ наблюдаетсяЖена, меняющая мужа совместно Прачечная 156 14 2 4 Основное блюдо 124 20 5 4 Ужин 77 11 7 13 Завтрак 82 36 15 7 Уборка 53 11 1 57 Посуда 32 24 4 53 Покупки 33 23 9 55 Официальный 12 46 23 15 За рулем 10 51 75 3 Финансы 13 13 21 66 Страхование 8 1 53 77 Ремонт 0 3160 2 Праздники 0 1 6 153# Ожидаемое количество круглый (chisq $ ожидаемый, 2)Жена, меняющая мужа совместно Прачечная 60.55 25,63 38,45 51,37 Основное блюдо 52,64 22,28 33,42 44,65 Ужин 37,16 15,73 23,59 31,52 Завтрак 48,17 20,39 30,58 40,86 Уборка 41,97 17,77 26,65 35,61 Посуда 38,88 16,46 24,69 32,98 Покупки 41,28 17,48 26,22 35,02 Официальная 33.03 13.98 20.97 28.02 На автомобиле 47,82 20,24 30,37 40,57 Финансы 38,88 16,46 24,69 32,98 Страхование 47,82 20,24 30,37 40,57 Ремонт 56,77 24.03 36,05 48,16 Выходные 55,05 23,30 34,95 46,70Характер зависимости между переменными строки и столбца
Как упоминалось выше, общая статистика хи-квадрат составляет 1944,456196.
Если вы хотите узнать, какие клетки вносят наибольший вклад в общую оценку хи-квадрат, вам просто нужно вычислить статистику хи-квадрат для каждой ячейки:
\ [ r = \ frac {o — e} {\ sqrt {e}} \]
Приведенная выше формула возвращает так называемые остатки Пирсона (r) для каждой ячейки (или стандартизованные остатки)
Клетки с наивысшими абсолютными стандартизованными остатками вносят наибольший вклад в общую оценку хи-квадрат.
ОстаткиПирсона можно легко извлечь из вывода функции chisq.test () :
раунд (остатки chisq $, 3)Жена, меняющая мужа совместно Прачечная 12.266 -2.298 -5.878 -6.609 Основное блюдо 9,836 -0,484 -4,917 -6,084 Ужин 6.537 -1.192 -3.416 -3.299 Завтрак 4,875 3,457 -2,818 -5,297 Уборка 1,702 -1,606 -4,969 3,585 Блюда -1,103 1,859 -4.163 3,486 Покупки -1,289 1,321 -3,362 3,376 Официальный -3,659 8,563 0,443 -2,459 Вождение -5,469 6,836 8,100 -5,898 Финансы -4,150 -0,852 -0,742 5,750 Страхование -5,758 -4,277 4,107 5,720 Ремонт -7,534 -4,290 20,646 -6,651 Праздники -7,419 -4,620 -4,897 15,556Давайте визуализируем остатки Пирсона с помощью пакета corrplot :
библиотека (корпплот) corrplot (chisq $ остатки, is.cor = FALSE)Тест независимости хи-квадрат в R
Для данной ячейки размер круга пропорционален сумме вклада ячейки.
Знак стандартизованных остатков также очень важен для интерпретации связи между строками и столбцами, как описано в блоке ниже.
- Положительные остатки отмечены синим цветом. Положительные значения в ячейках указывают на притяжение (положительную связь) между соответствующими переменными строки и столбца. 2}
\]
- r — остаток ячейки
# Вклад в процентах (%) contribЖена, меняющая мужа совместно Прачечная 7.738 0,272 1,777 2,246 Основное блюдо 4,976 0,012 1,243 1,903 Ужин 2,197 0,073 0,600 0,560 Завтрак 1,222 0,615 0,408 1,443 Уборка 0,149 0,133 1,270 0,661 Посуда 0,063 0,178 0,891 0,625 Покупки 0,085 0,090 0,581 0,586 Официальный 0,688 3,771 0,010 0,311 Вождение автомобиля 1,538 2,403 3,374 1,789 Финансы 0,886 0,037 0,028 1,700 Страхование 1,705 0,941 0,868 1,683 Ремонт 2.919 0.947 21,921 2,275 Праздники 2,831 1,098 1,233 12,445# Визуализировать вклад corrplot (contrib, is.cor = FALSE)Тест независимости хи-квадрат в R
Относительный вклад каждой ячейки в общую оценку хи-квадрат дает некоторое представление о характере зависимости между строками и столбцами таблицы непредвиденных обстоятельств.
Видно, что:
- Столбец «Жена» тесно связан с Прачечной, Обедом, Обедом
- Столбец «Муж» прочно связан со строкой Ремонт
- Столбец вместе часто связан со строкой Праздники
Из изображения выше видно, что клетки, в наибольшей степени влияющие на хи-квадрат, — это Жена / Прачечная (7.74%), Жена / Основная еда (4,98%), Муж / Ремонт (21,9%), Совместно / Праздники (12,44%).
Эти ячейки вносят около 47,06% в общую оценку хи-квадрат и, таким образом, составляют большую часть разницы между ожидаемыми и наблюдаемыми значениями.
Это подтверждает более раннюю визуальную интерпретацию данных. Как указывалось ранее, визуальная интерпретация может быть сложной, если таблица непредвиденных обстоятельств очень велика. В этом случае вклад одной ячейки в общую оценку хи-квадрат становится полезным способом установления характера зависимости.Доступ к значениям, возвращаемым функцией chisq.test ()
Результатом функции chisq.test () является список, содержащий следующие компоненты:
- статистика : значение статистики критерия хи-квадрат.
- параметр : степени свободы
- p.value : значение p теста
- наблюдаемое : наблюдаемое количество
- ожидается : ожидаемое количество
Формат кода R для использования для получения этих значений следующий:
# печать p-значения chisq $ p.значение # печать среднего chisq $ оценкаинформация
Этот анализ был проведен с использованием программного обеспечения R (версия 3.2.4).
Регрессияс двумя независимыми переменными Майкла Брэнника
Вопросы
Напишите уравнение регрессии необработанных баллов с двумя значениями ivs в нем.
В чем разница в интерпретации весов b в простой регрессии и множественной регрессии?
Опишите R-квадрат двумя разными способами, то есть используя две различные формулы.Объясните формулы.
Что произойдет с весами b , если мы добавим в уравнение регрессии новые переменные, которые сильно коррелируют с переменными, уже включенными в уравнение?
Почему мы указываем бета-веса (стандартизованные веса b )?
Напишите уравнение регрессии с бета-весами в нем.
Какие три фактора влияют на стандартную ошибку гири b ?
Как возможно иметь значимый R-квадрат и незначительные веса b ?
Линия регрессии
С одной независимой переменной мы можем записать уравнение регрессии как:
Где Y — наблюдаемая оценка зависимой переменной, a — точка пересечения, b — наклон, X — наблюдаемая оценка независимой переменной и e — ошибка или остаток.
Мы можем расширить это на любое количество независимых переменных:
(3,1)
Обратите внимание, что у нас есть k независимых переменных и наклон для каждой. У нас все еще есть одна ошибка и один перехват. Мы снова хотим выбрать оценки a и b , чтобы минимизировать сумму квадратов ошибок прогноза. Уравнение прогноза:
(3,2)
Найти значения b (наклоны) для k> 2 независимых переменных сложно, и вам действительно нужна матричная алгебра, чтобы увидеть вычисления.Это проще для k = 2 IV, которые мы здесь обсудим. Но основные идеи остаются неизменными независимо от того, сколько у вас независимых переменных. Если вы понимаете значение наклонов с двумя независимыми переменными, у вас, вероятно, все будет хорошо, независимо от того, сколько у вас есть.
Для случая с одной переменной вычисление b и a было:
Для случая с двумя переменными:
и
На этом этапе вы должны заметить, что все члены из случая одной переменной появляются в регистре двух переменных.В случае двух переменных в уравнении также появляется другая переменная X. Например, X 2 появляется в уравнении для b 1 . Обратите внимание, что члены, соответствующие дисперсии обеих переменных X, встречаются в наклонах. Также обратите внимание, что член, соответствующий ковариации X1 и X2 (сумма перекрестных произведений отклонений), также появляется в формуле для наклона.
Уравнение для a с двумя независимыми переменными:
Это уравнение является прямым обобщением случая для одной независимой переменной.
Числовой пример
Предположим, мы хотим спрогнозировать эффективность работы механиков Chevy на основе результатов теста на механические способности и результатов тестов на основе личностного теста, который измеряет сознательность. (На практике нам понадобится гораздо больше людей, но я хотел уместить это на слайде PowerPoint.)
Job Perf
Mech Apt
Сов
Y
Х1
Х2
X1 * Y
X2 * Y
Х1 * Х2
1
40
25
40
25
1000
2
45
20
90
40
900
1
38
30
38
30
1140
3
50
30
150
90
1500
2
48
28
96
56
1344
3
55
30
165
90
1650
3
53
34
159
102
1802
4
55
36
220
144
1980
4
58
32
232
128
1856
3
40
34
120
102
1360
5
55
38
275
190
2090
3
48
28
144
84
1344
3
45
30
135
90
1350
2
55
36
110
72
1980
4
60
34
240
136
2040
5
60
38
300
190
2280
5
60
42
300
210
2520
5
65
38
325
190
2470
4
50
34
200
136
1700
3
58
38
174
114
2204
Y
Х1
Х2
X1 * Y
X2 * Y
Х1 * Х2
65
1038
655
3513
2219
34510
Сумма
20
20
20
20
20
20
N
3.25
51,9
32,75
175,65
110,95
1725,5
M
1,25
7,58
5,24
84,33
54,73
474,60
SD
29.75
1091,8
521,75
USS
Мы можем собрать данные в такую матрицу:
л
Х 1
Х 2
Я
29,75
139.5
90,25
Х 1
0,77
1091,8
515,5
Х 2
0,72
0,68
521,75
Числа в таблице выше соответствуют следующим суммам квадратов, перекрестных произведений и корреляций:
Теперь мы можем вычислить коэффициенты регрессии:
Чтобы найти точку перехвата, имеем:
Следовательно, наше уравнение регрессии:
Y ‘= -4.10 + .09X1 + .09X2 или
Job Perf ‘= -4.10 + .09MechApt + .09Сознательность.
Визуальные представления регрессии
У нас есть 3 переменных, поэтому у нас есть 3 диаграммы рассеяния, которые показывают их отношения.
Поскольку мы вычислили уравнение регрессии, мы также можем просмотреть график зависимости Y ‘от Y или фактического значения от прогнозируемого Y.
Мы можем (как бы) просматривать график в трехмерном пространстве, где двумя предикторами являются оси X и Y, а ось Z является критерием, таким образом:
Этот график не очень хорошо показывает это, но проблему регрессии можно рассматривать как своего рода проблему поверхности отклика.Какова ожидаемая высота (Z) при каждом значении X и Y? Пример анимации показан в самом верху этой страницы (вращающийся рисунок). Решение этой проблемы линейной регрессией в этой размерности — это плоскость. Пакет plotly в R позволит вам «захватить» трехмерный график и повернуть его с помощью компьютерной мыши. Это позволяет более четко видеть поверхность отклика. Неподвижный вид прогнозируемых результатов механиков Chevy, произведенный Plotly:
R-квадрат (R 2 )
Так же, как и в простой регрессии, зависимая переменная рассматривается как линейная часть и ошибка.В множественной регрессии с линейной частью связано более одной переменной X. Когда мы запускаем множественную регрессию, мы можем вычислить долю дисперсии из-за регрессии (набор независимых переменных, рассматриваемых вместе). Эта пропорция называется R-квадрат. Мы используем заглавную R, чтобы показать, что это кратное R вместо одной переменной r . Мы также можем вычислить корреляцию между Y и Y ‘и возвести ее в квадрат. Если мы это сделаем, мы также найдем R-квадрат.
Y
Х1
Х2
Y ‘
Остаток
2
45
20
1.54
0,46
1
38
30
1,81
-0,81
3
50
30
2,84
0,16
2
48
28
2.50
-0,50
3
55
30
3,28
-0,28
3
53
34
3,45
-0,45
4
55
36
3.80
0,20
4
58
32
3,71
0,29
3
40
34
2,33
0,67
5
55
38
3.98
1,02
3
48
28
2,50
0,50
3
45
30
2,41
0,59
2
55
36
3.80
-1,80
4
60
34
4,06
-0,06
5
60
38
4,41
0,59
5
60
42
4.76
0,24
5
65
38
4,84
0,16
4
50
34
3,19
0,80
3
58
38
4.24
-1,24
M = 3,25
51,9
32,75
3,25
0
В = 1,57
57,46
27,46
1,05
0,52
USS = 29.83
19,95
9,88
Среднее значение Y равно 3,25, как и среднее значение Y ‘. Среднее значение остатков равно 0. Дисперсия Y составляет 1,57. Дисперсия Y ‘составляет 1,05, а дисперсия остатков составляет 0,52. Вместе дисперсия регрессии (Y ‘) и дисперсия ошибки (e) в сумме составляют дисперсию Y (1,57 = 1,05 + 0,52). R-квадрат равен 1,05 / 1,57 или 0,67. Если мы вычислим корреляцию между Y и Y ‘, мы обнаружим, что R =.82, который в квадрате также является R-квадратом 0,67. (Вспомните диаграмму рассеяния Y и Y ‘). R-квадрат — это доля дисперсии Y из-за множественной регрессии.
Проверка значимости R 2
Вы уже видели это однажды, но здесь это снова в новом контексте:
, который распределяется как F с k и (N-k-1) степенями свободы, когда нулевая гипотеза (что R-квадрат равен нулю в генеральной совокупности) верна.Теперь R 2 представляет собой множественную корреляцию, а не единственную корреляцию, которую мы видели в простой регрессии. В нашем последнем примере у нас есть 2 независимые переменные, 2 рэндов 0,67 и 20 человек, поэтому
р <0,01. (F , крит. для альфа = 0,01 составляет около 6).
Поскольку SStot = SSreg + SSres, мы можем вычислить эквивалентное F, используя суммы квадратов и соответствующую df.
, что согласуется с нашим предыдущим результатом в пределах ошибки округления.
Стандартные и нестандартные веса
С каждой переменной X будет связан один наклон или регрессионный вес. Каждый вес интерпретируется как изменение единицы измерения Y при изменении единицы измерения X, при этом остальные переменные X остаются постоянными. Если мы хотим делать точечные прогнозы (прогнозы фактического значения зависимой переменной) с учетом значений независимых переменных, это те веса, которые нам нужны. Например, если у нас есть средний балл бакалавриата и результаты SAT для человека и мы хотим спрогнозировать его средний балл первокурсника колледжа, нестандартные веса регрессии сделают свою работу.
Переменные с большим весом b должны говорить нам, что они более важны, потому что Y изменяется для некоторых из них быстрее, чем для других. Проблема с нестандартными или грубыми оценками b весов в этом отношении заключается в том, что они имеют разные единицы измерения и, следовательно, разные стандартные отклонения. Если бы мы измерили X = рост в футах, а не X = рост в дюймах, вес b для футов был бы в 12 раз больше, чем b для дюймов (12 дюймов на фут; в обоих случаях мы интерпретируем b как изменение единицы в Y, когда X изменяется на 1 единицу).Итак, когда мы измеряем разные переменные X в разных единицах, часть размера b относится к единицам измерения, а не к важности как таковой. Итак, что мы можем сделать, так это стандартизировать все переменные (как X, так и Y, каждый X по очереди). Если мы это сделаем, то все переменные будут иметь стандартное значение, равное единице, и связь с переменными X будет легко очевидна по размеру весов b — все будет интерпретировано как количество стандартных отклонений. что Y изменяется, когда каждый X изменяет одно стандартное отклонение.Стандартизированные уклоны называются бета-весами. Это чрезвычайно плохой выбор слов и символов, потому что мы уже использовали бета для обозначения значения популяции b (не вините меня; это часть литературы). Вообще говоря, при множественной регрессии бета будет относиться к стандартным весам регрессии, то есть к оценкам параметров, если не указано иное.
Уравнения регрессии с бета-весами
Поскольку мы используем стандартизованные оценки, мы снова попадаем в ситуацию z-значений.Как вы помните из сравнения корреляции и регрессии:
Но бета означает вес b , когда X и Y находятся в стандартных значениях, поэтому для случая простой регрессии r = beta, и мы имеем:
Предыдущие формулы, которые я дал для b , состояли из сумм квадратов и перекрестных произведений .
Но с оценками z мы будем иметь дело со стандартизованными суммами квадратов и перекрестных произведений. Стандартизированная усредненная сумма квадратов — 1
, а стандартизированная усредненная сумма перекрестных произведений — коэффициент корреляции
В итоге мы можем оценить бета-веса, используя корреляционную матрицу.При простой регрессии, как вы уже видели, r = beta. С двумя независимыми переменными,
и
, где r y1 — корреляция y с X1, r y2 — корреляция y с X2, а r 12 — корреляция X1 с X2. Обратите внимание, что две формулы почти идентичны, за исключением порядка первых двух символов в числителе.
Наша корреляционная матрица выглядит так:
Я
Х 1
Х 2
Я
1
Х 1
0.77
1
Х 2
0,72
0,68
1
Обратите внимание, что существует удивительно большая разница в бета-весах, учитывая величину корреляций.
Давайте посмотрим на это минутку, сначала на уравнение для бета-версии 1 . Числитель говорит, что бета 1 — это корреляция (X 1 и Y) минус корреляция (X 2 и Y), умноженная на корреляцию предиктора (X 1 и X 2 ).Знаменатель говорит о некотором увеличении числителя в зависимости от размера корреляции между X 1 и X 2 . Предположим, что r 12 равно нулю. Тогда r y2 r 12 равно нулю, а числитель r y1 . Знаменатель равен 1, поэтому результат будет r y1 , простая корреляция между X 1 и Y. Если корреляция между X 1 и X 2 равна нулю, бета-вес является простой корреляцией. С другой стороны, если корреляция между X 1 и X 2 равна 1.0 бета не определена, потому что мы делим на ноль. Таким образом, наша жизнь становится менее сложной, если корреляция между переменными X равна нулю.
Расчет R 2
Как я уже упоминал, один из способов вычислить R 2 — это вычислить корреляцию между Y и Y ‘и возвести ее в квадрат. Однако есть и другие способы расчета R 2 , и они важны для концептуального понимания того, что происходит при множественной регрессии.Если независимые переменные некоррелированы, то
Это говорит о том, что R 2 , доля дисперсии в зависимой переменной, приходящаяся на обе независимые переменные, равна сумме квадратов корреляций независимых переменных с Y. Это верно только в том случае, если IV ортогональны. (некоррелировано).
В нашем примере R 2 равно 0,67. Корреляции: r y1 = 0,77 и r y2 = 0,72. Если возвести в квадрат и сложить, мы получим.77 2 +.72 2 = 0,5929 + 0,5184 = 1,11, что явно слишком велико для R 2 , которое ограничено нулем и единицей.
Если IV коррелированы, то у нас есть общий X и, возможно, общий Y, и мы должны это учитывать. Две общие формулы можно использовать для расчета R 2 , когда IV коррелированы.
Это означает, что нужно умножить стандартизованный наклон (бета-вес) на корреляцию для каждой независимой переменной и сложить для расчета 2 RR.Это включает в себя как корреляцию (которая переоценивает общую сумму 2 рандов из-за общего Y), так и бета-вес (который недооценивает 2 рандов, поскольку он включает только уникальный Y и дисконтирует общий Y). При правильном сочетании они дают правильный R 2 . Обратите внимание, что когда r 12 равно нулю, тогда beta 1 = r y1 и beta 2 = r y2 , так что (beta 1 ) (r y1 ) = r 2 y1 , и у нас есть более ранняя формула, где R 2 — это сумма квадратов корреляций между X и Y.В нашем примере соответствующие числа (.52) .77 + (.37) .72 = .40 + .27 = 0,67, что согласуется с нашим предыдущим значением 2 рэндов.
Вторая формула, использующая только коэффициенты корреляции, —
Эта формула говорит, что R 2 — это сумма квадратов корреляций между X и Y с поправкой на общий X и общий Y. Обратите внимание, что член справа в числителе и переменная в знаменателе оба содержат r 12 , что является корреляцией между X1 и X2.Обратите внимание, что это уравнение также упрощает простую сумму квадратов корреляций, когда r 12 = 0, то есть когда IV ортогональны. В нашем примере
, что совпадает с нашим предыдущим значением в пределах ошибки округления.
Тесты коэффициентов регрессии
Каждый коэффициент регрессии представляет собой оценку наклона. При наличии более чем одной независимой переменной наклоны относятся к ожидаемому изменению Y, когда X меняет 1 единицу, УПРАВЛЯЯ ДРУГИМИ ПЕРЕМЕННЫМИ X.То есть b 1 — это изменение Y при изменении единицы измерения X 1 при сохранении постоянной X 2 , а b 2 — это изменение Y при изменении единицы измерения X 2 при постоянном X 1 . Мы рассмотрим это более формально после того, как введем частичную корреляцию. Мы хотели бы проверить, имеет ли наклон ( b ) какое-то значение, как правило, равен ли наклон нулю в генеральной совокупности. Для этого мы сравним значение b с его стандартной ошибкой, аналогично тому, что мы сделали для теста t , где мы сравнили разницу в средних значениях со стандартной ошибкой.
Стандартная ошибка веса b для задачи двух переменных:
, где s 2 y.12 — дисперсия оценки (дисперсия остатков). Стандартная ошибка веса b зависит от трех факторов. Дисперсия оценки говорит нам о том, насколько далеко точки отклоняются от линии регрессии (среднего квадрата расстояния). Большие ошибки в предсказании означают большую стандартную ошибку. Сумма квадратов IV также имеет значение.Чем больше сумма квадратов (дисперсия) X, тем меньше стандартная ошибка. Ограничение диапазона не только уменьшает размер корреляции, но также увеличивает стандартную ошибку веса b . Также имеет значение корреляция между независимыми переменными. Чем больше корреляция, тем больше стандартная ошибка веса b . Итак, чтобы найти значимые веса b , мы хотим минимизировать корреляцию между предикторами, максимизировать дисперсию предикторов и минимизировать ошибки прогнозирования.
Учитывайте это при планировании исследования. Если вы этого не сделаете, у вас могут возникнуть проблемы с питанием для теста значимости, и ваша тяжелая работа может не окупиться. Области, в которых прогнозирование плохое, будет труднее показать отношения (очевидно, но именно отсюда возникает дисперсия остатков). Если вы выбираете людей для исследования, убедитесь, что предикторы сильно различаются. Если вы проводите исследование на добровольцах в университете с высокой степенью отбора, у вас будет ограниченный диапазон когнитивных способностей, поэтому будет сложнее показать значительный регрессионный вес для теста когнитивных способностей.Тщательно выбирайте предикторы — если они сильно коррелированы, у вас может быть значительный R-квадрат, но незначительные веса регрессии. Возможно, вы заметили, что размер выборки явно не включен в формулу. Однако сумма квадратов для независимой переменной включена, и это будет увеличивать знаменатель по мере увеличения размера выборки, тем самым уменьшая стандартную ошибку. Таким образом, больший размер выборки, как обычно, приведет к большей мощности.
Отклонение прогноза
, а испытание веса b — t -тест с N-k -1 степенями свободы.
В нашем примере сумма квадратов ошибок составляет 9,79, а df — 20-2-1 или 17. Следовательно, наша дисперсия оценки составляет
.575871 или .58 после округления. Наши стандартные ошибки:
и S b2 = 0,0455, что следует из вычислений, которые идентичны, за исключением значения суммы квадратов для X 2 вместо X 1 .
Чтобы проверить значимость весов b , мы вычисляем статистику t
.
В нашем случае т = 0,0864 / 0,0313 или 2,75. Если мы сравним это с распределением t с 17 df , мы обнаружим, что оно значимо (из функции поиска мы находим, что p = 0,0137, что меньше 0,05).
Для b 2 , мы вычисляем t = 0,0876 / 0,0455 = 1,926, что имеет значение p , равное 0,0710, что несущественно. Обратите внимание, что корреляция r y2 равна 0,72, что является очень значимым ( p <.01), но b 2 не имеет значения.
Тесты R 2 по сравнению с тестами b
Поскольку веса b являются наклонами для уникальных частей Y (то есть той части Y, которая может быть однозначно отнесена к конкретному X в уравнении регрессии), и потому что корреляции между независимыми переменными увеличивают стандартные ошибки Для гирь b возможно наличие большого и значительного R 2 , но в то же время незначительные веса b (как в нашем примере с механикой Chevy).Также возможно найти значительный вес b без значительного R 2 . Это может произойти, когда у нас есть много независимых переменных (обычно более 2), все или большинство из которых имеют довольно низкую корреляцию с Y. Если одна из этих переменных имеет большую корреляцию с Y, R 2 может быть незначительным, потому что с таким большим количеством IV мы могли бы ожидать увидеть такое большое R 2 просто случайно. Если R 2 не имеет значения, обычно следует избегать интерпретации значимых весов b .В таких случаях весьма вероятно, что значительный вес b является ошибкой типа I.
Тестирование инкрементального R 2
Мы можем протестировать изменение R 2 , которое происходит, когда мы добавляем новую переменную в уравнение регрессии. Мы можем начать с 1 переменной и вычислить R 2 (или r 2 ) для этой переменной. Затем мы можем добавить вторую переменную и вычислить R 2 с обеими переменными в нем. Второй 2 рандов всегда будет равен или больше первого 2 рандов или больше.Если он больше, мы можем спросить, значительно ли он больше. Для этого вычисляем
, где R 2 L — большее R 2 (с большим количеством предикторов), k L — количество предикторов в большом уравнении, а k S — количество предикторов в меньшем уравнении. Когда ноль истинно, результат распределяется как F со степенями свободы, равными ( k L — k S ) и ( N — k L -1) .В нашем примере мы знаем, что R 2 y.12 = 0,67 (из более ранних вычислений), а также что r y1 = 0,77 и r y2 = 0,72. r 2 y1 = 0,59 и r 2 y2 = 0,52. Теперь мы можем увидеть, увеличивает ли добавление X1 или X2 к уравнению, содержащему другое, R 2 в значительной степени. Чтобы увидеть, добавляет ли X1 дисперсию, мы начнем с X2 в уравнении:
Наше критическое значение F (1,17) равно 4.
