Геометрия 10 Атанасян Контрольная 3 + ответы
Контрольная работа № 3 по геометрии в 10 классе с ответами по УМК Атанасян, базовый уровень (Просвещение). Геометрия 10 Атанасян Контрольная 2 «Перпендикулярность прямых и плоскостей» + ответы. Цитаты из пособия «Геометрия. Контрольные работы. 10–11 классы : учеб. пособие для общеобразоват. организаций : базовый уровень / М. А. Иченская» использованы в учебных целях. Ответы адресованы родителям.
Геометрия 10 класс (Атанасян)
Контрольная работа № 3 (Иченская)
К-3, Вариант 1
- Из точки О пересечения диагоналей квадрата ABCD проведён перпендикуляр ОН к плоскости квадрата. Докажите, что BD ⊥ НС.
- Через сторону KN прямоугольника KLMN проведена плоскость так, что длина проекции одной из сторон прямоугольника на эту плоскость равна 4 см. Найдите длину проекции диагонали КМ на эту плоскость, если KL = 12 см, LM = 3 см.
- Из точки А проведены к данной плоскости две наклонные, равные 2 см, угол между которыми равен 60°, а угол между их проекциями прямой. Найдите расстояние от точки А до данной плоскости.
К-3, Вариант 2
- Из вершины В квадрата ABCD проведён перпендикуляр BF к плоскости этого квадрата. Докажите, что АС ⊥ DF.
- Через вершину В треугольника АВС проведена плоскость, не совпадающая с плоскостью АВС и параллельная его стороне АС. Проекция треугольника АВС на эту плоскость – прямоугольный треугольник А1ВС1 с прямым углом В. Найдите сторону АС, если ВА1 = 9 см, ВС1 = 12 см.
- Из точки В проведены к данной плоскости две равные наклонные, угол между которыми равен 60°, а угол между их проекциями равен 90°. Найдите угол между каждой наклонной и её проекцией на плоскость.
К–3, Вариант 3
- Из середины D стороны АС равнобедренного треугольника АВС с основанием АС проведён к его плоскости перпендикуляр DK. Докажите, что АС ⊥ ВК.
- Через сторону АВ квадрата ABCD проведена плоскость. Проекция одной из сторон квадрата ABCD на эту плоскость равна 3 см. Найдите проекцию на эту плоскость одной из диагоналей квадрата, если известно, что АВ = 6 см.
- Из точки, отстоящей от плоскости на расстояние а, проведены две наклонные, образующие с плоскостью равные углы в 45°, а между собой угол в 60°. Найдите расстояние между концами наклонных.
К–3, Вариант 4
- Из точки О пересечения диагоналей ромба ABCD проведён перпендикуляр ОМ к его плоскости. Докажите, что BD ⊥ МС.
- Через вершину N равнобедренного треугольника MNL с основанием ML = 6 см проведена плоскость а параллельно стороне ML. Проекция одной из сторон этого треугольника на плоскость а равна 5 см. Найдите длину проекции на плоскость а медианы ND этого треугольника.
- Из точки М, отстоящей от плоскости на расстояние а, проведены две наклонные под углом 30° к плоскости, причём их проекции составляют между собой угол в 120°. Определите расстояние между концами наклонных.
Ответы на задачи из контрольной работы

Вы смотрели: Контрольная работа по геометрии в 10 классе «Перпендикулярность прямых и плоскостей» с ответами по УМК Атанасян, базовый уровень (Просвещение). Цитаты из пособия «Геометрия. Контрольные работы. 10–11 классы : базовый уровень / Иченская» использованы в учебных целях. Ответы адресованы родителям.
Геометрия 10 Атанасян Контрольная 3 + ответы.
Вернуться к Списку контрольных работ по геометрии в 10 классе (Атанасян)
ГДЗ к учебнику Атанасяна / контрольные работы / КА-1 Б1 геометрия 10 класс самостоятельные и контрольные работы Ершова, Голобородько
 Решение есть!
Решение есть!- 1 класс
- Математика
- Английский язык
- Русский язык
- Литература
- Окружающий мир
- 2 класс
- Математика
- Английский язык
- Русский язык
- Информатика
- Музыка
- Литература
- Окружающий мир
- Технология
- 3 класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Информатика
- Музыка
- Литература
- Казахский язык
- 4 класс
- Математика
- Русский язык
- Немецкий язык
- Музыка
- Литература
- Окружающий мир
- Казахский язык
- 5 класс
- Математика
- Английский язык
- Русский язык
- Физика
- Немецкий язык
- Украинский язык
ГДЗ по геометрии 10-11 класс Атанасян учебник Решебник
 Решение есть!
Решение есть!- 1 класс
- Математика
- Английский язык
- Музыка
- Литература
- Окружающий мир
- 2 класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Информатика
- Музыка
- Литература
- Окружающий мир
- Технология
- 3 класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Информатика
- Музыка
- Литература
- Окружающий мир
- Казахский язык
- 4 класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Информатика
- Музыка
- Литература
- Окружающий мир
- Казахский язык
- 5 класс
- Математика
- Английский язык
- Русский язык
- Физика
- Немецкий язык
- Украинский язык
- Биология
- История
- Информатика
- ОБЖ
ГДЗ к учебнику Атанасяна / контрольные работы / КА-1 А1 геометрия 10 класс самостоятельные и контрольные работы Ершова, Голобородько
 Решение есть!
Решение есть!- 1 класс
- Математика
- Английский язык
- Русский язык
- Музыка
- Литература
- Окружающий мир
- 2 класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Информатика
- Музыка
- Литература
- Окружающий мир
- Технология
- 3 класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Информатика
- Музыка
- Литература
- Окружающий мир
- Казахский язык
- 4 класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Информатика
- Музыка
- Литература
- Окружающий мир
- Казахский язык
- 5 класс
- Математика
- Английский язык
- Русский язык
- Физика
- Немецкий язык
- Украинский язык
Контрольные работы по геометрии: 10 класс: к учебнику Л.С. Атанасяна «Геометрия. 10-11 классы»


Пособие предназначено учителям математики старших классов, которые ведут преподавание курса геометрии по учебнику Л.С. Атанасяна «Геометрия, 10-11» издательства «Просвещение».
В пособии приведены тематический план и комплект контрольных работ на весь учебный год. Все работы даются в четырех равноценных вариантах, к которым приведены ответы.
В разделе «К учителю» даны подробные рекомендации по оцениванию качества выполнения контрольных работ и по эффективному использованию материалов раздела «Задания к тематическим зачетам», включающего основные теоремы курса и задачи к основным темам курса.
Без иллюстраций.
Бумага офсетная.
Список ссылок — выберите, чтобы скачать книгу «Контрольные работы по геометрии: 10 класс: к учебнику Л.С. Атанасяна «Геометрия. 10-11 классы»»:
Скачать «Контрольные работы по геометрии: 10 класс: к учебнику Л.С. Атанасяна «Геометрия. 10-11 классы»» в .PDF
Скачать «Контрольные работы по геометрии: 10 класс: к учебнику Л.С. Атанасяна «Геометрия. 10-11 классы»» в .EPUB
Скачать «Контрольные работы по геометрии: 10 класс: к учебнику Л.С. Атанасяна «Геометрия. 10-11 классы»» в .ZIP
Скачать «Контрольные работы по геометрии: 10 класс: к учебнику Л.С. Атанасяна «Геометрия. 10-11 классы»» в .FB2
Скачать «Контрольные работы по геометрии: 10 класс: к учебнику Л.С. Атанасяна «Геометрия. 10-11 классы»» в .MOBI
Скачать «Контрольные работы по геометрии: 10 класс: к учебнику Л.С. Атанасяна «Геометрия. 10-11 классы»» в .FB3
Скачать «Контрольные работы по геометрии: 10 класс: к учебнику Л.С. Атанасяна «Геометрия. 10-11 классы»» в .DOC
Скачать «Контрольные работы по геометрии: 10 класс: к учебнику Л.С. Атанасяна «Геометрия. 10-11 классы»» в .iOS.EPUB
Комментарии к книге:
ГДЗ по геометрии 10‐11 класс Атанасян Л.С.
авторы: Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Киселева Л.С., Позняк Э.Г..
Старшеклассники за годы учёбы уже практически досконально изучили математику. Им осталось немного до выпускных экзаменов. Хорошим подспорьем для подготовки к ЕГЭ станет онлайн-учебник – ГДЗ по геометрии 10‐11 класс Атанасян.
В десятом и одиннадцатом классе ученик изучает следующие темы по дисциплине:
- стереометрия, плоскость, аксиомы, теоремы;
- виды взаимного расположения прямых в пространстве: скрещивающиеся, параллельные, пересекающиеся;
- многогранники и тела вращения, вычисление их площади и объёма, сечение;
- векторы в пространстве, действия над ними.
Школьник учится обобщать и систематизировать полученные ранее знания по геометрии. Всё, что обучающийся изучал на плоскости теперь переносится в пространство.
Достоинства ГДЗ по геометрии за 10‐11 класс Атанасяна
Последние годы в школе становятся самыми сложными для ребёнка. На занятиях он должен показать всё, чему научился. Геометрия — непростой предмет, требует усидчивости и дисциплины. Чтобы решить задачи, нужно знать много теорем и уметь их правильно применять. Одними из трудных задач являются задания на доказательство. Некоторые преподаватели пропускают эти упражнения или упоминают их поверхностно, так как в ЕГЭ этот тип заданий не применяется. Но эти задачи помогают развивать у ребёнка логическое мышление, которое пригодится ученикам при выполнении практических работ. Хорошим помощником и подсказчиком для ученика в этом случае станет решебник.
Пособие с готовыми ответами подойдёт для подготовки к итоговой аттестации, контрольной работе или для выполнения домашнего задания. Сайт с ГДЗ доступен круглосуточно, обучающийся может воспользоваться решебником на телефоне дома и в школе. Подробное и грамотное решение даст ученику возможность разобраться с любой задачей, а чёткие и точные рисунки наглядно объяснят материал.
Необходимость использования онлайн-пособия в старших классах связано с тем, что:
- требуется подготовиться к экзамену;
- нужно усвоить пропущенный материал, так как непонятны следующие темы;
- не хватает времени на выполнение домашней работы;
- верные ответы помогут ребёнку оценить свои знания.
Но при использовании сборника нужно помнить, что бездумное списывание не даст знаний в предмете. Чтобы успешно усвоить дисциплину и сдать экзамен, требуется много заниматься дополнительно. Для этого нужно выполнять задания самостоятельно. Если же для решения задачи нет идей, можно воспользоваться номерами из решебника по геометрии для 10‐11 класса (авторы: Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б., Киселева Л. С., Позняк Э. Г.) как шаблоном. Задачником могут воспользоваться и преподаватели. При возникновении трудностей, которые могут возникнуть и у педагога, можно обратиться к пособию за поиском варианта решения.
Примечания к редакции по математике Глава 7 — Координатная геометрия (10-й класс)

Декартова система координат
В декартовой системе координат существует декартова плоскость, состоящая из двух числовых линий, перпендикулярных друг другу, т.е.е. ось x (горизонтальная) и ось y (вертикальная) , которая представляет две переменные. Эти две перпендикулярные линии называются координатной осью.
Точка пересечения этих двух линий называется центром или началом координатной плоскости. Его координаты (0, 0).
Любая точка на этой координатной плоскости представлена упорядоченной парой чисел.Пусть (a, b) — упорядоченная пара, тогда a — координата x, а b — координата y.
Расстояние до любой точки от оси Y называется ее координатой x или абсциссой , а расстояние до любой точки от оси x называется ее координатой y или ординатой .
Декартова плоскость разделена на четыре квадранта I, II, III и IV.

Уравнение прямой
Уравнение линии используется для построения графика линии на декартовой плоскости.
Уравнение линии записывается в форме пересечения наклона как
y = mx + b
, где m — наклон линии, а b — точка пересечения с y.

Чтобы сначала найти наклон линии, нам нужно преобразовать уравнение в форму пересечения наклона, тогда мы сможем легко получить наклон и точку пересечения по оси y.

Формула расстояния
Расстояние между любыми двумя точками A (x 1 , y 1 ) и B (x 2 , y 2 ) вычисляется по


Пример
Найдите расстояние между точками D и E на данном рисунке.

Решение

Это показывает, что это то же самое, что теорема Пифагора . Как в теореме Пифагора

Расстояние от исходной точки
Если нам нужно найти расстояние до любой точки от начала координат, то одна точка — это P (x, y), а другая точка — это сама начало координат, то есть O (0,0). Таким образом, согласно приведенной выше формуле расстояния, это будет

Формула сечения
Если P (x, y) — любая точка на отрезке AB, который делит AB в соотношении m: n, то координаты точки P (x, y) будут


Формула средней точки
Если P (x, y) является средней точкой отрезка AB, который делит AB в соотношении 1: 1, то координаты точки P (x, y) будут

Площадь треугольника

Здесь ABC — треугольник с вершинами A (x 1 , y 1 ), B (x 2 , y 2 ) и C (x 3 , y 3 ).Чтобы найти площадь треугольника, нам нужно провести перпендикуляры AP, BQ и CR от A, B и C, соответственно, к оси x. Теперь мы видим, что ABQP, APRC и BQRC — все трапеции.
Площадь треугольника ABC = Площадь трапеции ABQP + Площадь трапеции APRC — Площадь трапеции BQRC.

Следовательно,

Замечание : Если площадь треугольника равна нулю, то данные три точки должны быть коллинеарны.
Пример
Давайте посмотрим, как найти площадь четырехугольника ABCD, вершины которого — A (-4, -2), B (-3, -5), C (3, -2) и D (2, 3).
Если ABCD — четырехугольник, мы получаем два треугольника, соединяя A и C. Чтобы найти площадь четырехугольника ABCD, мы можем найти площадь ∆ ABC и ∆ ADC, а затем сложить их.




Площадь многоугольника
Подобно треугольнику, мы можем легко найти площадь любого многоугольника, если мы знаем координаты всех вершин многоугольника.
Если у нас есть многоугольник с числом вершин n, то формула для площади будет


Где x 1 — координата x вершины 1, а y n — координата y n-й вершины и т. Д.
Пример
Найдите площадь данного четырехугольника.

Решение
Найти площадь данного четырехугольника —


Площадь четырехугольника 45,5, так как площадь всегда положительна.
Центроид треугольника
Центроид треугольника — это точка, в которой все три медианы треугольника пересекаются друг с другом.

Здесь ABC — треугольник с вершинами A (x 1 , y 1 ), B (x 2 , y 2 ) и C (x 3 , y 3 ). Центроид треугольника — это точка с координатами (x, y).
Координаты центроида будут рассчитаны как

Примечания
В координатной геометрии многоугольники образованы координатами x и y его вершин. Итак, чтобы доказать, что данная цифра — это:
| No. | Фигуры из четырех точек | Доказать |
| 1. | Квадрат | Его четыре стороны равны, и диагонали также равны. |
| 2. | Ромб | Его четыре стороны равны. |
| 3. | Ромб, но не квадрат | Четыре стороны равны и диагонали не равны. |
| 4. | Прямоугольник | Его противоположные стороны равны, диагонали равны. |
| 5. | Параллелограмм | Его противоположные стороны равны. |
| 6. | Параллелограмм, но не прямоугольник | Его противоположные стороны равны, но диагонали не равны. |
| No. | Фигуры из трех точек | Доказать |
| 1. | Разносторонний треугольник | Если ни одна из его сторон не равна. |
| 2. | Равнобедренный треугольник | Если любые две стороны равны. |
| 3. | Равносторонний треугольник | Если все три стороны равны. |
| 4. | Правый треугольник | Если сумма квадратов любых двух сторон равна квадрату третьей стороны. |
Пример
Если координаты центра тяжести треугольника равны (1, 3), а две его вершины — (- 7, 6) и (8, 5), то какой будет третья вершина треугольника?
Решение
Пусть третья вершина треугольника будет P (x, y)
Поскольку центр тяжести треугольника равен (1, 3)
Следовательно,

Следовательно, координаты третьей вершины равны (2, — 2).


Особенности курса
- 728 Видео-лекции
- Примечания к редакции
- Документы за предыдущий год
- Интеллектуальная карта
- Планировщик исследования
- Решения NCERT
- Обсуждение Форум
- Контрольная бумага с видео-решением
Глава 10 Тест геометрии
Размер вставки (пикс.) 344 x 292429 x 357514 x 422599 x 487
ОПИСАНИЕ
Это демонстрирует, что даже если я не делал этого хорошо, я все же могу учиться на своих ошибках.
Текст главы 10 Тест на геометрию
r —- + E
+ Llko Cha pterQuiz
Mr. Grochowski
Geometry
rrr.rn «. Au & rres B, во время этого викторины, пожалуйста, попытайтесь показать все работы, так как эта викторина будет оцениваться с частичным зачетом. Не забудьте показать все единицы и оставить ответы в надлежащей форме. Пожалуйста, поместите все дроби в правильную сокращенную форму, кроме наклонов, и оставьте все радикалы в сокращенной форме. Пожалуйста, прочтите все вопросы внимательно. быть с тобой…
# 1 Определите следующее на рисунке ниже (предположим, что R — центр):
a) Хорда ffib) Радиан E {c) Диаметр $ [- d) Касательная линия5
e) Секущая линия 6 {flnnarc G
tl
b)
# 3
b)
Предположим, что все прямые касаются окружности. Решить для X
AL * + 1
fr-8D
-8-: l / 5
* L /) e-14
c)
/ D-3-t-lo
— Jp = — *
-4a =
D-.’
, l 1i Li’. «
S + Ll.r * 4x
tl
5
= I» -, f \ L —— * # 4
a)
Решить для X. L «\ kf, t \ | Ll. Cenl r \ 360.: _._ lo}.
/ o
. или r’3t’x- (c)
#r * 3r) \ f ,,,]. ‘il
Решите для v
b)
# 5
a)
# 6
a)
=, «1 (ae u go \
tx , 2zCq «) 9 c
Найдите значения x и y.
Y = qo»
X ‘QS’
C ts 11 ,..r, * «* — G) d) mz4 = 9o» \ / e) mz5 =! o ‘
t (mze’ F 6co
# 9 Найдите значения x и yI @ * eW *
96- 7 = lQt * o-lqz * lL $
, lbZX: fi, 4
X = n frF-
«; 1
/ oy ‘LGn’
L \ O
/ LlyrLJI, / go
zr? «Jr), Lr, — rso
lLlrla- 2 (l, r Lt !. rtoq» до
-lqqo @ * u-sane / oy -3 = Jeolon = 3oo
3o
24 года iyo, / o2-3x ‘,’ «-
1 * nr * at1 = kt- (q7) = / 3L
# 10 Найдите значение x:
b) a)
4.r = / s «t’9» x = t, r ‘!, X O.a & afr-
MPM2D Grade 10 Math Analytic Geometry Test — onstudynotes
Средняя точка
- M = ((x1 + x2) / (2)), ((y1 + y2) / (2))
Длина
Должен знать: Поиск формул уклона, средней точки и длины
Уравнения кругов
Свойства треугольников
- Свойство 1: Каждая медиана делит площадь треугольника пополам.
- Свойство 2: В любом треугольнике три медианы пересекаются в одной точке, центроид
- Свойство 3: средний сегмент составляет половину площади и половину длины и параллелен противоположным сторонам
- Свойство 4: Центроид разделяет линию в соотношении 2: 1
Свойства параллелограммов
- Свойство 1: Середины смежных сторон любого четырехугольника образуют параллелограмм
- Свойство 2: Противоположные стороны любого параллелограмма имеют одинаковую длину
- Свойство 3 : Диагонали параллелограмма делят друг друга пополам
Свойства трапеций
- Свойство 1: Отрезки трапеции параллельны параллельным сторонам
- Свойство 2: Сегменты линии, соединяющие середины непараллельных сторон, равны средней длине параллельных сторон.Верхняя сторона плюс сторона среднего сегмента, деленная на 2, равна длине непараллельной стороны
Свойства ромба
- Свойство 1: Все стороны равны по длине
- Свойство 2: Противоположные стороны параллельны, но не перпендикулярны
Собственность кругов
- Свойство 1: Диаметры окружности пересекаются в центре
- Свойство 2: Правые биссектрисы хорды проходят через центр окружности
- Свойство 3: Серединные перпендикулярные линии трех точек пересекаются в центре
- Свойство 4: Центр круга — это точка интереса правой биссектрисы сторон треугольника .
Найти кратчайшее расстояние от отрезка AB до C
- найти наклон, затем точку пересечения по оси Y отрезка AB
- Найдите наклон перпендикуляра линии AB
- Сопоставьте координаты C с перпендикулярным уклоном в формате y = mx + b
- Найдите точку интереса на линиях C и AB, чтобы увидеть, где ^ линия пересекается с линией AB путем подстановки исключения
- Найдите расстояние между POI и точкой C
Найдите центр круга с точками A, B и C, находящимися на окружности
- Предполагая, что AB и BC — хорды на окружности, находим их наклоны
- Получите перпендикулярный наклон этих хорд и средней точки
- Используя среднюю точку и перпендикулярные линии этих уклонов, получите уравнение правой биссектрисы этих хорд.
- Найдите точку интереса этих двух линий, и это будет ваш центр круга
Grade 10 Использование координатной геометрии.Упражнение 1 а. Найдите расстояние между точками A и B.
Презентация на тему: «10 класс по координатной геометрии. Упражнение 1 а. Найдите расстояние между А и В» — стенограмма презентации:
1 10 класс Использование координатной геометрии

2 Упражнение 1 а.Найдите расстояние между точками A и B.
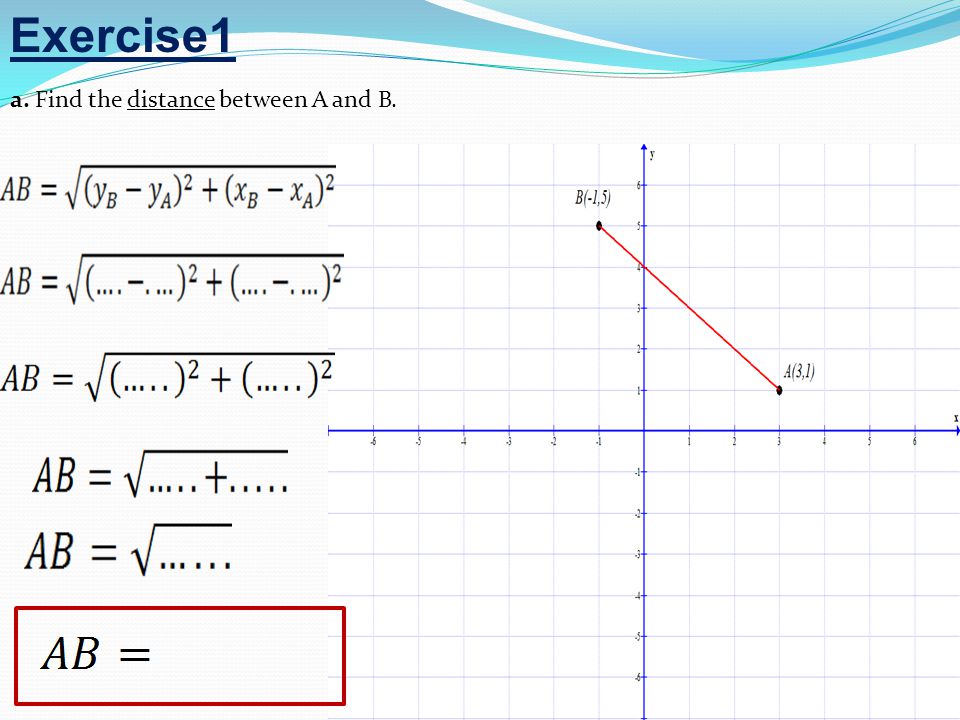
3 Упражнение 1 б. Найдите середину AB.
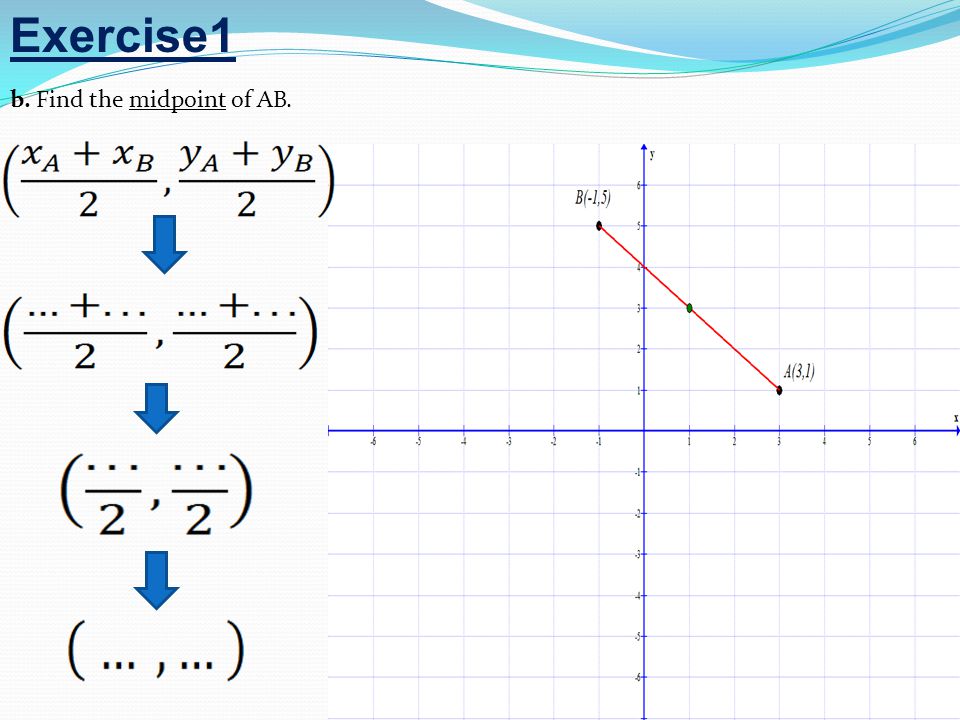
4 Упражнение 1 а. Найдите градиент интервала, соединяющего A и B.
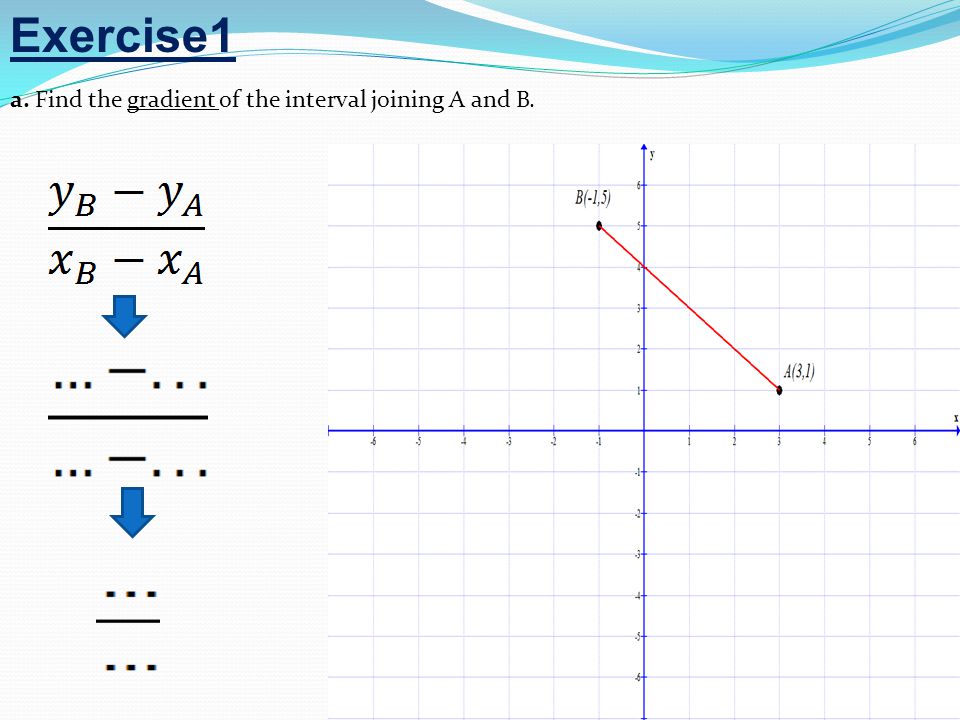
5 Расстояние AB Середина точек A и B Градиент прямой AB

6 Упражнение 2 а.Что такое уравнение AB? OC перпендикулярно AB. Пересечение оси Y с AB: Градиент AB: Итак, уравнение AB: y =
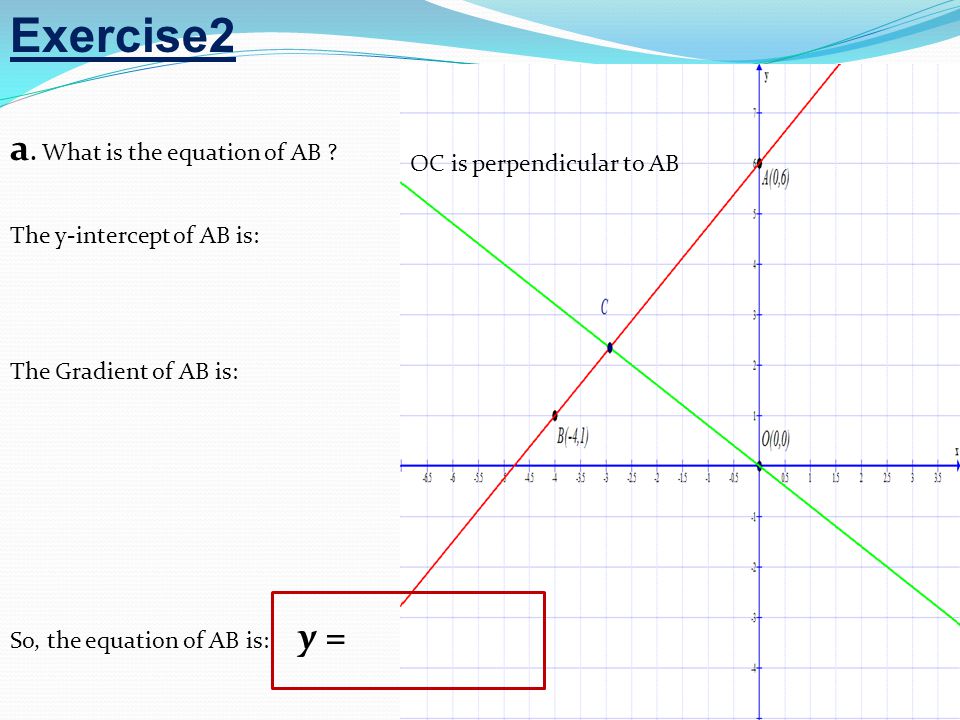
7 Упражнение 2 а. Что такое градиент ОС? OC перпендикулярно AB. Уравнение OC: y = b. Какое уравнение OC?
.