Контрольные работы по математике 10 класс
Контрольная работа «Параллельность прямых и плоскостей»
Вариант 1
1.Выберите верное утверждение
а) Любые четыре точки лежат в одной плоскости;
б) Любые три точки не лежат в одной плоскости;
в) Любые четыре точки не лежат в одной плоскости;
г) Через любые три точки, не лежащие на одной прямой, проходит плоскость и притом только одна;
Ответ________________
2. Назовите общую прямую плоскостей РВМ и МАВ.
а) РМ; б) А В; в) РВ; г) ВМ.
Ответ________________
3. Через вершины параллелограмма АВСД, лежащего в одной из двух параллельных плоскостей, проведены параллельные прямые, пересекающие вторую плоскость в точках А1, В1,С1, Д1.Тогда А1В1С1 Д1 представляет собой:
а) трапецию; б) ромб; в) параллелограмм; г) прямоугольник.
Ответ________________
4. Плоскость пересекает стороны АВ и ВС треугольника АВС в точках Д и Е соответственно, причем АС параллельна плоскости.
Найдите АС, если ВД: АД=3:4,ДЕ=10.
Ответ________________
5. Сторона ромба MCDN равна 4 см, MNKP -параллелограмм. Найдите периметр четырехугольника CDKP , если NK=8см, CMP=.
Ответ________________
Вариант 2
1. Выберите верное утверждение
а) Через любые три точки проходит плоскость и притом только одна;
б) Если две точки прямой лежат в одной плоскости, то и вся прямая лежит в этой плоскости;
в) Через прямую и точку, лежащую на ней, проходит единственная плоскость;
г) Нельзя провести плоскость через две параллельные прямые.
Ответ________________
2. Назовите общую прямую плоскостей AFD и DEF.
а) AF; б) FD; в) AE; г) ED.
Ответ________________
3. Через концы отрезка AB,не пересекающего плоскость и точку C – его середину, проведены параллельные прямые, пересекающие плоскость А1,В1,С1 соответственно. Найдите СС1, если
Найдите СС1, если
АА1=12, ВВ1=6.
а) 6; б) 9; в) 6 ; г) другой ответ.
Ответ________________
4. Плоскость пересекает стороны MP и KP треугольника MPK соответственно в точках N и E, причем сторона M K параллельна плоскости , M K=12, M N: NP=3:5.Найдите N E.
Ответ________________
5. Сторона ромба CDEK равна 8 см, CKMN -параллелограмм. Найдите периметр четырехугольника DEMN , если KM =6см, DCN=.
Ответ________________
Ответы.
1 вариант
2 вариантКонтрольные работы по алгебре 10 класс (базовый уровень)
КОНТРОЛЬНЫЕ РАБОТА
Тема: «Входная контрольная работа»
(коды КЭС: 1.3.4, 2.4.3, 2.5.1, 2.3.2, 3.1.3, 3.1.5, 3.1.4, 3.2.5, 2.3.4)
План работы:
План Входной контрольной работы по алгебре для учащихся 10 класса «А»
Расшифровка кодов 2 столбца представлена в Кодификаторе контролируемых элементов содержания (КЭС) и планируемых результатов обучения (ПРО) по предмету
№ задания | Код ПРО | Код КЭС | Элемент содержания | Тип задания (ВО, КО, РО) | Уровень сложности (Б, П) | Примерное время выполнения, мин. | Макс. балл за задание |
1 | 1.1 2.4 2.5 | 1.3.4 2.4.3 2.5.1 2.3.2 | Арифметические действия с рациональными числами. Рациональные выражения и их преобразования. Свойства квадратных корней. Формулы сокращенного умножения. | РО | Б | 5 | 1 |
2 | 3.1 | 3.1.3 | Квадратное уравнение. | РО | Б | 9 | 3 |
3 | 3.1 | 3.1.5 | Решение уравнений высших степеней. | РО | П | 8 | 2 |
4 | 3.2 | 3.1.4 | Решение рациональных уравнений. | РО | Б | 8 | 2 |
5 | 3. | 3.2.5 | Квадратные неравенства. | РО | Б | 7 | 2 |
6 | 3 | 2.3.4 | Текстовые задачи | РО | П | 8 | 2 |
Пояснение
Типы заданий:
ВО – с выбором ответа — ;
КО – с кратким ответом;
РО – с развернутым ответом
Уровень сложности:
Б – базовый;
П – повышенный
Текст контрольной работы
Вариант 1
1. Найдите значение выражения (1 балл)
Найдите значение выражения (1 балл)
—
2. Решите уравнение (1 балл за каждое уравнение)
А) 6×2-3x=0
Б) 25×2+2x-1=0
В) 25×2=1
3. Решите биквадратное уравнение (2 балла)
x4 -13×2+36=0
4. Решите неравенство (2 балла)
x2+4x+3≥0
5. (2 балла) Разность корней квадратного уравнения
x2-12x+q=0 равна 2. Найдите q.
Вариант 2
1. Найдите значение выражения (1 балл)
—
2. Решите уравнение (1 балл за каждое уравнение)
А) 5×2+20x=0
Б) x2-4x+1=0
В) 49×2=1
3. Решите биквадратное уравнение (2 балла)
x4 -29×2+100=0
4. Решите неравенство (2 балла)
x2-4x-5≥0
5. (2 балла) Разность корней квадратного уравнения
x2+x+с=0 равна 6. Найдите с.
Система оценивания
9-10 баллов (90-100%) — оценка «5»
7-8 баллов (75-89%) – оценка «4»
5-6 баллов (50-74%) – оценка «3»
№ 1 Тема: «« Степень с действительным показателем»
(коды КЭС: 1. 1.5, 1.1.6, 1.1.7 )
1.5, 1.1.6, 1.1.7 )
План работы:
План контрольной работы по ___алгебре_________ для учащихся ___10 А____ класса(ов)
Расшифровка кодов 2 столбца представлена в Кодификаторе контролируемых элементов содержания (КЭС) и планируемых результатов обучения (ПРО) по предмету
№ задания | Код ПРО | Код КЭС | Элемент содержания | Тип задания (ВО, КО, РО) | Уровень сложности (Б, П) | Примерное время выполнения, мин. | Макс. балл за задание |
1 | 1. | 1.1.5 1.1.6 1.1.7 | РО | Б | 5 | 2 | |
2 | 1.3 | 1.1.5 1.1.6 1.1.7 | РО | Б | 5 | 2 | |
3 | 1.3 | 1.1.5 1.1.6 1.1.7 | РО | П | 10 | 2 | |
4 | 1. | 1.1.5 1.1.6 1.1.7 | РО | П | 10 | 2 | |
5 | 1.3 | 1.1.5 1.1.6 1.1.7 | РО | П | 10 | 2 |
Пояснение
Типы заданий:
1) ВО – с выбором ответа — ;
2) КО – с кратким ответом;
3) РО – с развернутым ответом
Уровень сложности:
1) Б – базовый;
2)П – повышенный
Текст контрольной работы
Контрольная работа №1
Тема « Степень с действительным показателем»
В – 1 В — 2
1. Вычислить:
Вычислить:
1) 1)
2) 2)
2. Упростить выражение при
1) 1)
2) 2)
3. Сократить дробь 3. Сократить дробь
4. Сравнить числа: 4. Сравните числа
1) 1)
2) и 1. 2) и 1.
5. Найти сумму бесконечно убывающей
геометрической прогрессии,
если
Система оценивания
9-10 баллов (90-100%) — оценка «5»
7-8 баллов (75-89%) – оценка «4»
5-6 баллов (50-74%) – оценка «3»
5. Найти второй член бесконечно убывающей геометрической прогрессии, если сумма её членов равна , а знаменатель равен
Найти второй член бесконечно убывающей геометрической прогрессии, если сумма её членов равна , а знаменатель равен
№ 2 Тема: «« Степенная функция»
(коды КЭС: 2.1.3, 2.1.7., 3.1.4, 3.3.4 )
План работы:
План контрольной работы по ___алгебре_________ для учащихся ___10 А____ класса(ов)
Расшифровка кодов 2 столбца представлена в Кодификаторе контролируемых элементов содержания (КЭС) и планируемых результатов обучения (ПРО) по предмету
№ задания | Код ПРО | Код КЭС | Элемент содержания | Тип задания (ВО, КО, РО) | Уровень сложности (Б, П) | Примерное время выполнения, мин. | Макс. балл за задание |
1 | 3.1 | 2.1.3 2.1.7. | РО | Б | 5 | 2 | |
2 | 3.1 | 2.1.3 2.1.7. | РО | Б | 5 | 2 | |
3 | 3.1 | 3.1.4 3. | РО | П | 10 | 2 | |
4 | 3.1 | 3.1.4 3.3.4 | РО | П | 10 | 2 | |
5 | 3.1 | 2.1.3 2.1.7. 3.1.4 3.3.4 | РО | П | 10 | 2 |
Пояснение
Типы заданий:
1) ВО – с выбором ответа — ;
2) КО – с кратким ответом;
3) РО – с развернутым ответом
Уровень сложности:
1) Б – базовый;
2)П – повышенный
Текст контрольной работы
Контрольная работа №2
Тема «Степенная функция»
Вариант 1
1. Найти область определения функции .
Найти область определения функции .
2. Изобразить эскиз графика функции у = х7 и перечислить её основные свойства. Пользуясь свойствами этой функции:
1) сравнить с единицей (0,95)7; 2) сравнить и .
3. Решить уравнение:
1) 2) ; 3)
4. Установить, равносильны ли неравенства и <0.
5. Найти функцию, обратную к функции . Указать её область определения и множество значений. Является ли эта функция ограниченной?
Вариант 2
1. Найти область определения функции .
2. Изобразить эскиз графика функции у = х6 и перечислить её основные свойства. Пользуясь свойствами этой функции:
1) сравнить с единицей (1,001)6; 2) сравнить и .
3. Решить уравнение: 1) 2) .
3)
4. Установить, равносильны ли неравенства и .
5. Найти функцию, обратную к функции . Указать её область определения и множество значений. Является ли эта функция ограниченной?
Система оценивания
9-10 баллов (90-100%) — оценка «5»
7-8 баллов (75-89%) – оценка «4»
5-6 баллов (50-74%) – оценка «3»
№ 3 Тема: «« Показательная функция»
(коды КЭС: 2.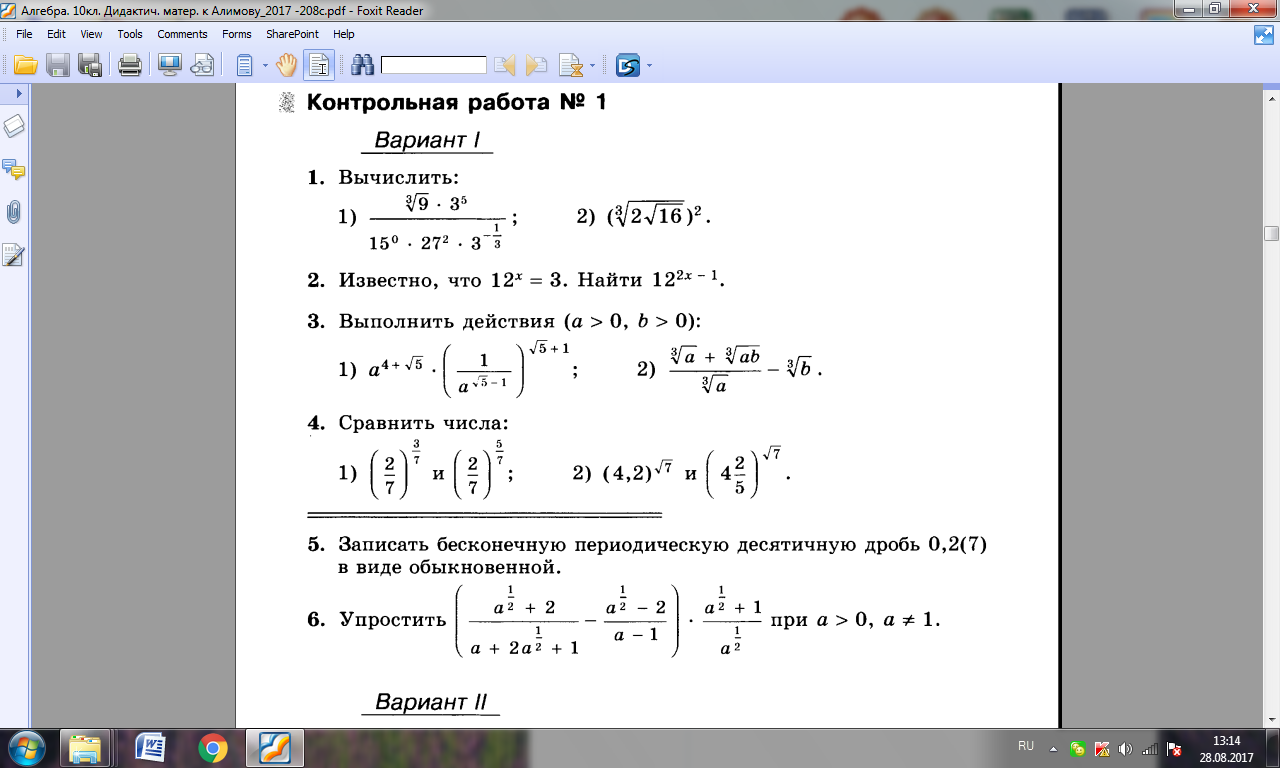 1.5, 2.3.3., 3.3.6 )
1.5, 2.3.3., 3.3.6 )
План работы:
План контрольной работы по ___алгебре_________ для учащихся ___10 А____ класса(ов)
Расшифровка кодов 2 столбца представлена в Кодификаторе контролируемых элементов содержания (КЭС) и планируемых результатов обучения (ПРО) по предмету
№ задания | Код ПРО | Код КЭС | Элемент содержания | Тип задания (ВО, КО, РО) | Уровень сложности (Б, П) | Примерное время выполнения, мин. | Макс. балл за задание |
1 | 3. | 2.1.5 2.2.3 3.3.6 | РО | Б | 5 | 1 | |
2 | 3.1 | 2.1.5 2.2.3 3.3.6 | РО | Б | 5 | 2 | |
3 | 3.1 | 2.1.5 2.2.3 3.3.6 | РО | П | 5 | 1 | |
4 | 3. | 2.1.5 2.2.3 3.3.6 | РО | П | 6 | 2 | |
5 | 3.1 | 2.1.5 2.2.3 3.3.6 | РО | П | 7 | 2 | |
6 | 3.1 | 2.1.5 2.2.3 3.3.6 | РО | П | 7 | 2 |
Пояснение
Типы заданий:
1) ВО – с выбором ответа — ;
2) КО – с кратким ответом;
3) РО – с развернутым ответом
Уровень сложности:
1) Б – базовый;
2)П – повышенный
Текст контрольной работы
Тема 3 «Показательная функция»
Вариант 1
1. Сравнить числа: 1) и ; 2) и .
Сравнить числа: 1) и ; 2) и .
2. Решить уравнение: 1) ; 2)
3. Решить неравенство >
4. Решить неравенство: 1) ; 2)
5. Решить систему уравнений
6. (Дополнительно) Решить уравнение
Вариант 2
1. Сравнить числа: 1) и ; 2) и .
2. Решить уравнение: 1) ; 2)
3. Решить неравенство .
4. Решить неравенство: 1) ; 2)
5. Решить систему уравнений
6. (Дополнительно) Решить уравнение
Система оценивания
9-10 баллов (90-100%) — оценка «5»
7-8 баллов (75-89%) – оценка «4»
5-6 баллов (50-74%) – оценка «3»
№ 4 Тема: «Логарифмическая функция»
(коды КЭС: 1.3, 1.4.5, 2.1.6, 2.2.4, 3.3.7 )
План работы:
План контрольной работы по ___алгебре_________ для учащихся ___10 А____ класса(ов)
Расшифровка кодов 2 столбца представлена в Кодификаторе контролируемых элементов содержания (КЭС) и планируемых результатов обучения (ПРО) по предмету
№ задания | Код ПРО | Код КЭС | Элемент содержания | Тип задания (ВО, КО, РО) | Уровень сложности (Б, П) | Примерное время выполнения, мин. | Макс. балл за задание |
1 | 2.1 2.3 3.1 1.3 | 1.3 | РО | Б | 5 | 1 | |
2 | 2.1 2.3 3.1 1.3 | 1.4.5 3.3.7 | РО | Б | 5 | 1 | |
3 | 3. 1.3 | 2.2.4 | РО | Б | 5 | 1 | |
4 | 2.1 2.3 | 2.1.6 | РО | Б | 6 | 2 | |
5 | 3.1 1.3 | 2.2.4 | РО | П | 7 | 2 | |
6 | 2. 2.3 | 2.1.6 | РО | П | 7 | 3 |
Пояснение
Типы заданий:
1) ВО – с выбором ответа — ;
2) КО – с кратким ответом;
3) РО – с развернутым ответом
Уровень сложности:
1) Б – базовый;
2)П – повышенный
Текст контрольной работы
Тема 4 «Логарифмическая функция»
Вариант 1
1. Вычислите:
2. Сравните числа и
3. Решите уравнение
4. Решите неравенство
5. Решите уравнение
6. Решите неравенство:
Вариант 2
1. Вычислите:
Вычислите:
2. Сравните числа и
3. Решите уравнение
4. Решите неравенство
5. Решите уравнение
6. Решите неравенство:
Система оценивания
9-10 баллов (90-100%) — оценка «5»
7-8 баллов (75-89%) – оценка «4»
5-6 баллов (50-74%) – оценка «3»
№ 5 Тема: «Тригонометрические формулы»
(коды КЭС: 1.2.3, 1.2.4, 1.2.5, 1.2.6, 1.2.7 )
План работы:
План контрольной работы по ___алгебре_________ для учащихся ___10 А____ класса(ов)
Расшифровка кодов 2 столбца представлена в Кодификаторе контролируемых элементов содержания (КЭС) и планируемых результатов обучения (ПРО) по предмету
№ задания | Код ПРО | Код КЭС | Элемент содержания | Тип задания (ВО, КО, РО) | Уровень сложности (Б, П) | Примерное время выполнения, мин. | Макс. балл за задание |
1 | 1.3 | 1.2.3 1.2.4 | РО | Б | 6 | 3 | |
2 | 1.3 | 1.2.5 1.2.6 | РО | Б | 4 | 1 | |
3 | 1.3 | 1.2.7 | РО | Б | 10 | 2 | |
4 | 1. | 1.2.5 1.2.6 | РО | Б | 10 | 2 | |
5 | 1.3 | 1.2.5 1.2.6 | РО | П | 10 | 2 |
Пояснение
Типы заданий:
1) ВО – с выбором ответа — ;
2) КО – с кратким ответом;
3) РО – с развернутым ответом
Уровень сложности:
1) Б – базовый;
2)П – повышенный
Текст контрольной работы
Тема №5 «Тригонометрические формулы»
Вариант 1
1. Найти значение выражения: 1) 2) 3)
Найти значение выражения: 1) 2) 3)
2. Вычислить:
3. Упростить выражение:
4. Доказать тождество:
5. Решить уравнение
Вариант 2
1. Найти значение выражения: 1) 2) 3)
2. Вычислить:
3. Упростить выражение:
4. Доказать тождество:
5. Решить уравнение
Система оценивания
9-10 баллов (90-100%) — оценка «5»
7-8 баллов (75-89%) – оценка «4»
5-6 баллов (50-74%) – оценка «3»
№ 6 Тема: «Тригонометрические уравнения»
(коды КЭС: 2.1.4)
План работы:
План контрольной работы по ___алгебре_________ для учащихся ___10 А____ класса(ов)
Расшифровка кодов 2 столбца представлена в Кодификаторе контролируемых элементов содержания (КЭС) и планируемых результатов обучения (ПРО) по предмету
№ задания | Код ПРО | Код КЭС | Элемент содержания | Тип задания (ВО, КО, РО) | Уровень сложности (Б, П) | Примерное время выполнения, мин. | Макс. балл за задание |
1 | 2.1 | 2.1.4 | РО | Б | 10 | 2 | |
2 | 2.1 | 2.1.4 | РО | Б | 10 | 2 | |
3 | 2.1 | 2.1.4 | РО | Б | 10 | 3 | |
4 | 2. | 2.1.4 | РО | Б | 10 | 3 | |
Пояснение
Типы заданий:
1) ВО – с выбором ответа — ;
2) КО – с кратким ответом;
3) РО – с развернутым ответом
Уровень сложности:
1) Б – базовый;
2)П – повышенный
Текст контрольной работы
Тема 6 «Тригонометрические уравнения»
Вариант 1
1. Решите уравнение:
2. Найдите решение уравнения на отрезке .
3. Решите уравнение:
; в)
4. Решите уравнение:
а)
Вариант 2
1. Решите уравнение:
а)
2. Найдите решение уравнения на отрезке .
3. Решите уравнение:
в)
4. Решите уравнение:
а)
Система оценивания
9-10 баллов (90-100%) — оценка «5»
7-8 баллов (75-89%) – оценка «4»
5-6 баллов (50-74%) – оценка «3»
Тема: «Итоговая контрольная работа»
(коды КЭС: 1.4.4.. 2.1.4, 2.2.3, 2.2.4, 3.1, 3.2, 3.3)
План работы:
План контрольной работы по ___алгебре_________ для учащихся ___10 А____ класса(ов)
Расшифровка кодов 2 столбца представлена в Кодификаторе контролируемых элементов содержания (КЭС) и планируемых результатов обучения (ПРО) по предмету
№ задания | Код ПРО | Код КЭС | Элемент содержания | Тип задания (ВО, КО, РО) | Уровень сложности (Б, П) | Примерное время выполнения, мин. | Макс. балл за задание |
1 | 1.3 | 1.4.4. 2.1.4 | РО | Б | 5 | 2 | |
2 | 2.1 | 2.2.3 | РО | Б | 5 | 2 | |
3 | 2.2 | 2.2.4 | РО | Б | 10 | 2 | |
4 | 2. | 3.1 | РО | Б | 10 | 2 | |
5 | 3.1 | 3.2 3.3 | РО | Б | 10 | 2 |
Пояснение
Типы заданий:
1) ВО – с выбором ответа — ;
2) КО – с кратким ответом;
3) РО – с развернутым ответом
Уровень сложности:
1) Б – базовый;
2)П – повышенный
Текст контрольной работы
Итоговая контрольная работа по алгебре и началам анализа.
Вариант 1
Базовый уровень
Вычислить:
а) ; в) ;
б) ; г) .
Вычислить:
.
Решите уравнение:
а) ; в) ;
б); г) .
Решите неравенство:
а) ; б).
Упростите выражения:
а); б).
Повышенный уровень
Решите уравнение:
.
Решите уравнение:
.
Решите уравнение:
.
а) Решите уравнение .
б) Найдите все корни этого уравнения, принадлежащие отрезку .
Вариант 2
Базовый уровень
Вычислить:
а) ; в) ;
б) ; г) .
Вычислить:
.
Решите уравнение:
а) ; в) ;
б); г) .
Решите неравенство:
а) ; б).
Упростите выражения:
а); б).
Повышенный уровень
Решите уравнение:
.
Решите уравнение:
.
Решите уравнение:
.
а) Решите уравнение .
б) Найдите все корни этого уравнения, принадлежащие отрезку .
Система оценивания
9-10 баллов (90-100%) — оценка «5»
7-8 баллов (75-89%) – оценка «4»
5-6 баллов (50-74%) – оценка «3»
Контрольная работа по математике 10 класс
Вариант 1 Задание № 1. Вычислить а) б) Задание № 2. Решить иррациональное уравнение Задание № 3 . Решить иррациональное неравенство Задание № 4. Решить показательное уравнение Задание № 5 . Решить показательное неравенство б) Задание № 6. а) б) в) Задание № 7. Решить логарифмическое уравнение Задание № 8. Вычислить а) б) в) | Вариант 2 Задание № 1. Вычислить а) б) Задание № 2. Решить иррациональное уравнение Задание № 3 . Решить иррациональное неравенство Задание № 4. Решить показательное уравнение Задание № 5 . Решить иррациональное неравенство б) Задание № 6. Вычислить а) б) в) Задание № 7. Решить логарифмическое уравнение Задание № 8. Вычислить а) б) в) |
Итоговая контрольная работа по геометрии за курс 10 класса
Вариант 1
Изобразите сечение конуса, проходящее через его высоту.
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 6. Объем параллелепипеда равен 48. Найдите третье ребро параллелепипеда, выходящее из той же вершины.
Объем параллелепипеда равен 48. Найдите третье ребро параллелепипеда, выходящее из той же вершины.
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые)
Найдите расстояние между вершинами A и С2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
Итоговая контрольная работа по геометрии за курс 10 класса
Вариант 2
Изобразите сечение конуса параллельное его основанию.
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 4 и 9. Объем параллелепипеда равен 216. Найдите третье ребро параллелепипеда, выходящее из той же вершины.
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые)
Найдите расстояние между вершинами D и С2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
ГДЗ по Алгебре за 10 класс Контрольные работы Глизбург В.
 И. Базовый уровень
И. Базовый уровеньАлгебра 10 класс Глизбург В.И. контрольные работы базовый уровень
Авторы: Глизбург В.И.
Ученики старшей школы отмечают полезность «ГДЗ по Алгебре 10 класс Контрольные работы Глизбург Мнемозина». Данный курс помогает углублять знания по математике, улучшает успеваемость по предмету и придает уверенности в своих возможностях.
Зачем нужен решебник
Большинство школьников сталкиваются с одной и той же проблемой при выполнении самостоятельной работы дома. Ученики берутся за множество задач одновременно, так как боятся что-то не сделать. В юной голове смешиваются все формулы, теоремы и аксиомы, что еще больше усложняет работу.
Множество ребят с высокой успеваемостью не могут проявить свои силы до конца только лишь из-за несобранности и неправильного распределения приоритетов.
- закреплять пройденные материалы;
- правильно оформлять решения задач;
- разбираться в формулах;
- обрести уверенность в собственных знаниях.
При такой качественной подготовке ученик не боится выходить к доске или отвечать на каверзные вопросы преподавателя. Данный сборник поможет быстро и эффективно подготовиться к ЕГЭ.
Что содержит решебник
«ГДЗ по Алгебре 10 класс Контрольные работы Глизбург В.И. Мнемозина» четко разделяется по видам контрольных работ. В составе сборника:
- 9 контрольных работ по 6 вариантов.

- Верные ответы на упражнения и задачки.
- Информация для справок.
Какая из контрольных вам попадется, зависит от учителя и уровня подготовки, поэтому стоит решить самостоятельно все варианты, опираясь при необходимости на готовые подробные ответы из представленного ресурса.
Все преимущества ГДЗ по алгебре за 10 класс Глизбург
Электронный помощник удобен в использовании, так как его не приходится носить в портфеле, его страницы не стираются, не рвутся и т.д. Главные его достоинства:
- Свободный доступ для компьютеров, смартфонов, планшетов.
- Пошагово расписанные решения и комментарии, ориентированные на возраст учащегося, для облегчения подготовки к экзаменам.
- Гибкий адаптивный поиск по номеру.
- Онлайн-режим и круглосуточная работа сервиса.
Итоговая контрольная работа по математике 10 класс
Вариант 1
Часть 1.
Вычислите:
Найдите значение выражения
3.На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой . Найдите значение производной функции f(x) в точке .
4. Найдите
5. Решите уравнение
6. Материальная точка движется прямолинейно по закону
(где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость (в м/с) в момент времени t = 9 с.
7. Найдите площадь поверхности правильной четырехугольной пирамиды, стороны основания которой равны 6 и высота равна 4.
8. На рисунке изображен график функции , определенной на интервале (−6; 8). Определите количество целых точек, в которых производная функции положительна.
Часть 2.
9. а) Решите уравнение
б) Укажите корни, принадлежащие отрезку
10. В правильной треугольной призме , все рёбра которой равны 2, найдите косинус угла между прямыми ВА1 и СА1 .
Вариант № 2
Часть 1.
1.Вычислите:.
2. Найдите значение выражения
3. На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой . Найдите значение производной функции f(x) в точке .
4.Найдите
5. Решите уравнение
6. Материальная точка движется прямолинейно по закону
(где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость в (м/с) в момент времени t = 6 с.
7. В правильной треугольной пирамиде SABC точка M – середина ребра AB, S – вершина. Известно, что BC = 3, а площадь боковой
поверхности пирамиды равна 45. Найдите длину отрезка SM.
8. На рисунке изображен график функции , определенной на интервале (−5; 5). Определите количество целых точек, в которых производная функции отрицательна.
Часть 2.
9. а) Решите уравнение
б) Найдите корни, принадлежащие отрезку
10. В правильной шестиугольной призме ABCDEF, все рёбра которой равны 1, найдите расстояние от точки В до прямой.
Вариант № 3
Часть 1.
Вариант №3.
1.Вычислите:.
2.Найдите значение выражения
3. На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой . Найдите значение производной функции f(x) в точке .
На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой . Найдите значение производной функции f(x) в точке .
4.Найдите
5.Решите уравнение
6. Материальная точка движется прямолинейно по закону
(где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость в (м/с) в момент времени
7.Стороны основания правильной четырёхугольной призмы равны 6, боковые рёбра равны 5. Найдите площадь поверхности этой призмы.
8.На рисунке изображен график функции y=f(x), определенной на интервале (−2; 12). Найдите сумму точек экстремума функции f(x).
Часть 2
9.а) Решите уравнение
б) Укажите корни, принадлежащие отрезку
10. В правильной шестиугольной пирамиде SABCDEF, боковые рёбра которой равны 5, а стороны основания – 3, найдите косинус угла между прямой CE и плоскостью SBC.
В правильной шестиугольной пирамиде SABCDEF, боковые рёбра которой равны 5, а стороны основания – 3, найдите косинус угла между прямой CE и плоскостью SBC.
Вариант 1
Часть 1.
Вычислите:
Найдите значение выражения
3.На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой . Найдите значение производной функции f(x) в точке .
4. Найдите
5. Решите уравнение
6. Материальная точка движется прямолинейно по закону
(где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость (в м/с) в момент времени t = 9 с.
7. Найдите площадь поверхности правильной четырехугольной пирамиды, стороны основания которой равны 6 и высота равна 4.
8. На рисунке изображен график функции , определенной на интервале (−6; 8). Определите количество целых точек, в которых производная функции положительна.
Часть 2.
9. а) Решите уравнение
б) Укажите корни, принадлежащие отрезку
10. В правильной треугольной призме , все рёбра которой равны 2, найдите косинус угла между прямыми ВА1 и СА1 .
Вариант № 2
Часть 1.
1.Вычислите:.
2. Найдите значение выражения
3. На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой . Найдите значение производной функции f(x) в точке .
4. Найдите
Найдите
5. Решите уравнение
6. Материальная точка движется прямолинейно по закону
(где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость в (м/с) в момент времени t = 6 с.
7. В правильной треугольной пирамиде SABC точка M – середина ребра AB, S – вершина. Известно, что BC = 3, а площадь боковой
поверхности пирамиды равна 45. Найдите длину отрезка SM.
8. На рисунке изображен график функции , определенной на интервале (−5; 5). Определите количество целых точек, в которых производная функции отрицательна.
Часть 2
9. а) Решите уравнение
б) Найдите корни, принадлежащие отрезку
10. В правильной шестиугольной призме ABCDEF, все рёбра которой равны 1, найдите расстояние от точки В до прямой.
В правильной шестиугольной призме ABCDEF, все рёбра которой равны 1, найдите расстояние от точки В до прямой.
Вариант № 3
Часть 1.
1.Вычислите:.
2.Найдите значение выражения
3.На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой . Найдите значение производной функции f(x) в точке .
4.Найдите
5.Решите уравнение
6. Материальная точка движется прямолинейно по закону
(где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость в (м/с) в момент времени
7.Стороны основания правильной четырёхугольной призмы равны 6, боковые рёбра равны 5. Найдите площадь поверхности этой призмы.
Найдите площадь поверхности этой призмы.
8.На рисунке изображен график функции y=f(x), определенной на интервале (−2; 12). Найдите сумму точек экстремума функции f(x).
Часть 2
9.а) Решите уравнение
б) Укажите корни, принадлежащие отрезку
10. В правильной шестиугольной пирамиде SABCDEF, боковые рёбра которой равны 5, а стороны основания – 3, найдите косинус угла между прямой CE и плоскостью SBC.
Критерии оценивания работы:
Каждое задание 1 части (№1-№8) оценивается в один балл, задания №9 2 части оценивается в 2 балла, задание №10 части 2 оценивается в 3 балла.
Критерии оценивания работы по алгебре и началам анализа:
Отметка | Количество баллов |
«5» | 10-13 |
«4» | 8-9 |
«3» | 5-7 |
«2» | 0-4 |
Итоговая контрольная работа (демоверсия) по математике за 10 класс
1105, ЕГЭ 2016, МАТЕМАТИКА,
Типовой вариант 1105, ЕГЭ 2016, МАТЕМАТИКА, 11 класс Инструкция по выполнению работы Экзаменационная работа состоит из двух частей, включающих в себя 19 заданий. Часть 1 содержит 8 заданий базового уровня
Часть 1 содержит 8 заданий базового уровня
КОНТРОЛЬНО-ИЗМЕРИТЕЛЬНЫЕ МАТЕРИАЛЫ
Муниципальное бюджетное общеобразовательное учреждение «Средняя общеобразовательная школа 1» Приложение к ОП СОО КОНТРОЛЬНО-ИЗМЕРИТЕЛЬНЫЕ МАТЕРИАЛЫ по текущей аттестации предмет: Математика. 10 класс составитель:
Подробнее4. Найдите значение выражения ,81.
Тренировочный вариант Основной государственный экзамен по МАТЕМАТИКЕ Тренировочный вариант Инструкция по выполнению работы Работа состоит из двух модулей: «Алгебра» и «Геометрия». Всего в работе 6 заданий.
ПодробнееПОЯСНИТЕЛЬНАЯ ЗАПИСКА
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Работа состоит из двух модулей: «Алгебра», «Геометрия». В модули «Алгебра» и «Геометрия» входят две части, соответствующие проверке на базовом и повышенном уровнях. При проверке базовой
При проверке базовой
ТРЕНИРОВОЧНЫЙ КИМ 02103
ОГЭ-9, 2016 г. Математика, 9 класс Тренировочный вариант 3 от 12.09.2015 1 / 9 Основной государственный экзамен по МАТЕМАТИКЕ Инструкция по выполнению работы Общее время экзамена 235 минут. Характеристика
ПодробнееСОДЕРЖАНИЕ Сроки Упражнения для
Тематическое планирование по алгебре и началам анализа (заочное отделение) в 1 классе Учебник: А.Г. Мордкович и др. в двух частях, Мнемозина 1 г Самостоятельные работы. Л.А. Александрова. Алгебра и начала
ПодробнееПовторение. Тема урока. урока
урока Дата проведения Вид контро ля Тема урока Использование ИКТ Повторение 3 четверть (40 часов) Глава 5. Производная (40 часов). 1 24 Числовые последовательности и их свойства. Прогрессии 2 24 Предел
ПодробнееТема 1: «Прямая и плоскость»
Тема : «Прямая и плоскость» Задание. Прямые, а и b пересекаются. Как расположены прямые, а и с относительно друг друга, если с параллельна b? ) скрещиваются, либо пересекаются; 2) скрещиваются, либо параллельны;
Прямые, а и b пересекаются. Как расположены прямые, а и с относительно друг друга, если с параллельна b? ) скрещиваются, либо пересекаются; 2) скрещиваются, либо параллельны;
Набережные Челны 2013 год
Муниципальное бюджетное общеобразовательное учреждение «Открытая (сменная) общеобразовательная школа 65» город Набережные Челны Республика Татарстан МЕТОДИЧЕСКОЕ ПОСОБИЕ по подготовке учащихся вечерней
ПодробнееПрограммы испытаний по математике
Программы испытаний по математике 1. Основные математические понятия и факты Арифметика, алгебра и начала анализа Натуральные числа (N). Простые и составные числа. Делитель, кратное. Наибольший общий делитель,
Подробнеевступительных испытаний по математике
УТВЕРЖДЕНО на заседании кафедры естественнонаучных и математических дисциплин Калужского филиала РАНХиГС «18» ноября 2013 г. , протокол _2 ПРОГРАММА вступительных испытаний по математике Настоящая программа
, протокол _2 ПРОГРАММА вступительных испытаний по математике Настоящая программа
Вариант 1 Профильный уровень
Работа репетиционного тестирования по математике 207 год Вариант Профильный уровень Инструкция по выполнению работы Работа состоит из двух частей, включающих в себя 9 заданий. Часть содержит 8 заданий
ПодробнееПРОГРАММА ПО МАТЕМАТИКЕ
ПРОГРАММА ПО МАТЕМАТИКЕ для поступающих в Поморский государственный университет имени М.В. Ломоносова на базе высшего или среднего специального профильного образования Вступительный экзамен по математике
ПодробнееПРОГРАММА ПО МАТЕМАТИКЕ
МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ ДЕПАРТАМЕНТ НАУЧНО-ТЕХНОЛОГИЧЕСКОЙ ПОЛИТИКИ И ОБРАЗОВАНИЯ ФГБОУ ВПО «ДОНСКОЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ УНИВЕРСИТЕТ» ПРОГРАММА ПО МАТЕМАТИКЕ Персиановский
ПодробнееСЕВЕРО-КАВКАЗСКИЙ СОЦИАЛЬНЫЙ ИНСТИТУТ
СОДЕРЖАНИЕ Пояснительная записка 3 Требования, предъявляемые к уровню подготовки поступающего на обучение 3 Содержание программы 4 Рекомендуемая литература 6 Общие правила проведения вступительного испытания
ПодробнееПояснительная записка
2 Пояснительная записка Программа разработана на основе обязательного минимума содержания среднего (полного) общего образования по математике. На испытании по математике поступающий должен показать: а)
На испытании по математике поступающий должен показать: а)
ТРЕНИРОВОЧНЫЙ КИМ 02101
ОГЭ-9, 2016 г. Математика, 9 класс Тренировочный вариант 1 от 30.08.2015 1 / 9 Основной государственный экзамен по МАТЕМАТИКЕ Инструкция по выполнению работы Общее время экзамена 235 минут. Характеристика
ПодробнееТРЕНИРОВОЧНЫЙ КИМ 02102
ТРЕНИРОВОЧНЫЙ КИМ 0202 ОГЭ-9, 206 г. Математика, 9 класс Тренировочный вариант 2 от 05.09.205 / 8 Основной государственный экзамен по МАТЕМАТИКЕ Инструкция по выполнению работы Общее время экзамена 25
ПодробнееАлгебра и начала анализа, ХI
Алгебра и начала анализа, ХI АЛГЕБРА И НАЧАЛА АНАЛИЗА По Положению о государственной (итоговой) аттестации выпускников XI(XII) классов общеобразовательных учреждений Российской Федерации учащиеся сдают
ПодробнееПрограммы для поступающих.
Программы для поступающих. Математика Настоящая программа состоит из трех разделов. В первом разделе перечислены основные математические понятия, которыми должен владеть поступающий как на письменном,
ПодробнееКонтрольная работа по теме «Функции» для 10 класса (4 варианта)
Вариант №1
1. Функция y = f (x) задана своим графиком (рис. 1). Найдите по графику:
- область определения:
Ответ - область значений функции:
Ответ - промежутки возрастания:
Ответ - нули функции:
Ответ - наибольшее значение функции:
Ответ
2. Найдите область определения функции
3. Постройте график функции
4. Постройте график функции
Постройте график функции
5. Решите уравнение
6. Решите уравнение
Вариант №2
1. Функция y = f (x) задана своим графиком (рис. 1). Найдите по графику:
- область определения:
Ответ - область значений функции:
Ответ - промежутки возрастания:
Ответ - нули функции:
Ответ - наибольшее значение функции:
Ответ
2. Найдите область определения функции:
3. Постройте график функции
4. Постройте график функции
5. Решите уравнение
6. Решите уравнение
Вариант №3
1. Функция y = f (x) задана своим графиком (рис. 1). Найдите по графику:
1). Найдите по графику:
- область определения:
Ответ - область значений функции:
Ответ - промежутки возрастания:
Ответ - нули функции:
Ответ - наибольшее значение функции:
Ответ
2. Найдите область определения функции:
3. Постройте график функции
4. Постройте график функции
5. Решите уравнение
6. Решите уравнение
Вариант №4
1. Функция y = f (x) задана своим графиком (рис. 1). Найдите по графику:
- область определения:
Ответ - область значений функции:
Ответ - промежутки возрастания:
Ответ - нули функции:
Ответ - наибольшее значение функции:
Ответ
2. Найдите область определения функции:
Найдите область определения функции:
3. Постройте график функции
4. Постройте график функции
5. Решите уравнение
6. Решите уравнение
MCAS 2013 Практический тест по математике для 10 класса
% PDF-1.6 % 353 0 объект > / ViewerPreferences> / Metadata 1901 0 R / Pages 349 0 R / OpenAction 858 0 R / StructTreeRoot 131 0 R / Type / Catalog / Lang (EN) / PageLabels 346 0 R >> эндобдж 1901 0 объект > поток 2012-09-20T10: 34: 13-04: 002012-09-20T12: 08: 54-04: 002012-09-20T12: 08: 54-04: 00Adobe InDesign CS4 (6.0.5)
 сделал: A678AABF2E03E211B6438BDEFA0C62BFadobe: DocId: INDD: c8b19f21-7b6f-11dd-адаб-808bb953f3f8proof: pdfxmp.iid: A578AABF2E03E211B6438BDEFA0C62BFxmp.did: 948718B636E2E111B2F5D5DD8B048274adobe: DocId: INDD: c8b19f21-7b6f-11dd-адаб-808bb953f3f8default
сделал: A678AABF2E03E211B6438BDEFA0C62BFadobe: DocId: INDD: c8b19f21-7b6f-11dd-адаб-808bb953f3f8proof: pdfxmp.iid: A578AABF2E03E211B6438BDEFA0C62BFxmp.did: 948718B636E2E111B2F5D5DD8B048274adobe: DocId: INDD: c8b19f21-7b6f-11dd-адаб-808bb953f3f8default iid: 928718B636E2E111B2F5D5DD8B0482742012-08-09T12: 03: 04-04: 00Adobe InDesign 6.0 /
iid: 928718B636E2E111B2F5D5DD8B0482742012-08-09T12: 03: 04-04: 00Adobe InDesign 6.0 / iid: 0E697F090EFCE11193A6809DFCEB648E2012-09-11T10: 12: 46-04: 00Adobe InDesign 6.0 /
iid: 0E697F090EFCE11193A6809DFCEB648E2012-09-11T10: 12: 46-04: 00Adobe InDesign 6.0 / iid: 72B5485E1CFCE11193A6809DFCEB648E2012-09-11T10: 26: 27-04: 00Adobe InDesign 6.0 /
iid: 72B5485E1CFCE11193A6809DFCEB648E2012-09-11T10: 26: 27-04: 00Adobe InDesign 6.0 / 0072.00 Inchesuuid: 84BA40C0A5CBDD11BDF4ACDE4BEA577 Duuid: 82BA40C0A5CBDD11BDF4ACDE4BEA577D
0072.00 Inchesuuid: 84BA40C0A5CBDD11BDF4ACDE4BEA577 Duuid: 82BA40C0A5CBDD11BDF4ACDE4BEA577DВопросы и решения по математике для 10-го класса
Консорциум Smarter Balanced Assessment Consortium (SBAC) — это стандартизированный тест, который включает в себя множество вопросов, усовершенствованных с помощью новых технологий.
Некоторые из них: Множественный выбор — один правильный ответ, Множественный выбор — несколько правильных ответов, Таблицы соответствия, Перетаскивание, Горячий текст, Заполнение таблицы, Графики, Уравнение / числовое значение, Расширенный составной ответ, Краткий ответ и многие другие.
Эта страница содержит несколько примеров вопросов вместе со ссылками на практические тесты по математике для 10 класса, которые дают вам представление о вопросах, которые ваши ученики, вероятно, увидят на тесте. После каждого типового вопроса следует объяснение ответа.Объяснение включает в себя важные аспекты задачи, которые вам, возможно, придется учитывать в отношении навыков, процессов и информации, которые должны знать ваши ученики.
Домен: уровень 10 >> Число и количество — система вещественных чисел
Пример вопроса: Оценить 9 150/300
- 18
- 9
- 3
- 81
Ответ Объяснение: 9 150/300 = 9 1/2 = квадратный корень из 9 = 3. В задаче с рациональным показателем числитель указывает степень, а знаменатель — корень. Однако в этой задаче показатель степени может быть уменьшен, поэтому сначала мы должны уменьшить его. Показатель 150/300 = 1/2. Таким образом, проблема становится 9 в степени 1/2. Знаменатель равен 2, поэтому мы извлекаем квадратный корень из 9, который равен 3. Числитель равен 1, поэтому мы возводим 3 в 1-ю степень и получаем ответ 3.
В задаче с рациональным показателем числитель указывает степень, а знаменатель — корень. Однако в этой задаче показатель степени может быть уменьшен, поэтому сначала мы должны уменьшить его. Показатель 150/300 = 1/2. Таким образом, проблема становится 9 в степени 1/2. Знаменатель равен 2, поэтому мы извлекаем квадратный корень из 9, который равен 3. Числитель равен 1, поэтому мы возводим 3 в 1-ю степень и получаем ответ 3.
Стандарты: HSN.RN.A.1
Нажмите здесь, чтобы попрактиковаться: Число и количество — система действительных чисел Вопросы по математике 10-го класса
Домен: Оценка 10 >> Количество и количество — количество
Пример вопроса: Перепишите x 1/2 в радикальной форме.
- √x
- √x 2
- 1 / √x
- -√x
Ответ Объяснение: В задаче с рациональным показателем числитель указывает степень, а знаменатель — корень. Поскольку проблема в том, что x 1/2 , знаменатель равен 2, что означает, что мы должны извлечь квадратный корень, а числитель равен 1, поэтому мы возведем его в первую степень, иначе экспонента не будет, поскольку показатель степени 1 редко бывает использовал. Это делает ответ квадратным корнем из x, записанным как √x.
Это делает ответ квадратным корнем из x, записанным как √x.
Стандарты: HSN.RN.A.1
Нажмите здесь, чтобы попрактиковаться: Число и количество 10-го класса — количество вопросов
Домен: уровень 10 >> Число и количество — комплексная система счисления
Пример вопроса: Полностью упростить i (7 − i)
- 7i − i 2
- 1 + 7i
- 6i
- −1 + 7i
Объяснение ответа: i (7 − i) = i * 7 − i * i = 7i − i 2 = 7i — (- 1) = 7i + 1 = 1 + 7i
Начните с использования метода распределения.Теперь упростим −i 2 = 1 по определению. Теперь переставьте и поместите реальную часть первой, а воображаемую — последней, чтобы она выглядела так: a + bi.
Стандарты: HSN.CN.A.2
Нажмите здесь, чтобы попрактиковаться: Математические числа и количество для 10 класса — вопросы по системе сложных чисел
Домен: Оценка 10 >> Число и количество — векторные и матричные количества
Пример вопроса: Вектор в стандартной форме имеет компоненты. Какая начальная точка?
Какая начальная точка?
- (0, 0)
- (3, 10)
- (6, 20)
- Недостаточно информации
Объяснение ответа: Поскольку вектор находится в стандартном положении, мы знаем, что начальная точка — это (0, 0) или начало координат.
Стандарты: HSN.VM.A.2
Нажмите здесь, чтобы попрактиковаться: Число и количество — Вопросы о векторных и матричных величинах для 10-го класса по математике
Область: 10 класс >> Алгебра — видение структуры в выражениях
Пример вопроса: Какое выражение эквивалентно 9x 2 — 16y 2 ?
- (3x — 4 года) (3x — 4 года)
- (3x + 4 года) (3x + 4 года)
- (3x + 4 года) (3x — 4 года)
- (3x — 4 года) 2
Ответ Объяснение: Студент должен понять, что выражение — это разница двух полных квадратов
Стандарты: HSA.SSE.A.2
Щелкните здесь, чтобы попрактиковаться: Алгебра — определение структуры выражений Вопросы для 10 класса по математике
Область: 10 класс >> Алгебра — арифметика с многочленами и рациональными выражениями
Пример вопроса: Вычислить f (x) = — a 3 + 6a − 7 при a = — 1 и сформулировать остаток.
- -14
- -12
- 14
- 12
Объяснение ответа: студент должен подставить — 1 в функцию следующим образом — (- 1) 3 +6 (−1) −7 = −12 и найти значение, чтобы получить остаток
Стандарты: HSA.APR.B.2
Щелкните здесь, чтобы попрактиковаться: Алгебра — Арифметика с многочленами и рациональными выражениями Вопросы для 10 класса по математике
Область: 10 класс >> Алгебра — создание уравнений
Пример вопроса: Соотношение персонала и гостей на гала-вечере было 3: 5. Всего в бальном зале присутствовало 576 человек. Сколько гостей было на гала-вечере?
- 276
- 300
- 360
- 216
Объяснение ответа: Установите соотношение гостей к общему количеству людей, 8/5 = x / 576.Решить крестным умножением. 8x = 2880. Разделите обе части на 8. Итак, x = 360.
Стандарты: HSA. CED.A.3
CED.A.3
Щелкните здесь, чтобы попрактиковаться: Алгебра — Создание уравнений Вопросы для 10 класса по математике
Область: 10 класс >> Алгебра — Рассуждение с помощью уравнений и неравенств
Пример вопроса: Решите квадратичный x 2 + 10x = −25.
- -10
- 10
- 5
- -5
Ответ Объяснение: Эту проблему можно легко решить, переставив уравнение так, чтобы оно решалось для нуля, а затем разложив на множители, как показано:
x 2 + 10x = −25
x 2 + 10x + 25 = 0
(x + 5) (x + 5) = 0
Поскольку оба фактора абсолютно одинаковы, у вас будет только одно решение этой проблемы.
х + 5 = 0
х = -5
Стандарты: HSA.REI.B.4
Щелкните здесь, чтобы попрактиковаться: Алгебра — Рассуждение с помощью уравнений и неравенств Вопросы для 10 класса по математике
Домен: уровень 10 >> Функции — функции интерпретации
Пример вопроса: Какой график может представлять график f (x) = sin (x)?
Ответ Пояснение: График функции sin всегда выглядит как волна. Единственная функция, которая может быть функцией sin, — это D.
Единственная функция, которая может быть функцией sin, — это D.
Стандарты: HSF.IF.C.7
Щелкните здесь, чтобы попрактиковаться: Functions — Interpreting Functions Questions for 10 Class Math
Домен: уровень 10 >> Функции — функции построения
Пример вопроса: Опишите, как можно получить график g (x) = x 3 -5, сдвигая f (x) = x 3 + 2.
- Сдвиг вправо 7 шт.
- Сдвиг влево 7 шт.
- Сдвиг на 7 единиц
- Сдвиг вниз на 7 единиц
Объяснение ответа: Единственное, что изменилось в двух уравнениях, — это точка пересечения по оси Y, которая управляет вертикальным смещением (вверх или вниз).Чтобы получить график g (x) путем сдвига графика f (x), вы должны сдвинуть f (x) вниз на 7 единиц, чтобы изменить значение от +2 до -5.
Стандарты: HSF.BF.B.3
Щелкните здесь, чтобы попрактиковаться: Functions — Building Functions Questions for 10 Grade 10 Math
Домен: уровень 10 >> Функции — функции интерпретации
Пример вопроса: Решите 3 x = 12, используя логарифмическую форму.
- x = ln12 / ln3
- x = ln (4)
- x = ln (9)
- Ни один из этих
Ответ Объяснение:
Решите, используя журналы следующим образом:
3 x = 12
x = log (основание 3) 12
x = ln12 / ln3
Стандарты: HSF.LE.A.4
Щелкните здесь, чтобы попрактиковаться: Functions — Interpreting Functions Questions for 10 Class Math
Домен: уровень 10 >> Функции — тригонометрические функции
Пример вопроса: В единичном круге видно, что tan (5π / 4) = 1. Какое значение cos (5π / 4)?
- −√2 / 2
- undefined
- √2 / 2
- –1
Ответ Пояснение:
Тригонометрическое отношение косинуса — это отношение длины соседней стороны к длине гипотенузы.Длина соседней стороны — это значение x в точке на единичной окружности. Гипотенуза — это радиус единичной окружности, поэтому гипотенуза равна 1. Таким образом, значение отношения косинуса любого угла в единичной окружности — это значение x точки на единичной окружности, которая соответствует этому углу. Тригонометрическое отношение касательной — это длина противоположной стороны, деленная на длину соседней стороны. Длина противоположной стороны — это значение y в точке на единичной окружности, а длина соседней стороны — это значение x в точке на единичной окружности.Гипотенуза — это радиус единичной окружности, поэтому гипотенуза равна 1. Таким образом, значение тангенциального отношения любого угла в единичной окружности — это отношение yx от точки на единичной окружности, которая соответствует этому углу. В этом вопросе tan (5π / 4) = 1. Это отношение берется из точки (−2 / √2, −2 / √2), которая соответствует углу с мерой 5π / 4 радиан. Таким образом, используя информацию выше, значение cos (5π4) совпадает со значением x в точке (−2 / √2, −2 / √2). Следовательно, значение cos (5π / 4) = −2 / √2.
Стандарты: HSF.TF.A.2
Щелкните здесь, чтобы попрактиковаться: Функции — Вопросы по тригонометрическим функциям для 10-го класса по математике
Домен: оценка 10 >> Геометрия — соответствие
Пример вопроса: Какими будут координаты точки S после применения следующего правила: (x + 3, y -2)?
- (1, -4)
- (-2, -2)
- (2, -2)
- (3, -2)
Ответ Объяснение: Ответ: B
Объяснение: Правило преобразования, которое дано, состоит в том, чтобы перевести точку на 3 единицы вправо и на 2 единицы вниз, как показано на следующей диаграмме:
Стандарты:
Щелкните здесь, чтобы попрактиковаться: Геометрия — вопросы на соответствие для 10 класса по математике
Домен: уровень 10 >> Геометрия — подобие, прямоугольные треугольники и тригонометрия
Пример вопроса: По какому свойству углы BAX и TSX могут быть сочтены совпадающими?
- Соответствующие углы
- Углы вертикальные
- Альтернативные внутренние углы
- Конгруэнтные углы
Ответ Объяснение: Ответ: A
Хотя это равные углы, вопрос задает свойство.Поскольку они находятся в соответствующих местах с поперечиной (AX), правильный ответ — A
.Стандарты: HSG.SRT.A.3
Щелкните здесь, чтобы попрактиковаться: вопросы по геометрии — подобию, прямоугольным треугольникам и тригонометрии для 10 класса по математике
Домен: класс 10 >> Геометрия — круги
Пример вопроса: Каково правило перевода и масштабный коэффициент расширения как Окружность F → Окружность F ‘?
- (х, у) → 1/4 (х, у + 10)
- (х, у) → 4 (х, у + 10)
- (х, у) → 1/4 (х + 10, у)
- (х, у) → 1/4 (х, у − 10)
Ответ Пояснение: Исходная окружность F имеет центр в точке (−5, −6) с радиусом 4 единицы.Смещенный / расширенный круг F ’имеет центр в точке (-5,4) с радиусом 1 единицы. Это означает, что центр был переведен на 10 единиц. В качестве преобразования этот перевод записывается как (x, y) → (x, y + 10). Круг F также был расширен в 1/4 раза, потому что радиус был уменьшен с 4 единиц до 1 единицы. В качестве преобразования это расширение записывается как (x, y) → 1/4 (x, y). Объединяя перевод и расширение, получаем правило (x, y) → 1/4 (x, y + 10).
Стандарты:
Щелкните здесь, чтобы попрактиковаться: Геометрия — Круги Вопросы для 10 класса по математике
Домен: уровень 10 >> Геометрия — выражение геометрических свойств уравнениями
Пример вопроса: Какое значение в числовой строке на рисунке ниже делит сегмент EF на две части с соотношением их длин 3: 1?
- -5
- -3
- -2
- –1
Объяснение ответа: Точка E находится на -7 на числовой прямой на рисунке, а точка F находится на 1.Таким образом, длина сегмента EF равна 8. Чтобы разделить сегмент на две части с соотношением их длин 3: 1, измените соотношение на 3x: 1x, чтобы разрешить изменение положения на числовой прямой. Затем установите сумму двух частей равной 8 и решите относительно x. 3x + 1x = 8; 4x = 8; x = 2. Теперь, когда вы знаете, что x = 2, найдите 3x, что равно 6. Найдите значение на числовой прямой, добавив 6 к положению точки E. −7 + 6 = -1. Значение на числовой прямой, которая делит сегмент EF в соотношении 3: 1, равно -1.
Стандарты: HSG.GPE.B.6
Щелкните здесь, чтобы попрактиковаться: Геометрия — Выражение геометрических свойств с помощью уравнений Вопросы для 10 класса по математике
Домен: оценка 10 >> Геометрия — геометрические измерения и размеры
Пример вопроса: Каков объем призмы, показанной ниже?
- 1350 см 3
- 1350 см
- 675 см 3
- 675 см
Ответ Пояснение: Используйте формулу объема пирамиды:
В = 1/2.a.c.h
В данном случае длина 15 см, длина основания 10 см, а высота 9 см. Следовательно:
V = 1 / 2.15.10.9 = 675 см 3
Стандарты: HSG.GMD.A.3
Щелкните здесь, чтобы попрактиковаться: Геометрия — геометрические измерения и вопросы о размерах для 10-го класса по математике
Домен: Уровень 10 >> Геометрия — Моделирование с помощью геометрии
Пример вопроса: Компания отправляет сферические пресс-папье в кубических ящиках.Окружность пресс-папье составляет 9π см. Если коробка подходит к сфере точно так, чтобы стороны сферы касались коробки, каков объем самой маленькой коробки, которую компания может использовать для доставки.
- 81 см 3
- 81 π см 3
- 729 см 3
- 1009 π см 3
Ответ Объяснение:
Обратите внимание, что диаметр сферы будет таким же, как и сторона кубической коробки.Используя значение окружности, можно определить диаметр пресс-папье.
C = πd9π
cm = πd9
cm = d
Так как диаметр равен по мере сторонам {\ dots}
V = s 3
V = (9 см) 3
V = 729 см 3
Стандарты: HSG.MG.A.3
Щелкните здесь, чтобы попрактиковаться: Геометрия — моделирование с помощью вопросов по геометрии для 10-го класса по математике
Домен: 10 класс >> Статистика и вероятность — интерпретация категориальных и количественных данных
Пример вопроса: Учитывая приведенный ниже график разброса, какой тип функции выражает корреляцию между двумя переменными?
- линейная
- Экспоненциальная
- Квадратичная
- Полярный
Ответ Объяснение: Обратите внимание, что тренд графика (красный) между точками данных образует линию.
Стандарты: HSS.ID.A.4
Щелкните здесь, чтобы попрактиковаться: Статистика и вероятности — Интерпретация категориальных и количественных данных Вопросы для 10 класса по математике
Домен: 10 класс >> Статистика и вероятность — делать выводы и обосновывать выводы
Пример вопроса: В рамках исследовательского проекта о поведении домашних животных была выбрана случайная выборка из 400 кошек. Исследование показало, что 60% кошек предпочитают спать в доме.Курица была любимой едой 35% этих кошек. Исследование также показало, что 85% кошек, которые предпочитали спать вне дома, имели другое любимое блюдо. Сколько кошек в выборке больше всего любили курицу и предпочитали спать внутри?
- 84
- 56
- 160
- 156
Объяснение ответа: Если в выборке 400 кошек и 60% кошек предпочли спать в помещении, то 400,0,60 = 240 кошек предпочли спать в помещении и 160 кошек предпочли спать на улице.Далее, если любимым блюдом 35% кошек, которые предпочитали спать внутри, была курица, то 240.0.35 = 84 кошки в выборке предпочли спать внутри и выбрали курицу в качестве своего любимого блюда.
Стандарты: HSS.IC.B.6
Щелкните здесь, чтобы попрактиковаться: Статистика и вероятности — Делать выводы и обосновывать выводы Вопросы для 10 класса по математике
Область: оценка 10 >> Статистика и вероятность — условная вероятность и правила вероятности
Пример вопроса: В студенческом совете есть одна предстоящая вакансия.В школе проводятся выборы, и у нее есть восемь равновероятных кандидатов. Класс AP Statistics хочет смоделировать результаты выборов, поэтому учащиеся должны выбрать подходящий метод моделирования. Они намерены провести испытания с симуляцией. Какой из этих методов будет наиболее подходящим?
- Вращайте колесо с восемью равными промежутками
- Подбросить монету восемь раз за каждые выборы
- Бросьте кости
- Бросок четыре кубика
Объяснение ответа: В вопросе указано, что существует восемь равновероятных кандидатов.Это означает, что каждый кандидат имеет одинаковые шансы на победу на выборах. Только вращающееся колесо с восемью равными ячейками могло смоделировать эту ситуацию, потому что колесо имеет равные шансы приземлиться на каждую ячейку.
Стандарты: HSS.IC.A.1
Щелкните здесь, чтобы попрактиковаться: Статистика и вероятность — условная вероятность и правила вероятностных вопросов для 10 класса по математике
Область: оценка 10 >> Статистика и вероятность — использование вероятности для принятия решений
Пример вопроса:
Используя приведенную выше диаграмму Венна, найдите P (C или E).
- 1/3
- 24/7
- 5/24
- Ни один из этих
Объяснение ответа: Просто посчитайте точки данных в кругах C и E. Их 8 из 24 общих точек данных, и, уменьшив, мы получим 8/24 = 1/3.
Стандарты: HSS.CP.B.7
Щелкните здесь, чтобы попрактиковаться: Статистика и вероятность — использование вероятности для принятия решений Вопросы по математике для 10 класса
Область: оценка 10 >> Статистика и вероятность — использование вероятности для принятия решений
Пример вопроса: Статистик работает в Sweet Shop USA, и ему было поручено выяснить, какова вероятность того, что неисправность машины для приготовления помадки приведет к повреждению всей партии помадки в процессе.Каждая неисправность машины обходится компании в 250 долларов. Статистик подсчитал вероятность того, что 1 из 20 партий фаджа будет потеряна из-за неисправности машины. Какова ожидаемая стоимость этих потерь за один месяц, если компания производит 20 партий помадки каждый день?
- $ 3750
- $ 150 000
- $ 7500
- $ 375
Объяснение ответа: Поскольку в большинстве месяцев 30 дней, мы предположим, что в месяце 30 дней. Мы можем использовать E (x) = x1p1 + x2p2 +… + xipi или просто вычислить следующим образом
E (X) =.05 * 250 * 30 = 375
Стандарты: HSS.MD.A.4
Щелкните здесь, чтобы попрактиковаться: Статистика и вероятность — использование вероятности для принятия решений Вопросы по математике для 10 класса
Математика средней школы (10, 11 и 12 классы)
Математика средней школы для 10, 11 и 12 классов представлены математические вопросы и задачи для проверки глубокого понимания математических концепций и вычислительных процедур. Предоставляются подробные решения и ответы на вопросы.
12 класс
11 класс
10 класс
Онлайн-калькуляторы
- Математические калькуляторы и решатели онлайн
- Онлайн-калькуляторы и решатели геометрии
- Калькулятор проверки делимости. Онлайн-калькулятор, который проверяет целые числа на видимость 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 и 13.
- Калькуляторы сложения, вычитания и умножения целых чисел. Три отдельных онлайн-калькулятора для сложения, вычитания и умножения целых чисел.
- Калькулятор частных и остатков. Онлайн-калькулятор, вычисляющий частное и остаток от деления двух целых чисел.
- Калькулятор наименьшего общего кратного (lcm). Вычислите наименьшее общее кратное двух натуральных чисел.
- Калькулятор наибольшего общего коэффициента (GCF). Вычислите наибольший общий делитель двух натуральных чисел.
- Калькулятор основных факторов. Разложите положительное целое число на простые множители.
- Калькулятор сложения дробей.Добавьте 2 или 3 дроби и уменьшите окончательный ответ.
- Калькулятор умножения дробей. Умножьте 2 дроби и уменьшите ответ.
- Калькулятор деления дробей. Разделите 2 дроби и уменьшите ответ.
- Калькулятор сокращения дробей. Перепишите дроби в уменьшенном виде.
Больше математики для начальной школы (4 и 5 классы) с бесплатными вопросами и задачи с ответами Домашняя страница
Автор — сообщить об этом объявлении по электронной почте
Экзамен по математике 10 класс
Ищете сертификационный экзамен, который поможет проверить ваши знания по основам математики и получить сертификат? StudySection запустил сертификационный экзамен по математике для учащихся 10-х классов.Эта серия экзаменов предназначена для лиц, обладающих хорошими знаниями и навыками в математике. Этот сертификационный экзамен — один из лучших вариантов онлайн-сертификации, признанный во всем мире. Пройдя эту серию экзаменов от StudySection, вы получите электронный сертификат и значок сертификации.
Сертификат по математике — это программа, предназначенная для улучшения ваших знаний по математике на уровне 10 класса. Наличие сильного математического опыта считается преимуществом для студентов, желающих поступить в аспирантуру.
По сравнению с хорошими знаниями математики, сертификат требует меньшего количества курсов и дает большую гибкость при выборе курсов. Этот сертификационный экзамен охватывает некоторые темы, такие как упрощение, вероятность, тригонометрия, числа, объем и площадь поверхности и т. Д. Все студенты имеют право на получение сертификата по математике, предоставляемого учебной секцией.
Этот экзамен состоит из нескольких вопросов с несколькими вариантами ответов. После того, как кандидат успешно сдал раздел «Бесплатный онлайн-сертификационный экзамен по основам математики», он / она сможет загрузить утвержденный сертификат, а также значок, который может помочь кандидату в продолжении профессиональной карьеры в области математики.Кандидаты, которые хотят сдать этот сертификационный онлайн-экзамен уровня 10 от StudySection, могут пройти его с легкостью и комфортом дома или на рабочем месте.
Темы, которые должны быть охвачены на онлайн-сертификационном экзамене по математике для 10-го класса, следующие:
- Вероятность
- СТАТИСТИКА
- Измерение
- КООРДИНАТНАЯ ГЕОМЕТРИЯ
- Система счисления
- Алгебра
- Тригнометрия
- Геометрия
Математический тест PSAT / NMSQT и PSAT 10
Математический тест охватывает ряд математических практик с упором на решение задач, моделирование, стратегическое использование инструментов и использование алгебраической структуры.
Важный:Попробуйте примерные вопросы по математике прямо сейчас
Это о реальном мире
Вместо того, чтобы проверять вас по каждой имеющейся математической теме, PSAT / NMSQT и PSAT 10 просят вас использовать математику, на которую вы будете полагаться больше всего в самых разных ситуациях. Вопросы к тесту по математике предназначены для отражения решения задач и моделирования, которые вы будете выполнять в:
- Колледж, курсы математики, естественных и социальных наук
- Рабочие места, которые у вас есть
- Твоя личная жизнь
Например, чтобы ответить на некоторые вопросы, вам нужно будет выполнить несколько шагов, потому что в реальном мире одного вычисления редко бывает достаточно для выполнения работы.
Краткая информация
- В большинстве математических вопросов будет несколько вариантов ответа, но некоторые, называемые сетками, просят вас придумать ответ, а не выбрать ответ.
- Математический тест разделен на две части: математический тест – калькулятор и математический тест – без калькулятора.
- Некоторые части теста включают несколько вопросов по одному сценарию.
Фокус
Тест по математике будет посвящен трем областям математики, которые играют наибольшую роль в широком спектре специальностей и профессий в колледже:
Тест по математике также включает дополнительные разделы математики, в том числе геометрию и тригонометрию, наиболее важные для подготовки к колледжу и карьеры.
Что измеряет математический тест
Свободное владение
Тест по математике — это шанс показать, что вы:
- Выполняйте процедуры гибко, точно, эффективно и стратегически.
- Быстро решайте проблемы, определяя и используя наиболее эффективные подходы к решению. Это может включать решение проблемы путем проверки, поиска ярлыка или реорганизации предоставленной вам информации.
Концептуальное понимание
Вы продемонстрируете свое понимание математических понятий, операций и отношений.Например, вас могут попросить установить связи между свойствами линейных уравнений, их графиками и контекстами, которые они представляют.
Приложения
Эти реальные проблемы требуют от вас анализа ситуации, определения основных элементов, необходимых для решения проблемы, математического представления проблемы и выполнения решения.
Использование калькулятора
Калькуляторы— важные инструменты, и чтобы добиться успеха после окончания школы, вам нужно знать, как и когда ими пользоваться.В части теста «Тест по математике — калькулятор» вы сможете сосредоточиться на сложном моделировании и рассуждениях, потому что калькулятор поможет вам сэкономить время.
Однако калькулятор, как и любой другой инструмент, настолько умен, насколько умен человек, который его использует. Тест по математике включает в себя несколько вопросов, по которым лучше не использовать калькулятор, даже если вам это разрешено. В этих случаях студенты, которые используют структуру или свою способность рассуждать, вероятно, закончат раньше, чем студенты, использующие калькулятор.
Тест по математике — часть теста без калькулятора облегчает оценку вашего владения математикой и вашего понимания некоторых математических понятий.Он также проверяет хорошо изученную технику и чувство чисел.
Справочные вопросы
Хотя большинство вопросов в тесте по математике представляют собой вопросы с несколькими вариантами ответов, 17 процентов — это вопросы с ответами учащихся, также известные как сетки. Вместо того, чтобы выбирать правильный ответ из списка вариантов, вам нужно будет решить проблемы и ввести свои ответы в сетки на листе для ответов.
Привязка ответов
- Отметьте не более одного кружка в любом столбце.
- Оцениваются только ответы, отмеченные кружком (вы не получите баллов за все, что написано в полях над кружками).
- Не имеет значения, в каком столбце вы начинаете вводить ответы; пока ответы записываются в области сетки, вы получите кредит.
- Сетка может содержать только четыре десятичных разряда и может содержать только положительные числа и ноль.
- Если проблема не указывает на иное, ответы можно вводить в сетку в виде десятичных или дробных чисел.
- Такие дроби не нужно сокращать до наименьшего значения.
- Все смешанные числа необходимо преобразовать в неправильные дроби перед записью в сетку.
- Если ответ — повторяющаяся десятичная дробь, учащиеся должны нанести на сетку наиболее точное значение, которое она сможет учесть.
Ниже приведен образец инструкций, которые студенты увидят на тесте.
Примеры вопросов
Узнайте о тесте по математике из первых рук, просмотрев образцы вопросов из PSAT / NMSQT и PSAT 10.
% PDF-1.4 % 1827 0 obj> эндобдж xref 1827 87 0000000016 00000 н. 0000003884 00000 н. 0000004089 00000 н. 0000004697 00000 н. 0000004743 00000 н. 0000004920 00000 н. 0000005098 00000 н. 0000005275 00000 н. 0000005994 00000 н. 0000006380 00000 н. 0000007181 00000 н. 0000007220 00000 н. 0000007307 00000 н. 0000007390 00000 н. 0000007471 00000 н. 0000007528 00000 н. 0000008034 00000 н. 0000010178 00000 п. 0000011875 00000 п. 0000012077 00000 п. 0000012454 00000 п. 0000012849 00000 п. 0000013142 00000 п. 0000013384 00000 п. 0000013688 00000 п. 0000013743 00000 п. 0000014061 00000 п. 0000014698 00000 п. 0000014742 00000 п. 0000014828 00000 п. 0000014910 00000 п. 0000016068 00000 н. 0000018074 00000 п. 0000018501 00000 п. 0000018529 00000 п. 0000018615 00000 п. 0000018933 00000 п. 0000019245 00000 п. 0000020541 00000 п. 0000021931 00000 п. 0000022383 00000 п. 0000022715 00000 п. 0000023019 00000 п. 0000023323 00000 п. 0000023560 00000 п. 0000023769 00000 п. 0000025126 00000 п. 0000025208 00000 п. 0000027273 00000 н. 0000028855 00000 п. 0000034004 00000 п. 0000038541 00000 п. 0000038681 00000 п. 0000039263 00000 п. 0000040030 00000 н. 0000041460 00000 п. 0000049060 00000 н. 0000049131 00000 п. 0000051431 00000 п. 0000051499 00000 н. 0000051567 00000 п. 0000051638 00000 п. 0000051728 00000 п. 0000051836 00000 п. 0000053358 00000 п. 0000053637 00000 п. 0000053953 00000 п. 0000054536 00000 п. 0000054781 00000 п. 0000056454 00000 п. 0000056727 00000 н. 0000057044 00000 п. 0000057117 00000 п. 0000057190 00000 п. 0000057333 00000 п. 0000057430 00000 п. 0000057488 00000 п. 0000057581 00000 п. 0000057637 00000 п. 0000057743 00000 п. 0000057799 00000 п. 0000057932 00000 п. 0000057988 00000 п. 0000058122 00000 п. 0000058177 00000 п. 0000003671 00000 н. 0000002081 00000 н. трейлер ] >> startxref 0 %% EOF 1913 0 obj> поток x ڔ UYPSW>! IM «f $ Xl \ $ R¦LHAM p:} tӎ] fCxjm {Ať? S
KY | Home
Информация о программе
Миссия KDE состоит в том, чтобы сотрудничать с округами, школами и заинтересованными сторонами в сфере образования для предоставления услуг, поддержки и руководства для обеспечения успеха для каждого ученика.На этом сайте размещены все инструменты, необходимые для районных координаторов по оценке, координаторов по оценке зданий, координаторов по технологиям и администраторов тестирования для подготовки и проведения итоговых оценок в Кентукки.
Важные датыВажные даты аттестации штата Кентукки и полевых испытаний.
Важные даты
PearsonAccess следующийPearsonAccess next служит точкой входа для всех служб Pearson, используемых школами и округами, участвующими в оценках штата Кентукки.
PearsonAccess следующий
Настройка технологииПодготовьте свою систему к компьютерным оценкам штата Кентукки.Получите доступ к техническим руководствам, руководствам пользователя и TestNav.
Технологическая установка
РесурсыДоступ к руководствам, сценариям и другим документам для подготовки и проведения оценок.
Ресурсы
Подготовка к экзаменуПользователи могут получить доступ к образцам элементов, руководствам по TestNav 8 и практическим тестам для подготовки к тестам в Кентукки.
Подготовка к экзамену
Выпущенные позицииЭти задания могут быть использованы для ознакомления экзаменаторов и студентов с экзаменом и форматом заданий.
Выпущенные позиции
ДокументыНовости для координаторов тестирования, администраторов тестирования, координаторов по технологиям, округов и школ.
Документы
ПоддержкаПомощь доступна через веб-форму, по телефону и в чате.


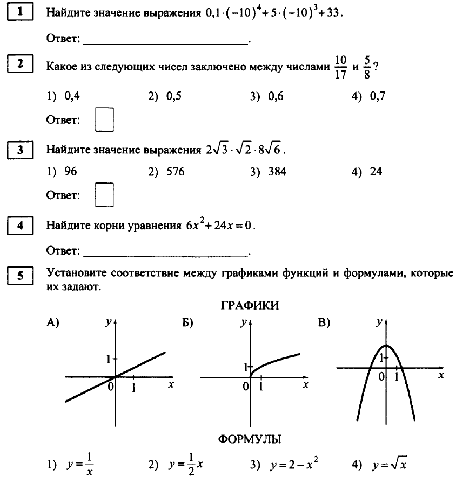
 Формула корней квадратного уравнения.
Формула корней квадратного уравнения. 2
2 3
3 3
3
 3.4
3.4 1
1 1
1
 1
1 1
1
 3
3
 1
1
 3
3 Вычислить
Вычислить