Алгебра 9 Макарычев К-9 В-1
Итоговая контрольная работа по алгебре за 9 класс с ответами и решениями. Алгебра 9 Макарычев К-9 В-1.
Алгебра 9 класс (Макарычев)
Контрольная работа № 9. Вариант 1
Итоговая контрольная работа за курс 9 класса
КР-9. Вариант 1 (транскрипт заданий)
№ 1. Упростите выражение ((x–y)/x – (y–x)/y) : (x+y)/xy.
№ 2. Решите систему уравнений
{ x2 + 2y = –2,
{ x + y = –1.
№ 3. Решите неравенство 3 + х ≤ 8x – (Зх + 7).
№ 4. Упростите выражение (a–3 • (a4)2) / a–6.
№ 5. Решите систему неравенств
{ x2 – 5x + 6 ≤ 0,
{ 2x – 5 ≤ 0.
№ 6. Постройте график функции у = х2 – 4. Укажите, при каких значениях х функция принимает положительные значения.
№ 7. В фермерском хозяйстве под гречиху было отведено два участка.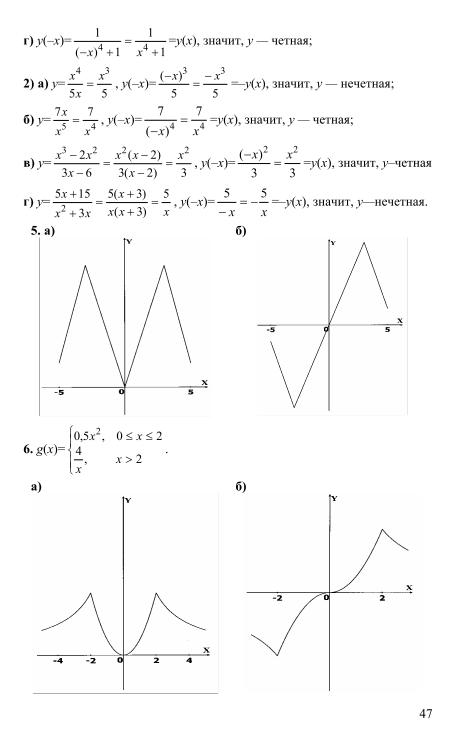
С первого собрали 105 ц гречихи, а со второго, площадь которого на 3 га больше, собрали 152 ц. Найдите площадь каждого участка, если известно, что урожайность гречихи на первом участке была на 2 ц с 1 га больше, чем на втором.
Алгебра 9 Макарычев К-9 В-1 ОТВЕТЫ:
КР-9. Ответы на Вариант 1.№ 1. х – у.
№ 2. (0; –1), (2;–3).
№ 3. [2,5; +∞). 4. а11.
№ 5. [2; 2,5].
№ 6. При x < –2 и x > 2.
№ 7. 5 и 8 га.
Смотреть РЕШЕНИЯ заданий Варианта 1 в тетради
Алгебра 9 Макарычев К-9 В-1. Итоговая контрольная работа по алгебре за 9 класс с ответами и решениями.
Другие варианты: К-9 Вариант 2 К-9 Вариант 3 К-9 Вариант 4
В учебных целях использованы цитаты из пособия:
«Алгебра. Дидактические материалы 9 класс / Макарычев, Миндюк, Крайнева — М.: Просвещение».
Представленная контрольная работа ориентирована на УМК Макарычева. Ответы адресованы родителям, которые смогут проконтролировать правильность выполнения заданий. Цитаты представлены в учебных целях, а также для ознакомления и покупки указанного учебного пособия.Список контрольных работ по алгебре в 9 классе для УМК Макарычев (Оглавление)
Контрольные работы по алгебре 9 класс (Макарычев Ю.Н.) | Материал по алгебре (9 класс) на тему:
Контрольная работа №9 (итоговая) 9 класс (Макарычев)
Вариант 1.
- Сократите дробь .
- Решите неравенство 5х – 7 ≥ 7х – 5.
- Решите уравнение х2 – 10х + 25 = 0.
- Сравните 56,78 ∙ 106 и 5,687 ∙ 107.
- Решите систему уравнений:
- Постройте график функции у = 7х – 5 и найдите, при каких значениях х значения у не меньше – 40.
- В арифметической прогрессии второй член равен 9, а разность равна 20. Найдите десятый член этой прогрессии и сумму первых десяти ее членов.
- Моторная лодка прошла против течения реки 8 км и вернулась обратно, затратив на обратный путь на 30 мин меньше, чем при движении против течения. Найдите скорость лодки в неподвижной воде, если скорость течения равна 4 км/ч.
- Сократите дробь .
- Решите неравенство
Контрольная работа №9 (итоговая) 9 класс (Макарычев)
Вариант 2
- Сократите дробь .
- Решите неравенство 3х – 8 ≥ 8х – 3.
- Решите уравнение х2 – 14х + 49 = 0.
- Сравните 4,567 ∙ 109 и 45,76 ∙ 108.
- Решите систему уравнений:
- Постройте график функции у = 6х – 7 и найдите, при каких значениях х значения у не больше – 49.
- В арифметической прогрессии второй член равен 11, а разность равна 30. Найдите десятый член этой прогрессии и сумму первых десяти ее членов.
- Моторная лодка прошла против течения реки 21 км и вернулась обратно, затратив на обратный путь на 20 мин меньше, чем при движении против течения. Найдите скорость лодки в неподвижной воде, если скорость течения равна 2 км/ч.
- Сократите дробь .
- Решите неравенство
Контрольная работа №9 (итоговая) 9 класс (Макарычев)
Вариант 1.
- Сократите дробь .
- Решите неравенство 5х – 7 ≥ 7х – 5.
- Решите уравнение х2 – 10х + 25 = 0.
- Сравните 56,78 ∙ 106 и 5,687 ∙ 107.
- Решите систему уравнений:
- Постройте график функции у = 7х – 5 и найдите, при каких значениях х значения у не меньше – 40.
- В арифметической прогрессии второй член равен 9, а разность равна 20. Найдите десятый член этой прогрессии и сумму первых десяти ее членов.
- Моторная лодка прошла против течения реки 8 км и вернулась обратно, затратив на обратный путь на 30 мин меньше, чем при движении против течения. Найдите скорость лодки в неподвижной воде, если скорость течения равна 4 км/ч.
- Сократите дробь .
- Решите неравенство
Контрольная работа №9 (итоговая) 9 класс (Макарычев)
Вариант 2
- Сократите дробь .
- Решите неравенство 3х – 8 ≥ 8х – 3.
- Решите уравнение х2 – 14х + 49 = 0.
- Сравните 4,567 ∙ 109 и 45,76 ∙ 108.
- Решите систему уравнений:
- Постройте график функции у = 6х – 7 и найдите, при каких значениях х значения у не больше – 49.
- В арифметической прогрессии второй член равен 11, а разность равна 30. Найдите десятый член этой прогрессии и сумму первых десяти ее членов.
- Моторная лодка прошла против течения реки 21 км и вернулась обратно, затратив на обратный путь на 20 мин меньше, чем при движении против течения. Найдите скорость лодки в неподвижной воде, если скорость течения равна 2 км/ч.
- Сократите дробь .
- Решите неравенство
Алгебра 9 Макарычев Контрольная № 1 с ответами
Контрольная работа № 1 по алгебре с ответами по УМК Макарычев и др. (Просвещение) Ответы на контрольные работы адресованы родителям, которые смогут проконтролировать правильность выполнения задания. Алгебра 9 Макарычев Контрольная № 1.
Цитаты использованы в учебных целях.
Алгебра 9 класс (Макарычев)
Контрольная работа № 1 Алгебра 9 класс (Макарычев) Контрольная работа № 1
К—1 (§ 1, 2). Вариант 1 (транскрипт):
• 1. Дана функция f(x)= 17х — 51. При каких значениях аргумента f(x) = 0, f(x) < 0, f(x) > 0? Является ли эта функция возрастающей или убывающей?
• 3. Сократите дробь
4. Область определения функции g (рис. 17) — отрезок [-2; 6]. Найдите нули функции, промежутки возрастания и убывания, область значений функции.
5. Сумма положительных чисел а и b равна 50. При каких значениях а и b их произведение будет наибольшим?
К—1 (§ 1, 2). Вариант 2 (транскрипт):
• 1. Дана функция g(x) = — 13х + 65. При каких значениях аргумента g(x) = 0, g(x) < О, g(x) > О? Является ли эта функция возрастающей или убывающей?
• 2. Разложите на множители квадратный трехчлен:
• 3. Сократите дробь
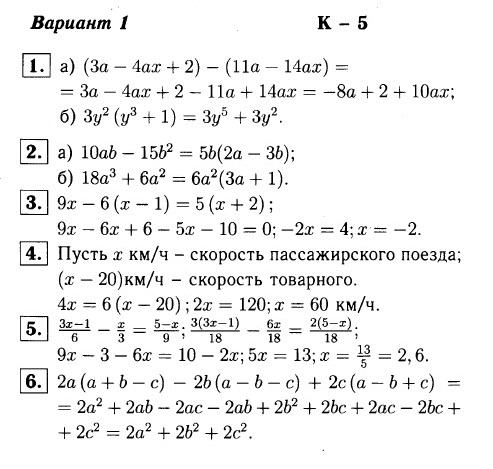Область определения функции f (рис. 18) — отрезок [-5; 4]. Найдите нули функции, промежутки возрастания и убывания, область значений функции.5. Сумма положительных чисел с и d равна 70. При каких значениях с и d их произведение будет наибольшим?
ОТВЕТЫ на контрольную работу:
Вернуться к Списку контрольных работ по алгебре 9 класс (Макарычев)
Вы смотрели: Контрольная работа № 1 по алгебре с ответами по УМК Макарычев и др. (Просвещение) Ответы на контрольные работы адресованы родителям, которые смогут проконтролировать правильность выполнения задания. Алгебра 9 Макарычев Контрольная № 1. Цитаты использованы в учебных целях.
Контрольные работы по алгебре 9 класс К учебнику Макарычева Глазков
Пособие 9 класса с самостоятельными-контрольными работами Глазкова, Варшавского, Гаиашвили к учебнику Макарычева по алгебре соответствует ФГОС ООО. Необходимое приложение к вышеуказанному учебнику Макарычева, рекомендованному МО РФ, состоящему ФПУ.
Содержит 18 самостоятельных, 6 контрольных работ. Они помогут формировать знания, умения, навыки уч-ся, предусмотренные курсом алгебры. Предназначены для оперативного контроля результатов обучения. Все работы представлены 4 вар-ми равной трудности. Содержит также ответы, рекомендации для подсчета баллов. Рекомендованное время выполнения одной самостоятельной работы — 30 м., а контрольной работы — 40. Выполнение работ поможет лучше освоить материал, даст учителям оперативную информацию о степени его усвоения. Адресован учителям, школьникам.ОГЛАВЛЕНИЕ
Предисловие 05
САМОСТОЯТЕЛЬНЫЕ РАБОТЫ 8
Функции их свойства 08
Квадратный трехчлен 15
Квадратичная функция ее график 17
Степенная функция. 22
Уравнения содной переменной 26
Дробные рациональные уравнения 29
Неравенства содной переменной 33
Уравнения сдвумя переменными 36
Неравенства сдвумя переменными 42
Арифметическая прогрессия 48
Геометрическая прогрессия 51
Элементы комбинаторики 55
58Итоговое повторение. 62
Итоговое повторение. 67
Итоговое повторение. 76
Итоговое повторение. 80
Итоговое повторение. 86
КОНТРОЛЬНЫЕ РАБОТЫ 90
Функции их свойства. 91
Степенная функция. 98
Неравенства содной переменной. 102
Неравенства сдвумя переменными Арифметическая — геометрическая прогрессии 107
Элементы комбинаторики …. 112
Ответы 131
Размер файла: 1 Мб; Формат: pdf/
Вместе с «Контрольные работы по алгебре 9 класс К учебнику Макарычева Глазков» скачивают:
ГДЗ к дидактическим материалам по алгебре 9 класс Макарычев
Издательство: Просвещение
Авторы: Ю.
Н. Макарычев, Н.Г. Миндюк, Л.Б. Крайнева
ГДЗ и решебник к дидактическим материалам по алгебре за 9 класс, авторов Макарычев, Миндюк, Крайнева 2014. Решение и ответы к контрольным и самостоятельным работам по алгебре за 9 класс.
Дополнительные упражнения для выпускника основной школы – шанс лучше подготовиться к экзаменам. В решебник по алгебре 9 класс (дидактические материалы, авторская разработка Макарычева) включены задания на все темы для более полного их усвоения и тренировки перед испытаниями.
Развернуто-детальные пояснения, включающие основные теоретические знания девятиклассника, помогают понять логику решения уравнений. Анализируя информацию, щедро предоставленную автором, ученик сможет выполнить конкретное задание и приобрести уверенность в своем умении их применять.
- Гдз по Алгебре за 9 класс можно найти тут
Самостоятельные работы
Контрольные работы
Итоговое повторение
Уравнения и неравенства с одной переменной
Уравнения и неравенства с двумя переменными
Арифметическая и геометрическая прогрессии
Элементы комбинаторики и теории вероятностей
Итоговый тест
Подпишись на нашу группу
Итоговая контрольная работа по алгебре 9 класс по учебнику Макарычева
Итоговая контрольная работа по алгебре 9 класс
Вариант 1
I часть (5 баллов)
В задании 1– 5 запиши ответ.
Верный ответ каждого задания оценивается одним баллом.
Функция задана формулой . Найдите .
Ответ:__________
При каких значениях х не определена функция
Ответ:__________
Найдите значение выражения .
Ответ:__________
Первый член арифметической прогрессии , а ее разность . Найдите восьмой член прогрессии.
Сколькими способами можно выбрать двух дежурных из 10 школьников.
Ответ:__________
II часть ( 4 балла)
Решение заданий 6 – 7 может иметь краткую запись без обоснования. Правильное решение каждого задания оценивается двумя баллами.
Решите систему уравнений
Постройте график функции . Найдите промежутки, на которых функция возрастает.
ІІІ часть (3 балла)
Решение 8 задания должно иметь обоснование.
Необходимо записать последовательные логические действия и объяснения. Правильное решение задания оценивается тремя баллами.
Найдите четыре числа, образующих геометрическую прогрессию, если первое число меньше третьего на 36, а второе меньше четвертого на 12.
Составила: Смолякова Ю.Л.
учитель математики
МОУ «Школа №48 г. Донецка»
Итоговая контрольная работа по алгебре 9 класс
Вариант 2
I часть (5 баллов)
В задании 1– 5 запиши ответ. Верный ответ каждого задания оценивается одним баллом.
Функция задана формулой . Найдите .
Ответ:__________
При каких значениях х не определена функция
Ответ:__________
Найдите значение выражения .
Ответ:__________
Первый член арифметической прогрессии , а ее разность .
Найдите девятый член прогрессии.
Ответ:__________
Сколькими способами можно выбрать из 12 учеников трех участников для участия в спартакиаде?
Ответ:__________
II часть ( 4 балла)
Решение заданий 6 – 7 может иметь краткую запись без обоснования. Правильное решение каждого задания оценивается двумя баллами.
Решите систему уравнений
Постройте график функции . Найдите промежутки, на которых функция убывает.
ІІІ часть (3 балла)
Решение 8 задания должно иметь обоснование. Необходимо записать последовательные логические действия и объяснения. Правильное решение задания оценивается тремя баллами.
Найдите четыре числа, образующих геометрическую прогрессию, у которой первый член больше третьего на 6, а второй – меньше четвертого на 3.
Составила: Смолякова Ю.
Л.
учитель математики
МОУ «Школа №48 г. Донецка»
ГДЗ к РТ по алгебре за 9 класс
Ответы на задания по алгебре за девятый класс к рабочей тетради Макарычев Ю.Н. Миндюк Н.Г. Крайнева Л.Б., Короткова Л.М.
Дидактические материалы Макарычев, Миндюк, Крайнева:Задания для школьных олимпиад:
Весенняя олимпиада: 12345678
Осенняя олимпиада: 12345678
Итоговое повторение по темам:
Арифметическая и геометрическая прогрессии: 123456789101112131415
Уравнения и неравенства с двумя переменными: 123456789101112
Уравнения и неравенства с одной переменной: 123456789101112131415161718
Функции: 123456789101112131415161718192021
Элементы комбинаторики и теории вероятностей: 12345678910111213141516171819
Итоговый тест: Вариант 1Вариант 2
Контрольные работы:
К-1:
Вариант 1: 12345
Вариант 2: 12345
Вариант 3: 12345
Вариант 4: 12345
К-2:
Вариант 1: 12345
Вариант 2: 12345
Вариант 3: 12345
Вариант 4: 12345
К-3:
Вариант 1: 12345
Вариант 2: 12345
Вариант 3: 12345
Вариант 4: 12345
К-4:
Вариант 1: 12345
Вариант 2: 12345
Вариант 3: 12345
Вариант 4: 12345
К-5:
Вариант 1: 12345
Вариант 2: 12345
Вариант 3: 12345
Вариант 4: 12345
К-6:
Вариант 1: 12345
Вариант 2: 12345
Вариант 3: 12345
Вариант 4: 12345
К-7:
Вариант 1: 12345
Вариант 2: 12345
Вариант 3: 12345
Вариант 4: 12345
К-8:
Вариант 1: 123456
Вариант 2: 123456
Вариант 3: 123456
Вариант 4: 123456
К-9:
Вариант 1: 1234567
Вариант 2: 1234567
Вариант 3: 1234567
Вариант 4: 1234567
Самостоятельные работы:
Вариант 1:С-1: 12345
С-2: 12345
С-3: 12345678
С-4: 12345
С-5: 12345
С-6: 123456
С-7: 123456
С-8: 123456
С-9: 123456
С-10: 1234567
С-11: 12345678
С-12: 123456
С-13: 12345678910
С-14: 12345678
С-15: 12345678
С-16: 123456
С-17: 12345
С-18: 123456
С-19: 123456
С-20: 123456
С-21: 1234567
С-22: 1234567
С-23: 12345
С-24: 1234
С-25: 12345678
С-26: 12345678910
С-27: 12345678910
С-28: 12345678910
С-29: 12345678
С-30: 12345678
С-31: 1234567
С-32: 1234567
Вариант 2:С-1: 12345
С-2: 12345
С-3: 12345678
С-4: 12345
С-5: 12345
С-6: 123456
С-7: 123456
С-8: 123456
С-9: 123456
С-10: 1234567
С-11: 12345678
С-12: 123456
С-13: 12345678910
С-14: 12345678
С-15: 1234568
С-16: 1234567
С-17: 12345
С-18: 123456
С-19: 123456
С-20: 123456
С-21: 1234567
С-22: 1234567
С-23: 12345
С-24: 1234
С-25: 12345678
С-26: 12345678910
С-27: 12345678910
С-28: 12345678910
С-29: 12345678
С-30: 12345678
С-31: 1234567
С-32: 1234567
Дидактические материалы Макарычев, Миндюк, Короткова:
Итоговая работа.
Телжаков:
Квадратная функция:123456789101112131415
Прогрессия:1234567891011121314151617
Степени:123456789101112131415161718
Тригонометрия:12345678910111213141516
Уравнения:123456789101112
Итоговая работа. Тихонов:
Прогрессия:123456789101112131415161718192021
Рациональные показатели:12345678910111213141516171819
Степенная функция:123456789101112131415161718192021222324
Тригонометрия:12345678910111213141516171819202122232425262728
Контрольные работы:
K-1А:
Вариант 1:12345
Вариант 2:12345
Вариант 3:12345
Вариант 4:12345
K-1:
Вариант 1:12345
Вариант 2:12345
Вариант 3:12345
Вариант 4:12345
K-2A:
Вариант 1:12345
Вариант 2:12345
Вариант 3:12345
Вариант 4:12345
K-2:
Вариант 1:123456
Вариант 2:123456
Вариант 3:123456
Вариант 4:123456
K-3:
Вариант 1:1234
Вариант 2:1234
Вариант 3:1234
Вариант 4:1234
K-3A:
Вариант 1:1234
Вариант 2:1234
Вариант 3:1234
Вариант 4:1234
K-4:
Вариант 1:12345
Вариант 2:12345
Вариант 3:12345
Вариант 4:1
K-4A:
Вариант 1:12345
Вариант 2:12345
Вариант 3:12345
Вариант 4:12345
K-5:
Вариант 1:12345
Вариант 2:12345
Вариант 3:12345
Вариант 4:12345
K-5A:
Вариант 1:1234
Вариант 2:1234
Вариант 3:1234
Вариант 4:1234
K-6:
Вариант 1:12345
Вариант 2:12345
Вариант 3:12345
Вариант 4:12345
K-6A:
Вариант 1:12345
Вариант 2:12345
Вариант 3:12345
Вариант 4:12345
K-7:
Вариант 1:12345
Вариант 2:12345
Вариант 3:12345
Вариант 4:12345
K-7A:
Вариант 1:12345
Вариант 2:12345
Вариант 3:12345
Вариант 4:12345
K-8:
Вариант 1:12345
Вариант 2:12345
Вариант 3:12345
Вариант 4:12345
K-8A:
Вариант 1:12345
Вариант 2:12345
Вариант 3:12345
Вариант 4:12345
K-9A:
Вариант 1:1234567
Вариант 2:1234567
Вариант 3:1234567
Вариант 4:1234567
K-9:
Вариант 1:1234
Вариант 2:1234
Вариант 3:1234
Вариант 4:1234
K-10:
Вариант 1:1234567
Вариант 2:1234567
Вариант 3:1234567
Вариант 4:1234567
Олимпиады:
Весна:12345678
Осень:12345678
Самостоятельные работы:
Вариант 1:
C-1:1234567
C-2:12345678
C-3:12345
C-4:12345
C-5:12345
C-6:123456
C-7:1234567
C-8:12345678
C-9:1234567
C-10:12345
C-11:123456
C-12:12345678910
C-13:123456789
C-14:123456
C-15:1234567
C-16:1234567
C-17:12345678
C-18:12345678910
C-19:12345678910
C-20:12345678910
C-21:12345678
C-22:123456
C-23:12345
C-24:1234567
C-25:1234567
C-26:12345678
C-27:12345678910
C-28:12345678
C-29:12345
C-30:1234567
C-31:123456
C-32:1234567
C-33:1234
C-34:12345678910
C-35:12345
C-36:1234567891011
C-37:123456891011
C-38:1234567
C-39:1234567
C-40:123456
C-41:12345678
C-42:12345
C-43:1234567
C-44:1234
C-45:123456
C-46:123467
C-47:123456
C-48:1234567
Вариант 2:
C-1:1234567
C-2:12345678
C-3:12345
C-4:12345
C-5:12345
C-6:123456
C-7:1234567
C-8:12345678
C-9:1234567
C-10:12345
C-11:123456
C-12:12345678910
C-13:123456789
C-14:123456
C-15:1234567
C-16:1234567
C-17:12345678
C-18:12345678910
C-19:12345678910
C-20:12345678910
C-21:12345678
C-22:123456
C-23:12345
C-24:1234567
C-25:1234567
C-26:12345678
C-27:12345678910
C-28:12345678
C-29:12345
C-30:1234567
C-31:123456
C-32:134567
C-33:1234
C-34:12345678910
C-35:12345
C-36:123457891011
C-37:1234567891011
C-38:1234567
C-39:1234567
C-40:123456
C-41:12345678
C-42:12345
C-43:1234567
C-44:1234
C-45:123456
C-46:1234567
C-47:123456
C-48:1234567
Повторение к главам 7-9:
Вариант 1:
П-1:1234
П-2:1234567891011
П-3:12345678910111213
П-4:12345678910111213141516
Вариант 2:
П-1:1234
П-2:123457891011
П-3:12345678910111213
П-4:12345678910111213141516
Поделись ответами с друзьями в социальных сетях:
| Сессия 1A Председатель: Катрина Лигетт Место проведения: Grand Ballroom | Сессия 1B Председатель: Ола Свенссон Расположение: Crystal Ballroom | |
| 8: 55-9: 15 | Коды для снятия отпечатков пальцев и приблизительная стоимость дифференциальной конфиденциальности Марк Бун, Джонатан Ульман, Салил Вадхан | Округление релаксации по сумме квадратов Боаз Барак, Джонатан А.  Кельнер, Дэвид Штюрер |
| 9: 20-9: 40 | Анализ Гаусса: оптимальные границы для сохранения конфиденциальности PCA Синтия Дворк, Кунал Талвар, Абхрадип Такурта, Ли Чжан | Аппроксимация постоянного коэффициента для сбалансированной резки в модели PIE Константин Макарычев, Юрий Макарычев, Аравиндан Виджаярагаван |
| 9: 45-10: 05 | Частные сопоставления и распределения Джастин Хсу, Чжийи Хуанг, Аарон Рот, Тим Рафгарден, Чживей Стивен Ву | Энтропия, оптимизация и подсчет Мохит Сингх, Нишит К.Вишной |
| 10: 05-10: 30 | Кофе-брейк | |
| Сессия 2A Председатель: Грегори Вэлиант Место: Grand Ballroom | Сессия 2B Председатель: Крис Уманс Расположение: Crystal Ballroom | |
| 10: 30-10: 50 | Полиномиальные границы для сеточной минорной теоремы Чандра Чекури, Юлия Чужой | Генераторы псевдослучайных чисел с оптимальной длиной начального числа для небулевых многоразмерных схем Сергей Артеменко, Ронен Шалтиэль |
| 10: 55-11: 15 | Теорема об исключенной полуинтегральной сетке для орграфов и задача направленных непересекающихся путей Кен-ичи Каварабаяши, Юсуке Кобаяши, Стефан Кройцер | Об алгоритмах дерандомизации, которые очень редко дают ошибки Одед Голдрайх, Ави Вигдерсон |
| 11: 20-11: 40 | Полицейские, грабители и угрожающие скелеты: мягкая декомпозиция для графов без второстепенных Иттай Абрахам, Сирил Гавой, Анупам Гупта, Офер Нейман, Кунал Талвар | Суперполиномиальные нижние оценки для однородных арифметических формул глубины 4 Нирадж Каял, Нутан Лимае, Чандан Саха, Шрикант Сринивасан |
| Нижние оценки для формул глубины 4, вычисляющих итеративное матричное умножение Эрве Фурнье, Нутан Лимай, Гийом Малод, Срикант Сринивасан | ||
| 11: 45-12: 05 | Определение свойств первого порядка нигде не плотных графов Мартин Гроэ, Стефан Крейцер, Себастьян Зиберц | Пределы уменьшения глубины для арифметических формул: все дело в верхнем веером Мринал Кумар, Шубханги Сараф |
| Суперполиномиальная нижняя оценка регулярных арифметических формул Нирадж Каял, Чандан Саха, Рампрасад Саптариши | ||
| 12: 05–1: 25 | Обед (самостоятельно) | |
| Сессия 3A Председатель: Ронитт Рубинфельд Место проведения: Grand Ballroom | Сессия 3B Председатель: Адам Смит Расположение: Crystal Ballroom | |
| 1: 30–1: 50 | Характеристика локально проверяемых аффинно-инвариантных свойств с помощью теорем разложения Юичи Йошида | Новые алгоритмы и нижние границы для схем с линейными пороговыми вентилями Райан Вильямс |
| 1: 55–2: 15 | L p -Testing Петр Берман, Софья Расходникова, Григорий Ярославцев | Формулы vs. Схемы для подключения на малых расстояниях Benjamin Rossman |
| 2: 20–2: 40 | Алгоритмы потоковой передачи турникета могут также быть линейными эскизами Йи Ли, Хай Л. Нгуен, Дэвид П. Вудрафф | На пути к более точным нижним границам формулы: подход с информационной сложностью к гипотезе о композиции KRW Дмитрий Гавинский, Ор Меир, Омри Вайнштейн, Ави Вигдерсон |
| 2: 45-3: 05 | Построение в линейном времени индексов сжатого текста в компактном пространстве Джамал Белаззуги | Преодоление барьера Мински-Паперта для цепей постоянной глубины Александр А.Шерстов |
| 3: 05-3: 30 | Кофе-брейк | |
| Сессия 4A Председатель: Брендан Люсьер Место проведения: Grand Ballroom | Сессия 4B Председатель: Томас Видик Расположение: Crystal Ballroom | |
| 3: 30-3: 50 | Экономическая эффективность требует взаимодействия Шахар Добзински, Ноам Нисан, Сигал Орен | Гомологические коды продуктов Сергей Бравый, Мэтью Гастингс |
| 3: 55-4: 15 | Образец сложности максимизации доходов Ричард Коул, Тим Рафгарден | Экспоненциальное улучшение точности для моделирования разреженных гамильтонианов Dominic W.  Берри, Эндрю М. Чайлдс, Ричард Клив, Робин Котари, Роландо Д. Сомма |
| 4: 20-4: 40 | Оптимальные конкурентные аукционы Нинг Чен, Ник Гравин, Пиньян Лу | Квантовый алгоритм для вычисления группы единиц произвольного числового поля степени Кирстен Эйзентрагер, Шон Халлгрен, Алексей Китаев, Фанг Сонг |
| Пленарные доклады Председатель: Давид Шмойс Расположение: Большой бальный зал | ||
| 4: 55-5: 15 | Соответствующий многогранник имеет экспоненциальную сложность расширения Thomas Rothvoss | |
| 5: 30-7: 30 | Лекции по премии Тьюринга Шафи Гольдвассер, Сильвио Микали | |
| Сессия 5A Председатель: Нихил Бансал Расположение: Большой бальный зал | Сессия 5B Председатель: Катрина Лигетт Расположение: Crystal Ballroom | |
| 8: 55-9: 15 | Primal Beats Dual on Online Packing LP в модели случайного порядка Thomas Kesselheim, Klaus Radke, Andreas Toennis, Berthold Voecking | Эффективный параллельный решатель для линейных систем SDD Ричард Пенг, Дэниел А.  Шпильман |
| 9: 20-9: 40 | Соревновательные алгоритмы на основе конкурентных равновесий: планирование без ясновидения при многогранных ограничениях Сунгджин Им, Джанардхан Кулкарни, Камеш Мунагала | Решение линейных систем SDD почти за миллионы 1/2 n Время Майкл Б. Коэн, Расмус Кинг, Гэри Л. Миллер, Якуб В. Пачоцки, Ричард Пэн, Ануп Рао, Шен Чен Сюй |
| 9: 45-10: 05 | Минимальное деление пополам фиксировано Параметр Tractable Марек Циган, Даниэль Локштанов, Марчин Пилипчук, Михал Пилипчук, Сакет Саураб | Оптимальные разложения матрицы CUR Христос Буцидис, Дэвид П.Вудрафф |
| 10: 05-10: 30 | Кофе-брейк | |
| Сессия 6A Председатель: Борис Аронов Место проведения: Большой бальный зал | Сессия 6B Председатель: Винод Вайкунтанатан Расположение: Crystal Ballroom | |
| 10: 30-10: 50 | От иерархических разделов к иерархическим покрытиям: оптимальные отказоустойчивые ключи для удвоения показателей Shay Solomon | Подбрасывание монет при любом постоянном смещении подразумевает одностороннее движение Итай Берман, Ифтах Хайтнер, Арис Тентес |
| 10: 55-11: 15 | Кратчайшие пути на многогранных поверхностях и ландшафтах Siu-Wing Cheng, Jiongxin Jin | Почти оптимально справедливый протокол трехстороннего подбрасывания монет Ифтах Хайтнер, Элиад Цфадиа |
| 11: 20-11: 40 | Вложение и канонизация графов ограниченного рода в логическое пространство Майкл Эльберфельд, Кен-ичи Каварабаяши | Надежные протоколы для безопасного расширения случайности и распределения ключей с использованием ненадежных квантовых устройств Карл А.  Миллер, Яоюнь Ши |
| 11: 45-12: 05 | Контрольная площадь поверхности с произвольной точностью Джо Ниман | Бесконечное расширение случайности с постоянным числом устройств Мэтью Кудрон, Генри Юэн |
| 12: 05–1: 45 | Обед (предоставляется на конференции) | |
| Сессия 7A Председатель: Нихил Бансал Расположение: Grand Ballroom | Сессия 7B Председатель: Адам Смит Расположение: Crystal Ballroom | |
| 1: 45-2: 05 | Средняя чувствительность пересечения полупространств Дэниел М.Кейн | Как использовать обфускацию неразличимости: отрицательное шифрование и многое другое Амит Сахаи, Брент Уотерс |
| 2: 10–2: 30 | От средней сложности к неправильной сложности обучения Амит Даниэли, Нати Линиал, Шай Шалев-Шварц | Как делегировать вычисления: сила доказательств отсутствия сигналов Яэль Тауман Калаи, Ран Раз, Рон Д.  Ротблюм |
| 2: 35-2: 55 | Сила локализации для эффективного изучения линейных разделителей с шумом Пранджал Авасти, Мария Флорина Балкан, Филип М.Длинный | Цепи, устойчивые к аддитивным атакам с приложениями для защиты вычислений Даниэль Генкин, Юваль Ишаи, Манодж М. Прабхакаран, Амит Сахаи, Эран Тромер |
| 3: 00–3: 20 | Бандиты с расходами на переключение: T 2/3 Сожаление Офер Декель, Цзянь Дин, Томер Корен, Ювал Перес | О существовании извлекаемых односторонних функций Нир Битански, Ран Канетти, Омер Панет, Алон Розен |
| 3: 25–3: 45 | Онлайн-изучение локальной структуры с помощью полуопределенного программирования Paul F.Кристиано | Black-Box Non-Black-Box Zero Knowledge Vipul Goyal, Rafail Ostrovsky, Alessandra Scafuro, Ivan Visconti |
| 3: 45-4: 15 | Кофе-брейк | |
| Сессия 8A Председатель: Брендан Люсьер Место проведения: Grand Ballroom | Сессия 8B Председатель: Миккель Торуп Расположение: Crystal Ballroom | |
| 4: 15-4: 35 | Дихотомии в вычислении равновесия и дополнительные алгоритмы поворота для нового класса неотделимой полезности Джугал Гарг, Рута Мехта, Виджай В.  Вазирани | Алгоритмы аппроксимации для двустороннего сопоставления с метрическими и геометрическими затратами Панкадж К. Агарвал, Р. Шараткумар |
| 4: 40-5: 00 | Сложность запроса приближенного равновесия Нэша Яков Бабиченко | Алгоритмы распределенной аппроксимации для взвешенных кратчайших путей Danupon Nanongkai |
| 5: 05-5: 25 | Постоянный рейтинг Bimatrix Games: PPAD-Hard Ruta Mehta | Параллельные алгоритмы для задач геометрического графа Александр Андони, Александр Николов, Кшиштоф Онак, Григорий Ярославцев |
| 8: 30-10: 30 | Деловая встреча (Большой бальный зал) | |
| Сессия 9A Председатель: Давид Шмойс Расположение: Большой бальный зал | Сессия 9B Председатель: Томас Видик Расположение: Crystal Ballroom | |
| 8: 55-9: 15 | PCA Фурье и надежная тензорная декомпозиция Navin Goyal, Santosh Vempala, Ying Xiao | Твердость окраски суперполилогарифмического гиперграфа с помощью длинных кодов низкой степени Венкатесан Гурусвами, Прахладх Харша, Йохан Хастад, Срикантх Шринивасан, Гириш Варма |
| 9: 20-9: 40 | Сглаженный анализ тензорных разложений Адитья Бхаскара, Моисей Чарикар, Анкур Моитра, Аравиндан Виджаярагаван | Аналитический подход к параллельным повторениям Ирит Динур, Дэвид Стеурер |
| 9: 45-10: 05 | Эффективная оценка плотности с помощью кусочно-полиномиальной аппроксимации Сиу Он Чан, Илиас Диакониколас, Рокко Серведио, Сяоруй Сан | Характеристика сопротивления сильной аппроксимации Субхаш Хот, Мадхур Тулсиани, Пратик Вора |
| 10: 05-10: 30 | Кофе-брейк | |
| Сессия 10A Председатель: Ола Свенссон Место проведения: Grand Ballroom | Сессия 10B Председатель: Миккель Торуп Расположение: Crystal Ballroom | |
| 10: 30-10: 50 | Сильно полиномиальный алгоритм максимизации обобщенного потока Ласло А.  Vegh | Зигзагообразная сортировка: простой детерминированный алгоритм сортировки без учета данных, выполняющийся за O (n log n) времени Майкл Т. Гудрич |
| 10: 55-11: 15 | Оракулы приблизительного расстояния с постоянным временем запроса Шири Чечик | Пороги обнаружения сообщества и слабое свойство Рамануджана Laurent Massoulie |
| 11: 20-11: 40 | Более быстрые кратчайшие пути для всех пар за счет сложности схемы Райан Уильямс | Распределенная вычислимость в византийских асинхронных системах Хаммурапи Мендес, Кристин Тассон, Морис Херлихи |
| 11: 45-12: 05 | Сублинейные декрементальные алгоритмы для достижимости от одного источника и кратчайших путей на ориентированных графах Моника Хензингер, Себастьян Кринингер, Данупон Нанонгкай | Являются ли параллельные алгоритмы без блокировок практически без ожидания? Дан Алистарх, Керен Ценсор-Гиллель, Нир Шавит |
| 12: 05–1: 45 | Обед (самостоятельно) | |
| Сессия 11A Председатель: Нихил Бансал Расположение: Grand Ballroom | Сессия 11B Председатель: Марк Браверман Расположение: Crystal Ballroom | |
| 1: 45-2: 05 | Многосторонний разрез, попарно реализуемые распределения и нисходящие пороги Анкит Шарма, Ян Вондрак | Каждый кодируемый списком код для высокого уровня шума имеет обильную частоту прокалывания, близкую к оптимальной Атри Рудра, Мэри Вуттерс |
| 2: 10–2: 30 | Кластер до того, как вы увидите галлюцинации: приблизительный дизайн сети с емкостью узлов и энергоэффективная маршрутизация Равишанкар Кришнасвами, Вишванат Нагараджан, Кирк Прухс, Клифф Штайн | Неповоротливые коды из аддитивной комбинаторики Дивеш Аггарвал, Евгений Додис, Шахар Ловетт |
| 2: 35-2: 55 | Алгоритмы аппроксимации для маршрутизации транспортных средств с ограничением сожаления и приложений для маршрутизации транспортных средств с ограничением расстояния Zachary Friggstad, Chaitanya Swamy | Преодоление квадратичного барьера для 3 LCC над реалами Зеев Двир, Шубханги Сараф, Ави Вигдерсон |
| 3: 00–3: 20 | Улучшенные алгоритмы аппроксимации для задач проектирования сети с ограниченными степенями и требованиями к подключению узлов Алина Эне, Али Вакилиан | Оптимальная частота ошибок для интерактивного кодирования I: адаптивность и другие настройки Мохсен Гаффари, Бернхард Хеплер, Мадху Судан |
| 3: 20-3: 50 | Кофе-брейк | |
| Сессия 12A Председатель: Давид Шмойс Расположение: Большой бальный зал | Сессия 12B Председатель: Марк Браверман Расположение: Crystal Ballroom | |
| 3: 50-4: 10 | Асимптотический порог k-SAT Amin Coja-Oghlan | Связь ограничена корнем ранга Шахар Ловетт |
| 4: 15-4: 35 | Порог соответствия для случайного регулярного теста NAE-SAT Цзян Дин, Аллан Слай, Nike Sun | Нижние границы связи через чувствительность критического блока Мика Гус, Тониан Питасси |
| 4: 40-5: 00 | Непроксимируемость для антиферромагнитных спиновых систем в области неединственности дерева Андреас Галанис, Даниэль Стефанкович, Эрик Вигода | Вычисления с полной памятью Гарри Бурман, Ричард Клив, Михал Коуки, Бруно Лофф, Флориан Спилман |
| 5: 05-5: 25 | Эффективный детерминированный приближенный счет для полиномиальных пороговых функций низкой степени Anindya De, Rocco A.Servedio | Наборы совпадений для полилинейных программ алгебраического разветвления с однократным чтением, в любом порядке Майкл А. Форбс, Рампрасад Саптариши, Амир Шпилка |
Якуб Опршал — Институт алгебры — ТУ Дрезден
Эта страница представляет собой отчет о моих исследованиях в качестве постдока, работающего над проектом ERC Мануэля Бодирски. Мое основное внимание было сосредоточено на применении универсальной алгебры к сложности бесконечного и многообещающего CSP.
Если вас интересуют мои текущие исследования, перейдите по адресу https://community.dur.ac.uk/jakub.oprsal/.
Препринты
Мои препринты на arXiv.
- с Якубом Булином, Андрей Крохин, Алгебраический подход к удовлетворению ограничений обещаний , препринт на arXiv.
- с Виктором Далмау, Марцином Козиком, Андреем Крохиным, Константином Макарычевым, Юрием Макарычевым, Робастные алгоритмы с полиномиальными потерями для почти единогласных CSP , препринт на arXiv.
ЖУРНАЛ Документы
- с Эрхардом Айхингером, Небойшей Мудрински, Сложность термальных представлений финитарных функций, Int. J. алгебры и вычислений. Vol. 28, No. 06, pp. 1101–1118 (2018) doi: 10.1142 / S0218196718500480. препринт на arXiv.
- с Libor Barto, Michael Pinsker, Страна чудес отражений , Isr. J. Math. (2018) 223: pp 363–398. DOI: 10.1007 / s11856-017-1621-9. http://rdcu.be/zYj8.
- Гипотеза о модулярности Тейлорса и связанные с ней проблемы для идемпотентных многообразий , Заказ 35 (2018) no.3: pp 433–460. DOI: 10.1007 / s11083-017-9441-4. http://rdcu.be/yAo1.
- Реляционное описание высших коммутаторов в алгебрах Мальцева , Algebra Univers. (2016), 76: 367–383. DOI: 10.1007 / s00012-016-0391-2.
- с Д. Донованом, Т. Григгсом, Т. МакКуртом, Д. Становски, Распределительные и антидистрибутивные тройные системы Мендельсона , Канадский математический бюллетень 59 (2016), нет. 1, 36–49. DOI: 10.4153 / CMB-2015-053-2.
Материалы конференции
- с Виктором Далмау, Марцином Козиком, Андреем Крохиным, Константином Макарычевым, Юрием Макарычевым, Надежные алгоритмы с полиномиальными потерями для почти единогласных CSP , Продолжение 28-го симпозиума ACM-SIAM.по дискретным алгоритмам, DOI: 10.1137 / 1.9781611974782.22.
- с А. Карпи, Г. Фичи Š. Голуб, М. Шортино, Universal Lyndon Words , MFCS 2014, LNCS, Vol. 8634, 2014, стр 135–146.
Конференц-переговоры
Удовлетворение ограничений обещаний , SSAOS, Шпиндлерув млин, 4 сентября 2018 г.
Блокаторы линейных условий Мальцева, Первая неделя алгебры, Сиена, 20 июня 2018 г.
- Алгебраический взгляд на выполнение ограничений обещания и жесткость раскраски d-раскрашиваемого графа в цвета 2d-1 , Schloß Dagstuhl, 5 июня 2018 г.
- О раскраске графа обещаний и условиях Мальцева , AAA96, Дармштадт, 1 июня 2018 г.
- Дополнение к функтору полиморфизма , AAA95, Братислава, 10 февраля 2018 г.
- Алгебраический подход к удовлетворению ограничений обещаний , BLAST 2017, Нэшвилл, Теннесси, 15 августа 2017 г.
- Бесконечные алгебры с несколькими подчиненными степенями , NSAC + AAA94, Нови-Сад, 15 июня 2017 г.
- Сложность термина в модулярных алгебрах сравнения , AAA93, Берн, 10 февраля 2017 г.
Зависящая от работы динамическая сложность формальных языков
1. Abboud, A., Backurs, A., Bringmann, K., Künnemann, M .: Детальная сложность анализа сжатых данных: количественная оценка улучшений по сравнению с распаковкой и решением . В: Уманс, К. (ред.) 58-й ежегодный симпозиум IEEE по основам компьютерных наук, FOCS 2017, Беркли, Калифорния, США, 15-17 октября 2017 г. С. 192–203. IEEE Computer Society (2017). 10.1109 / FOCS.2017.26
2.Аббуд, А., Бэкурс, А., Уильямс, В.В .: Если текущие алгоритмы клики оптимальны, то и синтаксический анализатор Valiant. SIAM J. Comput. 47 (6), 2527–2555 (2018)
3. Альструп, С., Хусфельдт, Т., Раухе, Т .: Динамические вложенные скобки. Инф. Comput. 193 (2), 75–83 (2004). 10.1016 / j.ic.2004.04.006, 10.1016 / j.ic.2004.04.006 [CrossRef]4. Бёргер, Э .: Абстрактные конечные автоматы: унифицированный вид моделей вычислений и структур проектирования систем. Аня. Pure Appl. Бревно. 133 (1-3), 149–171 (2005).10.1016 / j.apal.2004.10.007
5. Датта, С., Кулкарни, Р., Мукерджи, А., Швентик, Т., Цойме, Т .: Доступность в DynFO. J. ACM 65 (5), 33: 1–33: 24 (2018). 10.1145 / 3212685
6. Донг, Г., Су, Дж .: Инкрементальная оценка первого порядка запросов журнала данных. В: Языки программирования баз данных (DBPL-4), Труды четвертого международного семинара по языкам программирования баз данных — объектные модели и языки, Манхэттен, Нью-Йорк, США, 30 августа — 1 сентября 1993 г.стр. 295–308 (1993)
7. Донг, Г., Топор, Р. У .: Добавочная оценка запросов к журналу данных. В: Теория баз данных — ICDT’92, 4-я Международная конференция, Берлин, Германия, 14–16 октября 1992 г., Труды. С. 282–296 (1992). 10.1007 / 3-540-56039-4_48
8. Франдсен, Г.С., Хусфельдт, Т., Милтерсен, П.Б., Раухе, Т., Скайум, С .: Динамические алгоритмы для языков Дика. В: Akl, SG, Dehne, FKHA, Sack, J., Santoro, N. (eds.) Алгоритмы и структуры данных, 4-й международный семинар, WADS ’95, Кингстон, Онтарио, Канада, 16-18 августа 1995 г., Proceedings .Конспект лекций по информатике, т. 955. С. 98–108. Спрингер (1995). 10.1007 / 3-540-60220-8_54
9. Франдсен, Г.С., Милтерсен, П.Б., Скайум, С .: Динамические задачи с текстом. J. ACM 44 (2), 257–271 (1997). 10.1145 / 256303.256309
10. Галл Ф.Л .: Степени тензоров и быстрое умножение матриц. В: Международный симпозиум по символическим и алгебраическим вычислениям, ISSAC ’14, Кобе, Япония, 23-25 июля 2014 г., стр. 296–303 (2014)
11. Геладе, В., Марквардт, М., Швентик, Т. .: Динамическая сложность формальных языков. ACM Trans. Comput. Бревно. 13 (3), 19 (2012). 10.1145 / 2287718.2287719
12. Холм, Дж., Де Лихтенберг, К., Торуп, М .: Полилогарифмические детерминированные полностью динамические алгоритмы для связности, минимального остовного дерева, 2-ребер и двусвязности. J. ACM 48 (4), 723–760 (2001). 10.1145 / 502090.502095
13. Холм, Дж., Ротенберг, Э .: Полностью динамическое испытание планарности в полилогарифмическом времени. В кн .: Макарычев К., Макарычев Ю., Тулсиани, М., Камат, Г., Чужой, Дж. (Ред.) Материалы 52-го ежегодного симпозиума ACM SIGACT по теории вычислений, STOC 2020, Чикаго, Иллинойс, США, 22-26 июня 2020 г. 167–180. ACM (2020). 10.1145 / 3357713.3384249
14. Иммерман, Н .: Описательная сложность. Тексты для выпускников по информатике, Springer (1999). 10.1007 / 978-1-4612-0539-5
15. Иммерман, Н .: Описательная сложность. Springer Science & Business Media (2012)
16. JáJá, J .: Введение в параллельные алгоритмы.Аддисон-Уэсли (1992)
17. Либкин, Л .: Элементы теории конечных моделей. Спрингер (2004). 10.1007 / 978-3-662-07003-1
18. McNaughton, R., Papert, S .: Counter-Free Automata. MIT Press (1971)
19. Милтерсен, П. Б., Субраманиан, С., Виттер, Дж. С., Тамассия, Р.: Модели сложности для инкрементных вычислений. Теор. Comput. Sci. 130 (1), 203–236 (1994). 10.1016 / 0304-3975 (94) -7
20. Патнаик, С., Иммерман, Н .: Dyn-FO: параллельный динамический класс сложности.В: PODS. С. 210–221 (1994),
21. Шмидт, Дж., Швентик, Т., Тантау, Т., Вортмайер, Н., Цойме, Т .: Динамическая сложность формальных языков с учетом работы. CoRR abs / 2101.08735 (2021), https://arxiv.org/abs/2101.0873522. Швентик Т., Вортмайер Н., Цойме Т .: Эскизы динамической сложности. SIGMOD Рек. 49 (2), 18–29 (2020). 10.1145 / 3442322.3442325
23. Швентик, Т., Цойме, Т .: Динамическая сложность: последние обновления. SIGLOG News 3 (2), 30–52 (2016).10.1145 / 2948896.2948899
24. Шерлекар, Д.Д., Паваги, С., Рамакришнан, И.В .: O (1) параллельные алгоритмы инкрементного графа. В: Махешвари, С. (ред.) «Основы программных технологий и теоретической информатики», Пятая конференция, Нью-Дели, Индия, 16-18 декабря 1985 г., Труды. Конспект лекций по информатике, т. 206. С. 477–495. Спрингер (1985). 10.1007 / 3-540-16042-6_27
25. Штраубинг, Х .: Конечные автоматы, формальная логика и сложность схем. Биркхаузер Верлаг (1994)
26.Фоллмер, Х .: Введение в сложность схем: единый подход. Springer Science & Business Media (2013)
27. Уильямс В.В .: Умножение матриц быстрее, чем Копперсмит-Виноград. В: Karloff, H.J., Pitassi, T. (eds.) Proceedings of the 44th Symposium on Theory of Computing Conference, STOC 2012, New York, NY, USA, 19–22 мая 2012 г., стр. 887–898. ACM (2012). 10.1145 / 2213977.2214056
Исследовательские публикации Венкатесана Гурусвами.
Исследовательские публикации Венкатесана Гурусвами.Научные публикации
| АЛГОРИТМИЧЕСКИЙ
РЕЗУЛЬТАТЫ В СПИСКЕ ДЕКОДИРОВАНИЯ , Foundations and Trends® in
Теоретическая информатика , том 2, выпуск 2, 2007 г. Вы можете Скачать бесплатную копию книги (только для личного пользования ) можно здесь. Печатная и переплетенная версия этой статьи доступна по адресу 40% скидка от Now Publishers. |
подписок это список статей (соавторов), составленных мной, организованный тема / категория. Недавние статьи (начиная с 2005 года или около того) (пока) не разбиты на категории по темам. По каждой теме статьи упорядочены более или менее в задний ход хронологический порядок даты первой публикации. Я тоже обычно стараюсь чтобы сделать только самую последнюю версию (например,Журнал версия / подача, если таковая существует) имеющейся статьи.
Список DBLP публикаций Google Scholar стр. Цифровая библиотека ACM страница автора
документов (2006-настоящее время)
- Порог нулевой скорости для состязательного удаления битов меньше 1/2 , ECCC TR21-079 , 2021. (С сертификатом X.Он и Р. Ли)
- Улучшенные максимально восстанавливаемые LRC с использованием полиномов перекоса , ECCC TR21-025 , 2021 (с С. Гопи)
- Приближенное вершинное покрытие гиперграфа и обобщенная гипотеза Тузы , ECCC TR20-167 , 2020. (с С. Сандипом)
- AC-DC: Диагностика кривой усиления для группового тестирования Covid-19 , arxiv: 2011.05223 , 2021.(Совместно с Р. Габрисом, С. Паттабираманом, В. Рана, Ж. Рибейро, М. Черагчи, О. Миленковичем)
- Появится условная дихотомия логических упорядоченных обещаний CSP , ICALP 2021 . (Совместно с Й. Бракензиком и С. Сандипом)
- Линейная емкость Шеннона графов Кэли , ISIT 2021 , чтобы появиться. (Совместно с А. Рязановым)
- Границы линейного программирования для почти сбалансированных двоичных кодов , ISIT 2021 , чтобы появиться.(Совместно с А. Рязановым)
- Появится основанная на местности линза для кодированных вычислений , ISIT 2021 . (Совместно с М. Рудоу и К. В. Рашми)
- Полное опровержение всех полуслучайных логических CSP , SODA 2021 . (Совместно с Дж. Абаскалем и П. Котари)
- Явные коды с двумя удалениями с избыточностью, соответствующей экзистенциальной границе , SODA 2021 . (Совместно с J. H & aringstad)
- Эффективные линейные и аффинные коды для исправления вставок / удалений , SODA 2021 .(Совместно с К. Ченгом, Б. Хэуплером и X. Ли)
- Псевдобиномиальность липкого случайного блуждания , ITCS 2021 . (Совместно с В. Кумаром)
- Резкие пороговые значения для случайных кодов , ITCS 2021 . (Совместно с Дж. Мошеффом, Н. Решем, С. Сайласом, М. Вуттерсом)
- Арикан встречает Шеннон: полярные коды с почти оптимальной сходимостью к пропускной способности канала , STOC 2020 .(Совместно с А. Рязановым и Мин Е)
- Оптимально устойчивые коды для декодирования списков из вставок и удалений , STOC 2020 . (Совместно с Б. Хэуплером и А. Шахрасби)
- Твердость окраски d-к-1 Трехкратные графики с O (1) цветами , ICALP 2020 . (Совместно с С. Сандипом)
- Границы для декодирования списком и восстановления списка случайных линейных кодов , RANDOM 2020 . (Вместе с Р.Ли, Дж. Мошефф, Н. Реш, С. Сайлас, М. Вуттерс)
- Возвращение к сокращению алфавита в PCP Динура , ПРИБЛ. 2020 . (Совместно с Дж. Опрсалом и С. Сандипом)
- Устойчивое к утечкам разделение секретов в неразделенных моделях , ITC 2020 . (Совместно с Ф. Линем, М. Черагчи, Р. Сафави-Найни, Х. Ван)
- Симметричные полиморфизмы и эффективная разрешимость обещанных CSP , SODA 2020 .(Совместно с Я. Бракензиком)
- Твердость радужной окраски по полиморфизму низкой чувствительности , ПРИМЕР 2019 . (С Саем Сандипом)
- Жесткость потоковой передачи Unique Games , ПРИМЕР 2019 . (Вместе с Р. Тао)
- Построение максимально восстанавливаемых локальных кодов реконструкции через функциональные поля . ICALP 2019 . (Совместно с Л. Цзинь и К. Син)
- Превосходство Фредмана-Комлоса для идеального k-хеширования , ICALP 2019 .(Совместно с А. Рязановым)
- Почти оптимальное восстановление кодов Рида-Соломона с низкой субпакетизацией , ISIT 2019 . (Совместно с Х. Цзян)
- Экспоненциальная нижняя граница субпакетирования кодов MSR , STOC 2019 . (Совместно с О. Альрабиа)
- Мост между 0/1 и линейным программированием через случайные блуждания , STOC 2019 . (Совместно с Я. Бракензиком)
- CSP с глобальными модульными ограничениями: алгоритмы и надежность через полиномиальные представления , STOC 2019 .(Совместно с Й. Бракензиком и С. Гопи)
- Алгоритмическая поляризация для скрытых марковских моделей , ITCS 2019 . (Совместно с П. Наккираном и М. Суданом)
- Совместное использование секретов с двоичными общими ресурсами , ITCS 2019 . (Совместно с Ф. Линем, М. Черагчи, Р. Сафави-Найни и Х. Ван)
- Алгоритмическое сочетание LP и кольцевых уравнений для обещающих CSP , SODA 2019 . (Совместно с Я. Бракензиком)
- Максимально восстанавливаемые LRC: нижняя граница размера поля и конструкции для нескольких тяжелых четностей , SODA 2019 .(Совместно с С. Гопи и С. Еханиным)
- Аппроксимируемость норм матрицы p-> q: Обобщенное кривинское округление и сверхсжимающая твердость , SODA 2019 . (Совместно с В. Бхаттипролу, Э. Ли, М. Гошем, М. Тулсиани). Это объединенная расширенная аннотация, содержащая результаты следующих двух статей:
- Полярные коды с экспоненциально малой ошибкой при конечной длине блока , RANDOM 2018 . (Совместно с Дж. Бласиоком и М. Суданом)
- Какой длины могут быть оптимальные коды, ремонтируемые на месте? , СЛУЧАЙНОЕ 2018 .(Совместно с К. Синем и К. Юань)
- Явные коды расстояния 5 оптимальной длины с возможностью локального ремонта , Allerton 2018 . (Совместно с А. Бимером, Р. Коатни, Х. Лопесом, Ф. Пиньеро)
- Расширители размеров без потерь с помощью линеаризованных многочленов и схем подпространств , CCC 2018 . (Совместно с Н. Реш и К. Син)
- Общая сильная поляризация , STOC 2018 . (Вместе с Дж.Бласиок, П. Наккиран, А. Рудра и М. Судан)
- Коды epsilon-MSR: обращение к меньшему количеству кодовых блоков для точного ремонта , ISIT 2018 . (Совместно с С. Локамом и С. Викнешваром)
- О декодируемости случайных линейных рангово-метрических кодов по списку , ИСИТ 2018 . (Совместно с Н. Реш)
- Удовлетворение ограничений обещаний: алгебраическая структура и симметричная логическая дихотомия , SODA 2018 .(Совместно с Я. Бракензиком)
- Кодирование против удалений в не обращающих внимания и онлайн-моделях , SODA 2018 . (С Рэем Ли)
- Семейство тестов на диктатуру с идеальной полнотой для крышки этикеток 2-к-2 , Технический отчет ECCC TR17-141 , 2017. (Совместно с Й. Бракензиком)
- Декодирование списка с оптимальной скоростью по ограниченным алфавитам с использованием алгебро-геометрических кодов , Журнал , 2017.(С К. Син)
- Конструкции кода MDS с небольшой субпакетизацией и почти оптимальной полосой пропускания для восстановления , Публикация в журнале , 2017 г. (Совместно с А. Раватом, И. Тамо и К. Ефременко))
- Твердость радужной раскраски гиперграфов , FSTTCS 2017 , чтобы появиться. (Совместно с Р. Сакетом)
- Слабая развязка, полиномиальные складки и приблизительная оптимизация по сфере , FOCS 2017 .(Совместно с В. Бхаттипролу, М. Гошем, Э. Ли и М. Тулсиани)
- Стремление к сильным результатам несовместимости с идеальной полнотой , APPROX 2017 и ECCC TR17-080 . (Совместно с Я. Бракензиком)
- Сложность потоковой передачи аппроксимации Max 2CSP и Max Acyclic Subgraph , APPROX 2017 . (Совместно с А. Велингкером и С. Велусами)
- Населенный пункт через частично снятые коды , RANDOM 2017 .(Совместно с С. Л. Франк-Фишером и М. Вуттерсом)
- Эффективно декодируемые коды для двоичного канала удаления , СЛУЧАЙНО 2017 . (С Рэем Ли)
- Сертификаты суммы квадратов максимумов случайных тензоров на сфере , RANDOM 2017 . (Совместно с В. Бхаттипролу и Э. Ли)
- Дизайн подпространств на основе полей алгебраических функций , ICALP 2017 . (С Ч. Синем и Ч.Юаней)
- Улучшенная граница возможности декодирования списка нулевых ошибок канала 4/3 , ISIT 2017 . (С М. Далаи и Дж. Радхакришнаном)
- коды epsilon-MSR с малой подпакетизацией , ISIT 2017 . (Совместно с А. Раватом, И. Тамо и К. Ефременко)
- Коды MDS с небольшой субпакетизацией и почти оптимальной полосой пропускания для восстановления , SODA 2017 .(Совместно с А. Раватом)
- Подгонка устойчивой кривой Фурье и полиномиальной кривой , FOCS 2016 . (Совместно с Д. Цукерманом)
- Эффективно декодируемые коды вставки / удаления для режимов с высоким уровнем шума и высокой скоростью , ISIT 2016 . (С Рэем Ли)
- Новые результаты твердости для раскраски графиков и гиперграфов , CCC 2016 . (Совместно с Я. Бракензиком)
- Жесткие границы для дистилляции соглашения с помощью связи , CCC 2016 .(Совместно с Дж. Радхакришнаном)
- Восстановление кодов Рида-Соломона , STOC 2016 . (Совместно с М. Вуттерсом)
- Эффективное декодирование списка проколотых кодов Рида-Мюллера , IEEE Trans. Информация. Theory, 2017 (Совместно с Л. Цзинь и К. Син)
- Улучшенный предел доли корректируемых делеций , SODA’16, и IEEE Trans. Информация. Theory , 2017. (Совместно с Б. Бухом и Дж. Хэрингстадом)
- Эффективные коды с низким уровнем избыточности для исправления множественных удалений , SODA 2016 .(Совместно с Я. Бракензиком и С. Збарским)
- Почти оптимальная NP-твердость для Unique Coverage , SODA 2016 . (С Э. Ли)
- Простое доказательство твердости набора вершин обратной связи , Теория вычислений , 12 (6), 2016, 1-11. (С Э. Ли)
- Для характеристики сопротивления аппроксимации симметричных CSP , APPROX 2015 . (Вместе с Ыйуном Ли)
- Приблизительная раскраска гиперграфа при малом расхождении и связанных обещаниях , APPROX 2015 .(Совместно с В. Бхаттипролу и Э. Ли)
- Расширители размеров через конденсаторы рангов , RANDOM 2015 . (С Майклом Форбсом)
- Неприблизимость H-поперечного сечения / упаковки , ПРИМЕР 2015 . (Совместно с Ыйуном Ли).
- Коды удаления в высокошумном и высокоскоростном режимах , RANDOM 2015 . (С Кэрол Ван)
- Неравенство сумм энтропии и полиномиальная сходимость к пропускной способности Шеннона для всех алфавитов , CCC 2015 .(Совместно с А. Велингкером)
- Связь с несовершенно распределенной случайностью . ITCS 2015 . (Совместно с К. Канонном, Р. Мека и М. Суданом)
- Сильные результаты о несовместимости на сбалансированных радужных гиперграфах , SODA 2015 . (Вместе с Ыйуном Ли)
- Ограничения тестируемых аффинно-инвариантных кодов в высокоскоростном режиме , SODA 2015 . (Совместно с М. Суданом, А.Велингкер и К. Ван)
- (2 + eps) -SAT NP-жесткий , FOCS 2014 . (Совместно с П. Острином и Дж. Херингстадом).
- Явные коды метрики ранга, декодируемые списком с оптимальной избыточностью , RANDOM 2014 . (С Кэрол Ван)
- Наборы ударов для многочленов низкой степени с оптимальной плотностью , CCC 2014 . (Совместно с К. Син)
- Твердость окраски суперполилогарифмического гиперграфа с помощью длинных кодов низкой степени , STOC 2014 .(Совместно с П. Харшей, Дж. Херингстадом, С. Шринивасаном и Г. Вармой)
- Не гибкое кодирование против побитового вмешательства и взлома с разделенным состоянием , TCC 2014 . (Совместно с М. Черагчи)
- Вместимость немягких кодов , ITCS 2014 . (Совместно с М. Черагчи)
- Сложность аппроксимации CSP с ограничениями Balance / Hard , ITCS 2014 . (С Э. Ли)
- Округление SDP Лассерра с использованием выбора столбца и схем аппроксимации на основе спектра для разбиения графа и квадратичных IP-адресов , arXiv: 1312.3024 . (Совместно с А. К. Синопом)
- Оптимальная скорость декодирования списка свернутых алгебро-геометрических кодов над алфавитами постоянного размера , SODA 2014 . (Совместно с К. Син)
- Полярные коды: Скорость поляризации и полиномиальный зазор до емкости , FOCS 2013 . (Совместно с П. Ся)
- PCP через длинный код низкой степени и жесткость для ограниченной окраски гиперграфа , FOCS 2013 .(Совместно с И. Динуром)
- Явный подпространственные конструкции , ВОКС 2013 . (Совместно с С. Коппарти)
- Комбинаторные ограничения декодирования списка среднего радиуса , RANDOM 2013 . (Совместно с С. Нараянаном)
- Суперлинейные нижние границы для обработки многопроходных графов , CCC 2013 . (Совместно с К. Онаком)
- Список декодирования субкодов Рида-Соломона, алгебро-геометрических и Габидулина до границы Сингетона , STOC 2013 .(Совместно с К. Син)
- Непроксимируемость минимального вершинного покрытия на k-однородных k-долевых гиперграфах , ECCC TR13-071, 2013. (Совместно с С. Сачдевой и Р. Сакетом)
- CopyCatch: остановка групповых атак путем выявления локального поведения в социальных сетях , WWW 2013 . (Совместно с А. Бейтелем, В. Сюй, К. Палоу и К. Фалаутсосом)
- Ограниченная изометрия матриц Фурье и декодируемость случайных линейных кодов по списку , SODA 2013 .(Совместно с М. Черагчи и А. Велингкером)
- Аппроксимация неравномерного разреженного разреза с помощью обобщенных спектров , SODA 2013 . (Совместно с А. К. Синопом)
- Декодирование линейно-алгебраическим списком вариантов кодов Рида-Соломона , IEEE Trans. Информация. Теория , 59 (6): 3257-3268, 2013. (Совместно с К. Вангом)
- Постоянный фактор Разрывы интегральности Лассерра для задач разбиения графов , Рукопись , 2012.(Совместно с А. К. Синопом и Ю. Чжоу)
- Более быстрые решатели иерархии SDP для локальных алгоритмов округления , FOCS 2012 . (Совместно с А.К. Синопом).
- Аппроксимация ограниченного вхождения, упорядочивающая CSP , APPROX 2012 . (Совместно с Ю. Чжоу)
- Свернутые коды из башен функциональных полей и улучшенное декодирование списка оптимальных скоростей , STOC 2012 . (Совместно с К. Син)
- Список кодов подпространств декодирования из вставок и удалений , ITCS 2012.(Совместно с С. Нараянаном и К. Вангом)
- Оптимальная реконструкция матрицы низкого ранга на основе столбцов , SODA 2012. (Совместно с А. К. Синопом)
- Разрывы полиномиальной целостности для сильных SDP-релаксаций плотного k-подграфа , SODA 2012. (Совместно с А. Бхаскарой, М. Чарикаром, А. Виджаярагхаваном и Ю. Чжоу)
- Обход UGC из некоторых результатов оптимальной геометрической несовместимости , SODA 2012. (Совместно с П. Рагхавендрой, Р.Сакет, Ю. Ву)
- Иерархия Лассерра, высшие собственные значения и схемы аппроксимации для квадратичного целочисленного программирования с целями PSD , FOCS 2011. (Совместно с А. К. Синопом)
- Оптимальная скорость декодирования списка через производные коды , RANDOM 2011 . (Совместно с К. Вангом)
- Линейно-алгебраический список декодирования свернутых кодов Рида-Соломона , CCC 2011 .
- Нахождение пополам почти идеального графика , ICS 2011 .(Совместно с Ю. Макарычевым, П. Рагхавендрой, Д. Стеурером и Ю. Чжоу)
- Избежать случайного упорядочения сложно: каждый CSP упорядочивания устойчив к аппроксимации , SIAM J. Computing , 2011. (Совместно с Дж. Хэрингстадом, Р. Манокараном, П. Рагхавендрой и М. Чарикаром)
- Сложность поиска независимых множеств в ограниченных степенях (гипер) графах низкого хроматического числа , SODA 2011 . (Совместно с А. К. Синопом)
- Границы жесткой несовместимости для почти выполнимого рупорного SAT и набора точных попаданий , SODA 2011 .(Совместно с Ю. Чжоу)
- Коды для вычислительно простых каналов: явные конструкции с оптимальной скоростью , FOCS 2010 . (Совместно с А. Смитом)
- Соединение Шеннона и Хэмминга: список исправлений ошибок с оптимальной скоростью , ICM 2010 (приглашенный опрос)
- О недопустимости вершинного покрытия на k-разделных k-однородных гиперграфах , ICALP 2010 .(Совместно с Р. Сакетом)
- Зазоры SDP для 2-к-1 и других вариантов наклеек-крышек , ICALP 2010 . (Совместно с С. Хотом, Р. О’Доннеллом, П. Попатом, М. Тулсиани и Ю. Ву)
- О декодируемости списком Случайные линейные коды , STOC 2010 . (С Дж. Хэрингстад и С. Коппарти)
- Агностик обучение одночленов полупространствами сложно , FOCS 2009 .(Совместно с В. Фельдманом, П. Рагхавендрой и И Ву)
- Улучшены результаты неапроксимируемости для подграфа , максимально раскрашиваемого по k. ПРИМЕР 2009 . (Совместно с Синопом А.К.)
- Каждый CSP перестановки арности 3 устойчив к аппроксимации , CCC 2009 . (С М. Чарикаром и Р. Манокараном)
- Локально тестируемые коды требуют избыточных тестеров , CCC 2009 .(Совместно с Э. Бен-Сассоном, Т. Кауфманом, М. Суданом и М. Видерманом)
- Исправление ошибок до теоретико-информационного предела . версия html; Более красочное цифровое издание. Сообщения ACM , март 2009 г. (с А. Рудрой)
- Циклотомическая функция
поля, автоморфизмы Артина-Фробениуса и ошибка списка
коррекция с оптимальной скоростью , Алгебра и теория чисел , Vol.4 (2010), № 4, 433-463.
- Расширенная аннотация «Автоморфизмы Артина, циклотомические.
функциональных полей и кодов, декодируемых в свернутом виде », появившихся в STOC 2009 .
Вот версия arXiv.
- Расширенная аннотация «Автоморфизмы Артина, циклотомические.
функциональных полей и кодов, декодируемых в свернутом виде », появившихся в STOC 2009 .
- Список декодируемых тензорных произведений и чередующихся кодов . Расширенный договор в STOC 2009 . (Совместно с П. Гопаланом и П. Рагхавендрой)
- Распределение макс. И мин. С помощью древовидной структуры с нижней границей степени , Протоколы STOC 2009 .(Совместно с М. Х. Батени и М. Чарикаром)
- Преодолеть случайный порядок сложно: недопустимость максимального ациклического подграфа , FOCS 2008 . (Совместно с Р. Манокараном и П. Рагхавендрой)
- Евклидовы сечения с сублинейной случайностью и исправлением ошибок по действительным числам , RANDOM 2008 . (совместно с Дж. Ли и А. Вигдерсоном)
- Удовлетворение ограничений в небулевой области: алгоритмы аппроксимации и твердость Unique Games , ПРИБЛ. 2008 .Также отчет ECCC TR08-08 . (Совместно с П. Рагхавендрой)
- Явные перемежители для построения кода с повторным накоплением (RAA) , ISIT 2008 . (Совместно с В. Мачмоути)
- Мягкое декодирование, двойные коды BCH и улучшенные коды, декодируемые списком со смещением eps , IEEE Trans. Информация. Теория, 2010 . Версия конференции CCC 2008 . (Совместно с А. Рудрой)
- Усиление твердости в NP по детерминированным алгоритмам , J.N через коды расширителя , принято к Combinatorica , 2009. Conf. версия в SODA 2008 . (С Дж. Ли и А. Разборов)
- Непроксимируемость непересекающихся путей и маршрутизации с низкой перегрузкой на неориентированном графики , Combinatorica . (Совместно с М. Эндрюсом, Дж. Чужой, С. Ханной, К. Талвар, Л. Чжан)
- Лучшие двоичные коды с декодированием по списку за счет многоуровневой конкатенации, RANDOM 2007 ; Версия журнала в IEEE Trans.Информация. Теория . (Совместно с А. Рудрой)
- Несбалансированные расширители и экстракторы случайности из кодов Парвареша-Варди , Журнал ACM , 56 (4), 2009. (Совместно с К. Умансом и С. Вадханом)
- Трудность решения разреженных переопределенных линейных систем: PCP с 3 запросами по целым числам , Транзакции ACM по теории вычислений , 1 (2): (2009). Версия для конференции в STOC 2007 . (Совместно с П. Рагхавендрой)
- Жесткость маршрутизации с перегрузкой в направленных графах , КСД 2007 г. .(Совместно с Дж. Чужой, С. Ханной и К. Талваром)
Обзоры
- Bridging Shannon and Hamming: List Error-Correction with Optimal Rate , Proceedings of ICM 2010 (специальный опрос), август 2010 г.
- Исправление ошибок до теоретико-информационного предела . версия html; Более красочное цифровое издание. Сообщения ACM , март 2009 г. (с А. Рудрой)
- Список расшифровки двоичных кодов , Краткий обзор, 2009.
- Итеративное декодирование кодов проверки на четность с низкой плотностью , выпуск 90 Бюллетеня EATCS.
- Расшифровка списков и псевдослучайные конструкции , AAECC 2007 .
- Алгоритмические результаты при расшифровке списка , Основы и тенденции® в
Теоретическая информатика , том 2, выпуск 2, 2007 г.
- Расшифровка списка при усредненной сложности и псевдослучайности . Мини-обзор, ITW 2006 .
- Коды с исправлением ошибок и
Графики расширителя Новости SIGACT , 35 (3): 25-41,
Сентябрь 2004 г.
- Размышления о «Улучшенном»
Расшифровка Рида-Соломона и
Алгебро-геометрические коды » IEEE Information Theory Newsletter , 2002.(С М. Судан)
- Быстро
Смешивание цепей Маркова: сравнение методов , Неопубликовано , 2000.
- Доказательства на квартиру,
ускоряющаяся Вселенная и
$ \ Lambda $ CDM Model , Неопубликовано , 2000.
Теория кодирования
(статьи с 2006 г. и далее см. Выше)
- В. Гурусвами и С. Вадхан.
Нижняя граница размера списка для декодирования списка
Труды RANDOM 2005 . - В. Гурусвами и А. Рудра.
Коды, допускающие локальную проверку
Труды RANDOM 2005 . - В. Гурусвами и А. Рудра.
Ограничения на список кодов декодирования Рида-Соломона
IEEE Trans. Информация. Theory, август 2006 г. Предварительная версия в STOC 2005 . - В. Гурусвами и А. Варди.
Максимальное правдоподобное декодирование Рида-Соломона Коды NP-hard
IEEE Transactions on Information Theory 51 (7): 2249-2256 (2005).
Версия конференции в SODA 2005. - В. Гурусвами.
Коды исправления ошибок и Графики расширения
SIGACT News , 35 (3): 25-41, Сентябрь 2004 г. - В.
Гурусвами и П. Индик.
Расшифровка линейного временного списка с безошибочной настройкой
Материалы ICALP 2004 . - В.
Гурусвами, Д. Миччансио и О. Регев.
Сложность покрытия Радиус Проблема на решетках и кодах
Вычислительная сложность , 14 (2): 90-121, 2005.
Предварительная версия в Conference on Computational Complexity (CCC), 2004 . - Венкатесан
Гурусвами.
Лучшие экстракторы для лучших кодов?
Труды СКП 2004 . - Венкатесан Гурусвами и Петр Индик.
Эффективно декодируемые коды встреча Гилберта-Варшамова, направлявшегося в Низкие цены
Труды SODA 2004 . - Венкатесан Гурусвами.
Список Декодирование с дополнительной информацией
Труды сложности 2003 . - Венкатесан Гурусвами и Петр Индик.
Линейное время с кодированием и списком декодируемые коды
Труды ГКП 2003 . - Венкатесан Гурусвами и Игорь Шпарлинский.
Безусловное доказательство Герметичность Johnson Bound
Труды SODA 2003. - В. Гурусвами.
Пределы для перечисления декодируемости линейные коды
Труды ГПН 2002 . - В. Гурусвами и П. Индик.
Кодирование / декодирование линейного времени коды с близкими к оптимальным скорость
IEEE Trans. на Инфо. Theory , октябрь 2005 г. - В. Гурусвами и П. Индик.
Линейные временные коды, близкие к оптимальным для уникальной расшифровки и нового списка декодируемые коды над меньшими алфавитами
Труды ГПН 2002 . - Нога Алон, Венкатесан Гурусвами, Тали Кауфман и Мадху Судан.
Умение разгадывать секреты через расшифровку списка
Труды SODA 2002 . Публикуется в специальном выпуске ACM Transactions on Algorithms для статей SODA’02. - В. Гурусвами и П. Индик.
Линейные временные коды для коррекции максимально возможная доля ошибок .
Приглашен в службу Allerton 2001 . - Венкатесан Гурусвами и Мадху Судан.
Декодирование составных кодов с использованием мягкая информация
Труды Сложность 2002 . - В. Гурусвами и Мадху Судан.
Размышления об «Улучшенном» Расшифровка Рида-Соломона и Алгебро-геометрические коды »
Информационный бюллетень IEEE по теории информации, март 2002 г. . - В. Гурусвами и П. Индик.
На базе расширителя Конструкции эффективно декодируемых кодов
Труды ВОКС 2001 . - В. Гурусвами.
Список декодирования по стиранию: границы и код Конструкции
IEEE Trans. на Инфо. Теория , ноябрь 2003. - В. Гурусвами.
Конструкции кодов из числовых полей
IEEE Trans. на Инфо. Теория , 2003.
(Вот 2 страницы резюме.) - В. Гурусвами.
Список Расшифровка кодов исправления ошибок
Ph.Докторская диссертация, Массачусетский технологический институт, август 2001. - В. Гурусвами и М. Судан.
Расширения до Johnson Переплет
Рукопись , февраль 2001 г. - В. Гурусвами, Дж. Херингстад, М. Судан и Д. Цукерман.
Комбинаторный Границы для декодирования списка
IEEE Trans. по информации Теория , май 2002 г.
Приглашена предварительная версия. к 38-й ежегодной выставке Allerton Конференция по связи, управлению и вычислениям . - В. Гурусвами, А. Сахай и М. Судан.
Мягкое решение Расшифровка китайских остаточных кодов
Труды ВОКС 2000 . - В. Гурусвами и Мадху
Судан.
О представительствах Алгебро-геометрические коды для декодирования списков
IEEE Транзакции по теории информации , май 2001 г. - В. Гурусвами и М.
Судан.
Список алгоритмы декодирования некоторых сцепленных кодов
Материалы STOC 2000 . - Венкатесан Гурусвами и Мадху Судан.
Улучшено Расшифровка кодов Рида-Соломона и алгебро-геометрических кодов
IEEE Transactions on Теория информации , 45 (1999), стр. 1757-1767.
Алгоритмы аппроксимации, твердость Приближения, ПКП
(документы с 2006 г. и далее см. Выше)
- В. Гурусвами и Л. Тревизан.
Сложность принятия уникальных решений: приближение 1-в-kSAT
Труды APPROX 2005. - В. Гурусвами и С. Хот.
Твердость Max 3SAT без смешанных пунктов
Протоколы CCC 2005. - В. Гурусвами, Дж. Д. Хартлайн, А. Карлин, Д. Кемпе, К. Кеньон и Ф. МакШерри.
Вкл. Максимизирующая прибыль Цена без зависти
Труды SODA 2005. - В.
Гурусвами, Д. Миччансио и О. Регев.
Сложность покрытия Радиус Проблема на решетках и коды
Протоколы CCC 2004 ; Версия журнала в спецвыпуске Вычислительная сложность . - Моисей
Чарикар, Венкатесан Гурусвами и Энтони Вирт.
Кластеризация с качественной Информация
JCSS, октябрь 2005 г. (специальный выпуск). Предварительная версия FOCS 2003 . - И.
Динур, В. Гурусвами, С. Хот и О. Регев.
Новый многослойный PCP и твердость вершинного покрытия гиперграфа
SIAM J. Comput. 34 (5): 1129-1146 (2005)
Версия для конференции в STOC 2003. - И.
Динур, В. Гурусвами и С. Хот.
Vertex Cover на k -однородных гиперграфах трудно аппроксимировать в пределах коэффициента (k-3-eps)
Технический отчет ECCC TR02-027. - В.
Гурусвами и П. Индик.
Вложения и неприближаемость геометрических задач
Труды SODA 2003. - Л.
Энгебретсен и В.Гурусвами.
Ограничение превышает удовлетворение две переменные всегда легко?
Случайные структуры и алгоритмы , 2004 .. Предварительная версия в Proc. of RANDOM 2002. - В.
Гурусвами, Дж. Хастад
и М. Судан.
Твердость примерной раскраски гиперграфа
SIAM J. Comput. 31 (6): 1663-1686 (2002)
Предварительно версия появилась в FOCS 2000 (журнальная версия — значащая редакция). - М.
Чарикар,
В. Гурусвами, Р. Кумар, С. Раджагопалан и А. Сахай.
Комбинаторный Проблемы с выбором функций
Proc. ФОКС 2000 . - В.
Гурусвами и С. Кханна
На твердость 4-х окраски 3-х цветной граф
SIAM J. Disc. Math , 2004. (Предварительная версия в Proc. из Сложность 2000 , с. 188-197.) - В.
Гурусвами.
Результаты о несовместимости набора Проблемы расщепления и выполнимости без смешанных предложений
Algorithmica , 2003 (специальный выпуск для избранных статей из APPROX 2000.) - В.
Гурусвами, С. Кханна,
Р. Раджараман, Ф. Пасти,
М.
Яннакакис.
Почти оптимальное Результаты твердости и алгоритмы аппроксимации для путей, непересекающихся по ребрам. и связанные проблемы .
JCSS , 67 (3): 473-496, 2003.(Предварительный версия в Proc. КНД 1999 г. .) - Евгений Додис,
Венкатесан Гурусвами и Санджив
Ханна
Сегментация по 2 каталогам Проблема
Труды SODA 1999 . - Венкатесан
Гурусвами, Дэниел Левин,
Мадху Судан и Лука Тревизан
A точная характеристика NP с 3 запросами PCP
Труды FOCS 1998 . Также доступно как ECCC Technical Отчет TR98-034 .
[Техническое содержание этой статьи (даже версия ECCC) довольно трудно читать без знакомства с бумагой Хастада. Более автономная версия можно найти ниже в виде моей магистерской диссертации.] - В.
Гурусвами.
Эффективная проверка запросов Доказательства и улучшенные характеристики PCP NP
Магистерская работа, Массачусетский технологический институт, май 1999 г. Вот HTML абстрактный. - В.Гурусвами и Ч. Панду Ранган.
Прирожденная семья Задачи оптимизации со сколь угодно малым приближением пороги
Письма по обработке информации , 68 (1998), С. 241-248. - В.
Гурусвами и Ч.Панду Ранган.
Приблизительная окраска триклика для Размещение регистра
Письма об обработке информации , Vol. 60, 1996.
Другое Теоретические работы
Тезисов
- Расшифровка списка кодов исправления ошибок , Ph.Докторская диссертация, Массачусетский технологический институт, 2001.
- Эффективный запрос
Проверка доказательств и улучшенные характеристики PCP NP ,
Магистерская работа, Массачусетский технологический институт, май 1999 г.
Вот HTML автореферат диссертации. - Результаты несговорчивости для некоторых теоретико-графовых оптимизаций и Проблемы аппроксимации, кандидатская диссертация, Индийский институт Technology, Мадрас, май 1997 г.
Алгоритмический и структурный граф Теория
- В.Гурусвами. Перечислительный Аспекты некоторых классов Perfect Graphs , Discrete Математика , 205 (1999), стр. 97-117.
- В. Гурусвами, У. Ротикс, М.С. Маданлал, Дж. А. Маковски и Ч. Панду Ранган, Ограничения минимальных задач гаечного ключа , Информация и вычисления , 97 августа.
- В. Гурусвами и Ч. Панду Ранган. Алгоритмические аспекты клико-трансверсальные и независимые от кликов множества , Дискретный Прикладная математика , 100 (2000), стр.183-202.
- В. Гурусвами. Максимальный разрез на линейных и общих графиках , Дискретный Прикладная математика , 92 (1999), стр. 217-221.
- В. Гурусвами, Ч. Панду Ранган, М.С. Чанг, Г.Дж. Чанг и C.K. Вонг, Проблема вершинно-непересекающихся треугольников , Труды WG’98, Смоленицкий замок, Словакия, июнь 1998 г. Версия журнала в Computing .
- В. Гурусвами и Ч.Панду Ранган. Сложность графа Проблемы с упаковкой . Неопубликованная рукопись .
- В. Гурусвами и Ч. Панду Ранган. Алгоритмические аспекты Edge Доминирующие наборы . Неопубликованная рукопись .
- В. Гурусвами, Г. Мохан и К. Шива Рама Мурти, Вероятностная маршрутизация на многоступенчатом режиме с маршрутизацией по длине волны, гиперкубе и Debruijn Networks , Proc. четвертого Международная конференция по высокопроизводительным вычислениям (HiPC ’97).
- М.С. Маданлал, В. Гурусвами и Ч. Панду Ранган, Дерево Гаечный ключ на интервальных, перестановочных и правильных двудольных графах , Информация Письма о рассмотрении дела , Vol. 59, 1996.
- [ Бакалавриат
Тезис ] Результаты несговорчивости
для некоторой теоретико-графической оптимизации
и
Проблемы приближения , Индийский технологический институт,
Мадрас, май 1997 года.
Уведомление об авторских правах: Документы, распространяемые этим сервером, имеют был предоставляется как средство для обеспечения своевременного распространения научных и технические работы на некоммерческой основе.Copyright © и все права на него принадлежат авторам или другим авторским правам владельцев, несмотря на то, что они предложили здесь свои работы в электронном виде. Понятно, что все лица, копирующие это информация будет соответствовать условиям и ограничениям, налагаемым каждым авторское право. Эти работы не могут быть перепечатаны без явное разрешение правообладателей. Опубликованные документы ACM являются © Авторские права 199x принадлежат ACM, Inc.; Опубликованные документы Springer-Verlag являются © Springer-Verlag; и опубликованные документы IEEE © 199x IEEE, под этим условия.
| ВОСКРЕСЕНЬЕ | |
| 6:30 | Ужин, ресторан Джона Давенпорта на вершине Омни (только по приглашению) |
| ПОНЕДЕЛЬНИК | |
| 8:30 | Завтрак |
| 9:15 | Александр Барвинок (Мичиганский университет, Анн-Арбор), «Подсчет магических квадратов, таблица непредвиденных обстоятельств, целочисленные потоки и многое другое» (совместно с А.Самородницкий и А. Йонг) [Реферат] |
| 10:00 | Река Томас (Вашингтонский университет), «Малый чватальный ранг целочисленной матрицы» (совместно с Т. Богартом) [Аннотация] |
| 10:30 | Перерыв |
| 11:15 | Нильс Лауритцен (Университет Орхуса), «Наборы тестов и алгоритм Шарф-Шеллкросс» (совместно с А. Йенсеном и Б. Роуном) [Реферат] |
| 12:00 | Обед |
| 1:30 | Пабло Паррило (Массачусетский технологический институт), «Вычислительные методы для непрерывных игр» [Аннотация] |
| 2:15 | Моисей Чарикар (Принстонский университет), «Алгоритмический взгляд на гипотезу уникальных игр» [Аннотация] |
| 3:00 | Перерыв |
| 3:15 | Мишель Гоеманс (Массачусетский технологический институт), «Охватывающие деревья минимальной ограниченной степени» [Реферат] |
| 4:00 | Виджей Вазирани (Технологический институт Джорджии), «Рынки и первично-дуальная схема» [Реферат] |
| 6:30 | Ужин, кафе Union League (только по приглашениям) |
| ВТОРНИК | |
| 8:30 | Завтрак |
| 9:15 | Маргарет Райт (Нью-Йоркский университет), «Избранные недавние разработки в области оптимизации без производных» [Аннотация] |
| 10:00 | Роберт Дж.Вандербей (Принстонский университет), «Границы стохастически недоминируемых портфелей» (совместно с А. Рущинским) |
| 10:45 | Перерыв |
| 11:15 | Дэвид Шмойс (Корнельский университет), «Алгоритмы приближения для двухэтапных задач стохастического планирования» (совместно с М. Созио) [Аннотация] |
| 12:00 | Обед |
| 1:30 | Асуман Оздаглар (Массачусетский технологический институт), «Приближенные первичные решения и анализ скорости для субградиентных методов» (совместно с А.Недич) [Аннотация] |
| 2:15 | Ник Харви (Массачусетский технологический институт), «Рандомизированные алгебраические алгоритмы для задач сопоставления и матроидов» [Аннотация] |
Обновление! Деловая встреча в воскресенье отложена (чтобы было больше времени на обед). Он будет с , 8: 30–10: 00, . Вот версия этой программы для печати. Информация о конференцииВсе мероприятия будут проходить в отеле Hyatt Regency Bethesda. Конференц-залы расположены на уровне бальных залов отеля (на два уровня ниже главного вестибюля). Кофе-брейки и континентальные завтраки будут подаваться в фойе бального зала , на уровне бального зала. Залы Cartier / Tiffany будут использоваться в качестве зоны отдыха. Стойка регистрацииСтойка регистрации будет находиться в фойе Хаверфорд , на два уровня ниже главного вестибюля.Он будет открыт в субботу с 18:00 до 20:00 и вс-вт с 7:30 до 18:00. Доступ в ИнтернетБеспроводной доступ в Интернет будет доступен в зале Cartier / Tiffany, фойе бального зала и бальном зале Crystal (все на уровне бального зала). Информация о доступе к беспроводной сети будет доступна на стойке регистрации. ОбедыИз-за нехватки места обеды будут разделены между двумя залами. Посетители могут перейти в любую комнату.
Программа конференции
| ||
Теоретический семинар | Теоретическая информатика
Семинар теоретической группы CS в Университете Колорадо в Боулдере.
Наш теоретический семинар стартовал весной 2018 года. Следите за предстоящими выступлениями и / или подпишитесь на нашу рассылку cs-theory-announce!
Предстоящие переговоры
Все переговоры онлайн на осень 2020, весна 2021. Напишите текущему организатору (Бо Ваггонеру) ссылку на Zoom.
[Действия в период между уточнением информации]
13 августа 2021 г. (специальный, предсеместровый) Ювал Фильмус (Технион). Приблизительные полиморфизмы. 12-13 вечера MT, гибридный личный ECES 112 и виртуальный (электронная почта Джоша Грохоу для ссылки Zoom).
Аннотация: Какие булевы функции f: {0,1} n → {0,1} удовлетворяют f (x⊕y) = f (x) ⊕f (y)
… для всех x, y? линейные функции (100% режим).
… почти для всех x, y? функции, близкие к линейным (режим 99%).
… для многих x, y, более чем случайных функций? функции, коррелирующие с линейной функцией (режим 51%).
Все эти результаты классические.
Мы изучаем, что происходит, когда функция XOR заменяется произвольной булевой функцией.
На основе совместной работы с Гиладом Чейзом (Технион), Дор Минзером (Массачусетский технологический институт), Эльхананом Мосселем (Массачусетский технологический институт), Нитином Саурабом (IIIT Хайдарабад).
Прошедшие переговоры
Мы моделируем социальный выбор как действия, сопоставляющие состояния природы с (общественными) результатами. Функция социального выбора (или SCF) назначает действие каждому профилю субъективных предпочтений ожидаемой полезности по сравнению с действиями. SCF является стратегически устойчивым, если ни у одного агента никогда не было стимула искажать свои убеждения о состояниях природы или свою оценку результатов; он эффективен постфактум, если действие, выбранное в любом заданном профиле предпочтений, выбирает эффективный по Парето результат в каждом естественном состоянии.Мы предлагаем полную характеристику всех стратегически устойчивых и эффективных SCF. Выбранный акт должен выбирать наиболее предпочтительный исход какого-либо (возможно, другого) агента в каждом естественном состоянии. Набор состояний, в которых выбирается лучший результат агента, может варьироваться в зависимости от сообщаемого профиля убеждений; это объединение всех государств, закрепленных за ней набором двусторонних диктаторских и двусторонних согласованных правил назначения. Бумага: http://www.cireqmontreal.com/wp-content/uploads/cahiers/03-2017-cah.pdfАннотация: Для системы линейных уравнений ℓ i (x) = β i в n-векторе x переменных 0-1, мы вычисляем математическое ожидание exp {−∑iγ i (ℓ i (x) −β i ) 2 }, где x — вектор независимых случайных величин Бернулли, а γ i > 0 — константы. Алгоритм выполняется за квазиполиномиальное время n O (lnn) при некотором условии разреженности матрицы системы. Результат основан на отсутствии нулей аналитического продолжения математического ожидания для комплексных вероятностей, что также можно интерпретировать как отсутствие фазового перехода в модели Изинга с достаточно сильным внешним полем.В качестве примера рассмотрим задачу «сглаженного счета» совершенных паросочетаний в гиперграфах. https://arxiv.org/abs/2103.05488
Аннотация: Процедура Вейсфейлера-Лемана (WL) — широко используемый подход для проверки изоморфизма графов. Он работает путем итеративного вычисления инвариантной изоморфизма раскраски кортежей вершин. Между тем, декомпозиции являются фундаментальным инструментом в теории структурных графов и часто используются в подходах к решению проблемы изоморфизма графов.
В этом докладе я обсуждаю способность алгоритма WL идентифицировать графы путем их декомпозиции.В частности, я даю обзор нашего доказательства того, что двумерный алгоритм WL (2-WL) неявно вычисляет разложение графа на его 3-связные компоненты. Доказательство основывается на понимании того, что 2-WL обнаруживает пары вершин, разделяющих граф. Наш результат показывает, что определение размерности алгоритма, необходимого для различения двух заданных графов, сводится к определению размерности, необходимой для различения трехсвязных компонентов графов. Это довольно техническое утверждение позволяет сделать убедительные выводы для класса графов с ограниченной древовидной шириной и класса плоских графов.
Аннотация: Иммананты — это матричные функции, обобщающие детерминанты и перманенты. Учитывая неприводимый характер χ λ из S n для некоторого разбиения λ числа n, имманант, связанный с λ, является суммой-произведением перестановок π в S n , как и определитель, но с χ λ (π) играет роль sign (π).
Хартманн показал в 1985 году, что иммананты могут быть вычислены за полиномиальное время для знаковых символов. Точнее, для разбиения λ поля n с s частями пусть b (λ): = n − s подсчитывает клетки справа от первого столбца диаграммы Юнга λ.Имманант, связанный с λ, можно оценить за n O (b (λ)) раз.
Начиная с этого первоначального результата, были получены дополнительные результаты о жесткости для нескольких семейств имманантов, полученных из разбиений с неограниченным b (λ). Сюда входят перманенты, имманенты, связанные с персонажами-крючками, и другие классы. В этом выступлении мы завершаем картину жестких имманантных семейств: при стандартном предположении параметризованной сложности мы исключаем алгоритмы с полиномиальным временем для (корректных) имманантных семейств с неограниченным b (λ).Для имманантных семейств, в которых b (λ) даже полиномиально растет, мы устанавливаем трудность для #P и VNP. (См. ArXiv: 2102.04340.)
Аннотация: Мы даем простые итерационные методы вычисления приближенно оптимальных прямых и двойственных решений для задачи максимизации линейного функционала над выпуклым множеством K, заданным оракулом разделения. Наши методы основаны на вариантах классических алгоритмов фон Неймана и Франка-Вульфа.
Аннотация: В этом докладе я представлю некоторые недавние результаты об оптимальном обмане в играх Штакельберга.Недавняя работа в сообществе машинного обучения показала, что алгоритмы обучения, используемые для вычисления оптимальной стратегии лидера, которой он должен придерживаться в игре Штакельберга, подвержены манипуляциям со стороны ведомого. Такой алгоритм обучения работает, запрашивая лучшие ответы или выплаты последователя, который, следовательно, может обмануть алгоритм, отвечая так, как если бы его выплаты сильно отличались от того, что они есть на самом деле. Чтобы это стратегическое поведение было успешным, основная задача, с которой сталкивается последователь, состоит в том, чтобы точно определить выплаты, которые заставят алгоритм обучения вычислять обязательство, чтобы наилучшее реагирование на него максимизировало полезность ведомого в соответствии с его истинными выигрышами.Хотя эта проблема рассматривалась ранее, соответствующая литература была сосредоточена только на упрощенном сценарии, в котором пространство выигрыша ведомого конечно, таким образом, оставляя общую версию проблемы без ответа. Наши результаты восполняют этот пробел, показывая, что последователь всегда может вычислить (почти) оптимальные ложные выплаты в различных сценариях обучения между лидером и ведомым.
Аннотация: Мы описываем, как комбинаторные задачи перечисления / перечисления в сочетании со структурными свойствами гиперматриц / тензоров определяют критический аспект булевой функции, такой как сложность их формулы Де Моргана.В докладе не предполагается предварительное знакомство с гиперматрицами / тензорами.
Аннотация: Согласно ортодоксальной теории приближений, линейные программы (ЛП) плохо справляются с задачами max-cut и другими задачами удовлетворения ограничений и что для нетривиальных приближений необходимы полуопределенное программирование и спектральные методы. В этом выступлении я опишу два недавних результата, которые опровергают это убеждение: мы показываем, что LP субэкспоненциального размера могут (1) аппроксимировать максимальное сокращение до коэффициента, строго превышающего 0.5, и (2) удостоверяют max-разрез в графах ограниченного спектрального радиуса. Это решает сложность линейного расширения max-cut. Аналогичные результаты справедливы для Unique Games и других задач удовлетворения ограничений.
Основано на совместных работах с Райаном О’Доннеллом, Сэмом Хопкинсом и Лукой Тревизаном.
arXiv: https://arxiv.org/abs/1911.10304
Аннотация: Мы предлагаем теоретико-информационную основу для изучения обобщающих свойств алгоритмов машинного обучения. Наша структура связывает воедино существующие подходы, включая единые границы сходимости и новейшие методы адаптивного анализа данных.В частности, мы используем условную взаимную информацию (CMI) для количественной оценки того, насколько хорошо входные данные (т.е. обучающие данные) могут быть распознаны с учетом выходных данных (т.е. обученной модели) алгоритма обучения. Мы показываем, что границы CMI могут быть получены из размерности VC, схем сжатия, дифференциальной конфиденциальности и других методов. Затем мы показываем, что ограниченный CMI влечет за собой различные формы обобщения.
Совместная работа с Лидией Закинтиновой. См. Https://arxiv.org/abs/2001.09122
Abstract: Мы изучаем проблему изучения причинно-следственной максимизации персонализированной политики принятия решений на основе данных наблюдений с учетом возможных ненаблюдаемых искажений.Поскольку ценность политики и сожаление не могут быть однозначно идентифицированы, мы изучаем метод, который сводит к минимуму оценку сожаления наихудшего случая из-за набора неопределенности для весов склонности, который контролирует степень ненаблюдаемого искажения. Мы доказываем гарантии обобщения, которые гарантируют, что наша политика будет безопасна при применении на практике и фактически обеспечит максимально возможный единообразный контроль над диапазоном всех возможных сожалений населения, которые согласуются с возможной степенью смешения. Мы разрабатываем эффективные алгоритмические решения для вычисления этой противоречивой политики.Наконец, мы оцениваем и сравниваем наши методы на синтетических и полусинтетических данных. В частности, мы рассматриваем тематическое исследование персонализированной заместительной гормональной терапии, основанное на параллельном наблюдательном исследовании WHI и клиническом испытании. Мы демонстрируем, что скрытые искажения могут помешать существующим подходам к изучению политики и привести к неоправданному ущербу, в то время как наш надежный подход гарантирует безопасность и ориентирован на очевидные улучшения.
Работа выполнена совместно с Натаном Каллусом. Более ранняя версия этой работы была распространена как «Усовершенствование сомнительно надежной политики».
Abstract: Aaronson, Ambainis (2009) и Chailloux (2018) показали, что полностью симметричные (частичные) функции не допускают экспоненциального квантового ускорения запросов. Возникает естественный вопрос: насколько симметричной должна быть функция, чтобы она не могла демонстрировать большое квантовое ускорение? В этой работе мы доказываем, что симметрии гиперграфов в модели матрицы смежности допускают не более чем полиномиальное разделение между рандомизированными и квантовыми сложностями запросов. Мы также показываем, что примечательно то, что группы перестановок, построенные на основе этих симметрий, по существу являются единственными группами перестановок, которые предотвращают сверхполиномиальное квантовое ускорение.Мы докажем это, полностью охарактеризовав примитивные группы перестановок, которые допускают суперполиномиальные квантовые ускорения. Напротив, в модели списка смежности для графов с ограниченной степенью (где симметрия графа проявляется по-другому) мы демонстрируем проблему проверки свойств, которая показывает экспоненциальное квантовое ускорение. Эти результаты решают открытые вопросы, поставленные Амбаинисом, Чайлдсом и Лю (2010) и Монтанаро и де Вольф (2013).
Аннотация: Все известные эффективные алгоритмы для задач удовлетворения ограничений блокируются случайными примерами.Например, неизвестен эффективный алгоритм, который может q-раскрасить случайный граф со средней степенью (1 + ε) q ln q, даже если случайные графы остаются q-раскрашиваемыми для средней степени до (2 — o (1)) q ln q. Подобная неспособность найти решения при относительно низких плотностях ограничений известна для случайных CSP, таких как случайный k-SAT и других проблем на основе гиперграфов. Плотность ограничений, при которой алгоритмы не работают для каждого CSP, известна как «алгоритмический барьер» и доказуемо соответствует фазовому переходу в геометрии пространства решений [Achlioptas and Coja-Oghlan 2008].В этом выступлении я расскажу о своей недавней статье, которая направлена на то, чтобы пролить свет на следующий вопрос: может ли алгоритмический успех с точностью до барьера для каждого CSP быть приписан некоторому простому детерминированному свойству входных данных? В частности, я остановлюсь на проблеме раскраски графов и гиперграфов.
Abstract: Квантовая информатика — междисциплинарная область, тесно связанная с информатикой и физикой. В этой области есть алгоритмические инструменты с вычислительными приложениями в классической информатике и квантовой физике.В этом выступлении я расскажу о своей работе по разработке этих инструментов для решения задач оптимизации, машинного обучения и изучения квантовых систем. В частности, что касается информатики, я буду обсуждать квантовое ускорение для некоторых задач вычислительной геометрии с приложениями в машинном обучении и оптимизации. Я также опишу квантовые классические алгоритмы для решения задач машинного обучения, связанных с матрицами. Что касается физики, я представлю квантовые алгоритмы для моделирования открытых квантовых систем, а также эффективные конструкции псевдослучайных квантовых операторов.
Аннотация: Булева функция f на n-мерном гиперкубе называется k-хунтой, если она зависит только от некоторых k координат входных данных. Эти функции широко изучались в контексте PCP, теории обучения и тестирования свойств. В частности, флагманский результат тестирования свойств состоит в том, что k-хунт можно протестировать с помощью Õ (k) запросов, т. Е. Существует алгоритм, который, когда задан черный ящик для f, выполняет только Õ (k) запросов и принимает решение между следующие два случая:
- е — к-хунта.
- f находится по крайней мере на 0,01 далеко от каждой k-хунты g на расстоянии Хэмминга.
Удивительно, но сложность запроса полностью не зависит от внешнего измерения n. В этой работе мы добиваемся такой же качественной гарантии для шумоустойчивого варианта этой задачи. В частности, мы даем алгоритм запроса 2 k , чтобы различать следующие два случая.
- е это 0,48-близко к какой-то к-хунте.
- f — это минимум 0,49 далеко от каждой к-хунты.
Алгоритм и его доказательство правильности просты и модульны с использованием некоторых классических инструментов, таких как «случайные ограничения» с элементарными свойствами оператора шума на кубе.
Совместная работа с Эльхананом Мосселем и Джо Ниманом.
Аннотация: В этом докладе я рассмотрю теорию сложности вычислений и некоторые интересные квантовые обобщения некоторых популярных классов сложности. В частности, я рассмотрю два квантовых варианта полиномиальной иерархии и представлю несколько результатов, ограничивающих их вычислительную мощность.Для этого выступления не требуется никаких знаний о теории сложности или квантовой теории. Это совместная работа с Миклошом Сантой, Севагом Гарибианом, Аарти Сундарамом и Джастином Йиркой, а препринт можно найти по адресу https://arxiv.org/abs/1805.11139.
Аннотация: В этом докладе я рассмотрю несколько естественных квантовых проблем и, в частности, то, как проблемы меняются по мере изменения квантовых ресурсов. Я покажу, как с экономической точки зрения назначать «теневую цену» каждому квантовому ресурсу.Для этого я воспользуюсь теорией оптимизации и покажу, что теневые цены часто выдаются «бесплатно», если вы знаете, где их искать. Для этого выступления не требуется никаких знаний в области экономики, теории оптимизации или квантовой теории. Это совместная работа с Гэри Ау (Университет Саскачевана).
Аннотация: Первая демонстрация квантового превосходства в октябре 2019 г. стала крупным достижением экспериментальной физики. В то же время он опирался на важные достижения теоретической информатики.В этом докладе я опишу свою недавнюю работу, заложив теоретико-сложную основу эксперимента Google / UCSB по квантовому превосходству, предоставив доказательства того, что их устройство экспоненциально сложно моделировать с помощью классического компьютера. Этот перекресток между теорией сложности и квантовой физикой также предлагает новое понимание обеих дисциплин. Например, я объясню, как методы квантовой теории сложности могут быть использованы для решения чисто классических проблем. В частности, я опишу квантовый аргумент, который почти решает гипотезу о приближенной композиции степеней, обобщая почти 20-летнюю предыдущую работу.В другом направлении я покажу, что понятие вычислительной псевдослучайности из криптографии, основанной на сложности, имеет фундаментальное значение для физики черных дыр и теории квантовой гравитации.
Аннотация: Мы показываем, как два метода из статистической физики могут быть адаптированы для решения варианта пресловутой проблемы уникальных игр, потенциально открывая новые пути к гипотезе уникальных игр. Мы демонстрируем эффективные алгоритмы естественного обобщения Unique Games, основанные на приближении подходящей статистической суммы с помощью (i) области без нулей и полиномиальной интерполяции, и (ii) кластерного расширения.Мы также показываем, что небольшое улучшение параметров, для которых мы приводим результаты, опровергло бы гипотезу уникальных игр. На основе совместной работы с М. Колсоном, А. Колла, В. Пателем и Г. Регтсом.
Аннотация: Мы изучаем жесткую модель (независимые множества) на двудольных графах, используя кластерное разложение из статистической физики. Когда существует достаточный дисбаланс в степенях или летучести между сторонами (L, R) двудольного разделения, мы можем переписать жесткую статистическую сумму в терминах отклонений от независимых множеств, которые пусты с одной стороны двудольного разделения, и показать это выражение имеет сходящееся кластерное расширение.Это имеет интересные алгоритмические и вероятностные последствия. С алгоритмической стороны мы обращаемся к открытой проблеме приближенного подсчета и даем алгоритм с полиномиальным временем для аппроксимации статистической суммы для большого класса двудольных графов ограниченной степени; это включает, среди прочего, невзвешенный бирегулярный случай, когда степени удовлетворяют d R > = 7 d L log d L . Наш алгоритм аппроксимации основан на усечении расширения кластера. Как следствие этого метода, мы также доказываем, что базовая модель на таких графах демонстрирует экспоненциальное затухание корреляций за счет использования связей между расширением кластера и совместными кумулянтами.Совместная работа с Уиллом Перкинсом.
Abstract: Максимально восстанавливаемые коды — это коды, разработанные для распределенного хранилища, которые сочетают в себе быстрое восстановление после отказа одного узла и оптимальное восстановление после катастрофического отказа. Gopalan et al. [SODA 2017] изучил размер алфавита, необходимый для таких кодов в сеточных топологиях, и дал комбинаторную характеристику для него. Рассмотрим разметку ребер полного двудольного графа K n, n метками, исходящими из F 2 d , которое удовлетворяет следующему условию: для любого простого цикла сумма меток по его ребрам отлична от нуля .Минимальное d, где это возможно, контролирует размер алфавита, необходимый для максимально восстанавливаемых кодов в топологиях сетки n x n. До этой работы было известно, что d находится между (log n) 2 и n log n. Мы улучшаем обе оценки и показываем, что d линейно по n. Верхняя граница — это рекурсивная конструкция, которая превосходит случайную конструкцию. Для оценки снизу следует сначала связать проблему с числом независимости графа многогранника Биркгофа, а затем дать для нее точные оценки, используя теорию представлений симметрической группы.
(совместный с семинаром RCDS)
Аннотация: Сеть взаимосвязей между сегодняшними технологиями и обществом меняет многие традиционные способы ведения дел: Интернет вещей, биткойны, экономика совместного использования и истории о «фальшивых новостях», распространяемых в социальных сетях, все чаще находятся в общественном сознании. Таким образом, компьютерные ученые и инженеры должны все больше осознавать взаимосвязь между техническими характеристиками своих систем и личными целями пользователей, клиентов и противников.Я представлю недавние работы по двум проблемным областям: надежный дизайн стимулов для социальных сетей и гибкая координация и оптимизация в распределенных многоагентных спроектированных системах. В каждом из них, тщательно исследуя фундаментальные компромиссы, связанные с оптимальным дизайном, я стремлюсь развить более глубокое теоретическое понимание инструментов, которые помогут решить возникающие сегодня проблемы.
Аннотация: В классической онлайн-задаче принятия решения лицо, принимающее решение, которое пытается максимизировать свою ценность, проверяет последовательность поступающих элементов, чтобы узнать их значения (взятые из известных распределений), и решает, когда остановить процесс, беря текущий элемент. .Цель — доказать «неравенство пророка»: что она может делать примерно так же, как пророк с предвидением всех ценностей. В этой работе мы исследуем эту проблему, когда значения могут быть коррелированы. Мы рассматриваем естественную «линейную» корреляционную структуру, которая моделирует многие виды реальных поисковых задач. Ключевой проблемой является то, что алгоритмы на основе пороговых значений, которые обычно используются для устранения неравенства пророков, больше не гарантируют хорошей производительности. Мы связываем это препятствие с другой проблемой: небольшое «увеличение» значений поступающих элементов может снизить производительность многих алгоритмов.Мы используем эту интуицию, чтобы доказать границы (соответствие с постоянными факторами), которые плавно затухают в зависимости от степени корреляции поступающих элементов. Мы распространяем эти результаты на случай выбора нескольких элементов.
Совместная работа с Николь Имморлика и Сахил Сингла
Аннотация: Когда вы программируете свои собственные x == y , x.equals (y) или C.isSame (x, y) ; логика вашей программы имеет больше смысла, вы уменьшаете количество дубликатов, ускоряете поиск и фильтруете свои данные по тому, что важно. Но вы не можете предсказать, что f (x) == f (y) . Речь идет об улучшении эквивалентности с типами идентичности , чтобы убедиться, что когда вы судите о равенстве данных, ваша программа верит вам. Математика настоящая, но в ней есть практические и сложные задачи. Мы обсуждаем недавнюю теорию, практические инструменты для JVM и то, что это означает для сложности вычислений черного ящика.
Abstract: За сотни лет понимания природных систем физики разработали множество принципов динамики и точек зрения.Некоторые из этих методов, если их рассматривать (и абстрагироваться) через призму вычислений, могут привести к новым методам оптимизации и выборки для задач машинного обучения, статистики и теоретической информатики. Я представлю несколько недавних примеров из моих исследований такого взаимодействия между физикой и алгоритмами, например, алгоритм, вдохновленный гамильтоновой динамикой, для выборки из непрерывных распределений.
Основано на совместных работах с Ореном Мангуби.
Аннотация: Сопряжение — естественное понятие изоморфизма в символической динамике.Основной нерешенной проблемой в этой области является поиск алгоритма для определения сопряженности сдвигов конечного типа (SFT). В этом выступлении мы рассмотрим несколько связанных вычислительных проблем, ограниченных k-блочными кодами. Мы показываем, что предлагаемая k-блочная сопряженность находится в P, обнаружение k-блочной сопряженности является GI-трудным, уменьшение размера представления SFT через 1-блочную сопряженность является NP-полным, и распознавание того, является ли программный сдвиг SFT находится на P. Этот доклад не предполагает каких-либо предварительных знаний о символической динамике.На основе совместной работы с Рафом Фронгилло.
Аннотация: Мы обсудим понятие сертифицированного алгоритма. Сертифицированные алгоритмы обеспечивают гарантии производительности как в худшем, так и выходящем за его пределы. Во-первых, γ-сертифицированный алгоритм также является алгоритмом γ-приближения — он находит γ независимо от входных данных. Во-вторых, он точно решает γ-стабильные экземпляры (γ-стабильные экземпляры моделируют реальные экземпляры). Кроме того, сертифицированные алгоритмы обладают рядом других желательных свойств: они решают как максимизирующие, так и минимизирующие версии задачи (например,г. Max Cut и Min Uncut), решать слабостабильные экземпляры и решать проблемы с жесткими ограничениями.
Мы определим сертифицированные алгоритмы, опишем их свойства, представим структуру для разработки сертифицированных алгоритмов, предоставим примеры сертифицированных алгоритмов для максимального разреза / минимума неразрезанного, минимального многостороннего разреза, k-медианы и k-средних.
Беседа основана на совместной работе с Константином Макарычевым.
Аннотация: Мы обсуждаем вероятностный метод для различных формулировок раскраски графов и показываем, как «локальная занятость» дает общий язык для многих недавних результатов и приводит к некоторым новым приложениям.
Аннотация: Обучение с подкреплением — это подход к синтезу контроллеров, при котором агенты полагаются на сигналы вознаграждения для выбора действий, чтобы удовлетворить требования, неявные в сигналах вознаграждения. Часто неспециалистам приходится придумывать требования и их перевод для вознаграждения в условиях значительного дефицита времени, хотя ручной перевод требует времени и подвержен ошибкам. Для критически важных с точки зрения безопасности приложений обучения с подкреплением необходима строгая методология проектирования и, в частности, принципиальный подход к спецификации требований и к переводу целей в форму, требуемую алгоритмами обучения с подкреплением.
Формальная логика обеспечивает основу для строгого и однозначного определения требований к целям обучения. Однако алгоритмы обучения с подкреплением требуют, чтобы требования выражались в виде скалярных сигналов вознаграждения. Мы обсуждаем недавнюю технику, называемую предельной достижимостью, которая устраняет этот пробел, точно переводя логические требования в скалярную форму вознаграждения, необходимую в немодельном обучении с подкреплением. Этот метод позволяет синтезировать контроллеры, которые максимизируют вероятность удовлетворения заданных логических требований, используя готовые алгоритмы обучения с подкреплением без использования моделей.
Аннотация: Все корреляционные меры, классические и квантовые, должны быть монотонными относительно локальных операций. В этом докладе я охарактеризую монотонные формулы, которые представляют собой линейные комбинации энтропий фон Неймана, связанных с квантовым состоянием физической системы, состоящей из n частей. Затем я покажу, что эти формулы образуют многогранный выпуклый конус, который мы называем конусом монотонности, и перечислим его грани. Мы проиллюстрируем его структуру и докажем, что он эквивалентен конусу монотонных формул, вытекающих из сильной субаддитивности.Мы явно вычисляем его экстремальные лучи для n вплоть до 5. Я также рассмотрю симметричный конус монотонности, в котором формулы должны быть инвариантными относительно перестановок подсистем. Этот конус можно полностью описать для всех n. Кроме того, мы показываем, что эти результаты верны, даже когда состояния и операции должны быть классическими.
Аннотация: В сетевой маршрутизации пользователи часто ставят перед собой разные задачи при выборе наилучшего маршрута. Примером могут служить транспортные сети, где из-за неопределенности времени в пути водители могут выбирать между средним временем в пути и вариацией маршрута.Или они могут найти компромисс между временем и стоимостью, например, стоимостью, уплаченной в виде дорожных сборов.
Мы хотим понять влияние двух конфликтующих критериев при выборе маршрута, изучив полученное распределение трафика (равновесие) в сети. Мы исследуем две точки зрения на эту тему: (1) Как равновесная стоимость населения, не склонного к риску, сравнивается со стоимостью населения, нейтрального к риску? (т.е. сколько времени мы тратим на трафик из-за того, что не боимся риска) (2) Как равновесные затраты разнородной популяции сравниваются со стоимостью сопоставимой однородной группы пользователей?
Мы даем характеристики на оба вопроса выше.
Основано на совместной работе с Ричардом Коулом, Танасис Лианеас и Николасом Стир-Мозес.
В конце я упомяну текущую работу моей исследовательской группы по разработке алгоритмов и механизмов для энергосистем.
Аннотация: Квантовые вычисления стремительно переходят от научной фантастики к реальности. Недавний экспериментальный прогресс, достигнутый благодаря усилиям в академических кругах и промышленности, привел нас в новую эру, в которой масштабируемые квантовые компьютеры уже не за горами, а несовершенные квантовые системы в масштабе 50–100 кубитов будут реализованы в самом ближайшем будущем.По мере развития этой эпохи разрыв между теорией и экспериментом сокращается, и идеи теоретической информатики становятся все более важными для понимания этих квантовых устройств.Этот доклад направлен на описание моих исследований, направленных на разработку инструментов, необходимых для характеристики мощности квантовых вычислений как в ближайшем, так и в неопределенном будущем. Эти инструменты обеспечат основу для создания полезных квантовых алгоритмов следующего поколения, но также помогут направить ход квантового эксперимента.
Доклад будет доступен широкой аудитории информатики.
Abstract: Автоматизированные решения и политики, основанные на машинном обучении и стремлении к эффективности, пронизывают сегодняшнюю социальную жизнь. Я расскажу о трех довольно различных проявлениях этой реальности и некоторых вытекающих из них сложных вычислительных проблемах: Классификация эгоистичных агентов, например, при поступлении в колледж, может привести к игре, неэффективности и несправедливости; когда алгоритмы машинного обучения вводятся коммерческими производителями данных, необходимы новые формы проектирования вычислительных механизмов; наконец, оптимизация эффективности в играх с заторами, например за счет взимания платы за проезд на перегруженных маршрутах, может быть доказана при допущениях, которые неизбежно увеличивают неравенство в благосостоянии.Мы размышляем, не являются ли это симптомами и частями зарождающегося нового социального порядка.
Аннотация: В последние несколько лет несколько моих исследовательских проектов (совместных с сотрудниками) показывают, что полезно рассматривать линейные пространства матриц как линейный алгебраический аналог графов. В этом докладе я предложу такой аналог и объясню, почему такой аналог может иметь смысл. Затем я перечислю несколько соответствий между структурами на графах и структурами на матричных пространствах. К ним относятся идеальные сопоставления с матрицами полного ранга, сжатые подмножества и сжатые пространства, независимые множества против изотропных пространств, случайные графы и случайные матричные пространства и концепции изоморфизма.Эти соответствия играют важную роль в недавнем прогрессе в области некоммутативного рационального тестирования идентичности, образуют одно узкое место при помещении изоморфизма графов в P и предлагают возможный путь для постквантовой криптографии.Ниже приведены некоторые относящиеся к делу документы.
(1) Обобщенные последовательности Вонга и их приложения к проблемам Эдмондса, Дж. Иваниос, М. Карпински, И Цяо, М. Санта. arXiv: 1307.6429.
(2) Конструктивный некоммутативный ранг определяется за детерминированное полиномиальное время, по Г.Иваниос, И Цяо, К. В. Субрахманьям. arXiv: 1512.03531.
(3) Масштабирование операторов: теория и приложения, А. Гарг, Л. Гурвиц, Р. Оливейра, А. Вигдерсон. arXiv: 1511.03730.
(4) Линейные алгебраические аналоги проблемы изоморфизма графов и модели Эрдеша-Реньи, Ю. Ли, Ю. Цяо. arXiv: 1708.04501.
(5) От независимых множеств и раскраски вершин к изотропным пространствам и изотропным разложениям, X. Bei, S. Chen, J. Guan, Y. Qiao, X. Sun. В подготовке; бумага скоро будет доступна.
Аннотация: В задаче о k-разрезе гиперграфа входом является гиперграф вместе с константой k, и цель состоит в том, чтобы найти наименьшее подмножество гиперребер, удаление которых гарантирует, что оставшийся гиперграф имеет по крайней мере k компонент связности.Проблема k-разреза графа разрешима за полиномиальное время (Goldschmidt and Hochbaum, 1994), в то время как сложность проблемы k-разреза гиперграфа открыта. В этом докладе я представлю рандомизированный алгоритм с полиномиальным временем для решения проблемы k-разреза гиперграфа. На основе совместной работы с Чао Сюй и Силинь Ю.
Аннотация: В ближайшем будущем, вероятно, появятся квантовые компьютеры специального назначения с 50-70 качественными кубитами и управляемыми связями ближайших соседей. В этом выступлении я рассмотрю общие теоретические основы того, как использовать такие устройства для демонстрации «квантового превосходства»: то есть явного квантового ускорения для * некоторой * задачи, мотивированного целью опровергнуть расширенный тезис Черча-Тьюринга ( который говорит, что все физические системы могут быть эффективно смоделированы классическими компьютерами) с максимальной уверенностью.Эта часть выступления основана на совместной работе с Лиджи Чен, https://arxiv.org/abs/1612.05903. Затем, во второй части выступления, я расскажу о новой, еще не опубликованной работе о том, как эти эксперименты можно использовать для генерации криптографически сертифицированных случайных битов. Аннотация: Мы даем алгоритм времени m 1 + o (1) β o (1) для генерации равномерно случайных остовных деревьев в взвешенных графах с максимальным и минимальным весовым отношением β. В процессе мы проиллюстрируем, как можно преодолеть фундаментальные компромиссы при разбиении графа, удаляя вершины из графа с помощью дополнений Шура к связанной матрице Лапласа.Наша отправная точка — алгоритм Олдоса-Бродера, который выбирает случайное остовное дерево с помощью случайного блуждания. Как и в предыдущей работе, мы используем быстрые решатели лапласовской линейной системы, чтобы сократить случайное блуждание от вершины v до границы набора вершин, назначенных v, называемого «сокращателем». Мы отходим от предыдущей работы и представляем новый способ использования лапласовских решателей для сокращения пути. Чтобы ограничить объем работы по сокращению, мы показываем, что большинство шагов случайного блуждания происходит далеко от непосещенной вершины.Мы применяем это наблюдение, взимая плату за использование сокращателя S для шагов случайного блуждания в дополнении Шура, полученном путем удаления всех вершин в S, которые ему не присвоены.
Аннотация: Проблема кольцевого обучения с ошибками является кандидатом на квантово-безопасную задачу жесткой идеальной решетки, на которой будет основана будущая постквантовая криптография. Такие компании, как Google, уже развернули его, но действительно ли это сложно? Я объясню проблему и то, как ее можно использовать для криптографии, ее связь с другими проблемами решетки и точку зрения теоретиков чисел на ее сложность.
Резюме: Общая математическая проблема вычисления недорогих карт между двумя метрическими пространствами распространена во многих приложениях, включая регистрацию при обработке медицинских изображений, обнаружение функций при моделировании белков, реконструкцию эволюционных деревьев в филогеномике, поиск повторяющихся закономерностей в анализе данных и поиск простые представления данных в визуализации. Многие примеры общей проблемы доказуемо сложны, поэтому у нас есть дихотомия. С одной стороны, у нас есть общие алгоритмы с теоретическими гарантиями наихудшего случая, которые на практике являются чрезмерно медленными, а с другой — более быстрая эвристика, разработанная для конкретных приложений, но без гарантий.Дихотомия — это возможность — я использую параметризованную сложность, чтобы лучше понять сложность вычисления недорогих карт между метрическими пространствами на основе их геометрических и топологических свойств. Я специально нацелен на новые алгоритмы с лучшими гарантиями производительности, в частности, для случаев, представляющих практический интерес.В этом докладе я представляю параметризованную сложность: ветвь вычислительной сложности, которая классифицирует проблемы на основе их сложности по нескольким параметрам ввода в дополнение к размеру ввода; следовательно, он дает гораздо более детальную классификацию по сравнению с традиционным анализом наихудшего случая, основанным только на размере входных данных.Затем я представляю несколько параметризованных алгоритмов для вычисления недорогих карт между геометрическими объектами. Время работы этих алгоритмов параметризуется с учетом топологических и геометрических параметров входных объектов. Например, когда входом является граф, топологическим параметром может быть его ширина дерева, которая измеряет, насколько граф выглядит как дерево, а геометрическим параметром может быть внутренняя размерность метрического пространства, вызванная кратчайшими путями в графе.
Аннотация: Одним из полезных приложений теории характеров является изучение времен перемешивания случайных блужданий в группах.Понятие теории суперхарактеров побуждает к дальнейшему совершенствованию методов в этом приложении; в частности, он дает спектр вариантов, которые позволяют адаптировать теорию к потребностям лежащей в основе прогулки. Этот доклад фокусируется на индуцированных случайных блужданиях комбинаторных объектов, возникающих в результате разбиения множеств на группы. Мы исследуем, какие свойства разбиения множества дают желаемое поведение и как использовать результирующие теории представлений для вычисления собственных значений и собственных векторов для обхода.В этом проекте участвует множество студентов РЭУ.
Аннотация: Алгоритмы спектральной кластеризации находят кластеры в заданной сети, используя свойства собственных векторов матриц, связанных с сетью. В качестве первого шага вычисляется спектральное вложение, то есть отображение узлов в точки в реальном пространстве низкой размерности; затем используются алгоритмы геометрической кластеризации, такие как k-means, для кластеризации точек, соответствующих узлам.Такие алгоритмы работают настолько хорошо, что в некоторых приложениях, не связанных с сетевым анализом, таких как сегментация изображений, полезно связать сеть с данными, а затем применить спектральную кластеризацию к сети.Помимо применения в кластеризации, спектральные вложения являются ценным инструментом для уменьшения размерности и визуализации данных.
Эффективность алгоритмов спектральной кластеризации была строго обоснована в применении к сетям, исходящим из определенных вероятностных генеративных моделей.
Более поздняя разработка, которой посвящена эта лекция, представляет собой анализ спектральной кластеризации наихудшего случая, показывающий, что для каждого графа, который демонстрирует определенную кластерную структуру, такую структуру можно найти с помощью геометрических алгоритмов, применяемых к спектральному встраиванию. .
Такие результаты обобщают неравенство графа Чигера (классический результат в спектральной теории графов) и имеют дополнительные приложения в теории сложности вычислений и в чистой математике.
Аннотация: Дифференциальная конфиденциальность предлагает математическую основу для балансирования двух целей: получение полезной информации о конфиденциальных данных и защита конфиденциальности на индивидуальном уровне. Обнаружение ограничений дифференциальной конфиденциальности позволяет понять, какие анализы несовместимы с конфиденциальностью и почему.Эти идеи также помогают в поиске оптимальных алгоритмов сохранения конфиденциальности. В этом докладе я приведу примеры того, как и то и другое вытекает из нового понимания структуры дифференциальной конфиденциальности.Сначала я опишу отрицательные результаты анализа частных данных через соединение с криптографическими объектами, называемыми кодами снятия отпечатков пальцев. Эти результаты показывают, что (асимптотически) оптимальный способ решения естественных задач большой размерности — разложить их на множество более простых задач. Во второй части доклада я буду обсуждать концентрированную дифференциальную конфиденциальность — структуру, которая позволяет проводить более точный анализ, точно фиксируя состав более простых задач.
Аннотация: Фурье-аналитические и алгебраические методы привели к нескольким недавним достижениям в теоретической информатике. Эти методы обычно адаптированы для гиперкуба или других так называемых продуктовых областей; однако наблюдается растущий интерес к расширению горизонта за счет включения непродуктовых областей. Важным таким примером является пространство совершенных паросочетаний, нетривиальная алгебраическая структура которого оказалась проблематичной для современных алгебраических методов, основанных на гиперкубах.В этом докладе мы рассмотрим алгебраическую структуру совершенных паросочетаний с точки зрения теории представлений. Мы даем идеальные аналоги некоторых знакомых понятий и объектов в области булевых функций и обсуждаем несколько фундаментальных отличий, возникающих в неабелевой ситуации. Доклад завершится обзором некоторых результатов в области экстремальной комбинаторики, оптимизации и вычислительной сложности, которые были получены с этой алгебраической точки зрения.
Abstract: В этом докладе я опишу результат Гюнтнера, Тессеры и меня о свойствах аппроксимации и жесткости относительно гиперболических групп.Попутно мы увидим, что значит гиперболический граф и какое отношение парадокс Банаха-Тарского имеет к расширителям. Никаких предварительных знаний не требуется.
Аннотация: Изучается пространственная сложность рисования разрезов и лапласовских квадратичных форм графов. Мы показываем, что любая структура данных, которая приблизительно хранит размеры всех разрезов в неориентированном графе на n вершинах с точностью до ошибки 1 +, должна использовать Ω (n logn / 2 ) бит пространства в худшем случае, улучшая Ω (n / ϵ 2 ), оценка Andoni et al.и согласование с наиболее известной верхней границей, достигнутой с помощью спектральных распределителей. Наше доказательство основано на явлении жесткости для разрезающей (и спектральной) аппроксимации, которая может представлять независимый интерес: любые два d-регулярных графа, которые аппроксимируют разрезы друг друга значительно лучше, чем случайный граф, приближают, что полный граф должен перекрываться в постоянной доле их края.
Аннотация: Плоские кривые — один из самых фундаментальных объектов как в математике, так и в информатике. Помимо их очевидного использования в вычислительной геометрии и топологии, были найдены интересные приложения в оптимизации, теории узлов и многом другом.В этом выступлении мы вместе совершим путешествие по небольшой части ландшафта. Мы начнем с представлений плоских кривых и их деформаций, а также их внешнего вида и множества применений в различных дисциплинах математики и компьютерных наук. Затем мы сосредоточимся на дискретном представлении деформаций кривой, называемых гомотопическими движениями. Мы сделаем набросок идей, лежащих в основе нескольких недавних результатов по распутыванию плоских кривых с помощью гомотопических движений, их обобщению на поверхностях и последствиям для решения задач оптимизации плоских графов с использованием электрических преобразований.
Нет никаких предположений об исходных знаниях в топологии. Во время выступления будут заданы открытые вопросы (не ограничиваясь плоскими кривыми).
.