ГДЗ контрольная работа / К-2 / вариант 2 1 алгебра 7 класс дидактические материалы Звавич, Кузнецова
Решение есть!- 1 класс
- Математика
- Английский язык
- Русский язык
- Литература
- Окружающий мир
- 2 класс
- Математика
- Английский язык
- Русский язык
- Информатика
- Музыка
- Окружающий мир
- Технология
- 3 класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Музыка
- Литература
- Казахский язык
- 4 класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Информатика
- Музыка
- Литература
- Окружающий мир
- 5 класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Украинский язык
- Биология
Алгебра 7 Контрольная работа 2 с ответами (Макарычев)
Контрольная работа № 2 по алгебре в 7 классе с ответами по УМК Макарычев. Автор вопросов: Л.И.Мартышова (Контрольно-измерительные материалы). Цитаты из пособия использованы в учебных целях. Алгебра 7 Контрольная работа 2 «Уравнение с одной переменной». Ответы на контрольные работы адресованы родителям, которые смогут проконтролировать правильность выполнения задания.
Автор вопросов: Л.И.Мартышова (Контрольно-измерительные материалы). Цитаты из пособия использованы в учебных целях. Алгебра 7 Контрольная работа 2 «Уравнение с одной переменной». Ответы на контрольные работы адресованы родителям, которые смогут проконтролировать правильность выполнения задания.
Алгебра 7 класс (Макарычев)
Контрольная работа № 2
К-02. Вариант 1
- Решите уравнение: а) 3/4 • х = –8; б) 12,5 + 5х = 0; в) 18 – 0,2(3х – 70) = х.
- На одном складе было в 2 раза больше тонн яблок, чем на другом. Всего на складах 36 т. Сколько тонн яблок на каждом складе?
- При каком значении переменной а значение выражения За + 8 меньше значения выражения 5 – 6а на 15?
- Расстояние между пунктами А и В велосипедист проехал за 3 ч. На обратном пути он увеличил скорость на 2 км/ч. Поэтому на данный путь велосипедист затратил на 30 мин меньше. С какой скоростью ехал велосипедист из пункта А в пункт В?
- Решите уравнение |4x| = 2,8.

- Среди чисел 1, 2, 3, –1 выберите корни уравнения у2 – 2у – 3 = 0.
ОТВЕТЫ на Вариант 1
№1). а) –32/3; б) –2,5; в) 2,5.
№2). 24; 12.
№3). –2.
№4). 10 км/ч.
№5). –0,7; 0,7.
№6). –1; 3.
К-02. Вариант 2
- Решите уравнение: а) –4х = 4/7; б) –6х – 12,6 = 0; в) 26,9 – 0,8(3х + 40) = х.
- В одном мешке было на 12 кг сахара больше, чем в другом. Всего в обоих мешках было 72 кг сахара. Сколько килограммов сахара было в каждом мешке?
- При каком значении переменной х значение выражения 20 – Зх больше значения выражения 4 – 7х на 4?
- Расстояние между пунктами А и В мотоциклист проехал за 4 ч. На обратном пути он увеличил скоростью на 20 км/ч, поэтому затратил на обратный путь на 1 ч меньше. С какой скоростью ехал мотоциклист из А в В?
- Решите уравнение |5у| = 4,5.

- Среди чисел 1, 2, 3, –1 выберите корни уравнения у2 – 5у + 6 = 0.
ОТВЕТЫ на Вариант 2
№1). а) –1/7; б) 2,1; в) –1,5.
№2). 42; 30.
№3). –3.
№4). 60 км/ч.
№5). –0,9; 0,9.
№6). 2; 3.
Вы смотрели: Контрольная работа по алгебре в 7 классе с ответами по УМК Макарычев «Уравнение с одной переменной». Автор вопросов: Л.И.Мартышова (Контрольно-измерительные материалы). Цитаты из пособия использованы в учебных целях. Алгебра 7 Контрольная работа 2. Ответы на контрольные работы адресованы родителям.
Вернуться к Списку контрольных работ по алгебре в 7 классе (Мартышова. КИМ)
Контрольная работа К-2 вариант 2
Решебники, ГДЗ
- 1 Класс
- Математика
- Русский язык
- Английский язык
- Информатика
- Немецкий язык
- Литература
- Человек и мир
- Природоведение
- Основы здоровья
- Музыка
- Окружающий мир
- Технология
- 2 Класс
- Математика
- Русский язык
- Белорусский язык
- Английский язык
- Информатика
- Украинский язык
- Французский язык
- Немецкий язык
- Литература
- Человек и мир
- Природоведение
- Основы здоровья
- Музыка
- Окружающий мир
- Технология
- Испанский язык
- 3 Класс
- Математика
- Русский язык
- Белорусский язык
- Английский язык
- Информатика
- Украинский язык
- Французский язык
- Немецкий язык
- Литература
комплектов | Примечания, видео, контроль качества и тесты | 7 класс> Обязательная математика> Наборы
Наборы
Четко определенный набор вещей (предметов, чисел и т. Д.) Называется набором. Например: «простые числа меньше 10». Он определяет заметно
Д.) Называется набором. Например: «простые числа меньше 10». Он определяет заметно
Рис. Введение в концепции множества и диаграммы Венна
различных объекта, которые должны быть включены в коллекцию. Итак, 1, 2, 3, 5 и 7 попадают в коллекцию.
Член набора
Объекты, принадлежащие набору, называются элементами или элементами набора. Принадлежность члена к множеству обозначается символом или знаком «принадлежат» (то есть «\ (\ in \)»).
Например:
Возьмем набор, A = {3, 6, 9, 12, 15}.
В наборе A: 6, 9, 12 и 15 являются членами или элементами набора A. Итак, «3 \ (\ in \) A» читается как «3 принадлежит набору A» или «3 является член множества A ‘. Принимая во внимание, что число, кроме 3, 6, 9, 12 и 15, не принадлежит множеству A.
( Примечание: Символ ‘\ (\ in \)’ используется, когда какой-либо элемент не является членом какого-либо заданного набора).
Методы описания набора
Как правило, набор описывается следующими тремя способами:
- Метод описания
- Метод листинга
- Метод создания набора
- Метод описания:
В этом методе, набор описывается общим свойством члена набора в предложении внутри фигурных скобок. Например;
Например;
A = {нечетные числа меньше 10}
E = {четные числа от 7 до 20} - Метод листинга:
В этом методе набор представлен записью / включением его элементов в фигурные скобки. Например:
A = {1, 3, 5, 7, 9}
E = {8, 10, 12, 14, 16, 18} - Set-builderMethod:
В этом методе члены set представлены такой переменной, как x, y, z и т. д., и эта переменная описывает уникальное / общее свойство, разделяемое всеми членами (элементами) набора.Например:
A = {x: x — нечетное число меньше 10}, где читается как A — это набор всех значений x, такое tat x — нечетное число меньше 10.
Аналогично,
E = { z: z — четное число от 7 до 20}.
Кардинальное число набора
Число элементов в конечном наборе называется кардинальным числом набора. Он обозначается n (A), n (B) n (C) и т. Д. Например:
A = {2, 4, 6, 8, 10}
Здесь количество элементов множеств A равно 5. Итак, кардинальное число множества A равно n (A) = 5
Итак, кардинальное число множества A равно n (A) = 5
. Аналогично, M = {5, 10, 15}
∴ Кардинальное число набора M равно n (M) = 3.
Подмножество
Если A и B — два множества, и каждый элемент множества A также является элементом множества B, то A называется подмножеством B. Оно обозначается символом «⊆» как A ⊆ B. Например:
A = {целое число меньше 6}
, т.е. A = {0, 1,2, 3, 4, 5}
B = {нечетное число меньше 10}
, т.е. B = {1, 3, 5, 7 }
C = {четные числа меньше 9}
i.е. C = {2, 4, 6, 8}
D = {простые числа от 1 до 8}
т.е. D = {1, 2, 3 5, 7}
Здесь каждый элемент множеств B, C и D также является элементом множества A. Итак, B, множество C и множество D являются подмножествами множества A.
( Примечание: Пустой набор (Φ) — это подмножество каждого набора. Каждый набор является подмножеством самого себя )
- Надмножество
Если набор является подмножеством набора A, то набор A называется надмножеством B. Если обозначается как A⊇ B.
Если обозначается как A⊇ B. - Собственное подмножество
Набор ‘ A ‘называется собственным подмножеством множества B, если оно содержит хотя бы один элемент меньше, чем множество B.Обозначается символом «C». Символически мы пишем ABC, если A является правильным подмножеством B. Например:
A = {целое число меньше 6}
, т.е. A = {0, 1, 2, 3, 4, 5, 6}
B = { нечетное число меньше 7}
, т.е. B = {1, 3, 5}
Здесь B является подмножеством B, а множество B не равно множеству A. Итак, B является правильным подмножеством B, то есть A⊂ B .
( Примечание: Никакой набор не является правильным подмножеством самого себя. Нулевой набор или пустой набор является правильным подмножеством каждого набора). - Число подмножеств данного набора
Число подмножеств данного набора может быть получено с помощью формулы «2 n », где x — количество элементов данного набора.Например:
Set A = {a, b}
, т. е. n (A) = 2
е. n (A) = 2
Здесь возможными подмножествами набора A являются {a}, {b}, {a, b} иΦ. Итак, у него 4 подмножества.
, т.е. 2 n = 2 2 = 4
Универсальный набор
Универсальный набор — это набор, который имеет все элементы других данных наборов. Обозначается символом U или ξ (pxi). Например:
U = {a, b, c, d, e, f, g, h, i, o, u}
A = {a, b, c, d, e}
B = {a, e , i, o, u}
C = {b, d, f, g, i}
Здесь набор U — универсальный набор, который представляет собой набор алфавитов от a до j, а A, B и C — подмножества универсальный набор «U».
Венна — диаграмма
Схематическое изображение множеств называется Венн-диаграммой. Его разработал британский математик Джон Венн. Универсальный набор
Источник: Finingeometry.orgРис. Диаграммы Венна и конечная геометрия
‘U’ обычно обозначается прямоугольником, а другой набор — кружком.
Символы и их значение
| \ (\ in \) | ‘элемент’ или ‘принадлежит’ или ‘является членом содержимого’ |
| ∉ | ‘не элемент из ‘или’ не принадлежит ‘или’ не является членом ‘ |
| ⇒ | подразумевает, что |
| Iff | Если и только если |
| / или | , так что |
Эссе по периодическому тесту по математике для 7 класса
Республика ФилиппиныДепартамент образования
III регион
Подразделение Nueva Ecija
ПАЛАЯНСКАЯ ГОРОДСКАЯ НАЦИОНАЛЬНАЯ СТАРШАЯ ШКОЛА
Атате, город Палаян
Первый периодический тест по математике для 7 класса
С.2013 — 2014
НАИМЕНОВАНИЕ:
СОРТА И СЕКУНДА:
ТЕСТ I. МНОЖЕСТВЕННЫЙ ВЫБОР. Внимательно прочтите каждое утверждение. Напишите букву лучшего ответа по каждому пункту в графе перед числом.
1. Что из нижеперечисленного не описывает набор?
а. набор — четко определенная группа объектов |
б. наборы могут быть записаны в реестр или методом правил |
c. набор без какого-либо элемента называется пустым набором |
d. ни один из них |
2.Учитывая, что A = {2, 4, 6, 8} и B = {3, 4, 5}; найти A ∩B. а. {2, 3, 4, 5, 6, 8} | | c. {4} |
б. {} | | d. {2, 3, 5, 6, 8} |
3. Учитывая, что U = {1, 2, 3, 4, 5, 6, 7, 8},
A = {1, 3, 5, 8} и B = {2, 4, 6}; Найди’.
а. {2, 4, 6, 7} | | c. {4} |
б. {1, 3, 5, 8} | | d. {3, 5, 7} |
4. Что из следующего относится к количеству элементов данного набора? а. универсальный | | c. мощность |
б. элементы | | d.конечное множество |
5. Что из перечисленного НЕ является пустым?
а. A = {} | | c. A = {∅} |
б. набор без элемента | d. ни один из них |
6. Для вычитания целых чисел необходимо
a. изменить вычитаемое
b. изменить знак вычитаемого
c. применить правило сложения
применить правило сложения
d. изменить знак вычитаемого и
перейти к сложению
7. Какой набор чисел содержит отрицательные и положительные числа с нулем? а. натуральные числа | | c. подсчет чисел |
б.целые числа | d. целые числа |
8. Какое свойство действительных чисел показывает утверждение 3x + y = y + 3x? а. закрытие | | c. распределительный |
б. коммутативный | d. ассоциативный |
9. Сложение целых чисел с одинаковыми знаками означает ___
а. складывать числа и использовать их общий знак |
б. вычесть числа и использовать знак числа с большим абсолютным значением | c. Сложите числа и используйте знак плюса |
d. сложите числа и используйте знак минуса |
10.Что из следующего демонстрирует ассоциативное свойство? а. 2 (ab) = (2a) b | | c. 2 + (ab) = (2a) + b |
c. 2 + (a + b) = (a + b) | d. 2 (a + b) = 2a + 2b |
11. Что из следующего НЕ верно относительно операций с целыми числами? а. отрицательное время отрицательное равняется положительному |
б.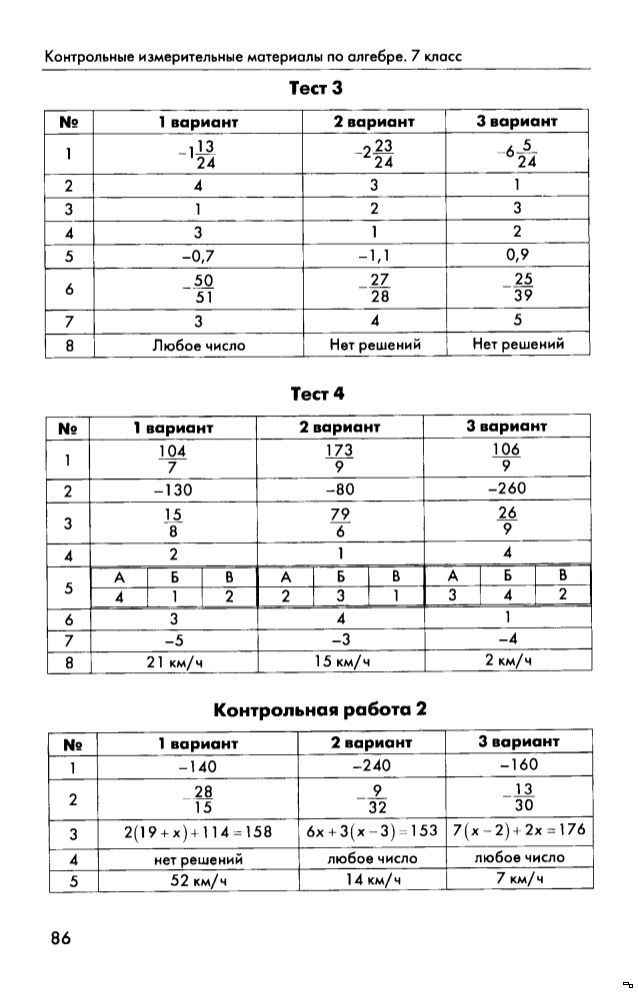 отрицательное деленное на положительное равно положительное |
отрицательное деленное на положительное равно положительное |
c. отрицательный плюс отрицательный равен отрицательному |
d. ни один из них |
12. Какое целое число равно (- 4) (- 3) (- 1)?
а.12 | | c. +4 |
б. -12 | d. — 3 |
13. Какое целое число равно (- 60) ÷ (- 5)?
а. 12 | | c. — 65 |
б. -12 | d. + 65 |
14. Какое целое число равно 11 — (- 11)?
а. 0 | | c. — 22 |
б. 22 | d. 1 |
15. Что из следующего неверно?
а. 5> 0 | | c. — 3> — 4 |
б. — 9> 5 | d. ни один из них |
16. В чем ценность | — 3 | • | — 7 | + | — 4 |?
a.14 | | c. 25 |
б. -25 | d.- 48 |
17. Сумма, обратная — 23, равна ____
.
а. 23 | | c. — 123 |
б. — 32 | d. — (- 23) |
18. Какое мультипликативное обратное число 8?
а. 18 | | c. 81 |
б. — 8 | d. ни один из них |
19. Набор {0, 1, 2, 3, 4, 5,…} известен как ste of _______ a. подсчет числа | | c. целые числа |
б. целые числа | d. рациональные числа |
целые числа | d. рациональные числа |
20. Какие из следующих дробей расположены в порядке убывания? а. 815, 23, 712, 49 | | c.23, 712, 815, 49 |
б. 23, 815, 712, 49 | d. ни один из них |
21. Простейшая форма произведения 615 • 38 —
.
а. 320 | | c. 740 |
б. 840 | d. 940 |
22. В повторяющейся десятичной системе счисления 0,1254712547… какая 19-я цифра находится справа от десятичной точки? а. 2 | | c. 5 |
б. 4 | d. 7 |
23. Какое свойство иллюстрируется уравнением
5 3 + 2 = 53 + (5) (2)?
а. закрытие | | c. распределительный |
б.коммутативный | d. ассоциативный |
24. Какой десятичный знак равен 139?
а. 0,4 | | c. 1.4 |
б. 0,4 | d. 1.4 |
25. Какая дробь равна десятичной 0,325?
а. 340 | | c. 1340 | …
Присоединяйтесь к StudyMode, чтобы прочитать полный документ
7-й класс Тест
- Ресурс исследования
- Исследовать
- Искусство и гуманитарные науки
- Бизнес
- Инженерная технология
- Иностранный язык
- История
- Математика
- Наука
- Социальная наука
Лучшие подкатегории
- Продвинутая математика
- Алгебра
- Основы математики
- Исчисление
- Геометрия
- Линейная алгебра
- Предалгебра
- Предварительный расчет
- Статистика и вероятность
- Тригонометрия
- другое →
Лучшие подкатегории
- Астрономия
- Астрофизика
- Биология
- Химия
- Науки о Земле
- Наука об окружающей среде
- Здравоохранение
- Физика
- другое →
Лучшие подкатегории
- Антропология
- Закон
- Политология
- Психология
- Социология
- другое →
Лучшие подкатегории
- Бухгалтерский учет
- Экономика
- Финансы
- Менеджмент
- другое →
Лучшие подкатегории
- Аэрокосмическая техника
- Биоинженерия
- Химическая промышленность
- Гражданское строительство
- Компьютерные науки
- Электротехника
- Промышленное проектирование
- Машиностроение
- Веб-дизайн
- другое →
Лучшие подкатегории
- Архитектура
- Связь
- Английский
- Гендерные исследования
- Музыка
- Исполнительское искусство
- Философия
- Религиоведение
- Письмо
- другое →
Примечания к редакции по математике Глава 9 — Рациональные числа (класс 7)
Натуральные числа
Все положительные целые числа, такие как 1, 2, 3, 4 ……. .это натуральные числа.
.это натуральные числа.
Целые числа
Все натуральные числа, включая 0, являются целыми числами.
Целые числа
Все отрицательные и положительные числа, включая 0, называются целыми числами.
Рациональные числа
Рациональные числа — это числа, которые могут быть выражены в форме p / q, где p и q — целые числа (q ≠ 0). Он включает в себя все натуральные, целые, дробные и целые числа.
Эквивалентные рациональные числа
Умножив или разделив числитель и знаменатель рационального числа на одно и то же целое число, мы можем получить другое рациональное число, эквивалентное данному рациональному числу.
Числа считаются эквивалентными, если они пропорциональны друг другу.
Пример
Следовательно, 1/2, 2/4, 4/8 эквивалентны друг другу, поскольку они равны друг другу.
Положительные и отрицательные рациональные числа
1. Положительные рациональные числа — это числа, числитель и знаменатель которых положительны.
Пример: 3/4, 12/24 и т. Д.
2. Отрицательные рациональные числа — это числа, у которых один из числителей или знаменателей отрицательный.
Пример: (-2) / 6, 36 / (- 3) и т. Д.
Примечание: Число 0 не является ни положительным, ни отрицательным рациональным числом.
Рациональные числа в числовой строке
Представление целых, натуральных и целых чисел в числовой строке выполняется следующим образом
Рациональные числа также могут быть представлены на числовой строке, например целыми числами, т.е. положительные рациональные числа находятся справа от 0, а отрицательные рациональные числа находятся слева от 0.
Представление рациональных чисел может быть выполнено на числовой прямой следующим образом
Рациональные числа в стандартной форме
Рациональное число находится в стандартной форме, если его знаменатель является положительным целым числом и нет общего делителя между числителем и знаменателем, кроме 1.
Если какое-либо данное рациональное число не находится в стандартной форме, мы можем привести его к его стандартной или низшей форме, разделив его числитель и знаменатель на их HCF, игнорируя его отрицательный знак.
Пример
Найдите стандартную форму от 18.12.
Решение
2/3 — это стандартная или простейшая форма 12/18
Сравнение рациональных чисел
1.Чтобы сравнить два положительных рациональных числа , нам нужно сделать их знаменатель одинаковым, тогда мы сможем легко их сравнить.
Пример
Сравните 4/5 и 3/8 и скажите, какой из них больше.
Решение
Чтобы сделать их знаменатель одинаковым, нам нужно взять НОК знаменателя обоих чисел.
LCM 5 и 8 равно 40.
2.Чтобы сравнить два отрицательных рациональных числа , мы сравниваем их, игнорируя их отрицательные знаки, а затем меняем порядок.
Пример
Сравните — (2/5) и — (3/7) и скажите, какой из них больше.
Решение
Для сравнения нам нужно сравнить их как обычные числа.
LCM 5 и 7 равно 35.
, изменив порядок чисел в обратном порядке.
3. Если у нас есть для сравнения одного отрицательного и одного положительного рационального числа , тогда ясно, что положительное рациональное число всегда будет больше, так как положительное рациональное число справа равно 0, а отрицательные рациональные числа слева. из 0.
из 0.
Пример
Сравните 2/5 и — (2/5) и скажите, какой из них больше.
Решение
Просто 2/5> — (2/5)
Рациональные числа между рациональными числами
Чтобы найти рациональные числа между двумя рациональными числами, мы должны сделать их знаменатель одинаковым, тогда мы сможем найти рациональные числа.
Пример
Найдите рациональные числа от 3/5 до 3/7.
Решение
Чтобы найти рациональные числа от 3/5 до 3/7, мы должны сделать их знаменатель одинаковым.
LCM 5 и 7 равно 35.
Следовательно, рациональные числа между 3/5 и 3/7 равны
.Это не единственные рациональные числа от 3/5 до 3/7.
Если мы найдем рациональные числа, эквивалентные 3/5 и 3/7, то мы сможем найти более рациональные числа между ними.
Следовательно, мы можем найти более рациональные числа между 3/5 и 3/7.
Примечание: Между любыми двумя рациональными числами находится n чисел рациональных чисел.
Операции с рациональными числами
1. Дополнение
а.Сложение двух рациональных чисел с одинаковым знаменателем
и. Мы можем добавить его, используя числовую строку .
Пример:
Складываем 1/5 и 2/5
Решение:
На числовой строке мы должны переместиться вправо от 0 до 1/5 единиц, а затем переместиться на 2/5 единиц вправо.
ii. Если нам нужно к сложить два рациональных числа , знаменатели которых совпадают, мы просто складываем их числители, а знаменатель остается прежним.
Пример
Добавьте 3/11 и 7/11.
Решение
Поскольку знаменатель тот же, мы можем просто сложить их числитель.
г. Сложение двух рациональных чисел с разными знаменателями
Если нам нужно сложить два рациональных числа с разными знаменателями, тогда мы должны взять НОК знаменателей и найти их эквивалентные рациональные числа с НОК в качестве знаменателя, а затем сложить их.
Пример
Складываем 2/5 и 3/7.
Решение
Чтобы сложить два рациональных числа, сначала нам нужно взять НОК знаменателей и найти эквивалентные рациональные числа.
LCM 5 и 7 равно 35.
г. Добавка обратная
Подобно целым числам, аддитивная инверсия рациональных чисел такая же.
Это показывает, что аддитивная величина, обратная 3/7, равна — (3/7)
Это показывает, что
2. Вычитание
Если нам нужно вычесть два рациональных числа, мы должны добавить аддитивное обратное рациональное число, которое вычитается, к другому рациональному числу.
а — б = а + (-b)
Пример
Вычтем 4/21 из 21 8/8.
Решение
и. В первом методе мы просто вычтем числитель, а знаменатель останется прежним.
ii. Во втором методе мы добавим аддитивную величину, обратную второму числу, к первому числу.
3. Умножение
а. Умножение рационального числа на положительное целое .
Чтобы умножить рациональное число на положительное целое, мы просто умножаем целое число на числитель, а знаменатель остается прежним.
Пример
г. Умножение рационального числа на отрицательное целое
Чтобы умножить рациональное число на отрицательное целое число, мы просто умножаем целое число на числитель, и знаменатель остается прежним, а полученное рациональное число будет отрицательным рациональным числом.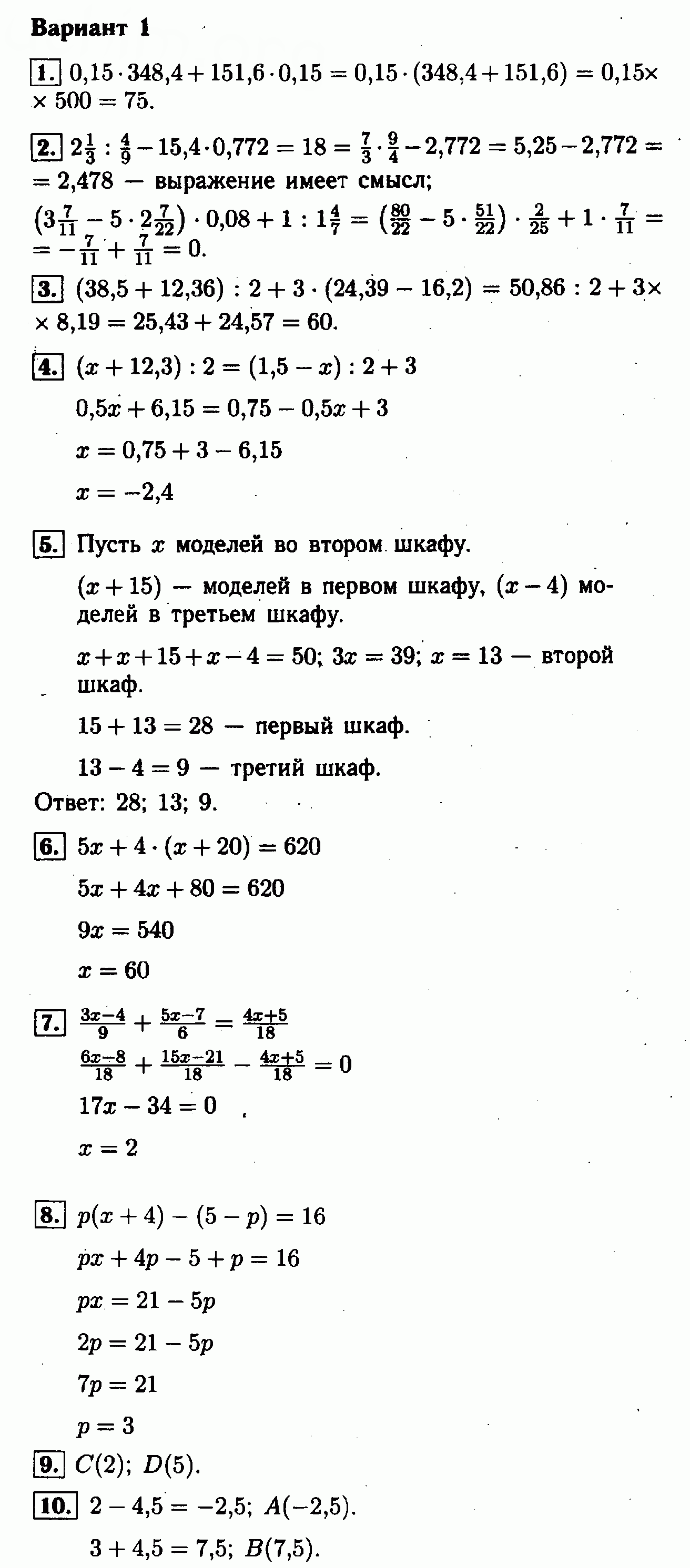
Пример
г. Умножение рационального числа на другое рациональное число
Чтобы умножить рациональное число на другое рациональное число, мы должны умножить числитель двух рациональных чисел и умножить знаменатель двух рациональных чисел.
Пример
Умножаем 3/7 и 5/11.
Решение
4.Подразделение
а. Взаимный
Обратное число — это множитель данного рационального числа, который дает произведение 1.
Взаимное значение a / b равно b / a
Произведение взаимного
Если мы умножим обратную величину рационального числа на это рациональное число, то произведение всегда будет 1.
Пример
г.Деление рационального числа на другое рациональное число
Чтобы разделить рациональное число на другое рациональное число, мы должны умножить величину, обратную рациональному числу, на другое рациональное число.
