 (1)
(1)Реферат
Закон Ома. История открытия. Различные виды закона Ома.
Содержание.
1. Общий вид закона Ома.
2. История открытия закона Ома, краткая биография ученого.
3. Виды законов Ома.
Закон Ома устанавливает зависимость между силой тока I в проводнике и разностью потенциалов (напряжением) U между двумя фиксированными точками (сечениями) этого проводника:
 (1)
(1)
 Коэффициент пропорциональности R , зависящий от геометрических и электрических свойств проводника и от температуры, называется омическим сопротивлением или просто сопротивлением данного участка проводника. Закон Ома был открыт в 1826 нем. физиком Г. Омом.
Коэффициент пропорциональности R , зависящий от геометрических и электрических свойств проводника и от температуры, называется омическим сопротивлением или просто сопротивлением данного участка проводника. Закон Ома был открыт в 1826 нем. физиком Г. Омом.
Георг Симон Ом родился 16 марта 1787 года в Эрлангене, в семье потомственного слесаря. После окончания школы Георг поступил в городскую гимназию. Гимназия Эрлангена курировалась университетом. Занятия в гимназии вели четыре профессора. Георг, закончив гимназию, весной 1805 года приступил к изучению математики, физики и философии на философском факультете Эрлангенского университета.
Проучившись три семестра, он принял приглашение занять место учителя математики в частной школе швейцарского городка Готтштадта.
В 1811 году он возвращается в Эрланген, заканчивает университет и получает степень доктора философии. Сразу же по окончании университета ему была предложена должность приват-доцента кафедры математики этого же университета.
В 1812 году Ом был назначен учителем математики и физики школы в Бамберге. В 1817 году он публикует свою первую печатную работу, посвященную методике преподавания "Наиболее оптимальный вариант преподавания геометрии в подготовительных классах". Ом занялся исследованиями электричества. В основу своего электроизмерительного прибора Ом заложил конструкцию крутильных весов Кулона. Результаты своих исследований Ом оформил в виде статьи под названием "Предварительное сообщение о законе, по которому металлы проводят контактное электричество". Статья была опубликована в 1825 году в "Журнале физики и химии", издаваемом Швейггером. Однако выражение, найденное и опубликованное Омом, оказалось неверным, что стало одной из причин его длительного непризнания. Приняв все меры предосторожности, заранее устранив все предполагаемые источники ошибок, Ом приступил к новым измерениям.
Появляется в свет его знаменитая статья "Определение закона, по которому металлы проводят контактное электричество, вместе с наброском теории вольтаического аппарата и мультипликатора Швейггера", вышедшая в 1826 году в "Журнале физики и химии".
В мае 1827 года "Теоретические исследования электрических цепей" объемом в 245 страниц, в которых содержались теперь уже теоретические рассуждения Ома по электрическим цепям. В этой работе ученый предложил характеризовать электрические свойства проводника его сопротивлением и ввел этот термин в научный обиход. Ом нашел более простую формулу для закона участка электрической цепи, не содержащего ЭДС: "Величина тока в гальванической цепи прямо пропорциональна сумме всех напряжений и обратно пропорциональна сумме приведенных длин. При этом общая приведенная длина определяется как сумма всех отдельных приведенных длин для однородных участков, имеющих различную проводимость и различное поперечное сечение".
В 1829 году появляется его статья "Экспериментальное исследование работы электромагнитного мультипликатора", в которой были заложены основы теории электроизмерительных приборов. Здесь же Ом предложил единицу сопротивления, в качестве которой он выбрал сопротивление медной проволоки длиной 1 фут и поперечным сечением в 1 квадратную линию.
В 1830 году появляется новое исследование Ома "Попытка создания приближенной теории униполярной проводимости".
Только в 1841 году работа Ома была переведена на английский язык, в 1847 году - на итальянский, в 1860 году - на французский.
16 февраля 1833 года, через семь лет после выхода из печати статьи, в которой было опубликовано его открытие, Ому предложили место профессора физики во вновь организованной политехнической школе Нюрнберга. Ученый приступает к исследованиям в области акустики. Результаты своих акустических исследований Ом сформулировал в виде закона, получившего впоследствии название акустического закона Ома.
Раньше всех из зарубежных ученых закон Ома признали русские физики Ленц и Якоби. Они помогли и его международному признанию. При участии русских физиков, 5 мая 1842 года Лондонское Королевское общество наградило Ома золотой медалью и избрало своим членом.
В 1845 году его избирают действительным членом Баварской академии наук. В 1849 году ученого приглашают в Мюнхенский университет на должность экстраординарного профессора. В этом же году он назначается хранителем государственного собрания физико-математических приборов с одновременным чтением лекций по физике и математике. В 1852 году Ом получил должность ординарного профессора. Ом скончался 6 июля 1854 года. В 1881 году на электротехническом съезде в Париже ученые единогласно утвердили название единицы сопротивления - 1 Ом.
В общем случае зависимость между I и U нелинейна, однако на практике всегда можно в определенном интервале напряжений считать её линейной и применять закон Ома; для металлов и их сплавов этот интервал практически неограничен.
Закон Ома в форме (1) справедлив для участков цепи, не содержащих источников ЭДС. При наличии таких источников (аккумуляторов, термопар, генераторов и т. д.) закон Ома имеет вид:
 (2)
(2)
где  — ЭДС всех источников, включённых в рассматриваемый участок цепи. Для замкнутой цепи закон Ома принимает вид:
— ЭДС всех источников, включённых в рассматриваемый участок цепи. Для замкнутой цепи закон Ома принимает вид:
 (3)
(3)
где  - полное сопротивление цепи, равное сумме внешнего сопротивления r и внутреннего сопротивления
- полное сопротивление цепи, равное сумме внешнего сопротивления r и внутреннего сопротивления  источника ЭДС. Обобщением закона Ома на случай разветвлённой цепи является правило 2-е Кирхгофа.
источника ЭДС. Обобщением закона Ома на случай разветвлённой цепи является правило 2-е Кирхгофа.
Закон Ома можно записать в дифференциальной форме, связывающей в каждой точке проводника плотность тока j с полной напряжённостью электрического поля. Потенциальное. электрическое поле напряжённости Е , создаваемое в проводниках микроскопическими зарядами (электронами, ионами) самих проводников, не может поддерживать стационарное движение свободных зарядов (ток), т. к. работа этого поля на замкнутом пути равна нулю. Ток поддерживается неэлектростатическими силами различного происхождения (индукционного, химического, теплового и т.д.), которые действуют в источниках ЭДС и которые можно представить в виде некоторого эквивалентного непотенциального поля с напряженностью E СТ, называемого сторонним. Полная напряженность поля, действующего внутри проводника на заряды, в общем случае равна E + E СТ . Соответственно, дифференциальный закон Ома имеет вид:
 или
или  , (4)
, (4)
где  - удельное сопротивление материала проводника, а
- удельное сопротивление материала проводника, а  - его удельная электропроводность.
- его удельная электропроводность.
Закон Ома в комплексной форме справедлив также для синусоидальных квазистационарных токов:
 (5)
(5)
где z - полное комплексное сопротивление:  , r – активное сопротивление, а x - реактивное сопротивление цепи. При наличии индуктивности L и емкости С в цепи квазистационарного тока частоты
, r – активное сопротивление, а x - реактивное сопротивление цепи. При наличии индуктивности L и емкости С в цепи квазистационарного тока частоты 
 .
.
Существует несколько видов закона Ома.
Закон Ома для однородного участка цепи (не содержащего источника тока): сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника:

Закон Ома для замкнутой цепи: сила тока в замкнутой цепи равна отношению ЭДС источника тока к суммарному сопротивлению всей цепи:

где R - сопротивление внешней цепи, r – внутреннее сопротивление источника тока.
R  - +
- +



R
Закон Ома для неоднородного участка цепи (участка цепи с источником тока):

 R
R 

 ;
; 
где  - разность потенциалов на концах участка цепи,
- разность потенциалов на концах участка цепи,  - ЭДС источника тока, входящего в участок.
- ЭДС источника тока, входящего в участок.
Способность вещества проводить ток характеризуется его удельным сопротивлением  либо проводимостью
либо проводимостью  . Их величина определяется химической природой вещества и условиями, в частности температурой, при которых оно находится. Для большинства металлов удельное сопротивление растет с температурой приблизительно по линейному закону:
. Их величина определяется химической природой вещества и условиями, в частности температурой, при которых оно находится. Для большинства металлов удельное сопротивление растет с температурой приблизительно по линейному закону:
 ;
; 
где  — удельное сопротивление при 0°С, t — температура по шкале Цельсия, а — коэффициент, численно равный примерно 1/273. Переходя к абсолютной температуре, получаем
— удельное сопротивление при 0°С, t — температура по шкале Цельсия, а — коэффициент, численно равный примерно 1/273. Переходя к абсолютной температуре, получаем

При низких температурах наблюдаются отступления от этой закономерности. В большинстве случаев зависимость  от T следует кривой 1 на рисунке.
от T следует кривой 1 на рисунке.

Величина остаточного сопротивления  в сильной степени зависит от чистоты материала и наличия остаточных механических напряжений в образце. Поэтому после отжига
в сильной степени зависит от чистоты материала и наличия остаточных механических напряжений в образце. Поэтому после отжига  заметно уменьшается. У абсолютно чистого металла с идеально правильной кристаллической решеткой при абсолютном нуле
заметно уменьшается. У абсолютно чистого металла с идеально правильной кристаллической решеткой при абсолютном нуле  .
.
У большой группы металлов и сплавов при температуре порядка нескольких градусов Кельвина сопротивление скачком обращается в нуль (кривая 2 на рисунке). Впервые это явление, названное сверхпроводимостью, было обнаружено в 1911 г. Камерлинг - Оннесом для ртути. В дальнейшем сверхпроводимость была обнаружена у свинца, олова, цинка, алюминия и других металлов, а также у ряда сплавов. Для каждого сверхпроводника имеется своя критическая температура Тк , при которой он переходит в сверхпроводящее состояние. При действии на сверхпроводник магнитного поля сверхпроводящее состояние нарушается. Величина критического поля HK , разрушающего сверхпроводимость, равна нулю при Т = Тк и растет с понижением температуры.
Полное теоретическое объяснение сверхпроводимости было дано в 1958 г. советским физиком Н. Н. Боголюбовым и его сотрудниками.
Зависимость электрического сопротивления от температуры положена в основу термометров сопротивления. Такой термометр представляет собой металлическую (обычно платиновую) проволоку, намотанную на фарфоровый или слюдяной каркас. Проградуированный по постоянным температурным точкам термометр сопротивления позволяет измерять с точностью порядка нескольких сотых градуса как низкие, так и высокие температуры.
Список использованной литературы:
Прохоров А. М. Физический энциклопедический словарь, М., 1983
Дорфман Я. Г. Всемирная история физики . М., 1979 Ом Г. Определение закона, по которому металлы проводят контактное электричество . – В кн.: Классики физической науки. М., 1989
Роджерс Э. Физика для любознательных , т. 3. М., 1971 Орир Дж. Физика , т. 2. М., 1981 Джанколи Д. Физика , т. 2. М., 1989
www.yurii.ru
РЕФЕРАТ
Дисциплина: Физика
Тема: «Законы Ома. Законы Кирхгофа»
Содержание реферата.
1.Краткая биография Ома, история открытия закона – стр.3.
2.Общий вид закона Ома – стр.5.
3.Виды законов Ома – стр.6.
4.Краткая биография Кирхгофа – стр.8.
5.Общий вид закона Кирхгофа – стр.9.
6.Виды законов Кирхгофа – стр.10.
7.Список использованной литературы – стр.15.
1.Краткая биография Ома, история открытия закона.
Георг Симон Ом родился 16 марта 1787 года в Эрлангене, в семье потомственного слесаря. После окончания школы Георг поступил в городскую гимназию. Гимназия Эрлангена курировалась университетом. Занятия в гимназии вели четыре профессора. Георг, закончив гимназию, весной 1805 года приступил к изучению математики, физики и философии на философском факультете Эрлангенского университета.
Проучившись три семестра, он принял приглашение занять место учителя математики в частной школе швейцарского городка Готтштадта.
В 1811 году он возвращается в Эрланген, заканчивает университет и получает степень доктора философии. Сразу же по окончании университета ему была предложена должность приват-доцента кафедры математики этого же университета.
В 1812 году Ом был назначен учителем математики и физики школы в Бамберге. В 1817 году он публикует свою первую печатную работу, посвященную методике преподавания "Наиболее оптимальный вариант преподавания геометрии в подготовительных классах". Ом занялся исследованиями электричества. В основу своего электроизмерительного прибора Ом заложил конструкцию крутильных весов Кулона. Результаты своих исследований Ом оформил в виде статьи под названием "Предварительное сообщение о законе, по которому металлы проводят контактное электричество". Статья была опубликована в 1825 году в "Журнале физики и химии", издаваемом Швейггером. Однако выражение, найденное и опубликованное Омом, оказалось неверным, что стало одной из причин его длительного непризнания. Приняв все меры предосторожности, заранее устранив все предполагаемые источники ошибок, Ом приступил к новым измерениям.
Появляется в свет его знаменитая статья "Определение закона, по которому металлы проводят контактное электричество, вместе с наброском теории вольтаического аппарата и мультипликатора Швейггера", вышедшая в 1826 году в "Журнале физики и химии".
В мае 1827 года "Теоретические исследования электрических цепей" объемом в 245 страниц, в которых содержались теперь уже теоретические рассуждения Ома по электрическим цепям. В этой работе ученый предложил характеризовать электрические свойства проводника его сопротивлением и ввел этот термин в научный обиход. Ом нашел более простую формулу для закона участка электрической цепи, не содержащего ЭДС: "Величина тока в гальванической цепи прямо пропорциональна сумме всех напряжений и обратно пропорциональна сумме приведенных длин. При этом общая приведенная длина определяется как сумма всех отдельных приведенных длин для однородных участков, имеющих различную проводимость и различное поперечное сечение".
В 1829 году появляется его статья "Экспериментальное исследование работы электромагнитного мультипликатора", в которой были заложены основы теории электроизмерительных приборов. Здесь же Ом предложил единицу сопротивления, в качестве которой он выбрал сопротивление медной проволоки длиной 1 фут и поперечным сечением в 1 квадратную линию.
В 1830 году появляется новое исследование Ома "Попытка создания приближенной теории униполярной проводимости".
Только в 1841 году работа Ома была переведена на английский язык, в 1847 году - на итальянский, в 1860 году - на французский.
16 февраля 1833 года, через семь лет после выхода из печати статьи, в которой было опубликовано его открытие, Ому предложили место профессора физики во вновь организованной политехнической школе Нюрнберга. Ученый приступает к исследованиям в области акустики. Результаты своих акустических исследований Ом сформулировал в виде закона, получившего впоследствии название акустического закона Ома.
Раньше всех из зарубежных ученых закон Ома признали русские физики Ленц и Якоби. Они помогли и его международному признанию. При участии русских физиков, 5 мая 1842 года Лондонское Королевское общество наградило Ома золотой медалью и избрало своим членом.
В 1845 году его избирают действительным членом Баварской академии наук. В 1849 году ученого приглашают в Мюнхенский университет на должность экстраординарного профессора. В этом же году он назначается хранителем государственного собрания физико-математических приборов с одновременным чтением лекций по физике и математике. В 1852 году Ом получил должность ординарного профессора. Ом скончался 6 июля 1854 года. В 1881 году на электротехническом съезде в Париже ученые единогласно утвердили название единицы сопротивления - 1 Ом.
2.Общий вид закона Ома.
Закон Ома устанавливает зависимость между силой тока Iв проводнике и разностью потенциалов (напряжением)Uмежду двумя фиксированными точками (сечениями) этого проводника:
 (1)
(1)
Коэффициент пропорциональности R, зависящий от геометрических и электрических свойств проводника и от температуры, называется омическим сопротивлением или просто сопротивлением данного участка проводника. Закон Ома был открыт в 1826 нем. физиком Г. Омом.
В общем случае зависимость между I иUнелинейна, однако на практике всегда можно в определенном интервале напряжений считать её линейной и применять закон Ома; для металлов и их сплавов этот интервал практически неограничен.
Закон Ома в форме (1) справедлив для участков цепи, не содержащих источников ЭДС. При наличии таких источников (аккумуляторов, термопар, генераторов и т. д.) закон Ома имеет вид:
 (2)
(2)
где  — ЭДС всех источников, включённых в рассматриваемый участок цепи. Для замкнутой цепи закон Ома принимает вид:
— ЭДС всех источников, включённых в рассматриваемый участок цепи. Для замкнутой цепи закон Ома принимает вид:
 (3)
(3)
где  - полное сопротивление цепи, равное сумме внешнего сопротивленияrи внутреннего сопротивления
- полное сопротивление цепи, равное сумме внешнего сопротивленияrи внутреннего сопротивления источника ЭДС. Обобщением закона Ома на случай разветвлённой цепи является правило 2-е Кирхгофа.
источника ЭДС. Обобщением закона Ома на случай разветвлённой цепи является правило 2-е Кирхгофа.
Закон Ома можно записать в дифференциальной форме, связывающей в каждой точке проводника плотность тока jс полной напряжённостью электрического поля. Потенциальное. электрическое поле напряжённостиЕ, создаваемое в проводниках микроскопическими зарядами (электронами, ионами) самих проводников, не может поддерживать стационарное движение свободных зарядов (ток), т. к. работа этого поля на замкнутом пути равна нулю. Ток поддерживается неэлектростатическими силами различного происхождения (индукционного, химического, теплового и т.д.), которые действуют в источниках ЭДС и которые можно представить в виде некоторого эквивалентного непотенциального поля с напряженностью EСТ,называемого сторонним. Полная напряженность поля, действующего внутри проводника на заряды, в общем случае равнаE+EСТ. Соответственно, дифференциальный закон Ома имеет вид:
 или
или , (4)
, (4)
где  - удельное сопротивление материала проводника, а
- удельное сопротивление материала проводника, а - его удельная электропроводность.
- его удельная электропроводность.
Закон Ома в комплексной форме справедлив также для синусоидальных квазистационарных токов:
 (5)
(5)
где z - полное комплексное сопротивление: ,r – активное сопротивление, аx- реактивное сопротивление цепи. При наличии индуктивностиLи емкостиСв цепи квазистационарного тока частоты
,r – активное сопротивление, аx- реактивное сопротивление цепи. При наличии индуктивностиLи емкостиСв цепи квазистационарного тока частоты
 .
.
3.Виды закона Ома.
Существует несколько видов закона Ома.
Закон Ома для однородного участка цепи(не содержащего источника тока): сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника:

Закон Ома для замкнутой цепи:сила тока в замкнутой цепи равна отношению ЭДС источника тока к суммарному сопротивлению всей цепи:

где R- сопротивление внешней цепи, r– внутреннее сопротивление источника тока.
R  - +
- +

R
Закон Ома для неоднородного участка цепи (участка цепи с источником тока):

 R
R 

 ;
;
где  - разность потенциалов на концах участка цепи,
- разность потенциалов на концах участка цепи, - ЭДС источника тока, входящего в участок.
- ЭДС источника тока, входящего в участок.
Способность вещества проводить ток характеризуется его удельным сопротивлением  либо проводимостью
либо проводимостью . Их величина определяется химической природой вещества и условиями, в частности температурой, при которых оно находится. Для большинства металлов удельное сопротивление растет с температурой приблизительно по линейному закону:
. Их величина определяется химической природой вещества и условиями, в частности температурой, при которых оно находится. Для большинства металлов удельное сопротивление растет с температурой приблизительно по линейному закону:
 ;
;
где  — удельное сопротивление при 0°С,t— температура по шкале Цельсия, а — коэффициент, численно равный примерно 1/273. Переходя к абсолютной температуре, получаем
— удельное сопротивление при 0°С,t— температура по шкале Цельсия, а — коэффициент, численно равный примерно 1/273. Переходя к абсолютной температуре, получаем

При низких температурах наблюдаются отступления от этой закономерности. В большинстве случаев зависимость  отTследует кривой1на рисунке.
отTследует кривой1на рисунке.

Величина остаточного сопротивления  в сильной степени зависит от чистоты материала и наличия остаточных механических напряжений в образце. Поэтому после отжига
в сильной степени зависит от чистоты материала и наличия остаточных механических напряжений в образце. Поэтому после отжига заметно уменьшается. У абсолютно чистого металла с идеально правильной кристаллической решеткой при абсолютном нуле
заметно уменьшается. У абсолютно чистого металла с идеально правильной кристаллической решеткой при абсолютном нуле .
.
У большой группы металлов и сплавов при температуре порядка нескольких градусов Кельвина сопротивление скачком обращается в нуль (кривая 2 на рисунке). Впервые это явление, названное сверхпроводимостью, было обнаружено в 1911 г. Камерлинг - Оннесом для ртути. В дальнейшем сверхпроводимость была обнаружена у свинца, олова, цинка, алюминия и других металлов, а также у ряда сплавов. Для каждого сверхпроводника имеется своя критическая температураТк, при которой он переходит в сверхпроводящее состояние. При действии на сверхпроводник магнитного поля сверхпроводящее состояние нарушается. Величина критического поляHK, разрушающего сверхпроводимость, равна нулю приТ =Тк и растет с понижением температуры.
Полное теоретическое объяснение сверхпроводимости было дано в 1958 г. советским физиком Н. Н. Боголюбовым и его сотрудниками.
Зависимость электрического сопротивления от температуры положена в основу термометров сопротивления. Такой термометр представляет собой металлическую (обычно платиновую) проволоку, намотанную на фарфоровый или слюдяной каркас. Проградуированный по постоянным температурным точкам термометр сопротивления позволяет измерять с точностью порядка нескольких сотых градуса как низкие, так и высокие температуры.
4.Краткая биография Кирхгофа.
Кирхгоф Густав Роберт(12.03.1824 – 17.10.1887) - немецкий физик.
Густав Кирхгоф родился в Кенигсберге в семье юриста. Окончив гимназию, он поступил в Кенигсбергский университет. После окончания университета Кирхгоф некоторое время преподавал в Берлине. В 1854 г. по совету химика Р. Бунзена Кирхгофа приглашают в Гейдельбергский университет, с которым связаны многие годы его небогатой внешними событиями жизни. Лишь безвременная смерть жены, оставившей ему четверых детей, и нелепый случай, сделавший его калекой, вынужденным передвигаться на кресле или с костылями, нарушили размеренный ход его жизни. Л. Больцман писал об этом так: «В жизни Кирхгофа не было ничего выдающегося, что соответствовало бы необычности его гения. Его жизнь была обычной жизнью немецкого профессора университета. Великие события происходили исключительно в его голове».
В начале своей научной деятельности Кирхгоф еще студентом начал исследовать законы распространения тока в электрических цепях. В 1849 г. он сформулировал свои знаменитые правила, которые до сих пор применяются для их расчета. В 1857 г. он опубликовал работу о распространении переменных токов по проводам, некоторые выводы которой предвосхитили теорию электромагнитного поля Максвелла.
Однако главный цикл работ Кирхгофа в Гейдельберге – анализ спектров излучения. Еще в 1855 г., сразу по приезде в Гейдельберг, Кирхгоф присоединился к исследованиям Р.Бунзена, который пытался установить химический состав солей по цвету пламени горелки (сейчас она так и называется бунзеновской горелкой). Кирхгоф сразу же заметил, что значительно более эффективным тестом на наличие того или иного вещества является анализ линейчатых спектров испускания этих веществ. Он сконструировал с помощью Бунзена новый, более совершенный, чем прежние, призматический спектроскоп и определил линии спектров множества элементов, открыв в процессе работы новые элементы - цезий и рубидий. Таким образом, Кирхгоф и Бунзен могут считаться создателями спектрального анализа, т.е. экспериментальной основы современной астрофизики.
Работа Кирхгофа по изучению спектров испускания элементов привела его к заключению о связи между спектральными линиями и темными линиями, обнаруженными Фраунгофером в спектре Солнца. Кирхгоф показал, что знаменитая желтая D-линия в спектре испускания натрия точно соответствует двум темным линиям в солнечном спектре. Это привело его к выводу, что атмосфера Солнца содержит натрий и этот натрий поглощает из непрерывного спектра солнечного излучения как раз ту часть, которая имеет длину волны, равную длине волны D-линии. Свою догадку Кирхгоф проверил в лаборатории, имитировав солнечный свет светом бунзеновской горелки и внеся в ее пламя поваренную соль.
Изучение связи между испусканием и поглощением излучения привело Кирхгофа к исследованию излучения нагретых тел. В 1862 г. он ввел понятие абсолютно черного тела и в качестве идеального излучателя (модель черного тела) предложил металлическую нагретую полость с маленькой дырочкой. Он сформулировал, опираясь на термодинамические соотношения, важнейший закон излучения черного тела: спектр излучения является универсальной функцией длины волны и температуры. Исследование излучения абсолютно черного тела стало на несколько десятилетий одной главных задач экспериментаторов и головной болью для теоретиков, так как классическая физика не могла объяснить наблюдаемого спектра излучения. Загадку излучения абсолютно черного тела разрешил в 1900 г. своей гипотезой квантов М.Планк, ученик Г.Кирхгофа. Поэтому без преувеличения можно сказать, что Кирхгоф внес важный вклад и в создание квантовой механики.
Кирхгоф был прекрасным лектором, хотя иногда немного суховатым. Правда, затем он великолепно редактировал и издавал свои лекции по разным вопросам теоретической физики. Многие германские физики в течение нескольких десятилетий учились по изданным лекциям Кирхгофа.
Несмотря на болезнь, лишавшую его подвижности, Кирхгоф был неутомимым исследователем и живым, интересным собеседником, любившим шутку. Однажды его банкир, под впечатлением от рассказов Кирхгофа о возможности определить химический состав Солнца, спросил: «Какой толк в том, что на Солнце есть золото, если я не могу перенести его на Землю и пощупать?» Несколькими годами спустя Кирхгоф получил золотую медаль Лондонского королевского общества и большую премию в золотых соверенах за свои исследования. Он вызвал своего банкира и передал ему свою награду, заметив шутливо: «Вот ваше золото из Солнца!»
5.Общий вид законов Кирхгофа.
Законы Кирхгофа являются одной из форм закона сохранения энергии и потому относятся к фундаментальным законам природы.
Середина XIX века как раз стала временем активных исследований свойств электрических цепей, и результаты этих исследований быстро находили практические применения. Базовые правила расчета простых цепей, такие как закон Ома, были уже достаточно хорошо проработаны. Проблема состояла в том, что из проводов и различных элементов электрических цепей технически уже можно было изготовлять весьма сложные и разветвленные сети — но никто не знал, как смоделировать их математически, чтобы рассчитать их свойства. Кирхгофу удалось сформулировать правила, позволяющие достаточно просто анализировать самые сложные цепи, и законы Кирхгофа до сих пор остаются важным рабочим инструментом специалистов в области электронной инженерии и электротехники.
Оба закона Кирхгофа формулируются достаточно просто и имеют понятную физическую интерпретацию. Первый закон гласит, что если рассмотреть любой узел цепи (то есть точку разветвления, где сходятся три или более проводов), то сумма поступающих в цепь электрических токов будет равна сумме исходящих, что, вообще говоря, является следствием закона сохранения электрического заряда. Например, если вы имеете Т-образный узел электрической цепи и по двум проводам к нему поступают электрические токи, то по третьему проводу ток потечет в направлении от этого узла, и равен он будет сумме двух поступающих токов. Физический смысл этого закона прост: если бы он не выполнялся, в узле непрерывно накапливался бы электрический заряд, а этого никогда не происходит.
Второй закон не менее прост. Если мы имеем сложную, разветвленную цепь, ее можно мысленно разбить на ряд простых замкнутых контуров. Ток в цепи может различным образом распределяться по этим контурам, и сложнее всего определить, по какому именно маршруту потекут токи в сложной цепи. В каждом из контуров электроны могут либо приобретать дополнительную энергию (например, от батареи), либо терять ее (например, на сопротивлении или ином элементе). Второй закон Кирхгофа гласит, что чистое приращение энергии электронов в любом замкнутом контуре цепи равно нулю. Этот закон также имеет простую физическую интерпретацию. Если бы это было не так, всякий раз, проходя через замкнутый контур, электроны приобретали или теряли бы энергию, и ток бы непрерывно возрастал или убывал. В первом случае можно было бы получить вечный двигатель, а это запрещено первым началом термодинамики; во втором — любые токи в электрических цепях неизбежно затухали бы, а этого мы не наблюдаем.
Самое распространенное применение законов Кирхгофа мы наблюдаем в так называемых последовательных и параллельных цепях.
В последовательной цепи (яркий пример такой цепи — елочная гирлянда, состоящая из последовательно соединенных между собой лампочек) электроны от источника питания по серии проводов последовательно проходят через все лампочки, и на сопротивлении каждой из них напряжение падает согласно закону Ома.
В параллельной цепи провода, напротив, соединены таким образом, что на каждый элемент цепи подается равное напряжение от источника питания, а это означает, что в каждом элементе цепи сила тока своя, в зависимости от его сопротивления. Пример параллельной цепи является — ламп «лесенкой»: напряжение подается на шины, а лампы смонтированы на поперечинах. Токи, проходящие через каждый узел такой цепи, определяются по второму закону Кирхгофа.
6.Виды законов Кирхгофа.
Первый закон Кирхгофаявляется следствием принципа непрерывности электрического тока, в соответствии с которым суммарный поток зарядов через любую замкнутую поверхность равен нулю, т.е. количество зарядов выходящих через эту поверхность должно быть равно количеству входящих зарядов. Основание этого принципа очевидно, т.к. при нарушении его электрические заряды внутри поверхности должны были бы либо исчезать, либо возникать без видимых причин.
Если заряды перемещаются внутри проводников, то они образуют в них электрический ток. Величина электрического тока может измениться только в узле цепи, т.к. связи считаются идеальными проводниками. Поэтому, если окружить узел произвольной поверхностью s(рис. 1), то потоки зарядов через эту поверхность будут тождественны токам в проводниках образующих узел и суммарный ток в узле должен быть равным нулю.
Для математической записи этого закона нужно принять систему обозначений направлений токов по отношению к рассматриваемому узлу. Можно считать токи направленные к узлу положительными, а от узла отрицательными. Тогда для узла рис. 1 уравнение Кирхгофа будет иметь вид I3+I4-I1-I2= 0 илиI3+I4=I1+I2.
Обобщая сказанное на произвольное число ветвей сходящихся в узле, можно сформулировать первый закон Кирхгофаследующим образом:
| | (1) |
или
| | (2) |
Очевидно, что обе формулировки равноценны и выбор формы записи уравнений может быть произвольным. Существенным является только соглашение о знаках токов для данной цепи, т.е. в пределах описания одной электрической цепи нельзя для разных узлов использовать разные знаки для токов направленных к узлам или от узлов.
При составлении уравнений по первому закону Кирхгофа направлениятоков в ветвях электрической цепивыбираютобычнопроизвольно. При этом необязательно даже стремиться, чтобы во всех узлах цепи присутствовали токи разных направлений. Может получиться так, что в каком-либо узле все токи сходящихся в нем ветвей будут направлены к узлу или от узла, нарушая тем самым принцип непрерывности. В этом случае в процессе определения токов один или несколько из них окажутся отрицательными, что будет свидетельствовать о протекании их в направлении противоположном принятому.
Второй закон Кирхгофасвязан с понятием потенциала электрического поля, как работы, совершаемой при перемещении единичного точечного заряда в пространстве. Если такое перемещение совершается по замкнутому контуру, то суммарная работа при возвращении в исходную точку будет равна нулю. В противном случае путем обхода контура можно было бы получать положительную энергию, нарушая закон ее сохранения.
Каждый узел или точка электрической цепи обладает собственным потенциалом и, перемещаясь вдоль замкнутого контура, мы совершаем работу, которая при возврате в исходную точку будет равна нулю. Это свойство потенциального электрического поля и описывает второй закон Кирхгофа в применении к электрической цепи.
Он также как и первый закон формулируется в двух вариантах, связанных с тем, что падение напряжения на источнике ЭДС численно равно электродвижущей силе, но имеет противоположный знак. Поэтому, если какая либо ветвь содержит сопротивление и источник ЭДС, направление которой согласно с направлением тока, то при обходе контура эти два слагаемых падения напряжения будут учитываться с разными знаками. Если же падение напряжения на источнике ЭДС учесть в другой части уравнения, то его знак будет соответствовать знаку напряжения на сопротивлении.
Сформулируем оба варианта второго закона Кирхгофа, т.к. они принципиально равноценны:
| | (3) |
Примечание: знак + выбирается перед падением напряжения на резисторе, если направление протекания тока через него и направление обхода контура совпадают; для падений напряжения на источниках ЭДС знак + выбирается, если направление обхода контура и направление действия ЭДС встречны независимо от направления протекания тока;
| | (4) |
Примечание: знак + для ЭДС выбирается в том случае, если направление ее действия совпадает с направлением обхода контура, а для напряжений на резисторах знак + выбирается, если в них совпадают направление протекания тока и направление обхода.
Здесь также как и в первом законе оба варианта корректны, но на практике удобнее использовать второй вариант, т.к. в нем проще определить знаки слагаемых.
С помощью законов Кирхгофа для любой электрической цепи можно составить независимую систему уравнений и определить любые неизвестные параметры, если число их не превышает число уравнений. Для выполнения условий независимости эти уравнения должны составляться по определенным правилам.
Общее число уравнений N в системе равно числу ветвей Nвминус число ветвей, содержащих источники тока NJ, т.е. N = Nв- NJ.
Наиболее простыми по выражениям являются уравнения по первому закону Кирхгофа, однако их число N1не может быть больше числа узлов Nуминус один.
Недостающие уравнения составляются по второму закону Кирхгофа, т.е.
| N1= Nу-1 ; | (5) |
| N2= N - N1= Nв- NJ- N1. | (6) |
Сформулируем алгоритм составления системы уравненийпо законам Кирхгофа :
studfiles.net
Федеральное агентство по образованию
Саратовский государственный социально-экономический университет
Марксовский филиал
Кафедра общих гуманитарных дисциплин
РЕФЕРАТ
По «Физике»
на тему: «Электрический ток. Закон Ома»
Студента 2 курса
Специальность: «Эуп пп»
Проверила : Старикова Н.Н.
Маркс – 2010
Электрический ток. Закон Ома
Если изолированный проводник поместить в электрическое поле />то на свободные заряды qв проводнике будет действовать сила />В результате в проводнике возникает кратковременное перемещение свободных зарядов. Этот процесс закончится тогда, когда собственное электрическое поле зарядов, возникших на поверхности проводника, скомпенсирует полностью внешнее поле. Результирующее электростатическое поле внутри проводника будет равно нулю (см. § 1.5).
Однако, в проводниках при определенных условиях может возникнуть непрерывное упорядоченное движение свободных носителей электрического заряда. Такое движение называется электрическим током. За направление электрического тока принято направление движения положительных свободных зарядов. Для существования электрического тока в проводнике необходимо создать в нем электрическое поле.
Количественной мерой электрического тока служит сила тока I– скалярная физическая величина, равная отношению заряда Δq, переносимого через поперечное сечение проводника (рис. 1.8.1) за интервал времени Δt, к этому интервалу времени:
Если сила тока и его направление не изменяются со временем, то такой ток называется постоянным.
/>
Рисунок 1.8.1.
Упорядоченное движение электронов в металлическом проводнике и ток I. S– площадь поперечного сечения проводника, />– электрическое поле
В Международной системе единиц СИ сила тока измеряется в амперах (А). Единица измерения тока 1 А устанавливается по магнитному взаимодействию двух параллельных проводников с током (см. § 1.16).
Постоянный электрический ток может быть создан только в замкнутой цепи, в которой свободные носители заряда циркулируют по замкнутым траекториям. Электрическое поле в разных точках такой цепи неизменно во времени. Следовательно, электрическое поле в цепи постоянного тока имеет характер замороженного электростатического поля. Но при перемещении электрического заряда в электростатическом поле по замкнутой траектории, работа электрических сил равна нулю (см. § 1.4). Поэтому для существования постоянного тока необходимо наличие в электрической цепи устройства, способного создавать и поддерживать разности потенциалов на участках цепи за счет работы сил неэлектростатического происхождения. Такие устройства называются источниками постоянного тока. Силы неэлектростатического происхождения, действующие на свободные носители заряда со стороны источников тока, называются сторонними силами.
Природа сторонних сил может быть различной. В гальванических элементах или аккумуляторах они возникают в результате электрохимических процессов, в генераторах постоянного тока сторонние силы возникают при движении проводников в магнитном поле. Источник тока в электрической цепи играет ту же роль, что и насос, который необходим для перекачивания жидкости в замкнутой гидравлической системе. Под действием сторонних сил электрические заряды движутся внутри источника тока противсил электростатического поля, благодаря чему в замкнутой цепи может поддерживаться постоянный электрический ток.
При перемещении электрических зарядов по цепи постоянного тока сторонние силы, действующие внутри источников тока, совершают работу.
Физическая величина, равная отношению работы Aстсторонних сил при перемещении заряда qот отрицательного полюса источника тока к положительному к величине этого заряда, называется электродвижущей силой источника(ЭДС):
/>
Таким образом, ЭДС определяется работой, совершаемой сторонними силами при перемещении единичного положительного заряда. Электродвижущая сила, как и разность потенциалов, измеряется в вольтах (В).
При перемещении единичного положительного заряда по замкнутой цепи постоянного тока работа сторонних сил равна сумме ЭДС, действующих в этой цепи, а работа электростатического поля равна нулю.
Цепь постоянного тока можно разбить на отдельные участки. Те участки, на которых не действуют сторонние силы (т. е. участки, не содержащие источников тока), называются однородными. Участки, включающие источники тока, называются неоднородными.
При перемещении единичного положительного заряда по некоторому участку цепи работу совершают как электростатические (кулоновские), так и сторонние силы. Работа электростатических сил равна разности потенциалов Δφ12= φ1– φ2между начальной (1) и конечной (2) точками неоднородного участка. Работа сторонних сил равна по определению электродвижущей силе />12, действующей на данном участке. Поэтому полная работа равна
U12= φ1– φ2+ />12.
Величину U12принято называть напряжениемна участке цепи 1–2. В случае однородного участка напряжение равно разности потенциалов:
U12= φ1– φ2.
Немецкий физик Г. Ом в 1826 году экспериментально установил, что сила тока I, текущего по однородному металлическому проводнику (т. е. проводнику, в котором не действуют сторонние силы), пропорциональна напряжению Uна концах проводника:
/>
где R= const.
Величину Rпринято называть электрическим сопротивлением. Проводник, обладающий электрическим сопротивлением, называется резистором. Данное соотношение выражает закон Ома для однородного участка цепи: сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника.
В СИ единицей электрического сопротивления проводников служит ом(Ом). Сопротивлением в 1 Ом обладает такой участок цепи, в котором при напряжении 1 В возникает ток силой 1 А.
Проводники, подчиняющиеся закону Ома, называются линейными. Графическая зависимость силы тока Iот напряжения U(такие графики называются вольт-амперными характеристиками, сокращенно ВАХ) изображается прямой линией, проходящей через начало координат. Следует отметить, что существует много материалов и устройств, не подчиняющихся закону Ома, например, полупроводниковый диод или газоразрядная лампа. Даже у металлических проводников при токах достаточно большой силы наблюдается отклонение от линейного закона Ома, так как электрическое сопротивление металлических проводников растет с ростом температуры.
Для участка цепи, содержащего ЭДС, закон Ома записывается в следующей форме:
IR= U12= φ1– φ2+ />= Δφ12+ />.
Это соотношение принято называть обобщенным законом Омаили законом Ома для неоднородного участка цепи.
На рис. 1.8.2 изображена замкнутая цепь постоянного тока. Участок цепи (cd) является однородным.
/>
Рисунок 1.8.2.
--PAGE_BREAK--Цепь постоянного тока
По закону Ома
IR= Δφcd.
Участок (ab) содержит источник тока с ЭДС, равной />.
По закону Ома для неоднородного участка,
Ir= Δφab+ />.
Сложив оба равенства, получим:
I(R+ r) = Δφcd+ Δφab+ />.
Но Δφcd= Δφba= – Δφab. Поэтому
/>
Эта формула выражет закон Ома для полной цепи: сила тока в полной цепи равна электродвижущей силе источника, деленной на сумму сопротивлений однородного и неоднородного участков цепи.
Сопротивление rнеоднородного участка на рис. 1.8.2 можно рассматривать как внутреннее сопротивление источника тока. В этом случае участок (ab) на рис. 1.8.2 является внутренним участком источника. Если точки aи bзамкнуть проводником, сопротивление которого мало по сравнению с внутренним сопротивлением источника (R<< r), тогда в цепи потечет ток короткого замыкания
/>
Сила тока короткого замыкания – максимальная сила тока, которую можно получить от данного источника с электродвижущей силой />и внутренним сопротивлением r. У источников с малым внутренним сопротивлением ток короткого замыкания может быть очень велик и вызывать разрушение электрической цепи или источника. Например, у свинцовых аккумуляторов, используемых в автомобилях, сила тока короткого замыкания может составлять несколько сотен ампер. Особенно опасны короткие замыкания в осветительных сетях, питаемых от подстанций (тысячи ампер). Чтобы избежать разрушительного действия таких больших токов, в цепь включаются предохранители или специальные автоматы защиты сетей.
В ряде случаев для предотвращения опасных значений силы тока короткого замыкания к источнику последовательно подсоединяется некоторое внешнее сопротивление. Тогда сопротивление rравно сумме внутреннего сопротивления источника и внешнего сопротивления, и при коротком замыкании сила тока не окажется чрезмерно большой.
Если внешняя цепь разомкнута, то Δφba= – Δφab= />, т. е. разность потенциалов на полюсах разомкнутой батареи равна ее ЭДС.
Если внешнее нагрузочное сопротивление Rвключено и через батарею протекает ток I, разность потенциалов на ее полюсах становится равной
Δφba= />– Ir.
На рис. 1.8.3 дано схематическое изображение источника постоянного тока с ЭДС равной />и внутренним сопротивлением rв трех режимах: «холостой ход», работа на нагрузку и режим короткого замыкания (к. з.). Указаны напряженность />электрического поля внутри батареи и силы, действующие на положительные заряды: />– электрическая сила и />– сторонняя сила. В режиме короткого замыкания электрическое поле внутри батареи исчезает.
/>
Рисунок 1.8.3.
Схематическое изображение источника постоянного тока: 1 – батарея разомкнута; 2 – батарея замкнута на внешнее сопротивление R; 3 – режим короткого замыкания
Для измерения напряжений и токов в электрических цепях постоянного тока используются специальные приборы – вольтметрыи амперметры.
Вольтметрпредназначен для измерения разности потенциалов, приложенной к его клеммам. Он подключается параллельноучастку цепи, на котором производится измерение разности потенциалов. Любой вольтметр обладает некоторым внутренним сопротивлением RB. Для того, чтобы вольтметр не вносил заметного перераспределения токов при подключении к измеряемой цепи, его внутреннее сопротивление должно быть велико по сравнению с сопротивлением того участка цепи, к которому он подключен. Для цепи, изображенной на рис. 1.8.4, это условие записывается в виде:
RB>> R1.
Это условие означает, что ток IB= Δφcd/ RB, протекающий через вольтметр, много меньше тока I= Δφcd/ R1, который протекает по тестируемому участку цепи.
Поскольку внутри вольтметра не действуют сторонние силы, разность потенциалов на его клеммах совпадает по определению с напряжением. Поэтому можно говорить, что вольтметр измеряет напряжение.
Амперметрпредназначен для измерения силы тока в цепи. Амперметр включается последовательно в разрыв электрической цепи, чтобы через него проходил весь измеряемый ток. Амперметр также обладает некоторым внутренним сопротивлением RA. В отличие от вольтметра, внутреннее сопротивление амперметра должно быть достаточно малым по сравнению с полным сопротивлением всей цепи. Для цепи на рис. 1.8.4 сопротивление амперметра должно удовлетворять условию
RA<< (r+ R1+ R2),
чтобы при включении амперметра ток в цепи не изменялся.
Измерительные приборы – вольтметры и амперметры – бывают двух видов: стрелочные (аналоговые) и цифровые. Цифровые электроизмерительные приборы представляют собой сложные электронные устройства. Обычно цифровые приборы обеспечивают более высокую точность измерений.
/>
Рисунок 1.8.4.
Включение амперметра (А) и вольтметра (В) в электрическую цепь
Последовательное и параллельное соединение проводников
Проводники в электрических цепях могут соединяться последовательно и параллельно.
При последовательном соединениипроводников (рис. 1.9.1) сила тока во всех проводниках одинакова:
I1= I2= I.
/>
Рисунок 1.9.1.
Последовательное соединение проводников
По закону Ома, напряжения U1и U2на проводниках равны
U1= IR1, U2= IR2.
Общее напряжение Uна обоих проводниках равно сумме напряжений U1и U2:
продолжение --PAGE_BREAK--U= U1+ U2= I(R1+ R2) = IR,
где R– электрическое сопротивление всей цепи. Отсюда следует:
R= R1+ R2.
При последовательном соединении полное сопротивление цепи равно сумме сопротивлений отдельных проводников.
Этот результат справедлив для любого числа последовательно соединенных проводников.
При параллельном соединении(рис. 1.9.2) напряжения U1и U2на обоих проводниках одинаковы:
U1= U2= U.
Сумма токов I1+ I2, протекающих по обоим проводникам, равна току в неразветвленной цепи:
I= I1+ I2.
Этот результат следует из того, что в точках разветвления токов (узлы Aи B) в цепи постоянного тока не могут накапливаться заряды. Например, к узлу Aза время Δtподтекает заряд IΔt, а утекает от узла за то же время заряд I1Δt+ I2Δt. Следовательно, I= I1+ I2.
/>
Рисунок 1.9.2.
Параллельное соединение проводников
Записывая на основании закона Ома
/>
где R– электрическое сопротивление всей цепи, получим
/>
При параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Этот результат справедлив для любого числа параллельно включенных проводников.
Формулы для последовательного и параллельного соединения проводников позволяют во многих случаях рассчитывать сопротивление сложной цепи, состоящей из многих резисторов. На рис. 1.9.3 приведен пример такой сложной цепи и указана последовательность вычислений.
/>
Рисунок 1.9.3.
Расчет сопротивления сложной цепи. Сопротивления всех проводников указаны в омах (Ом)
Следует отметить, что далеко не все сложные цепи, состоящие из проводников с различными сопротивлениями, могут быть рассчитаны с помощью формул для последовательного и параллельного соединения. На рис. 1.9.4 приведен пример электрической цепи, которую нельзя рассчитать указанным выше методом.
/>
Рисунок 1.9.4.
Пример электрической цепи, которая не сводится к комбинации последовательно и параллельно соединенных проводников
Цепи, подобные изображенной на рис. 1.9.4, а также цепи с разветвлениями, содержащие несколько источников, рассчитываются с помощью правил Кирхгофа.
Ссылки (links): www.physics.ru/courses/op25part2/content/chapter1/section/paragraph20/theory.html#1www.ronl.ru
Реферат на тему:
V — напряжение,I — сила тока,R — сопротивление.
Закон Ома — открыт в 1826 году, это физический закон, определяющий связь между напряжением, силой тока и сопротивлением проводника в электрической цепи. Назван в честь его первооткрывателя Георга Ома.
| Сила тока в участке цепи прямо пропорциональна напряжению, и обратно пропорциональна электрическому сопротивлению данного участка цепи. |
Закон Ома записывается формулой:
Где: I — сила тока (А), U — напряжение (В), R — сопротивление (Ом).
Следует иметь в виду, что закон Ома является фундаментальным (основным) и может быть применён к любой физической системе, в которой действуют потоки частиц или полей, преодолевающие сопротивление. Его можно применять для расчёта гидравлических, пневматических, магнитных, электрических, световых, тепловых потоков .
Георг Ом, проводя эксперименты с проводником, установил, что сила тока в проводнике пропорциональна напряжению
, приложенному к его концам:
или
Коэффициент пропорциональности назвали электропроводностью, а величину
принято именовать электрическим сопротивлением проводника.
Закон Ома был открыт в 1826 году.
Схема, иллюстрирующая три составляющие закона Ома
Диаграмма, помогающая запомнить закон Ома. Нужно закрыть искомую величину, и два других символа дадут формулу для её вычисления
Закон Ома для участка электрической цепи имеет вид:
где:
Закон Ома также применяется ко всей цепи, но в несколько изменённой форме:
где:
Сопротивление зависит как от материала, по которому течёт ток, так и от геометрических размеров проводника.
Полезно переписать закон Ома в так называемой дифференциальной форме, в которой зависимость от геометрических размеров исчезает, и тогда закон Ома описывает исключительно электропроводящие свойства материала. Для изотропных материалов имеем:
где:
Все величины, входящие в это уравнение, являются функциями координат и, в общем случае, времени. Если материал анизотропен, то направления векторов плотности тока и напряжённости могут не совпадать. В этом случае удельная проводимость является тензором ранга (1, 1).
Раздел физики, изучающий течение электрического тока в различных средах, называется электродинамикой сплошных сред.
Если ток является синусоидальным с циклической частотой ω, а цепь содержит не только активные, но и реактивные компоненты (ёмкости, индуктивности), то закон Ома обобщается; величины, входящие в него, становятся комплексными:
где:
При этом переход от комплексных переменных в значениях тока и напряжения к действительным (измеряемым) значениям может быть произведён взятием действительной или мнимой части (но во всех элементах цепи одной и той же!) комплексных значений этих величин. Соответственно, обратный переход строится для, к примеру, U = U0sin(ωt + φ) подбором такой , что
. Тогда все значения токов и напряжений в схеме надо считать как
Если ток изменяется во времени, но не является синусоидальным (и даже периодическим), то его можно представить как сумму синусоидальных Фурье-компонент. Для линейных цепей можно считать компоненты фурье-разложения тока действующими независимо.
Также необходимо отметить, что закон Ома является лишь простейшим приближением для описания зависимости тока от разности потенциалов и от сопротивления и для некоторых структур справедлив лишь в узком диапазоне значений. Для описания более сложных (нелинейных) систем, когда зависимостью сопротивления от силы тока нельзя пренебречь, принято обсуждать вольт-амперную характеристику. Отклонения от закона Ома наблюдаются также в случаях, когда скорость изменения электрического поля настолько велика, что нельзя пренебрегать инерционностью носителей заряда.
Закон Ома можно просто объяснить при помощи теории Друде:
wreferat.baza-referat.ru
Федеральное агентство по образованию
Саратовский государственный социально-экономический университет
Марксовский филиал
Кафедра общих гуманитарных дисциплин
РЕФЕРАТ
По «Физике»
на тему: «Электрический ток. Закон Ома»
Студента 2 курса
Специальность: «Эуп пп»
Проверила : Старикова Н.Н.
Маркс – 2010
Электрический ток. Закон Ома
Если изолированный проводник поместить в электрическое поле />то на свободные заряды qв проводнике будет действовать сила />В результате в проводнике возникает кратковременное перемещение свободных зарядов. Этот процесс закончится тогда, когда собственное электрическое поле зарядов, возникших на поверхности проводника, скомпенсирует полностью внешнее поле. Результирующее электростатическое поле внутри проводника будет равно нулю (см. § 1.5).
Однако, в проводниках при определенных условиях может возникнуть непрерывное упорядоченное движение свободных носителей электрического заряда. Такое движение называется электрическим током. За направление электрического тока принято направление движения положительных свободных зарядов. Для существования электрического тока в проводнике необходимо создать в нем электрическое поле.
Количественной мерой электрического тока служит сила тока I– скалярная физическая величина, равная отношению заряда Δq, переносимого через поперечное сечение проводника (рис. 1.8.1) за интервал времени Δt, к этому интервалу времени:
Если сила тока и его направление не изменяются со временем, то такой ток называется постоянным.
/>
Рисунок 1.8.1.
Упорядоченное движение электронов в металлическом проводнике и ток I. S– площадь поперечного сечения проводника, />– электрическое поле
В Международной системе единиц СИ сила тока измеряется в амперах (А). Единица измерения тока 1 А устанавливается по магнитному взаимодействию двух параллельных проводников с током (см. § 1.16).
Постоянный электрический ток может быть создан только в замкнутой цепи, в которой свободные носители заряда циркулируют по замкнутым траекториям. Электрическое поле в разных точках такой цепи неизменно во времени. Следовательно, электрическое поле в цепи постоянного тока имеет характер замороженного электростатического поля. Но при перемещении электрического заряда в электростатическом поле по замкнутой траектории, работа электрических сил равна нулю (см. § 1.4). Поэтому для существования постоянного тока необходимо наличие в электрической цепи устройства, способного создавать и поддерживать разности потенциалов на участках цепи за счет работы сил неэлектростатического происхождения. Такие устройства называются источниками постоянного тока. Силы неэлектростатического происхождения, действующие на свободные носители заряда со стороны источников тока, называются сторонними силами.
Природа сторонних сил может быть различной. В гальванических элементах или аккумуляторах они возникают в результате электрохимических процессов, в генераторах постоянного тока сторонние силы возникают при движении проводников в магнитном поле. Источник тока в электрической цепи играет ту же роль, что и насос, который необходим для перекачивания жидкости в замкнутой гидравлической системе. Под действием сторонних сил электрические заряды движутся внутри источника тока противсил электростатического поля, благодаря чему в замкнутой цепи может поддерживаться постоянный электрический ток.
При перемещении электрических зарядов по цепи постоянного тока сторонние силы, действующие внутри источников тока, совершают работу.
Физическая величина, равная отношению работы Aстсторонних сил при перемещении заряда qот отрицательного полюса источника тока к положительному к величине этого заряда, называется электродвижущей силой источника(ЭДС):
/>
Таким образом, ЭДС определяется работой, совершаемой сторонними силами при перемещении единичного положительного заряда. Электродвижущая сила, как и разность потенциалов, измеряется в вольтах (В).
При перемещении единичного положительного заряда по замкнутой цепи постоянного тока работа сторонних сил равна сумме ЭДС, действующих в этой цепи, а работа электростатического поля равна нулю.
Цепь постоянного тока можно разбить на отдельные участки. Те участки, на которых не действуют сторонние силы (т. е. участки, не содержащие источников тока), называются однородными. Участки, включающие источники тока, называются неоднородными.
При перемещении единичного положительного заряда по некоторому участку цепи работу совершают как электростатические (кулоновские), так и сторонние силы. Работа электростатических сил равна разности потенциалов Δφ12= φ1– φ2между начальной (1) и конечной (2) точками неоднородного участка. Работа сторонних сил равна по определению электродвижущей силе />12, действующей на данном участке. Поэтому полная работа равна
U12= φ1– φ2+ />12.
Величину U12принято называть напряжениемна участке цепи 1–2. В случае однородного участка напряжение равно разности потенциалов:
U12= φ1– φ2.
Немецкий физик Г. Ом в 1826 году экспериментально установил, что сила тока I, текущего по однородному металлическому проводнику (т. е. проводнику, в котором не действуют сторонние силы), пропорциональна напряжению Uна концах проводника:
/>
где R= const.
Величину Rпринято называть электрическим сопротивлением. Проводник, обладающий электрическим сопротивлением, называется резистором. Данное соотношение выражает закон Ома для однородного участка цепи: сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника.
В СИ единицей электрического сопротивления проводников служит ом(Ом). Сопротивлением в 1 Ом обладает такой участок цепи, в котором при напряжении 1 В возникает ток силой 1 А.
Проводники, подчиняющиеся закону Ома, называются линейными. Графическая зависимость силы тока Iот напряжения U(такие графики называются вольт-амперными характеристиками, сокращенно ВАХ) изображается прямой линией, проходящей через начало координат. Следует отметить, что существует много материалов и устройств, не подчиняющихся закону Ома, например, полупроводниковый диод или газоразрядная лампа. Даже у металлических проводников при токах достаточно большой силы наблюдается отклонение от линейного закона Ома, так как электрическое сопротивление металлических проводников растет с ростом температуры.
Для участка цепи, содержащего ЭДС, закон Ома записывается в следующей форме:
IR= U12= φ1– φ2+ />= Δφ12+ />.
Это соотношение принято называть обобщенным законом Омаили законом Ома для неоднородного участка цепи.
На рис. 1.8.2 изображена замкнутая цепь постоянного тока. Участок цепи (cd) является однородным.
/>
Рисунок 1.8.2.
--PAGE_BREAK--Цепь постоянного тока
По закону Ома
IR= Δφcd.
Участок (ab) содержит источник тока с ЭДС, равной />.
По закону Ома для неоднородного участка,
Ir= Δφab+ />.
Сложив оба равенства, получим:
I(R+ r) = Δφcd+ Δφab+ />.
Но Δφcd= Δφba= – Δφab. Поэтому
/>
Эта формула выражет закон Ома для полной цепи: сила тока в полной цепи равна электродвижущей силе источника, деленной на сумму сопротивлений однородного и неоднородного участков цепи.
Сопротивление rнеоднородного участка на рис. 1.8.2 можно рассматривать как внутреннее сопротивление источника тока. В этом случае участок (ab) на рис. 1.8.2 является внутренним участком источника. Если точки aи bзамкнуть проводником, сопротивление которого мало по сравнению с внутренним сопротивлением источника (R<< r), тогда в цепи потечет ток короткого замыкания
/>
Сила тока короткого замыкания – максимальная сила тока, которую можно получить от данного источника с электродвижущей силой />и внутренним сопротивлением r. У источников с малым внутренним сопротивлением ток короткого замыкания может быть очень велик и вызывать разрушение электрической цепи или источника. Например, у свинцовых аккумуляторов, используемых в автомобилях, сила тока короткого замыкания может составлять несколько сотен ампер. Особенно опасны короткие замыкания в осветительных сетях, питаемых от подстанций (тысячи ампер). Чтобы избежать разрушительного действия таких больших токов, в цепь включаются предохранители или специальные автоматы защиты сетей.
В ряде случаев для предотвращения опасных значений силы тока короткого замыкания к источнику последовательно подсоединяется некоторое внешнее сопротивление. Тогда сопротивление rравно сумме внутреннего сопротивления источника и внешнего сопротивления, и при коротком замыкании сила тока не окажется чрезмерно большой.
Если внешняя цепь разомкнута, то Δφba= – Δφab= />, т. е. разность потенциалов на полюсах разомкнутой батареи равна ее ЭДС.
Если внешнее нагрузочное сопротивление Rвключено и через батарею протекает ток I, разность потенциалов на ее полюсах становится равной
Δφba= />– Ir.
На рис. 1.8.3 дано схематическое изображение источника постоянного тока с ЭДС равной />и внутренним сопротивлением rв трех режимах: «холостой ход», работа на нагрузку и режим короткого замыкания (к. з.). Указаны напряженность />электрического поля внутри батареи и силы, действующие на положительные заряды: />– электрическая сила и />– сторонняя сила. В режиме короткого замыкания электрическое поле внутри батареи исчезает.
/>
Рисунок 1.8.3.
Схематическое изображение источника постоянного тока: 1 – батарея разомкнута; 2 – батарея замкнута на внешнее сопротивление R; 3 – режим короткого замыкания
Для измерения напряжений и токов в электрических цепях постоянного тока используются специальные приборы – вольтметрыи амперметры.
Вольтметрпредназначен для измерения разности потенциалов, приложенной к его клеммам. Он подключается параллельноучастку цепи, на котором производится измерение разности потенциалов. Любой вольтметр обладает некоторым внутренним сопротивлением RB. Для того, чтобы вольтметр не вносил заметного перераспределения токов при подключении к измеряемой цепи, его внутреннее сопротивление должно быть велико по сравнению с сопротивлением того участка цепи, к которому он подключен. Для цепи, изображенной на рис. 1.8.4, это условие записывается в виде:
RB>> R1.
Это условие означает, что ток IB= Δφcd/ RB, протекающий через вольтметр, много меньше тока I= Δφcd/ R1, который протекает по тестируемому участку цепи.
Поскольку внутри вольтметра не действуют сторонние силы, разность потенциалов на его клеммах совпадает по определению с напряжением. Поэтому можно говорить, что вольтметр измеряет напряжение.
Амперметрпредназначен для измерения силы тока в цепи. Амперметр включается последовательно в разрыв электрической цепи, чтобы через него проходил весь измеряемый ток. Амперметр также обладает некоторым внутренним сопротивлением RA. В отличие от вольтметра, внутреннее сопротивление амперметра должно быть достаточно малым по сравнению с полным сопротивлением всей цепи. Для цепи на рис. 1.8.4 сопротивление амперметра должно удовлетворять условию
RA<< (r+ R1+ R2),
чтобы при включении амперметра ток в цепи не изменялся.
Измерительные приборы – вольтметры и амперметры – бывают двух видов: стрелочные (аналоговые) и цифровые. Цифровые электроизмерительные приборы представляют собой сложные электронные устройства. Обычно цифровые приборы обеспечивают более высокую точность измерений.
/>
Рисунок 1.8.4.
Включение амперметра (А) и вольтметра (В) в электрическую цепь
Последовательное и параллельное соединение проводников
Проводники в электрических цепях могут соединяться последовательно и параллельно.
При последовательном соединениипроводников (рис. 1.9.1) сила тока во всех проводниках одинакова:
I1= I2= I.
/>
Рисунок 1.9.1.
Последовательное соединение проводников
По закону Ома, напряжения U1и U2на проводниках равны
U1= IR1, U2= IR2.
Общее напряжение Uна обоих проводниках равно сумме напряжений U1и U2:
продолжение --PAGE_BREAK--U= U1+ U2= I(R1+ R2) = IR,
где R– электрическое сопротивление всей цепи. Отсюда следует:
R= R1+ R2.
При последовательном соединении полное сопротивление цепи равно сумме сопротивлений отдельных проводников.
Этот результат справедлив для любого числа последовательно соединенных проводников.
При параллельном соединении(рис. 1.9.2) напряжения U1и U2на обоих проводниках одинаковы:
U1= U2= U.
Сумма токов I1+ I2, протекающих по обоим проводникам, равна току в неразветвленной цепи:
I= I1+ I2.
Этот результат следует из того, что в точках разветвления токов (узлы Aи B) в цепи постоянного тока не могут накапливаться заряды. Например, к узлу Aза время Δtподтекает заряд IΔt, а утекает от узла за то же время заряд I1Δt+ I2Δt. Следовательно, I= I1+ I2.
/>
Рисунок 1.9.2.
Параллельное соединение проводников
Записывая на основании закона Ома
/>
где R– электрическое сопротивление всей цепи, получим
/>
При параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Этот результат справедлив для любого числа параллельно включенных проводников.
Формулы для последовательного и параллельного соединения проводников позволяют во многих случаях рассчитывать сопротивление сложной цепи, состоящей из многих резисторов. На рис. 1.9.3 приведен пример такой сложной цепи и указана последовательность вычислений.
/>
Рисунок 1.9.3.
Расчет сопротивления сложной цепи. Сопротивления всех проводников указаны в омах (Ом)
Следует отметить, что далеко не все сложные цепи, состоящие из проводников с различными сопротивлениями, могут быть рассчитаны с помощью формул для последовательного и параллельного соединения. На рис. 1.9.4 приведен пример электрической цепи, которую нельзя рассчитать указанным выше методом.
/>
Рисунок 1.9.4.
Пример электрической цепи, которая не сводится к комбинации последовательно и параллельно соединенных проводников
Цепи, подобные изображенной на рис. 1.9.4, а также цепи с разветвлениями, содержащие несколько источников, рассчитываются с помощью правил Кирхгофа.
Ссылки (links): www.physics.ru/courses/op25part2/content/chapter1/section/paragraph20/theory.html#1www.ronl.ru
Марио Льоцци
ПЕРВЫЕ ИССЛЕДОВАНИЯ СОПРОТИВЛЕНИЯ ПРОВОДНИКОВ
Что такое проводник? Это чисто пассивная составная часть электрической цепи, отвечали первые исследователи. Заниматься его исследованием — значит попросту ломать себе голову над ненужными загадками, ибо только источник тока представляет собой активный элемент. Такой взгляд на вещи объясняет нам, почему ученые, по крайней мере до 1840 г., почти не проявляли интереса к тем немногим работам, которые проводились в этом направлении. Так, на втором съезде итальянских ученых, состоявшемся в Турине в 1840 г. (первый собирался в Пизе в 1839 г. и приобрел даже некое политическое значение), выступая в прениях по докладу, представленному Марианини, Де ла Рив утверждал, что проводимость большинства жидкостей не является абсолютной, «а скорее относительной и изменяется с изменением силы тока». А ведь закон Ома был опубликован за 15 лет до этого!
Среди тех немногих ученых, которые первыми стали заниматься вопросом проводимости проводников после изобретения гальванометра, был Стефано Марианини (1790—1866). К своему открытию он пришел случайно, изучая напряжение батарей. Он заметил, что с увеличением числа элементов вольтова столба электромагнитное воздействие на стрелку не увеличивается заметным образом. Это заставило Марианини сразу же подумать, что каждый вольтов элемент представляет собой препятствие для прохождения тока. Он делал опыты с парами «активными» и «неактивными» (т. е. состоящими из двух медных пластинок, разделенных влажной прокладкой) и опытным путем нашел отношение, в котором современный читатель узнает частный случай закона Ома, когда сопротивление внешней цепи не принимается во внимание, как это и было в опыте Марианини.
Георг Симон Ом (1789—1854) признавал заслуги Марианини, хотя его труды и не оказали Ому непосредственной помощи в работе. Ом вдохновлялся в своих исследованиях работой («Аналитическая теория тепла», Париж, 1822 г.) Жана Батиста Фурье (1768—1830)—одной из самых значительных научных работ всех времен, очень быстро получившей известность и высокую оценку среди математиков и физиков того времени. Ому пришла мысль, что механизм «теплового потока», о котором говорит Фурье, можно уподобить электрическому току в проводнике. И подобно тому как в теории Фурье тепловой поток между двумя телами или между двумя точками одного и того же тела объясняется разницей температур, точно так же Ом объясняет разницей «электроскопических сил» в двух точках проводника возникновение электрического тока между ними.
Придерживаясь такой аналогии, Ом начал свои экспериментальные исследования с определения относительных величин проводимости различных проводников. Применив метод, который стал теперь классическим, он подключал последовательно между двумя точками цепи тонкие проводники из различных материалов одинакового диаметра и изменял их длину так, чтобы получалась определенная величина тока. Первые результаты, которые ему удалось получить, сегодня кажутся довольно скромными.
Историки поражаются, например, тем, что по измерениям Ома серебро обладает меньшей проводимостью, чем медь и золото, и снисходительно принимают данное впоследствии самим Омом объяснение, согласно которому опыт проводился с серебряной проволокой, покрытой слоем масла, и это вводило в заблуждение относительно точного значения диаметра.
В то время имелось множество источников ошибок при проведении опытов (недостаточная чистота металлов, трудность калибровки проволоки, трудность точных измерений и т. п.). Важнейшим же источником ошибок была поляризация батарей. Постоянные (химические) элементы тогда еще не были известны, так что за время, необходимое для измерений, электродвижущая сила элемента существенно менялась. Именно эти причины, вызывавшие ошибки, привели к тому, что Ом на основании своих опытов пришел к логарифмическому закону зависимости силы тока от сопротивления проводника, включенного между двумя точками цепи.
После опубликования первой статьи Ома Поггендорф посоветовал ему отказаться от химических элементов и воспользоваться лучше термопарой медь — висмут, незадолго до этого введенной Зеебеком. Ом прислушался к этому совету и повторил свои опыты, собрав установку с термоэлектрической батареей, во внешнюю цепь которой включались последовательно восемь медных проволок одинакового диаметра, но разной длины. Силу тока он измерял с помощью своего рода крутильных весов, образуемых магнитной стрелкой, подвешенной на металлической нити. Когда ток, параллельный стрелке, отклонял ее, Ом закручивал нить, на которой она была подвешена, пока стрелка не оказывалась в своем обычном положении; сила тока считалась пропорциональной углу, на который закручивалась нить.
Ом пришел к выводу, что результаты опытов, проведенных с восемью различными проволоками, «могут быть выражены очень хорошо уравнением
X= a/ b+x,
где X означает интенсивность магнитного действия проводника, длина которого равна х, а а и b — константы, зависящие соответственно от возбуждающей силы и от сопротивления остальных частей цепи».
Условия опыта менялись: заменялись сопротивления и термоэлектрические пары, но результаты все равно сводились к приведенной выше формуле, которая очень просто переходит в известную нам, если X заменить силой тока, a —электродвижущей силой и b+x,—общим сопротивлением цепи.
Получив эту формулу, Ом пользуется ею для изучения действия мультипликатора Швейггера на отклонение стрелки и для изучения тока, который проходит во внешней цепи батареи элементов, в зависимости от того, как они соединены — последовательно или параллельно. Таким образом он объясняет (как это делается теперь в учебниках), чем определяется внешний ток батареи,— вопрос, который был довольно темным для первых исследователей.
Ом надеялся, что его экспериментальные работы откроют ему путь в университет, чего он так желал. Однако статьи прошли незамеченными. Тогда он оставил место преподавателя в кельнской гимназии и отправился в Берлин, чтобы теоретически осмыслить полученные результаты. В 1827 г. в Берлине он опубликовал свой главный труд «Die galvanische Kette, mathe-matisch bearbeitet» («Гальваническая цепь, разработанная математически»).
Эта теория, при разработке которой он вдохновлялся, как мы уже указывали, аналитической теорией теплоты Фурье, вводит понятия и точные определения электродвижущей силы, или «электроскопической силы», как ее называет Ом, электропроводности (Starke der Leitung) и силы тока. Выразив выведенный им закон в дифференциальной форме, приводимой современными авторами, Ом записывает его и в конечных величинах для частных случаев конкретных электрических цепей, из которых особенно важна термоэлектрическая цепь. Исходя из этого, он формулирует известные законы изменения электрического напряжения вдоль цепи.
Но теоретические исследования Ома также остались незамеченными, а если кто-нибудь и писал о них, то лишь для того, чтобы, высмеять «болезненную фантазию, единственной целью которой является стремление принизить достоинство природы». И лишь лет десять спустя его гениальные работы постепенно начали пользоваться должным признанием: в Германии их оценили Поггендорф и Фехнер, в России — Ленц, в Англии — Уитстон, в Америке — Генри, в Италии — Маттеуччи.
Одновременно с опытами Ома во Франции проводил свои опыты А. Беккерель, а в Англии — Барлоу. Опыты первого особенно замечательны введением дифференциального гальванометра с двойной обмоткой рамки и применением «нулевого» метода измерения. Опыты же Барлоу стоит упомянуть потому, что они экспериментально подтвердили постоянство силы тока во всей цепи. Этот вывод был проверен и распространен на внутренний ток батареи Фехнером в 1831 г., обобщен в 1851 г. Рудольфом Кольраушем (180Э—1858) на жидкие проводники, а затем еще раз подтвержден тщательными опытами Густава Нидмана (1826—1899).
ЭЛЕКТРИЧЕСКИЕ ИЗМЕРЕНИЯ
Беккерель применил дифференциальный гальванометр для сравнения электрических сопротивлений. На основе проведенных им исследований он сформулировал известный закон зависимости сопротивления проводника от его длины и сечения. Эти работы были продолжены Пуйе и описаны им в последующих изданиях его известных «Elements de physique experimentale» («Основы экспериментальной физики»), первое издание которых появилось в 1827 г. Сопротивления определялись методом сравнения.
Уже в 1825 г. Марианини показал, что в разветвляющихся цепях электрический ток распределяется по всем проводникам независимо от того, из какого материала они сделаны, вопреки утверждению Вольты, который полагал, что если одна ветвь цепи образуется металлическим проводником, а остальные — жидкими, то весь ток должен проходить по металлическому проводнику. Араго и Пуйе популяризировали во Франции наблюдения Марианини. Не зная еще закона Ома, Пуйе в 1837 г. воспользовался этими наблюдениями и законами Беккереля, чтобы показать, что проводимость цепи, эквивалентной двум разветвленным цепям, равна сумме проводимостей обеих цепей. Этой работой Пуйе положил начало изучению разветвленных цепей. Пуйе установил для них целый ряд терминов, которые живы и до сих пор, и некоторые частные законы, обобщенные Кирхгофом в 1845 г. в его известных «принципах»: в «узле» алгебраическая сумма сил токов равна нулю; в «петле» сумма произведений сопротивления каждого участка на соответствующую силу тока равна алгебраической сумме электродвижущих сил, действующих на участках этой петли.
Самый большой толчок для проведения электрических измерений, и в частности измерений сопротивления, был дан возросшими потребностями техники, и в первую очередь проблемами, возникшими с появлением электрического телеграфа. Впервые мысль об использовании электричества для передачи сигналов на расстояние родилась еще в XVIII веке. Вольта описал проект телеграфа, а Ампер еще в 1820 г. предлагал использовать электромагнитные явления для передачи сигналов. Идея Ампера была подхвачена многими учеными и техниками: в 1833 г. Гаусс и Вебер построили в Геттингене простейшую телеграфную линию, соединявшую астрономическую обсерваторию и физическую лабораторию. Но практическое применение телеграф получил благодаря американцу Самуэлу Морзе (1791—1872), которому в 1832 г. пришла удачная мысль создать телеграфный алфавит, состоящий всего из двух знаков. После многочисленных попыток Морзе в 1835 г. наконец удалось построить частным образом первую грубую модель телеграфа в Нью-Йоркском университете. В 1839 г. была проведена экспериментальная линия между Вашингтоном и Балтиморой, а в 1844 г. возникла организованная Морзе первая американская компания по коммерческой эксплуатации нового изобретения. Это было также первое практическое применение результатов научных изысканий в области электричества.
В Англии изучением и усовершенствованием телеграфа занялся Чарльз Уитстон (1802—1875), бывший мастер по изготовлению музыкальных инструментов. Понимая важность измерений сопротивления, Уитстон стал искать наиболее простые и точные методы таких измерений. Бывший в то время в ходу метод сравнения, как мы видели, давал ненадежные результаты, главным образом из-за отсутствия стабильных источников питания. Уже в 1840 г. Уитстон нашел способ измерения сопротивления независимо от постоянства электродвижущей силы и показал свое устройство Якоби. Однако статья, в которой это устройство описано и которую вполне можно назвать первой работой в области электротехники, появилась лишь в 1843 г. В этой статье дано описание знаменитого «мостика», названного затем в честь Уитстона. Фактически такое устройство было описано еще в 1833 г. Гюнтером Кристи и независимо от него в 1840 г. Марианини; оба они предлагали метод сведения к нулю, но их теоретические объяснения, при которых не учитывался закон Ома, оставляли желать лучшего.
Уитстон же был поклонником Ома и очень хорошо знал его закон, так что данная им теория «мостика Уитстона» ничем не отличается от приводимой сейчас в учебниках. Кроме того, Уитстон, чтобы можно было быстро и удобно изменять сопротивление одной стороны мостика для получения нулевой силы тока в гальванометре, включенном в диагональное плечо мостика, сконструировал три типа реостатов (само это слово было предложено им по аналогии с «реофором», введенным Ампером, в подражание которому Пекле ввел также термин «реометр»). Первый тип реостата с подвижной скобкой, применяемый и сейчас, был создан Уитстоном по аналогии со схожим приспособлением, применявшимся Якоби в 1841 г. Второй тип реостата имел вид деревянного цилиндра, вокруг которого была намотана часть подключенного в цепь провода, который легко перематывался с деревянного цилиндра на бронзовый. Третий тип реостата был похож на «магазин сопротивлений», который Эрнст Вернер Сименс (1816—1892), ученый и промышленник, в 1860 г. улучшил и широко распространил.
«Мостик Уитстона» дал возможность измерять электродвижущие силы и сопротивления.
Создание подводного телеграфа, пожалуй, еще более, нежели воздушного телеграфа, потребовало разработки методов электрических измерений. Опыты с подводным телеграфом начались еще в 1837 г., и одной из первых проблем, которую предстояло разрешить, было определение скорости распространения тока. Еще в 1834 г. Уитстон с помощью вращающихся зеркал, о чем мы уже упоминали в гл. 8, произвел первые измерения этой скорости, но полученные им результаты противоречили результатам Латимера Кларка, а последние в свою очередь не соответствовали более поздним исследованиям других ученых.
В 1855 г. Уильям Томсон (получивший впоследствии титул лорда Кельвина) объяснил причину всех этих расхождений. Согласно Томсону, скорость тока в проводнике не имеет определенной величины. Подобно тому как скорость распространения тепла в стержне зависит от материала, так и скорость тока в проводнике зависит от произведения его сопротивления на электрическую емкость. Следуя этой своей теории, которая в"«его времена подверглась ожесточенной критике, Томсон занялся проблемами, связанными с подводным телеграфом.
Первый трансатлантический кабель, соединивший Англию и Америку, функционировал около месяца, но затем испортился. Томсон рассчитал новый кабель, провел многочисленные измерения сопротивления и емкости, придумал новые передающие аппараты, из коих следует упомянуть астатический отражательный гальванометр, замененный «сифонным регистратором» его же изобретения. Наконец, в 1866 г. новый трансатлантический кабель успешно вступил в действие. Созданию этого первого большого электротехнического сооружения сопутствовала разработка системы единиц электрических и магнитных измерений.
Основа электромагнитной метрики была заложена Карлом Фридрихом Гауссом (1777—1855) в его знаменитой статье «Intensitas vis magneticae terrestris ad mensuram absolutam revocata» («Величина силы земного магнетизма в абсолютных мерах»), опубликованной в 1832 г. Гаусс заметил, что различные магнитные единицы измерения несоотносимы между собой, по крайней мере в большей своей части, и поэтому предложил систему абсолютных единиц, основанную на трех основных единицах механики: секунде (единице времени), миллиметре (единице длины) и миллиграмме (единице массы). Через них он выразил все остальные физические единицы и придумал ряд измерительных приборов, в частности магнетометр для измерения в абсолютных единицах земного магнетизма. Работу Гаусса продолжил Вебер, который построил много собственных приборов и приборов, задуманных еще Гауссом. Постепенно, особенно благодаря работам Максвелла, проводившимся в созданной Британской ассоциацией специальной комиссии по измерениям, которая издавала ежегодные отчеты с 1861 по 1867 г., возникла идея создать единые системы мер, в частности систему электромагнитных и электростатических мер.
Мысли о создании таких абсолютных систем единиц были подробно изложены в историческом отчете за 1873 г. второй комиссии Британской ассоциации. Созванный в Париже в 1881 г. Международный конгресс впервые установил международные единицы измерения, присвоив каждой из них название в честь какого-нибудь великого физика. Большая часть этих названий сохраняется до сих пор: вольт, ом, ампер, джоуль и т. д. После многих перипетий в 1935 г. была введена международная система Джорджи, или MKSQ, которая принимает за основные единицы метр, килограмм-массу, секунду и ом.
С «системами» единиц связаны «формулы размерностей», примененные впервые Фурье в его аналитической теории тепла (1822 г.) и распространенные Максвеллом, которым и установлены применяемые в них обозначения. Метрология прошлого века, основывавшаяся на стремлении объяснить все явления с помощью механических моделей, придавала большое значение формулам размерностей, в которых она хотела видеть не больше и не меньше как ключ к тайнам природы. При этом выдвигался ряд утверждений почти догматического характера. Так, чуть ли не обязательным догматом было требование, чтобы основных величин было непременно три. Но к концу века начали понимать, что формулы размерностей — это чистая условность, вследствие чего интерес к теориям размерностей стал постепенно падать.
Составила к.т.н. Савельева Ф.Н.
www.ronl.ru
Реферат
Закон Ома. История открытия. Различные виды закона Ома.
Содержание.
1. Общий вид закона Ома.
2. История открытия закона Ома, краткая биография ученого.
3. Виды законов Ома.
Закон Ома устанавливает зависимость между силой токаIв проводнике и разностью потенциалов (напряжением)Uмежду двумя фиксированными точками (сечениями) этого проводника:
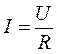 (1)
(1)
 Коэффициент пропорциональностиR, зависящий от геометрических и электрических свойств проводника и от температуры, называется омическим сопротивлением или просто сопротивлением данного участка проводника. Закон Ома был открыт в 1826 нем. физиком Г. Омом.
Коэффициент пропорциональностиR, зависящий от геометрических и электрических свойств проводника и от температуры, называется омическим сопротивлением или просто сопротивлением данного участка проводника. Закон Ома был открыт в 1826 нем. физиком Г. Омом.
Георг Симон Ом родился 16 марта 1787 года в Эрлангене, в семье потомственного слесаря. После окончания школы Георг поступил в городскую гимназию. Гимназия Эрлангена курировалась университетом. Занятия в гимназии вели четыре профессора. Георг, закончив гимназию, весной 1805 года приступил к изучению математики, физики и философии на философском факультете Эрлангенского университета.
Проучившись три семестра, он принял приглашение занять место учителя математики в частной школе швейцарского городка Готтштадта.
В 1811 году он возвращается в Эрланген, заканчивает университет и получает степень доктора философии. Сразу же по окончании университета ему была предложена должность приват-доцента кафедры математики этого же университета.
В 1812 году Ом был назначен учителем математики и физики школы в Бамберге. В 1817 году он публикует свою первую печатную работу, посвященную методике преподавания "Наиболее оптимальный вариант преподавания геометрии в подготовительных классах". Ом занялся исследованиями электричества. В основу своего электроизмерительного прибора Ом заложил конструкцию крутильных весов Кулона. Результаты своих исследований Ом оформил в виде статьи под названием "Предварительное сообщение о законе, по которому металлы проводят контактное электричество". Статья была опубликована в 1825 году в "Журнале физики и химии", издаваемом Швейггером. Однако выражение, найденное и опубликованное Омом, оказалось неверным, что стало одной из причин его длительного непризнания. Приняв все меры предосторожности, заранее устранив все предполагаемые источники ошибок, Ом приступил к новым измерениям.
Появляется в свет его знаменитая статья "Определение закона, по которому металлы проводят контактное электричество, вместе с наброском теории вольтаического аппарата и мультипликатора Швейггера", вышедшая в 1826 году в "Журнале физики и химии".
В мае 1827 года "Теоретические исследования электрических цепей" объемом в 245 страниц, в которых содержались теперь уже теоретические рассуждения Ома по электрическим цепям. В этой работе ученый предложил характеризовать электрические свойства проводника его сопротивлением и ввел этот термин в научный обиход. Ом нашел более простую формулу для закона участка электрической цепи, не содержащего ЭДС: "Величина тока в гальванической цепи прямо пропорциональна сумме всех напряжений и обратно пропорциональна сумме приведенных длин. При этом общая приведенная длина определяется как сумма всех отдельных приведенных длин для однородных участков, имеющих различную проводимость и различное поперечное сечение".
В 1829 году появляется его статья "Экспериментальное исследование работы электромагнитного мультипликатора", в которой были заложены основы теории электроизмерительных приборов. Здесь же Ом предложил единицу сопротивления, в качестве которой он выбрал сопротивление медной проволоки длиной 1 фут и поперечным сечением в 1 квадратную линию.
В 1830 году появляется новое исследование Ома "Попытка создания приближенной теории униполярной проводимости".
Только в 1841 году работа Ома была переведена на английский язык, в 1847 году - на итальянский, в 1860 году - на французский.
16 февраля 1833 года, через семь лет после выхода из печати статьи, в которой было опубликовано его открытие, Ому предложили место профессора физики во вновь организованной политехнической школе Нюрнберга. Ученый приступает к исследованиям в области акустики. Результаты своих акустических исследований Ом сформулировал в виде закона, получившего впоследствии название акустического закона Ома.
Раньше всех из зарубежных ученых закон Ома признали русские физики Ленц и Якоби. Они помогли и его международному признанию. При участии русских физиков, 5 мая 1842 года Лондонское Королевское общество наградило Ома золотой медалью и избрало своим членом.
В 1845 году его избирают действительным членом Баварской академии наук. В 1849 году ученого приглашают в Мюнхенский университет на должность экстраординарного профессора. В этом же году он назначается хранителем государственного собрания физико-математических приборов с одновременным чтением лекций по физике и математике. В 1852 году Ом получил должность ординарного профессора. Ом скончался 6 июля 1854 года. В 1881 году на электротехническом съезде в Париже ученые единогласно утвердили название единицы сопротивления - 1 Ом.
В общем случае зависимость междуIиUнелинейна, однако на практике всегда можно в определенном интервале напряжений считать её линейной и применять закон Ома; для металлов и их сплавов этот интервал практически неограничен.
Закон Ома в форме (1) справедлив для участков цепи, не содержащих источников ЭДС. При наличии таких источников (аккумуляторов, термопар, генераторов и т. д.) закон Ома имеет вид:
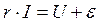 (2)
(2)
где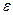 — ЭДС всех источников, включённых в рассматриваемый участок цепи. Для замкнутой цепи закон Ома принимает вид:
— ЭДС всех источников, включённых в рассматриваемый участок цепи. Для замкнутой цепи закон Ома принимает вид:
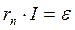 (3)
(3)
где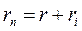 - полное сопротивление цепи, равное сумме внешнего сопротивленияrи внутреннего сопротивления
- полное сопротивление цепи, равное сумме внешнего сопротивленияrи внутреннего сопротивления источника ЭДС. Обобщением закона Ома на случай разветвлённой цепи является правило 2-е Кирхгофа.
источника ЭДС. Обобщением закона Ома на случай разветвлённой цепи является правило 2-е Кирхгофа.
Закон Ома можно записать в дифференциальной форме, связывающей в каждой точке проводника плотность токаjс полной напряжённостью электрического поля. Потенциальное. электрическое поле напряжённостиЕ, создаваемое в проводниках микроскопическими зарядами (электронами, ионами) самих проводников, не может поддерживать стационарное движение свободных зарядов (ток), т. к. работа этого поля на замкнутом пути равна нулю. Ток поддерживается неэлектростатическими силами различного происхождения (индукционного, химического, теплового и т.д.), которые действуют в источниках ЭДС и которые можно представить в виде некоторого эквивалентного непотенциального поля с напряженностьюEСТ,называемого сторонним. Полная напряженность поля, действующего внутри проводника на заряды, в общем случае равнаE+EСТ.Соответственно, дифференциальный закон Ома имеет вид:
 или
или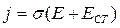 , (4)
, (4)
где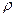 - удельное сопротивление материала проводника, а
- удельное сопротивление материала проводника, а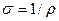 - его удельная электропроводность.
- его удельная электропроводность.
Закон Ома в комплексной форме справедлив также для синусоидальных квазистационарных токов:
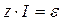 (5)
(5)
гдеz-полное комплексное сопротивление: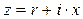 ,r– активное сопротивление, аx- реактивное сопротивление цепи. При наличии индуктивностиLи емкостиСв цепи квазистационарного тока частоты
,r– активное сопротивление, аx- реактивное сопротивление цепи. При наличии индуктивностиLи емкостиСв цепи квазистационарного тока частоты
 .
.
Существует несколько видов закона Ома.
Закон Ома для однородного участка цепи(не содержащего источника тока): сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника:
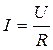
Закон Ома для замкнутой цепи:сила тока в замкнутой цепи равна отношению ЭДС источника тока к суммарному сопротивлению всей цепи:
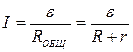
гдеR- сопротивление внешней цепи,r– внутреннее сопротивление источника тока.
R - +
- +



R
Закон Ома для неоднородного участка цепи(участка цепи с источником тока):
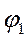
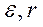 R
R

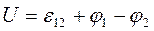 ;
;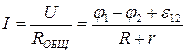
где - разность потенциалов на концах участка цепи,
- разность потенциалов на концах участка цепи,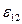 - ЭДС источника тока, входящего в участок.
- ЭДС источника тока, входящего в участок.
Способность вещества проводить ток характеризуется его удельным сопротивлением либо проводимостью
либо проводимостью . Их величина определяется химической природой вещества и условиями, в частности температурой, при которых оно находится. Для большинства металлов удельное сопротивление растет с температурой приблизительно по линейному закону:
. Их величина определяется химической природой вещества и условиями, в частности температурой, при которых оно находится. Для большинства металлов удельное сопротивление растет с температурой приблизительно по линейному закону:
 ;
;
где — удельное сопротивление при 0°С,t— температура по шкале Цельсия, а — коэффициент, численно равный примерно 1/273. Переходя к абсолютной температуре, получаем
— удельное сопротивление при 0°С,t— температура по шкале Цельсия, а — коэффициент, численно равный примерно 1/273. Переходя к абсолютной температуре, получаем

При низких температурах наблюдаются отступления от этой закономерности. В большинстве случаев зависимость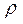 отTследует кривой1на рисунке.
отTследует кривой1на рисунке.
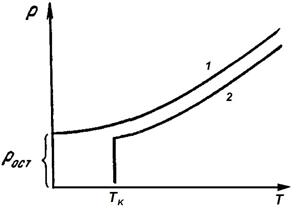
Величина остаточного сопротивления в сильной степени зависит от чистоты материала и наличия остаточных механических напряжений в образце. Поэтому после отжига
в сильной степени зависит от чистоты материала и наличия остаточных механических напряжений в образце. Поэтому после отжига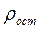 заметно уменьшается. У абсолютно чистого металла с идеально правильной кристаллической решеткой при абсолютном нуле
заметно уменьшается. У абсолютно чистого металла с идеально правильной кристаллической решеткой при абсолютном нуле .
.
У большой группы металлов и сплавов при температуре порядка нескольких градусов Кельвина сопротивление скачком обращается в нуль (кривая2на рисунке). Впервые это явление, названное сверхпроводимостью, было обнаружено в 1911 г. Камерлинг - Оннесом для ртути. В дальнейшем сверхпроводимость была обнаружена у свинца, олова, цинка, алюминия и других металлов, а также у ряда сплавов. Для каждого сверхпроводника имеется своя критическая температураТк,при которой он переходит в сверхпроводящее состояние. При действии на сверхпроводник магнитного поля сверхпроводящее состояние нарушается. Величина критического поляHK,разрушающего сверхпроводимость, равна нулю приТ=Тки растет с понижением температуры.
Полное теоретическое объяснение сверхпроводимости было дано в 1958 г. советским физиком Н. Н. Боголюбовым и его сотрудниками.
Зависимость электрического сопротивления от температуры положена в основу термометров сопротивления. Такой термометр представляет собой металлическую (обычно платиновую) проволоку, намотанную на фарфоровый или слюдяной каркас. Проградуированный по постоянным температурным точкам термометр сопротивления позволяет измерять с точностью порядка нескольких сотых градуса как низкие, так и высокие температуры.
Список использованной литературы:
Прохоров А. М.Физический энциклопедический словарь,М., 1983
Дорфман Я. Г.Всемирная история физики. М., 1979Ом Г.Определение закона, по которому металлы проводят контактное электричество. – В кн.: Классики физической науки. М., 1989
Роджерс Э.Физика для любознательных, т. 3. М., 1971Орир Дж.Физика, т. 2. М., 1981Джанколи Д.Физика, т. 2. М., 1989
superbotanik.net