Зако́ны Кирхго́фа (или правила Кирхгофа) — соотношения, которые выполняются между токами и напряжениями на участках любой электрической цепи. Правила Кирхгофа позволяют рассчитывать любые электрические цепи постоянного и квазистационарного тока.[1] Имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения многих задач теории электрических цепей. Применение правил Кирхгофа к линейной цепи позволяет получить систему линейных уравнений относительно токов, и соответственно, найти значение токов на всех ветвях цепи. Сформулированы Густавом Кирхгофом в 1845 году.

1. Формулировка

Для формулировки законов Кирхгофа, в электрической цепи выделяются узлы — точки соединения трёх и более проводников и контуры — замкнутые пути из проводников. При этом каждый проводник может входить в несколько контуров.

В этом случае законы формулируются следующим образом.

1.1. Первый закон

Первый закон Кирхгофа (Закон токов Кирхгофа, ЗТК) гласит, что алгебраическая сумма токов в любом узле любой цепи равна нулю (значения вытекающих токов берутся с обратным знаком):

$\sum\limits^n_{j=1}I_j=0.$

Иными словами, сколько тока втекает в узел, столько из него и вытекает. Данный закон следует из закона сохранения заряда. Если цепь содержит p узлов, то она описывается p − 1 уравнениями токов. Этот закон может применяться и для других физических явлений (к примеру, водяные трубы), где есть закон сохранения величины и поток этой величины.

1.2. Второй закон

Второй закон Кирхгофа (Закон напряжений Кирхгофа, ЗНК) гласит, что алгебраическая сумма падений напряжений по любому замкнутому контуру цепи равна алгебраической сумме ЭДС, действующих вдоль этого же контура. Если в контуре нет ЭДС, то суммарное падение напряжений равно нулю:

для постоянных напряжений $\sum^n_{k=1} E_k= \sum^m_{k=1}U_k=\sum^m_{k=1}R_kI_k;$ для переменных напряжений $\sum^n_{k=1} e_k= \sum^m_{k=1}u_k=\sum^m_{k=1}R_ki_k+\sum^m_{k=1}u_{L\,k}+\sum^m_{k=1}u_{C\,k}.$

Иными словами, при обходе цепи по контуру, потенциал, изменяясь, возвращается к исходному значению. Если цепь содержит ветвей, из которых содержат источники тока ветви в количестве mi~ , то она описывается m-mi-(p-1)~ уравнениями напряжений. Частным случаем второго правила для цепи, состоящей из одного контура, является закон Ома для этой цепи.

Законы Кирхгофа справедливы для линейных и нелинейных цепей при любом характере изменения во времени токов и напряжений.

Пример

На этом рисунке для каждого проводника обозначен протекающий по нему ток (буквой «I») и напряжение между соединяемыми им узлами (буквой «U»)

Например, для приведённой на рисунке цепи, в соответствии с первым законом выполняются следующие соотношения:

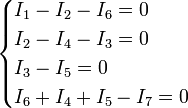
$\begin{cases} I_1-I_2-I_6=0\\ I_2-I_4-I_3=0\\ I_3-I_5=0\\ I_6+I_4+I_5-I_7=0\end{cases}$

Обратите внимание, что для каждого узла должно быть выбрано положительное направление, например здесь, токи, втекающие в узел, считаются положительными, а вытекающие — отрицательными.

В соответствии со вторым законом, справедливы соотношения:

$\begin{cases}U_2+U_4-U_6=0\\ U_3+U_5-U_4=0\end{cases}$

2. Особенности составления уравнений для расчёта токов

Законы Кирхгофа, записанные для узлов и контуров цепи, дают полную систему линейных уравнений, которая позволяет найти все токи и напряжения.
Перед тем, как составить уравнения, нужно произвольно выбрать:
- положительные направления токов в ветвях и обозначить их на схеме;
- положительные направления обхода контуров для составления уравнений по второму закону.
С целью единообразия рекомендуется для всех контуров положительные направления обхода выбирать одинаковыми (напр.: по часовой стрелке)
Если направление тока совпадает с направлением обхода контура (которое выбирается произвольно), перепад напряжения считается положительным, в противном случае — отрицательным.
При записи линейно независимых уравнений по второму закону, стремятся, чтобы в каждый новый контур, для которого составляют уравнение, входила хотя бы одна новая ветвь, не вошедшая в предыдущие контуры, для которых уже записаны уравнения по второму закону (достаточное, но не необходимое условие)

3. О значении для электротехники

Правила Кирхгофа имеют прикладной характер и позволяют наряду и в сочетании с другими приёмами и способами (метод эквивалентного генератора, метод контурных токов, метод узловых напряжений, принцип суперпозиции, способ составления потенциальной диаграммы) решать задачи электротехники. Правила Кирхгофа нашли широкое применение благодаря простой формулировке уравнений и возможности их решения стандартными способами линейной алгебры (методом Крамера, методом Гаусса и др.).

Существует мнение, согласно которому «Законы Кирхгофа» следует именовать «Правилами Кирхгофа», ибо они не отражают фундаментальных сущностей природы (и не являются обобщением большого количества опытных данных), а могут быть выведены из других положений и предположений.

4. Закон излучения

Закон излучения Кирхгофа — отношение излучательной способности любого тела к его поглощательной способности одинаково для всех тел при данной температуре для данной частоты для равновесного излучения и не зависит от их формы, химического состава и проч.

Примечания

Кирхгофа правила - slovari.yandex.ru/~книги/БСЭ/Кирхгофа правила/ — статья из Большой советской энциклопедии

Литература

Матвеев А. Н. Электричество и магнетизм. — Учебное пособие. — М.: Высшая школа, 1983. — 463 с.
Калашников С. Г. Электричество. — Учебное пособие. — М.: Физматлит, 2003. — 625 с.
Бессонов Л. А. Теоретические основы электротехники. Электрические цепи. — 11-е издание. — М.: Гардарики, 2007.

wreferat.baza-referat.ru

Реферат - Законы Ома. Законы Кирхгофа

определить число узлов и ветвей цепи Nуи Nв;
определить число уравнений по первому и второму законам N1и N2.;
для всех ветвей (кроме ветвей с источниками тока) произвольно задать направления протекания токов;
для всех узлов, кроме одного, выбранного произвольно, составить уравнения по первому закону Кирхгофа;
произвольно выбрать на схеме электрической цепи замкнутые контуры таким образом, чтобы они отличались друг от друга по крайней мере одной ветвью и чтобы все ветви, кроме ветвей с источниками тока, входили по крайней мере в один контур;
произвольно выбрать для каждого контура направление обхода и составить уравнения по второму закону Кирхгофа, включая в правую часть уравнения ЭДС действующие в контуре, а в левую падения напряжения на резисторах. Примечание: Знак ЭДС выбирают положительным, если направление ее действия совпадает с направлением обхода независимо от направления тока; а знак падения напряжения на резисторе принимают положительным, если направление тока в нем совпадает с направлением обхода.

Рассмотрим этот алгоритм на примере рис 2.

Здесь светлыми стрелками обозначены выбранные произвольно направления токов в ветвях цепи. Ток в ветви с R4не выбирается произвольно, т.к. в этой ветви он определяется действием источником тока.

Число ветвей цепи равно 5, а т.к. одна из них содержит источник тока, то общее число уравнений Кирхгофа равно четырем.

Число узлов цепи равно трем (a, b и c), поэтому число уравнений по первому закону Кирхгофа равно двум и их можно составлять для любой пары из этих трех узлов. Пусть это будут узлыaиb, тогда

a) J + IE1 = J + IR1 =IR3J + IR1 -IR3 = 0	(7)
b) IR3 + IE2 = IR1 + IR2IR3 + IE2 - IR1 - IR2 = 0	(8)

По второму закону Кирхгофа нужно составить два уравнения. Выберем два контура I и II так, чтобы все ветви, кроме ветви с источником тока попали по крайней мере в один из них, и зададим произвольно направление обхода как показано стрелками. Тогда

I) -E1 = IR1R1 + IR3R3	(9)
II) E2 = IR2R2	(10)

При выборе контуров и составлении уравнений все ветви с источниками тока должны быть исключены, т.е. контуры обхода не должны включать ветви с источниками тока.Это не означает что для контуров с источниками тока нарушается второй закон Кирхгофа. Просто при необходимости определения падения напряжения на источнике тока или на других элементах ветви с источником тока это можно сделать после решения системы уравнений. Например, нарис. 2можно создать замкнутый контур из элементовR3, R4,JиE2, и для него будет справедливым уравнение

IR3R3+E2+JR4+UJ= 0 ,

где UJ- падение напряжения на источнике токаJ.

Из сказанного выше очевидно, что законы Кирхгофа необязательно использовать в виде систем уравнений. Они справедливы всегда для любого узла и для любого замкнутого контура любой электрической цепи.

Современные средства математического анализа позволяют легко получить результат решения составленной выше системы уравнений, если она записана в матричной форме AX=B. Это можно сделать, например, для токов в качестве неизвестных.

Каждая строка матрицы Aдолжна соответствовать одному из уравнений (7)-(10). Поэтому в строки матрицыAнужно включить все коэффициенты при токах соответствующего уравнения,в той последовательности, в какой эти токи включены в координаты вектора неизвестных величин. Если какой-либо ток отсутствует в уравнении, то в качестве элемента матрицы нужно указать нуль. Для включения в матрицу уравнения по первому закону Кирхгофа удобнее записывать в форме (1) с нулевой правой частью, однако, для уравнения (7) нужно перенести ток источникаJв правую часть, т.к. он не входит в число неизвестных.

Вектор неизвестных токов Xпредставляет собой столбец, в который включены неизвестные токи в произвольной последовательности.

Вектор Bпредставляет собой столбец, координатами которого являются источники электрической энергии, действующие в цепи (правая часть уравнений (7)-(10)). Порядок включения их в столбец должен соответствовать порядку записи уравнений в строки матрицыA.

Составим матричное уравнение для схемы рис. 2, используя полученные ранее уравнения(7)-(8)и(9)-(10).

Здесь для упрощения восприятия строки записи помечены указателями на тот узел или контур, которому они соответствуют.

Список использованной литературы:

Прохоров А. М. Физический энциклопедический словарь, М., 1983

Дорфман Я. Г. Всемирная история физики. М., 1979

Ом Г. Определение закона, по которому металлы проводят контактное электричество. – В кн.: Классики физической науки. М., 1989

Роджерс Э. Физика для любознательных, т. 3. М., 1971 Орир Дж. Физика, т. 2. М., 1981 Джанколи Д. Физика, т. 2. М., 1989

studfiles.net

Реферат : Законы Кирхгофа

Академия ФСО России

Кафедра Физики

Тема:

«Законы Кирхгофа и их применение для расчета электрических цепей»

Орел-2009

Содержание

Первый закон Кирхгофа

Второй закон Кирхгофа

Расчет сложных цепей с помощью уравнений Кирхгофа

Первый закон Кирхгофа

Алгебраическая сумма токов в ветвях, сходящихся к любому узлу электрической цепи, тождественно равна нулю. Согласно этому закону, если к некоторому узлу цепи подсоединено n ветвей с токами i1, i2, ..., in, то в любой момент времени

где , если направление тока положительно и ориентировано от узла (ток выходит из узла), или , если ток входит в узел. Таким образом, любому узлу цепи соответствует уравнение, связывающее токи в ветвях цепи, соединенных с данным узлом.

В качестве примера приведем схему на рисунке 1.

Рис.1.

В соответствии с первым законом Кирхгофа:

Общее число уравнений, которое можно составить по первому закону Кирхгофа для цепи, равно числу узлов цепи .

Так, для четырех узлов графа (рисунок 2) можно составить следующие четыре уравнения:

Рис.2.

узел 1: ,

узел 2: ,

узел 3: ,

узел 4: .

Первый закон Кирхгофа часто называют законом Кирхгофа для токов и сокращенно в тексте обозначают ЗКТ.

Число независимых уравнений равно трем, так как любое из этих уравнений отличается от суммы трех остальных только знаком. Итак, если цепь содержит узлов, то для неё можно составить по первому закону Кирхгофа независимых уравнений. Совокупность из N узлов цепи, уравнения для которых образуют систему линейно независимых уравнений, называют совокупностью независимых узлов цепи.

Примеры на применение первого закона Кирхгофа. Параллельное соединение элементов

В качестве примера на применение первого закона Кирхгофа рассмотрим параллельное соединение нескольких элементов активных сопротивлений, конденсаторов, катушек индуктивности.

Особенностью параллельного соединения нескольких элементов является равенство напряжений, приложенных к зажимам любого из элементов, входящих в соединение. Цепь при таком соединении характеризуется только одним независимым узлом.

Пусть параллельно соединены n элементов активного сопротивления. Если выбрать направления отчетов токов в элементах такими как это показано на рисунке 3, то согласно первому закону Кирхгоффа при параллельном соединении элементов запишем:

ис.3.

;

учитывая, что , имеем ,

где .

Зависимость не отличается от зависимости между напряжением на зажимах и током в элементе активного сопротивления с проводимостью G. Следовательно, цепь, составленная из нескольких сопротивлении, включенных параллельно, может быть заменена одним активным сопротивлением, при этом проводимость эквивалентного элемента равна сумме проводимостей элементов, входящих в соединение.

При параллельном соединении конденсаторов (рисунок 4) ток ветви можно определить по формуле: .

Рис.4.

Для вычисления общего тока необходимо просуммировать токи ветвей:

где ..

Таким образом, при параллельном соединении нескольких конденсаторов эквивалентная ёмкость равна сумме емкостей, входящих в соединение.

В случае параллельного соединения катушек индуктивностей (рисунок 5) ток каждой из ветвей равен: .

Рис.5.

Уравнение для вычисления общего тока имеет вид:

Следовательно , то есть .

Это означает, что значение эквивалентной индуктивности будит меньше наименьшего из значений соединённых параллельно индуктивностей.

Второй закон Кирхгофа

Второй закон Кирхгофа формулируется следующим образом: алгебраическая сумма напряжений ветвей в любом контуре цепи тождественно равна нулю. Для замкнутого контура, изображённого на рисунке 6, можно записать соотношение:

Рис.6.

В соответствии со вторым законом Кирхгофа при обходе контура по часовой стрелке справедливо соотношение:

Изменение направления обхода эквивалентно изменению знаков напряжений на противоположные (умножению на минус единицу).

Примеры на применение второго закона Кирхгофа

Последовательное соединение элементов

Пусть n элементов активного сопротивления соединены последовательно (рисунок 7).

Рис.7.

В соответствии с выбранным направлением обхода по второму закону Кирхгофа получим уравнение:

характерной особенностью последовательного соединения является равенство токов в каждом из элементов, входящих в соединение.

При запишем:

, то есть .

Таким образом, при последовательном соединении нескольких резисторов эквивалентное сопротивление равно сумме сопротивлений, входящих в соединение.

При последовательном соединении катушек индуктивности (рисунок 8) можно записать:

Рис.8.

Если , то ,

следовательно .

Это означает, что эквивалентная индуктивность равна сумме индуктивностей, входящих в последовательное соединение.

В случае последовательного соединения конденсаторов (рисунок 9) по второму закону Кирхгофа можно записать:

Рис.9.

Заменяя получим: .

Обратная ёмкость всех конденсаторов, соединенных последовательно, равна сумме обратных ёмкостей конденсаторов, входящих в соединение:

При этом эквивалентная ёмкость соединения будет меньше наименьшей ёмкости конденсатора, входящего в последовательное соединение.

Расчет сложных цепей с помощью уравнений Кирхгофа

Пример 1

Далеко не во всех случаях цепь представляет собой совокупность лишь последовательно и параллельно соединенных ветвей. В качестве примера рассмотрим вариант расчета с помощью уравнений Кирхгофа электрической цепи (рисунок 10). Цепь содержит = 4 узлов и = 6 ветвей, включая источники напряжения.

Рис.10.

Для определения всех токов и напряжений в схеме достаточно найти значения токов во всех ветвях цепи. Зная ток, проходящий через любую из ветвей цепи, можно найти как напряжение этой ветви, так и напряжение между любой парой узлов цепи.

Если мы зададимся произвольно положительными направлениями токов в ветвях цепи и пронумеруем произвольно эти токи, то по первому закону Кирхгофа можно составить уравнений относительно токов в ветвях цепи.

По второму закону Кирхгофа будет линейно-независимых уравнений для напряжений ветвей схемы.

Совокупность из уравнений по первому закону Кирхгофа, и уравнений, составленных по второму закону Кирхгофа, образует систему линейно – независимых уравнений. Эта система будет неоднородной системой уравнений, так как ее свободными членами являются заданные напряжения источников.

Подобная система уравнений имеет единственное решение, позволяющее найти токи в ветвях цепи, а по ним и значения напряжений между любой парой узлов цепи.

Для примера составим систему уравнений по первому закону Кирхгофа (рисунок 10).

Число уравнений: .

Узел 1: ,

узел 2: ,

узел 3: .

В тоже время по второму закону Кирхгофа для контуров I, II, III можно составить систему из уравнений.

Контур I: ,

контур II: ,

контур III: .

Таким образом, решая систему из 6 уравнений с шестью неизвестными токами, например по методу Крамера, определим неизвестные. Если в цепи будет источник тока, то в системе уравнений неизвестным будет напряжение на зажимах этого источника, а ток через источник будет равен току задающего источника. Общее число неизвестных сохранится прежним.

Пример 2

Для цепи (рисунок 11) определить токи и , если E = 20 В, I0 = 2 A, R1 = 15 Ом, R2 = 85 Ом.

Рис.11.

Решение

Выберем направления токов , и обхода в контуре, составим уравнения по законам Кирхгофа. Число уравнений, составляемых по первому закону Кирхгофа:

Число уравнений по второму закону Кирхгофа:

Уравнение токов для узла 1:

. (a)

Уравнение по второму закону Кирхгофа:

. (б)

Подставим в уравнения (а) и (б) числовые значения получим:

Решив эту систему, определим токи и :

; .

Литература

Белецкий А.Ф. Теория линейных электрических цепей. – М.: Радио и связь, 1986.
Бакалов В.П. и др. Теория электрических цепей. – М.: Радио и связь, 1998.
Качанов Н. С. и др. Линейные радиотехнические устройства. М.: Воен. издат., 1974.
В.П. Попов Основы теории цепей – М.: Высшая школа, 2000

topref.ru

Реферат Правила Кирхгофа

скачать

Реферат на тему:

План:

1 Формулировка
- 1.1 Первый закон
- 1.2 Второй закон
2 Особенности составления уравнений для расчёта токов
3 О значении для электротехники
4 Закон излучения

Введение

Не следует путать с Принцип Керкгоффса.

1. Формулировка

В этом случае законы формулируются следующим образом.

1.1. Первый закон

$\sum\limits^n_{j=1}I_j=0.$

1.2. Второй закон

Пример

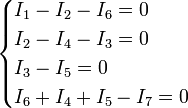
$\begin{cases} I_1-I_2-I_6=0\\ I_2-I_4-I_3=0\\ I_3-I_5=0\\ I_6+I_4+I_5-I_7=0\end{cases}$

В соответствии со вторым законом, справедливы соотношения:

$\begin{cases}U_2+U_4-U_6=0\\ U_3+U_5-U_4=0\end{cases}$

2. Особенности составления уравнений для расчёта токов

Законы Кирхгофа, записанные для узлов и контуров цепи, дают полную систему линейных уравнений, которая позволяет найти все токи и напряжения.
Перед тем, как составить уравнения, нужно произвольно выбрать:
- положительные направления токов в ветвях и обозначить их на схеме;
- положительные направления обхода контуров для составления уравнений по второму закону.
С целью единообразия рекомендуется для всех контуров положительные направления обхода выбирать одинаковыми (напр.: по часовой стрелке)
Если направление тока совпадает с направлением обхода контура (которое выбирается произвольно), перепад напряжения считается положительным, в противном случае — отрицательным.
При записи линейно независимых уравнений по второму закону, стремятся, чтобы в каждый новый контур, для которого составляют уравнение, входила хотя бы одна новая ветвь, не вошедшая в предыдущие контуры, для которых уже записаны уравнения по второму закону (достаточное, но не необходимое условие)

3. О значении для электротехники

4. Закон излучения

Примечания

Кирхгофа правила - slovari.yandex.ru/~книги/БСЭ/Кирхгофа правила/ — статья из Большой советской энциклопедии

Литература

Матвеев А. Н. Электричество и магнетизм. — Учебное пособие. — М.: Высшая школа, 1983. — 463 с.
Калашников С. Г. Электричество. — Учебное пособие. — М.: Физматлит, 2003. — 625 с.
Бессонов Л. А. Теоретические основы электротехники. Электрические цепи. — 11-е издание. — М.: Гардарики, 2007.

wreferat.baza-referat.ru

Смотрите также

..:::Новинки:::..

Windows Commander 5.11 Свежая версия.

Новая версия
IrfanView 3.75 (рус)

Обновление текстового редактора TextEd, уже 1.75a

System mechanic 3.7f
Новая версия

Обновление плагинов для WC, смотрим :-)

Весь Winamp
Посетите новый сайт.

WinRaR 3.00
Релиз уже здесь

PowerDesk 4.0 free
Просто - напросто сильный upgrade проводника.

..:::Счетчики:::..