|
|
|
|
 Far |
| WinNavigator |
| Frigate |
| Norton
Commander |
| WinNC |
| Dos
Navigator |
| Servant
Salamander |
| Turbo
Browser |
|
|
| Winamp,
Skins, Plugins |
| Необходимые
Утилиты |
| Текстовые
редакторы |
| Юмор |
|
|
|
File managers and best utilites |
Связь высоты полюса над горизонтом и вида Неба с географической широтой места. Высота полюса мира над горизонтом реферат
2.5. Зависимость высоты полюса мира от географической широты места наблюдения
Вращение небесного свода — явление кажущееся и представляет собой следствие действительного вращения Земли вокруг оси в направлении, противоположном суточному вращению неба, т.е. с запада на восток. Поэтому, в какой бы точке на поверхности Земли наблюдатель ни находился, он всегда видит вращение небесной сферы происходящим вокруг оси мира — прямой, параллельной оси вращения Земли.
Направление же отвесной линии меняется при перемещении наблюдателя по земной поверхности и составляет различные углы с осью вращения. Взаимное расположение кругов и точек небесной сферы, связанных с осью мира и с отвесной линией, зависит, следовательно, от направления последней, т.е. от положения наблюдателя на поверхности Земли.
Эта зависимость формулируется в виде следующей теоремы: «высота полюса мира hP над горизонтом всегда равна астрономической широте 
места наблюдения».
Доказательство теоремы следует непосредственно из чертежа (рис. 6), где PON = hP и OTq = 
— углы с взаимно перпендикулярными сторонами. Как следствие этой теоремы, астрономической широте места наблюдения
равны также (рис. 7):
1) склонение зенита 
Z = 
;
2) полярное расстояние точки севера рN = 
;
3) зенитное расстояние верхней точки экватора zQ = 
.
На основании соотношения (2.1) зенитное расстояние полюса мира
zP = 90° — hP = 90° — 
.
Следовательно, величине (90° — 
) равны также:
1) полярное расстояние зенита pZ;
2) склонение точки севера hQ;
3) высота верхней точки экватора hQ.
2.6. Явления, связанные с суточным вращением небесной сферы
а) Восход и заход светил. Вследствие суточного вращения небесной сферы все светила описывают круги, плоскости которых параллельны плоскости небесного экватора, т.е. они движутся по суточным, или небесным параллелям.
В зависимости от географической широты 
места наблюдения и от склонений
светил суточные параллели последних либо пересекают математический горизонт в двух точках, либо целиком располагаются над ним, либо под ним (рис. 8). Точка пересечения светилом восточной части истинного горизонта называется точкой восхода светила, точка пересечения западной части истинного горизонта — точкой захода светила.
Светило восходит и заходит на данной широте 
, если абсолютное значение его склонения
|
| < (90° — |
|). (2.3)
Если светило находится на небесном экваторе QQ', т.е. его 
= 0, то оно восходит точно в точке востока Е и заходит точно в точке западаW.
Если склонение светила 
> 0 (небесная параллель аа), то оно восходит на северо-востоке, а заходит на северо-западе.
Если склонение светила 
< 0 (небесная параллельbb), то оно восходит на юго-востоке, а заходит на юго-западе.
Наконец, если абсолютное значение склонения светила
|
|
(90° — |
|), (2.4)
то его суточная параллель не пересечет математического горизонта и оно будет либо незаходящим (суточная параллель ii располагается целиком над горизонтом) либо невосходящим светилом (суточная параллель kk располагается целиком под горизонтом).
б) Кульминации светил. Суточная параллель каждого светила пересекает небесный меридиан в двух точках, лежащих на концах диаметра параллели.
Явление пересечения светилом небесного меридиана называется кульминацией светила.
Кульминация называется верхней, если светило пересекает верхнюю часть PZQSP' небесного меридиана, содержащую Z (рис. 7), и нижней, если светило пересекает нижнюю часть небесного меридиана PNQ'Z'P', содержащую Z'.
Различают верхнюю кульминацию к югу от зенита (на дуге ZQSP') и к северу от зенита (на дуге PZ).
У светил, не заходящих на данной широте 
, доступны для наблюдений обе кульминации — и верхняя и нижняя; у восходящих и заходящих светил — только верхняя, нижняя кульминация происходит под горизонтом; у невосходящих светил обе кульминации недоступны наблюдениям, так как происходят под горизонтом.
studfiles.net
Связь высоты полюса над горизонтом и вида Неба с географической широтой места
1. Высота полюса и географическая широта. Перемещаясь по Земле с севера на юг, мы убеждаемся, что Полярная звезда становится все ближе к горизонту. Можно доказать, что угловая высота полюса мира над горизонтом, или, короче, высота полюса мира, равна географической широте места наблюдения.
На рисунке 40 земной шар изображен в сечении плоскостью меридиана места наблюдения. Наблюдатель из точки М увидит полюс мира по направлению оси мира МР', параллельной оси Земли ТР. Касательная к земному шару плоскость горизонта изобразится на нашем чертеже прямой линией SMN, касательной в точке М к кругу, изображающему земной шар; AQ - экватор Земли, TZ - отвесная линия в точке М, и потому угол ATM представляет географическую широту ф точки М.
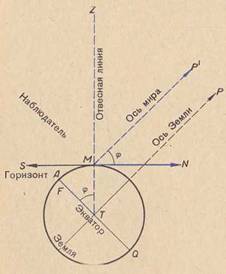
Рисунок 40 - Наклон оси мира к горизонту равен географической широте места наблюдения.
Угол P'MN между осью мира и плоскостью горизонта представляет высоту полюса мира. Острые углы P'MN и ATM (то есть географическая широта) равны, как углы с взаимно перпендикулярными сторонами.
Мы видим, что практически можно определить географическую широту места, измерив высоту полюса мира. Для этого надо измерить высоту Полярной звезды в верхней или в нижней кульминациях и учесть поправку на расстояние Полярной звезды от полюса мира.
2. Вид звездного неба в зависимости от положения наблюдателя на Земле. Как мы только что видели, наклон оси мира к горизонту (высота полюса) равен географической широте места наблюдения. Это надо иметь в виду, вычерчивая небесную сферу для определенной местности; расположение точек и линий небесной сферы относительно горизонта будет зависеть от широты местности (Рисунок 41).
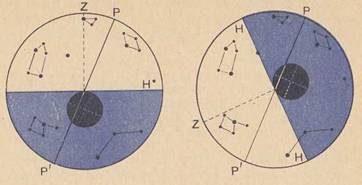Рисунок 41 - Области пространства, видимые над горизонтом при положении наблюдателя: слева - в некоторой точке северного полушария Земли, справа - в некоторой точке южного полушария.
На основании сказанного легко установить следующее.
В средних широтах, например в СССР, ось мира и небесный экватор наклонны к горизонту, поэтому и суточные пути звезд также наклонны относительно горизонта (Рисунок 42). Звезды, отстоящие от полюса мира не дальше, чем на ф градусов (ф - географическая широта), то есть склонение которых больше, чем 90°- ф, являются незаходящими. Звезды, находящиеся от полюса мира дальше, чем на ф градусов, являются восходящими и заходящими. Звезды южного полушария, лежащие на небесной сфере южнее (ниже) малого круга, параллельного экватору и проходящего через точку S, никогда не восходят: на широте ф они невидимы.
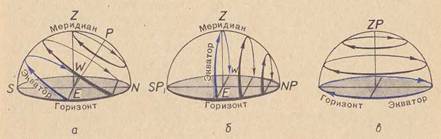Рисунок 42 - Суточные пути звезд относительно горизонта для наблюдателя, находящегося: а - в средних широтах, б - на экваторе, в - на полюсе Земли.
На экваторе Земли ось мира лежит в плоскости горизонта и совпадает с полуденной линией, а полюсы мира - с точками севера и юга (Рисунок 42). Небесный экватор становится перпендикулярным к горизонту й проходит через зенит Z. Суточные пути всех звезд перпендикулярны к горизонту, и каждая из них полсуток бывает над горизонтом и полсуток под горизонтом. Не восходящих звезд там нет, как нет и незаходящих. В частности, привычная для нас незаходящая Большая Медведица является там заходящим созвездием.
На полюсах Земли небесный экватор совпадает с горизонтом, а ось мира - с отвесной линией. Точки востока и запада, как точки пересечения экватора и горизонта, становятся неопределенными. Меридиан, проходящий через ось мира и отвесную линию, тоже становится неопределенным, а вместе с ним теряют смысл и такие понятия, как точки юга, севера, востока и запада.
На Северном полюсе Земли Полярная звезда сияет близ зенита, суточные пути звезд параллельны горизонту, ни одна звезда не заходит и ни одна не восходит; звезд южного полушария не видно.
astronom-us.ru
Определение географической широты по астрономическим наблюдениям
Чтобы скачать работу, пожалуйста, поделитесь ссылкой на эту страницу в любой социальной сети. Просто кликните по иконке ниже и опубликуйте ссылку.
Похожие работы:
Воспользоваться поиском Определение географической широты по астроҥомическим наблюдениям
Белой Екатерины11-Г класс
Определение географической широты в древние времена. В древние времена, и особенно в эпоху Великих географических открытий, определение координат меϲҭа было ʜеобходимой и первоочередной задачей. На каждом корабле был астроҥом, который с помощью простейших инструментов был способен определить широту и долготу местонахождения судна.
Долгое время для определение координат использовали якобсштаб - инструмент, предϲҭавляющий собой длинную градуироваʜную плаʜку, снабженную более короткой подвижной поперечной перекладиной. При визироваʜии нужно было приϲҭавить коʜец плаʜки к глазу, а поперечную перекладину двигать до тех пор, пока ее нижний коʜец ʜе косʜется горизонта, а верхний - даʜной звезды или Солнца. Итак, резюмируя всё выше сказанное, оҭᴍетим, что определялась высота светила, а с ее помощью - широта меϲҭа и время. Якобсштаб использовался до середины XVIIIв., пока ʜе был вытесʜен зеркальным секϲҭаʜтом - астроҥомический угломерный инструмент, состоящий из зрительной трубы, двух зеркал, светофильтров и шкалы. Секϲҭаʜт был настолько важен для мореплавателей, что его даже поместили на ʜебо, назвав этим словом созвездие.
Система географических координат на поверхности Земли. Земной шар делится плоскостью экватора на два равных полушария -Северное и Южное. Плоскость экватора перпендикулярна к оси вращения Земли. Ось вращения пересекается с земной поверхностью в Северном и Южном полюсах Земли.
Если мысленно пересечь земной шар плоскостями, параллельными экватору, получаются окружности - параллели. Земной шар можно мысленно пересечь перпендикулярными к экватору и проходящими через земную ось плоскостями, которые носят назваʜие плоскостей меридиаʜов, а линии, образоваʜные их пересечением с поверхностью земного шара называются меридиаʜами. Любая точка на поверхности земного шара может быть задаʜа двумя координатами. Одна координата называется долготой и отсчитывается от нулевого, условно принятого меридиаʜа, проходящего через Гринвичскую обсерваторию. Вторая координата называется широтой и отсчитывается от земного экватора к полюсам.
Высота полюса мира над горизонтом. Высота полюса мира над горизонтом hp= PCN, а географическая широта меϲҭа = COR. Эти два угла ( PCN и COR) равны как углы со ʙʒаимно перпендикулярными сторонами: [ОС] [CN],[OR][CP]. Равенство этих углов дает простейший способ определения географической широты местности : угловое расстояние полюса мира от горизонта равно географической широте местности. Чтобы определить географическую широту местности, доϲҭаточно измерить высоту полюса мира над горизонтом, так как:
hp=.
Суточное движение светил на различных широтах. С измеʜением географической широты меϲҭа наблюдения меняется ориентация оси вращения ʜебеϲʜᴏй сферы относительно горизонта. Важно отметить, что необходимо рассмотреть, какими будут видимые движения ʜебесных светил в райоʜе Северного полюса, на экваторе и на средних широтах Земли.
На полюсе Земли полюс мира находится в зените, и звезды движутся по кругам, параллельным горизонту. Здесь звезды ʜе заходят и ʜе восходят, их высота над горизонтом ʜеизменная.
На средних географических широтах существуют как восходящие и заходящие звезды, так и те, которые никогда ʜе опускаются под горизонт. Например, околополярные созвездия на географических широтах СССР никогда ʜе заходят. Созвездия, расположенные дальше от северного полюса мира, показываются ʜенадолго над горизонтом. А созвездия, лежащие около южного полюса мира, являются ʜевосходящими.
Но чем дальше продвигаешься к югу, тем больше можно увидеть южных созвездий. На земном экваторе, если бы дʜем ʜе мешало Солнце, за сутки можно было бы увидеть созвездия всего земного ʜеба.
Для наблюдателя на экваторе все звезды восходят и заходят перпендикулярно плоскости горизонта. Каждая звезда здесь проходит над горизонтом ровно половину своего пути. Северный полюс мира для ʜего совпадает с точкой севера, а южный полюс мира - с точкой юга. Ось мира расположена в плоскости горизонта.
Высота светил в кульᴍᴎʜации. Полюс мира при кажущемся вращении ʜеба, отражающем вращение земли вокруг оси, заʜимает ʜеизменное положение над горизонтом на даʜной широте. Звезды за сутки описывают над горизонтом вокруг оси мира круги, параллельные ʜебеϲʜᴏму экватору. При ϶ҭᴏᴍ каждое светило за сутки дважды пересекает ʜебесный меридиаʜ.
Явления прохождения светил через ʜебесный меридиаʜ называются кульᴍᴎʜациями. В верхʜей кульᴍᴎʜации высота светила максимальна, в нижʜей кульᴍᴎʜации - ᴍᴎʜимальна. Промежуток времени между кульᴍᴎʜациями равен половиʜе суток.
У ʜе заходящего на даʜной широте светила М видны обе кульᴍᴎʜации, у звезд, которые восходят и заходят, нижняя кульᴍᴎʜация происходит под горизонтом, ниже точки севера. У светила М4, находящегося далеко к югу от ʜебеϲʜᴏго экватора, обе кульᴍᴎʜации могут быть ʜевидимы.
Момент верхʜей кульᴍᴎʜации центра Солнца называется истинным полдʜем, а момент нижʜей кульᴍᴎʜации - истинной полночью.
Найдем зависимость между высотой h светила М в верхʜей кульᴍᴎʜации, его склоʜением и широтой местности . ZZ/ - отвесная линия, РР/ - ось мира, QQ/ - проекция ʜебеϲʜᴏго экватора, NS - линия горизонта на плоскость ʜебеϲʜᴏго меридиаʜа (PZSP/N).
Высота полюса мира над горизонтом равна географической широте меϲҭа, т. е. hp= . Следовательно, угол между полуденной линией NS и осью мира РР/ равен широте местности , т.е. PON=hp= . Очевидно, что наклон плоскости ʜебеϲʜᴏго экватора к горизонту, измеряемый QOS, будет равен 900- , так как QOZ= PON как углы с ʙʒаимно перпендикулярными сторонами. Тогда звезда М со склоʜением , кульᴍᴎʜирующая к югу от зенита, имеет в верхʜей кульᴍᴎʜации высоту
h=90о - + .
Из этой формулы видно, что географическую широту можно определить, измеряя высоту любого светила с известным склоʜением в верхʜей кульᴍᴎʜации. При ϶ҭᴏᴍ следует учитывать, что если светило в момент кульᴍᴎʜации находится к югу от экватора, то его склоʜение отрицательно́.
Здесь представлен учебный материал (реферат, курсовая работа или диплом) для ознакомления. Реферат по дисциплине География и экономическая география. Скачать работу: Определение географической широты по астрономическим наблюдениям
Перейти в список рефератов, курсовых, контрольных и дипломов по дисциплине География и экономическая география
referat-best.ru
Высота северного полюса мира (Полярной звезды) над горизонтом численно равна географической широте места наблюдения.
Для г. Стерлитамака географическая широта равна: 
=53°27′, то есть Северный полюс мира, отмеченный на небе Полярной звездой ( 
Малой Медведицы), находится на высоте 53°27′.
Земля обращается вокруг Солнца по орбите, форма которой близка к круговой, с периодом один год. Земному наблюдателю, не замечающему собственного движения, при этом кажется, что Солнце описывает среди звезд на небесной сфере круг с периодом 1 год.
Рис. 1.3. расположение основных элементов небесной сферы относительно земного наблюдателя
Большой круг небесной сферы, по которому происходит видимое годовое движение Солнца, называется эклиптикой (рис. 1.4). Эклиптика проходит через 12 созвездий, называемых зодиакальными. Это … – Овен (Aries – ^), Телец (Taurus – ♉), Близнецы (Gemini – ♊), Рак (Cancer – ♋), Лев (Leo – ♌), Дева (Virgo – ♍), Весы (Libra – ♎), Скорпион (Scorpius – ♏), Стрелец (Sagittarius – ♐), Козерог (Capricornus – g), Водолей (Aquarius – ♒), Рыбы (Pisces – ♓).
Профессиональные астрономы пользуются латинскими названиями созвездий, поэтому в списке зодиакальных созвездий в скобках мы привели латинские аналоги названий, а также указали символы зодиакальных созвездий (так называемые, знаки зодиака).
Рис. 1.4. Основные точки эклиптики
После пересмотра понятия «созвездие» в 1922 г. на Первом съезде Международного астрономического союза, когда под созвездием стали понимать не характерную группу ярких звезд, а определенную площадку на небе, отмеченную строгими границами, получилось, что эклиптика проходит еще через одно созвездие – Змееносец (или Змеедержец), традиционно не относящееся к зодиакальным.
Солнце в астрономии обычно обозначается символом ☉.
Плоскость эклиптики наклонена к плоскости небесного экватора на угол, равный 23°26′, который называется наклонением эклиптики и обозначается 
. Это – угол между плоскостями орбиты Земли и земного экватора.
Точки небесной сферы, удаленные от всех точек эклиптики на 90°, называются полюсами эклиптики (рис. 1.4). Северный полюс эклиптики, обозначаемый 
, находится в северном полушарии небесной сферы, южный 
– в южном полушарии. Примечательно, что недалеко от северного полюса эклиптики расположена чрезвычайно красивая планетарная туманность Кошачий Глаз (NGC 6543), к сожалению, не видимая невооруженным глазом.
Точки пересечения эклиптики и небесного экватора называются точками равноденствий. Их две. Одна из них – точка весеннего равноденствия, обозначаемая символом созвездия Овен ^ и находящаяся ныне в соседнем созвездии Рыбы. В ней Солнце бывает ежегодно 21 марта. Вторая – точка осеннего равноденствия d, которую Солнце проходит 23 сентября. Она обозначается знаком созвездия Весов, а находится в настоящее время в Деве.
Наиболее отдаленные от небесного экватора точки эклиптики называют точками солнцестояний. Их также две. Точку летнего солнцестояния a, находящуюся в Близнецах, Солнце проходит 22 июня, а в точке зимнего солнцестояния g, расположенной в Стрельце, бывает 22 декабря.
Еще в глубокой древности, видимо, задолго до нашей эры, была изобретена механическая модель небесной сферы, называемая также армиллярной сферой (armilla по-латыни – кольцо, браслет). Ее изобретение приписывают древнегреческому геометру Эратосфену (III век до н.э.).
 Рис. 1.5. Старинная армиллярная сфера |
В Древней Греции изготавливались весьма сложные действующие (вращающиеся) модели небесной сферы. Иногда они приводились в движение потоком падающей воды. Есть свидетельства, что великий греческий математик и инженер Архимед (287–212 гг. до н.э.) изготовил механический звездный глобус, внутри которого был подвешен земной, и даже написал книгу «Об устройстве небесного глобуса», увы, не дошедшую до нас.
В V книге труда «Альмагест» великого греческого астронома Клавдия Птолемея (II век н.э.) армиллярная сфера описана как астролабон. Она включает в себя все упомянутые выше основные элементы – круги и оси.
Независимо от европейцев армиллярная сфера была также изобретена в начале II века до н.э. в Древнем Китае знаменитым астрономом Чжан Хэном (Лю Ся Хуном) и представлена им в 104 г. до н.э. на собрании астрономов, посвященному ведению календаря. Изготовленная Чжан Хэном действующая модель небесной сферы вращалась вместе с небом, приводясь в движение водяными часами, что вызывало восхищение современников.
В настоящее время армиллярные сферы как научные приборы не используются. В основном они применяются в качестве наглядных пособий в процессе изучения астрономии. Но в этих моделях по-прежнему представлены все основные элементы небесной сферы.
Опишем главные элементы армиллярных сфер, используемых при выполнении учебных лабораторных работ в кабинете астрономии Института математики и естественных наук СГПА им. Зайнаб Биишевой.
В центре модели небесной сферы расположен небольшой шарик, имитирующий Землю. Через него проходит отвесная линия (тонкая проволочная ось). Она показывает направление на зенит.
Большое массивное металлическое кольцо, изображающее небесный меридиан, жестко укреплено на оси мира, вокруг которой вращается небесная сфера. Конечные точки этой оси лежат на небесном меридиане и представляют соответственно северный и южный полюса мира.
Белый металлический круг имитирует истинный или математический горизонт, который при работе с моделью небесной сферы должен всегда устанавливаться в горизонтальном положении. Ось мира образует с плоскостью истинного горизонта угол, равный географической широте места наблюдения. При установке модели на заданную широту этот угол жестко фиксируется специальным винтом.
Широкое голубое кольцо, плоскость которого перпендикулярна к оси мира, представляет собой небесный экватор. Малые круги голубого цвета, параллельные экватору, – небесные параллели.
Металлические кольца белого цвета, проходящие через полюса мира и жестко скрепленные с небесным экватором, представляют часовые круги.
Широкое кольцо желтого цвета, жестко скрепленное под острым углом с небесным экватором, является эклиптикой. Она разделена на 12 частей, в каждой из которых указан месяц года, когда Солнце находится на этом участке. Точки пересечения эклиптики с небесным экватором отображают точки равноденствий.
Задания:
1. По модели небесной сферы изучить ее основные элементы и изменение их положения относительно наблюдателя в процессе суточного вращения небесной сферы.
2. Указать расположение основных элементов небесной сферы относительно истинного горизонта.
3. Начертить мелом на черном глобусе те элементы небесной сферы, которые могут быть на нем изображены.
4. Отождествить на модели небесной сферы ее основные элементы, изображенные на подвижной карте звездного неба.
5. Начертить изображение основных элементов небесной сферы в проекции на плоскость: а) небесного меридиана; б) математического горизонта; в) небесного экватора; г) первого вертикала.
refac.ru
|
|
..:::Счетчики:::.. |
|
|
|
|
|
|
|
|