Реферат на тему:
Уравне́ния Э́йлера — Лагра́нжа (в физике также уравнения Лагранжа — Эйлера или уравнения Лагранжа) являются основными формулами вариационного исчисления, c помощью которых ищутся стационарные точки и экстремумы функционалов. В частности, эти уравнения широко используются в задачах оптимизации, и, совместно с принципом наименьшего действия, используются для вычисления траекторий в механике. В теоретической физике вообще это (классические) уравнения движения в контексте получения их из написанного явно выражения для действия (лагранжиана).
Использовнание уравнений Эйлера — Лагранжа для нахождения экстремума функционала в некотором смысле аналогично использованию теоремы дифференциального исчисления, утверждающей, что лишь в точке, где первая производная функции обращается в нуль, гладкая функция может иметь экстремум (в случае векторного аргумента приравнивается нулю градиент функции, то есть производная по векторному аргументу). Точнее говоря, это прямое обобщение соответствующей формулы на случай функционалов — функций бесконечномерного аргумента.
Уравнения были получены Леонардом Эйлером и Жозефом-Луи Лагранжем в 1750-х годах.
Пусть задан функционал
с подынтегральной функцией , обладающей непрерывными первыми частными производными и называемой функцией Лагранжа или лагранжианом, где через f' обозначена первая производная f по x. Если этот функционал достигает экстремума на некоторой функции
, то для неё должно выполняться обыкновенное дифференциальное уравнение
которое называется уравнением Эйлера — Лагранжа.
Рассмотрим стандартный пример: найти кратчайший путь между двумя точками плоскости. Ответом, очевидно, является отрезок, соединяющий эти точки. Попробуем получить его с помощью уравнения Эйлера — Лагранжа. Пусть точки, которые надо соединить, имеют координаты и
. Тогда длина пути
, соединяющего эти точки, может быть записана следующим образом:
Уравнение Эйлера — Лагранжа для этого функционала принимает вид:
откуда получаем, что
Таким образом, получаем прямую линию. Учитывая, что ,
, т. е. что она проходит через исходные точки, получаем верный ответ: отрезок, соединяющий точки.
Существует также множество многомерных вариантов уравнений Эйлера — Лагранжа.
только если удовлетворяет условию
В физических приложениях когда является лагранжианом (имеется в виду лагранжиан некоторой физической системы; то есть если J — действие для этой системы), эти уравнения — суть (классические) уравнения движения такой системы. Это утверждение может быть прямо обобщено и на случай бесконечномерного q.
где — независимые координаты,
,
,
доставляет экстремум если только f удовлетворяет уравнению в частных производных
Если n = 2 и L — функционал энергии, то эта задача называется «минимизацией поверхности мыльной плёнки».
В частности, вместо статического уравнения равновесия мыльной пленки, приведенного в качестве примера в предыдущем пункте, имеем в этом случае динамическое уравнение движения такой пленки (если, конечно, нам удалось изначально записать для нее действие, то есть кинетическую и потенциальную энергию).
Уравнение Эйлера — Лагранжа было получено в 1750-х годах Эйлером и Лагранжем при решении задачи об изохроне. Это проблема определения кривой, по которой тяжёлая частица попадает в фиксированную точку за фиксированное время, независимо от начальной точки.
Лагранж решил эту задачу в 1755 году и отослал решение Эйлеру. Развитый впоследствии метод Лагранжа и применение его в механике привело к формулировке лагранжевой механики. Переписка учёных привела к созданию вариационного исчисления (термин придумал Эйлер в 1766 году).
Вывод одномерного уравнения Эйлера — Лагранжа является одним из классических доказательств в математике. Оно основывается на основной лемме вариационного исчисления.
Мы хотим найти такую функцию , которая удовлетворяет граничным условиям
,
и доставляет экстремум функционалу
Предположим, что имеет непрерывные первые производные. Достаточно и более слабых условий, но доказательство для общего случая более сложно.
Если даёт экстремум функционалу и удовлетворяет граничным условиям, то любое слабое возмущение
, которое сохраняет граничные условия, должно увеличивать значение
(если
минимизирует его) или уменьшать
(если
максимизирует).
Пусть — любая дифференцируемая функция, удовлетворяющая условию
. Определим
Поскольку даёт экстремум для
, то
, то есть
Интегрируя по частям второе слагаемое, находим, что
Используя граничные условия на , получим
Отсюда, так как — любая, следует уравнение Эйлера — Лагранжа:
Лагранжиан может также зависеть и от производных f порядка выше, чем первый.
Пусть функционал, экстремум которого нужно найти, задан в виде:
Если наложить граничные условия на f и на её производные до порядка n − 1 включительно, а также предположить, что F имеет непрерывные первые производные, то можно, применяя интегрирование по частям несколько раз, вывести аналог уравнения Эйлера-Лагранжа и для этого случая:
Это уравнение часто называют уравнением Эйлера-Пуассона.
wreferat.baza-referat.ru
 Опубликовать
ОпубликоватьРеферат на тему:
Существует множество математических и физических объектов, названных в честь Леонарда Эйлера:
Категории: Объекты названные в честь людей, Списки Математика.
Текст доступен по лицензии Creative Commons Attribution-ShareAlike.www.wreferat.baza-referat.ru
Реферат на тему:
Уравне́ния Э́йлера — Лагра́нжа (в физике также уравнения Лагранжа — Эйлера или уравнения Лагранжа) являются основными формулами вариационного исчисления, c помощью которых ищутся стационарные точки и экстремумы функционалов. В частности, эти уравнения широко используются в задачах оптимизации, и, совместно с принципом наименьшего действия, используются для вычисления траекторий в механике. В теоретической физике вообще это (классические) уравнения движения в контексте получения их из написанного явно выражения для действия (лагранжиана).
Использовнание уравнений Эйлера — Лагранжа для нахождения экстремума функционала в некотором смысле аналогично использованию теоремы дифференциального исчисления, утверждающей, что лишь в точке, где первая производная функции обращается в нуль, гладкая функция может иметь экстремум (в случае векторного аргумента приравнивается нулю градиент функции, то есть производная по векторному аргументу). Точнее говоря, это прямое обобщение соответствующей формулы на случай функционалов — функций бесконечномерного аргумента.
Уравнения были получены Леонардом Эйлером и Жозефом-Луи Лагранжем в 1750-х годах.
Пусть задан функционал
с подынтегральной функцией , обладающей непрерывными первыми частными производными и называемой функцией Лагранжа или лагранжианом, где через f' обозначена первая производная f по x. Если этот функционал достигает экстремума на некоторой функции
, то для неё должно выполняться обыкновенное дифференциальное уравнение
которое называется уравнением Эйлера — Лагранжа.
Рассмотрим стандартный пример: найти кратчайший путь между двумя точками плоскости. Ответом, очевидно, является отрезок, соединяющий эти точки. Попробуем получить его с помощью уравнения Эйлера — Лагранжа. Пусть точки, которые надо соединить, имеют координаты и
. Тогда длина пути
, соединяющего эти точки, может быть записана следующим образом:
Уравнение Эйлера — Лагранжа для этого функционала принимает вид:
откуда получаем, что
Таким образом, получаем прямую линию. Учитывая, что ,
, т. е. что она проходит через исходные точки, получаем верный ответ: отрезок, соединяющий точки.
Существует также множество многомерных вариантов уравнений Эйлера — Лагранжа.
только если удовлетворяет условию
В физических приложениях когда является лагранжианом (имеется в виду лагранжиан некоторой физической системы; то есть если J — действие для этой системы), эти уравнения — суть (классические) уравнения движения такой системы. Это утверждение может быть прямо обобщено и на случай бесконечномерного q.
где — независимые координаты,
,
,
доставляет экстремум если только f удовлетворяет уравнению в частных производных
Если n = 2 и L — функционал энергии, то эта задача называется «минимизацией поверхности мыльной плёнки».
В частности, вместо статического уравнения равновесия мыльной пленки, приведенного в качестве примера в предыдущем пункте, имеем в этом случае динамическое уравнение движения такой пленки (если, конечно, нам удалось изначально записать для нее действие, то есть кинетическую и потенциальную энергию).
Уравнение Эйлера — Лагранжа было получено в 1750-х годах Эйлером и Лагранжем при решении задачи об изохроне. Это проблема определения кривой, по которой тяжёлая частица попадает в фиксированную точку за фиксированное время, независимо от начальной точки.
Лагранж решил эту задачу в 1755 году и отослал решение Эйлеру. Развитый впоследствии метод Лагранжа и применение его в механике привело к формулировке лагранжевой механики. Переписка учёных привела к созданию вариационного исчисления (термин придумал Эйлер в 1766 году).
Вывод одномерного уравнения Эйлера — Лагранжа является одним из классических доказательств в математике. Оно основывается на основной лемме вариационного исчисления.
Мы хотим найти такую функцию , которая удовлетворяет граничным условиям
,
и доставляет экстремум функционалу
Предположим, что имеет непрерывные первые производные. Достаточно и более слабых условий, но доказательство для общего случая более сложно.
Если даёт экстремум функционалу и удовлетворяет граничным условиям, то любое слабое возмущение
, которое сохраняет граничные условия, должно увеличивать значение
(если
минимизирует его) или уменьшать
(если
максимизирует).
Пусть — любая дифференцируемая функция, удовлетворяющая условию
. Определим
Поскольку даёт экстремум для
, то
, то есть
Интегрируя по частям второе слагаемое, находим, что
Используя граничные условия на , получим
Отсюда, так как — любая, следует уравнение Эйлера — Лагранжа:
Лагранжиан может также зависеть и от производных f порядка выше, чем первый.
Пусть функционал, экстремум которого нужно найти, задан в виде:
Если наложить граничные условия на f и на её производные до порядка n − 1 включительно, а также предположить, что F имеет непрерывные первые производные, то можно, применяя интегрирование по частям несколько раз, вывести аналог уравнения Эйлера-Лагранжа и для этого случая:
Это уравнение часто называют уравнением Эйлера-Пуассона.
www.wreferat.baza-referat.ru
Реферат на тему:
В математике (дифференциальных уравнениях), уравнение Коши — Эйлера (Эйлера — Коши) является частным случаем линейного дифференциального уравнения (см. линейное дифференциальное уравнение), приводимым к линейному дифференциальному уравнению с постоянными коэффициентами, которое имеет простой алгоритм решения.
Общий вид уравнения :
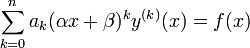 .
. Его частный случай :
 .
. Подстановка вида то есть
приводит уравнение к виду линейного дифференциального уравнения с постоянными коэффициентами.Действительно, заметим, что
,
и
.В соответствии с этим:
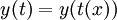
откуда
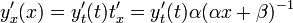
таким образом
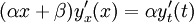
Вычислим очередную производную сложной функции
 ,
, что приводит к
 .
. и далее

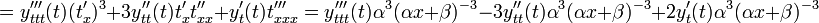
что, аналогично, приводит к
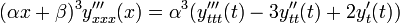
Эта цепь вычислений может быть продолжена до любого порядка n
Дано неоднородное уравнение
Определив подстановку (
), приходим к уравнению
После приведения имеем линейное неоднородное уравнение с постоянными коэффициентами
решение которого имеет вид
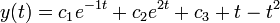
или в терминах
Общий вид уравнения :
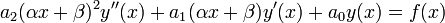 .
. Его частный случай :
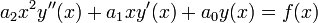 .
. Подстановкой то есть
или, соответственно,
приводится к виду линейного дифференциального уравнения второго порядка с постоянными коэффициентами.
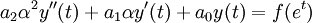 .
. или, соответственно,
 .
. Дано неоднородное уравнение
Определив подстановку (
), приходим к уравнению
После приведения имеем линейное неоднородное уравнение с постоянными коэффициентами
решение которого имеет вид
или в терминах
Рассмотрим однородное уравнения второго порядка вида:
 .
. Его решениями являются функции вида:
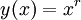 ,
,
где r — решения характеристического уравнения
 ,
, которое совпадает с характеристическим уравнением однородного уравнения с постоянными коэффициентами, полученного из исходного уравнения путём описанной выше замены переменной.
Дано однородное уравнение
Характеристическое уравнение которого имеет вид
 ,
, с решениями ,
.Тогда общее решение однородного уравнения
wreferat.baza-referat.ru
Линейные уравнения с переменными коэффициентами вида
 (6.8)
(6.8)
 (6.9)
(6.9)
или
 (6.10)
(6.10)
 (6.11)
(6.11)
называются уравнением Эйлера. Здесь  — постоянные коэффициенты.
— постоянные коэффициенты.
С помощью подстановки
 (6.12)
(6.12)
для уравнения (6.8), (6.9) и
 (6.13)
(6.13)
для уравнения (6.10), (6.11) оба эти уравнения сводятся к уравнению с постоянными коэффициентами. Для этого необходимо вычислить производные, например, от (6.12) по новой переменной t:

 , (6.14)
, (6.14)
…
……………………………………………………………
 .
.
Подставив значения (6.14) в уравнение (6.8), получим новое уравнение с постоянными коэффициентами
(6.14) в уравнение (6.8), получим новое уравнение с постоянными коэффициентами 
 , (6.15)
, (6.15)
которое называется преобразованным уравнением, по отношению к уравнению (6.8). Интегрируя это уравнение, находится решение  и далее после возвращения к старой переменной в соответствии с формулой (6.12) —
и далее после возвращения к старой переменной в соответствии с формулой (6.12) —  , найдем решение уравнения (6.8). Решения уравнений (6.9), (6.10), (6.11) находятся аналогичным способом.
, найдем решение уравнения (6.8). Решения уравнений (6.9), (6.10), (6.11) находятся аналогичным способом.
Пример 6.2. Найти решение уравнения:  .
.
▲ Полагая  или
или  , найдем
, найдем  .
.
Вычислим производные по новой переменной t, обозначив точками дифференцирование по t:

 .
.
Подставив  в исходное уравнение, получим
в исходное уравнение, получим
 .
.
Следовательно, мы получили однородное линейное уравнение. Его характеристическое уравнение  имеет корни
имеет корни  . Поскольку корни действительные и кратные, с кратностью равной двум, то общее решение будет иметь вид:
. Поскольку корни действительные и кратные, с кратностью равной двум, то общее решение будет иметь вид:
 .
.
Перейдя к переменной х, окончательно получим общее решение исходного уравнения
 .▲
.▲
Пример 6.3. Найти решение уравнения:
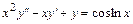 .
.
▲ Полагая  или
или  , найдем
, найдем  .
.
Вычислим производные по новой переменной t, обозначив точками дифференцирование по t:
 .
.
Подставив  в исходное уравнение, получим
в исходное уравнение, получим
 . (П6.3.1)
. (П6.3.1)
Это неоднородное линейное уравнение с постоянными коэффициентами и общее решение соответствующего ему однородного уравнения  имеет вид
имеет вид
 ,
,
Поскольку характеристическое уравнение  имеет двукратный корень равный единице:
имеет двукратный корень равный единице:  .
.
Частное решение уравнения (П6.3.1)можно получить методом неопределенных коэффициентов.
Поскольку параметры правой части неоднородного уравнения (П6.3.1) равны, соответственно, a =0, b = 1, q = 0, l = 0 и число  не совпадает ни с одним корнем характеристического уравнения, поэтому s=0, и m = max(q,l)= 0. Исходя из этого, можно выписать вид искомого частного решения:
не совпадает ни с одним корнем характеристического уравнения, поэтому s=0, и m = max(q,l)= 0. Исходя из этого, можно выписать вид искомого частного решения:

Вычислим производные от 


и подставив их в уравнение (П6.3.1), получим
 .
.
Приравняем коэффициенты при одинаковых функциях в правой и левой частях этого уравнения

Следовательно, частное решение уравнения (П6.3.1) имеет вид
 ,
,
а общее решение уравнения (П6.3.1) будет выглядеть так:
 .
.
Таким образом, общее решение исходного уравнения имеет вид:
 .▲
.▲
Частные решения однородного уравнения Эйлера (6.8), также можно получить, если использовать подстановку вида:
 (6.16)
(6.16)
Вычислив производные
 ,
,
и подставив их в уравнение (6.8) и сокращая на  , получим
, получим
 (6.17)
(6.17)
Это уравнение п-ой степени относительно k имеет п корней:  ; если все корни различны, то мы получаем п линейно независимых частных решений
; если все корни различны, то мы получаем п линейно независимых частных решений  , следовательно, общее решение будет иметь вид:
, следовательно, общее решение будет иметь вид:
 . (6.18)
. (6.18)
Пример 6.4. Найти решение уравнения:
 .
.
▲ Ищем решение в виде  , тогда уравнение (6.17) принимает вид:
, тогда уравнение (6.17) принимает вид:
 ,
,
откуда  . Мы видим, что корни действительные и различные, поэтому общее решение при х > 0 имеет вид
. Мы видим, что корни действительные и различные, поэтому общее решение при х > 0 имеет вид
 .▲
.▲
Кроме того, уравнение (6.17) будет характеристическим уравнением для преобразованного уравнения (6.15)
 ,
,
так как  . Следовательно, кратному корню
. Следовательно, кратному корню 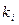 кратности a уравнения (6.17) будут соответствовать частные решения преобразованного уравнения
кратности a уравнения (6.17) будут соответствовать частные решения преобразованного уравнения

а общее решение преобразованного уравнения будет иметь вид:
 .
.
С учетом того, что  , общее решение уравнения Эйлера принимает вид:
, общее решение уравнения Эйлера принимает вид:
 .
.
Пример 6.5. Найти решение уравнения:  .
.
▲ Ищем решение в виде  , тогда уравнение (6.17) принимает вид:
, тогда уравнение (6.17) принимает вид:
 ,
,
откуда 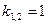 Мы видим, что корни кратные с кратностью равной 2, поэтому общее решение при х > 0 имеет вид:
Мы видим, что корни кратные с кратностью равной 2, поэтому общее решение при х > 0 имеет вид:  .▲
.▲
Комплексным сопряженным корням  кратности a уравнения (6.17) будут соответствовать частные решения
кратности a уравнения (6.17) будут соответствовать частные решения
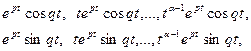
преобразованного уравнения или с учетом того, что  частные решения
частные решения
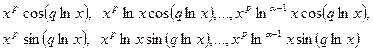
исходного уравнения Эйлера.
Пример 6.6. Найти решение уравнения:  .
.
▲ Ищем решение в виде  , тогда уравнение (6.17) принимает вид:
, тогда уравнение (6.17) принимает вид:
 ,
,
откуда 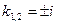 , Мы видим, что корни комплексные, поэтому общее решение при х > 0 имеет вид
, Мы видим, что корни комплексные, поэтому общее решение при х > 0 имеет вид
 .▲
.▲
Пример 6.7. Найти решение уравнения:
 .
.
▲ Это уравнение Эйлера вида (6.10), поэтому его решение ищем в виде  , тогда уравнение (6.17) принимает вид:
, тогда уравнение (6.17) принимает вид:
 ,
,
откуда  , Мы видим, что корни действительные и различные, причем среди них имеется двукратный корень-
, Мы видим, что корни действительные и различные, причем среди них имеется двукратный корень- . Поэтому частными решениями будут
. Поэтому частными решениями будут
 ,
,
а общее решение имеет вид
 .▲
.▲
refac.ru
Mathcad: решение дифференциальных уравнений и их систем
Для сравнения решений построим график Вычислим погрешности: Метод Рунге-Кутты Сравним решение, полученное методом Рунге-Кутты 4 порядка...
Mathcad: решение дифференциальных уравнений и их систем
Построим графики решений операторным методом и методом Эйлера Вычислим погрешности Метод Рунге-Кутты Построим графики решений операторным методом и методом...
Визуализация численных методов
Данный метод, как сказано выше, является одношаговым. Табулирование функции происходит поочередно в каждой точке. Для расчёта значения функции в очередном узле необходимо использовать значение функции в одном предыдущем узле...
Знакопеременные ряды
Приведём пример условно сходящегося ряда и его перестановку, которая уменьшает сумму ряда в два раза. Установим следующую формулу: Теорема (Эйлер): Выполняется равенство:...
Математическое моделирование и численные методы в решении технических задач
Теоретические сведения. Решить дифференциальное уравнение у/=f(x,y) численным методом - это значит для заданной последовательности аргументов х0, х1…, хn и числа у0, не определяя функцию у=F(x), найти такие значения у1, у2,…, уn, что уi=F(xi)(i=1,2,…, n) и F(x0)=y0...
Метод Рунге-Кутты четвертого порядка с автоматическим выбором шага интегрирования решения задачи Коши
Метод Эйлера для решения начальной задачи (2.1.1) был описан Эйлером в 1768 году. Этот метод весьма прост. Его глобальная погрешность имеет вид , где - постоянная, зависящая от задачи, и - максимальная длина шага. Если желательно, скажем...
Основы тригонометрических вычислений
Формула Эйлера утверждает, что для любого действительного числа выполнено следующее равенство: где -- основание натурального логарифма, -- мнимая единица. Формула Эйлера предоставляет связь между математическим анализом и тригонометрией...
Поведение фазовых траекторий динамических систем
Для интегрирования однородных линейных систем с постоянными коэффициентами применяется метод Эйлера...
Понятие о численных методах решения обыкновенных дифференциальных уравнений
Рассмотрим дифференциальное уравнение первого порядка, разрешенное относительно производной, то есть уравнение вида (1) относительно неизвестной функции y=y(x)...
Решение дифференциальных уравнений по методу Эйлера
Решить дифференциальное уравнение у/=f(x,y) численным методом - это значит для заданной последовательности аргументов х0, х1…, хn и числа у0, не определяя функцию у=F(x), найти такие значения у1, у2,…, уn, что уi=F(xi)(i=1,2,…, n) и F(x0)=y0. Таким образом...
Решение дифференциальных уравнений по методу Эйлера
В исправленном методе Эйлера мы находим средний тангенс наклона касательнй для двух точек: xm, ym и xm+h, ym+hym. Последняя точка есть та самая, которая в простом методе обозначалась xm+1, ym+1. Геометрический процесс нахождения точки xm+1...
Решение дифференциальных уравнений по методу Эйлера
Этот метод более точен. Рассмотрим дифференциальное уравнение (1) с начальным условием y(x0)=y0. Разобьем наш участок интегрирования на n равных частей. На малом участке [x0,x0+h] интегральную кривую заменим прямой линией. Получаем точку Мк(хк,ук). (рис...
Суммирование расходящихся рядов
Пусть дан ряд . Формула, выражающая “преобразование Эйлера” выглядит следующим образом . (20) При этом, как было доказано, из сходимости ряда в левой части вытекает сходимость ряда в правой части и равенство между их суммами...
Численные методы решения обыкновенных дифференциальных уравнений и систем
По условию выполнено соотношение: Пусть начальное значение искомой функции y(x0) =y0. Можно приближенно вычислить следующие значения...
Эйлеровы графы
№14 Можно ли нарисовать граф, изображённый а) на рисунке 2.10, а; б) на рисунке 2.10, б, не отрывая карандаш от бумаги и проводя каждое ребро ровно один раз? Ответ. а) Можно. б) Нельзя. Рисуя граф в каждую вершину, за исключением начальной и конечной...
math.bobrodobro.ru