WinNavigator

Frigate

Norton Commander

WinNC

Dos Navigator

Servant Salamander

Turbo Browser

Winamp, Skins, Plugins

Необходимые Утилиты

Текстовые редакторы

Юмор

File managers and best utilites

Курсовая работа: Теория тригонометрических функций. Тригонометрические функции реферат

Реферат - Тригонометрические функции 2

Тригонометрия – математическая дисциплина, изучающая зависимость между сторонами и углами треугольника, является разделом геометрии, тригонометрические функции являются объектом изучения математического анализа, а тригонометрические уравнения изучаются методами алгебры.

Тригонометрические функции возникли в Древней Греции в связи с исследованиями в астрономии и геометрии. Отношения сторон в прямоугольном треугольнике, которые по существу и являются тригонометрическими функциями, встречаются уже в Ш в. до н. э. в работах Евклида, Архимеда, Аполлония Пергского и др. Тригонометрия от греческих: trigonom – “треугольник”, metreo – “измеряю”, изучает зависимость между сторонами и углами треугольника.

Тригонометрия возникла из пратических нужд человека. С ее помощью можно определить расстояния до недоступных предметов. Она существенно упрощает процесс геодезической съемки местности, нужный для составления карт.

Зачатки тригонометрических познаний родились в древности. Жрецы постоянно наблюдали за небом, за перемещением звезд. На раннем этапе тригонометрия развивалась в тесной связи с астрономией и являлась ее вспомогательным разделом.

Исторически теоремы синусов сферической геометрии предшествовали теоремам плоской геометрии. Потребность людей в знаниях по астрономии, необходимых для исчисления времени, возникла прежде других потребностей человека, связанных с измерением углов. Исходя из геоцентрической гипетезы Вселенной, древнегреческие астрономы рассматривали Землю как шар, находящийся в центре небесной сферы, которая рвномерно вращается вокруг своей оси. При изучении закономерностей движения светил возникли многочисленные математические задачи, связанные со свойствами сферы и фигур, которые образуют на ней большие окружности.

Автором первого капитального сочинения о “сферике” – так называли сферическую геометрию древние греки – был, по-видимому, математик и астроном Евдокс Книдский (ок. 408-355 г.г. до н.э.). Но самым значительным произведением была “Сферика” Менелая Александрийского, греческого ученого, жившего в 1 в., который обощил результаты своих предшественников и получил большое количество новых результатов. Долгое время “Сферика” служила учебником для астрономов. Сферическая геометрия и сейчас нужна штурманам кораблей, которые по звездам определяют свои координаты, при геодезических съемках больших поверхностей Земли, при которых необходимо учитывать ее шарообразность.

Древнегреческие ученые разработали “тригонометрию хорд”, изложенную, выдающимся астрономом Птолемеем (П в.) в его работе “Альмагест”. Птолемей словесно, т.к. не было математической символики, вывел соотношения между хордами в круге, которые равносильны современным формулам для синуса половинного и двойного угла, суммы и разности двух углов.

Важный шаг сделан индийскими учеными, которые заменили хорды синусами. Это нововведение перешло в УШ в. в арабоязычную математику стран Ближнего и Среднего Востока. В 1Х – ХШ в.в. и “Сферика” Менелая, переведенная на арабский язык, внимательно изучалась математиками Ближнего и Среднего Востока. В ХП в. в переводе с арабского “Сферика” стала известна в Европе.

Математики Ближнего и Среднего Востока превратили тригонометрия из раздела астрономии в самостоятельную математическую дисциплину.В Х-Х1 в.в. они впервые доказали теорему синусов, открытие которой сыграло важнейшую роль в тригонометрии. Помимо синуса, были выведены другие функции и составлены таблицы для них.

Общепринятые понятия тригонометрии, а также обозначения и определения тригонометрических функций сформировались в процессе долгого исторического развития. Если, например, при введении основных тригонометрических понятий представляется естественным принимать радиус тригонометрического круга ( рис.1), равным единице, то эта, казалось бы, простая идея была усвоена только в Х-Х1 веке.

Рис. 1.

Лишь благодаря введению новых понятий, а также в результате разработки и усовершенствования математической символики, тригонометрия приобрела современный вид, наиболее удобный для решения вычислительных задач.

Современную форму теории тригонометрических функций и вообще тригонометрии придал в ХУШ в. в своих трудах Леонард Эйлер (1707 – 1783г.г.). Ему принадлежат определения тригонометрических функций и принятая в наши дни символика. Эйлер – крупнейший математик, в 1727 г. приехал в Россию по приглашению Петербургской академии наук, где получил большие возможности для работы и издания своих трудов, в списке которых более 800 названий по разным проблемам математики.

ЛИТЕРАТУРА.

1. Энциклопедический словарь юного математика.

2. Большая детская энциклопедия. Математика.

www.ronl.ru

Читать реферат по математике: "Тригонометрические функции"

(Назад) скачать (Cкачать работу)

Функция "чтения" служит для ознакомления с работой. Разметка, таблицы и картинки документа могут отображаться неверно или не в полном объёме!

Тригонометрические функции

Тригонометрия – слово греческое и в буквальном переводе означает измерение треугольников ( - треугольник, а - измеряю).

В данном случае измерение треугольников следует понимать как решение треугольников, т.е. определение сторон, углов и других элементов треугольника, если даны некоторые из них. Большое количество практических задач, а также задач планиметрии, стереометрии, астрономии и других приводятся к задаче решения треугольников.

Возникновение тригонометрии связано с землемерением, астрономией и строительным делом.

Впервые способы решения треугольников, основанные на изависимостях между сторонами и углами треугольника, были найдены древнегреческими астрономами Гиппархом (2 в. до н .э.) и Клавдием Птолемеем (2 в. н. э.). Пожднее зависимости между отношениями сторон треугольника и его углами начали называть тригонометрическими функциями.

Значительный вклад в развитие тригонометрии внесли арабские ученые аль-Батани (850-929) и Абу-ль-Вефа Мухамед-бен Мухамед (940-998), который составил таблицы синусов и тангенсов через 10’ с точностью до 1/604. Теорему синусов уже знали индийский ученый Бхаскара (р. 1114, год смерти неизвестен) и азербайджанский астроном и математик Насиреддин Туси Мухамед (1201-1274). Кроме того, Насиреддин Туси в своей работе “Трактат о полном четырехстороннике” изложил плоскую и сферическую тригонометрию как самостоятельную дисциплину.

Теорему тангенсов доказал Региомонтан (латинизированное имя немецкого астронома и математика Иоганна Мюллера (1436-1476)). Региомонтан составил также плдробные тригонометрические таблицы; благодаря его трудам плоская и сферическая тригонометрия стала самостоятельной дисциплиной и в Европе.

Дальнейшее развитие тригонометрия получила в трудах выдающихся астрономов Николая Коперника (1473-1543) – творца гелиоцентрической системы мира, Тихо Браге (1546-1601) и Иогана Кеплера (1571-1630), а также в работах математика Франсуа Виета (1540-1603), который полностью решил задачу об определениях всех элементов плоского или сферического треугольника по трем данным.

Долгое время тригонометрия носила чисто геометрический характер. Такою она была еще в средние века, хотя иногда в ней использовались и аналитические методы, особенно после появления логарифмов. Постепенно тригонометрия органически вошла в математический анализ, механику, физику и технические дисциплины.

Начиная с XVII в., тригонометрические функции начали применять к решению уравнений, задач механики, оптики, электричества, радиотехники, для описания колебательных процессов, распространения волн, движения различных механизмов, для изучения переменного электрического тока и т. д. Поэтому тригонометрические функции всесторонне и глубоко исследовались и приобрели важное значение для всей математики.

Аналитическая теория тригонометрических функций в основном была создана выдающимся математиком XVIII в. Леонардом Эйлером (1707-1783) членом Петербургской Академии наук.

Таким образом, тригонометрия, возникшая как наука о решении треугольников, со временем развилась и в науку о тригонометрических функциях.

Позднее часть тригонометрии, которая изучает свойства тригонометрических функций и зависимости между ними, начали называть гониометрией (в переводе – наука об измерении углов, от греч. - угол, - измеряю). Термин гониометрия в последнее время практически не употребляется.

Изучение свойств тригонометрических функций и зависимостей между ними отнесено к школьному курсу алгебры, а решение треугольников – к курсу геометрии.

Тригонометрические функции острого угла

В прямоугольном треугольнике, имеющем данный угол , отношения сторон не зависят от размеров треугольника. Рассмотрим два прямоугольных треугольника АВС и А1В1С1 (рис.1), имеющих равные углы А=А1 =. Из подобия этих треугольников имеем:

Если величину угла измерить, то написанные равенства остаются справедливыми, а измениться

лишь числовое значение отношений и т.д. Поэтому отношения

В1

можно рассматривать как функции угла .

Вc1 c а190 90 а Сb1 b С1 А1 А

Рис.1.

Синусом острого угла называется отношение противоположного этому углукатета к гипотенузе. Обозначают это так:

sin= Значения тригонометрических функций (отношений отрезков) являются отвлеченными числами.

Приближенные значения тригонометрических функций острого угла можно найти непосредственно согласно их определениям. Построив прямоугольный треугольник с острым углом и измерив его стороны, согласно определениям мы можемвычислить значение, например, sin.

Пользуясь тем, что значения тригонометрических функций не зависят от размеров треугольника, для вычисления значений sin углов =30; 45; 60 рассмотрим прямоугольный треугольник с углом =30; и катетом ВС=a=1, тогда гипотенуза этого треугольника с=2, а второй катет b=3; рассмотрим также треугольник с углом =45 и катетом a=1, тогда для этого треугольника c=2 и b=1.

Полученные результаты запишем в таблицу.

Рис.2.

Приближенные значения тригонометрических функций для углов от 0 до 90 можно получить построив четверть круга, радиус которогопримем за 1, и его дугу разделимна 45 равных частей. Тогда градусная мера каждой части будет равна 2.

90 N

B 520,79 а А b С 0,620 M Рис.3.

Радиусы АМ и АN разделим на 100 равных частей. Построим прямоугольный треугольник с вершиной в центре круга и катетом совпадающим с радиусом АМ и гипотенузой АВ=1. Если угол ВАС=, то по определению тригонометрических функций мы имеем:sin=а Для угла 52 на шкале радиуса АN находим, что а=0,79, а на шкале радиуса АМ находим, что b=0,62., то есть sin52=0,79.

Построив прямоугольные треугольники для углов =2, 4, 6, 8,…, 88, согласно рис.3., найдем значения (при аккуратных измерениях и вычислениях) с точностью до 0,01. Для углов 0 и 90 прямоугольных треугольников не существует. Однако, если гипотенуза АВ будет стремиться по положению к радиусу АМ, то угол 0, а катеты а0 и b1. В таком случае для полноты значений тригонометрических функций принимают, что

sin0=а=0; cos0=b=1.

Что касается значений tg и ctg, то при 0 отношение 0, т.е., а отношение при 0 неограниченно возрастает. Этот результат записывают как , где символ указывает, что величина неограниченно возрастает и не может быть выражена никаким числом, так как знак не является каким-либо числом. Таким образом, принимают, что tg0=0, а ctg0 не существует, что чаще записывают как ctg0=.

Рассуждая аналогично при 90 приходим к целесообразности принять что

sin90=1; cos90=0, tg90 не существует (tg90) и ctg90=0. Приведем таблицу значений синусов для углов от 0 до 90 с шагом 2, которую можно получить указанным выше способом.

градусы	0	2	4	6	8	10	12	14	16	18	20	22
sin	0,00	0,03	0,07	0,10	0,14	0,17	0,21	0,24	0,28	0,31	0,34	0,37
градусы	24	26	28	30	32	34	36	38	40	42	44	46
sin	0,41	0,44	0,47	0,50	0,53	0,56	0,59	0,62	0,64	0,67	0,69	0,72
градусы	48	50	52	54	56	68	60	62	64	66	68	70
sin	0,74	0,77	0,79	0,81	0,83	0,93	0,87	0,88	0,90	0,91	0,93	0,94
градусы	72	74	76

referat.co

Доклад - Тригонометрические функции 2

Рис. 1.

ЛИТЕРАТУРА.

1. Энциклопедический словарь юного математика.

2. Большая детская энциклопедия. Математика.

www.ronl.ru

Реферат Обратные тригонометрические функции

скачать

Реферат на тему:

План:

1 Основное соотношение
2 Функция arcsin
- 2.1 Свойства функции arcsin
- 2.2 Получение функции arcsin
3 Функция arccos
- 3.1 Свойства функции arccos
- 3.2 Получение функции arccos
4 Функция arctg
- 4.1 Свойства функции arctg
- 4.2 Получение функции arctg
5 Функция arcctg
- 5.1 Свойства функции arcctg
- 5.2 Получение функции arcctg
6 Функция arcsec
7 Функция arccosec
8 Производные от обратных тригонометрических функций
9 Интегралы от обратных тригонометрических функций
- 9.1 Неопределённые интегралы
10 Разложение в бесконечные ряды
11 Использование в геометрии

Введение

Обра́тные тригонометри́ческие фу́нкции (круговые функции, аркфункции) — математические функции, являющиеся обратными к тригонометрическим функциям. К обратным тригонометрическим функциям обычно относят шесть функций:

аркси́нус (обозначение: arcsin)
аркко́синус (обозначение: arccos)
аркта́нгенс (обозначение: arctg; в иностранной литературе arctan)
арккота́нгенс (обозначение: arcctg; в иностранной литературе arccot или arccotan)
арксе́канс (обозначение: arcsec)
арккосе́канс (обозначение: arccosec; в иностранной литературе arccsc)

Название обратной тригонометрической функции образуется от названия соответствующей ей тригонометрической функции добавлением приставки «арк-» (от лат. arc — дуга). Это связано с тем, что геометрически значение обратной тригонометрической функции можно связать с длиной дуги единичной окружности (или углом, стягивающим эту дугу), соответствующей тому или иному отрезку. Изредка в иностранной литературе пользуются обозначениями типа sin−1 для арксинуса и т. п.; это считается не совсем корректным, так как возможна путаница с возведением функции в степень −1.

1. Основное соотношение

$\arcsin x + \arccos x = \frac{\pi}{2}$ $\operatorname {arctg}\, x + \operatorname {arcctg}\, x = \frac{\pi}{2}$

2. Функция arcsin

График функции y = arcsinx.

Арксинусом числа m называется такое значение угла x, для которого $\sin x = m,\, -\frac{\pi}{2} \leqslant x \leqslant \frac{\pi}{2},\, |m|\leqslant 1.$

Функция y = sinx непрерывна и ограничена на всей своей числовой прямой. Функция y = arcsinx является строго возрастающей.

2.1. Свойства функции arcsin

2.2. Получение функции arcsin

Дана функция y = sinx. На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие y = arcsinx функцией не является. Поэтому мы рассмотрим отрезок, на котором она строго возрастает и принимает все значения области значений — $\left [ -\frac{\pi}{2}; \frac{\pi}{2} \right ]$ . Так как для функции y = sinx на интервале $\left [ -\frac{\pi}{2}; \frac{\pi}{2} \right ]$ каждому значению аргумента соответствует единственное значение функции, то на этом отрезке существует обратная функция y = arcsinx, график которой симметричен графику функции y = sinx на отрезке $\left [ -\frac{\pi}{2}; \frac{\pi}{2} \right ]$ относительно прямой y = x.

3. Функция arccos

График функции y = arccosx.

Арккосинусом числа m называется такое значение угла x, для которого $\cos x = m,\qquad 0 \leqslant x \leqslant \pi, |m|\leqslant 1.$

Функция y = cosx непрерывна и на всей своей числовой прямой. Функция y = arccosx является строго убывающей.

cos(arccosx) = x при $-1 \leqslant x \leqslant 1,$
arccos(cosy) = y при $0 \leqslant y \leqslant \pi.$
D(arccosx) = [ − 1;1], (область определения),
E(arccosx) = [0;π]. (область значений).

3.1. Свойства функции arccos

3.2. Получение функции arccos

Дана функция y = cosx. На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие y = arccosx функцией не является. Поэтому мы рассмотрим отрезок, на котором она строго убывает и принимает все свои значения — [0;π]. На этом отрезке y = cosx строго монотонно убывает и принимает все свои значения только один раз, а значит, на отрезке [0;π] существует обратная функция y = arccosx, график которой симметричен графику y = cosx на отрезке [0;π] относительно прямой y = x.

4. Функция arctg

График функции $y=\operatorname{arctg}\, x$ .

Арктангенсом числа m называется такое значение угла α, для которого $\operatorname{tg}\, \alpha = m , \qquad -\frac{\pi}{2} < \alpha < \frac{\pi}{2}.$

Функция $y=\operatorname{arctg} x$ непрерывна и ограничена на всей своей числовой прямой. Функция $y=\operatorname{arctg} x$ является строго возрастающей.

4.1. Свойства функции arctg

$\operatorname{arctg} x = \arcsin \frac{x}{\sqrt{1+x^2}}$

$\operatorname{arctg} x = 2 \operatorname{arccos} \frac{\sqrt{1+x^2}-1}{x}$

4.2. Получение функции arctg

Дана функция $y=\operatorname{tg}\, x.$ На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие $y=\operatorname{arctg}\, x$ функцией не является. Поэтому рассмотрим отрезок, на котором она строго возрастает и принимает все свои значения только один раз — $\left(-\frac{\pi}{2}; \frac{\pi}{2} \right).$ На этом отрезке $y=\operatorname{tg}\, x$ строго монотонно возрастает и принимает все свои значения только один раз, следовательно, на интервале $\left(-\frac{\pi}{2}; \frac{\pi}{2} \right)$ существует обратная $y=\operatorname{arctg}\, x$ , график которой симметричен графику $y=\operatorname{tg}\,x$ на отрезке $\left(-\frac{\pi}{2}; \frac{\pi}{2} \right)$ относительно прямой y = x.

5. Функция arcctg

График функции y=arcctg x

Арккотангенсом числа m называется такое значение угла x, для которого $\operatorname{ctg}\,x = m,\qquad 0 < x < \pi.$

Функция $y=\operatorname{arcctg}\, x$ непрерывна и ограничена на всей своей числовой прямой. Функция $y=\operatorname{arcctg}\, x$ является строго убывающей.

5.1. Свойства функции arcctg

$\operatorname{arcctg}\, (-x) = \pi - \operatorname{arcctg}\, x$ (график функции центрально-симметричен относительно точки $\left(0; \frac{\pi}{2}\right).$
$\operatorname{arcctg}\, x > 0$ при любых x.
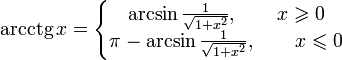
$\operatorname{arcctg}\, x = \left\{\begin{matrix} \arcsin \frac{1}{\sqrt{1+x^2}},\qquad x \geqslant 0 \\\pi-\arcsin \frac{1}{\sqrt{1+x^2}},\qquad x \leqslant 0\end{matrix}\right.$

5.2. Получение функции arcctg

Дана функция $y=\operatorname{ctg}\, x$ . На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие $y=\operatorname{arcctg}\, x$ функцией не является. Поэтому рассмотрим отрезок, на котором она строго убывает и принимает все свои значения только один раз — (0;π). На этом отрезке $y=\operatorname{ctg}\, x$ строго убывает и принимает все свои значения только один раз, следовательно, на интервале (0;π) существует обратная функция $y=\operatorname{arcctg}\, x$ , график которой симметричен графику $y=\operatorname{ctg}\, x$ на отрезке (0;π) относительно прямой y = x. График симметричен к арктангенсу

6. Функция arcsec

$\mathop{\operatorname{arcsec}}\, (x)\, = \operatorname{arccos} \left( \frac{1}{x}\right)\,$

7. Функция arccosec

$\mathop{\operatorname{arccosec}}\, (x)\, = \operatorname{arcsin} \left( \frac{1}{x}\right)\,$

8. Производные от обратных тригонометрических функций

$(\arcsin x)' = \frac{1}{\sqrt{1-x^2}}.$ $(\arccos x)' = \frac{-1}{\sqrt{1-x^2}}.$ $(\operatorname{arctg}\, x)' = \frac{1}{\ 1+x^2}.$ $(\operatorname{arcctg}\, x)' = -\frac{1}{\ 1+x^2}.$

9. Интегралы от обратных тригонометрических функций

9.1. Неопределённые интегралы

Для действительных и комплексных x:

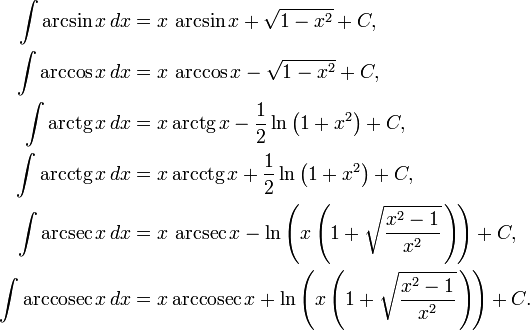
$\begin{align} \int \arcsin x\,dx &{}= x\,\arcsin x + \sqrt{1-x^2} + C,\\ \int \arccos x\,dx &{}= x\,\arccos x - \sqrt{1-x^2} + C,\\ \int \operatorname{arctg}\,x\,dx &{}= x\,\operatorname{arctg}\,x - \frac{1}{2}\ln\left(1+x^2\right) + C,\\ \int \operatorname{arcctg}\, x\,dx &{}= x\,\operatorname{arcctg}\, x + \frac{1}{2}\ln\left(1+x^2\right) + C,\\ \int \arcsec x\,dx &{}= x\,\arcsec x - \ln\left(x\left(1+\sqrt{{x^2-1}\over x^2}\,\right)\!\right) + C,\\ \int \operatorname{arccosec}\, x\,dx &{}= x\,\operatorname{arccosec}\, x + \ln\left(x\left(1+\sqrt{{x^2-1}\over x^2}\,\right)\!\right) + C. \end{align}$

Для действительных x ≥ 1:

$\begin{align} \int \arcsec x\,dx &{}= x\,\arcsec x - \ln\left(x+\sqrt{x^2-1}\right) + C,\\ \int \operatorname{arccosec}\, x\,dx &{}= x\,\operatorname{arccosec}\, x + \ln\left(x+\sqrt{x^2-1}\right) + C. \end{align}$ См. также Список интегралов от обратных тригонометрических функций

10. Разложение в бесконечные ряды

Для случая комплексного аргумента нижеприведенные ряды обычно принимаются как определение соответствующих функций.

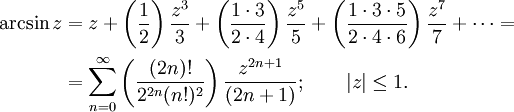
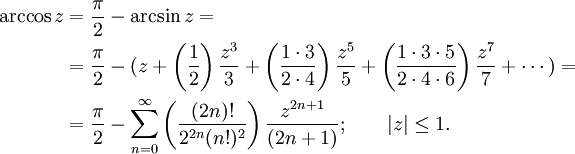
$\begin{align} \arcsin z & {}= z + \left( \frac {1} {2} \right) \frac {z^3} {3} + \left( \frac {1 \cdot 3} {2 \cdot 4} \right) \frac {z^5} {5} + \left( \frac{1 \cdot 3 \cdot 5} {2 \cdot 4 \cdot 6 } \right) \frac{z^7} {7} + \cdots =\\ & {}= \sum_{n=0}^\infty \left( \frac {(2n)!} {2^{2n}(n!)^2} \right) \frac {z^{2n+1}} {(2n+1)} ; \qquad | z | \le 1. \end{align}$ $\begin{align} \arccos z & {}= \frac {\pi} {2} - \arcsin z =\\ & {}= \frac {\pi} {2} - (z + \left( \frac {1} {2} \right) \frac {z^3} {3} + \left( \frac {1 \cdot 3} {2 \cdot 4} \right) \frac {z^5} {5} + \left( \frac{1 \cdot 3 \cdot 5} {2 \cdot 4 \cdot 6 } \right) \frac{z^7} {7} + \cdots ) =\\ & {}= \frac {\pi} {2} - \sum_{n=0}^\infty \left( \frac {(2n)!} {2^{2n}(n!)^2} \right) \frac {z^{2n+1}} {(2n+1)} ; \qquad | z | \le 1. 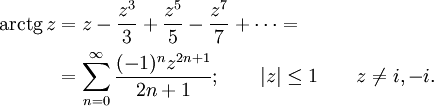\end{align}$ $\begin{align} \operatorname{arctg}\,z & {}= z - \frac {z^3} {3} +\frac {z^5} {5} -\frac {z^7} {7} +\cdots =\\ & {}= \sum_{n=0}^\infty \frac {(-1)^n z^{2n+1}} {2n+1} ; \qquad | z | \le 1 \qquad z \neq i,-i. 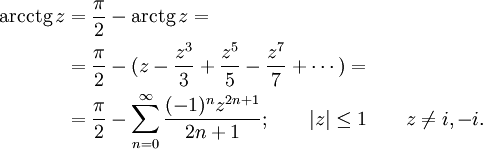\end{align}$ $\begin{align} \operatorname{arcctg}\,z & {}= \frac {\pi} {2} - \operatorname{arctg}\,z =\\ & {}= \frac {\pi} {2} - ( z - \frac {z^3} {3} +\frac {z^5} {5} -\frac {z^7} {7} +\cdots ) =\\ & {}= \frac {\pi} {2} - \sum_{n=0}^\infty \frac {(-1)^n z^{2n+1}} {2n+1} ; \qquad | z | \le 1 \qquad z \neq i,-i. 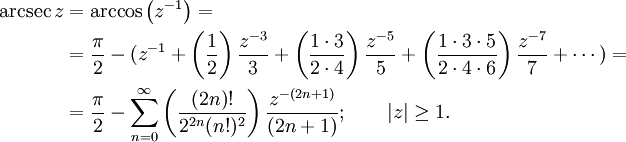\end{align}$ $\begin{align} \arcsec z & {}= \arccos\left(z^{-1}\right) =\\ & {}= \frac {\pi} {2} - (z^{-1} + \left( \frac {1} {2} \right) \frac {z^{-3}} {3} + \left( \frac {1 \cdot 3} {2 \cdot 4} \right) \frac {z^{-5}} {5} + \left( \frac{1 \cdot 3 \cdot 5} {2 \cdot 4 \cdot 6 } \right) \frac{z^{-7}} {7} + \cdots ) =\\ & {}= \frac {\pi} {2} - \sum_{n=0}^\infty \left( \frac {(2n)!} {2^{2n}(n!)^2} \right) \frac {z^{-(2n+1)}} {(2n+1)} ; \qquad \left| z \right| \ge 1. 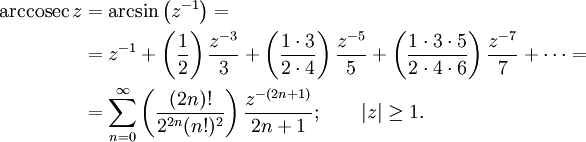\end{align}$ $\begin{align} \operatorname{arccosec}\,z & {}= \arcsin\left(z^{-1}\right) =\\ & {}= z^{-1} + \left( \frac {1} {2} \right) \frac {z^{-3}} {3} + \left( \frac {1 \cdot 3} {2 \cdot 4 } \right) \frac {z^{-5}} {5} + \left( \frac {1 \cdot 3 \cdot 5} {2 \cdot 4 \cdot 6} \right) \frac {z^{-7}} {7} +\cdots =\\ & {}= \sum_{n=0}^\infty \left( \frac {(2n)!} {2^{2n}(n!)^2} \right) \frac {z^{-(2n+1)}} {2n+1} ; \qquad \left| z \right| \ge 1. \end{align}$

Для арктангенса используется также более быстро сходящийся ряд, открытый Леонардом Эйлером:

$\operatorname{arctg}\,x = \frac{x}{1+x^2} \sum_{n=0}^\infty \prod_{k=1}^n \frac{2k x^2}{(2k+1)(1+x^2)}$

(член в сумме при n= 0 принимается равным 1).

11. Использование в геометрии

Прямоугольный треугольник ABC

Обратные тригонометрические функции используются для вычисления углов треугольника, если известны его стороны, например с помощью теоремы косинусов.

В прямоугольном треугольнике, эти функции от отношений сторон сразу дают угол:

α = arcsin (a/c) = arccos (b/c) = arctg (a/b) = arccosec (c/a) = arcsec (c/b) = arcctg (b/a)

wreferat.baza-referat.ru

Курсовая работа - Теория тригонометрических функций

--PAGE_BREAK--Слишком поспешное введение понятий синуса и косинуса «по окружности» приводит к трудностям при дальнейшем обучении: многие учащиеся испытывают затруднения с геометрическим истолкованием «тригонометрического языка». Таким образом, не получается создать надежный фундамент для успешного изучения материала. В учебнике Мордковича «Алгебра и начала анализа» на работу с числовой окружностью отводится 5 часов, что составляет почти 20% от 28 запланированных часов на изучение всей темы «Тригонометрические функции». Вообще говоря, здесь рассматриваются две математические модели: «числовая окружность» и «числовая окружность на координатной плоскости». То есть учащиеся обучаются работать одновременно в двух системах координат: в прямоугольной декартовой и криволинейной. Это поможет им в дальнейшем, когда понятия синуса и косинуса угла будут вводиться через координаты.

Здесь не только четко выделяется алгоритм построения точки на числовой окружности, но и проводится аналогия с числовой прямой, с указанием основных сходств и различий в построении точки на окружности и на прямой. Неплохо в учебнике Мордковича «Алгебра и начала анализа» мотивируется и само введение числовой окружности: «В реальной жизни двигаться приходится не только по прямой, но и по окружности. Будем считать беговую дорожку стадиона окружностью…». К тому же, уже на этапе изучения числовой окружности в неявном виде происходит подготовка к решению простейших тригонометрических уравнений и неравенств.

Например, рассматриваются задания типа: «Найти на числовой окружности точки с ординатой у = 1/2 и записать, каким числам tони соответствуют», «Найти на числовой окружности точки с абсциссой х tони соответствуют».

Итак, в учебнике Мордковича «Алгебра и начала анализа», в отличие от остальных учебников, проводится достаточно хорошая пропедевтическая работа для введения тригонометрических функций.

В учебнике Башмакова «Алгебра и начала анализа»также присутствуют элементы работы с числовой окружностью, но не в таком количестве как в Мордковиче.Здесь выделяется отдельный параграф «Вращательное движение и его свойства», в котором рассматриваются такие вопросы как построение точки по заданной мере угла и свойства вращательного движения.

В учебнике Колмогорова «Алгебра и начала анализа» в качестве подготовительной работы для введения тригонометрических функций выступает лишь повторение следующих вопросов:

- радианная мера угла (измерение углов в радианах, таблица значений тригонометрических функций (рассматривается исходя из геометрических соображений)),

- основные формулы тригонометрии (основное тригонометрическое тождество, формулы суммы и разности двух аргументов, формулы приведения, формулы суммы и разности синусов и косинусов, формулы двойного и половинного аргументов).

Вообще вопросы тригонометрии в этом учебнике рассматриваются в следующем порядке: тригонометрические преобразования – тригонометрические функции – тригонометрические уравнения и неравенства, в отличие от учебника Мордковича, по которому сначала изучаются функции, затем уравнения и неравенства, а только потом преобразования (как свойства функций).

Обучение же по учебникам Алимова «Алгебра и начала анализа»и Башмакова «Алгебра и начала анализа» предполагает изучение тригонометрических функций не в начале 10 класса (как это представлено в учебниках Колмогоров и Мордковича, а в конце него. Алимов предлагает приступить к изучению тригонометрии после изучения показательной и логарифмической функций. Причем, сначала изучаются тригонометрические преобразования, затем — тригонометрические уравнения и только после этого – тригонометрические функции. Такое расположение темы имеет ряд особенностей:

- изучение тригонометрических уравнений подразумевает изучение обратных тригонометрических функций. Таким образом, сначала учащиеся детально прорабатывают понятия арксинуса, арккосинуса и арктангенса, а затем только приступают к работе с синусом, косинусом и тангенсом, хотя с точки зрения логики, целесообразнее сделать наоборот;

- изучение тригонометрических функций после тригонометрических уравнений выкидывает из рассмотрения один из немаловажных методов решения тригонометрических уравнений – а именно графический метод (к тому времени мы ещё не умеем строить графики тригонометрических функций).

В учебнике же Башмакова «Алгебра и начала анализа» вообще предлагается изучать тригонометрию уже после изучения производной. Это позволяет вычислять приближенные значения тригонометрических функций в точках, тем самым облегчая их исследование, помогая при построении графиков и решении тригонометрических уравнений.

Что касается введения самих тригонометрических функций, то и здесь каждый из учебников имеет свои особенности. Начнем с определения синуса и косинуса. В учебнике Алимова дается следующее определение: «Сosх– это абсцисса точки единичной окружности, полученной поворотом точки Р (1;0) вокруг начала координат на угол х, а sinх – ее ордината». У Мордковича: «Если точка М числовой окружности соответствует числу t, то абсциссу точки М называют косинусом числа t, а ординату точки М называют синусом числа t». Эти два определения, в общем-то, принципиально не различаются, за исключением только того, что в учебнике Алимова тригонометрические функции определяются как функции углового аргумента, а в учебнике Мордковича как функции числового аргумента, да еще присутствуют различия в обозначении переменной (заметим, что при работе с числовой окружностью лучше употреблять символы sin t, cos t, tg t, ctg t, учитывая, что знак х в сознании детей ассоциируется с абсциссой в декартовой прямоугольной системе координат, а не с длиной пройденного по числовой окружности пути).

В учебнике же Колмогорова «Алгебра и начала анализа» как таковых определений синуса и косинуса нет, а вместо них присутствует фраза «… нетрудно понять, что ордината точки Рa — это синус угла a, а абсцисса этой точки – косинус угла a», а затем приведено геометрическое подтверждение этого факта. Благодаря этому, у учащихся не возникает недоумения по поводу того, почему раньше синусом называли отношение длин катета и гипотенузы, а сейчас откуда–то выплыли какие–то абсциссы и ординаты. В учебнике Мордковичаэтот факт тоже довольно неплохо пояснен, но с опозданием в 3 параграфа, а в учебнике Башмакова пояснение отсутствует вовсе.

Тангенс же во всех учебниках, за исключением Колмогорова,определяется как отношение синуса к косинусу. В учебнике же Колмогорова опять не дается четкого определения тангенса, а приводится лишь геометрическая интерпретация «ордината точки пересечения прямой ОРa(Рa— точка на единичной окружности) и касательной к окружности в точке (1;0) равна тангенсу угла a».

Определения котангенса авторы дают аналогично определениям тангенса за исключением учебника Алимова, в котором котангенс почему-то совсем игнорируется и не рассматривается как функция.

Остановимся подробнее на вопросах исследования и построения графиков тригонометрических функций.

В учебнике Мордковичапроцесс построения графика и исследования функции происходит следующим образом: уже известные ребятам факты обобщаются и формулируются как свойства функций. Сначала рассматриваются такие свойства функции y=sin(x), как область определения, множество значений, нечетность, возрастание на отрезке [0;p/2] и убывание на отрезке [p/2; 3p/2], ограниченность сверху и снизу, наибольшее и наименьшее значение. Затем составляется таблица основных значений функции на отрезке [0;p], строятся соответствующие точки и плавно соединяются.

Используя свойство нечетности синуса, полученный график отображается относительно начала координат на отрезок [-p;0], используя свойство периодичности, график функции достраивается на остальных отрезках длиной 2p. С опорой на построенный график, выделяется свойство непрерывности функции синус и область ее значений. Исследование функции cos х и построение ее графика как и во всех остальных учебниках основывается на том факте, что cos х = sin (х+p/2).

В учебнике Башмакова построение синусоиды происходит при помощи единичной окружности переносом значения синуса к соответствующим точкам оси ОХ. А затем, после построения графика, еще раз происходит возвращение к свойствам и к тому, как они проявляются на графике. В учебнике Колмогоров «Алгебра и начала анализа» синусоида строится подобно тому, как она строится в учебнике Башмакова, но все свойства функций за исключением области определения и множества значений рассматриваются в следующей теме «Основные свойства функций», а затем только переносятся на тригонометрические.

Отметим, что в учебниках Мордковича и Колмогорова не обоснован тот факт, что областью определения функций sin и cos является множество всех действительных чисел. Конечно, этот факт достаточно очевиден, но тем не менее учебник пишется не для учителя, а для учеников, а «мера очевидности», как известно, у всех разная. Поэтому не стоит забывать об обосновании даже очевидных фактов, ведь это приучает ребят к столь необходимой при изучении математики логической четкости и аккуратности мысли.

Что касается области значений тригонометрической функций, то ни в одном из учебников нет четкого обоснования данного свойства. Все «попытки» обоснования этого свойства сводятся к рассмотрению двойных неравенств:

-1 £ sin х £ 1 и -1 £ соs х £ 1, которые выполняются для всех значений х. Однако, отсюда совершенно не следует то, что в область значений данных функций входят все точки отрезка [-1;1].

При обосновании свойств четности и нечетности тригонометрических функций доказательство тождества sin(-х) = -sin(х) сводится в основном к симметричности точек х и –х, которая также четко не обоснована ни в одном из учебников.

Монотонность же тригонометрических функций во всех учебниках, за исключением Колмогорова,иллюстрируется с помощью числовой окружности. В учебнике в силу того, что тригонометрические преобразования изучаются перед тригонометрическими функциями, монотонность функции у= sin(х) обоснована более доказательно, но все же некоторые недочеты имеются.

При изучении свойства периодичности авторы учебников Мордкович, Алимов и Колмогоров дают следующее определение периодичности: «Функция f(x) называется периодической, если существует такое число Т¹0, что для любого х из области определения данной функции выполняется равенство f( x- T)= f( x)= f( x+ T). Число Т называется периодом функции f( x)».В учебнике Башмакова равенство f( x- T)= f( x)= f( x+ T) заменяется менее сильным равенством f( x)= f( x+ T), но зато снимаются ограничения на х. Здесь х может быть любым, а не только из области определения. Заметим, что для функций, областью определения которых является все множество R, эти два определения будут не только равносильными, но и одинаково корректными. Но если применять второе определение к функции у=sinÖх, то у учащихся может вызвать затруднения сравнение значений данной функции в точках, например, -p и p. Поэтому более целесообразным является использование первого определения.

Проанализируем теперь системы задач, направленные на отработку умений и навыков, которые предусмотрены программой по теме «Тригонометрические функции».

Система задач в учебнике Башмакова содержит в себе задания на перевод из градусной меры в радианную и наоборот, построение углов на единичной окружности, движение точки по окружности, определение тригонометрических функций, исследование и построение графиков комбинаций тригонометрических функций, нахождение значений тригонометрических функций в некоторых точках и их знаков на некоторых промежутках, нахождение производных комбинаций тригонометрических функций и вычисление приближенных значений тригонометрических функций.

В учебниках Алимоваи Колмогороваработе со свойствами комбинаций тригонометрических функций уделяется уже гораздо большее внимание, чем в учебнике Башмакова, присутствуют задачи теоретического плана, например, «Докажите, что если функция y=f(x) является периодической, то и y=k*f(x)+b тоже периодическая»,не остаются без практической отработки и гармонические колебания. В учебнике Алимоваприсутствует еще одна особенность: здесь подобрано большое количество задач с ограничением на переменную х, что помогает учащимся в осознании того факта, что «не всякие свойства функции, рассматриваемой на множестве всех действительных чисел, сохраняются при наложении ограничений на область определения этой функции».

Наиболее же полноценной из всех является система задач в учебнике Мордковича. Здесь, кроме всего уже вышеперечисленного, большое внимание уделено отработке навыков и умений работы с числовой окружностью, присутствуют задачи для работы с тригонометрическими функциями как числового, так и углового аргументов, используются функции, заданные кусочно, отрабатываются умения решать уравнения, содержащие тригонометрические функции, графическим методом.

Вообще, говоря о системе задач этих учебников, следует отметить некоторые недостатки учебника Башмакова «Алгебра и начала анализа».В идеале, решение каждой последующей задачи должно не только опираться на предыдущую, но и содержать какие–то дополнительные идеи. Здесь же не везде четко прослеживается система, да и по уровню сложности задачи не столь уж разнообразны.

Зато наличие отдельного задачника к учебнику Мордковича позволило дать в нем полноценную по объему систему упражнений, достаточную для работы в классе, для домашних заданий и повторения. Все задания дифференцированы по блокам, отдельно выделены даже устные и полуустные упражнения, что дает возможность более рационального использования учебного времени.

Таким образом, наиболее удачным учебным пособием в плане изучения темы «Тригонометрические функции» в курсе алгебры и начала анализа является учебно-методический комплект под редакцией А.Г. Мордковича, хотя оставлять без внимания остальные учебники тоже не стоит.

2.Теория обратных функций

Обратные тригонометрические функции

Определение обратной функции

Определение. Если функция f(x) задает взаимно однозначное соответствие между своей областью определения X и своей областью значений У (иными словами, если любым различным значениям аргумента соответствуют различные значения функции), то говорят, что функция f(x) имеет обратную функцию или что функция f(x) обратима.

Определение. Обратная функция — это правило, которое каждому числу у є У сопоставляет число х є X, причем y=f(x). Область определения обратной

функции есть множество У, область значений — X.

Теорема о корне. Пусть функция fвозрастает (или убывает) на промежутке I, число а — любое из значений, принимаемых fна этом промежутке. Тогда уравнение f(x)=aимеет единственный корень в промежутке I.

Доказательство. Рассмотрим возрастающую функцию f(в случае убывающей функции рассуждения аналогичны). По условию в промежутке I существует такое число b, что f(b)=a. Покажем, что b— единственный корень уравнения f(x)=a.

Допустим, что на промежутке I есть еще число с≠ Ь, такое что f(c)=a. Тогда или сb, или с>b. Но функция fвозрастает на промежутке I, поэтому соответственно либо f(c)f(b), либо f(c)>f(b). Это противоречит равенству f(c)= f(b)=a. Следовательно, сделанное предположение неверно и в промежутке I, кроме числа b, других корней уравнения f(x)=aнет.

Теорема об обратной функции. Если функция fвозрастает (или убывает) на промежутке I, то она обратима. Обратная к fфункция g, определенная в области значений fтакже является возрастающей (соответственно убывающей).

Доказательство. Положим для определенности, что функция fвозрастает. Обратимость функции f— очевидное следствие теоремы о корне. Поэтому остается доказать, что функция g, обратная к f, возрастает на множестве E(f).

Пусть х1 и х2 — произвольные значения из E(f), такие, что х2> х1 и пусть y1= g(х1), у2= g(х2). По определению обратной функции х1= f(y1) и х2= f(y2).

Воспользовавшись тем условием, что f— возрастающая функция, находим, что допущение y1≥y2 приводит к выводу f(y1) > f(y2), то есть х1 > х2. Это

противоречит предположению х2> х1Поэтому, y1> y2, то есть из условия х2> х1 следует, что g(x2)> g(х1). Что и требовалось доказать.

Исходная функция и обратная ей являются взаимно обратными.

Графики взаимно обратных функций

Теорема. Графики взаимно обратных функций симметричны относительно прямой у=х.

Доказательство. Заметим, что по графику функции fможно найти числовое значение обратной к fфункции gв произвольной точке а. Для этого нужно взять точку с координатой а не на горизонтальной оси (как это обычно делается), а на вертикальной. Из определения обратной функции следует, что значение g(a) равно b.

Таким образом, если считать, что выбрана несколько необычная система координат, то можно сказать, что график обратной к fфункции g— это график функции f(построенной в обычной системе координат).

Для того, чтобы изобразить график gв привычной системе координат, надо отразить график fотносительно прямой у=х.

Алгоритм составления обратной функции для функции y=f(x), x<img width=«13» height=«13» src=«ref-3_611821850-84.coolpic» v:shapes="_x0000_i1095">X.

1.Убедиться в том, что функция y=f(x) обратима на X.

2.Из уравнения y=f(x) х выразить через у, учитывая при этом, что х є X.

З.В полученном равенстве поменять местами х и у.

продолжение --PAGE_BREAK--2.2.Определение, свойства и графики обратных тригонометрических

функций

Арксинус

Функция синус возрастает на отрезке <img width=«65» height=«45» src=«ref-3_611821934-237.coolpic» v:shapes="_x0000_i1096"> и принимает все значения от -1 до 1. Следовательно, по теореме о корне для любого числа а, такого, что <img width=«40» height=«27» src=«ref-3_611822171-149.coolpic» v:shapes="_x0000_i1097">, в промежутке <img width=«65» height=«45» src=«ref-3_611821934-237.coolpic» v:shapes="_x0000_i1098"> существует единственный корень уравнения sinx= a. Это число и называют арксинусом числа а и обозначают arcsinа.

Определение.Арксинусом числа а, где <img width=«40» height=«27» src=«ref-3_611822171-149.coolpic» v:shapes="_x0000_i1099">, называется такое число из отрезка<img width=«65» height=«45» src=«ref-3_611821934-237.coolpic» v:shapes="_x0000_i1100">, синус которого равен а.

Свойства.

1. D(у) = [ -1;1 ]

2. Е(у) = [-π/2;π/2]

3. у (-х) = arcsin(-х) = — arcsin х – функция нечетная, график симметричен относительно точки О(0;0).

4. arcsin х = 0 при х = 0.

5. arcsin х > 0 при х є (0;1]

arcsin х при х є [-1;0)

6. у = arcsin х возрастает при любом х є [-1;1]

-1 ≤ х12 ≤ 1 arcsin х12 – функция возрастающая.

Арккосинус

Функция косинус убывает на отрезке [0;<img width=«15» height=«15» src=«ref-3_611827999-89.coolpic» v:shapes="_x0000_i1101">] и принимает все значения от -1 до 1. Поэтому для любого числа а, такого, что |а|<img width=«13» height=«16» src=«ref-3_611828088-88.coolpic» v:shapes="_x0000_i1102">1, на отрезке [0;<img width=«15» height=«15» src=«ref-3_611827999-89.coolpic» v:shapes="_x0000_i1103">] существует единственный корень в уравнении cosx=a. Это число в называют арккосинусом числа а и обозначают arcosа.

Определение. Арккосинусом числа а, где -1<img width=«13» height=«16» src=«ref-3_611828088-88.coolpic» v:shapes="_x0000_i1104"> а <img width=«13» height=«16» src=«ref-3_611828088-88.coolpic» v:shapes="_x0000_i1105">1, называется такое число из отрезка [0;<img width=«15» height=«15» src=«ref-3_611827999-89.coolpic» v:shapes="_x0000_i1106">], косинус которого равен а.

Свойства.

1. D(у) = [-1;1]

2. Е(у) = [0;π]

3. у(-х) = arccos(-х) = π — arccos х – функция не является ни четной, ни нечетной.

4. arccos х = 0 при х = 1

5. arccos х > 0 при х є [-1;1)

arccos х

6. у = arccos х убывает при любом х є [-1;1]

-1 ≤ х12 ≤ 1 arcsin х1 ≥ arcsin х2 – убывающая.

Арктангенс

Функция тангенс возрастает на отрезке-<img width=«72» height=«41» src=«ref-3_611834735-217.coolpic» v:shapes="_x0000_i1107">, следовательно, по теореме о корне уравнение tgx=a, где а — любое действительное число, имеет единственный корень х на интервале -<img width=«72» height=«41» src=«ref-3_611834735-217.coolpic» v:shapes="_x0000_i1108">. Этот корень называют арктангенсом числа а и обозначают arctga.

Определение. Арктангенсом числа a<img width=«13» height=«13» src=«ref-3_611821850-84.coolpic» v:shapes="_x0000_i1109">R называется такое число х <img width=«13» height=«13» src=«ref-3_611821850-84.coolpic» v:shapes="_x0000_i1110"><img width=«67» height=«45» src=«ref-3_611835337-243.coolpic» v:shapes="_x0000_i1111">,тангенс которого равен а.

Свойства.

1. D(у) = R

2. Е(у) = (-π/2;π/2)

3. у(-х) = у = arctg(-х) = — arctg х – функция является нечетной, график симметричен относительно точки О(0;0).

4. arctg х = 0 при х = 0

5. Функция возрастает при любом х є R

-∞ 1 2 arctg х12

6. Функция непрерывна при любом х є R.

Арккотангенс

Функция котангенс на интервале (0;<img width=«15» height=«15» src=«ref-3_611827999-89.coolpic» v:shapes="_x0000_i1112">) убывает и принимает все значения из R. Поэтому для любого числа а в интервале (0;<img width=«15» height=«15» src=«ref-3_611827999-89.coolpic» v:shapes="_x0000_i1113">) существует единственный корень уравнения ctgх = а. Это число а называют арккотангенсом числа а и обозначают arcctgа.

Определение.Арккотангенсом числа а, где а <img width=«13» height=«13» src=«ref-3_611821850-84.coolpic» v:shapes="_x0000_i1114"> R, называется такое число из интервала (0;<img width=«15» height=«15» src=«ref-3_611827999-89.coolpic» v:shapes="_x0000_i1115">),котангенс которого равен а.

Свойства.

1. D(у) = R

2. Е(у) = (0;π)

3. у(-х) = arcctg(-х) = π — arcctg х – функция не является ни четной, ни нечетной.

4. arcctg х = 0– не существует.

5. Функция у = arcctg х убывает при любом х є R

-∞ 1 2 arcctg х1 > arcctg х2

6. Функция непрерывна при любом х є R.

2.3 Тождественные преобразования выражений, содержащих обратные тригонометрические функцииПример 1. Упростить выражение:

а) <img width=«13» height=«20» src=«ref-3_611850390-73.coolpic» v:shapes="_x0000_i1116"><img width=«103» height=«24» src=«ref-3_611850463-520.coolpic» v:shapes="_x0000_i1117"> где <img width=«79» height=«23» src=«ref-3_611850983-283.coolpic» v:shapes="_x0000_i1118">

Решение. Положим <img width=«91» height=«24» src=«ref-3_611851266-364.coolpic» v:shapes="_x0000_i1119">. Тогда <img width=«93» height=«47» src=«ref-3_611851630-437.coolpic» v:shapes="_x0000_i1120"> и <img width=«71» height=«24» src=«ref-3_611852067-274.coolpic» v:shapes="_x0000_i1121"> Чтобы найти <img width=«29» height=«16» src=«ref-3_611852341-214.coolpic» v:shapes="_x0000_i1122"> <img width=«16» height=«20» src=«ref-3_611852555-92.coolpic» v:shapes="_x0000_i1123">, воспользуемся соотношением <img width=«136» height=«28» src=«ref-3_611852647-466.coolpic» v:shapes="_x0000_i1124"> Получаем <img width=«111» height=«28» src=«ref-3_611853113-375.coolpic» v:shapes="_x0000_i1125"> Но <img width=«93» height=«47» src=«ref-3_611851630-437.coolpic» v:shapes="_x0000_i1126">. На этом отрезке косинус принимает только положительные значения. Таким образом, <img width=«115» height=«32» src=«ref-3_611853925-409.coolpic» v:shapes="_x0000_i1127">, то есть <img width=«176» height=«32» src=«ref-3_611854334-684.coolpic» v:shapes="_x0000_i1128"> где <img width=«75» height=«20» src=«ref-3_611855018-255.coolpic» v:shapes="_x0000_i1129">.

б) <img width=«109» height=«24» src=«ref-3_611855273-552.coolpic» v:shapes="_x0000_i1130">

Решение.<img width=«519» height=«28» src=«ref-3_611855825-1524.coolpic» v:shapes="_x0000_i1131">

в) <img width=«88» height=«24» src=«ref-3_611857349-386.coolpic» v:shapes="_x0000_i1132">

Решение. Положим <img width=«81» height=«21» src=«ref-3_611857735-295.coolpic» v:shapes="_x0000_i1133">. Тогда <img width=«93» height=«47» src=«ref-3_611858030-436.coolpic» v:shapes="_x0000_i1134"> и <img width=«59» height=«21» src=«ref-3_611858466-164.coolpic» v:shapes="_x0000_i1135"> Найдем сначала <img width=«29» height=«16» src=«ref-3_611852341-214.coolpic» v:shapes="_x0000_i1136"> <img width=«16» height=«20» src=«ref-3_611852555-92.coolpic» v:shapes="_x0000_i1137">, для чего воспользуемся формулой <img width=«127» height=«51» src=«ref-3_611858936-501.coolpic» v:shapes="_x0000_i1138">, откуда <img width=«127» height=«51» src=«ref-3_611859437-502.coolpic» v:shapes="_x0000_i1139"> Так как <img width=«93» height=«47» src=«ref-3_611858030-436.coolpic» v:shapes="_x0000_i1140"> и на этом интервале косинус принимает только положительные значения, то <img width=«120» height=«51» src=«ref-3_611860375-484.coolpic» v:shapes="_x0000_i1141">.

Теперь найдем <img width=«40» height=«24» src=«ref-3_611860859-233.coolpic» v:shapes="_x0000_i1142">. Имеем <img width=«219» height=«56» src=«ref-3_611861092-775.coolpic» v:shapes="_x0000_i1143">. Это значит, что <img width=«168» height=«52» src=«ref-3_611861867-607.coolpic» v:shapes="_x0000_i1144">

г)<img width=«179» height=«24» src=«ref-3_611862474-734.coolpic» v:shapes="_x0000_i1145">

Решение. Воспользуемся известной формулой <img width=«281» height=«24» src=«ref-3_611863208-1084.coolpic» v:shapes="_x0000_i1146"> где <img width=«99» height=«19» src=«ref-3_611864292-421.coolpic» v:shapes="_x0000_i1147"> <img width=«99» height=«24» src=«ref-3_611864713-460.coolpic» v:shapes="_x0000_i1148">

д) <img width=«164» height=«24» src=«ref-3_611867571-635.coolpic» v:shapes="_x0000_i1150">

Решение.Из тригонометрии нам известно формула

Тогда

Пример2

. Вычислить:

а) <img width=«143» height=«55» src=«ref-3_611875300-861.coolpic» v:shapes="_x0000_i1155">

Решение. Пусть <img width=«133» height=«52» src=«ref-3_611876161-614.coolpic» v:shapes="_x0000_i1156"> Тогда <img width=«75» height=«20» src=«ref-3_611876775-337.coolpic» v:shapes="_x0000_i1157"> b <img width=«88» height=«47» src=«ref-3_611877112-385.coolpic» v:shapes="_x0000_i1158"> Более того, так как <img width=«61» height=«47» src=«ref-3_611877497-347.coolpic» v:shapes="_x0000_i1159"> то <img width=«80» height=«47» src=«ref-3_611877844-411.coolpic» v:shapes="_x0000_i1160">. Для вычисления <img width=«44» height=«47» src=«ref-3_611878255-336.coolpic» v:shapes="_x0000_i1161"> воспользуемся формулой <img width=«153» height=«24» src=«ref-3_611878591-575.coolpic» v:shapes="_x0000_i1162"> из нее следует, что <img width=«155» height=«53» src=«ref-3_611879166-716.coolpic» v:shapes="_x0000_i1163">.

Таким образом. Необходимо сначала найти <img width=«47» height=«16» src=«ref-3_611879882-281.coolpic» v:shapes="_x0000_i1164"> Так как <img width=«131» height=«48» src=«ref-3_611880163-556.coolpic» v:shapes="_x0000_i1165"> и ясно, что <img width=«75» height=«48» src=«ref-3_611880719-356.coolpic» v:shapes="_x0000_i1166">, то <img width=«96» height=«48» src=«ref-3_611881075-515.coolpic» v:shapes="_x0000_i1167">

Так как в интервале <img width=«80» height=«47» src=«ref-3_611877844-411.coolpic» v:shapes="_x0000_i1168">, <img width=«75» height=«23» src=«ref-3_611882001-403.coolpic» v:shapes="_x0000_i1169"> то <img width=«144» height=«53» src=«ref-3_611882404-696.coolpic» v:shapes="_x0000_i1170"> Итак, <img width=«139» height=«69» src=«ref-3_611883100-669.coolpic» v:shapes="_x0000_i1171"> и так как <img width=«92» height=«47» src=«ref-3_611883769-499.coolpic» v:shapes="_x0000_i1172"> а в этом интервале синус принимает только положительные значения, то <img width=«147» height=«53» src=«ref-3_611884268-705.coolpic» v:shapes="_x0000_i1173"> Таким образом, <img width=«212» height=«56» src=«ref-3_611884973-1069.coolpic» v:shapes="_x0000_i1174">

б) <img width=«163» height=«55» src=«ref-3_611886042-967.coolpic» v:shapes="_x0000_i1175">

Решение.Положим <img width=«196» height=«55» src=«ref-3_611887009-1050.coolpic» v:shapes="_x0000_i1176"> Тогда <img width=«72» height=«24» src=«ref-3_611888059-322.coolpic» v:shapes="_x0000_i1177"> и <img width=«156» height=«52» src=«ref-3_611888381-771.coolpic» v:shapes="_x0000_i1178"> Но <img width=«305» height=«52» src=«ref-3_611889152-1358.coolpic» v:shapes="_x0000_i1179"> Таким образом, <img width=«116» height=«48» src=«ref-3_611890510-578.coolpic» v:shapes="_x0000_i1180"> и, так как <img width=«91» height=«48» src=«ref-3_611891088-481.coolpic» v:shapes="_x0000_i1181"> получаем <img width=«61» height=«48» src=«ref-3_611891569-327.coolpic» v:shapes="_x0000_i1182"> Итак, <img width=«209» height=«55» src=«ref-3_611891896-1143.coolpic» v:shapes="_x0000_i1183">

в) <img width=«135» height=«52» src=«ref-3_611893039-778.coolpic» v:shapes="_x0000_i1184">

Решение. Так как <img width=«199» height=«28» src=«ref-3_611893817-731.coolpic» v:shapes="_x0000_i1185"> то <img width=«403» height=«52» src=«ref-3_611894548-1661.coolpic» v:shapes="_x0000_i1186">

г) <img width=«289» height=«55» src=«ref-3_611896209-1601.coolpic» v:shapes="_x0000_i1187">

Решение.

д)<img width=«193» height=«52» src=«ref-3_611902158-961.coolpic» v:shapes="_x0000_i1189">

Решение. Пусть <img width=«104» height=«48» src=«ref-3_611903119-472.coolpic» v:shapes="_x0000_i1190"> <img width=«107» height=«48» src=«ref-3_611903591-564.coolpic» v:shapes="_x0000_i1191"> Тогда <img width=«95» height=«47» src=«ref-3_611904155-465.coolpic» v:shapes="_x0000_i1192"> и <img width=«76» height=«48» src=«ref-3_611904620-411.coolpic» v:shapes="_x0000_i1193"> <img width=«96» height=«47» src=«ref-3_611905031-494.coolpic» v:shapes="_x0000_i1194"> и <img width=«84» height=«48» src=«ref-3_611905525-466.coolpic» v:shapes="_x0000_i1195">

Более того, так как <img width=«51» height=«48» src=«ref-3_611905991-358.coolpic» v:shapes="_x0000_i1196"> и <img width=«56» height=«48» src=«ref-3_611906349-380.coolpic» v:shapes="_x0000_i1197"><img width=«15» height=«23» src=«ref-3_611906729-73.coolpic» v:shapes="_x0000_i1198">то <img width=«77» height=«47» src=«ref-3_611906802-426.coolpic» v:shapes="_x0000_i1199"> и <img width=«83» height=«47» src=«ref-3_611907228-452.coolpic» v:shapes="_x0000_i1200"> Воспользуемся формулой <img width=«239» height=«28» src=«ref-3_611907680-901.coolpic» v:shapes="_x0000_i1201">

Необходимо сначала найти <img width=«48» height=«19» src=«ref-3_611908581-297.coolpic» v:shapes="_x0000_i1202"> <img width=«41» height=«20» src=«ref-3_611908878-261.coolpic» v:shapes="_x0000_i1203"> и <img width=«44» height=«23» src=«ref-3_611909139-315.coolpic» v:shapes="_x0000_i1204">.

Так как <img width=«131» height=«48» src=«ref-3_611880163-556.coolpic» v:shapes="_x0000_i1205"> и <img width=«105» height=«48» src=«ref-3_611910010-630.coolpic» v:shapes="_x0000_i1206">

В интервале <img width=«77» height=«47» src=«ref-3_611906802-426.coolpic» v:shapes="_x0000_i1207"> <img width=«81» height=«21» src=«ref-3_611911066-409.coolpic» v:shapes="_x0000_i1208">, то <img width=«87» height=«48» src=«ref-3_611911475-481.coolpic» v:shapes="_x0000_i1209">

Из основного тригонометрического тождества <img width=«137» height=«24» src=«ref-3_611911956-512.coolpic» v:shapes="_x0000_i1210"> найдем <img width=«60» height=«29» src=«ref-3_611912468-329.coolpic» v:shapes="_x0000_i1211"> <img width=«263» height=«48» src=«ref-3_611912797-1117.coolpic» v:shapes="_x0000_i1212"> Так как в интервале <img width=«77» height=«47» src=«ref-3_611906802-426.coolpic» v:shapes="_x0000_i1213"> <img width=«73» height=«23» src=«ref-3_611914340-375.coolpic» v:shapes="_x0000_i1214"> то <img width=«84» height=«48» src=«ref-3_611914715-442.coolpic» v:shapes="_x0000_i1215"> <img width=«52» height=«27» src=«ref-3_611915157-338.coolpic» v:shapes="_x0000_i1216"> также можем найти из основного тригонометрического тождества <img width=«143» height=«27» src=«ref-3_611915495-582.coolpic» v:shapes="_x0000_i1217"> <img width=«264» height=«48» src=«ref-3_611916077-1163.coolpic» v:shapes="_x0000_i1218"> Но так как в интервале <img width=«77» height=«47» src=«ref-3_611917240-444.coolpic» v:shapes="_x0000_i1219"> косинус принимает только положительные значения, то <img width=«87» height=«48» src=«ref-3_611917684-502.coolpic» v:shapes="_x0000_i1220">

Итак, <img width=«251» height=«48» src=«ref-3_611918186-1072.coolpic» v:shapes="_x0000_i1221"> Таким образом, <img width=«220» height=«52» src=«ref-3_611919258-1024.coolpic» v:shapes="_x0000_i1222">.

Пример3

.Проверьте справедливость равенства:

а) <img width=«253» height=«48» src=«ref-3_611920282-1110.coolpic» v:shapes="_x0000_i1223">

Решение. Положим <img width=«109» height=«48» src=«ref-3_611921392-553.coolpic» v:shapes="_x0000_i1224"> <img width=«107» height=«48» src=«ref-3_611921945-578.coolpic» v:shapes="_x0000_i1225">, <img width=«99» height=«48» src=«ref-3_611922523-512.coolpic» v:shapes="_x0000_i1226"> Тогда <img width=«96» height=«47» src=«ref-3_611905031-494.coolpic» v:shapes="_x0000_i1227"> и <img width=«63» height=«48» src=«ref-3_611923529-347.coolpic» v:shapes="_x0000_i1228"> <img width=«75» height=«23» src=«ref-3_611923876-377.coolpic» v:shapes="_x0000_i1229"> и <img width=«89» height=«48» src=«ref-3_611924253-505.coolpic» v:shapes="_x0000_i1230"> <img width=«79» height=«47» src=«ref-3_611924758-426.coolpic» v:shapes="_x0000_i1231">

Проверим в какой части четверти находятся левая и правая части равенства:

Левая часть: <img width=«135» height=«52» src=«ref-3_611925184-743.coolpic» v:shapes="_x0000_i1232">

Правая часть: <img width=«79» height=«52» src=«ref-3_611925927-499.coolpic» v:shapes="_x0000_i1233">

Рассмотрим равенство на промежутке <img width=«52» height=«52» src=«ref-3_611926426-374.coolpic» v:shapes="_x0000_i1234">, где монотонна любая тригонометрическая функция, но удобнее взять косинус от обеих частей.

Необходимо сначала найти <img width=«48» height=«19» src=«ref-3_611908581-297.coolpic» v:shapes="_x0000_i1237"><img width=«100» height=«47» src=«ref-3_611929368-616.coolpic» v:shapes="_x0000_i1238">

<img width=«261» height=«48» src=«ref-3_611929984-1095.coolpic» v:shapes="_x0000_i1239"> Но так как в промежутке <img width=«52» height=«52» src=«ref-3_611926426-374.coolpic» v:shapes="_x0000_i1240"> косинус принимает только положительные значения, то <img width=«88» height=«48» src=«ref-3_611931453-510.coolpic» v:shapes="_x0000_i1241">

Для вычисления <img width=«48» height=«47» src=«ref-3_611931963-385.coolpic» v:shapes="_x0000_i1242"> воспользуемся формулой <img width=«153» height=«47» src=«ref-3_611932348-731.coolpic» v:shapes="_x0000_i1243"> откуда <img width=«251» height=«69» src=«ref-3_611933079-1140.coolpic» v:shapes="_x0000_i1244"> и так как <img width=«87» height=«47» src=«ref-3_611934219-510.coolpic» v:shapes="_x0000_i1245"> а в этом промежутке <img width=«79» height=«47» src=«ref-3_611934729-508.coolpic» v:shapes="_x0000_i1246"> то <img width=«83» height=«48» src=«ref-3_611935237-492.coolpic» v:shapes="_x0000_i1247">

<img width=«45» height=«47» src=«ref-3_611935729-365.coolpic» v:shapes="_x0000_i1248"> найдем из формулы <img width=«13» height=«20» src=«ref-3_611850390-73.coolpic» v:shapes="_x0000_i1249"><img width=«149» height=«47» src=«ref-3_611936167-709.coolpic» v:shapes="_x0000_i1250"> <img width=«159» height=«48» src=«ref-3_611936876-740.coolpic» v:shapes="_x0000_i1251"> Так как в промежутке <img width=«87» height=«47» src=«ref-3_611934219-510.coolpic» v:shapes="_x0000_i1252"><img width=«76» height=«47» src=«ref-3_611938126-487.coolpic» v:shapes="_x0000_i1253"> то <img width=«79» height=«48» src=«ref-3_611938613-472.coolpic» v:shapes="_x0000_i1254">

Таким образом, <img width=«321» height=«52» src=«ref-3_611939085-1476.coolpic» v:shapes="_x0000_i1255"> а <img width=«76» height=«48» src=«ref-3_611940561-426.coolpic» v:shapes="_x0000_i1256">

Следовательно, равенство верно.

б) <img width=«155» height=«48» src=«ref-3_611940987-749.coolpic» v:shapes="_x0000_i1257">

Решение.Пусть <img width=«103» height=«48» src=«ref-3_611941736-537.coolpic» v:shapes="_x0000_i1258"> <img width=«89» height=«47» src=«ref-3_611942273-464.coolpic» v:shapes="_x0000_i1259">

Тогда <img width=«79» height=«23» src=«ref-3_611942737-363.coolpic» v:shapes="_x0000_i1260"> <img width=«96» height=«47» src=«ref-3_611905031-494.coolpic» v:shapes="_x0000_i1261">, а <img width=«101» height=«23» src=«ref-3_611943594-427.coolpic» v:shapes="_x0000_i1262">

Более того, так как <img width=«44» height=«48» src=«ref-3_611944021-318.coolpic» v:shapes="_x0000_i1263"> и <img width=«48» height=«47» src=«ref-3_611944339-318.coolpic» v:shapes="_x0000_i1264"> то <img width=«83» height=«47» src=«ref-3_611944657-444.coolpic» v:shapes="_x0000_i1265"> <img width=«77» height=«47» src=«ref-3_611945101-454.coolpic» v:shapes="_x0000_i1266">, <img width=«87» height=«47» src=«ref-3_611945555-494.coolpic» v:shapes="_x0000_i1267">.

Рассмотрим равенство на промежутке <img width=«52» height=«52» src=«ref-3_611926426-374.coolpic» v:shapes="_x0000_i1268">, где монотонна любая тригонометрическая функция, поэтому возьмем синус от обеих частей.

Следовательно, <img width=«159» height=«48» src=«ref-3_611949762-760.coolpic» v:shapes="_x0000_i1271">

продолжение --PAGE_BREAK--Пример4

.Доказать тождества.

а) <img width=«185» height=«52» src=«ref-3_611950522-631.coolpic» v:shapes="_x0000_i1272"> если <img width=«80» height=«20» src=«ref-3_611951153-257.coolpic» v:shapes="_x0000_i1273">

Доказательство. Вычислим значения тангенса от обеих частей равенства:

т.е. тангенсы равны.

Далее, так как <img width=«79» height=«23» src=«ref-3_611952788-276.coolpic» v:shapes="_x0000_i1275">то <img width=«148» height=«47» src=«ref-3_611953064-593.coolpic» v:shapes="_x0000_i1276">

Но по определению и <img width=«188» height=«52» src=«ref-3_611953657-681.coolpic» v:shapes="_x0000_i1277"> т.е. и <img width=«65» height=«23» src=«ref-3_611954338-336.coolpic» v:shapes="_x0000_i1278"> и <img width=«105» height=«52» src=«ref-3_611954674-341.coolpic» v:shapes="_x0000_i1279"> принадлежат одному и тому же промежутку монотонности тангенса. Тем самым тождество доказано.

б) arctg = arcsin <img width=«56» height=«47» src=«ref-3_611955015-195.coolpic» v:shapes="_x0000_i1280">

Доказательство.Вычислим значения тангенса от обеих частей равенства

tg(arctgx)=x

tg<img width=«532» height=«107» src=«ref-3_611955210-1714.coolpic» v:shapes="_x0000_i1281"> т.е. тангенсы равны.

Так как <img width=«168» height=«47» src=«ref-3_611956924-387.coolpic» v:shapes="_x0000_i1282">. Но и по определению <img width=«123» height=«41» src=«ref-3_611957311-291.coolpic» v:shapes="_x0000_i1283">т.е.

и <img width=«97» height=«47» src=«ref-3_611957602-268.coolpic» v:shapes="_x0000_i1284">, и arctgxпринадлежат одному и тому же промежутку монотонности тангенса.Что и требовалось доказать.

в) 2<img width=«159» height=«47» src=«ref-3_611957870-394.coolpic» v:shapes="_x0000_i1285">

Доказательство. Вычислим значения косинуса от обеих частей равенства

<img width=«280» height=«56» src=«ref-3_611959650-640.coolpic» v:shapes="_x0000_i1287">.

cos(arccosx)=x, т.е. косинусы равны.

Так как <img width=«107» height=«19» src=«ref-3_611960290-206.coolpic» v:shapes="_x0000_i1288"> и <img width=«152» height=«47» src=«ref-3_611960496-385.coolpic» v:shapes="_x0000_i1289">, т.е. и arccosx, и <img width=«101» height=«47» src=«ref-3_611960881-305.coolpic» v:shapes="_x0000_i1290"> принадлежат одному и тому же промежутку монотонности косинуса. Тем самым тождество доказано.

2.4.Задания, предлагаемые на вступительных экзаменах

Пример 1. Вычислить:

а)<img width=«101» height=«23» src=«ref-3_611961186-372.coolpic» v:shapes="_x0000_i1291">

б)<img width=«163» height=«45» src=«ref-3_611961558-424.coolpic» v:shapes="_x0000_i1292">

в)<img width=«164» height=«45» src=«ref-3_611961982-429.coolpic» v:shapes="_x0000_i1293">

Решение.а) Пусть arctg(-2) = γ. Тогда по определению арктангенса tgγ=-2 и γ<img width=«71» height=«45» src=«ref-3_611962411-247.coolpic» v:shapes="_x0000_i1294">. Отсюда <img width=«191» height=«48» src=«ref-3_611962658-464.coolpic» v:shapes="_x0000_i1295">. Из уравнения <img width=«133» height=«24» src=«ref-3_611963122-245.coolpic» v:shapes="_x0000_i1296"> находим, что <img width=«72» height=«41» src=«ref-3_611963367-206.coolpic» v:shapes="_x0000_i1297">. Поскольку γ<img width=«71» height=«45» src=«ref-3_611962411-247.coolpic» v:shapes="_x0000_i1298">, то sin γsinγ=-<img width=«28» height=«47» src=«ref-3_611963820-161.coolpic» v:shapes="_x0000_i1299">. Окончательно, <img width=«156» height=«45» src=«ref-3_611963981-502.coolpic» v:shapes="_x0000_i1300">.

б) Обозначим <img width=«171» height=«41» src=«ref-3_611964483-370.coolpic» v:shapes="_x0000_i1301">. Тогда <img width=«133» height=«41» src=«ref-3_611964853-301.coolpic» v:shapes="_x0000_i1302"> и <img width=«571» height=«47» src=«ref-3_611965154-1232.coolpic» v:shapes="_x0000_i1303">.

в) с учетом тождества <img width=«149» height=«41» src=«ref-3_611966386-314.coolpic» v:shapes="_x0000_i1304">, <img width=«63» height=«23» src=«ref-3_611966700-176.coolpic» v:shapes="_x0000_i1305">, получаем <img width=«67» height=«41» src=«ref-3_611966876-194.coolpic» v:shapes="_x0000_i1306">.

Пример 2.

Сравните два числа: <img width=«27» height=«41» src=«ref-3_611967070-139.coolpic» v:shapes="_x0000_i1307"> и <img width=«65» height=«41» src=«ref-3_611967209-211.coolpic» v:shapes="_x0000_i1308">.

Решение.Напишем сравнение <img width=«27» height=«41» src=«ref-3_611967070-139.coolpic» v:shapes="_x0000_i1309"> и <img width=«65» height=«41» src=«ref-3_611967209-211.coolpic» v:shapes="_x0000_i1310">. Взяв от обеих частей косинус, за счет его убывания получим обратное сравнение <img width=«83» height=«41» src=«ref-3_611967770-248.coolpic» v:shapes="_x0000_i1311">. Далее заметим, что <img width=«323» height=«48» src=«ref-3_611968018-702.coolpic» v:shapes="_x0000_i1312"> — известная величина. И задача сводится к числовому сравнению.

Следовательно, <img width=«83» height=«41» src=«ref-3_611969367-246.coolpic» v:shapes="_x0000_i1314">, а <img width=«27» height=«41» src=«ref-3_611967070-139.coolpic» v:shapes="_x0000_i1315"><img width=«65» height=«41» src=«ref-3_611967209-211.coolpic» v:shapes="_x0000_i1316">.

Пример 3.

Вычислить угол <img width=«208» height=«45» src=«ref-3_611969963-457.coolpic» v:shapes="_x0000_i1317">.

Решение. Из определений обратных тригонометрических функций следует

<img width=«279» height=«45» src=«ref-3_611970420-590.coolpic» v:shapes="_x0000_i1318">.

Следовательно, <img width=«65» height=«23» src=«ref-3_611971010-268.coolpic» v:shapes="_x0000_i1319">. Для нахождения <img width=«16» height=«15» src=«ref-3_611971278-88.coolpic» v:shapes="_x0000_i1320"> нужно вычислить значение какой-либо тригонометрической функции от <img width=«16» height=«15» src=«ref-3_611971278-88.coolpic» v:shapes="_x0000_i1321">, например, sin<img width=«16» height=«15» src=«ref-3_611971278-88.coolpic» v:shapes="_x0000_i1322"> или cos<img width=«16» height=«15» src=«ref-3_611971278-88.coolpic» v:shapes="_x0000_i1323">. Однако на интервале <img width=«39» height=«23» src=«ref-3_611971630-217.coolpic» v:shapes="_x0000_i1324"> функция синус немонотонна и угол <img width=«16» height=«15» src=«ref-3_611971278-88.coolpic» v:shapes="_x0000_i1325"> по найденному значению sin<img width=«16» height=«15» src=«ref-3_611971278-88.coolpic» v:shapes="_x0000_i1326"> определяется неоднозначно, а функция косинус монотонно убывает, следовательно, по значению cos<img width=«16» height=«15» src=«ref-3_611971278-88.coolpic» v:shapes="_x0000_i1327"> и угол <img width=«16» height=«15» src=«ref-3_611971278-88.coolpic» v:shapes="_x0000_i1328"> определяется однозначно.

Используя формулу для косинуса суммы, получим

Отсюда следует, что <img width=«16» height=«15» src=«ref-3_611971278-88.coolpic» v:shapes="_x0000_i1330">=<img width=«17» height=«41» src=«ref-3_611974796-119.coolpic» v:shapes="_x0000_i1331">.

Пример 4. Вычислите значение выражения <img width=«205» height=«48» src=«ref-3_611974915-536.coolpic» v:shapes="_x0000_i1332">.<img width=«12» height=«23» src=«ref-3_611975451-73.coolpic» v:shapes="_x0000_i1333">

Решение. 1) Найдём ОДЗ данного выражения:

Итак, данное выражение определено на промежутке <img width=«60» height=«48» src=«ref-3_611977152-234.coolpic» v:shapes="_x0000_i1335">.

2) Оценим, какие значения может принимать рассматриваемое выражение. Из неотрицательности выражений <img width=«56» height=«48» src=«ref-3_611977386-223.coolpic» v:shapes="_x0000_i1336"> и <img width=«56» height=«47» src=«ref-3_611977609-245.coolpic» v:shapes="_x0000_i1337"> следует справедливость неравенств: 0<img width=«145» height=«48» src=«ref-3_611977854-383.coolpic» v:shapes="_x0000_i1338">

<img width=«153» height=«47» src=«ref-3_611978237-437.coolpic» v:shapes="_x0000_i1339">.

Сложив неравенства одного знака, получим, что исходное выражение

<img width=«207» height=«48» src=«ref-3_611978674-541.coolpic» v:shapes="_x0000_i1340">может принимать значения из интервала <img width=«39» height=«23» src=«ref-3_611979215-220.coolpic» v:shapes="_x0000_i1341">.

3) На интервале <img width=«39» height=«23» src=«ref-3_611979215-220.coolpic» v:shapes="_x0000_i1342"> функция <img width=«29» height=«19» src=«ref-3_611979655-118.coolpic» v:shapes="_x0000_i1343"> является монотонной и, следовательно, зная её значение, можно однозначно определить и значение аргумента.

4) Найдём значение котангенса исходного выражения:

<img width=«548» height=«104» src=«ref-3_611979773-2176.coolpic» v:shapes="_x0000_i1344">.

Для преобразования полученного выражения применим следующее соотношения: <img width=«247» height=«49» src=«ref-3_611981949-788.coolpic» v:shapes="_x0000_i1345">если <img width=«113» height=«23» src=«ref-3_611982737-352.coolpic» v:shapes="_x0000_i1346">

<img width=«104» height=«23» src=«ref-3_611983089-329.coolpic» v:shapes="_x0000_i1347">при любых значениях <img width=«9» height=«16» src=«ref-3_611983418-81.coolpic» v:shapes="_x0000_i1348">.

Тогда получим, что <img width=«299» height=«92» src=«ref-3_611983499-991.coolpic» v:shapes="_x0000_i1349">

( с учётом ОДЗ) и, наконец, <img width=«417» height=«93» src=«ref-3_611985306-1427.coolpic» v:shapes="_x0000_i1351"> на ОДЗ рассматриваемого выражения.

5) В силу монотонности функции <img width=«29» height=«19» src=«ref-3_611979655-118.coolpic» v:shapes="_x0000_i1352"> на интервале <img width=«37» height=«23» src=«ref-3_611986851-225.coolpic» v:shapes="_x0000_i1353"> равенство <img width=«53» height=«21» src=«ref-3_611987076-148.coolpic» v:shapes="_x0000_i1354"> возможно лишь при <img width=«39» height=«41» src=«ref-3_611987224-149.coolpic» v:shapes="_x0000_i1355">.Следовательно, выражение <img width=«203» height=«48» src=«ref-3_611987373-537.coolpic» v:shapes="_x0000_i1356"> принимает значение <img width=«17» height=«41» src=«ref-3_611987910-117.coolpic» v:shapes="_x0000_i1357"> при <img width=«83» height=«45» src=«ref-3_611988027-269.coolpic» v:shapes="_x0000_i1358"> и не имеет смысла при других значениях x.

Ответ . <img width=«17» height=«41» src=«ref-3_611988296-116.coolpic» v:shapes="_x0000_i1359"> при <img width=«87» height=«45» src=«ref-3_611988412-280.coolpic» v:shapes="_x0000_i1360"><img width=«12» height=«23» src=«ref-3_611975451-73.coolpic» v:shapes="_x0000_i1361">не имеет смысла при<img width=«83» height=«45» src=«ref-3_611988765-276.coolpic» v:shapes="_x0000_i1362">.

Пример 5. Найдите множество значений функции <img width=«73» height=«21» src=«ref-3_611989041-165.coolpic» v:shapes="_x0000_i1363"> если x<img width=«140» height=«45» src=«ref-3_611989206-384.coolpic» v:shapes="_x0000_i1364">.

Решение.Заметим, что <img width=«217» height=«41» src=«ref-3_611989590-449.coolpic» v:shapes="_x0000_i1365">; так, что <img width=«233» height=«41» src=«ref-3_611990039-482.coolpic» v:shapes="_x0000_i1366">. Тогда при х<img width=«140» height=«45» src=«ref-3_611989206-384.coolpic» v:shapes="_x0000_i1367">функция cos2xдостигает максимума <img width=«131» height=«23» src=«ref-3_611990905-344.coolpic» v:shapes="_x0000_i1368">. Также <img width=«133» height=«45» src=«ref-3_611991249-366.coolpic» v:shapes="_x0000_i1369">, так как <img width=«135» height=«41» src=«ref-3_611991615-319.coolpic» v:shapes="_x0000_i1370">, а <img width=«112» height=«23» src=«ref-3_611991934-346.coolpic» v:shapes="_x0000_i1371">, так как <img width=«83» height=«41» src=«ref-3_611992280-233.coolpic» v:shapes="_x0000_i1372"> Так что минимум cos2x достигается при <img width=«540» height=«45» src=«ref-3_611992513-938.coolpic» v:shapes="_x0000_i1373">

Так что <img width=«84» height=«21» src=«ref-3_611993451-182.coolpic» v:shapes="_x0000_i1374">.

Пример 6. Найдите множество значений функции y=sin2x, если <img width=«131» height=«45» src=«ref-3_611993633-390.coolpic» v:shapes="_x0000_i1375">.

Решение.Так как arccosx-убывающая функция, то arccos<img width=«121» height=«41» src=«ref-3_611994023-308.coolpic» v:shapes="_x0000_i1376">, так что <img width=«93» height=«41» src=«ref-3_611994331-259.coolpic» v:shapes="_x0000_i1377">; <img width=«112» height=«41» src=«ref-3_611994590-296.coolpic» v:shapes="_x0000_i1378">.

Тогда <img width=«183» height=«41» src=«ref-3_611994886-419.coolpic» v:shapes="_x0000_i1379">, т.е. 2x находится во второй четверти, так, что sin2x – убывает. Значит, <img width=«567» height=«99» src=«ref-3_611995305-2140.coolpic» v:shapes="_x0000_i1380">

Так, что <img width=«140» height=«41» src=«ref-3_611997445-360.coolpic» v:shapes="_x0000_i1381"><img width=«61» height=«45» src=«ref-3_611997805-269.coolpic» v:shapes="_x0000_i1382">

Ответ:<img width=«61» height=«45» src=«ref-3_611997805-269.coolpic» v:shapes="_x0000_i1383">

Пример 7 . Решите систему уравнений <img width=«136» height=«72» src=«ref-3_611998343-457.coolpic» v:shapes="_x0000_i1384">

В ответе запишите значение <img width=«71» height=«23» src=«ref-3_611998800-198.coolpic» v:shapes="_x0000_i1385">

Решение.

Решим отдельно (*):

Система имеет вид:

Выберем <img width=«119» height=«41» src=«ref-3_612001894-291.coolpic» v:shapes="_x0000_i1389">

Ответ:<img width=«29» height=«41» src=«ref-3_612002185-140.coolpic» v:shapes="_x0000_i1390">

3. Уравнения, содержащие обратные тригонометрические функции

3.1. Уравнения, левая и правая части которых являются одноименными и

разноименными обратными тригонометрическими функциями Решение уравнений, левая и правая части которых представляют собой одноименные обратные тригонометрические функции различных аргументов, основывается, прежде всего, на таком свойстве этих функции, как монотонность.

Справедливы следующие равносильные переходы:

а) <img width=«183» height=«21» src=«ref-3_612002325-320.coolpic» v:shapes="_x0000_i1391">

б) <img width=«187» height=«21» src=«ref-3_612003351-324.coolpic» v:shapes="_x0000_i1393">

в) <img width=«165» height=«21» src=«ref-3_612004382-316.coolpic» v:shapes="_x0000_i1395">

г) <img width=«180» height=«21» src=«ref-3_612004918-335.coolpic» v:shapes="_x0000_i1397">

Замечание 1. Какой из двух равносильных систем пользоваться при решений уравнений а) и б), зависит от того, какое неравенство проще:

<img width=«60» height=«27» src=«ref-3_612005473-184.coolpic» v:shapes="_x0000_i1399"> (тогда использовать первую систему), или <img width=«59» height=«27» src=«ref-3_612005657-188.coolpic» v:shapes="_x0000_i1400"> (в этом случае используем вторую систему).

Пример 1. Решитьуравнение.

<img width=«252» height=«27» src=«ref-3_612005845-803.coolpic» v:shapes="_x0000_i1401">.

Ответ. x=-<img width=«15» height=«41» src=«ref-3_612007916-109.coolpic» v:shapes="_x0000_i1403">

Замечание 2. Решать неравенства, входящие в систему, необязательно. Достаточно проверить, удовлетворяют ли неравенству найденные корни уравнения.

Пример 2. Решить уравнение.

Ответ.<img width=«44» height=«45» src=«ref-3_612010757-196.coolpic» v:shapes="_x0000_i1408">.

Пример 3.arcsin(1+2х) = arcsin(2х<img width=«11» height=«20» src=«ref-3_612010953-79.coolpic» v:shapes="_x0000_i1409"> — х – 1). Запишем равносильную систему: <img width=«139» height=«51» src=«ref-3_612011032-416.coolpic» v:shapes="_x0000_i1410">

2х<img width=«11» height=«20» src=«ref-3_612010953-79.coolpic» v:shapes="_x0000_i1411"> — 3х -2 = 0, х<img width=«97» height=«23» src=«ref-3_612011527-185.coolpic» v:shapes="_x0000_i1412">.

Неравенство мы можем не решать, а подставить в него найденные корни.

Итак, х<img width=«52» height=«23» src=«ref-3_612011712-137.coolpic» v:shapes="_x0000_i1413"> удовлетворяет неравенству системы, а х<img width=«33» height=«23» src=«ref-3_612011849-114.coolpic» v:shapes="_x0000_i1414"> не удовлетворяет ему.

Ответ: <img width=«36» height=«21» src=«ref-3_612011963-117.coolpic» v:shapes="_x0000_i1415">

При решении уравнений, левая и правая части которых являются разноименными обратными тригонометрическими функциями, пользуются известными тригонометрическими тождествами. Решение их основано на следующих рассуждениях: пусть требуется решить уравнение

<img width=«164» height=«21» src=«ref-3_612012080-295.coolpic» v:shapes="_x0000_i1416">.

Предположим, что <img width=«19» height=«24» src=«ref-3_612012375-94.coolpic» v:shapes="_x0000_i1417">-решение этого уравнения. Обозначим

Тогда

Откуда

Итак

<img width=«305» height=«24» src=«ref-3_612013461-488.coolpic» v:shapes="_x0000_i1421"> (1)

Рассуждая аналогично, можно получить следующие переходы:

<img width=«258» height=«21» src=«ref-3_612013949-430.coolpic» v:shapes="_x0000_i1422"> (2)

(использована формула <img width=«91» height=«21» src=«ref-3_612014379-204.coolpic» v:shapes="_x0000_i1423">).

<img width=«304» height=«45» src=«ref-3_612014583-601.coolpic» v:shapes="_x0000_i1424"> (3)

(использована формула <img width=«124» height=«45» src=«ref-3_612015184-304.coolpic» v:shapes="_x0000_i1425">).

<img width=«300» height=«45» src=«ref-3_612015488-592.coolpic» v:shapes="_x0000_i1426"> (4)

(использована формула <img width=«120» height=«45» src=«ref-3_612016080-297.coolpic» v:shapes="_x0000_i1427">)

<img width=«297» height=«48» src=«ref-3_612016377-647.coolpic» v:shapes="_x0000_i1428"> (5)

(использована формула <img width=«117» height=«48» src=«ref-3_612017024-339.coolpic» v:shapes="_x0000_i1429">).

<img width=«306» height=«48» src=«ref-3_612017363-657.coolpic» v:shapes="_x0000_i1430"> (6)

(использована формула <img width=«127» height=«48» src=«ref-3_612018020-361.coolpic» v:shapes="_x0000_i1431">).

Замечание 3. Корнем каждого из уравнений (1)-(4) может быть только такое число <img width=«19» height=«24» src=«ref-3_612012375-94.coolpic» v:shapes="_x0000_i1432">, для которого <img width=«67» height=«24» src=«ref-3_612018475-175.coolpic» v:shapes="_x0000_i1433"> и <img width=«65» height=«24» src=«ref-3_612018650-174.coolpic» v:shapes="_x0000_i1434">. В противном случае множества

значений левой и правой частей уравнения не пересекаются.0> продолжение --PAGE_BREAK--Пример 4.решить уравнение

<img width=«188» height=«41» src=«ref-3_612018824-415.coolpic» v:shapes="_x0000_i1435">.

Решение.

Корень <img width=«64» height=«41» src=«ref-3_612020721-204.coolpic» v:shapes="_x0000_i1438"> является посторонним, так как при <img width=«140» height=«41» src=«ref-3_612020925-340.coolpic» v:shapes="_x0000_i1439"> и <img width=«69» height=«41» src=«ref-3_612021265-220.coolpic» v:shapes="_x0000_i1440">

Ответ.<img width=«20» height=«23» src=«ref-3_612021485-191.coolpic» v:shapes="_x0000_i1441">

При решении уравнений данного типа, содержащих параметры, становится актуальным вопрос о равносильности преобразований. Чтобы преобразования (1)-(4) сделать равносильными, следует учесть естественные ограничения, связанные с областями определения обратных тригонометрических функций и множествами их значений (см. замечание 3 ). Так, например,

Пример 5. Решить уравнение с параметром a:

<img width=«195» height=«21» src=«ref-3_612023522-336.coolpic» v:shapes="_x0000_i1444">.

Решение. Данное уравнение равносильно системе:

Графиком квадратного трехчлена <img width=«179» height=«24» src=«ref-3_612024599-301.coolpic» v:shapes="_x0000_i1446"> является парабола, ветви которой направлены вверх. Поскольку <img width=«99» height=«21» src=«ref-3_612024900-204.coolpic» v:shapes="_x0000_i1447">, то при любом а уравнение <img width=«60» height=«21» src=«ref-3_612025104-156.coolpic» v:shapes="_x0000_i1448">имеет ровно 2 корня, между которыми и заключено число 2а. поэтому только больший корень <img width=«36» height=«21» src=«ref-3_612025260-126.coolpic» v:shapes="_x0000_i1449"> удовлетворяет условию x>2a. Это корень <img width=«124» height=«47» src=«ref-3_612025386-322.coolpic» v:shapes="_x0000_i1450">.

Ответ. При любом <img width=«13» height=«15» src=«ref-3_612025708-84.coolpic» v:shapes="_x0000_i1451"> <img width=«124» height=«47» src=«ref-3_612025386-322.coolpic» v:shapes="_x0000_i1452">

3.2. Уравнения, решаемые другими методами

Уравнения, сводящиеся к алгебраическим

Некоторые уравнения могут быть свелены к алгебраическим уравнениям, при их решении приходиться использовать самые разнообразные преобразования.

Пример 1. arcsin 2 x –<img width=«17» height=«41» src=«ref-3_611987910-117.coolpic» v:shapes="_x0000_i1453">arcsinх+ <img width=«25» height=«44» src=«ref-3_612026231-146.coolpic» v:shapes="_x0000_i1454"> = 0. Пусть arcsin x = y, y <img width=«76» height=«45» src=«ref-3_612026377-270.coolpic» v:shapes="_x0000_i1455">

у<img width=«108» height=«44» src=«ref-3_612026647-283.coolpic» v:shapes="_x0000_i1456">, D = <img width=«117» height=«44» src=«ref-3_612026930-313.coolpic» v:shapes="_x0000_i1457">, y<img width=«91» height=«41» src=«ref-3_612027243-231.coolpic» v:shapes="_x0000_i1458">

arcsin x =<img width=«17» height=«41» src=«ref-3_612027474-116.coolpic» v:shapes="_x0000_i1459"> или arcsin x =<img width=«17» height=«41» src=«ref-3_612027590-119.coolpic» v:shapes="_x0000_i1460">

x=sin <img width=«17» height=«41» src=«ref-3_612027474-116.coolpic» v:shapes="_x0000_i1461"> , x=<img width=«27» height=«45» src=«ref-3_612027825-146.coolpic» v:shapes="_x0000_i1462"> x=sin<img width=«17» height=«41» src=«ref-3_612027590-119.coolpic» v:shapes="_x0000_i1463"> ,x=<img width=«16» height=«41» src=«ref-3_612028090-109.coolpic» v:shapes="_x0000_i1464">.

Ответ: <img width=«16» height=«41» src=«ref-3_612028090-109.coolpic» v:shapes="_x0000_i1465">;<img width=«27» height=«45» src=«ref-3_612027825-146.coolpic» v:shapes="_x0000_i1466">.

Пример 2. arccos2x – <img width=«25» height=«41» src=«ref-3_612028454-138.coolpic» v:shapes="_x0000_i1467"> arccosx +<img width=«25» height=«44» src=«ref-3_612028592-139.coolpic» v:shapes="_x0000_i1468">=0. Пустьarcros х= y, у<img width=«13» height=«13» src=«ref-3_611821850-84.coolpic» v:shapes="_x0000_i1469"> [0; <img width=«15» height=«15» src=«ref-3_611827999-89.coolpic» v:shapes="_x0000_i1470">]

y2 –<img width=«25» height=«41» src=«ref-3_612028454-138.coolpic» v:shapes="_x0000_i1471">y + <img width=«25» height=«44» src=«ref-3_612028592-139.coolpic» v:shapes="_x0000_i1472">=0, D =<img width=«116» height=«44» src=«ref-3_612029181-326.coolpic» v:shapes="_x0000_i1473">, <img width=«104» height=«41» src=«ref-3_612029507-255.coolpic» v:shapes="_x0000_i1474">

arccos x =<img width=«17» height=«41» src=«ref-3_611987910-117.coolpic» v:shapes="_x0000_i1475"> или arccos x = <img width=«17» height=«41» src=«ref-3_611974796-119.coolpic» v:shapes="_x0000_i1476">

x = cos<img width=«17» height=«41» src=«ref-3_611987910-117.coolpic» v:shapes="_x0000_i1477">, х=0 x = cos <img width=«17» height=«41» src=«ref-3_611974796-119.coolpic» v:shapes="_x0000_i1478">, x= <img width=«28» height=«45» src=«ref-3_612030234-148.coolpic» v:shapes="_x0000_i1479">

Ответ; 0; <img width=«28» height=«45» src=«ref-3_612030234-148.coolpic» v:shapes="_x0000_i1480">.

Пример 3.arctq2(3x + 2) + 2 arctq (3x + 2)=0.

Пусть arctq (3x + 2)=y, y<img width=«72» height=«41» src=«ref-3_612030530-221.coolpic» v:shapes="_x0000_i1481">

y2 + 2y=0, y (y + 2 )=0,

y=0 или y=-2 , -2<img width=«13» height=«16» src=«ref-3_612030751-86.coolpic» v:shapes="_x0000_i1482"><img width=«60» height=«41» src=«ref-3_612030837-201.coolpic» v:shapes="_x0000_i1483">

<img width=«12» height=«23» src=«ref-3_611975451-73.coolpic» v:shapes="_x0000_i1484"> arctq (3x + 2)=0, 3x + 2=tq 0, 3x + 2=0, х=<img width=«28» height=«41» src=«ref-3_612031111-129.coolpic» v:shapes="_x0000_i1485">

Ответ: <img width=«28» height=«41» src=«ref-3_612031111-129.coolpic» v:shapes="_x0000_i1486">

Пример

4.arcsin2x –<img width=«25» height=«41» src=«ref-3_612028454-138.coolpic» v:shapes="_x0000_i1487">arcsinx + <img width=«25» height=«44» src=«ref-3_612031507-136.coolpic» v:shapes="_x0000_i1488">= 0. Пустьarcsin x=y, y <img width=«76» height=«45» src=«ref-3_612026377-270.coolpic» v:shapes="_x0000_i1489"> .

y2 –<img width=«25» height=«41» src=«ref-3_612028454-138.coolpic» v:shapes="_x0000_i1490">y +<img width=«25» height=«44» src=«ref-3_612031507-136.coolpic» v:shapes="_x0000_i1491"> = 0, D = <img width=«65» height=«44» src=«ref-3_612032187-215.coolpic» v:shapes="_x0000_i1492">

Корней нет.

Ответ: корней нет

Пример 5. arctg2x –<img width=«25» height=«41» src=«ref-3_612032402-142.coolpic» v:shapes="_x0000_i1493">arctg x+ <img width=«25» height=«44» src=«ref-3_612032544-146.coolpic» v:shapes="_x0000_i1494">= 0.

Пусть arctg x=y, y<img width=«72» height=«41» src=«ref-3_612030530-221.coolpic» v:shapes="_x0000_i1495">

y2 –<img width=«25» height=«41» src=«ref-3_612032402-142.coolpic» v:shapes="_x0000_i1496">y +<img width=«25» height=«44» src=«ref-3_612032544-146.coolpic» v:shapes="_x0000_i1497"> = 0, D =<img width=«29» height=«44» src=«ref-3_612033199-158.coolpic» v:shapes="_x0000_i1498">, y<img width=«91» height=«41» src=«ref-3_612033357-233.coolpic» v:shapes="_x0000_i1499">

arctg x= <img width=«24» height=«41» src=«ref-3_612033590-126.coolpic» v:shapes="_x0000_i1500"> arctg x= <img width=«17» height=«41» src=«ref-3_612027590-119.coolpic» v:shapes="_x0000_i1501">

x=tg<img width=«24» height=«41» src=«ref-3_612033590-126.coolpic» v:shapes="_x0000_i1502"> х=1 x=tg <img width=«17» height=«41» src=«ref-3_612027590-119.coolpic» v:shapes="_x0000_i1503">, x=<img width=«27» height=«45» src=«ref-3_612034080-144.coolpic» v:shapes="_x0000_i1504">

Ответ: 1; <img width=«27» height=«45» src=«ref-3_612034080-144.coolpic» v:shapes="_x0000_i1505">

Уравнения, решаемые с помощью определений обратных тригонометрических функций

Пример 1.arcsin (x2 – 4x + 3)=0

x2 – 4x + 3= sin 0, а + в + с = 0, X1=1, X2=3

Проверка: x=1, arcsin 0=0 – верно, x =1 – корень уравнения

x=3, arcsin 0=0 – верно, x=3 – корень уравнения

Ответ: 0;3

Пример 2. 4 arctq( x2– 3x– 3 ) — <img width=«15» height=«15» src=«ref-3_611827999-89.coolpic» v:shapes="_x0000_i1506"> =0 . 4 arctq( x2— 3x– 3 ) = <img width=«15» height=«15» src=«ref-3_611827999-89.coolpic» v:shapes="_x0000_i1507">

arctq ( x2 – 3x – 3 ) =<img width=«17» height=«41» src=«ref-3_611974796-119.coolpic» v:shapes="_x0000_i1508">

x2 – 3x – 3= tq<img width=«17» height=«41» src=«ref-3_611974796-119.coolpic» v:shapes="_x0000_i1509"> , x2 – 3x – 3 = 1, x2 – 3x – 4 = 0, x1= -1,x2= 4

Проверка: x=-1, 4 arctq (1 + 3 – 3) – <img width=«15» height=«15» src=«ref-3_611827999-89.coolpic» v:shapes="_x0000_i1510"> = 0 – верно, x= -1 – корень уравнения

x=4, 4 arctq (16 – 12 – 3) – <img width=«15» height=«15» src=«ref-3_611827999-89.coolpic» v:shapes="_x0000_i1511"> =0-верно, x=4 – корень уравнения .

Ответ: -1;4

Пример 3. arrcos (x2 – 2) =<img width=«15» height=«15» src=«ref-3_611827999-89.coolpic» v:shapes="_x0000_i1512">, x2 – 2 = cos<img width=«15» height=«15» src=«ref-3_611827999-89.coolpic» v:shapes="_x0000_i1513">, x2 – 2= -1, x2=1, x<img width=«16» height=«25» src=«ref-3_612035140-88.coolpic» v:shapes="_x0000_i1514">=±1

Проверка: x=1, arrcos (1 – 2)= <img width=«15» height=«15» src=«ref-3_611827999-89.coolpic» v:shapes="_x0000_i1515"> – верно, x=1 – корень уравнения

x= -1, arrcos (1 – 2)= <img width=«15» height=«15» src=«ref-3_611827999-89.coolpic» v:shapes="_x0000_i1516"> – верно, x= -1 – корень уравнения.

Ответ: -1; 1

Пример 4. arcsin (x2 – 3x +<img width=«16» height=«41» src=«ref-3_612028090-109.coolpic» v:shapes="_x0000_i1517">)= <img width=«17» height=«41» src=«ref-3_612027590-119.coolpic» v:shapes="_x0000_i1518">.

x2 – 3x +<img width=«16» height=«41» src=«ref-3_612028090-109.coolpic» v:shapes="_x0000_i1519">=sin <img width=«17» height=«41» src=«ref-3_612027590-119.coolpic» v:shapes="_x0000_i1520"> , x2 – 3x= 0, x (x – 3)=0, x1=0, x2=3

Ответ: 0;3

Пример 5.6arcsin (x2 – 6x + 8,5) = <img width=«15» height=«15» src=«ref-3_611827999-89.coolpic» v:shapes="_x0000_i1521">.

arcsin (x2 – 6x + 8,5) = <img width=«17» height=«41» src=«ref-3_612027590-119.coolpic» v:shapes="_x0000_i1522">

x2 – 6x + 8,5 = sin <img width=«17» height=«41» src=«ref-3_612027590-119.coolpic» v:shapes="_x0000_i1523"> , x2 – 6x + 8,5 = 0,5,

x2 – 6x + 8 = 0, D =36 – 32=4, x<img width=«77» height=«23» src=«ref-3_612036189-164.coolpic» v:shapes="_x0000_i1524">

Ответ: 2;4

Уравнения, содержащие разные аргументы

Пример1. arcsin 6x + arcsin6<img width=«24» height=«24» src=«ref-3_612036353-113.coolpic» v:shapes="_x0000_i1029">x +<img width=«17» height=«41» src=«ref-3_611987910-117.coolpic» v:shapes="_x0000_i1525"> =0, arcsin 6x = -arcsin 6<img width=«24» height=«24» src=«ref-3_612036353-113.coolpic» v:shapes="_x0000_i1030">x – <img width=«17» height=«41» src=«ref-3_611987910-117.coolpic» v:shapes="_x0000_i1526">

sin (arcsin 6x) = -sin (arcsin 6<img width=«24» height=«24» src=«ref-3_612036353-113.coolpic» v:shapes="_x0000_i1031">x +<img width=«17» height=«41» src=«ref-3_611987910-117.coolpic» v:shapes="_x0000_i1527">)

6x = – cos arcsin 6<img width=«24» height=«24» src=«ref-3_612036353-113.coolpic» v:shapes="_x0000_i1032">x, где cos arcsin 6<img width=«24» height=«24» src=«ref-3_612036353-113.coolpic» v:shapes="_x0000_i1033">x=<img width=«151» height=«31» src=«ref-3_612037269-344.coolpic» v:shapes="_x0000_i1528">

6x= <img width=«68» height=«24» src=«ref-3_612037613-182.coolpic» v:shapes="_x0000_i1034">2 , 144x2 = 1, <img width=«12» height=«23» src=«ref-3_611975451-73.coolpic» v:shapes="_x0000_i1529">X<img width=«16» height=«25» src=«ref-3_612035140-88.coolpic» v:shapes="_x0000_i1530">= ±<img width=«16» height=«41» src=«ref-3_612028090-109.coolpic» v:shapes="_x0000_i1531">

Проверка: x =<img width=«16» height=«41» src=«ref-3_612028090-109.coolpic» v:shapes="_x0000_i1532">, arcsin<img width=«16» height=«41» src=«ref-3_612028090-109.coolpic» v:shapes="_x0000_i1533"> + arcsin <img width=«27» height=«45» src=«ref-3_612027825-146.coolpic» v:shapes="_x0000_i1534"> = — <img width=«17» height=«41» src=«ref-3_611987910-117.coolpic» v:shapes="_x0000_i1535"> — не верно, x=<img width=«16» height=«41» src=«ref-3_612028090-109.coolpic» v:shapes="_x0000_i1536">– посторонний корень

x= — <img width=«16» height=«41» src=«ref-3_612028090-109.coolpic» v:shapes="_x0000_i1537">, arcsin(-<img width=«16» height=«41» src=«ref-3_612028090-109.coolpic» v:shapes="_x0000_i1538">) + arcsin(-<img width=«27» height=«45» src=«ref-3_612027825-146.coolpic» v:shapes="_x0000_i1539">)= -<img width=«17» height=«41» src=«ref-3_611987910-117.coolpic» v:shapes="_x0000_i1540"> – верно, x= -<img width=«16» height=«41» src=«ref-3_612028090-109.coolpic» v:shapes="_x0000_i1541">– корень уравнения.

Ответ: — <img width=«16» height=«41» src=«ref-3_612028090-109.coolpic» v:shapes="_x0000_i1542">.

Пример 2. 2arrcos(-<img width=«16» height=«41» src=«ref-3_612039354-109.coolpic» v:shapes="_x0000_i1543">) = arrcos(x+ 3)

О. Д. З. <img width=«99» height=«69» src=«ref-3_612039463-377.coolpic» v:shapes="_x0000_i1544"> <img width=«92» height=«48» src=«ref-3_612039840-306.coolpic» v:shapes="_x0000_i1545"> , х= — 2.

<img width=«12» height=«23» src=«ref-3_611975451-73.coolpic» v:shapes="_x0000_i1546"> I способ: cos (2arrcos (-<img width=«16» height=«41» src=«ref-3_612039354-109.coolpic» v:shapes="_x0000_i1547">)) = cos (arcos (x + 3)). Вычислим cos (2arrcos (-<img width=«16» height=«41» src=«ref-3_612039354-109.coolpic» v:shapes="_x0000_i1548">)).

Пустьarccos (-<img width=«16» height=«41» src=«ref-3_612039354-109.coolpic» v:shapes="_x0000_i1549">) = α, α<img width=«13» height=«13» src=«ref-3_611821850-84.coolpic» v:shapes="_x0000_i1550"> [0; <img width=«15» height=«15» src=«ref-3_611827999-89.coolpic» v:shapes="_x0000_i1551">], cos α = — <img width=«16» height=«41» src=«ref-3_612039354-109.coolpic» v:shapes="_x0000_i1552">

cos2α= 2 cos2α– 1 = 2<img width=«105» height=«44» src=«ref-3_612040828-245.coolpic» v:shapes="_x0000_i1553">, тогда исходное уравнение принимает вид

x=4 – посторонний корень, т.к. не удовлетворяет О.Д.З.

IIспособ: Т.к. О.Д.З. включает одно значение, то только оно может быть корнем

уравнения или уравнение корней не имеет. Проверяем х = — 2.

2 arrcos1 = arcos(-2+ 3), 0 = 0 – верно, х = -2 – корень уравнения.

Ответ: -2 продолжение --PAGE_BREAK--Пример 3. arcsinx+ arcsin<img width=«57» height=«44» src=«ref-3_612041400-195.coolpic» v:shapes="_x0000_i1556">. sin (arcsin x) = sin (<img width=«17» height=«41» src=«ref-3_611987910-117.coolpic» v:shapes="_x0000_i1557">– arcsin <img width=«27» height=«44» src=«ref-3_612041712-140.coolpic» v:shapes="_x0000_i1558">)

x = cos (arcsin <img width=«27» height=«44» src=«ref-3_612041712-140.coolpic» v:shapes="_x0000_i1559">), x = <img width=«56» height=«48» src=«ref-3_612041992-218.coolpic» v:shapes="_x0000_i1560">, x2=1 – <img width=«24» height=«44» src=«ref-3_612042210-132.coolpic» v:shapes="_x0000_i1561">, 3x2 = 3 – x2, 4x2 = 3, х<img width=«16» height=«25» src=«ref-3_612035140-88.coolpic» v:shapes="_x0000_i1562">= ±<img width=«27» height=«45» src=«ref-3_612027825-146.coolpic» v:shapes="_x0000_i1563">

Проверка: x=<img width=«27» height=«45» src=«ref-3_612027825-146.coolpic» v:shapes="_x0000_i1564">, arcsin<img width=«27» height=«45» src=«ref-3_612027825-146.coolpic» v:shapes="_x0000_i1565"> + arcsin <img width=«16» height=«41» src=«ref-3_612028090-109.coolpic» v:shapes="_x0000_i1566">=<img width=«17» height=«41» src=«ref-3_611987910-117.coolpic» v:shapes="_x0000_i1567"> — верно, x=<img width=«27» height=«45» src=«ref-3_612027825-146.coolpic» v:shapes="_x0000_i1568"> — корень уравнения.

x=- <img width=«27» height=«45» src=«ref-3_612027825-146.coolpic» v:shapes="_x0000_i1569">, аrcsin(-<img width=«27» height=«45» src=«ref-3_612027825-146.coolpic» v:shapes="_x0000_i1570">) + arcsin(-<img width=«16» height=«41» src=«ref-3_612028090-109.coolpic» v:shapes="_x0000_i1571">) = <img width=«17» height=«41» src=«ref-3_611987910-117.coolpic» v:shapes="_x0000_i1572"> – неверно, x=- <img width=«27» height=«45» src=«ref-3_612027825-146.coolpic» v:shapes="_x0000_i1573"> — пост. кор. ур. Ответ:<img width=«27» height=«45» src=«ref-3_612027825-146.coolpic» v:shapes="_x0000_i1574">.

Уравнения, содержащие разные аркфункции

Пример1. arcos x – arcsin x = arrcos<img width=«24» height=«24» src=«ref-3_612036353-113.coolpic» v:shapes="_x0000_i1035">x. cos (arcos x – arcsin x) = cos (arcos<img width=«24» height=«24» src=«ref-3_612036353-113.coolpic» v:shapes="_x0000_i1036">x)

cos (arcos x) cos (arcsin x) + sin (arcos x) sin (arcsin x) = <img width=«24» height=«24» src=«ref-3_612036353-113.coolpic» v:shapes="_x0000_i1037">x

x<img width=«45» height=«24» src=«ref-3_612044389-138.coolpic» v:shapes="_x0000_i1038">2+ x<img width=«45» height=«24» src=«ref-3_612044389-138.coolpic» v:shapes="_x0000_i1039">2= <img width=«24» height=«24» src=«ref-3_612036353-113.coolpic» v:shapes="_x0000_i1040">x, 2x<img width=«45» height=«24» src=«ref-3_612044389-138.coolpic» v:shapes="_x0000_i1041">2= <img width=«24» height=«24» src=«ref-3_612036353-113.coolpic» v:shapes="_x0000_i1042">x, 2x<img width=«45» height=«24» src=«ref-3_612044389-138.coolpic» v:shapes="_x0000_i1043">2— <img width=«24» height=«24» src=«ref-3_612036353-113.coolpic» v:shapes="_x0000_i1044">x= 0,

x(2 <img width=«45» height=«24» src=«ref-3_612044389-138.coolpic» v:shapes="_x0000_i1045">2 - <img width=«24» height=«24» src=«ref-3_612036353-113.coolpic» v:shapes="_x0000_i1046"> ) = 0 , x=0 или 2 <img width=«45» height=«24» src=«ref-3_612044389-138.coolpic» v:shapes="_x0000_i1047">2= <img width=«24» height=«24» src=«ref-3_612036353-113.coolpic» v:shapes="_x0000_i1048">

4 – 4x2= 3 ,x2=<img width=«16» height=«41» src=«ref-3_612045782-111.coolpic» v:shapes="_x0000_i1575">, х<img width=«53» height=«41» src=«ref-3_612045893-172.coolpic» v:shapes="_x0000_i1576"> Проверка: x=0, arrcos0 – arc<img width=«16» height=«41» src=«ref-3_612028090-109.coolpic» v:shapes="_x0000_i1577">sin0 = arrcos0 – верно, x=0 – корень уравнения

х =<img width=«16» height=«41» src=«ref-3_612028090-109.coolpic» v:shapes="_x0000_i1578">, arrcos<img width=«16» height=«41» src=«ref-3_612028090-109.coolpic» v:shapes="_x0000_i1579">– arcsin<img width=«16» height=«41» src=«ref-3_612028090-109.coolpic» v:shapes="_x0000_i1580"> = arrcos<img width=«27» height=«45» src=«ref-3_612027825-146.coolpic» v:shapes="_x0000_i1581">– неверно, x=<img width=«16» height=«41» src=«ref-3_612028090-109.coolpic» v:shapes="_x0000_i1582">– посторонний корень

x= -<img width=«16» height=«41» src=«ref-3_612028090-109.coolpic» v:shapes="_x0000_i1583">, arrcos(-<img width=«16» height=«41» src=«ref-3_612028090-109.coolpic» v:shapes="_x0000_i1584">) – arcsin(-<img width=«16» height=«41» src=«ref-3_612028090-109.coolpic» v:shapes="_x0000_i1585">)= arrcos(-<img width=«27» height=«45» src=«ref-3_612027825-146.coolpic» v:shapes="_x0000_i1586">)– неверно, x= -<img width=«16» height=«41» src=«ref-3_612028090-109.coolpic» v:shapes="_x0000_i1587">–постор.корень.

Ответ: 0

Пример2. arcsin x – arcos x = arcsin (3x – 2)

sin (arcsin x – arccos x) = sin (arcsin (3x – 2))

sin(arcsin x) cos(arccos x) – sin(arccos x) cos(arcsin x) = 3x – 2

x2 – (1 – x2) – 3x + 2 =0, x2 – 1 + x2 – 3x + 2 = 0, 2x2 – 3x + 1 = 0, x1=1 , x2=<img width=«16» height=«41» src=«ref-3_612028090-109.coolpic» v:shapes="_x0000_i1588">

Проверка: x1=1, arcsin1 – arcos1 = arcsin(3 – 2), <img width=«48» height=«41» src=«ref-3_612047447-171.coolpic» v:shapes="_x0000_i1589">– верно, х =1- корень ур.

x2=<img width=«16» height=«41» src=«ref-3_612028090-109.coolpic» v:shapes="_x0000_i1590">, arcsin<img width=«16» height=«41» src=«ref-3_612028090-109.coolpic» v:shapes="_x0000_i1591"> – arсcos<img width=«16» height=«41» src=«ref-3_612028090-109.coolpic» v:shapes="_x0000_i1592"> = arcsin(3.<img width=«16» height=«41» src=«ref-3_612028090-109.coolpic» v:shapes="_x0000_i1593">– 2), <img width=«87» height=«41» src=«ref-3_612048054-229.coolpic» v:shapes="_x0000_i1594">-верно, x2=<img width=«16» height=«41» src=«ref-3_612028090-109.coolpic» v:shapes="_x0000_i1595">-кор.ур.

Ответ:<img width=«16» height=«41» src=«ref-3_612028090-109.coolpic» v:shapes="_x0000_i1596">;1.

При решении уравнений, содержащих разноимённые обратные тригонометрические функции, можно пользоваться тригонометрическими тождествами.

При решении многих уравнений такого рода бывает целесообразно не обсуждать вопрос о равносильности преобразований, а сразу переходить к уравнению-следствию и после его решения делать необходимую проверку.

Рассуждения могут быть примерно следующими.

Пусть требуется решить уравнение аrcsinf(x) = arсcosg(x).

Предположим, что х<img width=«9» height=«24» src=«ref-3_612048501-79.coolpic» v:shapes="_x0000_i1597"> — решение этого уравнения.

Обозначим аrcsinf(x<img width=«9» height=«24» src=«ref-3_612048501-79.coolpic» v:shapes="_x0000_i1598">) = arсcosg(x<img width=«9» height=«24» src=«ref-3_612048501-79.coolpic» v:shapes="_x0000_i1599">) через α. Тогда sinα = f(x<img width=«9» height=«24» src=«ref-3_612048501-79.coolpic» v:shapes="_x0000_i1600">), cosα. = g(x<img width=«9» height=«24» src=«ref-3_612048501-79.coolpic» v:shapes="_x0000_i1601">), откуда

f<img width=«11» height=«20» src=«ref-3_612010953-79.coolpic» v:shapes="_x0000_i1602">(x<img width=«9» height=«24» src=«ref-3_612048501-79.coolpic» v:shapes="_x0000_i1603">) + g<img width=«11» height=«20» src=«ref-3_612010953-79.coolpic» v:shapes="_x0000_i1604">(x<img width=«9» height=«24» src=«ref-3_612048501-79.coolpic» v:shapes="_x0000_i1605">) = 1.

Итак, аrcsinf(x) = arсcosg(x) <img width=«20» height=«16» src=«ref-3_612049212-91.coolpic» v:shapes="_x0000_i1606"> f<img width=«11» height=«20» src=«ref-3_612010953-79.coolpic» v:shapes="_x0000_i1607">(x) + g<img width=«11» height=«20» src=«ref-3_612010953-79.coolpic» v:shapes="_x0000_i1608">(x) = 1.

Аналогично получаем :

arctgf(x) = arctgg(x) <img width=«20» height=«16» src=«ref-3_612049212-91.coolpic» v:shapes="_x0000_i1609"> f(x) g(x) = 1. (По формуле tgxctgx= 1.)

аrcsinf(x) = arcctgg(x) <img width=«20» height=«16» src=«ref-3_612049212-91.coolpic» v:shapes="_x0000_i1610"> f<img width=«11» height=«20» src=«ref-3_612010953-79.coolpic» v:shapes="_x0000_i1611">(x) =<img width=«65» height=«45» src=«ref-3_612049722-218.coolpic» v:shapes="_x0000_i1612">. (По формуле sin<img width=«11» height=«20» src=«ref-3_612010953-79.coolpic» v:shapes="_x0000_i1613">x= <img width=«69» height=«45» src=«ref-3_612050019-226.coolpic» v:shapes="_x0000_i1614">

arctgf(x) = arсcosg(x) <img width=«20» height=«16» src=«ref-3_612049212-91.coolpic» v:shapes="_x0000_i1615"> <img width=«67» height=«45» src=«ref-3_612050336-218.coolpic» v:shapes="_x0000_i1616"> = g<img width=«11» height=«20» src=«ref-3_612010953-79.coolpic» v:shapes="_x0000_i1617">(x). . (По формуле cos<img width=«11» height=«20» src=«ref-3_612010953-79.coolpic» v:shapes="_x0000_i1618">x= <img width=«61» height=«45» src=«ref-3_612050712-214.coolpic» v:shapes="_x0000_i1619">

аrcsinf(x) = arctgg(x) <img width=«20» height=«16» src=«ref-3_612049212-91.coolpic» v:shapes="_x0000_i1620"> f<img width=«11» height=«20» src=«ref-3_612010953-79.coolpic» v:shapes="_x0000_i1621">(x) <img width=«79» height=«48» src=«ref-3_612051096-279.coolpic» v:shapes="_x0000_i1622">. (По формуле sin<img width=«11» height=«20» src=«ref-3_612010953-79.coolpic» v:shapes="_x0000_i1623">x= <img width=«61» height=«48» src=«ref-3_612051454-248.coolpic» v:shapes="_x0000_i1624">

arсcosg(x) = arcctgg(x) <img width=«20» height=«16» src=«ref-3_612049212-91.coolpic» v:shapes="_x0000_i1625"> f<img width=«11» height=«20» src=«ref-3_612010953-79.coolpic» v:shapes="_x0000_i1626">(x) <img width=«79» height=«48» src=«ref-3_612051096-279.coolpic» v:shapes="_x0000_i1627">. (По формуле соs<img width=«11» height=«20» src=«ref-3_612010953-79.coolpic» v:shapes="_x0000_i1628">x= <img width=«69» height=«48» src=«ref-3_612052230-265.coolpic» v:shapes="_x0000_i1629">

Приведём пример.

arсcos<img width=«47» height=«41» src=«ref-3_612052495-174.coolpic» v:shapes="_x0000_i1630"> = аrcsin <img width=«44» height=«41» src=«ref-3_612052669-174.coolpic» v:shapes="_x0000_i1631">. <img width=«183» height=«41» src=«ref-3_612052843-417.coolpic» v:shapes="_x0000_i1632">,

65х<img width=«11» height=«20» src=«ref-3_612010953-79.coolpic» v:shapes="_x0000_i1633"> + 78х — 143 = 0, т.к. а+в+с = 0, то х<img width=«8» height=«23» src=«ref-3_612053339-77.coolpic» v:shapes="_x0000_i1634"> = 1 и х<img width=«11» height=«23» src=«ref-3_612053416-79.coolpic» v:shapes="_x0000_i1635"> = <img width=«41» height=«41» src=«ref-3_612053495-172.coolpic» v:shapes="_x0000_i1636">

Проверка: х = 1, arсcos<img width=«21» height=«41» src=«ref-3_612053667-130.coolpic» v:shapes="_x0000_i1637"> = аrcsin <img width=«21» height=«41» src=«ref-3_612053797-127.coolpic» v:shapes="_x0000_i1638"> — верно, х = 1 – корень уравнения.

Х = <img width=«41» height=«41» src=«ref-3_612053495-172.coolpic» v:shapes="_x0000_i1639"> — посторнний корень, т.к. arсcos <img width=«93» height=«61» src=«ref-3_612054096-314.coolpic» v:shapes="_x0000_i1640"> = аrcsin <img width=«91» height=«61» src=«ref-3_612054410-314.coolpic» v:shapes="_x0000_i1641"> ,

arсcos(-<img width=«23» height=«41» src=«ref-3_612054724-142.coolpic» v:shapes="_x0000_i1642">) = аrcsin(-<img width=«24» height=«41» src=«ref-3_612054866-140.coolpic» v:shapes="_x0000_i1643">) — неверно. Ответ: 1.

Использование свойств монотонности обратных тригонометрических функций

Решить уравнение: arctg<img width=«215» height=«41» src=«ref-3_612055006-423.coolpic» v:shapes="_x0000_i1049"> .

Решение: Пусть х2 + х = t. Тогда уравнение примет вид arctg<img width=«145» height=«41» src=«ref-3_612055429-325.coolpic» v:shapes="_x0000_i1050">.

Функции Z= <img width=«25» height=«27» src=«ref-3_612055754-117.coolpic» v:shapes="_x0000_i1051"> Z= <img width=«43» height=«24» src=«ref-3_612055871-142.coolpic» v:shapes="_x0000_i1052">, y= arctgz и y= arcsinz являются монотонно

возрастающими. Поэтому функция y= arctg<img width=«23» height=«24» src=«ref-3_612056013-109.coolpic» v:shapes="_x0000_i1053"> +arcsin<img width=«43» height=«24» src=«ref-3_612055871-142.coolpic» v:shapes="_x0000_i1054"> также является

монотонно возрастающей.

Уравнение arctg<img width=«145» height=«41» src=«ref-3_612055429-325.coolpic» v:shapes="_x0000_i1055">.

имеет не более одного корня. Находим подбором t= 0 – корень данного уравнения.

Поэтому х2+ х = 0, х = 0, х = -1.

Ответ: -1; 0.

Использование ограниченности обратных тригонометрических функций

Решить уравнение: аrcsin(х ( х+у )) + аrcsin(у ( х+у )) = <img width=«15» height=«15» src=«ref-3_611827999-89.coolpic» v:shapes="_x0000_i1644">

Т.к. аrcsint<img width=«31» height=«41» src=«ref-3_612056678-141.coolpic» v:shapes="_x0000_i1645"> при <img width=«36» height=«27» src=«ref-3_612056819-143.coolpic» v:shapes="_x0000_i1646">, то левая часть уравнения не превосходит <img width=«73» height=«41» src=«ref-3_612056962-210.coolpic» v:shapes="_x0000_i1647">.

Знак равенства возможен, лишь если каждое слагаемое левой части равно <img width=«17» height=«41» src=«ref-3_611987910-117.coolpic» v:shapes="_x0000_i1648">.

Таким образом, уравнение равносильно системе: <img width=«239» height=«88» src=«ref-3_612057289-935.coolpic» v:shapes="_x0000_i1649">

Итак, х = у, тогда получаем уравнение 2х<img width=«11» height=«20» src=«ref-3_612010953-79.coolpic» v:shapes="_x0000_i1650"> = 1, х<img width=«65» height=«44» src=«ref-3_612058303-204.coolpic» v:shapes="_x0000_i1651">, у<img width=«65» height=«44» src=«ref-3_612058303-204.coolpic» v:shapes="_x0000_i1652">

Ответ: <img width=«159» height=«44» src=«ref-3_612058711-475.coolpic» v:shapes="_x0000_i1653">

3.3. Задания, предлагаемые в ЕГЭ

Пример 1. Решить уравнения:

а) <img width=«169» height=«45» src=«ref-3_612059186-458.coolpic» v:shapes="_x0000_i1654">.

Решение.Достаточно вначале выписать и решить систему неравенств, которые задают область определения и область значений арксинуса.

Проверка показывает, что x=-3 подходит.

Ответ.x=-3

б) <img width=«177» height=«41» src=«ref-3_612061618-384.coolpic» v:shapes="_x0000_i1656">

Решение.ОДЗ: <img width=«41» height=«19» src=«ref-3_612062002-126.coolpic» v:shapes="_x0000_i1657">. Вычисляя тангенсы обеих частей уравнения, получим

Ясно, что <img width=«83» height=«23» src=«ref-3_612064048-174.coolpic» v:shapes="_x0000_i1660"> являются корнями исходного уравнения; <img width=«51» height=«24» src=«ref-3_612064222-129.coolpic» v:shapes="_x0000_i1661"> — корень уравнения в силу нечетности функции арктангенс.

Ответ.<img width=«143» height=«24» src=«ref-3_612064351-225.coolpic» v:shapes="_x0000_i1662">

в) <img width=«209» height=«41» src=«ref-3_612064576-592.coolpic» v:shapes="_x0000_i1663">

Решение.ОДЗ: <img width=«41» height=«19» src=«ref-3_612062002-126.coolpic» v:shapes="_x0000_i1664">. По определению <img width=«308» height=«41» src=«ref-3_612065294-563.coolpic» v:shapes="_x0000_i1665"><img width=«12» height=«23» src=«ref-3_611975451-73.coolpic» v:shapes="_x0000_i1666">Вычисляя котангенсы обеих частей, получим эквивалентное уравнение (т.к. котангенс на интервале (0; <img width=«15» height=«15» src=«ref-3_611827999-89.coolpic» v:shapes="_x0000_i1667">) монотонно убывающая функция и, следовательно, из равенств котангенсов двух углов следует равенство этих углов):

Ответ. <img width=«92» height=«23» src=«ref-3_612066851-179.coolpic» v:shapes="_x0000_i1669">.

г) <img width=«179» height=«41» src=«ref-3_612067030-362.coolpic» v:shapes="_x0000_i1056">.

Решение.ОДЗ: <img width=«153» height=«56» src=«ref-3_612067392-441.coolpic» v:shapes="_x0000_i1057"> Запишем уравнение в эквивалентной форме:

<img width=«196» height=«44» src=«ref-3_612067833-402.coolpic» v:shapes="_x0000_i1058">.

Отметим, что

и, следовательно, вычисляя синусы обеих частей уравнения, мы получим в качестве следствия уравнение

Проверка показывает, что <img width=«41» height=«23» src=«ref-3_612069684-127.coolpic» v:shapes="_x0000_i1672"> является корнем исходного уравнения, а <img width=«47» height=«41» src=«ref-3_612069811-163.coolpic» v:shapes="_x0000_i1673"> ему не удовлетворяет:

Значение <img width=«20» height=«23» src=«ref-3_612070537-96.coolpic» v:shapes="_x0000_i1675"> появилось при переходе от исходного уравнения к уравнению-следствию.

Ответ. <img width=«44» height=«25» src=«ref-3_612070633-118.coolpic» v:shapes="_x0000_i1676">

д) <img width=«160» height=«22» src=«ref-3_612070751-596.coolpic» v:shapes="_x0000_i1677">

Решение.ОДЗ: <img width=«159» height=«56» src=«ref-3_612071347-487.coolpic» v:shapes="_x0000_i1678"> Отметим, что знаки обеих частей уравнения совпадают только на отрезке <img width=«44» height=«45» src=«ref-3_612071834-205.coolpic» v:shapes="_x0000_i1679">, где <img width=«231» height=«41» src=«ref-3_612072039-469.coolpic» v:shapes="_x0000_i1680"> (на отрезке <img width=«288» height=«45» src=«ref-3_612072508-611.coolpic» v:shapes="_x0000_i1681"> и, следовательно, уравнение не имеет решения). Но на отрезке <img width=«45» height=«45» src=«ref-3_612073119-203.coolpic» v:shapes="_x0000_i1682"> функция синус монотонна и, следовательно, взяв синусы обеих частей уравнения, на отрезке <img width=«43» height=«45» src=«ref-3_612073322-196.coolpic» v:shapes="_x0000_i1683"> получим уравнение, эквивалентное исходному: <img width=«12» height=«23» src=«ref-3_611975451-73.coolpic» v:shapes="_x0000_i1684"><img width=«524» height=«48» src=«ref-3_612073591-1623.coolpic» v:shapes="_x0000_i1685">

Ответ. <img width=«39» height=«41» src=«ref-3_612075214-145.coolpic» v:shapes="_x0000_i1686">

е) <img width=«163» height=«41» src=«ref-3_612075359-332.coolpic» v:shapes="_x0000_i1687">

Решение.Перепишем уравнение в виде

и перейдем к уравнению-следствию, взяв косинус от обеих частей

При таком решении необходима проверка. Легко видеть, что х=0 – корень уравнения.

Ответ. х=0.

продолжение --PAGE_BREAK--

www.ronl.ru

Реферат Тригонометрические функции 2

Математики Ближнего и Среднего Востока превратили тригонометрия из раздела астрономии в самостоятельную математическую дисциплину. В Х-Х1 в.в. они впервые доказали теорему синусов, открытие которой сыграло важнейшую роль в тригонометрии. Помимо синуса, были выведены другие функции и составлены таблицы для них.

Общепринятые понятия тригонометрии, а также обозначения и определения тригонометрических функций сформировались в процессе долгого исторического развития. Если , например, при введении основных тригонометрических понятий представляется естественным принимать радиус тригонометрического круга ( рис.1), равным единице, то эта, казалось бы, простая идея была усвоена только в Х-Х1 веке.

Рис. 1.

Если мы понимаем под синусом угла в прямоугольном треугольнике ОВС отношение катета ВС (линия синуса) к гипотенузе ОС (т.е. радиусу единичной окружности ), то в средние века термином «синус» обозначали саму линию синуса ВС. То же относится к косинусу, под которым понимали линию косинуса ОВ, и другим тригонометрическим функциям. Лишь благодаря введению новых понятий, а также в результате разработки и усовершенствования математической символики, тригонометрия приобрела современный вид, наиболее удобный для решения вычислительных задач.

ЛИТЕРАТУРА.1. Энциклопедический словарь юного математика.

2. Большая детская энциклопедия. Математика.

bukvasha.ru

Курсовая работа - Тригонометрические функции 2

Рис. 1.

ЛИТЕРАТУРА.

1. Энциклопедический словарь юного математика.

2. Большая детская энциклопедия. Математика.

www.ronl.ru

Смотрите также

..:::Новинки:::..

Windows Commander 5.11 Свежая версия.

Новая версия
IrfanView 3.75 (рус)

Обновление текстового редактора TextEd, уже 1.75a

System mechanic 3.7f
Новая версия

Обновление плагинов для WC, смотрим :-)

Весь Winamp
Посетите новый сайт.

WinRaR 3.00
Релиз уже здесь

PowerDesk 4.0 free
Просто - напросто сильный upgrade проводника.

..:::Счетчики:::..