Отдел образования, спорта и туризма Борисовского райисполкома
Государственное учреждение образования
«Средняя школа № 16 г. Борисова»
Треугольник Паскаля
Автор:
учащаяся 7 «А» класса
Абоян Елизавета Александровна,
домашний адрес: г. Борисов,
ул Смолевичская, д. 8, 76-51-80
Руководитель:
Ищук Ольга Эдуардовна, учитель математики
Борисов, 2016
Оглавление
В этом учебном году мы начали изучать новый предмет «геометрия».
Одна из глав курса геометрии называется «Треугольники». Меня очень заинтересовала данная тема. Я всегда хотела узнать много нового о треугольниках, об их происхождении и значении в нашей жизни. Ведь мир треугольников очень загадочен и интересен.
Треугольник - первая геометрическая фигура, встречающаяся в древних орнаментах. Изучая литературу, я узнала, что в Египте он символизировал триаду духовной воли, любви, интуиции и высшего разума человека, то есть его личность или душу.
Ацтеки использовали изображение треугольника с вершиной наверху, соединенного с перевернутым треугольником, в качестве символа временного цикла. Треугольник в сочетании с крестом образует алхимический знак Серы.
Равносторонний треугольник, символизирующий, по древнееврейской традиции, совершенство, у христиан означает Троицу - Отца, Сына и Святого Духа.
Существует множество видов треугольников, но больше всего меня заинтересовал треугольник Паскаля.
Проблема исследования:
Проблема моего исследования состоит в том, что я попыталась выявить и показать то, насколько широко треугольники используются в практической жизни.
Практическая значимость исследования:
Данная исследовательская работа может быть использован как дополнительный материал к урокам геометрии, для внеклассной работы по математике.
Цель исследования:
- ознакомиться с треугольником Паскаля и его применением как разновидностью треугольников;
Гипотеза:
Если числа треугольника Паскаля обладают особыми свойствами, то его можно считать уникальным для решения различных задач
Задачи:
- определить применение свойств чисел треугольника Паскаля;
- изучить литературу по теме «Треугольник Паскаля»;
- выявить свойства чисел, входящих в состав треугольника Паскаля;
- сформулировать вывод и итоги исследования;
Объект исследования: треугольник как геометрическая фигура
Предмет исследования: свойства треугольника Паскаля
Методы исследования:
- аналитико-статистическая работа со справочной, научно-познавательной и специальной литературой;
- поиск информации в интернет - ресурсах.
Направления работы:
- выбор проблемы, источников литературы, составление плана;
- работа с литературой и другими источниками;
- обработка полученных данных;
- анализ результатов, формулирование вывода;
- мультимедийная подготовка.
Основные этапы исследования: подготовительный; деятельностный;
Ход исследования: рефлексивный; аналитический; презентационный.
Моё первое знакомство с треугольником Паскаля произошло во время изучения темы «Возведение двучлена в степень» на уроке алгебры. Мне уже известны формулы квадрата суммы и квадрата разности, куба суммы и куба разности. Я заметила, что получить формулы для возведения двучлена в четвёртую, пятую и т.д. степень возможно, учитывая некоторую закономерность в коэффициентах и степенях каждого слагаемого.
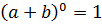
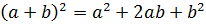
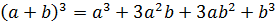
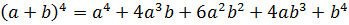
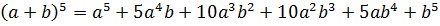
Коэффициенты всех строк можно расположить в виде треугольника:
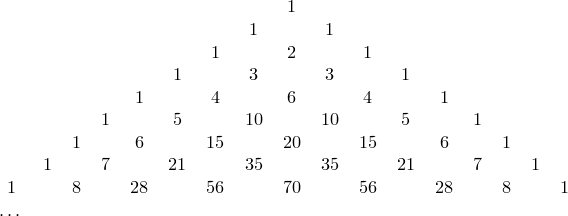
Таким образом я познакомилась с треугольником Паскаля и решила продолжить изучение арифметического треугольника.
Б
лез Паскаль (19 июня 1623, Клермон-Ферран, — 19 августа 1662, Париж) — французский математик, физик, литератор и философ.
Паскаль был первоклассным математиком. Он помог создать два крупных новых направления математических исследований. В возрасте шестнадцати лет написал замечательный трактат о предмете проективной геометрии и в 1654 году переписывался с Пьером де Ферма по теории вероятностей, что впоследствии оказало принципиальное влияние на развитие современной экономики.
Изучая разновидности треугольников, я выяснила, что треугольник Паскаля — арифметический треугольник, образованный биномиальными коэффициентами. Назван в честь Блеза Паскаля. В действительности, треугольник Паскаля был известен задолго до 1653 года - даты выхода "Трактата об арифметическом треугольнике". Так, этот треугольник воспроизведен на титульном листе учебника арифметики, написанном в начале XVI Петром Апианом, астрономом из Ингольтштадского университета. Изображен треугольник и на иллюстрации в книге одного китайского математика, выпущенной в 1303 году. Омар Хайям, бывший не только философом и поэтом, но и математиком, знал о существовании треугольника уже около 1100 года, в свою очередь, заимствовав его из более ранних китайских или индийских источников.
Ещё я узнала из книги "Математические новеллы" (М., Мир, 1974) Мартина Гарднера, что "Треугольник Паскаля так прост, что выписать его сможет даже десятилетний ребенок. В тоже время он таит в себе неисчерпаемые сокровища и связывает воедино различные аспекты математики, не имеющие на первый взгляд между собой ничего общего. Столь необычные свойства позволяют считать треугольник Паскаля одной из наиболее изящных схем во всей математике".
Я рассмотрела схему построения треугольника, предложенную Гуго Штейнгаузом в его классическом «Математическом калейдоскопе»: предположим, что вы входите в город как показано на схеме синей стрелкой, и можете двигаться только вперед, точнее, все время выбирая, вперед налево, или вперед направо. Узлы, в которые можно попасть только единственным образом, отмечены зелеными смайликами, точка, в которую можно попасть двумя способами, показана красным смайликом, а тремя, соответственно - розовыми. Это один из вариантов построения треугольника.
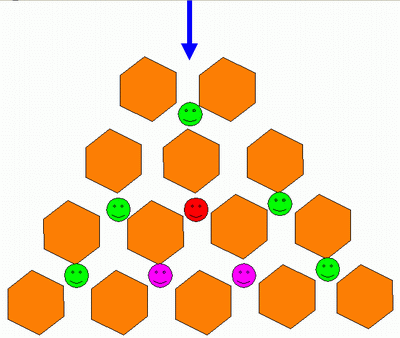
( Рисунок 1)
Изучая специальную литературу, я узнала, что еще проще объясняют устройство треугольника Паскаля слова: каждое число равно сумме двух расположенных над ним чисел.
Все элементарно, но сколько в этом таится чудес. Если очертить треугольник Паскаля, то получится равнобедренный треугольник. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Треугольник можно продолжать неограниченно. Он обладает симметрией относительно вертикальной оси, проходящей через его вершину. Вдоль диагоналей (насколько у треугольника могут быть диагонали, но не будем придираться, такая терминология встречается в публикациях), параллельных сторонам треугольника (на рисунке отмечены зелеными линиями) выстроены треугольные числа и их обобщения на случай пространств всех размерностей. Треугольные числа в самом обычном и привычном нам виде показывают, сколько касающихся кружков можно расположить в виде треугольника - как классический пример начальная расстановка шаров в бильярде. К одной монетке можно прислонить еще две - итого три - к двум можно приладить еще три - итого шесть.
Получили треугольные числа на рисунке: 3; 6; 10; 15.
Продолжая наращивать ряды с сохранением формы треугольника получим ряд 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66..., что и показывает вторая зеленая линия. Этот замечательный ряд, каждый член которого равен сумме натурального ряда чисел (55=1+2+3+4+5+6+7+8+9+10), содержит также множество знакомцев, хорошо известных любителям математики: 6 и 28 - совершенные числа, 36 - квадратное число, 8 и 21 - числа Фибоначчи.
Следующая зеленая линия покажет нам тетраэдральные числа - один шар мы можем положить на три - итого четыре, под три подложим шесть - итого десять, и так далее.
Чтобы найти сумму чисел, стоящих на любой диагонали от начала до интересующего нас места, достаточно взглянуть на число, расположенное снизу и слева от последнего слагаемого, (слева для правой диагонали, для левой диагонали будет справа, а вообще - ближе к середине треугольника). Пусть, например, мы хотим вычислить сумму чисел натурального ряда от 1 до 9. "Спустившись" по диагонали до числа 9, мы увидим слева снизу от него число 45. Оно то и дает искомую сумму. Чему равна сумма первых восьми треугольных чисел? Отыскиваем восьмое число на второй диагонали и сдвигаемся вниз и влево. Ответ: 120.
(Рисунок 2)
Треугольник Паскаля имеет применение в теории вероятностей и обладает замечательными свойствами.
Паскаль подробно исследовал свойства и применения своего "треугольника". Приведу для примера лишь 3 свойства "треугольника", найденные самим Паскалем; при этом буду исходить из того расположения "треугольника" на плоскости, какое было указанно Паскалем, и говорить о горизонтальных и вертикальных рядах.
Свойство 1: Каждое число А в таблице равно сумме чисел предшествующего горизонтального ряда, начиная с самого левого вплоть до стоящего непосредственно над числом А (в котором клетки, содержащие слагаемые, дающие в сумме А, заштрихованы). (Рисунок 4)
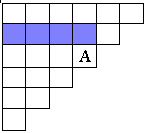
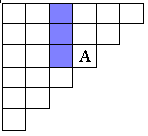
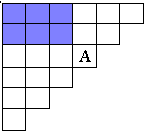
(Рисунок 4) (Рисунок 5) (Рисунок 6)
Свойство 2: Каждое число А в таблице равно сумме чисел предшествующего вертикального ряда, начиная с самого верхнего вплоть до стоящего непосредственно левее числа А. (Рисунок 5)
Свойство 3: Каждое число в таблице, будучи уменьшенным на единицу, равно сумме всех чисел, заполняющих прямоугольник, ограниченный теми вертикальными и горизонтальными рядами, на пересечении которых стоит число А (сами эти ряды в рассматриваемый прямоугольник не включаются). (Рисунок 6)
Блез Паскаль и другой великий француз, Пьер Ферма, стали основателями теории вероятностей, когда Паскаль и Ферма независимо друг от друга дали правильное объяснение так называемого парадокса раздела ставки. Два игрока играют в "безобидную" игру (т.е. шансы победить у обоих одинаковы), договорившись, что тот, кто первым выигрывает шесть партий, получит весь приз. Предположим, что игра остановилась до того, как один из них выиграл приз (например, первый игрок выиграл пять партий, а второй - три). Как справедливо разделить приз? Так, согласно одному решению следовало разделить приз в отношении 5 : 3, т.е. пропорционально выигранным партиям, согласно другому - в отношении 2 : 1 (здесь рассуждения велись, по всей видимости, следующим образом: поскольку первый игрок выиграл на две партии больше, что составляет третью часть от необходимых для победы шести партий, то он должен получить одну треть от приза, а оставшуюся часть нужно разделить пополам).
А между тем делить надо в отношении 7:1. И Паскаль, и Ферма рассматривали парадокс раздела ставки как задачу о вероятностях, установив, что справедливым является раздел, пропорциональный шансам первого игрока выиграть приз. Предположим, первому игроку осталось выиграть только одну партию, а второму для победы необходимо выиграть еще три партии, причем игроки продолжают игру и играют все три партии, даже если некоторые из них окажутся лишними для определения победителя. Для такого продолжения все 23 = 8 возможных исходов будут равновероятными. Так как второй игрок получает приз только при одном исходе (если он выиграл все три партии), а в остальных случаях побеждает первый игрок, справедливым является отношение 7 : 1.
В науке и практике часто встречаются задачи, решая которые приходится составлять различные комбинации из конечного числа элементов и подсчитывать число комбинаций. Такие задачи получили название комбинаторных задач.
Рассмотрим основные формулы комбинаторики:
Размещение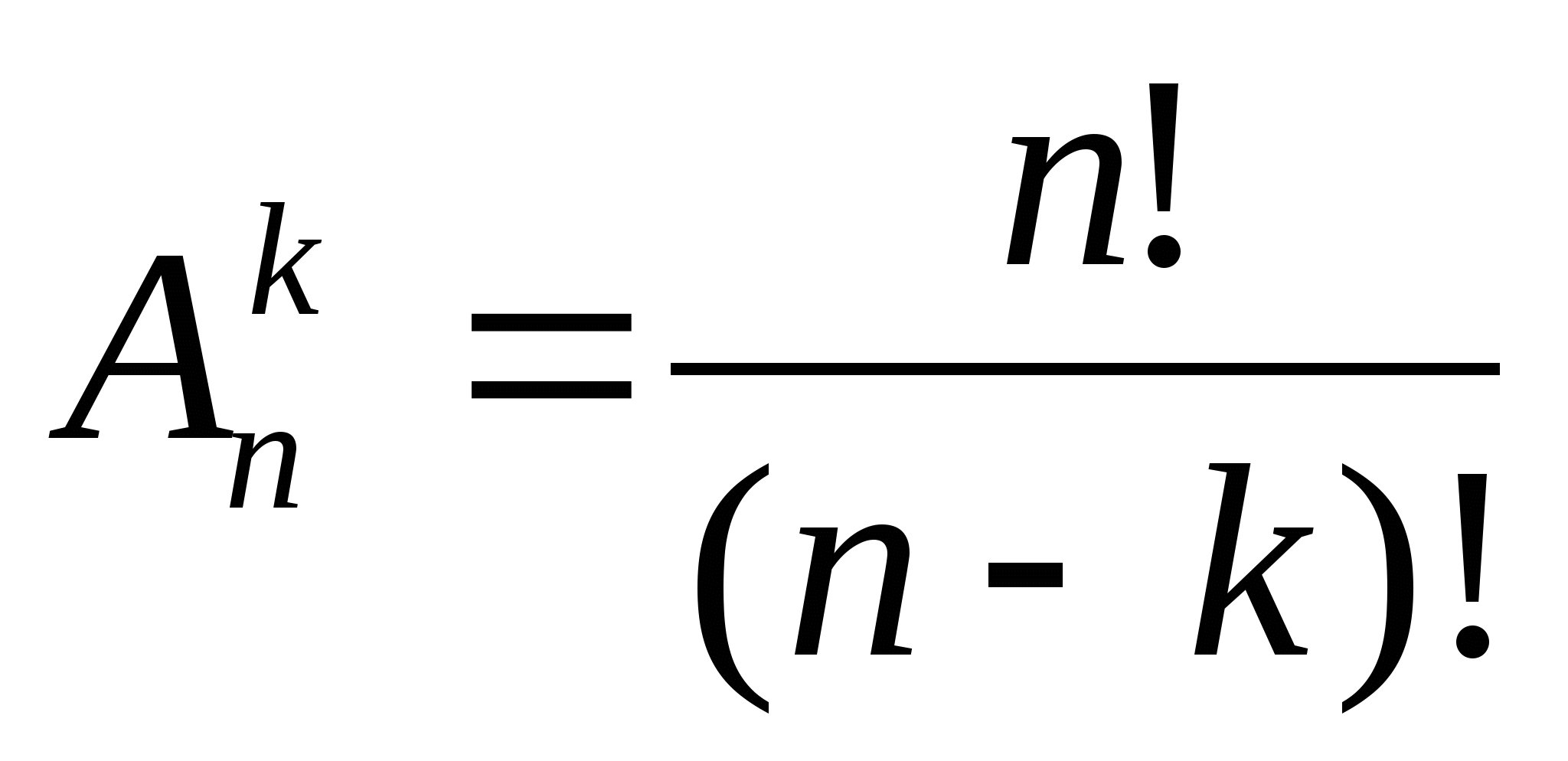 
Это любое упорядоченное подмножество m из элементов множества n.
Перестановки (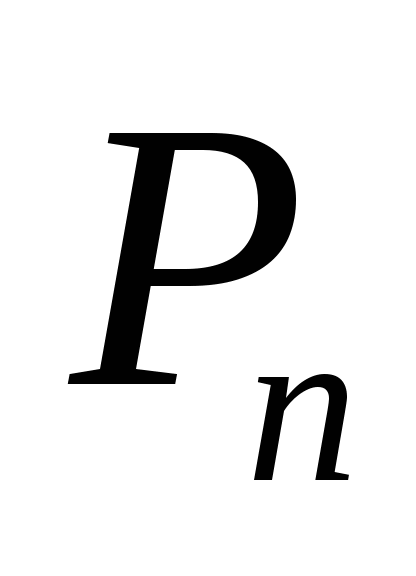
). Если k= n, то эти размещения называются перестановками.
Сочетания (
) – это любое подмножество из k – элементов, которые принадлежат множеству, состоящему из n – различных элементов.
.
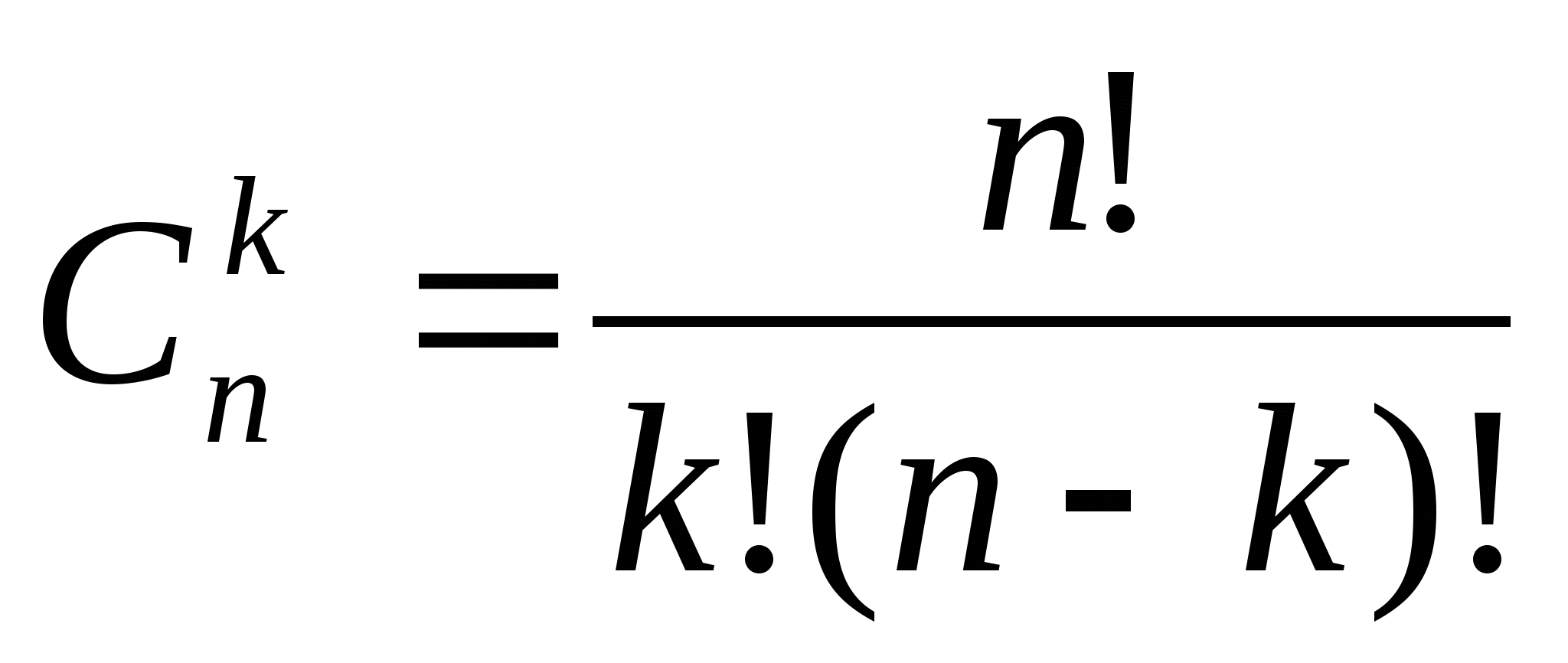В треугольнике Паскаля число, показывающее, сколькими способами можно выбрать k элементов из множества, содержащего n различных элементов, стоит на пересечении k-ой диагонали и n-ой строки. Чтобы вычислить сочетание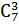 
, найду диагональ седьмую сверху и отсчитываю три числа по горизонтали. Получу число 35.
Можно использовать треугольник Паскаля и для вычисления размещений.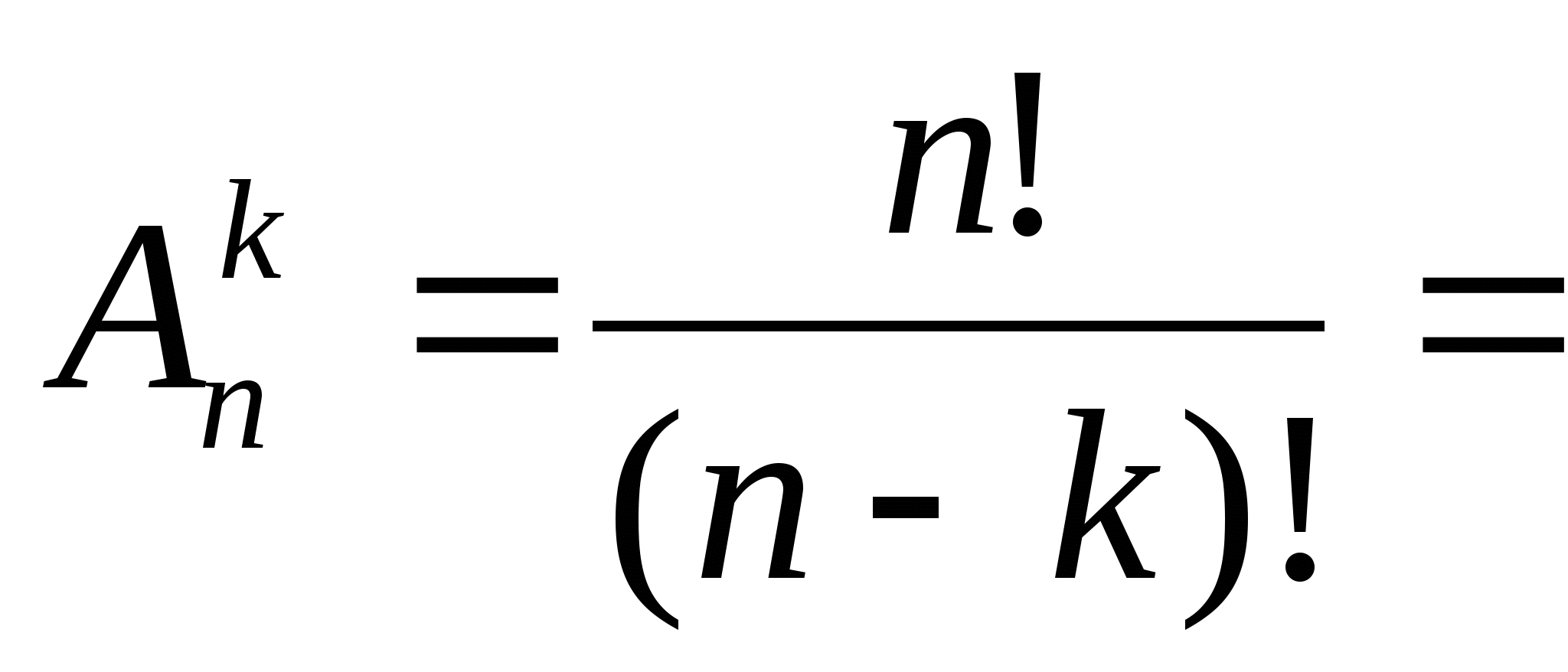 
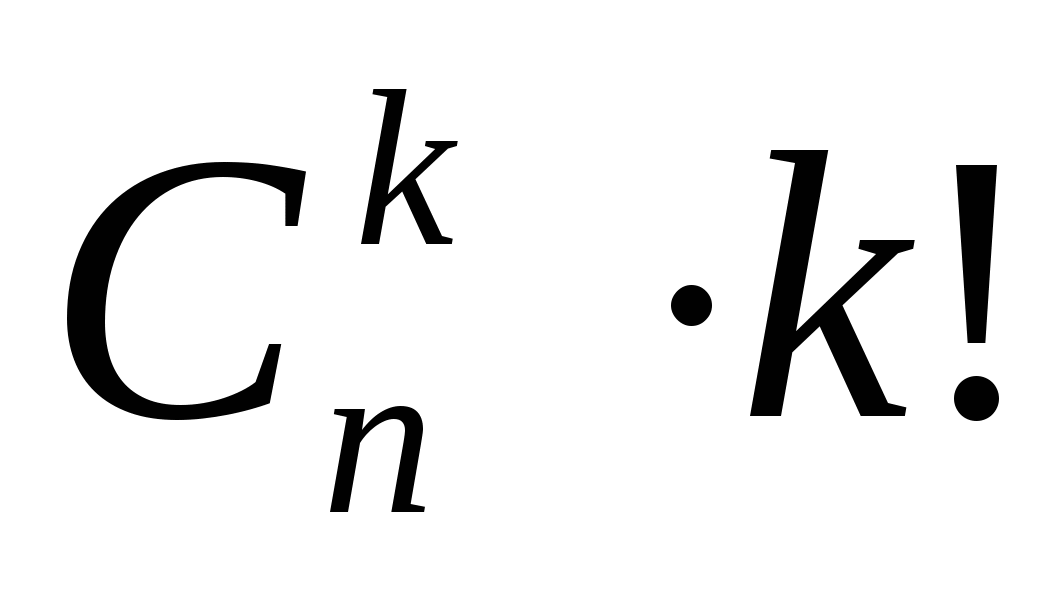.Если нам нужно посчитать 
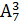, то зная что 
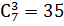, а 3!=6, получим значение данного размещения 210.
Я пришла к выводу, что рассмотренные свойства треугольника Паскаля подтверждают слова Мартина Гарднера о том, что треугольник Паскаля одна из наиболее изящных схем во всей математике.
Актуальность исследования обусловлена ежегодным усложнением заданий ЦТ, что требует углубленных знаний не только в алгебре, но и в геометрии.
В своей практической работе я подобрала ряд задач по теме «Треугольник Паскаля»
Задача 1. В магазине «Филателия» продается 8 различных наборов марок, посвященных спортивной тематике. Сколькими способами можно выбрать из них 3 набора?
Решение:
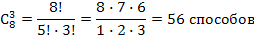
В
треугольнике Паскаля число, показывающее, сколькими способами можно выбрать k элементов из множества, содержащего n различных элементов, стоит на пересечении k-ой диагонали и n-ой строки.
Найду диагональ восьмую сверху и отсчитываю три числа по горизонтали. Получу число 56. (Рисунок 8)
Задача 2.Из шести врачей поликлиники двух необходимо отправить на курсы повышения квалификации. Сколькими способами это можно сделать?
Решение: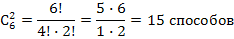
Найду диагональ шестую сверху и отсчитываю два числа по горизонтали. Получу число 15.
(Р(Рисунок 9)
Задача3. В пачке находятся одинаковые по размеру 7 тетрадей в линейку и 5 в клетку. Из пачки наугад берут 3 тетради. Какова вероятность того, что все три тетради окажутся в клетку?
Решение. Сначала найдём общее число возможных исходов, т.е. сколькими способами мы можем выбрать 3 тетради из 12 тетрадей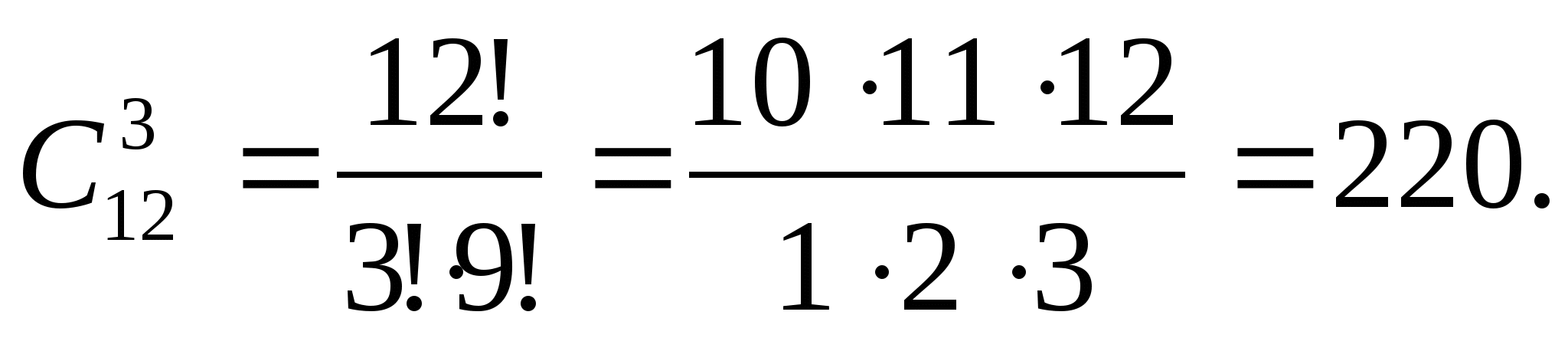 
А сколькими способами мы можем выбрать 3 тетради в клетку из имеющихся 5 тетрадей?
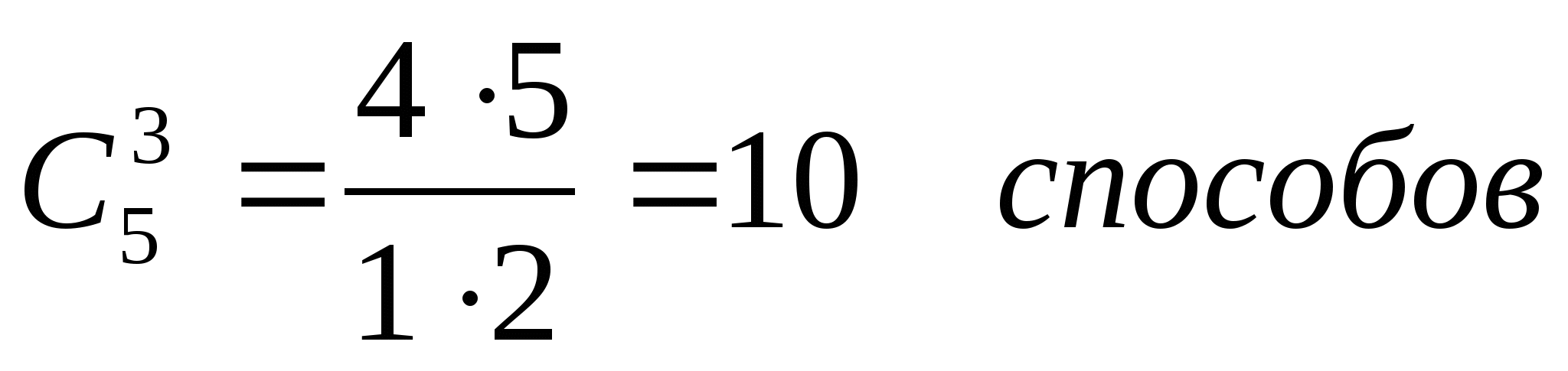
В
ероятностью Р наступления случайного события А называется отношение m/n, где n – число всех возможных исходов эксперимента, а m – число всех благоприятных исходов: Р(А)= m/n.
По формуле нахождения вероятности получим
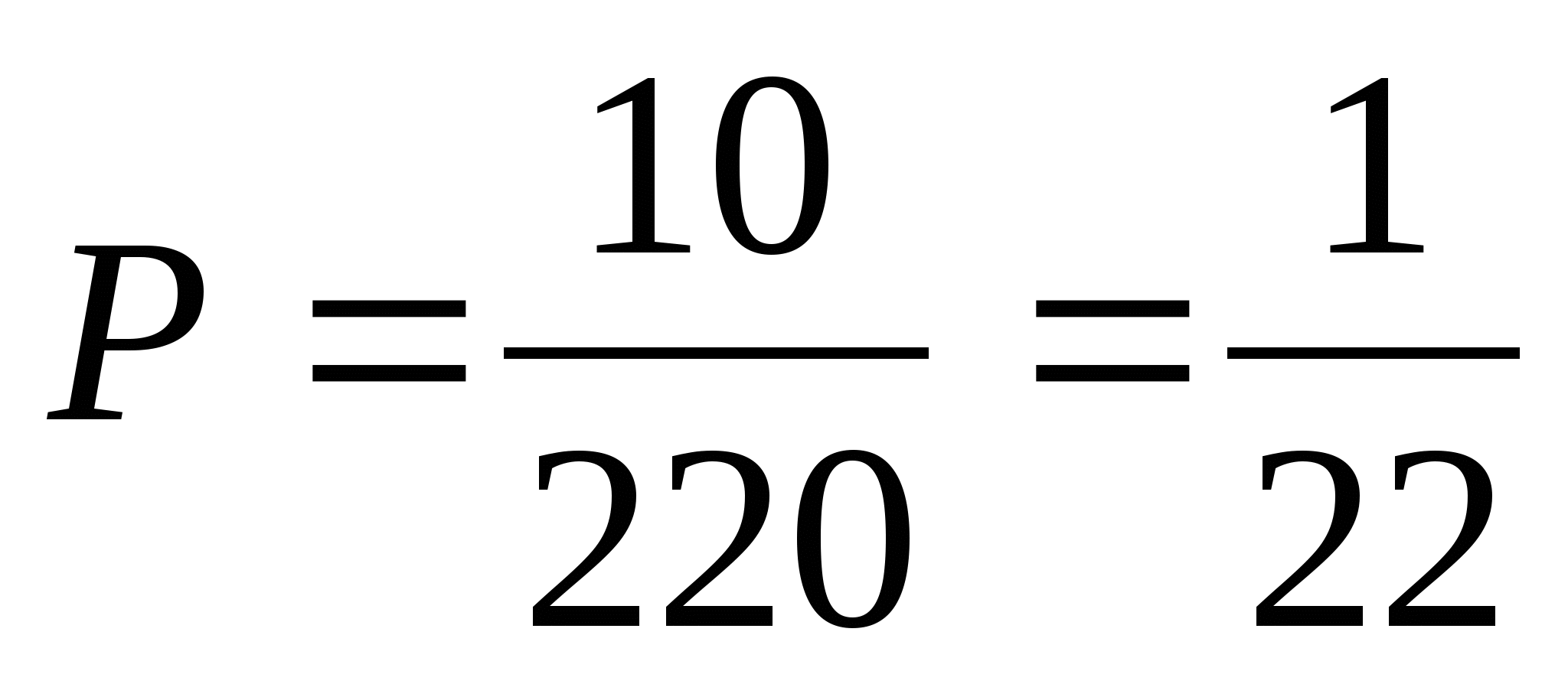
(Рисунок 10)
Задача4. На плоскости даны 10 прямых, причём среди них нет параллельных и через каждую точку их пересечения проходят ровно две прямые. Сколько у них точек пересечения?
Решение: ответ находится на пересечении -45 точек!
Задача 5. В сумке 10 мячей, пронумерованных от 1 до 10. Наугад вынимают 2 мяча. Какова вероятность того, что это будут мячи с номерами 7 и 3?
В
ынуть 2 мяча из 10 имеющихся можно 45 способами. Вероятность нашего события 2 из 45. (Рисунок 11)
В ходе проведения практического исследования я пришла к следующим выводам: при решении комбинаторных задач и задач по теории вероятностей можно пользоваться не только формулами комбинаторики, но и использовать свойства треугольника Паскаля
Работа по выбранной теме осуществлялась в полном соответствии с планом исследования, а именно: объект и предмет исследования, поставлены цели и задачи, а также определены ожидаемые результаты. Были указаны используемые методы исследования, определена проблема.
В данной работе была дана общая характеристика треугольника как геометрической фигуры, был детально рассмотрен треугольник Паскаля, его свойства.
Я пришла к выводу, что одной из наиболее известных и изящных численных схем во всей математике является треугольник Паскаля. Треугольник Паскаля - понятие значительно шире, чем мне представлялось. Он обладает не только удивительными свойствами, но и применялся в архитектуре средних веков для построения схем пропорциональности и для построения прямых углов землемерами и архитекторами. Используя треугольник Паскаля, можно решить задачи из теории вероятности и комбинаторики. С комбинаторными задачами я встречалась на уроках математики в 6 классе и при решении олимпиадных задач
Практическая значимость данной работы заключается в следующем: я, изучив много литературы по данному вопросу, получила дополнительные знания в области математики, укрепила свой интерес к этой науке.
Я узнала, что треугольник Паскаля применяется:
В курсе алгебры
При решении комбинаторных задач
Для решения различных задач в области физики
С появлением вычислительных машин построение треугольника Паскаля стало излюбленной задачкой для начинающих при изучении основ программирования.
Работа по данной теме оказалась интересной и полезной.
1. Абачиев С. К., Радужная фрактальность треугольника Паскаля / С. К. Абачиев, -- Минск, 1999.—168с.
2. Галкин Е.В. Нестандартные задачи по математике. Задачи логического характера. Книга для учащихся 5-11кл.Москва, «Просвещение», 1996г. – 194 с.
3. Мартин Гарднер. Глава 17. Неисчерпаемое очарование треугольника Паскаля / Математические новеллы. — Минск: Мир, 1974.— 456 с.
4. Треугольник Паскаля. В. А. Успенский. - 2 - е изд. – Москва: Наука, 1979. – 48с.
5. Фукс Д., Фукс М., Арифметика биномиальных коэффициентов / Квант. — 1970. — № 6. — С.17-25.
6. Энциклопедия для детей. Т 11. Математика / Глав. ред. М. Аксенова; метод. и отв. ред. В. Володин. – М.: Аванта+,2004. – 688с.
7. http://ru.wikipedia.org/wiki/
8. http://davaiknam.ru/text/volshebnij-treugolenik.
infourok.ru
Самарский филиал
Государственного образовательного учреждения
высшего профессионального образования города Москвы
«Московский городской педагогический университет»
Факультет информатики
Кафедра высшей математики и информатики
КУРСОВАЯ РАБОТА
Треугольник паскаля его свойства и приложения
Студента 4 курса
А.В. Копытов
Подпись________________
Научный руководитель:
Самара
2011
Оглавление
Введение ……………….……………………………………………………………..…..……3
Глава 1. Теоретические сведения о треугольнике паскаля его свойств и приложений..…………………………………………………………………………..……….5
§1.1. История Треугольника Паскаля ………………………………………………………..5
§1.2. Треугольник Паскаля.……………………………………………………………………6
§1.3. Свойства треугольника паскаля..……………………………………………………….8
§1.4. Администрирование базы данных……………………………………………………..12
§1.5. Администратор базы данных…………………………………………………………..13
Глава 2. Пример проектирования и администратирования баз данных …………...……..16
§2.1. Урок 1: Классические подходы в АБД………………………………………….......17
§2.2. Урок 2: Современные условия работы АБД………………… …………..…..….…19
§2.3. Урок 3 :Основные этапы и задачи проектирования баз данных……………....….22
Заключение..………………………………………………………………………..…….…....23
Библиография……………………………………………………………………………....….25
Введение
Треугольник Паскаля так прост, что выписать его сможет даже десятилетний ребенок. В то же время он таит в себе неисчерпаемые сокровища и связывает воедино различные аспекты математики, не имеющие на первый взгляд между собой ничего общего. Столь необычные свойства позволяют считать треугольник Паскаля одной из наиболее изящных схем во всей математике.
В нашей повседневной жизни мы широко используем раздел математики, называемый комбинаторным анализом. Этот раздел математики изучает так называемые конечные множества. Множество, состоящее из n элементов, называется n-элементным. Однако, мы можем выбрать k элементов из n-элементного множества. Каждая k-элементная часть n-элементного множества называется сочетанием из n элементов по k.
Цель исследования – ознакомиться с созданием баз данных, с сегодняшними проблемами и тенденциями развития.
Проблема исследования – изучение структуры и содержания системы задач по теме «Проектирование и администратирования баз данных» : технические средства и программное обеспечение» с позиции деятельностного подхода к обучению.
Объект исследования – процесс обучения информатике в основной школе.
Предмет исследования – система задач для изучения способов измерения информации учащимися 9-х классов.
Задачи исследования – 1) провести анализ психолого-педагогической, научно-методической, учебно-дидактической литературы; 2) определить методические принципы построения системы задач; 3) изучить задачи на измерение информации, приводимые в различных школьных учебниках по информатике; 4) разработать вариант системы задач для изучения способов измерения информации.
Методы исследования – анализ исторической, психолого-педагогической, научно-методической, учебно-дидактической литературы, учебников и учебных пособий по информатике; изучение опыта по организации деятельностного подхода к обучению; обобщение опыта работы автора в школе во время педагогической практики, анкетирование и тестирование учащихся 8-х классов, оценивание полученных результатов.
Глава 1. Теоретические сведения об проектировании и администратировании баз данных.
§1.1. История Треугольника Паскаля
Первое упоминание треугольной последовательности биномиальных коэффициентов под названием meru-prastaara встречается в комментарии индийского математика X века Халаюдхи к трудам другого математика, Пингалы. Треугольник исследуется также Омаром Хайямом около 1100 года, поэтому в Иране эту схему называют треугольником Хайяма. В 1303 году была выпущена книга «Яшмовое зеркало четырёх элементов» китайского математика Чжу Шицзе, в которой был изображен треугольник Паскаля на одной из иллюстраций; считается, что изобрёл его другой китайский математик, Ян Хуэй (поэтому китайцы называют его треугольником Яна Хуэя). На титульном листе учебника арифметики, написанном в 1529 году Петром Апианом, астрономом из Ингольтштадского университета, также изображён треугольник
Треугольник Паскаля был известен задолго до 1653 года - даты выхода "Трактата об арифметическом треугольнике". Так, этот треугольник воспроизведен на титульном листе учебника арифметики, написанном в начале XVI Петром Апианом, астрономом из Ингольтштадского университета. Изображен треугольник и на иллюстрации в книге одного китайского математика, выпущенной в 1303 году. Омар Хайям, бывший не только философом и поэтом, но и математиком, знал о существовании треугольника около 1100 года, в свою очередь, заимствовав его из более ранних китайских или индийских источников.
Мартин Гарднер пишет в книге "Математические новеллы" (М., Мир, 1974): "Треугольник Паскаля так прост, что выписать его сможет даже десятилетний ребенок. В тоже время он таит в себе неисчерпаемые сокровища и связывает воедино различные аспекты математики, не имеющие на первый взгляд между собой ничего общего. Столь необычные свойства позволяют считать треугольник Паскаля одной из наиболее изящных схем во всей математике".
А в 1653 году (в других источниках в 1655 году) вышла книга Блеза Паскаля «Трактат об арифметическом треугольнике»
Блез Паскаль, Blaise Pascal (родился 19 июня 1623 в Клермон-Ферране, ныне французский регион Овернь; умер 19 августа 1662 в Париже) - физик, математик, философ, писатель. Человек поразительных интеллектуальных способностей, проявившихся уже в раннем детстве. Его открытия в математике и физике заложили основы современной гидравлики и вычислительной техники, а сочинения повлияли на формирование литературного французского языка. Имя Паскаля носят единица измерения давления (1 Па), язык программирования "Паскаль" и университет в его родном городе.
§1.2. Треугольник Паскаля
Треугольник Паскаля — арифметический треугольник, образованный биномиальными коэффициентами. Назван в честь Блеза Паскаля.
Если очертить треугольник Паскаля, то получится равнобедренный треугольник. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Продолжать треугольник можно бесконечно. Строки треугольника симметричны относительно вертикальной оси. Имеет применение в теории вероятностей и обладает занимательными свойствами.
А еще проще объясняют устройство треугольника Паскаля слова: каждое число равно сумме двух расположенных над ним чисел. Все элементарно, но сколько в этом таится чудес.
На вершине треугольника стоит 1. Треугольник можно продолжать неограниченно. Он обладает симметрией относительно вертикальной оси, проходящей через его вершину. Вдоль диагоналей (насколько у треугольника могут быть диагонали, но не будем придираться, такая терминология встречается в публикациях), параллельных сторонам треугольника (на рисунке отмечены зелеными линиями) выстроены треугольные числа и их обобщения на случай пространств всех размерностей.
Даже беглого взгляда, брошенного на треугольник Паскаля, достаточно, чтобы отметить следующие любопытные факты: 10 ядер можно сложить и в виде тетраэдра и в виде плоского треугольника. А 56 гиперядер, образующих тетраэдр в пятимерном пространстве, можно уложить в обычный привычный трехмерный тетраэдр, однако, если бы мы попытались выложить из 56 ядер треугольник, то одно ядро осталось бы лишним.
§1.3. Свойства треугольника паскаля
§1.4. Администрирование базы данных
Администрирование базы данных – это функция управления базой данных (БД). Лицо ответственное за администрирование БД называется “Администратор базы данных” (АБД) или “Database Administrator” (DBA).
Функция “администрирования данных” стала активно рассматриваться и определяться как вполне самостоятельная с конца 60-х годов. Практическое значение это имело для предприятий, использующих вычислительную технику в системах информационного обеспечения для своей ежедневной деятельности.
Специализация этой функции с течением времени совершенствовалась, но качественные изменения в этой области стали происходить с началом использования так называемых интегрированных баз данных. Одна такая база данных могла использоваться для решения многих задач.
Таким образом, сформировалось определение БД как общего информационного ресурса предприятия, которое должно находиться всегда в работоспособном состоянии. И как для каждого общего ресурса значительной важности, БД стала требовать отдельного управления. Во многих случаях это было необходимо для обеспечения её повседневной эксплуатации, её развития в соответствии с растущими потребностями предприятия. К тому же БД и технология её разработки постоянно совершенствовались и уже требовались специальные знания высокого уровня для довольно сложного объекта, которым стала база данных. Отсюда функция управления базой данных и получила название “Администрирование базы данных”, а лицо ею управляющее стали называть “Администратор баз данных”.
freepapers.ru
Прогресс человечества во многом связан с открытиями, сделанными гениями. Одним из них является Блез Паскаль. Его творческая биография еще раз подтверждает истинность выражения Лиона Фейхтвангера «Талантливый человек, талантлив во всем». Все научные достижения этого великого ученого трудно перечесть. К их числу относится одно из самых элегантных изобретений в мире математики — треугольник Паскаля.
Блез Паскаль по современным меркам умер рано, в возрасте 39 лет. Однако за свою короткую жизнь он проявил себя как выдающийся физик, математик, философ и писатель. Благодарные потомки назвали в его честь единицу давления и популярный язык программирования Pascal. Он уже почти 60 лет используется для обучения написания различных кодов. Например, с его помощью каждый школьник может написать программу для вычисления площади треугольника на «Паскале», а также исследовать свойства схемы, о которой речь пойдет ниже.
Деятельность этого ученого с экстраординарным мышлением охватывает самые разные области науки. В частности, Блез Паскаль является одним из основателей гидростатики математического анализа, некоторых направлений геометрии и теории вероятностей. Кроме того, он:
Как уже было сказано, этот великий французский ученый внес огромный вклад в математическую науку. Одним из его безусловных научных шедевров является «Трактат об арифметическом треугольнике», который состоит из биномиальных коэффициентов, расставленных в определенном порядке. Свойства этой схемы поражают своим разнообразием, а сама она подтверждает пословицу «Все гениальное — просто!».
Справедливости ради нужно сказать, что на самом деле треугольник Паскаля был известен в Европе еще в начале 16 века. В частности, его изображение можно увидеть на обложке учебника арифметики известного астронома Петра Апиана из Ингольтштадского университета. Похожий треугольник представлен и в качестве иллюстрации в книге китайского математика Ян Хуэй, изданной в 1303 году. О его свойствах было известно также и замечательному персидскому поэту и философу Омару Хайяму еще в начале 12 века. Причем считается, что он познакомился с ним из трактатов арабских и индийских ученых, написанных ранее.
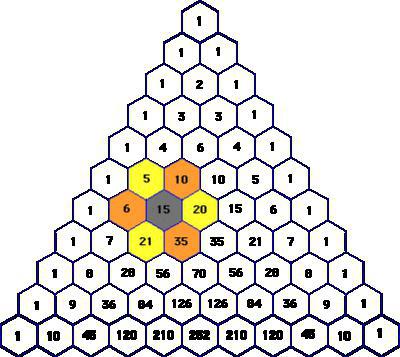
Прежде чем исследовать интереснейшие свойства треугольника Паскаля, прекрасного в своем совершенстве и простоте, стоит узнать, что он из себя представляет.
Говоря научным языком, эта числовая схема - бесконечная таблица треугольной формы, образованная из биномиальных коэффициентов, расположенных в определенном порядке. В его вершине и по бокам находятся цифры 1. Остальные позиции занимают числа, равные сумме двух чисел, расположенных над ними рядом выше. При этом все строки треугольника Паскаля симметричны относительно его вертикальной оси.
Треугольник Паскаля поражает своим совершенством. Для любой строки под номером n (n = 0, 1, 2…) верно:
Кроме того, сравнительно недавно, в 1972 году, было установлено еще одно свойство треугольника Паскаля. Для того чтобы его обнаружить, нужно записать элементы этой схемы в виде таблицы со сдвигом строк на 2 позиции. Затем отмечают числа, делящиеся на номер строки. Оказывается, что номер столбца, в котором выделены все числа, является простым числом.
Тот же трюк можно осуществить и по-другому. Для этого в треугольнике Паскаля заменяют числа на остатки от их деления на номер строки в таблице. Затем располагают строки в полученном треугольнике так, чтобы следующая из них начиналась правее на 2 колонки от первого элемента предыдущей. Тогда столбцы, имеющие номера, являющиеся простыми числами, будут состоять только из нулей, а в тех, у которых они составные, будет присутствовать хотя бы один ноль.
Как известно, так называется формула для разложения на слагаемые целой неотрицательной степени суммы двух переменных, которая имеет вид:
Присутствующие в них коэффициенты равны Cnm = n! / (m! (n - m)!), где m, представляет собой порядковый номер числа в строке n треугольника Паскаля. Иными словами, имея под рукой эту таблицу, можно легко возводить в степень любые числа, предварительно разложив их на два слагаемых.
Таким образом, треугольник Паскаля и бином Ньютона взаимосвязаны самым тесным образом.
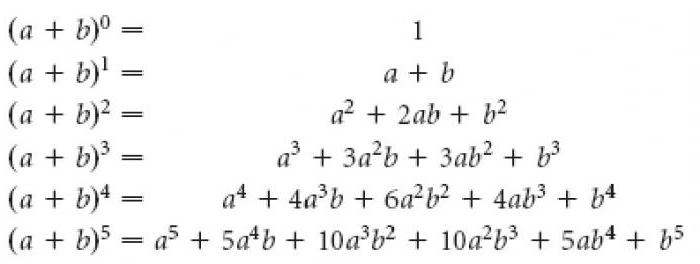
При внимательном изучении треугольника Паскаля можно обнаружить, что:
Такая интересная математическая схема, достаточно перспективная с точки зрения решения сложных задач, получается, если раскрасить четные числа Паскалевого изображения в один цвет, а нечетные — в другой.
Треугольник Серпинского можно выстроить и другим образом:
Самое интересное свойство треугольника Серпинского — его самоподобие, так как он состоит из 3-х своих копий, которые уменьшены в 2 раза. Оно позволяет отнести эту схему к фрактальным кривым, а они, как показывают новейшие исследования лучше всего подходят для математического моделирования облаков, растений, дельт рек, да и самой Вселенной.
Где используется треугольник Паскаля? Примеры задач, которые можно решать с его помощью, достаточно разнообразны и относятся к различным областям науки. Рассмотрим некоторые, наиболее интересные из них.
Задача 1. У некоторого большого города, обнесенного крепостной стеной, только одни входные ворота. На первом перекрестке основная дорога расходится на две. То же происходит и на любом другом. В город заходят 210 человек. На каждом из встречающихся перекрестков они делятся пополам. Сколько человек будет находить на каждом перекрестке, когда делиться будет уже невозможно. Ее ответом является 10 строка треугольника Паскаля (формула коэффициентов представлена выше), где по обе стороны от вертикальной оси расположены числа 210.
Задача 2. Имеется 7 наименований цветов. Нужно составить букет из 3 цветков. Требуется выяснить, сколькими различными способами это можно сделать. Эта задача из области комбинаторики. Для ее решения опять же используем треугольник Паскаля и получаем на 7 строке на третьей позиции (нумерация в обоих случаях с 0) число 35.
Теперь вы знаете, что изобрел великий французский философ и ученый Блез Паскаль. Его знаменитый треугольник при правильном использовании может стать настоящей палочкой-выручалочкой для решения множества задач, особенно из области комбинаторики. Кроме того, его возможно использовать для разгадывания многочисленных загадок, связанных с фракталами.
fb.ru
Вписанные и описанные окружности в треугольниках и четырехугольниках 28.05.2009/реферат, реферативный текст
Вписанная и описанная окружности в треугольниках и четырехугольниках, их определение и построение. Теорема Пифагора. Определение площади треугольника, трапеции и параллелограмма. Решение типовых задач по изложенным темам с применением полученных знаний.
Медианы треугольника 5.01.2010/реферат, реферативный текст
Медианы треугольника и их свойства. Открытие немецкого математика Г. Лейбница. Применение медиан в математической статистике. Основная сущность понятия "медиана тетраедра". Шесть доказательств теоремы о медианах. Теорема о медианах треугольника.
Методология изучения темы "Признаки равенства треугольников" 11.01.2004/курсовая работа
Теоретические сведения по теме "Признаки равенства треугольников". Методика изучения темы "Признаки равенства треугольников". Тема урока "Треугольник. Виды треугольников". "Свойства равнобедренного и равностороннего треугольников".
Окружности в треугольниках и четырехугольниках 16.06.2009/реферат, реферативный текст
Определение вписанной и описанной окружности, их свойства и признаки. Взаимное расположение прямой и окружности. Свойства прямоугольного треугольника и теорема Пифагора. Задачи с окружностью, вписанной и описанной в треугольниках и четырехугольниках.
Свойства и признаки треугольников 20.05.2009/презентация
Аксиомы: точки и прямые. Отрезки и их длины. Углы и их меры. Смежные и вертикальные углы. Параллельные прямые: определение, свойства. Треугольник и его элементы, признаки равенства. Треугольник и его виды: равнобедренный, равносторонний, прямоугольный.
Соотношение между сторонами и углами прямоугольного треугольника 17.05.2010/конспект урока
Ознакомление с понятиями синуса, косинуса, тангенса острого угла прямоугольного треугольника и основным тригонометрическим тождеством. Нахождение площади равнобедренного прямоугольного треугольная по заданному основанию и прилегающему к нему углу.
Умножение "треугольником" 6.02.2005/статья
Новый способ умножения чисел. Схожесть образующейся при вычислении матрицы из цифр, с треугольником относительна, но все же есть, особенно при умножении трехзначных чисел и выше. Треугольная матрица.
Площадь треугольника 8.11.2010/задача
Методика нахождения уравнения прямой исследуемого треугольника и параллельной ей стороне с использованием углового коэффициента. Определение уравнения высоты этого треугольника. Порядок и составление алгоритма вычисления площади данного треугольника.
Построение треугольника по трем элементам 11.01.2011/презентация
Методика и основные этапы построения треугольника по двум сторонам и медиане, проведенной к одной из них. Математическое и графическое изображение решения данного задания. Исследование условий для решения задачи и определение условия ее нерешаемости.
Фигуры постоянной ширины. Треугольник Рело 18.01.2011/курсовая работа
Ознакомление с понятием и основными свойствами кривых постоянной ширины. Треугольник Рело: исторические сведения, очертание, площадь. Особенности движения его вершины и центра. Применение исследуемой фигуры в грейферном механизме и кинопроекторах.
referat7.ru
Бином Ньютона — формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных, имеющая вид
где — биноминальные коэффициенты,
— неотрицательное целое число.
Это формула, представляющая выражение ( a + b ) n при положительном целом n в виде многочлена:
Заметим, что сумма показателей степеней для a и b постоянна и равна n.
Числа называются биномиальными коэффициентами.
Их можно вычислить, применяя только сложение, если пользоваться следующей схемой. В верхней строке пишем две единицы. Все последующие строки начинаются и заканчиваются единицей. Промежуточные числа в этих строках получаются суммированием соседних чисел из предыдущей строки. Эта схема называется треугольником Паскаля:
Первая строка в этой таблице содержит биномиальные коэффициенты для n = 1; вторая - для n = 2; третья - для n = 3 и т.д. Поэтому, если необходимо, например, разложить выражение:
( a + b )7 ,
мы можем получить результат моментально, используя таблицу:
Свойства биномиальных коэффициентов.
1. Сумма коэффициентов разложения ( a + b ) n равна 2 n .
Для доказательства достаточно положить a = b = 1. Тогда в правой части разложения бинома Ньютона мы будем иметь сумму биномиальных коэффициентов, а слева:
2. Коэффициенты членов, равноудалённых от концов разложения, равны.
Это свойство следует из соотношения:
3. Сумма коэффициентов чётных членов разложения равна сумме коэффициентов нечётных членов разложения; каждая из них равна
Для доказательства воспользуемся биномом: Здесь чётные члены имеют знак « + » , а нечётные - « - ». Так как в результате разложения получается 0, то следовательно, суммы их биномиальных коэффициентов равны между собой, поэтому каждая из них равна:
что и требовалось доказать.
3a1ka.livejournal.com
