Главная » Реферат » Теория пар сил на плоскости реферат

4. 2. Момент силы относительно точки в пространстве. Теория пар сил на плоскости реферат


Теория пар сил

Система двух равных по модулю параллельных противоположно направленных сил, называется парой сил.

Пара не имеет равнодействующую, её можно уравновесить только другой парой и можно представить в виде вектор-момента.

Свойства пар сил

  1. Пару сил можно переносить в плоскости её действия произвольно, не изменяя её действие.

  2. Момент пары не зависит от выбора центра.

Покажем, что сумма моментов сил относительно любого центра не зависит от выбора центра и равняется сумме момента.

Теорема об эквивалентности. Сложение пар сил в пространстве

Две пары, имеющие равные моменты – эквивалентны.

Продолжим векторы и отметим точки A и B.

Следовательно, две пары, имеющие равные моменты эквивалентны.

Можно произвольно менять модули сил и плечо пар, сохраняя неизменными их момент.

Перенос пары в параллельную плоскость

Пло­скости I и II должны быть параллельны, в частности, они могут совпадать.

Если приложить ии совместить точки при­ложения сил с проекциями точек, то получим:

Силы равны по модулю, поэтому их рав­нодействующие R и R' должны быть приложены в точке пересече­ния диагоналей прямоугольника ABB1A1, кроме того, они равны по модулю и направлены в проти­воположные стороны. Это означает, что они составляют систему, экви­валентную нулю.

Таким образом:

  1. Пару сил можно переносить в параллельную плоскость. Произвольно менять модули сил и плечо, сохраняя момент. Две пары можно привести к одному плечу.

  2. Пару сил можно перемещать в плоскости её действия.

Вектор – момент пары можно считать свободным вектором.

Если не плечо действует система пар сил, то складывая их геометрически получим главный вектор – момент равнодействующей пары, равный сумме векторов.

Понятие о статическом равновесии конструкции

Составляется уравнение относительно точки опрокидывания конструкции

–вес стены

Точка А – точка возможного опрокидывания

Муд=1,5Мопр

Мопр – момент опрокидывающий

Муд – удерживающий момент

Приведение силы к произвольному центру по методу Пуансо

Чтобы эффект действия сохранился нужно добавить равную и противоположную силу , которая образует присоединенную пару с плечомAB.

В результате приведения получаем силу , равную исходной и присоединенную пару.

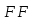с моментом M=Fh, можно представить в виде вектор – момента.

Так как вектор – момент свободный вектор, то его так же можно построить в точке B. Следовательно получаем: , которые можно приложить в точкуB.

Применяя метод Пуансо к системе сил, произвольно расположенных в пространстве можно получить условие равновесия любой произвольной системы в пространстве.

Приведение пространственной системы сил к произвольному центру. Условия равновесия пространственной системы

Требуется привести силы с центром О, с которым свяжем систему координат. Переносим F1 в точку О, прикладываем , которая образует пару, проделываем то же сF2.

Т.к. вектор-моменты пар являются параллельными векторами все их можно приложить к точке О.

Складывая их геометрически получим главный вектор момент:

Складывая F1, F2, Fn получаем главный вектор:

Ориентация векторов может быть определена с помощью косинусов.

Любую произвольную систему сил можно привести к любому центру и заменить двумя векторами M и R.

Если (=0 и=0) главный вектор и главный момент относительно любого центра равен нулю, то имеем условие равновесия произвольной системы сил.

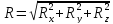
Эти уравнения представляют уравнения равновесия системы сил в пространстве в аналитической форме.

Таким образом для равновесия любой произвольной системы сил в пространстве необходимо и достаточно, чтобы сумма проекций на каждую координатную ось и сумма их моментов относительно каждой оси равнялись нулю.

Частные случаи приведения произвольной системы сил:

1) , т.е. условие равновесия системы сил.

2)т.е. система приводится к силе, равной главному вектору, приложенному к центру приведения. Тело может совершать поступательное движение.

3) , т.е. система приводится к паре сил с моментомM. Тело совершает вращательное движение.

4) и параллельны.

Так как M свободный вектор его можно переместить, тогда будет осуществляться поворот и перемещение. Тело может двигаться поступательно и вращаться, точки будут описывать винтовые линии.

5) и перпендикулярны. Тело может находиться в поступательном движении.

Вычислим :

Определение реакций связи в пространственной конструкции

Указать реакции или составляющие шарниров, составить уравнения равновесия.

Сумма проекций на координатные оси:

Сумма моментов относительно координатных осей:

Решив эти уравнения, можно найти все неизвестные силы. В конце решения необходимо сделать проверку.

studfiles.net

Глава 3. Теория пар сил на плоскости

3.1. Пара сил. Эквивалентность пар сил

Система двух параллельных сил, равных по модулю и направленных в противоположные стороны, называется парой сил или просто парой (рис. 3.1). Понятие о паре сил ввел в механику французский ученый Луи Пуансон (1777–1859).

Рис. 3.1. Пара сил

Пара сил – неуравновешенная система и не имеет равнодействующей. Пара сил производит на тело вращательное действие.

Вращательный эффект пары измеряется взятым со знаком «плюс» или «минус» произведением модуля одной из сил пары на ее плечо (момент пары):

.

Знак «плюс» ставится перед числовым значением момента в том случае, если пара стремится повернуть тело против хода часовой стрелки, и знак «минус» – если пара стремится повернуть тело по ходу часовой стрелки (рис. 3.2).

Рис. 3.2. Правило знаков момента пары сил

В Международной системе единиц (СИ) моменты пар выражаются в или .

Вращательное действие расположенной в данной плоскости пары зависит только от ее момента, поэтому для задания пары сил до­статочно указать числовое значение ее момента, а затем по данно­му или выбранному плечу определить силы пары или по силам подобрать необходимое плечо. Исходя из этого, на рисунках и схе­мах пары сил изображают иногда просто круговой стрелкой, харак­теризующей лишь направление вращающего действия. 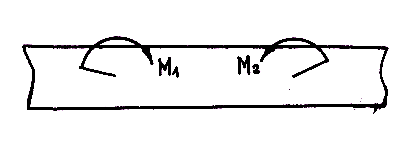Например, пары () и () (рис. 3.3, а), приложенные к брусу, можно условно изобразить круговыми стрелками, обозначив их M1 и M2 (рис. 3.3, б).

а

б

Рис. 3.3. Изображение пары сил

3.2. Сложение пар сил. Условие равновесия пар

Теорема: Система пар сил, действующих на тело в одной плоскости, эквивалентна паре сил с моментом, равным алгебраической сумме моментов пар системы.

Допустим, на тело действуют три пары, моменты которых M1, M2 и M3 известны (рис. 3.4).

Рис. 3.4. Система пар сил

Момент равнодействующей пары

,

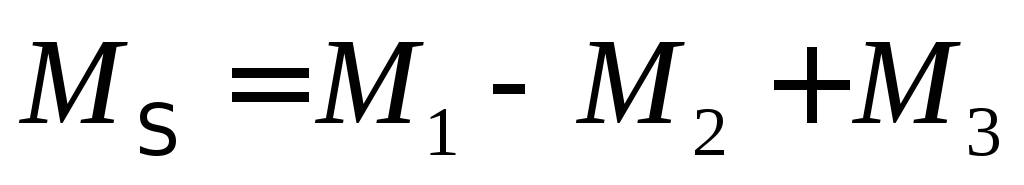Если в результате сложения пар , то действующие на тело пары сил образуют уравновешенную систему. Следовательно, необходимое и достаточное условие равновесия системы пар выражается одним уравнением:

,

т. е. для равновесия системы пар сил, действующих на тело в одной плоскости, необходимо и достаточно, чтобы алгебраическая сумма их моментов была равна нулю.

Значит, систему пар или одну пару можно уравновесить только парой.

3.3. Момент пары относительно точки

Задолго до появления понятия о паре сил и ее моменте в механике возникло понятие о моменте силы относительно точки. Первый, кто обратил внимание на важную роль в механике момента силы относительно точки, был Леонардо да Винчи (1452–1519), современную трактовку понятия момента силы относительно точки дал П. Вариньон (1654–1722).

Моментом силы относительно точки называется взятое со знаком «плюс» или «минус» произведение модуля силы на кратчайшее расстояние от точки до линии действия силы:

Точка О, относительно которой берется момент силы, называется центром момента. OВ = l – кратчайшее расстояние от центра момента до линии действия силы – называется плечом силы относительно данной точки. Знак «плюс» ставится в случае, если сила F стремится повернуть тело против хода часовой стрелки, а знак «минус» – в противоположном случае (правило знаков то же, что и у моментов пар сил). Момент силы относительно точки О на рис. 3.5 положительный.

Рис. 3.5. Момент силы относительно точки

studfiles.net

Теория пар сил - fiziku5.ru

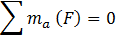
Могут использоваться 2 или 3 уравнения моментов.

Пример

Составим уравнение суммы всех сил на ось X и Y:

Сумма моментов всех сил относительно точки А:

Параллельные силы

Уравнение относительно точки А:

Уравнение относительно точки В:

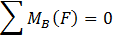
Сумма проекций сил на ось У:

Теория пар сил

Система двух равных по модулю параллельных противоположно направленных сил, называется парой сил.

Пара не имеет равнодействующую, её можно уравновесить только другой парой и можно представить в виде вектор-момента.

 

Свойства пар сил

1)  Пару сил можно переносить в плоскости её действия произвольно, не изменяя её действие.

2)  Момент пары не зависит от выбора центра.

Покажем, что сумма моментов сил относительно любого центра не зависит от выбора центра и равняется сумме момента.

Теорема об эквивалентности. Сложение пар сил в пространстве

Две пары, имеющие равные моменты – эквивалентны.

Продолжим векторы и отметим точки A и B.

Следовательно, две пары, имеющие равные моменты эквивалентны.

Можно произвольно менять модули сил и плечо пар, сохраняя неизменными их момент.

Перенос пары в параллельную плоскость

¯R^',¯R,¯(F_2 ),¯(F_1 ),h,¯(F_1^'' ),¯(F_2^'' ),¯(F_2^' ),¯(F_1^' ),А,В,А_2,В_2

 

Пло­скости I и II должны быть параллельны, в частности, они могут совпадать.

Если приложить и и совместить точки при­ложения сил с проекциями точек, то получим:

Силы равны по модулю, поэтому их рав­нодействующие R и R’ должны быть приложены в точке пересече­ния диагоналей прямоугольника ABB1A1, кроме того, они равны по модулю и направлены в проти­воположные стороны. Это означает, что они составляют систему, экви­валентную нулю.

Таким образом:

1)  Пару сил можно переносить в параллельную плоскость. Произвольно менять модули сил и плечо, сохраняя момент. Две пары можно привести к одному плечу.

2)  Пару сил можно перемещать в плоскости её действия.

Вектор – момент пары можно считать свободным вектором.

Если не плечо действует система пар сил, то складывая их геометрически получим главный вектор – момент равнодействующей пары, равный сумме векторов.

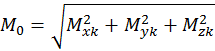
Понятие о статическом равновесии конструкции

 

Составляется уравнение относительно точки опрокидывания конструкции

– вес стены

Точка А – точка возможного опрокидывания

Муд=1,5Мопр

Мопр – момент опрокидывающий

Муд – удерживающий момент

Приведение силы к произвольному центру по методу Пуансо

Чтобы эффект действия сохранился нужно добавить равную и противоположную силу , которая образует присоединенную пару с плечом AB.

В результате приведения получаем силу , равную исходной и присоединенную пару.

с моментом M=Fh, можно представить в виде вектор – момента.

Так как вектор – момент свободный вектор, то его так же можно построить в точке B. Следовательно получаем: , которые можно приложить в точку B.

Применяя метод Пуансо к системе сил, произвольно расположенных в пространстве можно получить условие равновесия любой произвольной системы в пространстве.

Приведение пространственной системы сил к произвольному центру.

Условия равновесия пространственной системы

Требуется привести силы с центром О, с которым свяжем систему координат. Переносим F1 в точку О, прикладываем , которая образует пару, проделываем то же с F2.

Т. к. вектор-моменты пар являются параллельными векторами все их можно приложить к точке О.

Складывая их геометрически получим главный вектор момент:

Складывая F1, F2, Fn получаем главный вектор:

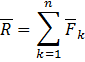
Ориентация векторов может быть определена с помощью косинусов.

Любую произвольную систему сил можно привести к любому центру и заменить двумя векторами M и R.

fiziku5.ru

Термех проба

10

Министерство образования и науки РФ

Федеральное государственное бюджетное образовательное

учреждение высшего профессионального образования

Забайкальский государственный университет

Кафедра теоретической механики

Р Е Ф Е Р А Т

По теме: «Эквивалентность пар сил в пространстве и на плоскости, их сложение и условие равновесия»

Студент: Садилов И.А.

Группа: СУС-13-2

Преподаватель: Геллер Ю.А.

г.Чита, 2014 г.

Содержание:

  1. Что такое пара сил…………………………………………………3

  2. Теорема о сумме моментов пары сил…………………………….3

  3. Теорема об эквивалентности пар сил……………………………4

  4. Теорема о переносе пары сил в параллельную плоскость…….5

  5. Теорема о сложении пар сил…………………………………….8

  6. Условия равновесия пар сил……………………………………..8

  7. Выводы…………………………………………………………….9

  8. Список используемой литературы………………………………10

ПАРА СИЛ

Парой сил называется система двух равных по модулю, параллельных и направленных в противоположные стороны сил, действующих на абсолютно твердое тело.

Плоскостью действия пары сил называется плоскость в которой расположены эти силы.

Плечом пары сил d называется кратчайшее расстояние между линиями действия сил пары.

Моментом пары сил называется вектор , модуль которого равен произведению модуля одной из сил пары на ее плечо и который направлен перпендикулярно плоскости действия сил пары в ту сторону, откуда пара видна стремящейся повернуть тело против хода часовой стрелки.

Рис. 4.1

Теорема о сумме моментов пары сил. Сумма моментов сил, входящих в состав пары, относительно любой точки не зависит от выбора этой точки и равна моменту этой пары сил.

Доказательство: Выберем произвольно точку О. Проведем из нее в точки А и В радиус-векторы (Смотри Рис. 4.2).

,

Что и требовалось доказать.

Рис. 4.2

Две пары сил называются эквивалентными, если их действие на твердое тело одинаково при прочих равных условиях.

Теорема об эквивалентности пар сил. Пару сил, действующую на твердое тело, можно заменить другой парой сил, расположенной в той же плоскости действия и имеющий одинаковый с первой парой момент.

Доказательство: Пусть на твердое тело действует пара сил .

Перенесем силу в точку , а силу в точку . Проведем через точки две любые параллельные прямые, пересекающие линии действия сил пары. Соединим точки отрезком прямой и разложим силы в точке и в точке по правилу параллелограмма.

Так как , то

и

Поэтому эквивалентна системе , а эта система эквивалентна системе , так как эквивалентна нулю.

Таким образом мы заданную пару сил заменили другой парой сил . Докажем, что моменты у этих пар сил одинаковы.

Момент исходной пары сил численно равен площади параллелограмма , а момент пары сил численно равен площади параллелограмма . Но площади этих параллелограммов равны, так как площадь треугольника равна площади треугольника .

Что и требовалось доказать.

Теорема о переносе пары сил в параллельную плоскость. Действие пары сил на твердое тело не изменится от переноса этой пары в параллельную плоскость.

Доказательство: Пусть на твердое тело действует пара сил в плоскости . Из точек приложения сил А и В опустим перпендикуляры на плоскость и в точках их пересечения с плоскостью приложим две системы сил и , каждая из которых эквивалентна нулю.

Сложим две равные и параллельные силы и . Их равнодействующая параллель-на этим силам, равна их сумме и приложена посредине отрезка в точке О.

Сложим две равные и параллельные силы и . Их равнодействующая параллель-на этим силам, равна их сумме и приложена посредине отрезка в точке О.

Так как , то система сил эквивалентна нулю и ее можно отбросить.

Таким образом пара сил эквивалентна паре сил , но лежит в другой, параллельной плоскости. Что и требовалось доказать.

Следствие: Момент пары сил, действующий на твердое тело, есть свободный вектор.

Две пары сил, действующих на одно и то же твердое тело, эквивалентны, если они имеют одинаковые по модулю и направлению моменты.

Теорема о сложении пар сил. Две пары сил, действующих на одно и то же твердое тело, и лежащие в пересекающихся плоскостях, можно заменить одной эквивалентной парой сил, момент которой равен сумме моментов заданных пар сил.

Доказательство: Пусть имеются две пары сил, расположенные в пересекающихся плоскостях. Пара сил в плоскости характеризуется моментом , а пара сил в плоскости характеризуется моментом .

Расположим пары сил так, чтобы плечо пар было общим и располагалось на линии пересечения плоскостей. Складываем силы, приложенные в точке А и в точке В, . Получаем пару сил .

Что и требовалось доказать.

Условия равновесия пар сил

Если на твердое тело действует несколько пар сил, как угодно расположенных в пространстве, то последовательно применяя правило параллелограмма к каждым двум моментам пар сил, можно любое количество пар сил заменить одной эквивалентной парой сил, момент которой равен сумме моментов заданных пар сил.

Теорема. Для равновесия пар сил, приложенных к твердому телу, необходимо и достаточно, чтобы момент эквивалентной пары сил равнялся нулю.

Теорема. Для равновесия пар сил, приложенных к твердому телу, необходимо и достаточно, чтобы алгебраическая сумма проекций моментов пар сил на каждую из трех координатных осей была равна нулю.

Условия равновесия системы сил

Векторная форма

Для равновесия произвольной системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы главный вектор системы сил был равен нулю и главный момент системы сил относительно любого центра приведения также был равен нулю.

Алгебраическая форма.

Для равновесия произвольной системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы три суммы проекций всех сил на оси декартовых координат были равны нулю и три суммы моментов всех сил относительно трех осей координат также были равны нулю.

Условия равновесия пространственной системы

параллельных сил

На тело действует система параллельных сил. Расположим ось Oz параллельно силам.

Уравнения

Для равновесия пространственной системы параллельных сил, действующих на твердое тело, необходимо и достаточно, чтобы сумма проекций этих сил была равна нулю и суммы моментов этих сил относительно двух координатных осей, перпендикулярным силам, также были равны нулю.

- проекция силы на ось Oz.

Выводы:

  1. Пару сил как жесткую фигуру можно как угодно поворачивать и переносить в ее плоскости действия.

  2. У пары сил можно изменять плечо и силы, сохраняя при этом момент пары и плоскость действия.

3.момент пары является свободным вектором и полностью определяет действие пары на абсолютно твердое тело. Для деформируемых тел теория пар неприменима.

ЛИТЕРАТУРА:

1. Кирсанов М.Н Теоретическая механика. Учебник для самоподготовки.

2.Тарг С.М Курс по Теоретической Механике.

studfiles.net

4. 2. Момент силы относительно точки в пространстве

29

Пример 4.1

Определить моменты сил Р1 = 10 кН, Р2 = 20 кН, Р3 = 30 кН, приложенных в вершинах квадрата АВСО (рис. 4. 3, а), относительно точки О, при стороне квадрата а = 0,2 м.

Решение:

1) Определяем момент силы Р1 = 10 кН относительно точки О.

Мо (Р1) = - Р1 . а =-10 . 0,2 =-2кНм

2) Определяем момент силы Р2 = 20 кН относительно точки О.

Мо (Р2) = Р2 . ОВ = 20. а√2 = 5,66 кНм

3) Определяем момент силы Р3 = 30 кН относительно точки О.

Мо (Р3) = - Р3 . ОД =-30 . а Соs 30° =-5,20кНм

Пример 4.2

Определить моменты сил Р1 = 10 кН, Р2 = 15 кН, Р3 = 30 кН, приложенных в вершинах А и В прямоугольного равнобедренного треугольника (рис. 4. 3, б), относительно точки О, при а = 0,3 м.

Решение:

Определяем момент силы Р1 = 10 кН относительно точки О.

Мо (Р1) = Р1 . ОС = 10. а Sin 45° = 2,12 кНм Определяем момент силы Р2 = 15 кН относительно точки О.

Мо (Р2) = Р2 . ОД = 15. а Sin 60° = 3,9 кНм Определяем момент силы Р3 = 30 кН относительно точки О.

Мо (Р3) = Р3 . 0 = 0

Пример 4.3

Определить моменты сил Р1 = 15 кН, Р2 = 20 кН, Р3 = 40 кН, приложенных в вершинах А, В, С прямоугольника (рис. 4. 3, в) и треугольников (рис. 4. 3, г, д, е), относительно точки О, при а = 0,6 м самостоятельно.

Результаты решения:

Рис. 3в Мо (Р1) = 9 кНм, Мо (Р2) =-10,39кНм, Мо (Р3) =-33,94кНм Рис. 3г Мо (Р1) =-4,5кНм, Мо (Р2) =-20,78кНм, Мо (Р3) = 20,78кНм Рис. 3д Мо (Р1) =-7,79кНм, Мо (Р2) =-12кНм, Мо (Р3) = 20,78 кНм Рис. 3е Мо (Р1) =-7,79кНм, Мо (Р2) =-18кНм, Мо (Р3) =-24кНм

Момент силы относительно точки в пространстве определяетсявектором, приложенным в этой точке, модуль которого равен произведению модуля силы на плечо.

30

Этот вектор перпендикулярен к плоскости, проведенной через моментную точку и линию действия силы и направлен так, чтобы вращение плоскости (если смотреть с конца вектора) происходило против хода часовой стрелки (рис. 4.4). Если из моментной точки О в точку приложения силы провести радиус – вектор r (рис. 4.4), то вектор момента силы можно выразить векторным произведением.

 

 

 

 

 

 

Мо (Р) =

r

*

р

(4.3)

Модуль момента силы

Мо (Р) = r . р Sinα = Р. d

5. ТЕОРИЯ ПАР СИЛ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ

5. 1. Пара сил. Момент пары сил на плоскости

Парой сил называется совокупность двух параллельных сил (линии действия которых не совпадают), равных по модулю и направленных в противоположные стороны.

Плоскость, в которой действуют силы, называется плоскостью действия пары.

Кратчайшее расстояние d между линиями действия сил, составляющих пару, называется плечом пары.

Если пару сил приложить к телу, находящемуся в покое, то оно будет совершать вращательное движение.

Пару сил нельзя уравновесить силой, так как она не имеет равнодействующей. Уравновесить пару можно только с помощью другой пары.

Вращательное действие пары на твердое тело характеризуют моментом пары.

Момент пары сил на плоскости – это скалярная величина, равная произведению одной из сил на плечо пары со знаком плюс или минус

Мо (Р1, Р1′) =± Р1 . d

Если вращение плоскости действия пары происходит против хода часовой стрелки, то момент пары считаем положительным, если по ходу часовой стрелки – отрицательным.

Выразим моменты пар сил на плоскости (рис. 5. 1, а):

Мо (Р1, Р1′) = Р1 . d1 Мо (Р2, Р2′) = - Р2 . d2

Поскольку пару сил характеризуют только моментом и в расчетах нужен лишь момент пары сил, то обычно для обозначения пары сил пользуются дуговой стрелкой в плоскости действия пары, которая показывает направление вращения пары и модуль момента М = М (Р1, Р1′) (рис. 5. 1, б). Численно момент пары можно определить как удвоенную площадь треугольника ОАВ,

31

основанием которого является одна из сил Р1, а вершиной О – точка приложения другой силы Р1′ (рис. 5. 1, б).

5. 2. Момент пары сил в пространстве. Эквивалентные пары

Пару сил характеризуют:

-плоскость действия;

-величина момента пары;

-направление вращения.

Момент пары в пространстве зависит от расположения плоскости действия и от направления, в котором пара стремится вращать тело, т.е. является векторной величиной.

Вектор, определяющий момент пары, называют вектор-моментом.Вектормомент пары равен по модулю произведению силы пары на ее плечо и направлен перпендикулярно к плоскости действия пары таким образом, чтобы вращение плоскости происходило против хода часовой стрелки, если смотреть с конца вектора (рис. 5. 2).

Эквивалентными называются пары, оказывающие на твердое тело одинаковое действие, т.е. вектор-моментыкоторых геометрически равны. Пары сил, расположенные в одной плоскости эквивалентны, если их моменты численно равны и совпадают по направлению вращения (рис. 5. 3).

Пара (Р1, Р1′) и пара (Р2, Р2′) эквивалентны, так как М (Р1, Р1′) = 20 кНм иМ (Р2, Р2′) = 20 кНм, а направление вращения одинаково (против хода часовой стрелки).

Определить эквивалентные пары на рис. 5. 4 самостоятельно.

Ответ. Первая и третья пары эквивалентны. Четвертая и шестая пары эквивалентны.

5. 3. Теоремы об эквивалентности пар

Теорема 1

Всякую пару сил, не изменяя ее действия на твердое тело, можно заменить другой парой, расположенной в той же плоскости, имеющей одинаковое с заданной парой направление вращения и равный по модулю момент.

Доказательство

Пусть на тело действуют пара сил (Р1, Р1′) в точках А и В (рис.5.5). Перенесем эти силы в точки Д и С, лежащие на их линиях действия. Приложим в точках С и Д две взаимно уравновешенные силы Т1 = - Т1′. Найдем равнодействующие:

R1 = Р1 + Т1, R1′ = Р1′ + Т1′

Получим новую пару сил (R1 , R1′). У пар (Р1, Р1′) и (R1 , R1′) одинаковое направление вращения.

Покажем, что обе пары имеют одинаковыйпо величине момент. M (Р1, Р1′) = Р1 . d1 M (R1, R1′) = R1 . d2

32

Р1

 

 

R1 =-----------

d2 = d1 Cosα

Cos α

 

 

 

Р1

. d1.

M (R1, R1′) =----------

d1 Cosα = Р1

Cos α

Таким образом, эти пары эквивалентны.

Следствия:

1.Действие пары сил на тело не изменится, если не изменяя момента пары переместить ее или повернуть в любое положение в плоскости действия

(рис.5.6).

2.Действие пары на тело не изменится, если не изменяя момента пары изменить силы пары и ее плечо. Во сколько раз уменьшаем силу, во столько раз увеличиваем плечо, и наоборот (рис. 5. 7).

Теорема

Действие пары сил на твердое тело не изменится, если пару сил перенести из данной плоскости в любую другую параллельную плоскость.

Доказательство

Рассмотрим твердое тело, на которое в плоскости I действует пара сил (Р1, Р1′). В произвольной плоскости II, параллельной плоскости I, проведем отрезок СД, параллельный и равный отрезку АВ (рис. 5. 8). В точках С и Д приложим уравновешенные силы Р2 = - Р2′ и Р3 = - Р3′. Модули этих сил выберем равными модулям сил заданной пары

Р1 = Р1′ = Р2 = Р2′ = Р3 = Р3′

Сложив силы Р′1 и Р3′, а также Р1 и Р2, найдем их равнодействующие R1 и R1′, которые приложены в точке пересечения диагоналей параллелограмма АВСД, равны помодулю и противоположно направлены.

Силы R1 и R1′ образуют уравновешенную систему сил, т.е. R1 + R1′ = 0, поэтому их можно устранить. Оставшаяся пара сил (Р2′, Р3) эквивалентна заданной, но расположена в параллельной плоскости.

Следствие

Вектор-моментпары является свободным вектором, т.е. его точку приложения можно переносить в любую точку тела, не изменяя модуль и направление.

33

 

б.

 

P'

 

 

2

 

M

d

 

P'1

А

d

2

1 О

 

P1

В

P

 

 

 

2

 

 

Рис. 5.1

M (P1,P'1)

P2

P'1

P1P'2

M (P2 ,P'2 )

Рис.5.2

P1

=2H

 

 

 

P2 =5Н

 

 

d=10м

 

 

 

d=4м

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

P'1

=2H

 

 

 

 

 

 

 

 

 

 

P'2

=5Н

 

 

 

 

 

 

 

 

 

 

Рис. 5.3

1.

P1=6H

d=4м

P'1=6H

4.

P'4 =6Н

A

_

P1'

2. 3.

P2 =12Н

d=2м

P'2 =12Н

5.

P4 =6Н

d=3м P5 =6H

P3 =3Н

d=8м

P'3 =3Н

d =3м

d=9м

P'6 =2Н

 

 

Рис.5.4

 

 

 

_

 

 

 

_

T1'

 

 

 

 

 

 

 

R1'

_ C

 

_

 

 

d2

 

 

P1'

1

 

 

 

a

P

 

 

 

a

_

 

 

 

 

 

D

 

R1

 

 

 

 

 

d1

 

_

 

 

 

_

T1

 

 

 

 

 

 

B

P1

 

 

_

P1

d

_

P1'

P1=4H

P2=2H

4м 8м

P2'=2H

P1'=4H

Рис. 5.7

_

P1d1

d2

_

P2

_

P1

d

_

P1'

Рис.5.6

P3=8H

_

P2

2м _

R'

P3'=8H

_

P1'

_

P1

d

_

P1'

_

 

_

II

P3'

 

 

 

 

M

 

O

 

 

_

_

 

 

R

B

 

I

P1

 

 

 

d _

A P1'

Рис. 5.8

 

_

 

_

_

 

Q2'

Q3

 

P2'

 

 

_

A _1

d

Q1'

 

 

B_

 

 

 

Q

 

Q3'

 

_

 

 

Q2

 

 

_

P3'

Рис.5.9

studfiles.net

STAT-L4

Теоретическая механика (Статика)

Краткое содержание: Пара сил. Теорема о сумме моментов пары сил. Теорема об эквивалентности пар сил. Теорема о переносе пары сил в параллельную плоскость. Теорема о сложении пар сил. Условия равновесия пар сил.

ПАРА СИЛ

Парой сил называется система двух равных по модулю, параллельных и направленных в противоположные стороны сил, действующих на абсолютно твердое тело.

Плоскостью действия пары сил называется плоскость в которой расположены эти силы.

Плечом пары сил d называется кратчайшее расстояние между линиями действия сил пары.

Моментом пары сил называется вектор , модуль которого равен произведению модуля одной из сил пары на ее плечо и который направлен перпендикулярно плоскости действия сил пары в ту сторону, откуда пара видна стремящейся повернуть тело против хода часовой стрелки.

Рис. 4.1

Теорема о сумме моментов пары сил. Сумма моментов сил, входящих в состав пары, относительно любой точки не зависит от выбора этой точки и равна моменту этой пары сил.

Доказательство: Выберем произвольно точку О. Проведем из нее в точки А и В радиус-векторы (Смотри Рис. 4.2).

,

Что и требовалось доказать.

Рис. 4.2

Две пары сил называются эквивалентными, если их действие на твердое тело одинаково при прочих равных условиях.

Теорема об эквивалентности пар сил. Пару сил, действующую на твердое тело, можно заменить другой парой сил, расположенной в той же плоскости действия и имеющий одинаковый с первой парой момент.

Доказательство: Пусть на твердое тело действует пара сил .

Перенесем силу в точку , а силу в точку . Проведем через точки две любые параллельные прямые, пересекающие линии действия сил пары. Соединим точки отрезком прямой и разложим силы в точке и в точке по правилу параллелограмма.

Так как , то

и

Поэтому эквивалентна системе , а эта система эквивалентна системе , так как эквивалентна нулю.

Таким образом мы заданную пару сил заменили другой парой сил . Докажем, что моменты у этих пар сил одинаковы.

Момент исходной пары сил численно равен площади параллелограмма , а момент пары сил численно равен площади параллелограмма . Но площади этих параллелограммов равны, так как площадь треугольника равна площади треугольника .

Что и требовалось доказать.

Выводы:

  1. Пару сил как жесткую фигуру можно как угодно поворачивать и переносить в ее плоскости действия.

  2. У пары сил можно изменять плечо и силы, сохраняя при этом момент пары и плоскость действия.

Теорема о переносе пары сил в параллельную плоскость. Действие пары сил на твердое тело не изменится от переноса этой пары в параллельную плоскость.

Доказательство: Пусть на твердое тело действует пара сил в плоскости . Из точек приложения сил А и В опустим перпендикуляры на плоскость и в точках их пересечения с плоскостью приложим две системы сил и , каждая из которых эквивалентна нулю.

Сложим две равные и параллельные силы и . Их равнодействующая параллель-на этим силам, равна их сумме и приложена посредине отрезка в точке О.

Сложим две равные и параллельные силы и . Их равнодействующая параллель-на этим силам, равна их сумме и приложена посредине отрезка в точке О.

Так как , то система сил эквивалентна нулю и ее можно отбросить.

Таким образом пара сил эквивалентна паре сил , но лежит в другой, параллельной плоскости. Что и требовалось доказать.

Следствие: Момент пары сил, действующий на твердое тело, есть свободный вектор.

Две пары сил, действующих на одно и то же твердое тело, эквивалентны, если они имеют одинаковые по модулю и направлению моменты.

Теорема о сложении пар сил. Две пары сил, действующих на одно и то же твердое тело, и лежащие в пересекающихся плоскостях, можно заменить одной эквивалентной парой сил, момент которой равен сумме моментов заданных пар сил.

Доказательство: Пусть имеются две пары сил, расположенные в пересекающихся плоскостях. Пара сил в плоскости характеризуется моментом , а пара сил в плоскости характеризуется моментом .

Расположим пары сил так, чтобы плечо пар было общим и располагалось на линии пересечения плоскостей. Складываем силы, приложенные в точке А и в точке В, . Получаем пару сил .

Что и требовалось доказать.

Условия равновесия пар сил.

Если на твердое тело действует несколько пар сил, как угодно расположенных в пространстве, то последовательно применяя правило параллелограмма к каждым двум моментам пар сил, можно любое количество пар сил заменить одной эквивалентной парой сил, момент которой равен сумме моментов заданных пар сил.

Теорема. Для равновесия пар сил, приложенных к твердому телу, необхо-димо и достаточно, чтобы момент эквивалентной пары сил равнялся нулю.

Теорема. Для равновесия пар сил, приложенных к твердому телу, необходимо и достаточно, чтобы алгебраическая сумма проекций моментов пар сил на каждую из трех координатных осей была равна нулю.

5

Лекция 3

01.11.03

studfiles.net

Глава 3. Теория пар сил на плоскости

3.1. Пара сил. Эквивалентность пар сил

Система двух параллельных сил, равных по модулю и направленных в противоположные стороны, называется парой сил или просто парой. Понятие о паре сил ввел в механику французский ученый Луи Пуансон (1777-1859).

Пара сил – неуравновешенная система и не имеет равнодействующей. Пара сил производит на тело вращательное действие.

Вращательный эффект пары измеряется взятым со знаком плюс или минус произведением модуля одной из сил пары на ее плечо (момент пары), т.е.

.

Знак «плюс» ставится перед числовым значением момента в том случае, если пара стремится повернуть тело против хода часовой стрелки, и знак «минус» если пара стремится повернуть тело по ходу часовой стрелки.

В Международной системе единиц (СИ) моменты пар выражаются в или .

Вращательное действие расположенной в данной плоскости пары зависит только от ее момента, поэтому для задания пары сил до­статочно указать числовое значение ее момента, а затем по данно­му или выбранному плечу можно определить силы пары или по силам подобрать необходимое плечо. Исходя из этого, на рисунках и схе­мах пары сил изображают иногда просто круговой стрелкой, харак­теризующей лишь направление вращающего действия. Например, пары ( ) и ( ), приложенные к брусу, можно условно изобразить круговыми стрелками, обозначив их 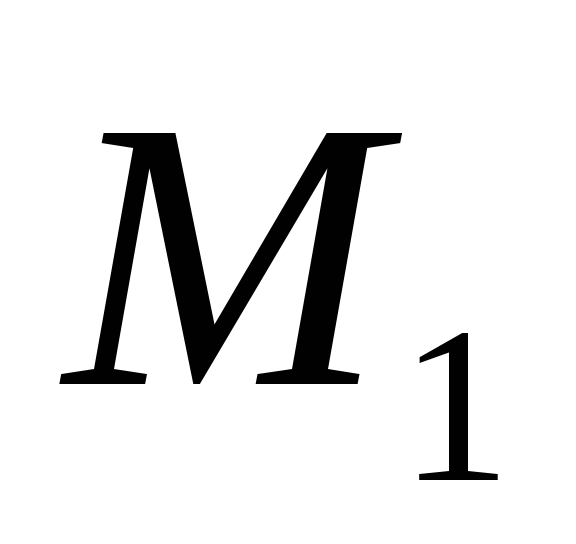и .

3.2. Сложение пар сил. Условие равновесия пар

Теорема: Система пар, действующих на тело в одной плоскости, эквивалентна паре сил с моментом, равным алгебраической сумме моментов пар системы.

Допустим, на тело действуют три пары, моменты которых известны.

Момент равнодействующей пары:

,

Если в результате сложения пар , то действующие на тело пары сил образуют уравновешенную систему. Следовательно, необходимое и достаточное условие равновесия системы пар выражается одним уравнением

,

т.е. для равновесия системы пар сил, действующих на тело в одной плоскости, необходимо и достаточно, чтобы алгебраическая сумма их моментов была равна нулю.

Значит, систему пар или одну пару можно уравновесить только парой.

3.3. Момент пары относительно точки

Задолго до появления понятия о паре сил и ее моменте в механике возникло понятие о моменте силы относительно точки. Первый, кто обратил внимание на важную роль в механике момента силы относительно точки, был Леонардо да Винчи (1452–1519), современную трактовку понятия момента силы относительно точки дал П. Вариньон (1654–1722).

Моментом силы относительно точки называется взятое со знаком «плюс» или «минус» произведение модуля силы на кратчайшее расстояние

от точки до линии действия силы, т.е.

Точка 0, относительно которой берется момент силы, называется центром момента. OВ = l – кратчайшее расстояние от центра момента до линии действия силы - называется плечом силы относительно данной точки. Знак “плюс” ставится в случае, если сила F стремится повернуть тело против хода часовой стрелки, а знак “минус” – в противоположном случае (правило знаков то же, что и у моментов пар сил). Момент силы относительно точки 0 на рисунке положительный.

studfiles.net

Смотрите также