Опубликовать ОпубликоватьРеферат на тему:
Теорема Фалеса — одна из теорем планиметрии.
В теореме нет ограничений на взаимное расположение секущих (она верна как для пересекающихся прямых, так и для параллельных). Также неважно, где находятся отрезки на секущих.
Доказательство в случае секущих
Доказательство в случае параллельных прямых
Проведем прямую BC. Углы ABC и BCD равны как внутренние накрест лежащие при параллельных прямых AB и CD и секущей BC, а углы ACB и CBD равны как внутренние накрест лежащие при параллельных прямых AC и BD и секущей BC. Тогда по первому признаку равенства треугольников треугольники ABC и DCB равны. Отсюда следует, что AC = BD и AB = CD. ■
Также существует обобщённая теорема Фалеса:
Параллельные прямые отсекают на секущих пропорциональные отрезки: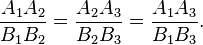
Теорема Фалеса является частным случаем обобщённой теоремы Фалеса, поскольку равные отрезки можно считать пропорциональными отрезками с коэффициентом пропорциональности, равным 1.
Если в теореме Фалеса равные отрезки начинаются от вершины (часто в школьной литературе используется такая формулировка), то обратная теорема также окажется верной. Для пересекающихся секущих она формулируется так:
| Если прямые, пересекающие стороны угла, отсекают на одной и на другой стороне угла равные (или пропорциональные) между собой отрезки, начиная от вершины, то такие прямые параллельны. |
В обратной теореме Фалеса важно, что равные отрезки начинаются от вершины
Таким образом (см. рис.) из того, что следует, что прямые
.
Если секущие параллельны, то необходимо требовать равенство отрезков на обеих секущих между собой, иначе данное утверждение становится неверным (контрпример — трапеция, пересекаемая линией, проходящей через середины оснований).
Аргентинская музыкальная группа Les Luthiers (исп.) представила песню, посвящённую теореме. В видеоклипе для этой песни[1] приводится доказательство для прямой теоремы для пропорциональных отрезков.
Категории: Теоремы, Планиметрия.
Текст доступен по лицензии Creative Commons Attribution-ShareAlike.wreferat.baza-referat.ru
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
Управление образования Советского района г. Красноярска
Использование теоремы Фалеса в современном мире
(Исследовательско – реферативная работа)
Работу выполнили:
Ученик 9 класса
Баландин Александр
Ученик 9 класса
Кузьмин Александр
Научные руководители:
Учитель математики Мальцева Т.Г
Учитель информатики Заболотникова Е.Ю.
Красноярск 2011
Содержание:
Цели и задачи проекта. 3
Аннотация 4
Введение 4
Теоретическая часть. 5
Исторические и биографические факты из жизни Фалеса.
Чем знаменит Фалес?
Практическая часть
Доказательство теоремы Фалеса. 17
Задачи на применение теоремы Фалеса. 18
Список литературы. 21
Цели и задачи проекта
Основная цель проекта:
Выяснить, чем знаменит Фалес и его теорема.
Вопросы учебной темы:
Кто ты, Фалес?
Почему теорема Фалеса так знаменита?
Как теорема Фалеса находит свое применение?
Методические задачи:
Научиться работать в паре,
Научиться обрабатывать и обобщать полученную информацию,
Научиться быстро и эффективно работать в сети Интернет,
Научиться создавать законченные информационные продукты.
Дидактические цели проекта:
С помощью дополнительной литературы, основанной на исторических фактах, познакомиться с открытиями и жизнью Фалеса и его последователей с точки зрения истории развития математики и других наук;
Рассмотреть теорему Фалеса, как источник замечательных математических открытий;
Изучение возможностей программы Power Point.
Аннотация.
Великий учёный Фалес Милетский основал одну из прекраснейших наук- геометрию. Известно, что Фалес Милетский имел титул одного из семи мудрецов Греции, что он был поистине первым философом, первым математиком, астрономом и вообще первым по всем наукам в Греции. Он был то же для Греции, что Ломоносов для России.
Введение.
Наиболее знаменитым из семи мудрецов был Фалес из Милета, ионийского города, греческой колонии в Малой Азии(ок.627-ок.547г. до н.э.).Фалеса также считают и первым философом, основателем Ионийской школы. Поскольку Фалес жил в Ионии, школа его была названа Ионийской.
Он умер в 546 году до н.э., и ему наследовал Анаксимандр, а вслед за ним шли Анаксимен, Анаксагор; Архелай, на ком И. ш. и закончилась.
Сочинения представителей Ионийской школы написаны на ионическом диалекте, в отличие от аттического диалекта произведений Платона и Аристотеля.
Ионийская школа – стихийно-материалистическое направление древнегреческой философии, возникшее и развившееся в ионийских колониях Греции в 6-4вв. до н.э.. Зародилась в г. Милет; её представители – Фалес, Анаксимандр и Анаксимен (милетская школа), Гераклит Эфесский. И. ш. принято противопоставлять пифагорейской, элейской и аттийской школам. Одна из основных идей, впервые выдвинутых философами И. ш. – мысль о единстве всего сущего, о происхождении всех вещей из некоторого единого первоначала, которое понималось при этом как та или иная вещественная стихия или как «беспредельное», из которого выделились основные противоположности тёплого и холодного.
Теоретическая часть.
Вода, по Фалесу, является первичным принципом или элементом, и на ней плавает Земля подобно кораблю, и землетрясение происходят из-за волнений этого вселенского моря.
В дерзновении своём он как бы сдвигает целые плиты и меняет демаркационные линии между реальным и мнимым, действительностью и грезой, ведь вопрошая обо всём мыслитель как бы выносит себя за пределы «всего», рассматривает его со стороны и ставит его под вопрос, выделяя себя, мыслящую в себе инстанцию из «всего», само «всё» как предмет уже в чём-то единиться, как бы округляется в «извне» взгляде философа. Ахиллес и Агамемнон – литература, как бы говорит Фалес, а я – Гомер, как автор я вижу нить сюжета, скрытую до поры от читателя и отдающую непрояснённостью судьбы героев. Так и Фалес, отстраняясь от всего, старается разглядеть сюжетную нить и драматургию, лицо, «физиономию» «всего», вставая на беспрецедентную точку «вне всего». Встав «по ту сторону» только и можно сказать о мире «всё». Фалес отверг всякую мысль о мнимости мира, его неподлинности, а значит и непознаваемости, сказав «есть» «всему», Фалес утвердил и свою позицию как наличествующую, сущую. Э.Р.Ф. как математик и астроном. В своё время Фалес был едва ли не единственным во всей Греции человеком, отдавшимся чистой науки и абстрактному мышлению без преследования каких-нибудь практических целей. Важнейшей заслугой Фалеса в области математики должно быть считаемо перенесение им из Египта в Грецию первых начал теоретической элементарной геометрии. Эвдем, по свидетельству Прокла, приписывает Фалес открытие следующих предложений. Вертикальные углы равны. Углы при основании равнобедренного треугольника равны. Треугольник определяется стороною и прилежащими к ней двумя углами. Диаметр делит круг на две равные части. Диоген Лаерний, в основании слов Памфилия, прибавляет к этому списку предложений ещё вписывание в круг прямоугольного треугольника. Что бы дать полный очерк геометрических знаний Фалеса, необходимо присоединить ещё ряд таких предложений, без которых приобретение первых делается невозможным, а именно предложений о параллельных линиях, о равносторонних, равнобедренных и разносторонних треугольниках, о параллелограммах и прочих сверх перечисленных «открытий» Фалеса в области теоретической геометрии, ему приписывается греческими писателями ещё решение двух геометрических задач практического характера, из которых одна состояла в определении расстояния корабля на море от Милетской гавани, а другая – в определении высоты пирамиды по длине её тени, а именно измеряя тень в тот час, когда она бывает равна своему телу. Поставив палку на конце тени, образуемой пирамидою, так что от солнечного света образовалось два треугольника, он показал, что отношение между величиною пирамиды и палки такое же, какое было между тенью пирамиды и тенью палки. В настоящее время в истории математики уже не существует никаких сомнений относительно того, что всё приписываемое Фалесу его соотечественниками геометрические «открытия» были в действительности простыми заимствованиями из египетской науки.
С именем Фалеса связывают многие остроумные и часто парадоксальные высказывания и ответы, которые так ценились греками. Так рассказывают, что он оставался неженатым: когда его мать в молодости побуждала его жениться, он отвечал « Слишком рано!», в зрелом возрасте «Слишком поздно!». А когда у него спрашивали, почему у него нет детей, он отвечал «Потому что люблю их». Фалес так же утверждал, что между жизнью и смертью нет разницы, а когда его спрашивали: «Почему ты в таком случае не умрёшь?», он отвечал «Именно поэтому».
Фалес был младше Солона лет на 10-15, но они были очень дружны, что видно, в частности, из письма, отправленного Фалесом Ферекиду. Этого письма, приведённого Диогеном Лаэрцким, могло и не быть, но описанные в нём события и отношения между людьми вполне правдоподобны. Фалес пишет: «После того как мы с Соломоном Афинским плавали на Крит ради наших там изысканий и плавали в Египет ради бесед с египетскими жрецами и звездочётами, право, мы были бы безумцами, если бы не поплыли и к тебе; говорю «мы», ибо и Солон приедет, если ты на то согласишься. Ты ведь домосед, в Ионии бываешь редко, новых людей видеть не будешь, и одна у тебя, как я полагаю, забота – о том, что ты пишешь. Мы же не пишем ничего, но зато странствуем по всей Элладе и Азии». О дружбе между Фалесом и Солоном свидетельствует и сам Плутарх, который, который рассказал о любопытном розыгрыше. «Когда Солон прибыл к Фалесу в Милет,- пишет Плутарх, - он удивлялся полному его равнодушию к браку и рождению детей. Фалес на этот раз промолчал, а спустя несколько дней подговорил одного приезжего рассказать, будто он недавно, десять дней назад, приехал из Афин. Солон спросил его, нет ли чего нового в Афинах. Приезжий, подученный Фалесом, сказал: «Ничего, только клянусь Зевсом, были похороны одного молодого человека, и провожал его весь город. Это был, как говорили, сын человека известного, первого в городе по своим нравственным качествам. Его самого не было; говорили, что он уже давно находится за границей».- «Какой несчастный!.. – воскликнул Солон. – А как его называли?» «Я слышал его имя, - отвечал тот, - да не помню; только много было разговоров об его уме и справедливости». Так при каждом ответе у Солона всё возрастал. Наконец, уже в полной тревоге он подсказал приезжему имя и спросил, не называли ли умершего Сыном Солона. Тот ответил утвердительно. Тогда Солон стал бить себя по голове, делать и говорить всё сказал: «Вот это, и удерживает меня от брака и рождения детей, что валит с ног и тебя, такого сильного человека. Что же касается этого рассказа, не бойся: это неправда». Отсюда, между прочим, следует, что семьи у Фалеса не было. Как сообщил Плутарх, Фалес усыновил ребёнка своей сестры, по имени Кабиста. Фалеса, же всегда считали естествоиспытателем, астрономом и математиком, изображали с циркулем в руке.
Народ говорил о семи мудрецах, к коим причислил Фалеса, Солона, Бианта, Питтака, Периандра, Клеобула и Хилона. В отношении первых трёх ни у кого сомнений не было, но с причислением остальных к лику мудрых велись ожесточённые споры. Одни называли либо Ферекида Сиросского, либо тирана Писистрата или какое-либо другое лицо, выдвигавшееся на соискание этого звания скорее из лести, чем по истинным достоинствам. Платон в «Протагоре» из названного списка убрал тирана Периандра, добавив Мисона, которому он, очевидно симпатизировал. Писал Фалес или нет, этого мы уже никогда не узнаем, но заслуги его перед наукой огромны, хотя и не всё время он ей посвятил. Находясь на службе у тирана Трасибула , Фалес плавал по Средиземному морю с торговой, а возможно, и государственно-дипламатической миссией. Сам он, скорее всего, в торговых сделках не участвовал, так как у него, похоже, не было устойчивого интереса к коммерческим делам. В древности говорили: «Ну, сущий Фалес», т.е. не от мира сего, отрешённый от повседневной суеты, думающий только о научных проблемах. Однако Аристотель рассказал один забавный случай, произошедший с Фалесом, который, будучи увлечённым и занятым учёным, тем не менее, мог провести успешную коммерческую сделку. «Этот рассказ о некоем, предвидении, - пишет Аристотель в «Политике», - использованном для того, чтобы нажить состояние, и его приписывают Фалесу, имея в виду его мудрость, но её можно рассматривать и с общей точки зрения. Когда его попрекали бедностью, утверждая, будто занятия философией никакой выгоды не приносят.
То, рассказывают, он, предвидя на основании астрономических данных богатый урожай оливок, ещё до истечения зимы роздал в задаток имевшуюся у него небольшую сумму денег всем владельцам маслобоен в Милете и на Хиосе, законтрактован их дёшево, так как никто с ним не конкурировал. Когда наступило время сбора оливок и сразу многим одновременно потребовались маслобойни, он, отдавая маслобойни на откуп на желательных ему условиях и собрав много денег, доказал, что философам при желании легко разбогатеть, но не это является предметом их стремлений. Так, говорят, Фалес дал доказательство своей мудрости. Этот случай, произошедший с Фалесом, вероятно, ещё в молодости, скорее подчёркивает его непрактичность, поскольку выставляется как исключение из правила, которому была подчинена его натура.
Платон, Аристотель и Плутарх, кивая на Фалеса, в унисон говорили, что мудрость надо отличать от рассудительности: первое касается знания природы, второе - выгоды для себя; Фалес был мудрым, но не рассудительным, (сейчас бы сказали, не расчётливым). Его жизнь в чём-то напоминает жизнь Галилея, который тоже по молодости торговал циркулями и подзорными трубами. Это занятие его увлекало так, что трудно было сказать, чем больше занята его голова - коммерцией или наукой. Но постепенно итальянского Фалеса – Галилея нередко сравнивают с античным мудрецом – захватила наука: все ночи напролёт он смотрел на звёзды, пока не ослеп.
Естественно, рано или поздно, знатному и мудрому Фалесу, на голову возвышающемуся над всеми остальными, чтобы не потерять её, пришлось «удалиться от государственных дел» и заняться науками. Знания качеств личности Писистрата и Трасибула помогает понять сложную политическую обстановку, в которой жил Фалес. Слава учёного пришла к Фалесу после предсказанного им солнечного затмения, которое описал Геродот: «Так как Алиатт, несмотря на требования Киаксара, не захотел выдать скифов, то у лидийцев с мидянами началась война. Пять лет длилась эта война, причём верх одерживали то мидяне, то побеждали лидийцы и однажды – даже в какой-то ночной битве. Так с переменным успехом продолжалась эта затяжная война, и на шестой год во время одной битвы внезапно день превратился в ночь. Это солнечное затмение предсказал ионянам Фалес Милетский и даже точно определил заранее год, в котором оно и наступило. Когда лидийцы и мидяне увидели, что день обратился в ночь, то прекратили битву и поспешно заключили мир». Нечего говорить о том, что занятия Фалеса в Египте также трактуются очень серьёзно. Это – крайне пессимистический взгляд на успехи Фалеса и, вообще, достижения всей античной науки.
Как показывает история исследования некоторых математических алгоритмов решения задач, которыми пользовались древние вавилоняне и египтяне, современные учёные не могут взять в толк, каким образом они могли быть найдены. Нашим современникам кажется, что для решения задач по нахождению площадей геометрических фигур, объёмов тел и прочих параметров требуются знания высших разделов математики – алгебры интегрально-дифферециального исчисления. Однако вполне работоспособные алгоритмы были найдены, причём некоторые из них три-четыре тысячи лет назад – мы просто не умеем их реконструировать. Может быть, не Фалес первый разделил год на365 дней, дал определение числа, как совокупности единиц и понял, что вписанный в круг треугольник, опирающийся на диаметр, всегда будет прямым, как об этом упоминается в различных древних источниках, но, по крайней мере, в его время об этом уже знали. Они говорят об уровне развития знаний той эпохи, в которой жил самый выдающийся учёный. Следовательно, мы смело можем говорить: Фалес или кто-то из его современников вполне понимал, что во всяком равнобедренном треугольников углы при основании равны, при пересечении двух прямых вертикальные углы равны, два треугольника равны, если два угла и одна сторона одного из них равны углам и одной стороне другого. Последняя теорема, как предполагается, использовалась Фалесом для нахождения расстояния до кораблей, находящихся в море. Нахождение Фалесом определенных отношений между элементами равнобедренного треугольника, ничем принципиальным не отличается от нахождений законов физики: и математические(стороны, углы, площади), и физические(сила, ускорение, масса) величины измеряются эмпирически, т.е. пришли к нам из опыта и используются нами в практической жизни. Интеллектуальные и чувственные образы тесно взаимосвязаны, так что разъединять их какой-либо преградой ненужно. Таким образом, математические объекты вполне можно отнести к естественнонаучным и рассматривать математику и естествознание, как одну рациональную науку, в которой используется один и тот же конструктивный подход. Нейгебауэр критиковал Фалеса за неудачное предположение, что причиной разлива Нила являются ветер, дующий с моря против его течения. Да, конечно, эта гипотеза ошибочна, но важно, что он над этим явлением размышлял и предложил рациональное объяснение, а не сводил дело к божественному гневу или милости, как это делали до него. Начиная с Фалеса люди повсеместно стали задаваться вопросами: почему сверкает молния, как возникает гром, что такое огонь, как связан он с теплом, откуда берётся ветер, что такое снег и лёд, как связаны они с холодом, из чего земля, животные и растительные ткани, какие причины приводят к землетрясению, наступлению холодов, образованию облаков и т.д. и т. д. Наука начинается там, где религии говорят «Нет!», где ищут решения, не прибегая к силам какого-либо Высшего Существа. И вот в этом Фалес был Первым! «Он первый нашёл путь Солнца от солнцестояния до солнцестояния; он первый ( по мнению некоторых) объявил, что размер Солнца составляет 1/720 часть [солнечного пути, а размеры Луны – такую же часть] лунного пути [ т.е. оба светила видны под углом 0,5 гр.]. Он первый назвал последний день месяца «тридесятым», [т.е. разделил год на 12 месяцев, в каждом из них было по 30 дней]. Он первый, как говорят иные, стал вести беседы о природе». Главное геометрическое достижение Фалеса состояла в том, что ему удалось открыть пропорциональность сторон подобных треугольников. Теперь на основе пропорции a/b=c/d, он мог производить измерение неизвестной величины по трём известным. Именно с помощью этой пропорции он нашёл высоту египетских пирамид.
Измерение расстояния до корабля, находящегося далеко в море, производилось тоже на основе этой пропорции. Выбрав на берегу базиса и вымерив с крайних его точек углы до корабля, геометр затем вычерчивал подобный треугольник небольших размеров и измерял у него две стороны, скажем, c и d; после этого ничего не стоило найти неизвестное расстояние до корабля – сторону b. Такого рода задачи и даже более сложного( нахождение площади круга, объём усечённой пирамиды и т.д.) умели решать в Египте. Это стало известно из найденных Московского и Риндовского папирусов, написанных около 2000 году до н.э. Однако этими знаниями овладел мудрый человек, живущий в ответственный для науки период. Далее можно пронаблюдать, как пропорция a/b = c/d через Пифагора, Демокрита и Архимеда легла в основу науки эпохи Зарождения и Итальянского Возрождения. Простота и универсальность пропорции позволило сделать множество математических и естественнонаучных открытий. Всё это говорит о том, что Фалес был не столько первым философом, сколько первым учёным, т.е. тем первым профессионалом, который все явления природы пытался Объяснить рациональными средствами. Но было в его объяснениях физического мира и такое, что отнести к рациональным соображениям можно лишь с изрядной натяжкой. Время жизни Фалеса, по Дильсу, 624 – 547 г. до н.э., расцвет сил (акме) 585г., дата славы 585г., предсказанное им солнечное затмение 28 мая 585г. По Таннери, время жизни Фалеса 637-558г. акме 597г., дата славы 586г., предсказанное им солнечное затмение 30 сентября 610г. Заслуги, которые приписывали Фалесу историки в новое время, можно резюмировать так: Фалес – родоначальник европейской науки, он перенёс с Востока в Грецию богатый запас эмпирических наблюдений и на основании этого обширного собрания фактов создал первые в истории мысли научно-теоритические построения. В частности, он – первый математик и создатель научной геометрии (преобразовал египетское искусство измерения в дедуктивную геометрию, покоящуюся на общих основаниях), астроном (предсказал полное затмение; открыл, что из созвездий наиболее точно север определяется Малой Медведицей, и т. д.), метеоролог (удачное предсказание урожая оливок), физик (ряд объяснений физических явлений). Как философов, он глава милетской школы и отец греческой философии. Точность его научных открытий, его деятельность не ограничивалась научно-теоретической областью, он также практически деятель с обширной сферой интересов: он – путешественник, купец (торгует солью), инженер, политик и государственный деятель. Наконец, известны его краткие изречения – практические советы морального характера. Основное положение Фалеса: вода есть начало всего. Нам неизвестно в точности, какой смысл заключён в этом положении. Прежде всего, идёт ли здесь речь о возникновении во времени или в вечной основе всего существующего? Говорит ли Фалес, что всё возникло из воды (учение, которое в 16 веке повторил Парацельс), или он указывает в воде постоянное начало, неизменно лежащее в основе изменчивых разнообразных форм природы? Далее, эта первая стихия есть ли вода, как одно из веществ природы, или под водой здесь разумеется всякая жидкость (т.е. первичным признаётся известное состояние матери), или, наконец, вода здесь есть объектированное качеств: влажность? Так расходятся взгляды учёных в истолковании положения Фалеса «вода есть начало всего», в котором, таким образом, и субъект и предикат двусмысленны для нас. Как говорит Дмитрий Фалерский в «Списке архонтов», Фалес был назван первым мудрецом в тот год, когда в Афинах был архонтом Дамасия, при котором были названы мудрецами известные семь. Принят же в число граждан Фалес был в Милете, куда он прибыл с Нейлеем, изгнанным из Финикии. Впрочем, по свидетельству большинства, он был природный милетец и знатного рода. Почти все философы древней Греции тщательно занимались математикой, в частности геометрией. Фалесу Мелецкому Прокл приписывает открытие или доказательство теорем о том, что диаметр делит круг пополам, что угол, вписанный в полуокружность, прямой, о равенстве вертикальных углов, о равенстве углов при основании равнобедренного треугольника и др. Эти положения были частично известны ещё вавилонянам и египтянам. Однако в отличии от вавилонской и египетской геометрии, имевшей преимущественно практический и прикладной характер, греческая геометрия характеризуется стремлением установить, что геометрические факты верны не только для отдельных частных случаев, а справедливы в любом случае. При помощи общих доказательств, с постепенным переходим от одной истины к другой, греческие математики создали геометрию как науку.
Направление строгой логической последовательности в геометрии первыми заложили геометры греческой ионийской школы, основателем которой был Фалес. Фалес был знаком и с вавилонской астрономией. Платон, знаменитый греческий философ четвёртого века до нашей эры, рассказывает, что Фалес, наблюдая звёзды, упал в колодец, а стоявшая рядом женщина посмеялась над ним, сказав: «Хочет знать, что делается на небе, а что у него под ногами, не видит…». Фалес сделал ряд открытий в области астрономии: установил время равноденствий и солнцестояний, определил продолжительность года, впервые наблюдал Малую Медведицу и т.п. Особенную славу ему принесло предсказание солнечного затмения, произошедшего в 585 году до н.э. Фалес был не только философом и учёным, но также государственным и общественным деятелем. Вот почему он был причислен к группе «семи мудрецов» древности.
Существуют разные версии смерти Фалеса.
1. Диоген Лаэрцкий в своём известном сочинении «О жизни, учёниях и изречениях знаменитых философов», появившемся где-то во 2-3вв., привёл письмо Анаксимена, посланное Пифагору, где сообщает о смерти своего учителя и друга. «Фалес, сын Эксамия, достигнув преклонных лет, несчастным образом скончался. Ночью он по своему обыкновению вышел со служанкой из дома, чтобы посмотреть на звёзды, и, созерцая их, свалился в канаву, о котором совсем запамятовал. Вот каков, по словам милетских жителей, был конец этого небоведца. Мы же, его собеседники, и сами, и дети наши, и коллеги наши по занятиям, сохранили память об этом муже и блюдем его заветы. Пусть же всякая наша речь начинается именем Фалеса». Во втором письме к Пифагору, который бежал от тирана Поликрата с острова Самос, расположенного недалеко от Милета, в италийский город Кратон, Анаксимен, жалуясь на тяжёлую жизнь, обронил такую фразу: «Как же помышлять Анаксимену о делах небесных, когда приходится страшиться гибели или рабства [на земле]. Возможно, в людской памяти как-то соединилась эта фраза с личностью Фалеса, но не с его гибелью.
2. В античности была распространена легенда, будто мудрец скончался от зноя, жажды и давки, когда смотрел на солнцепёке, как состязаются молодые и сильные гимнасты. Старик слишком приблизился к соревнующимся, пишет Диоген Лаэрцкий, и возбужденная толпа задавила его насмерть. Однако такой печальный финиш жизни этого выдающегося человека кажется маловероятным. Вряд ли могло так случиться, чтобы известного всей Элладе мыслителя задавила толпа болельщиков? Так что малопочётная гибель в канаве здесь кажется более предпочтительной, если только она действительно была вызвана желанием смотреть на звёзды.
3..Мудрец Фалес скончался в то время, когда смотрел гимнастическое состязание, от жары, жажды и бессилия, будучи уже престарелым. И на памятнике его написано: «Взирай на эту действительно малую могилу весьма мудрого Фалеса (слава же его достигает небес)». Имеется и у нас в первой из «Надписей», или в «Написанной в различных размерах», следующая надпись, относящаяся к нему: «Некогда смотревшего гимнастическое состязание мудреца Фалеса ты, о солнце Зевс, похитил из ристалища. Я восхваляю тебя за то, что увёл его поближе к небу, ибо, в самом деле, старик уже не мог более с земли видеть звёзды. Фалесу принадлежит изречение: «Познай самого себя», о котором Антисфен в «Диадохах» говорит, что оно принадлежит Фемоною и что его присвоил себе Хилон..
Сочинения Фалеса до нашего времени не сохранились.
Практическая часть.
Теорема
Докажем теорему Фалеса: если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.
Решение:
Пусть на прямой l1 отложены равные отрезки А1А2, А2А3, А3А4, …и через их концы проведены параллельные прямые, которые пересекают прямую l2 в точках В1, В2, В3, В4, … (рис.1). Требуется доказать, что отрезки В1В2, В2В3, В3В4, … равны друг другу. Докажем, например, что В1В2 = В2В3.
Рассмотрим сначала случай, когда прямые l1 и l2 параллельны (рис. 1, а). тогда А1А2 = В1В2 и А2А3 = В2В3 как противоположные стороны параллелограммов А1В1В2А2 и А2В2В3А3. так как А1А2 = А2А3, то и В1В2 = В2В3 если прямые l1 и l2 не параллельны, то через точку
В1 проведем прямую l, параллельную прямой l1 (рис.1, б). Она пересечет прямые А2В2 и А3В3 в некоторых точках С и D. Так как А1А2 = А2А3, то по доказанному В1С = СD. Отсюда получаем В1В2 = В2В3. Аналогично можно доказать, что В2В3 = В3В4 и т.д.
Задача
Через середину М стороны АВ треугольника АВС проведена прямая, параллельная стороне ВС. Эта прямая пересекает сторону АС в точке N. Докажите, что AN = NC.
Решение:
Через точку С проведем прямую, параллельную прямой АВ и обозначим буквой D точку пересечения этой прямой с прямой MN (рис. 2). Так как AM = МВ по условию, а MB = CD как противоположные стороны параллелограмма BCDM, то АМ = DC. Треугольники АМN и CDN равны по второму признаку равенства треугольников (АМ=CD,<1= <2 и <3=<4 как накрест лежащие углы при пересечении параллельных прямых АВ и CD секущими АС и МD), поэтому AN = NC.
^ Задача
Разделите данный отрезок АВ на n равных частей.
Решение:
Проведен луч АХ, не лежащий на прямой АВ, и на нем от точки А отложим последовательно n равных отрезков АА1, А1А2, …, Аn-1Аn (рис.3), т.е. столько равных отрезков, на сколько равных частей нужно разделить данный отрезок АВ (на рис. 3 n=5). Проведем прямую АnВ (точка Аn – конец последнего отрезка) и построим прямые, проходящие через точки А1 , А2 , …, Аn-1 и параллельные прямой АnВ. Эти прямые пересекают отрезок АВ в точках В1 , В2 , …, Вn-1, которые по теореме Фалеса делят отрезок АВ на n равных частей.
^ Задача
Разделите данный отрезок АВ на 8 равных частей.
Решение:
Проведен луч АХ, не лежащий на прямой АВ, и на нем от точки А отложим последовательно 8 равных отрезков АА1, А1А2, …, А7А8 (рис.3), т.е. столько равных отрезков, на сколько равных частей нужно разделить данный отрезок АВ (рис. 4). Проведем прямую А8В (точка А8 – конец последнего отрезка) и построим прямые, проходящие через точки А1 , А2 , …, А7 и параллельные прямой А8В. Эти прямые пересекают отрезок АВ в точках В1 , В2 , …, В7, которые по теореме Фалеса делят отрезок АВ на 8 равных частей.
Литература
Атанасян Л.С. и др. Геометрия. 7—9 классы : учеб. для общеобразоват. учреждений / [Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др.],М. : Просвещение, 1999.
Глейзер Г.И. История в математики в школе. Москва: Просвещение, 1983.
Малыгин К.Л. Элементы историзма в преподавании математики в средней школе. М: Учпедгиз 1963г.
Погорелов А.В. Геометрия 7 – 11 класс. Москва.: "Просвещение", 1995
Рыбников Л.А. История математики. Издательство МГУ, 1974 г.
Интернет ресурсы.
Планиметрия http://ru.wikipedia.org/wiki/
Милетская школа http://ru.wikipedia.org/wiki/
Теорема Фалеса http://ru.wikipedia.org/wiki/
4>2>
www.ronl.ru
Применение подобия к доказательству теорем и решению задач (Обобщение теоремы Фалеса. Теоремы Чевы и Менелая.)
1. Введение;
2. Обобщение теоремы Фалеса;
(a) Формулировка;
(b) Доказательство;
3. Теорема о пропорциональных отрезках;
4. Теорема Чевы;
(a) Формулировка;
(b) Доказательство;
5. Теорема Менелая;
(a) Формулировка;
(b) Доказательство;
6. Задачи и их решения;
7. Источники информации;
8. Вывод.
Мой реферат посвящен применению подобия к доказательству теорем и решению задач, а именно глубоко изучить обобщение теоремы Фалеса, теоремы Чевы и Менелая, которые не изучаются в школьной программе. Теме подобия, которая проходится в восьмом классе, отведено всего лишь 19 часов, что недостаточно для изучения этой темы более углубленно. В тему подобия входят: определение подобных треугольников, признаки подобия, отношение площадей подобных треугольников, средняя линия треугольника, пропорциональные отрезки и т.д.
Напомню определение подобных треугольников :
Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого. Оказывается, что у подобных треугольников не только отношение сходственных сторон, но и отношение любых других сходственных отрезков равно коэффициенту подобия. Например, отношение сходственных биссектрис AD и A1 D1 , т.е. биссектрис равных углов A и A1 в подобных треугольниках ABC и A1 B1 C1 , равно коэффициенту подобия k, отношение сходственных медиан AM и A1 M1 равно k и точно так же отношение сходственных высот AH и A1 h2 равно k.
С помощью данного материала, который изучается в школьной программе, мы можем решать довольно узкий круг задач. При создании своего реферата я собираюсь углубить свои знания по данной теме, что позволит решать более широкий круг задач на пропорциональные отрезки. В этом и заключается актуальность моего реферата.
Одна из теорем – это обобщение теоремы Фалеса. Сама теорема Фалеса проходится в восьмом классе. Но главными теоремами являются теоремы Чевы и Менелая.
Формулировка:
Параллельные прямые, пересекающие две данные прямые, отсекают на этих прямых пропорциональные отрезки.
Доказать:
=…=
.
Доказательство:
Докажем, например, что
Рассмотрим два случая:
1 случай
Прямые a и b параллельны. Тогда четырехугольники А1А2В2В1 и А2А3В3В2 – параллелограммы. Поэтому А1А2=В1В2 и А2А3=В2В3, откуда следует, что
2 случай
Прямые a и b не параллельны. Через точку А1 проведем прямую с, параллельную прямой b. Она пересечет прямые А2В2 и А3В3 в некоторых точках С2 и С3. Треугольники А1А2С2 и А1А3С3подобны по двум углам (угол А1 – общий, углы А1А2С2 и А1А3С3 равны как соответственные при параллельных прямых А2В2 и А3В3 секущей А2А3), поэтому
Отсюда по свойству пропорций получаем:
(1)
С другой стороны, по доказанному в первом случае имеем А1С2=В1В2, С2С3=В2В3. Заменяя в пропорции (1) А1С2 на В1В2 и С2С3 на В2В3, приходим к равенству
(2)
что и требовалось доказать.
На сторонах АС и ВС треугольника АВС отмечены точки К и М так, что АК:КС=m:n, BM:MC=p:q. Отрезки АМ и ВК пересекаются в точке О.
Доказать:
Доказательство:
Через точку М проведем прямую, параллельную ВК. Она пересекает сторону АС в точке D, и согласно обобщению теоремы Фалеса
Пусть АК=mx. Тогда в соответствии с условием задачи КС=nx, а так как KD:DC=p:q, то 
Снова воспользуемся обобщением теоремы Фалеса:
Аналогично доказывается, что 
.
Теорема названа в честь итальянского математика Джованни Чевы, который доказал её в 1678 году.
Формулировка:
Если на сторонах АВ, ВС и СА треугольника АВС взяты соответственно точки С1 , А1 и В1 , то отрезки АА1 , ВВ1 и СС1 пересекаются в одной точке тогда и только тогда, когда
(3)
Доказать:
1. 
(3)
2.отрезки АА1, ВВ1 и СС1 пересекаются в одной точке
Доказательство:
1. Пусть отрезки АА1, ВВ1 и СС1 пересекаются в одной точке О. Докажем, что выполнено равенство (3). По теореме о пропорциональных отрезках в треугольнике имеем:
и 
.
Левые части этих равенств одинаковы, значит, равны и правые части. Приравнивая их, получаем
.
Разделив обе части на правую часть, приходим к равенству (3).
2. Докажем обратное утверждение. Пусть точки С1, А1 и В1 взяты на сторонах АВ, ВС и СА так, что выполнено равенство (3). Докажем, что отрезки АА1, ВВ1 и СС1 пересекаются в одной точке. Обозначим буквой О точку пересечения отрезков АА1 и ВВ1 и проведем прямую СО. Она пересекает сторону АВ в некоторой точке, которую обозначим С2. Так как отрезки АА1, ВВ1 и СС1 пересекаются в одной точке, то по доказанному в первом пункте
. (4)
Итак, имеют место равенства (3) и (4).
Сопоставляя их, приходим к равенству 
=
, которое показывает, что точки C1 и C2 делят сторону AB в одном и том же отношении. Следовательно, точки C1 и C2 совпадают, и, значит, отрезки АА1, ВВ1 и СС1 пересекаются в точке O. Теорема доказана.
Формулировка:
Если на сторонах АВ и ВС и продолжении стороны АС (либо на продолжениях сторон АВ, ВС и АС) взяты соответственно точки С1 , А1, В1, то эти точки лежат на одной прямой тогда и только тогда, когда
(5)
Доказать:
1. (5)
2. точки А1,С1,В1 лежат на одной прямой
Доказательство:
1. Пусть точки А1,В1 и С1 лежат на одной прямой. Докажем, что выполнено равенство (5). Проведем AD,BE и CF параллельно прямой В1А1 (точка в лежит на прямой ВС). Согласно обобщению теоремы Фалеса имеем:
и 
Перемножая левые и правые части этих равенств, получаем
, откуда 
,
т.е. выполнено равенство (5).
2. Докажем обратное утверждение. Пусть точка В1 взята на продолжении стороны АС, а точки С1 и А1 – на сторонах АВ и ВС, причем так, что выполнено равенство (5). Докажем, что точки А1,В1 и С1 лежат на одной прямой, то по доказанному а первом пункте
(6)
Сопоставляя (5) и (6), приходим к равенству 
=
, которое показывает, что точки А1 и А2 делят сторону ВС в одном и том же отношении. Следовательно, точки А1 и А2 совпадают, и, значит, точки А1,В1 и С1 лежат на одной прямой. Аналогично доказывается обратное утверждение в случае, когда все три точки А1,В1 и С1 лежат на продолжениях соответствующих сторон. Теорема доказана.
Задача №1.
Условие:
В треугольнике АВС АD – медиана, точка О – середина медианы. Прямая ВО пересекает сторону АС в точке К.
Найти:
АК:КС=?:?
Решение: Пусть ВD = DС = а, АО = ОD = m. Прямая ВК пересекает две стороны и продолжение третьей стороны треугольника АDС. По теореме Менелая получаем
Задача №2.
Условие:
Пусть АD – медиана треугольника АВС. На стороне АD взята точка К так, что АК : КD = 3 : 1. Прямая ВК разбивает треугольник АВС на два.
Найти:
Решение: Пусть АD = DC = a, KD = m, тогда АК = 3m. Пусть Р – точка пересечения прямой ВК со стороной АС. Необходимо найти
отношение 
. Так как треугольники АВР и РВС имеют равные высоты, проведенные из вершины В, то 
По теореме Менелая для треугольника ADC и секущей РВ имеем
Итак, 
.
Задача №3.
Формулировка: Медианы треугольника пересекаются в одной точке. Точка пересечения делит каждую из них в отношении 2 : 1, считая от вершины.
Условие:
Медианы треугольника пересекаются в одной точке.
Доказать:
Точка пересечения делит каждую медиану в отношении 2 : 1, считая от вершины.
Доказательство: Пусть АМ1 , ВМ2 , СМ3 – медианы треугольника АВС. Чтобы доказать, что эти отрезки пересекаются в одной точке, достаточно показать, что 
Тогда по теореме Чевы (обратной) отрезки АМ1 , ВМ2 и СМ3 пересекаются в одной точке. Имеем:
Итак, доказано, что медианы треугольника пересекаются в одной точке.
Пусть О – точка пересечения медиан. Прямая М3 С пересекает две стороны треугольника АВМ2 и продолжение третьей стороны этого треугольника. По теореме Менелая
Рассматривая теорему Менелая для треугольников АМ1 С и АМ2 С, мы получаем, что
Теорема доказана.
Задача №4.
Формулировка:
Биссектрисы треугольника пересекаются в одной точке.
Доказать:
Биссектрисы треугольника пересекаются в одной точке.
Доказательство: Достаточно показать, что 
. Тогда по теореме Чевы (обратной) AL1, BL2, CL3 пересекаются в одной точке. По свойству биссектрис треугольника:
. Перемножая почленно полученные равенства, получаем: 
. Итак, для биссектрис треугольника равенство Чевы выполняется, следовательно, они пересекаются в одной точке. Теорема доказана.
Задача №5.
Формулировка:
Высоты остроугольного треугольника пересекаются в одной точке.
Доказать:
Высоты остроугольного треугольника пересекаются в одной точке.
Доказательство: Пусть АН1 , АН2, АН3 – высоты треугольника АВС со сторонами a, b, c. Из прямоугольных треугольников АВН2 и ВСН2 по теореме Пифагора выразим, соответственно, квадрат общего катета ВН2 , обозначив АН2 = х, СН2 = b – х.
(ВН2 )2 = с2 – х2 и (ВН2 )2 = а2 – (b – х)2 . приравнивая правые части полученных равенств, получаем с2 – х2 = а2 – (b – х)2 , откуда х = 
.
Тогда b –x = b - = 
.
Итак, АН2 = , СН2 = .
Аналогично рассуждая для прямоугольных треугольников АСН2 и ВСН3 , ВАН1 и САН1 , получим АН3 = 
, ВН3 = 
и ВН1 = 
,
СН1 = 
.
Для доказательства теоремы достаточно показать, что 
. Тогда по теореме Чевы (обратной) отрезки АН1 , ВН2 и СН3 пересекаются в одной точке. Подставив в левую часть равенства выражения длин отрезков АН3 , ВН3 , ВН1 , СН1 , СН2 и АН2 через а, b, с, убеждаемся, что равенство Чевы для высот треугольника выполняется. Теорема доказана.
Дополнительные главы по геометрии 8 класса (Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев, С. А. Шестаков, И. И. Юдина) - настоящее пособие является дополнением к учебнику `Геометрия, 7-9` авторов Л.С.Атанасяна, В.Ф.Бутузова и др. (М.: Просвещение, 1990 и последующие издания). Оно полностью соответствует программе углубленного изучения математики.
Сайты:
http://festival.1september.ru
http://www.problems.ru
С помощью обобщения теоремы Фалеса, теорем Чевы и Менелая, не изучаемых в школьной программе, можно быстрее и легче доказывать определенные теоремы и решать более широкий круг задач. Я смогла доказать такие теоремы: теорема о пропорциональных отрезках (с помощью обобщения теоремы Фалеса), теоремы о пересечении медиан, высот и биссектрис треугольника в одной точке (воспользовалась теоремами Чевы и Менелая).
www.yurii.ru
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
Управление образования Советского района г. Красноярска
Использование теоремы Фалеса в современном мире
(Исследовательско – реферативная работа)
Работу выполнили:
Ученик 9 класса
Баландин Александр
Ученик 9 класса
Кузьмин Александр
Научные руководители:
Учитель математики Мальцева Т.Г
Учитель информатики Заболотникова Е.Ю.
Красноярск 2011
Содержание:
Цели и задачи проекта. 3
Аннотация 4
Введение 4
Теоретическая часть. 5
Исторические и биографические факты из жизни Фалеса.
Чем знаменит Фалес?
Практическая часть
Доказательство теоремы Фалеса. 17
Задачи на применение теоремы Фалеса. 18
Список литературы. 21
Цели и задачи проекта
Методические задачи:
Научиться работать в паре,
Научиться обрабатывать и обобщать полученную информацию,
Научиться быстро и эффективно работать в сети Интернет,
Научиться создавать законченные информационные продукты.
Дидактические цели проекта:
С помощью дополнительной литературы, основанной на исторических фактах, познакомиться с открытиями и жизнью Фалеса и его последователей с точки зрения истории развития математики и других наук;
Рассмотреть теорему Фалеса, как источник замечательных математических открытий;
Изучение возможностей программы Power Point.
Аннотация.
Великий учёный Фалес Милетский основал одну из прекраснейших наук- геометрию. Известно, что Фалес Милетский имел титул одного из семи мудрецов Греции, что он был поистине первым философом, первым математиком, астрономом и вообще первым по всем наукам в Греции. Он был то же для Греции, что Ломоносов для России.
Введение.
Наиболее знаменитым из семи мудрецов был Фалес из Милета, ионийского города, греческой колонии в Малой Азии(ок.627-ок.547г. до н.э.).Фалеса также считают и первым философом, основателем Ионийской школы. Поскольку Фалес жил в Ионии, школа его была названа Ионийской.
Он умер в 546 году до н.э., и ему наследовал Анаксимандр, а вслед за ним шли Анаксимен, Анаксагор; Архелай, на ком И. ш. и закончилась.
Сочинения представителей Ионийской школы написаны на ионическом диалекте, в отличие от аттического диалекта произведений Платона и Аристотеля.
Ионийская школа – стихийно-материалистическое направление древнегреческой философии, возникшее и развившееся в ионийских колониях Греции в 6-4вв. до н.э.. Зародилась в г. Милет; её представители – Фалес, Анаксимандр и Анаксимен (милетская школа), Гераклит Эфесский. И. ш. принято противопоставлять пифагорейской, элейской и аттийской школам. Одна из основных идей, впервые выдвинутых философами И. ш. – мысль о единстве всего сущего, о происхождении всех вещей из некоторого единого первоначала, которое понималось при этом как та или иная вещественная стихия или как «беспредельное», из которого выделились основные противоположности тёплого и холодного.
Теоретическая часть.
Вода, по Фалесу, является первичным принципом или элементом, и на ней плавает Земля подобно кораблю, и землетрясение происходят из-за волнений этого вселенского моря.
В дерзновении своём он как бы сдвигает целые плиты и меняет демаркационные линии между реальным и мнимым, действительностью и грезой, ведь вопрошая обо всём мыслитель как бы выносит себя за пределы «всего», рассматривает его со стороны и ставит его под вопрос, выделяя себя, мыслящую в себе инстанцию из «всего», само «всё» как предмет уже в чём-то единиться, как бы округляется в «извне» взгляде философа. Ахиллес и Агамемнон – литература, как бы говорит Фалес, а я – Гомер, как автор я вижу нить сюжета, скрытую до поры от читателя и отдающую непрояснённостью судьбы героев. Так и Фалес, отстраняясь от всего, старается разглядеть сюжетную нить и драматургию, лицо, «физиономию» «всего», вставая на беспрецедентную точку «вне всего». Встав «по ту сторону» только и можно сказать о мире «всё». Фалес отверг всякую мысль о мнимости мира, его неподлинности, а значит и непознаваемости, сказав «есть» «всему», Фалес утвердил и свою позицию как наличествующую, сущую. Э.Р.Ф. как математик и астроном. В своё время Фалес был едва ли не единственным во всей Греции человеком, отдавшимся чистой науки и абстрактному мышлению без преследования каких-нибудь практических целей. Важнейшей заслугой Фалеса в области математики должно быть считаемо перенесение им из Египта в Грецию первых начал теоретической элементарной геометрии. Эвдем, по свидетельству Прокла, приписывает Фалес открытие следующих предложений. Вертикальные углы равны. Углы при основании равнобедренного треугольника равны. Треугольник определяется стороною и прилежащими к ней двумя углами. Диаметр делит круг на две равные части. Диоген Лаерний, в основании слов Памфилия, прибавляет к этому списку предложений ещё вписывание в круг прямоугольного треугольника. Что бы дать полный очерк геометрических знаний Фалеса, необходимо присоединить ещё ряд таких предложений, без которых приобретение первых делается невозможным, а именно предложений о параллельных линиях, о равносторонних, равнобедренных и разносторонних треугольниках, о параллелограммах и прочих сверх перечисленных «открытий» Фалеса в области теоретической геометрии, ему приписывается греческими писателями ещё решение двух геометрических задач практического характера, из которых одна состояла в определении расстояния корабля на море от Милетской гавани, а другая – в определении высоты пирамиды по длине её тени, а именно измеряя тень в тот час, когда она бывает равна своему телу. Поставив палку на конце тени, образуемой пирамидою, так что от солнечного света образовалось два треугольника, он показал, что отношение между величиною пирамиды и палки такое же, какое было между тенью пирамиды и тенью палки. В настоящее время в истории математики уже не существует никаких сомнений относительно того, что всё приписываемое Фалесу его соотечественниками геометрические «открытия» были в действительности простыми заимствованиями из египетской науки.
С именем Фалеса связывают многие остроумные и часто парадоксальные высказывания и ответы, которые так ценились греками. Так рассказывают, что он оставался неженатым: когда его мать в молодости побуждала его жениться, он отвечал « Слишком рано!», в зрелом возрасте «Слишком поздно!». А когда у него спрашивали, почему у него нет детей, он отвечал «Потому что люблю их». Фалес так же утверждал, что между жизнью и смертью нет разницы, а когда его спрашивали: «Почему ты в таком случае не умрёшь?», он отвечал «Именно поэтому».
Фалес был младше Солона лет на 10-15, но они были очень дружны, что видно, в частности, из письма, отправленного Фалесом Ферекиду. Этого письма, приведённого Диогеном Лаэрцким, могло и не быть, но описанные в нём события и отношения между людьми вполне правдоподобны. Фалес пишет: «После того как мы с Соломоном Афинским плавали на Крит ради наших там изысканий и плавали в Египет ради бесед с египетскими жрецами и звездочётами, право, мы были бы безумцами, если бы не поплыли и к тебе; говорю «мы», ибо и Солон приедет, если ты на то согласишься. Ты ведь домосед, в Ионии бываешь редко, новых людей видеть не будешь, и одна у тебя, как я полагаю, забота – о том, что ты пишешь. Мы же не пишем ничего, но зато странствуем по всей Элладе и Азии». О дружбе между Фалесом и Солоном свидетельствует и сам Плутарх, который, который рассказал о любопытном розыгрыше. «Когда Солон прибыл к Фалесу в Милет,- пишет Плутарх, - он удивлялся полному его равнодушию к браку и рождению детей. Фалес на этот раз промолчал, а спустя несколько дней подговорил одного приезжего рассказать, будто он недавно, десять дней назад, приехал из Афин. Солон спросил его, нет ли чего нового в Афинах. Приезжий, подученный Фалесом, сказал: «Ничего, только клянусь Зевсом, были похороны одного молодого человека, и провожал его весь город. Это был, как говорили, сын человека известного, первого в городе по своим нравственным качествам. Его самого не было; говорили, что он уже давно находится за границей».- «Какой несчастный!.. – воскликнул Солон. – А как его называли?» «Я слышал его имя, - отвечал тот, - да не помню; только много было разговоров об его уме и справедливости». Так при каждом ответе у Солона всё возрастал. Наконец, уже в полной тревоге он подсказал приезжему имя и спросил, не называли ли умершего Сыном Солона. Тот ответил утвердительно. Тогда Солон стал бить себя по голове, делать и говорить всё сказал: «Вот это, и удерживает меня от брака и рождения детей, что валит с ног и тебя, такого сильного человека. Что же касается этого рассказа, не бойся: это неправда». Отсюда, между прочим, следует, что семьи у Фалеса не было. Как сообщил Плутарх, Фалес усыновил ребёнка своей сестры, по имени Кабиста. Фалеса, же всегда считали естествоиспытателем, астрономом и математиком, изображали с циркулем в руке.
Народ говорил о семи мудрецах, к коим причислил Фалеса, Солона, Бианта, Питтака, Периандра, Клеобула и Хилона. В отношении первых трёх ни у кого сомнений не было, но с причислением остальных к лику мудрых велись ожесточённые споры. Одни называли либо Ферекида Сиросского, либо тирана Писистрата или какое-либо другое лицо, выдвигавшееся на соискание этого звания скорее из лести, чем по истинным достоинствам. Платон в «Протагоре» из названного списка убрал тирана Периандра, добавив Мисона, которому он, очевидно симпатизировал. Писал Фалес или нет, этого мы уже никогда не узнаем, но заслуги его перед наукой огромны, хотя и не всё время он ей посвятил. Находясь на службе у тирана Трасибула , Фалес плавал по Средиземному морю с торговой, а возможно, и государственно-дипламатической миссией. Сам он, скорее всего, в торговых сделках не участвовал, так как у него, похоже, не было устойчивого интереса к коммерческим делам. В древности говорили: «Ну, сущий Фалес», т.е. не от мира сего, отрешённый от повседневной суеты, думающий только о научных проблемах. Однако Аристотель рассказал один забавный случай, произошедший с Фалесом, который, будучи увлечённым и занятым учёным, тем не менее, мог провести успешную коммерческую сделку. «Этот рассказ о некоем, предвидении, - пишет Аристотель в «Политике», - использованном для того, чтобы нажить состояние, и его приписывают Фалесу, имея в виду его мудрость, но её можно рассматривать и с общей точки зрения. Когда его попрекали бедностью, утверждая, будто занятия философией никакой выгоды не приносят.
То, рассказывают, он, предвидя на основании астрономических данных богатый урожай оливок, ещё до истечения зимы роздал в задаток имевшуюся у него небольшую сумму денег всем владельцам маслобоен в Милете и на Хиосе, законтрактован их дёшево, так как никто с ним не конкурировал. Когда наступило время сбора оливок и сразу многим одновременно потребовались маслобойни, он, отдавая маслобойни на откуп на желательных ему условиях и собрав много денег, доказал, что философам при желании легко разбогатеть, но не это является предметом их стремлений. Так, говорят, Фалес дал доказательство своей мудрости. Этот случай, произошедший с Фалесом, вероятно, ещё в молодости, скорее подчёркивает его непрактичность, поскольку выставляется как исключение из правила, которому была подчинена его натура.
Платон, Аристотель и Плутарх, кивая на Фалеса, в унисон говорили, что мудрость надо отличать от рассудительности: первое касается знания природы, второе - выгоды для себя; Фалес был мудрым, но не рассудительным, (сейчас бы сказали, не расчётливым). Его жизнь в чём-то напоминает жизнь Галилея, который тоже по молодости торговал циркулями и подзорными трубами. Это занятие его увлекало так, что трудно было сказать, чем больше занята его голова - коммерцией или наукой. Но постепенно итальянского Фалеса – Галилея нередко сравнивают с античным мудрецом – захватила наука: все ночи напролёт он смотрел на звёзды, пока не ослеп.
Естественно, рано или поздно, знатному и мудрому Фалесу, на голову возвышающемуся над всеми остальными, чтобы не потерять её, пришлось «удалиться от государственных дел» и заняться науками. Знания качеств личности Писистрата и Трасибула помогает понять сложную политическую обстановку, в которой жил Фалес. Слава учёного пришла к Фалесу после предсказанного им солнечного затмения, которое описал Геродот: «Так как Алиатт, несмотря на требования Киаксара, не захотел выдать скифов, то у лидийцев с мидянами началась война. Пять лет длилась эта война, причём верх одерживали то мидяне, то побеждали лидийцы и однажды – даже в какой-то ночной битве. Так с переменным успехом продолжалась эта затяжная война, и на шестой год во время одной битвы внезапно день превратился в ночь. Это солнечное затмение предсказал ионянам Фалес Милетский и даже точно определил заранее год, в котором оно и наступило. Когда лидийцы и мидяне увидели, что день обратился в ночь, то прекратили битву и поспешно заключили мир». Нечего говорить о том, что занятия Фалеса в Египте также трактуются очень серьёзно. Это – крайне пессимистический взгляд на успехи Фалеса и, вообще, достижения всей античной науки.
Как показывает история исследования некоторых математических алгоритмов решения задач, которыми пользовались древние вавилоняне и египтяне, современные учёные не могут взять в толк, каким образом они могли быть найдены. Нашим современникам кажется, что для решения задач по нахождению площадей геометрических фигур, объёмов тел и прочих параметров требуются знания высших разделов математики – алгебры интегрально-дифферециального исчисления. Однако вполне работоспособные алгоритмы были найдены, причём некоторые из них три-четыре тысячи лет назад – мы просто не умеем их реконструировать. Может быть, не Фалес первый разделил год на365 дней, дал определение числа, как совокупности единиц и понял, что вписанный в круг треугольник, опирающийся на диаметр, всегда будет прямым, как об этом упоминается в различных древних источниках, но, по крайней мере, в его время об этом уже знали. Они говорят об уровне развития знаний той эпохи, в которой жил самый выдающийся учёный. Следовательно, мы смело можем говорить: Фалес или кто-то из его современников вполне понимал, что во всяком равнобедренном треугольников углы при основании равны, при пересечении двух прямых вертикальные углы равны, два треугольника равны, если два угла и одна сторона одного из них равны углам и одной стороне другого. Последняя теорема, как предполагается, использовалась Фалесом для нахождения расстояния до кораблей, находящихся в море. Нахождение Фалесом определенных отношений между элементами равнобедренного треугольника, ничем принципиальным не отличается от нахождений законов физики: и математические(стороны, углы, площади), и физические(сила, ускорение, масса) величины измеряются эмпирически, т.е. пришли к нам из опыта и используются нами в практической жизни. Интеллектуальные и чувственные образы тесно взаимосвязаны, так что разъединять их какой-либо преградой ненужно. Таким образом, математические объекты вполне можно отнести к естественнонаучным и рассматривать математику и естествознание, как одну рациональную науку, в которой используется один и тот же конструктивный подход. Нейгебауэр критиковал Фалеса за неудачное предположение, что причиной разлива Нила являются ветер, дующий с моря против его течения. Да, конечно, эта гипотеза ошибочна, но важно, что он над этим явлением размышлял и предложил рациональное объяснение, а не сводил дело к божественному гневу или милости, как это делали до него. Начиная с Фалеса люди повсеместно стали задаваться вопросами: почему сверкает молния, как возникает гром, что такое огонь, как связан он с теплом, откуда берётся ветер, что такое снег и лёд, как связаны они с холодом, из чего земля, животные и растительные ткани, какие причины приводят к землетрясению, наступлению холодов, образованию облаков и т.д. и т. д. Наука начинается там, где религии говорят «Нет!», где ищут решения, не прибегая к силам какого-либо Высшего Существа. И вот в этом Фалес был Первым! «Он первый нашёл путь Солнца от солнцестояния до солнцестояния; он первый ( по мнению некоторых) объявил, что размер Солнца составляет 1/720 часть [солнечного пути, а размеры Луны – такую же часть] лунного пути [ т.е. оба светила видны под углом 0,5 гр.]. Он первый назвал последний день месяца «тридесятым», [т.е. разделил год на 12 месяцев, в каждом из них было по 30 дней]. Он первый, как говорят иные, стал вести беседы о природе». Главное геометрическое достижение Фалеса состояла в том, что ему удалось открыть пропорциональность сторон подобных треугольников. Теперь на основе пропорции a/b=c/d, он мог производить измерение неизвестной величины по трём известным. Именно с помощью этой пропорции он нашёл высоту египетских пирамид.
Измерение расстояния до корабля, находящегося далеко в море, производилось тоже на основе этой пропорции. Выбрав на берегу базиса и вымерив с крайних его точек углы до корабля, геометр затем вычерчивал подобный треугольник небольших размеров и измерял у него две стороны, скажем, c и d; после этого ничего не стоило найти неизвестное расстояние до корабля – сторону b. Такого рода задачи и даже более сложного( нахождение площади круга, объём усечённой пирамиды и т.д.) умели решать в Египте. Это стало известно из найденных Московского и Риндовского папирусов, написанных около 2000 году до н.э. Однако этими знаниями овладел мудрый человек, живущий в ответственный для науки период. Далее можно пронаблюдать, как пропорция a/b = c/d через Пифагора, Демокрита и Архимеда легла в основу науки эпохи Зарождения и Итальянского Возрождения. Простота и универсальность пропорции позволило сделать множество математических и естественнонаучных открытий. Всё это говорит о том, что Фалес был не столько первым философом, сколько первым учёным, т.е. тем первым профессионалом, который все явления природы пытался Объяснить рациональными средствами. Но было в его объяснениях физического мира и такое, что отнести к рациональным соображениям можно лишь с изрядной натяжкой. Время жизни Фалеса, по Дильсу, 624 – 547 г. до н.э., расцвет сил (акме) 585г., дата славы 585г., предсказанное им солнечное затмение 28 мая 585г. По Таннери, время жизни Фалеса 637-558г. акме 597г., дата славы 586г., предсказанное им солнечное затмение 30 сентября 610г. Заслуги, которые приписывали Фалесу историки в новое время, можно резюмировать так: Фалес – родоначальник европейской науки, он перенёс с Востока в Грецию богатый запас эмпирических наблюдений и на основании этого обширного собрания фактов создал первые в истории мысли научно-теоритические построения. В частности, он – первый математик и создатель научной геометрии (преобразовал египетское искусство измерения в дедуктивную геометрию, покоящуюся на общих основаниях), астроном (предсказал полное затмение; открыл, что из созвездий наиболее точно север определяется Малой Медведицей, и т. д.), метеоролог (удачное предсказание урожая оливок), физик (ряд объяснений физических явлений). Как философов, он глава милетской школы и отец греческой философии. Точность его научных открытий, его деятельность не ограничивалась научно-теоретической областью, он также практически деятель с обширной сферой интересов: он – путешественник, купец (торгует солью), инженер, политик и государственный деятель. Наконец, известны его краткие изречения – практические советы морального характера. Основное положение Фалеса: вода есть начало всего. Нам неизвестно в точности, какой смысл заключён в этом положении. Прежде всего, идёт ли здесь речь о возникновении во времени или в вечной основе всего существующего? Говорит ли Фалес, что всё возникло из воды (учение, которое в 16 веке повторил Парацельс), или он указывает в воде постоянное начало, неизменно лежащее в основе изменчивых разнообразных форм природы? Далее, эта первая стихия есть ли вода, как одно из веществ природы, или под водой здесь разумеется всякая жидкость (т.е. первичным признаётся известное состояние матери), или, наконец, вода здесь есть объектированное качеств: влажность? Так расходятся взгляды учёных в истолковании положения Фалеса «вода есть начало всего», в котором, таким образом, и субъект и предикат двусмысленны для нас. Как говорит Дмитрий Фалерский в «Списке архонтов», Фалес был назван первым мудрецом в тот год, когда в Афинах был архонтом Дамасия, при котором были названы мудрецами известные семь. Принят же в число граждан Фалес был в Милете, куда он прибыл с Нейлеем, изгнанным из Финикии. Впрочем, по свидетельству большинства, он был природный милетец и знатного рода. Почти все философы древней Греции тщательно занимались математикой, в частности геометрией. Фалесу Мелецкому Прокл приписывает открытие или доказательство теорем о том, что диаметр делит круг пополам, что угол, вписанный в полуокружность, прямой, о равенстве вертикальных углов, о равенстве углов при основании равнобедренного треугольника и др. Эти положения были частично известны ещё вавилонянам и египтянам. Однако в отличии от вавилонской и египетской геометрии, имевшей преимущественно практический и прикладной характер, греческая геометрия характеризуется стремлением установить, что геометрические факты верны не только для отдельных частных случаев, а справедливы в любом случае. При помощи общих доказательств, с постепенным переходим от одной истины к другой, греческие математики создали геометрию как науку.
Направление строгой логической последовательности в геометрии первыми заложили геометры греческой ионийской школы, основателем которой был Фалес. Фалес был знаком и с вавилонской астрономией. Платон, знаменитый греческий философ четвёртого века до нашей эры, рассказывает, что Фалес, наблюдая звёзды, упал в колодец, а стоявшая рядом женщина посмеялась над ним, сказав: «Хочет знать, что делается на небе, а что у него под ногами, не видит…». Фалес сделал ряд открытий в области астрономии: установил время равноденствий и солнцестояний, определил продолжительность года, впервые наблюдал Малую Медведицу и т.п. Особенную славу ему принесло предсказание солнечного затмения, произошедшего в 585 году до н.э. Фалес был не только философом и учёным, но также государственным и общественным деятелем. Вот почему он был причислен к группе «семи мудрецов» древности.
Существуют разные версии смерти Фалеса.
1. Диоген Лаэрцкий в своём известном сочинении «О жизни, учёниях и изречениях знаменитых философов», появившемся где-то во 2-3вв., привёл письмо Анаксимена, посланное Пифагору, где сообщает о смерти своего учителя и друга. «Фалес, сын Эксамия, достигнув преклонных лет, несчастным образом скончался. Ночью он по своему обыкновению вышел со служанкой из дома, чтобы посмотреть на звёзды, и, созерцая их, свалился в канаву, о котором совсем запамятовал. Вот каков, по словам милетских жителей, был конец этого небоведца. Мы же, его собеседники, и сами, и дети наши, и коллеги наши по занятиям, сохранили память об этом муже и блюдем его заветы. Пусть же всякая наша речь начинается именем Фалеса». Во втором письме к Пифагору, который бежал от тирана Поликрата с острова Самос, расположенного недалеко от Милета, в италийский город Кратон, Анаксимен, жалуясь на тяжёлую жизнь, обронил такую фразу: «Как же помышлять Анаксимену о делах небесных, когда приходится страшиться гибели или рабства [на земле]. Возможно, в людской памяти как-то соединилась эта фраза с личностью Фалеса, но не с его гибелью.
2. В античности была распространена легенда, будто мудрец скончался от зноя, жажды и давки, когда смотрел на солнцепёке, как состязаются молодые и сильные гимнасты. Старик слишком приблизился к соревнующимся, пишет Диоген Лаэрцкий, и возбужденная толпа задавила его насмерть. Однако такой печальный финиш жизни этого выдающегося человека кажется маловероятным. Вряд ли могло так случиться, чтобы известного всей Элладе мыслителя задавила толпа болельщиков? Так что малопочётная гибель в канаве здесь кажется более предпочтительной, если только она действительно была вызвана желанием смотреть на звёзды.
3..Мудрец Фалес скончался в то время, когда смотрел гимнастическое состязание, от жары, жажды и бессилия, будучи уже престарелым. И на памятнике его написано: «Взирай на эту действительно малую могилу весьма мудрого Фалеса (слава же его достигает небес)». Имеется и у нас в первой из «Надписей», или в «Написанной в различных размерах», следующая надпись, относящаяся к нему: «Некогда смотревшего гимнастическое состязание мудреца Фалеса ты, о солнце Зевс, похитил из ристалища. Я восхваляю тебя за то, что увёл его поближе к небу, ибо, в самом деле, старик уже не мог более с земли видеть звёзды. Фалесу принадлежит изречение: «Познай самого себя», о котором Антисфен в «Диадохах» говорит, что оно принадлежит Фемоною и что его присвоил себе Хилон..
Сочинения Фалеса до нашего времени не сохранились.
Практическая часть.
Теорема
Докажем теорему Фалеса: если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.
Решение:
Пусть на прямой l1 отложены равные отрезки А1А2, А2А3, А3А4, …и через их концы проведены параллельные прямые, которые пересекают прямую l2 в точках В1, В2, В3, В4, … (рис.1). Требуется доказать, что отрезки В1В2, В2В3, В3В4, … равны друг другу. Докажем, например, что В1В2 = В2В3.
Рассмотрим сначала случай, когда прямые l1 и l2 параллельны (рис. 1, а). тогда А1А2 = В1В2 и А2А3 = В2В3 как противоположные стороны параллелограммов А1В1В2А2 и А2В2В3А3. так как А1А2 = А2А3, то и В1В2 = В2В3 если прямые l1 и l2 не параллельны, то через точку
В1 проведем прямую l, параллельную прямой l1 (рис.1, б). Она пересечет прямые А2В2 и А3В3 в некоторых точках С и D. Так как А1А2 = А2А3, то по доказанному В1С = СD. Отсюда получаем В1В2 = В2В3. Аналогично можно доказать, что В2В3 = В3В4 и т.д.
Задача
Через середину М стороны АВ треугольника АВС проведена прямая, параллельная стороне ВС. Эта прямая пересекает сторону АС в точке N. Докажите, что AN = NC.
Решение:
Через точку С проведем прямую, параллельную прямой АВ и обозначим буквой D точку пересечения этой прямой с прямой MN (рис. 2). Так как AM = МВ по условию, а MB = CD как противоположные стороны параллелограмма BCDM, то АМ = DC. Треугольники АМN и CDN равны по второму признаку равенства треугольников (АМ=CD,
Задача
Разделите данный отрезок АВ на n равных частей.
Решение:
Проведен луч АХ, не лежащий на прямой АВ, и на нем от точки А отложим последовательно n равных отрезков АА1, А1А2, …, Аn-1Аn (рис.3), т.е. столько равных отрезков, на сколько равных частей нужно разделить данный отрезок АВ (на рис. 3 n=5). Проведем прямую АnВ (точка Аn – конец последнего отрезка) и построим прямые, проходящие через точки А1 , А2 , …, Аn-1 и параллельные прямой АnВ. Эти прямые пересекают отрезок АВ в точках В1 , В2 , …, Вn-1, которые по теореме Фалеса делят отрезок АВ на n равных частей.
Задача
Разделите данный отрезок АВ на 8 равных частей.
Решение:
Проведен луч АХ, не лежащий на прямой АВ, и на нем от точки А отложим последовательно 8 равных отрезков АА1, А1А2, …, А7А8 (рис.3), т.е. столько равных отрезков, на сколько равных частей нужно разделить данный отрезок АВ (рис. 4). Проведем прямую А8В (точка А8 – конец последнего отрезка) и построим прямые, проходящие через точки А1 , А2 , …, А7 и параллельные прямой А8В. Эти прямые пересекают отрезок АВ в точках В1 , В2 , …, В7, которые по теореме Фалеса делят отрезок АВ на 8 равных частей.
Литература
Атанасян Л.С. и др. Геометрия. 7—9 классы : учеб. для общеобразоват. учреждений / [Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др.],М. : Просвещение, 1999.
Глейзер Г.И. История в математики в школе. Москва: Просвещение, 1983.
Малыгин К.Л. Элементы историзма в преподавании математики в средней школе. М: Учпедгиз 1963г.
Погорелов А.В. Геометрия 7 – 11 класс. Москва.: "Просвещение", 1995
Рыбников Л.А. История математики. Издательство МГУ, 1974 г.
Интернет ресурсы.
Планиметрия /wiki/
Милетская школа /wiki/
Теорема Фалеса /wiki/
gigabaza.ru
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
Управление образования Советского района г. Красноярска
Использование теоремы Фалеса в современном мире
(Исследовательско – реферативная работа)
Работу выполнили:Ученик 9 класса
Баландин Александр
Ученик 9 класса
Кузьмин Александр Научные руководители:
Учитель математики Мальцева Т.Г
Учитель информатики Заболотникова Е.Ю. Красноярск 2011
Содержание:
Цели и задачи проекта. 3
Аннотация 4
Введение 4
Теоретическая часть. 5
Цели и задачи проекта
Аннотация.
Великий учёный Фалес Милетский основал одну из прекраснейших наук- геометрию. Известно, что Фалес Милетский имел титул одного из семи мудрецов Греции, что он был поистине первым философом, первым математиком, астрономом и вообще первым по всем наукам в Греции. Он был то же для Греции, что Ломоносов для России. Введение.
Наиболее знаменитым из семи мудрецов был Фалес из Милета, ионийского города, греческой колонии в Малой Азии(ок.627-ок.547г. до н.э.).Фалеса также считают и первым философом, основателем Ионийской школы. Поскольку Фалес жил в Ионии, школа его была названа Ионийской.
Он умер в 546 году до н.э., и ему наследовал Анаксимандр, а вслед за ним шли Анаксимен, Анаксагор; Архелай, на ком И. ш. и закончилась.
Сочинения представителей Ионийской школы написаны на ионическом диалекте, в отличие от аттического диалекта произведений Платона и Аристотеля.
Ионийская школа – стихийно-материалистическое направление древнегреческой философии, возникшее и развившееся в ионийских колониях Греции в 6-4вв. до н.э.. Зародилась в г. Милет; её представители – Фалес, Анаксимандр и Анаксимен (милетская школа), Гераклит Эфесский. И. ш. принято противопоставлять пифагорейской, элейской и аттийской школам. Одна из основных идей, впервые выдвинутых философами И. ш. – мысль о единстве всего сущего, о происхождении всех вещей из некоторого единого первоначала, которое понималось при этом как та или иная вещественная стихия или как «беспредельное», из которого выделились основные противоположности тёплого и холодного.
Теоретическая часть.
Вода, по Фалесу, является первичным принципом или элементом, и на ней плавает Земля подобно кораблю, и землетрясение происходят из-за волнений этого вселенского моря.
В дерзновении своём он как бы сдвигает целые плиты и меняет демаркационные линии между реальным и мнимым, действительностью и грезой, ведь вопрошая обо всём мыслитель как бы выносит себя за пределы «всего», рассматривает его со стороны и ставит его под вопрос, выделяя себя, мыслящую в себе инстанцию из «всего», само «всё» как предмет уже в чём-то единиться, как бы округляется в «извне» взгляде философа. Ахиллес и Агамемнон – литература, как бы говорит Фалес, а я – Гомер, как автор я вижу нить сюжета, скрытую до поры от читателя и отдающую непрояснённостью судьбы героев. Так и Фалес, отстраняясь от всего, старается разглядеть сюжетную нить и драматургию, лицо, «физиономию» «всего», вставая на беспрецедентную точку «вне всего». Встав «по ту сторону» только и можно сказать о мире «всё». Фалес отверг всякую мысль о мнимости мира, его неподлинности, а значит и непознаваемости, сказав «есть» «всему», Фалес утвердил и свою позицию как наличествующую, сущую. Э.Р.Ф. как математик и астроном. В своё время Фалес был едва ли не единственным во всей Греции человеком, отдавшимся чистой науки и абстрактному мышлению без преследования каких-нибудь практических целей. Важнейшей заслугой Фалеса в области математики должно быть считаемо перенесение им из Египта в Грецию первых начал теоретической элементарной геометрии. Эвдем, по свидетельству Прокла, приписывает Фалес открытие следующих предложений. Вертикальные углы равны. Углы при основании равнобедренного треугольника равны. Треугольник определяется стороною и прилежащими к ней двумя углами. Диаметр делит круг на две равные части. Диоген Лаерний, в основании слов Памфилия, прибавляет к этому списку предложений ещё вписывание в круг прямоугольного треугольника. Что бы дать полный очерк геометрических знаний Фалеса, необходимо присоединить ещё ряд таких предложений, без которых приобретение первых делается невозможным, а именно предложений о параллельных линиях, о равносторонних, равнобедренных и разносторонних треугольниках, о параллелограммах и прочих сверх перечисленных «открытий» Фалеса в области теоретической геометрии, ему приписывается греческими писателями ещё решение двух геометрических задач практического характера, из которых одна состояла в определении расстояния корабля на море от Милетской гавани, а другая – в определении высоты пирамиды по длине её тени, а именно измеряя тень в тот час, когда она бывает равна своему телу. Поставив палку на конце тени, образуемой пирамидою, так что от солнечного света образовалось два треугольника, он показал, что отношение между величиною пирамиды и палки такое же, какое было между тенью пирамиды и тенью палки. В настоящее время в истории математики уже не существует никаких сомнений относительно того, что всё приписываемое Фалесу его соотечественниками геометрические «открытия» были в действительности простыми заимствованиями из египетской науки.
С именем Фалеса связывают многие остроумные и часто парадоксальные высказывания и ответы, которые так ценились греками. Так рассказывают, что он оставался неженатым: когда его мать в молодости побуждала его жениться, он отвечал « Слишком рано!», в зрелом возрасте «Слишком поздно!». А когда у него спрашивали, почему у него нет детей, он отвечал «Потому что люблю их». Фалес так же утверждал, что между жизнью и смертью нет разницы, а когда его спрашивали: «Почему ты в таком случае не умрёшь?», он отвечал «Именно поэтому».
Фалес был младше Солона лет на 10-15, но они были очень дружны, что видно, в частности, из письма, отправленного Фалесом Ферекиду. Этого письма, приведённого Диогеном Лаэрцким, могло и не быть, но описанные в нём события и отношения между людьми вполне правдоподобны. Фалес пишет: «После того как мы с Соломоном Афинским плавали на Крит ради наших там изысканий и плавали в Египет ради бесед с египетскими жрецами и звездочётами, право, мы были бы безумцами, если бы не поплыли и к тебе; говорю «мы», ибо и Солон приедет, если ты на то согласишься. Ты ведь домосед, в Ионии бываешь редко, новых людей видеть не будешь, и одна у тебя, как я полагаю, забота – о том, что ты пишешь. Мы же не пишем ничего, но зато странствуем по всей Элладе и Азии». О дружбе между Фалесом и Солоном свидетельствует и сам Плутарх, который, который рассказал о любопытном розыгрыше. «Когда Солон прибыл к Фалесу в Милет,- пишет Плутарх, - он удивлялся полному его равнодушию к браку и рождению детей. Фалес на этот раз промолчал, а спустя несколько дней подговорил одного приезжего рассказать, будто он недавно, десять дней назад, приехал из Афин. Солон спросил его, нет ли чего нового в Афинах. Приезжий, подученный Фалесом, сказал: «Ничего, только клянусь Зевсом, были похороны одного молодого человека, и провожал его весь город. Это был, как говорили, сын человека известного, первого в городе по своим нравственным качествам. Его самого не было; говорили, что он уже давно находится за границей».- «Какой несчастный!.. – воскликнул Солон. – А как его называли?» «Я слышал его имя, - отвечал тот, - да не помню; только много было разговоров об его уме и справедливости». Так при каждом ответе у Солона всё возрастал. Наконец, уже в полной тревоге он подсказал приезжему имя и спросил, не называли ли умершего Сыном Солона. Тот ответил утвердительно. Тогда Солон стал бить себя по голове, делать и говорить всё сказал: «Вот это, и удерживает меня от брака и рождения детей, что валит с ног и тебя, такого сильного человека. Что же касается этого рассказа, не бойся: это неправда». Отсюда, между прочим, следует, что семьи у Фалеса не было. Как сообщил Плутарх, Фалес усыновил ребёнка своей сестры, по имени Кабиста. Фалеса, же всегда считали естествоиспытателем, астрономом и математиком, изображали с циркулем в руке.
Народ говорил о семи мудрецах, к коим причислил Фалеса, Солона, Бианта, Питтака, Периандра, Клеобула и Хилона. В отношении первых трёх ни у кого сомнений не было, но с причислением остальных к лику мудрых велись ожесточённые споры. Одни называли либо Ферекида Сиросского, либо тирана Писистрата или какое-либо другое лицо, выдвигавшееся на соискание этого звания скорее из лести, чем по истинным достоинствам. Платон в «Протагоре» из названного списка убрал тирана Периандра, добавив Мисона, которому он, очевидно симпатизировал. Писал Фалес или нет, этого мы уже никогда не узнаем, но заслуги его перед наукой огромны, хотя и не всё время он ей посвятил. Находясь на службе у тирана Трасибула , Фалес плавал по Средиземному морю с торговой, а возможно, и государственно-дипламатической миссией. Сам он, скорее всего, в торговых сделках не участвовал, так как у него, похоже, не было устойчивого интереса к коммерческим делам. В древности говорили: «Ну, сущий Фалес», т.е. не от мира сего, отрешённый от повседневной суеты, думающий только о научных проблемах. Однако Аристотель рассказал один забавный случай, произошедший с Фалесом, который, будучи увлечённым и занятым учёным, тем не менее, мог провести успешную коммерческую сделку. «Этот рассказ о некоем, предвидении, - пишет Аристотель в «Политике», - использованном для того, чтобы нажить состояние, и его приписывают Фалесу, имея в виду его мудрость, но её можно рассматривать и с общей точки зрения. Когда его попрекали бедностью, утверждая, будто занятия философией никакой выгоды не приносят.
То, рассказывают, он, предвидя на основании астрономических данных богатый урожай оливок, ещё до истечения зимы роздал в задаток имевшуюся у него небольшую сумму денег всем владельцам маслобоен в Милете и на Хиосе, законтрактован их дёшево, так как никто с ним не конкурировал. Когда наступило время сбора оливок и сразу многим одновременно потребовались маслобойни, он, отдавая маслобойни на откуп на желательных ему условиях и собрав много денег, доказал, что философам при желании легко разбогатеть, но не это является предметом их стремлений. Так, говорят, Фалес дал доказательство своей мудрости. Этот случай, произошедший с Фалесом, вероятно, ещё в молодости, скорее подчёркивает его непрактичность, поскольку выставляется как исключение из правила, которому была подчинена его натура.
Платон, Аристотель и Плутарх, кивая на Фалеса, в унисон говорили, что мудрость надо отличать от рассудительности: первое касается знания природы, второе - выгоды для себя; Фалес был мудрым, но не рассудительным, (сейчас бы сказали, не расчётливым). Его жизнь в чём-то напоминает жизнь Галилея, который тоже по молодости торговал циркулями и подзорными трубами. Это занятие его увлекало так, что трудно было сказать, чем больше занята его голова - коммерцией или наукой. Но постепенно итальянского Фалеса – Галилея нередко сравнивают с античным мудрецом – захватила наука: все ночи напролёт он смотрел на звёзды, пока не ослеп.
Естественно, рано или поздно, знатному и мудрому Фалесу, на голову возвышающемуся над всеми остальными, чтобы не потерять её, пришлось «удалиться от государственных дел» и заняться науками. Знания качеств личности Писистрата и Трасибула помогает понять сложную политическую обстановку, в которой жил Фалес. Слава учёного пришла к Фалесу после предсказанного им солнечного затмения, которое описал Геродот: «Так как Алиатт, несмотря на требования Киаксара, не захотел выдать скифов, то у лидийцев с мидянами началась война. Пять лет длилась эта война, причём верх одерживали то мидяне, то побеждали лидийцы и однажды – даже в какой-то ночной битве. Так с переменным успехом продолжалась эта затяжная война, и на шестой год во время одной битвы внезапно день превратился в ночь. Это солнечное затмение предсказал ионянам Фалес Милетский и даже точно определил заранее год, в котором оно и наступило. Когда лидийцы и мидяне увидели, что день обратился в ночь, то прекратили битву и поспешно заключили мир». Нечего говорить о том, что занятия Фалеса в Египте также трактуются очень серьёзно. Это – крайне пессимистический взгляд на успехи Фалеса и, вообще, достижения всей античной науки.
Как показывает история исследования некоторых математических алгоритмов решения задач, которыми пользовались древние вавилоняне и египтяне, современные учёные не могут взять в толк, каким образом они могли быть найдены. Нашим современникам кажется, что для решения задач по нахождению площадей геометрических фигур, объёмов тел и прочих параметров требуются знания высших разделов математики – алгебры интегрально-дифферециального исчисления. Однако вполне работоспособные алгоритмы были найдены, причём некоторые из них три-четыре тысячи лет назад – мы просто не умеем их реконструировать. Может быть, не Фалес первый разделил год на365 дней, дал определение числа, как совокупности единиц и понял, что вписанный в круг треугольник, опирающийся на диаметр, всегда будет прямым, как об этом упоминается в различных древних источниках, но, по крайней мере, в его время об этом уже знали. Они говорят об уровне развития знаний той эпохи, в которой жил самый выдающийся учёный. Следовательно, мы смело можем говорить: Фалес или кто-то из его современников вполне понимал, что во всяком равнобедренном треугольников углы при основании равны, при пересечении двух прямых вертикальные углы равны, два треугольника равны, если два угла и одна сторона одного из них равны углам и одной стороне другого. Последняя теорема, как предполагается, использовалась Фалесом для нахождения расстояния до кораблей, находящихся в море. Нахождение Фалесом определенных отношений между элементами равнобедренного треугольника, ничем принципиальным не отличается от нахождений законов физики: и математические(стороны, углы, площади), и физические(сила, ускорение, масса) величины измеряются эмпирически, т.е. пришли к нам из опыта и используются нами в практической жизни. Интеллектуальные и чувственные образы тесно взаимосвязаны, так что разъединять их какой-либо преградой ненужно. Таким образом, математические объекты вполне можно отнести к естественнонаучным и рассматривать математику и естествознание, как одну рациональную науку, в которой используется один и тот же конструктивный подход. Нейгебауэр критиковал Фалеса за неудачное предположение, что причиной разлива Нила являются ветер, дующий с моря против его течения. Да, конечно, эта гипотеза ошибочна, но важно, что он над этим явлением размышлял и предложил рациональное объяснение, а не сводил дело к божественному гневу или милости, как это делали до него. Начиная с Фалеса люди повсеместно стали задаваться вопросами: почему сверкает молния, как возникает гром, что такое огонь, как связан он с теплом, откуда берётся ветер, что такое снег и лёд, как связаны они с холодом, из чего земля, животные и растительные ткани, какие причины приводят к землетрясению, наступлению холодов, образованию облаков и т.д. и т. д. Наука начинается там, где религии говорят «Нет!», где ищут решения, не прибегая к силам какого-либо Высшего Существа. И вот в этом Фалес был Первым! «Он первый нашёл путь Солнца от солнцестояния до солнцестояния; он первый ( по мнению некоторых) объявил, что размер Солнца составляет 1/720 часть [солнечного пути, а размеры Луны – такую же часть] лунного пути [ т.е. оба светила видны под углом 0,5 гр.]. Он первый назвал последний день месяца «тридесятым», [т.е. разделил год на 12 месяцев, в каждом из них было по 30 дней]. Он первый, как говорят иные, стал вести беседы о природе». Главное геометрическое достижение Фалеса состояла в том, что ему удалось открыть пропорциональность сторон подобных треугольников. Теперь на основе пропорции a/b=c/d, он мог производить измерение неизвестной величины по трём известным. Именно с помощью этой пропорции он нашёл высоту египетских пирамид.
Измерение расстояния до корабля, находящегося далеко в море, производилось тоже на основе этой пропорции. Выбрав на берегу базиса и вымерив с крайних его точек углы до корабля, геометр затем вычерчивал подобный треугольник небольших размеров и измерял у него две стороны, скажем, c и d; после этого ничего не стоило найти неизвестное расстояние до корабля – сторону b. Такого рода задачи и даже более сложного( нахождение площади круга, объём усечённой пирамиды и т.д.) умели решать в Египте. Это стало известно из найденных Московского и Риндовского папирусов, написанных около 2000 году до н.э. Однако этими знаниями овладел мудрый человек, живущий в ответственный для науки период. Далее можно пронаблюдать, как пропорция a/b = c/d через Пифагора, Демокрита и Архимеда легла в основу науки эпохи Зарождения и Итальянского Возрождения. Простота и универсальность пропорции позволило сделать множество математических и естественнонаучных открытий. Всё это говорит о том, что Фалес был не столько первым философом, сколько первым учёным, т.е. тем первым профессионалом, который все явления природы пытался Объяснить рациональными средствами. Но было в его объяснениях физического мира и такое, что отнести к рациональным соображениям можно лишь с изрядной натяжкой. Время жизни Фалеса, по Дильсу, 624 – 547 г. до н.э., расцвет сил (акме) 585г., дата славы 585г., предсказанное им солнечное затмение 28 мая 585г. По Таннери, время жизни Фалеса 637-558г. акме 597г., дата славы 586г., предсказанное им солнечное затмение 30 сентября 610г. Заслуги, которые приписывали Фалесу историки в новое время, можно резюмировать так: Фалес – родоначальник европейской науки, он перенёс с Востока в Грецию богатый запас эмпирических наблюдений и на основании этого обширного собрания фактов создал первые в истории мысли научно-теоритические построения. В частности, он – первый математик и создатель научной геометрии (преобразовал египетское искусство измерения в дедуктивную геометрию, покоящуюся на общих основаниях), астроном (предсказал полное затмение; открыл, что из созвездий наиболее точно север определяется Малой Медведицей, и т. д.), метеоролог (удачное предсказание урожая оливок), физик (ряд объяснений физических явлений). Как философов, он глава милетской школы и отец греческой философии. Точность его научных открытий, его деятельность не ограничивалась научно-теоретической областью, он также практически деятель с обширной сферой интересов: он – путешественник, купец (торгует солью), инженер, политик и государственный деятель. Наконец, известны его краткие изречения – практические советы морального характера. Основное положение Фалеса: вода есть начало всего. Нам неизвестно в точности, какой смысл заключён в этом положении. Прежде всего, идёт ли здесь речь о возникновении во времени или в вечной основе всего существующего? Говорит ли Фалес, что всё возникло из воды (учение, которое в 16 веке повторил Парацельс), или он указывает в воде постоянное начало, неизменно лежащее в основе изменчивых разнообразных форм природы? Далее, эта первая стихия есть ли вода, как одно из веществ природы, или под водой здесь разумеется всякая жидкость (т.е. первичным признаётся известное состояние матери), или, наконец, вода здесь есть объектированное качеств: влажность? Так расходятся взгляды учёных в истолковании положения Фалеса «вода есть начало всего», в котором, таким образом, и субъект и предикат двусмысленны для нас. Как говорит Дмитрий Фалерский в «Списке архонтов», Фалес был назван первым мудрецом в тот год, когда в Афинах был архонтом Дамасия, при котором были названы мудрецами известные семь. Принят же в число граждан Фалес был в Милете, куда он прибыл с Нейлеем, изгнанным из Финикии. Впрочем, по свидетельству большинства, он был природный милетец и знатного рода. Почти все философы древней Греции тщательно занимались математикой, в частности геометрией. Фалесу Мелецкому Прокл приписывает открытие или доказательство теорем о том, что диаметр делит круг пополам, что угол, вписанный в полуокружность, прямой, о равенстве вертикальных углов, о равенстве углов при основании равнобедренного треугольника и др. Эти положения были частично известны ещё вавилонянам и египтянам. Однако в отличии от вавилонской и египетской геометрии, имевшей преимущественно практический и прикладной характер, греческая геометрия характеризуется стремлением установить, что геометрические факты верны не только для отдельных частных случаев, а справедливы в любом случае. При помощи общих доказательств, с постепенным переходим от одной истины к другой, греческие математики создали геометрию как науку.
Направление строгой логической последовательности в геометрии первыми заложили геометры греческой ионийской школы, основателем которой был Фалес. Фалес был знаком и с вавилонской астрономией. Платон, знаменитый греческий философ четвёртого века до нашей эры, рассказывает, что Фалес, наблюдая звёзды, упал в колодец, а стоявшая рядом женщина посмеялась над ним, сказав: «Хочет знать, что делается на небе, а что у него под ногами, не видит…». Фалес сделал ряд открытий в области астрономии: установил время равноденствий и солнцестояний, определил продолжительность года, впервые наблюдал Малую Медведицу и т.п. Особенную славу ему принесло предсказание солнечного затмения, произошедшего в 585 году до н.э. Фалес был не только философом и учёным, но также государственным и общественным деятелем. Вот почему он был причислен к группе «семи мудрецов» древности.
Существуют разные версии смерти Фалеса.
1. Диоген Лаэрцкий в своём известном сочинении «О жизни, учёниях и изречениях знаменитых философов», появившемся где-то во 2-3вв., привёл письмо Анаксимена, посланное Пифагору, где сообщает о смерти своего учителя и друга. «Фалес, сын Эксамия, достигнув преклонных лет, несчастным образом скончался. Ночью он по своему обыкновению вышел со служанкой из дома, чтобы посмотреть на звёзды, и, созерцая их, свалился в канаву, о котором совсем запамятовал. Вот каков, по словам милетских жителей, был конец этого небоведца. Мы же, его собеседники, и сами, и дети наши, и коллеги наши по занятиям, сохранили память об этом муже и блюдем его заветы. Пусть же всякая наша речь начинается именем Фалеса». Во втором письме к Пифагору, который бежал от тирана Поликрата с острова Самос, расположенного недалеко от Милета, в италийский город Кратон, Анаксимен, жалуясь на тяжёлую жизнь, обронил такую фразу: «Как же помышлять Анаксимену о делах небесных, когда приходится страшиться гибели или рабства [на земле]. Возможно, в людской памяти как-то соединилась эта фраза с личностью Фалеса, но не с его гибелью.
2. В античности была распространена легенда, будто мудрец скончался от зноя, жажды и давки, когда смотрел на солнцепёке, как состязаются молодые и сильные гимнасты. Старик слишком приблизился к соревнующимся, пишет Диоген Лаэрцкий, и возбужденная толпа задавила его насмерть. Однако такой печальный финиш жизни этого выдающегося человека кажется маловероятным. Вряд ли могло так случиться, чтобы известного всей Элладе мыслителя задавила толпа болельщиков? Так что малопочётная гибель в канаве здесь кажется более предпочтительной, если только она действительно была вызвана желанием смотреть на звёзды.
3..Мудрец Фалес скончался в то время, когда смотрел гимнастическое состязание, от жары, жажды и бессилия, будучи уже престарелым. И на памятнике его написано: «Взирай на эту действительно малую могилу весьма мудрого Фалеса (слава же его достигает небес)». Имеется и у нас в первой из «Надписей», или в «Написанной в различных размерах», следующая надпись, относящаяся к нему: «Некогда смотревшего гимнастическое состязание мудреца Фалеса ты, о солнце Зевс, похитил из ристалища. Я восхваляю тебя за то, что увёл его поближе к небу, ибо, в самом деле, старик уже не мог более с земли видеть звёзды. Фалесу принадлежит изречение: «Познай самого себя», о котором Антисфен в «Диадохах» говорит, что оно принадлежит Фемоною и что его присвоил себе Хилон..
Сочинения Фалеса до нашего времени не сохранились.
Практическая часть.
Теорема
Докажем теорему Фалеса: если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.
Решение:Пусть на прямой l1 отложены равные отрезки А1А2, А2А3, А3А4, …и через их концы проведены параллельные прямые, которые пересекают прямую l2 в точках В1, В2, В3, В4, … (рис.1). Требуется доказать, что отрезки В1В2, В2В3, В3В4, … равны друг другу. Докажем, например, что В1В2 = В2В3.
Рассмотрим сначала случай, когда прямые l1 и l2 параллельны (рис. 1, а). тогда А1А2 = В1В2 и А2А3 = В2В3 как противоположные стороны параллелограммов А1В1В2А2 и А2В2В3А3. так как А1А2 = А2А3, то и В1В2 = В2В3 если прямые l1 и l2 не параллельны, то через точку
В1 проведем прямую l, параллельную прямой l1 (рис.1, б). Она пересечет прямые А2В2 и А3В3 в некоторых точках С и D. Так как А1А2 = А2А3, то по доказанному В1С = СD. Отсюда получаем В1В2 = В2В3. Аналогично можно доказать, что В2В3 = В3В4 и т.д.
Задача Через середину М стороны АВ треугольника АВС проведена прямая, параллельная стороне ВС. Эта прямая пересекает сторону АС в точке N. Докажите, что AN = NC. Решение: Через точку С проведем прямую, параллельную прямой АВ и обозначим буквой D точку пересечения этой прямой с прямой MN (рис. 2). Так как AM = МВ по условию, а MB = CD как противоположные стороны параллелограмма BCDM, то АМ = DC. Треугольники АМN и CDN равны по второму признаку равенства треугольников (АМ=CD,
Задача Разделите данный отрезок АВ на n равных частей. Решение: Проведен луч АХ, не лежащий на прямой АВ, и на нем от точки А отложим последовательно n равных отрезков АА1, А1А2, …, Аn-1Аn (рис.3), т.е. столько равных отрезков, на сколько равных частей нужно разделить данный отрезок АВ (на рис. 3 n=5). Проведем прямую АnВ (точка Аn – конец последнего отрезка) и построим прямые, проходящие через точки А1 , А2 , …, Аn-1 и параллельные прямой АnВ. Эти прямые пересекают отрезок АВ в точках В1 , В2 , …, Вn-1, которые по теореме Фалеса делят отрезок АВ на n равных частей. 
Задача Разделите данный отрезок АВ на 8 равных частей. Решение: Проведен луч АХ, не лежащий на прямой АВ, и на нем от точки А отложим последовательно 8 равных отрезков АА1, А1А2, …, А7А8 (рис.3), т.е. столько равных отрезков, на сколько равных частей нужно разделить данный отрезок АВ (рис. 4). Проведем прямую А8В (точка А8 – конец последнего отрезка) и построим прямые, проходящие через точки А1 , А2 , …, А7 и параллельные прямой А8В. Эти прямые пересекают отрезок АВ в точках В1 , В2 , …, В7, которые по теореме Фалеса делят отрезок АВ на 8 равных частей.
Литература
4>2>
mognovse.ru
