(1*)Московский Институт Электронной Техники
(Технический Университет)
Кафедра Высшей математики - I.
по курсу «Численные методы» на тему
«Приближённое решение краевых задач
математической физики методом сеток».
Вариант 2.
Выполнила: Безуглова Е.А.
Группа: МП-38.
Руководитель: Лесин В.В.
Москва, 2002 г.
Методические указания и постановка задачи.
1. Тема.
Приближенное решение краевых задач математической физики методом сеток.
2. Цель работы.
Изучить основные понятия теории конечно-разностных методов решения краевых задач математической физики и уметь применять их на практике. Численное решение задачи осуществляется на персональной ЭВМ в среде MATLAB. Преимущество использования этой среды — богатый набор командных программ, реализующих большинство стандартных задач линейной алгебры и методов оптимизации, а также статистической обработки результатов. MATLAB обладает также хорошими графическими возможностями отображения результатов.
3. Порядок работы.
Познакомиться с основными понятиями метода сеток и методикой численного решения разностных уравнений, аппроксимирующих краевую задачу. Наиболее полно все основные понятия метода сеток изложены в [1,2]. Достаточной теоретической базой может служить методическое пособие [3].
Классифицировать уравнение и проверить корректность постановки данной в варианте краевой задачи и соответствие её физическому смыслу.
Разобраться с методикой построения явных и неявных разностных схем конечно-разностных систем для данного типа уравнения.
Разобраться с устойчивыми методами решения явной и неявной схем.
Реализовать программу, осуществляющую решение в среде MATLAB.
Получить численные результаты для своего варианта. Оформить их в виде таблиц, построить необходимые кривые и поверхности уровней, иллюстрирующие решение задачи.
Оформить курсовую работу в соответствии с общим требованиями к курсовым работам. В теоретической части должны быть кратко освещены следующие вопросы:
Классификация уравнения. Вскрыть физический смысл тех явлений, которые описываются данной математической постановкой задачи.
Понятия: сеточный шаблон, порядок аппроксимации разностных схем, сходимость, устойчивость решения.
Классификация задач.
Линейное уравнение второго порядка в частных производных в общем случае имеет вид:
(1*)
где a, b, c, d, e, g, f - известные функции от x и y. Если a, b, c, d, e, g – константы, то (1*) называется уравнением с постоянными коэффициентами. Если f(x, y)=0, то уравнение является однородным.
Уравнение (1) называется эллиптическим, если D < 0; гиперболическим,
если D > 0; параболическим, если D = 0. D - дискриминант квадратичной формы :
При помощи невырожденного преобразования U(x, y) 
уравнение (1) можно привести к одному из следующих канонических видов:
эллиптический
гиперболический
параболический
Постановка задач. При математическом описании физического процесса надо прежде всего поставить задачу, т. е. сформулировать условия, достаточные для однозначного определения процесса. Дифференциальные уравнения имеют бесчисленное множество решений, поэтому для однозначного определения процесса необходимы также дополнительные условия краевые и начальные. Краевые и начальные условия зависят от типа уравнения. Задача, в которой поставлены краевые и начальные условия называется смешанной задачей.
Краевые задачи для уравнения Пуассона.
Исследование стационарных процессов различной физической природы часто приводит к необходимости решать уравнения эллиптического типа. Простейшим и наиболее распространённым уравнением этого типа является уравнение Пуассона:
Однородное уравнение Пуассона (при 
) называется уравнением Лапласа. Такими уравнениями описываются явления электростатики или магнитостатики. В частности, потенциал
электрического поля, образованного системой электродов и объёмным зарядом частиц с плотностью
, удовлетворяет всюду внутри области, не занятой электродами, уравнению:
, 
(1)
при условии, что на границе области (на электродах) поддерживаются заданные значения потенциала:
,
, (2)
где 
- граница областиG, 
- функция, определённая на всех точках границы.
Уравнения (1) и (2) называют первой краевой задачей для уравнения Пуассона.
Подобной же постановке удовлетворяет задача стационарного двумерного распределения температуры в пластине конечной толщины, если внутри пластины распределены по заданному закону источники (стоки) тепла, описываемые функцией 
, а на границах пластины поддерживается заданная температура.
Возможны и другие постановки краевых задач для уравнения Пуассона. Например:
, 
,
где 
- производная по нормали к граничной кривой в точке
границы Г. Это есть вторая краевая задача, или задача Неймана.
Метод сеток.
Метод сеток состоит в сведении решения краевой задачи к решению алгебраических уравнений для так называемой сеточной функции. Для этого область G непрерывного изменения аргумента заменяется областью дискретного его изменения. Дифференциальный оператор заменяется некоторым разностным оператором. Краевые и начальные условия заменяются на соответствующие разностные аналоги. Выберем в области, где ищется решение дифференциального уравнения, некоторое конечное множество точек, в которых и будем искать решение уравнения. Ясно, что чем больше мы возьмем таких точек, тем точнее решим уравнение. Множество таких точек называется сеткой, отдельные точки – узлы сетки. Функция, определенная в узлах сетки, называется сеточной функцией.
Пусть ωh – сетка в некоторой области G, Hh – линейное пространство сеточных функций, заданных на ωh ; H0 –линейное пространство гладких функций 
(x) ; 
- норма в H0 ; 
- норма в Hh. Предполагается, что:
существует оператор проектирования Ph такой, что
Ph
=
h
Hhдля любого 
H0
нормы 
и 
согласованы, т. е. 
||Ph
|| = 
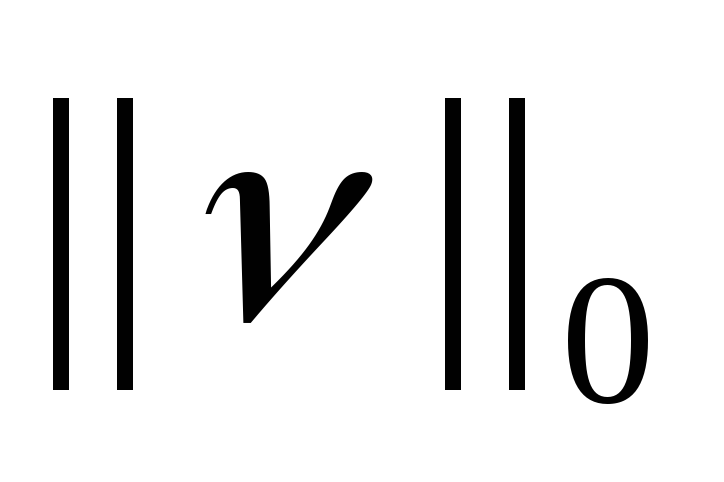
Рассмотрим некоторый дифференциальный оператор λ, заданный в H0, и оператор λh, преобразующий сеточную функцию 
hв сеточную функцию λh
h, заданную на ωh.
Погрешностью аппроксимации оператора λ разностным оператором λh называется сеточная функция ψh = λh
h– (λ
)h, в сеточном пространстве Hh , где 
h= Ph
, (λ
)h= Ph(λ
), 
- любая функция из H0. Если при этом
|| ψh||h= ||λh
h - (λ
)h||h = O(hm), то разностный оператор λh аппроксимирует дифференциальный оператор λ с порядком m>0.
При формулировке соответствующей разностной задачи необходимо аппроксимировать не только дифференциальное уравнение, но и краевые и начальные условия.
Разностная аппроксимация простейших дифференциальных операторов.
Пусть дан линейный дифференциальный оператор L, действующий на функцию v=v(x). Заменяя входящие в Lv производные разностными отношениями, получим вместо Lv разностное выражение Lhvh, являющееся линейными комбинациями значений сеточной функции vh на некотором множестве узлов сетки, называемом шаблоном. Такая приближенная замена Lv на Lhvh называется аппроксимацией дифференциального оператора разностным оператором ( или разностной аппроксимацией оператора L).
Изучение разностных аппроксимаций оператора L вначале производят локально, т.е. в любой фиксированной точке x области h. Прежде чем приступать к разностной аппроксимации оператора необходимо выбрать шаблон, т.е. указать множество соседних с узлом хi узлов, в которых значения сеточной функции vh(xi)=v(xi) могут быть использованы для аппроксимации оператора L.
Обозначим: (x)=Lhv(x)-Lv(x) при h0. Величина (x) называется погрешностью разностной аппроксимации Lv в точке х.
Говорят, что Lh аппроксимирует дифференциальный оператор L с порядком m>0 в точке х, если
(x)=Lhv(x)-Lv(x)=О(hm).
studfiles.net
Решение. Метод Крылова основан на свойстве квадратной матрицы обращать в нуль свой характеристический многочлен.
Согласно теореме Гамильтона-Кали, всякая квадратная матрица является корнем своего характеристического многочлена и, следовательно, обращает его в нуль.
Пусть
– (1)
характеристический многочлен.
Заменяя в выражении (1) величину на
, получим
. (2)
Возьмем произвольный ненулевой вектор
. (3)
Умножим обе части выражения (2) на :
(4)
Положим
, (5)
т.е.
(6)
Учитывая (5), выражение (4) запишем в виде
, (7)
или в виде
Решаем систему (7). Если эта система имеет единственное решение, то ее корни являются коэффициентами характеристического многочлена (1).
Если известны коэффициенты и корни
характеристического многочлена, то метод Крылова дает возможность найти соответствующие собственные векторы по следующей формуле:
(8)
Здесь – векторы, использованные при нахождении коэффициентов
методом Крылова, а коэффициенты
определяются по схеме Горнера
(9)
Используя все выше сказанное, развернем характеристический определитель матрицы А= методом Крылова.
Выберем в качестве начального следующий вектор:
,
Вычислим
Составим матричное уравнение
, или
Полученную систему уравнений решим методом Жордана-Гаусса.
| | | | | | | |
| 1 | 9 | 2 | 0 | -72 | -61 | -61 |
| -1 | 1 | 0 | -3 | -3 | -3 | |
| 30 | 5 | 1 | -167 | -131 | -131 | |
| 2 | 1 | 2/9 | 0 | -8 | -61/9 | -61/9 |
| 0 | 11/9 | 0 | -11 | -88/9 | -88/9 | |
| 0 | -15/9 | 1 | 657/9 | 651/9 | 651/9 | |
| 3 | 1 | 0 | 0 | -6 | -5 | -5 |
| 0 | 1 | 0 | -9 | -8 | -8 | |
| 0 | 0 | 1 | 58 | 59 | 59 | |
| 4 | 1 | 0 | 0 | |||
| 0 | 1 | 0 | ||||
| 0 | 0 | 1 |
Таким образом характеристическое уравнение матрицы имеет вид
2. Для определения собственных чисел матрицы
необходимо решить полученное характеристическое уравнение третьей степени
Данное кубическое уравнение невозможно решить стандартными средствами. Воспользуемся для этой цели числовыми методами, а точнее методами приближенного вычисления.2.1 Исследование функции.
Вычислим первую и вторую производные данной функции
Необходимо выбрать интервал, на котором будем находить решение.
Для отделения корней существует несколько способов. Наиболее популярные из них – графический и аналитический.
В литературе рассматриваются эти способы по отдельности. По заданию курсовой работы требуется отделить корни каждым из этих способов. Рискну нарушить это требование, и объединить эти два способа в один. То есть исследовать функцию аналитически и по результатам исследования построить приблизительный график функции.
Областью значений исходного уравнения является вся ось .
Приравняв первую производную к нулю, мы можем получить критические точки данной функции (точки минимумов и максимумов, или же точки, в которых функция не определена).
Стоит отметить, что для вычисления квадратного корня, также применимы числовые методы, на которых и основаны микрокалькуляторы и программы для ЭВМ. Данные методы основаны на логарифмировании корня и последующего вычисления.
вычисляется при помощи числового ряда
Уравнение имеет решение
,
. Изменив знак равенства на знак неравенства (< или >), можем найти промежутки возрастания и убывания функции.Функция возрастает на промежутке
и убывает на промежутке
. Подставив в исходное уравнение значения критических точек, имеем в результате для
и для
.
Приравняв вторую производную к нулю, мы можем найти точку перегиба и, соответственно, найти интервал, на котором функция выпуклая и вогнутая.
Далее необходимо найти, интервалы, в которых график функции пересекает ось .
Сразу можно определиться, что так при значение функции больше нуля, а при
- меньше нуля, то одна из точек пересечения, будет лежать на данном интервале. Произведя не хитрые математические вычисления значения функции для
, сузим интервал до
.
Далее рассмотрим оставшиеся два интервала.
Известно, что при - значение функции отрицательно, а в первой критической точке положительно, то будем сужать этот промежуток. В данном случае применим метод половинного деления.
| | |
| 0 | 58 |
| -100 | -1059042 |
| -50 | -139492 |
| -25 | -19092 |
| -12 | -2426 |
| -6 | -320 |
| -3 | 4 |
| -5 | -172 |
| -4 | -66 |
| | |
| 4 | -10 |
| 100 | 939158 |
| 50 | 109608 |
| 25 | 11708 |
| 12 | 814 |
| 6 | 4 |
| 5 | -12 |
Следующий будет от и до бесконечности.
Произведем аналогичные вычисления и получим промежуток
На основании произведенного анализа построим график исходной функции.
2.2 Метод хорд.
Сразу необходимо заметить, что существуют два случая (варианта) при решении методом хорд.
Случай первый. Первая и вторая производные функции имеют одинаковые знаки, т.е. .
В этом случае итерационный процесс осуществляем по формуле
Случай второй. Первая и вторая производные функции имеют разные знаки, т.е. .
В этом случае итерационный процесс осуществляем по формуле
Для оценки точности приближение можно воспользоваться формулой
,
где при
,
– точное значение корня.
Итак решим наше уравнение методом хорд с точностью
.
2.2.1 Интервал .
Так как первая и вторые производные в точке, от которой мы начинаем работать имеют различные знаки, то работаем по второму варианту.
Результаты вычисления приведены в таблице.
| | | | | |
| -4,0000000 | -3,0000000 | -66,0000000 | 4,0000000 | 0,0740741 |
| -4,0000000 | -3,1142857 | -66,0000000 | -2,3688397 | 0,0438674 |
| -4,0000000 | -3,0440850 | -66,0000000 | 1,5901736 | 0,0294477 |
| -4,0000000 | -3,0901012 | -66,0000000 | -0,9879693 | 0,0182957 |
| -4,0000000 | -3,0610770 | -66,0000000 | 0,6456578 | 0,0119566 |
| -4,0000000 | -3,0798611 | -66,0000000 | -0,4086778 | 0,0075681 |
| -4,0000000 | -3,0678974 | -66,0000000 | 0,2640772 | 0,0048903 |
| -4,0000000 | -3,0755972 | -66,0000000 | -0,1684077 | 0,0031187 |
| -4,0000000 | -3,0706743 | -66,0000000 | 0,1083107 | 0,0020058 |
| -4,0000000 | -3,0738353 | -66,0000000 | -0,0692833 | 0,0012830 |
| -4,0000000 | -3,0718112 | -66,0000000 | 0,0444729 | 0,0008236 |
| -4,0000000 | -3,0731096 | -66,0000000 | -0,0284836 | 0,0005275 |
| -4,0000000 | -3,0722776 | -66,0000000 | 0,0182690 | 0,0003383 |
| -4,0000000 | -3,0728111 | -66,0000000 | -0,0117068 | 0,0002168 |
| -4,0000000 | -3,0724692 | -66,0000000 | 0,0075061 | 0,0001390 |
| -4,0000000 | -3,0726884 | -66,0000000 | -0,0048109 | 0,0000891 |
| -4,0000000 | -3,0725479 | -66,0000000 | 0,0030843 | 0,0000571 |
| -4,0000000 | -3,0726380 | -66,0000000 | -0,0019770 | 0,0000366 |
en.coolreferat.com
Интеграл можно вычислить методами:
А). Левых прямоугольников Б). Правых прямоугольников В). Трапеций Г.) Средних прямоугольников Д.) Симпсона.
2. Первая и вторая производная функции f(x) должны сохранять свой знак для уточнения корня методами:
а). бисекции б). хорд в). итераций г). Ньютона.
3. Последовательность решения системы линейных уравнений методом итераций:
Приведение системы к виду
Выбор метрики
Расчет определителя системы
Выбор начального приближения
Проверка условий сходимости
Процесс итераций
4. Завышенное значение интеграла будет получено методом ……………прямоугольников.
Напишите формулу для вычисления второй производной «в центре».
Необходимо сделать не менее …………. итераций, чтобы найти корень уравнения с точностью методом бисекции на отрезке [0; 1].
Чтобы построить полином Лагранжа 6-ой степени необходимо ………узлов интерполяции.
При уточнении корня уравнения на отрезке [a; b] методом хорд в качестве начального приближения следует взять b, если………..
При уточнении корня уравнения на отрезке [a; b] методом хорд в качестве начального приближения следует взять a, если………..
При каких условиях метод Ньютона не определен? Приведите пример.
Какой из концов отрезка [a; b] следует выбрать в качестве начального приближения в методе Ньютона, если , и ?
Какой из концов отрезка [a; b] следует выбрать в качестве начального приближения в методе Ньютона, если , и ?
Сформулируйте достаточное условие сходимости итерационного процесса при нахождении корня уравнения.
Почему итерационные методы являются самоисправляющимися ?
Запишите условие прекращения итераций для нахождения корня уравнения с точностью .
При каких значениях условием прекращения итераций для нахождения корня с точностью можно считать условие ?
Докажите, что если определить функцию по формуле , где , а знак совпадает со знаком на отрезке [a; b], то уравнение эквивалентно уравнению , а функция удовлетворяет достаточному условию сходимости.
Напишите достаточное условие сходимости метода итераций для метрики
Напишите достаточное условие сходимости метода итераций для метрики
Напишите достаточное условие сходимости метода итераций для метрики
Решение системы линейных уравнений найдено с точностью , если выполняется условие:
Скорость сходимости метода Зейделя выше, чем метода простых итераций, когда выполняется условие сходимости: А). Б). В).
Напишите интерполяционную формулу Лагранжа.
Выведите формулу для оценки погрешности численного дифференцирования «назад».
Погрешность численного дифференцирования по «центральной» формуле оценивается из неравенства : а). б). в).
Если значения функции y(x) рассчитываются с погрешностью , то оптимальный шаг численного дифференцирования по «центральной» формуле следует определять из соотношения: a). б). в). .
Какие ограничения накладываются на распределение узлов интерполяции по отрезку интерполирования при построении полинома Лагранжа?
Необходимо определить производную …….-го порядка от функции f(x), чтобы оценить погрешность интерполяции этой функции полиномом Лагранжа 5-ой степени.
Как изменится оптимальный шаг численного дифференцирования по «центральной» формуле, если погрешность , с которой рассчитываются значения функции y(x), уменьшится втрое?
Расчет интеграла методом ……………… прямоугольников даст завышенное значение.
При расчете интеграла по формуле Симпсона подынтегральная функция на отрезке длиной аппроксимируется полиномом ……..-ой степени.
Погрешность метода «средних» прямоугольников оценивается из неравенства: а). б) в)
Напишите неравенство для оценки погрешности метода трапеций.
Погрешность по методу Рунге для квадратурной формулы Симпсона оценивается из приближенного равенства: а). б). в). г). .
Квадратурная формула Чебышева с n узлами дает точный результат для полинома степени ….. .
Квадратурная формула Гаусса с n узлами дает точный результат для полинома степени ….. .
Если вторая производная подынтегральной функции f(x) неизвестна, то погрешность численного интегрирования методом трапеций можно оценить по формуле (приведите формулу):
Если вторая производная подынтегральной функции f(x) неизвестна, то погрешность численного интегрирования методом средних прямоугольников можно оценить по формуле (приведите формулу):
Если первая производная подынтегральной функции f(x) неизвестна, то погрешность численного интегрирования методом левых прямоугольников можно оценить по формуле (приведите формулу):
Если первая производная подынтегральной функции f(x) неизвестна, то погрешность численного интегрирования методом правых прямоугольников можно оценить по формуле (приведите формулу):
Если четвертая производная подынтегральной функции f(x) неизвестна, то погрешность численного интегрирования методом Симпсона можно оценить по формуле (приведите формулу):
Система уравнений называется плохо обусловленной, если ………
Вычислите интеграл по формуле Симпсона при n = 2 и сравните с точным значением.
Найдите минимальное число частей n, на которое необходимо разбить отрезок интегрирования, чтобы найти интеграл с точностью по формуле Симпсона.
Найдите минимальное число частей n, на которое необходимо разбить отрезок интегрирования, чтобы найти интеграл с точностью по формуле левых прямоугольников.
Найдите минимальное число частей n, на которое необходимо разбить отрезок интегрирования, чтобы найти интеграл с точностью по формуле трапеций.
Найдите минимальное число частей n, на которое необходимо разбить отрезок интегрирования, чтобы найти интеграл с точностью по формуле средних прямоугольников.
Найдите минимальное число частей n, на которое необходимо разбить отрезок интегрирования, чтобы найти интеграл с точностью по формуле правых прямоугольников.
Найдите минимальное число частей n, на которое необходимо разбить отрезок интегрирования, чтобы найти интеграл с точностью по формуле Симпсона.
Корень уравнения f(x)=0 отделен на отрезке [a; b]. С какой точностью будет найден корень после n итераций метода деления отрезка пополам?
Покажите, что метод хорд можно применить для нахождения корня уравнения на отрезке [0.5; 2].
В каких случаях метод Ньютона не определен?
Необходимо найти корень уравнения на отрезке [0.2; 0.5] методом итераций. Можно ли выразить функцию как ? (Ответ обосновать.)
Найти интерполяционный полином Лагранжа первой степени для функции, заданной таблично:
x
0.5
0.7
f (x)
2
2.4
Найти интерполяционный полином Лагранжа первой степени для функции, заданной таблично:
x
0.5
1
f (x)
2
3
Найти интерполяционный полином Лагранжа первой степени для функции, заданной таблично:
x
0.7
1
f (x)
2.4
3
Дана таблица значений функции
x
1.5
1.6
1.7
4.48
4.95
5.47
Оценитe погрешность интерполяции этой функции полиномом Лагранжа второй степени в точке x = 1.57 .
Найдите погрешность квадратурной формулы, составленной следующим образом:
(здесь и -квадратурные формулы «средних» прямоугольников и трапеций).
www.ronl.ru
