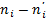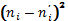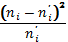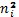|
|
|
|
 Far Far |
 WinNavigator WinNavigator |
 Frigate Frigate |
 Norton
Commander Norton
Commander |
 WinNC WinNC |
 Dos
Navigator Dos
Navigator |
 Servant
Salamander Servant
Salamander |
 Turbo
Browser Turbo
Browser |
|
|
 Winamp,
Skins, Plugins Winamp,
Skins, Plugins |
 Необходимые
Утилиты Необходимые
Утилиты |
 Текстовые
редакторы Текстовые
редакторы |
 Юмор Юмор |
|
|
|
File managers and best utilites |
Проверка статистических гипотез. Статистическая проверка гипотез реферат
Статистическая проверка гипотез | Рефераты KM.RU
Курсовая работа по дисциплине: «Статистика»
Выполнил: ст. гр.МНЖ-31
Саратовский государственный технический университет
Саратов 2010
Введение
Под статистической гипотезой понимается всякое высказывание о виде неизвестного распределения, или параметрах генеральной совокупности известных распределений, или о независимости выборок, которое можно проверить статистически, то есть опираясь на результаты наблюдений в случайной выборке.
Использование гипотез необходимо для развития любой отрасли науки: биологии, медицины, техники и др. В экономике сфера применения статистических гипотез ограничена. Это объясняется тем, что в естественных науках можно организовать эксперимент в виде случайной бесповторной выборки, в которой отдельные наблюдения стохастически независимы. В экономике строгое выполнение этого условия порой невозможно.
В результате выполнения курсовой работы получаются практические навыки определения характеристик случайной выборки и установления нормальности распределения случайной величины при заданном уровне значимости.
Нормальное распределение наиболее часто встречается в задачах управленческой и маркетинговой деятельности. Таким образом, предлагаемая курсовая работа содержит часть инструментария, необходимого современному экономисту и руководителю.
Условие задачи
Дано статистическое распределение выборки:
| хi | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
| ni | 5 | 13 | 20+(m+n) | 30-(m+n) | 19 | 10 | 3 |
Где xi – результаты измерений, ni- частоты, с которыми встречаются значения xi . xi=0, 2*m+0, 3*(i-1)*n.
Методом произведений найти выборочные: среднюю, дисперсию, среднее квадратическое отклонение.
Построить нормальную кривую.
Проверить гипотезу о нормальности Х при уровне значимости α=0, 05.
Решение задачи
1 Найдем методом произведений выборочные: среднюю, дисперсию и среднее квадратическое отклонение. Воспользуемся методом произведений, для чего составляем таб.1
m=3; n=4.
| хi | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
| ni | 5 | 13 | 27 | 23 | 19 | 10 | 3 |
xi=0, 2*m+0, 3*(i-1)*n.
x1=0, 2*3+0, 3*(1-1)*4=0, 6
x2=0, 2*3+0, 3*(2-1)*4=1, 8
x3=0, 2*3+0, 3*(3-1)*4=3
x4=0, 2*3+0, 3*(4-1)*4=4, 2
x5=0, 2*3+0, 3*(5-1)*4=5, 4
x6=0, 2*3+0, 3*(6-1)*4=6, 6
x7=0, 2*3+0, 3*(7-1)*4=7, 8
| хi | ni | ui | niui | niui2 | ni (ui+1)2 |
| 0, 6 | 5 | -2 | -10 | 20 | 5 |
| 1, 8 | 13 | -1 | -13 | 13 | 0 |
| 3 | 27 | 0 | 0 | 0 | 27 |
| 4, 2 | 23 | 1 | 23 | 23 | 92 |
| 5, 4 | 19 | 2 | 38 | 76 | 171 |
| 6, 6 | 10 | 3 | 30 | 90 | 160 |
| 7, 8 | 3 | 4 | 12 | 48 | 75 |
| n=∑ni=100 | ∑niui=80 | ∑ niui2=280 | ∑ ni (ui+1)2=530 |
В качестве ложного нуля принимаем С=3 – варианта с наибольшей частотой 27. Шаг выборки h=x2-x1=1, 8-0, 6=1, 2. Тогда условные варианты определяем по формуле:
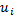 =
=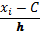 =
= 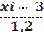
Подсчитываем условные варианты ui и заполняем все столбцы.
Последний столбец служит для контроля вычислений по тождеству:
∑ ni (ui+1)2=∑ niui2+2∑ niui+n.
Контроль: 530=270+2*80+100.
Вычисления произведены верно. Найдем условные моменты.
M1*=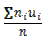 =
=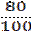 =0, 8; M2*=
=0, 8; M2*=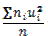 =
= =2, 8.
=2, 8.
Вычисляем выборочную среднюю:
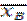 =M1* * h + C= 0, 8*1, 2+3=3, 96
=M1* * h + C= 0, 8*1, 2+3=3, 96
Находим выборочную дисперсию:
dB= [ M2*- (M1*)2]* h3= [2, 8 - (0, 8)2]*1, 22=3, 1
Определим выборочное среднее квадратическое отклонение:
σB=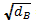 =
=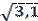 =1, 76
=1, 76
2 Строим нормальную кривую.
Для облегчения вычислений все расчеты сводим в таб.2
| xi | ni | xi | ui= |
| ni'=68, 18*φ(ui) |
| 0, 6 | 5 | -3, 36 | -1, 90 | 0, 0656 | 4 |
| 1, 8 | 13 | -2, 16 | -1, 22 | 0, 1895 | 13 |
| 3 | 27 | -0, 96 | -0, 54 | 0, 3448 | 24 |
| 4, 2 | 23 | 0, 24 | 0, 13 | 0, 3918 | 28 |
| 5, 4 | 19 | 1, 44 | 0, 81 | 0, 2637 | 20 |
| 6, 6 | 10 | 2, 64 | 1, 50 | 0, 1295 | 9 |
| 7, 8 | 3 | 3, 84 | 2, 18 | 0, 0371 | 2 |
| 100 | n= |
Заполняем первые три столбца.
В четвертом столбце записываем условные варианты по формуле, указанной в «шапке» таблицы. В пятом столбце находим значения функции:
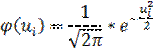
Функции φ(ui) четная, т.е. φ(ui)= φ(-ui).
Значения функции φ(ui) в зависимости от аргумента ui (берутся положительные ui, т.к. функция φ(ui) четная) находим из таблицы.
Теоретические частоты теоретической кривой находим по формуле:
 =
=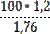 φ(ui)=68, 18*φ(ui)
φ(ui)=68, 18*φ(ui)
И заполняем последний столбец. Отметим, что в последнем столбце частоты 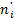 округляются до целого числа и
округляются до целого числа и  .
.
В системе координат  строим нормальную (теоретическую) кривую по выравнивающим частотам
строим нормальную (теоретическую) кривую по выравнивающим частотам 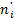 (они отмечены кружками) и полигон наблюдаемых частот (они отмечены крестиками). Полигон наблюдаемых частот построен в системе координат
(они отмечены кружками) и полигон наблюдаемых частот (они отмечены крестиками). Полигон наблюдаемых частот построен в системе координат  .
.
3 Проверим гипотезу о нормальности Х при уровне значимости α=0, 05.
Вычислим 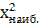 , для чего составим расчетную таблицу 3.
, для чего составим расчетную таблицу 3.
| ni |
|
|
|
|
|
|
| 5 | 4 | 1 | 1 | 0, 25 | 25 | 6, 25 |
| 13 | 13 | 0 | 0 | 0 | 169 | 13 |
| 27 | 24 | 3 | 9 | 0, 38 | 729 | 30, 38 |
| 23 | 28 | -5 | 25 | 0, 89 | 529 | 18, 89 |
| 19 | 20 | -1 | 1 | 0, 05 | 361 | 18, 05 |
| 10 | 9 | 1 | 1 | 0, 11 | 100 | 11, 11 |
| 3 | 2 | 1 | 1 | 0, 5 | 9 | 4, 5 |
| 100 | 100 | X2наиб=2, 18 | 102, 18 |
Суммируя числа пятого столбца, получаем X2наиб=2, 18
Суммируя числа последнего столбца, получаем 102, 18.
Контроль: X2наиб=2, 18
∑ −∑ni =102, 18−100= 2, 18
−∑ni =102, 18−100= 2, 18
Совпадение результатов подтверждает правильность вычислений.
Найдем число степеней свободы, учитывая, что число групп выборки (число различных вариантов) 7. 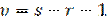 , где s- число различных значений xi.
, где s- число различных значений xi. 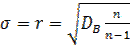 , т.е r=2.υ = s−2=>υ = 7−2−1=4
, т.е r=2.υ = s−2=>υ = 7−2−1=4
По таблице критических точек распределения х2, по уровню значимости α=0, 05 и числу степеней свободы ν=4 находим 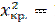 9, 5.
9, 5.
Так как 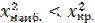 то нет оснований отвергать нулевую гипотезу. Другими словами, расхождение эмпирических и теоретических частот незначимое. Следовательно, данные наблюдений согласуются с гипотезой о нормальном распределении генеральной совокупности.
то нет оснований отвергать нулевую гипотезу. Другими словами, расхождение эмпирических и теоретических частот незначимое. Следовательно, данные наблюдений согласуются с гипотезой о нормальном распределении генеральной совокупности.
Найдем доверительный интервал для оценки неизвестного МО М(Х), пологая, что Х имеет нормальное распределение, среднее квадратическое отклонение σ=σx=σB=1, 76 и доверительная вероятность γ=0, 95.
Известен объем выборки: n=100, выборочная средняя 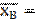
3, 96.
Из соотношения 2Ф(t)= γ получим Ф(t)=0, 475. По таблице находим параметр t=1, 96.
Найдем точность оценки
δ =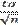 =
= 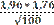 =0, 34
=0, 34
Доверительный интервал таков:
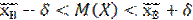
Или 3, 96-0, 34<M(X)<3, 96+0, 34  3, 62<M(X)<4, 3.
3, 62<M(X)<4, 3.
Надежность γ=0, 95 указывает, что если произведено достаточно большое число выборок, то 95% из них определят такие доверительные интервалы, в которых параметр действительно заключен
Список литературы
Для подготовки данной работы были использованы материалы с сайта http://referat.ru/
Дата добавления: 05.10.2011
www.km.ru
Реферат Проверка статистических гипотез
скачатьРеферат на тему:
План:
- Введение
- 1 Статистические гипотезы
- 1.1 Определения
- 1.2 Пример
- 2 Этапы проверки статистических гипотез
- 3 Виды критической области
Введение
Проверки статистических гипотез — класс базовых задач в математической статистике.
1. Статистические гипотезы
1.1. Определения
Пусть в (статистическом) эксперименте доступна наблюдению случайная величина X, распределение которой неизвестно полностью или частично. Тогда любое утверждение, касающееся
называется статистической гипотезой. Гипотезы различают по виду предположений, содержащихся в них:
- Статистическая гипотеза, однозначно определяющая распределение
, то есть
, где
какой-то конкретный закон, называется простой.
- Статистическая гипотеза, утверждающая принадлежность распределения
к некоторому семейству распределений, то есть вида
, где
— семейство распределений, называется сложной.
На практике обычно требуется проверить какую-то конкретную и как правило простую гипотезу H0. Такую гипотезу принято называть нулевой. При этом параллельно рассматривается противоречащая ей гипотеза h2, называемая конкурирующей или альтернативной.
Выдвинутая гипотеза нуждается в проверке, которая осуществляется статистическими методами, поэтому гипотезу называют статистической. Для проверки гипотезы используют критерии, позволяющие принять или опровергнуть гипотезу.
В большинстве случаев статистические критерии основаны на случайной выборке фиксированного объема
из распределения
. В последовательном анализе выборка формируется в ходе самого эксперимента и потому её объем является случайной величиной (см. Последовательный статистический критерий).
1.2. Пример
Пусть дана независимая выборка из нормального распределения, где μ — неизвестный параметр. Тогда
, где μ0 — фиксированная константа, является простой гипотезой, а конкурирующая с ней
— сложной.
2. Этапы проверки статистических гипотез
- Формулировка основной гипотезы H0 и конкурирующей гипотезы h2. Гипотезы должны быть чётко формализованы в математических терминах.
- Задание вероятности α, называемой уровнем значимости и отвечающей ошибкам первого рода, на котором в дальнейшем и будет сделан вывод о правдивости гипотезы.
- Расчёт статистики φ критерия такой, что:
- её величина зависит от исходной выборки
;
- по её значению можно делать выводы об истинности гипотезы H0;
- сама статистика φ должна подчиняться какому-то известному закону распределения, так как сама φ является случайной в силу случайности
.
- её величина зависит от исходной выборки
- Построение критической области. Из области значений φ выделяется подмножество
таких значений, по которым можно судить о существенных расхождениях с предположением. Его размер выбирается таким образом, чтобы выполнялось равенство
. Это множество
и называется критической областью.
- Вывод об истинности гипотезы. Наблюдаемые значения выборки подставляются в статистику φ и по попаданию (или непопаданию) в критическую область
выносится решение об отвержении (или принятии) выдвинутой гипотезы H0.
3. Виды критической области
Выделяют три вида критических областей:
F-критерий | Q-критерий Розенбаума | t-критерий Стьюдента | U-критерий Манна-Уитни | Z-критерий | Критерий Бартлетта | Критерий Колмогорова | Критерий Кохрена | Критерий отношения правдоподобия | Критерий Пирсона | Критерий Уилкоксона | Критерий Фридмана
wreferat.baza-referat.ru
Реферат Статистическая гипотеза
скачатьРеферат на тему:
План:
- Введение
- 1 Статистические гипотезы
- 1.1 Определения
- 1.2 Пример
- 2 Этапы проверки статистических гипотез
- 3 Виды критической области
Введение
Проверки статистических гипотез — класс базовых задач в математической статистике.
1. Статистические гипотезы
1.1. Определения
Пусть в (статистическом) эксперименте доступна наблюдению случайная величина X, распределение которой неизвестно полностью или частично. Тогда любое утверждение, касающееся
называется статистической гипотезой. Гипотезы различают по виду предположений, содержащихся в них:
- Статистическая гипотеза, однозначно определяющая распределение
, то есть
, где
какой-то конкретный закон, называется простой.
- Статистическая гипотеза, утверждающая принадлежность распределения
к некоторому семейству распределений, то есть вида
, где
— семейство распределений, называется сложной.
На практике обычно требуется проверить какую-то конкретную и как правило простую гипотезу H0. Такую гипотезу принято называть нулевой. При этом параллельно рассматривается противоречащая ей гипотеза h2, называемая конкурирующей или альтернативной.
Выдвинутая гипотеза нуждается в проверке, которая осуществляется статистическими методами, поэтому гипотезу называют статистической. Для проверки гипотезы используют критерии, позволяющие принять или опровергнуть гипотезу.
В большинстве случаев статистические критерии основаны на случайной выборке фиксированного объема
из распределения
. В последовательном анализе выборка формируется в ходе самого эксперимента и потому её объем является случайной величиной (см. Последовательный статистический критерий).
1.2. Пример
Пусть дана независимая выборка из нормального распределения, где μ — неизвестный параметр. Тогда
, где μ0 — фиксированная константа, является простой гипотезой, а конкурирующая с ней
— сложной.
2. Этапы проверки статистических гипотез
- Формулировка основной гипотезы H0 и конкурирующей гипотезы h2. Гипотезы должны быть чётко формализованы в математических терминах.
- Задание вероятности α, называемой уровнем значимости и отвечающей ошибкам первого рода, на котором в дальнейшем и будет сделан вывод о правдивости гипотезы.
- Расчёт статистики φ критерия такой, что:
- её величина зависит от исходной выборки
;
- по её значению можно делать выводы об истинности гипотезы H0;
- сама статистика φ должна подчиняться какому-то известному закону распределения, так как сама φ является случайной в силу случайности
.
- её величина зависит от исходной выборки
- Построение критической области. Из области значений φ выделяется подмножество
таких значений, по которым можно судить о существенных расхождениях с предположением. Его размер выбирается таким образом, чтобы выполнялось равенство
. Это множество
и называется критической областью.
- Вывод об истинности гипотезы. Наблюдаемые значения выборки подставляются в статистику φ и по попаданию (или непопаданию) в критическую область
выносится решение об отвержении (или принятии) выдвинутой гипотезы H0.
3. Виды критической области
Выделяют три вида критических областей:
F-критерий | Q-критерий Розенбаума | t-критерий Стьюдента | U-критерий Манна-Уитни | Z-критерий | Критерий Бартлетта | Критерий Колмогорова | Критерий Кохрена | Критерий отношения правдоподобия | Критерий Пирсона | Критерий Уилкоксона | Критерий Фридмана
wreferat.baza-referat.ru
|
|
..:::Счетчики:::.. |
|
|
|
|
|
|
|
|


 =xi−3, 96
=xi−3, 96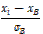 =
=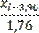
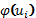
 =100
=100