Исследовательская работа на тему " Симметрия вокруг нас". Симметрия вокруг нас реферат

Исследовательская работа на тему " Симметрия вокруг нас"

Исследовательская работа на тему:

«Симметрия вокруг нас»

Секция математики

Работу выполнили:

ученики 6б класса

Руководитель работы:

учитель математики Дутова Е.Г.

МБОУ « Гимназия №1» с. Красногвардейское

2013--2014 уч. год

Оглавление:

1.Введение ………………………………………………………………стр.3

2. Симметрия в математике …………………………………………стр.4 - 6

3. Симметрия в зоологии …………………………………………….стр.6 -8

4.Симметрия в технике и транспорте ………………………....…..стр.8 - 10

5.Симметрия в архитектуре ……………………………………..…стр.10 -12

6.Симметрия в искусстве………………………….………………стр.12 - 16

7. Симметрия в ботанике…………………………………………..стр.16 - 17

8.Приложение……………………………………………………………стр.18

9.Список литературы ………………………………...…………………стр.19

Новым в науке явилось не выявление принципа симметрии, а выявление его всеобщности.

В. И. Вернадский

Цели исследовательской работы:

• изучение понятия симметрии и её видов (центральная, осевая, поворотная, зеркальная и др.),

• проведение исследовательской работы по изучению явлений симметрии в зоологии, ботанике, архитектуре, живописи, транспорте и технике,

• приобретение навыков самостоятельной работы с большими объемами информации (например, из СМИ, Интернет, из энциклопедий по математике и других учебных пособий по предмету).

Задачи исследовательской работы:

• создание иллюстративного компьютерного материала по всем разделам исследования симметрии: в зоологии, ботанике, архитектуре, живописи, транспорте и технике,

• написать доклады и сделать выводы о своей исследовательской работе,

• публично выступить с презентацией своей творческой работы,

• научится работать в группе и индивидуально, для достижения поставленной цели.

Этапы исследовательской работы:

• выбор интересующей темы исследования и распределение по группам,

• обсуждение плана исследования и промежуточных результатов,

• работа с разными информационными источниками;

• промежуточные консультации в группе и с учителем,

• публичное выступление с показом презентационного материала.

Методы исследовательской работы:

Сбор и структурирование собранного материала на различных этапах исследования.

Выполнение рисунков, чертежей; фотографий.

Предполагаемое практическое применение:

Возможность применения полученных знаний: при решении предметных задач,

в повседневной жизни, при изучении тем на других предметах.

Использование результатов исследования в виде презентаций учителями – предметниками, в качестве вспомогательного материала при проведении интегрированных уроков по различным учебным дисциплинам.

Используемая аппаратура: Цифровой фотоаппарат, мультимедийное оборудование.

Примечание: Все выполненные работы содержат не только информационный, но и научный материал. Каждый раздел имеет компьютерную презентацию, которая иллюстрирует каждое направление исследования.

1. Симметрия в математике.

«Стоя перед черной доской и рисуя на ней мелом разные фигуры, я вдруг был поражен мыслью: почему симметрия приятна глазу? Что такое симметрия? Это врожденное чувство, отвечал я сам себе»

Л.Н. Толстой.

Симметрия сквозь века.

По преданию термин «симметрия» придумал скульптор Пифагор Регийский, живший в городе Регул. Отклонение от симметрии он определил термином «асимметрия». О нем нам говорили как о первом скульпторе, в творчестве которого была сделана попытка соблюсти ритм и соразмерность. Кроме того, Пифагор прославился реалистическим изображением человеческих жил, вен и волос.

Древние греки полагали, что Вселенная симметрична просто потому, что она прекрасна. Считая сферу наиболее симметричной и совершенной формой, они делали вывод о сферичности Земли и её движении по сфере вокруг некоего «центрального огня», где двигались также 6 известных тогда планет вместе с Луной, Солнцем, звёздами. Древнегреческий философ и математик Пифагор Самосский (VI в. до н.э.) и пифагорейцы предпочитали вместо слова «симметрия» пользоваться словом «гармония». Последователи Пифагора Самосского пытались связать симметрию с числом. Каждой вещи, учили пифагорейцы, соответствует определённое отношение чисел, которое они называли логосом. Поэтому познание вещей заключалось для них познанием логоса. Гармония является божественной и заключается в числовых отношениях.

Широко используя идею гармонии и симметрии, учёные древности любили обращаться не только к сферическим формам, но и к правильным многогранникам, для построения которых они использовали «золотое отношение». У правильных многогранников грани – правильные многоугольники одного вида, а углы между гранями равны. Древние греки установили поразительный факт: существует всего пять правильных выпуклых многогранников, названия которых связаны с числом граней, - тетраэдр, октаэдр, икосаэдр, куб, додекаэдр.

Все правильные многогранники обладают и зеркальной, и поворотной симметрией. А идея симметрии являлась отправным пунктом для учёных прошлых веков в теориях о строении материи и Вселенной. Правильные многогранники изучал и сам Пифагор Самосский (V в. до н.э.), математик, философ, религиозный авторитет, основатель одной из первых математических школ. Но впервые их подробно описал Платон, поэтому математики стали называть эти фигуры Платоновыми телами. Платон сводил гармонию к пространственной симметрии. По Платону космос сферичен, а в центре сферы расположена Земля. И пифагорейцы, и Платон полагали, что материя состоит из четырёх основных элементов – огня, земли, воздуха и воды. Согласно их теории, атомы этих элементов имели форму Платоновых тел: атомы огня – форму тетраэдра, земли – форму куба, воздуха – форму октаэдра, а атомы воды – форму икосаэдра. Додекаэдр считался местожительством богов, неким эфиром.

«Симметрия - это некая «средняя мера», – считал Аристотель. Аристотель говорил о симметрии, как о таком состоянии, которое характеризуется соотношением крайностей. Из этого высказывания следует, что Аристотель, пожалуй, был ближе всех к открытию одной из самых фундаментальных закономерностей природы - закономерности о ее двойственности. Проходя сквозь века термин «симметрия» обрастал различными толкованиями. Римский врач Гален (II в. н. э.) из Пергама под симметрией понимал покой души и уравновешенности.

Идея симметрии увлекла немецкого астронома Иогана Кеплера. Кеплер пытался построить геометрическую модель мира. Модель Солнечной системы Кеплера была создана 400 лет назад. В сферу Сатурна он вписал куб, а в куб вписал сферу Юпитера. В сферу Юпитера он вписал тетраэдр – сферу Марса, а в сферу Марса был вписан додекаэдр, в который Кеплер вписал сферу Земли. Вычислив в соответствии со своей схемой радиусы планетных сфер, он обнаружил, что отношения этих радиусов хорошо согласуются с данными, полученными из наблюдений. Это побудило Кеплера думать, что ему удалось объяснить строение солнечной системы на основе единой геометрической схемы, использующей 6 планет и 5 Платоновых тел. Но Кеплер заблуждался: планет в Солнечной системе было не 6, а 9, отношения радиусов планетных сфер случайно совпали с отношениями в геометрической схеме. Современная наука рассматривает Вселенную с позиций единства симметрии и асимметрии.

Герман Вейль – это немецкий математик. Его деятельность приходится на первую половину ХХ века. Именно он сформулировал определение симметрии, установил по каким признакам усмотреть наличие или, наоборот, отсутствие симметрии в том или ином случае. Таким образом, математически строгое представление сформировалось сравнительно недавно – в начале ХХ века. Оно достаточно сложное.

Герман Клаус Хуго Вейль родился в городе Эльмсхорне (Германия). В 1908 году окончил Геттингенский университет, в том же году защитил диссертацию и получил степень доктора философии. С 1908 до 1913 г. читал лекции в Геттингенском университете в качестве приват-доцента. С 1913 по 1930 г. - профессор Цюрихского политехнического института. В 1930 - 1933 гг. работает в Геттингенском университете. 1933 по 1955 г.г. читает лекции в Принстонском институте перспективных исследований (США). Член Национальной Академии Наук США. Автор книги «Симметрия». Герман Вейль - один из крупнейших ученых XX века, оставил глубокий след во многих разделах математики и математической физики. Вейлю, в частности, мы обязаны тем, что отдаем себе сегодня полный отчет в значении для математики и физики общего понятия симметрии. Герман Вейль сказал: “Симметрия является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство “

Обратимся к словарю: Современный энциклопедический словарь: СИММЕТРИЯ (от греческого symmetria - соразмерность), в широком смысле - инвариантность (неизменность) структуры, свойств, формы (например, в геометрии, кристаллографии) материального объекта относительно его преобразований (т. е. изменений ряда физических условий). Симметрия лежит в основе сохранения законов.

Большой энциклопедический словарь: СИММЕТРИЯ - в геометрии - свойство геометрических фигур. Две точки, лежащие на одном перпендикуляре к данной плоскости (или прямой) по разные стороны и на одинаковом расстоянии от нее, называются симметричными относительно этой плоскости (или прямой). Фигура (плоская или пространственная) симметрична относительно прямой (оси симметрии) или плоскости (плоскости симметрии), если ее точки попарно обладают указанным свойством. Фигура симметрична относительно точки (центр симметрии), если ее точки попарно лежат на прямых, проходящих через центр симметрии, по разные стороны и на равных расстояниях от него.

Толковый словарь русского языка Д.Н.Ушакова: СИММЕТРИЯ, симметрии, мн. нет, ж. (греч. symmetria). Пропорциональность, соразмерность в расположении частей целого в пространстве, полное соответствие (по расположению, величине) одной половины целого другой половине. Симметрия в планировке зданий на площади. Соблюдать симметрию.

Новый словарь русского языка под редакцией Т.Ф.Ефремовой: Симметрия ж. род. Соразмерное, пропорциональное расположение частей чего-л. по отношению к центру, середине.

Толковый словарь живого великорусского языка В.И.Даля: СИММЕТРИЯ ж. греч, соразмер, соразмерность, равно (или разно) подобие, равномерие, равнообразие, соответствие, сходность; одинаковость, либо соразмерное подобие расположенья частей целого, двух половин; сообразие, сообразность; противоравенство, противоподобие. Симметрическое расположенье дома, фасада, равнообразное на обе половины. Полная симметрия докучает, а изящное разнообразие красит и тешит вкус. Словарь синонимов русского языка: Симметрия - см. согласие, соответствие

Мы же обратимся и еще раз вспомним те определения, которые даны нам в учебнике.

Определение. Две точки А и А1 называются симметричными относительно прямой а, если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему. Каждая точка прямой а считается симметричной самой себе.

Определение. Фигура называется симметричной относительно прямой а, если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре. Прямая а называется осью симметрии фигуры. Говорят также, что фигура обладает осевой симметрией. Приведём примеры геометрических фигур, обладающие осевой симметрией. У неразвёрнутого угла одна ось симметрии - прямая, на которой расположена биссектриса угла. Равнобедренный треугольник имеет одну ось симметрии, а равносторонний треугольник - три оси симметрии. Прямоугольник и ромб, не являющиеся квадратами имеют по две оси симметрии, а квадрат - четыре оси симметрии. У окружности их бесконечно много - любая прямая, проходящая через её центр, является осью симметрии.

Определение. Две точки А и А1 называются симметричными относительно точки О, если О - середина отрезка АА1. Точка О считается симметричной самой себе.

Определение. Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре. Точка О называется центром симметрии фигуры. Говорят также, что фигура обладает центральной симметрией. Приведём примеры фигур, обладающие центральной симметрией. Простейшими фигурами, обладающими центральной симметрией, является окружность и параллелограмм. Центром симметрии окружности является центр окружности, а центром симметрии параллелограмма - точка пересечения его диагоналей. О симметрии графиков функций уместно говорить, когда функция является четной или нечетной.

Зеркальная симметрия: «Что может быть больше похоже на мою руку или мое ухо, чем их собственное отражение в зеркале? И все же руку, которую я вижу в зеркале, нельзя поставить на место настоящей руки» Иммануил Кант. Зеркально симметричным считается объект, состоящий из двух половин, которые являются зеркальными двойниками по отношению друг к другу. На рисунке приведен простой пример объекта и его зеркального двойника - треугольник АВС и треугольник А1В1С1 (здесь М N - пересечение плоскости зеркала с плоскостью рисунка). Каждой точке объекта соответствует определенная точка зеркального двойника. Эти точки находятся на одном перпендикуляре к прямой MN , по разные стороны и на одинаковом расстоянии от нее (рис. 1).

Обычно считают, что наблюдаемый в зеркале двойник является точной копией самого объекта. В действительности это не совсем так. Зеркало не просто копирует объект, а меняет местами (переставляет) передние и задние по отношению к зеркалу части объекта. В сравнении с самим объектом его зеркальный двойник оказывается "вывернутым" вдоль направления перпендикулярного к плоскости зеркала. Этот эффект хорошо виден на одном рисунке и фактически незаметен на другом. Эту плоскость называют плоскостью симметрии. Предположим, что одна половина объекта является зеркальным двойником по отношению к другой его половине. Такой объект называют зеркально симметричным. Он преобразуется сам в себя при отражении в соответствующей зеркальной плоскости.

Проведем эксперимент. Напишем на листе бумаги заглавными печатными буквами два слова "КОФЕ" и "ЧАЙ". Затем возьмем зеркало и поставим его вертикально так, чтобы линия пересечения плоскости зеркала с плоскостью листа делила эти слова по горизонтали. Зеркало не подействовало на слово " КОФЕ ", тогда как слово "ЧАЙ" оно изменило до неузнаваемости. Этот " фокус " имеет простое объяснение. Разумеется, зеркало одинаковым образом отражает нижнюю половину обеих слов. Однако в отличие от слова " ЧАЙ " слово " КОФЕ " обладает горизонтальной осью симметрии, именно поэтому оно не искажается при отражении в зеркале (рис. 2).

Поворотная симметрия. Говорят, что объект обладает поворотной симметрией, если он совмещается сам с собой при повороте на угол 360˚/n, где n – натуральное число. Центр симметрии называют осью вращения n-го порядка.

2. Симметрия в зоологии.

Зоология – наука о животных. Она изучает многообразие животного мира, особенности строения и деятельности тела животных, их развития, распределения по земле и отношений к окружающей (живой и мертвой) природе. Конечная цель ее - выяснение законов, управляющих явлениями животного мира, объяснение с их помощью происхождение современного мира животных и установление естественной системы животных. Существует множество таких законов, и один из них это закон - симметрия. Как связаны животный мир и симметрия?

Симметрия простейших организмов. Эрнст Геккель (1834 - 1919) - немецкий естествоиспытатель, основоположник филогенетического направления дарвинизма. Основные научные работы посвящены филогенезу (историческому развитию) растений и животных, зоологии беспозвоночных. Эрнст Геккель проводил свои зоологические исследования в лаборатории и в ходе экспедиций на остров Мадейра, на Цейлон, в Египет и Алжир. Геккель публикует монографии по радиоляриям, глубоководным медузам, сифонофорам, глубоководным рыбам-удильщикам и другим обитателям подводного мира. С 1861г. Геккель - приватдоцент, а в 1865 - 1909гг. - профессор Йенского университета. Умение рисовать помогло Геккелю в его работе по систематизации морских простейших. Рассматривая эти существа с помощью микроскопа, Геккель одновременно рисовал их внешний вид и строение. Первые организмы на Земле, плавающие в толще воды одноклеточные, имели максимально возможную симметрию – шаровую, они появились примерно 3.5 млрд. лет назад. Например, радиолярии. Геккель описал новые виды, обитающие в индийском океане, настоящий размер радиолярии – мене миллиметра. Пораженный открывшейся ему красотой живых форм, он создал альбом под названием «Красота форм в природе». На рисунках можно увидеть плоскости и центры симметрии. Эти рисунки хорошо иллюстрируют многовековую идею о том, что красота и строение живых организмов непосредственно связаны с симметрией.

Представитель простейших - пресноводная гидра (рис. 3). Тело достигает 1-1, 5см. Ловчие щупальца короче тела. Гидру можно обнаружить на водной растительности. Для этого необходимо выловить водоросли и оставить их на некоторое время в банке с водой, чтобы гидра расправилась. На расправившейся гидре можно увидеть тело, щупальца, окружающие ротовое отверстие, подошву. Питается гидра, захватывая своими щупальцами мелких животных. Гидру относят к многоклеточным животным, так как её тело образовано большим количеством клеток. Биологи подтверждают, что через тело гидры можно провести несколько плоскостей симметрии. Такой тип симметрии тела животного в биологии называется лучевой. Лучевая симметрия способствует тому, что животное может ловить добычу и чувствовать приближение опасности с любой стороны. Именно поэтому животные, ведущие малоподвижный образ жизни, внешне похожи на зонтики, шары и цветки растений.

Симметрия подводного мира. Для представителей подводного мира характерна центральная (поворотная) симметрия. Медуза – обладает лучевой (центральной симметрией). Морская звезда. Звездообразные или пятиугольные иглокожие. Величина колеблется от 2 см до 1 м, хотя большинство — 12—24 см. Многие виды ярко окрашены. Обнаружив двустворчатого моллюска, морская звезда обхватывает его раковину руками, присасывается к ней своими ножками и за счет мышечного напряжения раздвигает створки, для принятия пищи. Ось симметрии этих животных показывает направление силы тяжести. Морская звезда обладает поворотной симметрией пятого порядка.

Радиальная симметрия — форма симметрии, сохраняющаяся при вращении объекта вокруг определённой точки или прямой. Часто эта точка совпадает с центром тяжести объекта, то есть той точкой, в которой пересекается бесконечное количество осей симметрии. Подобными объектами могут быть круг, шар, цилиндр или конус. Тело морских ежей обычно почти сферическое, размером от 2—3 до 30 см; покрыто рядами известковых пластинок. Пластинки, как правило, соединены неподвижно и образуют плотный панцирь (скорлупу), не позволяющий ежу изменять форму. По форме тела (и некоторым иным признакам) морские ежи подразделяются на правильных и неправильных. У правильных ежей форма тела почти круглая, и построены они по строго радиальной пятилучевой симметрии. У неправильных ежей форма тела уплощённая, и у них различимы передний и задний концы тела.

Симметрия в животном мире диктуется условиями жизни. Это хорошо видно на примере рыбы камбалы. У камбалы, как и у других рыб, имеется вертикальная плоскость симметрии. Взрослая камбала лежит на дне. Ее глаза, рот, плавники переползают на одну сторону, и ее плоскость симметрии поворачивается на 90º. Камбала приобретает симметрию тела вращения, т.е. поворотную центральную симметрию.

Животные, которые способны передвигаться в каком-то избранном направлении, приобрели двустороннюю симметрию тела (осевую). На ее появление оказало влияние направление движения животного и направление силы тяжести. Однако большинство животных нашей планеты, например, майский жук, речной рак, слон, имеют одинаковые парные органы на левой и на правой сторонах тела. Такие животные появились значительно позже кишечнополостных в процессе исторического развития. Через их тело можно мысленно провести только одну плоскость, делящую их на две зеркально одинаковые половины. Такая симметрия тела называется двусторонней. Она характерна для всех активно передвигающихся животных. Двусторонняя (билатеральная) симметрия — симметричность относительно зеркального отражения. Асимметризация по оси «перед–зад» происходила при взаимодействии с пространственным полем, когда понадобилось быстрое движение (спастись от хищника, догнать жертву). В результате, в передней части тела оказались главные рецепторы и мозг. Билатерально симметричные организмы господствуют последние 650–800 млн. лет. Это ракообразные, рыбы, все прогрессивные формы: млекопитающие, птицы, насекомые. В этих направлениях животное устремляется за пищей или спасается от опасности. По нашим наблюдениям, осевая симметрия присуща большому количеству видов животных. Еж, Сова, Божья коровка, Бабочка, Паук и другие животные обладают осевой симметрией. Например, у бабочки симметрия проявляется с математической строгостью (рис. 4). Такая симметрия способствует поступательному движению живого организма. Почему же в природе царит симметрия? Чем обусловлена эта упорядоченность, пропорциональность?

По данным науки, первые многоклеточные животные появились в воде; они произошли от колониальных простейших – жгутиковых, похожих на вольвокс, и располагались в толще воды во взвешенном состоянии, и любое перемещение для них было безразлично. Поэтому первые многоклеточные имели форму шара. По мере развития и усложнения организмов под действием силы тяжести они стали различать «верх» и «низ» и потеряли симметрию шара. Животные, ведущие прикреплённый образ жизни, такие, как гидра, приобрели симметрию, которая способствует ловле добычи и защиты от врагов, появляющихся с любой стороны. Ось симметрии этих животных показывает направление силы тяжести. Те животные, которые способны были передвигаться в каком- то избранном направлении, приобрели двустороннюю симметрию тела. На её появление важное влияние оказало как направление силы тяжести, так и направление движения животного. Для двустороннесимметричных видов характерно наличие двух примерно одинаковых частей тела, что помогает им сохранять равновесие, прямолинейно передвигаться, быстрее находить пищу и т. д.

Владимир Николаевич Беклемишев советский зоолог, действительный член АМН СССР выделил три типа симметрии (шаровая, радиальная, билатеральная) расположив их в эволюционный ряд. Считая полностью асимметричную амёбу более примитивным существом, чем одноклеточные организмы шаровой симметрии (радиолярии), он поместил её в начало ряда. Билатерально симметричные организмы считались “венцом” эволюции.

Выводы:

►Симметрию живого существа определяет направление его движения. Для живых существ, для которых ведущим направлением является направление движения “вперед”, наиболее характерна осевая симметрия. Так как в этом направлении животные устремляются за пищей и в этом же спасаются от преследователей. А нарушение симметрии привело бы к торможению одной из сторон и превращению поступательного движения в круговое.

►Центральная симметрия чаще встречается в форме животных, обитающих под водой.

►Асимметрию можно наблюдать на примере простейших животных.

3. Симметрия в технике и транспорте.

В жизни такого большого города, как Жуковский транспорт играет значительную роль. И мы ежедневно сталкиваемся с различными его проявлениями. Наш город признан городом авиации. В Жуковском очень много предприятий и институтов, которые разрабатывают и испытывают новые виды самолётов. Так же, в нашем городе одна из самых длинных взлётных полос в России. 27 января 2007года городу Жуковскому был присвоен статус наукограда.

В технике красота, соразмерность механизмов часто бывает связана с их надежностью, устойчивостью в работе. Симметричная форма дирижабля, самолета, подводной лодки, автомобиля и т.д. обеспечивает хорошую обтекаемость воздухом или водой, а значит, и минимальное сопротивление движению. В технике существует своего рода постулат: наиболее целесообразные и функционально совершенные изделия являются наиболее красивыми. В подтверждение этого постулата приведем слова генерального авиаконструктора О.К. Антонова: "Мы прекрасно знаем, что красивый самолет летает хорошо, а некрасивый плохо, а то и вообще не будет летать. Это не суеверие, а совершенно материалистическое положение... конструктор может идти часто от красоты к технике, от решений эстетических к решениям техническим". Самолёт обладает осевой симметрией: Детали самолёта тоже симметричны.

Железнодорожный транспорт. С Москвой Жуковский связан железной дорогой Казанского направления. Время пути по железной дороге до станции метро Выхино 31 минута, а до Казанского вокзала 55 минут. Своё 70-летие отметила старейшая в России детская железная дорога, протянувшаяся почти на 5 км от подмосковного Жуковского до посёлка Кратово. Свою историю дорога ведёт с 1937 года. С идеей создать узкоколейку, где бы школьники могли учиться профессии для поступления в железнодорожные учебные заведения, обратились к Наркомату путей сообщения в 1935 году пионеры Раменского района. Глава ведомства Лазарь Каганович одобрил предложение, и начались строительные работы. Станция «Юность» Малой Московской детской железной дороги, напротив платформы Отдых.

Первые паровозы в России были построены русскими механиками и изобретателями, отцом и сыном Черепановыми — Ефимом Алексеевичем и Мироном Ефимовичем. Черепановыми было создано около 20 различных паровых машин, работавших на нижнетагильских заводах. В 1834 г. они построили первый русский паровоз, а в 1835 г. — второй, более мощный. С развитием науки и техники стремление человека к симметричности форм сохраняется. Мы продемонстрируем её на примере вида электровоза спереди.

Симметрия автомобиля. Интерьер автомобиля производит впечатление своей симметрией и объемом" Взгляните на силуэт автомобиля, - предложил специально обученный человек, - Так выглядит практически любая машина, оставленная в снегопад без движения. Ветер плавно обдувает ее кузов, оставляя где-то больше снега, а где-то меньше. Стало быть, силуэт этот подсказан самой природой, а потому он более чем гармоничен". Машина, как и любой вид транспорта, обладает осевой продольной симметрией. Некоторые детали машин имеют центральную симметрию: колесо автомобиля, шестеренка и др. При моделировании автомобильных дисков, для расчетов применяют поворотную симметрию. Регулировка схождения колес автомобиля производится относительно продольной оси симметрии машины. Для наземного вида транспорта в большей степени характерна осевая симметрия. Причиной этого является направление его движения.

В процессе нашей исследовательской деятельности мы пришли к выводу, что центральная симметрия не совместима с формой наземного и подземного транспорта. Причиной этого служит его направление движения. При рассмотрении вида сверху трамвая, электровоза, телеги, мы видим, что ось симметрии проходит вдоль направления движения. Таким образом, центральную симметрию следует искать в воздушном и подводном транспорте, т. е. в таких видах, где направления: вперед, назад, вправо, влево, – равноценны. Один из таких видов транспорта – это воздушный транспорт.

Понятие "аэростат", или летательный аппарат легче воздуха, возникло в результате слияния двух слов: aer - воздух и statos - стоящий неподвижно (греч.). Подъемная сила аэростата создается заключенным в газонепроницаемую оболочку гелием или водородом - газами, плотность которых меньше плотности воздуха, либо горячим воздухом. Аэростаты делятся на свободные, то есть аэростаты свободного полета, и привязные аэростаты (змейковые), поднимаемые на привязном тросе вручную либо с помощью лебедки. Современные аэростаты - это надежные и безопасные средства, используемые как для воздухоплавания, так и для решения разнообразных специальных задач. Привязные аэростаты получили большое распространение в качестве действенного средства наружной рекламы. На основе привязных аэростатов реализован, например, аттракцион "Аэролифт", поднимающий пассажиров на высоту 150 - 200 метров. Аэростат обладает осевой симметрией в продольном разрезе, а сверху: центральной симметрией (рис.5). Один из воздушных видов транспорта – это воздушный шар.

Первый полет на воздушном шаре в России совершил известный французский гастролер-воздухоплаватель Жак Гарнерен вместе со своей женой в 1803 году. Воздушный шар поднялся с Васильевского острова и пролетев над городом благополучно приземлился. Полет был совершен в присутствии "императорской фамилии и великого стечения зрителей". Развитие советского воздушного флота сопровождалось широким распространением в авиации парашюта. В процессе создания новых типов самолетов летчики и испытатели, проводя рискованные эксперименты на опытных машинах, видели в парашюте своего верного помощника. Замечательное изобретение Г. Е. Котельникова нашло широчайшее применение не только как надежное спасательное средство, но и как спортивный снаряд одного из любимейших массовых видов советского спорта. Показательные прыжки с парашютом, проводившиеся в аэроклубах Осоавиахима, привлекали множество молодежи, охотно вступавшей в парашютные кружки. Авиационный парашют – это русское изобретение.

Первые испытания парашюта были проведены 2 июня 1912 года с помощью автомобиля. Машину разогнали, и Котельников дернул за спусковой ремень. Привязанный за буксировочные крюки парашют мгновенно раскрылся. В 1911 году Котельников зарегистрировал свое изобретение - ранцевый парашют свободного действия.

В 1927 году летчик-испытатель М. М. Громов совершил прыжок с самолета, вошедшего в "штопор", из которого, несмотря на все усилия, вывести машину не удалось. Вслед за Громовым спаслись с помощью парашюта и ряд других летчиков. Эти случаи убедительно показали отличные качества и надежность действия авиационного парашюта. Его именем названа улица в Москве, площадь в нашем городе Жуковском.

Транспорт будущего. Надувное тормозное устройство. Дальнейшее развитие парашют получил в изобретении нашими учеными “надувного тормозного устройства”. Оно предназначено для спуска грузов и человека с орбиты. Надувное тормозное устройство представляет собой эластичную оболочку, наполняемую в космосе. Она имеет гибкую теплозащиту и дополнительную надувную оболочку. Впервые спускаемый аппарат с надувной тормозной системой был запущен 9 февраля 2000 года и впоследствии потерян из-за неисправностей в тормозной системе. Вид сверху этого устройства представляет собой круг. А круг, как мы знаем, не только обладает осевой симметрией, но и центральной. Центр симметрии совпадает с центром круга. Задача спасения людей в чрезвычайных ситуациях может быть успешно решена с помощью предлагаемой системы спасения, созданной на основе надувного тормозного устройства. В то же время, это единственное в мире устройство, предназначенное для широкого применения – от возврата грузов и экстренной эвакуации из космоса до осуществления мягкой посадки на другие планеты, в частности, на Марс.

Выводы:

►Вид сверху и вид спереди различных видов транспорта обладает либо центральной, либо осевой симметрией.

►Для наземного вида транспорта в большей степени характерна осевая симметрия. Причиной этого является направление его движения.

►Центральная симметрия чаще встречается в форме воздушного и подводного транспорта, для которого направления: вправо, влево, вперед, назад, – равноценны.

►Модели транспорта будущего в той же степени, что и модели настоящего и прошлого обладают различными видами симметрии.

4. Симметрия в архитектуре.

Прекрасные образцы симметрии демонстрируют произведения архитектуры. Большинство зданий зеркально - симметричны. Общие планы построек, фасады, орнаменты, карнизы, колонны обнаруживают соразмерность, гармонию. Много примеров использования симметрии дает старая русская архитектура: колокольни, сторожевые башни, внутренние опорные столбы.

Архитектура – удивительная область человеческой деятельности. В ней тесно переплетены и строго уравновешены наука, техника искусство. Только соразмерное, гармоничное единство этих начал делает возводимое человеком сооружение памятником архитектуры, неподвластным времени, подобно памятникам литературы.

Архитектура бесконечно разнообразна. И все же самый древний храм и современный дом, подобно человеческим лицам, имеют множество общих черт. В своем творчестве архитекторы располагают только строительным материалом и пространством. Все остальное в архитектурном облике здания архитектор создает собственной фантазией. В качестве художественных средств он использует композицию, пропорциональное соотношение здания и его частей, живопись и скульптуру, окружающую природу и застройку.

Композиция зданий. От нее в первую очередь зависит впечатление, которое производит архитектурное сооружение. Сочетание различных объемов высоких и низких, прямолинейных и криволинейных, чередование пространств открытых и закрытых. Это, пожалуй, основные приемы, которые использует зодчий, создавая архитектурные композиции (рис 6).

Наиболее ясны и уравновешены здания с симметричной композицией. Такие здания были характерны для архитектуры эпохи классицизма. Под классицизмом понимают архитектурный стиль, распространённый в Европе в XVIII — начале XIX вв., главной чертой которого было обращение к формам античного зодчества как к эталону гармонии, простоты, строгости, логической ясности и монументальности.

Мы предлагаем Вам прогуляться по городу Жуковскому и особенно обратить внимание на композиции зданий нашего города, на их симметричность.

Прогулка по городу Жуковскому. В древности здесь были глухие места с множеством озер и болот. Огромные лесные массивы тянулись от села Быково до реки Москвы. Первые поселения появились в этом районе в начале XX века, когда владелец Московской железной дороги Николай Карлович фон Мекк выкупил у князя Прозоровского-Голицына большой участок леса и основал станцию Прозоровская (в последствии Кратово) и дачный поселок. Поблизости он решил построить город-сад, в котором будет все, что нужно для удобной, здоровой и благополучной жизни его обитателей. В 1912 году, приглашенные им, молодые архитекторы В. Н. Семенов, А. И. Таманян, А. В. Щусев, А. И. Шанецкий и Н. Н. Бунятов разработали проект. В короткие сроки выполнили все изыскания и в густом сосновом бору, на водоразделе рек Москвы и Хрипанки приступили к возведению нескольких жилых домов — с водопроводом, канализацией, хозяйственными постройками — и первых корпусов уникального больничного городка Начавшаяся в 1914 году мировая война остановила стройку. Проект не удалось полностью осуществить, но заложенные в нем идеи в дальнейшем широко применяли при создании новых микрорайонов и дачных поселков не только в России, но и далеко за ее пределами. Использовали их и при строительстве города Жуковского. По окончании войны в окрестностях поселка Прозоровского появились новые санатории, железнодорожная платформа и дачный поселок Отдых. Одна из красивейших усадьб барона фон Мекк в данное время называется Домом культуры «Стрела». Очевидна симметричность, стройность и пропорциональность этой постройки. Центральной симметрией обладает памятник архитектуры – фонтан.

Архитектуре классицизма в целом присуща регулярность планировки и четкость объемной формы. Основой архитектурного языка классицизма стал ордер, в пропорциях и формах близкий к античности, симметрично-осевые композиции, сдержанность декоративного убранства. Симметрично – осевые композиции при планировке города.

Храмы города Жуковского. Устройство храма зиждется на принципах симметрии, которые должны тщательно соблюдаться архитектором. Они обусловлены пропорцией. Пропорция есть соответствие между частями и целым. Отсюда получаются принципы симметрии. Без симметрии и пропорции не может быть принципов устройства храма, то есть, если нет точного соотношения между его частями, каковое существует в хорошо слаженном человеке.

Церковь Иконы Божией Матери Иверская в Жуковском. Деревянная шатровая церковь с покрытыми бочками боковыми притворами, достаточно точно воспроизводящая облик памятников Русского Севера. Служит крестильной церковью при Пантелеймоновском храме. Храм крестово-купольного типа, центрально – симметричный.

Церковь Михаила Архангела в Жуковском. Новая церковь, устроенная в приспособленном кирпичном здании. Помещение перестроено, сооружён деревянный купол с шатром, притвор со звонницей.

Церковь Пантелеимона Целителя в Жуковском Новая церковь, выстроенная на основе старого корпуса городской больницы. Завершена двускатными кровлями с главками, шатровая колокольня пристроена в 1997. В настоящее время главный городской храм.

Церковь Покрова Пресвятой Богородицы при Центральной городской больнице в Жуковском. Церковь на территории Центральной городской больницы. Первоначально Космодамианский храм был устроен в приспособленном помещении, в 2004-2007 выстроена отдельная Покровская церковь с приделом Космы и Дамиана - однокупольная кирпичная постройка эклектичной архитектуры. Симметричная постройка. Центрально – симметричный купол.

Церковь Преображения Господня в Жуковском. Большой каменный двухэтажный храм, возводящийся рядом с Пантелеймоновской и Иверской церквами. Пятикупольный шестистолпный храм строится в духе городских соборов начала XVI века.

Церковь Иконы Божией Матери Державная в Кратово. Первоначально церковь была устроена в здании дореволюционной постройки. Ныне выстроен одноглавый каменный четырехстолпный храм в духе новгородской архитектуры. Приделы Царе-Никольский и Всех Святых, в Земле Российской просиявших. Храм построен в старом новгородско-псковском стиле.

Пятый дом. Говорят, «возле арки, за углом» есть в Жуковском «пятый дом», дорогу к которому может показать любой житель, не спрашивая названия улицы. Говорят, с этого дома уникальной архитектуры начинался город Жуковский. Считается, что именно здесь началось строительство нашего города. Здание симметрично, это подчеркнуто арками и оконными проемами.

За 60 лет город вырос практически на пустом месте. Здание детской поликлиники, начало 1950-х годов. Здание центральной городской больницы, начало XXI века. Кафе «Студенческое» (начало 1960-х годов) и Кафе «Глиссада» (январь 2008 г). Пересечение улиц Чкалова и Горького (конец 1950-х годов, январь 2008 г). Улица Гагарина 1962 год, улица Гагарина начало XXI века. Средняя школа №5 - одно из старейших зданий города. Нашей школе 46 лет. Здание мэрии можно отнести к одному из современных сооружений, обладающих симметрией.

Примером удивительного сочетания симметрии и асимметрии является Покровский собор (храм Василия Блаженного) на Красной площади в Москве. Эта причудливая композиция из десяти храмов, каждый из которых обладает центральной симметрией, в целом не имеет ни зеркальной, ни поворотной симметрии. Симметричные архитектурные детали собора кружатся в своем асимметричном, беспорядочном танце вокруг его центрального шатра: они то поднимаются, то опускаются, то как бы набегают друг на друга, то отстают, создавая впечатление радости и праздника. Без своей удивительной асимметрии храм Василия Блаженного просто немыслим!

Пример современной архитектуры в городе Жуковском. Торговые центры: «Навигатор» и «Клод Моне» На первый взгляд эти сооружения абсолютно несимметричны. Но в них присутствуют элементы, обладающие тем или иным видом симметрии. В данное время важнейшей задачей градостроительства является строительство жилья и объектов инфраструктуры. Строится много зданий современной архитектуры.

Мы живем, находясь под воздействием с одной стороны, симметрии и необходимости, а с другой - асимметрии и случайности и используя в своей практике диалектику симметрии - асимметрии. Например, строители современных мостов, высотных зданий, башен знают, что конструкция не должна быть безупречно симметричной из-за опасности возникновения резонансных колебаний, которые могут привести к ее разрушению. Поэтому симметрию конструкций сознательно нарушают, вводя в нее отдельные асимметричные элементы, т. е. чистая симметрия, может оказаться опасной. Она неустойчива.

Выводы:

►Принципы симметрии являются основополагающими для любого архитектора, но вопрос о соотношении между симметрией и асимметрией каждый архитектор решает по-разному. Асимметричное в целом сооружение может являть собой гармоническую композицию симметричных элементов.

►Удачное решение определяется талантом зодчего, его художественным вкусом и его пониманием прекрасного. Прогуляйтесь по нашему городу и убедитесь, что удачных решений может быть очень много, но неизменным остается одно – стремление архитектора к гармонии, а это в той или иной степени связано с симметрией.

5. Симметрия в искусстве.

«Назначение и цель гармонии - упорядочить части, вообще говоря, различные по природе, неким совершенным соотношением так, чтобы они одна другой соответствовали, создавая красоту» Л.Б. Альберти.

У многих народов с древнейших времен симметрия воспринималась как символ стабильности и гармонии. В изобразительном искусстве симметрия (в переводе с греческого языка — соразмерность) также стала одним из основных способов композиции. Симметричная композиция легко воспринимается зрителем, сразу привлекая внимание к центру картины, в котором и находится то главное, относительно которого разворачивается действие. В древнерусской живописи сложилась образная система, иллюстрирующая религиозные сюжеты. Традиционная композиция иконы чаще всего симметрична, а главные персонажи выделены своим центральным местоположением. Зримый образ Всевышнего обычно располагался строго в центре пространства иконы как символ и смысл первоосновы мира. Симметричные, гармоничные пропорции, создающие впечатление покоя и величественности, подчеркивали несовершенство и хаотичность земного бытия.

Для анализа симметрии изображения лучше обратиться к хранящейся в Эрмитаже картине гениального итальянского художника и ученого Леонардо да Винчи «Мадонна Литта». Обратите внимание: фигуры мадонны и ребенка вписываются в правильный треугольник, который вследствие своей симметричности особенно ясно воспринимается глазом зрителя. Благодаря этому мать и ребенок сразу же оказываются в центре внимания, как бы выдвигаются на передний план. Голова мадонны совершенно точно, но в то же время естественно помещается между двумя симметричными окнами на заднем плане картины. В окнах просматриваются спокойные горизонтальные линии пологих холмов и облаков. Все это создает ощущение покоя и умиротворенности, усиливаемое за счет гармоничного сочетания голубого цвета с желтоватыми и красноватыми тонами.

Внутренняя симметрия картины хорошо ощущается. А что можно сказать об асимметрии? Асимметрия хорошо проявляется, например, в тельце ребенка, которое неправильно разрезает упомянутый выше треугольник. И, кроме того, есть одна в высшей степени выразительная деталь. Благодаря взаимной замкнутости, завершенности линий фигуры мадонны создается впечатление полного безразличия мадонны к окружающему миру, и в частности к зрителю. Мадонна вся сосредоточена на младенце; она нежно держит его, нежно глядит на него. Все ее мысли сосредоточены только на нем. И вдруг вся эта замкнутость картины в себе исчезает, как только мы встречаемся со взглядом ребенка. Именно здесь внутренняя уравновешенность композиции нарушается: спокойный и внимательный взгляд обращен прямо на зрителя, через него картина раскрывается во внешний мир. Попробуйте мысленно убрать эту чудесную асимметрию, повернуть лицо младенца к матери, соединить их взгляды. Разве вы не чувствуете, что от этого картина сразу беднее, менее выразительнее? Получается, что всякий раз, когда мы, восхищаемся тем или иным произведением искусства, говорим о гармонии, красоте, эмоциональности воздействия, мы тем самым касаемся одной и той же неисчерпаемой проблемы – проблемы соотношения между симметрией и асимметрией.

Художники эпохи Возрождения часто использовали язык симметрии в построении своих композиций. Это следовало из их логики понимания картины как изображения идеального мироустройства, где царит разумная организованность и уравновешенность, которые человек может познать и осмыслить. В удивительной картине "Обручение девы Марии" великий Рафаэль воспроизвел такой образ мира, существующего по законам гармонии и строгой логики. Использованный принцип симметрии создает впечатление покоя и торжественности и в то же время некой отстраненности от зрителя. Вход в изящную ротонду и кольцо, одеваемое Иосифом на руку Марии, совпадают с центральной осью симметрии картины. Перекликаются движения фигур юношей и девушек, расположенных справа и слева от основной группы. Симметричными дорожками из гранитных плит вымощена площадь перед храмом. Такое соотношение элементов углубляет образный смысл произведения, наполняет его многогранной символикой.

Художники, хотя и часто прибегают к симметрии, используют ее очень осторожно. Поясним эту мысль аналогией с весами. Если весы находятся в равновесии, то их коромысло горизонтально, чашки весов расположены симметрично относительно опоры весов. Но стоит на одну из чашек положить дополнительный груз, как равновесие нарушится, коромысло наклонится, чашки начнут двигаться. Исчезла симметрия - нарушилось равновесие, появилась асимметрия- система пришла в движение. Таким образом, строгая симметрия воспринимается как покой, равновесие, небольшое отклонение от симметрии воспринимается как динамика, движение. Проанализируем с этих позиций картину А.Рублева "Троица". Симметричная в целом композиция этой картины (расположение трех ангелов симметрично) в деталях асимметрична, и это создает впечатление динамики действия, повышает выразительность произведения искусства. Что хотел показать художник в картине "Троица", используя симметрию? Скорее всего, уравновешенность и покой, которые несут эти три ангела.

Конечно, чаще всего в изобразительном искусстве мы говорим о неполной симметрии. Существует некоторая "обращенность" к центру, создающая композиционное равновесие. В картине "Три богатыря" русского художника В. Васнецова по небу движутся тяжелые облака, колышется спелая нива, волнуются могучие кони, с трепещущими от ветра гривами. Сами герои полны сдерживаемой силы: вся группа чуть сдвинута влево, один из богатырей выдвигает меч, другой прикрывает ладонью глаза, третий, наклонив голову, прислушивается. Из-за этих небольших отклонений от строгой симметричности возникает ощущение внутренней свободы персонажей, их готовности к движению. В главном же композиция картины, близкая к симметрии, помогает художнику воплотить образ неприступной "богатырской заставы", непоколебимых защитников русской земли, их спокойствия и уверенности.

Среди современных художников в жанре “математического искусства” наиболее успешно выступает голландский художник Мориц Эшер. «Если мы создаём мир, то пусть он будет не абстрактным и туманным. Пусть он будет представлен конкретными узнаваемыми вещами» М.К. Эшер. Голландский художник Мориц Корнилис Эшер создал уникальные и очаровательные работы, в которых использованы или показаны широкий круг математических идей, в том числе и идей симметрии. “Я часто ощущаю большую близость к математикам, чем к коллегам-художникам”, — писал сам Эшер. Ему же приписывают слова: “Все мои произведения — это игры. Серьезные игры”. Его литографии, гравюры на дереве, мозаику можно увидеть в кабинетах математиков и других ученых во всех уголках мира (рис 7).

Морицу Эшеру более повезло как ученому, чем как художнику. В его гравюрах и литографиях видели ключи к доказательству теорем или оригинальные контрпримеры, бросающие вызов здравому смыслу. На худой конец их воспринимали как прекрасные иллюстрации к научным трактатам по кристаллографии, теории групп, когнитивной психологии или компьютерной графике. Голландский художник Мориц Корнелиус Эшер родился 17 июня 1898 года в провинции Голландии. В доме, котором родился Эшер, сейчас находится музей. Учитель рисования заметил талант у мальчика и научил его делать гравюры по дереву. В 1916 году Эшер выполняет свою первую графическую работу, гравюру на фиолетовом линолеуме - портрет своего отца.

В городе Гарлеме он берет уроки рисования у Самюэля Джесерена, оказавшего формирующее влияние на жизнь и творчество Эшера. Эшер начинает экспериментировать в новом для себя направлении, уже тогда в его работах встречаются зеркальные отображения, кристаллические фигуры и сферы, идеи симметрии, замощения плоскости. Конец двадцатых годов оказалась очень плодотворным периодом для Морица. Его работы демонстрировались на многих выставках Голландии, а к 1929 году его популярность достигла такого уровня, что за один год прошли пять персональных выставок в Голландии и Швейцарии. Именно в этот период картины Эшера впервые были названы механическими и "логическими". Среди его восторженных поклонников были и математики, которые видели в его работах оригинальную визуальную интерпретацию некоторых математических законов. Это более интересно тем, что сам Эшер не имел специального математического образования. В процессе своей работы он черпал идеи из математических статьей, в которых рассказывалось о мозаичном разбиении плоскости, проецировании трехмерных фигур на плоскость и неевклидовой геометрии. Он был очарован всевозможными парадоксами и в том числе "невозможными фигурами". Наиболее интересными для изучения идеями Эшера являются всевозможные разбиения плоскости и логика трехмерного пространства. Т В 1950 году проходит его первая персональная выставка в Соединенных Штатах и начинают покупаться его работы. 27 апреля 1955 года Морица Эшера посвящают в рыцари и он становится дворянином. ". В период с 1950 по 1960 годы он создал свои наиболее известные картины (литографии, гравюры на дереве и металле), в том числе и с невозможными конструкциями, в которых он мастерски исследовал пластические аспекты понятий бесконечности и симметрии, а также особенности психологического восприятия сложных трёхмерных объектов. Творчество Эшера проникло во многие сферы жизни: его работы исследуют математики, используют ученые и психологи, его произведения становятся иллюстрациями романов, обложками пластинок, став неотъемлемой принадлежностью современности. В середине 50-х годов Эшер объединяет мозаику с фигурами, уходящими в бесконечность. В 1971 году Морис Эшер скончался в возрасте 73 лет. Эшер прожил достаточно долго, чтобы увидеть книгу "Мир М. К. Эшера", переведенную на английский язык и остался ею очень доволен. Его автопортрет, созданный в конце жизни, так же парадоксален, как и остальные картины. Творец здесь похож на свои произведения. Точные детали создают странную гармонию целого. Наверно, сам того не желая, Мориц Эшер оставил здесь свидетельство не только своего внешнего облика и стиля, но и своего характера.

Симметрию в живописи можно проследить на примерах картин жуковских художников С.А.Петрик, В. С. Самарыча, Н. А. Щеулова., В. Пименова.

Важная часть фотографического искусства – композиция. Слово «композиция» (compositio) по-латыни означает «соединение» или «приведение в порядок». «Компоновать» — значит складывать отдельные части в целостное произведение. Задача композиции заключается в том, чтобы отдельные элементы, из которых состоит общая картина, связать между собой, соединить в одно неразрывное целое. В хорошо скомпонованной фотографии ни одна часть не может быть удалена, и ничто не может быть добавлено без того, чтобы не нарушилось художественное качество. И, наоборот, если фотография плохо скомпонована, то из нее можно без ущерба удалить ту или иную часть и также без ущерба добавить новую. При рассматривании фотографии взгляд должен естественно переходить с одного предмета на другой, полностью воспринимая изображение, оставаясь при этом в границах кадра. Всякая фотография состоит из нескольких — иногда очень многих — частей. Каждая часть обладает некоторым качеством, привлекающим наше внимание. Одни части композиции привлекают наше внимание сильнее, другие — слабее. Это зависит, прежде всего, от смысловой значимости объекта, которую фотограф выявляет размером объекта, его цветовым пятном и, наконец, его местоположением на изобразительной плоскости. Например, две части композиции будут уравновешены, если они имеют одинаковую зрительную тяжесть, т.е. привлекают внимание зрителя в одинаковой степени. Равновесие может быть достигнуто на основе симметрии, т.е. когда обе части расположены одинаково по отношению к какой-либо оси, например горизонтальной. Композиция состоит из нескольких больших и малых деталей, расположенных таким образом, что группа с одной стороны горизонтальной оси уравновешивает группу, помещенную с другой стороны. Но не всегда возможно уравновесить отдельные части изображения относительно оси или центра. Чаще равновесие частей проводится не на основе симметрии (асимметричная композиция).

Отражение в воде - единственный пример горизонтальной симметрии в природе. Быть может, в этом и состоит тайна его очарования?...Мы любуемся пейзажами художников, удачными снимками. Горы красиво отражаются на поверхности озера, придавая снимку законченность. Поверхность озера играет роль зеркала и воспроизводит отражение с геометрической точностью. Поверхность воды есть плоскость симметрии... Как скучно было бы жить в мире, где нет водных зеркал! Бывало, выйдешь на берег тихого озера — и ахнешь: мир, прекрасный всегда, сейчас прекрасен вдвойне. С доскональной точностью он повторен в озерной глади. И это придает ему особую значительность. Чудо отражения глубоко повлияло на человека, на развитие у него чувства прекрасного. Быть может, именно возле водных зеркал человек впервые задумался о законах симметрии? Ведь отражения так наглядно и глубоко выражают суть этих законов. На планете Земля много разнообразных зеркал: и крохотных, эфемерных — вроде весенних лужиц; и гигантских, океанических — сомасштабных самой бесконечности. Великолепна и таинственна двойная бездна! Вот когда чувство гармонии, питаемое симметрией отражений, обретает космическую наполненность. Приглядимся внимательно к озерному зеркалу. Для физика это пленка поверхностного натяжения; возникает она благодаря особому распределению сил в молекулах воды, граничащих с воздушной средой. Для биолога озерное зеркало — среда жизни, интереснейшая экологическая ниша, а для фотографа – зеркало души и гармонии.

Выводы:

►Симметричная композиция легко воспринимается зрителем, сразу привлекая внимание к центру картины, репродукции, фотографии, в которой и находится то главное, относительно которого разворачивается действие.

►Художники исходят из основных законов природной симметрии, вместе с тем они выявляют "чуть заметные отклонения от нее". Об этом говорил известный художник О. Ренуар: "Два глаза, даже на самом красивом лице, всегда чуть-чуть различны, нос никогда не находится в точности над серединой рта; долька апельсина, листья на деревьях, лепестки цветка никогда не бывают в точности одинаковыми".

►Симметрия и асимметрия создают впечатление динамики действия, повышают выразительность произведения искусства, будут всегда, находится рядом и волновать зрителя.

6. Симметрия в ботанике.

Ботаника – наука о растениях. Ботаника – охватывает огромный круг проблем: их систематику; развитие в течение геологического времени; возможности хозяйственного использования растений; закономерности внешнего и внутреннего строения растений. Наше исследование было направлено на выявление примеров симметрии в растениях, то есть мы занимались последней из этих проблем – проблемой поиска закономерностей внешнего строения растений.

В 5 веке до н. э. на явление симметрии в живой природе обратили внимание в Древней Греции пифагорейцы, в связи с развитием ими учения о гармонии. В 19 веке появлялись отдельные работы, касающиеся этой темы. А в 1961 году, как результат многовековых исследований, посвященных поиску красоты и гармонии окружающей нас природы, появилась наука биосимметрика.

У биологических объектов встречаются следующие типы симметрии:

• сферическая симметрия — симметричность относительно вращений в трёхмерном пространстве на произвольные углы.

• симметрия n-порядка — симметричность относительно поворотов на угол 360°/n вокруг какой-либо оси.

• двусторонняя (билатеральная) симметрия — симметричность относительно зеркального отражения.

• трансляционная симметрия — симметричность относительно сдвигов пространства в каком-либо направлении на некоторое расстояние.

Характерная для растений симметрия конуса хорошо видна на примере фактически любого дерева. Дерево при помощи корневой системы поглощает влагу и питательные вещества из почвы, т.е. снизу, а остальные жизненно важные функции выполняется кроной, т.е. наверху. Вертикальная ориентация оси корпуса характеризует симметрию дерева. Ярко выраженной симметрией обладают листья, цветы, ветви, плоды. Нарушение некоторых из условий определяющих симметрию дерева как симметрию конуса, приводит к искривлению стволов и однобоко развитой кроны дерева. Четко выраженной симметрией обладают листья клена, дуба и т. д. Например, лист клена обладает осевой, зеркальной симметрией (рис 8).

В природе встречается взаимное расположение лепестков разных видов:

зеркально равные, совместимо и зеркально равные, совместимо равные. Расположение лепестков относительно закономерно друг друга может быть: симметричным, хаотичным, асимметричным.

ПЕРЕНОСНАЯ (ТРАНСЛЯЦИОННАЯ) СИММЕТРИЯ. О такой симметрии говорят тогда, когда при переносе фигуры вдоль прямой на какое-то расстояние кратное этой величине, она совмещается сама с собой. Веточка акации имеет зеркальную и переносную симметрию, а веточка боярышника обладает скользящей осью симметрии, с последующим зеркальным отражением. А цветок одуванчика обладает симметрией шара (сферической симметрией).

Центральную симметрию можно наблюдать на изображении следующих цветов: лук, цветок одуванчика, цветок кувшинки, цветок мать и мачехи. Цветок ромашки обладает центральной симметрией, только в случае четного количества лепестков. Её сердцевина представляет собой окружность, и поэтому центрально симметрична, так как мы знаем, что окружность имеет центр симметрии. В случае же нечетного количества лепестков, например анютины глазки, цветок обладает только осевой симметрией. Барвинок обладает поворотной симметрией пятого порядка и не обладает зеркальной симметрией.

О крапиве: Сорвите лист крапивы и посчитайте зубчики с левой и правой стороны. Вы убедитесь, что с одной и другой стороны одинаковое число зубцов.

О ягодах. Рассмотрим разрез любой из ягод. В поперечном разрезе она представляет собой окружность, а окружность, как нам известно, имеет центр симметрии. В продольном разрезе, например, ягода клубники обладает осевой симметрией. Поперечный разрез фруктов обладает центральной симметрией.

О грибах. Гриб в продольном разрезе обладает осевой симметрией, а шляпка гриба – центральной симметрией. Далее производится показ презентации «Геометрия цветка».

Выводы:

►По нашим наблюдениям, в любом растении можно найти какую-то его часть, обладающую осевой или центральной симметрией.

Это могут быть листья, цветы, стебли, стволы деревьев, плоды, и более мелкие части, такие как сердцевина цветка, пестик, тычинки и другие.

► Осевая симметрия присуща различным видам растений и грибам, и их частям.

►Центральная симметрия наиболее характерна для плодов растений и некоторых цветов.

►Симметрия – общее свойство объектов окружающего мира, асимметрия же отражает индивидуальные свойства объектов.

►Мы пришли к главному выводу, что симметрия в основе всего, она – первооснова Красоты…

Симметрия – это не только математическое понятие. Его заимствовали из природы. А так как человек – это часть природы, то человеческое творчество во всех его проявлениях тяготеет к симметрии. Симметрия в живой природе: в животном и растительном мире, – передается генетически из поколения в поколение. Можно сказать, что на симметрии держится весь мир. Когда мы видим проявления симметрии в разных областях жизни, мы невольно испытываем чувство удовлетворения тем всеобщим порядком, который царит в природе. Но симметрия – общее свойство объектов окружающего мира, асимметрия же отражает индивидуальные свойства объектов. Мир существует благодаря единству симметрии и асимметрии.

Приложение

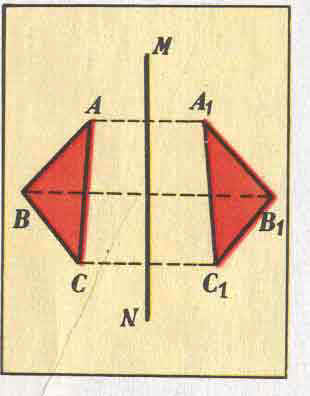
рис. 1 рис .2

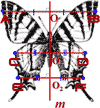
рис.3 рис.4

рис.5 рис.6

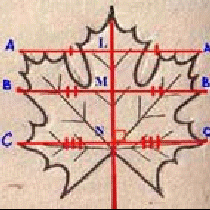
рис.7 рис.8

Список литературы:

1. Смирнова Е.С. Курс наглядной геометрии: Просвещение 2002

2. Шарыгин И. Ф. Ерганжиева Л.Н Наглядная геометрия- М: Мирос, 1992

3. Волошилов А.В. Пифагор – М: Просвещение , 1993

4. Сонин А.С Постижение совершенства – М: Здание, 1987

5. Тарасов Л.В Этот удивительный симметричный мир – М: Просвещение, 1982

6. Гончар В.В Модели многогранников. – М. АКИМ, 1998

7. Веннинджер М. Модели многогранников.- М: Мир, 1974

8. Александровская Л. Мы учимся летать. Издательство «ММедия», 2007

9. Иллюстрированный энциклопедический словарь. М.Терра, 1998.

10. Гусев А. С. МордковичА.Г. .Справочные материалы М: Просвещение 1998.

11. Атанасян Л.С. Учебник по геометрии для 7 - 9классов.

12. Выгодский. М.Я. Справочник по элементарной математике М., 1968г..

Ресурсы сети Интернет:

http://www.edu.sbor.net:8001/files/gios/metod_kabinet/konkurs/samodurova/razn/

Symmetry_web.htm

http://www bse.chemport.ru/simmetriya_(v_matematike).shtml  · 

http://www lib.mexmat.ru/books/11811  

http://www method.vladimir.rcde.ru/getblob.asp?id=1100000280  · 86 КБ

http://wwwobgon.com/archive/relcom.wheels/4k1y4f4o4h2y2b4m4l4b3w4b4j4i4g2b1x4i1z2e2d4c1w2f4j2c2c3w1w4e3y4f4c3u2m2a3t4q1u3v4h5f.html  · 10 КБ

http://www sholast.ru/story/simmetrija_v_biologii.html  · 30 КБ

www.sunhome.ru/image/14714  · 28 КБ

http://wwwwww.bymath.net/studyguide/geo/sec/geo22.htm  · 25 КБ

http://www gatchina3000.ru/great-soviet-encyclopedia/bse/102/213.htm  · 17 КБ

http://www olig.ru/forums/index.php?showtopic=103634  · 64 КБ

www.sunhome.ru/image/14325  · 27 КБ

http://www grigor.volnet.ru/lektion/l9.3.htm  · 28 КБ

http://www likt590.ru/project/matematika/5/  · 2 КБ

http://www letopisi.ru.netflow.ru/index.php?title=Симметрия_в_архитектуре&  · 10 КБ

http://www .mavicanet.ru/lite/rus/21575.html  · 13 КБ

http://dic.academic.ru

http://www.proza.ru/texts/2005/12/26-13.html

http://www.mccme.ru/free-books/prasolov/planim/gl17.htm

http://www.likt590.ru/project/matematika/5/index1.html

http://fio.ifmo.ru/archive/group19/c1wu9/str01a.htm

http://www.studik.ru/721953159144679/%D1%80%D0%B5%D1%84%D0%B5%D1%80%D0%B0%08

http://www.be.sci-lib.com/article093717.html

http://www.bestreferat.ru/referat-76256.html

http://www.edu-zone.net/show/71231.html

http://nature.web.ru/db/msg.html?mid=1175978&s=

infourok.ru

Реферат симметрия в природе номинация «Математика вокруг нас»

казенное учреждение

Кулустайская средняя общеобразовательная школа

РЕФЕРАТ

СИММЕТРИЯ В ПРИРОДЕ

НОМИНАЦИЯ «Математика вокруг нас»

МОКУ Кулустайской СОШ

Бурмистрова Клава Руководитель учитель математики

Бородина Галина Васильевна

с. Усть – Кивда, 2013г.

Введение………………………………………………………………….… 1

Основная часть…………………………………………….…………….. 2

1. Основные понятия о симметрии и геометрии природы………………. 2

1.1. Виды симметрии……………………………………………………….. 2

1.2. Симметрия в живой природе ………………………............................. 3

1.3. Симметрия в кристаллах……………………………………………….. 7

1.4.Симметрия в снежинках …………………............................................. 8 Заключение……………………………………………………………...…… 10

Литература………………………...…………………………………...………11

Введение

Аристотель

Симметрия является одной из наиболее фундаментальных и одной из наиболее общих закономерностей мироздания: живой, неживой природы и общества. Понятие симметрии проходит через всю многовековую историю человеческого творчества. Знаменитый академик В.И. Вернадский считал, что «… представление о симметрии слагалось в течение десятков, сотен, тысяч поколений. Правильность его проверена реальным опытом и наблюдением, бытом человечества в разнообразнейших природных условиях». Понятие «симметрия» выросло на изучении живых организмов и живого вещества, в первую очередь человека. Само понятие, связанное с понятием красоты или гармонии, было дано великими греческими ваятелями, и слово «симметрия» этому явлению отвечающее, приписывается скульптуру Пифагору из Регнума (Южная Италия, тогда Великая Греция), жившему в V веке до нашей эры». А другой известный академик А.В. Шубников (1887-1970) в предисловии к своей книге «Симметрия» писал: «Изучение археологических памятников показывает, что человечество на заре своей культуры уже имело представление о симметрии и осуществляло ее в рисунке и в предметах быта. Надо полагать, что применение симметрии в первобытном производстве определялось не только эстетическими мотивами, но и в известной мере и уверенностью человека в большей пригодности для практики правильных форм.

Симметрии посвящены такие строчки:

О, симметрия! Гимн тебе пою! Тебя повсюду в мире узнаю. Ты в Эйфелевой башне, в малой мошке, Ты в елочке, что у лесной дорожки. С тобою в дружбе и тюльпан, и роза, И снежный рой – творение мороза!

В этом учебном году я изучала по геометрии центральную и осевую симметрии. Мы говорили о том, что многие листья деревьев и лепестки цветов симметричны относительно среднего стебля. Я видела красоту кристаллов, выращенных моими одноклассниками из поваренной соли на уроках физики. И я задалась целью выяснить: ближе познакомиться с симметрией в царстве природы и выяснить, чем она обусловлена. Для ее реализации мною были сформулированы следующие задачи:

1.Познакомиться подробнее с иными видами симметрии.

2.Выявить причины, обуславливающие симметрию в природе.

Основная часть

1. Основные понятия о симметрии и геометрии природы

В математике рассматриваются различные виды симметрии.

В планиметрии знакомые виды симметрии: осевая симметрия (симметрия относительно прямой), центральная симметрия (симметрия относительно точки).

Две точки А и А1 называются симметричными относительно прямой а, если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему.

Фигура называется симметричной относительно прямой а, если для каждой точки фигуры симметричная ей точка относительно прямой а, также принадлежит этой фигуре.

Две точки А и А1 называются симметричными относительно точки О, если О – середина отрезка АА1.

Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре.

В стереометрии вводится еще один вид симметрии - зеркальная симметрия (симметрия относительно плоскости).

Две точки А и А1 называются симметричными относительно плоскости α, если эта плоскость проходит через середину отрезка АА1 и перпендикулярна к нему.

Фигура называется симметричной относительно плоскости α, если для каждой точки фигуры симметричная ей точка относительно плоскости, также принадлежит этой фигуре.

Есть и иные виды симметрии это:

1. Винтовая симметрия.
2. Поворотная симметрия.
3. Переносная симметрия

Природа – удивительный творец и мастер. Все живое в природе обладает свойством симметрии.

Нас окружают различные цветы, деревья. Подует ветерок, и листок с дерева упадет прямо на рукав. Форма его не является случайной, она строго закономерна. Листок как бы склеен из двух более или менее одинаковых половинок. Одна из этих половинок расположена зеркально относительно другой, совсем так, как располагаются друг относительно друга отражение какого- либо предмета в зеркале и сам предмет. Чтобы убедиться в этом, можно поставить зеркальце с прямым краем на линию, идущую вдоль черенка и разделяющую пластинку листа пополам. Заглянув в зеркальце, увидишь, что отражение правой половины листа более или менее точно заменяет его левую половину и, наоборот, левая половина листка в зеркальце как бы перемещается на место правой половины. Плоскость, разделяющая листок на две зеркально равные части (которая сейчас совпадает с плоскостью зеркала), называется «плоскостью симметрии». Ботаники и зоологи называют такую симметрию билатеральной (в переводе с латинского дважды боковой). Такой тип организации характерен для большинства беспозвоночных, в особенности для кольчатых червей и для членистоногих – ракообразных, паукообразных, насекомых, бабочек; для позвоночных – рыб, птиц, млекопитающих. Впервые двусторонняя симметрия появляется у плоских червей, у которых передний и задний концы тела различаются между собой. Если сверху посмотреть на любое насекомое и мысленно провести посередине прямую (плоскость), то левые и правые половинки насекомых будут одинаковыми и по расположению, и по размерам, и по окраске. Ведь мы ни разу не видели, чтобы у жука или стрекозы, у любого другого насекомого лапы слева были бы ближе к голове, чем справа, а правое крыло божьей коровки было бы больше, чем левое. Такого в природе не бывает, иначе бы насекомые не смогли бы летать. Если посмотреть на красавицу бабочку с яркой расцветкой, она тоже состоит из двух одинаковых половинок. Даже пятнистый узор на ее крыльях подчиняется такой геометрии

И выглянувший из травы жучок, и промелькнувшая мошка, и сорванная ветка, - все подчиняется «билатеральной симметрии». Итак, повсюду в лесу мы наталкиваемся на билатеральную симметрию. Может быть, любое существо обладает плоскостью симметрии и, следовательно, подходит тем самым под билатеральную симметрию.

На первый взгляд может показаться, что подходит, но не все так просто, как кажется. Возле куста скромно выглядывает из травы обыкновенный поповник (ромашка).

Имеет ли такое «цветочное солнышко» плоскость симметрии? Конечно! Без всякого труда можно его разрезать на две зеркально равные половинки по линии, проходящей через центр цветка и продолжающейся воль середины любого из лепестков или между ними. Это, однако, не все. Ведь лепестков-то много, и вдоль каждого лепестка можно обнаружить плоскость симметрии. Значит, этот цветок обладает многими плоскостями симметрии, и все они пересекаются в его центре. Сходным образом, можно охватить и геометрию подсолнечника, василька, колокольчика.

Кроме зеркальной в природе можно наблюдать и так называемую винтовую симметрию.

Если рассмотреть веточку с листьями, то можно заметить, что основания черешков располагаются по винтовой линии, каждый следующий лист прикреплен выше и в сторону от предыдущего. Если соединить последовательно основания листьев ниткой, то она обовьется вокруг стебля по правильной винтовой линии. Проследив за расположением листьев по этой спирали, можно заметить, что листья расположены одни над другими. Часть спирали, заключенная между двумя такими листьями, называется в ботанике “циклом”. Листорасположение обозначают в виде дроби, в числителе которой число оборотов одного цикла спирали, а в знаменателе – число листьев в одном цикле. Наиболее распространенные типы листорасположений: 1/3, 2/5, 3/8,5/13 и т.д. Ботаники давно заметили, что этот ряд отличается одной любопытной и довольно неожиданной особенностью: каждая из этих дробей, начиная с третьей, получается из предыдущих путем сложения их числителей и знаменателей. Числители и знаменатели дают ряд Фибоначчи: 1, 2, 3, 5, 8… и 2, 3, 5, 8, 13… Например, у бука - 1/3, или 120°, у дуба и абрикоса — 2/5, у груши и тополя — 3/8, у ивы и миндаля — 5/13 и т.д. Такое расположение позволяет листьям наиболее эффективно получать влагу и солнечный свет.

Искусству конструирования можно научиться у природы. Простейшие морские организмы – радиолярии (в пер. с лат. Это название означает «золотой диск»). В них все приспособлено к морской среде обитания: отростки – для координации движения, колючки - для защиты от морских хищников, форма – для сохранения устойчивости в воде. Эти организмы живут как на поверхности моря, так и на разных его глубинах. Радиолярии незаметны невооруженным глазом. Но если посмотреть в микроскоп, то откроется фантастическая природная геометрия симметрий разного порядка.

1.3.Симметрия в кристаллах.

Однако симметрия существует и там, где ее не видно на первый взгляд. Физик скажет, что всякое твердое тело – кристалл. Знаменитый кристаллограф Евграф Степанович Федоров сказал: “Кристаллы блещут симметрией”. Химик скажет, что все тела состоят из молекул, а молекулы состоят из атомов. А многие атомы располагаются в пространстве по принципу симметрии.

Кристаллы одни из самых красивых и загадочных творений природы, нахождение в природе крупных однородных кристаллов - явление нечастое. Однако мелкокристаллические вещества встречаются весьма часто. Так, например, почти все горные породы: гранит, песчаники известняк кристалличны. В настоящее время кристаллы имеют большое распространение в науке и технике. Кристаллами обычно называют твердые тела, образующиеся в природных или лабораторных условиях и имеющие вид многогранников, которые напоминают строгие геометрические построения. Поверхность таких фигур ограничена более или менее совершенными плоскостями- гранями, пересекающимися по прямым линиям- ребрам. Точки пересечения ребер образуют вершины. Кристаллы обычно твердые тела.

Кристаллов в природе существует великое множество и так же много существует различных форм кристаллов. Было установлено, что все кристаллы построены из элементарных частиц, расположенных в строгом порядке внутри кристаллического тела. Рассматривая различные кристаллы, можно у видеть, что все они разные по форме, но любой из них представляет симметричное тело. Симметричность - одно из основных свойств кристаллов. Всего существует 32 вида симметрии идеальных форм кристалла.

Нельзя не увидеть симметрию в огранённых драгоценных камнях. Многие гранильщики стараются придать бриллиантам форму тетраэдра, куба, октаэдра или икосаэдра.

1.4. Симметрия в снежинках.

В течении долгих лет геометрия кристаллов казалась таинственной неразрешимой загадкой. В 1619 великий немецкий математик и астроном Йоган Кеплер обратил внимание на симметрию снежинок. Он попытался объяснить ее тем, что кристаллы построены из мельчайших одинаковых шариков, теснейшим образом присоединенных друг к другу (вокруг центрального шарика можно в плотную разложить только шесть таких же шариков). По пути, намеченному Кеплером пошли в последствии Роберт Гук и М. В. Ломоносов. Они так же считали, что элементарные частицы кристаллов можно уподобить плотно упакованным шарикам. В наше время принцип плотнейших шаровых упаковок лежит в основе структурной кристаллографии. Через 50 лет после Кеплера датский геолог, кристаллограф и анатом Николас Стенон впервые сформулировал основные понятия о формировании кристаллов: "Рост кристалла происходит не изнутри, как у растений, но путем наложения на внешние плоскости кристалла мельчайших частиц, приносящихся извне некоторой жидкостью". Эта идея о росте кристаллов в результате отложения на гранях все новых и новых слоев вещества сохранила свое значение.

Фотографии и рисунки снежинок можно найти во многих учебниках физики в главах, в которых рассказывают о симметрии.

Большая часть дождевых капель начинает свою жизнь как снежные кристаллы, тающие, прежде чем они упадут на землю. Однако только холодные, находящиеся на большой высоте перистые облака состоят из кристалликов льда. В основном же облака представляют собой скопление маленьких водяных капелек, удерживающихся в воздухе так же, как частички дыма.

Хотя снежные кристаллы многообразны, их можно классифицировать по трем основным формам; шестиугольные призматические столбики, тонкие шестиугольные пластины и разветвлённые звёзд. . Изучение кристаллов льда с помощью рентгеновских лучей показало, что молекулы воды в кристалле льда расположены так, что каждая из молекул окружена шестью соседями. Центры этих молекул образуют правильный шестиугольник. Что же касается причин различия форм кристаллов, то до недавнего времени ученые не могли прийти к единому мнению. По некоторым гипотезам форма кристалликов должна в основном определяться степенью перенасыщения окружающего воздуха парами воды, а не температурой облака. Но исследования показали, что кристаллы различной формы вырастают при различных температурах.

Особенно интересны узоры, которыми покрываются зимой окна квартир, автобусов. При резком похолодании температура окон становится ниже температуры воздуха в помещении. На них и оседают молекулы пара, находящиеся во влажном воздухе в комнате, образуя красивые узоры. При этом тоже очень важно, чтобы воздух в комнате был не очень влажным. В противном случае пар сначала сконденсируется на стекле и затем замерзает, образуя слой льда. Узоры не появляются на окне, если открыта форточка. В этом случае температура воздуха в комнате у стекла понижается, став такой же, как и температура самого стекла. В ледяных узорах, можно увидеть большинство форм, которые могут принимать снежные кристаллы.

Трудно найти человека, который не имел бы какого-либо представления о симметрии, объясняющей наличие определенного порядка, закономерности в расположении частей окружающего мира. С симметрией мы встречаемся везде – в природе, технике, искусстве, науке. Понятие симметрии проходит через всю многовековую историю человеческого творчества. Принципы симметрии играют важную роль в физике и математике, химии и биологии, технике и архитектуре, живописи и скульптуре, поэзии и музыке. Законы природы, управляющие неисчерпаемой в своём многообразии картиной явлений, в свою очередь, подчиняются принципам симметрии.

Существует множество видов симметрии в природе, но при всем многообразии живых организмов, принцип симметрии действует всегда, и этот факт еще раз подчеркивает гармоничность нашего мира. В своём реферате я внимание уделила симметрии живой и неживой природы, но это только малая часть, доступная для моего понимания. В дальнейшем я хотел бы изучить мир симметрии более глубоко. ЛИТЕРАТУРА

1. Атанасян Л.С. Геометрия 7-9. М.:Просвещение, 2012г..
2. Атанасян Л.С. Геометрия 10-11. М.:Просвещение, 2010г.
3. Азевич А.И. Двадцать уроков гармонии М.: Школа-Пресс,1998г.
4. Стюарт И. Какой формы снежинка. Магические цифры в природе. М.: Мир книги 2007г.

5. http://www.wikiznanie.ru/ru-wz/index.php/

6. Фото из сети Интернет

nenuda.ru

Реферативно-исследовательская работа "Симметрия вокруг нас"

Реферативно-исследовательская работа

«

Симметрия вокруг нас»

Учащегося 8а класса

 МОУСОШ№1 им. Пушкина

Пудовкина Александра

2011/2012 уч. год

ПЛАН:

ВВЕДЕНИЕ

Симметрия в математике.

Симметрия в природе.

Симметрия в литературе.

Симметрия в искусстве и архитектуре.

Симметрия в технике.

ЗАКЛЮЧЕНИЕ

ЛИТЕРАТУРА

ВВЕДЕНИЕ

«...быть прекрасным значит быть симметричным и соразмерным».

Платон

Симме́трия (от греч. symmetria — соразмерность) 

Симметрия является уникальным свойством природы, представление о котором слагалось в течение десятков, сотен, тысяч поколений. Изучение археологических памятников показывает, что человечество на заре своей культуры уже имело представление о симметрии и осуществляло ее в рисунке и в предметах быта.Применение симметрии в первобытном производстве определялось не только эстетическими мотивами, но и уверенностью человека в большей пригодности для практики правильных форм.

Первоначальное понятие о геометрической симметрии как о гармонии пропорций, как о «соразмерности», что и означает в переводе с греческого слово «симметрия», с течением времени приобрело универсальный характер, и было осознано как всеобщая идея инвариантности (т. е. неизменности) относительно некоторых преобразований. Таким образом, геометрический объект или физическое явление считаются симметричными, если с ними можно сделать что-то такое, после чего они останутся неизменными.

Например, пятиконечная звезда, будучи повернута на 72° (360°:5), займет первоначальное положение, а  будильник одинаково звенит в любом углу комнаты. Первый пример дает понятие об одном из видов геометрической симметрии — поворотной, а второй иллюстрирует важную физическую симметрию — однородность и изотропность (равнозначность всех направлений) пространства. Благодаря, этому виду  симметрии все физические приборы (в том числе и будильник) одинаково работают в разных точках пространства, если, конечно, не изменяются окружающие физические условия. Легко вообразить, какая бы царила на Земле неразбериха, если бы эта симметрия была нарушена!

Таким образом, не только симметричные формы окружают нас повсюду, но и сами многообразные физические и биологические законы гравитации, электричества и магнетизма, ядерных взаимодействий, наследственности пронизаны общим для всех них принципом симметрии. Действительно, еще Платон мыслил атомы четырех стихий — земли, воды, огня и воздуха — геометрически симметричными в виде правильных многогранников. И хотя сегодня «атомная физика» Платона кажется наивной, принцип симметрии и через два тысячелетия остается основополагающим принципом современной физики атома. За это время наука прошла путь от осознания симметрии геометрических тел к пониманию симметрии физических явлений.

В современном понимании симметрия — это общенаучная философская категория, характеризующая структуру организации систем. Важнейшим свойством симметрии является сохранение (инвариантность) тех или иных признаков (геометрических, физических, биологических и т. д.) по отношению к вполне определенным преобразованиям.

Симметрия в математике.

В «Современный словарь иностранных слов»  под симметрией понимается «соразмерность, полное соответствие в расположении частей целого относительно средней линии, центра.  Расположение точек относительно точки (центра симметрии),  прямой (оси симметрии) или плоскости (плоскости симметрии), при котором каждые две соответствующие точки, лежащие на одной прямой, проходящей через центр симметрии, на одном перпендикуляре к оси или плоскости симметрии, находятся от них на одинаковом расстоянии.

Симметрия простых геометрических форм: равнобедренный треугольник с одной осью симметрии; прямоугольник с двумя осями симметрии; квадрат, имеющий четыре оси симметрии. В кубе можно провести девять осей симметрии 

"Тела Платона": 1 — тетраэдр, 2 — куб, 3 — октаэдр, 4 — додекаэдр, 5 — икосаэдр 

В математике слово «симметрия» имеет не меньше семи значений (среди них симметричные полиномы, симметрические матрицы). В логике существуют симметричные отношения.

Плоская фигура, симметричная относительно прямой АВ; точка М преобразуется в М’ при отражении (зеркальном) относительно АВ.

Звездчатый правильный многоугольник, обладающий симметрией восьмого порядка относительно своего центра.

Куб, имеющий прямую AB осью симметрии третьего порядка, прямую CD — осью симметрии четвёртого порядка, точку О — центром симметрии. Точки М и M' куба симметричны как относительно осей AB и CD, так и относительно центра О.

В математике слово «симметрия» имеет не меньше семи значений (среди них симметричные полиномы, симметрические матрицы). В логике существуют симметричные отношения.

Симметрия в природе

В отличие от искусства или техники, красота в природе не создаётся, а лишь фиксируется, выражается. Среди бесконечного разнообразия форм живой и неживой природы в изобилии встречаются такие совершенные образы, чей вид неизменно привлекает наше внимание. К числу таких образов относятся некоторые кристаллы, многие растения. 

 Примеры трансляции подобия в природных формах. Лист подчиняется принципу зеркальной симметрии с одновременным уменьшением элементов (направленностью симметрии), цветок отличается соединением радиальной и спиральной (в трех измерениях) симметрии.    Подобным же образом строятся динамично-симметричные формы раковин, листьев папоротника.

Интересно интерпретируется понятие симметрии в биологии. Там описывается шесть различных видов симметрии. Мы узнаем, например, что гребневики дисимметричны, а цветки львиного зева отличаются билатеральной симметрией.

Аксиальная симметрия: а — лист плюща; б — медуза Aurelia insulinda; в — цветок флокса. При повороте этих фигур вокруг оси симметрии равные части каждого из них совпадут друг с другом соответственно 1, 4, 5 раз (оси 1, 4, 5-го порядка). Лист плюща асимметричен.

Биообъекты с совершенной точечной симметрией. Радиолярии: модель аденовируса в форме икосаэдра.

Биообъекты с совершенной точечной симметрией. Радиолярии: частица аденовируса в форме икосаэдра.

Актиноморфная симметрия; а — бабочка; б — лист кислицы;

 Бабочке свойственна двусторонняя, или билатеральная, симметрия.

В книгах по химии часто можно встретить обозначения L- и D- кислота, производные от латинских слов laevus — левый и dexter — правый.

Теперь нам уже нетрудно сообразить, что вещество, носящее название «декстро-энерген», должно быть оптически активным и притом правовращающим.

в

Диссимметрические D- и L-биообъекты: а — цветки анютиных глазок; б — раковины прудовика;; г — листья бегонии.

Биообъекты с совершенной точечной симметрией. Радиолярии: а — шарообразная Ethmosphaera polysyphonia, содержащая бесконечное число осей бесконечного порядка + бесконечное число плоскостей симметрии + центр симметрии; б — кубические Hexastylus marginatus и Lithocubus geometricus, характеризующиеся симметрией куба; в — додекаэдрическая Circorhegma dodecahedra, характеризующаяся симметрией правильных многогранников — додекаэдра и икосаэдра.

Симметрия проявляется в многообразных структурах и явлениях неорганического мира и живой природы. В мир неживой природы очарование симметрии вносят кристаллы.

 Каждая снежинка- это маленький кристалл замерзшей воды. Форма снежинок может быть очень разнообразной, но все они обладают симметрией - поворотной симметрией 6-го порядка и, кроме того, зеркальной симметрией.

Радиальная симметрия снежинок

Схема образования тел шестилучевой симметрии

Кристалл–твердое тело, имеющее естественную форму многогранника. Характерная особенность того или иного вещества состоит в постоянстве углов между соответственными гранями и ребрами для всех образов кристаллов одного и того же вещества.

Что же касается формы граней, числа граней и ребер и величины кристалла, то для одного и того же вещества они могут значительно отличаться друг от друга.

Для каждого данного вещества существует своя, присущая только ему идеальная форма его кристалла. Эта форма обладает свойством симметрии, т.е. свойством кристаллов совмещаться с собой в различных положениях путём поворотов, отражений, параллельных переносов. Среди элементов симметрии различаются оси симметрии, плоскости симметрии, центр симметрии, зеркальные оси.

Внутреннее устройство кристалла представляется в виде пространственной решётки, в одинаковых ячейках которой, имеющих форму параллелепипедов, размещены по законам симметрии одинаковые мельчайшие частицы - молекулы, атомы, ионы и их группы. Многие, если не все, кристаллы более или менее легко раскалываются по некоторым строго определённым плоскостям. Это явление называется спайностью и свидетельствует о том, что механические свойства кристаллов анизотропны, т. е. не одинаковы по разным направлениям.

Симметрия внешней формы кристалла является следствием его внутренней симметрии - упорядоченного взаимного расположения в пространстве атомов (молекул).

У водо-растворимых кристаллов органических соединений зеркальная симметрия молекул прослеживается как в твердом, так и в растворенном состоянии. Известный пример — винная кислота. Она встречается в виде левых и правых кристаллов. Соответственно ведет себя и ее раствор. Под правым направлением здесь всегда понимается направление по часовой стрелке. Таким образом, левая винная кислота вращает плоскость поляризации против часовой стрелки. Нидерландский физико-химик Якоб Хендрик Вант-Гофф (1852—1911) объяснил такое поведение винной кислоты, исходя из строения ее молекулы.При одном и том же химическом составе можно написать три разные структурные формулы винной кислоты. Каждый из двух центральных атомов углерода в любом случае связан с группой СООН. В органической химии эта группа — отличительный признак кислоты. Проглотив таблетку аспирина или попробовав на язык уксус, вы ощущаете кисловатый вкус, он обусловлен именно присутствием группы СООН. Для нас, однако, важнее правая и левая связи атомов углерода. Они связывают либо атом водорода, либо группу ОН. Именно здесь кроется возможность возникновения двух зеркально-симметричных вариантов их взаимного расположения и, помимо того, третьего варианта, который симметричен сам по себе.

Молекула винной кислоты

В пространстве существуют тела, обладающие винтовой симметрией, т.е. совмещаемые со своим первоначальным положением после поворота на какой-либо угол вокруг оси, дополненного сдвигом вдоль той же оси. Если данный угол поделить на 360 градусов– рациональное число, то поворотная ось оказывается также осью переноса. 

Фигура, обладающая винтовой симметрией, которая осуществляется переносом вдоль вертикальной оси, дополненным вращением вокруг неё на 90°.

Симметрия в литературе и языках.

Существуют языки, в которых начертание знаков опирается на наличие симметрии. Так, в китайской письменности иероглиф означает именно истинную середину.

Многие буквы русского языка обладают осевой и центральной симметрией. Если мы поместим буквы перед зеркалом, расположив его параллельно строке, то заметим, что те из них, у которых ось симметрии проходит горизонтально, можно прочесть и в зеркале. А вот те, у которых ось расположена вертикально или отсутствует вовсе, становятся «нечитабельными».

В то время как симметричные фигуры полностью соответствуют своему отражению, несимметричные отличны от него: из спирали, закручивающейся справа налево, в зеркале получится спираль, закручивающаяся слева направо. 

Латинское N выглядит у них, как И, а S и Z получаются наоборот. Если мы внимательно посмотрим на буквы латинского алфавита (а это ведь тоже, в сущности, плоские фигуры!), то увидим среди них симметричные и несимметричные. У таких букв, как N,S , Z, нет ни одной оси симметрии (равно как и у F, G, J, L, Р, О и R). Но N,S и Z особенно легко пишутся «наоборот», так-так имеют центр симметрии. У остальных прописных букв есть как минимум по одной оси симметрии. Буквы А, М, Т, U, V, W и Y можно разделить пополам продольной осью симметрии. Буквы В, С, D, Е, I, К — поперечной осью симметрии. У букв Н, О и Х имеется по две взаимно перпендикулярные оси симметрии. (тот же эксперимент можно провести с любым алфавитом европейской группы).

Симметрия в искусстве и архитектуре.

СИММЕ́ТРИЯ (греч. symmetria — "соразмерность", от syn — "вместе" и metreo — "измеряю") — основополагающий принцип самоорганизации материальных форм в природе и формообразования в искусстве. Закономерное расположение частей формы относительно центра или главной оси. Уравновешенность, правильность, согласованность частей, объединенных в целое.

В архитектуре оси симметрии используются как средства выражения архитектурного замысла.

Симметрия "Мирового дерева" в изобразительном искусстве. Изображение дерева в искусстве древней Месопотамии (по В. Хенце). 

 Симметрия "Мирового дерева" в изобразительном искусстве. "Любовное дерево". Польская народная вышивка. XIX в. 

 Ажурные звезды, полученные способом декупюра (вырезанием из сложенного вчетверо листа бумаги) 

 Схемы рисунков сцепного кружева

Орнамент; осью переноса является любая прямая, соединяющая центры двух каких-либо завитков.

Бордюр, накладывающийся на себя или переносом на некоторый отрезок вдоль горизонтальной оси, или отражением (зеркальным) относительно той же оси и переносом вдоль неё на отрезок, вдвое меньший.

Фигуры, обладающие симметрией переноса: верхняя фигура имеет также бесконечное множество вертикальных осей симметрии (второго порядка), т. е. плоскостей отражения.

Принцип симметрии сказывается в образах многих мифологических существ, прежде всего миксантропических (составных). Таковы амфисбена (двусторонняя ящерица) или фантастическое существо китайской мифологии: Дзяо-дзе ("обжора"), которое изображали на обеденных блюдах в качестве предостережения от переедания. Дзяо-дзе имеет одну голову и два тела, расходящиеся влево и вправо. Передняя пара ног служит обоим туловищам. За оскаленную пасть это существо называют также "маской людоеда".

В искусстве западноевропейского Барокко архитекторы, скульпторы, живописцы использовали композиционные схемы, основанные на поворотной симметрии. Таковы композиции П. П. Рубенса "Охота на львов", "Союз земли и воды".

Мы обнаружим, что симметрия существует в музыке и хореографии (в танце).Она зависит здесь от чередования тактов. Оказывается, многие народные песни и танцы построены симметрично.

Симметрия в технике

Принцип зеркальной симметрии широко применяется в технике. Легко установить, что каждая симметричная плоская фигура может быть с помощью зеркала совмещена сама с собой. Достойно удивления, что такие сложные фигуры, как пятиконечная звезда или равносторонний пятиугольник, тоже симметричны. Как это вытекает из числа осей, они отличаются именно высокой симметрией.

В трехмерном мире пространственных тел, где мы с вами живем, существуют плоскости симметрии. «Зеркало» всегда имеет на одно измерение меньше, чем мир, который оно отражает.

Угловое зеркало с прямым углом между составляющими его зеркалами отличается еще некоторыми интересными свойствами. Если смастерить его из двух маленьких зеркал, то можно убедиться в том, что в таком зеркале с прямоугольным раствором (а сейчас речь только о нем) отраженный луч света всегда параллелен падающему лучу. Это очень важное свойство. Но не единственное! При повороте углового зеркала вокруг оси, соединяющей зеркала (в определенных пределах), отраженный луч не изменит своего направления.

Свойство отраженного луча сохранять направление при повороте углового зеркала вокруг оси находит широкое применение в технике. Так, в трехгранном зеркальном уголковом отражателе луч сохраняет постоянное направление, несмотря на весьма сильные качания зеркала. По форме такое зеркало представляет собой кубик с отрезанным уголком. И в этом случае на практике используют не три зеркала, а соответствующую стеклянную призму с зеркальными гранями.

Важной областью применения трехгранного зеркала служит уголковый отражатель (кошачий глаз, катофот) на велосипедах, мотоциклах, сигнальных предохранительных щитах, ограничителях проезжей части улицы. С какой бы стороны ни упал свет на такой отражатель, световой рефлекс всегда сохраняет направление источника света.

Большую роль трехгранные зеркальные уголковые отражатели играют в радиолокационной технике. Самолеты и крупные стальные корабли отражают луч радара. Несмотря на значительное рассеяние его, той небольшой доли отраженных радиоволн, которая возвращается к радару, обычно достаточно для распознания объекта.

Хуже обстоит дело с маленькими суденышками, сигнальными поплавками и пластиковыми парусными яхтами. У небольших предметов отражение слишком слабое. Пластиковые яхты так же «прозрачны» для радиоволн, на которых работает радарная техника, как оконные стекла для солнечного света. Поэтому парусные яхты и сигнальные буйки оснащают металлическими уголковыми отражателями. Длина граней у такого «зеркала» всего около 30 см, но этого довольно, чтобы возвращать достаточно мощное эхо.

Прямоугольные призмы, как бы «складывающие» ход луча «гармошкой», сохраняя его необходимую длину, заданную фокусным расстоянием линзы, позволяют уменьшать габариты оптических приборов. В призматических биноклях лучи света при помощи таких приборов обращаются на 180°.

В технике оси симметрии наиболее четко обозначаются там, где требуется оценить отклонение от нулевого положения, например на руле грузовика или на штурвале корабля.

ЗАКЛЮЧЕНИЕ

«Принцип симметрии охватывает все новые области. Из области кристаллографии, физики твердого тела он вошел в область химии, в область молекулярных процессов и в физику атома. Нет сомнения, что его проявления мы найдем в еще более далеком от окружающих нас комплексов мире электрона, и ему подчинены будут явления квантов», – это слова академика В. И. Вернадского, занимавшегося изучением  принципов симметрии в неживой природе.

Симметрия, проявляясь в самых различных объектах материального мира, несомненно, отражает наиболее общие, наиболее фундаментальные его свойства.Поэтому исследование симметрии разнообразных природных объектов и сопоставление его результатов является удобным и надежным инструментом познания основных закономерностей существования материи.

 Можно увидеть, что это кажущаяся простота уведет нас далеко в мир науки и техники и позволит время от времени подвергать испытанию способности нашего мозга (так как именно он запрограммирован на симметрию).

ЛИТЕРАТУРА

1. Современный словарь иностранных слов. М.: Русский язык,

1993г.Советский энциклопедический словарь М.: Советская энциклопедия, 1980г.

2. Урманцев Ю.А. Симметрия природы и природа симметрии М.: Мысль,

1974г.

3. Пидоу Дэн Геометрия и искусство М.: Мир, 1979г.

4. Шафрановский И.И. Симметрия в геологии Л.: Недра, 1975г.

5. Трофимов В. Введение в геометрическом многообразии с симметриями

М.: МГУ 1989г.

nsportal.ru

Смотрите также

• 
  Внешние носители информации реферат
• 
  Теория массового обслуживания реферат
• 
  Экономическая мысль средневековья реферат
• 
  Реферат по биологии паразитизм
• 
  Паразитизм реферат по биологии
• 
  Гиппократ основоположник медицины реферат
• 
  Экспертиза промышленной безопасности реферат
• 
  Реферат педагогика в медицине
• 
  Реферат биологическая обратная связь
• 
  Биологическая обратная связь реферат
• 
  Наполеон и россия реферат