|
|
|
|
 Far Far |
 WinNavigator WinNavigator |
 Frigate Frigate |
 Norton
Commander Norton
Commander |
 WinNC WinNC |
 Dos
Navigator Dos
Navigator |
 Servant
Salamander Servant
Salamander |
 Turbo
Browser Turbo
Browser |
|
|
 Winamp,
Skins, Plugins Winamp,
Skins, Plugins |
 Необходимые
Утилиты Необходимые
Утилиты |
 Текстовые
редакторы Текстовые
редакторы |
 Юмор Юмор |
|
|
|
File managers and best utilites |
Вентили, триггеры и сумматоры. Реферат триггеры и сумматоры
Сумматоры
Количество просмотров публикации Сумматоры - 34
Схема, осуществляющая суммирование по этим правилам, принято называть полусумматором (рис. 8.31, а). Логику ее работы иллюстрирует табл. 8.2.
Сумма Sj = 1 получается при условии, что одно из слагаемых равно единице. Сигнал переноса в следующий разряд Pi+l появляется при условии, что оба слагаемых равны единице. Условное обозначение полусумматора показано на рис. 8.31, б.
Триггеры
Триггеры наряду с логическими элементами являются основными элементами цифровых ИМС. Каждый триггер предназначен для хранения одной единицы информации — бита. Основу триггера составляет кольцо из двух инверторов (рис. 8.33, а), ĸᴏᴛᴏᴩᴏᴇ принято обозначать в виде электронной защелки (рис. 8.33, б).
Читайте также
Сумматором называется электронное устройство, выполняющее арифметическое суммирование кодов чисел. Обычно сумматоры представляют собой комбинацию одноразрядных суммирующих схем. При сложении двух чисел, независимо от системы счисления, в каждом разряде производится... [читать подробнее].
Шифраторы и дешифраторы Шифратор преобразует сигнал, поданный только в один входной провод, в выходной параллельный двоичный код, который появится на выходах шифратора. Чтобы шифратор откликался на входной сигнал только одного провода, его схему делают... [читать подробнее].
Сумматоры – схема складывает четырехразрядное двоичное число Аi c четырехразрядным двоичным числом Вi и на выходе формирует двоичную сумму Si. Для расширения сумматора в схеме предусмотрен вход переполнения Пвх и выход переполнения Пвых. На схемах электрически –... [читать подробнее].
Сумматором называют устройство, осуществляющее арифметическое сложение двоичных чисел. Сумматор является одним из основных элементов ЭВМ, выполняющим арифметические операции. Сложение многоразрядных двоичных чисел производится однотипными действиями,... [читать подробнее].
Сумматором называют устройство, осуществляющее арифметическое сложение двоичных чисел. Сумматор является одним из основных элементов ЭВМ, выполняющим арифметические операции. Сложение многоразрядных двоичных чисел производится однотипными действиями,... [читать подробнее].
Ограничители расхода Ограничителем расхода называется клапан, предназначенный для ограничения расхода в гидросистеме или на каком-либо ее участке. Рис.6.8. Ограничитель расхода: а - принципиальная схема; б - зависимость Q=f(&... [читать подробнее].
Различают однонаправленные демультиплексоры, в которых цифровая информация передается в одном направлении. А также двунаправленные демультиплексоры, где цифровая и аналоговая информация передается в обе стороны. Обозначение демультиплексора DMX (1 – n), где n –... [читать подробнее].
Они строятся из одноразрядных сумматоров. Число одноразрядных сумматоров равно разрядности слагаемых. При этом одноразрядные сумматоры связаны между собой только цепями переносов. Схема четырехразрядного сумматора показана на рис. 2.27. Рис. 2.27. Четырехразрядный... [читать подробнее].
При обработке больших массивов десятичных чисел значительная часть времени расходуется на перевод чисел из одной системы счисления в другую. В этом случае целесообразно выполнять обработку данных непосредственно в десятичной системе счисления. При этом для... [читать подробнее].
Поскольку дешифратор со стробированием может быть использовани и как демультиплексор, его называют дешифратор-демультиплексор. Поэтому в качестве демультиплексора применяют дешифратор, на вход стробирования которого подаётся информационный входной... [читать подробнее].
referatwork.ru
НОУ ИНТУИТ | Лекция | Счетные схемы ЭВМ. Счетчики и сумматоры
Аннотация: Рассматривается принцип действия счётных схем как основы построения арифметических устройств.
Счетными схемами, лежащими в основе построения арифметических устройств ЭВМ, являются счетчики и сумматоры. Любые, даже самые сложные, вычислительные схемы представляют собой комбинацию счетчиков различных разновидностей и сумматоров, реализующих вычисления, как правило, в дополнительном коде (подробно кодирование информации в двоичном коде и соответствующая арифметика представлены в "Заключение" ).
Двоичные счетчики
Счетчиком называют функциональный узел, предназначенный для счета сигналов [1, c. 252].
По мере поступления входных сигналов счетчик последовательно перебирает свои состояния в определенном для данной схемы порядке. В частности, двоичные счетчики, рассматриваемые в настоящем пособии, перебирают последовательность двоичных кодов. В том случае, если последовательность выдается с возрастанием кода, счетчик называется суммирующим, если код уменьшается с приходом каждого счетного сигнала, то счетчик называется вычитающим. Если в счетчике предусмотрено переключение из суммирующего режима в вычитающий и обратно, он называется реверсивным. Количество схем счетчиков огромно [1, 2, 3]. Их изучение является отдельной, обширной темой, и задачей данного курса не является.
Простейший синхронный суммирующий счетчик можно построить на счетных, или Т -триггерах (от англ . toggle - кувыркаться). Счетным Т -триггером называют так называемый JK -триггер, который работает в счетном режиме, когда на J- и K -входы постоянно подана логическая 1. JK -триггер представляет собой соединение двух однотактных D -триггеров-защелок (рис. 9.1.а), на С -входы которых поступают противоположные уровни сигналов.
При подаче 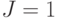 и
и 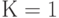 на выходе нижнего элемента И будет постоянный логический 0, поскольку
на выходе нижнего элемента И будет постоянный логический 0, поскольку 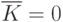 . А состояние верхнего элемента И будет определяться состоянием выхода
. А состояние верхнего элемента И будет определяться состоянием выхода  всей схемы. Если в предыдущий момент времени
всей схемы. Если в предыдущий момент времени  , а
, а 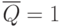 то на выходе элемента И-ИЛИ будет логическая
то на выходе элемента И-ИЛИ будет логическая 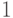 . При
. При  она записывается в первый D -триггер, а при отрицательном фронте на
она записывается в первый D -триггер, а при отрицательном фронте на  - во второй D -триггер и выдается на выход
- во второй D -триггер и выдается на выход  всей схемы: формируется передний фронт импульса
всей схемы: формируется передний фронт импульса 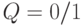 . При
. При  на инверсном выходе схемы
на инверсном выходе схемы 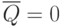 . Этот сигнал переведет при
. Этот сигнал переведет при  первый D -триггер в нулевое состояние, а при
первый D -триггер в нулевое состояние, а при  - второй D -триггер и выход
- второй D -триггер и выход  всей схемы переводится в нулевое состояние схемы (формируется задний фронт импульса
всей схемы переводится в нулевое состояние схемы (формируется задний фронт импульса  ) так, как показано на рис. 9.1,б.
) так, как показано на рис. 9.1,б.
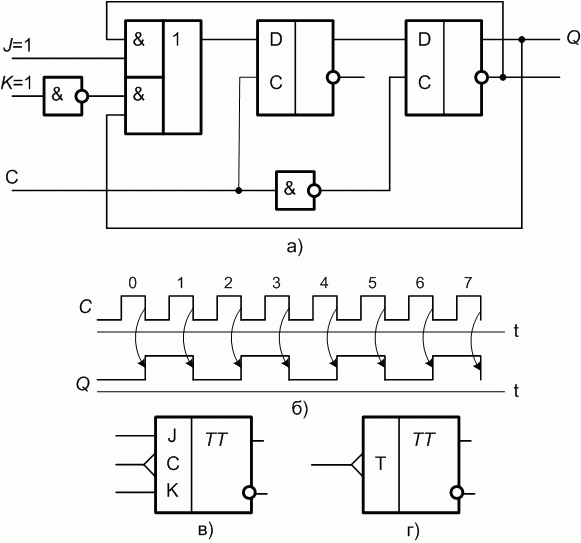 Рис. 9.1. JK-триггер: а - функциональная схема; б - временная диаграмма работы; в - УГО JK-триггера; г - УГО счетного Т-триггера
Рис. 9.1. JK-триггер: а - функциональная схема; б - временная диаграмма работы; в - УГО JK-триггера; г - УГО счетного Т-триггераТаким образом, в счетном режиме частота входных сигналов уменьшается в два раза. Факт переключения триггера в противоположное состояние при прохождении заднего фронта сигнала  отображается на УГО динамическим входом в виде треугольника (рис. 9.1,в и г). Все ранее рассмотренные управляющие сигналы были статическими.
отображается на УГО динамическим входом в виде треугольника (рис. 9.1,в и г). Все ранее рассмотренные управляющие сигналы были статическими.
При последовательном соединении нескольких счетных Т-триггеров получаем схему простейшего синхронного счетчика (рис. 9.2,а). При этом выход самого последнего триггера будет являться самым старшим разрядом двоичного кода на выходе счетчика, выход самого первого триггера - младшим разрядом в соответствии с временной диаграммой, представленной на рис. 66,б. Данной схеме соответствует УГО на рис. 9.2.б. Как правило, у счетчиков предусматриваются вход  для принудительного сброса в нулевое состояние (когда все триггеры схемы сброшены в
для принудительного сброса в нулевое состояние (когда все триггеры схемы сброшены в  ) и выход переноса
) и выход переноса 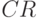 , устанавливаемый в 1 в том случае, когда прошла вся последовательность импульсов (рис. 9.2,в). Для схемы 3-разрядного счетчика, представленной на рис. 9.2, это коды от 000_{2} до 111_{2}.
, устанавливаемый в 1 в том случае, когда прошла вся последовательность импульсов (рис. 9.2,в). Для схемы 3-разрядного счетчика, представленной на рис. 9.2, это коды от 000_{2} до 111_{2}.
 увеличить изображениеРис. 9.2. Суммирующий двоичный счетчик: а - функциональная схема; б - временная диаграмма работы; в - УГО
увеличить изображениеРис. 9.2. Суммирующий двоичный счетчик: а - функциональная схема; б - временная диаграмма работы; в - УГОВыход переноса может быть использован для последовательного соединения нескольких счетчиков с целью повышения разрядности подсчитываемого числа. Такие схемы называются схемами с последовательным переносом. Существуют также и более сложные схемы с параллельным переносом [1, c. 257-262].
Сумматоры
Сумматором называют функциональный узел, выполняющий сложение одно- или многоразрядных двоичных чисел в соответствии с правилами двоичного сложения.
Подробно вопросы двоичной арифметики освещены в "Заключение" . Правила двоичного сложения можно представить в виде таблицы истинности будущей логической схемы (табл. 9.1) двоичного сумматора и построить эту схему по принципам, изложенным в лекции 3.
Для текущего разряда суммы  логическое выражение имеет вид:
логическое выражение имеет вид:

причем согласно карте Карно, представленной на рис. 9.3,а, данное выражение не минимизируется. Для выходного переноса 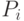 минимизация возможна, поэтому логическое выражение согласно рис. 9.3,б, получается следующим:
минимизация возможна, поэтому логическое выражение согласно рис. 9.3,б, получается следующим:

 Рис. 9.3. Карты Карно для одноразрядного сумматора: а - для текущего разряда суммы; б - для текущего разряда выходного переноса
Рис. 9.3. Карты Карно для одноразрядного сумматора: а - для текущего разряда суммы; б - для текущего разряда выходного переносаСхема одноразрядного сумматора и его УГО представлены на рис. 9.4.
www.intuit.ru
Сумматор. Триггер
Сумматор — это электронная логическая схема, выполняющая суммирование двоичных чисел.
Многоразрядный двоичный сумматор, предназначенный для сложения много разрядных двоичных чисел, представляет собой комбинацию одноразрядных сумматоров.
Одноразрядный двоичный сумматор есть устройство с тремя входами и двумя выходами.
Если требуется складывать двоичные слова длиной два и более бит, то можно использовать последовательное соединение таких сумматоров.
Что должен делать сумматор? Он должен последовательно, разряд за разрядом (начиная с конца), складывать «единицы» и «нули» первого и второго слагаемого Причем здесь возможны такие четыре варианта 0+0,1+0, 0+1 и 1+1 Первые три операции прекрасно выполнила бы одна схема ИЛИ в первом случае на ее выходе не было бы сигнала, а во втором и третьем на выходе появлялся бы импульс И это как раз соответствовало бы известным правилам сложения 0+0=0, 1+0=1 и 0+1=1 Что же касается четвертого сочетания слагаемых, 1 + 1, то схема ИЛИ, конечно, не годится под действием двух одновременных импульсов на ее входах она дала бы один стандартный выходной импульс, что соответствовало бы операции 1+1=1 А нам нужно, чтобы получилось 1+1=0 с переносом «единицы» в следующий разряд .Здесь тоже все начинается со схемы ИЛИ - именно на ее вход одновременно подаются импульсы обоих слагаемых Но с выхода ИЛИ они идут на выход «сумма» не сразу, а через элемент И1 Как известно, схема И срабатывает только в том случае, если у нее на входе есть одновременно два сигнала, И1, И2 .Это значит, что «единица» пройдет из ИЛИ через И1 на выход сумматора только в том случае, если на вход И1 вместе с этой «единицей» придет второй сигнал, в данном случае от логического элемента НЕ Посмотрим, в каких случаях это происходит
Оба слагаемых подаются не только на ИЛИ, но одновременно еще и на элемент И2, а с него сигнал поступает как раз на интересующий нас элемент НЕ .В первых трех случаях 0+0,1+0 и 0+1 элемент И2 не срабатывает, так как на его входе нет необходимых для этого двух - именно двух и только двух! - одновременных импульсов А значит, в этих случаях с И2 на элемент НЕ ничего не поступает, этот элемент не срабатывает, и на его выходе действует нормальное выходное напряжение Не забывайте, что элемент НЕ делает все наоборот сигнал на его выходе существует, когда на вход элемента ничего не подается . А когда на вход сигнал подается - на выходе элемента НЕ сигнал исчезает В итоге получается если на входах сумматора нет импульсов (0+0), то на его выходе тоже нет импульса-в этом случае на входе И1 действует только сигнал, поступающий с НЕ, а его одного недостаточно для срабатывания И1, элемент И2 пока не срабатывает, на его вход тоже ничего не поступает, если на входах сумматора появляется только один импульс (1+0 или 0+1), то на выходе «сумма» импульс появится-теперь на входе И1, кроме напряжения, как и прежде поступающего с НЕ, появляется еще один сигнал - с ИЛИ, этих двух сигналов, с ИЛИ и с НЕ, недостаточно для того чтобы сработал элемент И1, и на его выходе, то есть на выходе «сумма», появился импульс (1+0=1, 0+1=1), элемент И2 все еще не срабатывает на его входе один импульс, а этого мало, если на входах сумматора одновременно появятся два импульса (1+1), то на выходе «сумма» будет «ноль» хотя к И1, как и раньше, пройдет сигнал с ИЛИ, но исчезнет сигнал с НЕ Потому что под действием двух одновременных входных импульсов (1+1) сработает наконец И2 и при этом на входе НЕ появится сигнал, а на выходе исчезнет И таким образом из-за исчезновения сигнала на выходе НЕ не сработает И1, а значит, на выходе «сумма» окажется «ноль» Вот этого как раз мы и добивались, чтобы при появлении «единиц» одновременно на обоих входах сумматора на его выходе «сумма» был «ноль» Потому что 1+1=10, то есть в первом разряде при сложении должен появиться «ноль», а во второй нужно перенести «единицу», что же касается «единицы», то ее снимают с выхода «перенос», то есть с выхода И2, и направляют в линию задержки ЛЗ.Там эта «единица» ждет, пока на входах сумматора появятся импульсы или паузы следующего разряда (« ноль пишем, один в уме »), и в нужный момент добавляется к ним Чтобы решить эту задачу до конца, приходится собирать несколько более сложную схему, но это же, как говорится, детали Принцип действия сумматора остается без изменений выполняя определенные логические операции, он складывает любые двоичные числа, перенося при необходимости «единицу» в следующий разряд и безошибочно формируя последовательность импульсов и пауз, в которых отображен результат сложения, записана сумма двух чисел Если добавить к сумматору простейшее устройство вывода информации, например перо с электромагнитным приводом, то получится законченная электронная счетная машина для выполнения операции «сложение»
Триггер.
Важнейшей структурной единицей оперативной памяти компьютера, а также внутренних регистров процессора является триггер. Это устройство позволяет запоминать, хранить и считывать информацию (каждый триггер может хранить 1 бит информации). Термин "триггер" происходит от английского слова trigger - защелка, спусковой крбчок. Для обозначения этой схемы в английском языке чаще употребляется термин flip - flop, что в переводе охначает - хлопанье. Это звукопдрожательное название электронной схемы указывает на ее способность почти мгновенно переходить (перебрасываться) из одного устойчивого состояния в другое и наоборот.
Самый простой триггер – RS-триггер (R и S соответственно от английских слов reset - сброс и set - установка). Такой триггер можно построить из двух логических элементов «ИЛИ» и двух элементов «НЕ» или двух модулей "ИЛИ-НЕ".
В обычном состоянии на входы триггера подан сигнал 0, и триггер хранит 0. Для записи 1 на вход S (установочный) подается сигнал 1. Последовательно рассмотрев прохождение сигнала по анимированной схеме, видим, что триггер переходит в это состояние и будет устойчиво находится в нем и после того, как сигнал на входе S исчезнет. Триггер запомнил 1, то есть с выхода триггера Q можно считать 1. В этот момент, повторное нажатие на кнопку, подающую единицу на установочный вход ничего не изменяет.
Для того чтобы сбросить информацию и подготовиться к приему новой, подается сигнал 1 на вход R (сброс), после чего триггер возвратиться к исходному "нулевому" состоянию, что хорошо заметно на анимации. Если в процессе демонстрации возникнет необходимость построить таблицу истинности работы логического модуля "ИЛИ-НЕ"
stud24.ru
Вентили, триггеры и сумматоры
Вентиль представляет собой логический элемент, который принимает одни двоичные значения и выдает другие в зависимости от своей реализации. Так, например, есть вентили, реализующие логическое умножение (конъюнкцию), сложение (дизъюнкцию) и отрицание.
Триггеры и сумматоры – это относительно сложные устройства, состоящие из более простых элементов – вентилей.
Триггер способен хранить один двоичный разряд, за счет того, что может находиться в двух устойчивых состояниях. В основном триггеры используется в регистрах процессора.
Сумматоры широко используются в арифметико-логических устройствах (АЛУ) процессора и выполняют суммирование двоичных разрядов.
Законы алгебры логики
Для логических величин обычно используются три операции:
1. Конъюнкция – логическое умножение (И) – and, &, ∧.
2. Дизъюнкция – логическое сложение (ИЛИ) – or, |, v.
3. Логическое отрицание (НЕ) – not,.
Логические выражения можно преобразовывать в соответствии с законами алгебры логики:
1. Законы рефлексивностиa ∨ a = aa ∧ a = a
2. Законы коммутативностиa ∨ b = b ∨ aa ∧ b = b ∧ a
3. Законы ассоциативности(a ∧ b) ∧ c = a ∧ (b ∧ c)(a ∨ b) ∨ c = a ∨ (b ∨ c)
4. Законы дистрибутивностиa ∧ (b ∨ c) = a ∧ b ∨ a ∧ ca ∨ b ∧ c = (a ∨ b) ∧ (a ∨ c)
5. Закон отрицания отрицания( a) = a
6. Законы де Моргана(a ∧ b) = a ∨ b(a ∨ b) = a ∧ b
7. Законы поглощенияa ∨ a ∧ b = aa ∧ (a ∨ b) = a
Логические элементы. Вентили
В основе построения компьютеров, а точнее аппаратного обеспечения, лежат так называемые вентили. Они представляют собой достаточно простые элементы, которые можно комбинировать между собой, создавая тем самым различные схемы. Одни схемы подходят для осуществления арифметических операций, а на основе других строят различную память ЭВМ.
Простейший вентиль представляет собой транзисторный инвертор, который преобразует низкое напряжение в высокое или наоборот (высокое в низкое). Это можно представить как преобразование логического нуля в логическую единицу или наоборот. Т.е. получаем вентиль НЕ.
Соединив пару транзисторов различным способом, получают вентили ИЛИ-НЕ и И-НЕ. Эти вентили принимают уже не один, а два и более входных сигнала. Выходной сигнал всегда один и зависит (выдает высокое или низкое напряжение) от входных сигналов. В случае вентиля ИЛИ-НЕ получить высокое напряжение (логическую единицу) можно только при условии низкого напряжении на всех входах. В случае вентиля И-НЕ все наоборот: логическая единица получается, если все входные сигналы будут нулевыми. Как видно, это обратно таким привычным логическим операциям как И и ИЛИ. Однако обычно используются вентили И-НЕ и ИЛИ-НЕ, т.к. их реализация проще: И-НЕ и ИЛИ-НЕ реализуются двумя транзисторами, тогда как логические И и ИЛИ тремя.
Выходной сигнал вентиля можно выражать как функцию от входных.
Транзистору требуется очень мало времени для переключения из одного состояния в другое (время переключения оценивается в наносекундах). И в этом одно из существенных преимуществ схем, построенных на их основе.
Сумматор и полусумматор
Арифметико-логическое устройство процессора (АЛУ) обязательно содержит в своем составе такие элементы как сумматоры. Эти схемы позволяют складывать двоичные числа.
Как происходит сложение? Допустим, требуется сложить двоичные числа 1001 и 0011. Сначала складываем младшие разряды (последние цифры): 1+1=10. Т.е. в младшем разряде будет 0, а единица – это перенос в старший разряд. Далее: 0 + 1 + 1(от переноса) = 10, т.е. в данном разряде снова запишется 0, а единица уйдет в старший разряд. На третьем шаге: 0 + 0 + 1(от переноса) = 1. В итоге сумма равна 1100.
Полусумматор
Теперь не будем обращать внимание на перенос из предыдущего разряда и рассмотрим только, как формируется сумма текущего разряда. Если были даны две единицы или два нуля, то сумма текущего разряда равна 0. Если одно из двух слагаемых равно единице, то сумма равна единицы. Получить такие результаты можно при использовании вентиля ИСКЛЮЧАЮЩЕГО ИЛИ.
Перенос единицы в следующий разряд происходит, если два слагаемых равны единице. И это реализуемо вентилем И.
Тогда сложение в пределах одного разряда (без учета возможной пришедшей единицы из младшего разряда) можно реализовать изображенной ниже схемой, которая называется полусумматором. У полусумматора два входа (для слагаемых) и два выхода (для суммы и переноса). На схеме изображен полусумматор, состоящий из вентилей ИСКЛЮЧАЮЩЕЕ ИЛИ и И.
Сумматор
В отличие от полусумматора сумматор учитывает перенос из предыдущего разряда, поэтому имеет не два, а три входа.
Чтобы учесть перенос приходится схему усложнять. По-сути она получается, состоящей из двух полусумматоров.

Рассмотрим один из случаев. Требуется сложить 0 и 1, а также 1 из переноса. Сначала определяем сумму текущего разряда. Судя по левой схеме ИСКЛЮЧАЮЩЕЕ ИЛИ, куда входят a и b, на выходе получаем единицу. В следующее ИСКЛЮЧАЮЩЕЕ ИЛИ уже входят две единицы. Следовательно, сумма будет равна 0.
Теперь смотрим, что происходит с переносом. В один вентиль И входят 0 и 1 (a и b). Получаем 0. Во второй вентиль (правее) заходят две единицы, что дает 1. Проход через вентиль ИЛИ нуля от первого И и единицы от второго И дает нам 1.
Проверим работу схемы простым сложением 0 + 1 + 1 = 10. Т.е. 0 остается в текущем разряде, и единица переходит в старший. Следовательно, логическая схема работает верно.
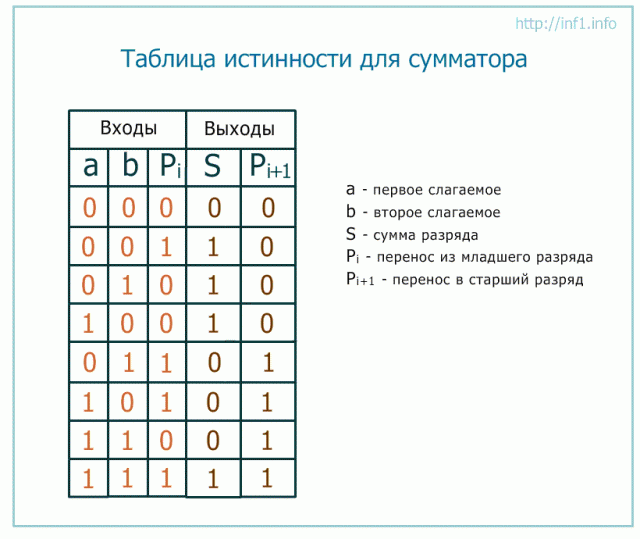
Работу данной схемы при всех возможных входных значениях можно описать следующей таблицей истинности.
infopedia.su
|
|
..:::Счетчики:::.. |
|
|
|
|
|
|
|
|


