Математика, которая мне нравится. Реферат теорема морли
Теорема Морли | Математика, которая мне нравится
 Фрэнк Морли (1860–1937) — английский математик, известный своими работами по алгебре и геометрии. Морли любил придумывать задачи, и за более чем 50 лет своей работы со времени окончания Кембриджского университета он опубликовал более 60 задач в Educational Times. Большинство этих задач — геометрические. Морли очень хорошо играл в шахматы. Одни раз он даже выиграл у чемпиона мира по шахматам Эмануэля Ласкера (примеч. Интересно, что Ласкер тоже занимался математикой, и одна из теорем названа его именем — теорема Ласкера — Нётер). Морли внес огромный вклад в развитие математики в США. В течение 30 лет он был редактором журнала American Journal of Mathematics, работал и в журнале Bulletin of the American Mathematical Society, в 1919–20 годах был президентом Американского математического общества.
Фрэнк Морли (1860–1937) — английский математик, известный своими работами по алгебре и геометрии. Морли любил придумывать задачи, и за более чем 50 лет своей работы со времени окончания Кембриджского университета он опубликовал более 60 задач в Educational Times. Большинство этих задач — геометрические. Морли очень хорошо играл в шахматы. Одни раз он даже выиграл у чемпиона мира по шахматам Эмануэля Ласкера (примеч. Интересно, что Ласкер тоже занимался математикой, и одна из теорем названа его именем — теорема Ласкера — Нётер). Морли внес огромный вклад в развитие математики в США. В течение 30 лет он был редактором журнала American Journal of Mathematics, работал и в журнале Bulletin of the American Mathematical Society, в 1919–20 годах был президентом Американского математического общества.
Самым известным результатом Фрэнка Морли является теорема о трисектрисах треугольника, носящая его имя.
Сначала определим трисектрису, а затем докажем теорему.
Определение. Трисектрисой угла называется каждый из двух лучей, делящих этот угол на три равные части.
Теорема Морли. Точки пересечения смежных трисектрис углов произвольного треугольника являются вершинами равностороннего (правильного) треугольника.
Доказательство. Нужно доказать, что треугольник  равносторонний.
равносторонний.

Используя обозначения, приведенные на рисунке, поскольку в треугольнике  сумма углов
сумма углов  , имеем
, имеем
![Rendered by QuickLaTeX.com \[\alpha+\beta+\gamma+\pi/3.\]](/800/600/http/hijos.ru//wp-content/ql-cache/quicklatex.com-ea0ea12d9b1aacccdd8516e4fa9e2e2a_l3.png)
Возьмем произвольный равносторонний треугольник  . Пусть
. Пусть  — точки на высотах треугольника
— точки на высотах треугольника  (или на продолжениях высот) такие, что
(или на продолжениях высот) такие, что
![Rendered by QuickLaTeX.com \[\angle XPY=\angle XPZ=\alpha+\frac{\pi}{6},\]](/800/600/http/hijos.ru//wp-content/ql-cache/quicklatex.com-bf3f56d6b107e47c4dcd73a1e925f251_l3.png)
![Rendered by QuickLaTeX.com \[\angle YQZ=\angle YQX=\beta+\frac{\pi}{6},\]](/800/600/http/hijos.ru//wp-content/ql-cache/quicklatex.com-920dd76292c03a8bc80b72b477bc4b86_l3.png)
![Rendered by QuickLaTeX.com \[\angle ZRX=\angle ZRY=\gamma+\frac{\pi}{6}.\]](/800/600/http/hijos.ru//wp-content/ql-cache/quicklatex.com-746d3186cf1e829ac5b791ebfc5fac88_l3.png)

Пусть  — точка пересечения
— точка пересечения  и
и  ,
,  — точка пересечения
— точка пересечения  и
и  , и
, и  — точка пересечения
— точка пересечения  и
и  . Тогда в четырехугольнике
. Тогда в четырехугольнике 
![Rendered by QuickLaTeX.com \[\angle AQX=2\beta+\frac{\pi}{3},\]](/800/600/http/hijos.ru//wp-content/ql-cache/quicklatex.com-bfde8e6dd12a69ab99fa49b645395019_l3.png)
![Rendered by QuickLaTeX.com \[\angle ARX=2\gamma+\frac{\pi}{3},\]](/800/600/http/hijos.ru//wp-content/ql-cache/quicklatex.com-9522853b8908cb0c30d87227d344a099_l3.png)
![Rendered by QuickLaTeX.com \[\angle QXR=2\alpha+\beta+\gamma+\frac{\pi}{3}.\]](/800/600/http/hijos.ru//wp-content/ql-cache/quicklatex.com-d081769adb445de759151178a8abd49d_l3.png)
Следовательно,  . Аналогично,
. Аналогично,  и
и  .
.
Проведем окружность с центром в точке  , касающуюся
, касающуюся  . Так как
. Так как  — биссектриса
— биссектриса  , то эта окружность также касается
, то эта окружность также касается  . Теперь проведем касательные к окружности
. Теперь проведем касательные к окружности  и
и  . Обозначим через
. Обозначим через  точку пересечения этих касательных. Тогда
точку пересечения этих касательных. Тогда
![Rendered by QuickLaTeX.com \[\angle XBT=\angle XBZ=\beta\]](/800/600/http/hijos.ru//wp-content/ql-cache/quicklatex.com-6073ab54f38634e0a2940a61e185383b_l3.png)
и
![Rendered by QuickLaTeX.com \[\angle XCU=\angle XCY=\gamma.\]](/800/600/http/hijos.ru//wp-content/ql-cache/quicklatex.com-cdb0e6aae978174f30f85054e79ad4de_l3.png)
Тогда сумма углов  и
и  в четырехугольнике
в четырехугольнике  равна
равна
![Rendered by QuickLaTeX.com \[\displaystyle 2\alpha+\frac{\pi}{3}+2\beta+2\gamma=\pi,\]](/800/600/http/hijos.ru//wp-content/ql-cache/quicklatex.com-aa99f10c053ec9fa33806814bdaf52d7_l3.png)
откуда  . Другими словами,
. Другими словами,  — прямая, так что точки
— прямая, так что точки  и
и  совпадают. Следовательно,
совпадают. Следовательно,  . Аналогично определяются углы треугольников
. Аналогично определяются углы треугольников  и
и  , откуда получаем, что углы треугольника
, откуда получаем, что углы треугольника  равны
равны  и
и  . Если необходимо, этот треугольник можно заменить подобным ему, который будет совпадать с
. Если необходимо, этот треугольник можно заменить подобным ему, который будет совпадать с  .
.
Источники: http://www.cut-the-knot.org/triangle/Morley/sb3.shtml
http://www-history.mcs.st-andrews.ac.uk/Biographies/Morley.html
hijos.ru
Исследовательская работа по теме трисекция угла страница 4
3. Теорема Морлея (или Теорема Морли).
Фрэнк Морли (1860–1937) — английский математик, известный своими работами по алгебре и геометрии. Морли любил придумывать задачи, и за более чем 50 лет своей работы со времени окончания Кембриджского университета он опубликовал более 60 задач в Educational Times. Большинство этих задач — геометрические. Морли очень хорошо играл в шахматы. Одни раз он даже выиграл у чемпиона мира по шахматам Эмануэля Ласкера (примеч. Интересно, что Ласкер тоже занимался математикой, и одна из теорем названа его именем — теорема Ласкера — Нётер). Морли внес огромный вклад в развитие математики в США. В течение 30 лет он был редактором журнала American Journal of Mathematics, работал и в журнале Bulletin of the American Mathematical Society, в 1919–20 годах был президентом Американского математического общества.
Самым известным результатом Фрэнка Морли является теорема о трисектрисах треугольника, носящая его имя.
Сначала определим трисектрису, а затем докажем теорему.
Определение. Трисектрисой угла называется каждый из двух лучей, делящих этот угол на три равные части.
Теорема Морли. Точки пересечения смежных трисектрис углов произвольного треугольника являются вершинами равностороннего (правильного) треугольника.
Доказательство. Нужно доказать, что треугольник XYZ - равносторонний.
Обратиться к приложению – рисунок 8.
Используя обозначения, приведённые в рисунке, поскольку в трeугольнике ABC сумма углов 3 α + 3 β + 3 γ = 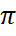 , имеем α + β + γ +
, имеем α + β + γ + 
Возьмём произвольный равносторонний треугольник XYZ. Пусть P, Q, R – точки на высотах треугольника ABC, такие что:
∟ XPY = ∟XPZ = α + 
∟ YQZ = ∟YQX = β + 
∟ZRX = ∟ZRY = γ + 
Пусть A — точка пересечения QZ и RY, B — точка пересечения PX и PZ, и C — точка пересечения PY и QX. Тогда в четырехугольнике XRAQ:
∟AQX = 2 ß + 
∟ARX = 2γ + 
∟QXR = 2α + β + γ + 
Обратиться к приложению – рисунок 9.
Следовательно, ∟ZAY = α .
Аналогично, ∟ XBZ = β и ∟YCX = γ .
Проведем окружность с центром в точке X, касающуюся PB. Так как PX — биссектриса ∟BPC, то эта окружность также касается PC. Теперь проведем касательные к окружности BT и CU. Обозначим через V точку пересечения этих касательных. Тогда
∟ XBT = ∟ XBZ = β и ∟XCU = ∟XCY = γ.
Тогда сумма углов P, B и C в четырехугольнике PBVC равна 2 α +  + 2 β + 2 γ =
+ 2 β + 2 γ = 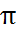 ,
,
Откуда ∟ TVU = 0 . Другими словами, BTUVC — прямая, так что точки T, U, и V совпадают. Следовательно, ∟ XBC = 3, ∟ XCB = γ . Аналогично определяются углы треугольников YCA и ZAB , откуда получаем, что углы треугольника ABC равны 3 α, 3 β и 3 γ . Если необходимо, этот треугольник можно заменить подобным ему, который будет совпадать с треугольником ABC.
4. Вывод
Несмотря на то, что уже тысячи лет великие умы человечества ищут способы осуществления трисекции угла с помощью циркуля и линейки, до сих пор решения не найдено. Это говорит о том, что она действительно не осуществима для большинства углов. Но всё равно находятся те, кто пытается предложить свой вариант решения, но впоследствии они опровергаются из-за какого-то маленького недочёта. Я оказалась в числе тех, кто остался не равнодушным к этой задачи и кто потратил своё время на поиск своего, уникального решения. Я не жалею, я однажды открыла для себя задачу о трисекции угла, ведь, благодаря процессу построения чертежей и выполнению доказательства, человек ищет какие-то алгоритмы, которые помогает ему мыслить логически. А без логики человеку в современном мире приходится очень тяжело. Я считаю, что каждому необходимо хотя бы пытаться находить различные способы решения одной и той же задачи, так как это развивает человека, заставляет его мыслить рационально. Надеюсь, что в следующей моей работе я представлю во внимание ещё более интересную неразрешимую или ещё не доказанную задачу, постараюсь в ней разобраться и найти какие-нибудь пути её разрешения
infourok.ru
Тема реферата (2) - Реферат
Муниципальное общеобразовательное учреждение
«Средняя общеобразовательная школа №87»
Тема реферата:
Три знаменитые задачи древности.
Выполнил: Мурзыков А. В.
ученик 10 класса Б.
Руководители:
Кулеш Людмила Егоровна,
учитель математики;
Троегубова Татьяна Сергеевна,
учитель информатики.
Северск -2009.
Содержание:
Введение………………………………………………………………3
1.Задача о квадратуре круга………………………………………… 4
2.Число π………………………………………………………………8
3.Задача о трисекции угла……………………………………………9
4. Теорема Морлея…………………………………………………...15
5.Задача об удвоении площади круга………………………..……..16
Заключение…………………………………………………………...18
Список источников…………………………………………………..19
Приложение 1………………………………………………………...21
Приложение 2………………………………………………………...22
Введение
Искусство построения геометрических фигур при помощи циркуля и линейки было в высокой степени развито в Древней Греции. Однако древним геометрам никак не удавалось выполнить некоторые построения, используя лишь циркуль и линейку, а построения, выполненные с помощью других инструментов, не считались геометрическими. К числу таких задач относятся так называемые три знаменитые классические задачи древности: о квадратуре круга, о трисекции угла, об удвоении площади круга.
Я считаю эту тему актуальной, потому что очень полезно изучать методы решений данных задач древними учёными, так как большинство методов и способов решений различных задач сохранились и до наших дней и используются в современной математике.
Я хотел больше узнать о возможных способах решения этих задач древними учёными, которые могли использовать только подручные материалы для решения такого рода задач.
Целью моей работы будет углубление в историю математики и задач, представленных в моём реферате.
Перед собой поставил следующие задачи:
1.Изучить литературу и источники Интернет по данной теме.
2.Обработать информацию.
3.Сделать свои выводы.
4.Выполнить и представить презентацию в Power Point.
Моя работа состоит из пяти глав. Мной были изучены и обработаны материалы 9 литературных источников, среди которых учебная, справочная, научная литература и Интернет-ресурсы. Оформлено приложение, подготовлена презентация, сделанная в редакторе Power Point.
1.Задача о квадратуре круга
Одной из древнейших и самых популярных математических задач, занимавшей умы людей на протяжении 3 – 4 тысячелетий, является задача о квадратуре круга, т.е. о построении с помощью циркуля и линейки квадрата, равновеликому данному кругу.
Е сли обозначить радиус круга через r, то речь будет идти о построении квадрата, площадь которого равна πr2, а сторона равна r
сли обозначить радиус круга через r, то речь будет идти о построении квадрата, площадь которого равна πr2, а сторона равна r . Теперь известно, что число π - отношение окружности к своему диаметру – число иррациональное. Оно выражается бесконечной непериодической десятичной дробью 3,1415926… и было, между прочим, вычислено с 707 десятичными знаками математиком В. Шенксом. Этот результат вместе с формулой вычислений он обнародовал в 1837 году. Ни одна ещё задача подобного рода не решалась с таким огромным приближением и с точностью, далеко превышающее отношение микроскопических расстояний к телескопическим.
. Теперь известно, что число π - отношение окружности к своему диаметру – число иррациональное. Оно выражается бесконечной непериодической десятичной дробью 3,1415926… и было, между прочим, вычислено с 707 десятичными знаками математиком В. Шенксом. Этот результат вместе с формулой вычислений он обнародовал в 1837 году. Ни одна ещё задача подобного рода не решалась с таким огромным приближением и с точностью, далеко превышающее отношение микроскопических расстояний к телескопическим.
Шенкс вычислял. Следовательно, он стоял в противоречии с требованиями задачи о квадратуре круга, где требовалось найти решение построением. Работа, сделанная Шенксом, в сущности бесполезна – или почти бесполезна. Но, с другой стороны, она может служить довольно убедительным доказательством противного тому, кто, убедившись доказательствами Линдеманна и других или не зная о них, до сих пор ещё надеется, что можно найти точное отношение длины окружности к диаметру. Можно вычислить приближенное значение π (и корня квадратного из π), удовлетворяющее тем или иным практическим потребностям. Однако не в практическом отношении интересовала людей задача о квадратуре круга, а интересовала её принципиальная сторона: возможно ли точно решить эту задачу, выполняя построения с помощью только циркуля и линейки.
Следы задачи о квадратуре круга можно усмотреть ещё в древнеегипетских и вавилонских памятниках II тысячелетия до н.э. Однако непосредственная постановка задачи о квадратуре круга встречается впервые в греческих сочинениях V в. до н.э. В своём произведении «О изгнании » Плутарх рассказывает, что философ и астроном Анаксагор (500 – 428 г. до н.э.) находясь в тюрьме, отгонял печаль размышлениями над задачей о квадратуре круга. В комедии « Птицы » (414 г. до н.э.) знаменитый греческий поэт Аристофан, шутя на тему о квадратуре круга, вкладывает в уста Астронома Метона следующие слова:
Возьму линейку, проведу прямую,
И мигом круг квадратом обернётся,
Посередине рынок мы устроим,
А от него уж улицы пойдут –
Ну, как на Солнце! Хоть оно само
И круглое, а ведь лучи прямые!..
Эти стихи говорят о том, что задача уже была к тому времени очень популярна в Греции. Один из современников Сократа – софист Антифон считал, что квадратуру круга можно осуществить следующим образом: впишем в круг квадрат и, разделяя пополам дуги, соответствующие его сторонам, построим правильный вписанный восьмиугольник, затем шестнадцатиугольник и так далее, пока не получим многоугольник, который в силу малости сторон сольётся с окружностью. Но так как можно построить квадрат равновеликий любому многоугольнику, то и круг можно квадрировать. Однако уже Аристотель доказал, что это будет только приближённое, но не точное решение задачи, так как многоугольник никогда не может совпасть с кругом.
К вадратурой круга занимался также самый знаменитый геометр V века до н.э. – Гиппократ Хиосский. У многих занимавшихся этой задачей возникало сомнение, возможно ли вообще построить прямолинейную фигуру, равновеликую криволинейной. Эта возможность была доказана Гиппократом, построившим лунообразные фигуры (Рис. 1), известных под названием «гиппократовых луночек». В полукруг с диаметром BC вписан равнобедренный прямоугольный треугольник BAC (BC=AC). На AB и AC, как на диаметрах, описываются полуокружности.
вадратурой круга занимался также самый знаменитый геометр V века до н.э. – Гиппократ Хиосский. У многих занимавшихся этой задачей возникало сомнение, возможно ли вообще построить прямолинейную фигуру, равновеликую криволинейной. Эта возможность была доказана Гиппократом, построившим лунообразные фигуры (Рис. 1), известных под названием «гиппократовых луночек». В полукруг с диаметром BC вписан равнобедренный прямоугольный треугольник BAC (BC=AC). На AB и AC, как на диаметрах, описываются полуокружности.
Фигуры-мениски ALBM и ADCE, ограниченными круговыми дугами, и называются луночками.
По теореме Пифагора:
BC =AB
=AB +AC
+AC =2AC
=2AC . (1)
. (1)
Рис. 1
Отношение  площадей кругов или полукругов BMAEC и AECD равно, как впервые доказал сам Гиппократ, отношению квадратов соответствующих диаметров
площадей кругов или полукругов BMAEC и AECD равно, как впервые доказал сам Гиппократ, отношению квадратов соответствующих диаметров  , которые в силу (1) равно 2. Итак, площадь сектора OAC равна площади полукруга, построенного на диаметре AC. Если из обеих этих равных площадей вычесть площадь сегмента ACE, то и получим, что площадь треугольника AOC равна площади луночки ADCE, или сумма площадей обеих луночек равна площади равнобедренного треугольника BCA. Гиппократ нашёл и другие луночки, допускающие квадратуру, и продолжал свои изыскания в надежде дойти до квадратуры круга, что ему, конечно, не удалось.
, которые в силу (1) равно 2. Итак, площадь сектора OAC равна площади полукруга, построенного на диаметре AC. Если из обеих этих равных площадей вычесть площадь сегмента ACE, то и получим, что площадь треугольника AOC равна площади луночки ADCE, или сумма площадей обеих луночек равна площади равнобедренного треугольника BCA. Гиппократ нашёл и другие луночки, допускающие квадратуру, и продолжал свои изыскания в надежде дойти до квадратуры круга, что ему, конечно, не удалось.
Различные другие попытки, продолжавшиеся в течение тысячелетий, найти квадратуру круга оканчивались неудачей. Лишь в 80-х годах 19века было строго доказано, что квадратура круга с помощью циркуля и линейки невозможна. Задача о квадратуре круга становится разрешимой, если применять, кроме циркуля и линейки, еще и другие средства построения. Так, еще в 4веке до н.э. греческие математики Динострат и Менехм пользовались для решения задачи одной кривой, которая была найдена еще в 5веке до н.э. Гиппием Элидским. Однако ученых Древней Греции и их последователей такие решения, находящиеся за пределами применения циркуля и линейки, не удовлетворяли. Будучи сначала чисто геометрической задачей, квадратура круга превратилась в течение веков в исключительно важную задачу арифметико-алгебраического характера, связанную с числом  , и содействовала развитию новых понятий и идей в математике.
, и содействовала развитию новых понятий и идей в математике.
Квадратура круга была в прежние времена самой заманчивой и соблазнительной задачей. Армия «квадратурщиков» неустанно пополнялась каждым новым поколением математиков. Все усилия были тщетны, но число их не уменьшалось. В некоторых умах доказательство, что решение не может быть найдено, зажигало ещё большее рвение к изысканиям. Что эта задача до сих пор не потеряла своего интереса, лучшим доказательством служит появление до сих попыток её решить.
Квадратура круга
Под словами «Квадратура круга» понимают как задачу точного построения квадрата, равновеликого кругу, так и задачу вычисления площади круга с тем или иным приближением. Задачу о точной квадратуре круга пытались решить первоначально с помощью циркуля и линейки. Математика древности знала ряд случаев, когда с помощью этих инструментов удавалось преобразовать криволинейную фигуру в равновеликую ей прямолинейную (например, гиппократовы луночки). Попытки решения задачи о квадратуре круга, продолжавшиеся в течение тысячелетий, неизменно оканчивались неудачей. С 1775 года Парижская Академия наук, а затем и другие академии стали отказываться от рассмотрения работ, посвященных квадратуре круга. В 19 веке было дано научное обоснование этого отказа: строго установлена неразрешимость квадратуры круга с помощью циркуля и линейки.
Если радиус круга равен r, то сторона равновеликого этому кругу квадрата равна r . Таким образом, задача сводится к следующей: осуществить построение, в результате которого данный отрезок (r) был бы умножен на данное число (
. Таким образом, задача сводится к следующей: осуществить построение, в результате которого данный отрезок (r) был бы умножен на данное число ( ). Однако графическое умножение отрезка на число осуществимо циркулем и линейкой, если упомянутое число — корень алгебраического уравнения с целыми коэффициентами, разрешимого в квадратных радикалах. Таким образом, окончательная ясность в вопросе о квадратуре круга могла быть достигнута на пути изучения арифметической природы числа π. В конце 18 века немецким математиком И. Ламбертом и французским математиком А. Лежандром была установлена иррациональность числа π. В 1882 немецкий математик Ф. Линдеман доказал, что число π (а значит и
). Однако графическое умножение отрезка на число осуществимо циркулем и линейкой, если упомянутое число — корень алгебраического уравнения с целыми коэффициентами, разрешимого в квадратных радикалах. Таким образом, окончательная ясность в вопросе о квадратуре круга могла быть достигнута на пути изучения арифметической природы числа π. В конце 18 века немецким математиком И. Ламбертом и французским математиком А. Лежандром была установлена иррациональность числа π. В 1882 немецкий математик Ф. Линдеман доказал, что число π (а значит и  ) трансцендентно, то есть не удовлетворяет никакому алгебраическому уравнению с целыми коэффициентами. Теорема Линдемана положила конец попыткам решения задачи о квадратуре круга с помощью циркуля и линейки. Задача о квадратуре круга становится разрешимой, если расширить средства построения. Уже греческим геометрам было известно, что квадратуру круга можно осуществить, используя трансцендентные кривые; первое решение задачи о квадратуре круга было выполнено Диностратом (4 в. до н. э.) при помощи специальной кривой — так называемой квадратрисы. [7]
) трансцендентно, то есть не удовлетворяет никакому алгебраическому уравнению с целыми коэффициентами. Теорема Линдемана положила конец попыткам решения задачи о квадратуре круга с помощью циркуля и линейки. Задача о квадратуре круга становится разрешимой, если расширить средства построения. Уже греческим геометрам было известно, что квадратуру круга можно осуществить, используя трансцендентные кривые; первое решение задачи о квадратуре круга было выполнено Диностратом (4 в. до н. э.) при помощи специальной кривой — так называемой квадратрисы. [7]
Гиппократовы луночки
Гиппократовы луночки, три фигуры, указанные Гиппократом Хиосским, каждая из которых ограничена дугами двух окружностей и для каждой из которых с помощью циркуля и линейки можно построить равновеликие прямолинейные фигуры. Построение одной из гиппократовых луночек ясно из рисунка. Площадь заштрихованной гиппократовой луночки равна площади равнобедренного треугольника АВС. Другие гиппократовы луночки получаются более сложным путём.

Гиппократ Хиосский (Hippokrates)
(вторая половина 5 века до н. э.) - древнегреческий геометр, автор первого систематического сочинения по геометрии (не дошедшего до нас), которое, вероятно, охватывало материал первых 4 книг «Начал» Евклида. В поисках решения квадратуры круга Гиппократ Хиосский нашёл квадратуры трёх так называемых гиппократовых луночек. [8]
2.Число π
Число π - число, равное отношению длины окружности к длине её диаметра. Число π является трансцендентным числом, его приближенное значение равно 3,1415926...
Открывателями числа π можно считать людей доисторического времени, которые при плетении корзин заметили, что для того, чтобы получить корзину нужного диаметра, необходимо брать прутья в 3 раза длиннее его. Найдены таблички из обожженной глины в Месопотамии, на которых зафиксирован данный факт. Египтяне почти за 2000 лет до н.э. заметили, что диаметр окружности не содержится точно 3 раза в её длине. С этого времени начинается изучение числа π, которое продолжается и до наших дней.
Изучение числа π шло вместе с поиском решения задачи о построении квадрата, равновеликого окружности, т.е. о построении с помощью циркуля и линейки отрезка, равного по длине окружности.
Леонардо Фибоначчи около 1220 года определил три первых точных десятичных знака числа π. В XVI в. Андриан Антонис определил шесть точных десятичных знаков числа π, а Франсуа Виет вычислил первые девять точных десятичных знаков этого числа. Но необходимо отметить, что китайским математикам уже в V веке были известны шесть точных знаков числа π. После Виета в Европе началась гонка за вычислением точных десятичных знаков числа. Фламандский математик Андриан ван Роомен вычисляет 15 точных десятичных знаков числа π. Но математическим подвигом можно назвать вычисления голландского математика Лудольфа ван Цейлена, который получил 35 точных десятичных знаков числа π. В его честь число π было названо современниками "Лудольфово число".[1]
3.Задача о трисекции угла
Знаменитой была в древности и задача о трисекции угла (от латинских слов trio – три и section – рассечение, разрезание), т.е. о разделении угла на три равные части с помощью циркуля и линейки.
Г оворят, что такое ограничение вспомогательных приборов было введено знаменитым греческим философом Платоном.
оворят, что такое ограничение вспомогательных приборов было введено знаменитым греческим философом Платоном.
Так, деление прямого угла на три равные части умели производить ещё пифагорейцы, основываясь на том, что в равностороннем треугольнике каждый угол равен 60о. Пусть требуется разделить на три равные части прямой угол MAN . Откладываем на полупрямой AN произвольный отрезок AC, на котором строим равносторонний треугольник ACB. Так как угол CAB равен 60о, то  = 30о.
= 30о.
 Построим биссектрису AD угла САВ, получаем искомое деление прямого угла MAN
Построим биссектрису AD угла САВ, получаем искомое деление прямого угла MAN
на три равных угла:  ,
,  ,
,  .
.
Задача о трисекции угла оказывается разрешимой и при некоторых других частных значениях угла (например, для углов в  , п – натуральное число), однако не в общем случае, т.е. любой угол невозможно разделить на три равных части с помощью только циркуля и линейки. Это было доказано лишь в первой половине ХIХ в.
, п – натуральное число), однако не в общем случае, т.е. любой угол невозможно разделить на три равных части с помощью только циркуля и линейки. Это было доказано лишь в первой половине ХIХ в.

Рис. 3, а, б, в: конхоида Никомеда
Задача о трисекции угла становится разрешимой и в общем случае, если не ограничиваться в геометрических построениях одними только классическими инструментами, циркулем и линейкой. Попытки решения задачи с помощью инструментов и средств были предприняты еще в V в. до н.э. Так, например, Гиппий Элидский, знаменитый софист, живший около 420 г. до н.э., пользовался для трисекции угла квадратрисой. Александрийский математик Никомед (II в. до н.э.) решил задачу о трисекции угла с помощью одной кривой, названной конхоидой Никомеда (рис. 3), и дал описание прибора для черчения этой кривой.

Рис. 4 Рис. 5
Интересное решение задачи о трисекции угла дал Архимед в своей книге «Леммы», в которой доказывается , что если продолжить хорду АВ (рис.4) окружности радиуса r на отрезок BC= r и провести через С диаметр FE, то дуга BF будет втрое меньше дуги АЕ. Действительно на основе теорем о внешнем угле треугольника и о равенстве углов при основании равнобедренного треугольника имеем:
 ,
,

 ,
,
значит,

О тсюда следует так называемый способ «вставки» для деления на три равные части угла AOE. Описав окружность с центром O и радиусом OE и OA, проводим диаметр EF. Линейку CB на которой нанесена длина CB радиуса r (например, помощью двух штрихов), прикладываем и двигаем так, чтобы её точка C скользила по продолжению диаметра (EF), а сома линейка всё время проходила бы через точку A окружности, пока точка B линейки не окажется на окружности. Тогда угол BCF и будет искомой третьей частью угла AOE (Рис.5). Как видно, в этом приёме используется вставка отрезка CB между продолжением диаметра EF и окружностью так, чтобы продолжение отрезка CB прошло через заданную точку A окружности. В указанном выше построении применяется, помимо циркуля, не просто линейка как инструмент для проведения прямых, а линейка с делениями, которая даёт длину определённого отрезка.
тсюда следует так называемый способ «вставки» для деления на три равные части угла AOE. Описав окружность с центром O и радиусом OE и OA, проводим диаметр EF. Линейку CB на которой нанесена длина CB радиуса r (например, помощью двух штрихов), прикладываем и двигаем так, чтобы её точка C скользила по продолжению диаметра (EF), а сома линейка всё время проходила бы через точку A окружности, пока точка B линейки не окажется на окружности. Тогда угол BCF и будет искомой третьей частью угла AOE (Рис.5). Как видно, в этом приёме используется вставка отрезка CB между продолжением диаметра EF и окружностью так, чтобы продолжение отрезка CB прошло через заданную точку A окружности. В указанном выше построении применяется, помимо циркуля, не просто линейка как инструмент для проведения прямых, а линейка с делениями, которая даёт длину определённого отрезка.
Вот ещё одно решение задачи о трисекции угла при помощи линейки с двумя насечками предложенное Кемпе:
Рис. 6
Пусть дан какой – либо угол ABC; и пусть на лезвии нашей линейки обозначены 2 точки, P и Q (см. ту же фигуру, внизу)
Построение.
На одной из сторон угла откладываем от вершины B прямую BA = PQ. Делим ВА пополам в точке М; проводим линии  и
и  .
.
Возьмём теперь нашу линейку и приспособим её к уже полученной фигуре так, чтобы точка Р линейки лежала на прямой КМ, точка Q лежала бы
на прямой LM, и в тоже время продолжение PQ линейки проходило бы через вершину данного угла В. тогда прямая ВР и есть искомая, отсекающая третью часть угла В.
Доказательство:
 как накрест лежащие. Разделим PQ пополам и середину N соединим с М прямой NM. Точка N есть середина гипотенузы прямоугольного треугольника PQM, а потому PN = NМ, а, следовательно, треугольник PNM равнобедренный, и значит
как накрест лежащие. Разделим PQ пополам и середину N соединим с М прямой NM. Точка N есть середина гипотенузы прямоугольного треугольника PQM, а потому PN = NМ, а, следовательно, треугольник PNM равнобедренный, и значит

Внешний же 
Вместе с тем  .
.
Значит, 
Итак: 
(Ч.Т.Д.).
Приведённое выше решение задачи принадлежит Кемпле, который при этом поднял вопрос, почему Евклид не воспользовался делением линейки и процессом её приспособления для доказательства 4-й теоремы своей первой книги, где вместо этого он накладывает стороны одного треугольника на стороны другого. На это может ответить только, что в задачу Евклида и не входило отыскивание некоторой точки по средствам измерения и процесса приспособления линейки. В своих рассуждениях и доказательствах он просто накладывает фигуру на фигуру – и только.
Задача о трисекции угла возникла в Древней Греции примерно в V веке до н.э. из потребностей архитектуры и строительной техники. Древним грекам удалось решить задачу о трисекции прямого угла при помощи циркуля и линейки. Р. Декарт высказал предположение о неразрешимости задачи о трисекции произвольного угла при помощи циркуля и линейки без засечек. Это утверждение было доказано в 1837 году Ванцелем.
Следствия, открытые в процессе решения задачи о трисекции угла.
В 15 веке самаркандский ученый применил трисекцию угла к составлению весьма точных тригонометрических таблиц.
В 16 веке французский математик Ф. Виет на основе трисекции угла нашел тригонометрическое решение квадратного уравнения.
Павловым К. К.было рассмотрено четыре способа построения трисектрисы угла:
при помощи циркуля и линейки без засечек
решение Гиппея при помощи квадратрисы (рис.1 и 2).
решение Паппа Александрийского при помощи конхоиды Никомеда
решение Архимеда при помощи циркуля и линейки с двумя засечками .
При изучении первого способа построения автором были решены следующие задачи:
трисекция угла в 900, 450, 22,50,... π /2n, где n – натуральное число (все эти углы образуют бесконечно малую геометрическую прогрессию со знаменателем q =1/2).
трисекция угла в 1800.
трисекция угла в 3600.


Рис. 1. Квадратриса. Рис. 2. Трисекция угла при помощи
квадратрисы.
Сравнительный анализ различных способов построения представлен в таблице. Здесь под легкостью построения понимается использование вспомогательных средств, а коэффициент точности высчитывается по методике, описанной в курсе начертательной геометрии (Виноградов В.Н., Ройтман И.А.).
Сравнительный анализ способов построения трисектрисы угла.
(см приложение 2, таблица 1)
Из приведенной таблицы видно, что задача трисекции угла в 90° решается всеми четырьмя способами. Любой острый угол можно разделить на 3 равные части только при использовании вспомогательных средств (2,3 и 4 способы), а углы α = π /2n, где n- натуральное число можно разделить на 3 равные части при помощи циркуля и линейки.
Использование вспомогательных средств уменьшают легкость и точность построения. [9]
4.Теорема Морлея
Теорема Морлея о трисектрисах — одна из самых удивительных теорем геометрии треугольника. Трисектрисами угла называются два луча, делящие угол на три равные части.
Т еорема утверждает:
еорема утверждает:
Точки пересечения смежных трисектрис углов произвольного треугольника являются вершинами равностороннего треугольника.
На чертеже три разноцветных угла при каждой вершине большого треугольника равны. Теорема утверждает, что независимо от выбора большого треугольника маленький фиолетовый треугольник будет равносторонним.
Теорема была открыта в 1904 году Франком Морлеем (Frank Morley). Тогда он упомянул об этой теореме своим друзьям, а опубликовал её двадцать лет спустя в Японии. За это время она была независимо опубликована как задача в журнале «Educational Times».[6]
5.Задача об удвоении куба
Удвоение куба – так называется третья классическая задача древнегреческой математики. Эта задача наряду с двумя первыми сыграла большую роль в развитии математических методов.
З адача состоит в построении куба, имеющий объём, вдвое больше объёма данного куба. Если обозначить через а ребро данного куба, то длина ребра х искомого куба должно удовлетворять уравнению
адача состоит в построении куба, имеющий объём, вдвое больше объёма данного куба. Если обозначить через а ребро данного куба, то длина ребра х искомого куба должно удовлетворять уравнению
x3 = 2a3, или x = 
Задача является естественным обобщением аналогичной задачей об удвоении квадрата, которая решается просто: стороной квадрата, площадь которого равна 2а2, служит отрезок длиной а , т.е. диагональ данного квадрата со стороной а. Наоборот удвоение куба, объём которого равен 2а3, т.е. отрезок х, равный
, т.е. диагональ данного квадрата со стороной а. Наоборот удвоение куба, объём которого равен 2а3, т.е. отрезок х, равный  , не может быть построен при помощи циркуля и линейки. Однако это было доказано лишь в первой половине XIX века.
, не может быть построен при помощи циркуля и линейки. Однако это было доказано лишь в первой половине XIX века.
Задача об удвоении куба носит так же название «делосской задачи» в связи со следующей легендой.
На острове Делос (в Эгейском море) распространялась эпидемия чумы. Когда жители острова обратились к оракулу за советом, как избавится от чумы, они получили ответ: «Удвойте жертвенник храма Аполлона». Сначала они считали, что задача легка. Так как жертвенник имел форму куба, они построили новый жертвенник, ребро которого было в два раза больше ребра старого жертвенника. Делосцы не знали, что таким образом они увеличили объём куба не в 2 раза, а в 8 раз. Чума ещё больше усилилась, и в ответ на вторичное обращение к оракулу последний посоветовал: «Получше изучайте геометрию…» Согласно другой легенде, бог приписал удвоение жертвенникам не потому, что ему нужен вдвое больший жертвенник, а потому, что хотел упрекнуть греков, «которые не думают о математике и не дорожат геометрией».
Задачей удвоения куба еще в V веке до н.э. занимался Гиппократ Хиосский, который впервые свел ее к решению следующей задачи: построить «два средних пропорциональных» отрезка х, у между данными отрезками а, b, т.е. найти х и у, которые удовлетворяли в следующей непрерывной пропорции:
а : х = х : у = у : b (1)
Одно из механических решений задач об удвоении куба, относящееся к IV веку до н.э., основано на методе двух средних пропорциональных. Отложим на стороне прямого угла отрезок AO=а, где а - длина ребра куба, а на другой его стороне – отрезок OB=2а. На продолжениях сторон прямого угла стараемся найти такие точки M и N , чтобы (АМ) и (ВN) были перпендикулярны к (MN); тогда OM = х и ON = у будут двумя серединами пропорциональными между отрезками AO и BO. Для этого устраивается угольник с подвижной линейкой.
Имеем:
AO: OM = OM : ON = ON : OB,
или
а : х = х : у = у : 2а.
Отсюда

или
 ,
,
т.е.
 .
.
Это значит, что отрезок OM искомый.
Архит Тарентский дал интересное стереометрическое решение «делосской задачи». После него, кроме Евдокса, дали свои решения Эратосфен, Никомед, Аполлоний, Герон, Папп и другие.
Заключение.
Итак, выполнив эту работу, я узнал много нового и интересного о знаменитых классических задачах древности, о людях, посвятивших себя решению данных задач, познакомился с историей возникновения данных задач, методами их решения.
Изучив весь этот материал, я понял, что все старания решить три знаменитые задачи при известных ограничивающих условиях (циркуль и линейка) привели только к доказательству, что подобное решение невозможно. Но, несмотря на это, интерес к этим классическим задачам не пропадает и сегодня. Многие современные математики пытаются решить эти знаменитые задачи.
Мне было интересно узнать, что при попытках решить эти задачи было сделано огромное число открытий, имеющих гораздо больший интерес и значение, чем сами поставленные задачи. Попытка Колумба открыть новый путь в Индию, плывя всё на запад, окончилась, как известно, неудачей. Но гениальная попытка великого человека привела к «попутному» открытию целой новой части света, перед богатством и умственным развитием которого бледнеют ныне все сокровища Индии. И теперь я знаю, что так необходимо и так должно было случиться.
В своей работе я обобщил собранный по теме реферата материал и подготовил для его защиты презентацию, сделанную в редакторе Power Point. Мне было интересно работать над выбранной темой реферата.
Древность завещала решение всех трёх задач нашим временам.
Список источников
http://images.google.ru/imgres?imgurl=http://www.distedu.ru/mirror/_math/www.tmn.fio.ru/works/07x/304/images/har7-8.jpg&imgrefurl=http://www.distedu.ru/mirror/_math/www.tmn.fio.ru/works/07x/304/d7.htm&usg=__b5S9TbEmekccqcjSzQap7pafKbI=&h=802&w=695&sz=105&hl=ru&start=41&um=1&tbnid=Q441sIJ77zsafM:&tbnh=143&tbnw=124&prev=/images%3Fq%3D%25D0%25BA%25D0%25B2%25D0%25B0%25D0%25B4%25D1%2580%25D0%25B0%25D1%2582%25D1%2583%25D1%2580%25D0%25B0%2B%25D0%25BA%25D1%2580%25D1%2583%25D0%25B3%25D0%25B0%26start%3D40%26ndsp%3D20%26um%3D1%26hl%3Dru%26lr%3D%26newwindow%3D1%26sa%3DN
Большая Советская Энциклопедия.
http://www.hawwa-sulamjt.narod.ru/4.htm
http://images.google.ru/imgres?imgurl=http://bibliotekar.ru/chip/222.jpg&imgrefurl=http://bibliotekar.ru/chip/1195-20.htm&usg=__f4qgALvuFPVhknx2EEJBdILbiLA=&h=235&w=619&sz=19&hl=ru&start=24&um=1&tbnid=Je6x9qlMpZqZzM:&tbnh=52&tbnw=136&prev=/images%3Fq%3D%25D0%25BA%25D0%25B2%25D0%25B0%25D0%25B4%25D1%2580%25D0%25B0%25D1%2582%25D1%2583%25D1%2580%25D0%25B0%2B%25D0%25BA%25D1%2580%25D1%2583%25D0%25B3%25D0%25B0%26start%3D20%26ndsp%3D20%26um%3D1%26hl%3Dru%26lr%3D%26newwindow%3D1%26sa%3DN
http://images.google.ru/imgres?imgurl=http://www.sciteclibrary.ru/ris-stat/st107/01.gif&imgrefurl=http://www.sciteclibrary.ru/rus/catalog/pages/2194.html&usg=__7m2njynOFsCC418zMhNh6KEufm8=&h=725&w=425&sz=56&hl=ru&start=27&um=1&tbnid=9Prz7Ynvs6k8UM:&tbnh=140&tbnw=82&prev=/images%3Fq%3D%25D1%2582%25D1%2580%25D0%25B8%25D1%2581%25D0%25B5%25D0%25BA%25D1%2586%25D0%25B8%25D1%258F%2B%25D1%2583%25D0%25B3%25D0%25BB%25D0%25B0%26start%3D20%26ndsp%3D20%26um%3D1%26hl%3Dru%26lr%3D%26newwindow%3D1%26sa%3DN
http://images.google.ru/imgres?imgurl=http://upload.wikimedia.org/wikipedia/commons/thumb/6/68/Morley_triangle.png/300px-Morley_triangle.png&imgrefurl=http://ru.wikipedia.org/wiki/%25D0%25A2%25D0%25B5%25D0%25BE%25D1%2580%25D0%25B5%25D0%25BC%25D0%25B0_%25D0%259C%25D0%25BE%25D1%2580%25D0%25BB%25D0%25B5%25D1%258F&usg=__zTZzKoORKn_wx47PjHNWWZFunu0=&h=226&w=300&sz=21&hl=ru&start=40&um=1&tbnid=vV0065iGQd1R7M:&tbnh=87&tbnw=116&prev=/images%3Fq%3D%25D1%2582%25D1%2580%25D0%25B8%25D1%2581%25D0%25B5%25D0%25BA%25D1%2586%25D0%25B8%25D1%258F%2B%25D1%2583%25D0%25B3%25D0%25BB%25D0%25B0%26start%3D20%26ndsp%3D20%26um%3D1%26hl%3Dru%26lr%3D%26newwindow%3D1%26sa%3DN
О квадратуре круга (Архимед, Гюйгенс, Ламберт, Лежандр). С приложением истории вопроса, пер. с нем., 3 изд., М. — Л., 1936; Стройк Д. Я., Краткий очерк истории математики, пер. с нем.,2 изд., М., 1969.
Кольман Э., История математики в древности, М., 1961, с. 103—05.
http://images.google.ru/imgres?imgurl=http://stf.karelia.ru/teleconf/1999/fig1-3.jpg&imgrefurl=http://stf.karelia.ru/teleconf/1999/doklad-19.htm&usg=__qjkz6siQyEkg4sfh2GpqOsY5FBo=&h=389&w=388&sz=29&hl=ru&start=8&um=1&tbnid=pSVSzNiuZJlK3M:&tbnh=123&tbnw=123&prev=/images%3Fq%3D%25D1%2582%25D1%2580%25D0%25B8%25D1%2581%25D0%25B5%25D0%25BA%25D1%2586%25D0%25B8%25D1%258F%2B%25D1%2583%25D0%25B3%25D0%25BB%25D0%25B0%26um%3D1%26hl%3Dru%26lr%3D%26newwindow%3D1%26sa%3DG
Приложение 1.
Памятник числу π.

Приложение 2
Таблица 1.
Сравнительный анализ способов построения трисектрисы угла.
| Авторы решения | Использован-ные средства и инструмен- ты | Лег- кость пост-роения | Точность | Возможное использование |
| для острого угла | для прямого угла | для тупого угла | для угла от 180° до 360° |
| Древние Греки | Циркуль и линейка без засечек | + + | С уменьшением угла точность уменьшается | + для угла α = π /2n, где n- натураль-ное число | + | - | Только для угла 180° и 360° |
| Архимед | Циркуль и линейка с двумя засечками | - | Менее точно по сравнению с первым способом | + | + | -? | -? |
| Папп Александрийский | Конхоида Никомеда, циркуль, линейка | - | Менее точно по сравнению с 1,2,4 | + | + | -? | -? |
| Гиппей | Открытая им квадратриса, циркуль, линейка | - | Менее точно, чем 1, но более точно, чем 2 и 3. Чем точнее построена квадратриса, тем точнее трисекция | + | + | + | + |
refdb.ru
Теорема Морли - WikiVisually
1. Теорема – In mathematics, a theorem is a statement that has been proved on the basis of previously established statements, such as other theorems, and generally accepted statements, such as axioms. A theorem is a consequence of the axioms. The proof of a theorem is a logical argument for the theorem statement given in accord with the rules of a deductive system. The proof of a theorem is interpreted as justification of the truth of the theorem statement. In light of the requirement that theorems be proved, the concept of a theorem is fundamentally deductive, in contrast to the notion of a scientific law, many mathematical theorems are conditional statements. In this case, the proof deduces the conclusion from conditions called hypotheses or premises, however, the conditional could be interpreted differently in certain deductive systems, depending on the meanings assigned to the derivation rules and the conditional symbol. Although they can be written in a symbolic form, for example, within the propositional calculus. In some cases, a picture alone may be sufficient to prove a theorem, because theorems lie at the core of mathematics, they are also central to its aesthetics. Theorems are often described as being trivial, or difficult, or deep and these subjective judgments vary not only from person to person, but also with time, for example, as a proof is simplified or better understood, a theorem that was once difficult may become trivial. On the other hand, a theorem may be simply stated. Fermats Last Theorem is a particularly well-known example of such a theorem, logically, many theorems are of the form of an indicative conditional, if A, then B. Such a theorem does not assert B, only that B is a consequence of A. In this case A is called the hypothesis of the theorem and B the conclusion. The theorem If n is an natural number then n/2 is a natural number is a typical example in which the hypothesis is n is an even natural number. To be proved, a theorem must be expressible as a precise, nevertheless, theorems are usually expressed in natural language rather than in a completely symbolic form, with the intention that the reader can produce a formal statement from the informal one. It is common in mathematics to choose a number of hypotheses within a given language and these hypotheses form the foundational basis of the theory and are called axioms or postulates. The field of known as proof theory studies formal languages, axioms. Some theorems are trivial, in the sense that they follow from definitions, axioms, a theorem might be simple to state and yet be deep
2. Треугольник – A triangle is a polygon with three edges and three vertices. It is one of the shapes in geometry. A triangle with vertices A, B, and C is denoted △ A B C, in Euclidean geometry any three points, when non-collinear, determine a unique triangle and a unique plane. This article is about triangles in Euclidean geometry except where otherwise noted, triangles can be classified according to the lengths of their sides, An equilateral triangle has all sides the same length. An equilateral triangle is also a polygon with all angles measuring 60°. An isosceles triangle has two sides of equal length, some mathematicians define an isosceles triangle to have exactly two equal sides, whereas others define an isosceles triangle as one with at least two equal sides. The latter definition would make all equilateral triangles isosceles triangles, the 45–45–90 right triangle, which appears in the tetrakis square tiling, is isosceles. A scalene triangle has all its sides of different lengths, equivalently, it has all angles of different measure. Hatch marks, also called tick marks, are used in diagrams of triangles, a side can be marked with a pattern of ticks, short line segments in the form of tally marks, two sides have equal lengths if they are both marked with the same pattern. In a triangle, the pattern is no more than 3 ticks. Similarly, patterns of 1,2, or 3 concentric arcs inside the angles are used to indicate equal angles, triangles can also be classified according to their internal angles, measured here in degrees. A right triangle has one of its interior angles measuring 90°, the side opposite to the right angle is the hypotenuse, the longest side of the triangle. The other two sides are called the legs or catheti of the triangle, special right triangles are right triangles with additional properties that make calculations involving them easier. One of the two most famous is the 3–4–5 right triangle, where 32 +42 =52, in this situation,3,4, and 5 are a Pythagorean triple. The other one is a triangle that has 2 angles that each measure 45 degrees. Triangles that do not have an angle measuring 90° are called oblique triangles, a triangle with all interior angles measuring less than 90° is an acute triangle or acute-angled triangle. If c is the length of the longest side, then a2 + b2 > c2, a triangle with one interior angle measuring more than 90° is an obtuse triangle or obtuse-angled triangle. If c is the length of the longest side, then a2 + b2 < c2, a triangle with an interior angle of 180° is degenerate
3. Правильный треугольник – In geometry, an equilateral triangle is a triangle in which all three sides are equal. In the familiar Euclidean geometry, equilateral triangles are also equiangular and they are regular polygons, and can therefore also be referred to as regular triangles. Thus these are properties that are unique to equilateral triangles, the three medians have equal lengths. The three angle bisectors have equal lengths, every triangle center of an equilateral triangle coincides with its centroid, which implies that the equilateral triangle is the only triangle with no Euler line connecting some of the centers. For some pairs of triangle centers, the fact that they coincide is enough to ensure that the triangle is equilateral, in particular, A triangle is equilateral if any two of the circumcenter, incenter, centroid, or orthocenter coincide. It is also equilateral if its circumcenter coincides with the Nagel point, for any triangle, the three medians partition the triangle into six smaller triangles. A triangle is equilateral if and only if any three of the triangles have either the same perimeter or the same inradius. A triangle is equilateral if and only if the circumcenters of any three of the triangles have the same distance from the centroid. Morleys trisector theorem states that, in any triangle, the three points of intersection of the adjacent angle trisectors form an equilateral triangle, a version of the isoperimetric inequality for triangles states that the triangle of greatest area among all those with a given perimeter is equilateral. That is, PA, PB, and PC satisfy the inequality that any two of them sum to at least as great as the third. By Eulers inequality, the triangle has the smallest ratio R/r of the circumradius to the inradius of any triangle, specifically. The triangle of largest area of all those inscribed in a circle is equilateral. The ratio of the area of the incircle to the area of an equilateral triangle, the ratio of the area to the square of the perimeter of an equilateral triangle,1123, is larger than that for any other triangle. If a segment splits an equilateral triangle into two regions with equal perimeters and with areas A1 and A2, then 79 ≤ A1 A2 ≤97, in no other triangle is there a point for which this ratio is as small as 2. For any point P in the plane, with p, q, and t from the vertices A, B. For any point P on the circle of an equilateral triangle, with distances p, q. There are numerous triangle inequalities that hold with equality if and only if the triangle is equilateral, an equilateral triangle is the most symmetrical triangle, having 3 lines of reflection and rotational symmetry of order 3 about its center. Its symmetry group is the group of order 6 D3
4. Кубика – Here F is a non-zero linear combination of the third-degree monomials x3, y3, z3, x2y, x2z, y2x, y2z, z2x, z2y, xyz. These are ten in number, therefore the cubic curves form a space of dimension 9. Each point P imposes a single linear condition on F, if we ask that C pass through P, if two cubics pass through a given set of nine points, then in fact a pencil of cubics does, and the points satisfy additional properties, see Cayley–Bacharach theorem. A cubic curve may have a point, in which case it has a parametrization in terms of a projective line. Otherwise a non-singular cubic curve is known to have nine points of inflection and this can be shown by taking the homogeneous version of the Hessian matrix, which defines again a cubic, and intersecting it with C, the intersections are then counted by Bézouts theorem. However, only three of these points may be real, so that the others cannot be seen in the projective plane by drawing the curve. The nine inflection points of a non-singular cubic have the property that every line passing through two of them contains exactly three inflection points, the real points of cubic curves were studied by Isaac Newton. The real points of a non-singular projective cubic fall into one or two ovals, the other oval, if it exists, does not contain any real inflection point and appears either as an oval or as two infinite branches. Like for conic sections, a line cuts this oval at, at most, a non-singular cubic defines an elliptic curve, over any field K for which it has a point defined. This does depend on having a K-rational point, which serves as the point at infinity in Weierstrass form, there are many cubic curves that have no such point, for example when K is the rational number field. The singular points of a plane cubic curve are quite limited, one double point. A reducible plane cubic curve is either a conic and a line or three lines, and accordingly have two points or a tacnode, or up to three double points or a single triple point if three lines. Suppose that ABC is a triangle with sidelengths a = | BC |, b = | CA |, relative to ABC, many named cubics pass through well-known points. Examples shown below use two kinds of coordinates, trilinear and barycentric. To convert from trilinear to barycentric in an equation, substitute as follows, x ↦ bcx, y ↦ cay, z ↦ abz, to convert from barycentric to trilinear, use x ↦ ax, y ↦ by. Many equations for cubics have the form f + f + f =0, in the examples below, such equations are written more succinctly in cyclic sum notation, like this, [cyclic sum f =0. The cubics listed below can be defined in terms of the conjugate, denoted by X*. Let LA be the reflection of line XA about the angle bisector of angle A
5. Япония – Japan is a sovereign island nation in Eastern Asia. Located in the Pacific Ocean, it lies off the eastern coast of the Asia Mainland and stretches from the Sea of Okhotsk in the north to the East China Sea, the kanji that make up Japans name mean sun origin. 日 can be read as ni and means sun while 本 can be read as hon, or pon, Japan is often referred to by the famous epithet Land of the Rising Sun in reference to its Japanese name. Japan is an archipelago consisting of about 6,852 islands. The four largest are Honshu, Hokkaido, Kyushu and Shikoku, the country is divided into 47 prefectures in eight regions. Hokkaido being the northernmost prefecture and Okinawa being the southernmost one, the population of 127 million is the worlds tenth largest. Japanese people make up 98. 5% of Japans total population, approximately 9.1 million people live in the city of Tokyo, the capital of Japan. Archaeological research indicates that Japan was inhabited as early as the Upper Paleolithic period, the first written mention of Japan is in Chinese history texts from the 1st century AD. Influence from other regions, mainly China, followed by periods of isolation, from the 12th century until 1868, Japan was ruled by successive feudal military shoguns who ruled in the name of the Emperor. Japan entered into a period of isolation in the early 17th century. The Second Sino-Japanese War of 1937 expanded into part of World War II in 1941, which came to an end in 1945 following the bombings of Hiroshima and Nagasaki. Japan is a member of the UN, the OECD, the G7, the G8, the country has the worlds third-largest economy by nominal GDP and the worlds fourth-largest economy by purchasing power parity. It is also the worlds fourth-largest exporter and fourth-largest importer, although Japan has officially renounced its right to declare war, it maintains a modern military with the worlds eighth-largest military budget, used for self-defense and peacekeeping roles. Japan is a country with a very high standard of living. Its population enjoys the highest life expectancy and the third lowest infant mortality rate in the world, in ancient China, Japan was called Wo 倭. It was mentioned in the third century Chinese historical text Records of the Three Kingdoms in the section for the Wei kingdom, Wa became disliked because it has the connotation of the character 矮, meaning dwarf. The 倭 kanji has been replaced with the homophone Wa, meaning harmony, the Japanese word for Japan is 日本, which is pronounced Nippon or Nihon and literally means the origin of the sun. The earliest record of the name Nihon appears in the Chinese historical records of the Tang dynasty, at the start of the seventh century, a delegation from Japan introduced their country as Nihon
6. Прямая Симсона – In geometry, given a triangle ABC and a point P on its circumcircle, the three closest points to P on lines AB, AC, and BC are collinear. The line through these points is the Simson line of P, the concept was first published, however, by William Wallace in 1797. If P and Q are points on the circumcircle, then the angle between the Simson lines of P and Q is half the angle of the arc PQ. In particular, if the points are diametrically opposite, their Simson lines are perpendicular, let H denote the orthocenter of the triangle ABC, then the Simson line of P bisects the segment PH in a point that lies on the nine-point circle. Given two triangles with the circumcircle, the angle between the Simson lines of a point P on the circumcircle for both triangles doesnt depend of P. The set of all Simson lines, when drawn, form an envelope in the shape of a known as the Steiner deltoid of the reference triangle. The construction of the Simson line that coincides with a side of the triangle yields a nontrivial point on this side line. This point is the reflection of the foot of the altitude about the midpoint of the line being constructed. Furthermore this point is a tangent point between the side of the triangle and its Steiner deltoid. A quadrilateral that is not a parallelogram has one and only one point, called the Simson point. The Simson point of a trapezoid is the point of intersection of the two nonparallel sides, no convex polygon with at least 5 sides has a Simson line. The method of proof is to show that ∠ N M P + ∠ P M L =180 ∘. P C A B is a quadrilateral, so ∠ P B N + ∠ A C P = ∠ P B A + ∠ A C P =180 ∘. P M N B is a quadrilateral, so ∠ P B N + ∠ N M P =180 ∘. Now P L C M is cyclic, so ∠ P M L = ∠ P C L =180 ∘ − ∠ A C P, therefore ∠ N M P + ∠ P M L = ∠ A C P + =180 ∘. Let ABC be a triangle, let a line ℓ through circumcenter O, let AP, BP, CP meet ℓ at Ap, Bp, Cp respectively. Let A0, B0, C0 the projections of Ap, Bp, Cp onto BC, CA, AB, moreover, the new line passes through the midpoint of OH, where H the orthocenter of ΔABC. If ℓ passes through P, the line coincides with the Simson line, let a circumconic of the triangle ABC, let Q, P be two points on the plane
7. Окружность девяти точек – In geometry, the nine-point circle is a circle that can be constructed for any given triangle. It is so named because it passes through nine significant concyclic points defined from the triangle and these nine points are, The midpoint of each side of the triangle The foot of each altitude The midpoint of the line segment from each vertex of the triangle to the orthocenter. Its center is the nine-point center of the triangle, the diagram above shows the nine significant points of the nine-point circle. Points D, E, and F are the midpoints of the three sides of the triangle, points G, H, and I are the feet of the altitudes of the triangle. Points J, K, and L are the midpoints of the segments between each altitudes vertex intersection and the triangles orthocenter. For an acute triangle, six of the lie on the triangle itself. But soon after Feuerbach, mathematician Olry Terquem himself proved the existence of the circle and he was the first to recognize the added significance of the three midpoints between the triangles vertices and the orthocenter. Thus, Terquem was the first to use the name nine-point circle, the circle which passes through the feet of the altitudes of a triangle is tangent to all four circles which in turn are tangent to the three sides of the triangle. The triangle center at which the incircle and the nine-point circle touch is called the Feuerbach point, the radius of a triangles circumcircle is twice the radius of that triangles nine-point circle. Figure 3 A nine-point circle bisects a line segment going from the triangles orthocenter to any point on its circumcircle. Figure 4 The center N of the nine-point circle bisects a segment from the orthocenter H to the circumcenter O, the nine-point center N is one-fourth of the way along the Euler line from the centroid G to the orthocenter H, HN = 3NG. The nine-point circle of a triangle is the circumcircle of both the reference triangles medial triangle and its orthic triangle. The center of all rectangular hyperbolas that pass through the vertices of a triangle lies on its nine-point circle, examples include the well-known rectangular hyperbolas of Keipert, Jeřábek and Feuerbach. This fact is known as the Feuerbach conic theorem, if an orthocentric system of four points A, B, C and H is given, then the four triangles formed by any combination of three distinct points of that system all share the same nine-point circle. This is a consequence of symmetry, the sides of one triangle adjacent to a vertex that is an orthocenter to another triangle are segments from that second triangle, a third midpoint lies on their common side. Consequently, these four triangles have circumcircles with identical radii, let N represent the common nine-point center and P be an arbitrary point in the plane of the orthocentric system. As P approaches N the locus of P for the corresponding constant K, furthermore the nine-point circle is the locus of P such that PA2+PB2+PC2+Ph3 = 4R2. The centers of the incircle and excircles of a triangle form an orthocentric system, the nine-point circle created for that orthocentric system is the circumcircle of the original triangle
8. Замечательные точки треугольника – For example the centroid, circumcenter, incenter and orthocenter were familiar to the ancient Greeks, and can be obtained by simple constructions. Each of these classical centers has the property that it is invariant under similarity transformations, in other words, for any triangle and any similarity transformation, the center of the transformed triangle is the same point as the transformed center of the original triangle. This invariance is the property of a triangle center. It rules out other points such as the Brocard points which are not invariant under reflection. All centers of an equilateral triangle coincide at its centroid, the definitions and properties of thousands of triangle centers have been collected in the Encyclopedia of Triangle Centers. Even though the ancient Greeks discovered the classic centers of a triangle they had not formulated any definition of a triangle center. After the ancient Greeks, several special points associated with a triangle like the Fermat point, nine-point center, symmedian point, Gergonne point, as of 11 November 2014, Clark Kimberlings Encyclopedia of Triangle Centers contains an annotated list of 6,102 triangle centers. A real-valued function f of three variables a, b, c may have the following properties, Homogeneity, f = tn f for some constant n. Bisymmetry in the second and third variables, f = f, if a non-zero f has both these properties it is called a triangle center function. If f is a triangle center function and a, b, c are the side-lengths of a triangle then the point whose trilinear coordinates are f, f, f is called a triangle center. This definition ensures that triangle centers of similar triangles meet the criteria specified above. By convention only the first of the three coordinates of a triangle center is quoted since the other two are obtained by cyclic permutation of a, b, c. This process is known as cyclicity, every triangle center function corresponds to a unique triangle center. Different functions may define the same triangle center, for example the functions f1 = 1/a and f2 = bc both correspond to the centroid. Two triangle center functions define the same triangle center if and only if their ratio is a function symmetric in a, b and c, even if a triangle center function is well-defined everywhere the same cannot always be said for its associated triangle center. For example let f be 0 if a/b and a/c are both rational and 1 otherwise, then for any triangle with integer sides the associated triangle center evaluates to 0,0,0 which is undefined. In some cases these functions are not defined on the whole of ℝ3, for example the trilinears of X365 are a1/2, b1/2, c1/2 so a, b, c cannot be negative. Furthermore in order to represent the sides of a triangle they must satisfy the triangle inequality, so, in practice, every functions domain is restricted to the region of ℝ3 where a ≤ b + c, b ≤ c + a, and c ≤ a + b
9. Трисекция угла – Angle trisection is a classical problem of compass and straightedge constructions of ancient Greek mathematics. It concerns construction of an equal to one third of a given arbitrary angle. The problem as stated is generally impossible to solve, as proved by Pierre Wantzel in 1837, however, although there is no way to trisect an angle in general with just a compass and a straightedge, some special angles can be trisected. For example, it is straightforward to trisect a right angle. It is possible to trisect an angle by using tools other than straightedge. For example, neusis construction, also known to ancient Greeks, involves simultaneous sliding and rotation of a marked straightedge, other techniques were developed by mathematicians over the centuries. Because it is defined in terms, but complex to prove unsolvable. These solutions often involve mistaken interpretations of the rules, or are simply incorrect, three problems proved elusive, specifically, trisecting the angle, doubling the cube, and squaring the circle. The problem of angle trisection reads, Construct an angle equal to one-third of an arbitrary angle. Pierre Wantzel published a proof of the impossibility of trisecting an arbitrary angle in 1837. Wantzels proof, restated in modern terminology, uses the algebra of field extensions. However Wantzel published these results earlier than Galois and did not use the connection between field extensions and groups that is the subject of Galois theory itself. The problem of constructing an angle of a given measure θ is equivalent to constructing two segments such that the ratio of their length is cos θ. From a solution to one of two problems, one may pass to a solution of the other by a compass and straightedge construction. The triple-angle formula gives an expression relating the cosines of the angle and its trisection. It follows that, given a segment that is defined to have unit length and this equivalence reduces the original geometric problem to a purely algebraic problem. Every irrational number which is constructible in a step from some given numbers is a root of a polynomial of degree 2 with coefficients in the field generated by these numbers. Therefore, any number which is constructible by a sequence of steps is a root of a polynomial whose degree is a power of two
10. Построение с помощью циркуля и линейки – The idealized ruler, known as a straightedge, is assumed to be infinite in length, and has no markings on it and only one edge. The compass is assumed to collapse when lifted from the page, more formally, the only permissible constructions are those granted by Euclids first three postulates. It turns out to be the case that every point constructible using straightedge, the ancient Greek mathematicians first conceived compass-and-straightedge constructions, and a number of ancient problems in plane geometry impose this restriction. The ancient Greeks developed many constructions, but in cases were unable to do so. Gauss showed that some polygons are constructible but that most are not, some of the most famous straightedge-and-compass problems were proven impossible by Pierre Wantzel in 1837, using the mathematical theory of fields. In spite of existing proofs of impossibility, some persist in trying to solve these problems, in terms of algebra, a length is constructible if and only if it represents a constructible number, and an angle is constructible if and only if its cosine is a constructible number. A number is constructible if and only if it can be using the four basic arithmetic operations. Circles can only be starting from two given points, the centre and a point on the circle. The compass may or may not collapse when its not drawing a circle, the straightedge is infinitely long, but it has no markings on it and has only one straight edge, unlike ordinary rulers. It can only be used to draw a segment between two points or to extend an existing segment. The modern compass generally does not collapse and several modern constructions use this feature and it would appear that the modern compass is a more powerful instrument than the ancient collapsing compass. However, by Proposition 2 of Book 1 of Euclids Elements, although the proposition is correct, its proofs have a long and checkered history. Eyeballing it and getting close does not count as a solution and that is, it must have a finite number of steps, and not be the limit of ever closer approximations. One of the purposes of Greek mathematics was to find exact constructions for various lengths, for example. The Greeks could not find constructions for these three problems, among others, Squaring the circle, Drawing a square the same area as a given circle, doubling the cube, Drawing a cube with twice the volume of a given cube. Trisecting the angle, Dividing a given angle into three smaller angles all of the same size, for 2000 years people tried to find constructions within the limits set above, and failed. All three have now been proven under mathematical rules to be generally impossible, the ancient Greek mathematicians first attempted compass-and-straightedge constructions, and they discovered how to construct sums, differences, products, ratios, and square roots of given lengths. They could also construct half of an angle, a square whose area is twice that of another square, a square having the same area as a given polygon
wikivisually.com
Теорема Морли — Википедия (с комментариями)
Материал из Википедии — свободной энциклопедии
У этого термина существуют и другие значения, см. Морли. Теорема Морли[1], или теорема Морлея[2] о трисектрисах — одна из интереснейших теорем геометрии треугольника. Трисектрисами угла называются два луча, делящие угол на три равные части.
Формулировка

На чертеже три разноцветных угла при каждой вершине большого треугольника равны. Независимо от выбора большого треугольника маленький фиолетовый треугольник будет равносторонним.
История
Теорема была открыта в 1904 году Фрэнком Морли в связи с изучением свойств кубических кривых. Тогда он упомянул об этой теореме своим друзьям, а опубликовал её двадцать лет спустя в Японии. За это время она была независимо опубликована как задача в журнале Educational Times[en].
Вариации и обобщения
- Если рассмотреть также внешние трисектрисы (то есть трисектрисы внешних углов треугольника), то среди точек пересечения этих 12 прямых существует 27 троек точек, образующих правильные треугольники.
Замечание
Существуют точки Морлея −1-я и 2-я, связанные с треугольником Морлея (1ST AND 2ND Morley Centers)faculty.evansville.edu/ck6/tcenters/recent/morley.html (см. Недавно открытые точки (центры) треугольника)
См. также
Напишите отзыв о статье "Теорема Морли"
Примечания
Отрывок, характеризующий Теорема Морли
Под влиянием выпитого вина и после дней, проведенных в уединении с своими мрачными мыслями, Пьер испытывал невольное удовольствие в разговоре с этим веселым и добродушным человеком. – Pour en revenir a vos dames, on les dit bien belles. Quelle fichue idee d'aller s'enterrer dans les steppes, quand l'armee francaise est a Moscou. Quelle chance elles ont manque celles la. Vos moujiks c'est autre chose, mais voua autres gens civilises vous devriez nous connaitre mieux que ca. Nous avons pris Vienne, Berlin, Madrid, Naples, Rome, Varsovie, toutes les capitales du monde… On nous craint, mais on nous aime. Nous sommes bons a connaitre. Et puis l'Empereur! [Но воротимся к вашим дамам: говорят, что они очень красивы. Что за дурацкая мысль поехать зарыться в степи, когда французская армия в Москве! Они пропустили чудесный случай. Ваши мужики, я понимаю, но вы – люди образованные – должны бы были знать нас лучше этого. Мы брали Вену, Берлин, Мадрид, Неаполь, Рим, Варшаву, все столицы мира. Нас боятся, но нас любят. Не вредно знать нас поближе. И потом император…] – начал он, но Пьер перебил его. – L'Empereur, – повторил Пьер, и лицо его вдруг привяло грустное и сконфуженное выражение. – Est ce que l'Empereur?.. [Император… Что император?..] – L'Empereur? C'est la generosite, la clemence, la justice, l'ordre, le genie, voila l'Empereur! C'est moi, Ram ball, qui vous le dit. Tel que vous me voyez, j'etais son ennemi il y a encore huit ans. Mon pere a ete comte emigre… Mais il m'a vaincu, cet homme. Il m'a empoigne. Je n'ai pas pu resister au spectacle de grandeur et de gloire dont il couvrait la France. Quand j'ai compris ce qu'il voulait, quand j'ai vu qu'il nous faisait une litiere de lauriers, voyez vous, je me suis dit: voila un souverain, et je me suis donne a lui. Eh voila! Oh, oui, mon cher, c'est le plus grand homme des siecles passes et a venir. [Император? Это великодушие, милосердие, справедливость, порядок, гений – вот что такое император! Это я, Рамбаль, говорю вам. Таким, каким вы меня видите, я был его врагом тому назад восемь лет. Мой отец был граф и эмигрант. Но он победил меня, этот человек. Он завладел мною. Я не мог устоять перед зрелищем величия и славы, которым он покрывал Францию. Когда я понял, чего он хотел, когда я увидал, что он готовит для нас ложе лавров, я сказал себе: вот государь, и я отдался ему. И вот! О да, мой милый, это самый великий человек прошедших и будущих веков.]wiki-org.ru
 Фрэнк Морли (1860–1937) — английский математик, известный своими работами по алгебре и геометрии. Морли любил придумывать задачи, и за более чем 50 лет своей работы со времени окончания Кембриджского университета он опубликовал более 60 задач в Educational Times. Большинство этих задач — геометрические. Морли очень хорошо играл в шахматы. Одни раз он даже выиграл у чемпиона мира по шахматам Эмануэля Ласкера (примеч. Интересно, что Ласкер тоже занимался математикой, и одна из теорем названа его именем — теорема Ласкера — Нётер). Морли внес огромный вклад в развитие математики в США. В течение 30 лет он был редактором журнала American Journal of Mathematics, работал и в журнале Bulletin of the American Mathematical Society, в 1919–20 годах был президентом Американского математического общества.
Фрэнк Морли (1860–1937) — английский математик, известный своими работами по алгебре и геометрии. Морли любил придумывать задачи, и за более чем 50 лет своей работы со времени окончания Кембриджского университета он опубликовал более 60 задач в Educational Times. Большинство этих задач — геометрические. Морли очень хорошо играл в шахматы. Одни раз он даже выиграл у чемпиона мира по шахматам Эмануэля Ласкера (примеч. Интересно, что Ласкер тоже занимался математикой, и одна из теорем названа его именем — теорема Ласкера — Нётер). Морли внес огромный вклад в развитие математики в США. В течение 30 лет он был редактором журнала American Journal of Mathematics, работал и в журнале Bulletin of the American Mathematical Society, в 1919–20 годах был президентом Американского математического общества. равносторонний.
равносторонний.
 сумма углов
сумма углов  , имеем
, имеем![Rendered by QuickLaTeX.com \[\alpha+\beta+\gamma+\pi/3.\]](/800/600/http/hijos.ru//wp-content/ql-cache/quicklatex.com-ea0ea12d9b1aacccdd8516e4fa9e2e2a_l3.png)
 — точки на высотах треугольника
— точки на высотах треугольника ![Rendered by QuickLaTeX.com \[\angle XPY=\angle XPZ=\alpha+\frac{\pi}{6},\]](/800/600/http/hijos.ru//wp-content/ql-cache/quicklatex.com-bf3f56d6b107e47c4dcd73a1e925f251_l3.png)
![Rendered by QuickLaTeX.com \[\angle YQZ=\angle YQX=\beta+\frac{\pi}{6},\]](/800/600/http/hijos.ru//wp-content/ql-cache/quicklatex.com-920dd76292c03a8bc80b72b477bc4b86_l3.png)
![Rendered by QuickLaTeX.com \[\angle ZRX=\angle ZRY=\gamma+\frac{\pi}{6}.\]](/800/600/http/hijos.ru//wp-content/ql-cache/quicklatex.com-746d3186cf1e829ac5b791ebfc5fac88_l3.png)

 — точка пересечения
— точка пересечения  и
и  ,
,  — точка пересечения
— точка пересечения  и
и  , и
, и  — точка пересечения
— точка пересечения  и
и  . Тогда в четырехугольнике
. Тогда в четырехугольнике 
![Rendered by QuickLaTeX.com \[\angle AQX=2\beta+\frac{\pi}{3},\]](/800/600/http/hijos.ru//wp-content/ql-cache/quicklatex.com-bfde8e6dd12a69ab99fa49b645395019_l3.png)
![Rendered by QuickLaTeX.com \[\angle ARX=2\gamma+\frac{\pi}{3},\]](/800/600/http/hijos.ru//wp-content/ql-cache/quicklatex.com-9522853b8908cb0c30d87227d344a099_l3.png)
![Rendered by QuickLaTeX.com \[\angle QXR=2\alpha+\beta+\gamma+\frac{\pi}{3}.\]](/800/600/http/hijos.ru//wp-content/ql-cache/quicklatex.com-d081769adb445de759151178a8abd49d_l3.png)
 . Аналогично,
. Аналогично,  и
и  .
.  , касающуюся
, касающуюся  . Так как
. Так как  — биссектриса
— биссектриса  , то эта окружность также касается
, то эта окружность также касается  . Теперь проведем касательные к окружности
. Теперь проведем касательные к окружности  и
и  . Обозначим через
. Обозначим через  точку пересечения этих касательных. Тогда
точку пересечения этих касательных. Тогда![Rendered by QuickLaTeX.com \[\angle XBT=\angle XBZ=\beta\]](/800/600/http/hijos.ru//wp-content/ql-cache/quicklatex.com-6073ab54f38634e0a2940a61e185383b_l3.png)
![Rendered by QuickLaTeX.com \[\angle XCU=\angle XCY=\gamma.\]](/800/600/http/hijos.ru//wp-content/ql-cache/quicklatex.com-cdb0e6aae978174f30f85054e79ad4de_l3.png)
 и
и  равна
равна![Rendered by QuickLaTeX.com \[\displaystyle 2\alpha+\frac{\pi}{3}+2\beta+2\gamma=\pi,\]](/800/600/http/hijos.ru//wp-content/ql-cache/quicklatex.com-aa99f10c053ec9fa33806814bdaf52d7_l3.png)
 . Другими словами,
. Другими словами,  — прямая, так что точки
— прямая, так что точки  и
и  . Аналогично определяются углы треугольников
. Аналогично определяются углы треугольников  и
и  , откуда получаем, что углы треугольника
, откуда получаем, что углы треугольника  и
и  . Если необходимо, этот треугольник можно заменить подобным ему, который будет совпадать с
. Если необходимо, этот треугольник можно заменить подобным ему, который будет совпадать с  .
.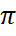 , имеем α + β + γ +
, имеем α + β + γ + 

 + 2 β + 2 γ =
+ 2 β + 2 γ = 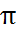 ,
, сли обозначить радиус круга через r, то речь будет идти о построении квадрата, площадь которого равна πr2, а сторона равна r
сли обозначить радиус круга через r, то речь будет идти о построении квадрата, площадь которого равна πr2, а сторона равна r . Теперь известно, что число π - отношение окружности к своему диаметру – число иррациональное. Оно выражается бесконечной непериодической десятичной дробью 3,1415926… и было, между прочим, вычислено с 707 десятичными знаками математиком В. Шенксом. Этот результат вместе с формулой вычислений он обнародовал в 1837 году. Ни одна ещё задача подобного рода не решалась с таким огромным приближением и с точностью, далеко превышающее отношение микроскопических расстояний к телескопическим.
. Теперь известно, что число π - отношение окружности к своему диаметру – число иррациональное. Оно выражается бесконечной непериодической десятичной дробью 3,1415926… и было, между прочим, вычислено с 707 десятичными знаками математиком В. Шенксом. Этот результат вместе с формулой вычислений он обнародовал в 1837 году. Ни одна ещё задача подобного рода не решалась с таким огромным приближением и с точностью, далеко превышающее отношение микроскопических расстояний к телескопическим. вадратурой круга занимался также самый знаменитый геометр V века до н.э. – Гиппократ Хиосский. У многих занимавшихся этой задачей возникало сомнение, возможно ли вообще построить прямолинейную фигуру, равновеликую криволинейной. Эта возможность была доказана Гиппократом, построившим лунообразные фигуры (Рис. 1), известных под названием «гиппократовых луночек». В полукруг с диаметром BC вписан равнобедренный прямоугольный треугольник BAC (BC=AC). На AB и AC, как на диаметрах, описываются полуокружности.
вадратурой круга занимался также самый знаменитый геометр V века до н.э. – Гиппократ Хиосский. У многих занимавшихся этой задачей возникало сомнение, возможно ли вообще построить прямолинейную фигуру, равновеликую криволинейной. Эта возможность была доказана Гиппократом, построившим лунообразные фигуры (Рис. 1), известных под названием «гиппократовых луночек». В полукруг с диаметром BC вписан равнобедренный прямоугольный треугольник BAC (BC=AC). На AB и AC, как на диаметрах, описываются полуокружности.  =AB
=AB площадей кругов или полукругов BMAEC и AECD равно, как впервые доказал сам Гиппократ, отношению квадратов соответствующих диаметров
площадей кругов или полукругов BMAEC и AECD равно, как впервые доказал сам Гиппократ, отношению квадратов соответствующих диаметров  , которые в силу (1) равно 2. Итак, площадь сектора OAC равна площади полукруга, построенного на диаметре AC. Если из обеих этих равных площадей вычесть площадь сегмента ACE, то и получим, что площадь треугольника AOC равна площади луночки ADCE, или сумма площадей обеих луночек равна площади равнобедренного треугольника BCA. Гиппократ нашёл и другие луночки, допускающие квадратуру, и продолжал свои изыскания в надежде дойти до квадратуры круга, что ему, конечно, не удалось.
, которые в силу (1) равно 2. Итак, площадь сектора OAC равна площади полукруга, построенного на диаметре AC. Если из обеих этих равных площадей вычесть площадь сегмента ACE, то и получим, что площадь треугольника AOC равна площади луночки ADCE, или сумма площадей обеих луночек равна площади равнобедренного треугольника BCA. Гиппократ нашёл и другие луночки, допускающие квадратуру, и продолжал свои изыскания в надежде дойти до квадратуры круга, что ему, конечно, не удалось. , и содействовала развитию новых понятий и идей в математике.
, и содействовала развитию новых понятий и идей в математике.
 оворят, что такое ограничение вспомогательных приборов было введено знаменитым греческим философом Платоном.
оворят, что такое ограничение вспомогательных приборов было введено знаменитым греческим философом Платоном. = 30о.
= 30о. Построим биссектрису AD угла САВ, получаем искомое деление прямого угла MAN
Построим биссектрису AD угла САВ, получаем искомое деление прямого угла MAN ,
,  ,
,  , п – натуральное число), однако не в общем случае, т.е. любой угол невозможно разделить на три равных части с помощью только циркуля и линейки. Это было доказано лишь в первой половине ХIХ в.
, п – натуральное число), однако не в общем случае, т.е. любой угол невозможно разделить на три равных части с помощью только циркуля и линейки. Это было доказано лишь в первой половине ХIХ в.

 ,
,
 ,
,
 тсюда следует так называемый способ «вставки» для деления на три равные части угла AOE. Описав окружность с центром O и радиусом OE и OA, проводим диаметр EF. Линейку CB на которой нанесена длина CB радиуса r (например, помощью двух штрихов), прикладываем и двигаем так, чтобы её точка C скользила по продолжению диаметра (EF), а сома линейка всё время проходила бы через точку A окружности, пока точка B линейки не окажется на окружности. Тогда угол BCF и будет искомой третьей частью угла AOE (Рис.5). Как видно, в этом приёме используется вставка отрезка CB между продолжением диаметра EF и окружностью так, чтобы продолжение отрезка CB прошло через заданную точку A окружности. В указанном выше построении применяется, помимо циркуля, не просто линейка как инструмент для проведения прямых, а линейка с делениями, которая даёт длину определённого отрезка.
тсюда следует так называемый способ «вставки» для деления на три равные части угла AOE. Описав окружность с центром O и радиусом OE и OA, проводим диаметр EF. Линейку CB на которой нанесена длина CB радиуса r (например, помощью двух штрихов), прикладываем и двигаем так, чтобы её точка C скользила по продолжению диаметра (EF), а сома линейка всё время проходила бы через точку A окружности, пока точка B линейки не окажется на окружности. Тогда угол BCF и будет искомой третьей частью угла AOE (Рис.5). Как видно, в этом приёме используется вставка отрезка CB между продолжением диаметра EF и окружностью так, чтобы продолжение отрезка CB прошло через заданную точку A окружности. В указанном выше построении применяется, помимо циркуля, не просто линейка как инструмент для проведения прямых, а линейка с делениями, которая даёт длину определённого отрезка. и
и  .
. как накрест лежащие. Разделим PQ пополам и середину N соединим с М прямой NM. Точка N есть середина гипотенузы прямоугольного треугольника PQM, а потому PN = NМ, а, следовательно, треугольник PNM равнобедренный, и значит
как накрест лежащие. Разделим PQ пополам и середину N соединим с М прямой NM. Точка N есть середина гипотенузы прямоугольного треугольника PQM, а потому PN = NМ, а, следовательно, треугольник PNM равнобедренный, и значит

 .
.



 еорема утверждает:
еорема утверждает:  адача состоит в построении куба, имеющий объём, вдвое больше объёма данного куба. Если обозначить через а ребро данного куба, то длина ребра х искомого куба должно удовлетворять уравнению
адача состоит в построении куба, имеющий объём, вдвое больше объёма данного куба. Если обозначить через а ребро данного куба, то длина ребра х искомого куба должно удовлетворять уравнению
 , т.е. диагональ данного квадрата со стороной а. Наоборот удвоение куба, объём которого равен 2а3, т.е. отрезок х, равный
, т.е. диагональ данного квадрата со стороной а. Наоборот удвоение куба, объём которого равен 2а3, т.е. отрезок х, равный  , не может быть построен при помощи циркуля и линейки. Однако это было доказано лишь в первой половине XIX века.
, не может быть построен при помощи циркуля и линейки. Однако это было доказано лишь в первой половине XIX века.
 ,
, .
.
