При изучении этой темы необходимо обеспечитьусвоение детьми рациональных вычислительных приемов сложения и вычитания в пределах первого десятка; сформировать прочные вычислительные навыки; добиться запоминания наизусть результатов сложения и вычитания, а также состава чисел из слагаемых.
В органической связи с изучением сложения и вычитания включаются элементы алгебры и геометрии: дети знакомятся с математическими выражениями, уравнениями и неравенствами. Рассматриваются геометрические фигуры, выполняются упражнения на составление фигур, измерение и черчение отрезков, вычленение фигур из заданной фигуры.
Задачи изучения темы:
1. Разъяснить смысл действий сложения и вычитания.
2. Сформировать вычислительные приемы сложения и вычитания.
3. Сформировать навыки табличного сложения и вычитания в тесной связи с усвоением состава чисел в пределах 10.
4. Ознакомить с названиями компонентов и результатов действий сложения и вычитания. Рассмотреть сумму, разность как выражение.
6. Разъяснить взаимосвязь между суммой и слагаемыми.
Методику ознакомления с вычислительными приемами можно изобразить в соответствии с планом изучения в виде схемы:
|
|
|
|
| | | | |
|
|
|
План изучения:
1. Подготовительный этап: раскрытие конкретного смысла действий сложения и вычитания, запись и чтение примеров, случаи прибавления и вычитания 1, на основе образования последовательности натуральных чисел.
2. Изучение приемов присчитывания и отсчитывания группами: по 2, по3, по 4.
3. Изучение приема перестановки слагаемых для случаев прибавления 5, 6, 7, 8, 9. Таблицы сложения и состав чисел из слагаемых.
4. Изучение приема вычитания на основе знания связи между суммой и слагаемыми для случаев вычитания 5, 6, 7, 8, 9.
Подготовительная работа к изучению сложения и вычитания начинается с первых уроков. Рассматриваются случаи а±1, а±2. На практике, при решении задач необходимо показать, что операции объединения множеств соответствует действие сложения, а операции удаления части множества – действие вычитания. Когда прибавляют, становится больше, чем было; когда вычитают, становится меньше.
К концу изучения нумерации учащиеся должны прочно усвоить способы образования любого числа первого десятка присчитыванием и отсчитыванием единицы и, используя этот прием (а не пересчитывание), свободно выполнять сложение и вычитание с единицей. Постепенно дети обобщают свои наблюдения и формулируют выводы: прибавить 1 к числу—значит назвать следующее за ним число; вычесть 1 из числа — значит назвать предшествующее ему число. На специально отведенном уроке приводят в систему все изученные случаи а±1, под руководством учителя дети составляют таблицы «прибавить I» и «вычесть I» и затем заучивают их наизусть.
На втором этапе рассматривают случаи сложения и вычитания вида: а±2, а±3, а±4, результаты которых находятся присчитыванием или отсчитыванием.
Чтобы подчеркнуть, с одной стороны, сходство вычислительных приемов, а с другой стороны, противоположный характер действий сложения и вычитания, случаи «прибавить 2» и «вычесть 2» так же, как позднее случаи «прибавить З» и «вычесть З», затем «прибавить 4» и «вычесть 4», изучаются одновременно в сопоставлении друг с другом.
Работа над вычислительными навыками строится по такому плану:
1) подготовительные упражнения;
2) знакомство с приемами вычисления;
3) закрепление знания приемов, выработка вычислительного навыка;
4) составление и заучивание таблиц.
Рассмотрим методику ознакомления с вычислительным приемом «прибавить и вычесть 2».
На подготовительном этапе (за 1—2 урока до изучения темы) рекомендуется научить детей решать примеры в два действия вида: 64-1+1, 9-1-1, чтобы дети закрепили умения прибавлять и вычитать единицу и накопили наблюдения: если прибавим (вычтем) 1 и еще 1, то всего прибавим (вычтем) 2. Вначале решение таких примеров иллюстрируют действиями с предметами, например: «Положите 4 синих квадрата, придвиньте 1 желтый квадрат. Сколько квадратов получилось? Придвиньте еще 1 желтый квадрат. Сколько квадратов получилось? Запишите пример: 4+1+1, объясните, как решаем такой пример (к 4 прибавить 1, получится 5; к 5 прибавить 1, получится 6».
Так же рассматривается пример 7 - 1 – 1.
На уроке по ознакомлению с новыми приемами вычислений вначале так же выполняют несколько подготовительных упражнений, а потом объясняют сам прием.
Затем приступают к рассмотрению приема прибавления и вычитания числа 2.
Учитель ставит цель перед детьми - научиться прибавлять и вычитать число 2. Решение первых примеров выполняется с опорой на предметное действие. Решается пример 4+2. Пусть эти букеты на окне изображают число 4, а эти 2 букета на столе — число 2. Покажите, как эти 2 букета присоединить к тем 4 букетам (ученик переносит цветы на окно: сначала один букет, потом второй). Запишем то, что сделал Вова. Сколько сначала к 4 прибавили? Сколько получилось? Как же можно прибавить 2 к 4? Чтобы прибавить 2 к 4, надо прибавить сначала 1 к 4, получится 5, а потом прибавить к 5 еще 1, получится 6).
На доске запись:
4+2=6
4+1=5
5+1=6
Далее ученики выполняют задание: рисуют в тетрадях, например, 7 яблок, затем 2 яблока раскрашивают, записывают пример 7—2 и, опираясь на свою практическую работу (сначала раскрасили 1 яблоко, а потом еще 1 яблоко), объясняют, как вычесть 2 (из 7 вычесть 1, получится 6; из 6 вычесть 1, получится 5).
В таком же плане рассматривается еще пара заданий (например, по иллюстрациям в учебнике), а затем уже переходят к решению примеров с пояснением приемов вычислений. В результате такой работы дети к концу урока усваивают, как можно прибавить 2 к любому числу и как вычесть 2 из любого числа.
С помощью аналогичных упражнений раскрываются приемы вычислений для случаев а±3 и а±4. Чтобы дети применяли здесь свои умения прибавлять и вычитать 2, при решении примеров на сложение и вычитание с числами 3 и 4, они должны представить 3 как 2 и 1 или как 1 и 2, а число 4 как 2 и 2. Приемы вычислений также иллюстрируют действиями с предметами и на первых порах несколько примеров решают с подробной записью приема.
Для приема а±4 запись может быть такой: 5+4=5+2+2, 10-4=10-2-2. Такие записи готовят учащихся к изучению свойств арифметических действий.
Упражнения выполняются до тех пор, пока не станут прочными навыками. Вначале примеры решаются с подробными пояснениями приема вычисления вслух, постепенно пояснения сокращаются, затем проговариваются кратко про себя. С целью выработки навыков включаются устные упражнения (устный счет, игры «молчанка», «эстафета», «лесенка», «круговые примеры» и др.). Очень полезны арифметические диктанты - устные вычисления с показом ответов разрезными цифрами или записью ответов в тетрадях. Выполняются также разнообразные письменные упражнения в решении примеров и задач. Особенно ценны упражнения с элементами творчества, догадки: составить примеры, задачи, исправить неверно решенные примеры, вставить пропущенное число или знак действия в примерах: -3=7. 8-=6, 8+0=10; 6*4=10, 6*4=2.
Эффективными для формирования вычислительных навыков являются упражнения с равенствами и неравенствами: сравнить выражения и вставить знаки «>», «<» или «=»: 7+2*7, 10—З* 4; проверить, правильно ли поставлены знаки в заданных равенствах и неравенствах: 6+4<10, 6+3>10, 8+2=10; вставить подходящее число, чтобы получилась верная запись: 10-4<, 5+2>, 5+3=.
Сравнение выражений выполняют на основе сравнения их значений (5+2>6, так как 7 больше, чем 6), поэтому дети с помощью таких упражнений закрепляют навыки вычислений.
Важно, чтобы учащиеся поняли, что, сложив два числа, получаем новое число и что соответственно это число может быть выражено суммой двух чисел: если 6+2=8, то 8=6+2; если 5+3=8, то 8=5+3 и т. д. С этой целью предлагают специальные упражнения, например: «Составьте примеры на сложение с ответом 7 и замените число 7 суммой по образцу 0+0=7, 7==+».
Завершающим моментом в работе над каждым из приемов (а±2, а±3, а±4 является составление и заучивание таблиц). Часть каждой таблицы составляется коллективно под руководством учителя, часть - самостоятельно. Одновременно с таблицами сложения и вычитания полезно составить таблицу состава чисел из слагаемых, например:
2+2=4 4=2+2 4-2=2
3+2=5 5=3+2 5-2=3
4+2=6 6=4+2 6-2=4
…
8+2=10 10=8+2 10-2=8
На этом этапе изучения сложения и вычитания учащиеся знакомятся с терминами: сложение, вычитание, слагаемое, сумма, а позднее с терминами — уменьшаемое, вычитаемое, разность.
|
Сначала эти термины употребляет учитель (например, когда диктует примеры детям для устного счета), однако надо детей всемерно побуждать к употреблению этих новых слов, предлагая им читать примеры по-разному (при проверке самостоятельной работы), заполнять таблицы вида:
| Слагаемое | ||||
| Слагаемое | ||||
| Сумма |
Полезно проследить попутно, как изменяется сумма (разность) - увеличивается или уменьшается и при каких условиях это происходит.
На следующем, третьем этапе изучают прием сложения для случаев «прибавить 5, 6, 7, 8, 9». При сложении в пределах 10 в этих примерах второе слагаемое больше первого (1+9, 2+7, 3+5, 4+6 и т. п.). Если при вычислениях применить перестановку слагаемых, то все эти случаи сведутся к ранее изученным видам: а+1, а+2, а+3, а+4. Чтобы применение приема перестановки было осознано детьми, целесообразно вначале раскрыть им суть переместительного свойства сложения.
С переместительным свойством сложения можно ознакомить детей так. Учащимся предлагают, например, положить 4 синих треугольника и придвинуть к ним 3 красных треугольника. Сколько всего треугольников? Как узнать? (Записывают 4+3=7.) Затем дается задание поменять местами синие и красные треугольники и к 3 красным треугольникам придвинуть 4 синих треугольника. Записывают, какой пример теперь решили (3+4=7). Читают оба примера с названием чисел при сложении. Сравнивают примеры, т. е. находят, чем примеры отличаются и чем они похожи (слагаемые переставлены, их поменяли местами, а сумма получилась одинаковая).
Аналогично рассматривают еще 2-3 такие пары примеров (по иллюстрации на доске, по картинкам в учебнике и т. п.). Затем с помощью учителя дети формулируют вывод: от перестановки слагаемых сумма не изменяется.
Далее раскрывают прием перестановки слагаемых, т. е. показывают, когда именно в вычислениях используют переместительное свойство. С этой целью решают задачи практического характера. Например, надо сложить вместе 2 мешка и 7 мешков муки, стоящие порознь. Как удобнее это сделать: принести 2 мешка к 7 мешкам или 7 мешков к двум мешкам? Дети, опираясь на жизненные наблюдения, дают ответ на вопрос задачи. Затем решают с пояснением пары примеров вида: 1+3, 34-1, 2+4, 4+2; сравнивают приемы вычислений и выясняют, как быстрее сложить числа. На основе таких упражнений дети приходят к выводу: легче к большему числу прибавить меньшее, чем к меньшему прибавить большее, а переставлять числа при сложении всегда можно - сумма от этого не изменяется.
Затем показывают, как использовать прием перестановки при решении примеров и задач на сложение в пределах 10 (прибавить 5, 6, 7, 8, 9). В процессе упражнений у детей формируется умение применять прием перестановки слагаемых. После этого составляется краткая таблица сложения в пределах 10, зная которую можно решать все примеры на сложение в пределах первого десятка:
2+2=4
3+2=5
4+2=6 3+3=6
5+2=7 4+3=7
6+2=8 5+3=8 4+4=8
7+2=9 6+3=9 5+4=9
8+2=10 7+3=10 6+4=10 5+5=10
Рассмотрев таблицу, дети сами могут пояснить, почему включены только эти случаи и почему не включены остальные.
На данном этапе продолжается работа над усвоением состава чисел из слагаемых. Систематически предлагаются учащимся задания на замену каждого из чисел второго пятка суммой слагаемых, на дополнение этих чисел до указанного числа (например, до 10, до 9), на подбор монет (например, какими двумя монетами можно уплатить 6 коп., 7 коп., 8 коп., 10 коп.?). Это подготавливает детей к изучению вычитания на следующем этапе.
На четвертом этапе изучается прием вычитания, основанный на связи между суммой и слагаемыми для нахождения результатов в случаях «вычесть 5, 6, 7, 8, 9». Чтобы решить, скажем, пример 10 - 8, надо заменить число 10 суммой чисел 8 и 2 и вычесть из нее одно слагаемое - 8, получим другое слагаемое - 2. Для использования такого приема надо знать состав чисел из слагаемых, а также знать, как связаны между собой сумма и слагаемые.
Подготовка к усвоению связи между компонентами и результатом действия сложения проводится с самого начала работы над сложением и вычитанием. С этой целью предусматриваются специальные упражнения: по данному рисунку (1 большой мяч и 2 маленьких мяча) составить примеры на сложение и вычитание или же по одному и тому же рисунку составить задачу на сложение и задачу на вычитание; решить и сравнить пары примеров вида: 4+3 н 7-3.
Ознакомлению со связью между компонентами и результатом действия сложения отводится специальный урок. Работу над новым материалом можно провести так.
Учитель предлагает детям проиллюстрировать красными и синими кружками пример на сложение (5+4=9). Пример читают с названием чисел при сложении. Затем предлагают из всех кружков убрать (отодвинуть) красные кружки, выясняют, какие кружки остались и сколько их. Записывают новый пример: 9—5=4 и читают, называя числа так, как они назывались в первом примере (из суммы 9 вычли первое слагаемое, получили второе слагаемое 4).
5 + 4 = 9
----------------
9 - 5 = 4
Аналогично рассматривают пример: 9-4=5.
Подобных упражнений надо выполнить достаточное количество, чтобы на основе своих наблюдений дети смогли сами сделать вывод: если из суммы вычесть первое слагаемое, получится второе слагаемое; если из суммы вычесть второе слагаемое, получится первое слагаемое.
Для закрепления знаний связи между суммой и слагаемыми учащиеся выполняют такие упражнения: по данному при' меру на сложение составляют два примера на вычитание и решают их (2+4=6, 6—4= , 6—2== ), с тремя данными числами (4, 3, 7) составляют и решают четыре примера(4+3,3+4, 7-4, 7-3).
Знание связи между компонентами и результатом действия сложения используется для нахождения результатов вычитания (случаи «вычесть 5, 6, 7, 8, 9»). На уроке, посвященном ознакомлению детей с этим приемом вычитания, прежде всего, повторяют состав чисел 6, 7, 8 и др., а также закрепляют знание изученной взаимосвязи.
Затем приступают к раскрытию нового приема вычитания. Учитель предлагает детям объяснить, как можно решить пример 10 - 8 (на доске прикреплены кружки на резинке, с помощью которых удобно провести объяснение). Учащиеся, как правило, сначала называют прием отсчитывания (вычесть 5 и ещё 3, вычесть 4 и 4 и т. п.). Выслушав предложения детей, учитель ставит задачу - найти более удобный прием вычисления.
«Вот у нас записан состав числа 10 из различных слагаемых. 10 - это 8 и еще сколько? (10 - это 8 и 2. Обозначает на кружках состав числа 10.) Этот пример будет нашим помощником. Если из суммы 8 и 2 вычесть 8, сколько получится? (Получится 2, записывает ответ, показывает на кружках, повторяет рассуждение.) Теперь нам надо решить пример 10 - 6. Кто догадался, какими слагаемыми надо заменить число 10, чтобы вычесть число б? Назовите пример – помощник.
Аналогично рассматриваются другие примеры.
На следующих уроках для выработки навыка вычислений включаются разнообразные упражнения.
В процессе изучения сложения и вычитания выполняются упражнения с нулем: 2 – 2, 4 – 4, 6 + 0, 5 – 0.
Заканчивается работа над «Десятком» повторением и закреплением. Важно достичь беглости вычислений.
Вопросы и задания для самостоятельной работы
1. Каков смысл действий сложения и вычитания при теоретико-множественном подходе к изучению курса математики?
2. Перечислите группы вычислительных приемов и укажите теоретические основы их изучения в концентре «Десяток».
3. Укажите виды упражнений с числом «нуль».
megaobuchalka.ru
Место изучения темы: 1 класс
Цели:
Задачи:
Наглядные пособия и дидактический материал
1) Таблица классная настенная с названиями чисел при сложении и вычитании вида:
| слагаемое | слагаемое | сумма | ||
| + | = |
2) Набор подвижных цифр и знаков
3) Набор геометрических фигур различных видов и разного цвета
4) Набор карточек с числовыми фигурами, иллюстрирующими числа 1-5
5) Наборы предметных картинок для составления задач
Содержание и особенности изучения темы
Сложение и вычитание в пределах 10 составляют основу выполнения устных и письменных вычислений за пределами первого десятка.
Конкретный смысл сложения и вычитания осознается детьми в процессе действий с множествами предметов и находит применение при решении задач. Сложение рассматривается как объединение множеств, не имеющих общих элементов. Вычитание - как удаление части множества. Сложение связывается с увеличением числа элементов данного множества; вычитание – с уменьшением числа элементов данного множества.
Значительное место в этой теме отводится знакомству с названиями компонентов и результатов действий и осознанию связей между ними, а также усвоению свойств арифметических действий.
Включаются также элементы алгебры и геометрии: дети знакомятся с математическими выражениями (сумма, разность ), учатся их читать и записывать, приступают к сравнению выражений, на основе чего получают числовые равенства и неравенства вида: 4+2>7, 7-3<7+3, 3+2=2+3. Здесь же учащиеся знакомятся с уравнениями вида x-3=7, 5+x=9 и учатся их решать. Закрепляются умения чертить и измерять отрезки, включаются задачи на составление геометрических фигур из заданных, и на вычленение знакомых геометрических фигур из данной фигуры.
Изучение сложения вычитания в пределах 10 проводится по такому плану:
1. Подготовительный этап: раскрытие конкретного смысла действий сложения и вычитания, запись и чтение примеров, случаи прибавить и вычесть 1, где результаты находятся на основе знания свойства натурального ряда чисел (когда к числу прибавляем 1, получаем число, следующее за ним при счете, а когда вычитаем из числа 1, то получаем предыдущее число).
2. Изучение приемов присчитывания и отсчитывания по одному и группами для случаев 
2, 3, 4.
3. Изучение приема перестановки слагаемых для случаев + 5, 6, 7, 8, 9. Таблица сложения и состав чисел из слагаемых.
4. изучение приема вычитания на основе знания связи между суммой и слагаемыми для случаев – 5,6, 7, 8, 9.
Подготовительная работа к изучению сложения и вычитания начинается с первых уроков рассмотрения нумерации. Выполняя многократно операции над множествами, дети уясняют, что операции объединения соответствует действие сложения, а операции удаления части множества – действие вычитания. Также обращается внимание детей на то, что, когда прибавляют, то становится больше, чем было; когда вычитают, становится меньше.
К концу изучения нумерации учащиеся должны прочно усвоить способы образования любого числа первого десятка присчитыванием и отсчитыванием единицы, и используя этот прием ( а не пересчитывание ), свободно выполнять сложение и вычитание с единицей. Постепенно дети обобщают свои выводы и формулируют выводы: прибавить 1 числу - значит назвать следующее за ним число; вычесть 1 из числа – значит назвать предшествующее ему число. На специально отведенном уроке приводят в систему все случаи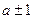 
, под руководством учителя дети составляют таблицы «прибавить 1» и «вычесть 1» и затем заучивают их наизусть.
На втором этапе рассматриваются случаи сложения и вычитания вида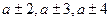 
, результаты которых находят присчитыванием или отсчитыванием по частям.
Работа над вычислительными навыками строится по такому плану:
1) подготовительные упражнения;
2) знакомство с приемами вычисления;
3) закрепление знания приемов, выработка вычислительного навыка;
4) составление и заучивание таблиц.
Рассмотрим методику ознакомления с вычислительным приемом «прибавить и вычесть 2».
На подготовительном этапе дети учатся решать примеры в два действия 2+1+1, 9-1-1, чтобы закрепить умения прибавлять и вычитать единицу и накопить наблюдения: если прибавим (вычтем) 1 и еще 1, то всего прибавим (вычтем) 2.
На уроке по ознакомлению с новыми приемами вычислений учитель ставит цель перед детьми – научиться прибавлять и вычитать число 2. Решение первых примеров выполняется с опорой на предметное действие. Решается пример 4+2. Пусть эти букеты на окне изображают число 4, а эти 2 букета на столе – число 2. Покажите как2 букета присоединить к тем 4 (ученик переносит цветы на окно: сначала один букет, затем второй).Запишем то, что сделал Вова. Сколько сначала к 4 прибавили? Сколько получилось? Как же можно прибавить 2 к 4? Чтобы прибавить 2 к 4, надо прибавить сначала 1 к 4, получится 5, а потом прибавить к 5 еще 1, получится 6.
На доске запись:
4 + 2 = 6
4 + 1 = 5
5 + 1 = 6
Далее ученики выполняют задание: рисуют в тетради 7 яблок, затем 2 яблока раскрашивают, записывают пример 7-2 и, опираясь на свою практическую работу (сначала раскрасили 1, а потом еще 1 яблоко), объясняют, как вычесть 2.
В таком же плане рассматриваются еще несколько заданий, затем переходят к решению примеров с пояснением приемов вычислений.
С помощью аналогичных упражнений раскрываются приемы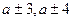 
. Приемы вычислений также иллюстрируют действиями с предметами и на первых порах несколько примеров решают с подробной записью на доске
| 4 + 3 = 7 | 9 – 3 = 6 | |||
| 4 + 2 = 6 | 9 – 1 = 8 | |||
| 6 + 1 = 7 | 8 – 2 = 6 |
Для приемов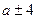 
запись может быть такой же, но целесообразнее начать записывать по-другому: 5 + 4 = 5 + 2 + 2 = 9, 10 – 4 = 10 – 2 - 2 = 6.
Вначале примеры решаются с подробными пояснениями вслух, постепенно пояснения сокращаются, затем проговариваются кратко про себя. С целью выработки навыков включаются устные упражнения ( устный счет, игры «молчанка», «эстафета», «лесенка», «круговые примеры» ). Очень полезны арифметические диктанты. Особенно полезны творческие упражнения: составить задачи, примеры, исправить неверно решенные примеры, вставить пропущенное число или знак действия - 3 = 7, 8 - = 6, 8 + = 10; 6 * 4 = 10, 6 * 4 = 2.
Эффективными для формирования вычислительных навыков являются упражнения с равенствами и неравенствами: сравнить выражения и вставить знаки: 7 + 2 * 7, 10 – 3 * 4; проверить, правильно ли поставлены знаки: 6 + 4<10, 6 +3>10,8 +2 =10; вставить подходящее число, чтобы получилось верная запись: 10 – 4<, 5 + 2>, 5 + 3=.
Сравнение выражений выполняют на основе сравнения их значений, поэтому дети с помощью таких упражнений закрепляют навыки вычислений.
Завершает работу над каждым из приемов 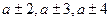составление и заучивание таблиц. Часть каждой таблицы составляется коллективно под руководством учителя, часть – самостоятельно. Одновременно с таблицами сложения и вычитания полезно составить таблиц состава чисел из слагаемых, например:
| 2 + 2 = 4 | 4 = 2 + 2 | 4 – 2 = 2 | ||||
| 3 + 2 = 5 | 5 = 3 + 2 | 5 – 2 = 3 | ||||
| 4 + 2 = 6 | 6 = 4 + 2 | 6 – 2 = 4 | ||||
| … | … | … | ||||
| 8 + 2 = 10 | 10 = 8 + 2 | 10 – 2 = 8 |
На этом этапе учащиеся знакомятся с терминами сложение, вычитание, слагаемое, сумма, а позднее с терминами – уменьшаемое, вычитаемое, разность.
На третьем этапе изучают прием сложения для случаев «прибавить 5, 6, 7, 8, 9». Если при вычислениях применить перестановку слагаемых, то все эти случаи сведутся к ранее изученным видам а + 1, а + 2, а + 3, а + 4. Для этого знакомятся с переместительным свойством сложения.
Раскрыть прием перестановки слагаемых, т. е. показать, когда именно в вычислениях используют переместительное свойство можно при решении практической задачи. Например, надо сложить вместе 2 мешка и 7 мешков муки, стоящие порознь. Как удобнее это сделать: принести 2 мешка к 7 или 7 мешков к двум? На основе таких упражнений дети приходят к выводу: легче к большему числу прибавить меньшее, а переставлять числа всегда можно – сумма от этого не изменится.
Затем показывают, как использовать прием перестановки слагаемых при решении примеров и задач на сложение в пределах 10. После этого составляется таблица сложения в пределах 10. Дети сами могут пояснить, почему включены только эти случаи и почему не включены остальные.
На четвертом этапе изучается прием вычитания, основанный на связи между суммой и слагаемыми для нахождения результатов в случаях «вычесть 5, 6, 7, 8, 9». Взаимосвязь между суммой и слагаемыми рассматривается в теме «Нахождение неизвестного слагаемого». Оперируя с конкретными предметными множествами (демонстрационные и индивидуальные средства наглядности), учащиеся самостоятельно приходят к выводу: если из суммы двух слагаемых вычесть одно слагаемое, то получим другое слагаемое (индуктивный метод: неполная индукция).
В ходе работы над темой дети знакомятся с задачами на увеличение (уменьшение) числа, связанными со сравнением двух множеств предметов. Они должны осознать, что означают выражения «во втором на 2 больше (меньше), чем в первом», научиться сводить задачи этого вида к задачам на нахождение суммы и остатка на основе рассуждения: «На 2 больше, значит, столько же и еще 2», «На 3 меньше, значит, столько же без 3».
В процессе изучения сложения и вычитания продолжается формирование понятия числа нуль. Выполняя действия над множествами, учащиеся постепенно усваивают, что число нуль – это характеристика пустого множества. В конце работы над темой включаются случаи сложения и вычитания с нулем 6 + 0, 6 – 0.
megaobuchalka.ru
Разделы: Начальная школа
Цель:
- Сегодня на уроке математики работаем над темой “сложение и вычитание в пределах 10”. На уроке мы покажем, как умеем работать, считать, решать задачи, помогать друг другу. Итак, успех зависит от внимания.
Игра “Поспевай – не зевай”
Задача:
К серой цапле на урок Прилетели 7 сорок А из них лишь 3 сороки Приготовили урок Сколько лодырей – сорок Прилетело на урок? (4)
- Как узнали? - Кого называют лодырем? (Лентяй, тот который ленится, лодырничает)
Знакомство с произведением. (В сказке лягушка любила путешествовать по городам). Наша лягушка-квакушка любит путешествовать по числовому ряду
2 + 6 = 8 10 – 6 = 4 5 + 1 = 6 3 – 2 = 1 9 – 2 = 7 7 + 3 = 10
У него 4 лапки Лапки – цап-царапки Пара чутких ушей Он гроза для всех мышей. (Кот)
Повторим состав чисел. (Дети ответы показывают на пальцах.)
Вывод: повторили состав чисел, вспомнили, как читаются математические выражения.
Вывод: Чтобы узнать на сколько одно число больше или меньше другого, надо из большего вычесть меньшее.
- На какой вопрос отвечают эти слов? (Кто?)- К какой группе отнесём? (Птицы).
-Какая птица может ходить по дну водоёма? Для проверки выбора ответа воспользуйтесь цепочкой примеров?
Оляпка - певчая птичка бурого цвета с белой грудкой. Она может нырять и бегать по дну водоёма, цепляясь за неровности дна, камешки. На дне ловит насекомых, червей и мальков рыб. Пойманную добычу птичка всегда выносит на берег и съедает. Перья у оляпки не намокают, так как они обильно смазаны жиром. Спасаясь от врага, оляпка ныряет в воду.
Теперь посмотрите на нашу птичку. Из каких геометрических фигур состоит наша птичка? Покажите треугольники. Круг. Овал. Точка
- Рассмотрите картинку. Составьте задачу.
Девочек – 3 чел. Мальчиков - ? на 2 больше 3 + 2 = 5Ответ: 5 мальчиков.
| Девочек – 3 чел. Мальчиков – 5 чел. |  |
Какой вопрос можно поставить? |
| Выпиши нужные цифры в примеры. | Раскрась картинки по своему настроению |
|
|
|
xn--i1abbnckbmcl9fb.xn--p1ai
Разделы: Начальная школа
Цели урока:
Оборудование: рисунки Ёжика и Кроша (см. приложение 2 ), карточки для взаимотренажа (ВТр) (см. приложение 1), учебник.
Структура урока:
Ход урока
I. ИВУ.
II. ВМД.
- Чтобы включиться в работу мы поиграем в игру “Третий лишний”. Я называю три слова, а вы должны доказать, что одно из слов лишнее.
III. Минутка чистописания.
- Прописать числа 9 и 10.
- Повторение состава чисел.
Игра “Отгадай пару чисел”.
-Учитель говорит, что он задумал два числа, если их сложить, получится 9. Ученики отгадывают эти числа. Аналогично для числа 10.
IV. Взаимотренаж.
- Работа по карточкам в парах постоянного состава (ППС) (см. приложение 1).
V. Решение примеров.
1)- Из какого мультфильма эти герои? (“Смешарики.”)
- Назовите героев.
Учитель сообщает, что Ёжик и Крош ходили в лес за грибами.
- Какие грибы растут в лесу?
- Назовите съедобные грибы? Несъедобные?
На доске написаны названия грибов, которые они нашли. Ученики должны решить примеры и узнать, сколько грибов собрал каждый из героев.
| Ёжик | Крош | ||
| Сыроежки 6 | лисички 10 | маслята 5 | подосиновики 3 |
| Подосиновики 1 | волнушки 2 | лисички 7 | волнушки 4 |
| 3+7-8= | 4+5-6= |
| 2+6-7= | 10-6+0= |
| 1+9= | 9-4= |
| 3+3= | 9-2= |
Ученики читают пример с нужным ответом и говорят, сколько грибов нашли герои.
- Прочитайте пример с ответом 6.
2) Решение задачи для смекалистых из учебника стр. 33.
3) Из учебника стр.33 №4
Примеры составляются и решаются устно.
- Как называются числа при вычитании?
VI. Физкультминутка “Мельница”.
Наклонимся вперёд, Руки в стороны. Ветер дует, завывает, Нашу мельницу вращает. Раз, два, три, четыре – Завертелась, закружилась.
(Исходное положение – наклон вперёд, руки в стороны, стойка ноги врозь.
1- правой рукой коснуться пола, 2- смена положения рук.)
VII. Решение задач.
1) Составить задачи по картинкам и решить. (учебник стр.33 №1)
Решение задач по рядам.
Аналогично составляются задачи о пирожном в пакете и на тарелке.
2) К задачам №2 и №3 ученики записывают решение самостоятельно.(по учебнику стр.33)
VIII. Геометрический материал.
- Из 7 палочек нужно составить 3 треугольника.
Ответ:
IX. Итог урока.
Рефлексия.
Дать каждому ребёнку листочек.
- Изобразите на этом листочке своё отражение, а затем приклеить на доску, чтобы составить фотографию класса.
Приложение 1.
Лицевая сторона карточки:
| №1 1) 4+5= 2) 3+2= 3) 6+4= 4) 1+8= 5) 5+3= 6) 7+2= |
№2 1) 8-8= 2) 6-5= 3) 9-3= 4) 10-2= 5) 5-4= 6) 7-6= |
№3 1) 9-5= 2) 5-1= 3) 2-2= 4) 4-3= 5) 8-4= 6) 10-7= |
№4 1) 2+3= 2) 5+4= 3) 1+9= 4) 6+3= 5) 7+1= 6) 4+2= |
| №5 1) 9-7= 2) 8-4= 3) 5-3= 4) 7-7= 5) 10-4= 6) 4-2= |
№6 1) 8-7= 2) 4-2= 3) 3-1= 4) 7-7= 5) 6-5= 6) 4-4= |
№7 1) 9+1= 2) 1+5= 3) 3+7= 4) 4+5= 5) 3+2= 6) 5+1= |
№8 1) 4-3= 2) 10-7= 3) 9-3= 4) 6-2= 5) 2-1= 6) 6-6= |
Обратная сторона карточки:
| Ответ №4 1) 5 2) 9 3) 10 4) 9 5) 8 6) 6 |
Ответ №3 1) 4 2) 4 3) 0 4) 1 5) 4 6) 3 |
Ответ №2 1) 0 2) 1 3) 6 4) 8 5) 1 6) 1 |
Ответ №1 1) 9 2) 5 3) 10 4) 9 5) 8 6) 9 |
| Ответ №8 1) 1 2) 3 3) 6 4) 4 5) 1 6) 0 |
Ответ №7 1) 10 2) 6 3) 10 4) 9 5) 5 6) 6 |
Ответ №6 1) 1 2) 2 3) 2 4) 0 5) 1 6) 0 |
Ответ №5 1) 2 2) 4 3) 2 4) 0 5) 6 6) 2 |
Приложение 2.
xn--i1abbnckbmcl9fb.xn--p1ai
Цели : закрепить вычислительные умения и навыки, навык решения задач; развивать логическое мышление, развивать умение наблюдать и сравнивать. Пробуждать интерес к предмету через игру; закрепить знание компонентов при сложении и вычитании.
Ход урока.
Орг. Момент.
2.Устный счет.
-Какое время года на улице.?
-Какая погода?
Мы совершим путешествие в лес.
17 пуночек сели в одну кормушку 8 в другую. Сытно их брюшкам. Вот и спрошу я ребята у вас. Сколько птичек мы кормим сейчас?
К серой цапле на урок
Прилетело 37 сорок.
А из них 3 сороки приготовили уроки.
Сколько лодырей сорок прилетело на урок.
3 человека ждали поезда 3 часа.
Сколько времени ждал каждый?
Летела стая гусей,2 спереди , 1 сзади,2 сзади, 1 впереди.
Сколько было гусей?
3.Решить примеры на снежинках.
Дуют ветры в феврале.
Воют в трубах громко.
Змейкой мчится по земле
Легкая поземка.
36-7=. 40+25=
98-8=, 16+56=.
Наперекор снегам и вьюгам. Летим на лыжах друг за другом
1 10 99 0 16 17 23 86 50.
На какие две группы можно поделить эти числа?
3 13 23 33………
Продолжить ряд.
4.Работа над ранее изученным материалом .
Каких животных мы можем встретить в лесу?
Самое маленькое однозначное число.
Самое большое двухзначное число.
Назвать соседей числа 99 .83, 13.
Какое число предшествует числу 39,60.
Следует за числом 90 63.
1 слагаемое 23 ,2 слагаемое 9 сумма?
Уменьшаемое 35,вычитаемое 6, разность?
Увеличить 16 на 14.
Уменьшить 77 на 17.
На сколько 36 меньше 40?
На сколько 50 больше 40?
5.Вычисли и сделай проверку.
Кто в лесу холодном
Рыщет злой и голодный?
62+28, 90-17, 18+22, 86-35, 43+48.
6.Решение задачи.
Дальше вдруг сугроб огромный!
Развалился вдоль и вширь.
Этот снежный богатырь.
Объезжать его мы стали-
И задачу увидали
В команде лыжников мальчиков19 человек , а девочек на 3 больше .
Сколько всего человек в команде?
-Задача простая или составная?
-Что узнаем первым действием? Вторым действием?
-Как изменить вопрос, чтобы задача решалась вычитанием.
7.Ребусы 2 *
8.Физ-ка.
9. Запиши выражения и вычисли.
К числу 56 прибавить разность чисел 90 и54.
Из числа 87 вычесть сумму чисел 78 и 2.
К разности чисел 100 и79 прибавить сумму чисел67 и10.
(Задания на птичках .Какие птички? Чем питаются?)
10.Решить уравнения.(Назвать компоненты.)
Х- 8 =5 38-х=30 х+10=50
11.Состав чисел.
В лесу можно встретить домик лесника. Из каких геометрических фигур состоит домик лесника? Какие геометрические фигуры знаете?
Составить выражения с ответом 17.
17
4 7 6 5
6 8 3 4
1 9 7 8
5 2 8 7
Найдите периметр со сторонами 3 см и 4 см.
12. Поставить знаки + -.
( задание приготовила лисичка, прочитать слово которое получится.
26 * 30* 8 =48 34*7*7=20
78*9*9=60 63*(20*7)=50
13.Работа с величинами. ( Помоги белочке.)
а* а+с 91 см*9 дм
а* а-в 1ч*60 мин.
14.Итог .Д/з.
Очень жаль, что путь недолог.
Возвращаться нам пора.
Но на следующем уроке.
Вновь продолжится игра!
Открытый урок по математике во 2 классе. Учитель Серикова Е .В.
^ Литературный К. В. Н .
Цели: проверить знания по изученному материалу, развивать речь уч-ся , логическое мышление .
Приветствие команд.
1.Привет друзья! Сегодня в школе
Большой и интересный день.
Мы приготовили веселый
Наш школьный К. В. Н.
К.В.Н. соревнование
В остроумии и знании
Чтобы этот вечер К.В.Н.
Вам по душе пришелся всем
Нужно знания иметь прочные
Быть веселым и находчивым
И соревнуясь вместе с вами ,
Мы останемся друзьями.
Итак, пусть борьба кипит сильней
И наша дружба вместе с ней.
Разминка.
( исправить ошибки в стихах )
В чаще голову задрав.
Воет с голоду жираф.( волк)
Кто в малине знает толк,
Косолапый бурый волк. (медведь)
Дочерей и сыновей
Учит хрюкать муравей (свинья)
4.Кто любит по ветвям носится
Конечно, рыжая лисица (белка)
5.Быстрее всех от страха
Несется черепаха. (заяц.)
6. По горной круче проходил
Обросший шерстью крокодил. ( баран)
7.В темной лужице своей
Громко квакал Бармалей (лягушонок)
8. С пальмы вниз, на пальму снова
Ловко прыгает корова.( обезьяна.)
Загадки о сказочных героях.
( пед. сов. 05. 4 номер, стр 14.)
По одному слову угадать сказку.
Зеркало (Сказка о мертво царевне.)
Кувшин. (Лиса и журавль.)
Лук и стрела. (Царевна лягушка.)
Топор. (Каша из топора.)
Яйцо. (Курочка ряба.)
Зайчик. (Колобок , Лиса и заяц.)
Конь.(Конек- Горбунок)
Кольцо ( Волшебное колечко).
Составить слова.
( возьмите по одному слову из левого столбика по порядку и правого на выбор , чтобы при сложении их получилось новое слово.
сено овод
банк рот
стол ежи
зал глаз
свет ода
яр вал
воз очки
газ елка
гриб марка
чувство яр
бор
Игра со зрителями. ( загадки) . Уроки знаний .стр- 7, 8.
Конкурс пословиц.
( отгадать пословицу по словам.)
1.Труд-лень.(Труд человека кормит , а лень портит.)
2. Труд- рыбка. (Без труда не вытащишь и рыбки из пруда.)
3.Шило –мешок.( Шило в мешке не утаишь)
4. Язык-дело ( Не спеши языком , торопись делом)
5. Лес-дерево.(Чем дальше в лес ,тем больше дров)
6. Дело-мастер.(Дело мастера боится.)
Конкурс капитанов.
( каждая команда работает самостоятельно. тесты. стр-8.9 № 6 2005.
1. Лучший в мире крокодил. Гена.
2.Сколько козлят у многодетной козы. 7.
3. Самая известная курочка. Ряба.
4. Кто тянул репку перед жучкой Внучка.
5.Гордость Варвары красы. Коса.
6. Мальчик-луковка Чиполлино
7. Крокодиловая речка Африке. Лимпопо.
8. Скатерть сказочная. Самобранка.
9. Назовите братьев Чук и Гек.
10. Дедушка любитель зайцев Мазай.
11. Девочка с голубыми волосами Мальвина.
12. Девочка , которая растаяла весной Снегурочка.
13. Воздыхатель Мальвины. Пьеро
14. Былинный богатырь из города Мурома. Илья.
Загадки в пословицах и поговорках.
чем меньше пословиц –подсказок для этого понадобится, тем лучше.
пед. сов. 05. №6 стр 5.
Живые синонимы.
( вспомнить как и о ком у нас говорят в народе, используя названия птиц.)
11. Могучий , как орел
2. Вольный, как птица
3. Важный или спокойный, как гусь
4. Важный или надутый, как гусь
5. Верность лебединая
6. Любовь голубиная
7. Взгляд хищный, как у ястреба
8. Взгляд зоркий , как у сокола
9. Болтать или трещать, как сорока
10. Ворковать, как голубь
Учитель начальных классов : Серикова Е.В.
К В Н по окружающему миру
на тему « Земля- наш общий дом»
Конкурс «Овощная грядка»
1.Под каждым кустом сидит клубком. ( картофель)
2.Красна девица, росла в темнице, а коса на улице.(морковь)
3.Над землей трава, под землей – алая голова (свекла)
4. Летом в огороде , свежие , зеленые; а зимой –в бочке, желтые , соленые.( огурцы)
5.Растет на грядке зеленая ветка, а на ней красные детки.(помидор)
6.Среди бахчи зеленые мячи, налетела детвора – от мячей одна кора (арбуз)
7.Рос ребенок – не знал пеленок , а как стал стариком- сто пеленок на нем ( капуста)
8.В землю крошка, а из земли лепешка (репа)
9.Прежде чем его мы съели , все наплакаться успели ( лук)
10. Хоть я сахарной зовусь , но дождя я не боюсь.(Сахарная свекла)
Конкурс для любознательных.
( на столе карточки с цифрами, показать правильный ответ)
1.Чем измеряют температуру воздуха.
а) барометром б) термометром в) линейкой г) градусником.
2. От какой точки на термометре ведут отсчет температуры воздуха?
а) от самого нижнего деления.
б) от нулевой отметки.
в)от самого нижнего деления.
3.При какой температуре теплее?
а) +10 б) -20 в) о
4. Кто не впадает в зимнюю спячку?
а) медведь б) ёж в) белка.
5.Какой орган называют «мотором» всего организма?
а)сердце б) лёгкие в) мозг
6.С помощью какого органа человек дышит ?
а) мозг б) сердце в)лёгкие
7. Что при дыхании поглощают живые существа из воздуха?
а)Азот б) кислород в) углекислый газ.
8. Чем питаются растения ?
а) кислород б) углекислый газ.
3.Конкурс « Загадочное животное»
(расшифровать животное)
1. льдоша (лошадь) соль (лось) вайруме (муравей )
зока (коза ) бакоса (собака ) кабел (белка)
4 конкурс.
«Наша голубая планета.» (конкурс капитанов) .
Каждая команда самостоятельно должна выбрать из данного списка съедобные растения.
(рожь , пшеница ,белена, рис , волчье лыко, картофель, дурман, ландыш, огурец, мухомор, сыроежки.)
1.Как называется естественный спутник земли?
2.Какая из звезд ближе всех расположена к земле?(солнце)
3.Сколько планет входят в солнечную систему?
4 Солнце –это планета или звезда?
5.Самая маленькая планета солнечной системы?
6.Самая большая планета солнечной системы?
7.Сколько материков на нашей планете ?
8.Сколько океанов на планете земля?
9.Как называется уменьшенная модель земли?
10.Кто совершил первый полет в космос?
5 конкурс. «РОМАШКА»
(задания на лепестках ромашки)
6 конкурс « Музыкальная шкатулка»
(инсценировка песни о животном)
Подведение итогов конкурса. Награждение.
Название этого красивого крупного цветка переводится с латинского как « меч» . По легенде, он вырос на месте гибели двух друзей_ гладиаторов.
В одной из сказок братьев Гримм принцесса заснула на сто лет, так как уколола шипами этого цветка.
Легенда гласит , что этот цветок беседует ночью со звездами, не случайно и его название переводится как звезда.
Эти белые полевые цветы служили зонтиками для гномов.
Назовите животное, которое является одним из самых крупных быков мира. Его рост достигает 2 метров, вес доходит до тонны. Могучее телосложение не мешает ему быть быстрым и ловким в движениях.
Это хищный зверь. Обладает острым зрением и тонким слухом Прекрасно лазает по деревьям, устраивает в ветвях засаду и охотится на крупных животных, например оленей. Хорошо плавает ,промышляет рыбной ловлей, обучает этому и своих котят.
льдоша соль зока
вайруме бакоса кабел
Учитель начальных классов: Серикова Е.В.
www.ronl.ru
КОЧЕНЕВСКОГО РАЙОНА
НОВОСИБИРСКОЙ ОБЛАСТИ
УРОК – СКАЗКА
ПО МАТЕМАТИКЕ В 1 КЛАССЕ
«СЛОЖЕНИЕ И ВЫЧИТАНИЕ В ПРЕДЕЛАХ 10. ЗАКРЕПЛЕНИЕ».
УЧИТЕЛЬ НАЧАЛЬНЫХ КЛАССОВ
II КВАЛИФИКАЦИОННОЙ КАТЕГОРИИ
ТРОЦЕНКО ТАТЬЯНА АЛЕКСЕЕВНА
2007 Г.
Тема: Сложение и вычитание в пределах 10. Закрепление.
Образовательные задачи:
Обучающая - развивать навыки счета от 1 до 20 и состав чисел 10; формирование умений находить последующие и предыдущие числа; умение находить значение числового выражения, опираясь на знания состава числа; уметь читать, записывать и сравнивать любые числа в пределах 10; упражнять учащихся измерять длину отрезков в сантиметрах с помощью линейки; решать примеры и задачи на сложение и вычитание в пределах 10; воспитывать культуру общения.
Развивающая – развитие памяти, внимания, логическое мышление, речь.
Дидактические средства:
- демонстрационный материал (сюжетные картинки – «дед», «бабка», «внучка», «Жучка», «кошка», «мышка», «репка»).
- учебная тетрадь Моро на печатной основе № 1, цветные карандаши, ручка, линейка,
^
I. Организационный момент. Сообщение целей урока.
Долгожданный дан звонок –
Начинается урок.
Вступительное слово:
- Ребята, мы сегодня отправимся в сказку « Репка» на новый лад.
Тут затеи и задачи,
Игры, шутки, все для вас!
Пожелаем все удачи –
За работу, в добрый час.
^
- Посадил «Дед» репку ( на доске появляется рис. Деда и репки ).
Выросла репка большая - пребольшая, да не простая а математическая. Стал «Дед» репку тянуть не может вытянуть. Тянет - потянет, вытянуть не может. И вдруг «репка» говорит человеческим голосом:
- Ответь-ка «Дед» на мои вопросы математические, может быть тогда сможешь вытянуть меня из земли.
(- Давайте, ребята, поможем «Деду» ответить на вопросы «репки») 1.Разминка:
- Сколько дней в неделе?
- Какой день недели сегодня?
- Какое сегодня число?
- Какое сейчас время года?
- Какой месяц осени сейчас идет?
- Сколько месяцев в году?
- С какого месяца начинается год?
- Какой самый короткий месяц в году?
2.Устный счет:
- Счет от 1 до 20 (и обратно)
- Расставить числа по порядку: 1 5 3 6 2 10 8 7 4 9;
- Счет от 3 до 8; от 7 до 10; от 9 до 6; от 7 до 2;
- Назови соседей чисел: 3, 6, 8:
- Между числами кто живет?: 3 и 5; 7 и 9; 4 и 6;
- Назовите следующее число за числом: 3; 7; 5; 2;
- Назовите предыдущее число числу: 6; 8; 10; 4;
- Состав чисел: 8; 9; 10.
- 2 6 10 - Что вы можете сказать о них?
- Назовите самое большое и самое маленькое число в данном ряду.
- На сколько 2 меньше, чем 10? На сколько 10 больше, чем 2.
3.Физминутка
4.Сравнить числа ( обозначить соответствующим числом количество фигур и сравнить числа).
а)
>
3
> 2
4 5
б) 10 * 8 6 * 2 0 * 5 4 * 9
в) 4 -1 * 6 10 * 5 + 5 9 – 3 * 9
г) – А как можно уровнять? 3 - * = 2 3 = 2 + *
д) Какое число надо вставить чтобы запись была верной? * > 4
3
5.Самостоятельная работа (у каждого ученика листочки с заданием).
Расставить знаки « >», «
2 * 4 +3 6 * 8 + 1 9 - 2 * 5 5 * 1 + 6
- Не вытянул «Дед» «репку». Ничего у него не получилось. Позвал он на помощь «Бабку» ( картинка). Тянут они, потянут, вытянуть они не могут.
Спрашивает тут «репка»: « А не умеете ли вы считать и сравнивать? Вот тогда может и вытяните меня.
( Поможем ребята «Деду» и Бабке» выполнить задания «репки»? )
6.Работа в тетради Моро с. 5, №2, № 3, № 4. (Проверка))
- Обрадовалась «репка», что ей такие сообразительные «Дед» с «Бабкой» попались и спрашивает:
- А не умеете ли вы примеры решать?
- Нечего делать, принялись «Дед» и «Бабка» примеры решать.( Давайте поможем быстрее решить примеры «Деду» и «Бабке»?)
7. Работа в тетради Моро с. 5, № 5)
а)- Что значит + 1? - 1? (ответы детей)
7+1 10- 1
5+1 6-1
8+1 7-1
2+1 4-1
( ответы дети показывают на карточках)
б) Найдите примеры с ответом 4 и закрасьте красным цветом:
4 – 2 3 + 1 6 + 1
5 – 1 5 - 4 1 + 3
2 + 1 2 + 2 3 - 2
Найдите примеры с ответом 5 и закрасьте зеленым цветом:
1 + 4 3 + 1 4 + 1
5 – 3 3 + 2 5 - 2
6 – 1 4 – 3 2 + 3
Показать карточки с нужным ответом:
2 + ? = 10 5 + 5 = ? 8 + ? = 10
* + 7 = 10 ? + 9 = 10 6 + ? = 10
- Снова стали тянуть «репку», но вытянуть не могут. Позвали они «Внучку»
( картинка ). А «Внучка» у них была веселая, любила она петь и танцевать.
Давайте потанцуем вместе с «Внучкой». ( звучит музыка)
8. Физминутка
В хоровод встал серый зайка
И поет: «Я был зазнайкой,
А теперь могу считать-
Раз, два, три, четыре, пять,
Прибавляю, отнимаю,
Математику я знаю
И поэтому с утра
Я кричу: « Ура! Ура!»
- Тут «репка» и говорит «Внучке»: « Как ты хорошо танцуешь, внучка! А
знаешь ли, ты, геометрические фигуры?» (Давайте поможем «Внучке»?)
а) – Как называются эти фигуры? – Какая из них лишняя? Почему?
б) – Какая фигура лишняя и почему?
в) - Измерить отрезки. (у каждого карточка с фигурами). Молодцы, ребята!
- «Внучка» за « Бабку», «Бабка» за «Дедку», «Дедка» за «репку», тянут – потянут, вытянуть не могут. Позвали они «Жучку». Прибежала «Жучка» (картинка ).
- А «Репка» и говорит: « Из разных цифр сделаны бусы,
А в тех кружках, где чисел нет,
Расставьте минусы и плюсы,
Чтобы данный получить ответ».
- Поможем « Жучке?»
- Справились мы вместе с «Жучкой». А теперь попробуем вытянуть «репку»:
«Жучка» за «Внучку», «Внучка» за «Бабку», «Бабка» за «Дедку», «Дедка» за «репку» , тянут – потянут, вытянуть не могут. Позвали они «Кошку».
Прибежала на помощь «Кошка». (картинка). А «репка» ее просит:
« Попробуй решить задачу». А «Кошка не умеет решать задачи. Давайте вместе с «Кошкой» поучимся решать задачи.
- Послушайте задачу:
« У Коли было 3 машинки. Ему подарили еще 2 машинки. Сколько всего машинок стало у Коли?
- Кто повторит задачу? ( повторяют задачу 2 ученика)
- Сколько было машинок? ( 3)
- Сколько подарили машинок? (2)
- Как это можно записать?
( с помощью карточек с цифрами делают запись: 3 + 2 = 5).
- Больше стало машинок или меньше?
- Как по разному можно прочитать эту запись?
«У Ани было 4 конфеты. Одну конфету она съела. Сколько конфет у нее осталось? ( 2 ученика повторяют задачу)
- Сколько у Ани было конфет? (4)
- Сколько она съела? (1)
- Сколько конфет осталось?(3)
- Как записать? ( делают запись: 4 – 1 = 3
- Больше стало конфет или меньше?
- Как по разному можно прочитать выражение?
- Вот и справились мы с задачами.
К. за Ж., Ж. за Вн., Вн. за Б., Б. за Д., Д. за Р., тянут - потянут, вытянуть не могут. Позвали они «Мышку». Прибежала «Мышка» ( картинка)
- А «репка» говорит: « Вот вам последнее задание. Если вы не выполните это задание, то не вытянуть вам меня».
- Поможем «Мышке?»
9. Работа в тетради Моро с. 6.
- Молодцы! Справились с заданием.
Тянут- потянут – и вытянули «Репку». Но без вашей помощи, ребята, они не смогли бы вытянуть «репку».
^
- Понравился вам урок?
- Что вы делали на уроке?
( Всем дарят «Репку» ).
ПРИЛОЖЕНИЕ 4
Из фигур, представленных на кар точках, выбрать ту. которую можно поместить вместо знака вопроса. Недостающей может быть одна из фигур любого ряда и расположения.
ЦЕЛЬ: Вызвать у детей интерес к решению задачи. Учить путем зрительного и мыслительного анализа рядов фигур по горизонтали выбирать недостающую из 6 предложенных фигур. Упражнять детей в доказательстве решения.
МАТЕРИАЛ: Таблица и карточки с изображенными на них фигурами.
ХОД РАБОТЫ: « Посмотрите внимательно на эту задачу, она нарисована».
«Я расскажу, как надо ее решать.Нужно рассмотреть сначала первый, верхний ряд фигур ( показывает), затем второй, средний. А в третьем ряду, нижнем, одной фигу не хватает. На ее месте стоит знак вопроса.
Недостающую фигуру надо выбрать из фигур, нарисованных на карточках, и поместить на это место, вот сюда ( показывает).
База данных защищена авторским правом © kursovaya-referat.ru 2017При копировании материала укажите ссылку
kursovaya-referat.ru
С этим файлом связано 184 файл(ов). Среди них: 0-0-0-97-20, 0-0-0-96-20, 0-0-0-95-20, 0-0-0-93-20, 0-0-0-92-20, 0-0-0-91-20, 0-0-0-90-20, 0-0-0-89-20, 0-0-0-88-20, 0-0-0-87-20 и ещё 174 файл(а).Показать все связанные файлы Математика 1 классТип учебного занятия: урок общения и систематизации знанийТема: «Сложение и вычитание в пределах 10»Цель:
• обобщить и систематизировать знания обучающихся по теме;
• отработать умения по теме «Сложение и вычитание», научить применять их на практике;
• развивать смекалку, мышление;
• воспитывать интерес к предмету.
Знаем: Умеем:
• ± 1 • + и -
• ± 2 • решать задачи
• ± 3 • сравнивать
• части задачи
• правила сравнения
•
ХОД УРОКА:
| № УЭ | Учебный материал с указанием задания | Управление обучением |
| УЭ 1.0 | Организационный момент Цель: подготовка учащихся к работе на занятии- Долгожданный дан звонок Начинается урок! | Самоорганизация |
| УЭ 2.0 | Актуализация опорных знаний Цель: обеспечить мотивацию и принятие учащимися цели учебно-познавательной деятельности, активизация опорных знаний. | |
| УЭ 2.1 | Устный счет. Математическая разминка Задачи на смекалку. - Дети лепили снежную бабу. После прогулки на батарее сохло 8 варежек. Сколько детей лепили снежную бабу? - Из какой посуды нельзя ничего съесть? - Наступил декабрь. Распустились 3 ромашки, а потом – еще 1. Сколько цветов распустилось?- А хотите узнать, какой герой к нам сегодня придет на урок? - За каждое правильно выполненное задание, у нас будет появляться часть этого героя. | Самоопределение Самоутверждение Самовыражение |
| 2.2 | Веселые задачи
А навстречу три тигренка С водопоя шли домой. Сосчитайте поскорей, Сколько встретилось зверей? (7)
Три из них сломались, Сколько же осталось? (6)
- Что ты, белочка, несешь? Задала лиса вопрос. Я несу своим детишкам Два ореха и три шишки. Ты, лиса, мне подскажи: Сколько будет два да три? (5)
Он в окно глядит, считает. Сколько их в футбол играет? (4)- Как решали? (Складывали и вычитали) | Обратная связь (сигналы) Самоопределение Самоутверждение |
| 2.3 | Игра «Наряди математическую ёлочку» - Какой скоро нас ждет праздник? (Ученики объединяются в группы. Считают примеры (прикреплены к елке), выбирают правильный ответ (записан в елочном шаре), доказывают)
5 + 3 9 – 2 8 + 2 7 – 3 | Работа в больших группах |
| 2.4 | Назовем тему урока - Сложение и вычитание чисел в пределах 10 Знаем: Умеем: ± 1 + и - ± 2 решать задачи ± 3 сравнивать части задачи смекать правила сравнения | Вывод темы урока и целеполагания |
| УЭ 3.0 | Отработка материала Цель: отработать приемы сложения и вычитания при выполнении заданий различного уровня. | |
| 3.1 | Работа над задачами (в учебнике) I в. II в. с. 102 №2 с. 102 №3 Разбор задачи. - Из чего состоит задача? (Сделать ловушку – убрать одну часть задачи) - Чего не хватает? - Предлагаю составить по вариантам решение и рассказать друг другу. (2 ученика работают у доски) - Какое умение отрабатывали? | Работа в ППС Сверка с доской Подведение итога |
| 3.2 | Работа с ребусами. (на парту) - Что видите? (Неравенство и равенство) - Что предлагаете сделать? - Решите, покажите, какие знаки нужно вставить? 6 * 3 * 1 > 8 7 * 3 * 2 = 2 - Какое умение отрабатывали? | Работа в МГ Подведение итога |
| 3.3 | Карточка (учащиеся работают в карточке) Карточка
Ответ:
 9 – 3 = 7 + 2 =
5 + 3 = 6 – 2 =
- 1 - 3 + 2 - 3 + 1 - 2 8 → → → → → → =
(Учитель проверяет и делает вывод: кто справился, кто затруднился) - Кому легко? - Кому трудно? - Кому было интересно на уроке? - Чем запомнился? | Самостоятельная работа по карточке Самовыражение Самоутверждение Рефлексия Итог урока |
| 3.4 | Работа в тетради - Откройте тетради на стр. 28 - Раскрасьте рисунок. - Кто же к нам сегодня пришел на урок? (Снеговик) - А ничего интересного вы не заметили? (Он держит большую снежинку) - А хотите узнать, что на ней написано? (27 декабря приглашаю на новогоднюю ёлку) | Работа в тетради |
| УЭ 4.0 | Итог урока Цель: подвести итог урока.- Назовите тему урока. - Кому было легко? - Кому трудно? - Молодцы! | Беседа по подведению итога работы на уроке |
Составила: С. Н. Шабырова
| Ребусы | Ребусы |
| 6 * 3 * 1 > 87 * 3 * 2 = 2 | 6 * 3 * 1 > 87 * 3 * 2 = 2 |
| Ребусы | Ребусы |
| 6 * 3 * 1 > 87 * 3 * 2 = 2 | 6 * 3 * 1 > 87 * 3 * 2 = 2 |
| Ребусы | Ребусы |
| 6 * 3 * 1 > 87 * 3 * 2 = 2 | 6 * 3 * 1 > 87 * 3 * 2 = 2 |
| Ребусы | Ребусы |
| 6 * 3 * 1 > 87 * 3 * 2 = 2 | 6 * 3 * 1 > 87 * 3 * 2 = 2 |
| Ребусы | Ребусы |
| 6 * 3 * 1 > 87 * 3 * 2 = 2 | 6 * 3 * 1 > 87 * 3 * 2 = 2 |
Задание: реши примеры и найди ответы
6 + 3 =
9 – 2 =
7 – 3 =
5 + 3 =
8 + 2 =
перейти в каталог файловtrig.zodorov.ru
6 + 3 
