
Для решения большинства задач в прикладных науках необходимо знать местоположение объекта или точки, которое определяется с помощью применения одной из принятых систем координат. Кроме того, имеются системы высот, которые также определяют высотное местонахождение точки на поверхности Земли.
Координаты – числовые или буквенные значения, с помощью которых можно определить место, где расположена точка на местности. Как следствие, система координат – это совокупность однотипных значений, имеющих одинаковый принцип нахождения точки или объекта.
Нахождение местоположения точки требуется для решения многих практических задач. В такой науке, как геодезия, определение местонахождения точки в заданном пространстве – главная цель, на достижении которой строится вся последующая работа.

Большинство систем координат, как правило, определяют расположение точки на плоскости, ограниченной только двумя осями. Для того чтобы определить позицию точки в трехмерном пространстве, применяется также система высот. С ее помощью можно узнать точное местонахождение искомого объекта.
Системы координат определяют местоположение точки на территории земной поверхности, задавая ей три значения. Принципы их расчета различны для каждой координатной системы.

Основные пространственные системы координат, применяемые в геодезии:
Все системы имеют свою начальную точку отсчета, величины для местонахождения объекта и области применения.
Основной фигурой, применяемой для отсчета геодезических координат, является земной эллипсоид.
Эллипсоид – трехмерная сжатая фигура, которая наилучшим образом представляет собой фигуру земного шара. Ввиду того что земной шар – математически неправильная фигура, вместо нее для определения геодезических координат используют именно эллипсоид. Это облегчает осуществление многих расчетов для определения положения тела на поверхности.
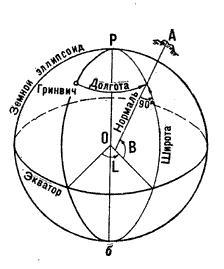
Геодезические координаты определяются тремя значениями: геодезической широтой, долготой и высотой.
Для решения высокоточных задач высшей геодезии необходимо различать геодезические и географические координаты. В системе, применяемой в инженерной геодезии, таких различий, ввиду небольшого пространства, охватываемого работами, как правило, не делают.
Для определения геодезических координат в качестве плоскости отсчета используют эллипсоид, а для определения географических – геоид. Геоид является математически неправильной фигурой, более приближенной к фактической фигуре Земли. За его уровненную поверхность принимают ту, что продолжена под уровнем моря в его спокойном состоянии.

Географическая система координат, применяемая в геодезии, описывает позицию точки в пространстве с указанием трех значений. Определение географической долготы совпадает с геодезической, так как точкой отсчета также будет нулевой меридиан, называемый Гринвичским. Он проходит через одноименную обсерваторию в городе Лондоне. Географическая широта определяется от экватора, проведенного на поверхности геоида.
Высота в системе местных координат, применяемой в геодезии, отсчитывается от уровня моря в его спокойном состоянии. На территории России и стран бывшего Союза отметкой, от которой производят определение высот, является Кронштадтский футшток. Он расположен на уровне Балтийского моря.
Полярная система координат, применяемая в геодезии, имеет другие нюансы произведения измерений. Она применяется на небольших участках местности для определения относительного местоположения точки. Началом отсчета может являться любой объект, отмеченный как исходный. Таким образом, с помощью полярных координат нельзя определить однозначное местонахождение точки на территории земного шара.
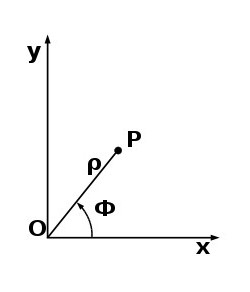
Полярные координаты определяются двумя величинами: углом и расстоянием. Угол отсчитывается от северного направления меридиана до заданной точки, определяя ее положение в пространстве. Но одного угла будет недостаточно, поэтому вводится радиус-вектор – расстояние от точки стояния до искомого объекта. С помощью этих двух параметров можно определить местоположение точки в местной системе.
Как правило, эта система координат используется для выполнения инженерных работ, проводимых на небольшом участке местности.
Прямоугольная система координат, применяемая в геодезии, также используется на небольших участках местности. Главным элементом системы является координатная ось, от которой происходит отсчет. Координаты точки находятся как длина перпендикуляров, проведенных от осей абсцисс и ординат до искомой точки.
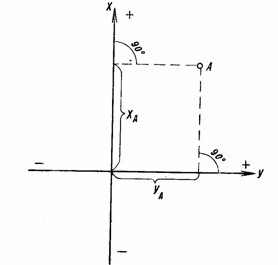
Северное направление оси Х и восточное оси У считаются положительными, а южное и западное – отрицательными. В зависимости от знаков и четвертей определяют нахождение точки в пространстве.
Координатная зональная система Гаусса-Крюгера схожа с прямоугольной. Различие в том, что она может применяться для всей территории земного шара, а не только для небольших участков.
Прямоугольные координаты зон Гаусса-Крюгера, по сути, являются проекцией земного шара на плоскость. Она возникла в практических целях для изображения больших участков Земли на бумаге. Искажения, возникающие при переносе, считаются незначительными.
Согласно этой системе, земной шар делится по долготе на шестиградусные зоны с осевым меридианом посередине. Экватор находится в центре по горизонтальной линии. В итоге насчитывается 60 таких зон.

Каждая из шестидесяти зон имеет собственную систему прямоугольных координат, отсчитываемую по оси ординат от осевого меридиана Х, а по оси абсцисс – от участка земного экватора У. Для однозначного определения местоположения на территории всего земного шара перед значениями Х и У ставят номер зоны.
Значения оси Х на территории России, как правило, являются положительными, в то время как значения У могут быть и отрицательными. Для того чтобы избежать знака минус в величинах оси абсцисс, осевой меридиан каждой зоны условно переносят на 500 метров на запад. Тогда все координаты становятся положительными.
Система координат была предложена Гауссом в качестве возможной и рассчитана математически Крюгером в середине двадцатого века. С тех пор она используется в геодезии в качестве одной из основных.
Системы координат и высот, применяемые в геодезии, используются для точного определения положения точки на территории Земли. Абсолютные высоты отсчитываются от уровня моря или другой поверхности, принятой за исходную. Кроме того, имеются относительные высоты. Последние отсчитываются как превышение от искомой точки до любой другой. Их удобно применять для работы в местной системе координат с целью упрощения последующей обработки результатов.
Помимо вышеперечисленных, имеются и другие системы координат, применяемые в геодезии. Каждая из них имеет свои преимущества и недостатки. Есть также свои области работы, для которых актуален тот или иной способ определения местоположения.
Именно цель работы определяет, какие системы координат, применяемые в геодезии, лучше использовать. Для работы на небольших территориях удобно использовать прямоугольную и полярную системы координат, а для решения масштабных задач необходимы системы, позволяющие охватить всю территорию земной поверхности.
fb.ru
Количество просмотров публикации Системы координат применяемые в геодезии - 496
Для определения положения точек в масштабе всей Земли в геодезии используют три системы координат – астрономическую, геодезическую и геоцентрическую пространственную прямоугольную систему.
Астрономические координаты - это угловые величины и определяющие положение точек земной поверхности относительно земного экватора и начального меридиана.
Рис. 2
Астрономическая широта- φ - это угол, составляемый направлением отвесной линии в данной точке с плоскостью земного экватора. Широты отсчитываются к северу и югу от экватора и соответственно называются северными и южными.
Астрономическая долгота λ - это двугранный угол между плоскостью начального меридиана и плоскостью меридиана данной точки. Долготы отсчитываются на восток и на запад от начального меридиана и называются восточными и западными. Астрономические координаты могут, определятся из астрономических наблюдений.
Координаты геодезические определяют положение точек земное поверхности на референц-эллипсоиде.
Геодезическая широта В - угол, составленный направлением нормали к референц-эллипсоиду в данной точке с плоскостью геодезического экватора.
Геодезическая долгота L - двугранный угол между плоскостью геодезического меридиана данной точки и плоскостью начального меридиана.
Геодезические координаты вычисляются по результатам наземных геодезических измерений, спроектированных на поверхность референц-эллипсоида.
При составлении планов и карт местности обычно используется левая система плоских прямоугольных координат (рис. 3).
Рис.3
В этой системе вертикальная линия, ориентируемая на север, является осью абсцисс, а горизонтальная направлением на восток - осью ординат. Нумерация четвертой здесь идёт по ходу часовой стрелки; знаки функций те же, что я в левой системе плоских прямоугольных координат. В случае если ось абсцисс совмещается с более выгодным направлением, то такая система координат принято называть условной.
Системы высот. Для определения высот точек Земли относительно некоторой отсчетной уровенной поверхности используется несколько систем высот.
Высотой (отметкой, альтитудой) точки называют расстояние, измеренное по отвесной линии от отсчетной уровенной поверхности до данной точки. Абсолютная (ортометрическая) высота H отсчитывается от поверхности геоида, относительная (условная) H¢ – от произвольной уровенной поверхности, геодезическая – от поверхности референц-эллипсоида (рис.4).
В России за начало отсчета высот принят средний уровень Балтийского моря в районе Кронштадского футштока, и наша система высот принято называть Балтийской (нормальной). В ней отсчетной поверхностью служит квазигеоид – фигура, близкая к поверхности геоида. Балтийская система в пределах одного метра отличается от Адриатической системы (Австрия) и Северной (Германия). Сам уровень Балтийского моря выше уровня Черного моря на 0,7 м и, что самое любопытное, близкие друг к другу уровни Тихого и Атлантического океанов в районе Панамского канала отличаются по высоте на 0,6 м. Все это следует иметь в виду при использовании картографических материалов разных стран.
Вместе с тем, следует знать, что горизонтальные поверхности, перпендикулярные вектору силы тяжести, не параллельны между собой (они сжимаются у полюса) и в связи с этим высоты точек, лежащих на некоторой уровенной поверхности, уменьшаются по мере приближения к полюсу. Это уменьшение выражается формулой
,
где - разность широт точек, выраженная в радианной мере.
К примеру, воды озера Байкал, расположенные на средней широте jср=53,5°, с размахом широт 4,3° и средней высотой H=450 м на севере и юге отличаются по высоте на 0,2 м.
Превышением принято называть разность высот двух точек. На небольшой территории (в несколько десятков квадратных километров) величина h не зависит от принятой системы высот, получается, что
.
referatwork.ru
Количество просмотров публикации Системы координат, применяемые в геодезии - 641
Для определения положения точек в геодезии применяют пространственные прямоугольные, геодезические и плоские прямоугольные координаты.
Пространственные прямоугольные координаты. Начало системы координат расположено в центре O земного эллипсоида (рис. 2.2).
| | Рис. 2.2. Земной эллипсоид и координаты: Х, Y , Z – пространственные прямоугольные; B, L, H - геодезические; G - Гринвич |
Ось Z направлена по оси вращения эллипсоида к северу. Ось Х лежит в пересечении плоскости экватора с начальным - гринвичским меридианом. Ось Y направлена перпендикулярно осям Z и X на восток.
Геодезические координаты. Геодезическими координатами точки являются ее широта͵ долгота и высота (рис. 2.2).
Геодезической широтой точки М принято называть угол В, образованный нормалью к поверхности эллипсоида, проходящей через данную точку, и плоскостью экватора.
Широта отсчитывается от экватора к северу и югу от 0° до 90° и принято называть северной или южной. Северную широту считают положительной, а южную - отрицательной.
Плоскости сечения эллипсоида, проходящие через ось OZ, называются геодезическими меридианами.
Геодезической долготой точки М принято называть двугранный угол L, образованный плоскостями начального (гринвичского) геодезического меридиана и геодезического меридиана данной точки.
Долготы отсчитывают от начального меридиана в пределах от 0° до 360° на восток, или от 0° до 180° на восток (положительные) и от 0° до 180° на запад (отрицательные).
Геодезической высотой точки М является ее высота Н над поверхностью земного эллипсоида.
Геодезические координаты с пространственными прямоугольными координатами связаны формулами
X = (N + H)cosB cosL,
Y = (N+H)cosB sinL,
Z = [(1 - e2) N+H] sinB,
где e - первый эксцентриситет меридианного эллипса и N -радиус кривизны первого вертикала.При этом N=a/(1 - e2 sin2B)1/2.
Геодезические и пространственные прямоугольные координаты точек определяют с помощью спутниковых измерений, а также путем их привязки геодезическими измерениями к точкам с известными координатами.
Отметим, что наряду с геодезическими существуют еще астрономические широта и долгота. Астрономическая широта j это - угол, составленный отвесной линией в данной точке с плоскостью экватора. Астрономическая долгота l – угол между плоскостями Гринвичского меридиана и проходящего через отвесную линию в данной точке астрономического меридиана. Астрономические координаты определяют на местности из астрономических наблюдений.
Астрономические координаты отличаются от геодезических потому, что направления отвесных линий не совпадают с направлениями нормалей к поверхности эллипсоида. Угол между направлением нормали к поверхности эллипсоида и отвесной линией в данной точке земной поверхности принято называть уклонением отвесной линии.
Обобщением геодезических и астрономических координат является термин – географические координаты.
Плоские прямоугольные координаты. Для решения задач инженерной геодезии от пространственных и геодезических координат переходят к более простым – плоским координатам, позволяющим изображать местность на плоскости и определять положение точек двумя координатами х и у.
Поскольку выпуклую поверхность Земли изобразить на плоскости без искажений нельзя, введение плоских координат возможно только на ограниченных участках, где искажения так малы, что ими можно пренебречь. В России принята система прямоугольных координат, основой которой является равноугольная поперечно–цилиндрическая проекция Гаусса. Поверхность эллипсоида изображается на плоскости по частям, называемым зонами. Зоны представляют из себясферические двуугольники, ограниченные меридианами, и простирающиеся от северного полюса до южного (рис. 2.3). Размер зоны по долготе равен 6°. Центральный меридиан каждой зоны принято называть осевым. Нумерация зон идет от Гринвича к востоку.
| | Рис. 2.3. Деление поверхности Земли на координатные зоны: G – Гринвич |
Долгота осевого меридиана зоны с номером N равна:
l0 = 6°× N - 3° .
Осевой меридиан зоны и экватор изображаются на плоскости прямыми линиями (рис. 2.4). Осевой меридиан принимают за ось абсцисс x, а экватор - за ось ординат y. Их пересечение (точка O) служит началом координат данной зоны.
| | Рис. 2.4. Изображение координатной зоны на плоскости: О – начало координат (х0=0; у0=500 км). |
Чтобы избежать отрицательных значений ординат, координаты пересечения принимают равными x0 = 0, y0 = 500 км, что равносильно смещению оси х к западу на 500 км.
Чтобы по прямоугольным координатам точки можно было судить, в какой зоне она расположена, к ординате y слева приписывают номер координатной зоны.
Пусть к примеру, координаты точки А имеют вид:
xА= 6 276 427 м
yА = 12 428 566 м
Эти координаты указывают на то, что точка А находится на расстоянии 6276427 м от экватора, в западной части (y < 500 км) 12-ой координатной зоны, на расстоянии 500000 - 428566 = 71434 м от осевого меридиана.
Для пространственных прямоугольных, геодезических и плоских прямоугольных координат в России принята единая система координат СК-95, закрепленная на местности пунктами государственной геодезической сети и построенная по спутниковым и наземным измерениям по состоянию на эпоху 1995 ᴦ.
Местные системы прямоугольных координат.При строительстве различных объектовчасто используют местные (условные) системы координат, в которых направления осей и начало координат назначают, исходя из удобства их использования в ходе строительства и последующей эксплуатации объекта.
Так, при съемке железнодорожной станции ось у направляют по оси главного железнодорожного пути в направлении возрастания пикетажа, а ось х – по оси здания пассажирского вокзала.
При строительстве мостовых переходов ось х обычно совмещают с осью моста͵ а ось y идет в перпендикулярном направлении.
При строительстве крупных промышленных и гражданских объектов оси x и y направляют параллельно осям строящихся зданий.
4.Метод проекций в геодезии
Плоский многоугольник abede является ортогональной проекцией пространственного многоугольника ABCDE.
Другая имеющая весьма важное значение в геодезии проекция принято называть центральной. Суть ее состоит в следующем. Возьмем произвольную точку О (рис. 3) и соединим ее со всеми вершинами многоугольника ABCDE, находящегося на земной поверхности. Полученные в пересечении с горизонтальной плоскостью PQ точки abede и будут центральными проекциями точек ABCDE,
Плоский многоугольник abode принято называть центральной проекцией многоугольника ABCDE.
referatwork.ru
Геодезические координаты определяют положение точки земной поверхности на референц-эллипсоиде (рис.7).
Геодезическая широта B – угол, образованный нормалью к поверхности эллипсоида в данной точке и плоскостью его экватора. Широта отсчитывается от экватора к северу или югу от 0° до 90° и соответственно называется северной или южной широтой.
Геодезическая долгота L – двугранный угол между плоскостями геодезического меридиана данной точки и начального геодезического Гринвичского меридиана.
Долготы точек, расположенных к востоку от начального меридиана, называются восточными, а к западу – западными.

Рисунок 7 - Система геодезических координат
Астрономическая широта и долгота определяют положение точки земной поверхности относительно экваториальной плоскости и плоскости начального астрономического меридиана (рис.8).

Рисунок 8 - Система астрономических координат
Астрономическая широта– угол, образованный отвесной линией в данной точке и экваториальной плоскостью.
Астрономическая долгота– двугранный угол между плоскостями астрономического меридиана данной точки и начального астрономического меридиана.
Плоскостью астрономического меридиана является плоскость, проходящая через отвесную линию в данной точке и параллельная оси вращения Земли.
Астрономическая широта и долгота определяются астрономическими наблюдениями.
Геодезические и астрономические координаты отличаются (имеют расхождение) из-за отклонения отвесной линии от нормали к поверхности эллипсоида. При составлении географических карт этим отклонением пренебрегают.
Географические координаты – величины, обобщающие две системы координат: геодезическую и астрономическую, используют в тех случаях, когда отклонение отвесных линий от нормали к поверхности не учитывается (рис.9).

Рисунок 9 - Система географических координат
Географическая широта– угол, образованный отвесной линией в данной точке и экваториальной плоскостью.
Географическая долгота– двугранный угол между плоскостями меридиана данной точки с плоскостью начального меридиана.
При решении инженерно-геодезических задач в основном применяют плоскую прямоугольную геодезическую и полярную системы координат.
Для определения положения точек в плоской прямоугольной геодезической системе координат используют горизонтальную координатную плоскость ХОУ (рис. 10), образованную двумя взаимно перпендикулярными прямыми. Одну из них принимают за ось абсцисс X, другую – за ось ординат Y, точку пересечения осей О – за начало координат.

Рисунок 10 - Плоская прямоугольная система координат
Изучаемые точки проектируют с математической поверхности Земли на координатную плоскость ХОУ. Так как сферическая поверхность не может быть спроектирована на плоскость без искажений (без разрывов и складок), то при построении плоской проекции математической поверхности Земли принимается неизбежность данных искажений, но при этом их величины должным образом ограничивают. Для этого применяется равноугольная картографическая проекция Гаусса – Крюгера (проекция названа по имени немецких ученых, предложивших данную проекцию и разработавших формулы для её применения в геодезии), в которой математическая поверхность Земли проектируется на плоскость по участкам – зонам, на которые вся земная поверхность делится меридианами через 6° или 3°, начиная с начального меридиана (рис. 11).

Рисунок 11 - Деление математической поверхности Земли на шестиградусные зоны
В пределах каждой зоны строится своя прямоугольная система координат. С этой целью все точки данной зоны проецируются на поверхность цилиндра (рис. 12, а), ось которого находится в плоскости экватора Земли, а его поверхность касается поверхности Земли вдоль среднего меридиана зоны, называемого осевым. При этом соблюдается условие сохранения подобия фигур на земле и в проекции при малых размерах этих фигур.

Рисунок 12 - Равноугольная картографическая проекция Гаусса – Крюгера (а) и зональная система координат (б):
1 – зона, 2 – координатная сетка, 3 – осевой меридиан, 4 – проекция экватора на поверхность цилиндра, 5 – экватор,6 – ось абсцисс – проекция осевого меридиана, 7 – ось ординат – проекция экватора
После проектирования точек зоны на цилиндр, он развертывается на плоскость, на которой изображение проекции осевого меридиана и соответствующего участка экватора будет представлена в виде двух взаимно перпендикулярных прямых (рис. 12, б). Точка пересечения их принимается за начало зональной плоской прямоугольной системы координат, изображение северного направления осевого меридиана – за положительную ось абсцисс, а изображение восточного направления экватора – за положительное направление оси ординат.
Для всех точек на территории нашей страны абсциссы имеют положительное значение. Чтобы ординаты точек также были только положительными, в каждой зоне ординату начала координат принимают равной 500 км (рис. 12, б). Таким образом, точки, расположенные к западу от осевого меридиана, имеют ординаты меньше 500 км, а к востоку – больше 500 км. Эти ординаты называют преобразованными.
На границах зон в пределах широт от 30° до 70° относительные ошибки, происходящие от искажения длин линий в этой проекции, колеблются от 1 : 1000 до 1 : 6000. Когда такие ошибки недопустимы, прибегают к трехградусным зонам.
На картах, составленных в равноугольной картографической проекции Гаусса – Крюгера, искажения длин в различных точках проекции различны, но по разным направлениям, выходящим из одной и той же точки, эти искажения будут одинаковы. Круг весьма малого радиуса, взятый на уровенной поверхности, изобразится в этой проекции тоже кругом. Поэтому говорят, что рассматриваемая проекция конформна, т. е. сохраняет подобие фигур на сфере и в проекции при весьма малых размерах этих фигур. Таким образом, изображения контуров земной поверхности в этой проекции весьма близки к тем, которые получаются.
Четверти прямоугольной системы координат нумеруются. Их счет идет по ходу стрелки от положительного направления оси абсцисс (рис.13).

Рисунок 13 - Четверти прямоугольной системы координат
Если за начало плоской прямоугольной системы координат принять произвольную точку, то она будет называться относительной или условной.
studfiles.net