|
|
|
|
 Far Far |
 WinNavigator WinNavigator |
 Frigate Frigate |
 Norton
Commander Norton
Commander |
 WinNC WinNC |
 Dos
Navigator Dos
Navigator |
 Servant
Salamander Servant
Salamander |
 Turbo
Browser Turbo
Browser |
|
|
 Winamp,
Skins, Plugins Winamp,
Skins, Plugins |
 Необходимые
Утилиты Необходимые
Утилиты |
 Текстовые
редакторы Текстовые
редакторы |
 Юмор Юмор |
|
|
|
File managers and best utilites |
Творческий проект "Откуда появились цифры?". Реферат о числах 5 класс
Творческий проект "Откуда появились цифры?"

Разделы: Работа с дошкольниками
Как люди научились считать
Учиться считать люди начали в незапамятные времена, а учителем у них была сама жизнь.
Древние люди добывали себе пищу главным образом охотой. На крупного зверя – бизона или лося – приходилось охотиться всем племенем: в одиночку ведь с ним не справишься. Командовал облавой обычно самый старый и опытный охотник. Чтобы добыча не ушла, ее надо было окружить, ну вот хотя бы так: пять человек справа, семь сзади, четыре слева. Тут уж без счета никак не обойдешься! И вождь первобытного племени справлялся с этой задачей. Даже в те времена, когда человек не знал таких слов, как “пять” или “семь”, он мог показать числа на пальцах рук.

Кстати сказать, пальцы сыграли немалую роль в истории счета. Особенно когда люди начали обмениваться друг с другом предметами своего труда. Так, например, желая обменять, сделанное им копье с каменным наконечником на пять шкурок для одежды, человек клал на землю свою руку и показывал, что против каждого пальца его руки нужно положить шкурку. Одна пятерня означала 5, две – 10. Когда рук не хватало, в ход шли и ноги. Две руки и одна нога – 15, две руки и две ноги – 20.
Так люди начинали учиться считать, пользуясь тем, что дала им сама природа, – собственной пятерней.
Часто говорят: “Знаю, как свои пять пальцев”. Не с этого ли далекого времени пошло это выражение, когда знать, что пальцев пять, значило то же, что уметь считать?
Пальцы были первыми изображениями чисел. Очень сложно было складывать и вычитать. Загибаешь пальцы – складываешь, разгибаешь – вычитаешь. Когда люди еще не знали, что такое цифры, в ход при счете шли и камешки, и палочки. В старину, если крестьянин-бедняк брал в долг у богатого соседа несколько мешков зерна, он выдавал вместо расписки палочку с зарубками – бирку. На палочке делали столько зарубок, сколько было взято мешков. Эту палочку раскалывали: одну половинку должник отдавал богатому соседу, а другую оставлял себе, чтобы тот потом не требовал вместо трех мешков пять. Если давали деньги друг другу в долг, тоже отмечали это на палочке. Словом, в старину бирка служила чем-то вроде записной книжки.
Как люди научились записывать цифры
Проходили многие-многие годы. Менялась жизнь человека. Люди приручили животных, на земле появились первые скотоводы, а затем и земледельцы. Постепенно росли знания людей, и чем дальше, тем больше увеличивалась потребность в умении считать и мерить. Скотоводам приходилось пересчитывать свои стада, а при этом счет мог идти уже сотнями и тысячами. Земледельцу надо было знать, сколько земли засеять, чтобы прокормить себя до следующего урожая. А время посева? Ведь, если посеять не во время, урожая не получишь!

Счет времени по лунным месяцам уже не годился. Нужен был точный календарь. К тому же людям все чаще приходилось сталкиваться с большими числами, запомнить которые трудно или даже невозможно. Нужно было придумать, как их записывать.
В разных странах и в разные времена это делалось по-разному. Очень разные и порою даже забавные эти “цифры” у разных народов. В Древнем Египте числа первого десятка записывали соответствующим количеством палочек. Вместо цифры “3” – три палочки. А вот для десятков уже другой знак – вроде подковы.

У древних греков, например, вместо цифр, были буквы. Буквами обозначались цифры и в древних русских книгах: “А” - это один, “Б” - два, “В” – три и т.д.

У древних римлян были другие цифры. Мы и сейчас пользуемся иногда римскими цифрами. Их можно увидеть и на циферблате часов, и в книге, где обозначается номер главы. Если внимательно рассмотреть, римские цифры похожи на пальцы. Один – это один палец; два – два пальца; пять – это пятерня с отставленным большим пальцем; шесть – это пятерня да еще один палец.




Все-таки, откуда же взялись те десять цифр, которыми мы пользуемся сегодня? Наши современные цифры пришли к нам из Индии через арабские страны, поэтому их и называют арабскими. Происхождение каждой из девяти арабских цифр хорошо видно, если их записать в “угловатой” форме.

Эти цифры произошли от счета по пальцам. Цифру “1” писали так же, как и сейчас, палочкой, цифру “2” – двумя палочками, только не стоячими, а лежачими. Когда эти две палочки быстро писали одну под другой, их соединяли косой черточкой, как мы соединяем буквы в слова. Вот и получился значок, напоминающий нашу теперешнюю двойку. Тройка получалась при скорописи из трех палочек, лежащих одна под другой. В пятерке можно узнать кулак с отставленным пальцем, даже само слово “пять” происходит от слова “пясть” – кисть руки.
От арабов к нам пришло и слово “цифра” от слова “сифр”. Цифрами называют все десять значков для записи чисел, которыми мы пользуемся: 0, 1, 2, 3, 4, 5, …….
Современное слово “нуль” появилось гораздо позже, чем “цифра”. Оно происходит от латинского слово “нулла” – “никакая”. Изобретение нуля считается одним из важнейших математических открытий. При новом способе записи чисел значение каждой написанной цифры стало прямо зависеть от нее.
позиции, места в числе. При помощи десяти цифр можно записать любое, даже самое большое число, и сразу ясно, какая цифра что обозначает.
Магия чисел
Какую цифру вы любите больше всего? Семерку? Пятерку? А может, единицу? Вас удивляет такой вопрос: как можно любить, или не любить какие - то цифры, числа? Однако не все так думают. У некоторых есть числа “плохие” и “хорошие”, например, число 7 – хорошее, а 13 – плохое и т.д. Впервые мистическое отношение к числам возникло несколько тысяч лет назад, а в середине века широко распространилось по всей Европе. Была даже целая наука – нумерология, в которой каждое имя имело свое число, получаемое при переводе букв имени в цифры.
Детей заинтересовало значение числа 7.
Ведь очень многое в жизни связано с этой цифрой. Дети-дошкольники, когда им исполняется 7 лет, идут в школу; 7 цветов радуги; 7 дней в неделе; 7 звезд в созвездии Большой медведицы; 7 нот нотной грамоты.
Цифру 7 всегда связывали с понятием везения (удачи). Иногда эту цифру называют знаком ангела.
Семь считали магическим, священным числом. Это объяснялось еще и тем, что человек воспринимает окружающий мир (свет, запахи, вкус, звуки) через семь “отверстий” в голове (два глаза, два уха, две ноздри, рот).
Нередко, приписывая числу 7 таинственную силу, знахари вручали больному семь разных лекарств, настоянных на семи разных травах, и советовали пить семь дней.
Это волшебное число 7 широко использовалось в сказках “Белоснежка и семь гномов”, “Волк и семеро козлят”, “Цветик-семицветик”; в мифах древнего мира.
Отголоски почитания этого числа дошли и до наших дней, когда в речи употребляются пословицы и поговорки типа:
- Семь раз отмерь, один раз отрежь.
- Семеро одного не ждут.
- Лук – от семи недуг.
- Семь бед – один ответ.
- Семь пядей во лбу.
- Семь пятниц на неделе.
Много еще можно узнать о значении числа 7, однако каждое число имеет свое магическое значение.
А сколько звезд на небе? Сколько животных в зоопарке? А сколько ходит детей в детский сад? Дети скоро пойдут в школу и научатся считать и записывать большое количество предметов с помощью этих простых, но нужных десяти цифр.
xn--i1abbnckbmcl9fb.xn--p1ai
Проект по математике "Возникновение чисел" 5 класс
Муниципальное общеобразовательное учреждение
«Средняя общеобразовательная школа № 2» п. Бабынино
IV школьная научно-исследовательская конференция
« Одаренные дети – будущее России»
НОУ «Эрудит»
Исследовательский проект
«ВОЗНИКНОВЕНИЕ ЧИСЕЛ»
секция физико-математическая
Автор: ученица 5 класса
Мамонова София
Руководитель: учитель математики
Кочанова Евгения Владимировна
Оглавление
Введение. стр. 3
Глава I. Возникновение чисел
1.1. О происхождении арифметики. Счет. стр.4-5
1.2. Системы счисления стр.6
1.3 Письменная нумерация. Цифры разных времен стр.7-8
Глава II.
Заключение. стр.
Список использованной литературы. стр. Приложения:
Приложение 1
Приложение 2
Приложение 3
Приложение 4
Приложение 5
Введение
Мы … никогда не стали бы разумными,
если бы исключили число из человеческой
жизни.
Платон
Ни для кого не секрет, что наша жизнь наполнена цифрами и числами: день рождения, день недели, магазинный ценник, номер телефона. В настоящее время наше общество постоянно пользуется числами, чтобы что-то купить или продать, позвонить, узнать время. К тому же у каждого человека есть различные цифры, опознающие его: в паспорте, свидетельстве о рождении, кредитной карточке. Мы встречаемся с числами на каждом шагу и настолько с этим свыклись, что почти не отдаём себе отчёта, насколько важны они в нашей жизни. Но ведь когда-то же этих обозначений не существовало. А тогда откуда они взялись? И почему именно такие, а не иначе? И вообще много ли их существовало? Но когда же впервые люди стали считать? Кто же их этому научил?
Меня очень заинтересовали эти вопросы, ответы на которые я постаралась найти, выполнив информационно-реферативный проект: «Возникновение чисел».
Цель данной работы - расширить свои знания о некоторых страницах истории чисел.
Задачи:
Изучить литературу об истории возникновения чисел;
Обобщить информацию, связанную с историей возникновения чисел.
Методы работы (теоретические и эмпирические методы исследования):
- анализ литературы;
- анкетирование учащихся.
Глава I. Возникновение чисел
1.1.О происхождении арифметики. Счет.
С арифметикой мы входим, как говорил М.В. Ломоносов, во «врата учености» и начинаем наш долгий и нелегкий, но увлекательный путь познания мира. Слово «арифметика» происходит от греческого arithmos, что значит «число». [1]
Велико значение арифметики в повседневной жизни. Без счета, без умения правильно складывать, вычитать, умножать и делить числа немыслимо развитие человеческого общества. Четыре арифметических действия, правила устных и письменных вычислений изучаются, начиная с начальных классов. Все эти правила не были выдуманы или открыты одним человеком. Арифметика возникла из повседневной практики, из жизненных нужд людей в их трудовой деятельности. [5]
Еще в самые отдаленные времена людям приходилось считать различные предметы, с которыми они встречались в повседневной жизни. Было время, когда человек умел считать только до двух. Число «два» связывалось с органами зрения и слуха и вообще с конкретной парой предметов. «Глаза» у индийцев, «крылья» у тибетцов означало также «два». Если предметов было больше двух, то первобытный человек говорил просто «много». [1]
Так, например, племя ботокудов, жившее в Бразилии, выражало числа только словами «один» и «много». Появление элемента «два» объясняется выявлением возможности взять по одному предмету в каждую руку. На первоначальном этапе счёта человек связывал это понятие с понятием обеих рук, в которых находится по одному предмету в каждой. [6] Лишь постепенно человек научился считать до трех, затем пяти, десяти. [1] При выражении понятия «три» встретилось затруднение: у человека нет третьей руки; это затруднение было преодолено, когда человек догадался помещать третий предмет у своих ног. Таким образом, «три» характеризовалось поднятием обеих рук и указанием на ноги. Отсюда сравнительно характерно произошло выделение и понятие «четыре». На первой ступени развития счета человек еще отнюдь не пользовался наименованием чисел, а выражал их или у ног, или соответствующими телодвижениями или жестами.
Развитие счёта пошло значительно быстрее, когда человек догадался обратиться к самому близкому ему, самому естественному счётному аппарату – к своим пальцам. Участие пальцев в счёте помогло человеку переступить за число четыре, так как когда все пальцы на одной руке стали считаться равноценными единицами, это сразу позволило довести счёт до пяти. Дальнейшее развитие счёта потребовало усложнения счётного аппарата, и человек нашёл выход, привлекая к счёту сначала пальцы второй руки, а затем, распространяя свой приём, на пальцы ног: для племён, не носивших обуви, использование пальцев ног было вполне естественным.
Так, для выражения числа «двадцать» индейцы из Южной Америки противопоставляют пальцы на руках пальцам на ногах.
На этой ступени развития человек уже отказывается от необходимости брать пересчитываемые предметы в руку или класть к ногам. В математику входит первая абстракция, заключающаяся в том, что пересчитываемые предметы заменяются какими-либо другими однородными между собой предметами или знаками: камешками, узелками, ветками, зарубками. [6] ( Приложение1)
С развитием производства и торговли счет распространяется на множества, содержащие все большее и большее число предметов. Люди в своей практической деятельности не могли обходиться без измерения расстояний, площадей земельных участков, вместимости. Потребность в измерениях привела к возникновению и развитию, как приемов измерений, так и техники счета и правил действия над числами. ( Приложение 2)
Таким образом, возникновение и развитие чисел связано с трудовой деятельностью людей, с развитием общества. [1]
1.2.Системы счисления
Известно, что счет у нас ведется десятками: десять единиц образуют один десяток, десять десятков – одну сотню, иными словами: десять единиц первого разряда образуют одну единицу второго разряда, десять единиц второго разряда – одну единицу третьего разряда и так далее.
Такой способ счета, группами в десять, которым мы пользуемся, называется десятичной системой счисления или десятичной нумерацией. [1]
Система счисления – это способ записи чисел в виде, удобном для прочтения и выполнения арифметических операций. [5]
Почему за основание десятичной системы счисления принимается число 10? Никаких особых математических преимуществ у числа 10 по сравнению с другими нет. Использование его, как основания системы счисления исторически объясняется только тем, что первым счетным аппаратом человека были десять пальцев рук. Счет по пальцам рук, которым пользовались наши предки, положил начало системе счисления. [4]
Лузин Н.Н. поэтому поводу сказал следующее: «Преимущества десятичной системы не математические, а зоологические. Если бы на руках было бы не десять пальцев, а восемь, то человечество пользовалось восьмеричной системой счисления». [5]
Однако были племена и народы, в Африке, которые при счете пользовались лишь пятью пальцами одной руки, считали пятками: у них выработалась пятеричной система счисления, в которой основой служит число пять. Следы пятеричной системы сохранились и в скандинавских языках. [1]
Некоторые племена в качестве счетного аппарата применяли не сами пальцы рук, а их суставы. В этом случае счет иногда развивался тоже достаточно продуктивно и оформлялся в стройные системы. Здесь процесс счета протекал таким образом: большой палец одной руки является счетчиком суставов остальных пальцев этой руки; так как на каждом из остальных четырех пальцев этой руки содержится по три сустава, то следующий за суставом выше единицей являлось число 12, что и послужило двенадцатеричной системой счисления. Этот процесс иногда не останавливался на двенадцати, а продолжался далее, причем каждый палец другой руки служил единицей высшего разряда, т.е. представлял собой 12, и после отсчета всех пальцев на второй руке создавалась новая единица высшего разряда 12х5, то есть 60. Возможно, что такого рода счет способствовал созданию шестидесятеричной системы счисления, имевшей большое распространение в древнем Вавилоне и перешедшей позднее ко многим другим народам.
Следы двенадцатеричной и шестнадцатеричной систем счисления сохранились и до нашего времени. Стоит вспомнить хотя бы счет часов в сутках, измерение углов градусами, минутами и секундами. [6]
Древнейшей из всех является двоичная система счисления, которой пользовались древние египтяне.
Двадцатеричная система возникла у народов, считавших не только с помощью пальцев рук, но и пальцев ног. Этой системой пользовались также индейцы племени Майя.
В настоящее время почти все народы мира пользуются десятичной системой счисления. [1] Однако это не означает, что эта система всегда была единственной: некоторые народы перешли к десятичной системе уже в более поздние времена, а ранние пользовались другой системой. [6]
В связи с развитием ЭВМ широкое применение нашли двоичная, восьмеричная, троичная системы. Для современных вычислительных машин эти системы оказались более удобными, чем десятичная. [4]
1.3.Письменная нумерация. Цифры разных времен
Как бы велико ни было число, его можно записать с помощью всего лишь десяти числовых знаков, цифр: 1.2,3,4,5, 6,7,8,9,0. Современные цифры были выработаны на протяжении многих веков. Для запоминания чисел люди пользовались зарубками на деревьях и на палках и узлами на веревках. Далее естественно стали обозначать число «один» одной чертой, «два» -двумя, «три»-тремя черточками и так далее. Следы таких цифр имеются, например, в римской системе: I, II, III. Но с развитием производства и культуры, когда появилась нужда записывать большие числа, стало неудобно пользоваться черточками. Тогда стали вводить особые знаки для отдельных чисел. Каждое число, как и каждое слово, обозначалось особым значком, иероглифом.
Вот, например, как выглядят китайские иероглифические цифры. ( Приложение 3)
В древнем Египте единица изображена колом, десяток – как бы парой рук, сотня – свернутым пальмовым листом, тысяча – цветком лотоса, сто тысяч – лягушкой.
( Приложение 4). Вот, например, как будет выглядеть число 1245386 в египетской записи.( Приложение 5)
В дальнейшем появляются особые обозначения отдельных звуков, то есть буквы. Было время, когда буквами пользовались и в качестве цифр. Так поступали древние греки, евреи, славяне и другие народы. Чтобы отличить буквы от чисел, славяне ставили над буквами, изображающие числа, особый знак, названный «титло». Эта нумерация, называемая алфавитной, также оказалась со временем неудобной.
(Приложение 6)
Потребности практики, развитие производства и торговли способствовали созданию более удобных, современных цифр и образованию современной письменной нумерации.
Всем известны римские цифры : I V X L C D M.
1 5 10 50 100 500 1000
( Приложение 7)
Некоторые из этих семи знаков служили и буквами. Римляне обозначали буквой М тысячу. Вот, например, как записывалось число 38784: XXXVIIImDCCLXXXIV. Неудобна была римская нумерация по сравнению с нашей десятичной: записи длинные, умножение и деление в письменном виде производить невозможно. Все действия нужно производить в уме. Даже, чтобы прочитать число, нужно устно складывать или вычитать, потому, что каждая из семи римских цифр означает всюду, где бы она ни стояла, одно и тоже число. В современной же письменной нумерации не только вид, начертание цифры, но и ее место, ее положение, ее позиция среди других цифр имеет значение. Например, в числе 15 цифра 5 означает пять единиц, а в числе 53 та же цифра 5 означает пять десятков. Именно поэтому наша нумерация называется позиционной.
Она, как и современные цифры, возникла много лет назад в Индии. [1] Кроме того, в Индии получило распространение употребление нуля для указания соответствующих разрядных единиц, что тоже сыграло большую роль в усовершенствовании числовых записей и облегчении операций над числами. Цифровые знаки Индии не совпадают по очертаниям с современными цифрами, но все же имеют с ними в некоторых случаях большое сходство. Так, например, очень походили на современные цифры индийские знаки, изображавшие единицу, семерку и нуль. Остальные знаки в течение многих веков, отделяющих нас от времени их происхождения, сильно видоизменялись. [6]
В течение многих столетий, переходя от народа к народу, старинные индийские цифры много раз изменялись, пока приняли современную форму. [1]
( Приложение 8)
Арабы заимствовали у индийцев цифры и позиционную десятичную систему, которую европейцы, в свою очередь заимствовали у арабов. Поэтому наши цифры, в отличие от римских, стали называть арабскими. Правильнее было бы их называть индийскими. Они употребляются в нашей стране, начиная с семнадцатого века. Римские же цифры применяются лишь в исключительных случаях. [1]
ГЛАВА II. Развитие теории простых чисел.
Развитие теории простых чисел имеет большое значение для многих разделов математики.
В натуральном ряду простые числа расположены очень загадочно. Найти порядок их чередования пытались и пытаются многие математики, начиная с Эвклида.
Такой способ (решето Эратосфена) открыл греческий математик Эратосфен.
Великий математик П. Ферма в одном из своих писем утверждал, что любое простое число вида х = 4n + 1 является суммой двух квадратов.
Попробуем представить таким способом некоторые числа, например: 5; 13; 17; 29; 37:
5 = 4·1+1=12+22;
13 = 4·3+1=22+32;
17 = 4·4+1=42+12;
29 = 4·7+1=22+52;
37 = 4·9+1=62+12.
Ценный вклад в теорию чисел внес другой великий математик – Л. Эйлер.
В 1755 году, после многих лет упорного труда, Эйлеру удалось найти доказательство этого предложения П. Ферма.
В наше время поиск больших простых чисел выполняют на электронных вычислительных машинах.
«Охота» за общей формулой, с помощью которой можно выразить любое простое число, началась ещё в древности, но до сих пор не увенчалась успехом.
Если многие математики разных стран занимались числами, то у нас появился ещё один вопрос – есть ли числа, носящие имена великих математиков?
Наши поиски привели к следующим открытиям и знакомству с интересными числами.
Заключение.
Проведя анкетирование учащихся моего класса и двух других классов нашей школы, знают ли они из какой страны к нам пришли числа, я получила следующие результаты, которые представлены на диаграмме.( Приложение )
Из полученной информации можно сделать следующий вывод: очень мало учащихся, знают о том, откуда к нам пришли числа.
Список использованной литературы.
Глейзер Г.И. История математики в школе
Григорьева Г.И. Математика. Предметная неделя в школе.-М.: Издательство «Глобус»,2010.-198с.
Депман И. Я. За страницами учебника математики. – М.; Просвещение,1989.
Нагибин Ф.Ф. Математическая шкатулка.-М.:Просвещение,1988.-160с.
Электронный энциклопедический словарь юного математика
Интернет-ресурс
Приложение 1
Узлы, применявшиеся в старину для изображения чисел
Приложение 2

Межевание у древних египтян ( примерно XV в. до н.э.)
Приложение 3

Китайские иероглифические цифры
Приложение 4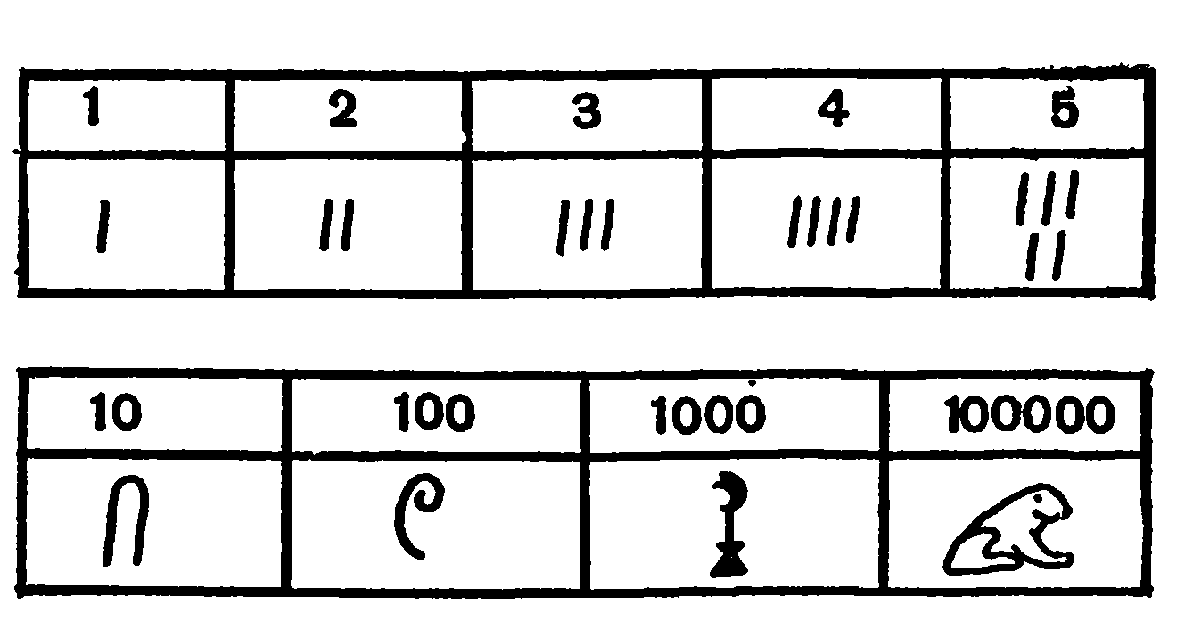
Египетские иероглифические цифры
Приложение 5

Приложение 6
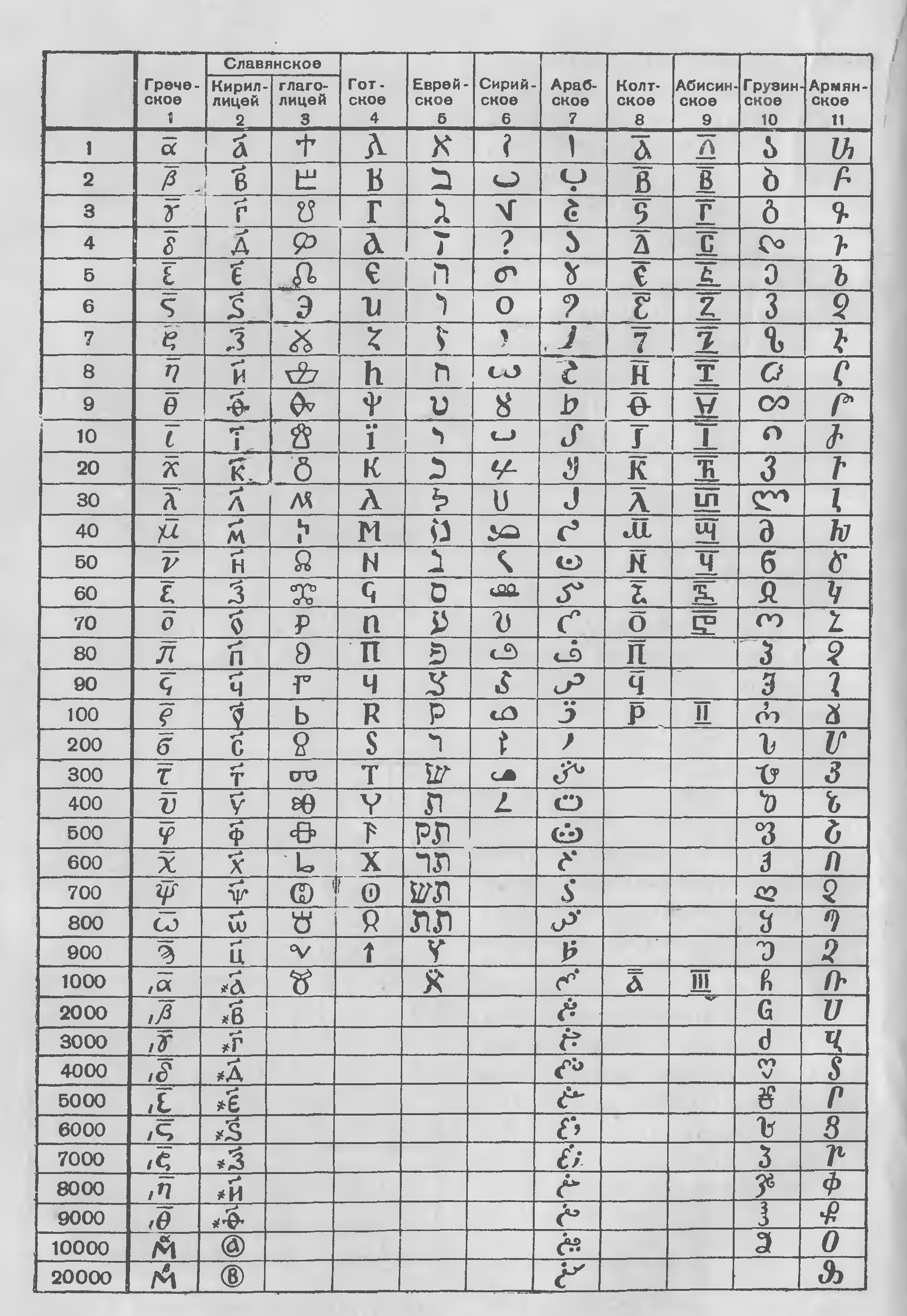
Алфавитная нумерация у разных народов
Приложение 7
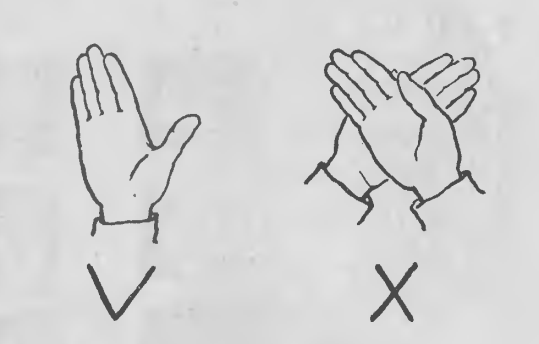
Римская нумерация
Приложение 8

Эволюция индийских цифр от XII века до средины XV века
infourok.ru
Доклад по теме"Числа великаны"
Две стихии господствуют в математике – числа и фигуры с их бесконечным многообразием свойств и взаимосвязей. Само возникновение понятия числа — одно из гениальнейших проявлений человеческого разума. Действительно, числами не только что-то измеряют, ими сравнивают, вычисляют, даже рисуют, проектируют, сочиняют, играют, делают умозаключения, выводы. Когда- то числа служили только для решения практических задач. А потом их стали изучать, узнавать их свойства.
Открытия в науке о числах делали Пифагор, Архимед, немецкий ученый Карл Гаусс, французские математики Алексис Клеро, Эверист Галуа, Шюке и др. Сначала люди умели называть лишь маленькие числа, а потом все больше и больше. Они создали разные системы исчисления, такие как двоичная, десятичная, шестидесятеричная.
Около 2.5- 3 тысяч лет до нашей эры египтяне придумали свою числовую систему. Своя система счисления была у римлян. В древности применялась и алфавитная система записи чисел. Любопытны были различные методы обозначения чисел. Но у всех этих методов был один недостаток: по мере увеличения чисел нужны были все новые и новые знаки.
Величайший ученый Древней Греции Архимед уже в III в. до н.э. написал книгу

« Исчисление песчинок», в которой он опровергает ложное мнение людей о том, будто бы число песчинок на земле столь велико, что его нельзя выразить, а числа больше этого и вообще якобы не существуют. Архимед доказывает, что если наполнить песчинками пространство всего мира, всю вселенную, которую он принимает за огромный шар с диаметром около 15000000000 километров, то число песчинок не превысит 1063. Это есть единица с 63 нулями. Таким образом, в «Псаммите» Архимед показал, что счёт можно продолжить неограниченно, то есть натуральный ряд бесконечен.
Впрочем, египтяне, римляне, греки с большими числами в своей практике не встречались. И когда древнегреческий математик Архимед научился называть громадные числа и изложил свое открытие в своей книге, на это никто не обратил внимание
Человечество развивалось и двигалось вперед. Люди пытались вычислить площадь земли, расстояние от земли до солнца, расстояние между звездами, изучали молекулы, атомы. Появилась необходимость в обозначении больших чисел. Ученые задумались: «Есть ли предел у числового ряда, как назвать и записать большое число?» В жизни мы эти числа почти не встречаем. Только в науке нужны большие числа.
Но изучение чисел и их свойств необходимо современному человеку для развития логического мышления, памяти, творческого решения задач. В школьном курсе «математика» не изучается тема «числа — великаны», но узнав, что существуют числа больше миллиарда, у нас возник интерес и желание больше узнать об этих числах. Безусловно, мало знать, как называются самые большие числа в мире, имеющие собственное название. Интересно узнать и посмотреть на то, как они записываются, где встречаются в жизни.
Это и обусловило выбор темы работы: «Числа — великаны».
Актуальность: расширить свой кругозор в употреблении чтения многозначных чисел- великанов в области астрономии, химии, физики.
Объект исследования: удивительный мир чисел
Предмет исследования: числа — великаны
Цель – знакомство с названием чисел — великанов, умение их читать.
Гипотеза «Если узнаем историю возникновения чисел, системы счисления и название классов, тогда легко будем читать и писать большие числа. Сможем избежать трудностей при чтении, сталкиваясь на практике с числами- великанами»
В истории математики сложилось так, что числа-великаны имеют свои названия и записи в двух вариантах. Их называют «длинная шкала» и «короткая шкала».
Например, число квинтиллион может быть записано таким образом:
1 000 000 000 000 000 000 = 1018 (согласно короткой шкале)
или так:
1 000 000 000 000 000 000 000 000 000 000 = 1030 (согласно длинной шкале)
Такое различие в значениях для одного и того числа начинается буквально с биллиона, – числа, записанного с помощью 9 нулей (по короткой шкале) и с 12 нулями (по длинной).
До биллиона (как видно из таблицы ниже) различия в записи чисел, являющихся степенями тысячи, нет.

В чем разница наименования чисел-великанов в системе короткой шкалы и длинной шкалы?
Названия числа в системе короткой шкалы формируется так:
латинской числительное + «- иллион».
Например,
1) секстиллион = «sexta» (шестая) + «-иллион»:
1 000 000 000 000 000 000 000 = 10001 + 6 = 1000 * 10006 .
1) нониллион = «nona» (девятая) + «- иллион»:
1 000 000 000 000 000 000 000 000 000 000 = 10001 + 9 = 1000 * 10009 .
Исключение составляет название слова «миллион»; оно образовано от латинского «mille»( что означало «тысяча») + «-он» . То есть, миллион – это тысяча тысяч.
Система названий чисел-великанов по короткой шкале используется всего лишь в
нескольких странах: США, Великобритании, Канаде, России, Украине, Турции и
Греции.
Вот примеры значений чисел-великанов и их названий:

Обратите внимание, что некоторые из названных стран используют чаще слово «миллиард», нежели слово «биллион» (тысяча миллионов). А ведь «миллиард» уже по своему строению относится к системе с длинной шкалой.
Здесь названия чисел строятся по такому принципу: к латинскому числительному добавляется суффикс «-он», следующее за ним число ( то есть в 1000 раз большее) образуется из того же самого числительного по-латыни, но с окончанием «-ард».
Например, за триллионом в системе длинной шкалы идёт триллиард (тысяча триллионов), а только потом квадриллион, за ним идет квадриллиард (тысяча квадриллионов) и т. д.
В числах-великанах количество нулей определяется так: если в этой системе число оканчивается «-иллион», то оно вычисляется по такой формуле 6•x (где x — числительное латинское) . А если оканчивается на «-иллиард», то 6•x+3.
Например, квадриллион имеет 6•4 = 24 нуля (kvadra – четыре), а квадриллиард имеет
6•4 + 3 = 27 нулей
| Название | Значение | ||
| Короткаяшкала | Длиннаяшкала | ||
| тысяча | 103 | 103 | |
| миллион | 106 | 106 | |
| миллиард | (109) | 109 | |
| биллион | 109 | 1012 | |
| биллиард | — | 1015 | |
| триллион | 1012 | 1018 | |
| триллиард | — | 1021 | |
| квадриллион | 1015 | 1024 | |
| квадриллиард | — | 1027 | |
| квинтиллион | 1018 | 1030 | |
| квинтиллиард | — | 1033 | |
| секстиллион | 1021 | 1036 | |
| секстиллиард | — | 1039 | |
| септиллион | 1024 | 1042 | |
| септиллиард | — | 1045 | |
| октиллион | 1027 | 1048 | |
| октиллиард | — | 1051 | |
| нониллион | 1030 | 1054 | |
| нониллиард | — | 1057 | |
| дециллион | 1033 | 1060 | |
| дециллиард | — | 1063 | |
Произношение чисел, идущих далее, часто различается.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Интересные факты с числами-великанами.
Факт 1.
Суэцкий канал считается границей между Азией и Африкой. По нему могут проплыть самые крупные грузовые суда и танкеры, имеющие максимальную грузоподъемность 240.000 тонн. Сегодня его считают инженерным чудом: кораблям не нужно огибать Африку, чтобы например из Роттердама добраться в Токио. Суэцким каналом пользуются нефтяные танкеры и суда, перевозящие древесину, руду и зерно. В 2010 году через канал прошли 17993 корабля. Значит, к окончанию 2013 года их примерно было 17993 * 3 = 53979 и они перевезли грузов около 53979 * 240000 = 12 954 960 000 т, т.е. 13 миллиардов тонн или 13 триллионов кг груза.

Факт 2.
Фонтан Фахда в Джидде (Саудовская Аравия) внесен в Книгу рекордов Гиннеса как самый высокий фонтан в мире. Он находится в прибрежном заливе и извергает соленую воду, которую качает всего лишь 2 насоса. Он состоит из одного мощного столба воды, который устремляется вертикально в воздух со скоростью 374 км/час,
выбрасывая по 625 литров в секунду запасов Красного Моря на высоту 312 метров.
Масса воды в воздухе превышает 18 тонн.

Факт3
Солнеченая система

Масса Земли - 5 978 000 000 000 000 000 000 000 кг
Факт 4
Масса планет.

Масса Венеры 4.81068 · 1024 (Килограмм)Масса Земли 5.97600 · 1024 (Килограмм)Масса Луны 0.07350 · 1024 (Килограмм)Масса Марса 0.63345 · 1024 (Килограмм)Масса Меркурия 0.32868 · 1024 (Килограмм)
Масса Нептуна 101.59200 · 1024 (Килограмм)Масса Плутона 0.01195 · 1024 (Килограмм)Масса Сатурна 561.80376 · 1024 (Килограмм)Масса Солнца 1989000.00000 · 1024 (Килограмм)Масса Урана 86.05440 · 1024 (Килограмм)Масса Юпитера 1876.64328 · 1024 (Килограмм)
ФАКТ 5
Самый большой океан –Тихий, его площадь – 178 684 тыс.км2; Глубина тоже наибольшая – 4 281 метр . 
Факт 6
Наибольшая высота суши над уровнем моря- горы Джомолунгма (Эверест) – 8848 метров. Сколько этажей имел бы дом высотой в эту гору, если считать, что расстояние между этажами 4 м? 8 848 : 4 = 2 212 (этажей). 
Применение чисел — великанов в жизни
При исследовании проблемы среди учащихся 4-7, и 8-9 классов одной из школ было проведено анкетирование. Были представлены следующие вопросы:
- Какое число самое большое?
- Запишите число миллион, миллиард, триллион, квадриллион, и др.?
- Как называется число с 12 нулями?
- Существуют ли числа более чем с 12 нулями?
- Что больше биллион или миллиард?
Результаты следующие:
Из 36 опрошенных 10 учащихся самым большим числом назвали триллион, 21 учащихся — миллиард, а 3 ученика– квадриллион, 2 ученика – другие классы. 20 из опрошенных правильно записали числа миллион, миллиард, у четырех не хватает нулей, 10 учащихся правильно записали триллион, 2 квадриллион.
На вопрос «Как называется число с 12 нулями?» 19 учеников назвали правильный ответ. У других нет ответа.
На последний вопрос из опрошенных 19 учеников ответили – «да», 8 – «наверно», 8 учеников ответили «не знаю», 1 – нет.
В повседневной практике, даже при сложнейших вычислениях, редко используются числа больше миллиарда. Астрономы, физики и химики, имеющие дело с большими числами, предпочитают записывать числа с помощью степени числа десять. Мы с трудом ориентируемся в больших числах, даже миллион как следует, себе не представляем.
Как представить себе 1 000 000 учащихся? Чтобы это представить, посчитаем, на сколько километров протянулась бы шеренга в 1 000 000 учащихся, если бы каждые 2 из них заняли 1м. Почти от Москвы до Санкт-Петербурга протянулась бы эта шеренга. Каких размеров достигнет обыкновенный комар, увеличенный в миллион раз?
Длина комара приблизительно равна 5 мм. 5 мм x1 000 000 = 5 000 000мм = 5 км.
Рост человека, увеличенный в миллион раз, достигает 1700км.
Миллион можно назвать карликом по сравнению с таким числом, как миллиард. Если мы начнем считать подряд до миллиарда в 12 – летнем возрасте, то закончим счет глубоким стариком 100 – летнего возраста, работая ежедневно по 6 часов в сутки.
Миллиард – это не просто великан, а великанище. Ведь совсем небольшой промежуток времени – 1 минута. А миллиард таких минут – эта более 19 столетий. Секунда времени в сравнении с часом нам кажется мгновением. Но миллиард секунд – это около 32 лет.
Часто можно встретиться с числовыми великанами. Они присутствуют всюду вокруг и даже внутри нас самих — надо лишь уметь рассмотреть их. Небо над головой, песок под ногами, воздух вокруг нас, кровь в нашем теле — все скрывает в себе невидимых великанов из мира чисел.
Числовые исполины небесных пространств для большинства людей не являются неожиданными. Хорошо известно, что зайдет ли речь о числе звезд вселенной, об их расстояниях от нас и между собою, об их размерах, весе, возрасте — во всех случаях мы неизменно встречаемся с числами, подавляющими воображение своей огромностью. Недаром выражение «астрономическое число» сделалось крылатым. Многие, однако, не знают, что даже и те небесные тела, которые астрономы часто называют «маленькими», оказываются настоящими великанами, если применить к ним привычную земную мерку. Существуют в нашей солнечной системе планеты, которые, ввиду их незначительных размеров, получили у астрономов наименование «малых». Среди них имеются и такие, поперечник которых равен нескольким километрам. В глазах астронома, привыкшего к исполинским масштабам, они так малы, что, говоря о них, он пренебрежительно называет их «крошечными». Но они представляют собой «крошечные» тела только рядом с другими небесными светилами, еще более огромными: на обычную же человеческую мерку они далеко не миниатюрны. Возьмем такую «крошечную» планету с диаметром 3 км. По правилам геометрии легко рассчитать, что поверхность такого тела заключает 28 кв. км, или 28 000 000 кв. м. На 1 кв. м может поместиться стоя человек 7. Значит, на 28 миллионах кв. м найдется место для 196 миллионов человек.
Песок под нашими ногами также вводит нас в мир числовых исполинов. Недаром сложилось издавна выражение: «бесчисленны, как песок морской». Древние недооценивали многочисленность песка, считая ее одинаковой с многочисленностью звезд. В старину не было телескопов, а простым глазом мы видим на небе всего около 3500 звезд (в одном полушарии). Песок на морском берегу в миллионы раз многочисленнее, чем звезды, доступные невооруженному зрению.
Каждый кубический сантиметр окружающего нас воздуха (это примерно портновский наперсток) заключает в себе 27 квинтиллионов молекул, в крошечной капли крови плавает пять миллионов мелких телец красного цвета.
Практическая часть
Задачи с применением чисел- великанов
Мы можем решить такие задачи.
Задача 1.
Какой объем воды выкачали насосы фонтана Фахда с момента его открытия (1983г.) за 30 лет?
1) За 1 секунду: 625 л воды
2) За 1 час: 625 л * 3600 сек. = 2 250 000 л.
3) За 1 сутки: 2 250 000 л * 24 ч. = 54 000 000 л.
4) 1 год: 54 000 000 л. * 365 дн. = 19 710 000 000 л.
5) За 30 лет: 19 710 000 000 л. * 30 лет = 591 300 000 000 л.
Задача 2.
Объем воды Красного Моря составляет 251 тысячу кубометров. На сколько лет хватило бы беспрерывной работы фонтана Фахда, если бы вода не возвращалась назад в море?
1) Объем воды: 251 000 м3 = 251 000 000 л.
2) За 1 год фонтан выкачивает 19 710 000 000 л.
3) 19 710 000 000 л. больше, чем 251 000 000 л. Значит, запас воды в Красном Море закончился бы раньше, чем через год.
4) За 1 сутки фонтан извергает 54 000 000 л. воды. Тогда 251 000 000 л : 54 000 000 л ≈ 4,6 суток.
То есть, менее чем за 5 дней фонтан прекратил бы свою работу , а Красное Море было бы вычерпано до капельки.
Задача №3
Сколько времени потребуется человеку, чтобы сосчитать миллиард зерен, если он в минуту будет считать по 100 зерен.
Решение: По нашему условию, сосчитать до миллиарда человеку потребуется
1 000 000000:100=10 000 000 мин. Или (10 000 000:60=166 667), т. е. Примерно 170 000 ч. или (170000:24=7000) около 7000 суток, т. е. Более 16 лет беспрерывного счета.
Задача №4
В нашей стране проживают около 250 млн. человек. Если все люди встанут в одну шеренгу, то какой длины будет эта шеренга? (Пусть каждый человек занимает место длиной в 50см).
Решение: 250 000 000·50 =12 500 000 000см, т.е. 125 000 км
Список задач на тему «Числа великаны» см. Приложение.
Заключение
Проделанная исследовательская работа помогла узнать, как зародилась наука о числах, как она развивалось, какие трудности встречались на ее пути и какие ученые занимались изучением чисел и их свойств.Узнав историю возникновения чисел, систем счисления, название классов, расширили свой кругозор в области математики, а именно по вопросу числа- великаны.Были удивлены, что числа великаны и названия их появились давно. Оказывается, они окружают нас повсюду. Подробно изучив классы, можем называть и записывать числа- великаны, использовать знания при решении задач.
Через практическую деятельность – вычисления, сравнения попытались представить, насколько эти числа огромны. Полученные знания помогут в дальнейшем в изучении предметов физика, химия, астрономия.
Планируем продолжить изучение чисел их свойств. Зная, что существуют числа- великаны, хочется иметь представление о числах- карликах.
Гипотеза «Если узнаем историю возникновения чисел, системы счисления и название классов, тогда легко будем читать и писать большие числа. Сможем избежать трудностей при чтении, сталкиваясь на практике с числами- великанами» нашла свое утверждение.
Литература
1. Депман И. Я.,Виленкин Н.Я. За страницами учебника математики: пособие для учащихся 5-6 классов средней школы.М.Просвещение,1989
2.Депман И. Я. Мир чисел. М.: Детская литература,1982
3.Кординский Б. А.,Ахадов Л. А.Удивительный мир чисел: книга для учащихся. М.Просвещение,1986
4.Литцман В. Великаны и карлики в мире чисел. М,1959.
5.Нагибин Ф. Ф., Канин Е. С.Математическая шкатулка. М.Просвещение,1988
6. Интернет ресурсы: http://yandex.ru/images; wikipedia.org; http://pandia.org.
План.
1.Вступление: Цель. Задачи работы.Гипотеза.
2.Исторические сведения возникновения чисел-великанов.
3. Обозначение чисел-великанов:
а) короткая шкала,
б) длинная шкала.
4. Интересные факты
5. Применение чисел-великанов.
6.Практическая часть (задачи).
7.Заключение.
8. Приложение
9.Литература.
Числа-великаны и их названия.

Выполнили: ученицы 5 «Г» класса
МБОУ «СОШ №48»
г. Астрахань
Ляликова Екатерина, Бакалым Анастасия
Учитель: Макеева Ю.К.
multiurok.ru
|
|
..:::Счетчики:::.. |
|
|
|
|
|
|
|
|


