 Гладкая
поверхность (без трения):
Гладкая
поверхность (без трения):
Связи и реакции связей
Тело называется свободным, если его перемещение в пространстве ничем не ограничено. В противном случае тело называется несвободным, а тела, ограничивающие перемещения данного тела, ¾ связями. Силы, с которыми связи действуют на данное тело, называются реакциями связей.
Основные виды связей и их реакции:
1.
 Гладкая
поверхность (без трения):
Гладкая
поверхность (без трения):
Реакция гладкой поверхности направлена по нормали к этой поверхности (перпендикулярна общей касательной).
2.
 Опорная точка
(ребро):
Опорная точка
(ребро):
Реакция перпендикулярна опирающейся поверхности.
3. Идеальная нить (гибкая, невесомая, нерастяжимая):
 Примеры: моделирует трос,
канат, цепь, ремень,…
Примеры: моделирует трос,
канат, цепь, ремень,…
Реакция идеальной нити направлена по нити к точке подвеса.
4. Идеальный стержень (жесткий, невесомый стержень, на концах которого шарниры):
 |
Реакция связи направлена по стержню.
В отличие от нити стержень может работать и на сжатие.
5. Цилиндрический шарнир:
Такая связь позволяет телу перемещаться вдоль оси, поворачиваться вокруг оси шарнира, но не позволяет точке закрепления перемещаться в плоскости, перпендикулярной оси шарнира. Реакция лежит в плоскости, перпендикулярной оси шарнира, и проходит через нее. Положение этой реакции не определено, но она может быть представлена двумя взаимно перпендикулярными составляющими
 |
|||
 |
|||
6. Сферический шарнир:
Такая связь не дает точке закрепления тела перемещаться ни в одном из направлений. Положение реакции не определено, но она может быть представлена тремя взаимно перпендикулярными составляющими.
 |
|||
 |
|||
7. Подпятник:
 Реакция данной связи
задается аналогично предыдущему случаю.
Реакция данной связи
задается аналогично предыдущему случаю.
8. Жесткая заделка:
Такая связь препятствует перемещению и повороту вокруг точки закрепления. Контакт тела со связью осуществляется по поверхности. Имеем распределенную систему сил реакции, которая, как будет показано, может быть заменена одной силой и парой сил.
Аксиома освобождаемости от связей:
Всякое несвободное тело можно считать свободным, если мысленно освободиться от связей, а их действие заменить соответствующими реакциями.
www.referatmix.ru
Связи и реакции связей
Тело называется свободным, если его перемещение в пространстве ничем не ограничено. В противном случае тело называется несвободным, а тела, ограничивающие перемещения данного тела, ¾ связями. Силы, с которыми связи действуют на данное тело, называются реакциями связей.
Основные виды связей и их реакции:
1. Гладкая поверхность (без трения):
Реакция гладкой поверхности направлена по нормали к этой поверхности (перпендикулярна общей касательной).2. Опорная точка (ребро):Реакция перпендикулярна опирающейся поверхности.3. Идеальная нить (гибкая, невесомая, нерастяжимая):
Примеры: моделирует трос, канат, цепь, ремень,…
Реакция идеальной нити направлена по нити к точке подвеса.4. Идеальный стержень (жесткий, невесомый стержень, на концах которого шарниры):
Реакция связи направлена по стержню.
В отличие от нити стержень может работать и на сжатие.5. Цилиндрический шарнир:Такая связь позволяет телу перемещаться вдоль оси, поворачиваться вокруг оси шарнира, но не позволяет точке закрепления перемещаться в плоскости, перпендикулярной оси шарнира. Реакция лежит в плоскости, перпендикулярной оси шарнира, и проходит через нее. Положение этой реакции не определено, но она может быть представлена двумя взаимно перпендикулярными составляющими
6. Сферический шарнир:
Такая связь не дает точке закрепления тела перемещаться ни в одном из направлений. Положение реакции не определено, но она может быть представлена тремя взаимно перпендикулярными составляющими.
7. Подпятник:
Реакция данной связи задается аналогично предыдущему случаю.8. Жесткая заделка:
Такая связь препятствует перемещению и повороту вокруг точки закрепления. Контакт тела со связью осуществляется по поверхности. Имеем распределенную систему сил реакции, которая, как будет показано, может быть заменена одной силой и парой сил.
Аксиома освобождаемости от связей:
Всякое несвободное тело можно считать свободным, если мысленно освободиться от связей, а их действие заменить соответствующими реакциями.
bukvasha.ru
Тело, которое может совершать из данного положения любые перемещения в пространстве, называется свободным.
Тело, перемещениям которого препятствуют какие-нибудь другие, скрепленные или соприкасающиеся с ним тела, называется несвободным. Все то, что ограничивает перемещение данного тела, называют связью.
Сила, с которой данная связь действует на тело, препятствующая тем или иным его перемещениям, называется реакцией связи. Реакция связи направлена в сторону противоположную той, куда связь не дает перемещаться телу.
Принцип освобождаемости от связей: несвободное твердое тело можно рассматривать как свободное, если его мысленно освободить от связей, заменив их действие реакциями. В статике этот принцип позволяет рассматривать равновесие несвободного твердого тела как свободного под действием активных(заданных)сил и реакций связей.
Рассмотрим наиболее часто встречающиеся типы связей на плоскости и направления их реакций.
1. Гладкая плоскость (поверхность) или опора
Реакция N гладкой плоскости (поверхности) или опоры направлена по общей нормали к поверхностям соприкасающихся тел в точке их касания и приложена к этой точке.
2. Гибкая нить (провода, канаты, цепи, ремни)
Реакция Т направлена вдоль нити к точке подвеса.
3. Невесомый стержень с шарнирами
Реакция N невесомого стержня направлена вдоль стержня. Обычно реакция Nизображается от тела по стержню, в предположении, что в равновесии стержень растянут.
4. Неподвижный цилиндрический шарнир илиподшипник
Реакция RAцилиндрического шарнира может иметь любое направление в плоскости, перпендикулярной оси вращения, т. е. в плоскостиАху. Обычно ее раскладывают на две составляющие ХАи YAпо двум взаимноперпендикулярным направлениям.
5. Шарнирно-подвижная опора (опора на катках)
Реакция R проходит через ось шарнира и направлена перпендикулярно к опорной плоскости.
6. Жесткая заделка
Нахождение реакции жесткой заделки сводится к определению составляющих ХАи YAпрепятствующих линейному перемещению балки в плоскости действия сил, и алгебраической величине момента mA, препятствующего вращению балки под действием приложенных к ней сил.
Аксиома связей (принцип освобождения от связей) — одна из аксиом теоретической механики. Может быть сформулирована следующим образом:
Всякое несвободное тело можно рассматривать как свободное, если отбросить связи и заменить их действие реакциями этих связей.
При этом под связью понимается всё то, что ограничивает движение тела.
Простейший пример применения аксиомы связей: если на горизонтальной поверхности (например, на столе) в поле тяжести Земли (то есть, в "обычных" земных условиях) лежит тело, то мы можем мысленно отбросить горизонтальную поверхность и заменить её действие силой реакции этой поверхности.
Приступая к решению задания, необходимо разобраться в условии задачи и рисунке, а затем:
1. Составить расчетную схему, которая включает:
- объект равновесия,
- активные (заданные) силы,
- силы реакции, заменяющие действия отброшенных связей.
2. Определить вид полученной системы сил и выбрать, соответствующие ей, уравнения равновесия;
3. Выяснить, является ли задача статически определимой;
4. Составить уравнения равновесия и определить из них силы реакции;
5. Сделать проверку полученных результатов.
При замене связей (опор) силами реакций помнить:
- если связь препятствует перемещению тела только в одном каком-нибудь направлении, то направление ее реакции противоположно этому направлению;
- если же связь препятствует перемещению тела по многим направлениям, то силу реакции такой связи изображают ее составляющими, показывая их параллельно выбранным координатным осям  и
и  .
.
Решение уравнений равновесия будет тем проще, чем меньшее число неизвестных будет входить в каждое из них. Поэтому, при составлении уравнений равновесия следует:
1) координатные оси  и
и  располагать так, чтобы одна из осей была перпендикулярна к линии действия хотя бы одной из неизвестных сил, в этом случае проекция неизвестной силы исключается из соответствующего уравнения равновесия;
располагать так, чтобы одна из осей была перпендикулярна к линии действия хотя бы одной из неизвестных сил, в этом случае проекция неизвестной силы исключается из соответствующего уравнения равновесия;
2) за центр моментов выбирать точку, в которой пересекаются линии действия наибольшего числа неизвестных сил реакций, тогда моменты этих сил не войдут в уравнение моментов.
Если сила  в плоскости
в плоскости  имеет две составляющие ее силы
имеет две составляющие ее силы  и
и  , то при вычислении момента силы
, то при вычислении момента силы  вокруг некоторой точки О, полезно применить теорему Вариньона, вычислив сумму моментов составляющих ее сил относительно этой точки (см. рис. 4).
вокруг некоторой точки О, полезно применить теорему Вариньона, вычислив сумму моментов составляющих ее сил относительно этой точки (см. рис. 4).
Если к телу в числе других сил приложена пара сил, то ее действие учитывается только в уравнении моментов сил, куда вносится момент этой пары, с соответствующим, знаком.
Пример 1. Шар веса  опирается в точке
опирается в точке  на наклонную плоскость, образующую с вертикалью угол
на наклонную плоскость, образующую с вертикалью угол  , и привязан к стене веревкой, которая образует с вертикалью угол
, и привязан к стене веревкой, которая образует с вертикалью угол  (рис.13а). Определить реакцию плоскости в точке
(рис.13а). Определить реакцию плоскости в точке 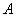 и натяжение веревки.
и натяжение веревки.

Рис.13
Решение: Обозначим искомую реакцию плоскости, направленную по нормали  к этой плоскости, через
к этой плоскости, через  , а натяжение веревки – через
, а натяжение веревки – через  . Линия действия всех трех сил
. Линия действия всех трех сил  и
и  пересекаются в центре шара
пересекаются в центре шара  . Примем вертикаль и горизонталь в точке
. Примем вертикаль и горизонталь в точке  за координатные оси и найдем проекции сил
за координатные оси и найдем проекции сил  и
и  на эти оси:
на эти оси:
 ,
,  ,
,  ,
,
 ,
,  ,
, 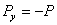 .
.
Так как данная система сходящихся сил является плоской, то условия равновесия (4) имеют вид
1) 
2) 
Умножив первое уравнение на  , а второе на
, а второе на  и сложив их, получим
и сложив их, получим
 .
.
Затем из первого уравнения находим
 .
.
В случае, когда веревка, удерживающая шар, параллельна наклонной плоскости  , получим
, получим  ,
,  .
.
Для решения этой же задачи графическим способом, необходимо построить замкнутый силовой многоугольник. Построение силового многоугольника всегда нужно начинать с известных, заданных сил. Из произвольной точки  (рис.13б) проведем вектор
(рис.13б) проведем вектор  , параллельный данной силе
, параллельный данной силе  , длина которого в выбранном масштабе изображает модуль этой силы. Затем через точки
, длина которого в выбранном масштабе изображает модуль этой силы. Затем через точки  и
и 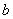 проводим прямые, параллельные линиям действия искомых сил
проводим прямые, параллельные линиям действия искомых сил  и
и  , которые пересекутся в точке
, которые пересекутся в точке  . Векторы
. Векторы  и
и  определяют искомые силы
определяют искомые силы  и
и  .Чтобы найти направление искомых сил на силовом треугольнике , нужно обойти этот треугольник по его периметру, причем направление этого обхода определяется направлением данной силы
.Чтобы найти направление искомых сил на силовом треугольнике , нужно обойти этот треугольник по его периметру, причем направление этого обхода определяется направлением данной силы  . Измерив длину сторон
. Измерив длину сторон  и
и  и зная масштаб, в котором построена сила
и зная масштаб, в котором построена сила  , найдем численные значения сил
, найдем численные значения сил  и
и  .
.
studfiles.net

Очевидно, что перенос точки приложения силы вдоль ее линии действия не может изменить главного вектора системы, так как при этой операции вектор каждой силы остается неизменным. Главный момент также не изменится, так как момент силы не зависит от положения точки приложения силы на ее линии действия.
Рассмотрим теперь вторую операцию. Пусть в точке А приложены две силыF1 иF2 (рис.16) Заменим их одной силойF , найденной по правилу параллелограмма:
F = F1 + F2.
Найдем момент силы F относительно точкиО.
mO (F ) =rA ×F =rA ×(F1 +F2 ) =rA ×F1 +rA ×F2 =mO (F1 ) +mO (F2 ).
Таким образом, применение этой элементарной операции приводит к замене в выражениях главного вектора и главного момента двух слагаемых их геометрической суммой. Очевидно, что главный вектор и главный момент при этом не изменяются.
4.1.Гладкая поверхность. Гладкой считается поверхность, трением о которую можно пренебречь. Гладкое тело, опирающееся на гладкую поверхность, может скользить вдоль этой поверхности и не может перемещаться по нормали к ней.
Реакция гладкой поверхности направлена по общей нормали к соприкасающимся поверхностям тела и опоры и приложена в точке их контакта (рис.17). В случае шероховатых поверхностей трение можно исключить при
Рис.17
Рис.18
помощи катков (рис.18), соединенных с телом и устанавливаемых на опорную плоскость. Реакция катков направлена по нормали к опорной плоскости.
4.2 Точечная опора (острие, гладкий выступ).Реакция точечной опоры направлена по нормали к поверхности тела (рис.19).
4.3. Нить, на которой подвешено тело (рис. 20), не дает ему удаляться от точки

подвеса. Реакция направлена вдоль нити от точки ее закрепления на данном теле.
4.4. Цилиндрический шарнир состоит из болта и надетой на него втулки. Такое закрепление допускает перемещение вдоль оси шарнира и вращение вокруг нее. Реакция шарнира приложена в точке контакта болта и втулки и направлена по общей нормали к соприкасающимся поверхностям. Положение точки контакта зависит от приложенных к телу активных сил, поэтому направление реакции шарнира заранее неизвестно (рис.21), и ее раскладывают на двевзаимно-перпендикулярныесоставляющие, параллельные координатным осям (рис.22).
YC | RC |
|
|
| Уа |
| RB |
С | А | Ха | В |
| XC |
|
|
Рис. 21 |
|
| Рис.22 |
4.5. Подшипник – опора вала, допускающая его вращение вокруг своей оси и перемещение вдоль этой оси. Реакция подшипника лежит в плоскости, перпендикулярной оси вала и раскладывается на двевзаимно-перпендикулярныесоставляющие (рис.23).
z | ZB |
|
|
|
|
|
|
|
| ||||||||||
|
|
|
|
|
|
|
| ||||||||||||
ZA |
|
|
|
|
|
|
|
| |||||||||||
A |
|
|
|
|
|
|
|
|
| B | y | ZA |
|
|
| YA | |||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
XA | XB |
| А |
|
|
|
| ||||||||||||
|
|
|
|
|
| ||||||||||||||
|
|
|
|
|
| ||||||||||||||
x |
|
|
|
|
|
|
|
| XA | ||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
|
|
|
| Рис.23 |
|
|
|
|
|
|
|
| Рис.24 | ||||||
4.6. Подпятник представляет собой опору вала, позволяющую ему перемещаться только в одном направлении вдоль оси вала и поворачиваться вокруг нее. Реакция подпятника (рис.24) раскладывается на три взаимноперпендикулярные составляющие.
SB | 4.7. Реакция тонкого невесомого стержня, шарнирно | |
B | соединенного концами с телом и опорой, направлена вдоль | |
стержня (рис. 25). Это следует из того, что опорный стержень | ||
| ||
| находится в равновесии под действием двух приложенных в | |
A | шарнирах сил, а в этом случае на основании аксиомы 1 силы | |
| направлены вдоль прямой, соединяющей точки их приложения. | |
|

4.8. | Жесткая заделка. При таком закреплении балки (рис.26) исключается | |||||
| УА |
|
| ее поворот, горизонтальные и вертикальные перемещения, | ||
|
|
| поэтому реакция такой связи состоит | из пары сил с | ||
|
|
| A ХА | |||
МА |
|
| моментом МA, препятствующей повороту | балки, и двух | ||
|
|
|
| |||
|
|
| Рис.26 | взаимно-перпендикулярныхсилXA,УА. |
| |
|
|
|
|
| ||
5. ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ К ДВУМ СИЛАМ. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ СИЛ.
Доказательство. Докажем эту теорему для системы, состоящей из трех сил. Пусть к твердому телу в точках А, В иС приложены силыF1, F2 иF3 (рис.27).
|
| D |
| F311 |
|
| F31 |
| |
|
| F21 | C | F3 |
|
| P2 |
| F31 |
|
| 11 |
| |
| B | F3 | F |
|
| F211 |
| ||
|
|
| ||
|
| A |
|
|
F21 |
| F211 |
| |
| F2 | P1 | Н | |
|
|
| ||
Будем считать, что эти силы не лежат в одной плоскости. Проведем через точку А и силуF2 плоскость П, а через точкуА и силуF3 - плоскость Н. Выберем на линии
пересечения этих плоскостей произвольную точку D. Соединим точкиА иD с точкамиВ иС. Разложим силуF2 на две составляющиеF21 иF211 , направленные по прямымАВ иВD и перенесем эти составляющие по линиям их действия в точки
А и D.
Разложим силу |
|
|
|
| F31и | F311 , направленные по прямым | DС и | ||||||
F3 на составляющие | |||||||||||||
AС, | и перенесем эти составляющие вдоль их линий действия в точки А | и D. | |||||||||||
Силы | F21и | F31 , приложенные в точкеD, заменим, используя правило | |||||||||||
параллелограмма, одной силой |
|
| Силы |
| , | ||||||||
P2 , приложенной в той же точке. | F1 | ||||||||||||
F211и | F311 , приложенные в точкеА, заменим, используя дважды | правило | |||||||||||

параллелограмма, одной силой Р1 . Таким образом, исходная система сил{F1, F2 , F3} оказалась замененной системой{P1, P2 }. Так как при этом применялись только элементарные операции, то системы{P1, P2 }и{F1, F2 , F3 }оказались эквивалентными, и, следовательно, их главные векторы и главные моменты не изменились:
R F = RP , MO F = MO P .
Если плоскости П и Н сливаются, то точку D можно брать где угодно в этих плоскостях.
Теорема доказана для системы, состоящей из трех сил. Если система состоит из большего числа сил, то, повторяя эту операцию несколько раз, приведем к двум силам и любую заданную систему сил.
Операция замены системы сил эквивалентной системой, состоящей из двух сил, называется приведением данной системы сил к двум силам.
5.2.Теорема о равновесии системы сил. Для равновесия произвольной системы сил необходимо и достаточно, чтобы главный вектор и главный момент относительно любого центра равнялись нулю.
Доказательство необходимости. Пусть система сил{F1 , F2 ,..., Fn }∞ 0 .
Докажем, что главный вектор системы равен нулю и главный момент относительно любого центра также равен нулю:
|
| F =0, |
| OF | = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||
R | M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||
|
| Заменим |
| эту | систему | эквивалентной системой | P2 | В | ||||||||||||||||||||
двух сил { |
| , | P2}. | { |
| , |
|
| Fn}∞{ |
| , |
| }∞0. |
|
| |||||||||||||
|
|
|
|
|
|
| ||||||||||||||||||||||
|
| F1 | F2 ,..., | P1 | P2 |
|
| |||||||||||||||||||||
P1 |
| rB | ||||||||||||||||||||||||||
|
| Если | система | { |
| , |
|
| }∞0 , то на основании |
| О | |||||||||||||||||
|
| P1 | P2 |
| ||||||||||||||||||||||||
первой аксиомы заключаем, что силы |
| и |
| равны |
|
| ||||||||||||||||||||||
P1 | P2 |
| Рис.28. | |||||||||||||||||||||||||
по модулю и направлены по одной прямой в противоположные стороны (рис.28). Главный вектор R P =P1 + P2 = 0 .
Главный момент системы M OP = rA ×P1 +rB ×P2 = (rA −rB ) ×P1 = ВA ×P1 =0 векторыBА иP1 направлены по одной прямой.
Следовательно, | будут равны нулю главный вектор и главный момент системы | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
{ |
|
| , |
|
| ,..., |
|
|
|
|
|
| }, т.е. |
|
|
|
|
| F =0, |
|
|
| F = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||
F | F | F |
|
| R | M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||||||||||||||||||||
1 | 2 |
|
|
|
| n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| O |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||
|
|
| Доказательство достаточности. Пусть главный вектор и главный момент | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
системы { |
|
| , |
| ,..., |
|
| }равны нулю: |
|
|
| F = 0; |
|
| F = | 0 . (рис.28). | ||||||||||||||||||||||||||||||||||||||||||||||||
F | F | F | R | M | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
| 1 | 2 |
|
|
| n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| O |
|
|
|
|
| Fn}∞ 0 . | |||||||||||||||||||||
Докажем, что система находится в равновесии: { |
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
F1, | F2 ,..., | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
| Преобразуем |
|
| систему |
| { |
|
|
|
| Fn} в |
| эквивалентную систему двух сил | |||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
| F1, | F2 ,..., |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
{ |
| , |
| }: | { |
| , |
| ,..., |
|
| }∞ | { |
| , |
|
| }, |
| Тогда, |
|
| P = |
| F | =0. |
| P | = |
| + |
| = 0. | |||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
P | P | F | F | F |
| P | P |
| R | R | R | P | P | |||||||||||||||||||||||||||||||||||||||||||||||||||
1 |
| 2 |
| 1 |
|
|
|
| 2 |
|
|
| n |
|
|
|
|
| 1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 2 | ||||||||||||||||||||||||
|
| Следовательно, |
|
|
|
|
| = − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||||||
|
|
| P2 |
| P1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||||||||||||||
Определим главный момент системы {P1, P2 } относительно точкиО:
studfiles.net
Тело называется свободным , если его перемещение в пространстве ничем не ограничено. В противном случае тело называется несвободным , а тела, ограничивающие перемещения данного тела, ¾ связями . Силы, с которыми связи действуют на данное тело, называются реакциями связей .
Основные виды связей и их реакции:
1.  Гладкая поверхность (без трения):
Гладкая поверхность (без трения):
Реакция гладкой поверхности направлена по нормали к этой поверхности (перпендикулярна общей касательной).
2.  Опорная точка (ребро):
Опорная точка (ребро):
Реакция перпендикулярна опирающейся поверхности.
Возможно вы искали - Контрольная работа: по Отечественной истории 3
3. Идеальная нить (гибкая, невесомая, нерастяжимая):
 Примеры: моделирует трос, канат, цепь, ремень,…
Примеры: моделирует трос, канат, цепь, ремень,…
Реакция идеальной нити направлена по нити к точке подвеса.
4. Идеальный стержень (жесткий, невесомый стержень, на концах которого шарниры):
 |
Реакция связи направлена по стержню.
Похожий материал - Сочинение: Христианские мотивы в стихах из романа Б.Л. Пастернака Доктор Живаго
В отличие от нити стержень может работать и на сжатие.
5. Цилиндрический шарнир:
Такая связь позволяет телу перемещаться вдоль оси, поворачиваться вокруг оси шарнира, но не позволяет точке закрепления перемещаться в плоскости, перпендикулярной оси шарнира. Реакция лежит в плоскости, перпендикулярной оси шарнира, и проходит через нее. Положение этой реакции не определено, но она может быть представлена двумя взаимно перпендикулярными составляющими
 |
 |
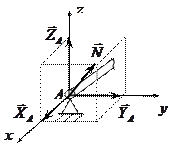
6. Сферический шарнир:
Такая связь не дает точке закрепления тела перемещаться ни в одном из направлений. Положение реакции не определено, но она может быть представлена тремя взаимно перпендикулярными составляющими.
 |
 |
Очень интересно - Курсовая работа: Внебюджетные фонды 11
7. Подпятник:
 Реакция данной связи задается аналогично предыдущему случаю.
Реакция данной связи задается аналогично предыдущему случаю.
8. Жесткая заделка:
Такая связь препятствует перемещению и повороту вокруг точки закрепления. Контакт тела со связью осуществляется по поверхности. Имеем распределенную систему сил реакции, которая, как будет показано, может быть заменена одной силой и парой сил.
Аксиома освобождаемости от связей:
Всякое несвободное тело можно считать свободным, если мысленно освободиться от связей, а их действие заменить соответствующими реакциями.
Вам будет интересно - Реферат: Особенности внебюджетных фондов
К-во Просмотров: 52
Бесплатно скачать Реферат: Связи и реакции связей
cwetochki.ru
Тело, перемещению которого в пространстве препятствует какие-нибудь другие тела, скрепленные или соприкасающиеся с данным, называется несвободным. Все то, что ограничивает перемещение данного тела в пространстве, называется связями.
Пример. Груз висит на веревке, ящик стоит на полу и т.д.
Сила, с которой данная связь действует на тело, препятствуя тем или иным его перемещениям, называется силой реакции (противодействия) связи или просто реакцией связи.
Силы, приложенные к телу, но не являющиеся реакциями, называются активными.
Направление силы реакции связи противоположно той, куда связь не дает перемещаться телу.
1. Гладкая поверхность
Р еакция связиN гладкой поверхности или опоры направлена по нормали к поверхностям соприкасающихся тел в точке касания и приложена в этой точке.
еакция связиN гладкой поверхности или опоры направлена по нормали к поверхностям соприкасающихся тел в точке касания и приложена в этой точке.
а) б) в)
Рис. 1.5
Если одна из соприкасающихся поверхностей является точкой, то реакция направлена по нормали к другой поверхности (рис. 1.5).
2. Нить, стержень.
Р

 еакция Т натянутой нити и нагруженного стержняS направлена вдоль этих связей и приложена в точке контакта (рис. 1.6).
еакция Т натянутой нити и нагруженного стержняS направлена вдоль этих связей и приложена в точке контакта (рис. 1.6).
а) б)
Рис. 1.6
3 . Цилиндрический шарнир (подшипник, петля).
. Цилиндрический шарнир (подшипник, петля).
Р

 еакцияR цилиндрического шарнира лежит в плоскости, перпендикулярной оси шарнира, и может иметь любое направление в этой плоскости. Для определения R ее раскладывают на два взаимноперпендикулярных направления: Rx и Ry (рис. 1.7).
еакцияR цилиндрического шарнира лежит в плоскости, перпендикулярной оси шарнира, и может иметь любое направление в этой плоскости. Для определения R ее раскладывают на два взаимноперпендикулярных направления: Rx и Ry (рис. 1.7).
Рис. 1.7
4 . Подвижная шарнирная опора.
. Подвижная шарнирная опора.
Р еакция связиR направлена перпендикулярно плоскости возможного перемещения шарнира (рис. 1.8).
еакция связиR направлена перпендикулярно плоскости возможного перемещения шарнира (рис. 1.8).
5
Рис. 1.8
а)
б)
Рис. 1.9
. Шаровый шарнир и подпятник (рис. 1.9, рис. 1.10).а) б)
Рис. 1.10
Р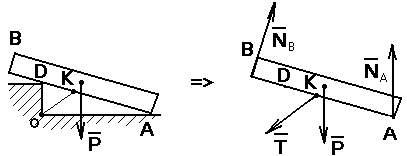 еакция шарового шарнира и подпятника может иметь любое направление в пространстве.
еакция шарового шарнира и подпятника может иметь любое направление в пространстве.
А
Рис. 1.11
а)
б)
ксиома связей. Всякое несвободное тело можно рассматривать как свободное, если отбросить связи и заменить их действие реакциями этих связей (рис. 1.11). 
Сложение сил
Геометрический способ сложения сил
В
а)
б)
Рис. 1.12
еличина, равная геометрической сумме сил какой-либо системы называется главным вектором этой системы сил. П


 усть на твердое тело действует плоская система сил (F1, F2, F3, …, Fn) (рис. 1.12).
усть на твердое тело действует плоская система сил (F1, F2, F3, …, Fn) (рис. 1.12).
И

 з произвольно выбранной точки О откладывается векторF1, из его конца откладывается вектор F2 и т.д. Вектор R, замыкающий силовой многоугольник, является результирующим:
з произвольно выбранной точки О откладывается векторF1, из его конца откладывается вектор F2 и т.д. Вектор R, замыкающий силовой многоугольник, является результирующим:

Пусть на тело действуют две силы, лежащие в одной плоскости (рис. 1.13).


 .
.
Р
Рис. 1.13
езультирующая сила определяется по правилу параллелограмма, модуль силы определяется по теореме косинусов или синусов:  ;
;  .
.
Сложение трех сил не лежащих в одной плоскости
Р ассмотрим три силы
ассмотрим три силы ,
,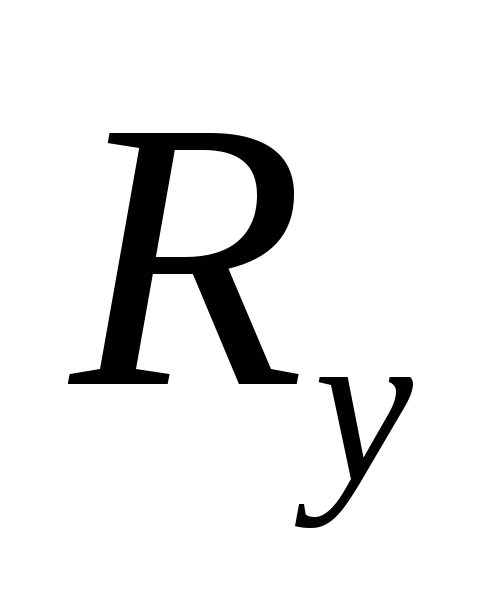 ,
, не лежащие в одной плоскости (рис. 1.14). Результирующая сила
не лежащие в одной плоскости (рис. 1.14). Результирующая сила равна:
равна:
 .
.
Направление силы определим по направляющим косинусам:

Рис. 1.14
; ;
;  .
.Разложение сил
Разложение сил по двум заданным направлениям
П
 усть надо силуF разложить по направлениям AB и AD (рис. 1.15).
усть надо силуF разложить по направлениям AB и AD (рис. 1.15).

Рис. 1.15
.Задача сводится к построению параллелограмма, у которого стороны расположены по направлениям AB и AD и данная сила F является диагональю. Тогда стороны параллелограмма будут искомыми силами.
Разложение сил по трем заданным направлениям.

П
Рис. 1.16
усть направления силы не лежат в одной плоскости. Тогда задача сводится к построению параллелепипеда, у которого диагональю является данная сила, а ребра параллельны заданным направлениям (рис. 1.16).  .
.
Вопросы для самоконтроля
Что изучает статика?
Что такое абсолютно твердое тело?
Основные виды связей и их реакции?
Геометрическое сложение сил?
Задачи, рекомендуемые для самостоятельного решения: 1.1 – 1.6 [2]
Литература: [1], [3], [4].
Лекция 2.
Действия над силами. Система сходящихся сил

Проекция силы на ось и на плоскость
П роекция силы на ось. Пусть сила F образует с осью OX угол (рис. 2.1), тогда проекция этой силы на ось будет:
роекция силы на ось. Пусть сила F образует с осью OX угол (рис. 2.1), тогда проекция этой силы на ось будет:
Fx = Fcos.
П
Рис. 2.1
роекция силы на ось есть величина скалярная. П

 роекция силы на плоскость. Проекцией силы F на плоскость OXY называется вектор Fxy = OB1, заключенный между проекциями начала и конца силы F на эту плоскость (рис. 2.2.)
роекция силы на плоскость. Проекцией силы F на плоскость OXY называется вектор Fxy = OB1, заключенный между проекциями начала и конца силы F на эту плоскость (рис. 2.2.)
П

Рис. 2.2
роекция силы на плоскость есть величина векторная, так как она кроме численного значения характеризуется направлением на плоскости. По модулюFxy = Fcos, где - угол между направлением силы F и ее проекцией Fxy. А налитический способ задания сил. Для аналитического способа задания силы необходимо выбрать систему координат OXYZ и спроектировать силу на оси координат (рис. 2.3).
налитический способ задания сил. Для аналитического способа задания силы необходимо выбрать систему координат OXYZ и спроектировать силу на оси координат (рис. 2.3).
Направляющие косинусы определяются по формулам:


Рис. 2.3
; ;
;  .
. 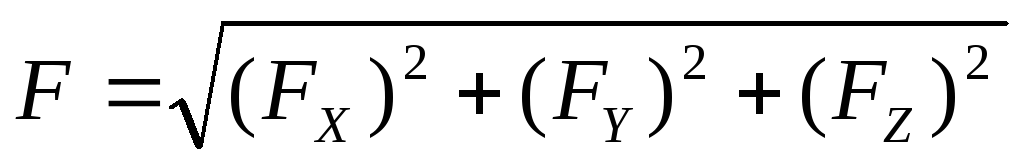 .
.
Для плоской системы сил:
 ;
;  ;
;  ;
;  .
.
studfiles.net
Связи и реакции связей - раздел Механика, Теоретическая механика
Все законы и теоремы статики справедливы для свободного твердого тела.
Все тела делятся на свободные и связанные.
Свободным называется тело, которое не испытывает никаких препятствий для перемещения в пространстве в любом направлении. Если же тело связано с другими телами, которые ограничивают его движение в одном или нескольких направлениях, то оно является несвободным. Тела, которые ограничивают движение рассматриваемого тела, называют связями.
При взаимодействии между телом и его связями возникают силы, противодействующие возможным движениям тела. Эти силы действуют на тело со стороны связей и называются реакциями связей.
Реакция связи всегда противоположна тому направлению, по которому связь препятствует движению тела. Существование реакцией основывается аксиомой связей используют принцип освобождения от связей. Не изменяя равновесия тела, каждую связь можно отбросить, заменяя ее реакцией. Определение реакций связей является одной из наиболее важных задач статики.
Все связи можно разделить на несколько типов.


Рис. 1.6
1) Связь – гладкая опора (без трения).
Реакция опоры приложена в точке опоры и всегда направлена перпендикулярно опоре (рис. 1.7).
2) Гибкая связь (нить, веревка, трос, цепь). Груз подвешен на двух нитях (рис. 1.6). Реакция нити направлена вдоль нити от тела, при этом нить может быть только растянута.
3) Жесткий стержень. На схемах стержни изображают толстой сплошной линией (рис. 1.8).
 Стержень может быть сжат или растянут. Реакция стержня направлена вдоль стержня. Стержень работает на растяжение или сжатие. Точное направление реакции определяют, мысленно убрав стержень и рассмотрев возможные перемещения тела без этой связи.
Стержень может быть сжат или растянут. Реакция стержня направлена вдоль стержня. Стержень работает на растяжение или сжатие. Точное направление реакции определяют, мысленно убрав стержень и рассмотрев возможные перемещения тела без этой связи.
Возможным перемещением точки называется такое бесконечно малое мысленное перемещение, которое допускается в данный момент наложенными на него связями.
 Убираем стержень 1, в этом случае стержень 2 падает вниз. Следовательно, сила от стержня 1 (реакция) направлена вверх. Убираем стержень 2. В этом случае точка А
Убираем стержень 1, в этом случае стержень 2 падает вниз. Следовательно, сила от стержня 1 (реакция) направлена вверх. Убираем стержень 2. В этом случае точка А
рис 1.8 опускается вниз, отодвигаясь от стены. Следовательно, реакция стержня 2 направлена к стене.
 4) Сферический шарнир.Этот вид вид связи закрепляет тело таким образом, что оно не может
4) Сферический шарнир.Этот вид вид связи закрепляет тело таким образом, что оно не может
Рис. 1.9
совершать никаких поступательных перемещений в пространстве, а может только поворачивается относительно трех координатных осей, проходящих через центр шарнира. Для нахождения модуля и направления реакции R ее необходимо заменить тремя составляющими x, y, z с линями действия, параллельными осями координат.
Рис. 1.10
5) Шарнирно – неподвижная опора.(рис. 1.10,а). Эта опора препятствует любому поступательному перемещению системы в ее плоскости, но дает ей возможность свободно поворачиваться вокруг оси шарнира (трением в шарнире пренебрегаем). Схематически такая опора изображается двумя стержнями (рис. 1.10, б), шарнирно соединенными на одном конце. Реакция такой опоры проходит через ось шарнира, но неизвестна как по модулю, так и по направлению и, следовательно, характеризуется двумя неизвестными величинами. Для их нахождения реакцию Rвнеобходимо заменить двумя взаимно перпендикулярными составляющими RВхи RВу,.
6)Шарнирно-подвижная опора(рис. 1.10,в). Эта опора препятствует лишь перемещению, перпендикулярному к опорной плоскости, но не препятствует перемещению оси шарнира параллельно этой плоскости. Реакция шарнирно-подвижной опоры всегда перпендикулярна опорной плоскости. Таким образом, для шарнирно-подвижной опоры неизвестна только величина реакции. Схематически такая опора изображается в виде одного стержня с шарнирами по концам (рис. 1.10, г). Реакция такой опоры проходит через ось шарнира и направлена вдоль стержня.
 Шарнирно – неподвижная и шарнирно – подвижная опоры являются опорами балочных систем.
Шарнирно – неподвижная и шарнирно – подвижная опоры являются опорами балочных систем.
7)Защемление или «заделка». Любые перемещения точки крепления не возможны.
Под действием внешних сил в опоре возникают реактивная сила и реактивный момент Mr, препятствующий повороту (рис. 1.11).
Реактивную силу принято представлять в виде двух составляющих вдоль осей координат R = Rx + Ry.
рис. 1.11
– Конец работы –
Эта тема принадлежит разделу:
Теоретическая механика... Введение... Любое явление в ок ружающем нас макромире связано с движением следовательно не может не иметь того или иного...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Связи и реакции связей
Аксиомы статики Условия, при которых тело может находиться в равновесии, выводиться из нескольких основных положений, прим
Определение равнодействующей геометрическим способом Знать геометрический способ определения равнодействующей системы сил, условия равновесия плоской систе
Равнодействующая сходящихся сил Равнодействующую двух пересекающихся сил можно определить с помощью параллелограмма или треугольника си
Проекция силы на ось Проекция силы на ось определяется отрезком оси, отсекаемым перпендикулярами, опущенными на ось из начал
Определение равнодействующей системы сил аналитическим способом Величина равнодействующей равна векторной (геометрической) сумме векторов системы сил. Определяем равноде
Условия равновесия плоской системы сходящихся сил в аналитической форме Исходя из того, что равнодействующая равна нулю, получим:
Методика решения задач Решение каждой задачи можно условно разделить на три этапа. Первый этап: Отбрасываем внешние связи сис
Пара сил и момент силы относительно точки Знать обозначение, модуль и определение моментов пары сил и силы относительно точки, условия равновесия с
Эквивалентность пар Две пары сил считаются эквивалентными в том случае, если после замены одной пары другой парой механическо
Опоры и опорные реакции балок Правило для определения направления реакций связей ( рис.1.22). Шарнирно-подвижная опора допускает п
Приведение силы к точке. Произвольная плоская система сил представляет собой систему сил, линии действия которых расположены в пло
Приведение плоской системы сил к данной точке Метод приведения одной силы к данной точке можно при
Влияние точки приведения Точка приведения выбрана произвольно. Произвольная плоская система сил представляет собой систему сил, ли
Теорема о моменте равнодействующей (теорема Вариньона) В общем случае произвольная плоская система сил приводится к главному вектору F'гл и к главному мо
Условие равновесия произвольно плоской системы сил 1)При равновесии главный вектор системы равен нулю (=0)
Балочные системы. Определение реакций опор и моментов защемления Иметь представление о видах опор и возникающих реакциях в опорах. Знать три формы уравнений равн
Виды нагрузок По способу приложения нагрузки делятся на сосредоточенные и распределенные. Если реально передача нагрузк
Момент силы относительно точки Момент силы относительно оси характеризуется вращательным эффектом, создаваемым силой, стремящейся пове
Вектор в пространстве В пространстве вектор силы проецируется на три взаимно перпендикулярные оси координат. Проекции вектора
Приведение произвольной пространственной системы сил к центру О Дана пространственная система сил (рис. 7.5а). Приведем ее к центру О. Силы необходимо параллельно пе
Некоторые определения теории механизмов и машин При дальнейшем изучении предмета теоретической механики, в особенности при решении задач, мы столкнемся с
Ускорение точки Векторная величина, характеризующая быстроту измене
Ускорение точки при криволинейном движении При движении точки по криволинейном траектории скорость меняет свое направление. Представим себе точку М
Равномерное движение Равномерное движение — это движение с постоянной скоростью: v = const. Для прямолинейного ра
Неравномерное движение При неравномерном движении численные значения скорости и ускорения меняются. Уравнение неравноме
Тема 2.2 Простейшие движения твердого тела Иметь представление о поступательном движении, его особенности и параметрах, о вращательном движении тел
Вращательное движение Движение, при котором по крайнем мере точки твердого тела или неизменяемой системы остаются неподвижными,
Частные случаи вращательного движения Равномерное вращение (угловая скорость постоянна): ω = const. Уравнение (закон) равн
Скорости и ускорения точек вращающегося тела Тело вращается вокруг точки О. Определим параметры движения точки Л, расположенной на расстоянии
Преобразование вращательного движения Преобразование вращательного движения осуществляется разнообразными механизмами, которые называются
Основные определения Сложным движением считают движение, которое можно разложить на несколько простых. Простыми движениям
Плоскопараллельное движение твердого тела Плоскопараллельным, или плоским, называется такое движение твердого тела, при котором все точки тел
Метод определения мгновенного центра скоростей Скорость любой точки тела можно определять с помощью мгновенного центра скоростей. При этом сложно
Тема 3.2 Понятие трения Абсолютно гладких и абсолютно твердых тел в природе не существует, и поэтому при перемещении одного тела по
Трение скольжения Трением скольжения называется трение движения, при котором скорости тел в точке касания различ
Свободная и несвободная точки Материальная точка, движение которой в пространстве не ограничено какими-нибудь связями, называется сво
Принцип кинетостатики (принцип Даламбера) Принцип кинетостатики используют для упрощения решения ряда технических задач. Реально силы инерции
Работа постоянной силы на прямолинейном пути Работа силы в общем случае численно равна произведению модуля силы на длину пройденного мм пути и на косин
Работа постоянной силы на криволинейном пути Пусть точка М движется по дуге окружности и сила
Мощность Для характеристики работоспособности и быстроты совершения работы введено понятие мощности.
Коэффициент полезного действия Способность тела при переходе из одного состояния в другое совершать работу называется энергией.
Закон изменения количества движения Количеством движения материальной точки называется векторная величина, равная произведению массы точк
Потенциальная и кинитецеская энергия Существуют две основные формы механической энергии: потенциальная энергия, или энергия положения,
Закон изменения кинетической энергии Пусть на материальную точку массой m действует постоянная сила
Основы динамики системы материальных точек Совокупность материальных точек, связанных между собой силами взаимодействия, называется механической с
Основное уравнение динамики вращающегося тела Пусть твердое тело под действием внешних сил вращает
Моменты инерции некоторых тел Момент инерции сплошного цилиндра (рис. 3.19) Моме
Сопротивление материалов Иметь представление о видах расчетов в сопротивлении материалов, о классификации нагрузок, о внутренних
Тема 4.1 Основные положения. Гипотезы и допущения Практика показывает, что все части конструкций под действием нагрузок деформируются, т. е. изменяет сво
Внешние силы Всопротивлении материалов под внешними воздействиями подразумевается не только силовое взаимо
Деформации линейные и угловые. Упругость материалов В отличие от теоретической механики, где изучалось взаимодействие абсолютно жестких (недеформируемых) тел,
Допущения и ограничения, принятые в сопротивлении материалов Реальные строительные материалы, из которых возводятся различные здания и сооружения, представляют собой
Виды нагрузок и основных деформаций В процессе работы машин и сооружений их узлы и детали воспринимают и передают друг другу различные на
Формы элементов конструкции Все многообразие форм сводится к трем видам по одному признаку. 1. Брус — любое тело, у которого дл
Метод сечений. Напряжение Знать метод сечений, внутренние силовые факторы, составляющие напряжений. Уметь определять виды
Растяжение и сжатие Растяжением или сжатием называют вид нагружения, при котором в поперечном сечении бруса возникает
Центральное растяжение прямого бруса. Напряжения Центральным растяжением или сжатием называется такой вид деформации, при котором в любом поперечном сечен
Напряжения при растяжении и сжатии При растяжении и сжатии в сечении действует только нормальное напряжение. Напряжения в поперечных се
Продольные и поперечные деформации. Закон Гука Иметь представление о продольных и поперечных деформациях и их связи. Знать закон Гука, зависимо
Закон Гука при растяжении и сжатии Напряжения и деформации при растяжении и сжатии связаны между собой зависимостью, которая называется зако
Формулы для расчета перемещений поперечных сечений бруса при растяжении и сжатии. Используем известные формулы. Закон Гука σ=Еε. Откуда
Механические испытания. Статические испытания на растяжение и сжатие Это стандартные испытания: оборудование — стандартная разрывная машина, стан- дартный образец (кругл
Механические характеристики Механические характеристики материалов, т. е. величины, характеризующие их прочность, пластичность, упруго
allrefers.ru