|
|
|
|
 Far |
| WinNavigator |
| Frigate |
| Norton
Commander |
| WinNC |
| Dos
Navigator |
| Servant
Salamander |
| Turbo
Browser |
|
|
| Winamp,
Skins, Plugins |
| Необходимые
Утилиты |
| Текстовые
редакторы |
| Юмор |
|
|
|
File managers and best utilites |
Свойства пары сил. Реферат на тему пара сил
Пара сил
1. Пара сил - система двух сил, приложенных к телу в двух разных точках:
- равных по модулю
- параллельных
- противоположно направленных
2. Плечо пары сил – кратчайшее расстояние между линиями действия сил пары.
Момент пары сил
Момент пары сил - произведение модуля любой силы на плечо пары (модуль силы х плечо)
Свойства пары сил
1. Сумма проекций на любую ось сил пары равна нулю
F2cosα – F1cosα = 0
2. Сумма моментов сил пары относительно любой точки плоскости равна моменту пары.
momo(
) = - F1d = - Fd
momo(
) = + F2l = +Fl
momo(
) + momo(
) = - Fd + Fl = - F(d-l) = - Fh
Следовательно, пару сил нельзя заменить равнодействующей.
Самостоятельная работа обучающегося по теме 1.3. (1 час – все)
1. Составить глоссарий основных понятий по теме «Пара сил» - арх, ‘эзс – 1 час
1. Решение задач на определение моментов сил относительно точки: авто – 1час
Тема 1.4. Плоская система произвольно расположенных сил
– (4 час арх, 2час авто, эзс)
Основные понятия
1. Плоская система сил – система сил, линии действия которых лежат в одной плоскости.
2. На плоскости могут быть приложены силы:
А) произвольно расположенные;
Б) пары сил;
В) силы, сходящиеся в одной точке.
3. Плоская система произвольно расположенных сил – все силы или линии их действия не пересекаются в одной точке.
Приведение плоской системы сил к заданному центру
1. Пусть на твёрдое тело действует система сил 
2. Приложим в точке Опо 2 уравновешенные силы:
А) одна равна и параллельна заданной: 
Б) другая сила равна заданной, но противоположно направлена
3. В итоге на тело действует:
А) система сходящихся сил 
Б) система пар сил с моментами
4. Систему сходящихся сил заменяем равнодействующей
Или в соответствии с тем, что 
и т.д.
5. В соответствии со вторым свойством пары сил найдём алгебраическую сумму моментов всех пар
Мо =m1+m2+ …+mn
Лемма Пуансо
1. В результате произвольную плоскую систему сил можно заменить:
- одной силой, равной геометрической сумме всех сил, приложенных в произвольно выбранном центре и
- моментом,равным алгебраической сумме моментов присоединенных пар
2. Принятые определения:
А) точка о – центр приведения
Б) главный вектор– векторR, равный геометрической сумме всех сил. Его значение не зависит от выбора центра приведения.
В) главный момент– момент МО, равный алгебраической сумме моментов присоединённых пар. Его значение зависит от выбора центра приведения (величина плеча будет меняться).
Частные случаи приведения
1. R0=0,M0≠0 – система эквивалентна паре сил с моментом, равным главному моменту системы, который в этом случае не зависит от выбора центра приведения;
2. R0≠0,M0=0 – система эквивалентна равнодействующей R. Главный вектор в данном случае – является равнодействующей.
3. R0≠0,M0≠0 – система эквивалентна равнодействующей R, приложенной в новом центре приведения, расположенном от прежнего на расстоянии d = Мо\R
4. R=0,M0=0 – плоская система сил находится в равновесии;
Теорема Вариньона (о моменте равнодействующей плоской системы сил)
Момент равнодействующей плоской системы сил относительно произвольного центра О равен алгебраической сумме моментов всех сил системы относительно этого центра.
Аналитические уравнения равновесия плоской системы сил
Условие равновесия выражается тремя уравнениями – основные уравнения равновесия:
2. Варианты записи уравнений равновесия – в зависимости от расположения сил
или
Класссификация нагрузок
Сосредоточенная
Распределённая: по линии, по поверхности, по объёму
Изгибающий момент
Балочные системы
1. Объект решения задач статики – балки (или балочные системы)
2. Балка – деталь в виде прямого бруса с опорами в двух (или более) точках.
Виды опор
1. Шарнирно-подвижная: вращение вокруг своей оси (шарнир) + поступательное перемещение (подвижная)
2. Шарнирно-неподвижная: вращение вокруг своей оси (шарнир)
3. Жёсткая заделка(защемление): препятствует любому перемещению.
Решение задач на определение опорных реакций
С помощью трёх уравнений равновесия определяют реакции опор (если число реакций связи не превышает трёх):
1. Показать нагрузки
2. Обозначают нагрузки
3. Освобождаются от опор и заменяют их действие на балку реакциями
4. Составляют уравнение равновесия
5. Решают уравнения равновесия и определяют из них опорные реакции
6. Проверка решения
Определение усилий в стержнях плоских ферм – вырезанием узлов
1. Аналитический способ
2. Графический способ – построением диаграммы Максвелла – Кремоны
Элементы теории трения
ТЕМА 1.5. ЭЛЕМЕНТЫ ТЕОРИИ ТРЕНИЯ (авто - 1 час)
Самостоятельная работа обучающегося (авто – 1час)
1. Решение задач по индивидуальным заданиям
1. Понятие о трении
Сила трения возникает при соприкосновении тел и препятствует передвижению одного тела по поверхности другого.
2. Виды сил трения:
А) трение скольжения
Б) трение скольжения
3. Трение скольжения– сопротивление, возникающее при относительном перемещении одного тела по поверхности другого.
4. Законы трения:
А) Сила трения Fтрнаправлена в сторону, противоположную относительной скорости скольжения
Б) Сила трения не зависит от площади контактирующих поверхностей
В) Модуль силы трения пропорционален нормальному давлению (чем больше нормальное давление, тем больше сила трения).
5. По рисунку:
А) сила тяжести mg– вниз (чем большеmg, тем больше опорная реакцияN(вектор)
Б) тело движется вниз = сила трения направлена вверх по наклонной плоскости
В) гладкая поверхность = опорная реакция N(вектор) направлена перпендикулярна плоскости
Г) по аксиоме 3 строим диагональ параллелограмма R(равнодействующая)
6. Виды сил трения скольжения:
А) сила трения при покое Fтр
foN
Б) сила трения при движении Fтр
fN
N– сила нормального давления
fo– коэффициент трения покоя
f– коэффициент трения скольжения – зависит от скорости скольжения тел.
Оба коэффициента зависят от материала и физического состояния поверхностей
7. Трение качения– сопротивление, возникающее при качении одного тела к другому.
8. Виды связей:
А) идеальные (без трения)
Б) реальные (с трением)
Самостоятельная работа обучающихся – 3час эзс, 4час арх,
1. Решить задачи по определению опорных реакций для однопролётной балки по вариантам
2. Решить задачи на определение усилий в стержнях фермы по вариантам
3. Сравнить способы определения усилий, сделать краткий анализ о преимуществах и недостатках каждого метода - результат оформить в виде таблицы
Авто – 2час
1. Выполнение расчётно-графической работы на определение опорных реакций балочных систем
studfiles.net
2.1.6. Пара сил и ее свойства
Парой силназывается система двух равных по модулю, параллельных и направленных в противоположные стороны сил, действующих на твердое тело (рис. 2.1.15).Плоскость
, содержащая линии действия сил пары
и
называетсяплоскостью действия сил пары. Расстояние
между линиями действия сил пары называетсяплечом пары.
Определим значение момента пары относительно произвольного центра О.Согласно правилу параллелограмма -вектор-момент парыравен геометрической сумме моментов сил пары
и
, т.е.
,
откуда, учитывая, что по определению пары сил 
, получаем
. (2.1.20)
Модуль момента пары равен
. (2.1.21)
Алгебраическое значение момента пары сил равно
, где
. (2.1.22)
Момент пары считается положительным, если он стремится вращать тело против хода часовой стрелки иотрицательным, если - по ходу часовой стрелки.
Из выражений (2.1.20) и (2.1.21) видно, что вектор-момент 
пары перпендикулярен плоскости действия сил
и
и не зависит от положения в пространстве центраО,так как, где бы мы не выбрали центр, вектор
сохраняет своё значение. Таким образом, не нарушая величину и направление вектора-момента пары
, плоскость действия
сил пары можно параллельно переносить как угодно в пространстве.
На основе изложенного можно сформулировать следующие свойства пар. Действие пары на твердое тело не изменится, если:
1) перенести пару в плоскости ее действия в любое другое положение;
2) перенести пару в любую другую плоскость, параллельную плоскости ее действия;
3) модуль сил пары увеличить (или уменьшить) в несколько раз, а её плечо уменьшить (или увеличить) во столько же раз.
Если пары сил расположены в одной или параллельных плоскостях, то они складываются алгебраически. Если же пары сил расположены в пересекающихся плоскостях, то они складываются геометрически.
2.1.7. Пара трения качения
В
технических задачах приходится учитывать не только трение скольжения, но и, так называемое, трение качения, мерой действия которого являетсямомент пары трения качения. Рассмотрим цилиндрический каток, лежащий на горизонтальной плоскости (2.1.16,а). Если никакие активные силы, кроме силы тяжести
, на каток не действуют, то сила
уравновешивается нормальной реакцией
опорной поверхности и каток сохраняет состояние покоя.
Приложим к катку горизонтальную силу 
(рис.2.1.16,б). Тогда в точке
касания Авозникнет сила трения
, препятствующая скольжению катка по плоскости, а точка приложения нормальной реакции
сместится относительно точкиАв сторону действия силы
на некоторое расстояниеh. Это объясняется тем, что, из-за деформации, каток фактически соприкасается с плоскостью по небольшой площадке с центром в точкеА. После приложения силы
, нагрузка на левую половину площадки уменьшится, а на правую половину возрастёт. В итоге линия действия нормальной реакции
сместится вправо и возникнет пара сил (
,
) с плечомhи моментом
. Эта пара, препятствующая качению катка по плоскости, называется парой трения качения, а её момент
- моментом трения качения.
При увеличении силы 
от нуля плечоhи момент
возрастают до предельных значений, при которых каток начинает катиться:
. (2.1.23)
Величина 
, имеющая размерность длины, называется коэффициентом трения качения; его значения определяются опытным путём и приводятся в технических справочниках. Коэффициент
и момент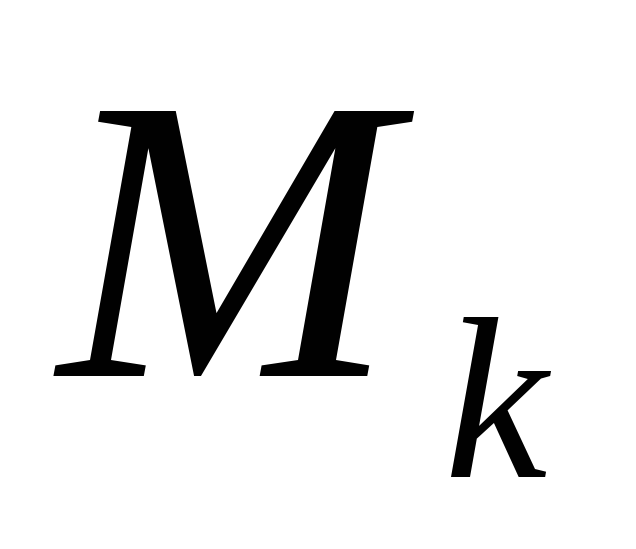
тем меньше, чем твёрже соприкасающиеся тела и чем чище обработаны их поверхности.
После начала качения момент 
независимо от величины силы
равен предельному значению
.
2.1.8. Система сил. Главный вектор и главный момент системы сил Системой силназываютлюбую совокупность сил, действующих на тело
или механическую систему одновременно. Всякую систему сил можно привести к произвольному центру, заменив её эквивалентной системой сил. Рассмотрим приведение одной силы к данному центру,не лежащему на линии действия этой силы(метод Пуансо).
Пусть к свободному твердому телу в точке
приложена сила
(рис. 2.1.17). Возьмем произвольную точку
(центр приведения) и проведем через нее и силу
плоскость
. Приложим в центре
уравновешенную систему сил
,
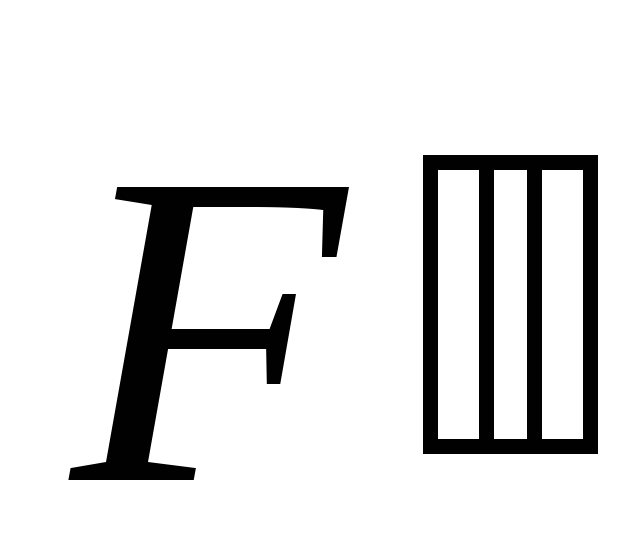; равных по модулю
и параллельных ей. Система сил
эквивалентна силе
. С другой стороны, ее можно рассматривать как состоящую из силы
, геометрически равной силе
, но приложенной в центре
, и пары
, называемойприсоединенной. Легко видеть, что момент присоединенной пары
геометрически равен моменту силы
относительно центра
:
. Используя символ эквивалентности систем сил, напишем
∞
.
Итак, сила, приложенная в какой-либо точке тела эквивалентна равной ей силе, приложенной в произвольно выбранном центре, и паре, момент которой равен моменту данной силы относительно этого центра.
Пусть на свободное твердое тело действует система сил 
, рас-положенных как угодно в пространстве и приложенных в точках
. Приведем все данные силы к произвольно центру
. В результате получим силы
,,равные данным силам и приложенные в центре
и присоеди-ненные пары
. Моменты
этих присоединенных пар равны моментам данных сил относительно центра приведения:
. (2.1.24)
Складывая силы 
, приложенные в центре
по правилу многоугольника, получаем одну силу
. Так как силы
равны геометрически данным силам
, то можно записать
. (2.1.25)
Вектор 
, равный геометрической сумме всех сил системы, называетсяглавным вектором системы сил.
Складывая присоединенные пары 
, получим одну пару с моментом
, равным геометрической сумме моментов присоединенных пар
. (2.1.26)
Учитывая (2.1.24), находим
. (2.1.27)
Вектор 
, равный геометрической сумме моментов всех сил системы относительно центра приведения
, называетсяглавным моментом системы сил относительно этого центра.
Таким образом, произвольную систему сил, приложенную к свободному твердому телу, можно привести к одной силе, равной главному вектору системы сил, и приложенной в центре приведения и к одной паре с моментом, равным главному моменту этой системы относительно центра приведения. Не следует отождествлять главный вектор
c равнодействующей, так как он заменяет систему сил в сочетании с главным моментом, в то время как равнодействующая
, если она существует, одна заменяет систему сил.
При переносе центра приведения главный вектор не изменяется, а главный момент в общем случае изменяется.
Вопросы для самопроверки по теме 2.1
Почему сила является векторной величиной?
Что такое инертность материальных тел?
Если точка не взаимодействует с другими материальными телами, то в каком состоянии она должна находиться?
Сформулируйте основной закон механики.
Разложите вектор силы по координатным осям.
Какой принцип механики позволяет изучать механику несвободных материальных тел?
В каком случае момент силы относительно точки равен нулю?
Что называется моментом силы относительно оси?
В каких случаях момент силы относительно оси равен нулю?
Что называется парой сил? Чему равен момент пары?
Как направлен, где приложен вектор момента пары?
Сформулируйте свойства пары сил.
Как складываются пары, лежащие в одной плоскости; в пересекающихся плоскостях?
Определите момент пары трения качения.
Приведите силу к любой произвольно взятой точке твердого тела.
16. Что называется главным вектором системы сил?
17. Дайте определение главного момента произвольной системы сил относительно центра приведения.
18.Изменятся ли главный вектор и главный момент системы сил при переносе центра приведения в другое положение?
studfiles.net
Пара сил. Момент пары сил. Теоремы о парах.
Количество просмотров публикации Пара сил. Момент пары сил. Теоремы о парах. - 1571
Пара сил – система двух равных по модулю, параллельных и направленных в противоположные стороны сил, действующих на абсолютно твердое тело. Действие пары сил на твердое тело сводится к некоторому вращательному эффекту, который характеризуется величиной – момент пары. Он определяется:
Его модулем = F*d. d – расстояние между линиями действия сил пары, принято называть плечом пары.
Положением в пространстве плоскости действия пары.
Направлением поворота пары в этой плоскости.
Момент пары сил – вектор m(или M), модуль которого равен произведению модуля одной из сил пары, на ее плечо, и который направлен перпендикулярно плоскости действия пары в ту сторону, откуда пара видна стремящейся повернуть тело против хода часовой стрелки.
Две пары, лежащие в || плоскостях и имеющие одинаковый момент эквивалентны.
Все пары в пересекающихся плоскостях можно заменить одной парой с моментом, равным сумме моментов этих пар. Размещено на реф.рфДля абсолютно твердого тела пара – свободный вектор, определяемы только моментом. Момент перпендикулярен плоскости образуемой парой.
Пару можно заменить параллельной ей равной силе и парой с моментом, равным произведению этой силы на расстояние до новой точки приложения.
Теоремы о парах. 1) Две пары, лежащие в одной плоскости, можно заменить одной парой, лежащей в той же плоскости, с моментом, равным сумме моментов данных двух пар. Размещено на реф.рф . 2) Две пары, имеющие геометрически равные моменты, эквиваленты. 3) Не нарушая состояния твердого тела, пару сил можно переносить в плоскости ее действия. Т.е. момент пары сил является свободным вектором. 4) Система нескольких пар сил эквивалента одной паре, момент которой равен векторной сумме моментов данных пар. Размещено на реф.рфТ.е. система пар приводится к одной паре, момент которой равен сумме моментов всех пар. Размещено на реф.рфУсловие равновесия пар сил:
– геометрическая сумма их моментов равна 0. Пары сил, расположенные в одной плоскости, взаимно уравновеш-тся, в случае если алгебраическая сумма их моментов åМi=0.
Момент силы относительно точки– вектор, численно равный произведению модуля силы на плечо и направленный перпендикулярно плоскости, содержащей силу и точку, в такую сторону, чтобы смотря ему навстречу, видеть силу стремящейся повернуться против хода час.стрелки. Плечо "h"– кратчайшее расстояние от точки до линии действия силы.
– момент силы равен векторному произведению вектора
на вектор
. Модуль векторного произведения:
R×F×sina= F×h. Для плоской сист. сил обычно находят не вектор момента͵ а только его модуль:
±F×h, >0 – против час.стр.; <0 – по час.стр. Размещено на реф.рфСвойства момента силы: 1) момент силы не изменяется при переносе точки приложения силы вдоль ее линии действия; 2) момент силы относит. точки =0 только тогда, когда сила =0 или когда линия действия силы проходит через точку (ᴛ.ᴇ. плечо =0). В случае если x,y,z – координаты точки приложения силы, Fx, Fy, Fz – проекции силы на оси координат и точка 0 – начало координат, то
=(yFz – zFy)
+(zFx – xFz)
+(xFy – yFx)
, откуда проекции момента силы на оси коорд.: М0x(
)=yFz – zFy; М0y(
)=zFx – xFz; М0z(
)=xFy – yFx.
Главный вектор – векторная сумма всех сил, приложенных к телу. Главный момент относительно центра –векторная сумма моментов всех сил, приложенных к телу относительно того же центра.
Теорема (лемма) о параллельном переносе силы: сила приложенная в какой-либо точке тверд. тела, эквивалента такой же силе, приложенной в любой др. Размещено на реф.рфточке этого тела, и паре сил, момент которой равен моменту данной силы относительно новой точки приложения.
referatwork.ru
Свойства пары сил | Физика
В учебниках физики описан такой способ определения центра тяжести: пластинку произвольной формы подвешивают на нитке за какую-нибудь ее точку (рис. 51). Когда установится равновесие, через эту точку подвеса проводят на пластинке вертикаль. Центр тяжести находится, конечно, на этой линии. Потом пластинку подвешивают за другую точку. Проводят вертикальную линию, проходящую через эту точку. На пересечении двух линий и находится центр тяжести.
Я проводил опыт иначе. Пластинку я положил на поверхность стола и тянул за нитку так, чтобы пластинка скользила по горизонтальной плоскости. Но лучше я покажу вам это непосредственно на опыте (рис. 52). Смотрите, пластинка поворачивается, и вот направление натянутой нити проходит через центр тяжести, помеченный мной заранее на основании обычного опыта с отвесом. Прикрепим теперь нитку в другой точке и повторим опыт. Направление натянутой нити даст нам новую прямую, и в точке пересечения этих прямых находится центр тяжести пластинки.
Между этими способами имеется большое сходство. Но как объяснить такой поворот пластинки в моем опыте? Постараюсь объяснить этот вопрос так, чтобы вам все было понятно. Я расскажу вам про удивительные свойства пары сил. Знание этих свойств имеет огромное значение для техники. Всюду: в машинах, станках, на заводе, на транспорте — вы видите, как вращаются валы, оси, шкивы. А чем вызывается вращение? Парой сил! Даже когда вам кажется, что вращение происходит под действием только одной силы, например когда вы открываете или закрываете дверь за ручку, то в действительности и тут имеется пара сил — вторая сила возникает в петлях двери.
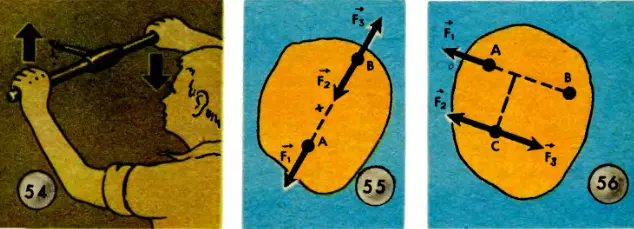
Парой сил или просто парой в механике называют две равные по модулю, параллельные, противоположно направленные силы, приложенные к телу таким образом, чтобы они не оказались на одной прямой (рис. 53). Равнодействующей пара сил не имеет. Под действием пары сил тело вращается. И уравновесить пару одной силой нельзя. Для этого потребуется другая пара сил, которая бы вращала тело в обратную сторону. Конечно, вращающее действие этой второй пары должно быть равно вращающему действию первой. А от чего зависит вращающее действие пары сил? Конечно, от модуля сил, составляющих пару сил.
Но не только от этого. Вращающее действие пары зависит и от расстояния между силами, составляющими пару. Чтобы увеличить действие пары сил, буравы, винтовые прессы и т. п. снабжают рукоятками (рис. 54), и, чем длиннее рукоятка, чем больше будет расстояние между силами, тем большим будет вращающее действие пары. Расстояние между параллельными силами пары (по перпендикулярному к ним направлению) называют плечом пары сил.
Вращающее действие пары измеряют произведением модуля силы на плечо. Такое произведение называют моментом пары.
Здесь уместно немного поговорить о слове «момент». Дело в том, что это слово в обычной разговорной речи и в механике имеет совсем разные значения. В разговорной речи «момент» означает «очень короткий промежуток времени». Так, например, говорят: «в один момент», «моментально». В механике же термин «момент» имеет иное значение; оно не связано с понятием времени. В переводе с латинского momentum означает «движущая сила», «толчок»; в английской литературе слово momentum переводится как «импульс». Однако в русской научной литературе это слово связывают не с импульсом, а с вращением. Рассматривая вращающиеся тела, используют понятия «момент силы», «момент импульса» («момент количества движения»), «момент инерции». При этом часто «момент силы» для краткости называют просто «моментом». Помня об этом, не удивляйтесь, почему при расчетах балок, осей важно находить «изгибающие моменты», при расчете валов - «крутящие моменты» и т. д.
Момент сил вы изучали в школе и даже решали задачи на равновесие рычагов, используя правило моментов. Я уже говорил, что и при действии одной силы, если она не проходит через ось вращения тела, мы имеем в сущности пару сил. Вторая сила возникает в качестве противодействия оси телу, деформирующему ось. Ведь если бы не было оси, то тело стало бы удаляться под действием приложенной силы. Ось же удерживает его.
Встречающееся определение, согласно которому плечом силы называется перпендикуляр, опущенный из оси вращения на линию действия силы, полностью совпадает с определением плеча пары сил как кратчайшего расстояния между параллельными силами, составляющими пару.
Теперь я предложу вам новый вопрос: что вы знаете о переносе точки приложения силы?
Точку приложения силы можно переносить по линии действия силы. Мы хотим перенести точку приложения силы 
из точки A в точку B (рис. 55). Приложим в точке B две противоположные силы 
и 
, равные по модулю силе . Это не окажет никакого влияния на тело: ведь силы уравновешены. Но можно считать, что уравновешены и силы и . Значит, их можно отбросить и тогда останется только сила , равная по модулю силе и так же направленная, но приложенная в точке B.
А теперь я покажу вам, что случится, если мы перенесем силу не в точку B на линии действия силы, а в какую-нибудь точку C вне этой линии (рис. 56). Будем рассуждать так. Приложим в точке C две силы, равные по модулю и параллельные силе . Можно ли теперь отбросить силы и , как это только что делали? Конечно нет! Это не уравновешенные силы, это пара сил, и она должна вызывать вращение тела.
Итак, если силу перенести не по линии ее действия, это не проходит безнаказанно: появляется еще так называемая «присоединенная пара». Действие этой пары тем больше, чем дальше в сторону от линии AB мы выбираем точку C, потому что силы-то те же, но плечо, а значит, и момент больше. В случае если точку приложения выбрать на линии действия сил, плечо обращается в нуль и никакой пары не присоединяется. Вот почему и говорят, что точку приложения силы можно переносить только по линии действия силы.
Пары, имеющие равные моменты, называются эквивалентными парами (рис. 57).
Я могу вам доказать, что в отличие от одной силы пару можно переносить в любое место плоскости, в которой она расположена, и притом совершенно безнаказанно. При этом не обязательно даже сохранять прежнее направление сил, т. е. пару можно поворачивать как угодно, лишь бы момент пары и направление вращения, ею вызываемого (по или против часовой стрелки), оставались прежними.
Вот смотрите: приложим в точках C и D (|CD| = |AB|) по две противоположные силы, т. е. как бы две противоположные пары. Одна из них, отмеченная черточками (рис. 58, а), стремится вращать тело в одну сторону, другая — в противоположную. Следовательно, пары уравновешиваются, но можно считать уравновешенными и первоначальную пару с плечом AB, и противоположную ей с плечом CD (перечеркнутую). Тогда останется лишь одна пара с плечом CD, вращающая тело в ту же сторону, что и первоначальная. Значит, можно сказать, что мы пару с плечом AB перенесли на плечо CD. Разве это не удивительное свойство пары сил?
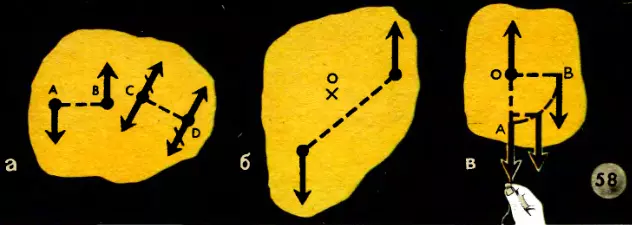
Неужели новая пара действует так же, как первоначальная? Ведь ось-то вращения тоже переместилась? Всякая пара сил, где бы она ни была расположена в той же плоскости, вращает тело вокруг оси, проходящей через центр тяжести (центр масс) тела, т. е. через току O (рис. 58, б). Вот еще одно удивительное свойство пары сил.
Но почему же?! Какое отношение имеет к этому всему центр тяжести? Дело в том, что пара сил не имеет равнодействующей. Следовательно, в этом случае не удастся свести движение тела к движению центра тяжести. Поскольку на центр тяжести не действует никакая сила, то он должен оставаться в покое, быть неподвижным. Других неподвижных точек у тела быть не может, так как две неподвижные точки, не лежащие на оси вращения, не позволили бы телу вращаться.
Значит, где же проходит ось вращения (ведь ось вращения неподвижна)? Только через центр тяжести и нигде больше! Если направление приложенной силы не проходит через центр тяжести, то мы можем ее перенести, как я объяснял, в центр тяжести, но тогда появится присоединенная пара. Тело начнет поворачиваться, как вы и видели на опыте (см. рис. 52). При этом плечо пары и ее момент будут все уменьшаться (рис. 58, в), пока направление тянущей нити не станет проходить через центр тяжести. Тогда вращение прекратится и тело будет двигаться поступательно.
Вот и все, что я хотел рассказать вам об удивительных свойствах пары сил. То, что вы узнали, имеет большое значение в технике. Для плавного хода машин необходимо, чтобы вращающиеся части были хорошо уравновешены (балансированы), т. е. чтобы ось вращения проходила через центр масс вала, шкива, якоря электрического генератора или двигателя, иначе установка будет вибрировать и может разрушиться.
phscs.ru
|
|
..:::Счетчики:::.. |
|
|
|
|
|
|
|
|