Определенный интеграл. Реферат на тему определенный интеграл

Реферат: Определенный интеграл

ИНТЕГРАЛ (от лат. Integer - целый) - одно из важнейших понятий математики, возникшее в связи с потребностью, с одной стороны отыскивать функции по их производным (например, находить функцию, выражающую путь, пройденный движущейся точкой, по скорости этой точки), а с другой - измерять площади, объемы, длины дуг, работу сил за определенный промежуток времени и т. п.

Символ введен Лейбницем (1675 г.). Этот знак является изменением латинской буквы S (первой буквы слова сумма). Само слово интеграл придумал Я. Бернулли (1690 г.). Вероятно, оно происходит от латинского integero, которое переводится как приводить в прежнее состояние, восстанавливать. (Действительно, операция интегрирования “восстанавливает” функцию, дифференцированием которой получена подынтегральная функция.) Возможно происхождение слова интеграл иное: слово integer означает целый.

В ходе переписки И. Бернулли и Г. Лейбниц согласились с предложением Я. Бернулли. Тогда же , в 1696г., появилось и название новой ветви математики - интегральное исчисление (calculus integralis), которое ввел И. Бернулли.

Другие известные вам термины, относящиеся к интегральному исчислению, появились значительно позднее. Употребляющееся сейчас название первообразная функция заменило более раннее “примитивная функция”, которое ввел Лагранж (1797 г.). Латинское слово primitivus переводится как “начальный”: F(x)= - начальная (или первоначальная, или первообразная) для функции f(x), которая получается из F(x) дифференцированием.

В современной литературе множество всех первообразных для функции f(x) называется также неопределенным интегралом. Это понятие выделил Лейбниц, который заметил, что все первообразные функции отличаются на произвольную постоянную. А называют определенным интегралом (обозначение ввел К. Фурье (1768-1830), но пределы интегрирования указывал уже Эйлер).

Возникновение задач интегрального исчисления связано с нахождением площадей и объемов. Ряд задач такого рода был решен математиками древней Греции. Античная математика предвосхитила идеи интегрального исчисления в значительно большей степени, чем дифференциального исчисления. Большую роль при решении таких задач играл исчерпывающий метод, созданный Евдоксом Книдским (ок. 408 - ок. 355 до н. э.) и широко применявшийся Архимедом (ок. 287 - 212 до н. э.).

Однако Архимед не выделил общего содержания интеграционных приемов и понятий об интеграле, а тем более не создал алгоритма интегрального исчисления. Ученые Среднего и Ближнего Востока в IX - XV веках изучали и переводили труды Архимеда на общедоступный в их среде арабский язык, но существенно новых результатов в интегральном исчислении они не получили.

Деятельность европейских ученых в это время была еще более скромной. Лишь в XVI и XVII веках развитие естественных наук поставило перед математикой Европы ряд новых задач, в частности задачи на нахождение квадратур (задачи на вычисление площадей фигур), кубатур (задачи на вычисление объемов тел) и определение центров тяжести .

Труды Архимеда, впервые изданные в 1544 (на латинском и греческом языках), стали привлекать широкое внимание, и их изучение явилось одним из важнейших отправных пунктов развития интегрального исчисления. Архимед предвосхитил многие идеи интегрального исчисления. Но потребовалось более полутора тысяч лет, прежде чем эти идеи нашли четкое выражение и были доведены до уровня исчисления.

Математики XVII столетия, получившие многие новые результаты, учились на трудах Архимеда. Активно применялся и другой метод - метод неделимых, который также зародился в Древней Греции. Например, криволинейную трапецию они представляли себе составленной из вертикальных отрезков длиной f(x) , которым тем не менее приписывали площадь, равную бесконечно малой величине f(x)dx. В соответствии с таким пониманием искомая площадь считалась равной сумме S = бесконечно большого числа бесконечно малых площадей. Иногда даже подчеркивалось, что отдельные слагаемые в этой сумме - нули, но нули особого рода, которые сложенные в бесконечном числе, дают вполне определенную положительную сумму.

На такой кажущейся теперь по меньшей мере сомнительной основе И. Кеплер (1571 - 1630 гг.) в своих сочинениях “Новая астрономия” (1609 г.) и “Стереометрия винных бочек” (1615 г.) правильно вычислил ряд площадей (например площадь фигуры, ограниченной эллипсом) и объемов (тело резалось на бесконечно тонкие пластинки).

Эти исследования были продолжены итальянскими математиками Б. Кавальери (1598 - 1647 годы) и Э. Торричелли (1608 -1647 годы).

В XVII веке были сделаны многие открытия, относящиеся к интегральному исчислению. Так, П. Ферма уже в 1629 году решил задачу квадратуры любой кривой y =, где N - целое (т. е. вывел формулу ), и на этой основе решил ряд задач на нахождение центров тяжести. И. Кеплер при выводе своих знаменитых законов движения планет, фактически опирался на идею приближенного интегрирования. И. Барроу (1603-1677 года), учитель Ньютона, близко подошел к пониманию связи интегрирования и дифференцирования. Большое значение имели работы по представлению функции в виде степенных рядов.

Однако при всей значимости результатов, полученных математиками XVII столетия, исчисления еще не было. Необходимо было выделить общие идеи, лежащие в основе решения многих частных задач, а также установить связь операций дифференцирования и интегрирования, дающую достаточно точный алгоритм. Это сделали Ньютон и Лейбниц, открывшие независимо друг от друга факт, известный вам под названием формулы Ньютона - Лейбница. Тем самым окончательно оформился общий метод. Предстояло еще научиться находить первообразные многих функций, дать логические основы нового исчисления и т. п. Но главное уже было сделано: дифференциальное и интегральное исчисление создано.

Методы математического анализа активно развивались в следующем столетии (в первую очередь следует назвать имена Л. Эйлера, завершившего систематическое исследование интегрирования элементарных функций, и И. Бернулли). В развитии интегрального исчисления приняли участие русские математики М. В. Остроградский (1801 - 1862 гг.), В. Я. Буняковский (1804 - 1889 гг.), П. Л. Чебышев (1821 - 1894 гг.). Принципиальное значение имели, в частности, результаты Чебышева, доказавшего, что существуют интегралы, не выразимые через элементарные функции.

Строгое изложение теории интеграла появилось только в прошлом веке, Решение этой задачи связано с именами О. Коши, одного из крупнейших математиков немецкого ученого Б. Римана (1826 - 1866 гг.), французского математика Г. Дарбу (1842 - 1917).

Ответы на многие вопросы, связанные с существованием площадей и объемов фигур, были получены с созданием К. Жорданом (1826 - 1922 гг.) теории меры.

Различные обобщения понятия интеграла уже в начале нашего столетия были предложены французскими математиками А. Лебегом (1875 - 1941 гг.) и А. Данжуа (1884 - 1974) советским математиком А. Я. Хичиным (1894 -1959 гг.)

1). Афанасенко Е. И. Детская энциклопедия т.2., М., “Просвещение”, 1964.

2). Вавилов В. В. Задачи по математике. Начало анализа., М., “Наука”, 1990.

3).Евграфов Н. Н. Курс физики для подготовительных отделений вузов., М., “Высшая школа”, 1984.

4). Колмогоров А. Н. Алгебра и начала анализа., М., “Просвещение”, 1990.

5). Пинсий А. А. Физика., М., “Просвещение”, 1994.

6). Прохоров А. М. Большая Советская энциклопедия т.10., М., “Советская энциклопедия”, 1972.

7). Сканави М. И. Сборник задач по математике для поступающих во втузы., М., “Высшая школа”, 1988.

8). Яковлев Т. Х. Пособие по математике для поступающих в вузы., М., “Наука”, 1988.

www.neuch.ru

Определенный интеграл — реферат

Федеральное агентство  по образованию

Государственное образовательное  учреждение

высшего профессионального  образования

«Южно-Уральский государственный  университет»

Кафедра Экономической  теории и мировой экономики

РЕФЕРАТ

ПО КУРСУ  «МАТЕМАТИКА»

НА ТЕМУ «ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ»

Выполнил:

Студент группы   ЗЭУ-234 (Шумиха)

Ф.И.О Спирин Дмитрий Александрович

Проверил: Семакина Е.А.

Шумиха

2011

СОДЕРЖАНИЕ

I. ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ

  1. Понятие определенного интеграла……………………………………….…..3

  2. Геометрический смысл определенного интеграла…………………….…….5

  3. Основные свойства определенного интеграла……………………….………6

  4. Формула Ньютона–Лейбница…………………………………………………7

  5. Замена переменной в определенном интеграле……………………………...9

  6. Интегрирование по частям……………………………………………………11

II. ПРИМЕНЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ

  1. Площадь криволинейной трапеции…………………………………………13

  2. Объем тела вращения…………………………………………………………19

  3. Длина дуги плоской кривой………………………………………………….22

  4. Несобственные интегралы с бесконечными пределами интегрирования..24

  5. Несобственные интегралы от неограниченных функций………………….27

Литература…………………………………………………………………..........29

I. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

1. Понятие определенного интеграла

Пусть функция  определена на отрезке , . Выполним следующие операции:

1. разобьем отрезок точками на n частичных отрезков ;
2. в каждом из частичных отрезков , выберем произвольную точку и вычислим значение функции в этой точке ;
3. найдем произведения , где – длина частичного отрезка , ;
4. составим сумму

, (1) которая называется интегральной суммой функции y = f(x) на отрезке [а, b]. С геометрической точки зрения интегральная сумма представляет собой сумму площадей прямоугольников, основаниями которых являются частичные отрезки , а высоты равны соответственно (рис. 1). Обозначим через длину наибольшего частичного отрезка ;

5. найдем предел интегральной суммы, когда .

Рис. 1

Определение. Если существует конечный предел интегральной суммы (1) и он не зависит ни от способа разбиения отрезка на частичные отрезки, ни от выбора точек в них, то этот предел называется определенным интегралом от функции на отрезке и обозначается .

Таким образом, .

В этом случае функция  называется интегрируемой на . Числа а и b называются соответственно нижним и верхним пределами интегрирования, – подынтегральной функцией, – подынтегральным выражением, – переменной интегрирования; отрезок называется промежутком интегрирования.

Теорема 1. Если функция непрерывна на отрезке , то она интегрируема на этом отрезке.

2. Геометрический смысл определенного интеграла

Пусть на отрезке  задана непрерывная неотрицательная функция . Криволинейной трапецией называется фигура, ограниченная сверху графиком функции y = f(x), снизу – осью Ох, слева и справа – прямыми x = a и x = b (рис. 2).

Рис. 2

Определенный интеграл от неотрицательной функции с геометрической точки зрения численно равен площади криволинейной трапеции, ограниченной сверху графиком функции , слева и справа – отрезками прямых и , снизу – отрезком оси Ох.

3. Основные свойства определенного интеграла

1. Значение определенного интеграла не зависит от обозначения переменной интегрирования: .

2. Определенный интеграл с одинаковыми пределами интегрирования равен нулю:

3. Если , то, по определению, полагаем
4. Постоянный множитель можно выносить за знак определенного интеграла:
5. Определенный интеграл от алгебраической суммы двух функций равен алгебраической сумме определенных интегралов от этих функций:

.

6. Если функция  интегрируема на и , то

.

7. (теорема о среднем). Если функция непрерывна на отрезке , то на этом отрезке существует точка , такая, что .

4. Формула Ньютона–Лейбница

Вычисление определенных интегралов через предел интегральных сумм связано с большими трудностями. Поэтому существует другой метод, основанный на тесной связи, существующей между понятиями определенного и неопределенного интегралов.

Теорема 2. Если функция непрерывна на отрезке и – какая-либо ее первообразная на этом отрезке, то справедлива следующая формула:

, (2), которая называется формулой Ньютона–Лейбница. Разность принято записывать следующим образом:

,

где символ называется знаком двойной подстановки.

Таким образом, формулу (2) можно записать в виде:

.

Нахождение определенных интегралов с помощью формулы Ньютона-Лейбница осуществляется в два этапа: на первом этапе находят некоторую первообразную для подынтегральной функции ; на втором – находится разность значений этой первообразной на концах отрезка .

Пример 1. Вычислить интеграл .

Решение. Для подынтегральной функции произвольная первообразная имеет вид . Так как в формуле Ньютона-Лейбница можно использовать любую первообразную, то для вычисления ин- теграла возьмем первообразную, имеющую наиболее простой вид: . Тогда .

Пример 2. Вычислить интеграл .

Решение. По формуле Ньютона-Лейбница имеем:

.

5. Замена переменной в определенном интеграле

Теорема 3. Пусть функция непрерывна на отрезке . Тогда, если: 1) функция и ее производная непрерывны при ; 2) множеством значений функции при является отрезок ; 3) , , то справедлива формула

, (3), которая называется формулой замены переменной в определенном интеграле.

Заметим, что, как и в случае неопределенного интеграла, использование замены переменной позволяет упростить исходный интеграл, приблизив его к табличному. При этом в отличие от неопределенного интеграла в данном случае нет необходимости возвращаться к исходной переменной интегрирования – достаточно лишь найти новые пределы интегрирования и (для этого надо решить относительно переменной t уравнения и )).

На практике часто  вместо подстановки  используют подстановку . В этом случае нахождение новых пределов интегрирования по переменной t упрощается: , .

Пример 3. Вычислить интеграл

Решение. Введем новую  переменную по формуле . Определим и . Возведя в квадрат обе части равенства , получим , откуда . Находим новые пределы интегрирования. Для этого в формулу подставим старые пределы и . Получим: , откуда и, следовательно, ; , откуда и, следовательно, . Таким образом:

 .

Пример 4. Вычислить интеграл .

Решение. Воспользуемся  универсальной тригонометрической подстановкой. Положим , откуда , . Найдем новые пределы интегрирования: если , то ; если , то . Значит, . Следовательно:

.

Пример 5. Вычислить интеграл .

Решение. Положим , тогда , откуда . Находим новые пределы интегрирования: ; . Имеем: . Следовательно:

.

6. Интегрирование по частям

Теорема 4. Пусть функции и имеют непрерывные производные на отрезке . Тогда имеет место следующая формула интегрирования по частям:

. (4)

Доказательство

Так как , то функция является первообразной для функции . Тогда по формуле Ньютона–Лейбница получаем

,

откуда

.

Пример 6. Вычислить .

Решение. Положим , отсюда . По формуле (4) находим

 .

Пример 7. Вычислить .

Решение. Пусть , тогда . Применяя формулу интегрирования по частям, получаем

 .

Пример 8. Вычислить .

Решение. Полагая , определяем . Следовательно:

[к полученному интегра-лу снова  применяем формулу интегрирования  по частям: ; следовательно: ] = =

.

II. Применение определенных интегралов. Несобственные интегралы

1. Площадь криволинейной трапеции

Пусть функция  неотрицательна и непрерывна на отрезке . Тогда, согласно геометрическому смыслу определенного интеграла, площадь криволинейной трапеции, ограниченной сверху графиком этой функции, снизу – осью , слева и справа – прямыми и (см. рис. 2) вычисляется по формуле

. (5)

Пример 9. Найти площадь фигуры, ограниченной линией и осью .

Решение. Графиком функции  является парабола, ветви которой направлены вниз. Построим ее (рис. 3). Чтобы определить пределы интегрирования, найдем точки пересечения линии (параболы) с осью (прямой ). Для этого решаем систему уравнений

Получаем: , откуда , ; следовательно, , .

Рис. 3

Площадь фигуры находим по формуле (5):

(кв. ед.).

Если функция  неположительна и непрерывна на отрезке , то площадь криволинейной трапеции, ограниченной снизу графиком данной функции, сверху – осью , слева и справа – прямыми и , вычисляется по формуле

. (6)

В случае если функция  непрерывна на отрезке и меняет знак в конечном числе точек, то площадь заштрихованной фигуры (рис. 4) равна алгебраической сумме соответствующих определенных интегралов:

. (7)

Рис. 4

Пример 10. Вычислить площадь фигуры, ограниченной осью и графиком функции при .

Рис. 5

Решение. Сделаем чертеж (рис. 5). Искомая площадь представляет собой сумму площадей и . Найдем каждую из этих площадей. Вначале определим пределы интегрирования, решив систему Получим , . Следовательно:

 ;

.

Таким образом, площадь  заштрихованной фигуры равна

(кв. ед.).

Рис. 6

Пусть, наконец, криволинейная трапеция ограничена сверху и снизу графиками непрерывных на отрезке функций и ,  а слева и справа – прямыми и (рис. 6). Тогда ее площадь вычисляется по формуле

. (8)

Пример 11. Найти площадь фигуры, ограниченной линиями и .

referat911.ru

Курсовая работа на тему: Определенный интеграл страница 5

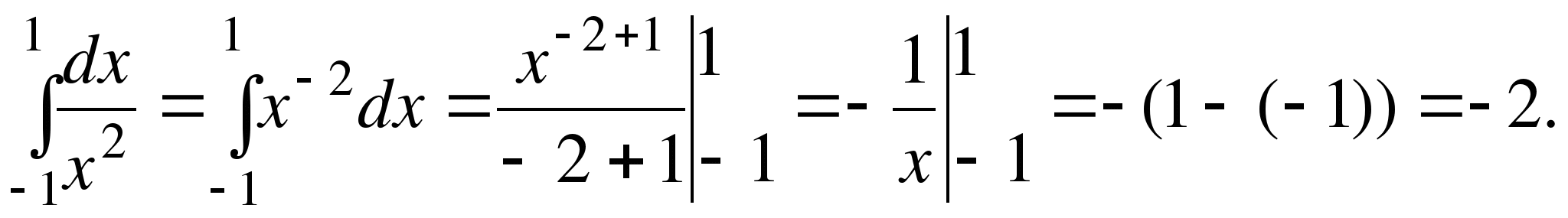
мы получим неверный результат, так как определенный интеграл от функции положительной 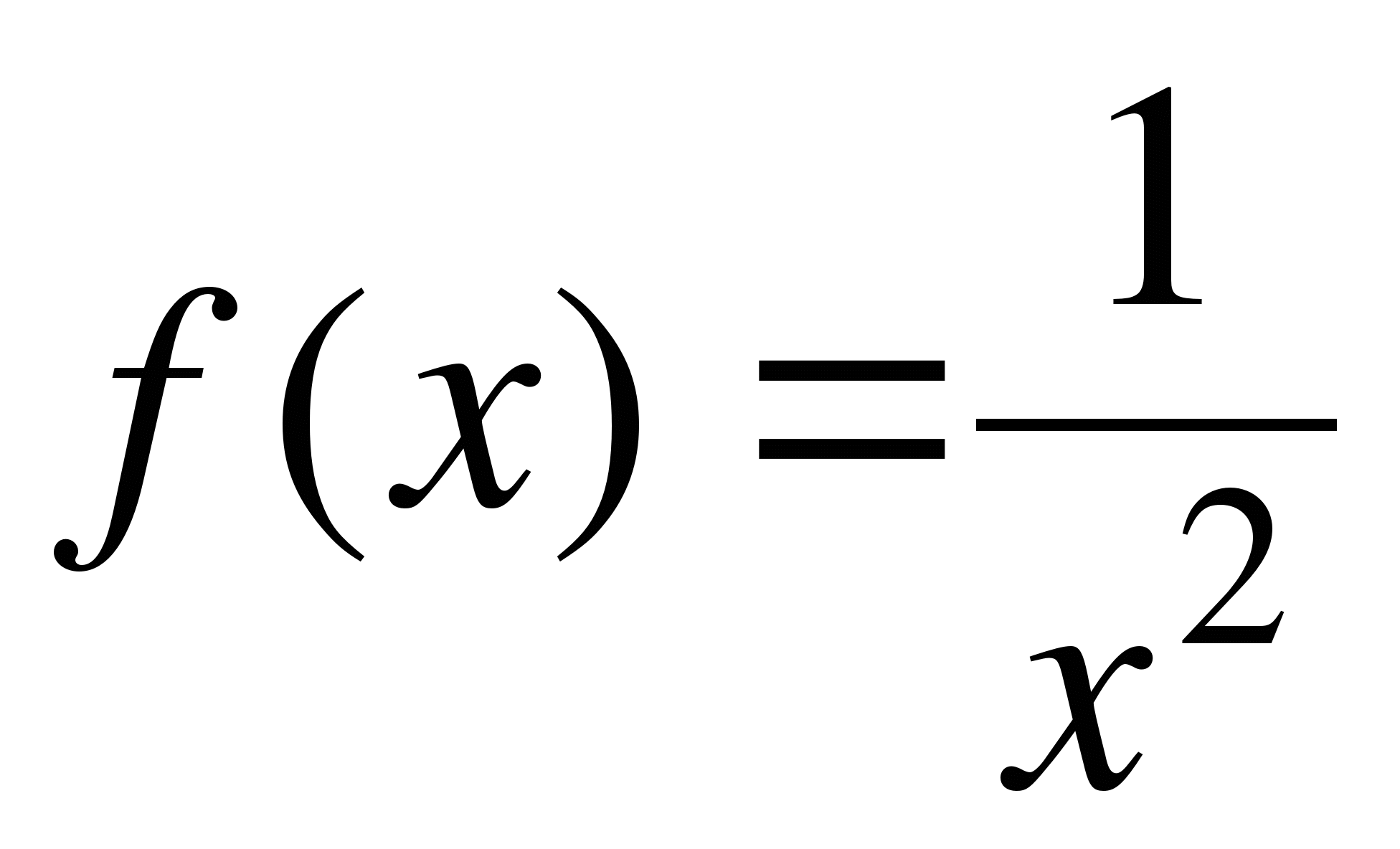во всем промежутке интегрирования, не может быть отрицательным числом.

Дело в том, что в заданном промежутке [-1, 1] подинтегральная функция 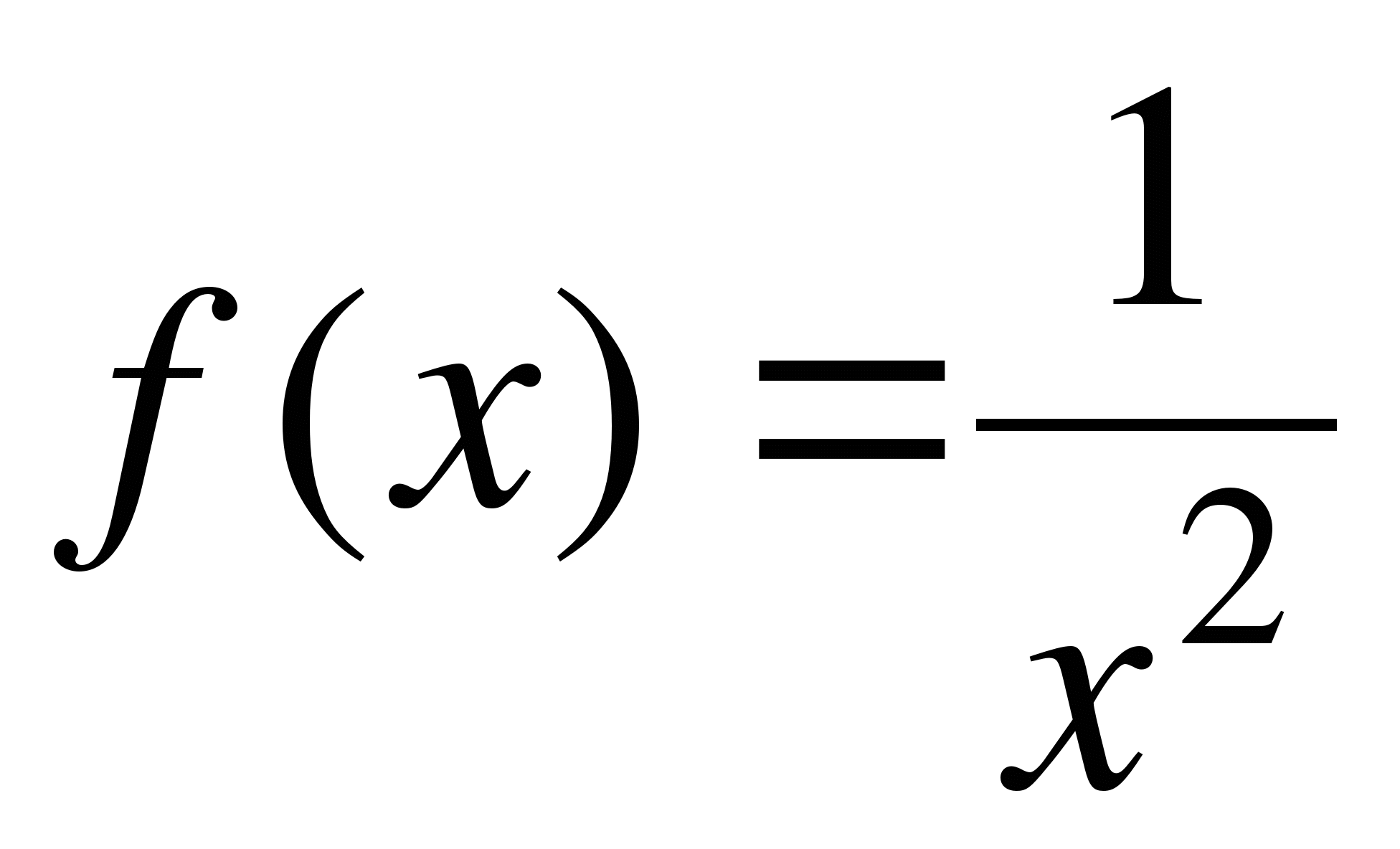в точке имеет разрыв 2–го рода и поэтому мы не имели право использовать формулу Ньютона – Лейбница.

б) В данном случае подинтегральная функция 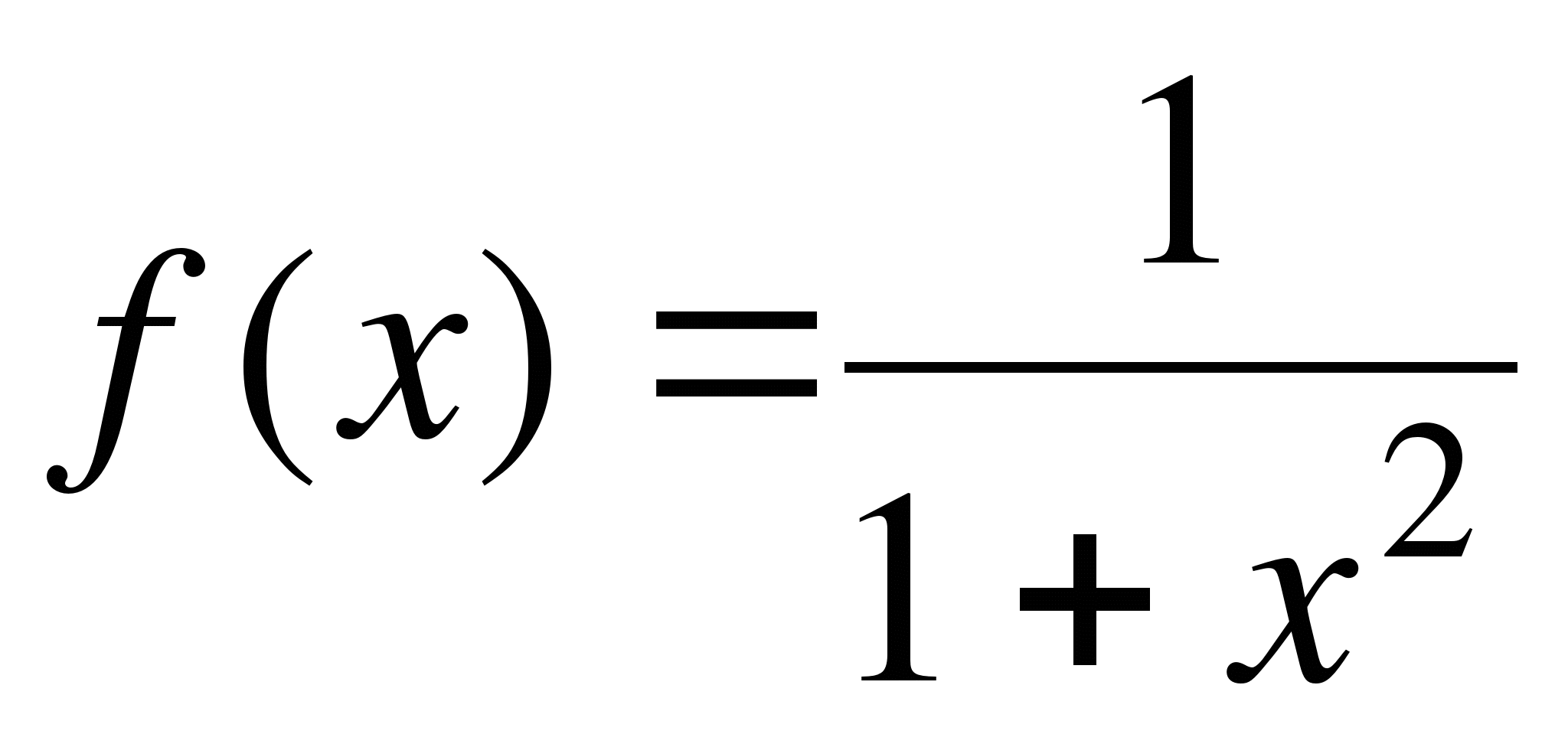- непрерывна в промежутке [-1, 1], и ее первообразная известна по таблице неопределенных интегралов: 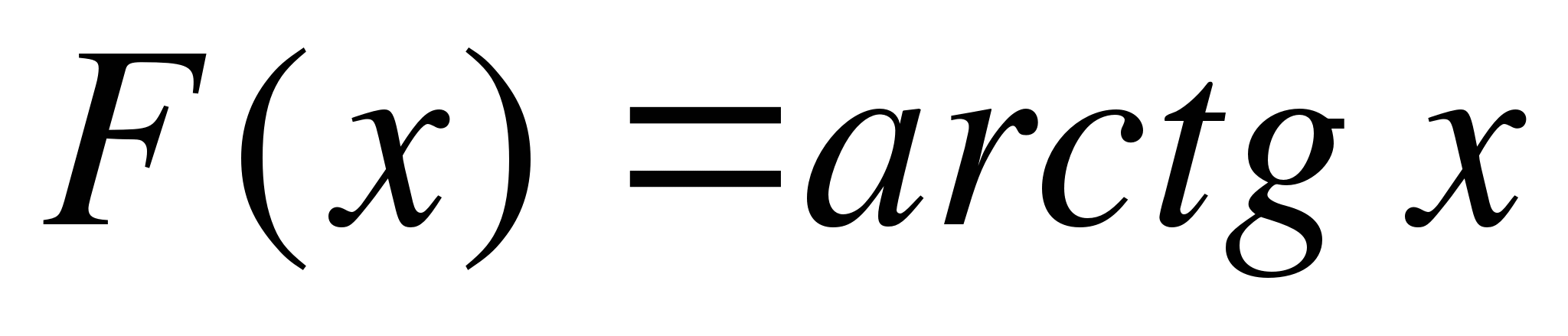. Следовательно, по формуле Ньютона – Лейбница получим

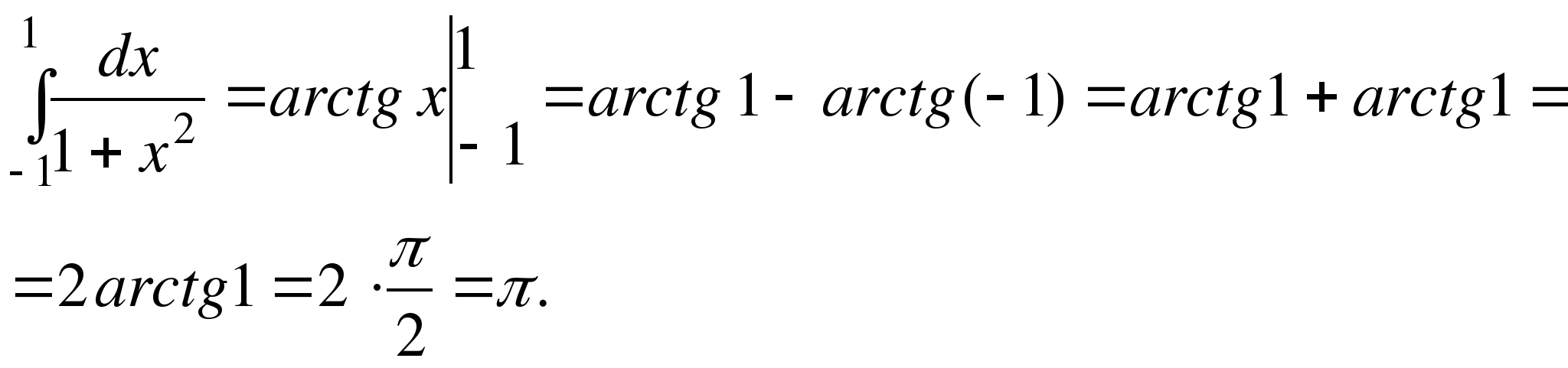
в) Введем подстановку 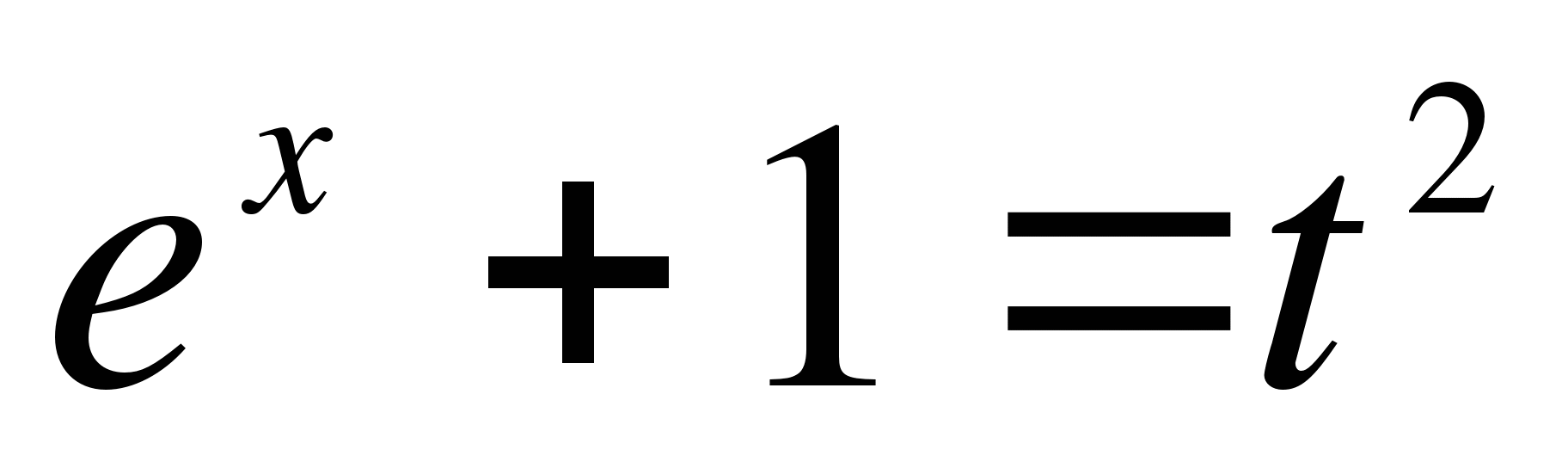(или ).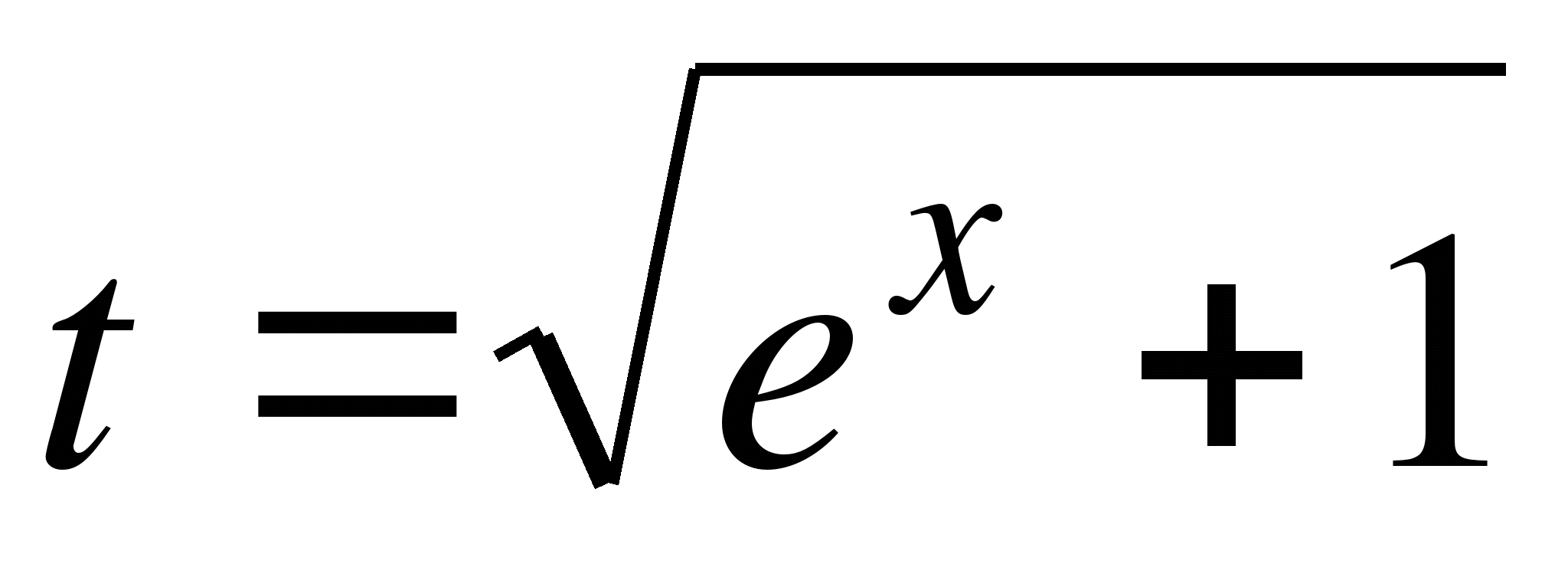

Проверим условие 1) – 3):

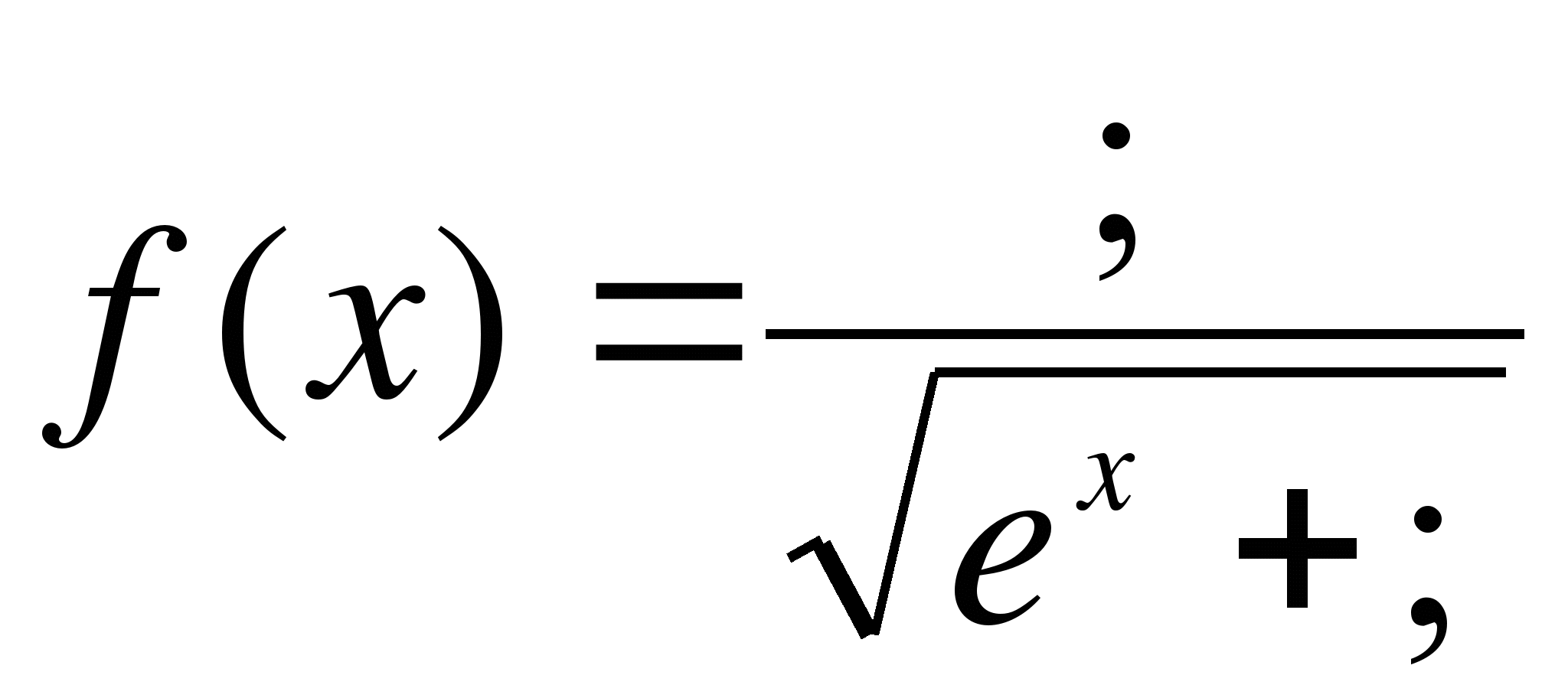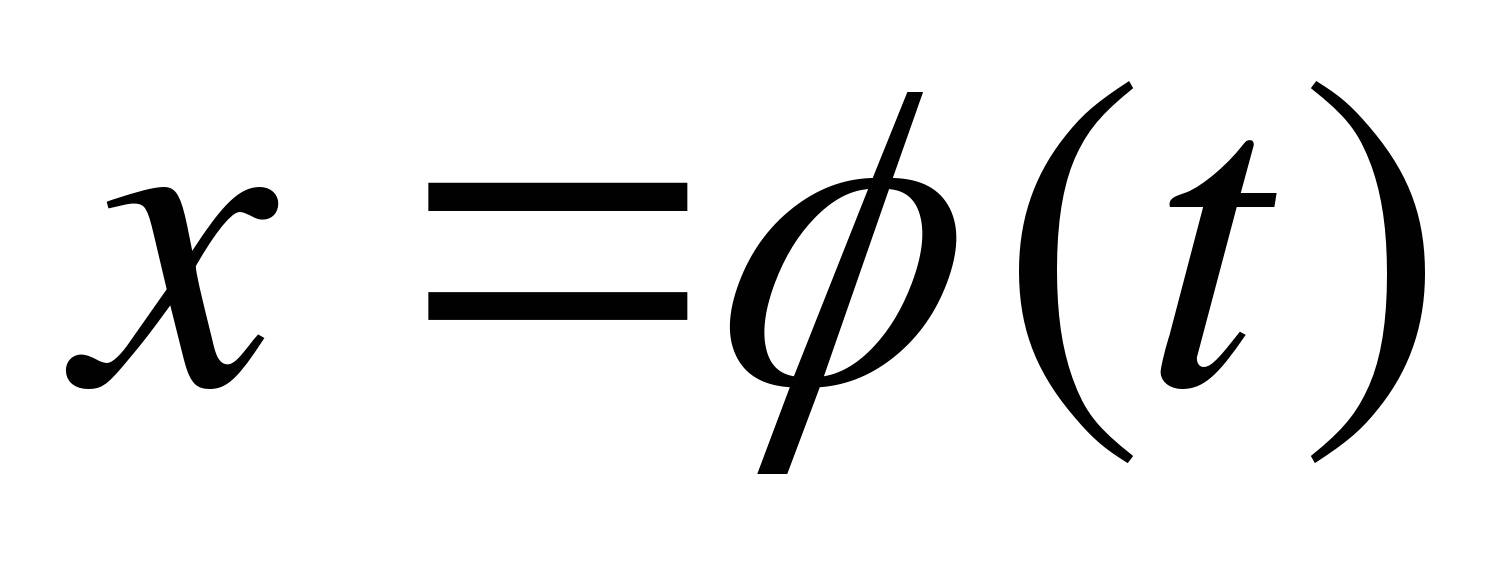1) функция - непрерывна на отрезке [0,1], т.е. найдем функцию из подстановки

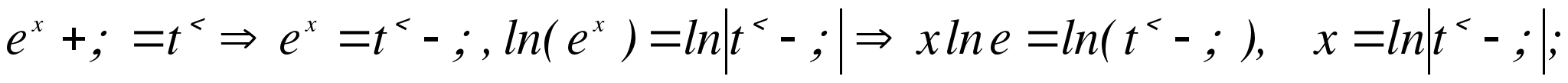2) функция 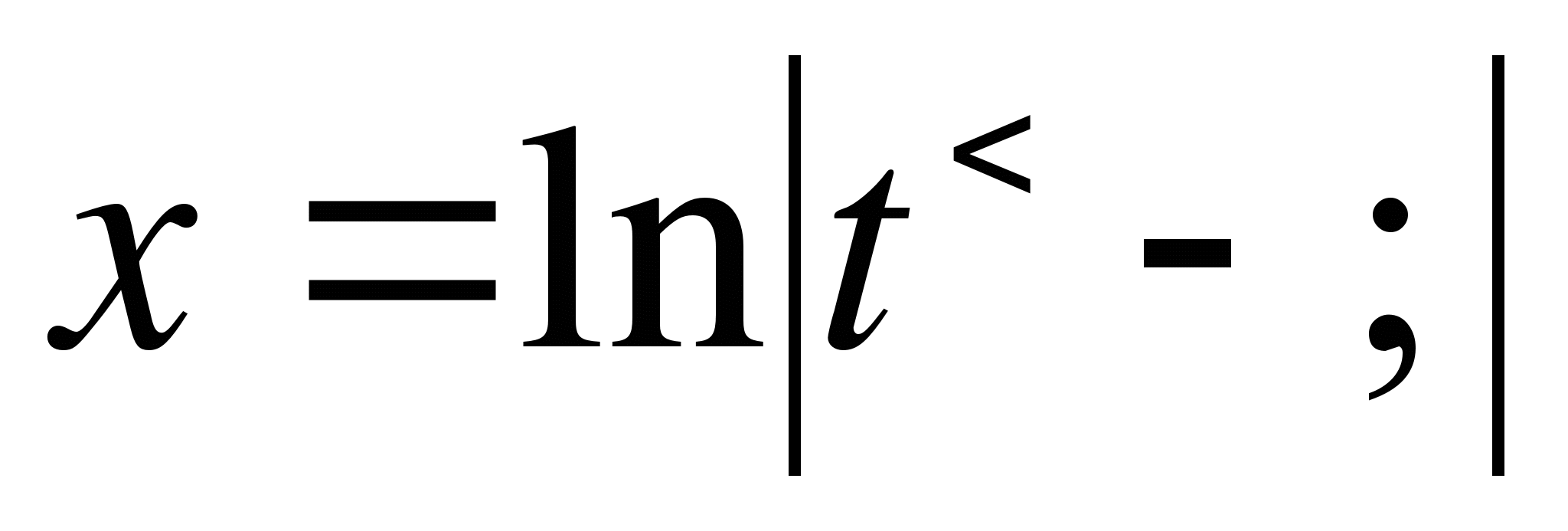и ее производная - непрерывны на отрезке [α, β], где при x=0 и x=ln2, соответственно, найдем из ,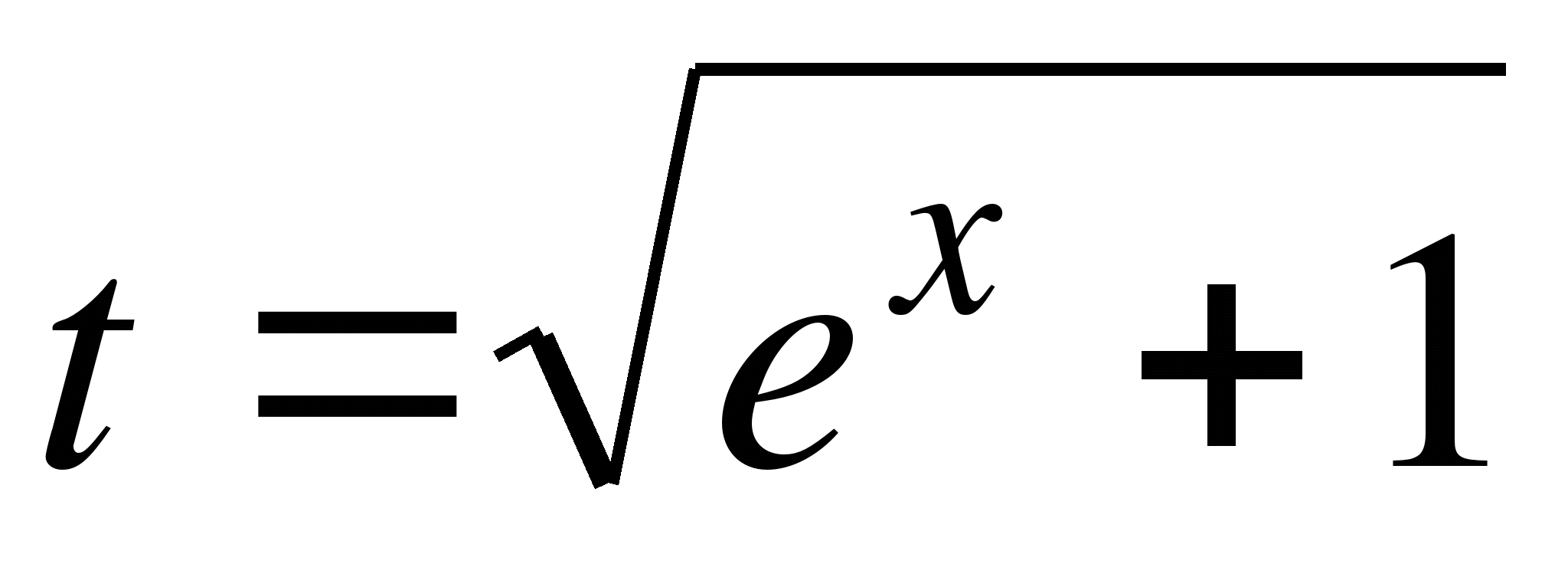

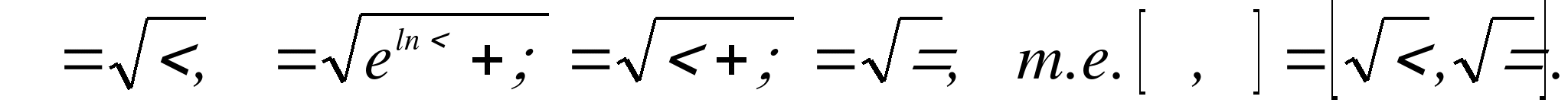
Следовательно, замена переменной в данном случае законна. Тогда, из 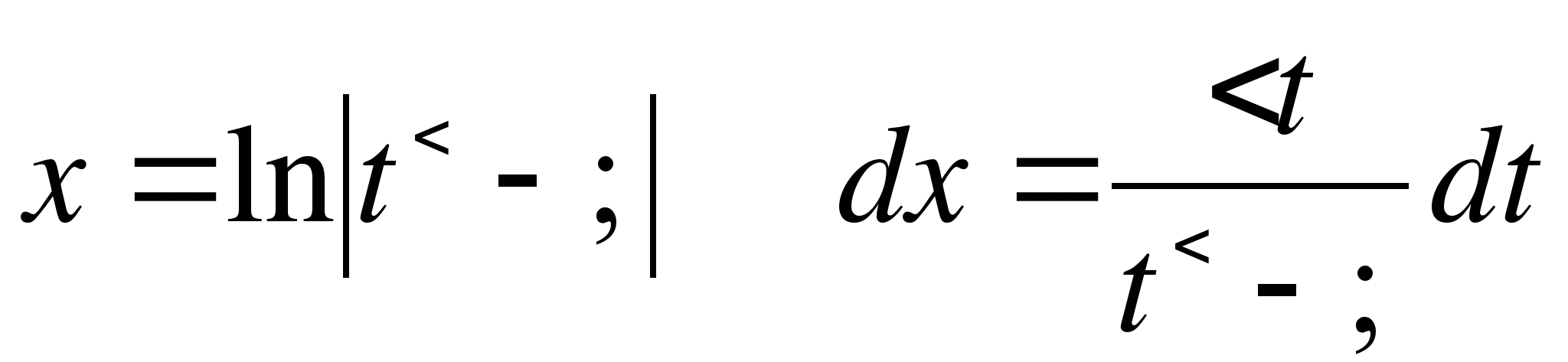и по формуле (2) получим:

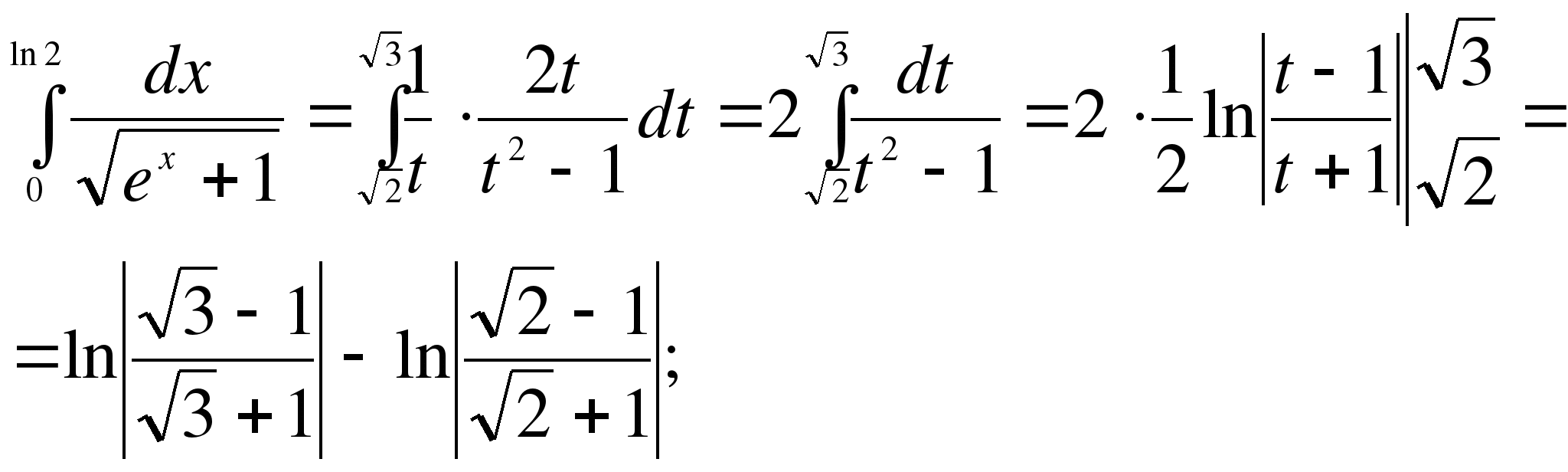
г) Введем подстановку 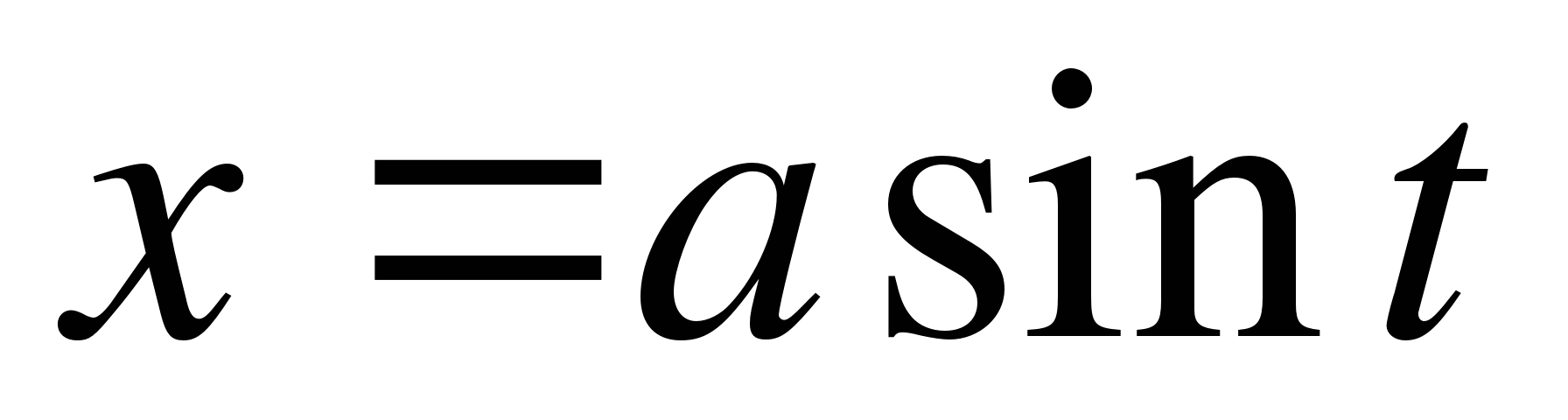. Проверим условия 1) – 3):

1) функция 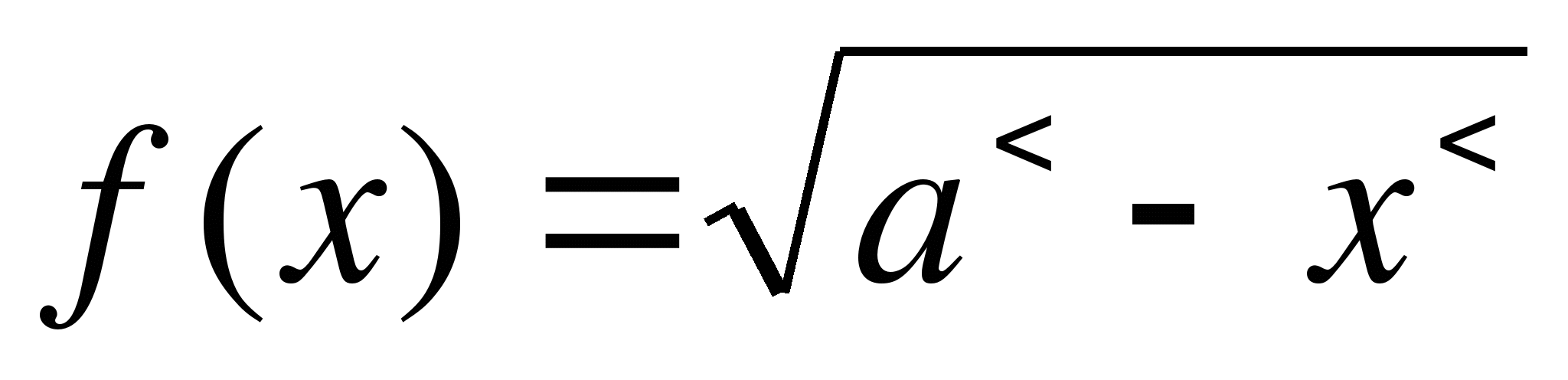- непрерывна в промежутке [0, a];

2) функция 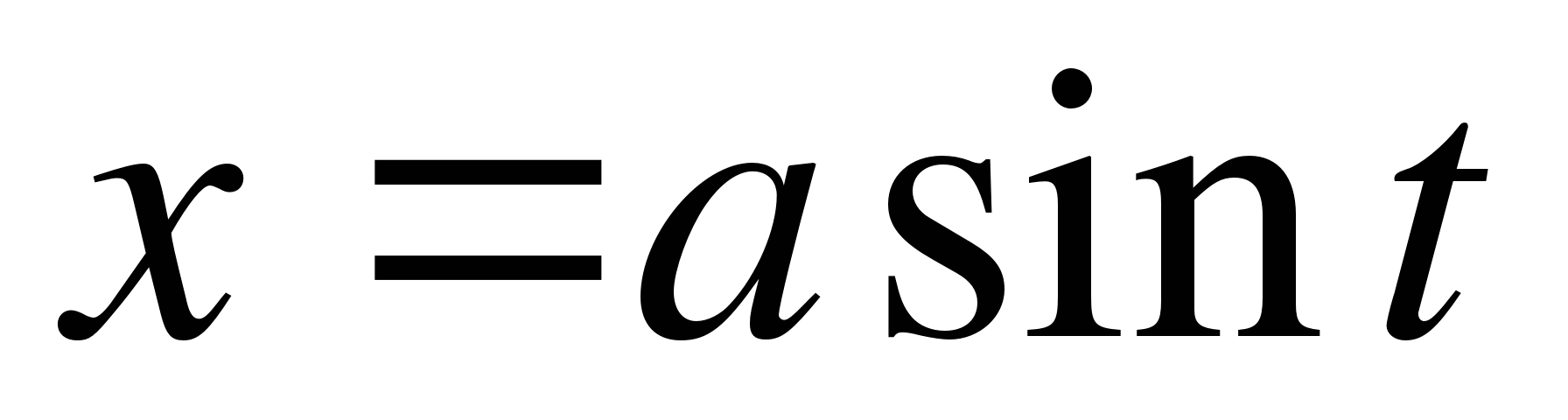и ее производная - непрерывны в промежутке [α,β], где при 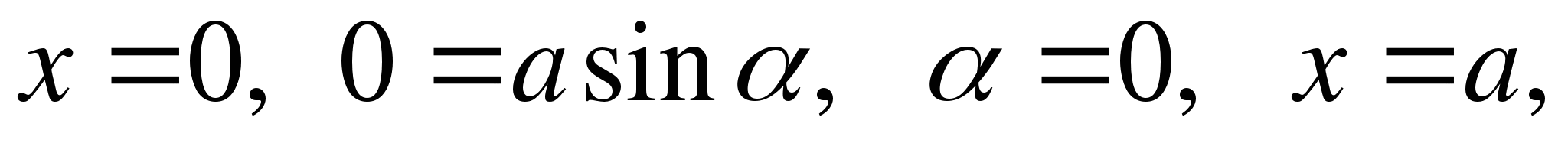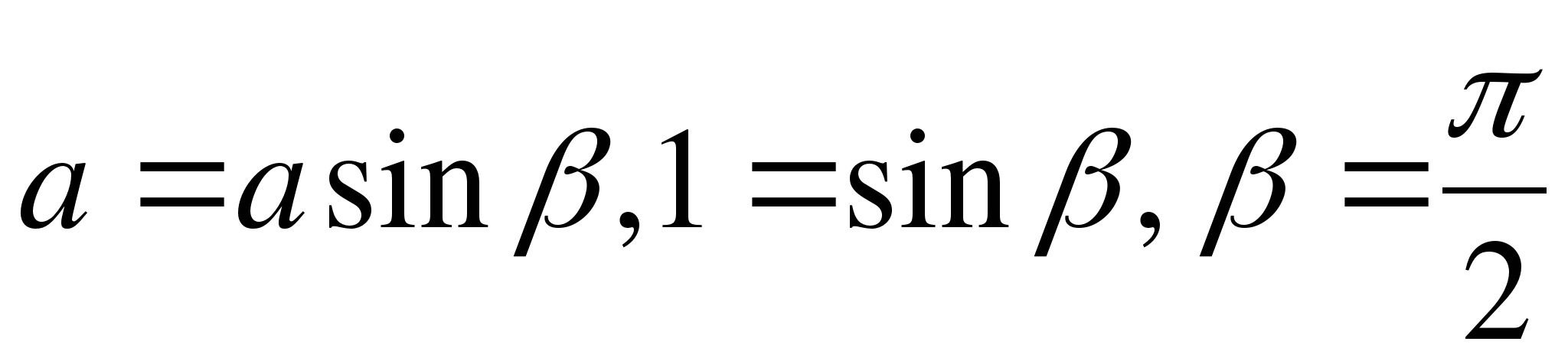. Отсю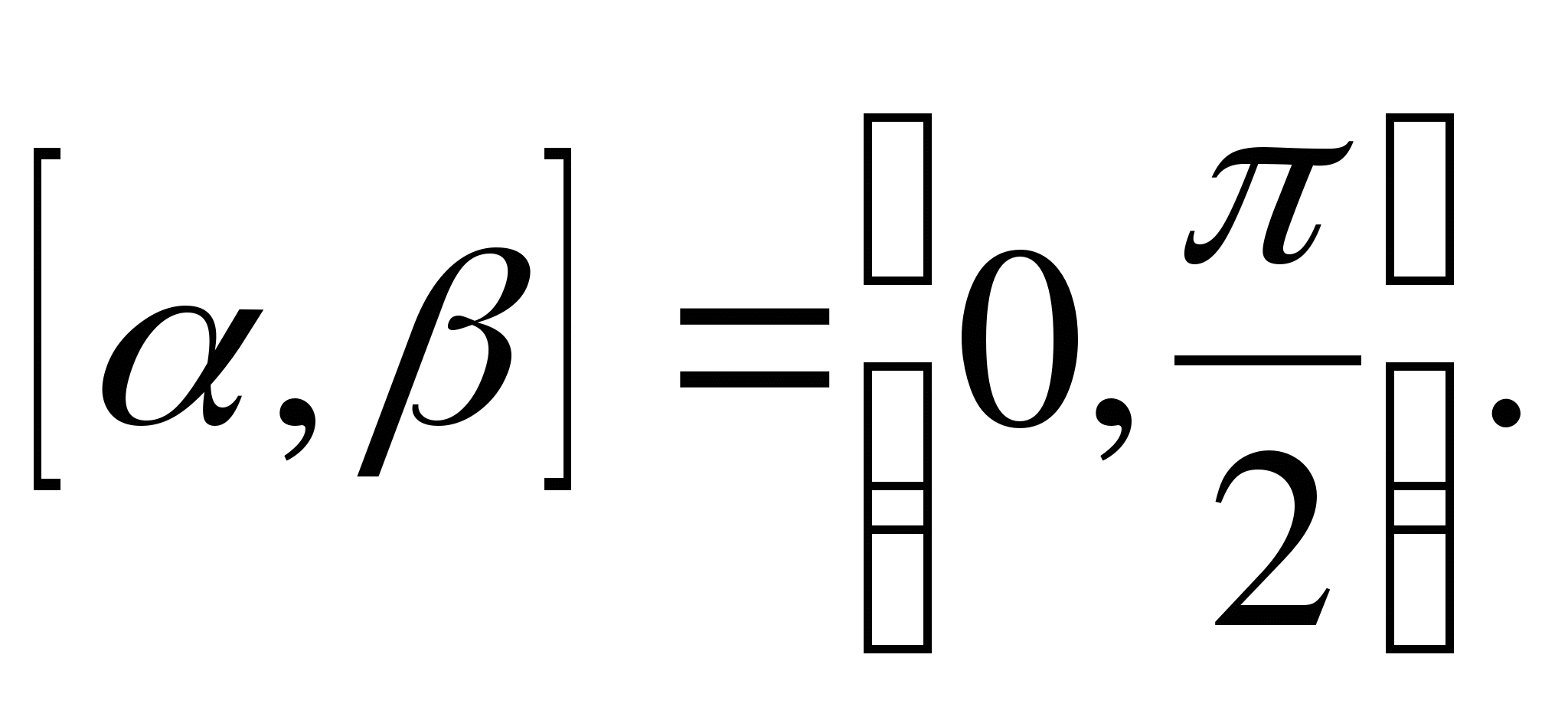да Тогда .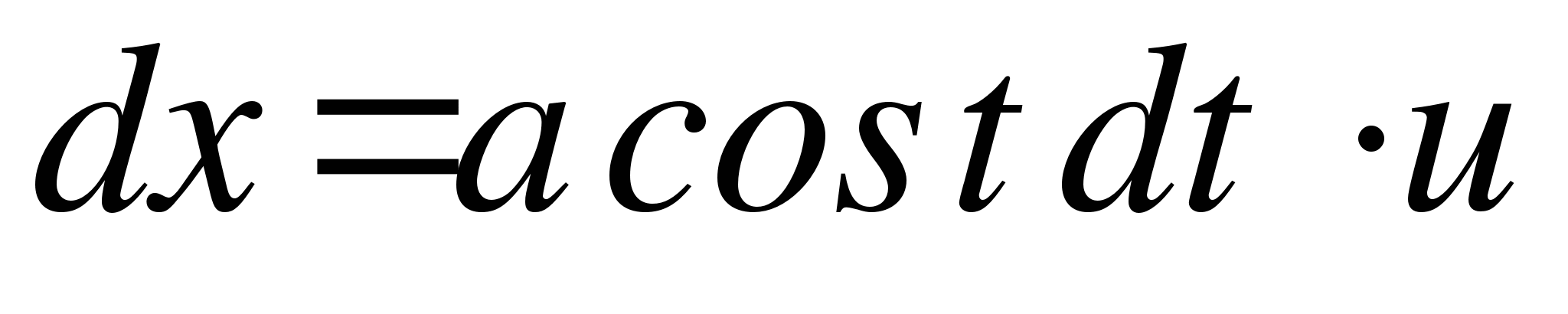

П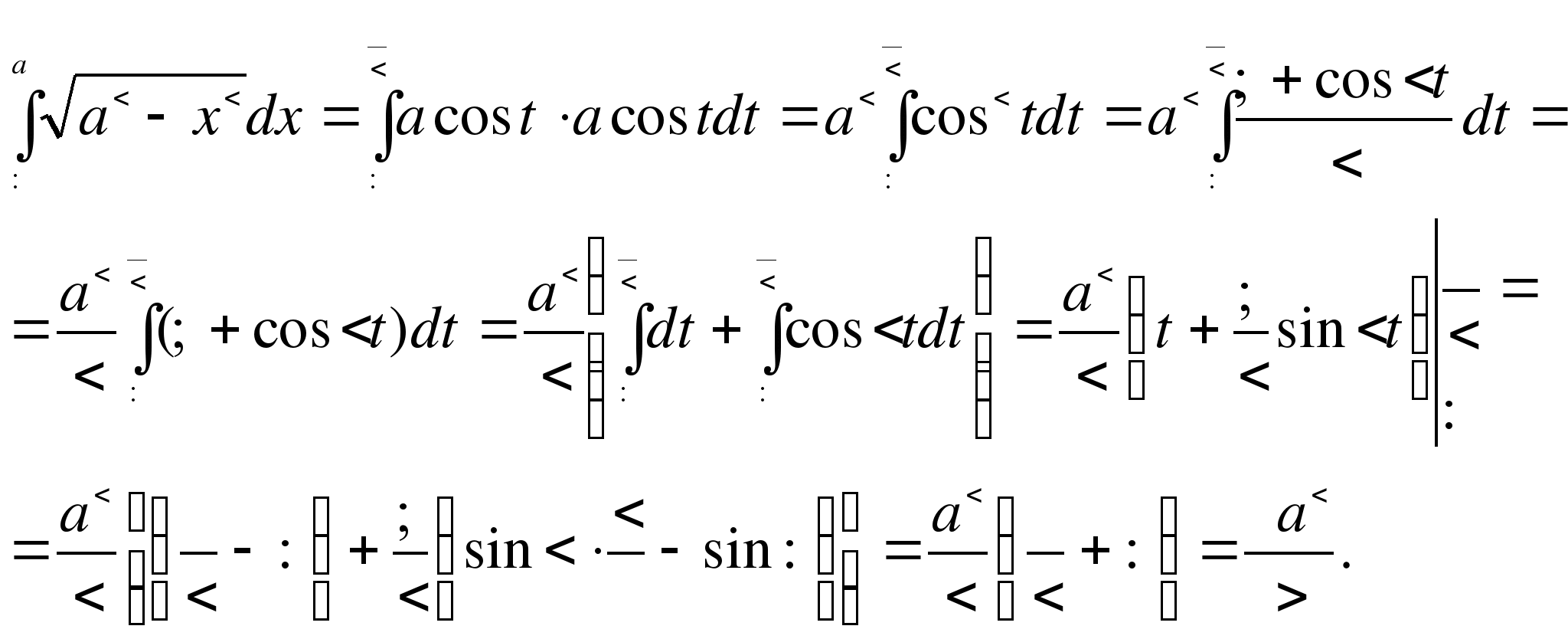о формуле замены переменной, получим:

д) Для вычисления определенного интеграла 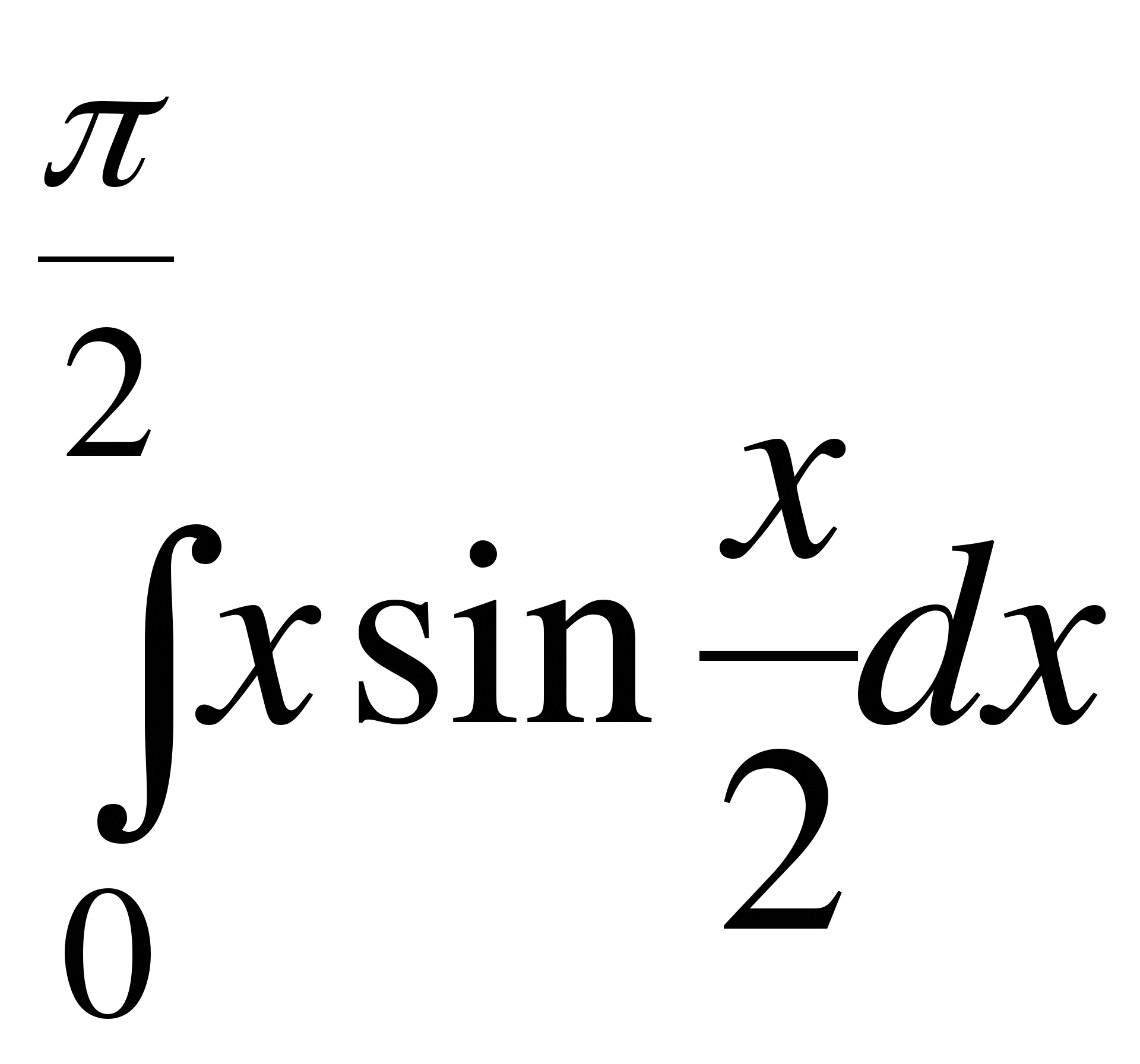, воспользуемся формулой (3) интегрирования по частям в определенном интеграле.

Обозначим

Легко заметить, что функции u = x и v = 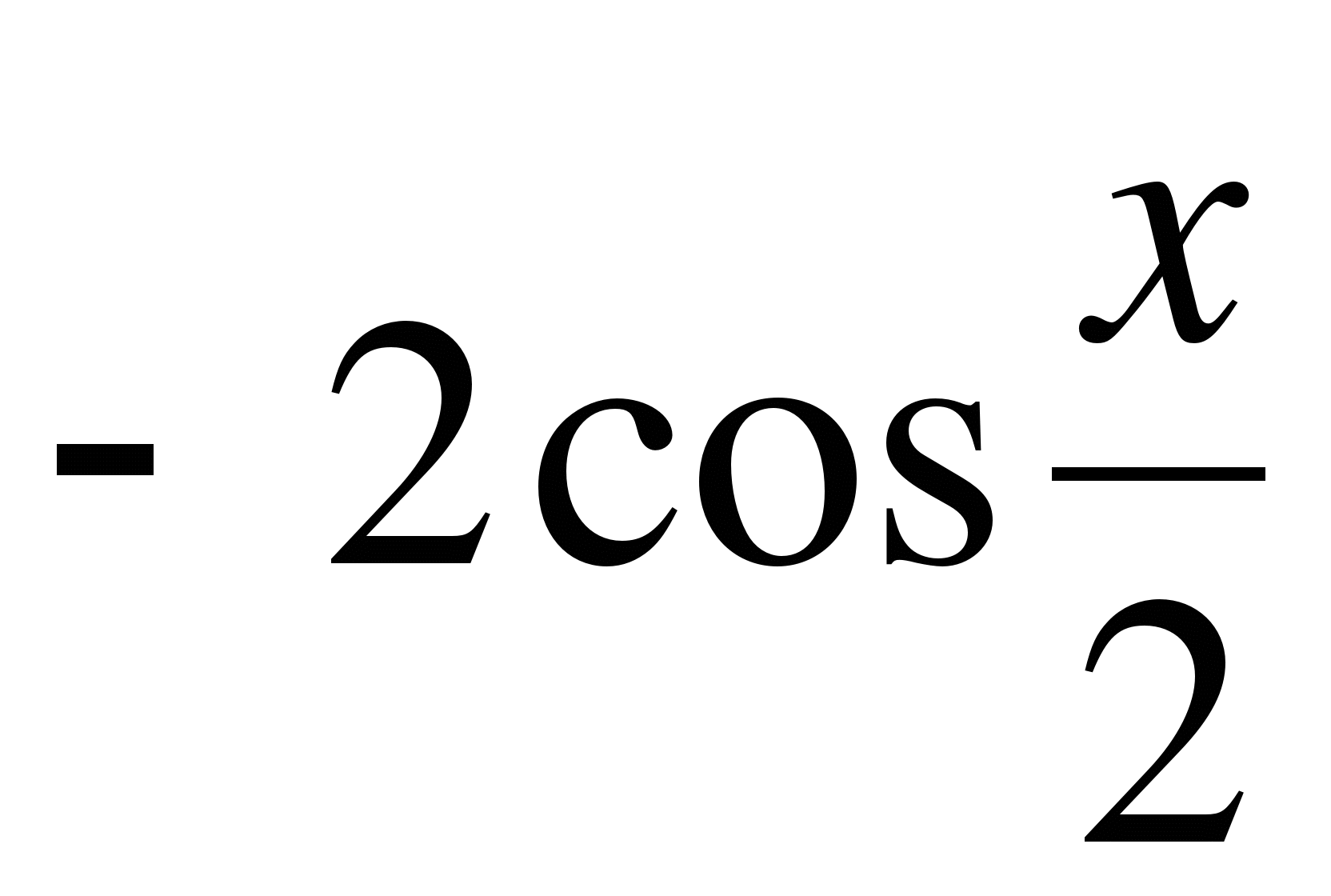- непрерывны в промежутке 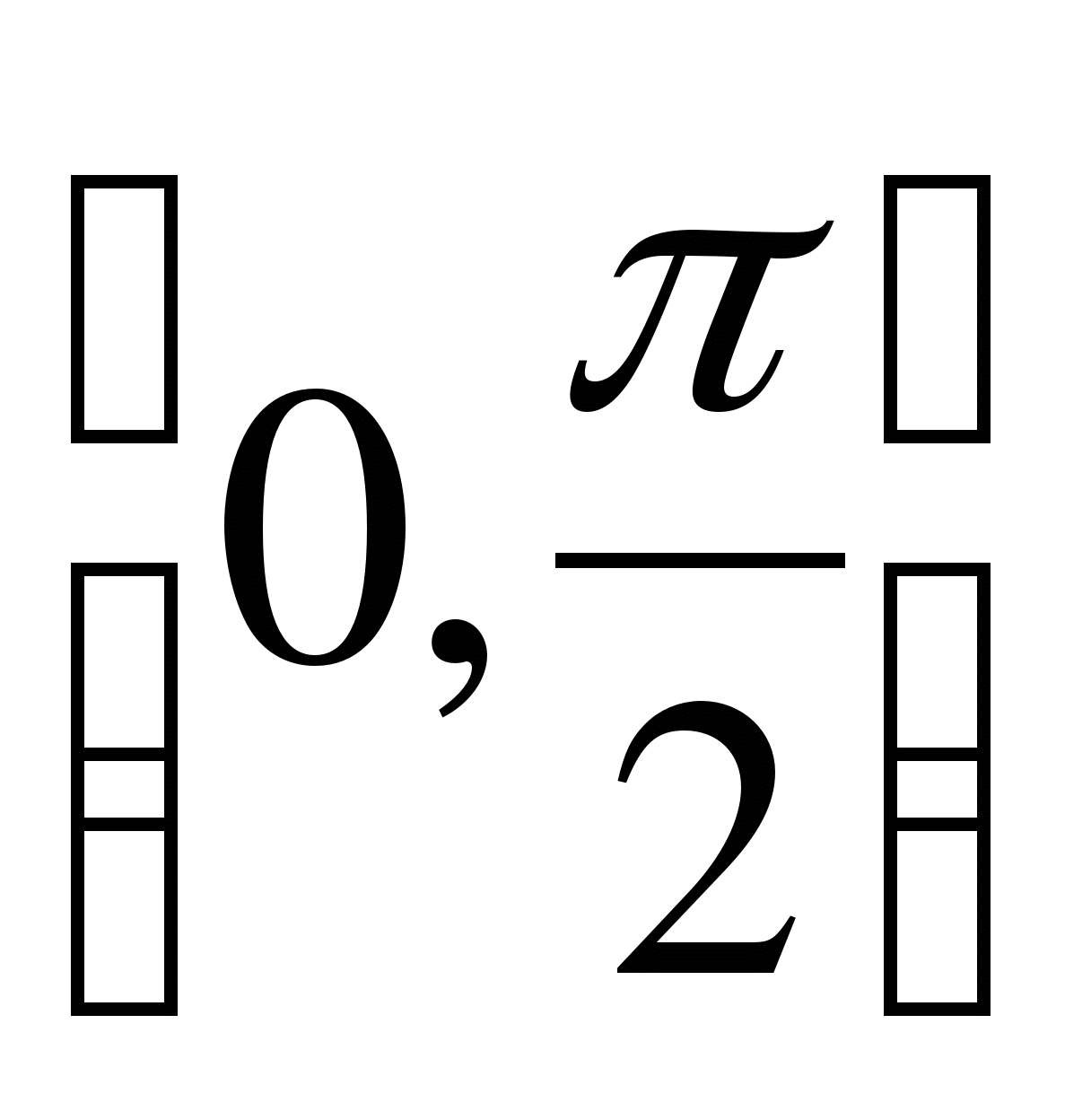и имеют в каждой точке этого промежутка непрерывные производные 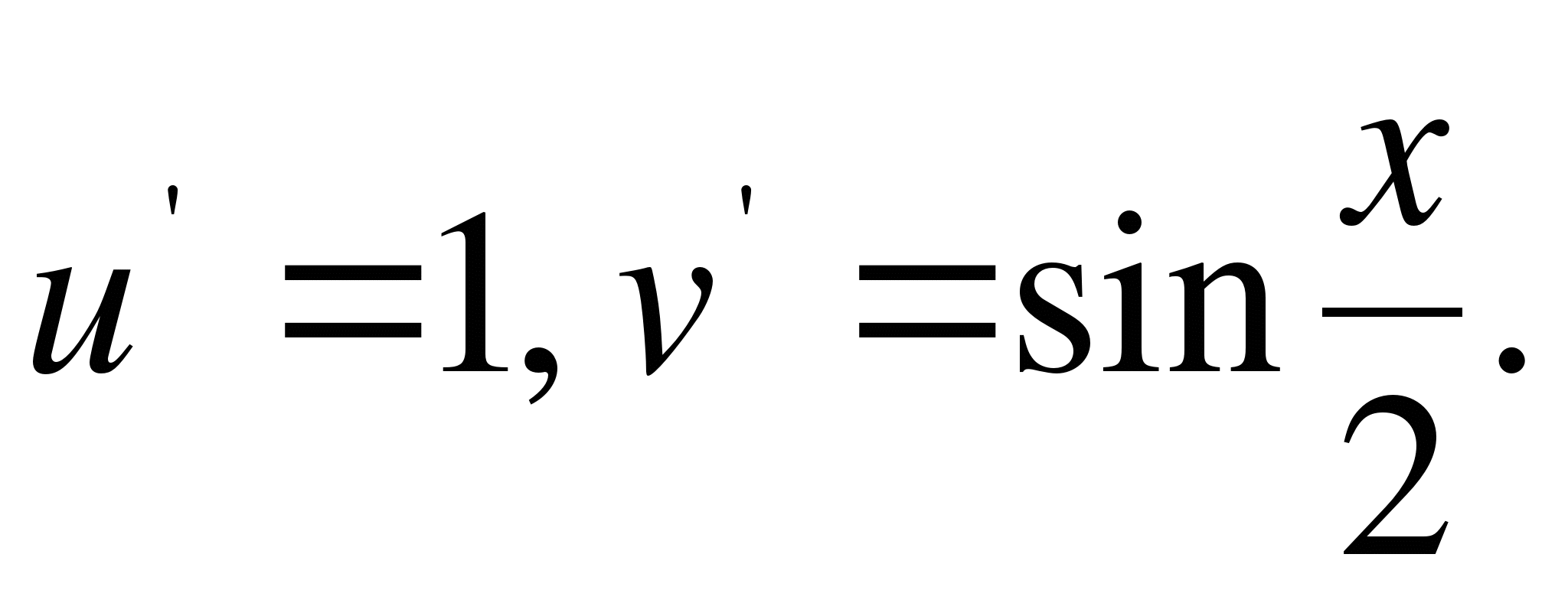Следовательно, по формуле (3) будем иметь:

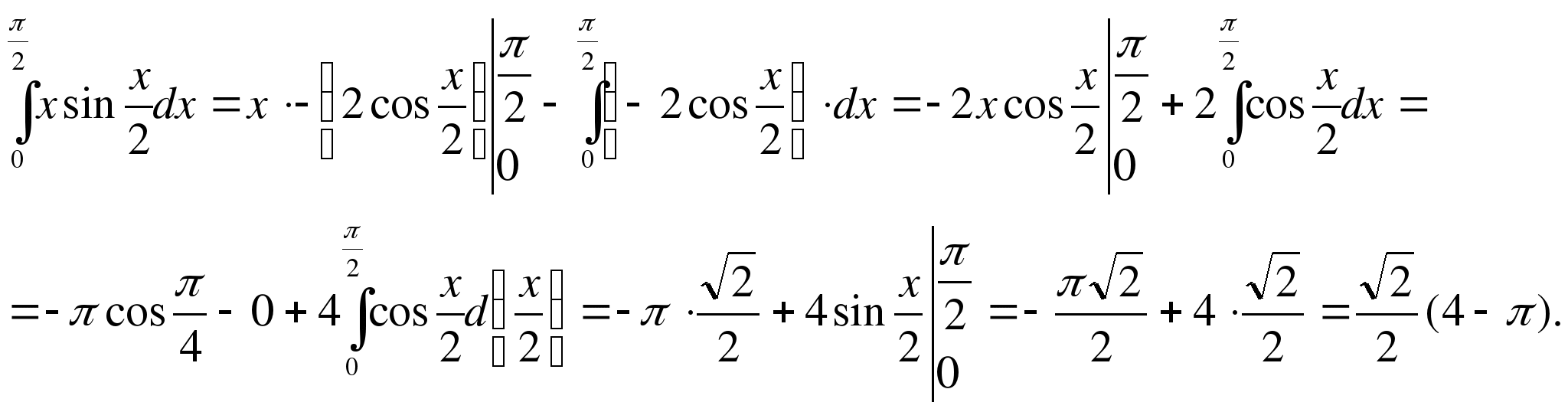
Лабораторная работа №7

Тема: Формула Ньютона – Лейбница. Замена переменной в определенном интеграле. Формула интегрирования по частям.

Теоретические вопросы

1. Объясните равенство 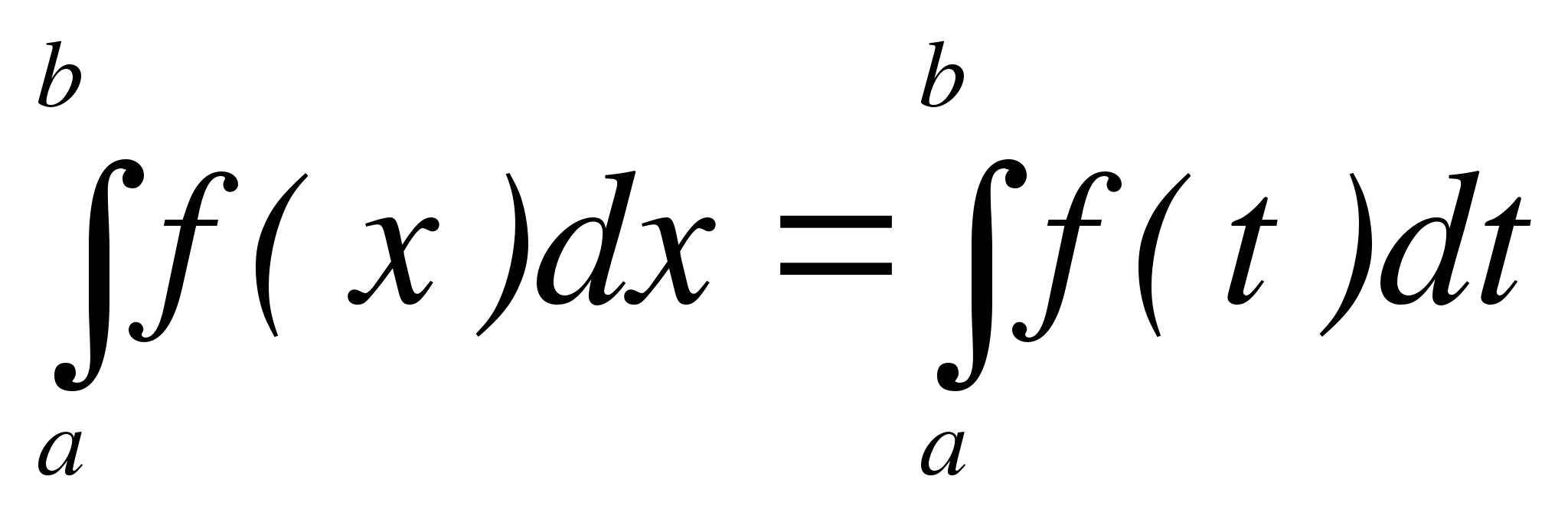, исходя из формулы Ньютона-Лейбница?

2. При каких условиях справедлива формула

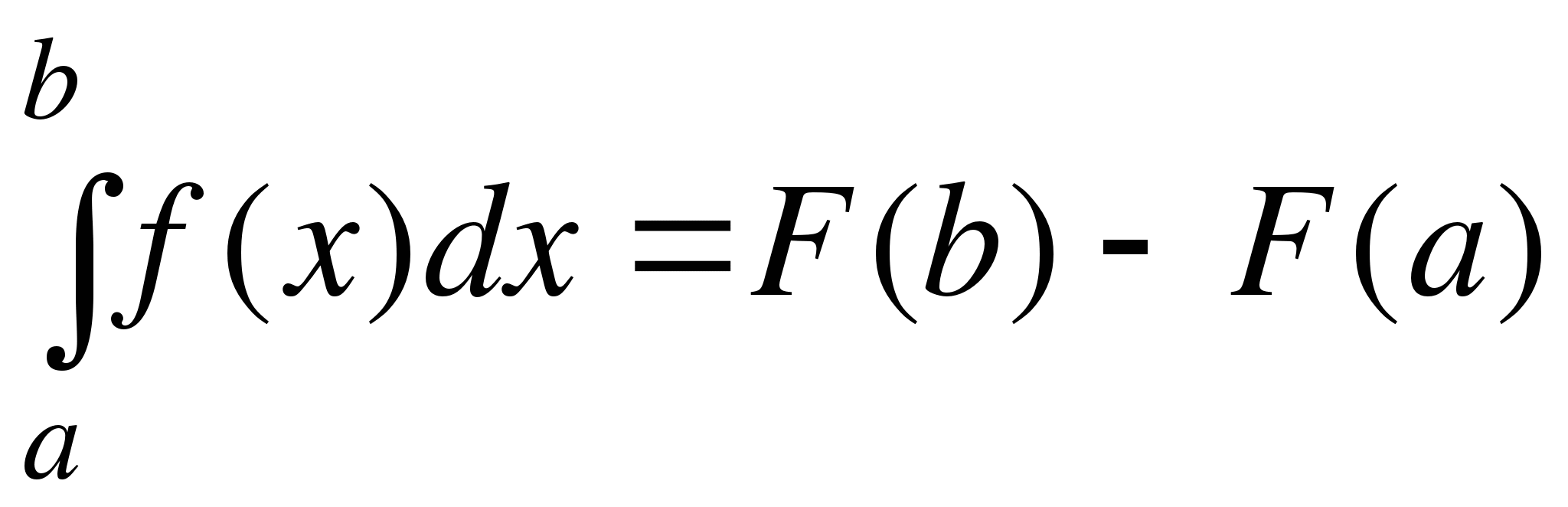
Ньютона – Лейбница? Докажите эту формулу.

3. Почему формула Ньютона - Лейбница называют основной формулой интегрального исчисления?

4. При каких условиях справедлива формула

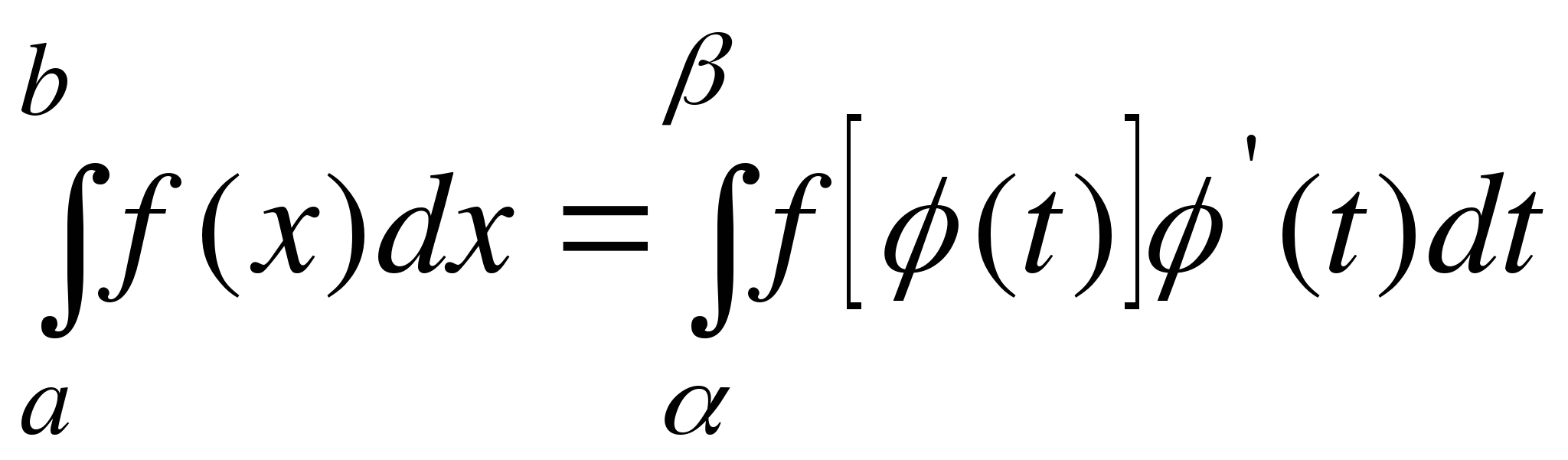
замены переменной в определенном интеграле? как найти новые пределы α и β интегрирования?

5. Почему при замене переменной в определенном интеграле можно не возвращаться к старой переменной?

6. Докажите формулу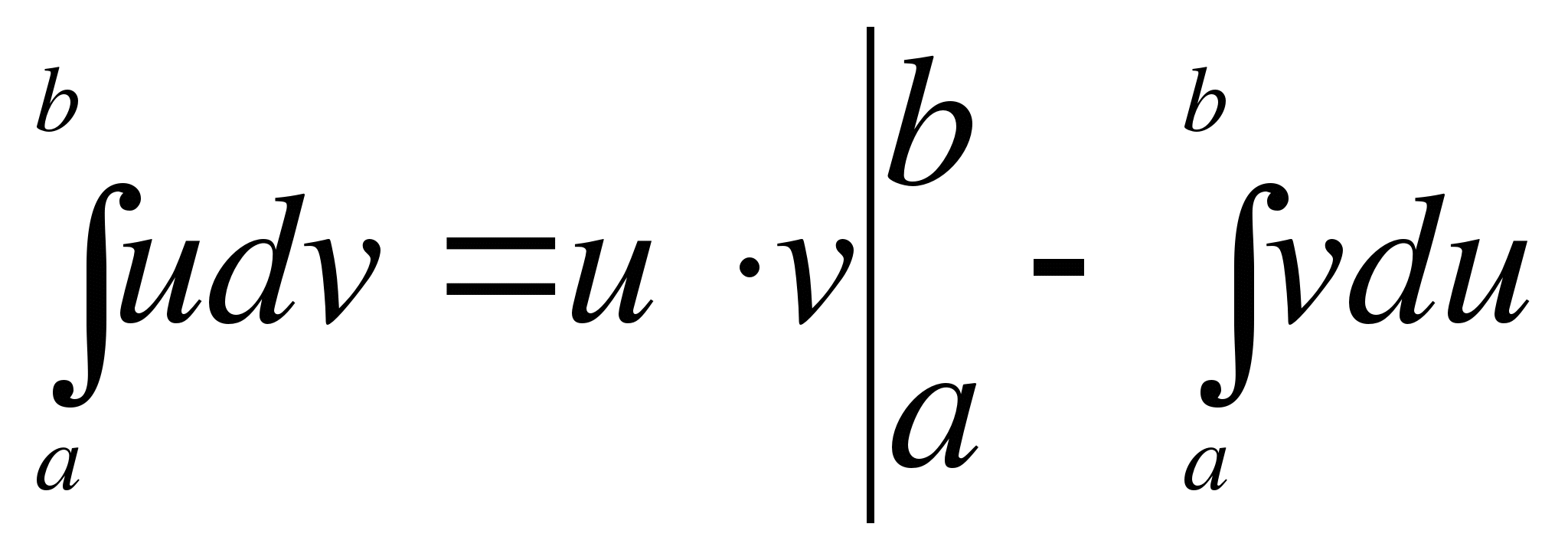 интегрирования по частям в определенном интеграле. При каких условиях она справедлива?

Упражнения

1. Вычислить с помощью формулы Ньютона - Лейбница следующие интегралы:

II. Методом замены переменной вычислить интегралы:

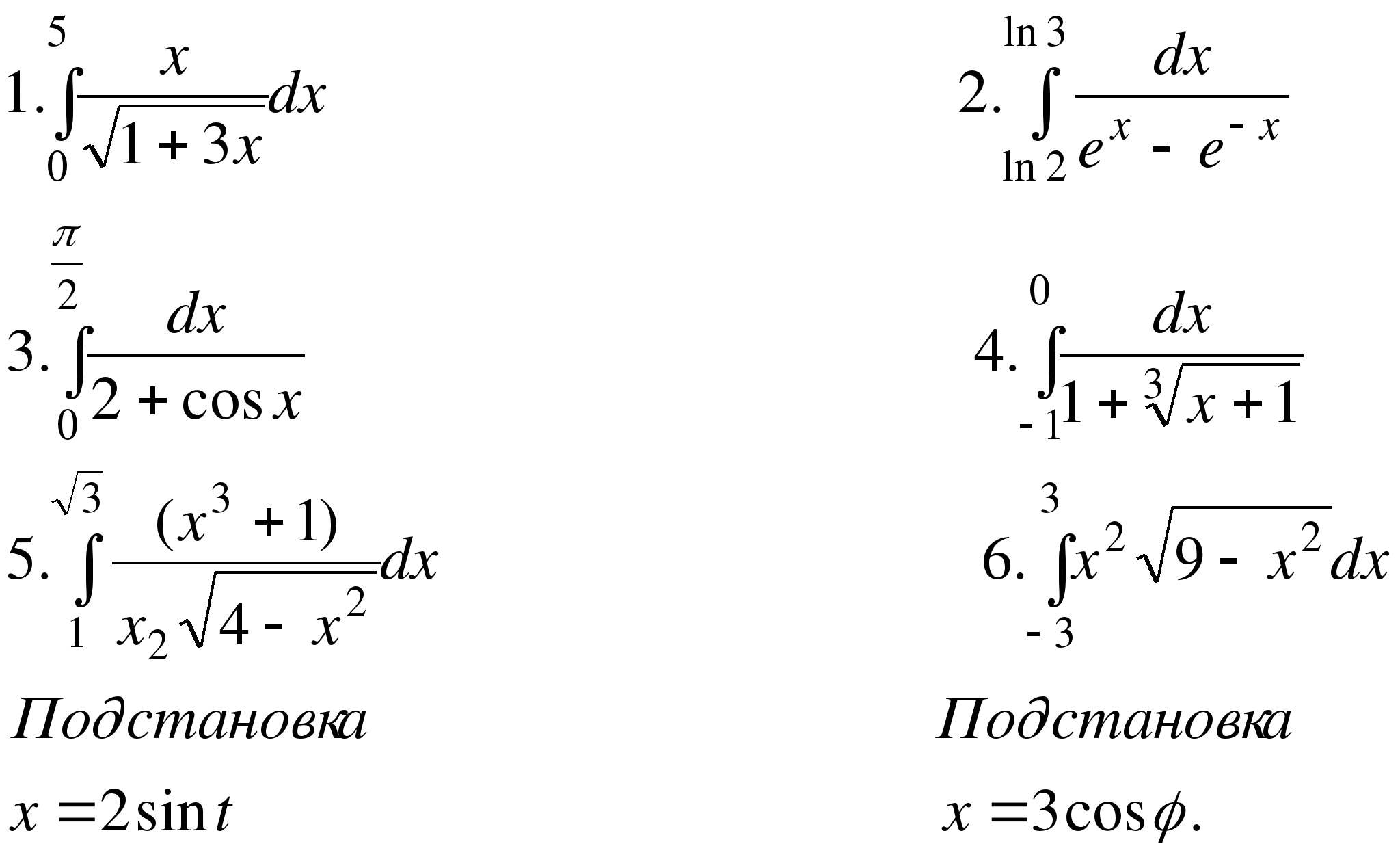
III. С помощью формулы интегрирования по частям вычислить интегралы:

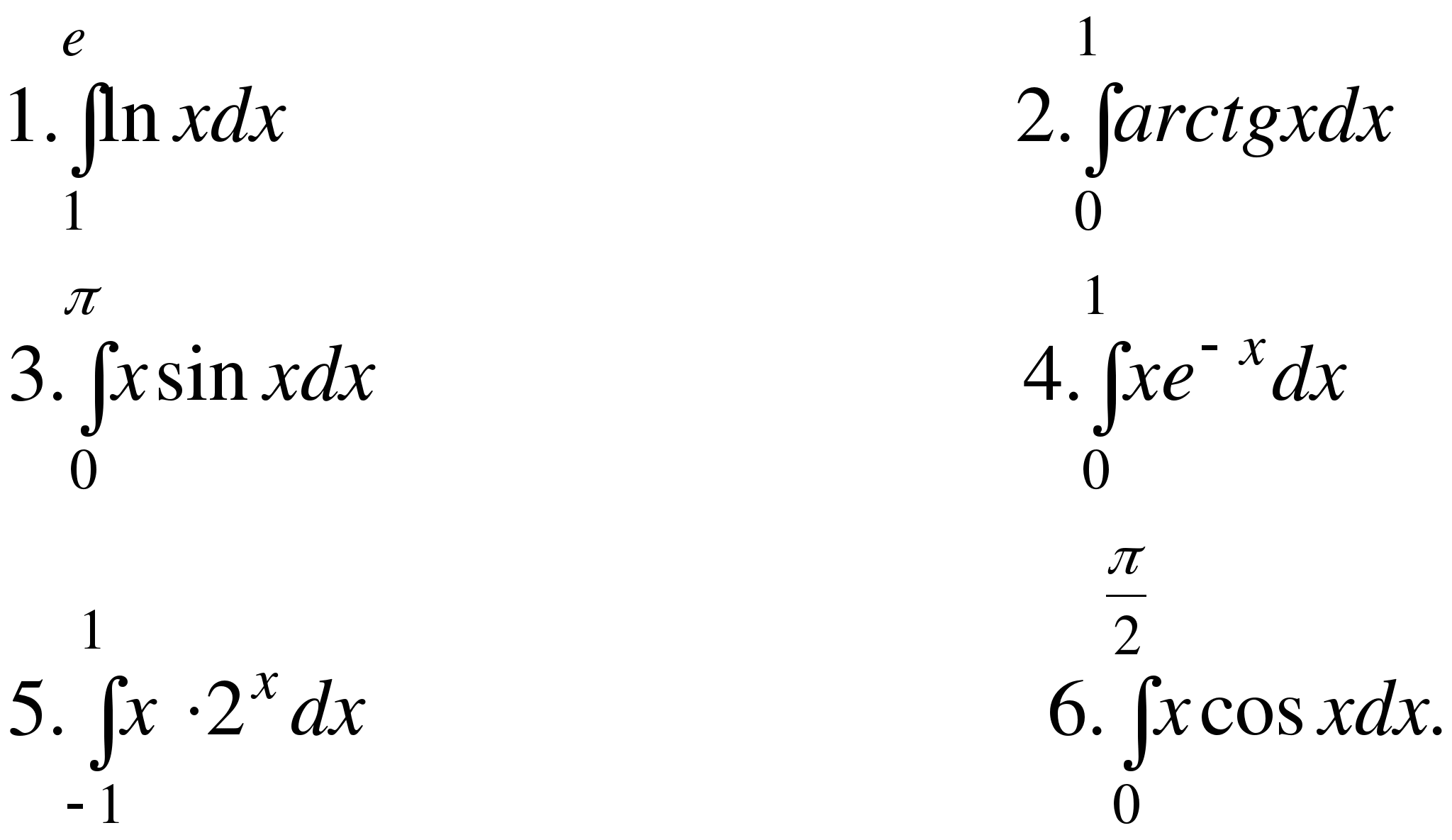
IV.Найти среднее значение функции y=f(x) на отрезке [a,b]:

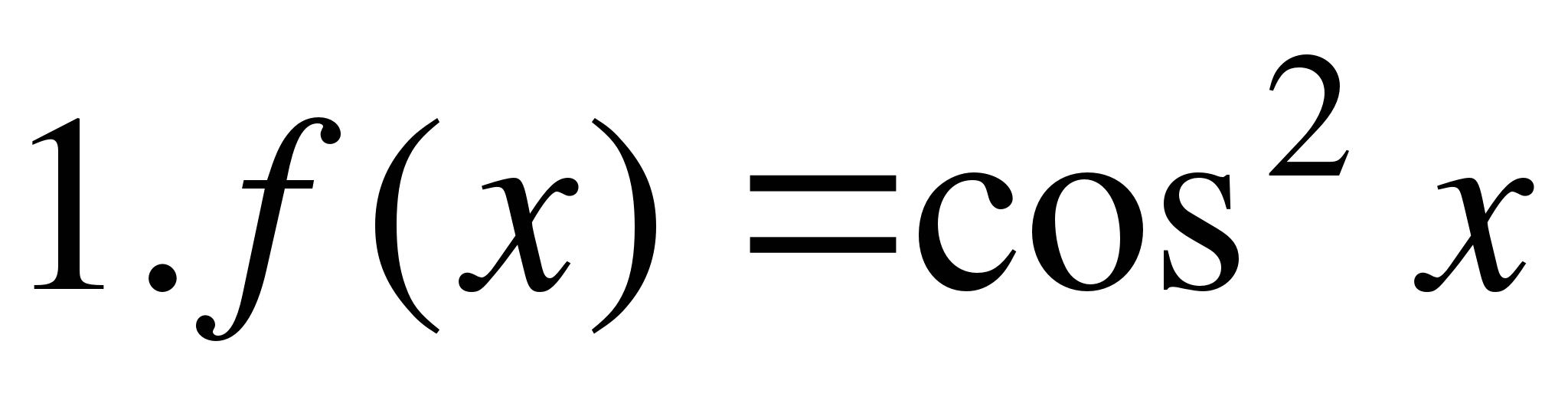на отрезке [0;π];

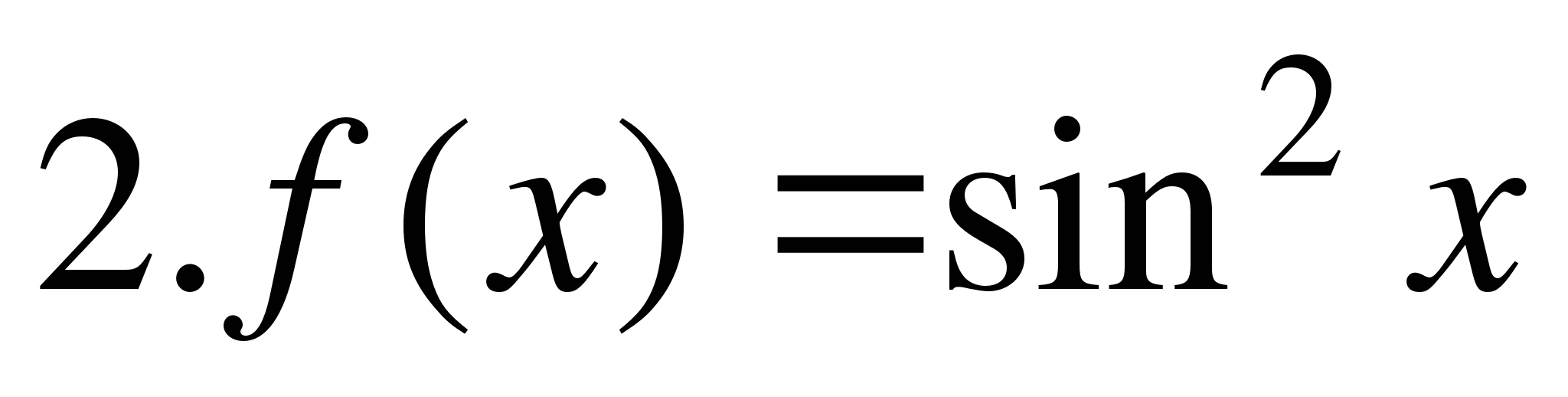на отрезке [0;π];

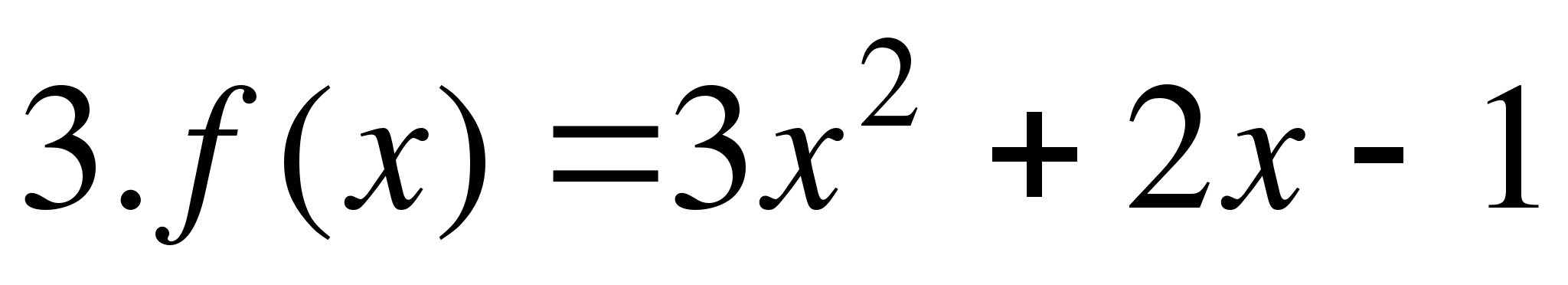на отрезке [1;5];

4.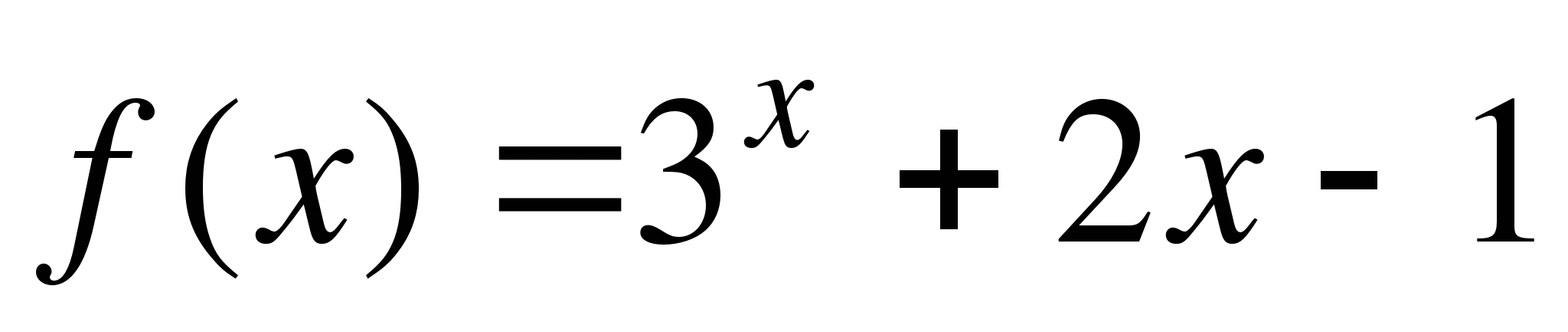 на отрезке [0;3].

§ 9. Несобственные интегралы

В определении определенного интеграла 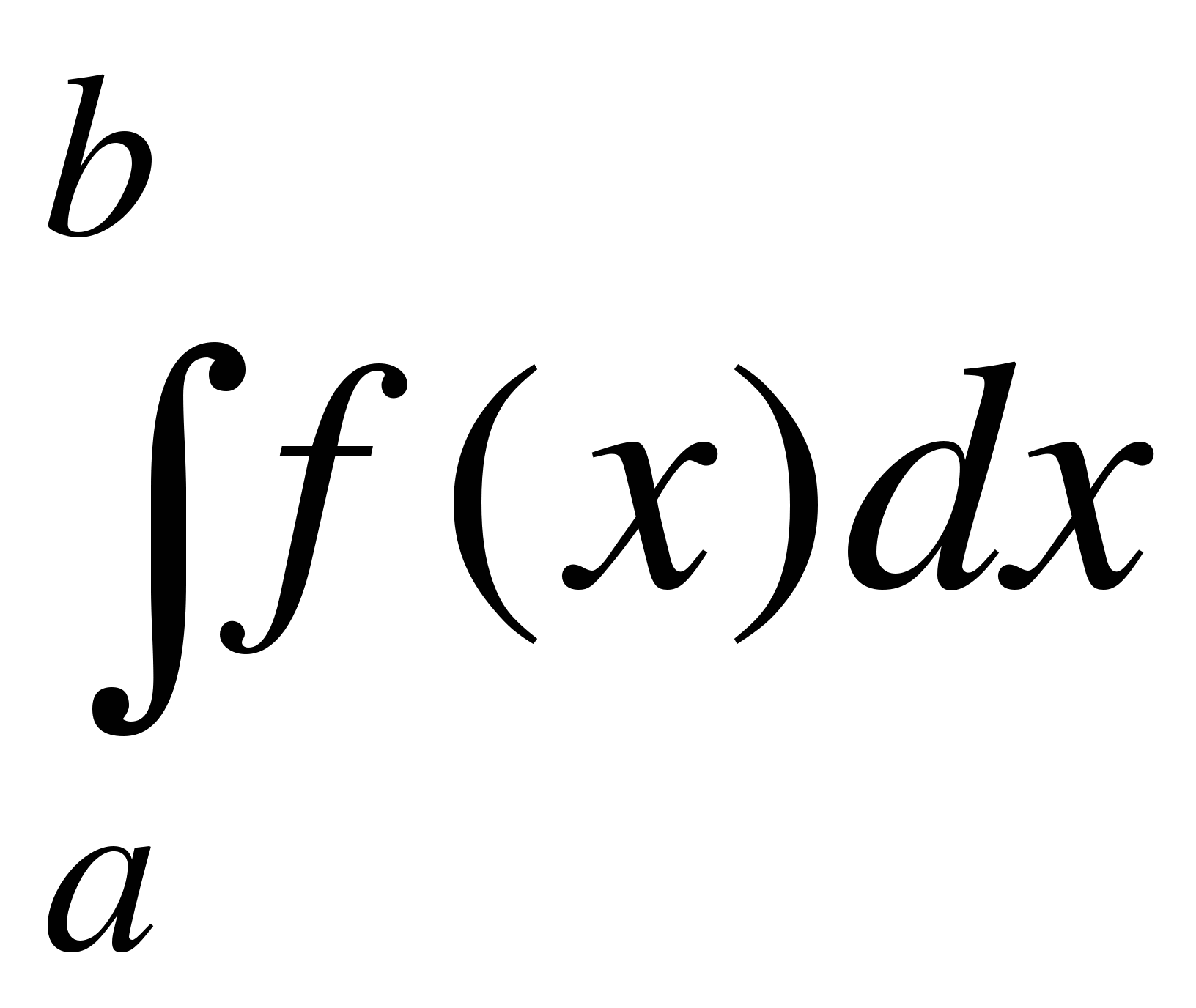мы считали пределы конечными числами, а подинтегральную функцию f(x) – ограниченной в промежутке [a, b]. Поэтому приведенное ранее определение определенного интеграла теряет смысл, если не выполняется хотя бы одно из указанных условий, то есть когда подинтегральная функция неограниченна в промежутке интегрирования или когда промежуток интегрирования бесконечен. Однако и в этих случаях иногда удается обобщить понятие определенного интеграла. В результате такого обобщения и возникает понятие о так называемых несобственных интегралах.

infourok.ru

Смотрите также

• 
  Реферат на тему история вышивки
• 
  Реферат на тему дизельное топливо
• 
  Природные зоны 7 класс реферат
• 
  Опрос как метод исследования реферат
• 
  Надзор за страховой деятельностью реферат
• 
  Мартин лютер реферат по истории
• 
  Реферат на тему раздаточная коробка
• 
  Реферат на тему путешественники россии
• 
  Реферат на тему витамин б
• 
  Интеллектуальная собственность в интернете реферат
• 
  Гален и его учение реферат