 .
.Реферат
по теме:
«Шестое математическое действие»
Выполнила:
ученица 8 класса
Руководитель:
учитель математики
Содержание
1. Введение.
2. С корнем квадратным - сквозь историю.
3. День квадратного корня.
4. Из истории возникновения формулы корней квадратного уравнения.
5. Квадратный корень из числа
6. Основные тождества для квадратных корней
7. Извлечение квадратного корня из произведения, дроби и степени
10. Геометрические приложения.
11. Заключение.
12. Список литературы.
Введение
«Многие вещи нам не понятны не потому,
что наши понятия слабы; но потому, что
сии вещи не входят в круг наших понятий.»
Козьма Прутков
«Мысли и афоризмы», № 66.
В ходе решения некоторых математических задач приходится оперировать с квадратными корнями, поэтому важно знать правила действий с ними, научиться преобразовывать выражения, их содержащие, а также знать историю возникновения квадратных корней.
Цель настоящего реферата – изучение правил действий с квадратными корнями и способов преобразования выражений их содержащих. Для извлечения квадратного корня существуют таблицы квадратов. Для двухзначных чисел, можно разложить число на простые множители и извлечь квадратный корень из произведения. Таблицы квадратов бывает недостаточно, извлечение корня разложением на множители - трудоёмкая задача, которая тоже не всегда приводит к желаемому результату. Я постаралась найти способы, которые бы позволили извлечь квадратный корень в любом случае.
С корнем квадратным - сквозь историю
Начиная с XIII в. итальянские и другие европейские математики обозначали корень латинским словом «Radix» («корень») или сокращённо R. В XV в. Н. Шюке писал: R212 вместо 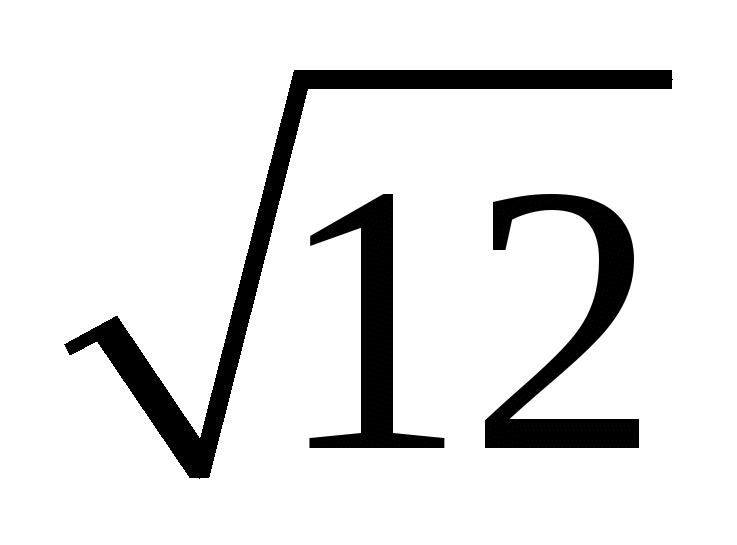 .
.
Ныне применяемый знак корня произошёл от обозначения, которое применяли немецкие математики XV-XVI вв., называвшие алгебру «Косс», а алгебраистов «коссистами». (Математики XII-XV вв. писали свои произведения на латинском языке. Они называли неизвестное res – вещь. Итальянские математики перевели res словом cosa. Последний термин был заимствован немцами, откуда и появились «Косс» и «коссисты».)
Впоследствии образовался знак ˅ , близкий к современному символу корня, но без верхней черты. Этот знак встречается впервые в немецкой алгебре «Быстрый и красивый счёт при помощи искусных правил алгебры, обычно называемых Косс», изданной в 1525 г. в Страсбурге. Автором этой книги был уроженец Чехии, учитель математики в Вене Криштоф Рудольф из Явора (княжество, принадлежавшее в то время богемскому королевству). Книга пользовалась успехом и переиздавалась на протяжении XVI в. и вплоть до 1615 г. Знаком корня пользовались в XVI в. М. Штифель, С. Стевин и др.
В 1626 г. нидерландский математик А. Жирар, сочетая знак Рудольфа с

 2 3
2 3
показателями Шюке, ввёл близкое к современному обозначение , и т.д. Это обозначение стало вытеснять знак R. Однако долгое время писали, например a+b ( вместо современного 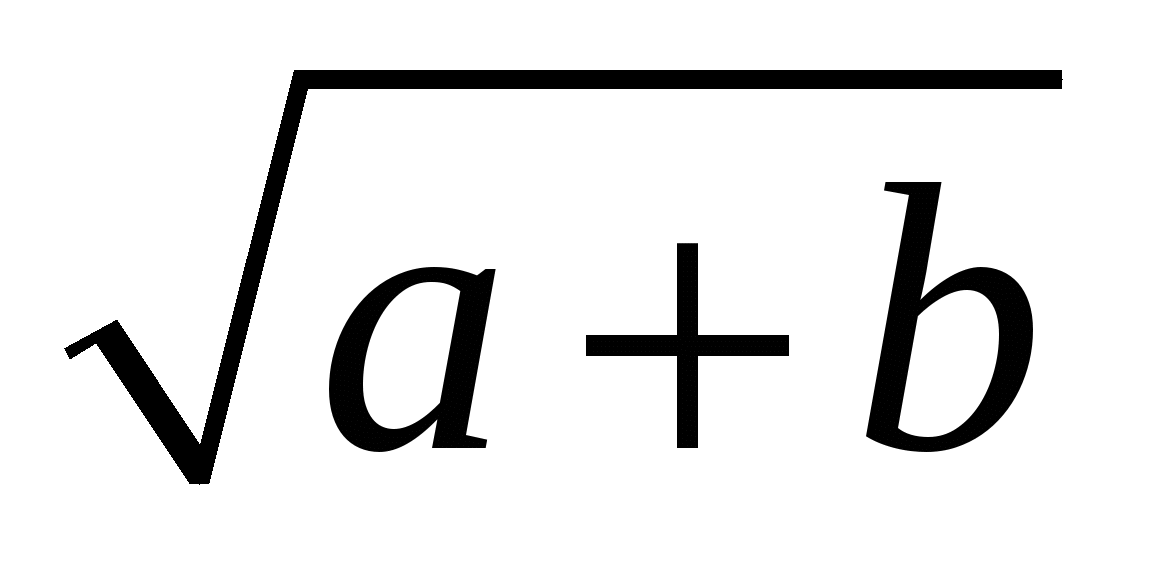 ). Лишь в 1637 г. Рене Декарт соединил знак корня с горизонтальной чертой, применив в своей «Геометрии» современный знак корня
). Лишь в 1637 г. Рене Декарт соединил знак корня с горизонтальной чертой, применив в своей «Геометрии» современный знак корня 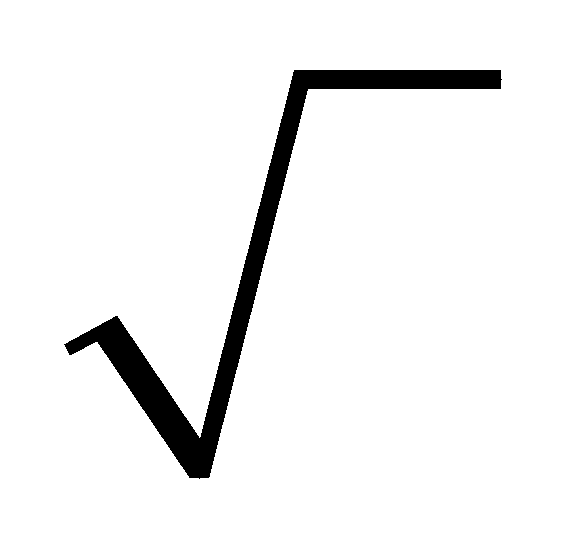 .
.

 Однако запись у Декарта несколько отличается от современной. У него, например, записано:
Однако запись у Декарта несколько отличается от современной. У него, например, записано: 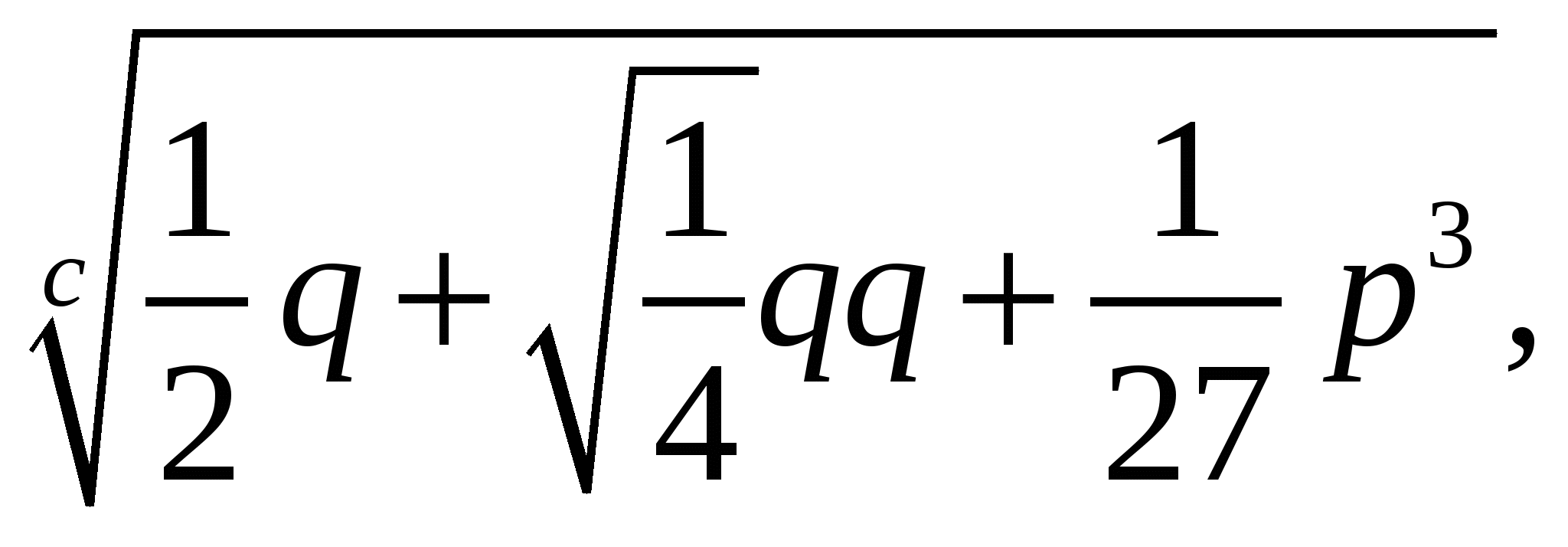
где буква с поставлена вместо латинского слова cubicus, что означает кубический. В современной записи это выражение будет выглядеть так: 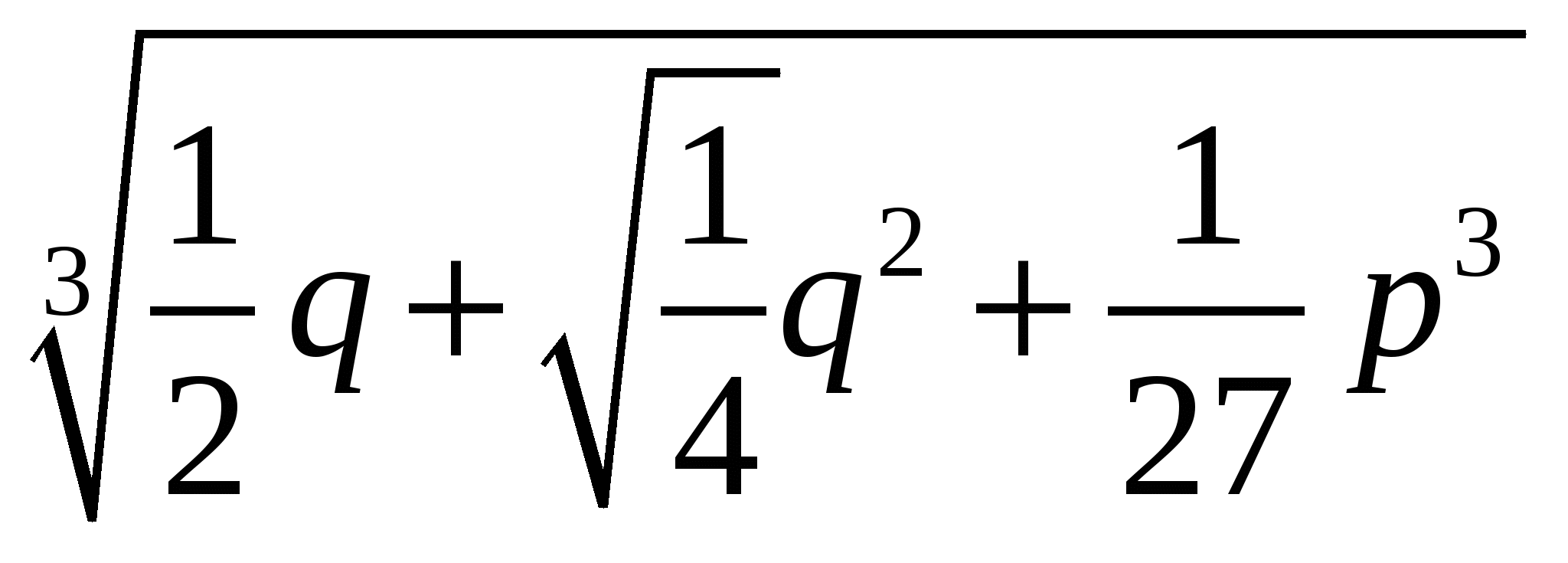 .
.
Ещё ближе к современному применял обозначение радикала Ньютон в «Универсальной арифметике» (1685 г.). Впервые запись корня, точно совпадающая с ныне принятой, встречается в книге француза Ролля «Руководство алгебры», написанной в 1690 г. Современный знак корня окончательно вошёл во всеобщее употребление лишь в начале XVIII в. 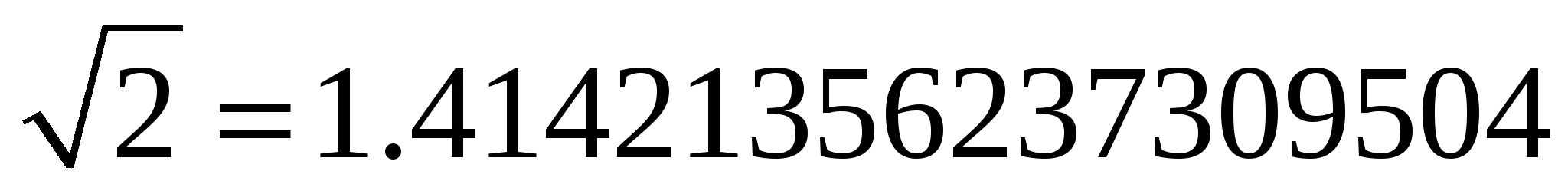

Вавилонская табличка (около 1800—1600 г. до н. э.) с вычислением 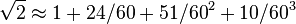
Интерес к квадратному корню из двух возник давно. В собрании Вавилонских исторических ценностей, хранящемся в Йельском университете (Нью-Хейвен, штат Коннектикут), есть круглая глиняная табличка, относящаяся к 1750 г. до нашей эры. На ней изображен рассеченный диагоналями квадрат и четкими клинописными знаками выписаны три цифры. Когда их прочли, стало ясно, что без малого четыре тысячи лет назад в Вавилоне умели определять диагональ квадрата по его стороне, умножая ее длину на квадратный корень из двух. Цифры на табличке как раз и представляют собой эту величину, выведенную с точностью до пятого знака: 1, 24, 51, 10. Ну что ж, это совсем неплохое приближение к истине, ведь
1 + 24/60+51/602+10/603=1,41421.
Невольно хочется повторить: это подсчитано в XVIII веке до нашей эры!
За пять столетий до нашей эры школа Пифагора сделала одно из величайших математических открытий. Пифагорейцы пытались доказать, что любое число может быть выведено путем сложения, вычитания, умножения и деления положительных целых чисел. А корень квадратный из двух — число иррациональное и конечным числом таких операций не получается. Это и было обнаружено последователями Пифагора. Однако они любили всяческую секретность и «законспирировали» свое открытие на долгие годы.
Его доказательство впервые появилось в «Началах» Евклида около 300 г. до нашей эры. А затем примерно в 140 г. нашей эры Теону из Смирны удалось разработать интереснейший алгоритм вычисления корня квадратного из двух; этот алгоритм стал предтечей всей методики использования непрерывных дробей.
Еще ученые Вавилона (более 4000 лет назад) умели находить приближенное значение квадратного корня из любого натурального числа. Правило, применявшееся в Вавилоне, таково: Вавилонские математики (II тысячелетие до н. э.) разработали для извлечения квадратного корня особый численный метод. Начальное приближение для 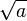 рассчитывалось исходя из ближайшего к корню (в меньшую сторону) натурального числа
рассчитывалось исходя из ближайшего к корню (в меньшую сторону) натурального числа 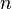 . Представив подкоренное выражение в виде:
. Представив подкоренное выражение в виде: 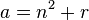 , получаем:
, получаем: 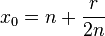 , затем применялся итеративный процесс уточнения, соответствующий методу Ньютона:
, затем применялся итеративный процесс уточнения, соответствующий методу Ньютона:
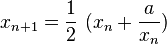
Итерации в этом методе очень быстро сходятся. Для 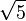 , например,
, например, 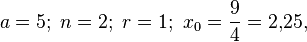 и мы получаем последовательность приближений:
и мы получаем последовательность приближений:
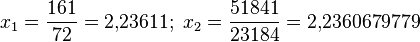
В заключительном значении верны все цифры, кроме последней.
Аналогичные задачи и методы встречаются в древнекитайской «Математике в девяти книгах». Древние греки сделали важное открытие:  — иррациональное число. Детальное исследование, выполненное Теэтетом Афинским (IV век до н. э.), показало, что если корень из натурального числа не извлекается нацело, то его значение иррационально.
— иррациональное число. Детальное исследование, выполненное Теэтетом Афинским (IV век до н. э.), показало, что если корень из натурального числа не извлекается нацело, то его значение иррационально.
Чтобы извлечь корень из натурального числа с, его разлагают на сумму а2 + b (число а должно быть наибольшим таким, что а2 < с), тогда квадратный корень из с приближенно вычисляют по формуле:
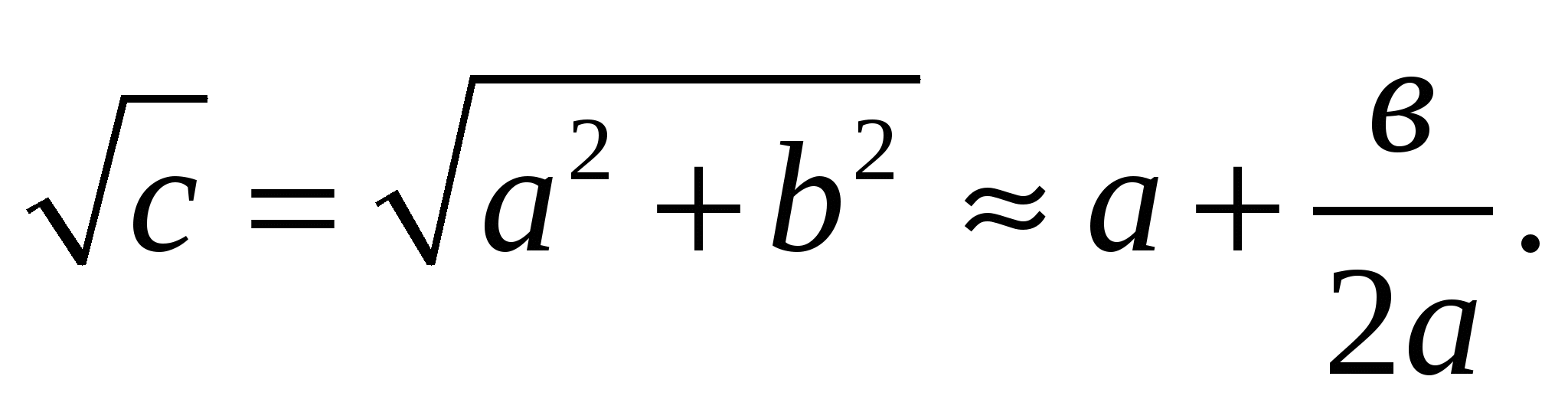
Например,
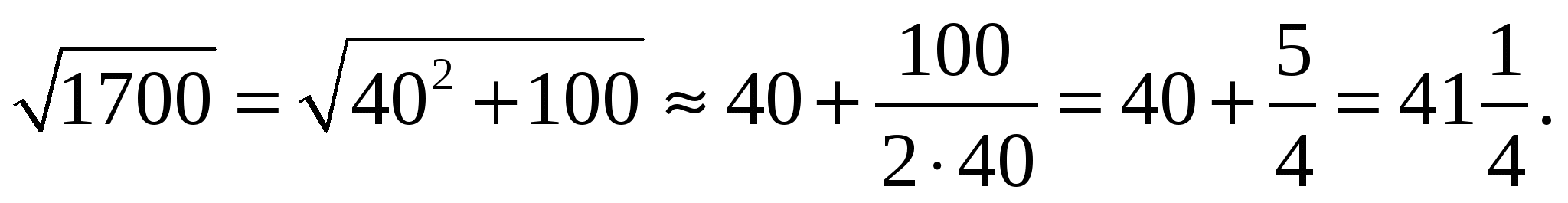
Грекам был известен вавилонский метод приближенного нахождения квадратного корня. Например, у Герона Александрийского (около 1 в.) написано:
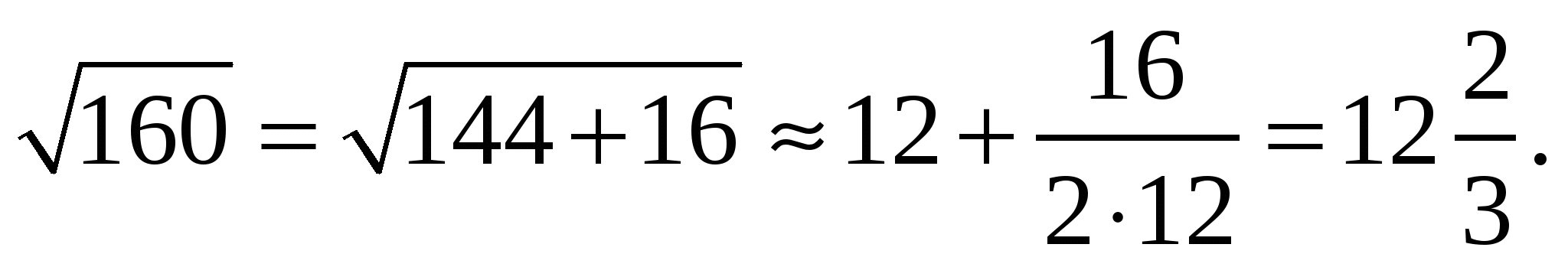
День квадратного корня

03.03.2009
«День квадратного корня» отмечают математики Калифорнии. Третье число третьего месяца девятого года, считают они, в «переводе» на математический язык означает «трижды три девять», или же «три как квадратный корень из девяти».
Учитель математики из города Редвуд Рон Гордон даже организовал специальное соревнование. Победитель получит, естественно, 339 долларов.
Дочь учителя создала специальный сайт в Интернете, где фанаты «Дня квадратного корня», которых, как оказалось, сотни, предлагают свои варианты празднования этой даты.
В частности, самыми популярными «атрибутами» математического праздника являются вареные кубики из корнеплодов и выпечка в форме математического знака квадратного корня.
Каждое столетие имеет в своих календарных «закромах» 9 дней квадратного корня. В ХХI веке предыдущий раз такой день наступал 2 февраля 2004 года (2–2-4). Следующего же придется ждать 7 лет: он наступит 4 апреля 2016 года (4–4-16). А в прошлом, 2009 году, случилась полностью «квадратная» дата  01.04.09, 16:25. Она встречается намного реже, чем другие дни квадратных корней.
01.04.09, 16:25. Она встречается намного реже, чем другие дни квадратных корней.
Из истории возникновения формулы корней квадратного уравнения
Задачи на квадратные уравнения встречались уже в 499 г. в Древней Индии. Часто они были в стихотворной форме. Вот одна из задач знаменитого индийского математика XII века Бхаскары:
«Обезьянок резвых стаяВ cласть поевши развлекалась,Их в квадрате часть восьмаяНа поляне забавлялась,А 12 по лианам …Стали прыгать, повисая,Сколько было обезьянок,Ты скажи мне, в этой стае?»
Уже в то время он знал о двузначности корней квадратных уравнений:
(x/8)2 + 12 = x
Формулы решения квадратных уравнений в Европе были впервые изложены в “Книге абака”, написанной в 1202 году итальянским математиком Леонардом Фибоначчи. И лишь в XVII веке, благодаря трудам Жирара, Декарта, Ньютона и других ученых, способ решения квадратных уравнений принимает современный вид.
Квадратный корень из числа
Зная время t, можно найти путь при свободном падении по формуле: 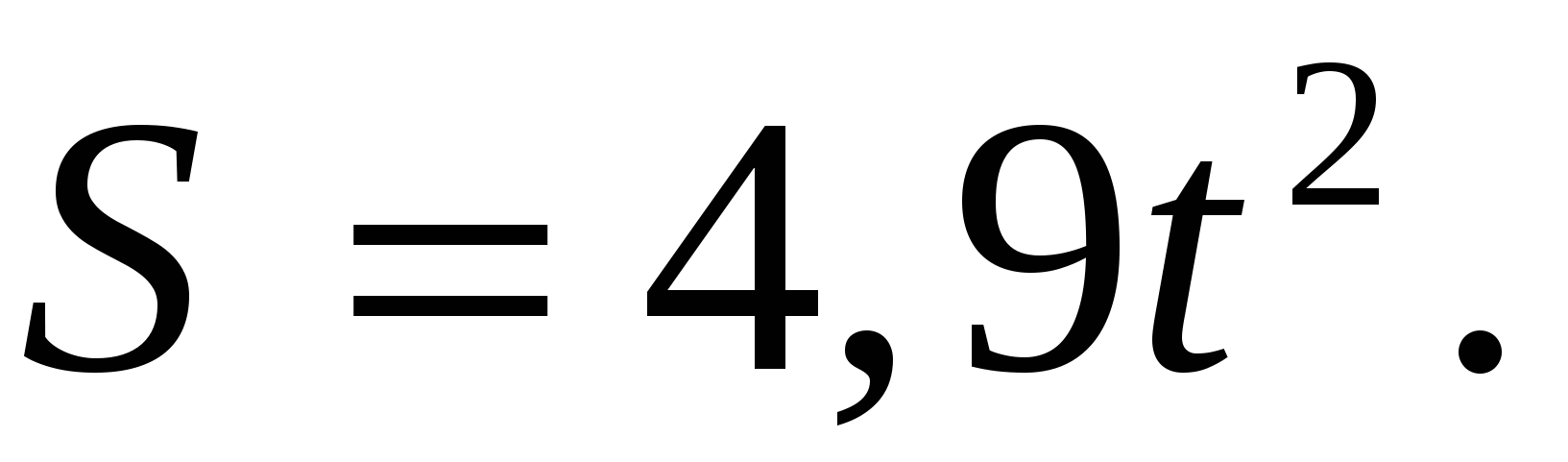 Решим обратную задачу.
Решим обратную задачу.
Задача. Сколько секунд будет падать камень, сброшенный с высоты 122,5 м?
Чтобы найти ответ, нужно решить уравнение  Из него находим, что
Из него находим, что  Теперь осталось найти такое положительное число t, что его квадрат равняется 25. Этим числом является 5, так как
Теперь осталось найти такое положительное число t, что его квадрат равняется 25. Этим числом является 5, так как 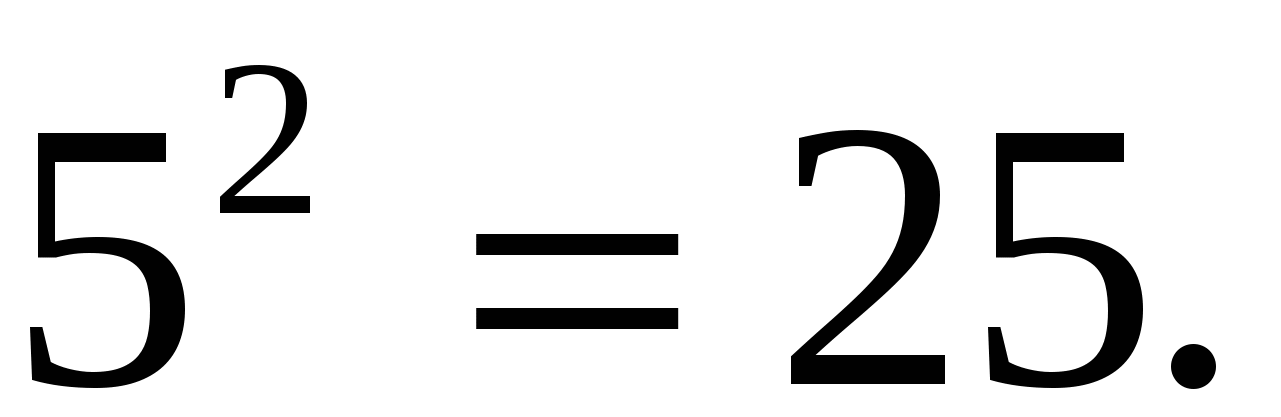 Значит, камень будет падать 5 с.
Значит, камень будет падать 5 с.
Искать положительное число по его квадрату приходится и при решении других задач, например при отыскании длины стороны квадрата по его площади. Введем следующее определение:
Определение. Неотрицательное число, квадрат которого равен неотрицательному числу а, называется квадратным корнем из а. Это число обозначают 
Таким образом 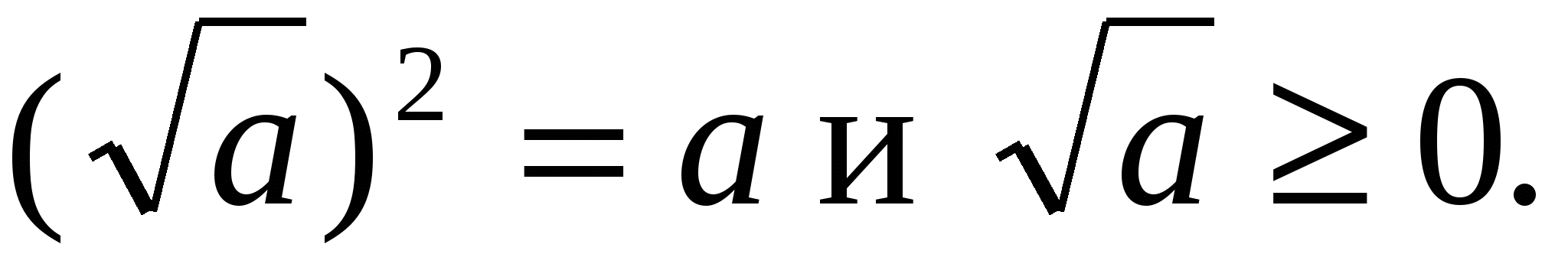
Пример. Так как
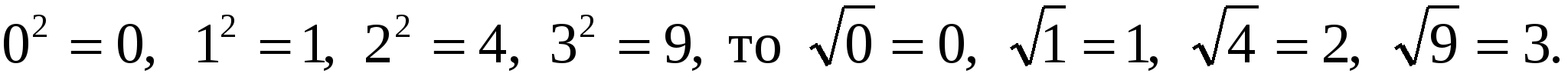
Из отрицательных чисел нельзя извлекать квадратные корни, так как квадрат любого числа или положителен, или равен нулю. Например, выражение 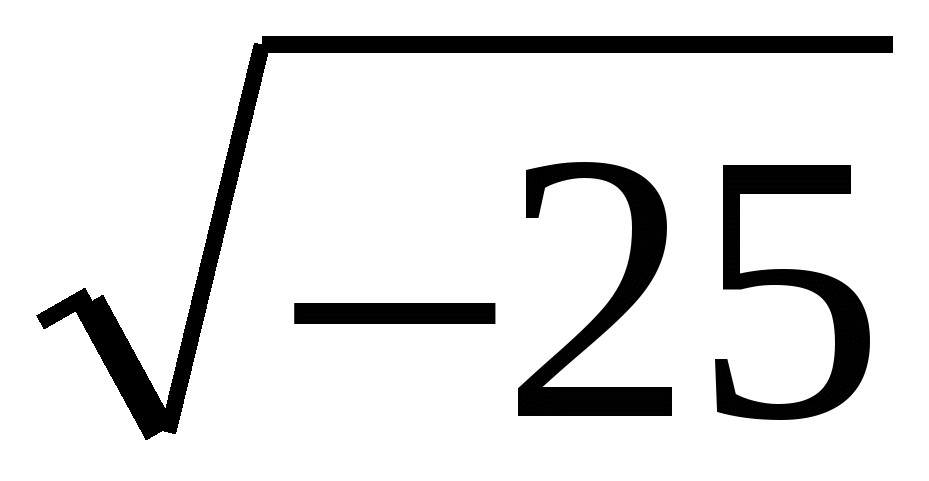 не имеет числового значения.
не имеет числового значения.
В записи  знак
знак  называют знаком радикала (от латинского "радикс" - корень), а число а - подкоренным числом. Например, в записи
называют знаком радикала (от латинского "радикс" - корень), а число а - подкоренным числом. Например, в записи  подкоренное число равно 25. Так как
подкоренное число равно 25. Так как 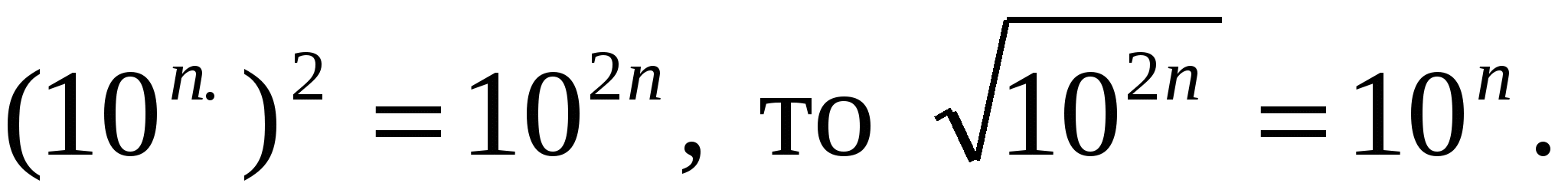
 Это означает, что квадратный корень из числа, записанного единицей и 2n нулями, равен числу, записываемому единицей и n нулями:
Это означает, что квадратный корень из числа, записанного единицей и 2n нулями, равен числу, записываемому единицей и n нулями:
 = 10…0
= 10…0
2n нулей n нулей
Аналогично доказывается, что
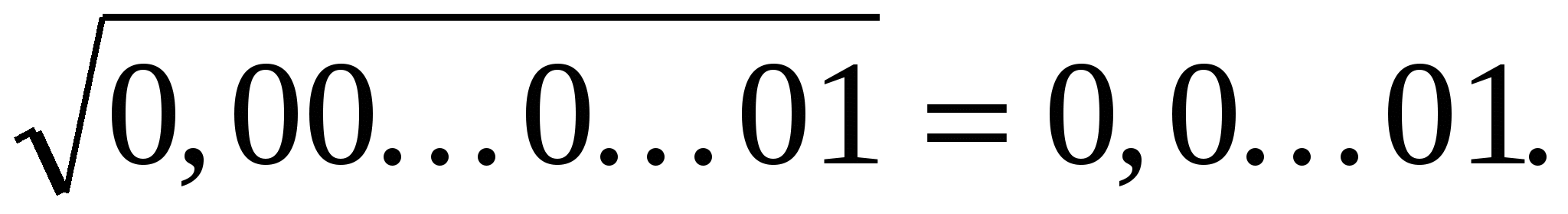
2n нулей n нулей
Например,
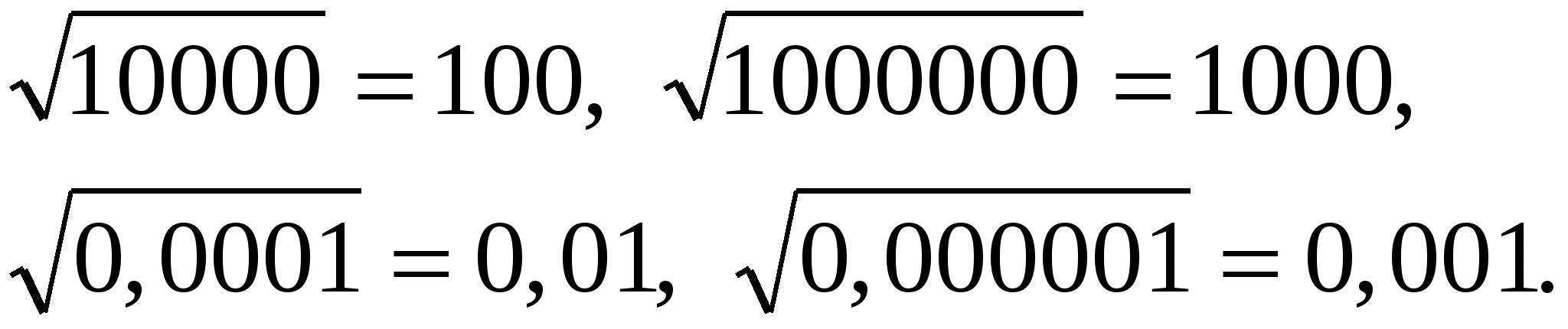
Основные тождества для квадратных корней
Из определения квадратного корня вытекает, что равенство
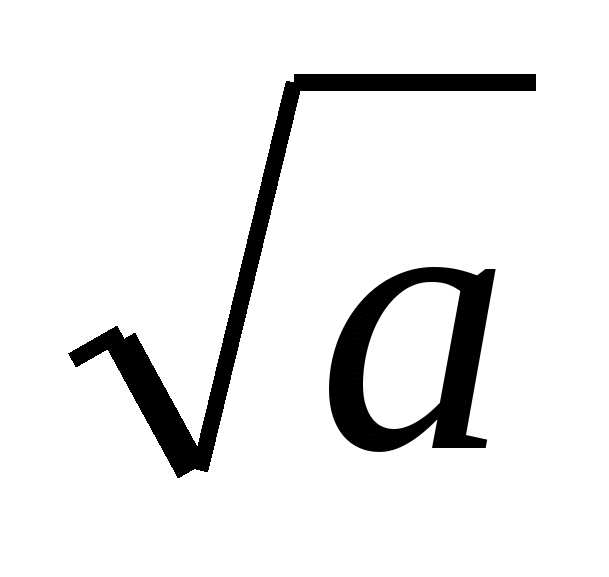 =х, где а
=х, где а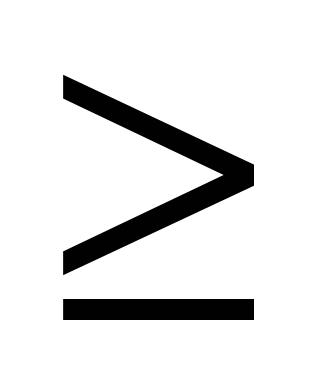 0, верно в том и только в том случае, когда х2=а, причем х
0, верно в том и только в том случае, когда х2=а, причем х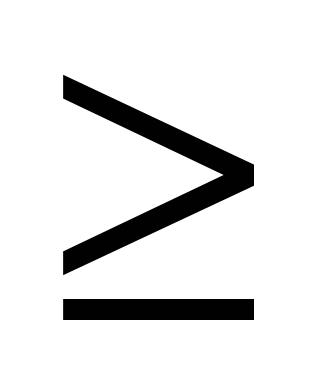 0. Заменяя в равенстве х2=а переменную х на
0. Заменяя в равенстве х2=а переменную х на 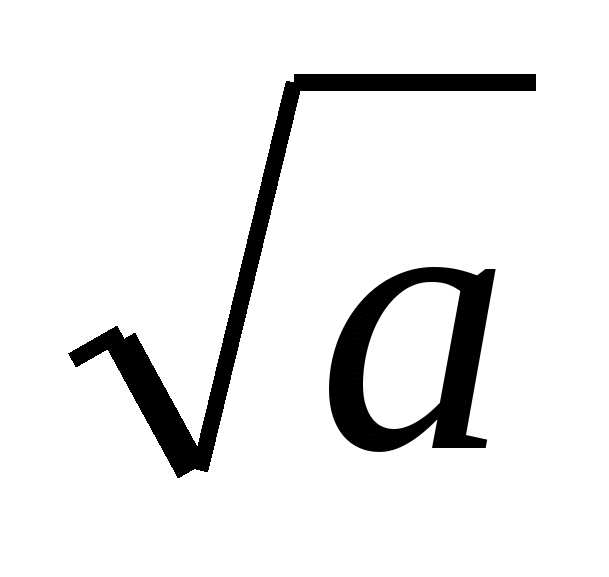 , получаем тождество
, получаем тождество  2=а, (1)
2=а, (1)
верное для всех а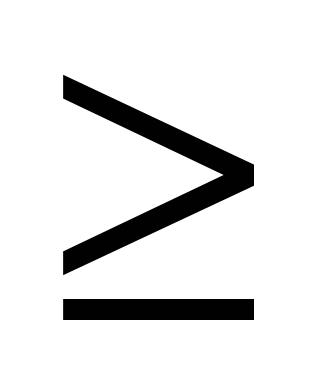 0. Заменяя в равенстве
0. Заменяя в равенстве 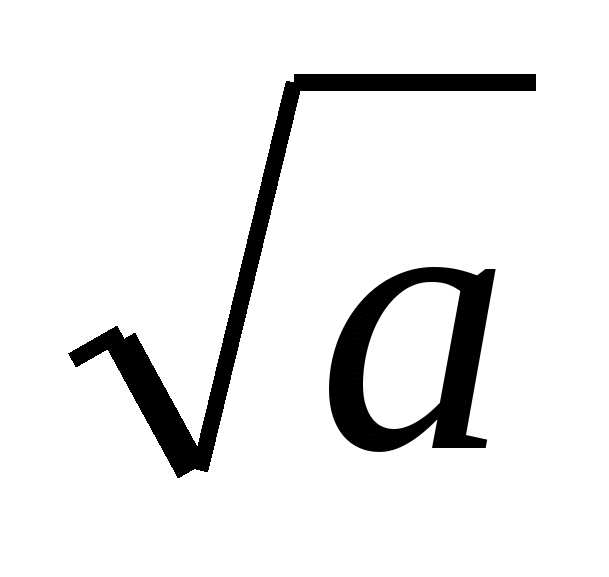 =х переменную а на х2, получаем тождества
=х переменную а на х2, получаем тождества 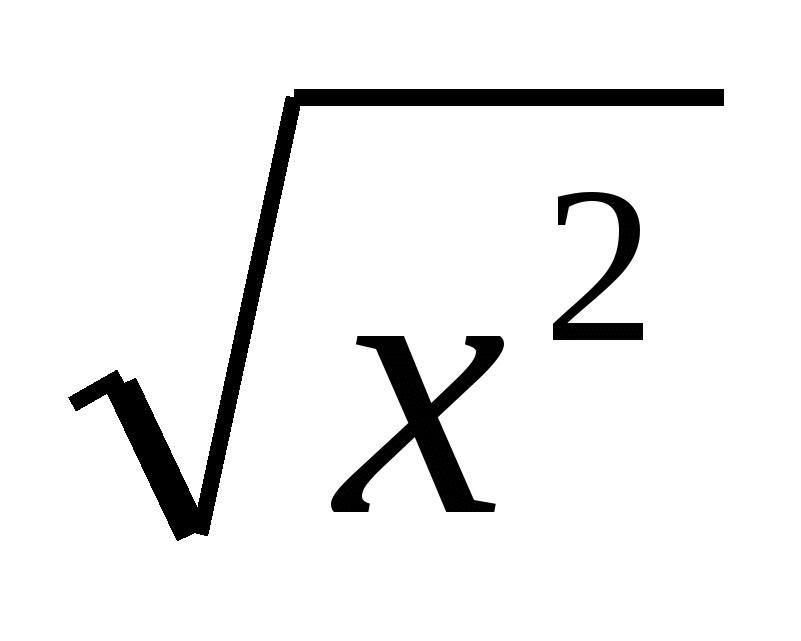 = х, (2)
= х, (2)
которое верно для всех х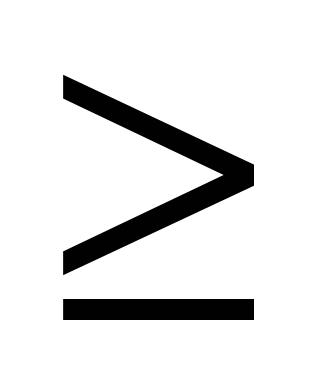 0.
0.
Например, 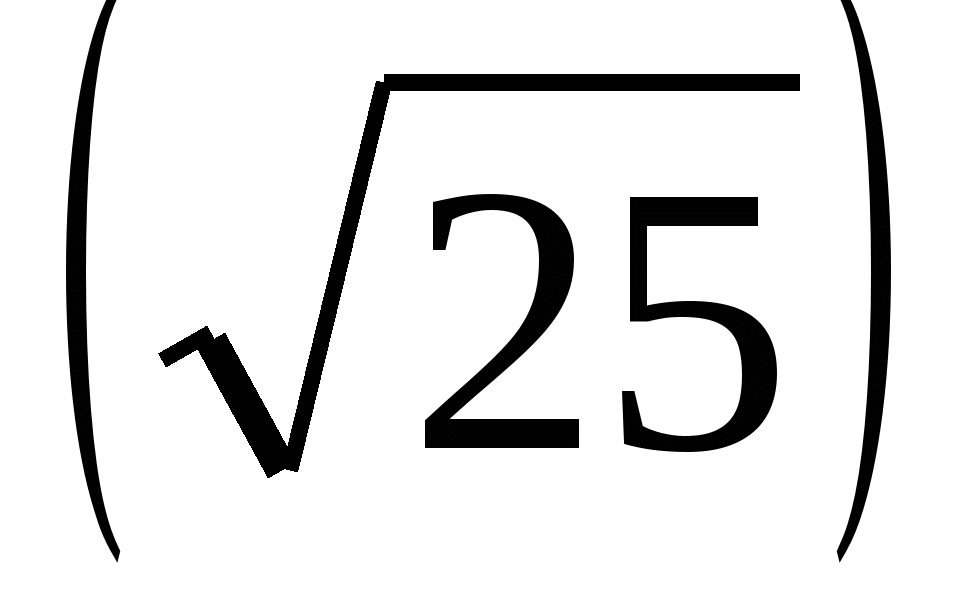 2 = 25;
2 = 25; 2 = 8;
2 = 8; 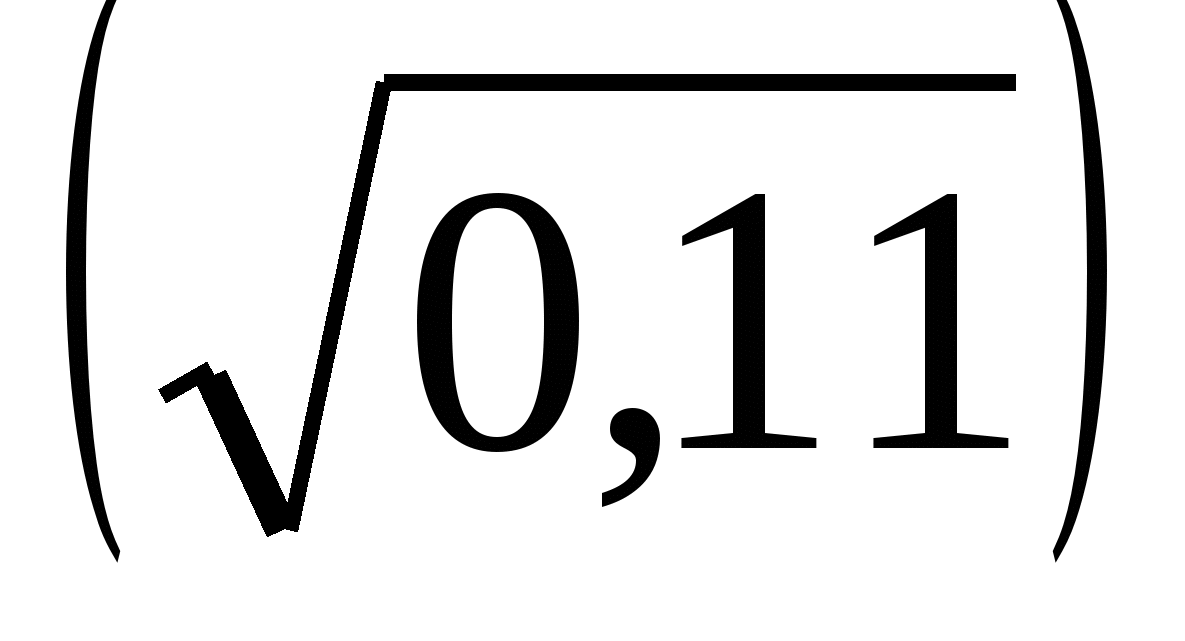 2 = 0,11;
2 = 0,11; 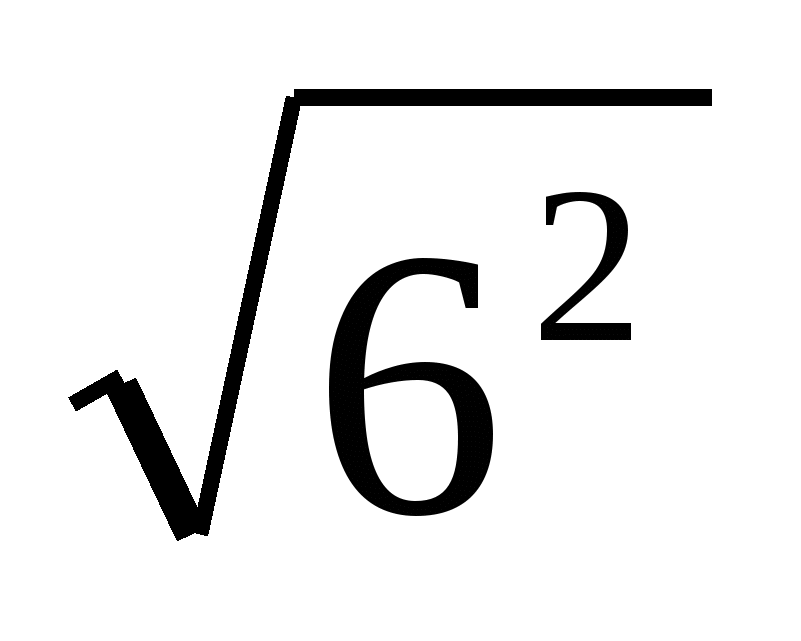 = 6;
= 6; 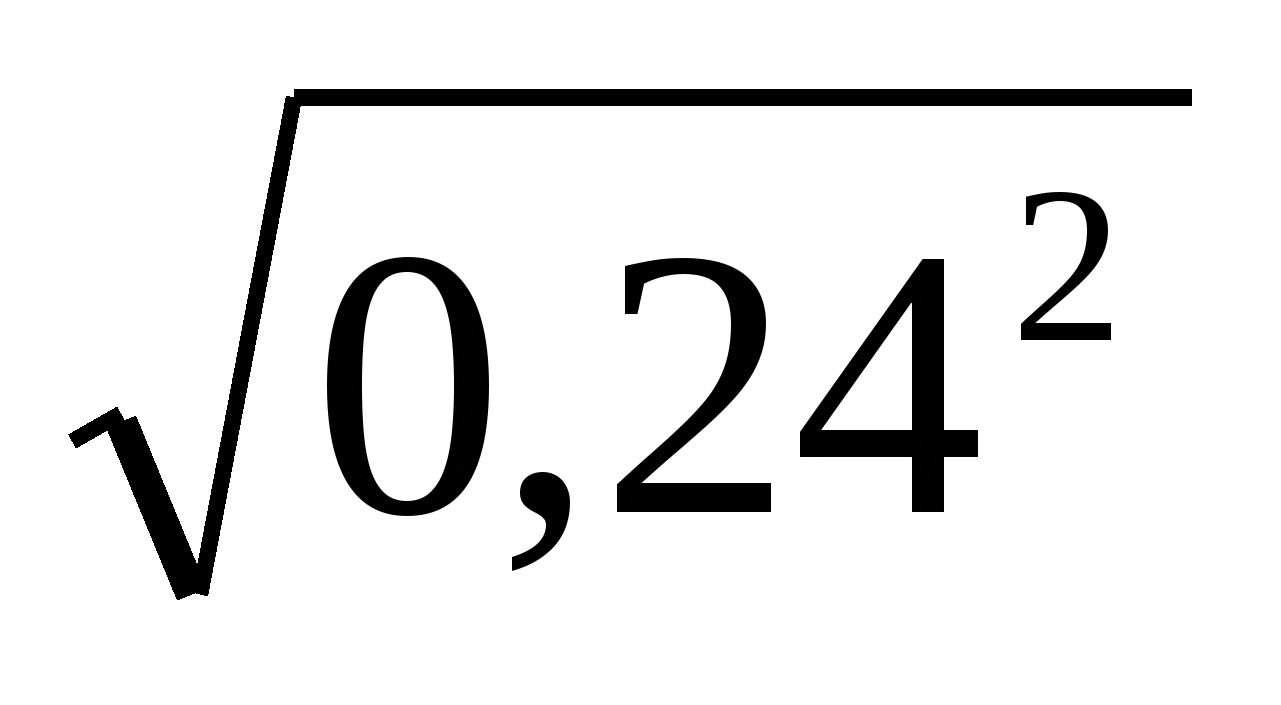 =0,24.
=0,24.
Формулы 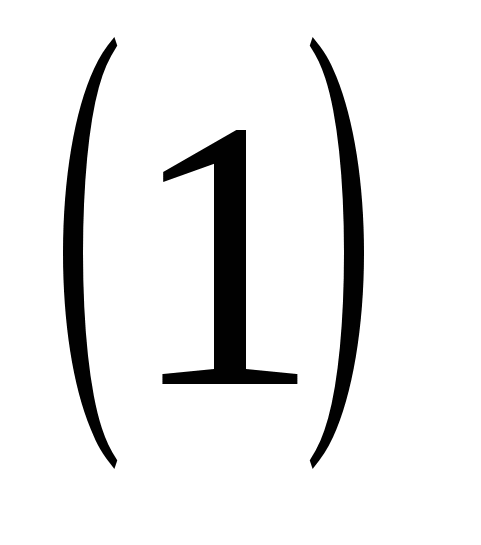 и
и  показывают , что для неотрицательных чисел операции возведения в квадрат и извлечения квадратного корня взаимно обратны Т.е. если выполнить над каким – нибудь неотрицательным числом сначала одну из этих операций, а потом другую, то число не изменится.
показывают , что для неотрицательных чисел операции возведения в квадрат и извлечения квадратного корня взаимно обратны Т.е. если выполнить над каким – нибудь неотрицательным числом сначала одну из этих операций, а потом другую, то число не изменится.
Если а – отрицательное число, то равенство 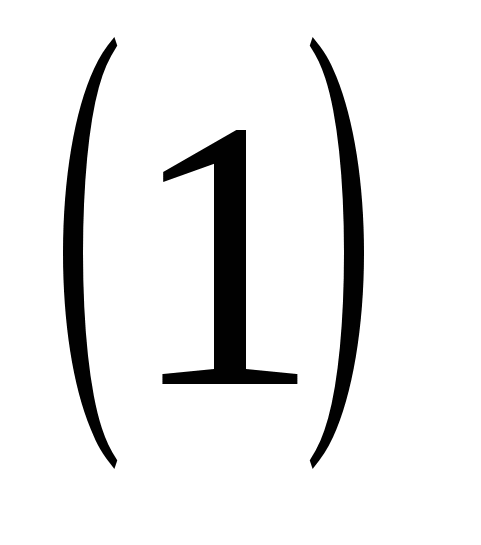 неверно, так как
неверно, так как 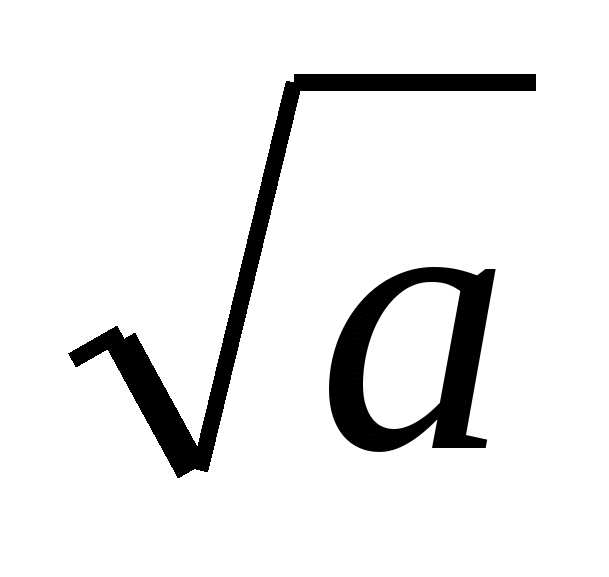 не имеет числового значения. При отрицательных значениях х неверно и равенство
не имеет числового значения. При отрицательных значениях х неверно и равенство  . Например,
. Например, 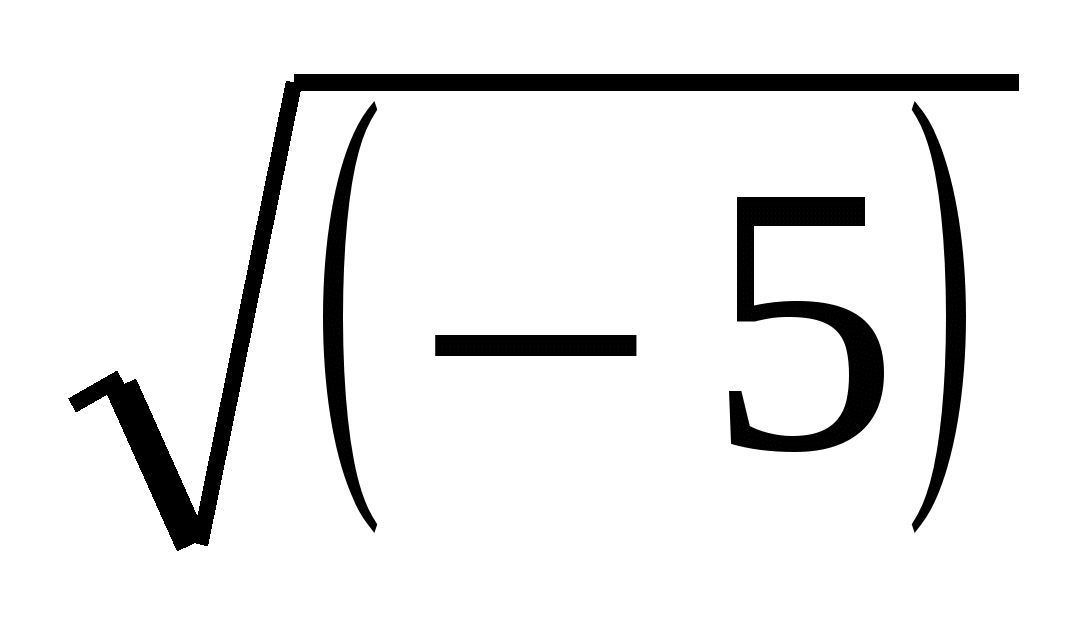 2 =
2 =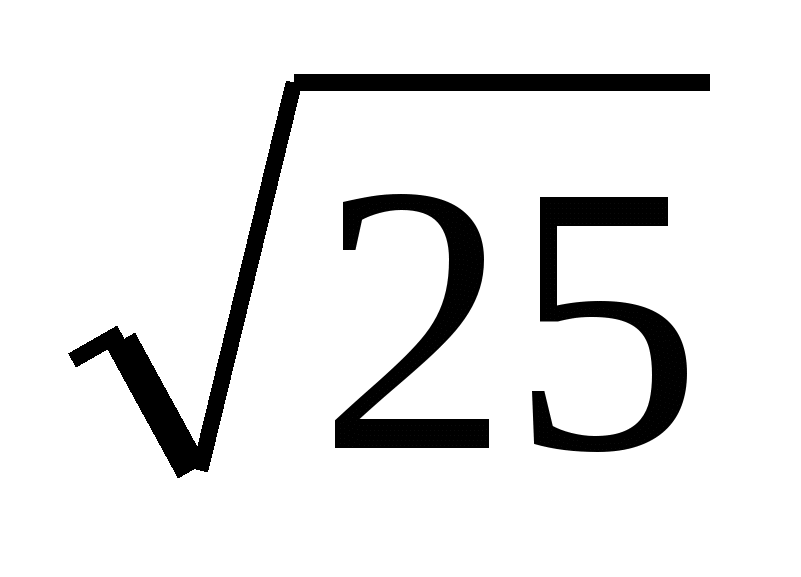 =5, а не –5. Так как х2 =
=5, а не –5. Так как х2 =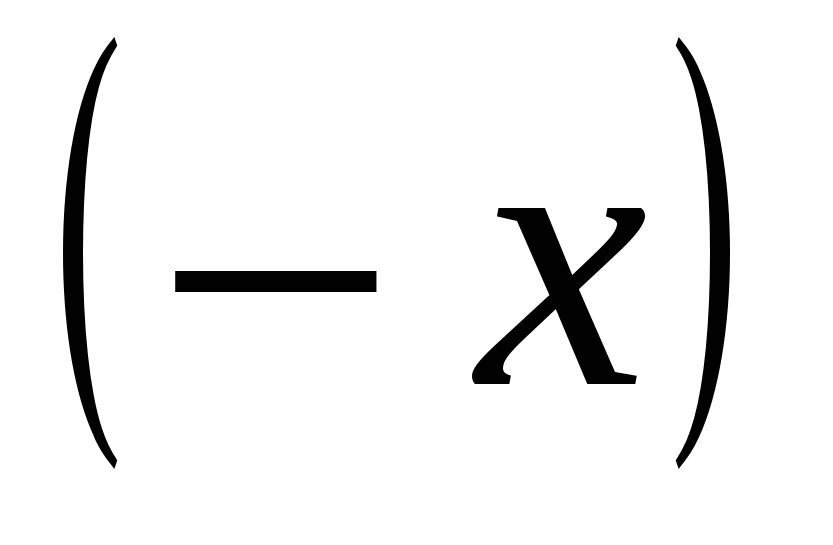 2, а при х < 0 имеем –х> 0,
2, а при х < 0 имеем –х> 0,
то при х< 0 верно равенство 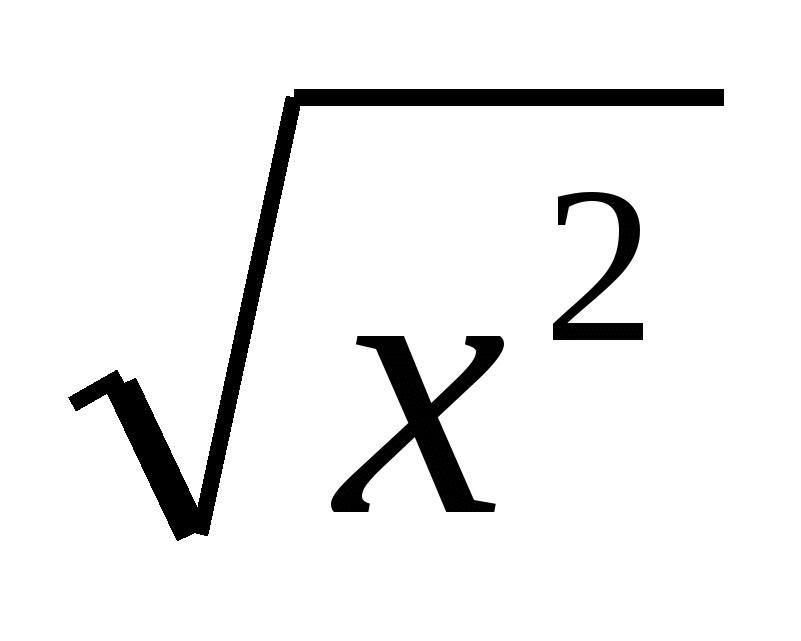 =
= 2 = - х (3)
2 = - х (3)
Итак,
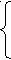 x, если х
x, если х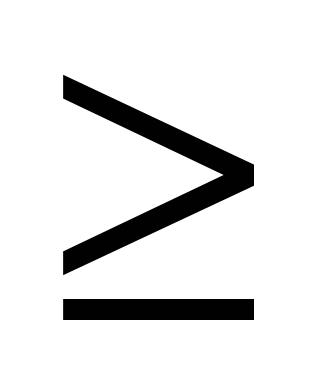 0,
0,
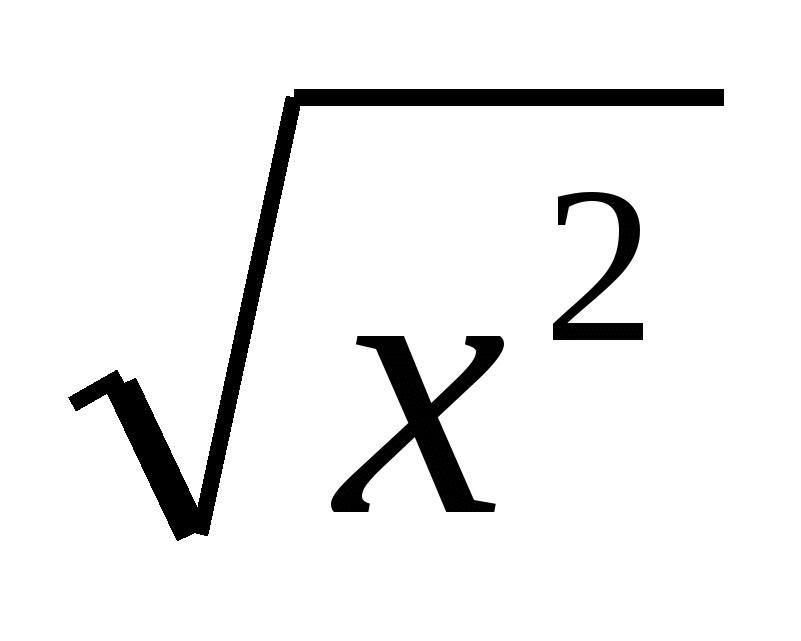 = -х, если х < 0.
= -х, если х < 0.
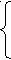 Но мы знаем, что х, если х
Но мы знаем, что х, если х 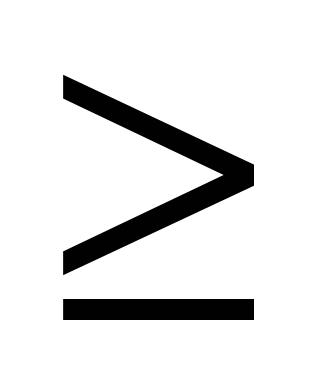 0,
0,
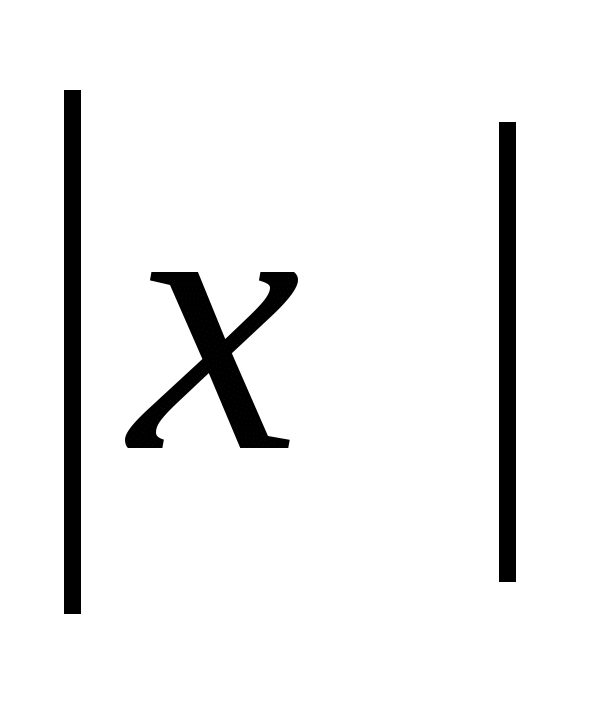 =
=
-х, если х < 0.
Поэтому для всех чисел х верно равенство
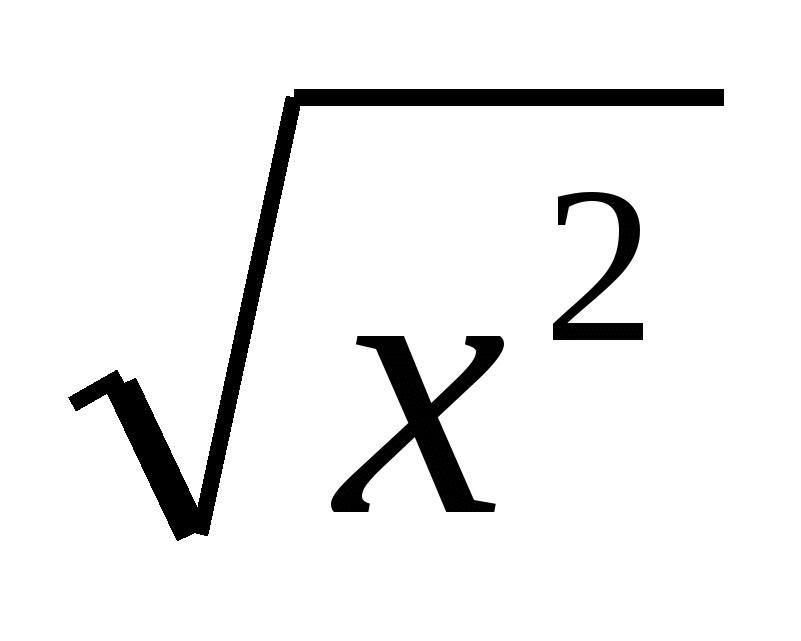 =
= 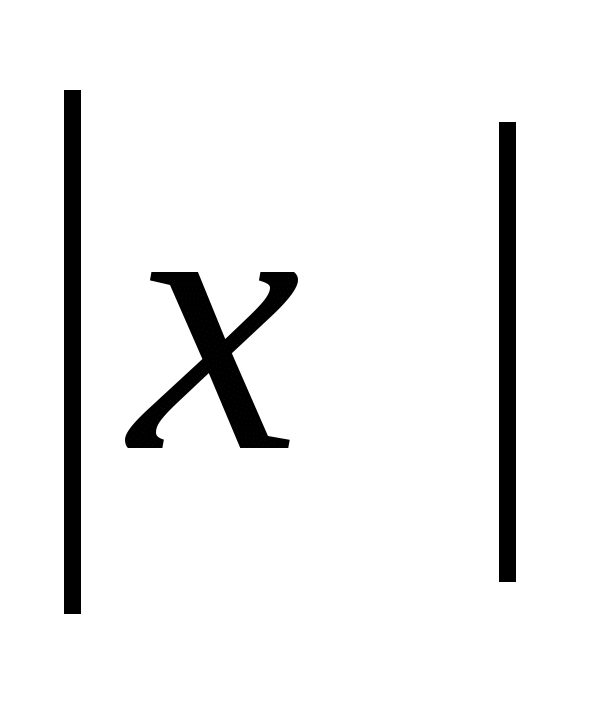 . (4)
. (4)
Например, 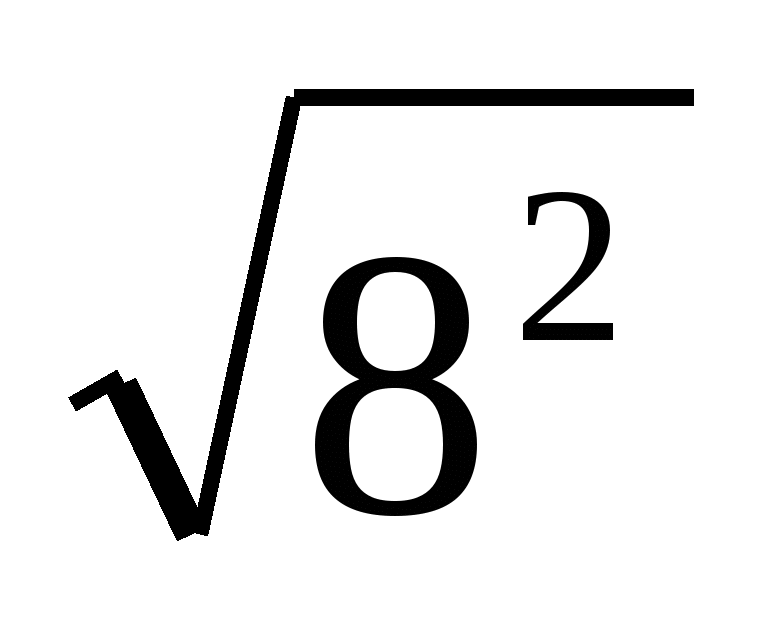 =
=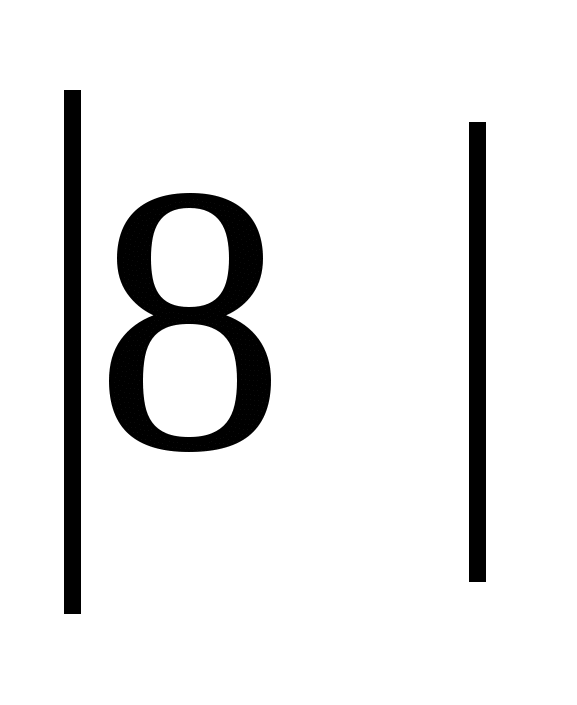 =8,
=8, 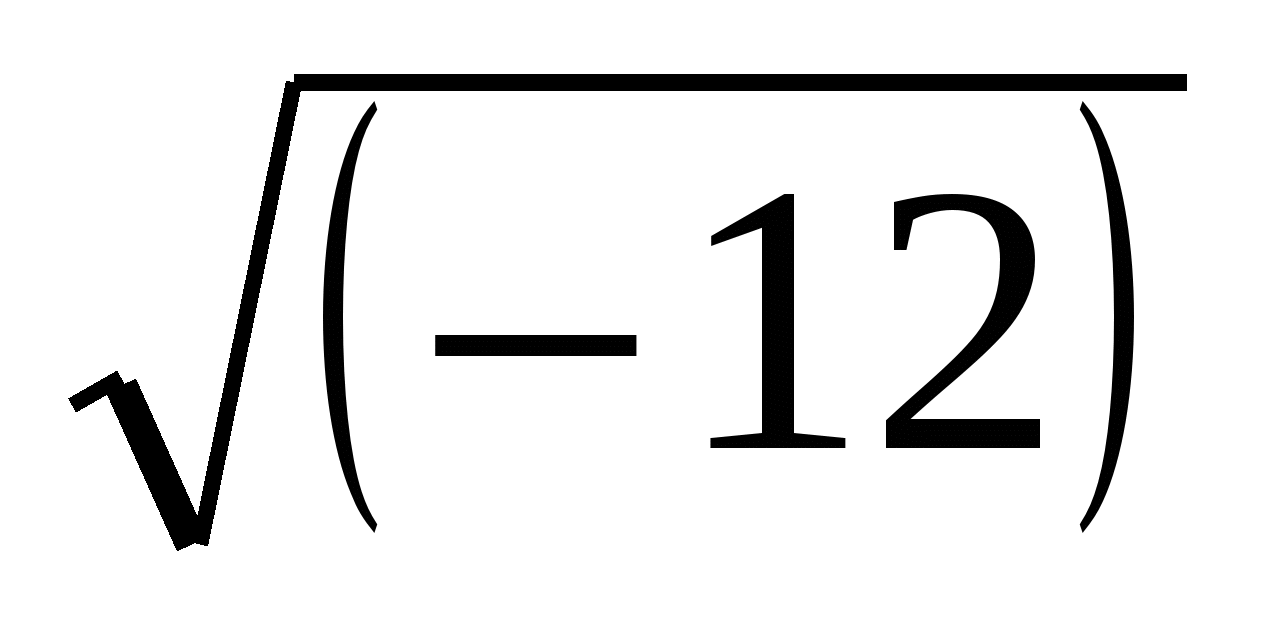 2 =
2 = 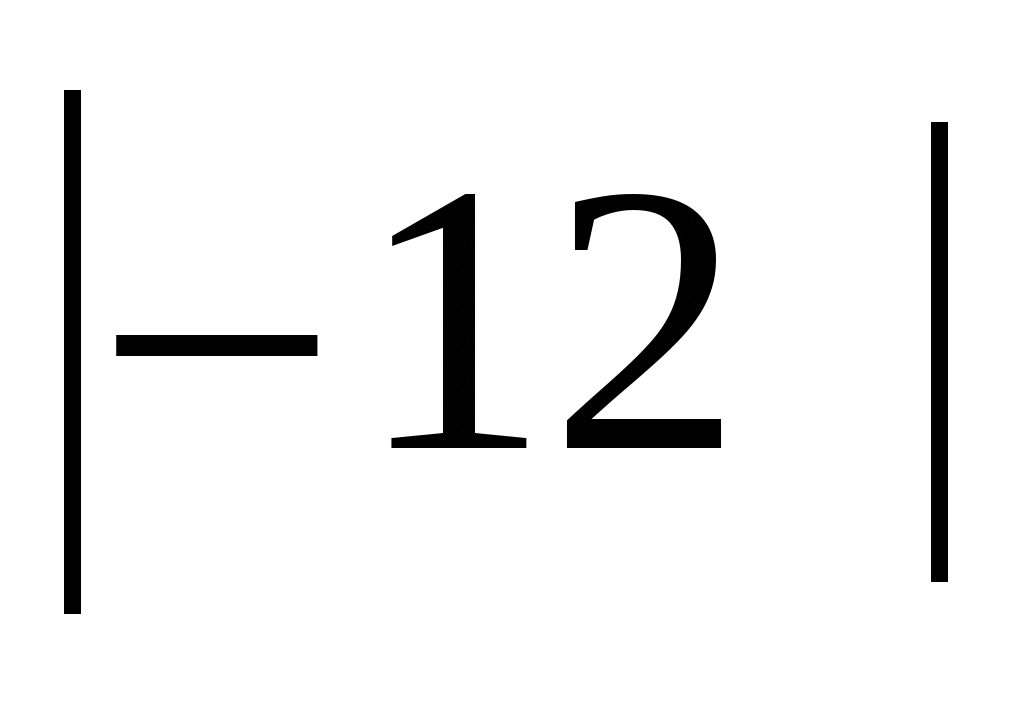 = 12
= 12
П р и м е р 1. Упростим выражение 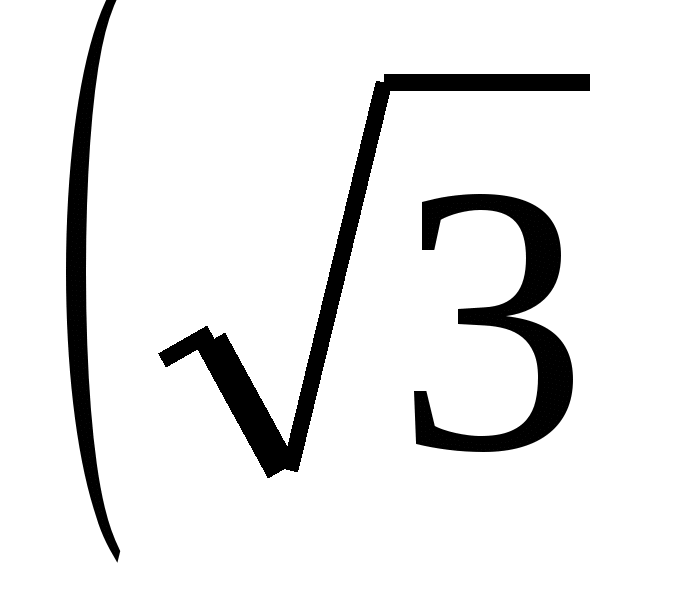 +
+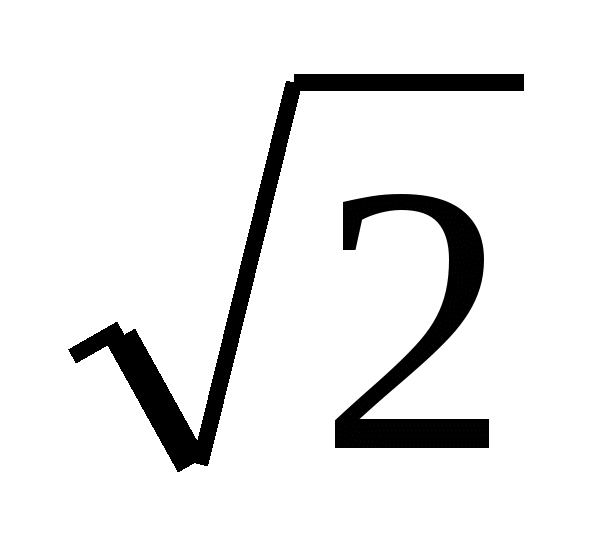
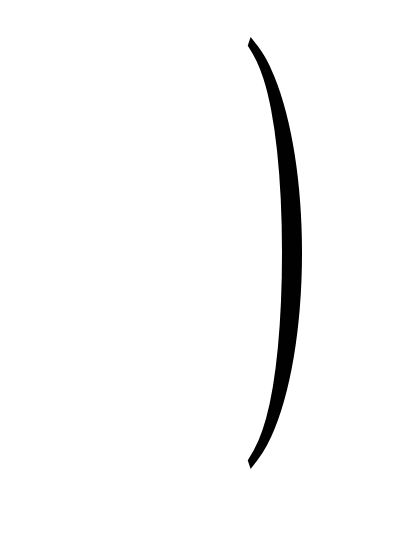 2 +
2 + 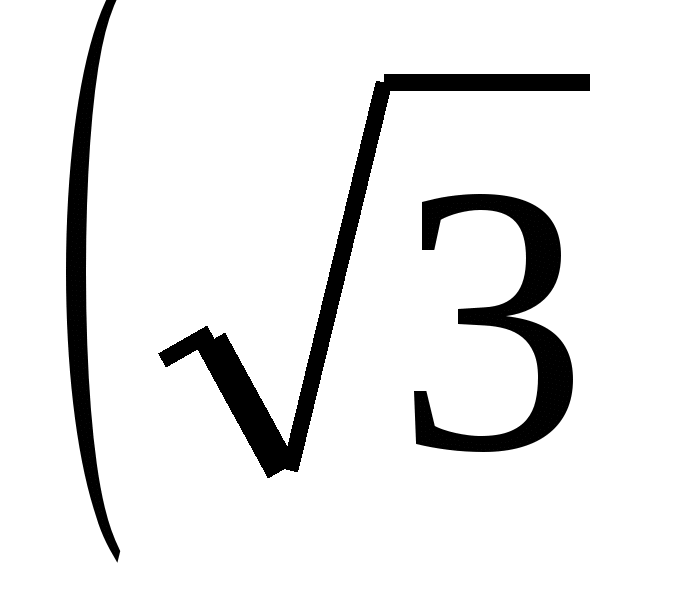 -
- 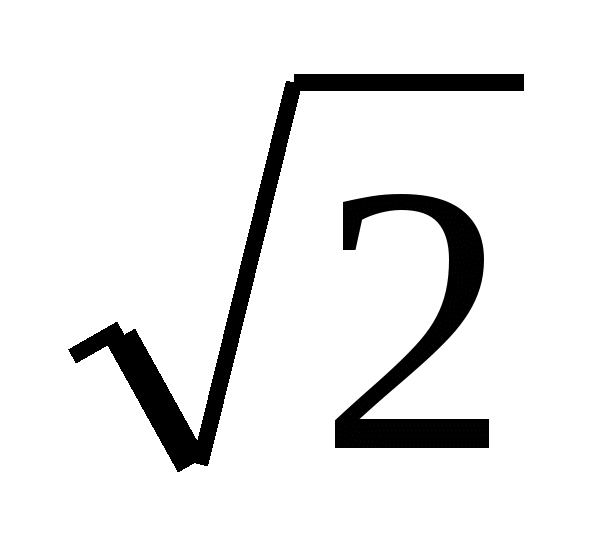
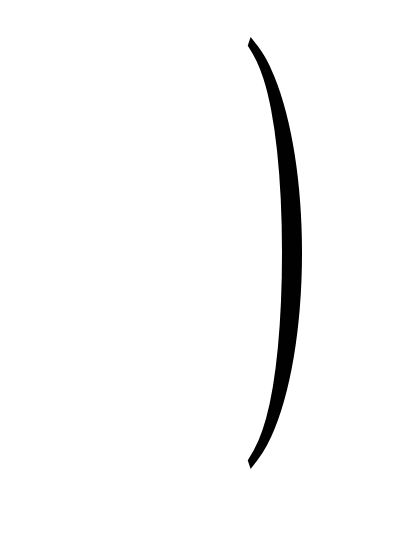 2.
2.
Р е ш е н и е. Так как 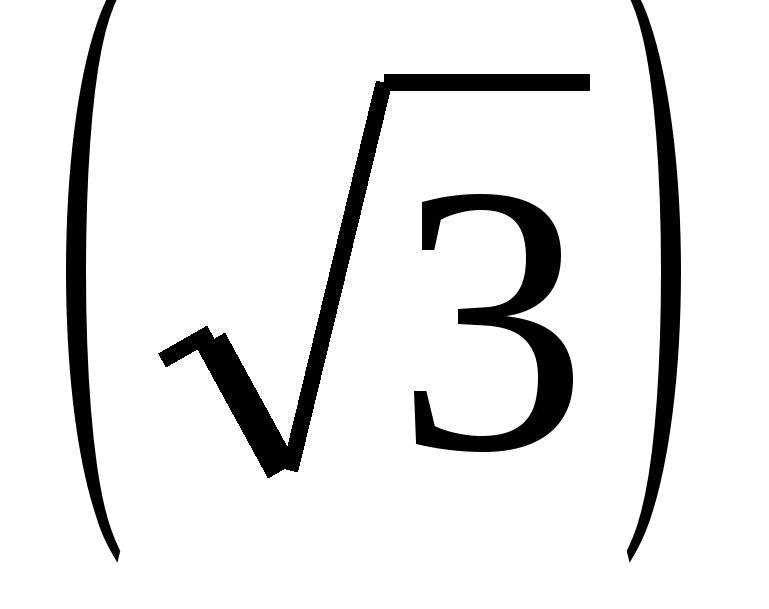 2 = 3,
2 = 3, 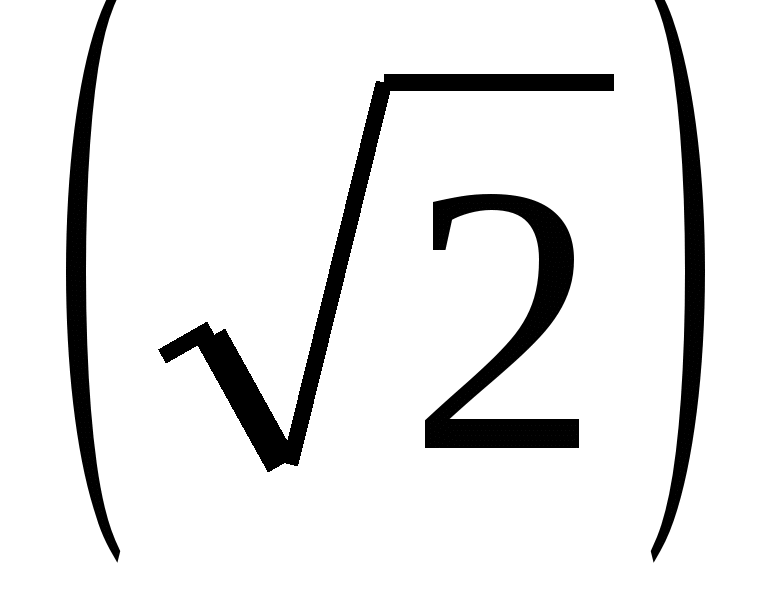 2 = 2, то
2 = 2, то 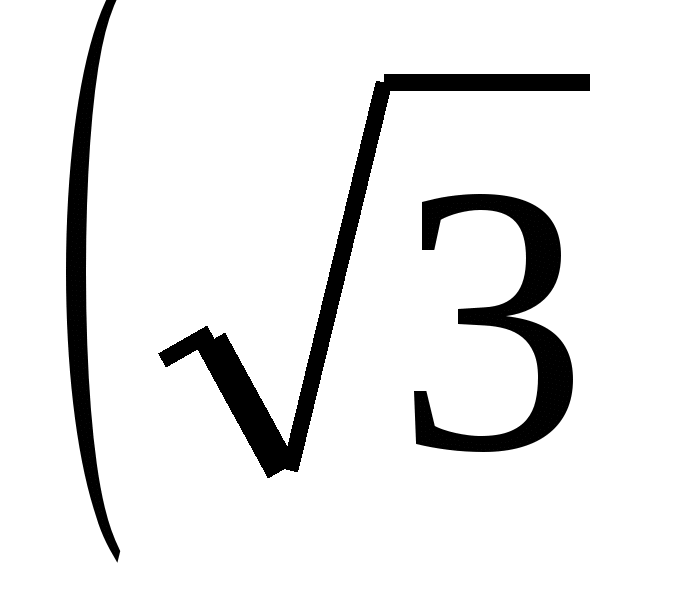 +
+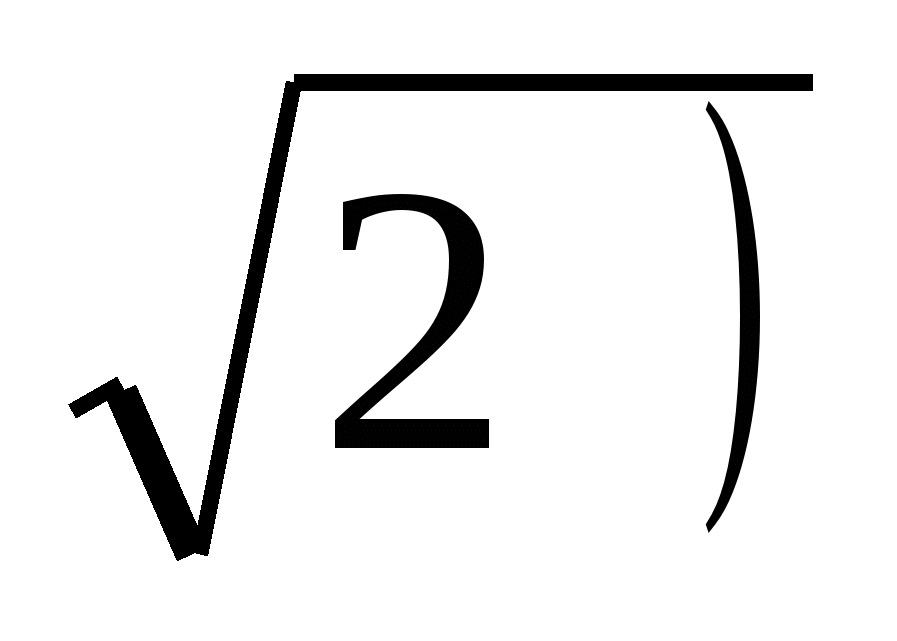 2 +
2 + 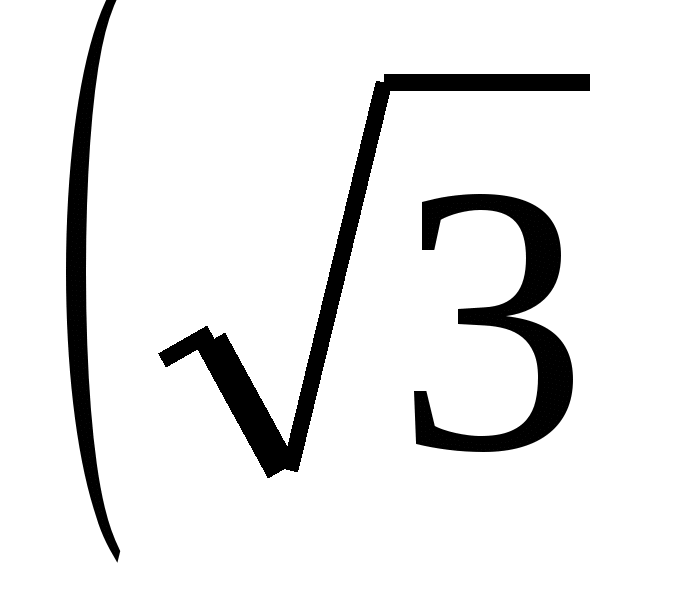 -
- 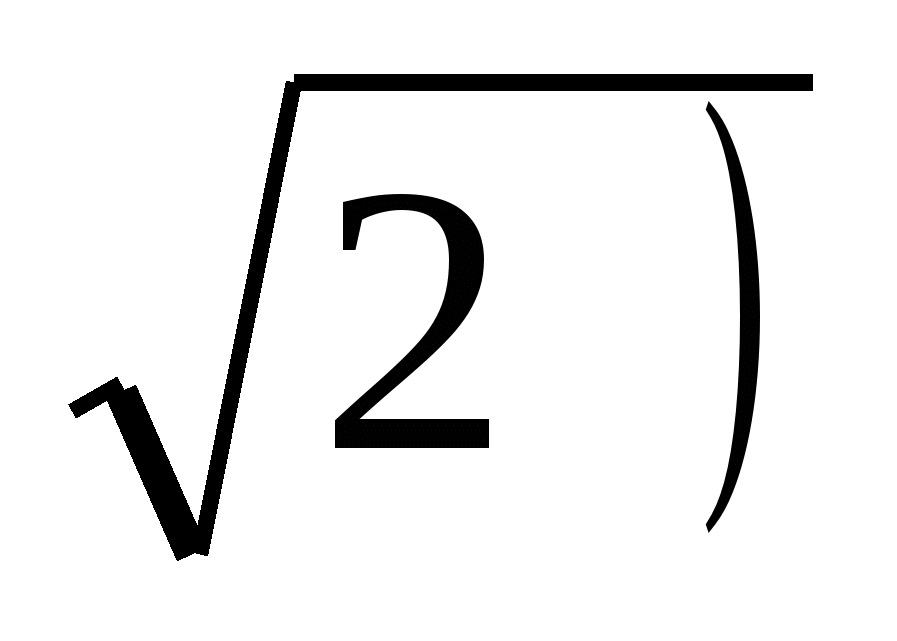 2 =
2 =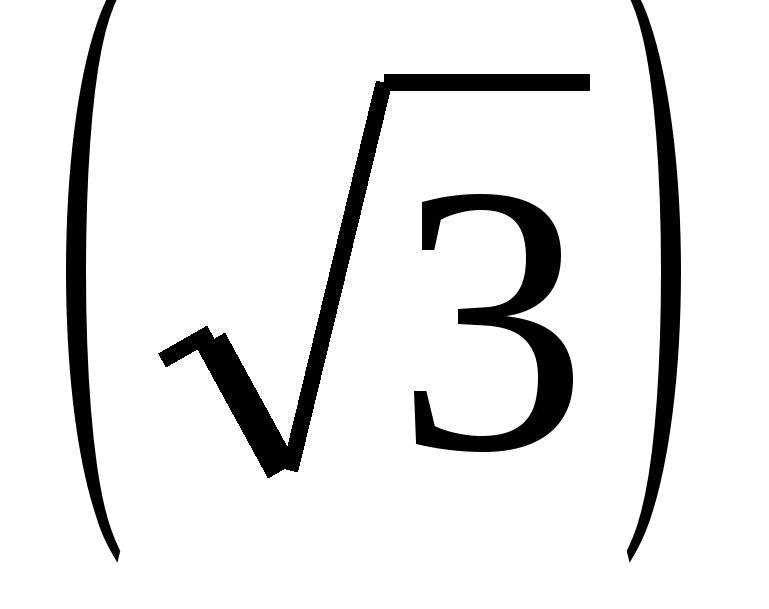 2 +2
2 +2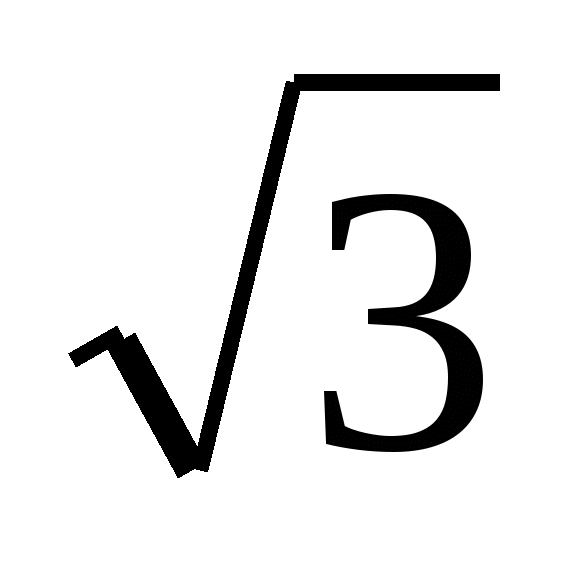

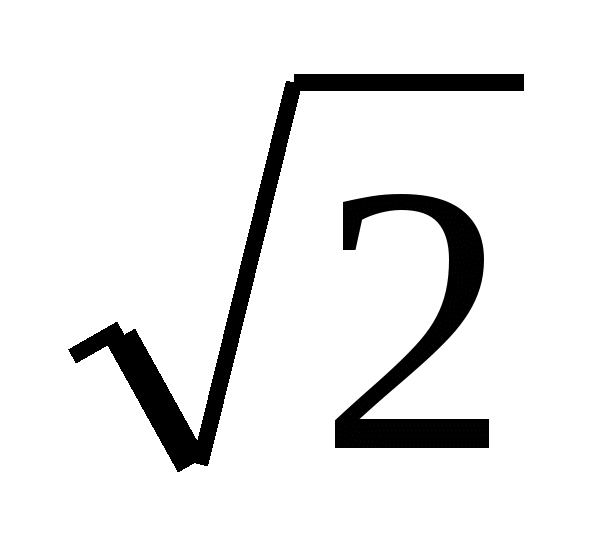 +
+ 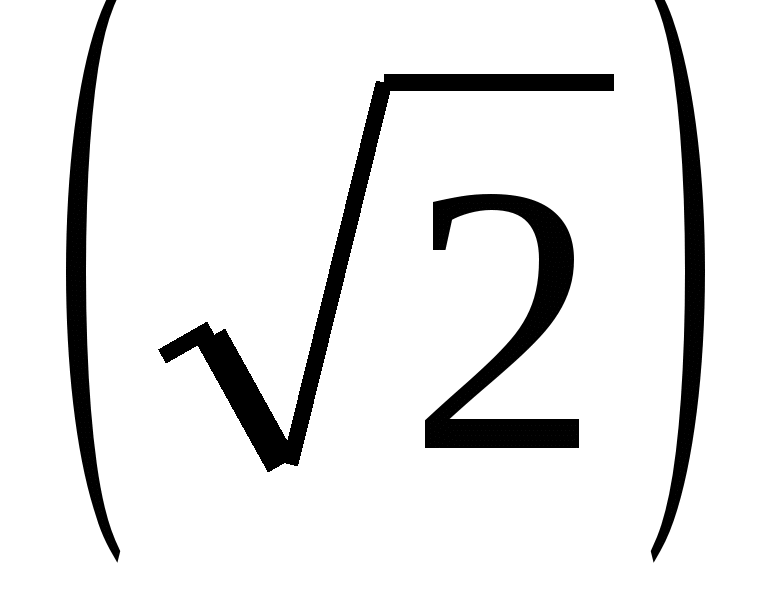 2 +
2 +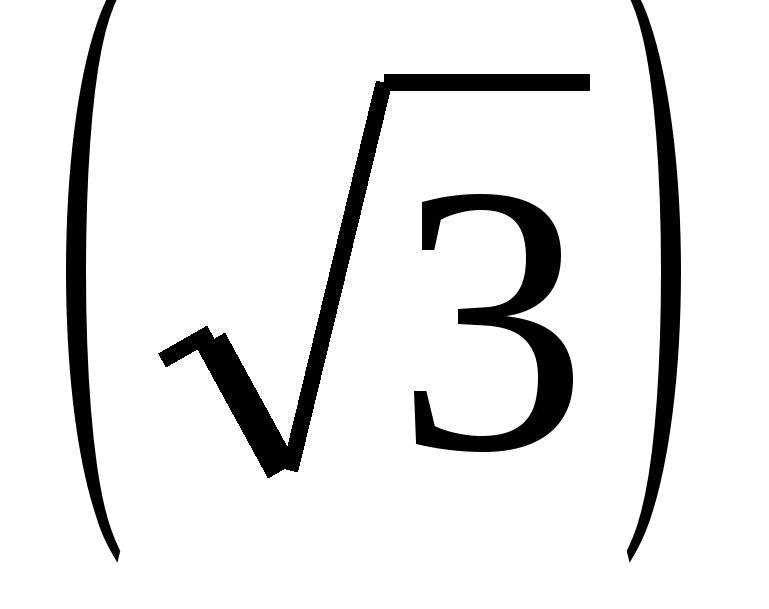 2 – 2
2 – 2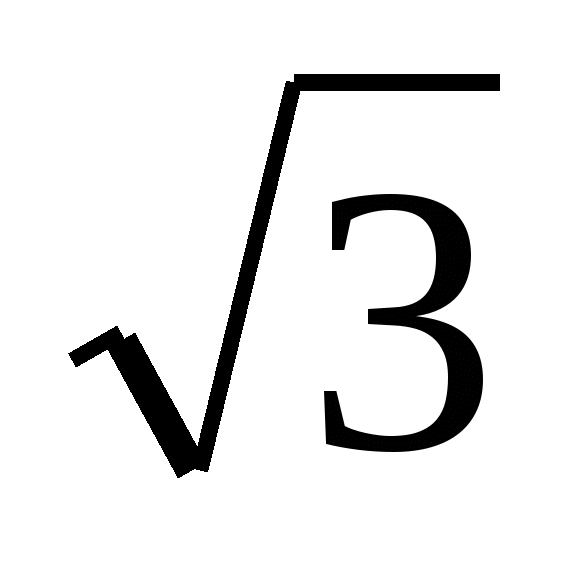

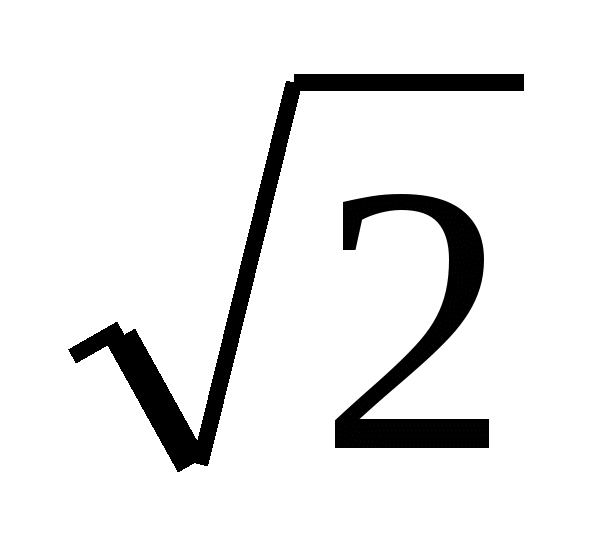 +
+ 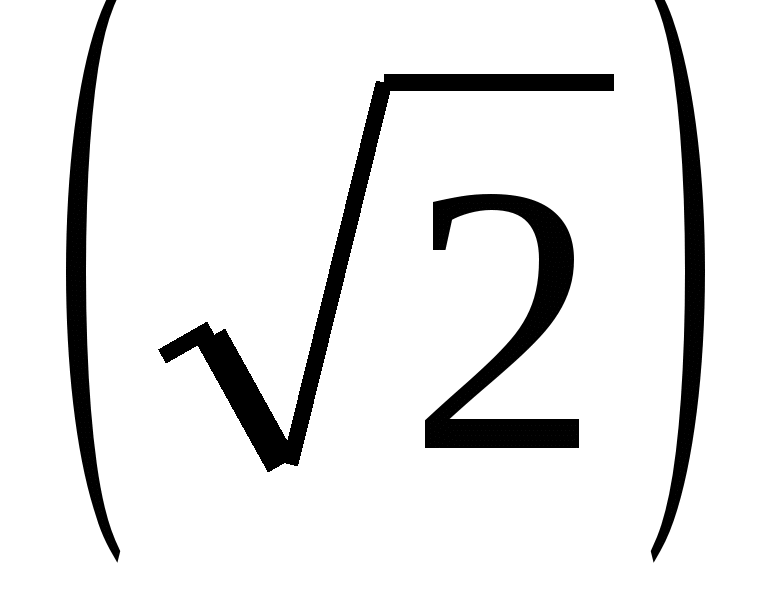 2 =2
2 =2
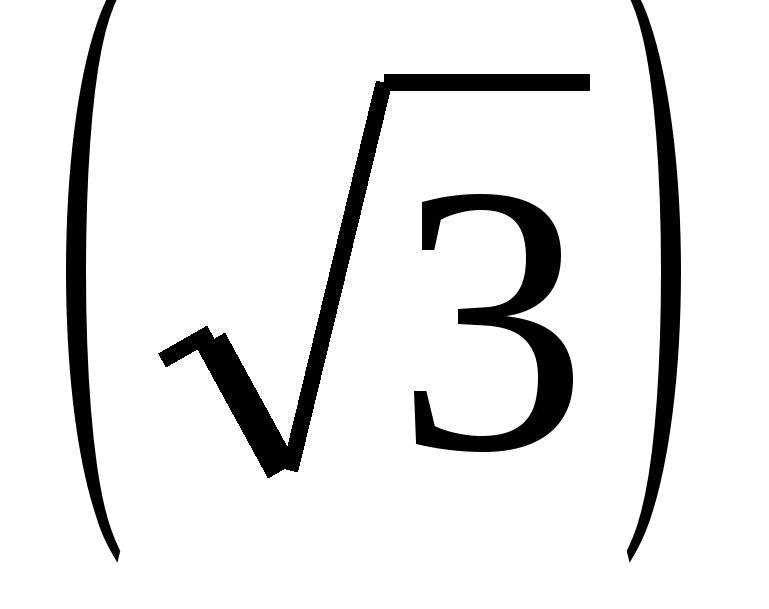 2 + 2
2 + 2 
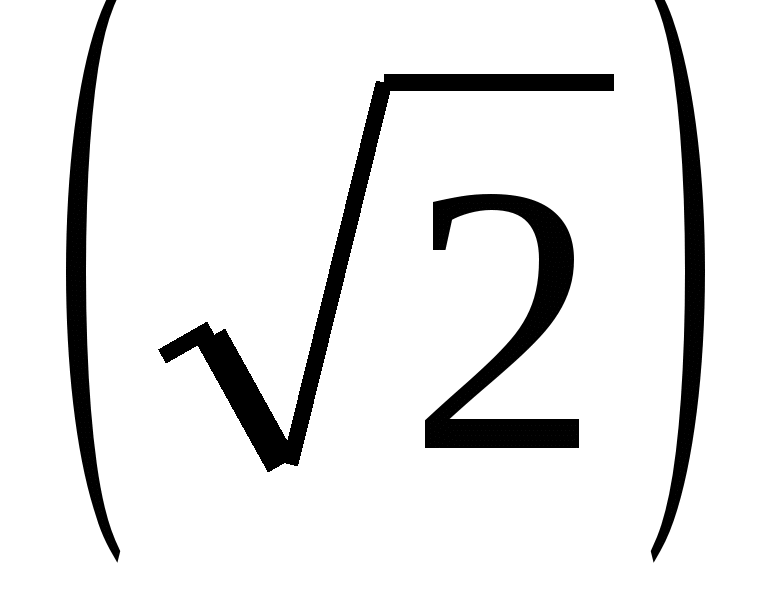 2 = 2
2 = 2  3 + 2
3 + 2  2 = =10.
2 = =10.
П р и м е р 2. Найдем значения выражения 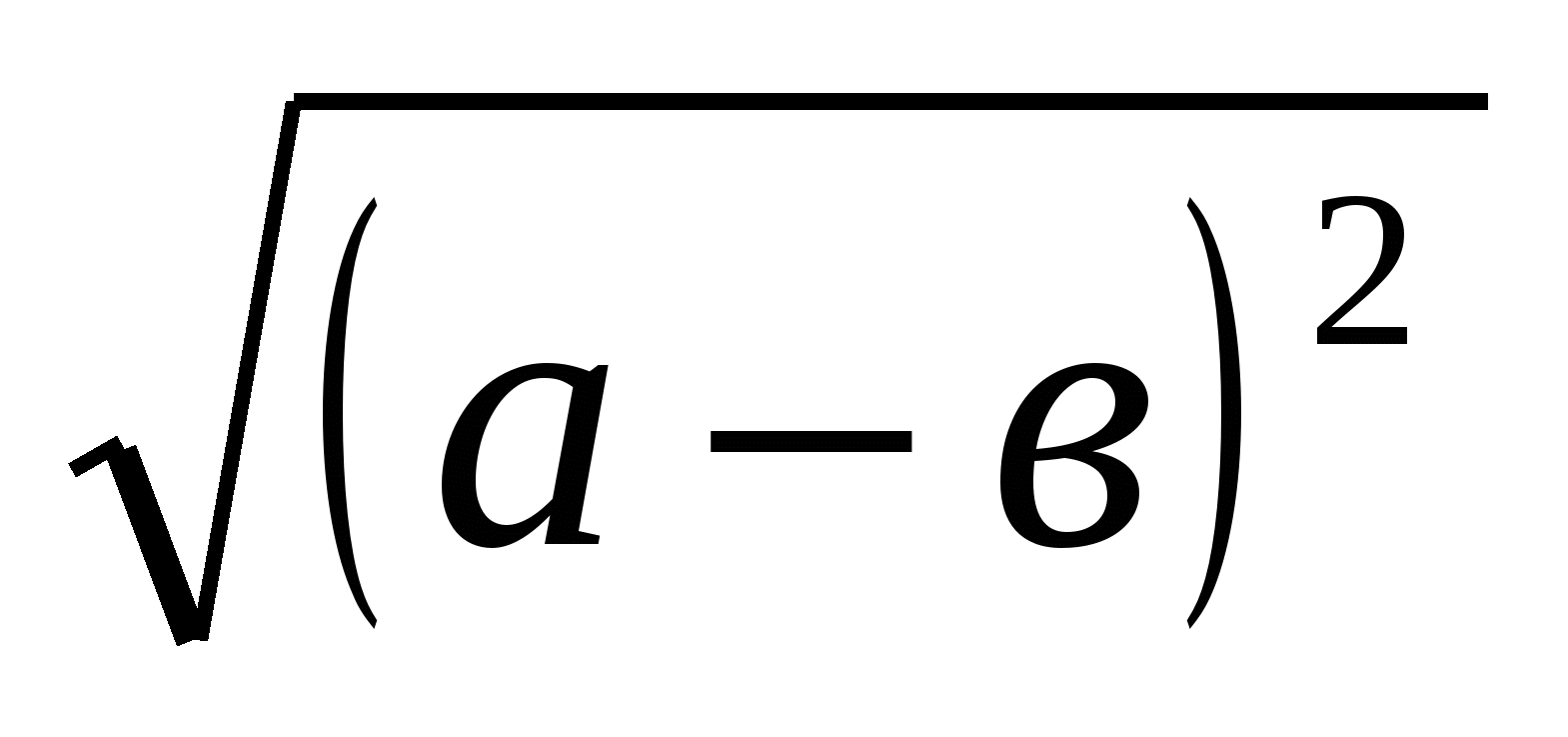 при а = 2,1
при а = 2,1
b = 3,6
Р е ш е н и е. При любом значении х выполняется равенство
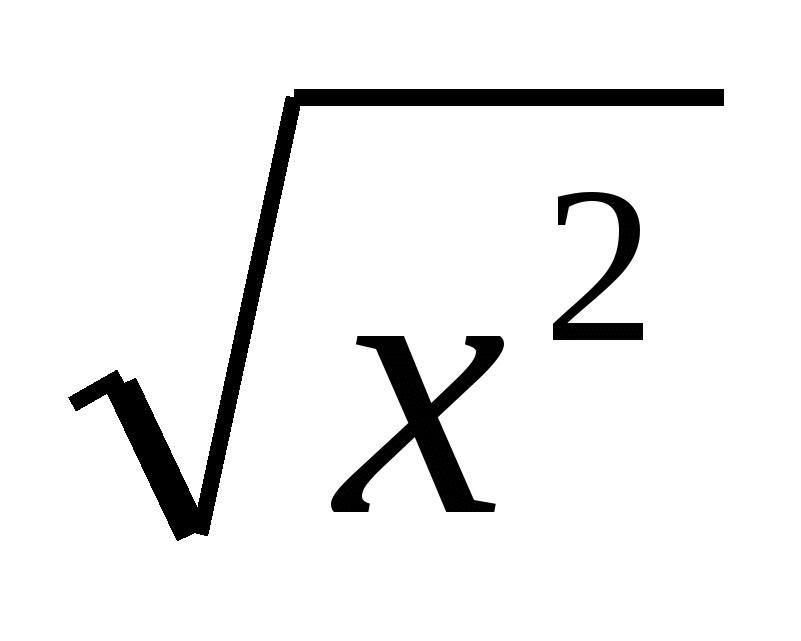 =
= 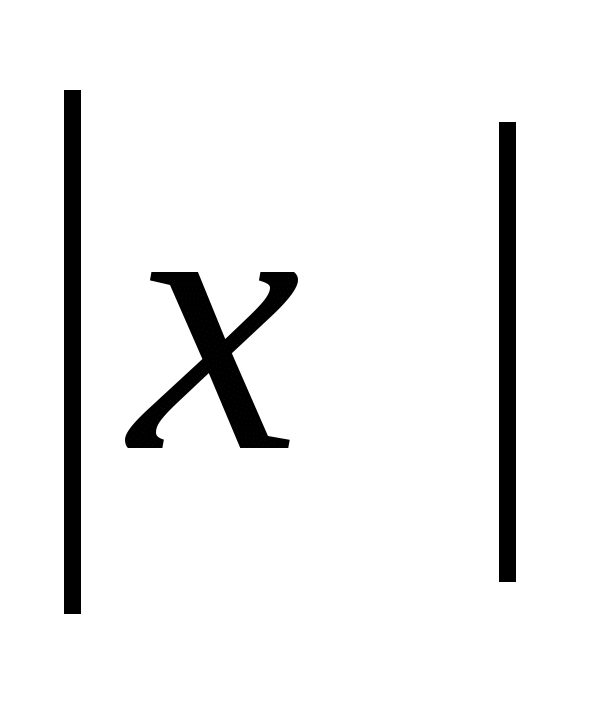 . Поэтому
. Поэтому 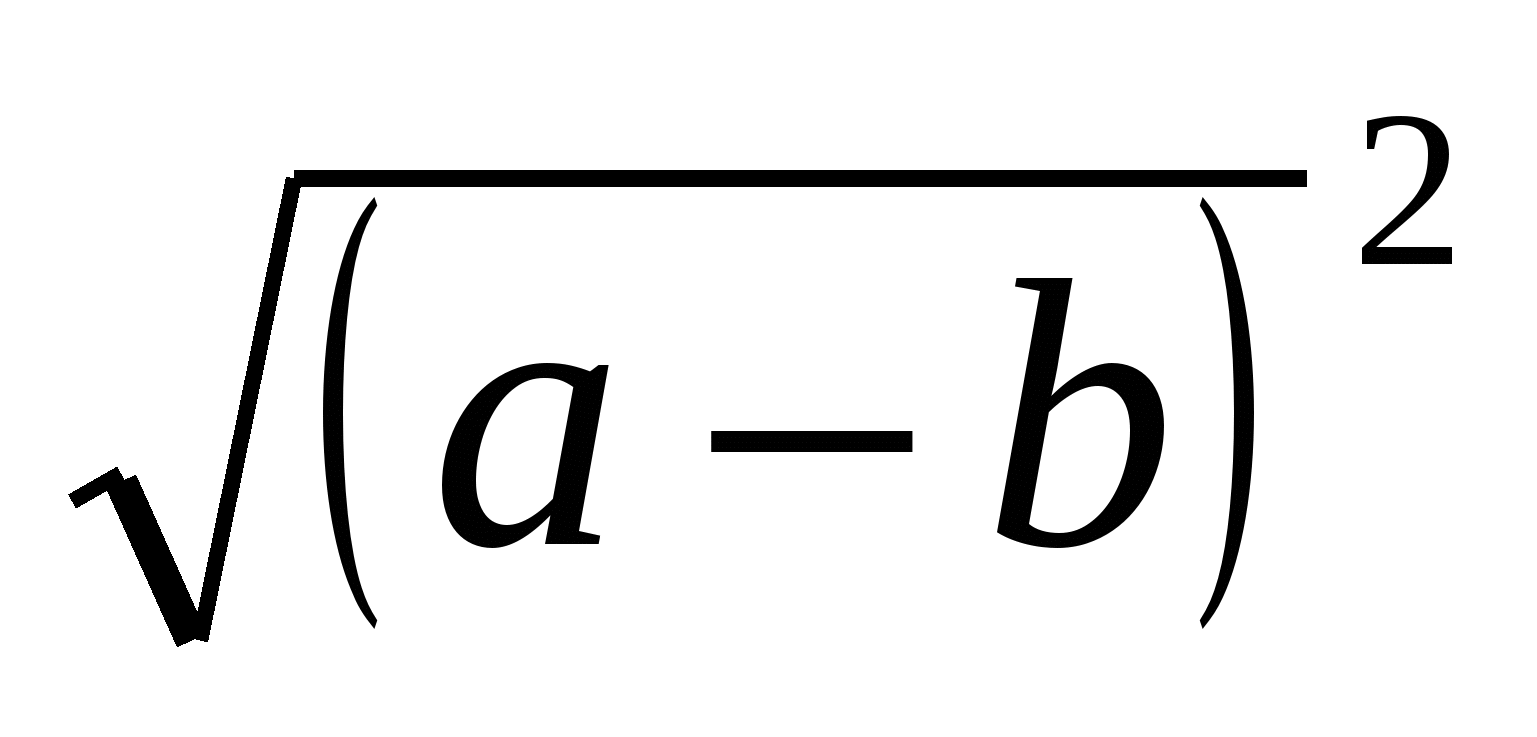 =
= 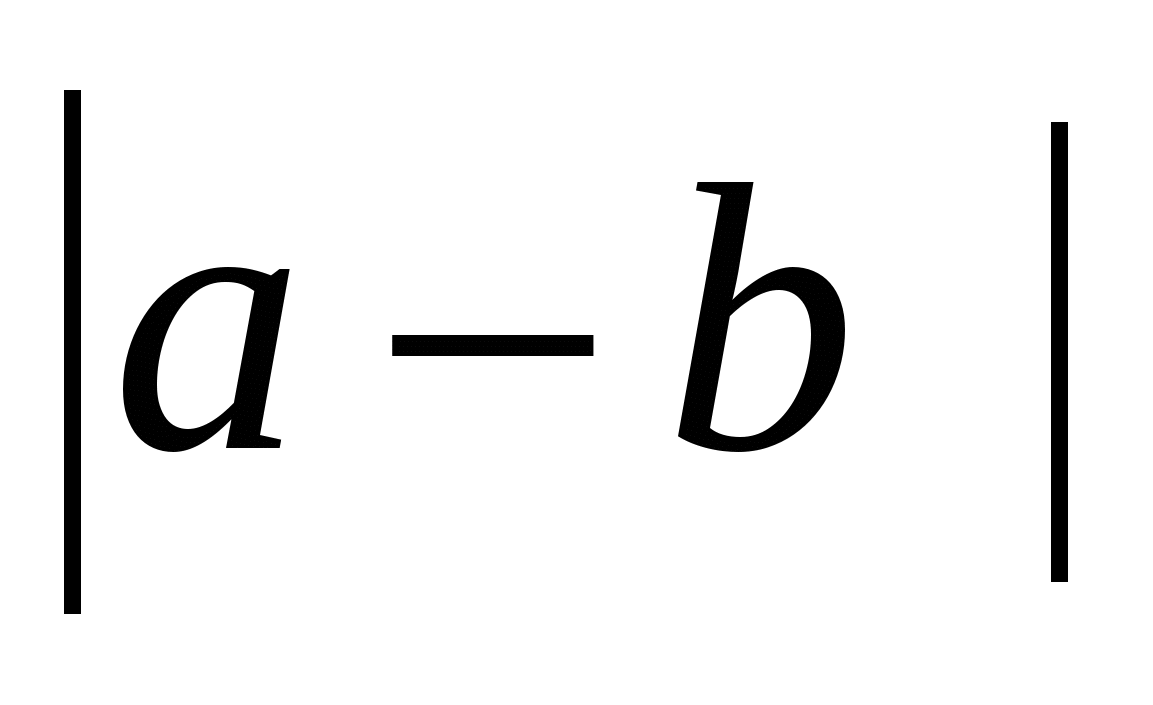 . Но
. Но 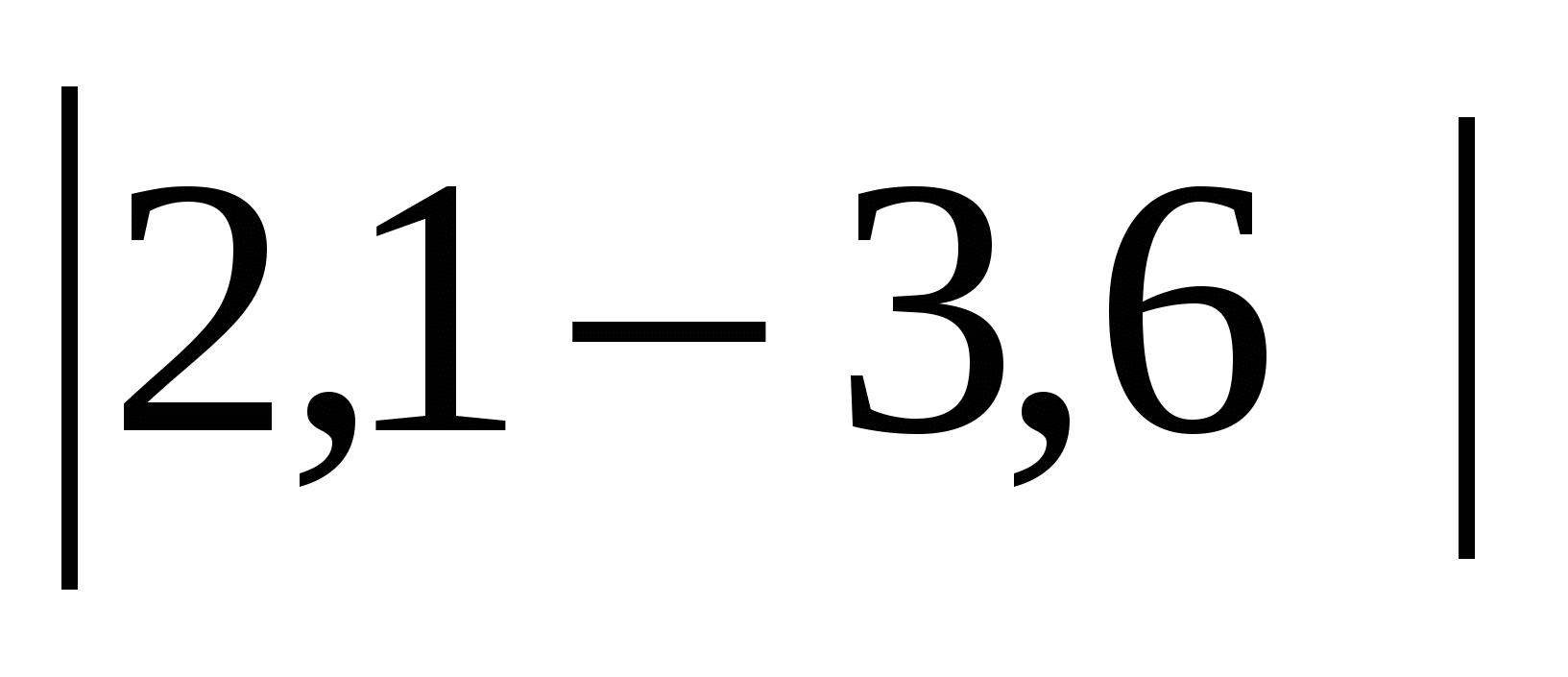 =
=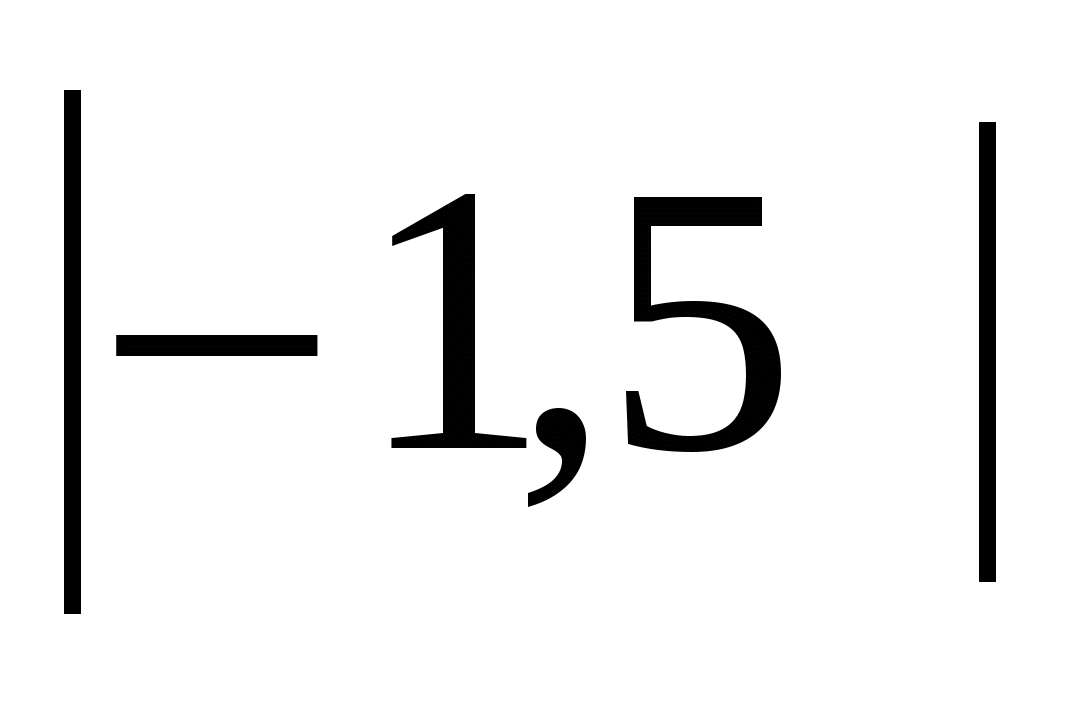 = 1,5. Значит, при а = 2,1; b =3,6 имеем
= 1,5. Значит, при а = 2,1; b =3,6 имеем 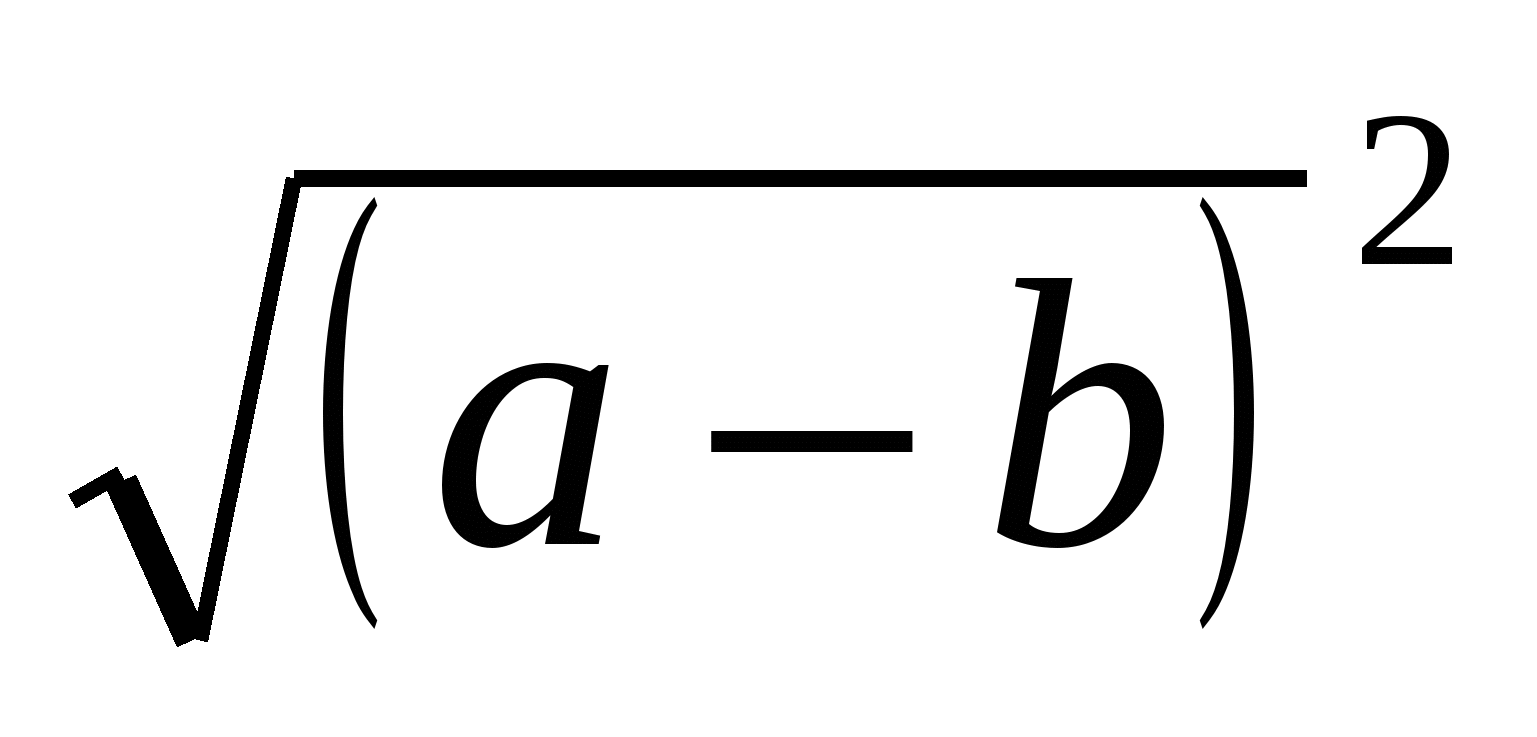 =1,5.
=1,5.
Выражения 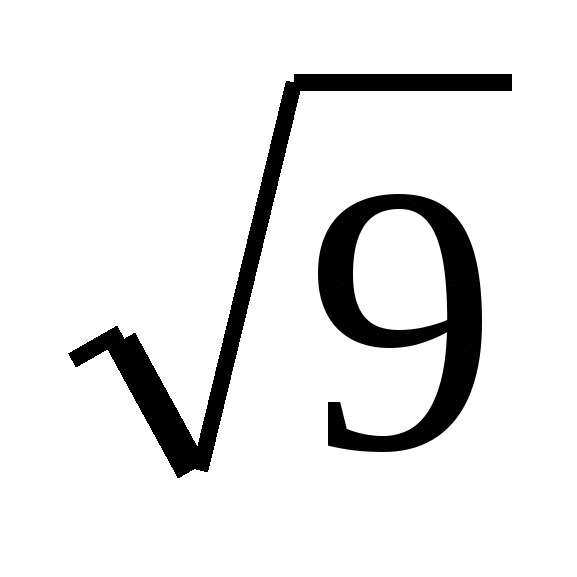
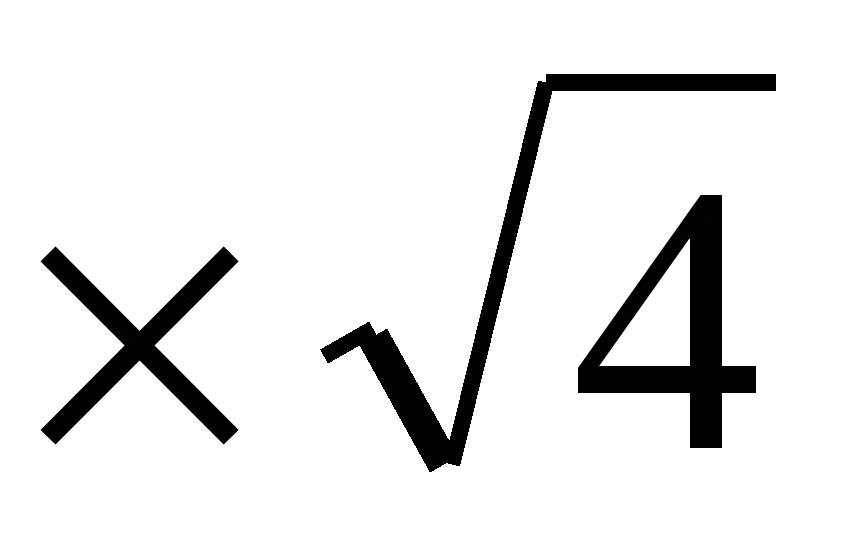 и
и 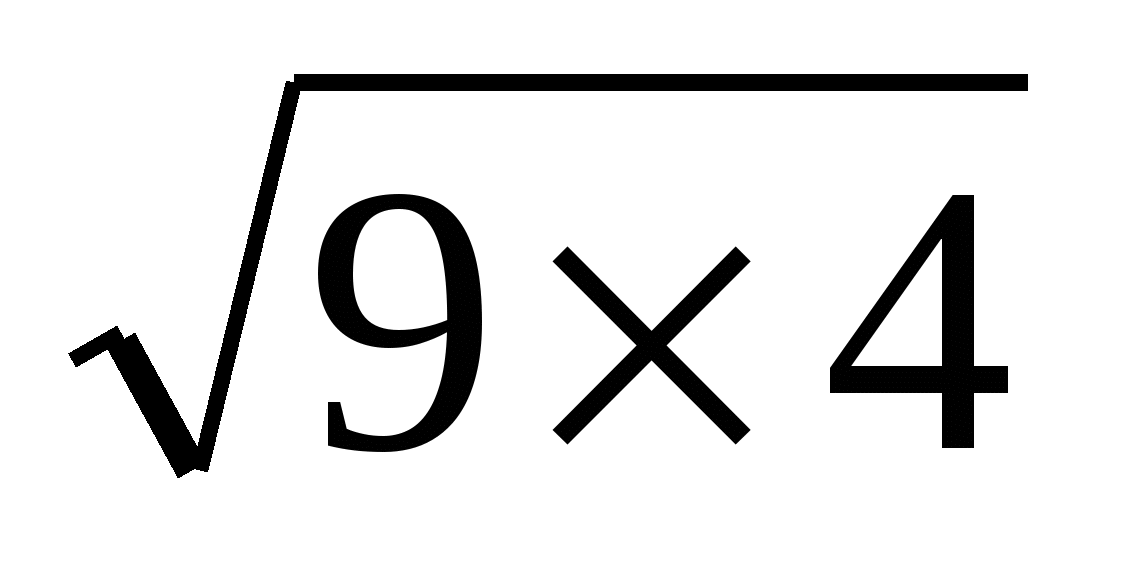 имеют одно и то же значение 6.
имеют одно и то же значение 6.
В самом деле, 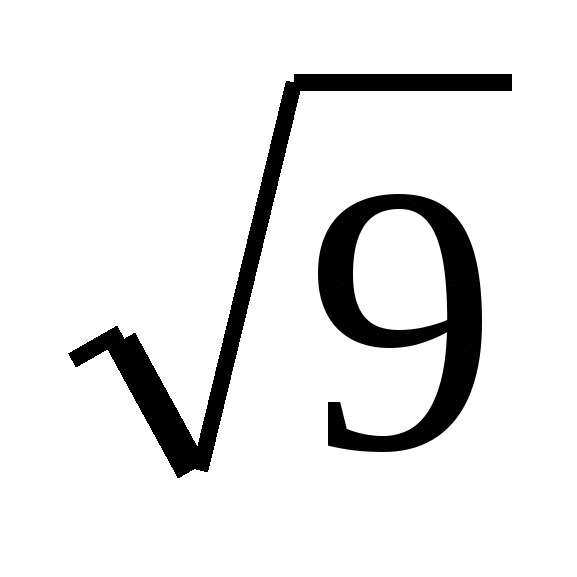 = 3,
= 3, 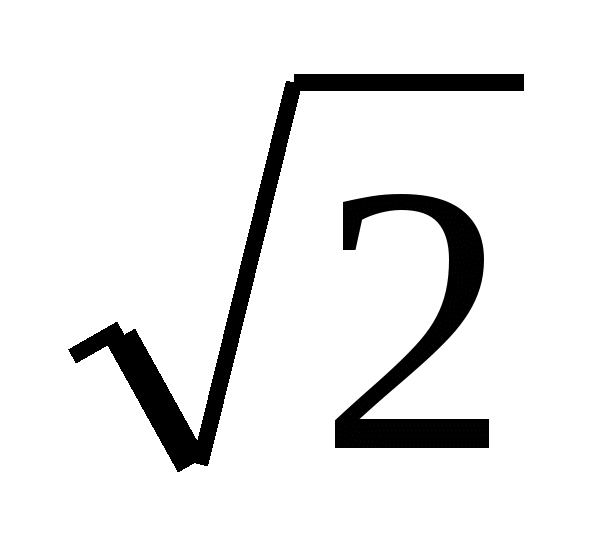 = 2,
= 2, 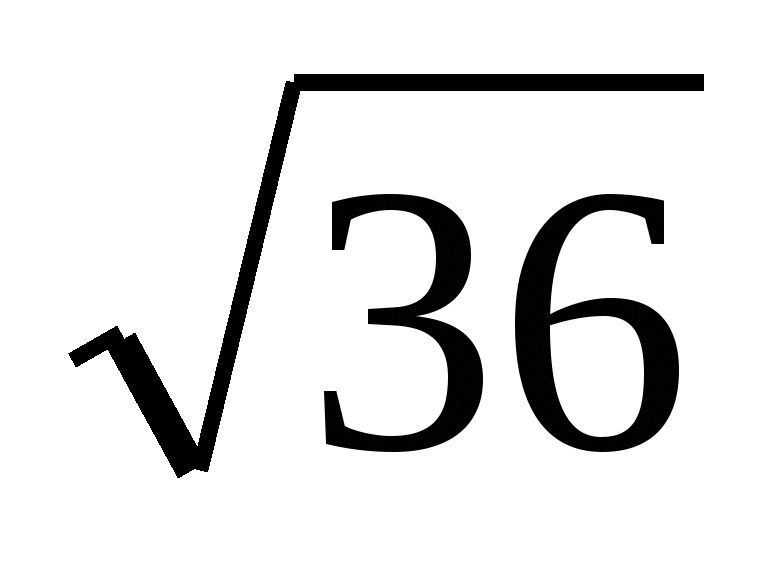 = 6, поэтому
= 6, поэтому 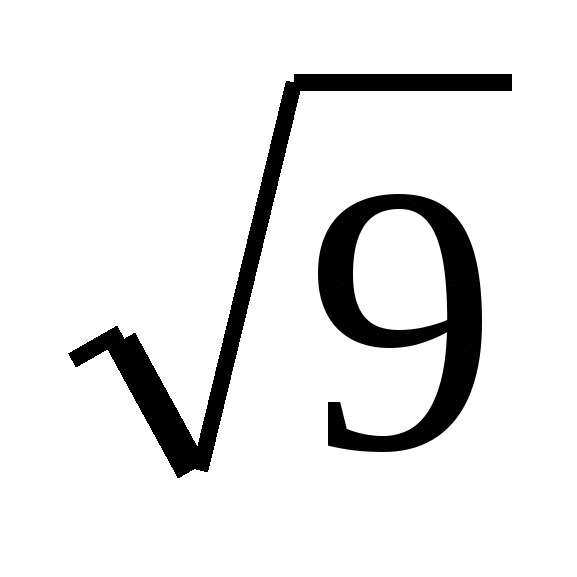

 = 3
= 3  2 = 6 и
2 = 6 и 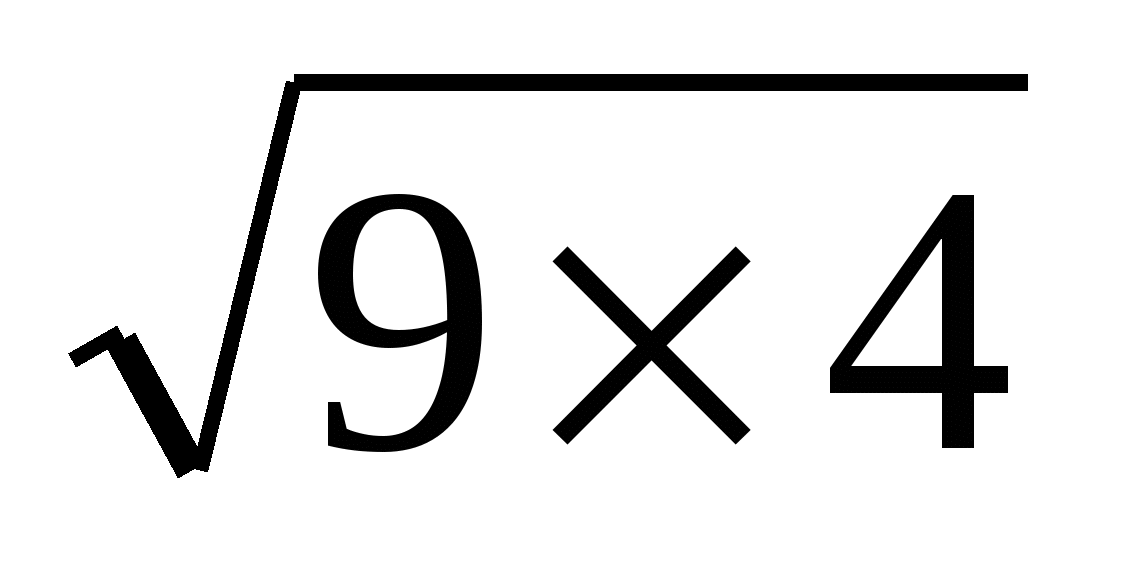 = =
= =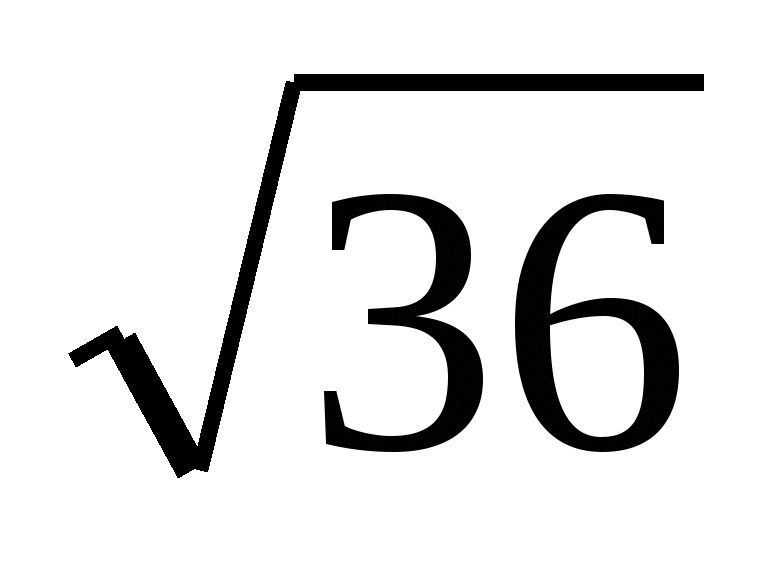 = 6. Равенство
= 6. Равенство 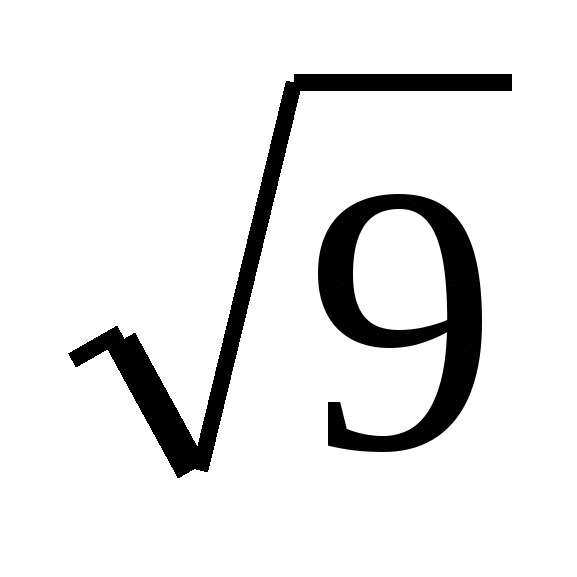

 =
=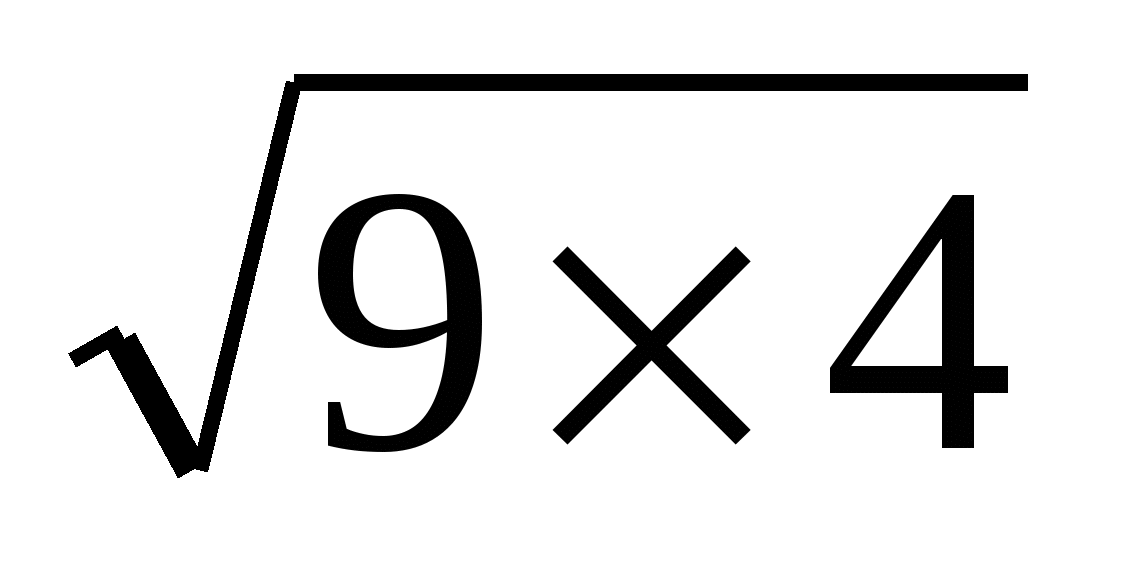 - частный случай общего утверждения :
- частный случай общего утверждения :
Т е о р е м а 1. Квадратный корень из произведения двух неотрицательных чисел равен произведению квадратных корней из этих чисел, т.е. при а 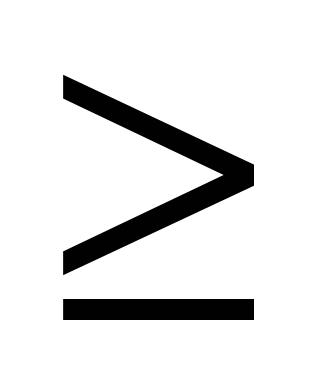 0, b
0, b 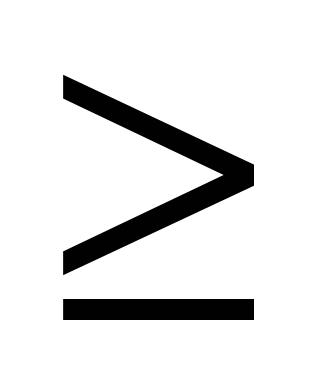 0 имеем
0 имеем 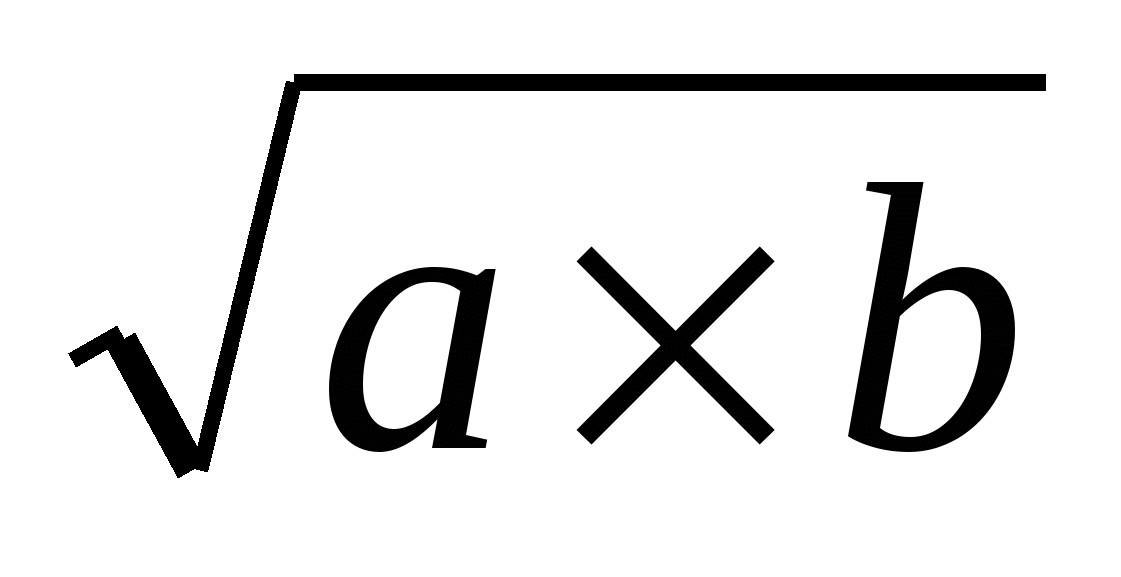 =
= 

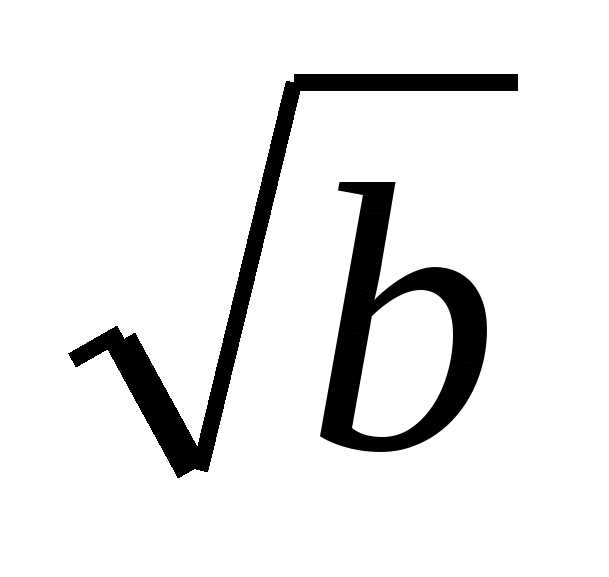 (1)
(1)
 Д о к а з а т е л ь с т в о. Пусть число а и b неотрицательны.
Д о к а з а т е л ь с т в о. Пусть число а и b неотрицательны.
Тогда по правилу возведения в степень имеем
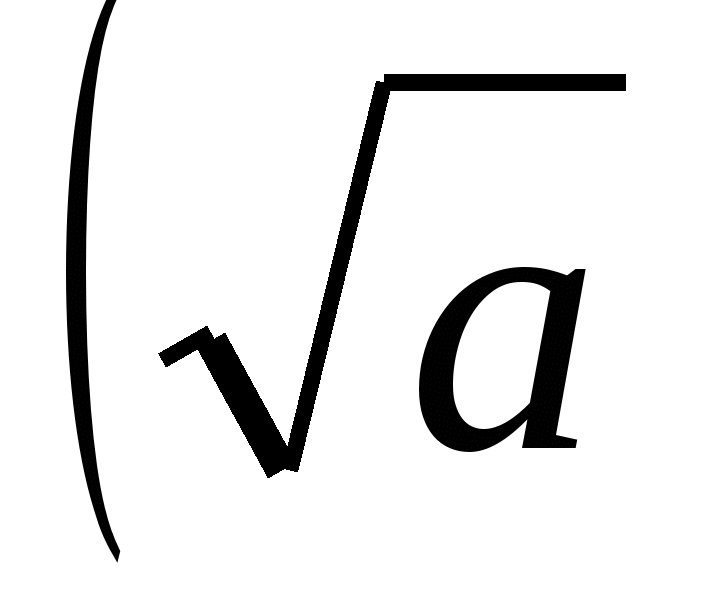

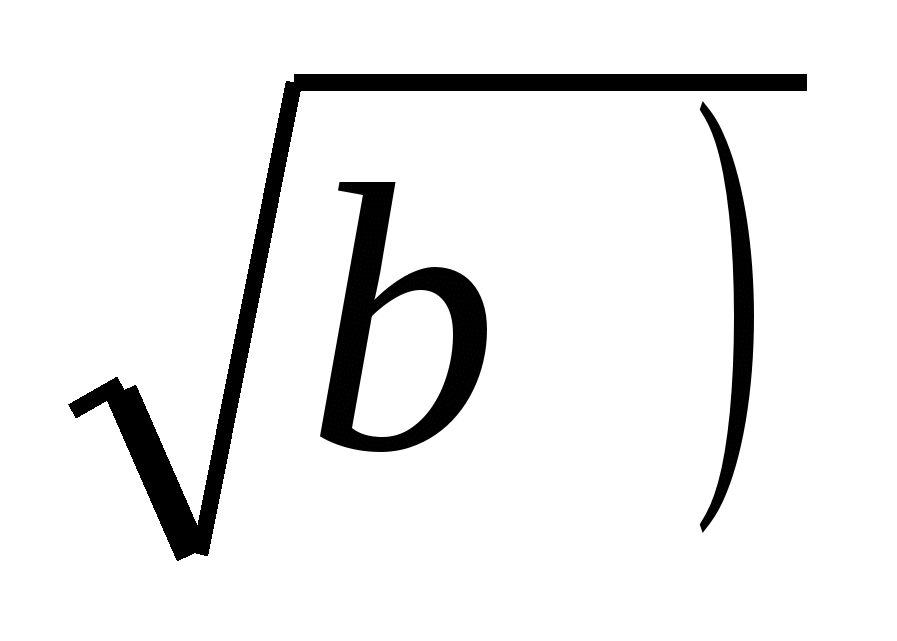 2 =
2 = 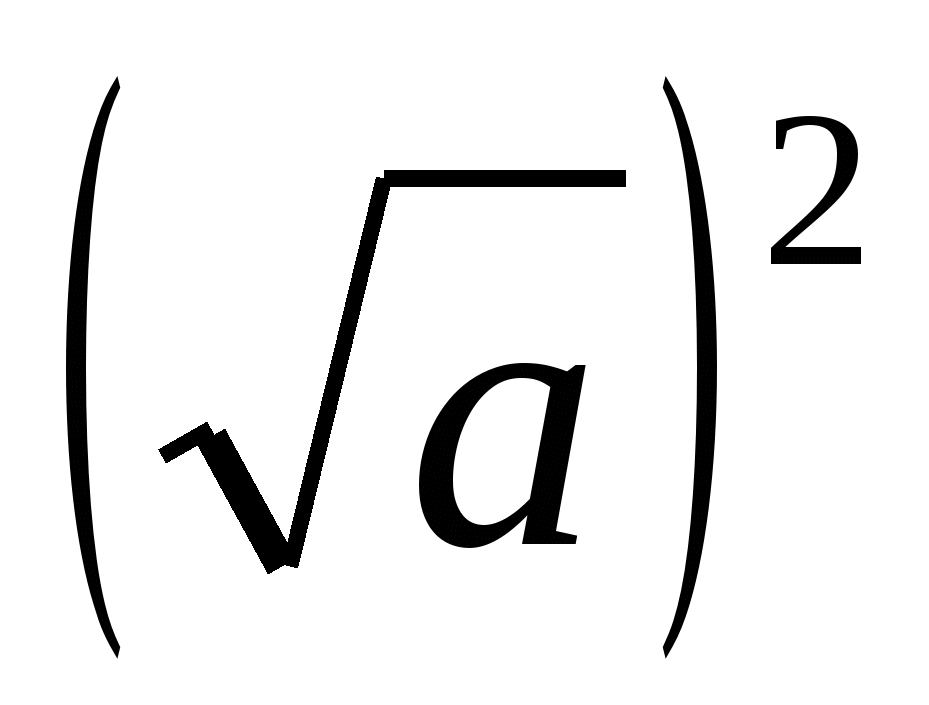


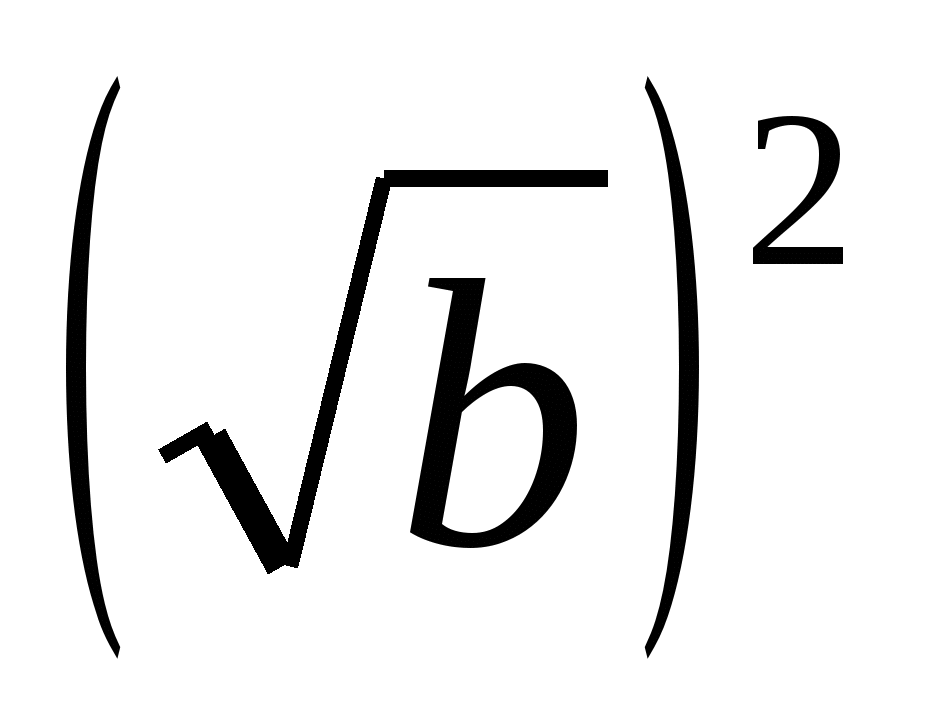 = а
= а  b
b
Кроме того, 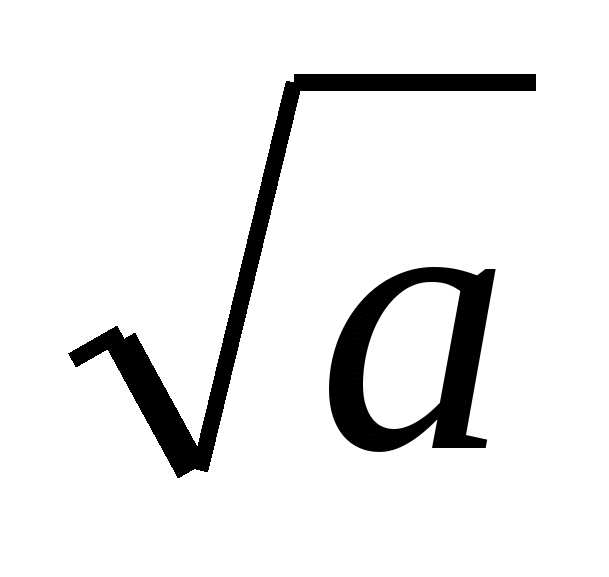

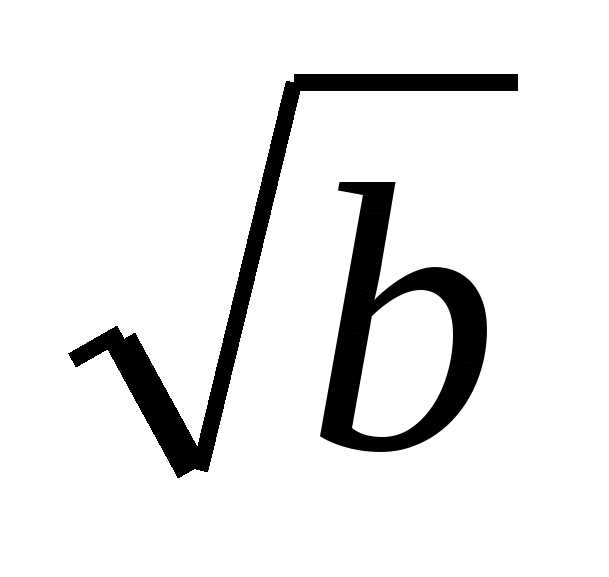 - неотрицательное число как произведение двух неотрицательных чисел
- неотрицательное число как произведение двух неотрицательных чисел 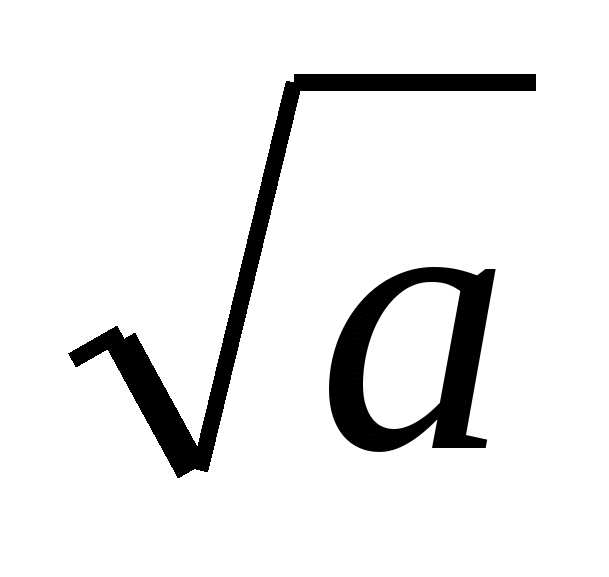 и
и 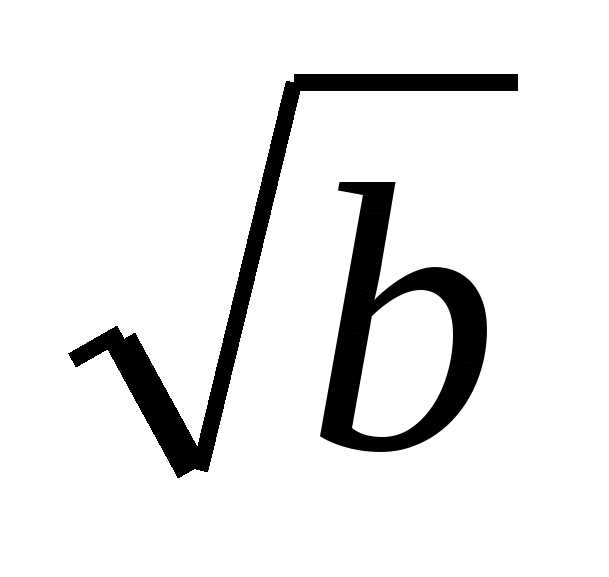 . Поэтому
. Поэтому 

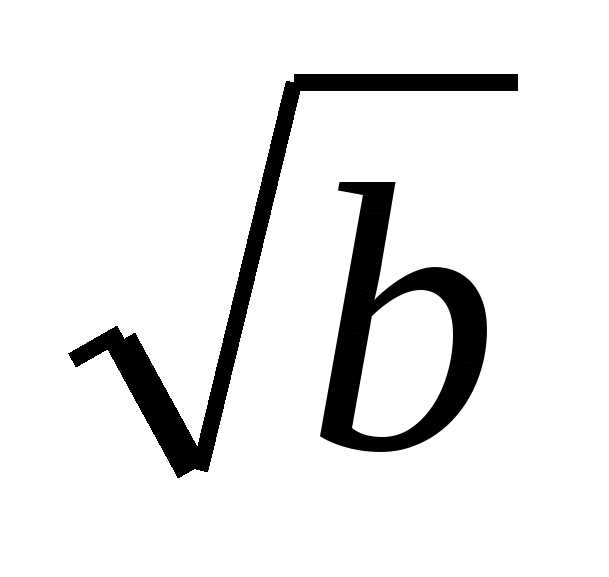 =
= 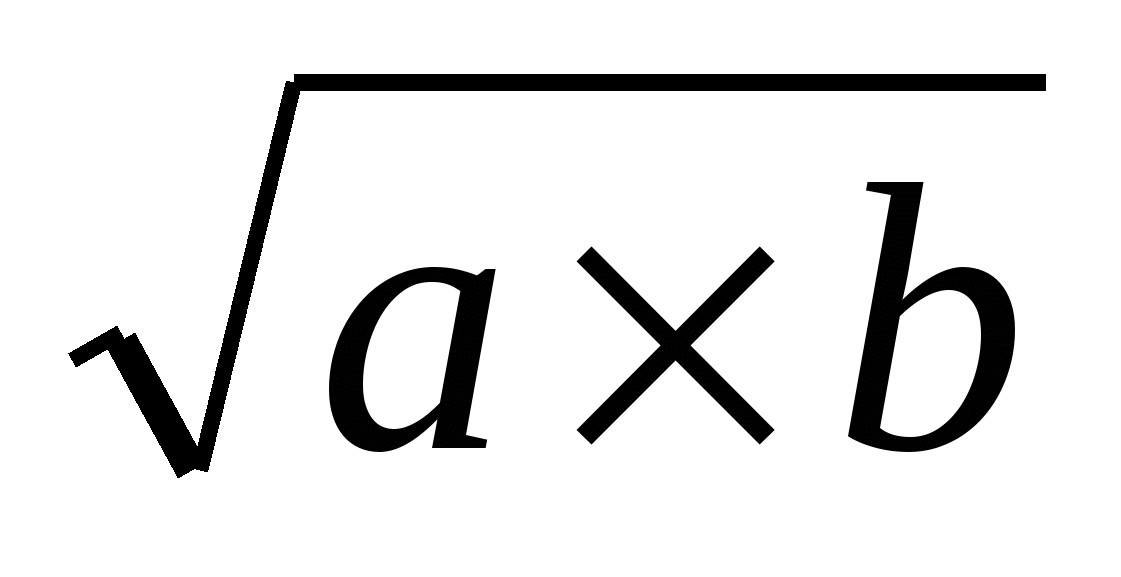
П р и м е р 1. Найдем значения выражения 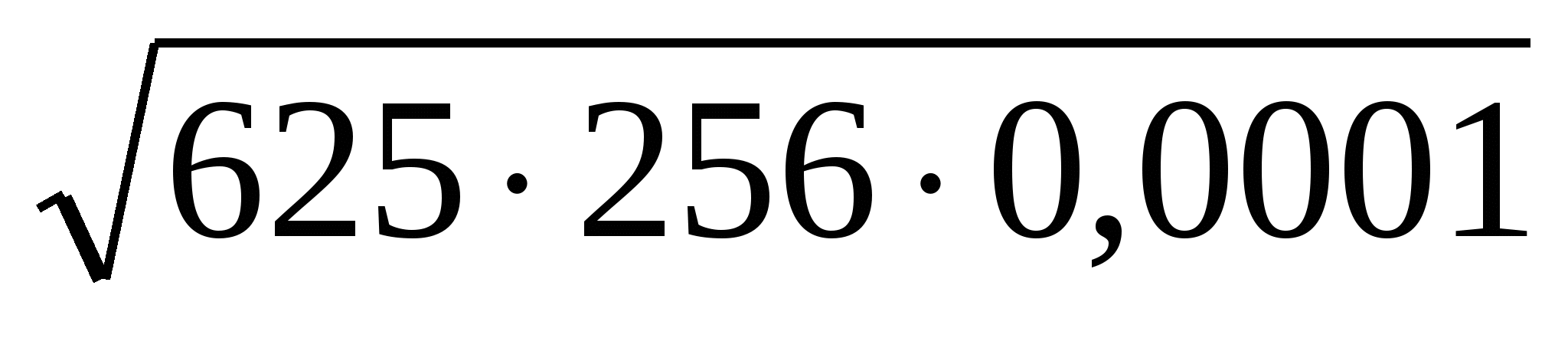
Р е ш е н и е. Мы имеем 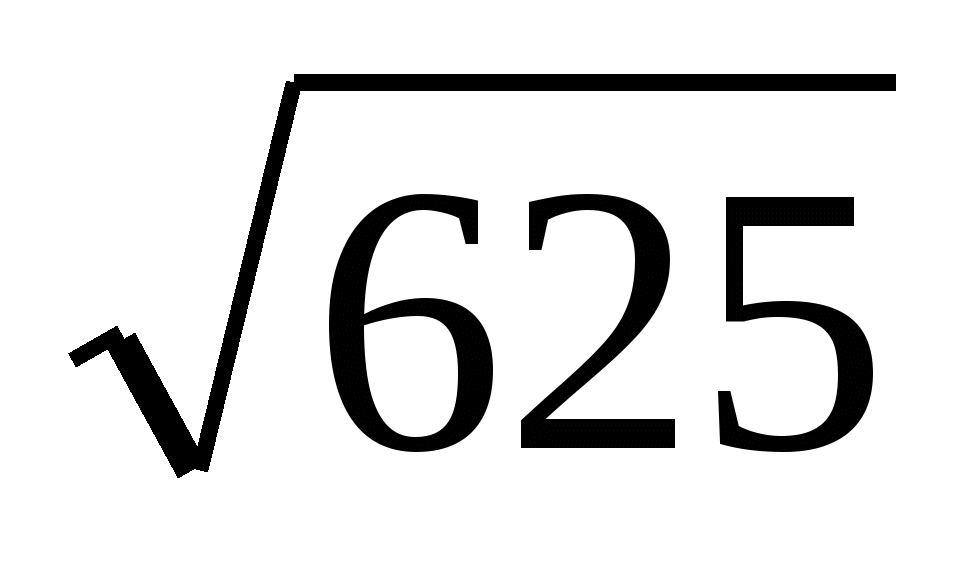 = 25,
= 25, 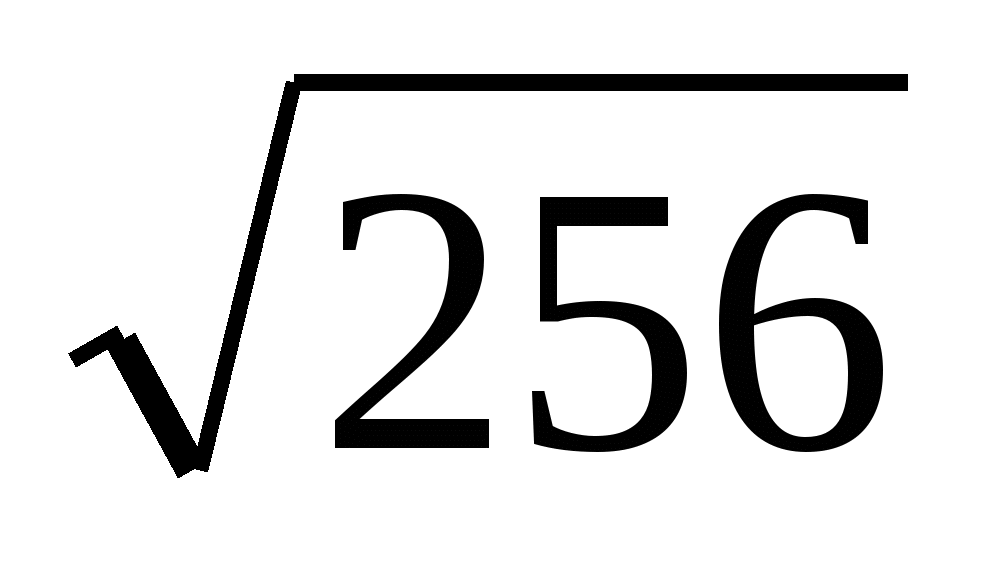 = 16,
= 16,  = 0,01,
= 0,01,
и потому 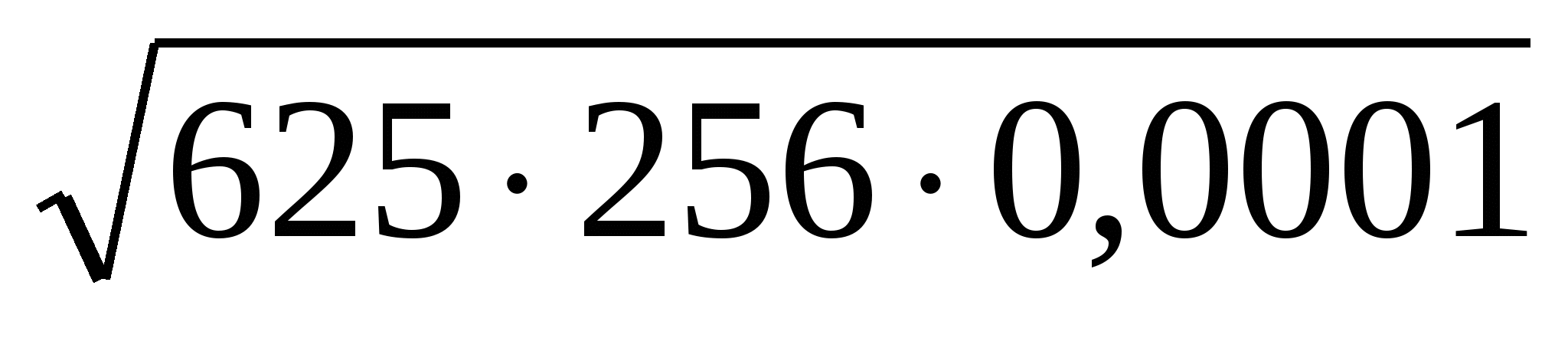 = 25
= 25 16
16 0,01= 4.
0,01= 4.
Аналогично доказывается, что  =
=  (2)
(2)
Преобразование выражений
При преобразовании выражении, содержащих квадратные корни, оказывается полезной следующая формула:
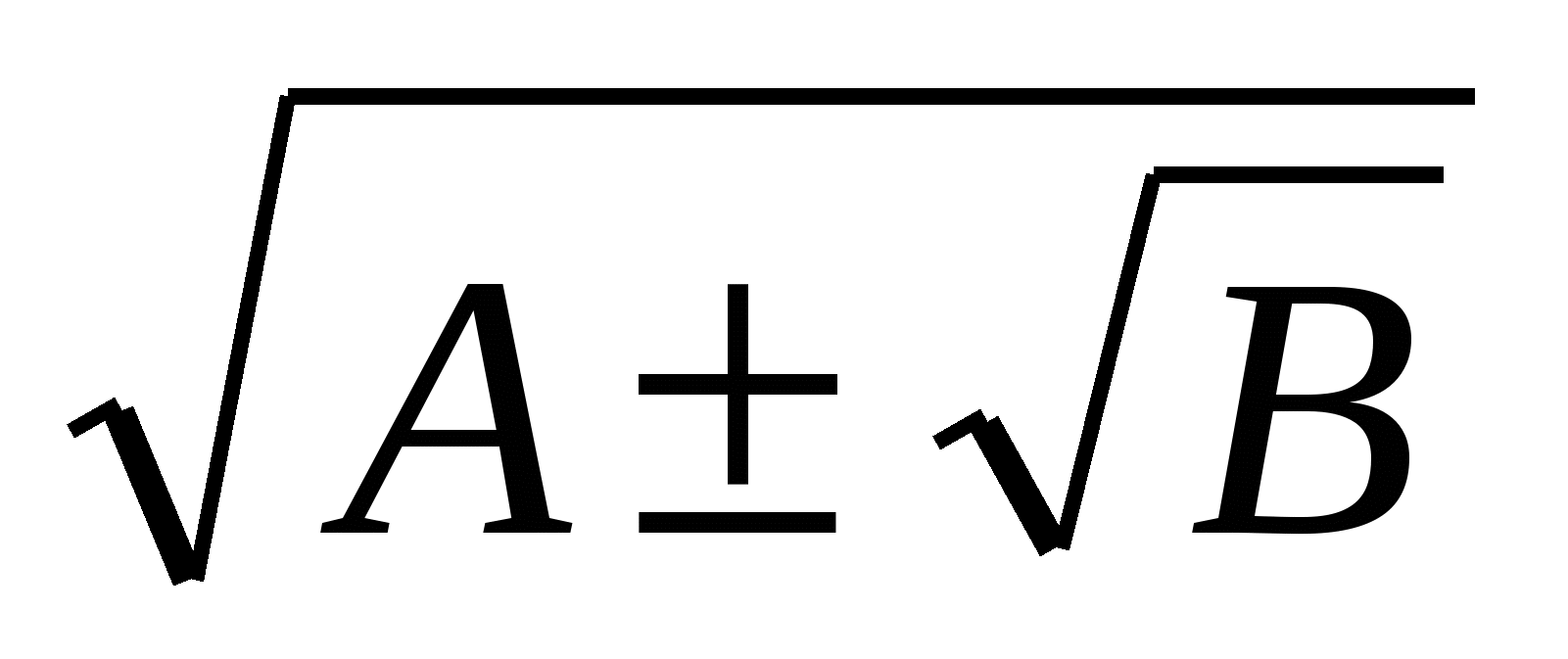 =
= 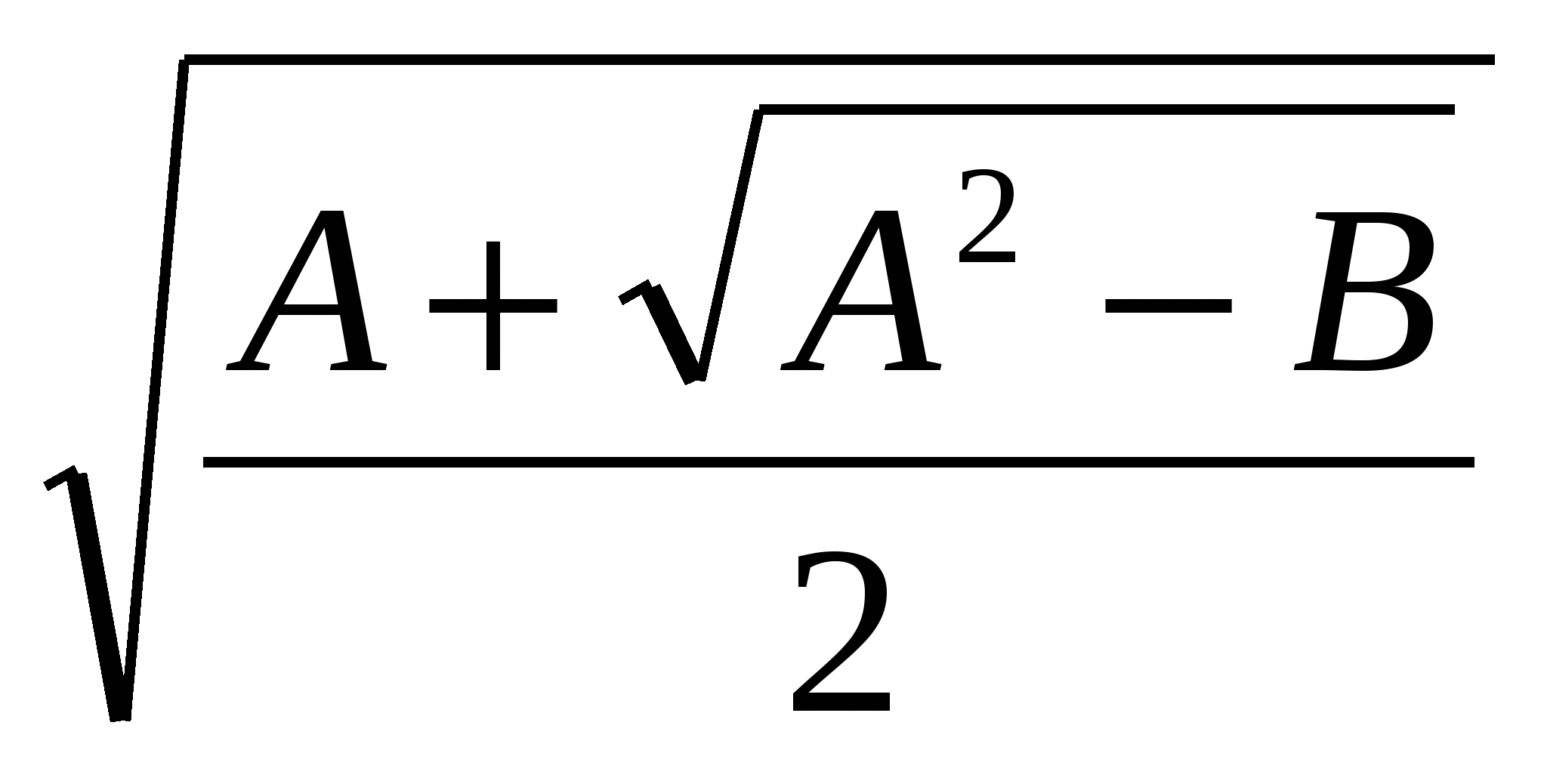

 ,
,
где А2 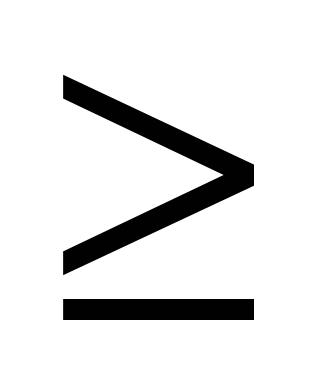 В (в обеих частях равенства одновременно берутся знаки “ плюс “ и “ минус “). Чтобы доказать это равенство, заметим, во-первых, что и левая, и правая его части являются при А
В (в обеих частях равенства одновременно берутся знаки “ плюс “ и “ минус “). Чтобы доказать это равенство, заметим, во-первых, что и левая, и правая его части являются при А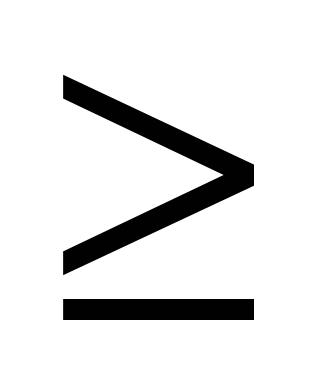 0, В
0, В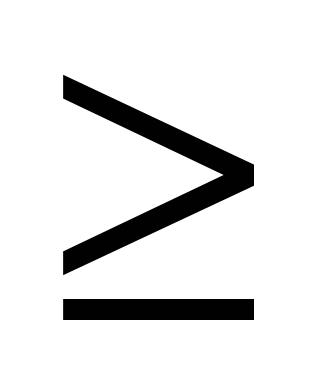 0, А2 – В
0, А2 – В 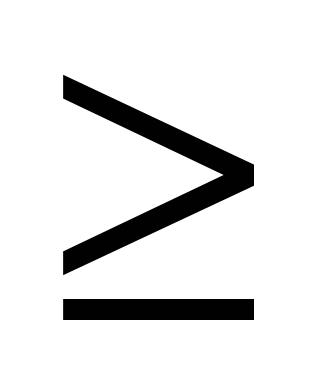 0 неотрицательными числами. Возведем теперь обе части равенства
0 неотрицательными числами. Возведем теперь обе части равенства 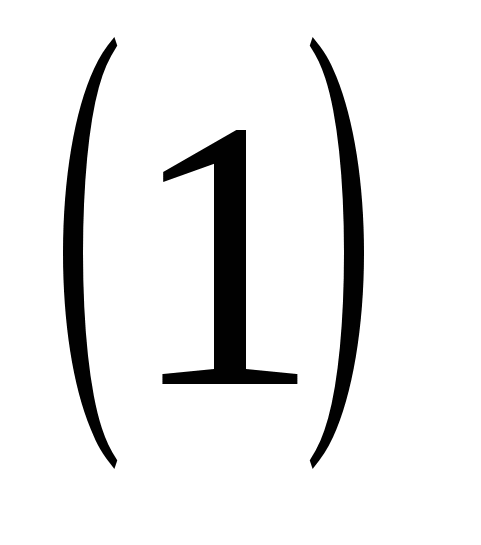 в квадрат. В левой части имеем А
в квадрат. В левой части имеем А 
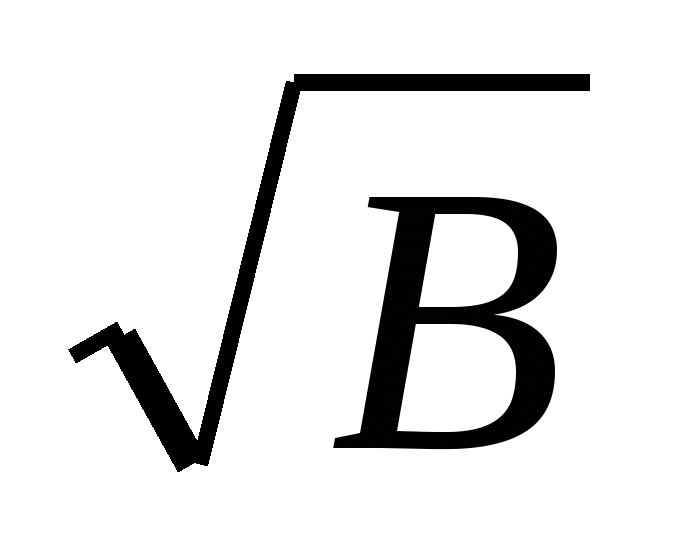 , в правой части по формуле квадрата суммы или разности получаем
, в правой части по формуле квадрата суммы или разности получаем
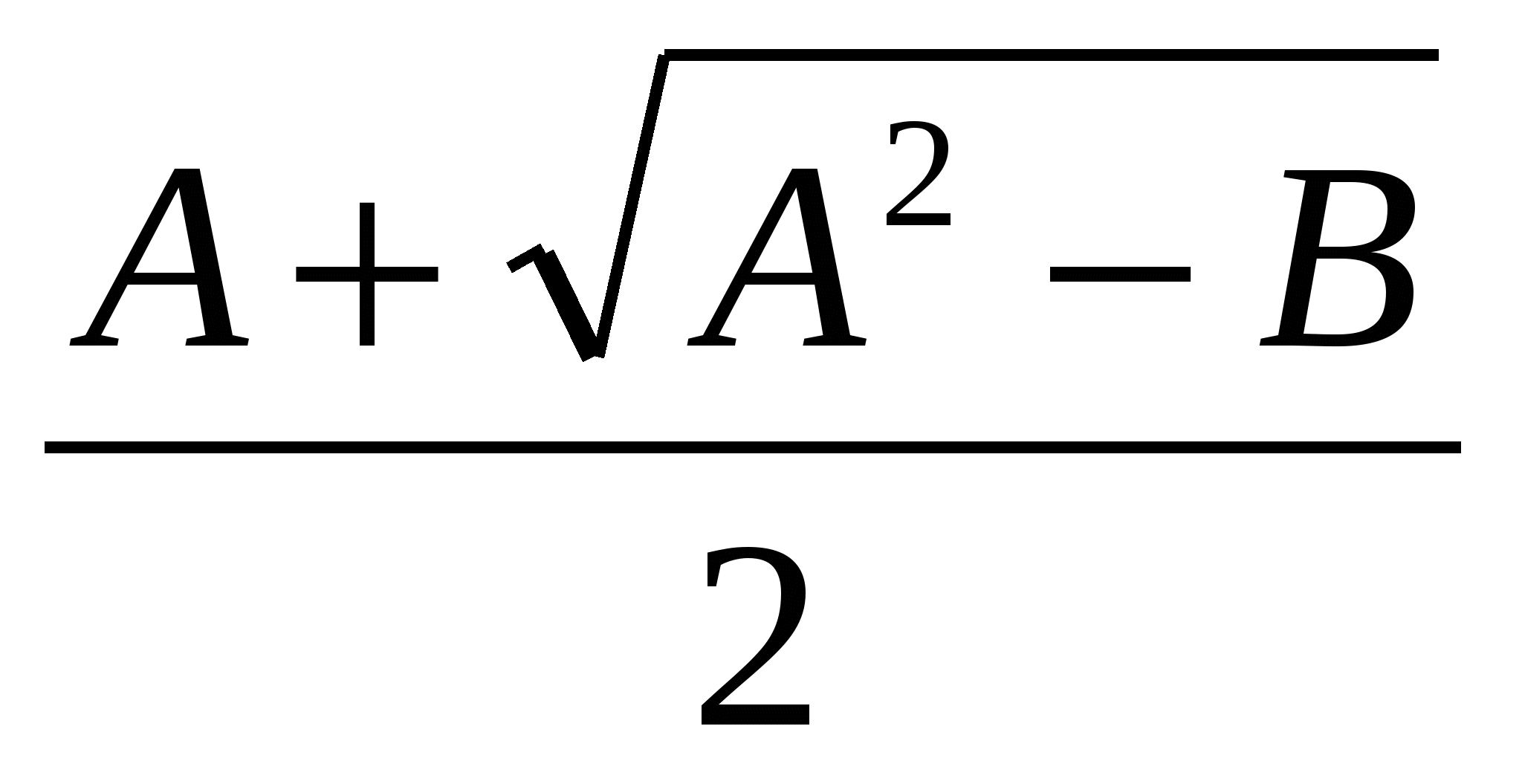
 2
2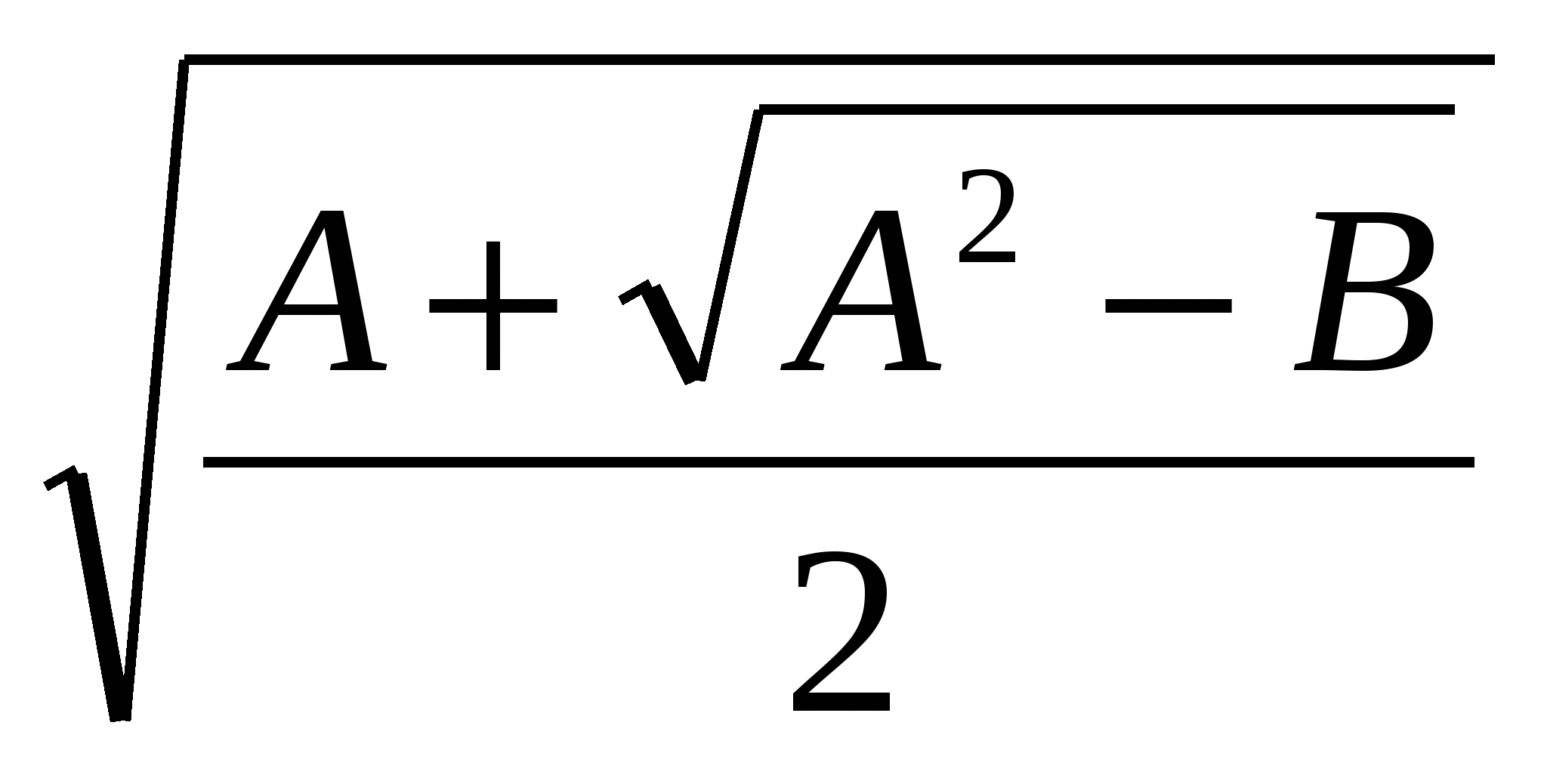

 +
+ 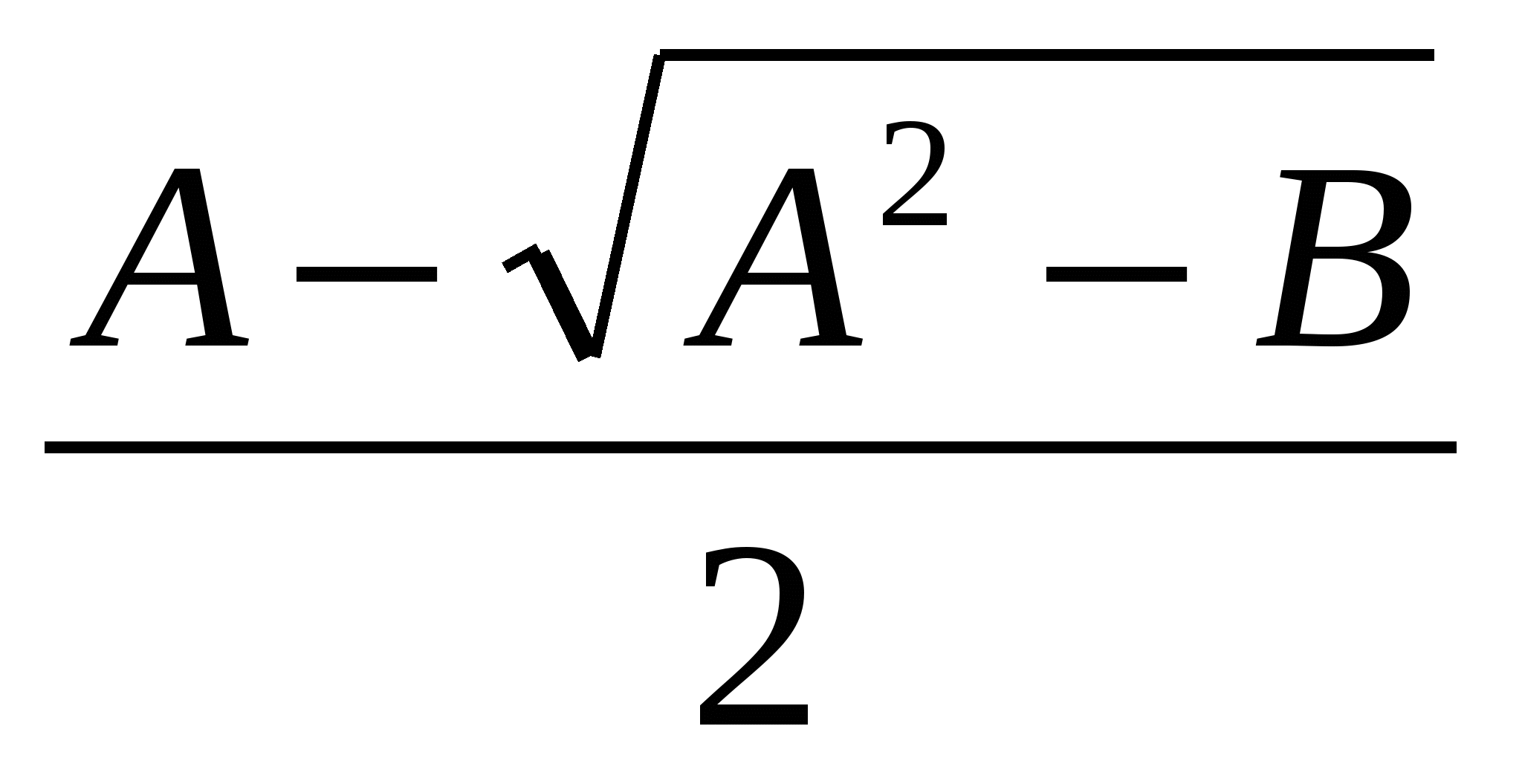 =
=
= А  2
2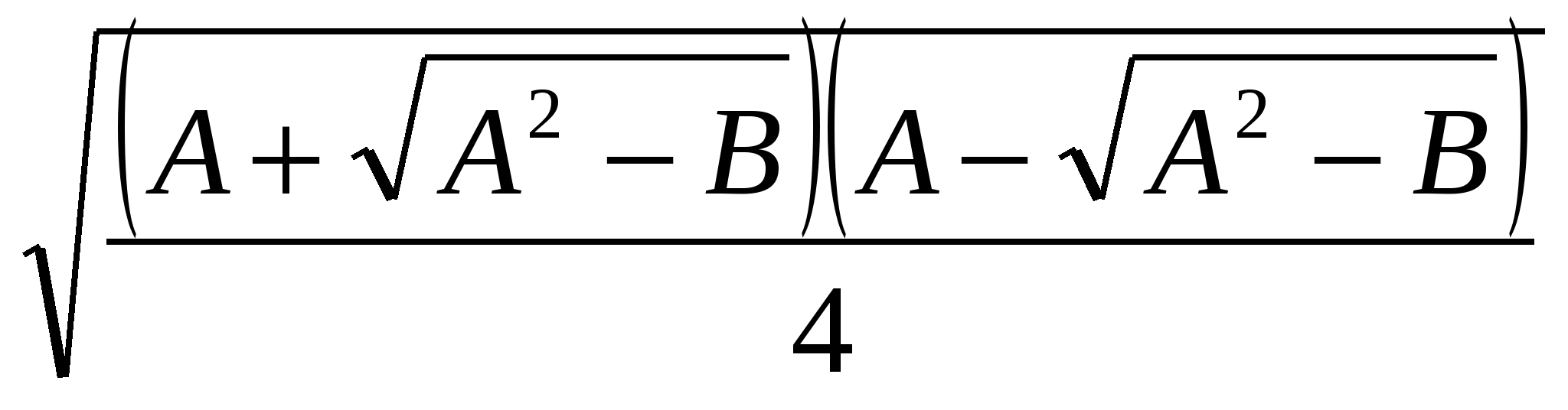 = А
= А  2
2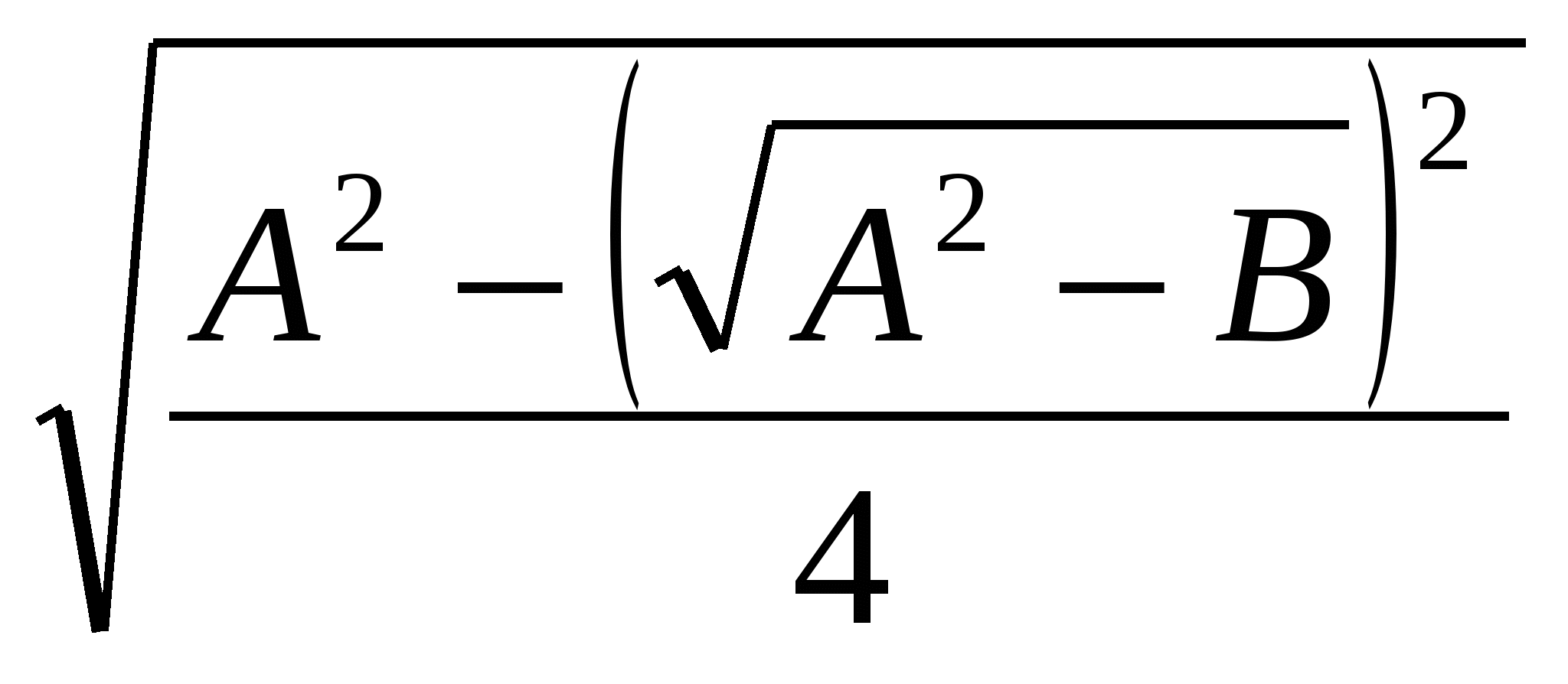 =
=
= А  2
2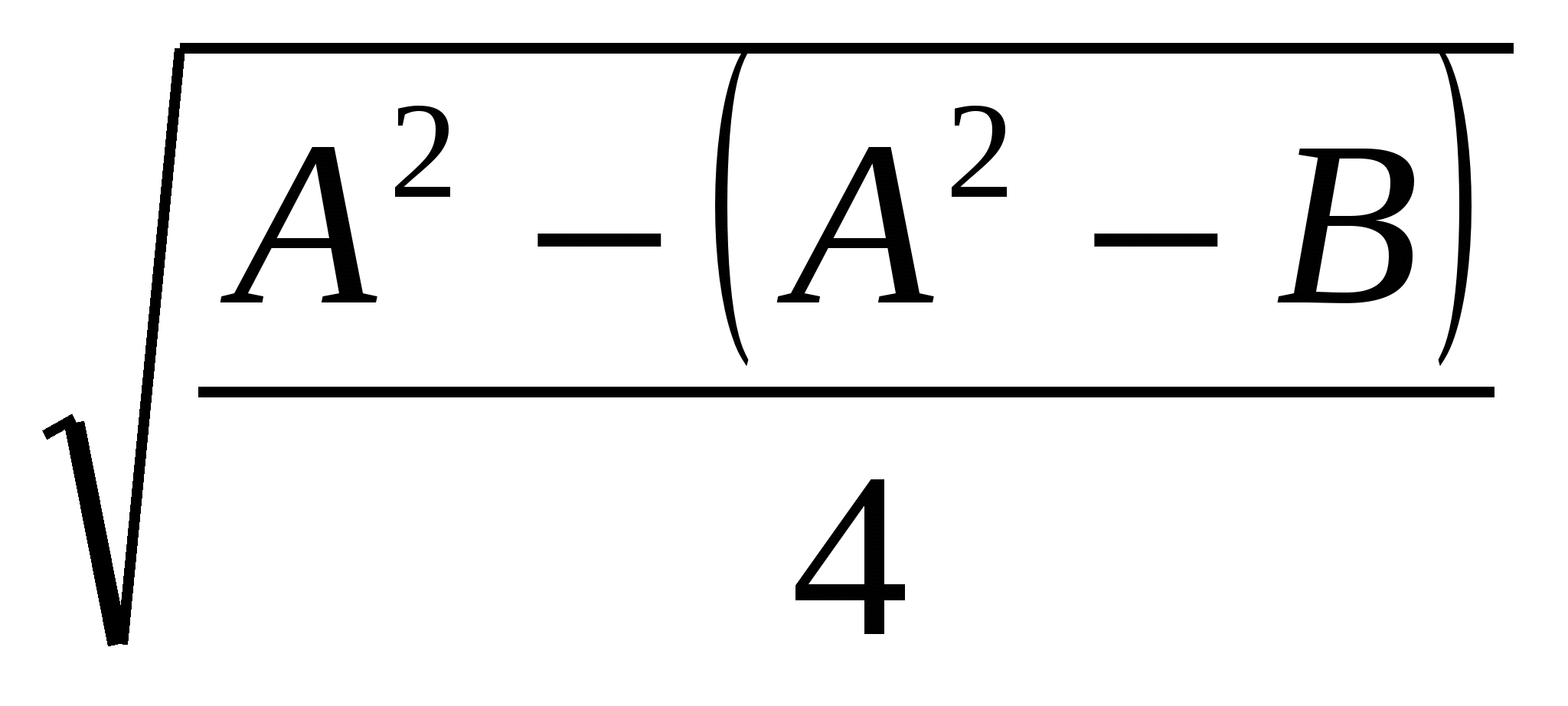 = А
= А  2
2 = А
= А 
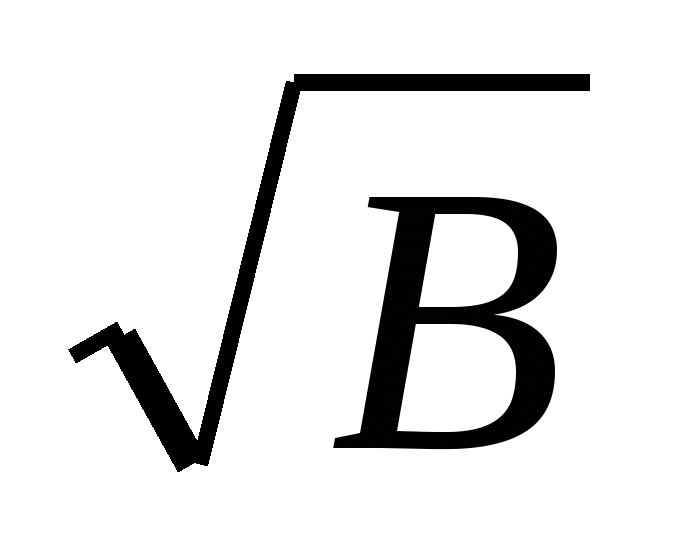 .
.
Таким образом, квадраты обеих частей равенства 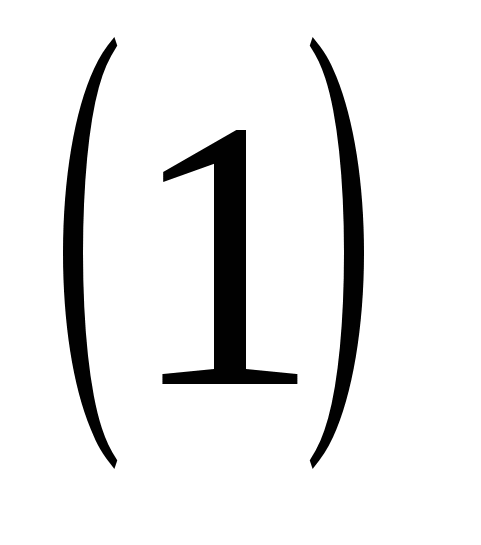 оказались одинаковыми, а поскольку эти части – неотрицательные числа, то равенство
оказались одинаковыми, а поскольку эти части – неотрицательные числа, то равенство 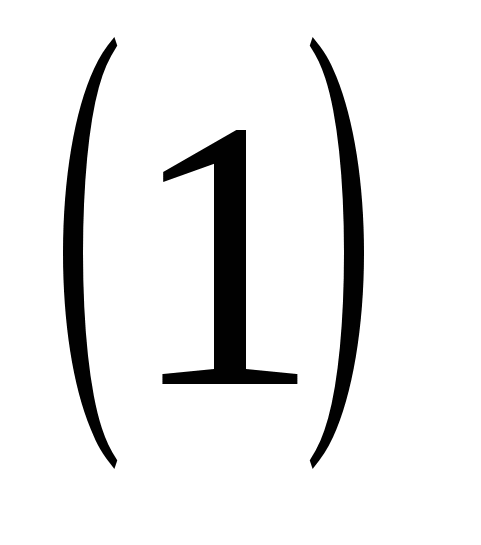 доказано.
доказано.
П р и м е р 1. Упростим выражение 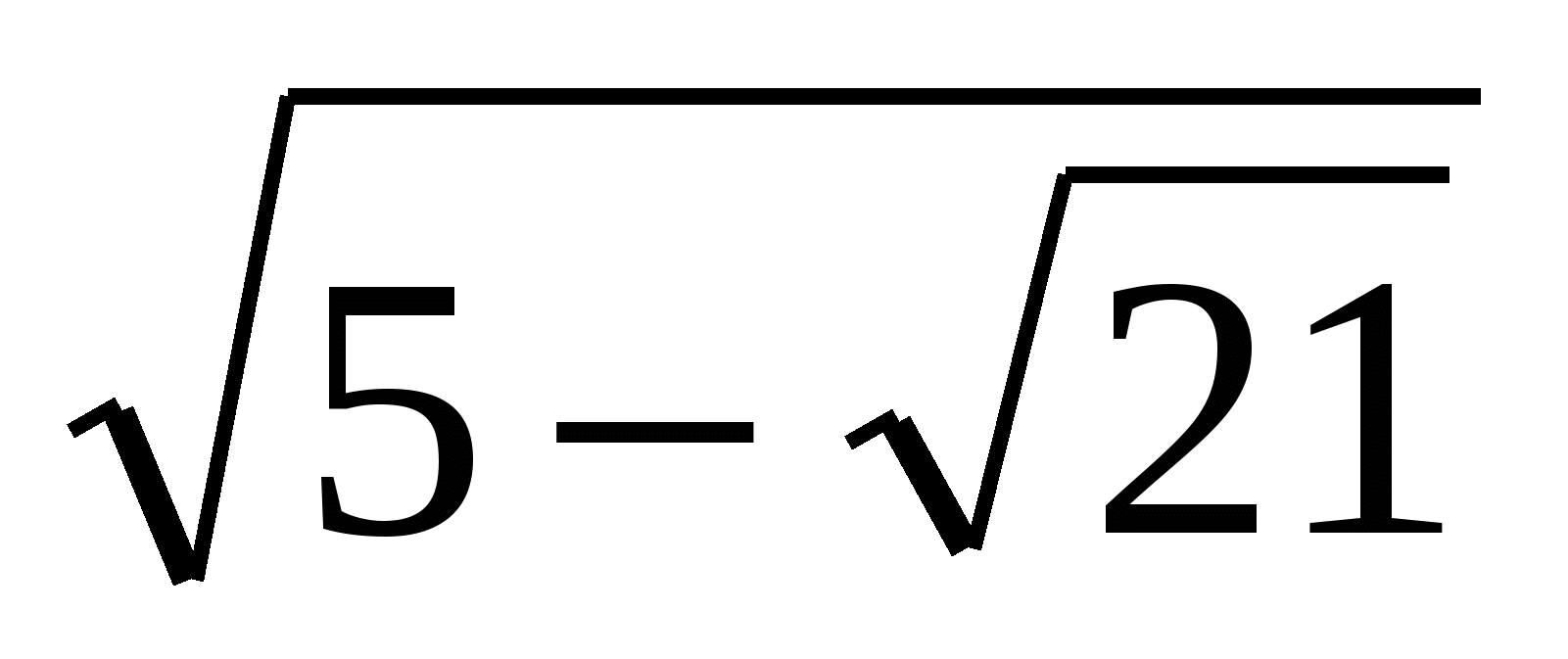 .
.
1-й с п о с о б. В одном случае имеем А = 5, В = 21, А2 – В =
= 52 – 21 = 4, и поэтому по формуле 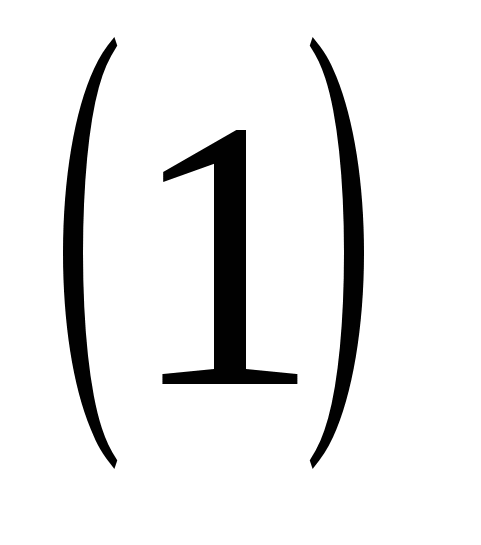
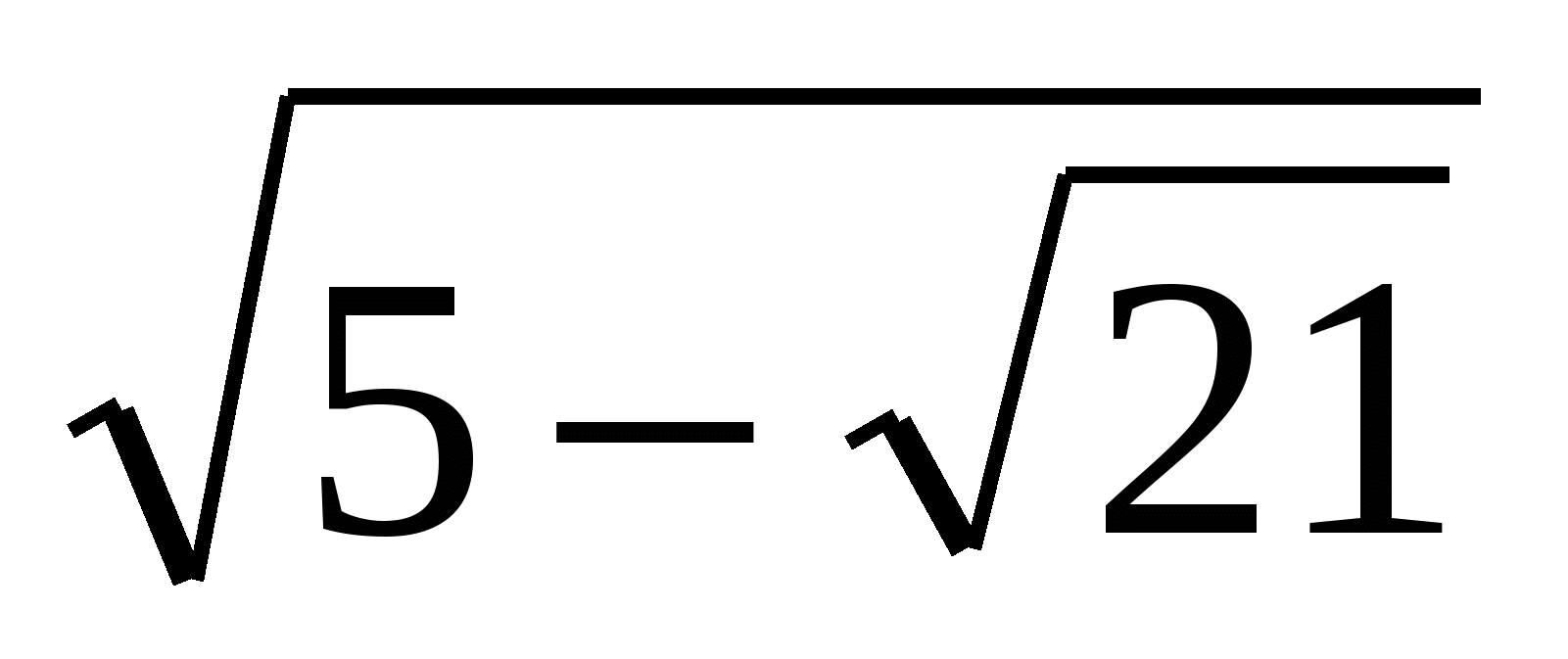 =
= 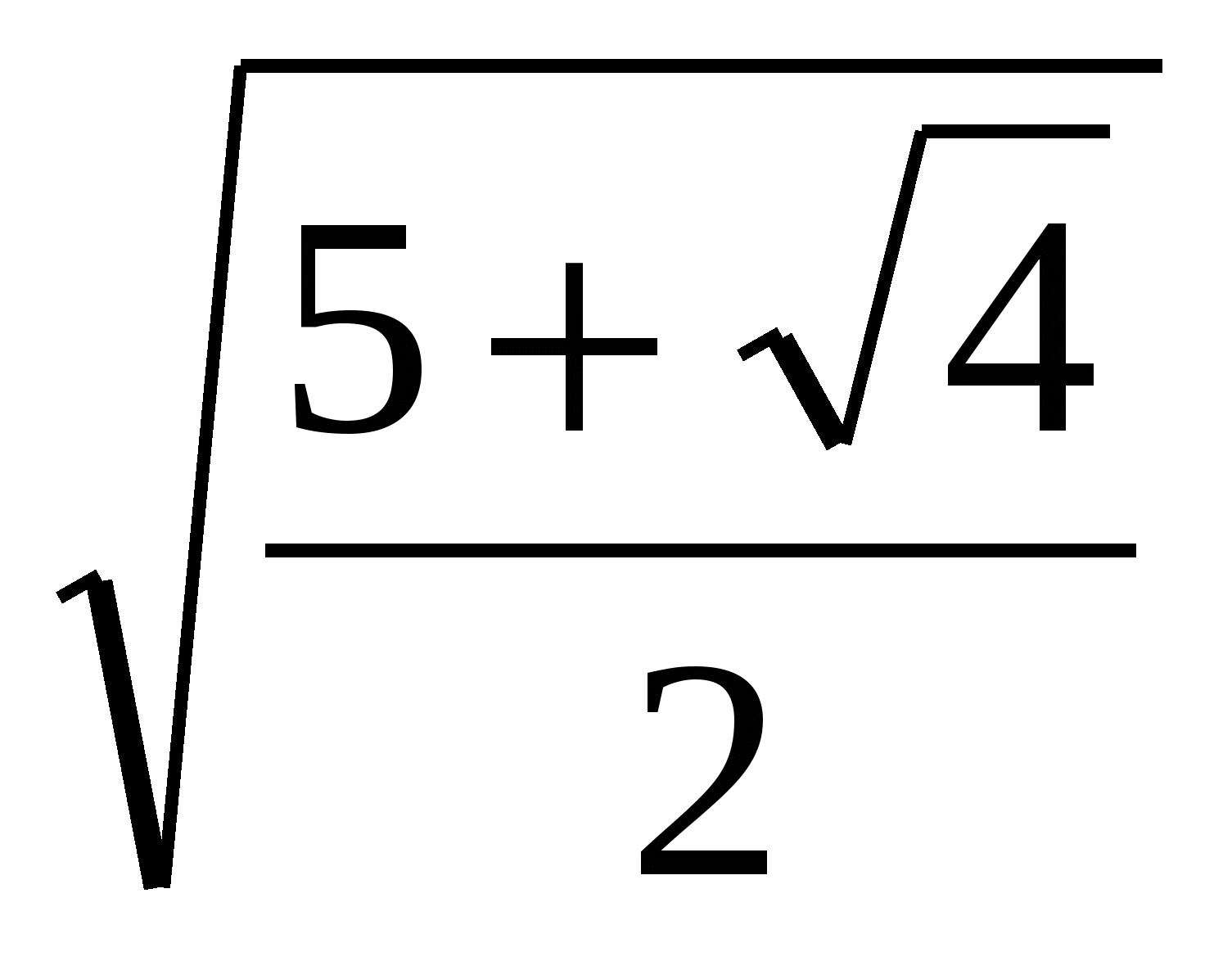 -
- 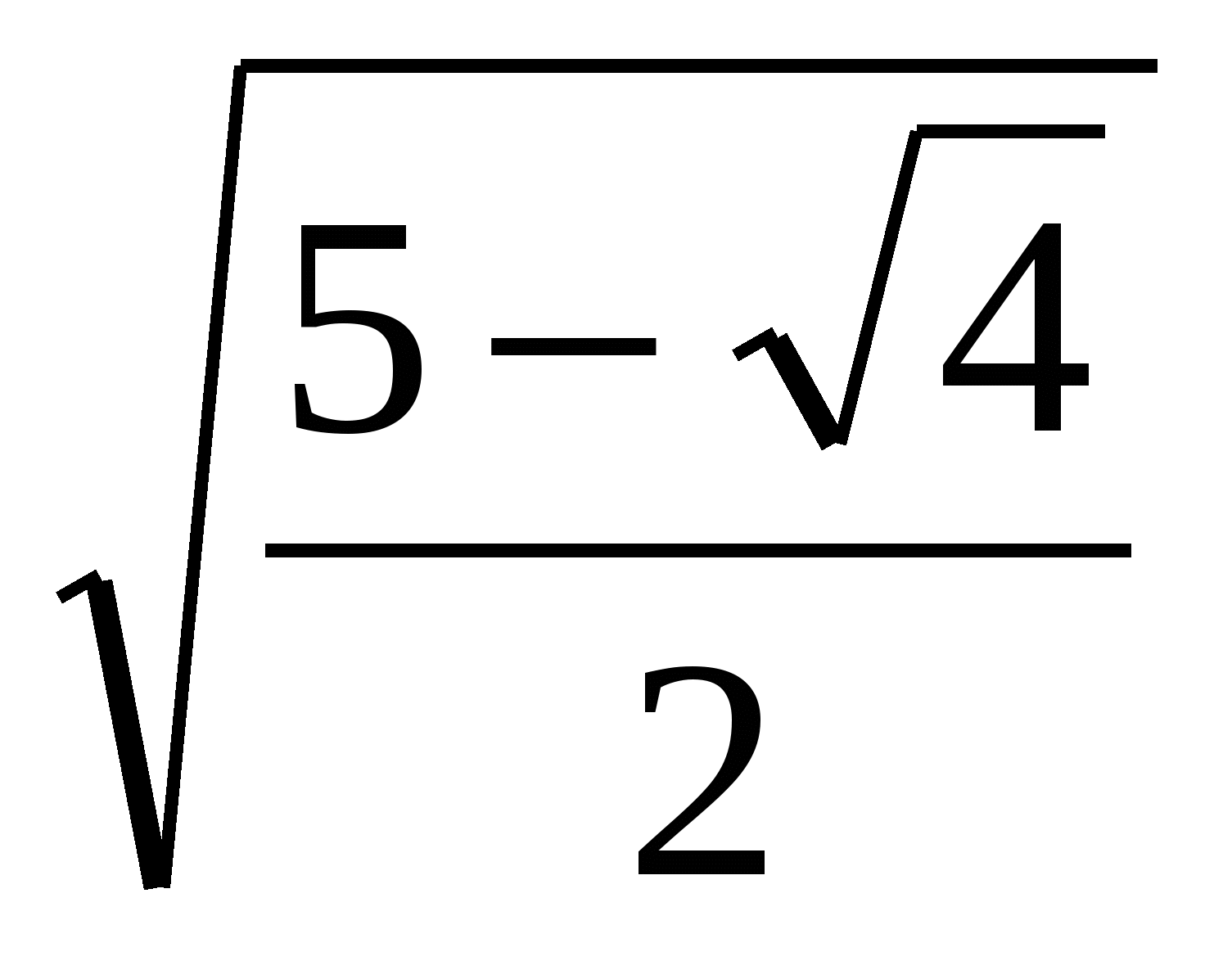 =
= 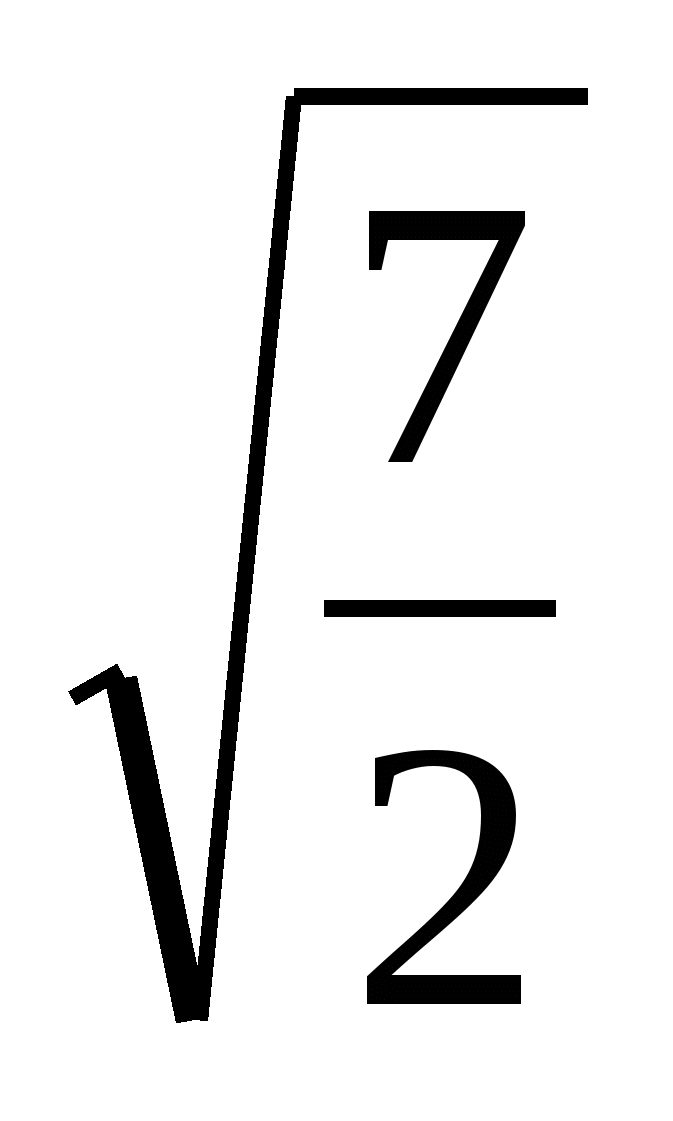 -
- 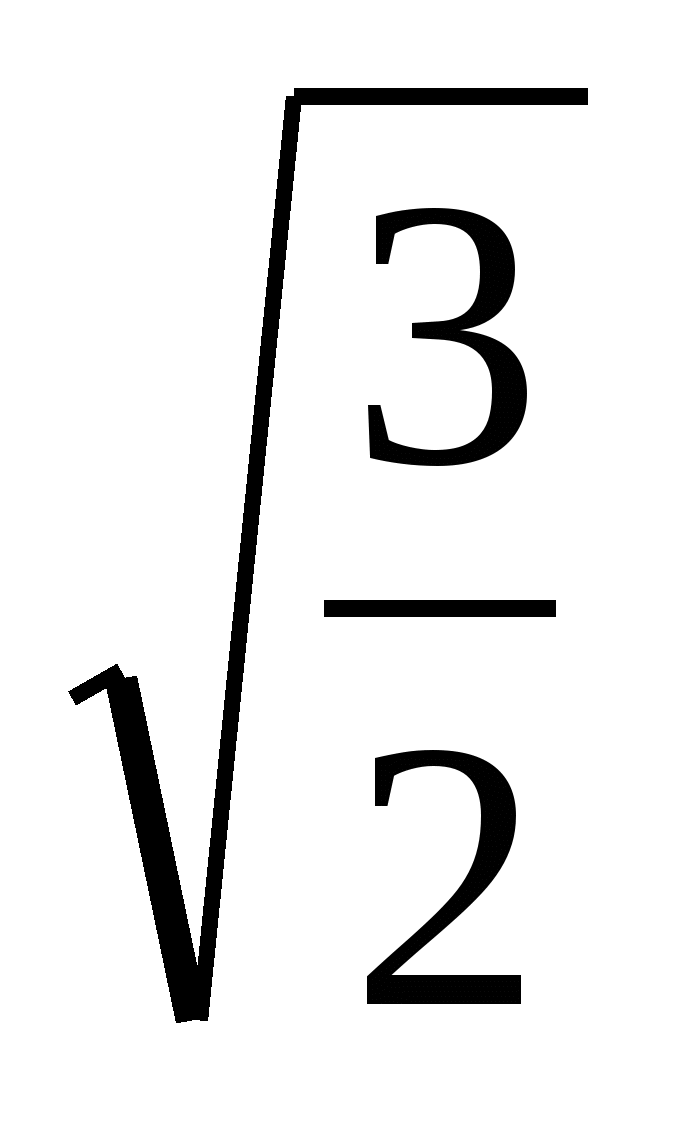 .
.
2-й с п о с о б. Приведем подкоренное выражение к полному квадрату:
5 - 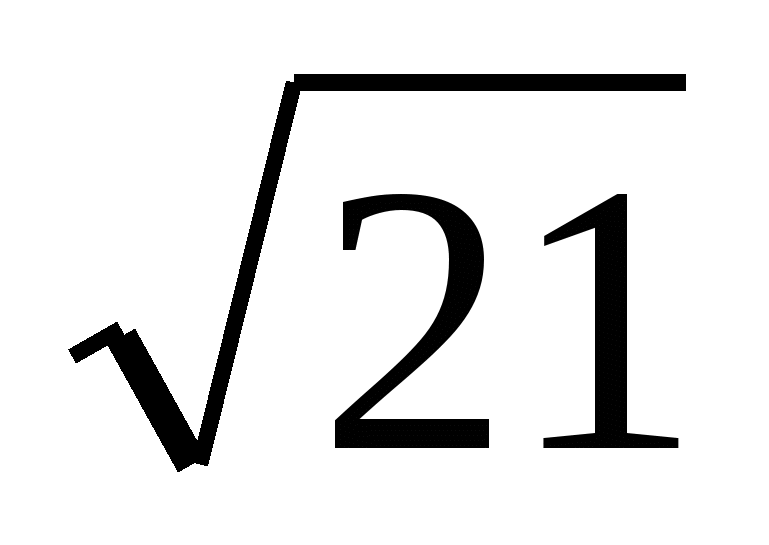 =
= 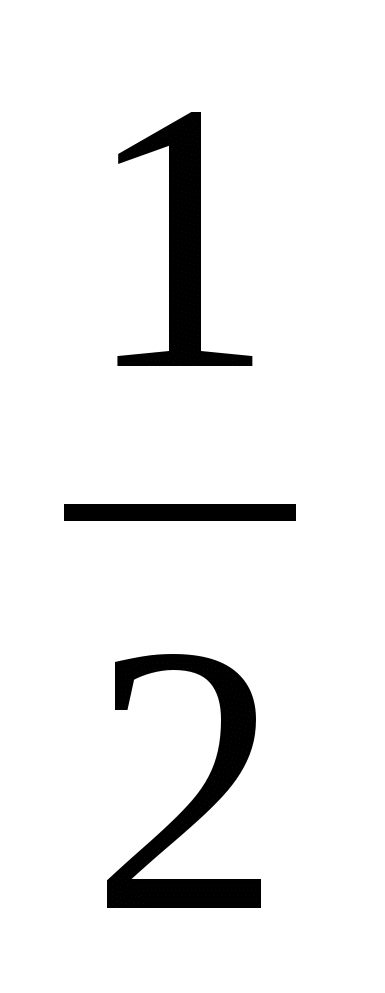
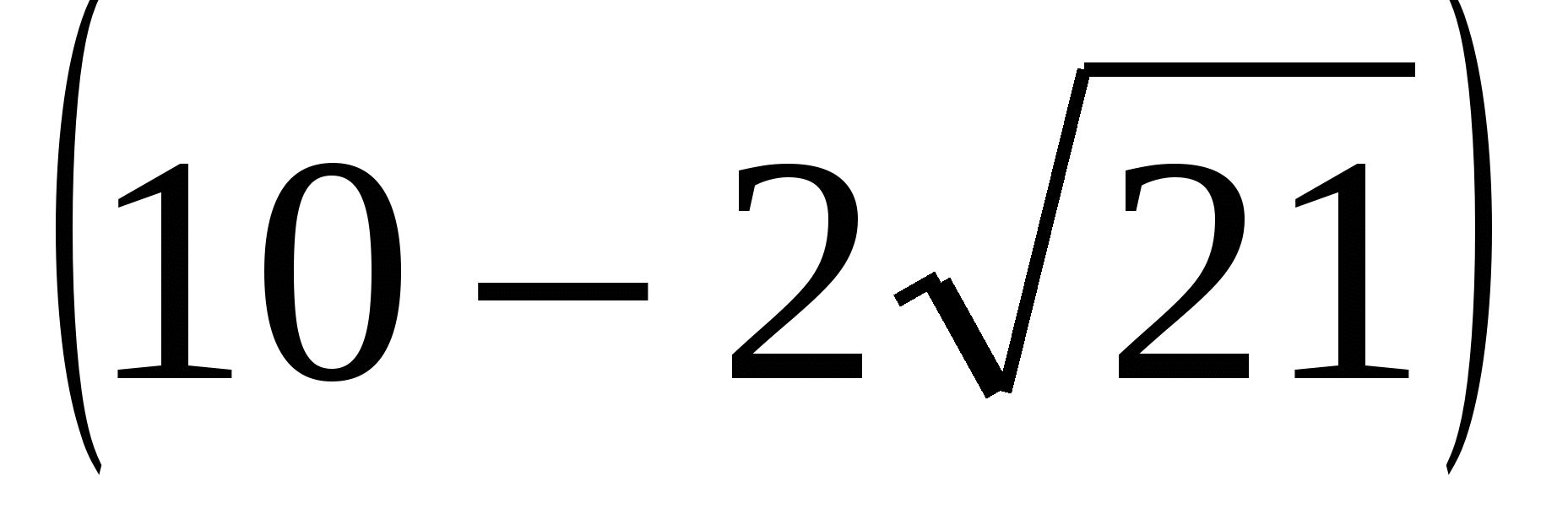 =
= 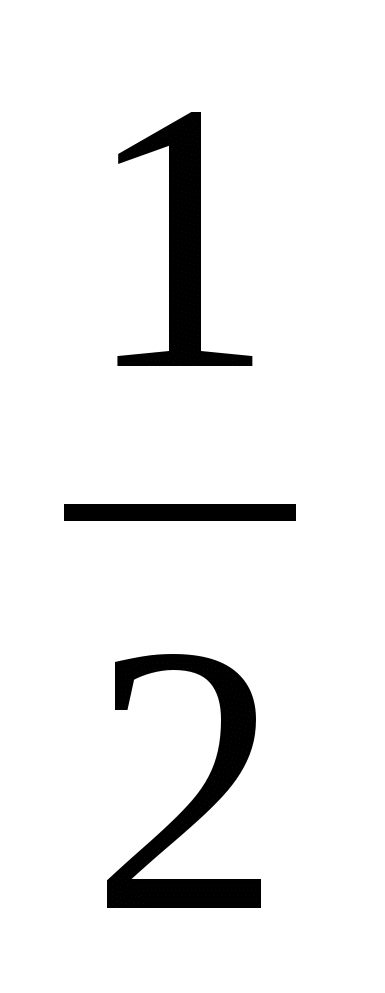
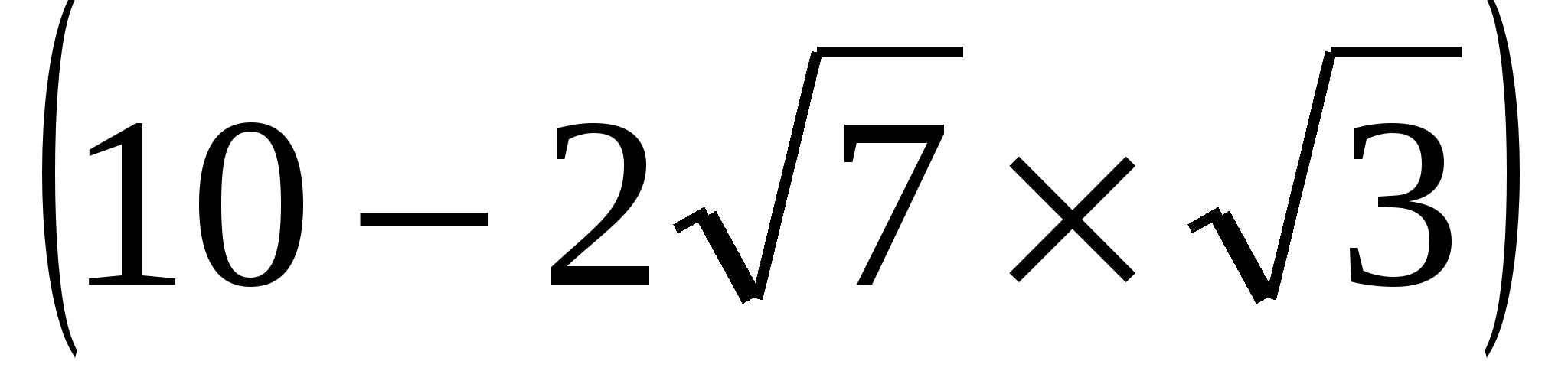 =
=
=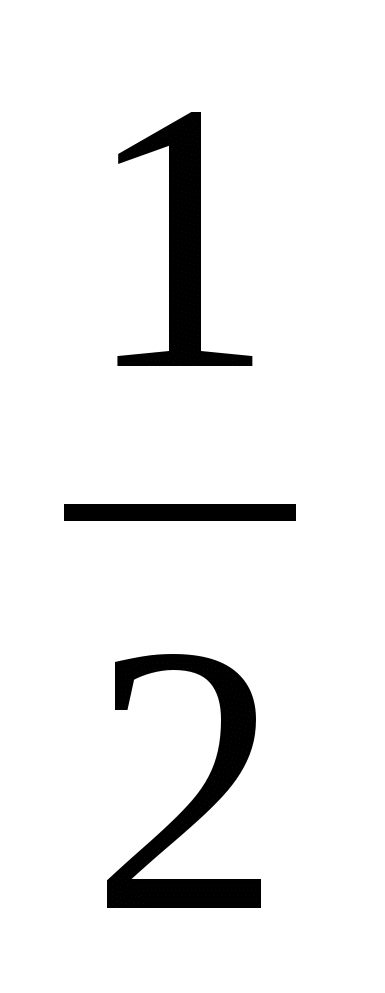
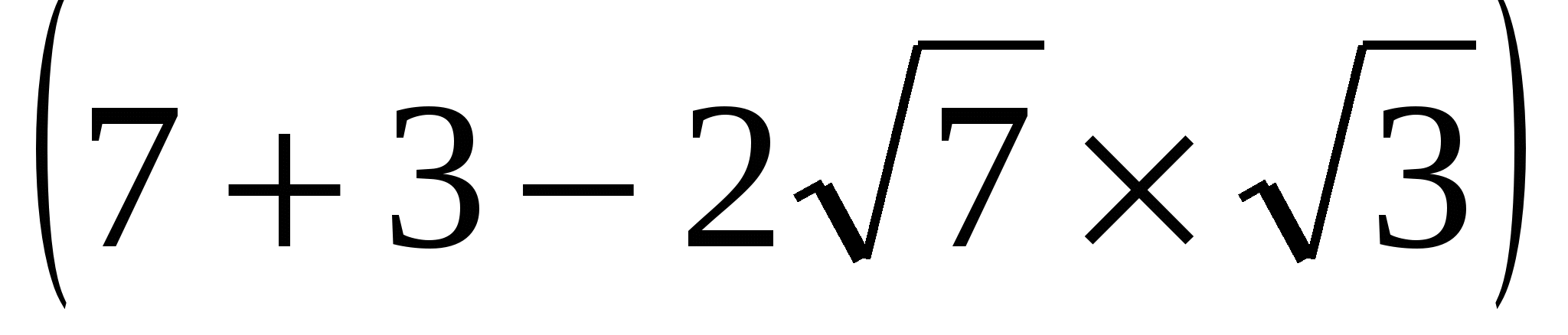 =
= 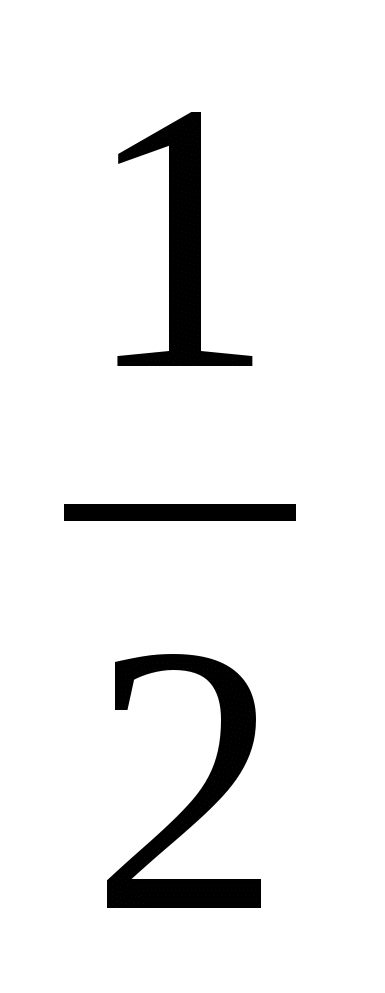
 =
= 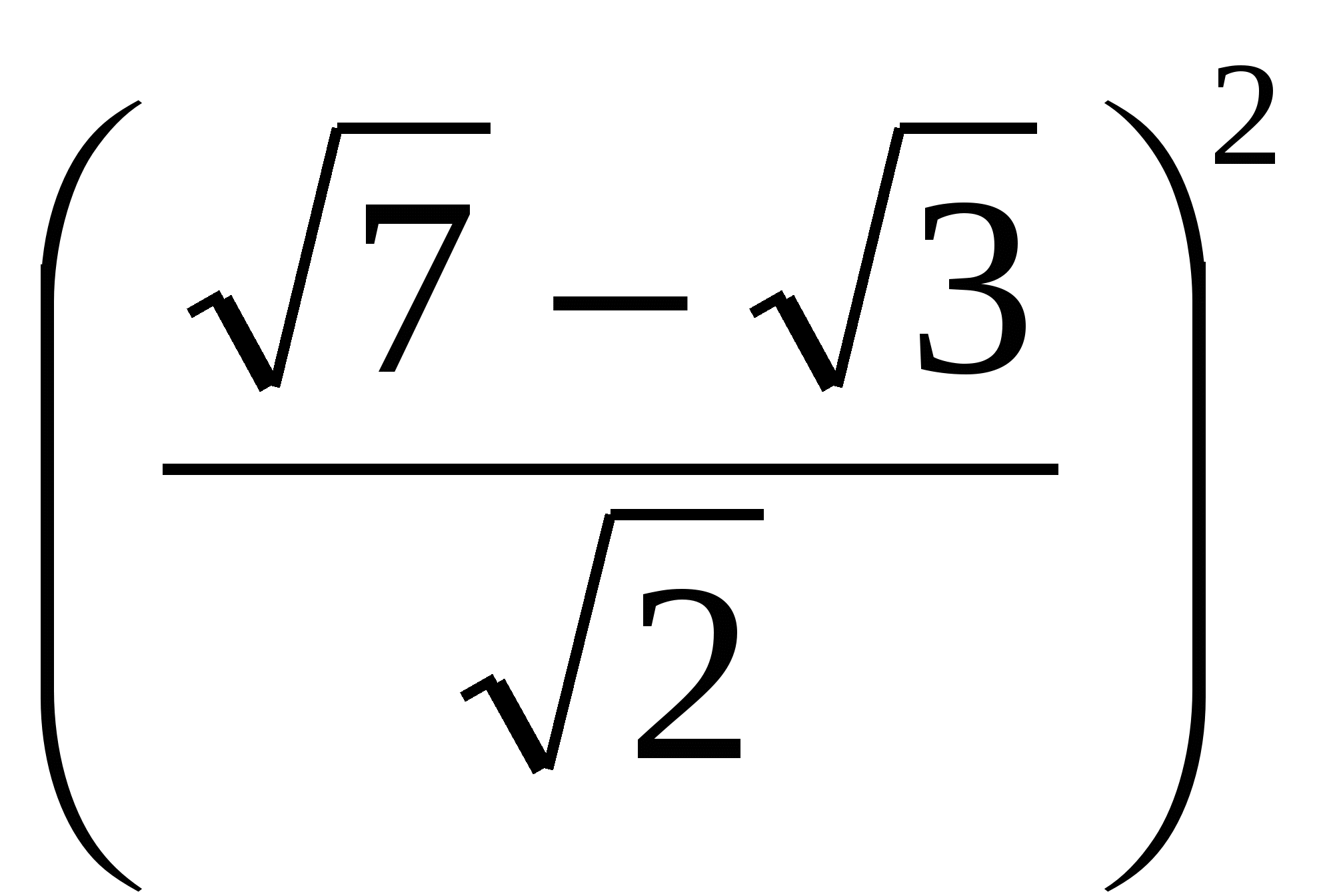 .
.
Поэтому 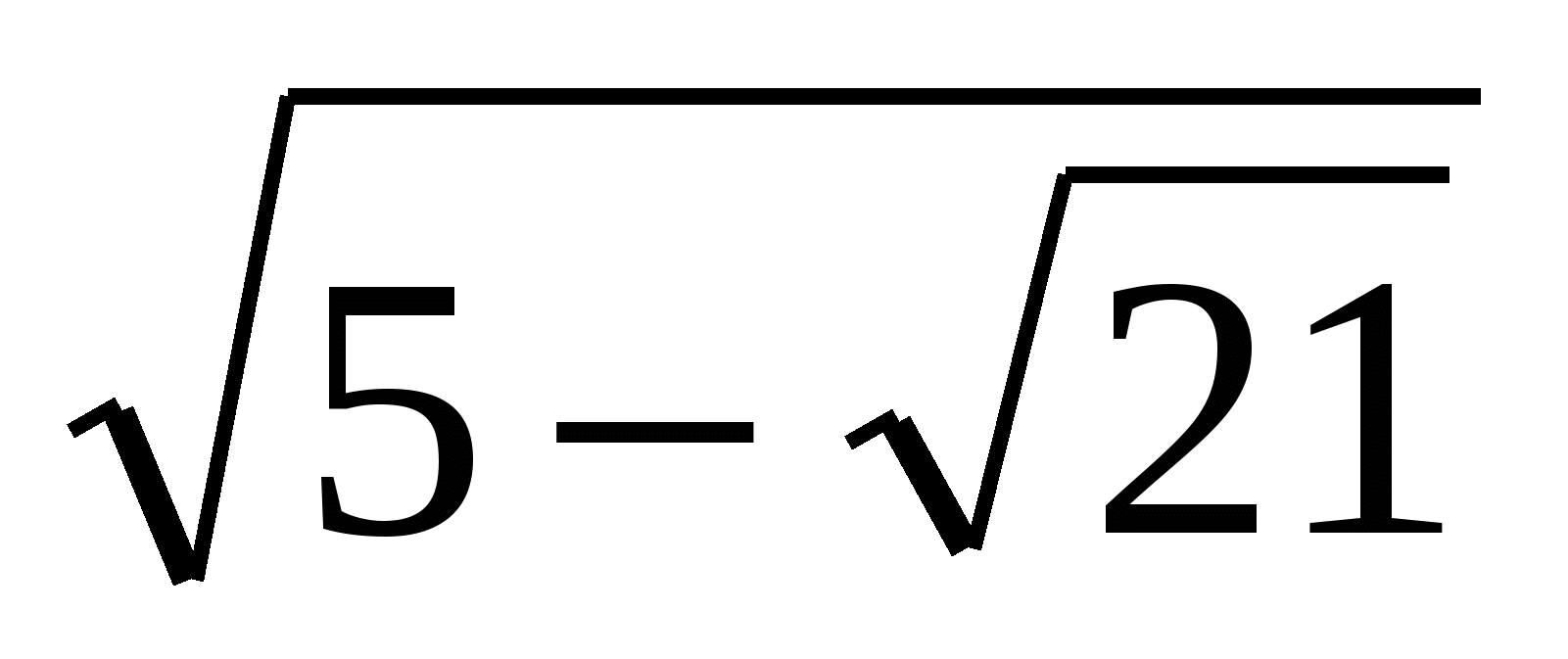 =
= 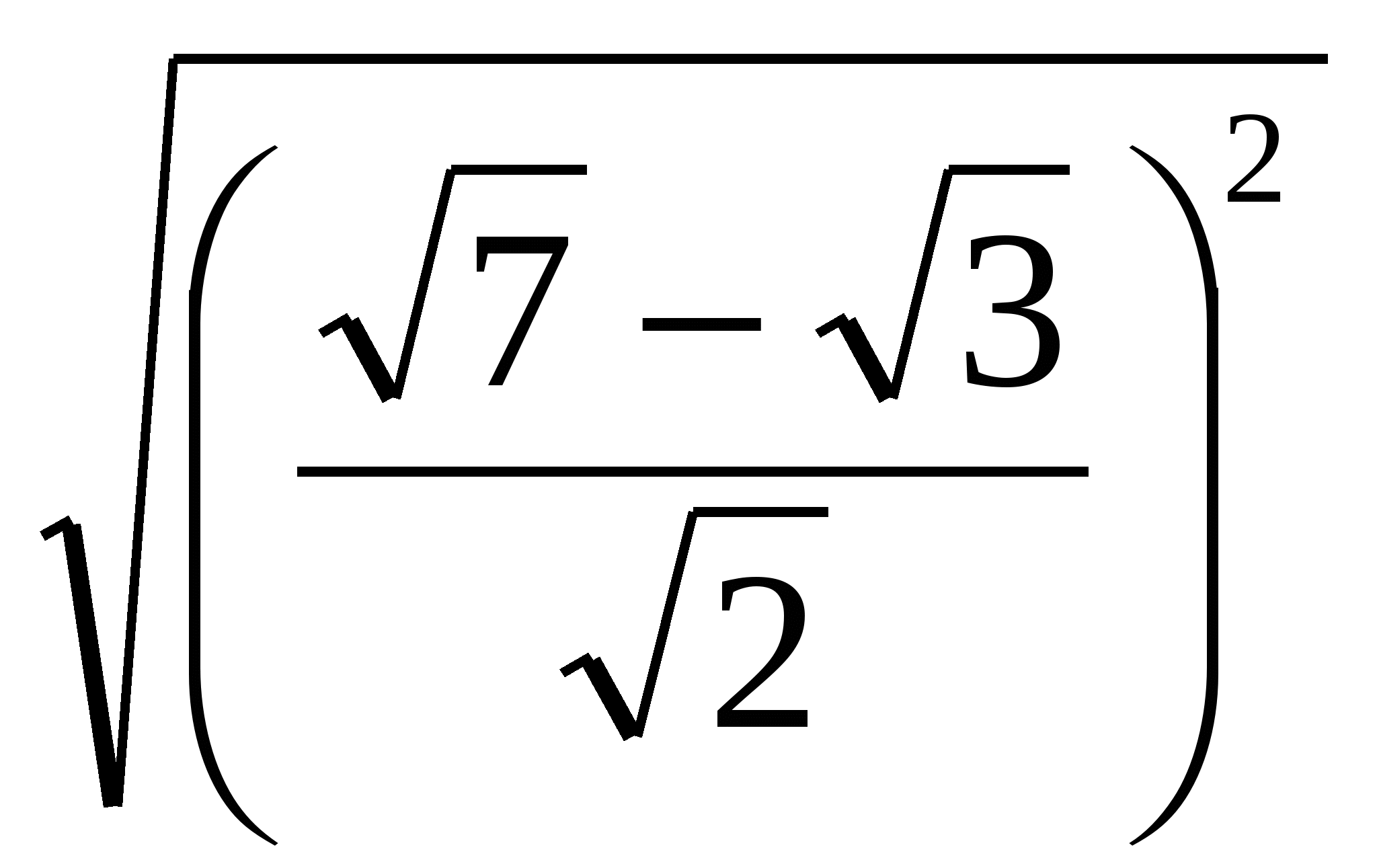 =
= 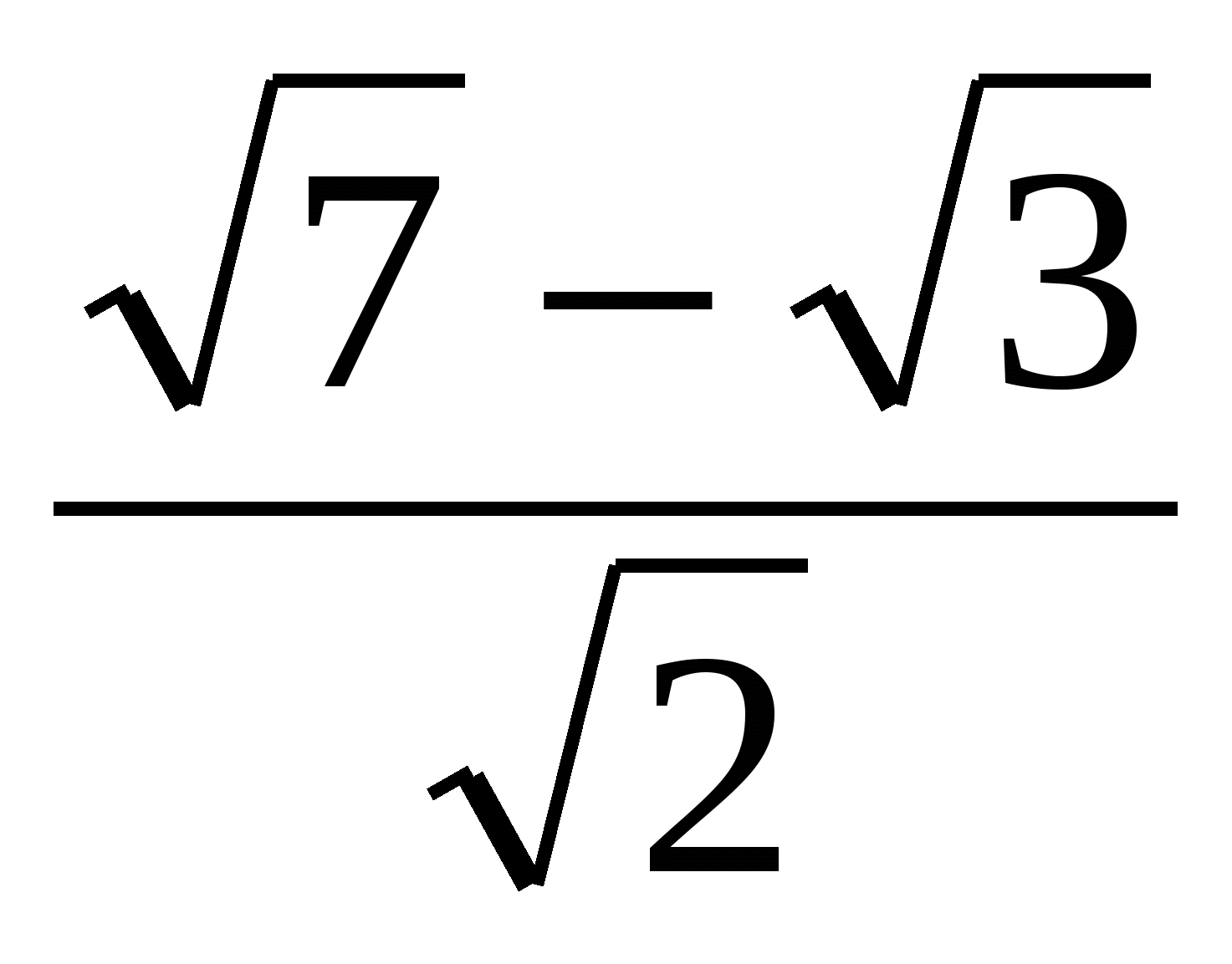
. П р и м е р 2. Упростить выражение 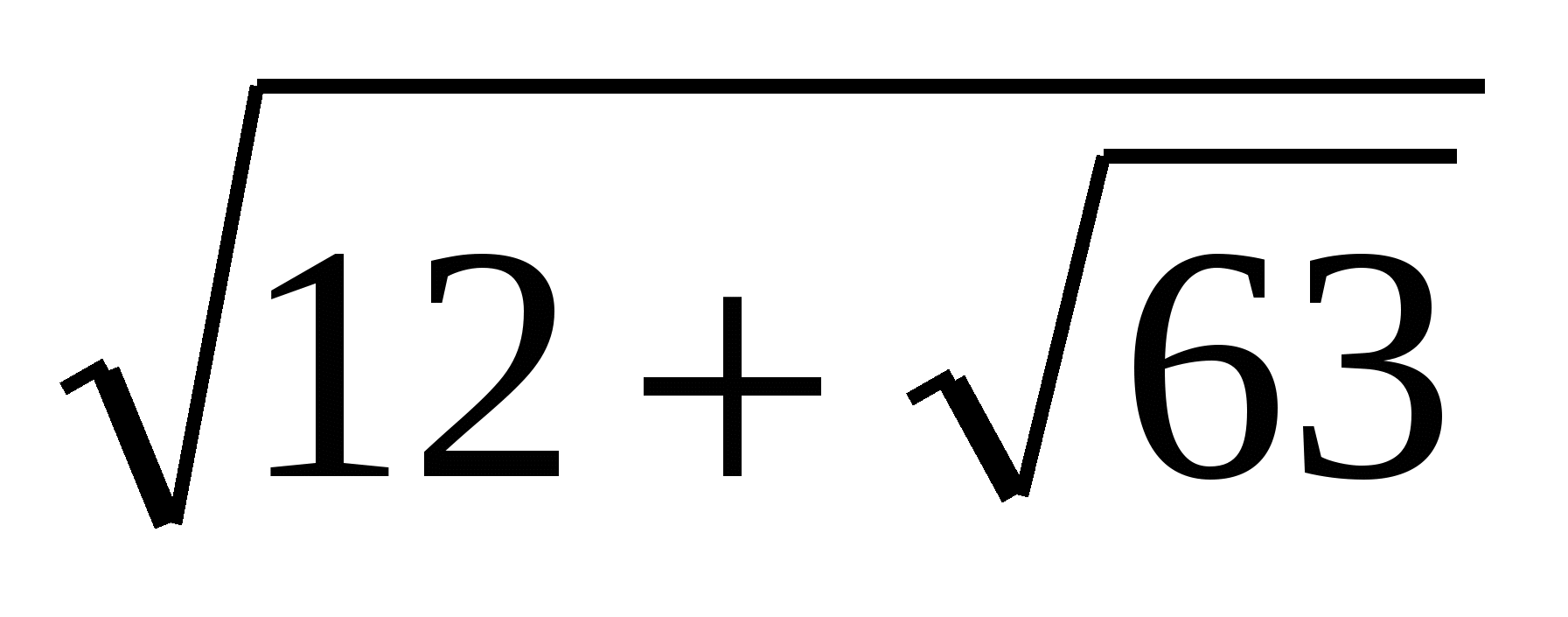
1-й с п о с о б:
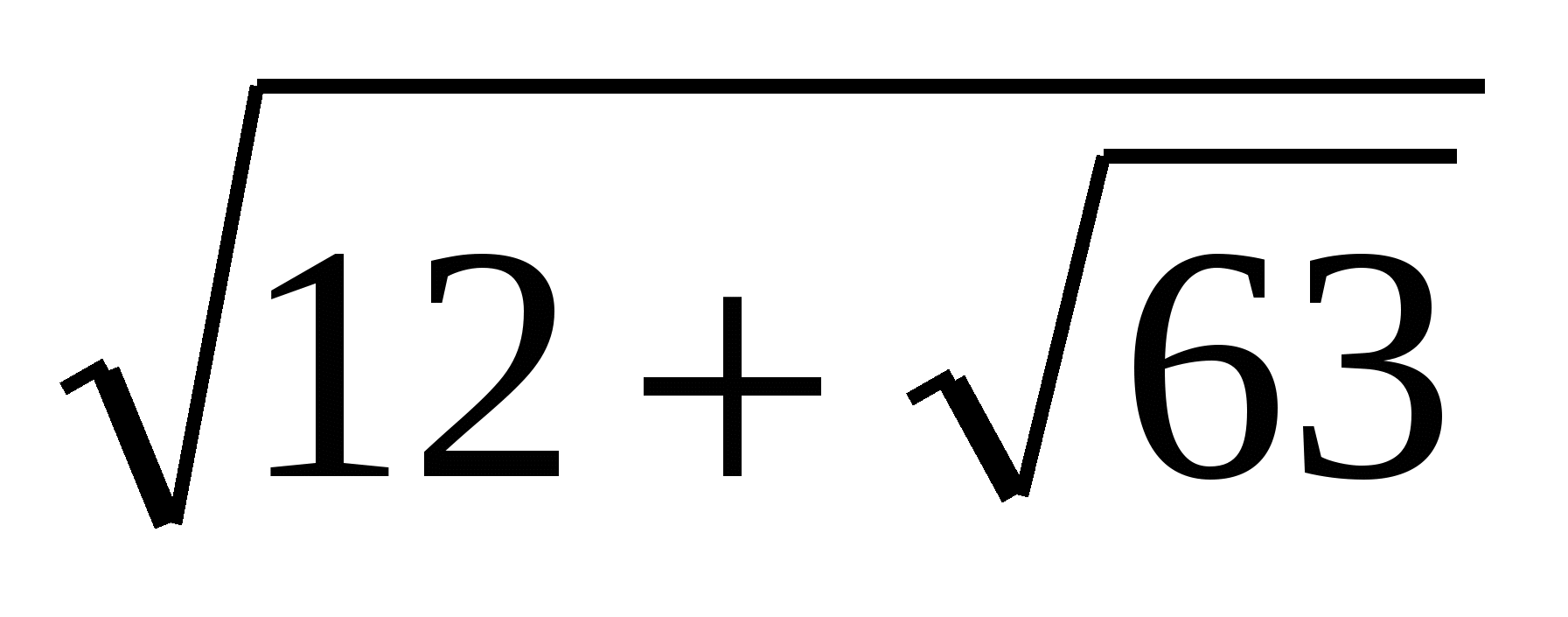 =
=  +
+ 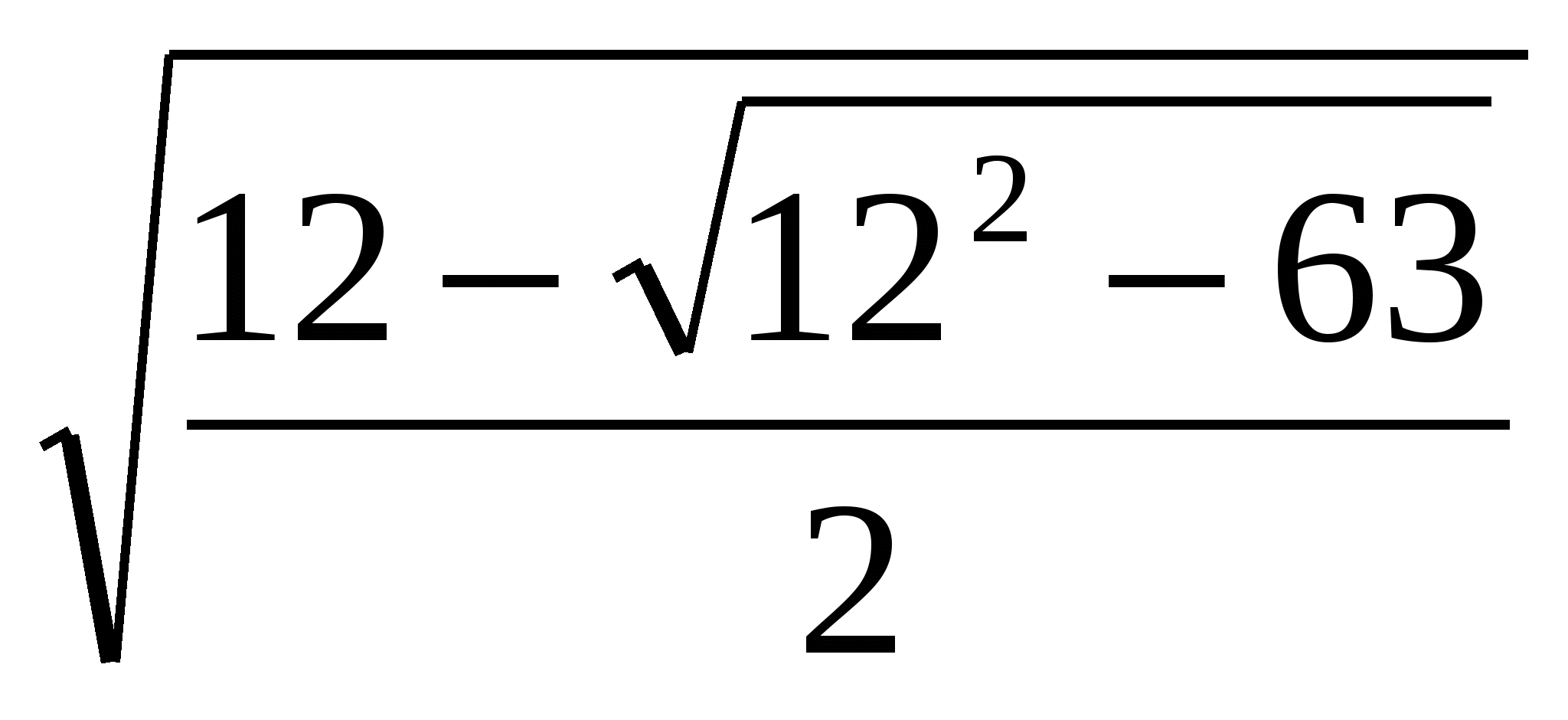 =
=
= 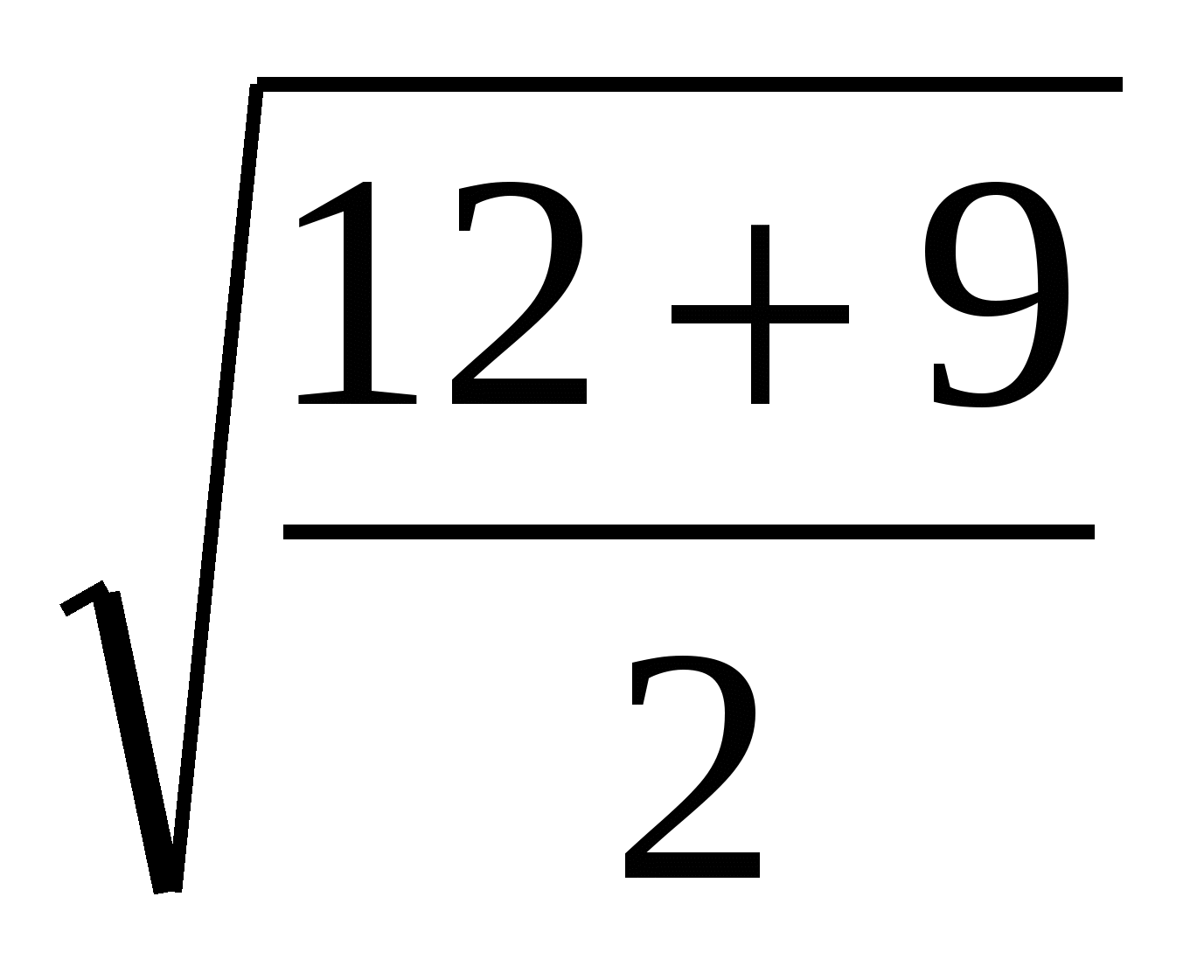 +
+ 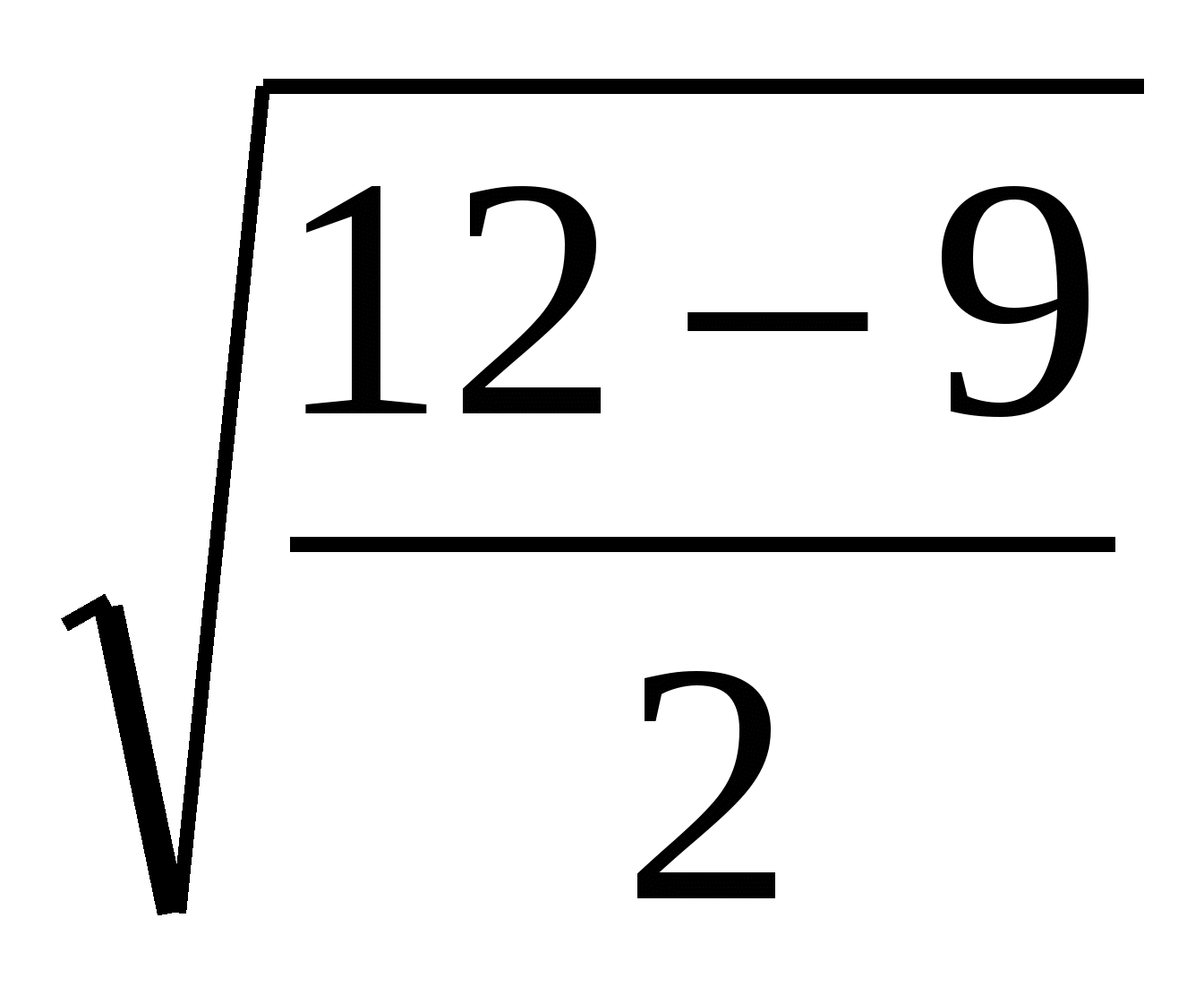 =
= 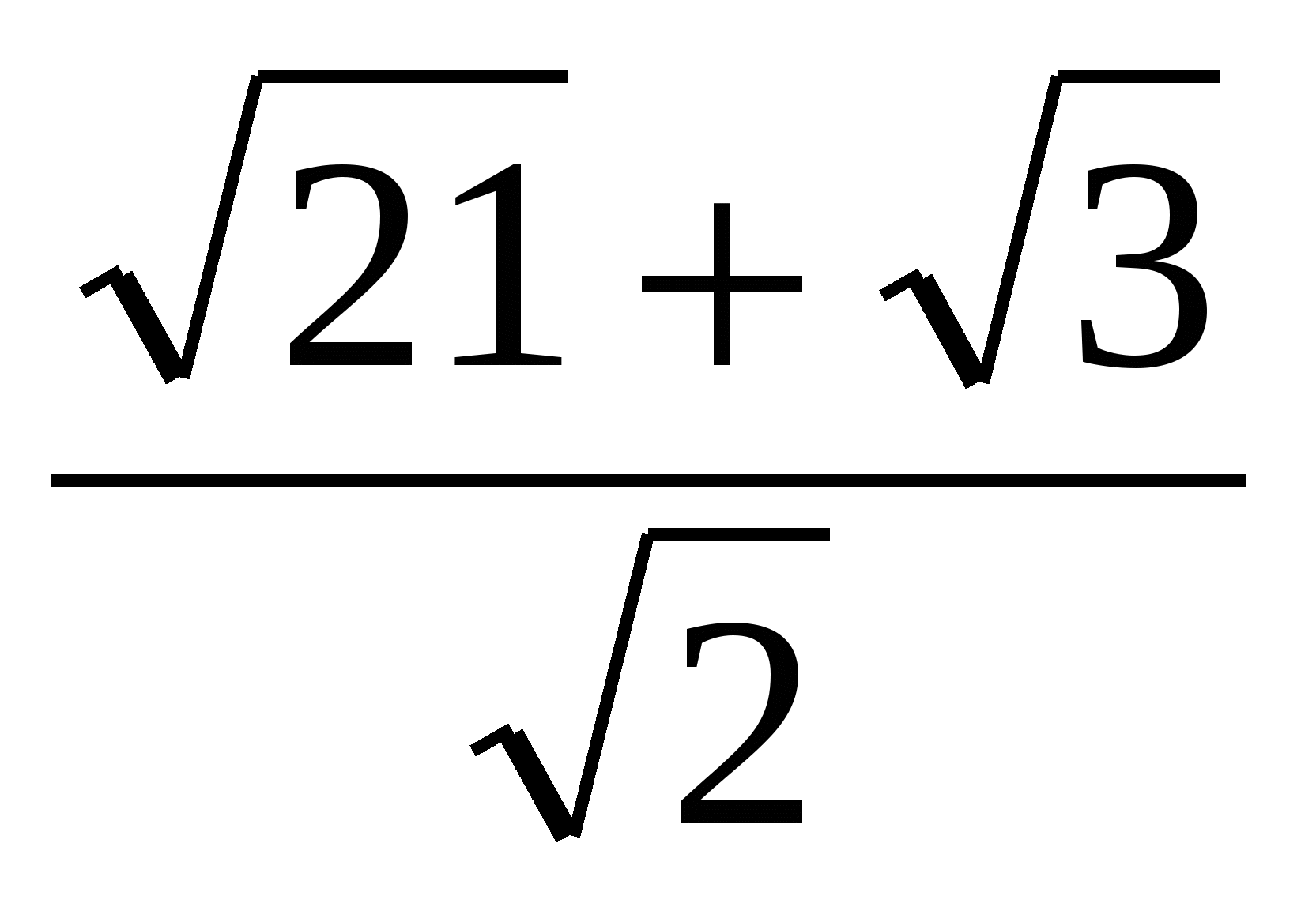
2-й с п о с о б:
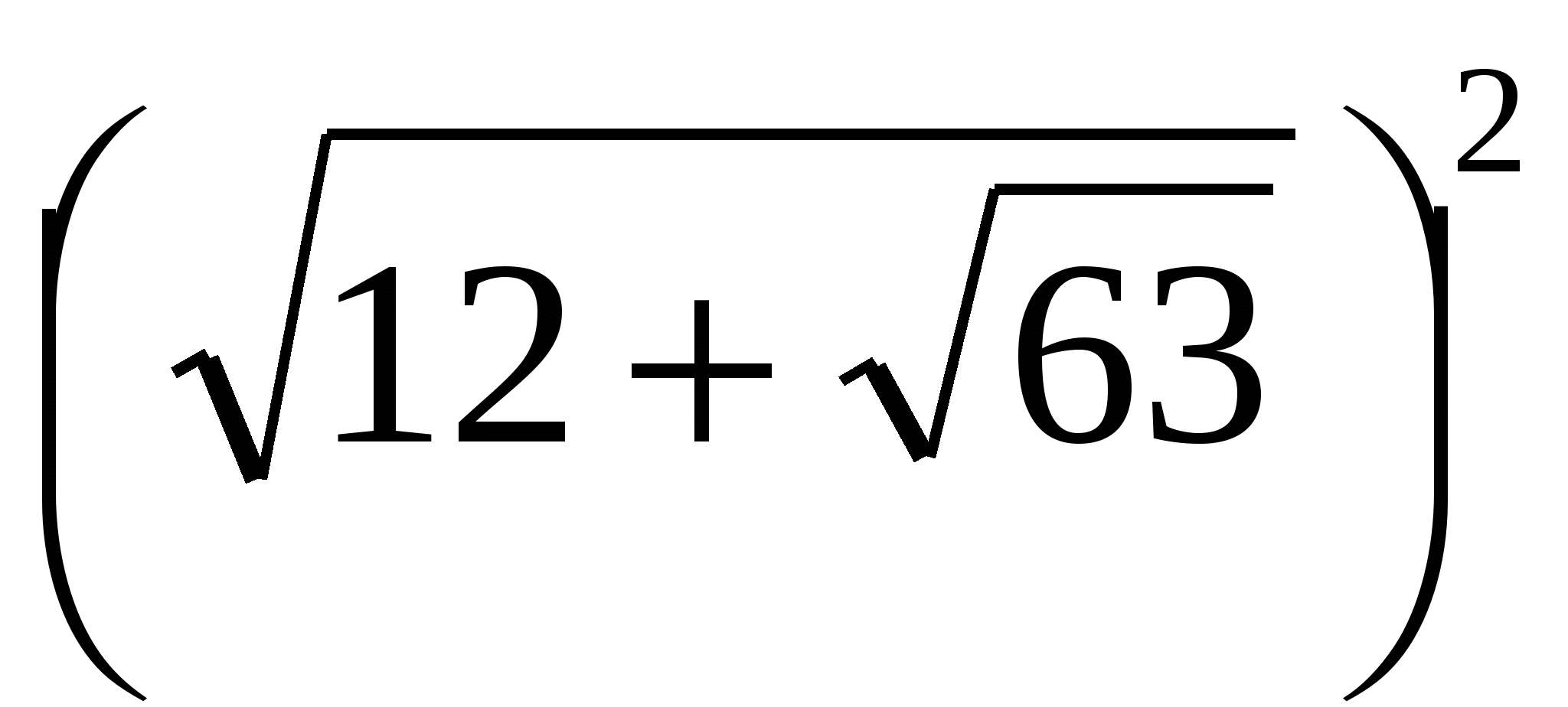 =
= 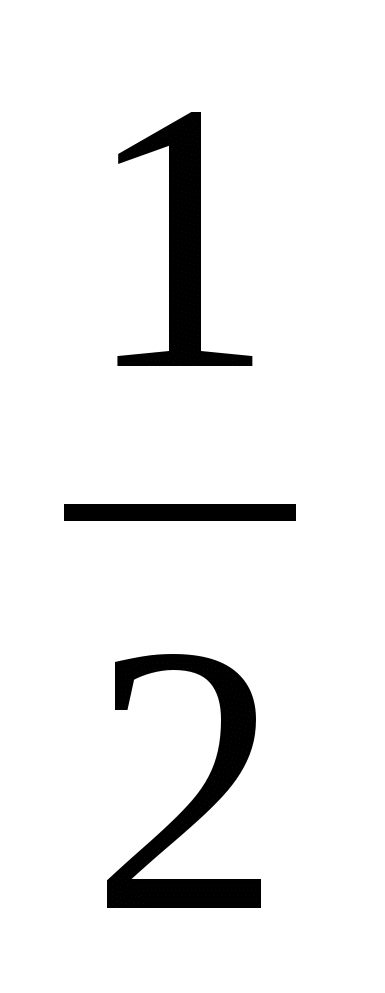
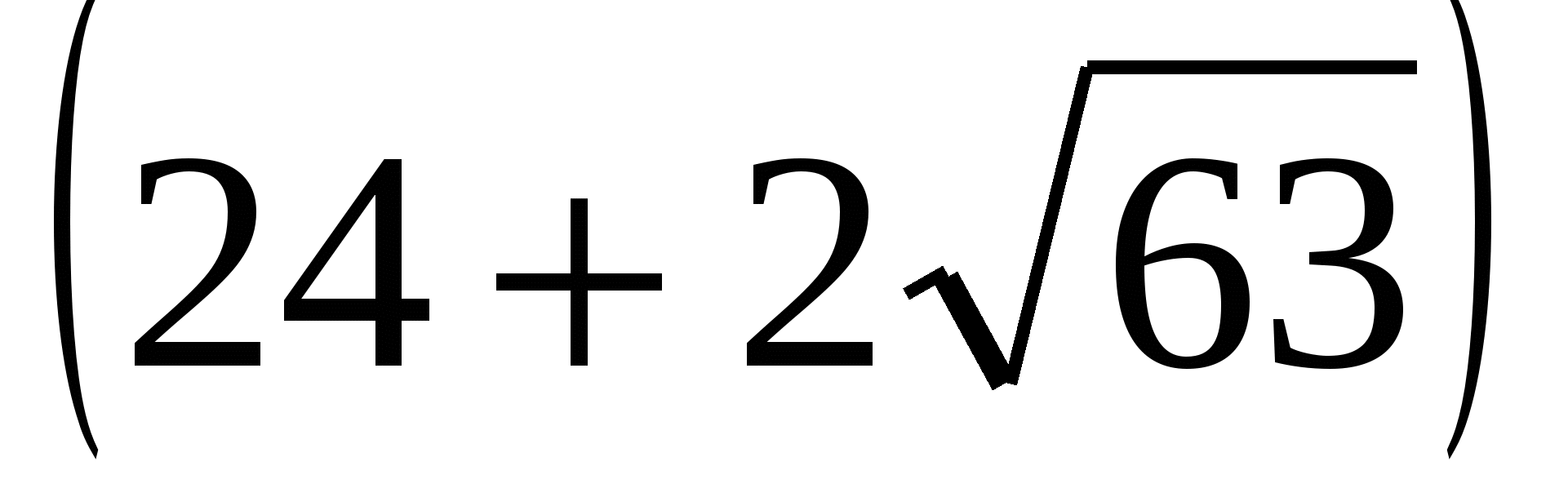 =
= 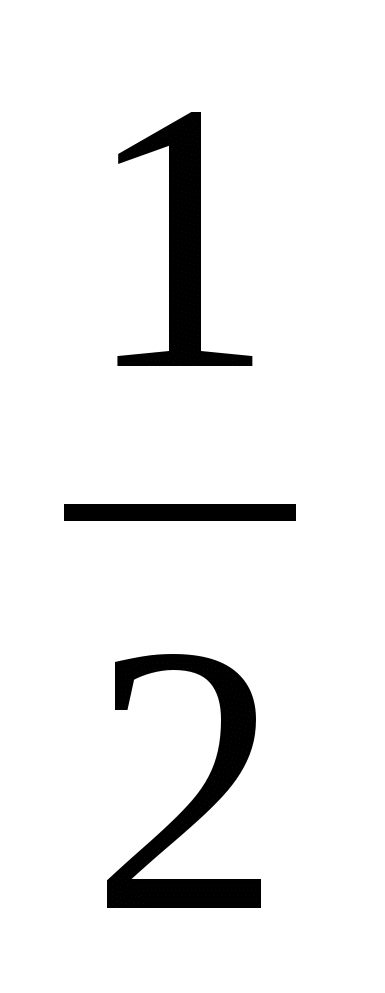
 =
=
= 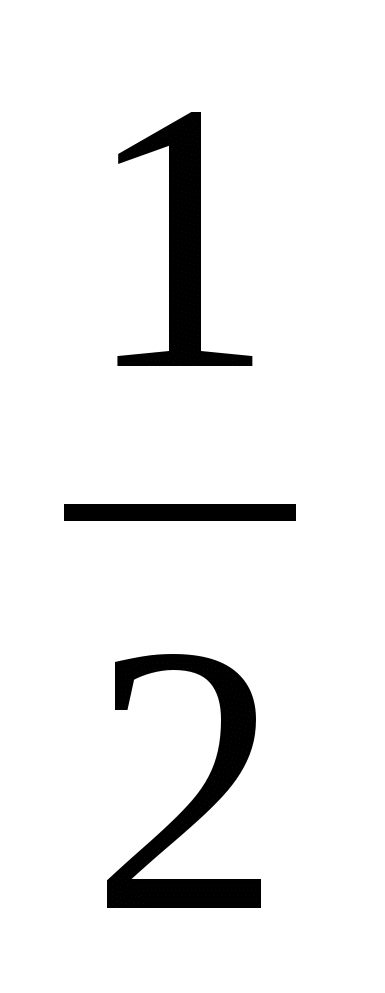
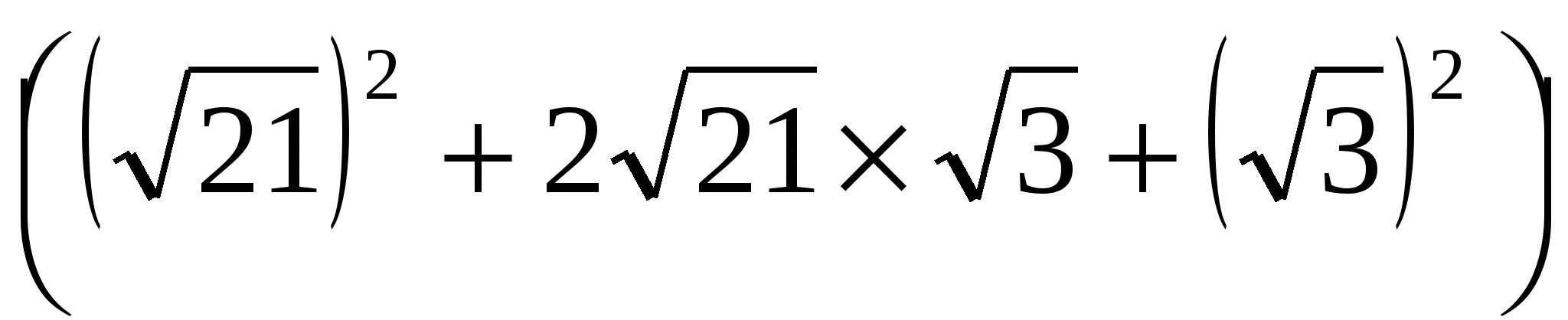 =
= 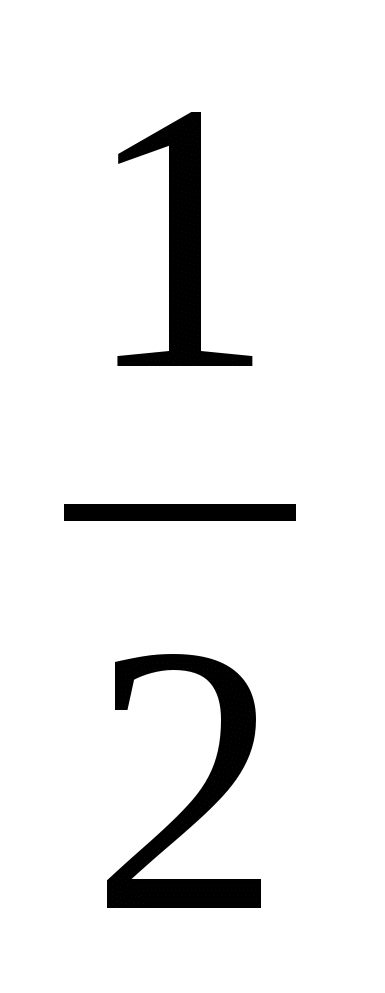
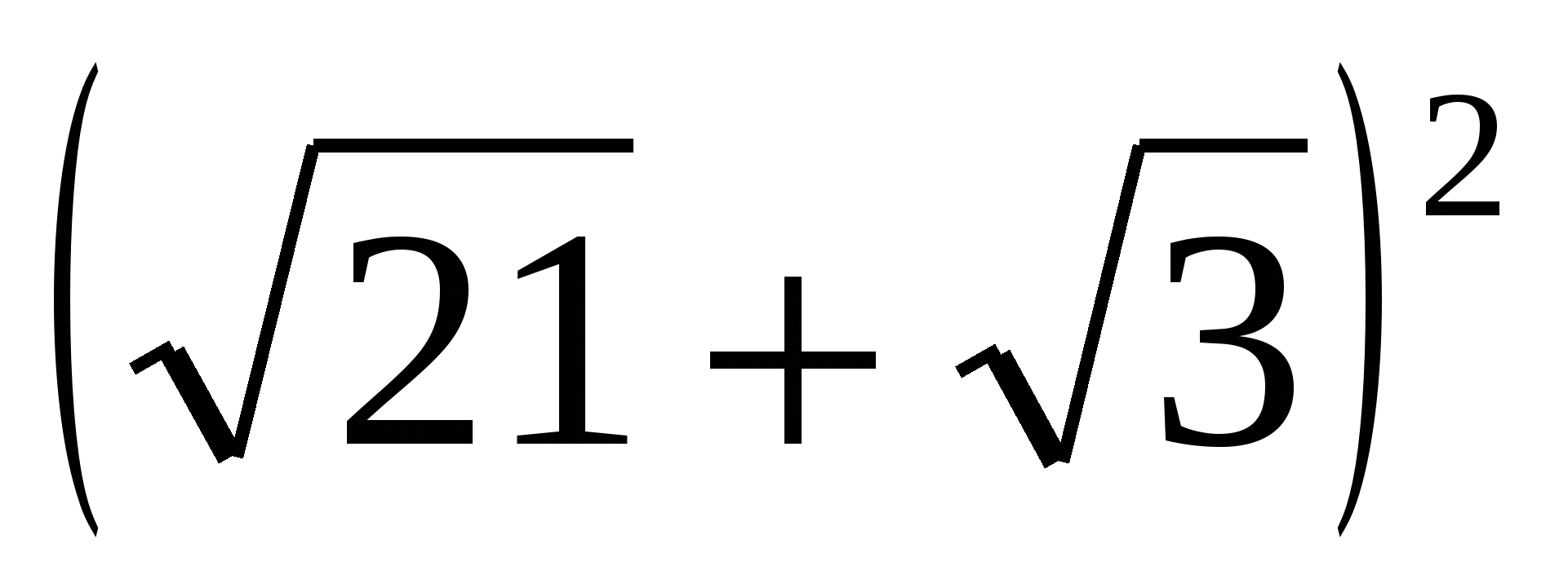
Поэтому 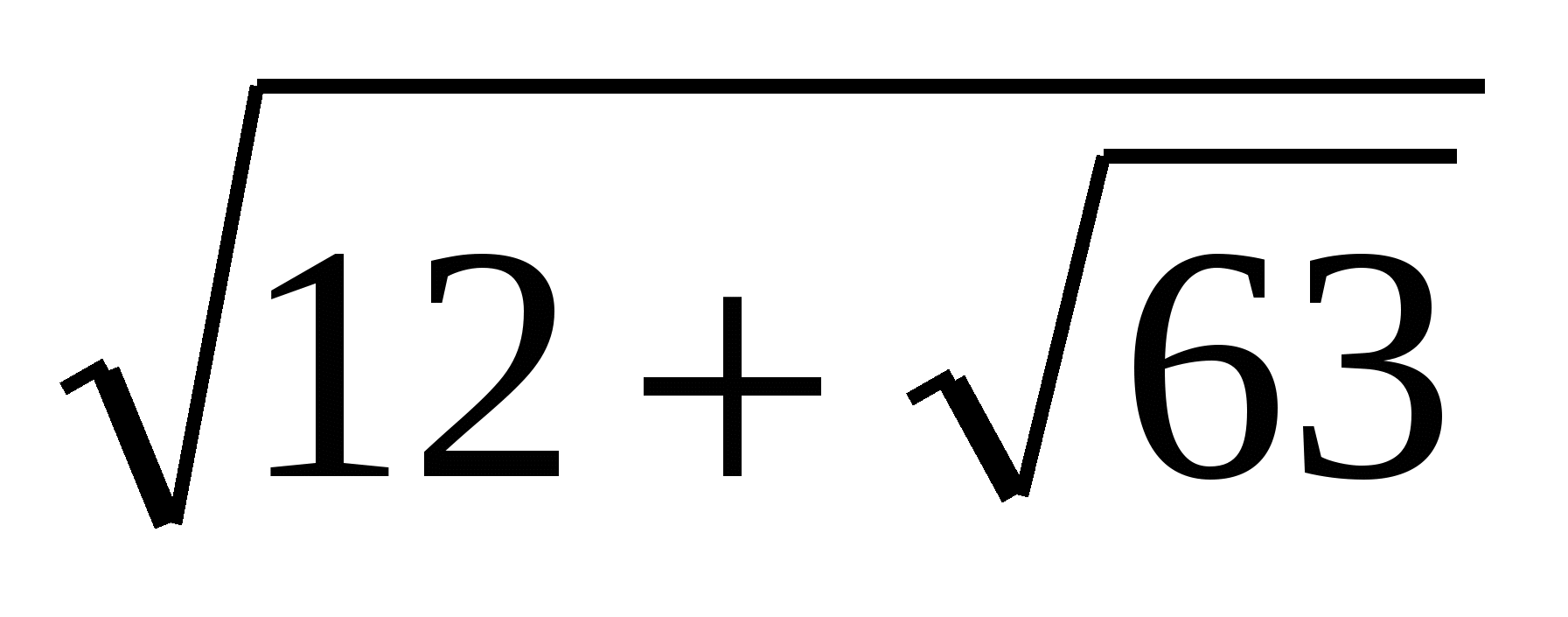 =
= 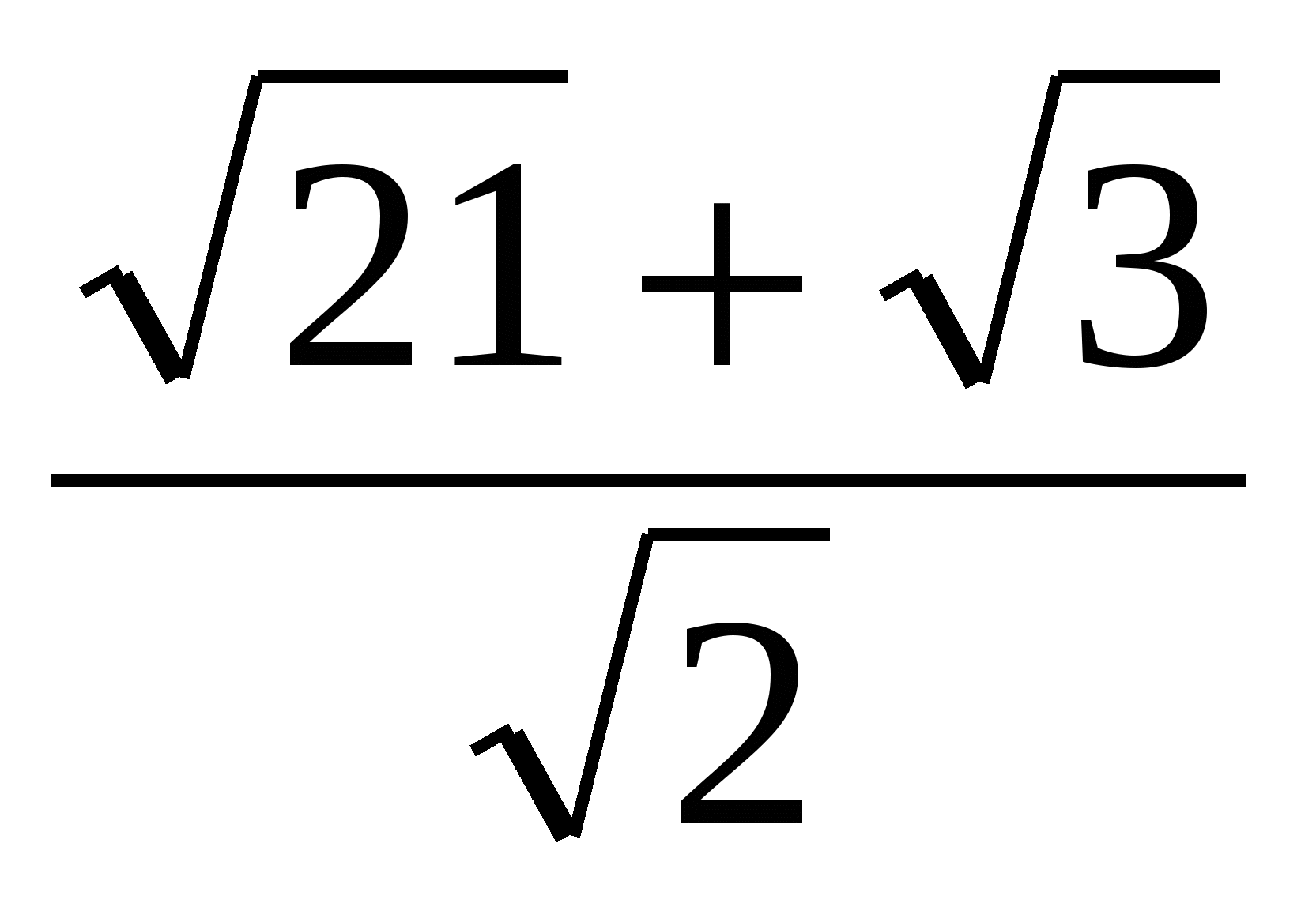
П р и м е р 3. Упростить выражение 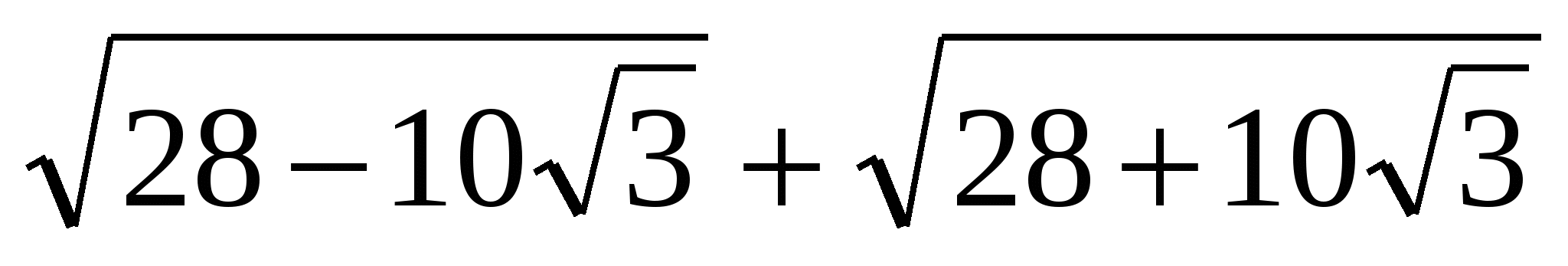
Решение.
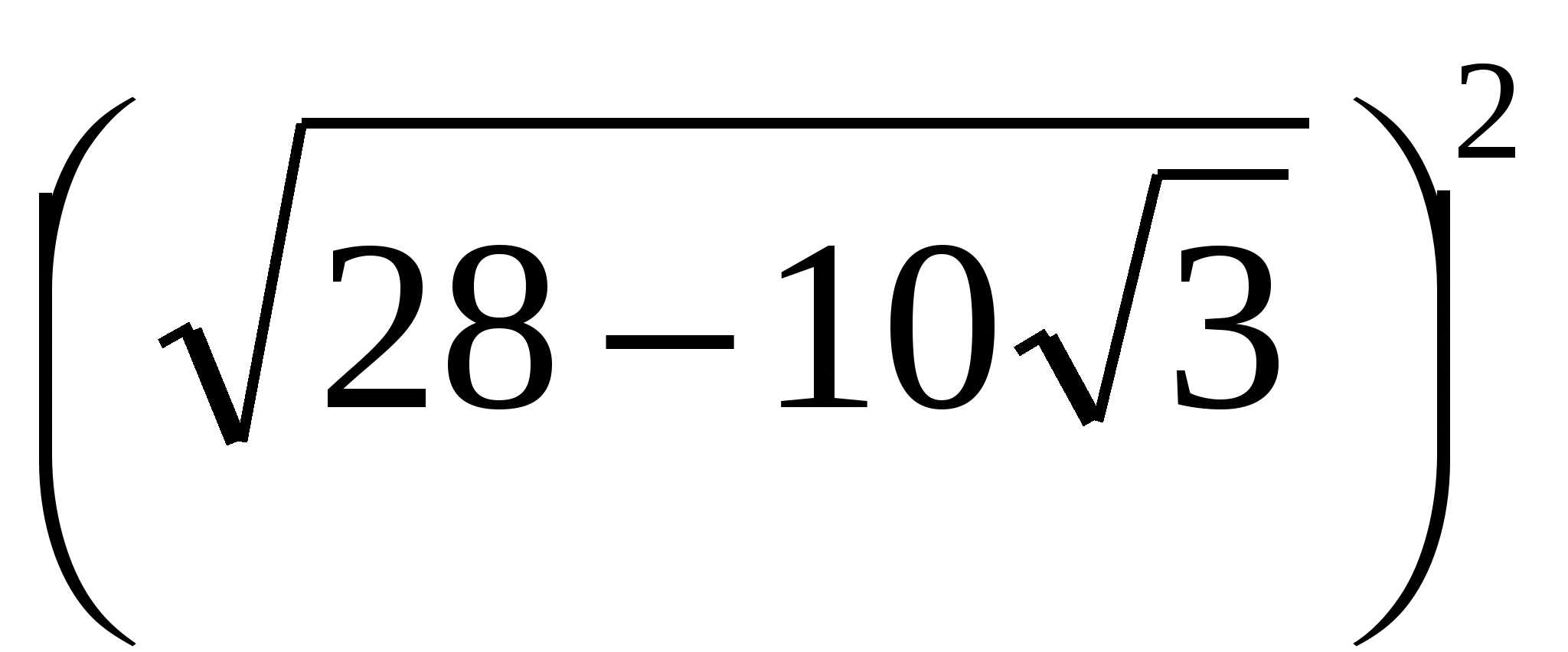 = 28 – 10
= 28 – 10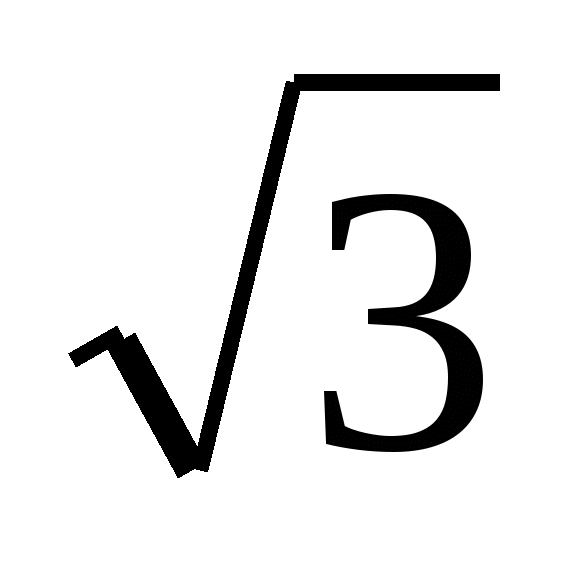 = 25 – 10
= 25 – 10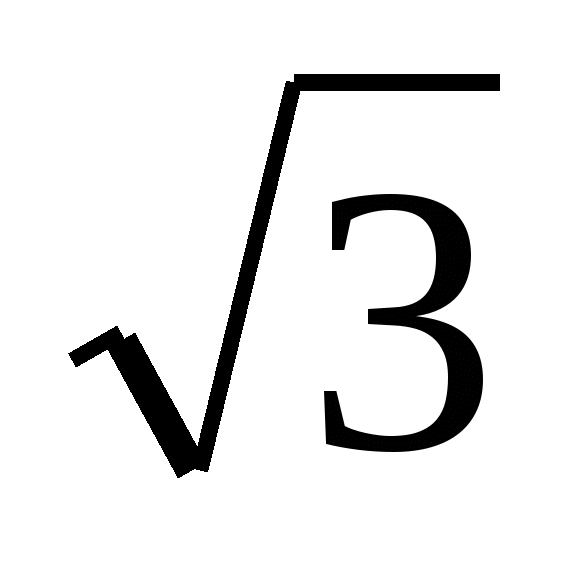 +3 =
+3 =
= 52 – 10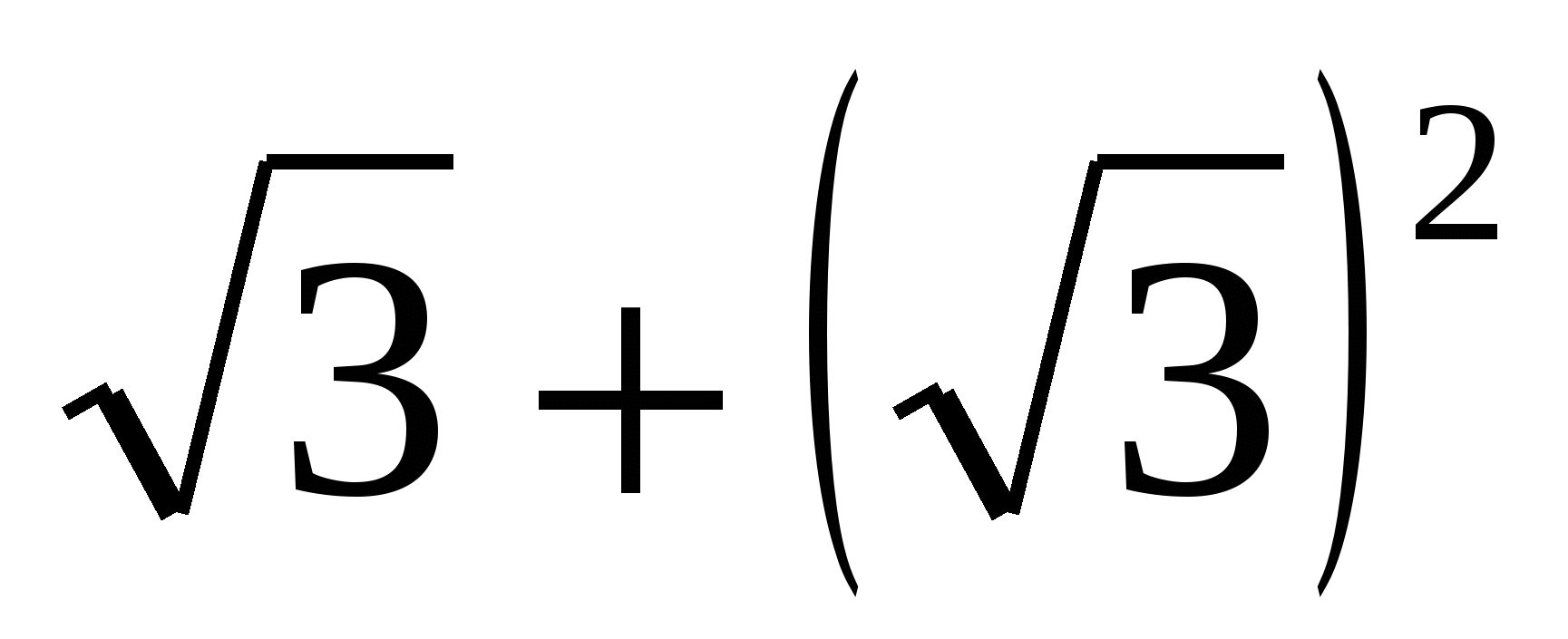 =
= 
Поэтому 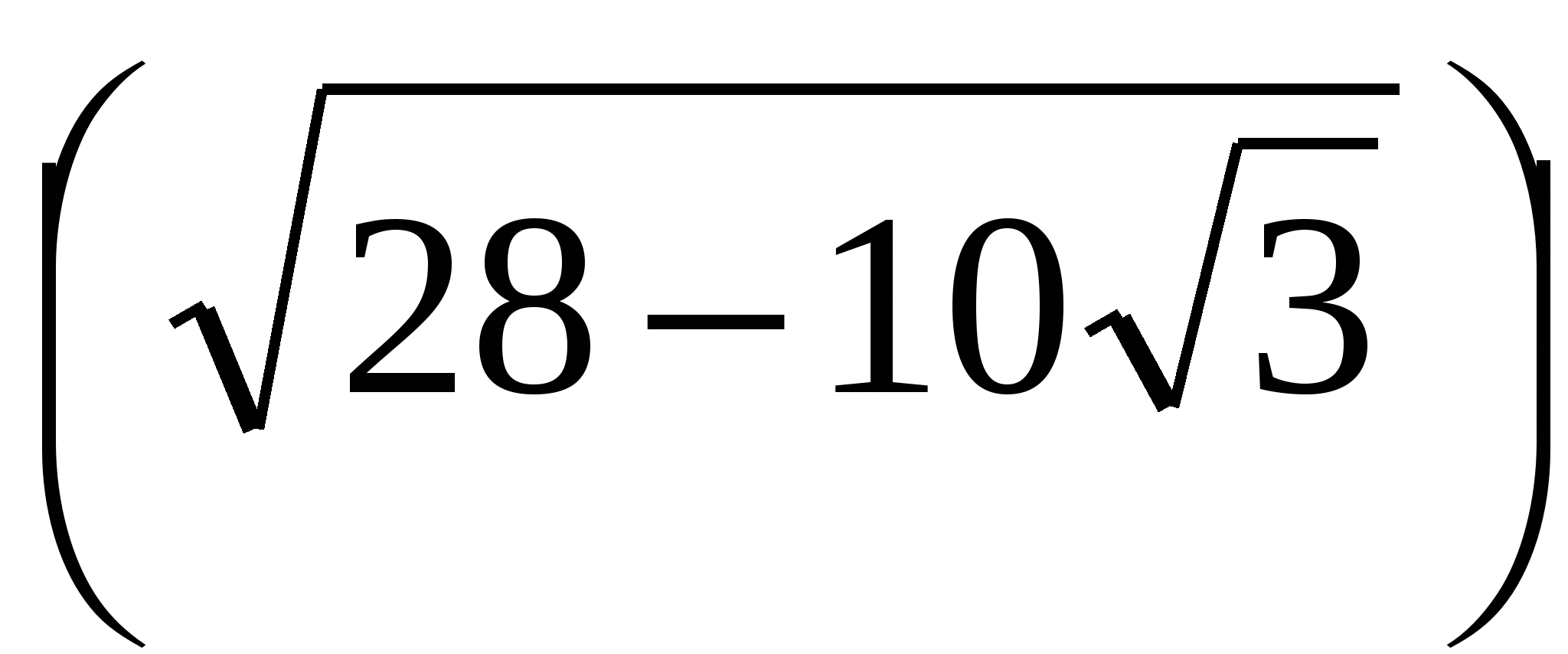 = 5 –
= 5 – 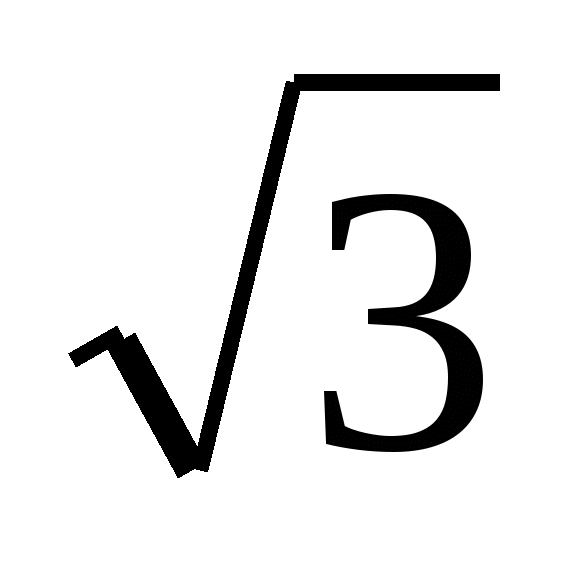
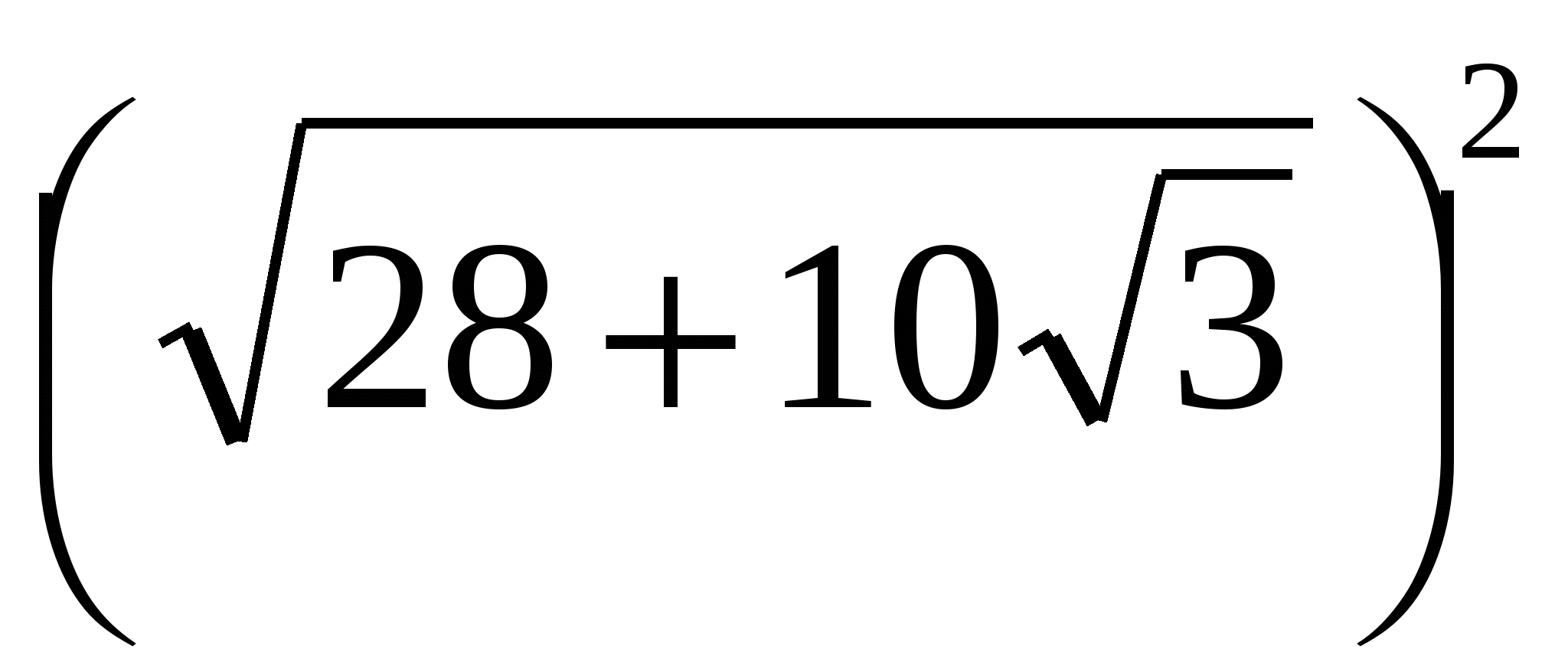 = 28 + 10
= 28 + 10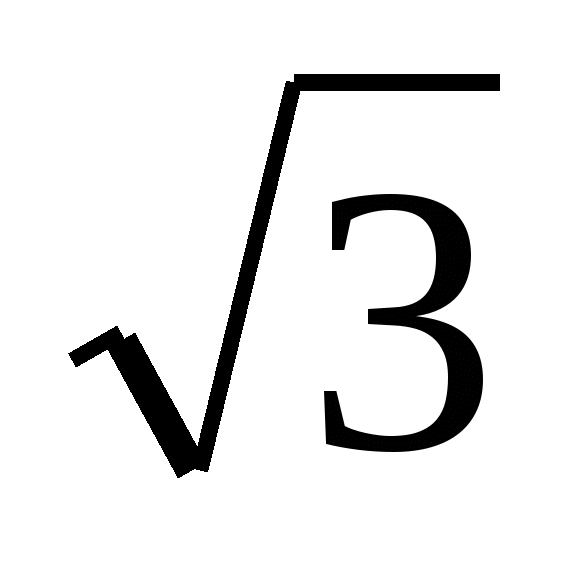 = 25 + 10
= 25 + 10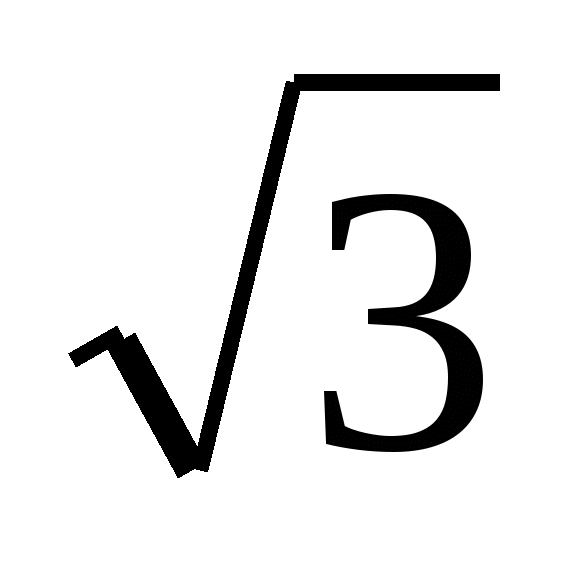 + 3 =
+ 3 = 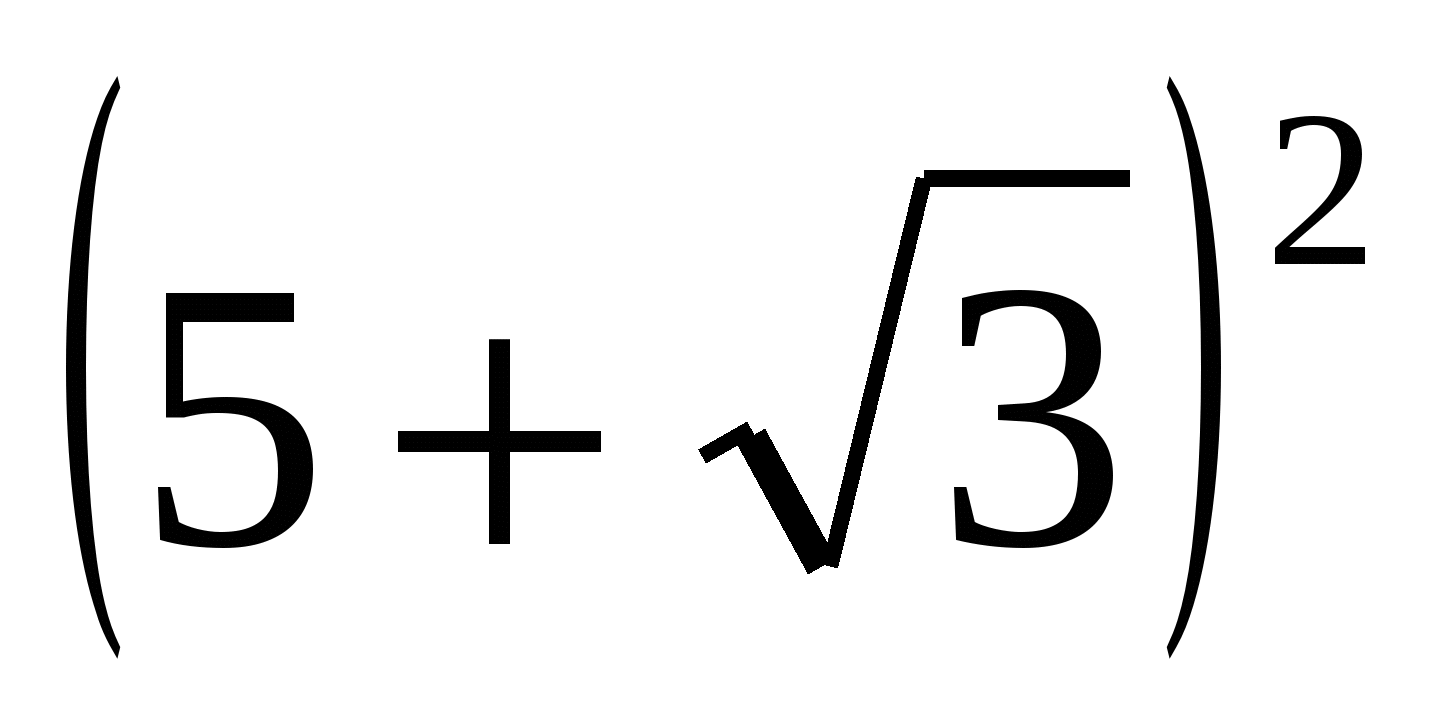
Поэтому 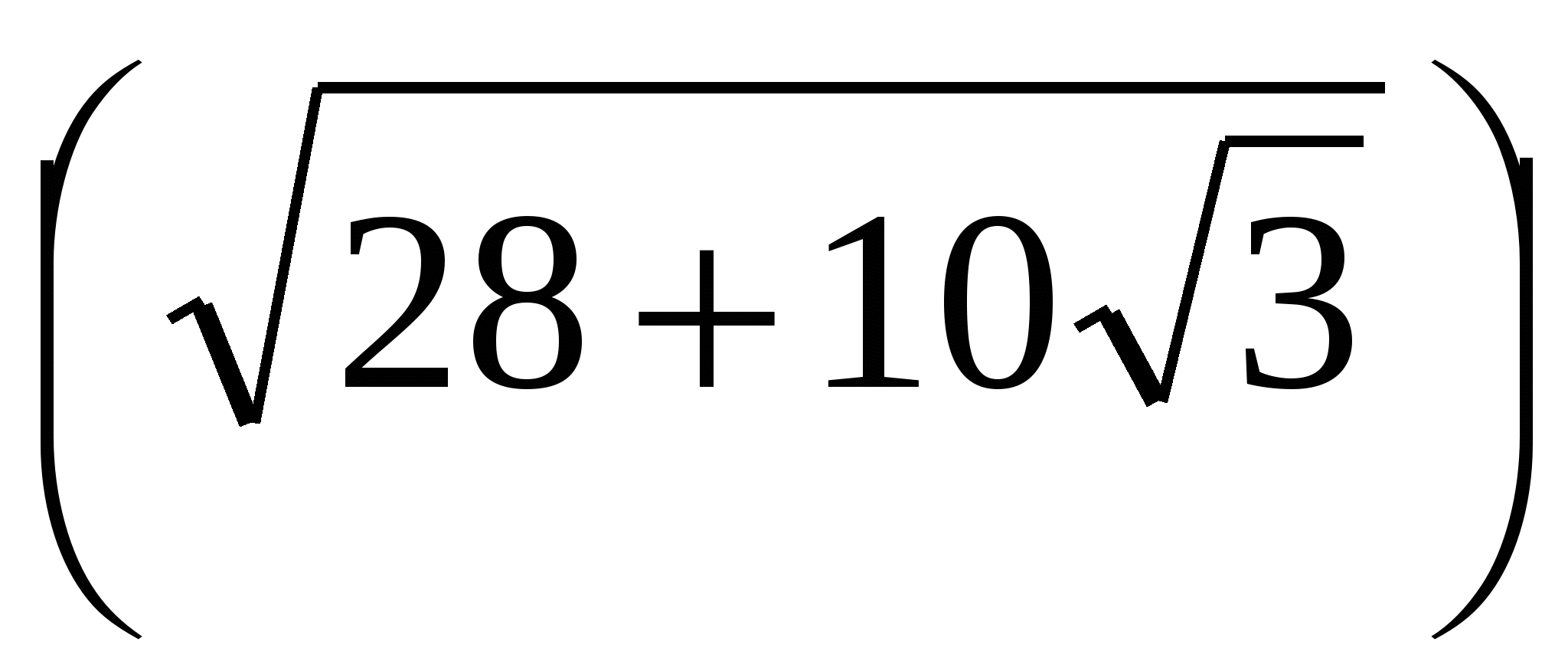 = 5 +
= 5 + 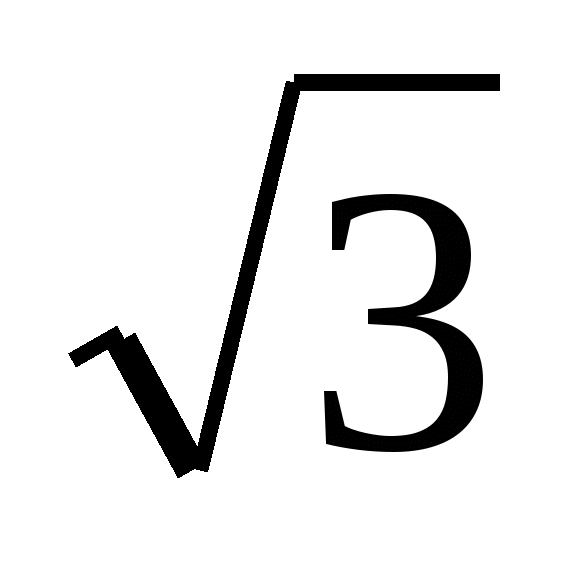

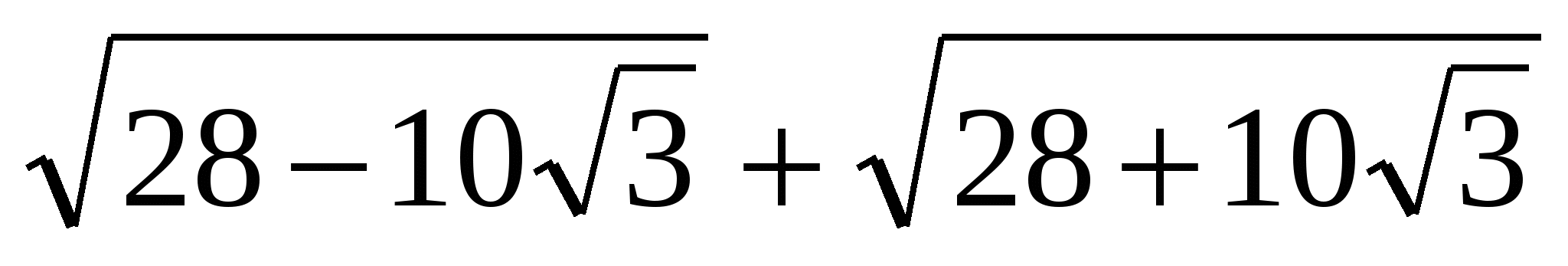 =
=
= 5 – 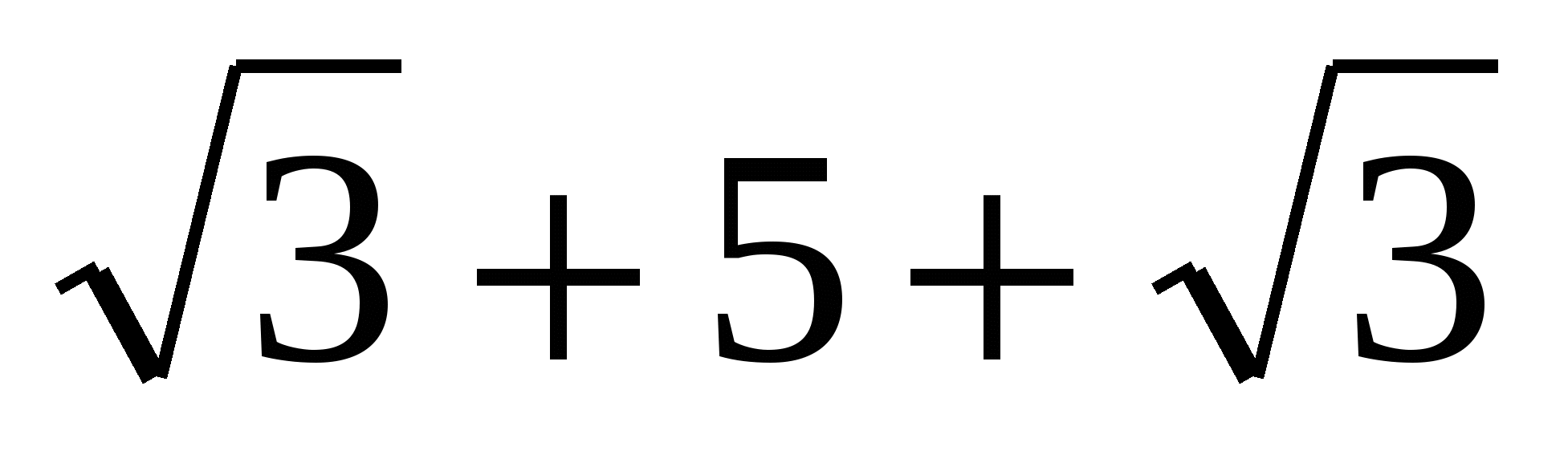 = 5 + 5 = 10
= 5 + 5 = 10
Пример 4. Упростить 
Решение.
1. 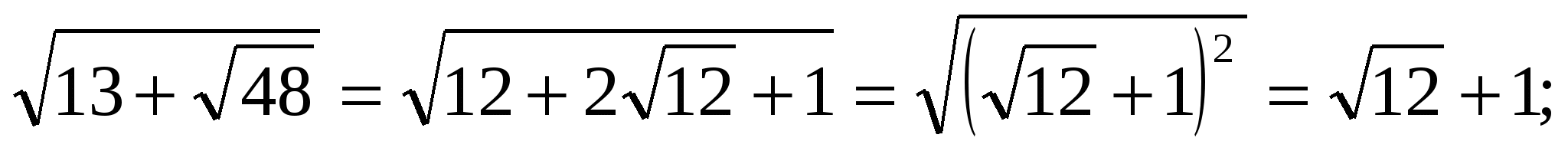
2. 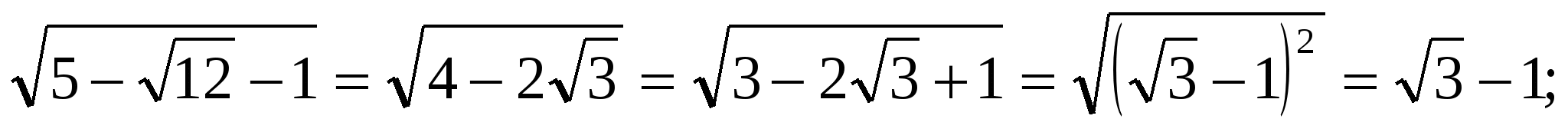
3. 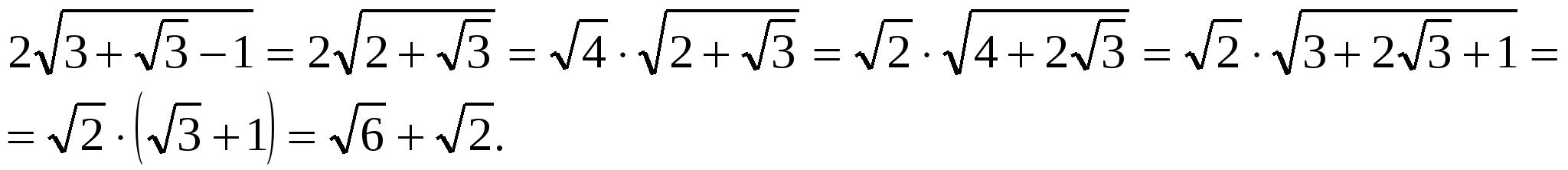
Ответ: 
Пример 5. Какое из чисел больше: 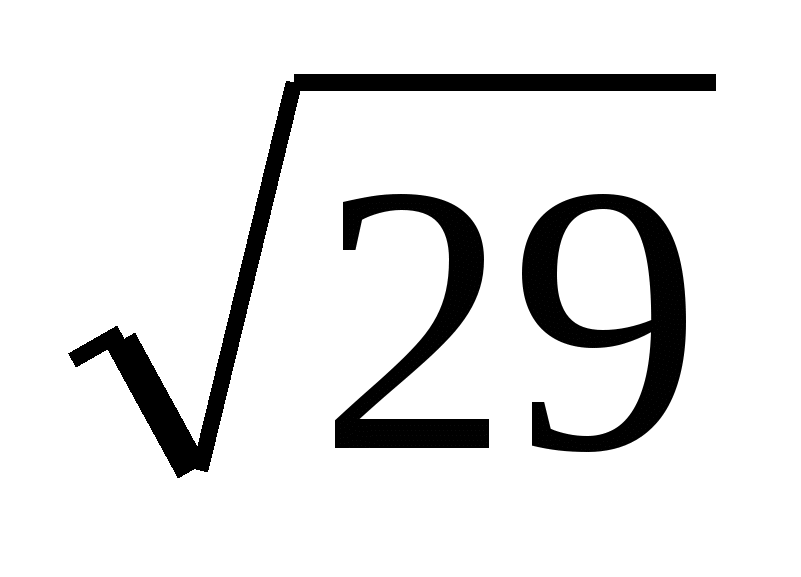 или
или  ?
?
Решение.
Очевидно, что 
Оценим сумму 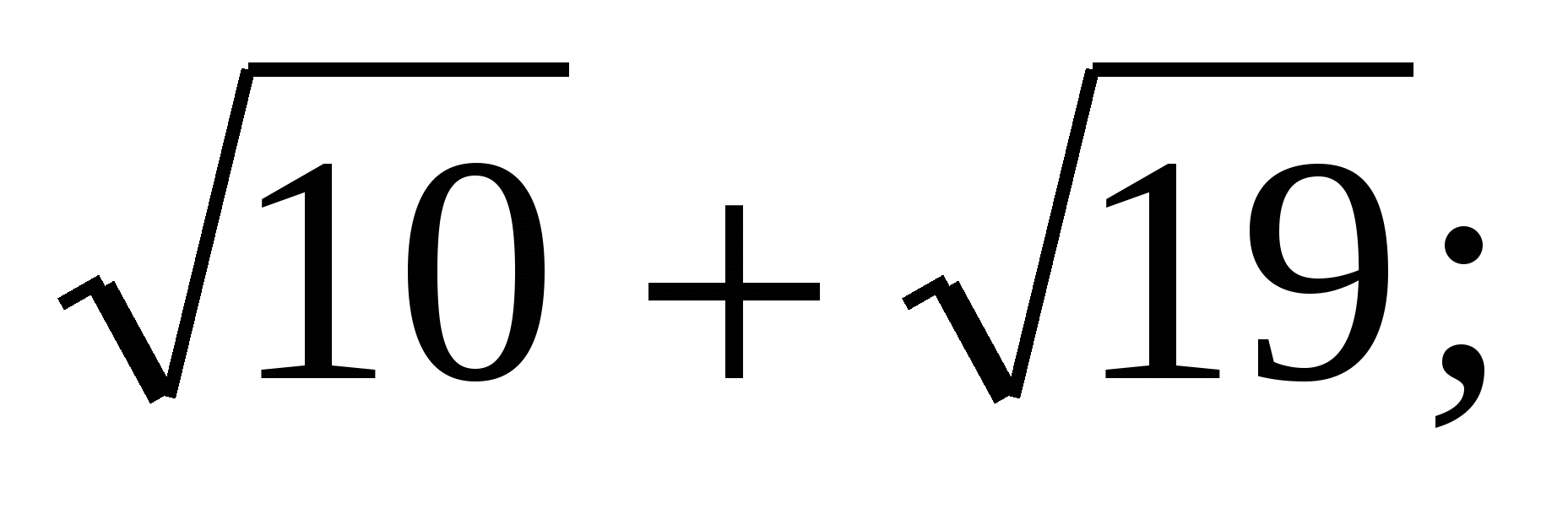
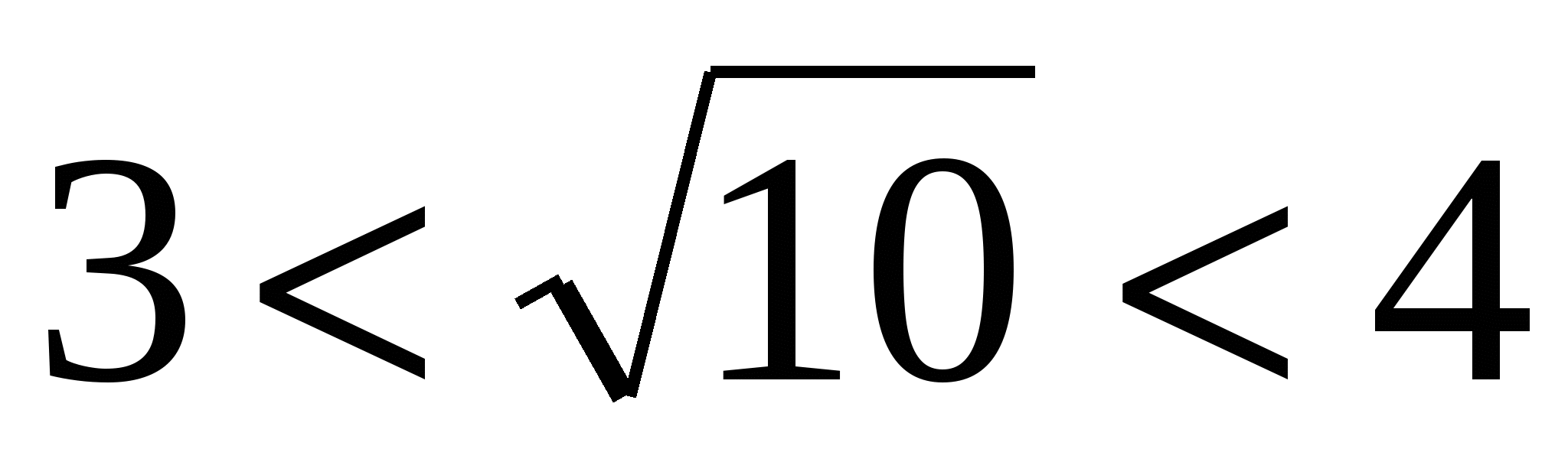
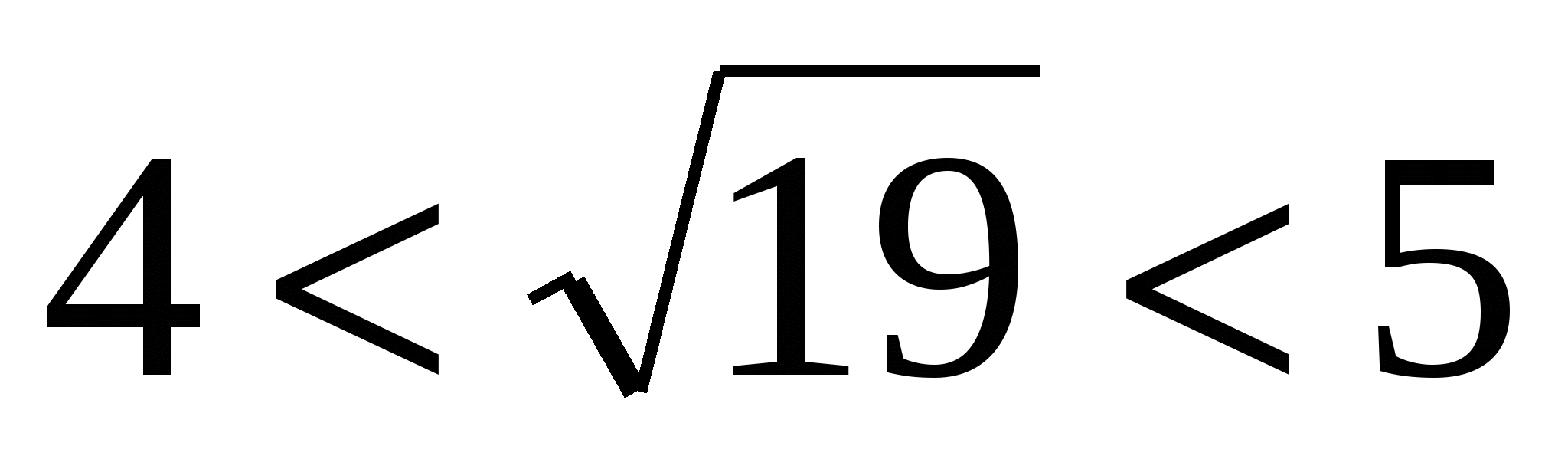
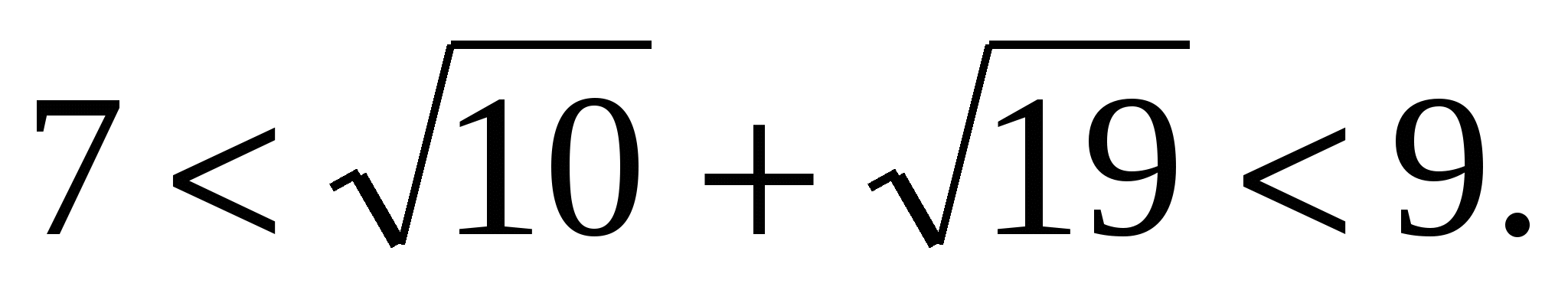
Так как 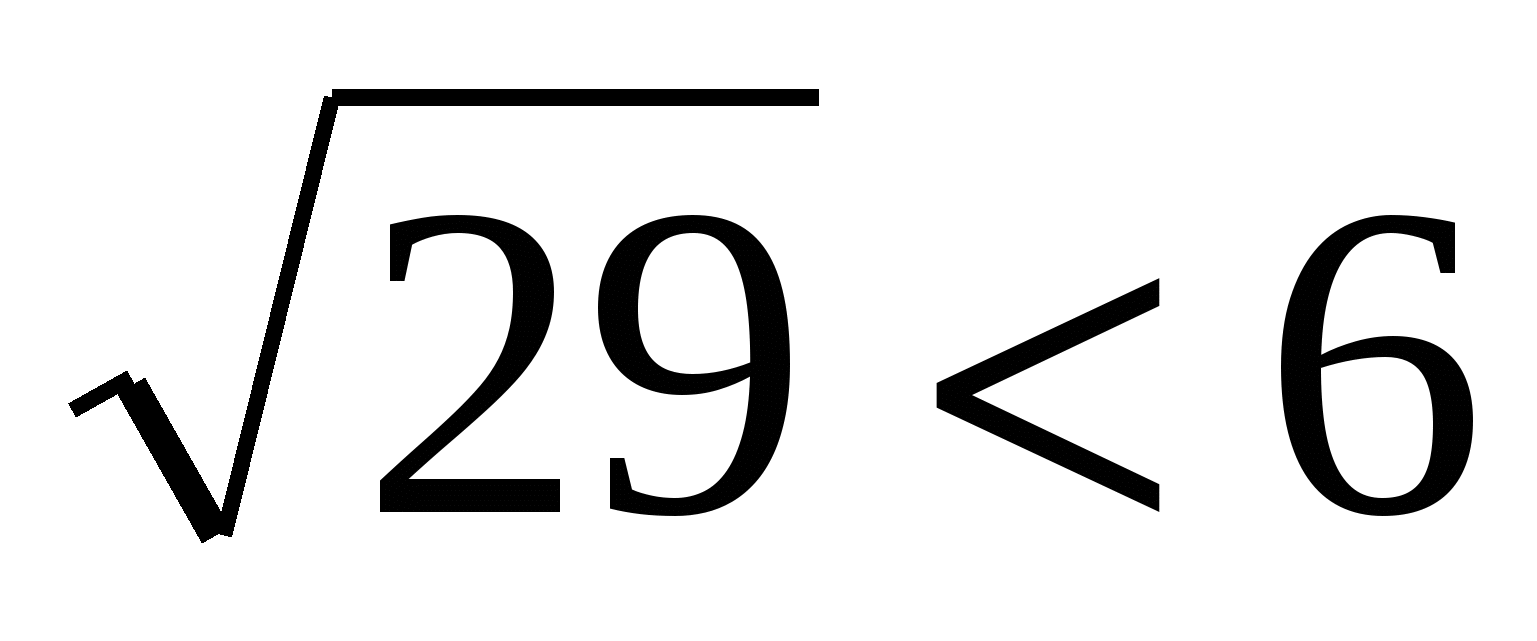 , а
, а 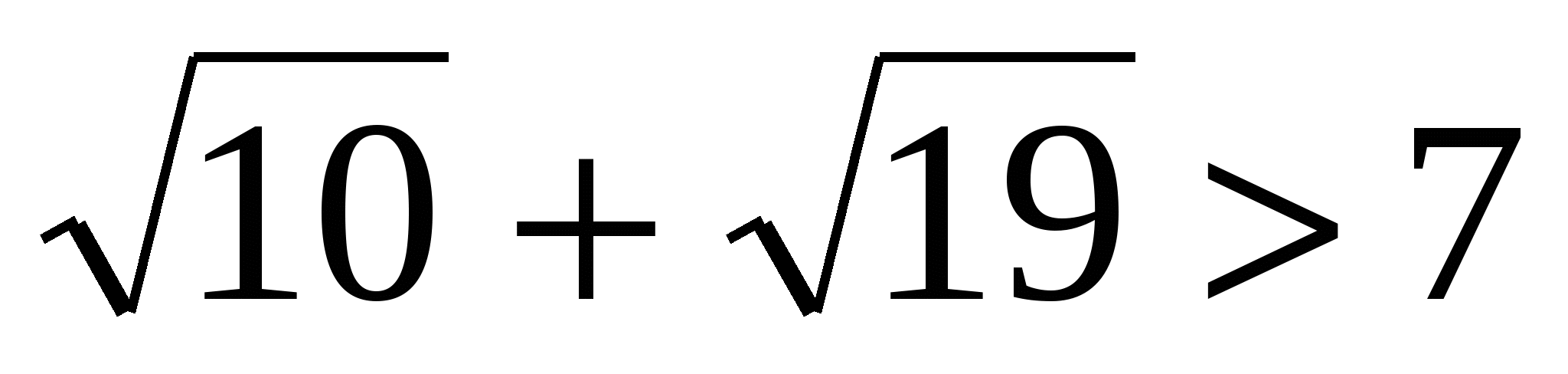 , то
, то 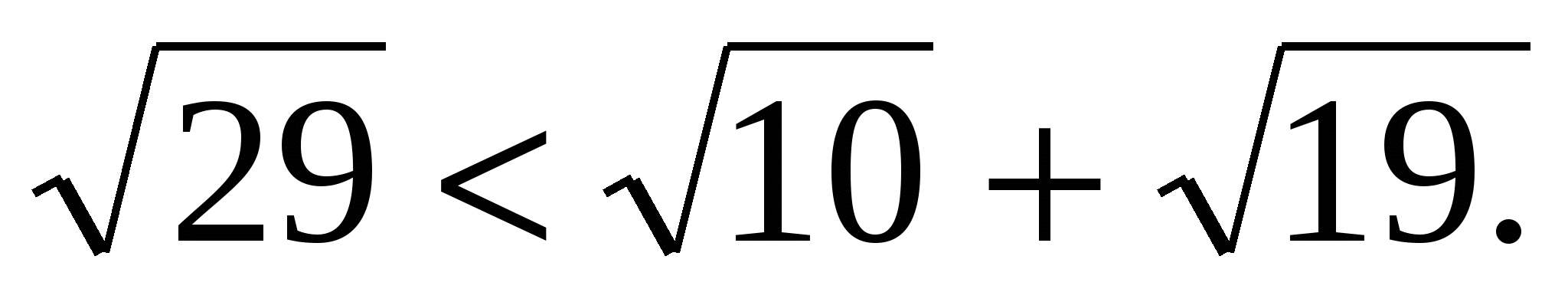
Ответ: 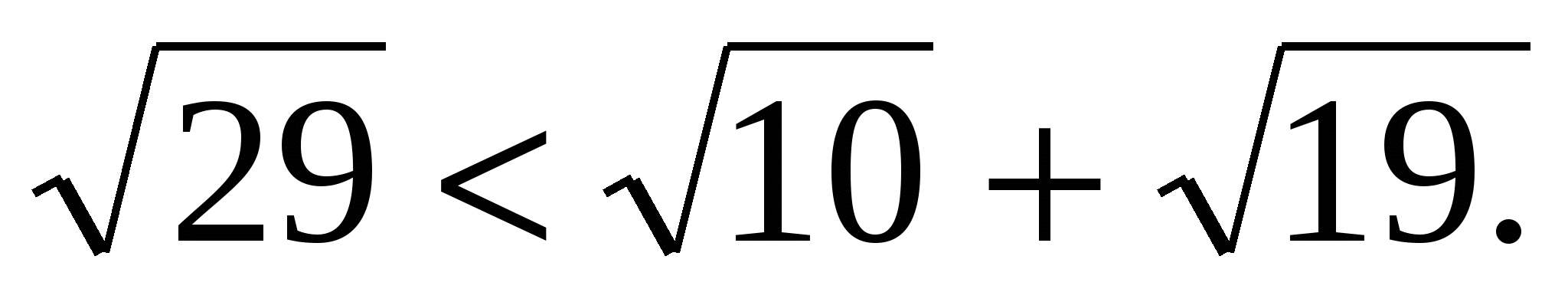
Пример 6. Вычислить: 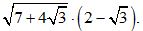
Внесение множителя под знак корня
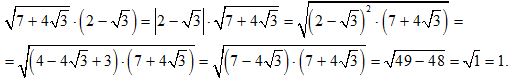
При внесении множителя под знак корня учитываются правила:
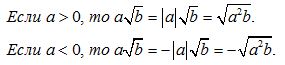
Пример7. Вычислить: 
Так как 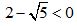 , то
, то
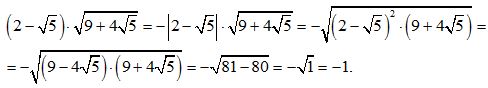
Ответ: -1.
Пример 8. Упростить выражение 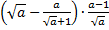 .
.
Решение. Учтем, что данное выражение имеет смысл не при всех возможных значениях переменной, т. к. в данном выражении присутствуют квадратные корни и дроби, что приводит к «сужению» области допустимых значений. ОДЗ:
 (
(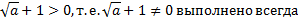 ).
).
Приведем выражение в скобках к общему знаменателю и распишем числитель последней дроби как разность квадратов:
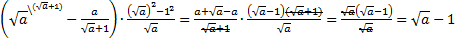 при
при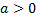 .
.
Ответ. 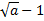 при
при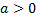 .
.
Пример 9. Упростить выражение 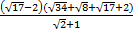 .
.
Решение. Видно, что вторая скобка числителя имеет неудобный вид и нуждается в упрощении, попробуем разложить ее на множители с помощью метода группировки.
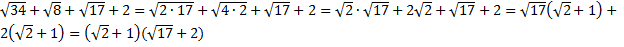 Для возможности выносить общий множитель мы упростили корни путем их разложения на множители. Подставим полученное выражение в исходную дробь:
Для возможности выносить общий множитель мы упростили корни путем их разложения на множители. Подставим полученное выражение в исходную дробь:
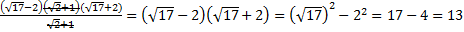 .
.
После сокращения дроби применяем формулу разности квадратов.
Ответ. 13.
Пример 10. Освободиться от иррациональности (корней) в знаменателе: а) 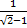 ; б)
; б) 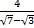 .
.
Решение. а) Для того чтобы избавиться от иррациональности в знаменателе, применяется стандартный метод домножения и числителя и знаменателя дроби на сопряженный к знаменателю множитель (такое же выражение, но с обратным знаком). Это делается для дополнения знаменателя дроби до разности квадратов, что позволяет избавиться от корней в знаменателе. Выполним этот прием в нашем случае:
 .
.
б) выполним аналогичные действия:
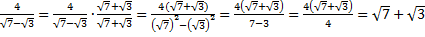 .
.
Ответ.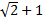 ;
; 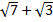 .
.
Алгоритм извлечения квадратного корня столбиком
Этот способ позволяет найти приближённое значение корня из любого действительного числа с любой наперёд заданной точностью.
Для ручного извлечения корня применяется запись, похожая на деление столбиком. Пусть извлекается корень из целого числа A. В отличие от деления снос производится группами по две цифры, причём группы следует отмечать, начиная с десятичной запятой (в обе стороны), дописывая необходимым количеством нулей.
Найти an, квадрат которого наиболее близко подходит к группе старших разрядов числа A, оставаясь меньше последнего.
Провести вычитание из старших разрядов A квадрата числа an.
Удвоить an.
Сдвинуть остаток от вычитания на 2 разряда влево, а величину 2an – на один разряд влево. Под сдвигом в данном алгоритме понимается умножение / деление на степени 10, что соответственно является сдвигом влево и вправо.
Приписать справа от остатка вычитания два следующих старших разряда числа A.
Сравнить полученное число с нулём.
Если полученное число не равно 0, то найти такое 2an − 1, которое, будучи умноженным на  , даст в результате число, меньшее полученного на четвёртом шаге, но наиболее близкое к нему по значению. Перейти к п. 3.
, даст в результате число, меньшее полученного на четвёртом шаге, но наиболее близкое к нему по значению. Перейти к п. 3.
Если в п. 6 получено равенство, то перейти к п. 4, предварительно приписав справа от an нуль.
После получения количества цифр, равного 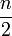 , прекратить вычисления (если требуется целое значение) или продолжать до необходимой точности, записывая получающиеся цифры после запятой.
, прекратить вычисления (если требуется целое значение) или продолжать до необходимой точности, записывая получающиеся цифры после запятой.
Описанная последовательность действий в математике получила название алгоритма извлечения квадратного корня.
Чтобы извлечь квадратный корень из данного целого числа, разбивают его справа налево на грани, по две цифры в каждой, кроме первой (крайней левой), в которой может быть и одна цифра.
Чтобы найти первую цифру корня, извлекают квадратный корень из первой грани.
Чтобы найти вторую цифру, из первой грани вычитают квадрат первой цифры корня, к остатку сносят вторую грань и число десятков получившегося числа делят на удвоенную первую цифру корня; полученное целое число снова подвергают испытанию.
Испытание проводится так: за вертикальной чертой (слева от остатка) пишут удвоенное, ранее найденное число корня, и к нему с правой стороны приписывают испытуемую цифру; получившееся после этой приписки число умножают на испытуемую цифру. Если после умножения получится число, больше остатка, то испытуемая цифра не годится и надо испытать следующую меньшую цифру.
Следующие цифры корня находят с помощью того же приёма.
Если после снесения грани число десятков получившегося числа окажется меньше делителя, т.е. меньше удвоенной найденной части корня, то в корне ставят 0, сносят следующую грань и продолжают действие дальше.
Пример. Извлечём корень 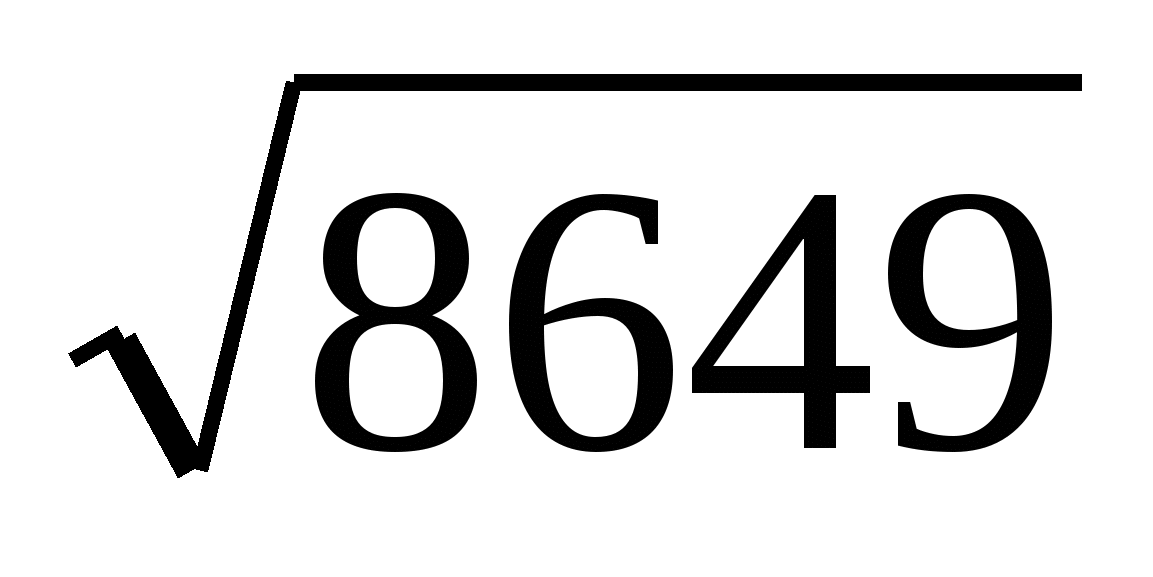 .
.
1-й шаг. Число 8649 разбиваем на грани справа налево; каждая из которых должна содержать две цифры. Получаем две грани: 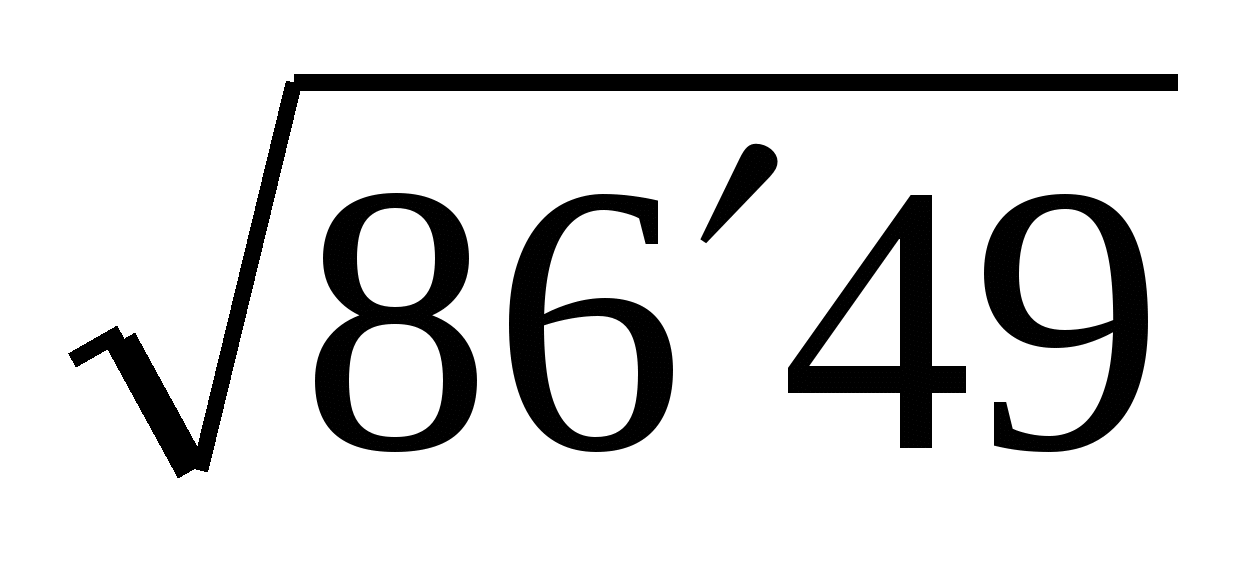 .
.
2-й шаг. Извлекаем квадратный корень из первой грани 86, получаем 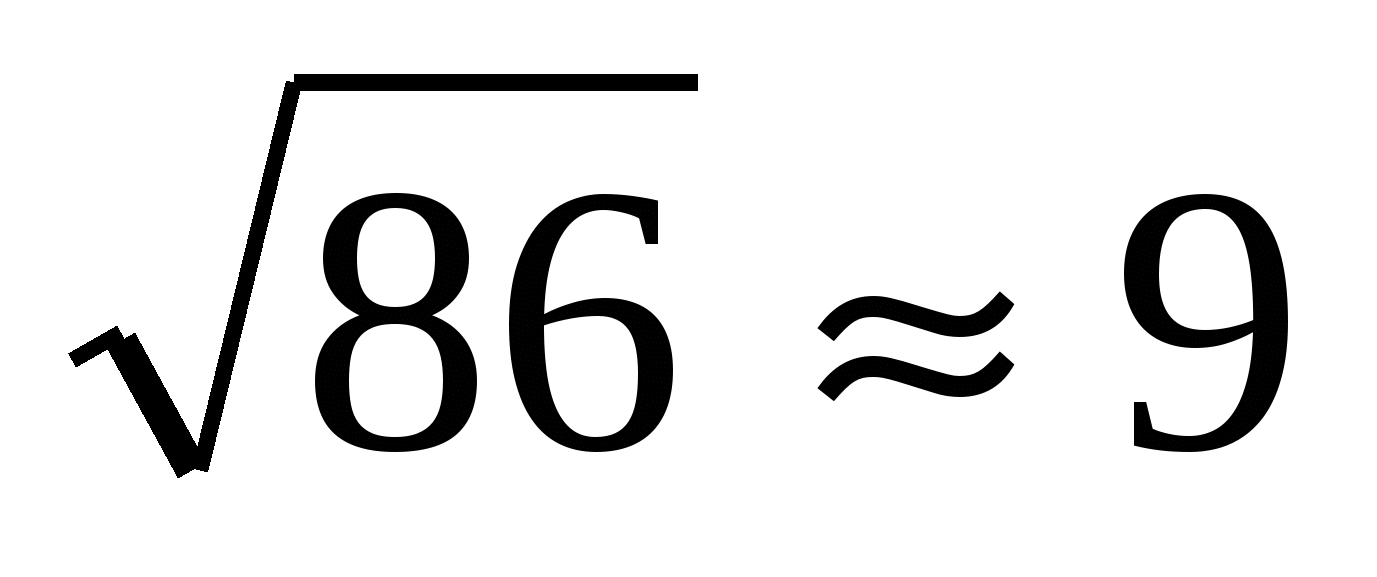 с недостатком. Цифра 9 – это первая цифра корня.
с недостатком. Цифра 9 – это первая цифра корня.
3-й шаг. Число 9 возводим в квадрат (92= 81) и число 81 вычитаем из первой грани, получаем 86 – 81 = 5. Число 5 – первый остаток.
4-й шаг. К остатку 5 приписываем вторую грань 49, получаем число 549.
5-й шаг. Удваиваем первую цифру корня 9 и, записывая слева, получаем:
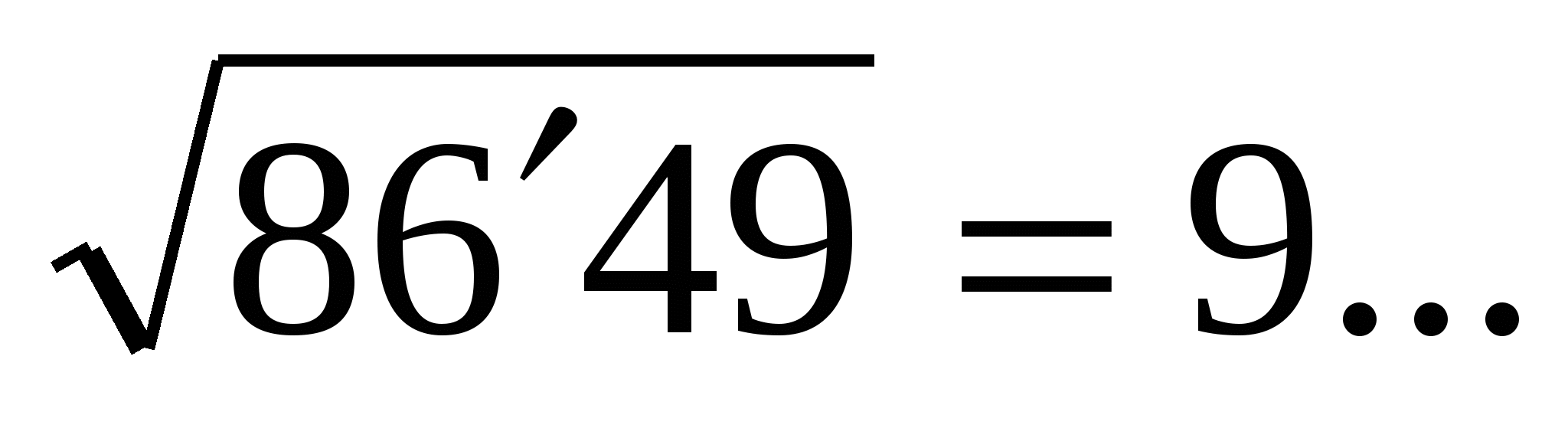
¯ 81
18… ¯¯¯¯¯549¯¯¯¯¯
К числу 18 нужно приписать такую наибольшую цифру, чтобы произведение числа, которое мы получим, на эту цифру было бы либо равно числу 549, либо меньше, чем 549. Это цифра 3. Она находится путем подбора: количество десятков числа 549, то есть число 54 делится на 18, получаем 3, так как 183 ∙ 3 = 549. Цифра 3 – это вторая цифра корня.
6-й шаг. Находим остаток 549 – 549 = 0. Так как остаток равен нулю, то мы получили точное значение корня – 93. Процесс извлечения корня закончился. Число 93 – двузначное, так как подкоренное число 8649 содержит две грани. Корень из числа содержит столько цифр, сколько граней содержит это число.
Аналогично извлекают квадратный корень из десятичных дробей. Только подкоренное число разбивают на грани так, чтобы запятая была между гранями, т.е. от запятой влево и вправо. Если в крайней правой грани окажется одна цифра, то её дополняют дописыванием к числу нуля.
Извлечение квадратного корня из целого числа «нацело».
Пример: найдём √212521
№
Шаги алгоритма
Пример
Комментарии
1
Разбить число на группы по 2 цифры в каждой справа налево
21’ 25’ 21
Общее число образовавшихся групп определяет количество цифр в ответе
2
Для первой группы цифр подобрать цифру, квадрат которой будет наибольшим, но не превосходящим числа первой группы
1 группа – 21
42=16
16<21
цифра - 4
Найденная цифра записывается в ответе на первом месте
3
Из первой группы цифр вычесть найденный на шаге 2 квадрат первой цифры ответа
_21’ 25’ 21
16
5
4
К остатку, найденному на шаге 3, приписать справа (снести) вторую группу цифр
_21’ 25’ 21
16__
525
5
К удвоенной первой цифре ответа приписать справа такую цифру, чтобы произведение полученного в результате числа на эту цифру было наибольшим, но не превосходила числа, найденного на шаге 4
4*2=8
цифра – 6
86*6=516
516<525
Найденная цифра записывается в ответе на втором месте
6
Из числа, полученного на шаге 4 вычесть число, полученное на шаге 5. Снести к остатку третью группу
_21’ 25’ 21
16
_525
516
921
7
К удвоенному числу, состоящему из первых двух цифр ответа, приписать справа такую цифру, чтобы произведение полученного в результате числа на эту цифру был наибольшим, но не превосходило числа, полученного на шаге 6
46*2=92
цифра 1
921*1=921
Найденная цифра записывается в ответе на третьем месте
8
Записать ответ
√212521=461
Извлечение квадратного корня из целого числа (корень не извлекается «нацело»).
Пример: найдём √123456
№
Шаги алгоритма
Пример
Комментарии
1
Установить точность извлечения 1/10m
m = 3
Определить количество знаков в ответе после запятой
2
Разбить число на группы по 2 цифры в каждой справа налево
12’ 34’ 56
3
Создать группы в дробной части числа, приписав, справа нули
12’ 34’ 56’, 00’ 00’ 00
Количество приписываемых нулей сокращается с заявленной точностью. В нашем примере – 6 нулей
(3 группы, так как m=3)
4
Использовать алгоритм 1, начиная со 2 шага
√12”34”56”00”00”00=351,363
_9_
_334
325
_956
701
_25500
21069
443100
421596
_2150400
2108169
42231
Извлечение квадратного корня из десятичной дроби.
Пример: найдём √104,2441
№
Шаги алгоритма
Пример
Комментарии
1
Разбить число на группы по 2 цифры в каждой
1’ 04’, 24’ 41
Цифры, входящие в целую часть числа разбить справа налево, а цифры, входящие в дробную часть – слева направо
2
Установить точность
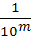
m = 4
1’ 04’, 24’ 41’ 00’ 00
Если число группы в дробной части больше m, отбросить лишнее; если меньше m - составить недостающие группы из нулей
3
Использовать алгоритм 1, начиная со 2 шага
√104,25520000=10,2105
1
_00425
404
_2152
2041
_1110000
1001025
108975
Извлечение квадратного корня из обыкновенной дроби.
Пример: найдём 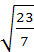
№
Шаги алгоритма
Пример
Комментарии
1
Установить точность извлечения
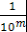 , m=2
, m=2
2
Обратить обыкновенную дробь в десятичную
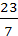 =2,4285
=2,4285
Число десятичных знаков поле запятой определяется заявленной точностью, удвоив её
3
Извлечь приближенный корень из десятичной дроби, полученной на шаге 2(использовать алгоритм 1)
-√2,4285≈1,55
_1
_142
125
_1785
1525
260
Геометрические приложения
К извлечению квадратных корней сводятся многие геометрические задачи. Например, в курсе геометрии доказывают теорему Пифагора: квадрат длины гипотенузы прямоугольного треугольника равен сумме квадратов длин катетов этого треугольника. Индийцы две тысячи лет тому назад доказывали ее с помощью следующего чертежа.
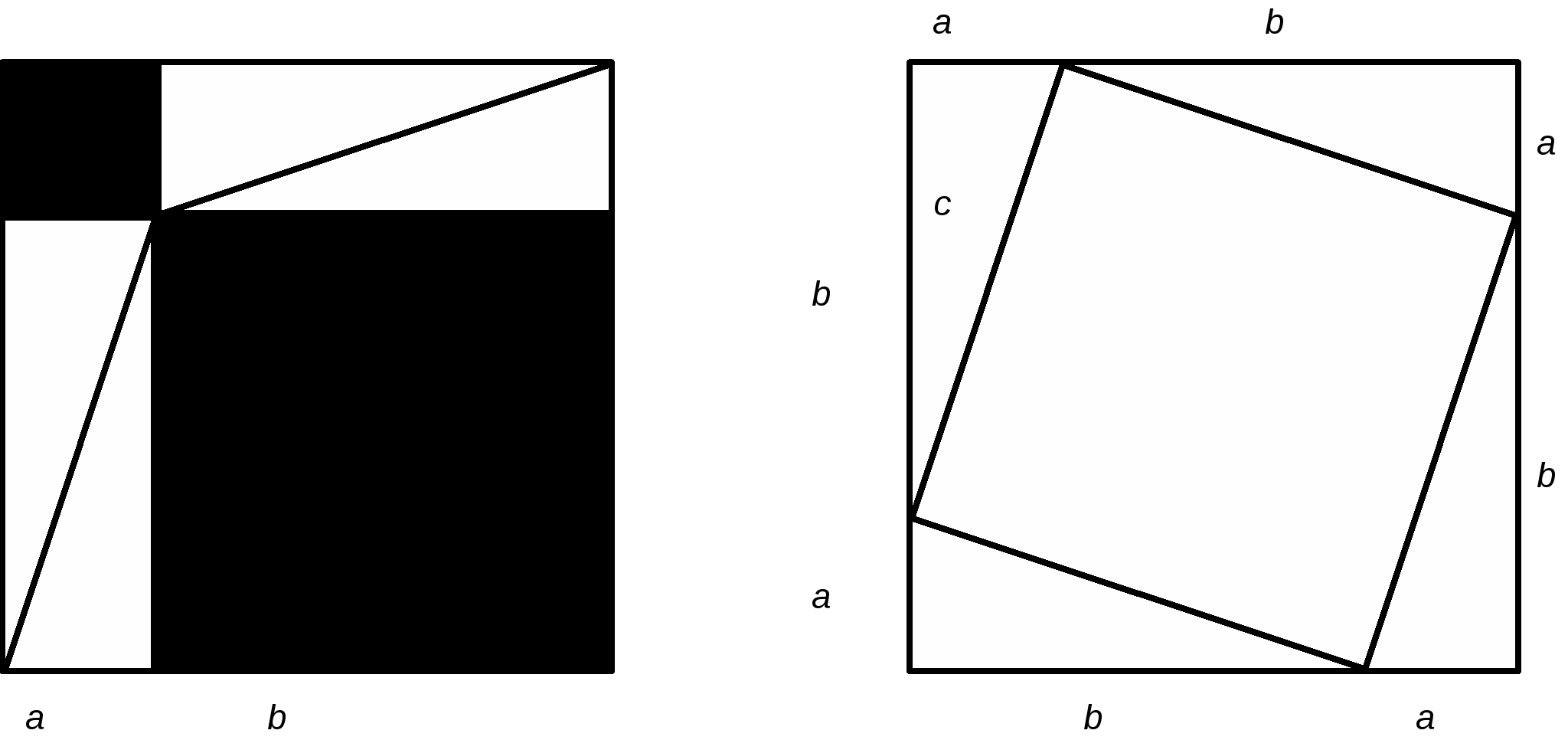
Рисунок № 1.
Видим, что площади заштрихованных фигур в обоих квадратах равны, но в одном случае площадь равна 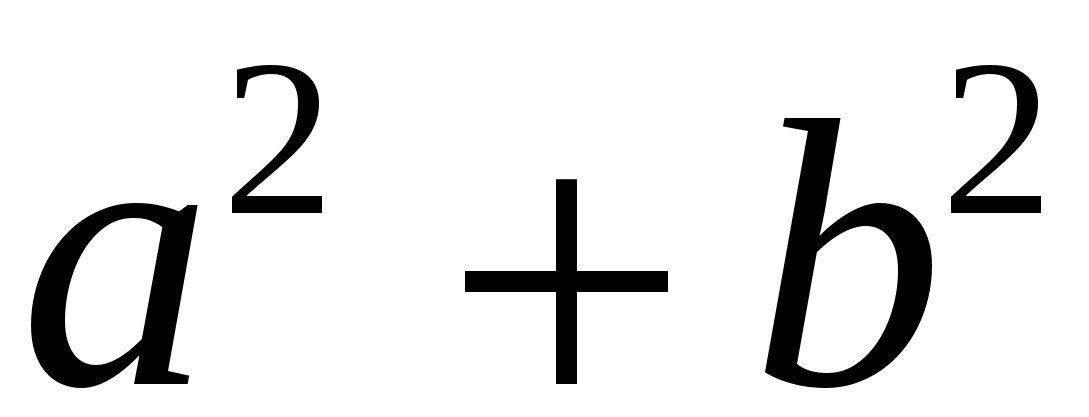 , а в другом -
, а в другом - 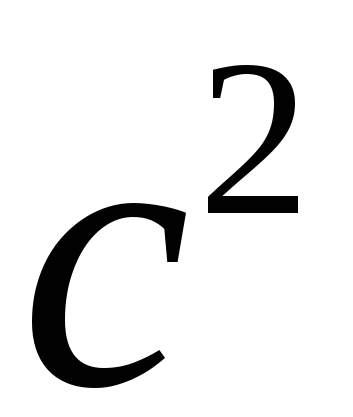 . Значит,
. Значит,  .
.
Из теоремы Пифагора следует, что расстояние между точками
М(х1;у1) и N(x2;y2) координатной плоскости (рис.2) выражается формулой
MN=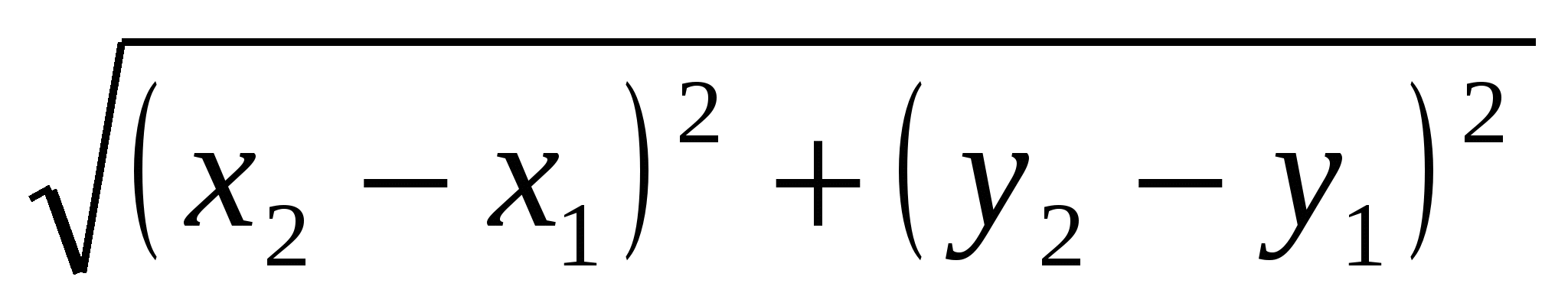 . (1)
. (1)
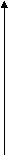
y N


 y2
y2

 y2-y1
y2-y1

 у1 M х2-х1
у1 M х2-х1
О х1 х2 x
Рис.2
Пример 1: Найдем расстояние от вершины дерева до конца его тени, если высота дерева равна 12 м, а длина тени -- 16 м.
Решение: По теореме Пифагора имеем
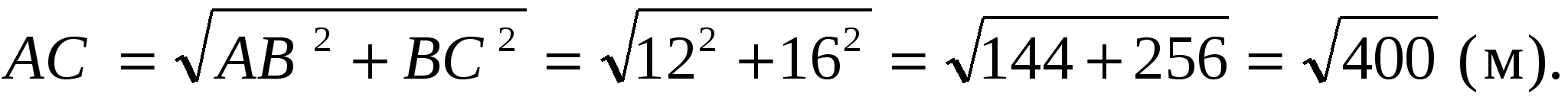
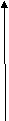 12 (х1;у1)
12 (х1;у1)
 (х2;у2)
(х2;у2)
16
Так как 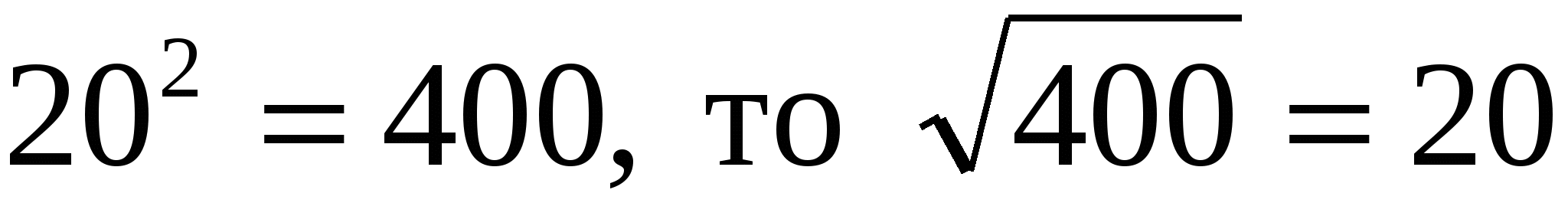 , т. е. расстояние равно 20 м.
, т. е. расстояние равно 20 м.
По формуле (1) мы получим тот же самый результат.
Пример 2: Найдем расстояние между точками М (3; 1)и N(8; -11) координатной плоскости.
Решение: По формуле (1) имеем
MN = 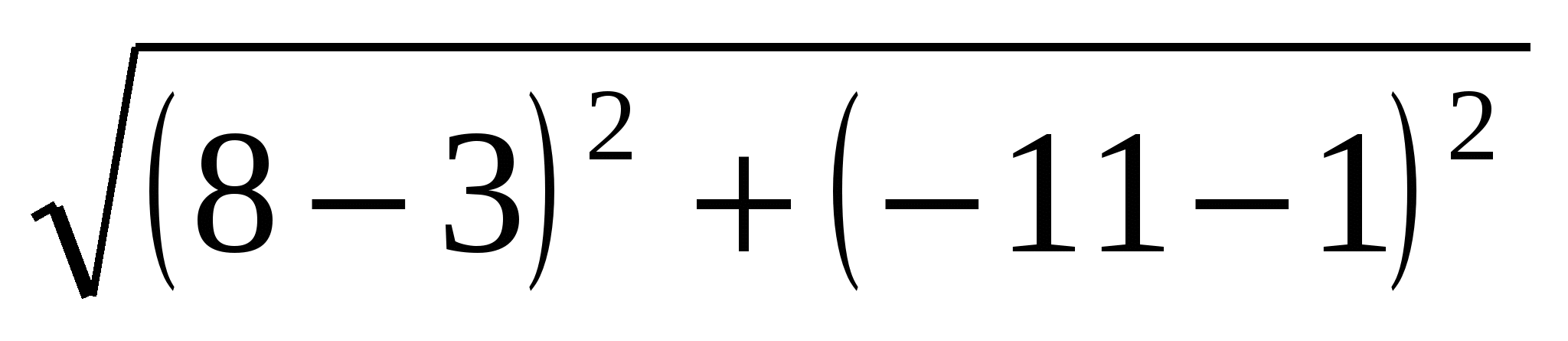 =
= 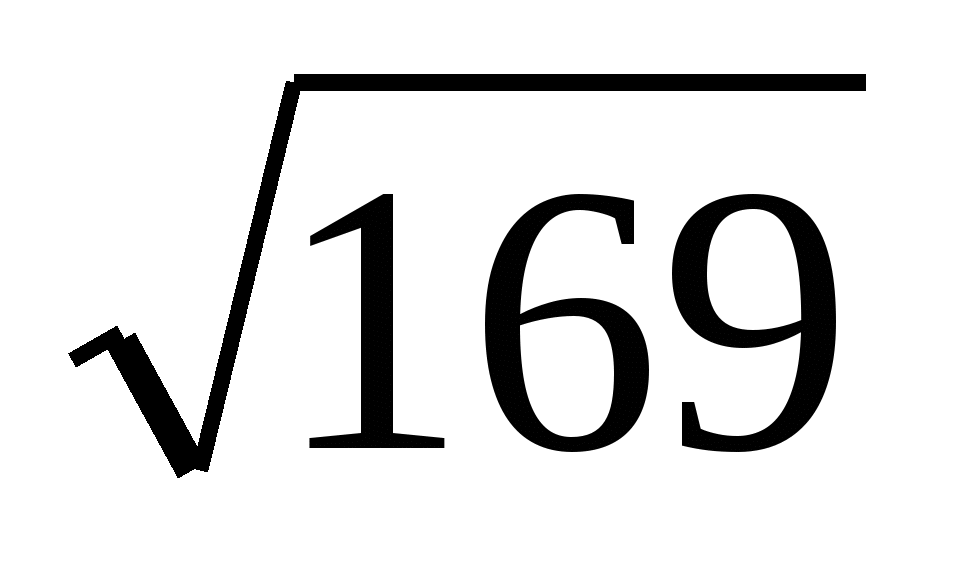 =13
=13
Заключение
Сложение и умножение имеют по одному обратному действию, которые называются вычитанием и делением. Пятое математическое действие - возведение в степень - имеет два обратных: разыскание основания и разыскание показателя. Разыскание основания есть шестое математическое действие и называемое извлечением корня. Нахождение показателя - седьмое действие - называется логарифмированием. Причину того, что возведение в степень имеет два обратных действия, в то время как сложение и умножение - только по одному, понять нетрудно: оба слагаемых (первое и второе) равноправны, их можно поменять местами; то же верно относительно умножения; однако числа, участвующие в возведении в степень, т. е. основание и показатель степени, неравноправны между собой; переставить их, вообще говоря, нельзя (например, 35не равно53). Поэтому разыскание каждого из чисел, участвующих в сложении и умножении, производится одинаковыми приемами, а разыскание основания степени и показателя степени выполняется различным образом.
В результате работы над рефератом, я расширила свои знания об арифметическом квадратном корне, узнала историю его возникновения и написания, рассмотрела задачи вычисление, на упрощение выражений, на избавление от иррациональности в знаменателе, научилась извлекать столбиком квадратный корень из многозначных чисел, десятичных дробей, обыкновенных дробей.
Данная тема является очень важной хотя и не очень понятной на первый взгляд. Каждый школьник должен научиться извлекать квадратный (или энный) корень, ведь при решении различных алгебраических или геометрических задач не обойтись без них. Даже в физике будут встречаться формулы, содержащие корни квадратные.
Я считаю, что полученные мною знания пригодятся для дальнейшего изучения алгебры и других предметов, а также для успешной сдачи экзаменов.
Список литературы
1. Алгебра: Учеб. Для 8 кл. сред.шк.\ Ш.А.Алимов, Ю.М.Колягин, Ю.В.Сидоров и др. – 2 изд.М.:-Просвещение, 2013г
2. Маковецкий П. В. «Смотри в корень», Сборник любопытных задач и вопросов, Москва издательство «Наука» 2008 г., 448 стр.
3.Петраков И.С. «Математические кружки в 8–10 классах»: Кн. для учителя. – М.: Просвещение, 1987 г.
4. Энциклопедия для детей. Т. 11. Математика/ Глав. ред. М. Аксенова. М.: Аванта+плюс. 2004 г.
5. Перельман Я. И. «Занимательная алгебра», Москва издательство «Наука» 2000 г., 200 стр.
6. «Большая Советская Энциклопедия»
7. Интернет-сайт «Научные термины», www. izviliny.ru/science terms.
8. Интернет-сайт «Школа перспектива», www. sys-tema.ru.
infourok.ru
ВведениеВ ходе решения некоторых математических задач приходится оперировать с квадратными корнями. Поэтому важно знать правила действий с квадратными корнями и научиться преобразовывать выражения, их содержащие. Цель – изучение правил действий с квадратными корнями и способов преобразования выражений с квадратными корнями. Мы знаем, что некоторые рациональные числа выражаются бесконечными периодическими десятичными дробями, как, например, число 1/1998=0,000500500500… Но ничто не мешает вообразить и число, в десятичном разложении которого не обнаружится никакого периода. Такие числа называются иррациональными. История иррациональных чисел восходит к удивительному открытию пифагорейцев еще в VI в. до н. э. А началось все с простого, казалось бы, вопроса: каким числом выражается длина диагонали квадрата со стороной 1? Диагональ разбивает квадрат на 2 одинаковых прямоугольных треугольника, в каждом из которых она выполняет роль гипотенузы. Поэтому, как следует из теоремы Пифагора, длина диагонали квадрата равна. Сразу же возникает соблазн достать микрокалькулятор и нажать клавишу извлечения квадратного корня. На табло мы увидим 1,4142135. Более совершенный калькулятор, выполняющий вычисления с высокой точностью покажет 1,414213562373. А с помощью современного мощного компьютера
можно вычислить с точностью до сотен, тысяч, миллионов знаков после запятой. Но даже самый высокопроизводительный компьютер, сколько бы долго он ни работал, никогда не сможет ни рассчитать все десятичные цифры, ни обнаружить в них какой-либо период. И хотя у Пифагора и его учеников компьютера не было, обосновали этот факт именно они. Пифагорейцы доказали, что у диагонали квадрата и его стороны общей меры (т.е. такого отрезка, который целое число раз откладывался бы и на диагонали, и на стороне) не существует. Следовательно, отношение их длин – число
– нельзя выразить отношением некоторых целых чисел m и n. А коль скоро это так, добавим мы, десятичное разложение числа
не обнаруживает никакой регулярной закономерности. По следам открытия пифагорейцев Как доказать, что число
иррационально? Предположим, существует рациональное число m/n=
. Дробь m/n будем считать несократимой, ведь сократимую дробь всегда можно привести к несократимой. Возведя обе части равенства, получим
. Отсюда заключаем, что m – число четное, то есть m=2К. Поэтому
и, следовательно,
, или
. Но тогда получим что и n четное число, а этого быть не может, поскольку дробь m/n несократима. Возникает противоречие. Остается сделать вывод, что наше предположение неверно и рационального числа m/n, равного
не существует.
\* MERGEFORMATРис. 1 Видим, что площади заштрихованных фигур в обоих квадратах равны, но в одном случае площадь равна
, а в другом –
. Значит,
. Из теоремы Пифагора следует, что расстояние между точками М (х1; у1) и N (x2; y2) координатной плоскости (рис. 2) выражается формулой MN=
(1) Пример 1. Найдем расстояние от вершины дерева до конца его тени, если высота дерева равна 12 м, а длина тени – 16 м. Решение. По теореме Пифагора имеем
Так как
, т.е. расстояние равно 20 м. Пример 2. Найдем расстояние между точками М (3; 1) и N (8; -11) координатной плоскости. Решение. По формуле (1) имеем MN =
=
=13
= – х, если х < 0. Поэтому для всех чисел х верно равенство
=
. (4) Например,
=
=8,
2 =
= 12. Пример 1. Упростим выражение
+
2 +
-
2. Р е ш е н и е. Так как
2 = 3,
2 = 2, то
+
2 +
-
2 =
2 + 2
+
2 +
2 – 2
+
2 =2
2 + 2
2 = 2
3 + 2
2 = =10. Пример 2. Найдем значения выражения
при а = 2,1; b = 3,6 Решение. При любом значении х выполняется равенство
=
. Поэтому
=
. Но
=
= 1,5. Значит, при а = 2,1; b =3,6 имеем
=1,5.
где А2 В (в обеих частях равенства одновременно берутся знаки «плюс» и «минус «). Чтобы доказать это равенство, заметим, во-первых, что и левая, и правая его части являются при А
0, В
0, А2 – В
0 неотрицательными числами. Возведем теперь обе части равенства
в квадрат. В левой части имеем А
, в правой части по формуле квадрата суммы или разности получаем
2
+
= = А
2
= А
2
= = А
2
= А
2
= А
. Таким образом, квадраты обеих частей равенства
оказались одинаковыми, а поскольку эти части – неотрицательные числа, то равенство
доказано. Пример 1. Упростить выражение
. 1-й способ. В одном случае имеем А = 5, В = 21, А2 – В = = 52 – 21 = 4, и поэтому по формуле
=
–
=
–
. 2-й способ. Приведем подкоренное выражение к полному квадрату: 5 –
=
=
= =
=
=
.
Поэтому =
=
Пример 2. Упростить выражение
1-й способ:
=
+
= =
+
=
2-й способ. Приведем подкоренное выражение к полному квадрату:
Пример 3. Упростить выражение
Решение.
Ответ: 10. Пример 4. Упростить
Решение. 1.
2.
3.
Ответ:
Пример 5. Какое из чисел больше:
или
? Решение. Очевидно, что
Оценим сумму
Так как
, а
, то
Ответ:
www.coolreferat.com
Квадратные корни
Введение
В ходерешения некоторых математических задач приходится оперировать с квадратнымикорнями. Поэтому важно знать правила действий с квадратными корнями и научитьсяпреобразовывать выражения, их содержащие. Цель – изучение правил действий сквадратными корнями и способов преобразования выражений с квадратными корнями.
Мы знаем, чтонекоторые рациональные числа выражаются бесконечными периодическими десятичнымидробями, как, например, число 1/1998=0,000500500500… Но ничто не мешаетвообразить и число, в десятичном разложении которого не обнаружится никакогопериода. Такие числа называются иррациональными.
Историяиррациональных чисел восходит к удивительному открытию пифагорейцев еще в VI в.до н. э. А началось все с простого, казалось бы, вопроса: каким числомвыражается длина диагонали квадрата со стороной 1?
Диагональразбивает квадрат на 2 одинаковых прямоугольных треугольника, в каждом изкоторых она выполняет роль гипотенузы. Поэтому, как следует из теоремыПифагора, длина диагонали квадрата равна/>.Сразу же возникает соблазн достать микрокалькулятор и нажать клавишу извлеченияквадратного корня. На табло мы увидим 1,4142135. Более совершенный калькулятор,выполняющий вычисления с высокой точностью покажет 1,414213562373. А с помощьюсовременного мощного компьютера /> можновычислить с точностью до сотен, тысяч, миллионов знаков после запятой. Но дажесамый высокопроизводительный компьютер, сколько бы долго он ни работал, никогдане сможет ни рассчитать все десятичные цифры, ни обнаружить в них какой-либопериод.
И хотя уПифагора и его учеников компьютера не было, обосновали этот факт именно они.Пифагорейцы доказали, что у диагонали квадрата и его стороны общей меры (т.е.такого отрезка, который целое число раз откладывался бы и на диагонали, и настороне) не существует. Следовательно, отношение их длин – число /> – нельзя выразитьотношением некоторых целых чисел m и n. А коль скоро это так, добавим мы,десятичное разложение числа /> необнаруживает никакой регулярной закономерности.
По следамоткрытия пифагорейцев
Как доказать,что число /> иррационально?Предположим, существует рациональное число m/n=/>. Дробь m/n будем считатьнесократимой, ведь сократимую дробь всегда можно привести к несократимой.Возведя обе части равенства, получим />. Отсюдазаключаем, что m – число четное, то есть m=2К. Поэтому /> и,следовательно, />, или />. Но тогда получим что и n четное число, а этогобыть не может, поскольку дробь m/n несократима. Возникает противоречие.
Остаетсясделать вывод, что наше предположение неверно и рационального числа m/n, равного />не существует.
1. Квадратный корень из числа
Зная время t,можно найти путь при свободном падении по формуле: /> Решимобратную задачу.
Задача. Сколько секунд будетпадать камень, сброшенный с высоты 122,5 м?
Чтобы найтиответ, нужно решить уравнение /> Из негонаходим, что /> Теперь осталось найтитакое положительное число t, что его квадрат равняется 25. Этим числом является5, так как /> Значит, камень будетпадать 5 с.
Искатьположительное число по его квадрату приходится и при решении других задач,например при отыскании длины стороны квадрата по его площади. Введем следующееопределение.
Определение. Неотрицательноечисло, квадрат которого равен неотрицательному числу а, называется квадратнымкорнем из а. Это число обозначают />
Таким образом/>
Пример. Так как
/>
Изотрицательных чисел нельзя извлекать квадратные корни, так как квадрат любогочисла или положителен, или равен нулю. Например, выражение /> не имеет числовогозначения.
В записи /> знак /> называют знаком радикала(от латинского «радикс» – корень), а число а – подкоренным числом.Например, в записи /> подкоренноечисло равно 25. Так как /> Этоозначает, что квадратный корень из числа, записанного единицей и2nнулями, равен числу, записываемому единицей и n нулями:
/> = 10…0
2n нулей n нулей
Аналогичнодоказывается, что /> 2n нулей n нулей
Например, />
2. Вычислениеквадратных корней
Мы знаем, чтоне существует рационального числа, квадрат которого равен 2. Это означает, что /> не может быть рациональнымчислом. Он является иррациональным числом, т.е. записывается в виденепериодической бесконечной десятичной дроби, причем первые десятичные знакиэтой дроби имеют вид 1,414… Чтобы найти следующий десятичный знак, надо взятьчисло 1.414х, где х может принимать значения 0, 1, 2, 3, 4, 5, 6,7, 8, 9, возвести по порядку эти числа в квадрат и найти такое значениех,при котором квадрат меньше, чем 2, но следующий за ним квадрат больше, чем 2.Таким значением является х=2. Далее повторяем то же самое с числами вида1,4142х. Продолжая этот процесс, получаем одну за другой цифры бесконечнойдесятичной дроби, равной />.
Аналогичнодоказывается существование квадратного корня из любого положительногодействительного числа. Разумеется, последовательное возведение в квадрат весьматрудоемкое занятие, и потому существуют способы быстрее находить десятичныезнаки квадратного корня. С помощью микрокалькулятора можно найти значение /> с восемью верными цифрами.Для этого достаточно ввести в микрокалькулятор число а>0 и нажатьклавишу /> – на экране высветится 8цифр значения />. В некоторыхслучаях приходится использовать свойства квадратных корней, которые мы укажемниже.
Еслиточность, даваемая микрокалькулятором, недостаточна, можно воспользоватьсяспособом уточнения значения корня, даваемым следующей теоремой.
Теорема. Если а – положительноечисло и /> – приближенное значениедля /> по избытку, то /> – приближенноезначение для /> по недостатку.
Доказательство.
По условию x1><sub/>/> и потому х12>a,/><1. Но />2 = /> = a/>. Т.к. /><1, то a/><a. Значит, />а и /> — приближенное значение для/> по недостатку.
Аналогичнодоказывается, что если /> – приближенноезначение для /> по недостатку, то /> – приближенное значение /> по избытку.
Поскольку /> и /> являются приближеннымизначениями для /> по избытку и понедостатку, то в качестве лучшего приближения для /> естественновыбрать среднее арифметическое этих чисел, т.е. число х2 = />/>.А чтобы получить еще более точное значение для />,надо взять среднее арифметическое чисел />,т.е. число х3 = />/>. Так вычисляются одно за другимвсе лучшие и лучшие приближенные значения для />.Приближения ведут до тех пор, пока два полученных значения /> не совпадут в пределахзаданной точности. Можно доказать, что каждое приближение примерно удваиваетчисло верных десятичных знаков.
Пример1. Уточнимпо формуле х2 = />/> приближение
х1 = 1,414для />.
Решение.
В нашемслучае а=2. Поэтому
х1 = />(1,414 + 1,4144271) +1,4142135…
Выполнив ещеодно приближение, мы убедимся, что все выписанные знаки полученного ответаверны, т.е. число верных знаков удвоилось.
Пример2. Найдем приближенноезначение для /> с точностью до 0,0001.
Решение.
Выберем запервое приближение для /> число 2. Тогдавторое приближение вычисляется так:
х2 = />= 2,25/>
Далее имеем
х3 =/>= 2,2361,
х4=/>=2,2361.
Значит, сточностью до 0,0001 имеем />=2,2361.
Ответ: />
3. Геометрическиеприложения
К извлечениюквадратных корней сводятся многие геометрические задачи. Например, в курсегеометрии доказывают теорему Пифагора: квадрат длиныгипотенузы прямоугольного треугольника равен сумме квадратов длин катетов этоготреугольника. Индийцы две тысячи лет тому назад доказывали ее с помощьюследующего чертежа.
/>
Рис. 1
Видим, чтоплощади заштрихованных фигур в обоих квадратах равны, но в одном случае площадьравна />, а в другом – />. Значит, />.
Из теоремы Пифагораследует, что расстояние между точками
М (х1; у1) и N (x2; y2) координатной плоскости(рис. 2) выражается формулой
MN=/> (1)
Пример1. Найдем расстояние отвершины дерева до конца его тени, если высота дерева равна 12 м, а длинатени – 16 м.
Решение. Потеореме Пифагора имеем
/>
Так как />, т.е. расстояние равно 20 м.
Пример2. Найдем расстояние междуточками М (3; 1) и N (8; -11) координатной плоскости.
Решение.
По формуле(1) имеем MN = />= />=13
4. Основные тождества для квадратныхкорней
Изопределения квадратного корня вытекает, что равенство/>/>=х,где а/>0, верно в том и только втом случае, когда<sup/>х2=а, причем х/>0. Заменяя в равенстве х2=апеременную х на />, получаемтождество />2=а, (1)
верное длявсех а/>0. Заменяя в равенстве />=х переменную а на х2,получаем тождества
/>= х, (2)
которое вернодля всех х/>0.
Например, />2 = 25;/>2 = 8; />2 = 0,11; />= 6; />=0,24.
Формулы /> и /> показывают, что длянеотрицательных чисел операции возведения в квадрат и извлечения квадратногокорня взаимно обратны, т.е. если выполнить над каким-нибудь неотрицательнымчислом сначала одну из этих операций, а потом другую, то число не изменится.
Если а –отрицательное число, то равенство /> неверно,так как /> не имеет числовогозначения. При отрицательных значениях х неверно и равенство />. Например, />2 =/>=5, а не –5. Так как х2=/>2, а при х< 0 имеем – х> 0,
то при х<0 верно равенство />=/>2 = – х (3)
Итак,
/>x, если х/> 0,
/>= – х, если х < 0.
Но мы знаем,что х, если х /> 0,
/>/>=
– х, если х< 0.
Поэтому длявсех чисел х верно равенство
/>= />. (4)
Например, />=/>=8, />2 = />= 12.
Пример1. Упростим выражение />+/>/>2+ /> — />/>2.
Р е ш е н ие. Так как />2 = 3, />2 = 2, то />+/>2 + /> — />2 =/>2 +
2/>/>/> + />2 +/>2 – 2/>/>/> + />2 =2/> />2 + 2 /> />2 = 2 /> 3 + 2 /> 2 = =10.
Пример2. Найдемзначения выражения /> при а = 2,1; b = 3,6
Решение. Прилюбом значении х выполняется равенство
/>= />. Поэтому />= />. Но />=/>= 1,5. Значит, при а = 2,1;b =3,6 имеем /> =1,5.
5. Извлечениеквадратного корня из произведения, дроби и степени
Выражения />/> и /> имеют одно и то жезначение 6.
В самом деле,/>= 3, />= 2, /> = 6, поэтому />/>/>= 3 /> 2 = 6 и />= =/>= 6. Равенство />/>/>=/> – часный случай общегоутверждения.
Теорема1. Квадратныйкорень из произведения двух неотрицательных чисел равен произведению квадратныхкорней из этих чисел, т.е. при а /> 0, b/> 0 имеем />= /> /> />
Доказательство.
Пусть числа аи b неотрицательны.
Тогда поправилу возведения в степень имеем
/> /> />2 = />/>/> />= а /> b
Кроме того, /> /> /> – неотрицательное числокак произведение двух неотрицательных чисел /> и/>. Поэтому /> /> />= />
Пример 1. Найдем значения выражения/>
Решение.
Мы имеем /> = 25, />= 16, />= 0,01,
и потому /> =25/>16/>0,01= 4.
Аналогичнодоказывается, что /> = />
Теорема2.Квадратный корень из дроби с неотрицательным числителем и положительнымзнаменателем равен частному от деления квадратного корня из числителя на квадратныйкорень из знаменателя, т.е. при а /> 0 и b> 0 имеем />
Теорема3.Прилюбом значении а и при любом b/> 0 верно равенство />
6. ПреобразованиевыраженийПрипреобразовании выражении, содержащих квадратные корни, оказывается полезной следующаяформула:
/>= /> /> />,
где А2/> В (в обеих частях равенства одновременно берутсязнаки «плюс» и «минус «). Чтобы доказать это равенство, заметим, во-первых, чтои левая, и правая его части являются при А/> 0,В/> 0, А2 – В /> 0 неотрицательными числами.Возведем теперь обе части равенства /> в квадрат.В левой части имеем А /> />, в правой части по формулеквадрата суммы или разности получаем
/> /> 2/> /> /> + />=
= А /> 2/> = А /> 2/> =
= А /> 2/> = А /> 2/> = А /> />.
Таким образом,квадраты обеих частей равенства /> оказалисьодинаковыми, а поскольку эти части – неотрицательные числа, то равенство />доказано.
Пример1. Упроститьвыражение />.
1-й способ. В одном случае имеем А= 5, В = 21, А2 – В =
= 52– 21 = 4, и поэтому по формуле />
/>= /> – /> = /> – />.
2-й способ. Приведем подкоренное выражениек полному квадрату:
5 – />= />/>=/>/>=
=/>/>=/>/> =/>.
Поэтому />= />= />
Пример2.Упроститьвыражение />
1-й способ:
/>= /> + />=
= /> + />= />
2-й способ.Приведемподкоренное выражение к полному квадрату: />
/>
Пример3. Упростить выражение />
Решение.
/>/>
Ответ: 10.
Пример4. Упростить />
Решение.
1. />
2. />
3. />
Ответ: />
Пример5. Какое из чисел больше: /> или />?
Решение.
Очевидно, что/>
Оценим сумму /> />
/>
/>
Так как />, а />, то />
Ответ: />
7. Алгоритмизвлечения квадратного корня столбикомЭтот способпозволяет найти приближённое значение корня из любого действительного числа слюбой наперёд заданной точностью.
Для ручногоизвлечения корня применяется запись, похожая на деление столбиком. Пустьизвлекается корень из целого числа A. Вотличие от деления снос производится группами по две цифры, причём группыследует отмечать, начиная с десятичной запятой (в обе стороны), дописываянеобходимым количеством нулей.
Найти an, квадрат которого наиболее близкоподходит к группе старших разрядов числа A,оставаясь меньше последнего.
Провестивычитание из старших разрядов A квадратачисла an.
Удвоить an.
Сдвинутьостаток от вычитания на 2 разряда влево, а величину 2an –на один разряд влево. Под сдвигом в данном алгоритме понимается умножение /деление на степени 10, что соответственно является сдвигом влево и вправо.
Приписатьсправа от остатка вычитания два следующих старших разряда числа A.
Сравнитьполученное число с нулём.
Еслиполученное число не равно 0, то найти такое 2an− 1, которое, будучи умноженным на />,даст в результате число, меньшее полученного на четвёртом шаге, но наиболееблизкое к нему по значению. Перейти к п. 3.
Если в п. 6получено равенство, то перейти к п. 4, предварительно приписав справа от an нуль.
Послеполучения количества цифр, равного />, прекратитьвычисления (если требуется целое значение) или продолжать до необходимойточности, записывая получающиеся цифры после запятой.
Описаннаяпоследовательность действий в математике получила название алгоритма извлеченияквадратного корня.
1. Чтобыизвлечь квадратный корень из данного целого числа, разбивают его справа налевона грани, по две цифры в каждой, кроме первой (крайней левой), в которой можетбыть и одна цифра.
2. Чтобынайти первую цифру корня, извлекают квадратный корень из первой грани.
3. Чтобынайти вторую цифру, из первой грани вычитают квадрат первой цифры корня, костатку сносят вторую грань и число десятков получившегося числа делят наудвоенную первую цифру корня; полученное целое число снова подвергаютиспытанию.
4. Испытаниепроводится так: за вертикальной чертой (слева от остатка) пишут удвоенное,ранее найденное число корня, и к нему с правой стороны приписывают испытуемуюцифру; получившееся после этой приписки число умножают на испытуемую цифру.Если после умножения получится число, больше остатка, то испытуемая цифра негодится и надо испытать следующую меньшую цифру.
5. Следующиецифры корня находят с помощью того же приёма.
6. Еслипосле снесения грани число десятков получившегося числа окажется меньшеделителя, т.е. меньше удвоенной найденной части корня, то в корне ставят 0,сносят следующую грань и продолжают действие дальше.
Пример.Извлечём корень />.
1-й шаг. Число 8649 разбиваем награни справа налево; каждая из которых должна содержать две цифры. Получаем двеграни: />.
2-й шаг. Извлекаем квадратныйкорень из первой грани 86, получаем /> снедостатком. Цифра 9 – это первая цифра корня.
3-й шаг. Число 9 возводим вквадрат (92<sub/>= 81) и число 81 вычитаем из первой грани,получаем 86 – 81 = 5. Число 5 – первый остаток.
4-й шаг. К остатку 5 приписываемвторую грань 49, получаем число 549.
5-й шаг. Удваиваем первую цифрукорня 9 и, записывая слева, получаем:
/>
¯ 81
18… ¯¯¯¯¯549¯¯¯¯¯
К числу 18нужно приписать такую наибольшую цифру, чтобы произведение числа, которое мыполучим, на эту цифру было бы либо равно числу 549, либо меньше, чем 549. Этоцифра 3. Она находится путем подбора: количество десятков числа 549, то естьчисло 54 делится на 18, получаем 3, так как 183 ∙ 3 = 549. Цифра 3 – этовторая цифра корня.
6-й шаг. Находим остаток 549 –549 = 0. Так как остаток равен нулю, то мы получили точное значение корня – 93.Процесс извлечения корня закончился. Число 93 – двузначное, так как подкоренноечисло 8649 содержит две грани. Корень из числа содержит столько цифр, сколькограней содержит это число.
Аналогичноизвлекают квадратный корень из десятичных дробей. Только подкоренное числоразбивают на грани так, чтобы запятая была между гранями, т.е. от запятой влевои вправо. Если в крайней правой грани окажется одна цифра, то её дополняют дописываниемк числу нуля.
Заключение
Данная работа посвящена квадратнымкорням. Рассмотрены правила действий с квадратными корнями, способыпреобразования выражений, содержащих квадратные корни, геометрические приложения.В работе приведены примеры действий с квадратными корнями и преобразованиявыражений с ними. Рассмотрен алгоритм извлечения квадратного корня.
Такимобразом, цель достигнута, задачи выполнены.
Список использованныхисточников1. Алгебра: Учеб. пособие для8 кл. / Е.П. Кузнецова и др; под ред. Л.Б. Шнепермана. – 2 изд. –Мн.: Нар. асвета, 2005.
2. Алгебра: Учеб. для 8‑хкл. общеобразоват. шк. с углубл. изучением математики / К.О. Ананченко идр. – Мн.: Нар. асвета, 1994.
3. Петраков И.С.«Математические кружки в 8–10 классах»: Кн. для учителя. – М.:Просвещение, 1987 г.
4. Энциклопедия для детей.Т. 11. Математика/ Глав. ред. М. Аксенова. М.: Аванта+плюс. 2004 г.
edportal.net
Операции со степенями.
1. При умножении степеней с одинаковым основанием их показатели складываются:
a m · a n = a m + n .
2. При делении степеней с одинаковым основанием их показатели вычитаются.

3. Степень произведения двух или нескольких сомножителей равна произведению степеней этих сомножителей.
( abc… ) n = a n · b n · c n …
4. Степень отношения (дроби) равна отношению степеней делимого (числителя) и делителя (знаменателя):
( a / b ) n = a n / b n .
5. При возведении степени в степень их показатели перемножаются:
( a m ) n = a m n .
П р и м е р . ( 2 · 3 · 5 / 15 ) ² = 2 ² · 3 ² · 5 ² / 15 ² = 900 / 225 = 4 .
Операции с корнями. Во всех нижеприведенных формулах символ 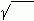 означает арифметический корень (подкоренное выражение положительно).
означает арифметический корень (подкоренное выражение положительно).
1. Корень из произведения нескольких сомножителей равен произведению корней из этих сомножителей:

2. Корень из отношения равен отношению корней делимого и делителя:

3. При возведении корня в степень достаточно возвести в эту степень подкоренное число:

4. Если увеличить степень корня в n раз и одновременно возвести в n-ую степень подкоренное число, то значение корня не изменится:

5. Если уменьшить степень корня в n раз и одновременно извлечь корень n-ой степени из подкоренного числа, то значение корня не изменится:

Расширение понятия степени. До сих пор мы рассматривали степени только с натуральным показателем; но действия со степенями и корнями могут приводить также к отрицательным, нулевым и дробным показателям. Все эти показатели степеней требуют дополнительного определения.
Степень с отрицательным показателем. Степень некоторого числа с отрицательным (целым) показателем определяется как единица, делённаяна степень того же числа с показателем, равным абсолютной велечине отрицательного показателя:

Теперь формула a m : a n = a m - n может быть использована не только при m , большем, чем n , но и при m , меньшем, чем n .
П р и м е р . a4 : a7 = a 4 - 7 = a -3 .
Если мы хотим, чтобы формула a m : a n = a m - n была справедлива при m = n , нам необходимо определение нулевой степени.
Степень с нулевым показателем. Степень любого ненулевого числа с нулевым показателем равна 1.
П р и м е р ы . 2 0 = 1, ( – 5 ) 0 = 1, ( – 3 / 5 ) 0 = 1.
Степень с дробным показателем. Для того, чтобы возвести действительное число а в степень m / n , нужно извлечь корень n–ой степени изm-ой степени этого числа а :

О выражениях, не имеющих смысла. Есть несколько таких выражений.
Случай 1.
 где a ≠ 0 , не существует.
где a ≠ 0 , не существует.
В самом деле, если предположить, что x – некоторое число, то в соответствии с определением операции деления имеем: a = 0· x, т.e. a = 0, что противоречит условию: a ≠ 0
Случай 2.
 - любое число.
- любое число.
В самом деле, если предположить, что это выражение равно некоторому числу x, то согласно определению операции деления имеем: 0 = 0 · x . Но это равенство имеет место при любом числе x, что и требовалось доказать.
Случай 3.
Если считать, что правила действий со степенями распространяются и на степени с нулевым основанием, то
0 0 - любое число.
Действительно,

Р е ш е н и е . Рассмотрим три основных случая:
1) x = 0 – это значение не удовлетворяет данному уравнению
( Почему? ).
2) при x > 0 получаем: x / x = 1, т.e. 1 = 1, откуда следует,
что x – любое число; но принимая во внимание, что в
нашем случае x > 0 , ответом является x > 0 ;
3) при x < 0 получаем: – x / x = 1, т.e. –1 = 1, следовательно,
в этом случае нет решения.
Таким образом, x > 0.
uclg.ru