
Понятие длины отрезка и ее измерения были уже использованы неоднократно, в частности, когда рассматривали натуральное число как меру величины. В этом пункте мы только обобщим представления о длине отрезка как геометрической величине.
В геометрии длина - это величина, характеризующая протяженность отрезка, а также других линий (ломаной, кривой). В нашем курсе будет рассмотрено только понятие длины отрезка. При его определении будем использовать введенное в теме 18 понятие «отрезок состоит из отрезков».
Определение. Длиной отрезка называется положительная величина, обладающая следующими свойствами: 1) равные отрезки имеют равные длины; 2) если отрезок состоит из двух отрезков, то его длина равна сумме длин его частей.
Эти свойства длины отрезка используются при ее измерении. Чтобы измерить длину отрезка, нужно иметь единицу длины. В геометрии такой единицей является длина произвольного отрезка.
Как показано в теме 18, результатом измерения длины отрезка является положительное действительное число - его называют численным значением длины отрезка при выбранной единице длины или мерой длины данного отрезка. Если обозначить длину отрезка буквой X, единицу длины - Е, а получаемое при измерении действительное число - буквой а, то можно записать: а=mЕ (Х) или Х = а∙Е.
Получаемое при измерении длины отрезка положительное действительное число должно удовлетворять ряду требований:
1. Если два отрезка равны, то численные значения их длин тоже равны.
2. Если отрезок х состоит из отрезков х1 и х2, то численное значение его длины равно сумме численных значений длин отрезков х1 и х2.
3. При замене единицы длины численное значение длины данного отрезка увеличивается (уменьшается) во столько раз, во сколько новая единица меньше (больше) старой.
4. Численное значение длины единичного отрезка равно единице.
Доказано, что положительное действительное число, являющееся мерой длины заданного отрезка, всегда существует и единственно. Доказано также, что для каждого положительного действительного числа существует отрезок, длина которого выражается этим числом.
Заметим, что часто, ради краткости речи, численное значение длины отрезка называют просто длиной. Например, в задании «Найдите длину данного отрезка» под словом «длина» подразумевается численное значение длины отрезка. Не менее часто допускают и другую вольность - говорят: «Измерь отрезок» вместо «Измерь длину отрезка».
Задача. Построить отрезок, длина которого 3,2Е. Каким будет численное значение длины этого отрезка, если единицу длины Е увеличить в 3 раза ?
Решение. Построим произвольный отрезок и будем считать его единичным. Затем построим прямую, отметим на ней точку А и отложим от нее 3 отрезка, длины которых равны Е. Получим отрезок АВ, длина которого 3Е (рис. 1).

Чтобы получить отрезок длиной 3,2Е, надо ввести новую единицу длины. Для этого единичный отрезок надо разбить либо на 10 равных частей, либо на 5, поскольку 0,2 =  . Если от точки В отложить отрезок, равный
. Если от точки В отложить отрезок, равный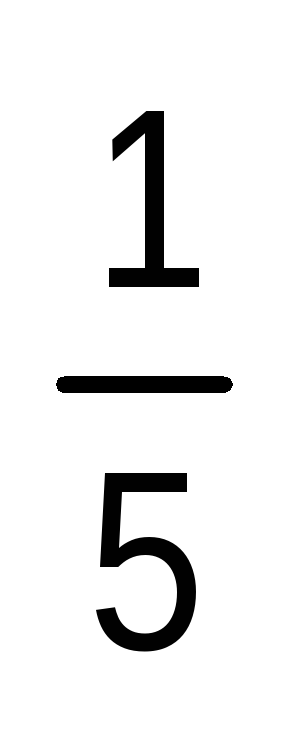 единичного, то длина отрезка АС будет равна 3,2Е.
единичного, то длина отрезка АС будет равна 3,2Е.
Чтобы выполнить второе требование задачи, воспользуемся свойством 3, согласно которому при увеличении единицы длины в 3 раза численное значение длины данного отрезка уменьшается в 3 раза. Разделим 3,2 на 3, получим:
3,2 : 3 == 3 : 3 =
: 3 =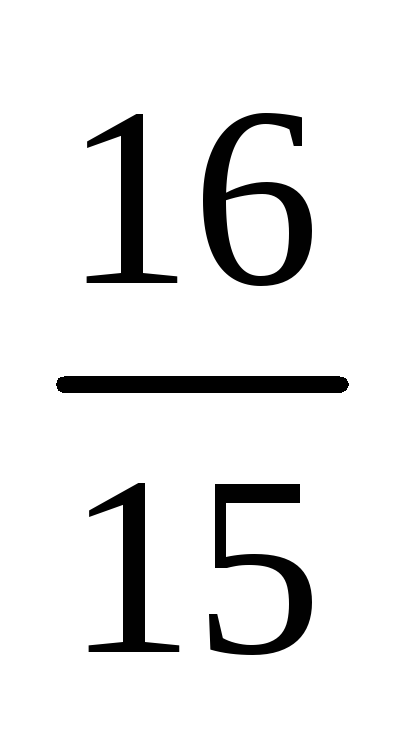 = 1
= 1 . Таким образом, при единице длины 3Е численное значение длины построенного отрезка АС будет равно 1
. Таким образом, при единице длины 3Е численное значение длины построенного отрезка АС будет равно 1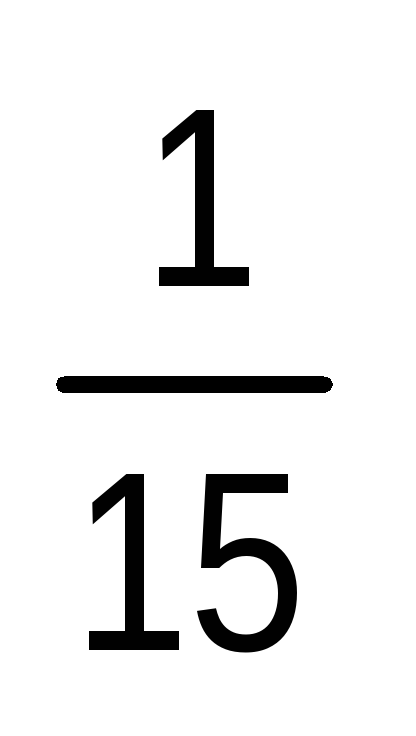 .
.
studfiles.net
Понятие длины отрезка и ее измерения были уже использованы неоднократно, в частности, когда рассматривали натуральное число как меру величины. В этом пункте мы только обобщим представления о длине отрезка как геометрической величине.
В геометрии длина - это величина, характеризующая протяженность отрезка, а также других линий (ломаной, кривой). В нашем курсе будет рассмотрено только понятие длины отрезка. При его определении будем использовать введенное в теме 18 понятие «отрезок состоит из отрезков».
Определение.Длиной отрезка называется положительная величина, обладающая следующими свойствами: 1) равные отрезки имеют равные длины; 2) если отрезок состоит из двух отрезков, то его длина равна сумме длин его частей.
Эти свойства длины отрезка используются при ее измерении. Чтобы измерить длину отрезка, нужно иметь единицу длины. В геометрии такой единицей является длина произвольного отрезка.
Как показано в теме 18, результатом измерения длины отрезка является положительное действительное число - его называют численным значением длины отрезка при выбранной единице длины или мерой длины данного отрезка. Если обозначить длину отрезка буквой X, единицу длины - Е, а получаемое при измерении действительное число - буквой а, то можно записать: а=mЕ (Х) или Х = а∙Е.
Получаемое при измерении длины отрезка положительное действительное число должно удовлетворять ряду требований:
1. Если два отрезка равны, то численные значения их длин тоже равны.
2. Если отрезок х состоит из отрезков х1 и х2, то численное значение его длины равно сумме численных значений длин отрезков х1 и х2.
3. При замене единицы длины численное значение длины данного отрезка увеличивается (уменьшается) во столько раз, во сколько новая единица меньше (больше) старой.
4. Численное значение длины единичного отрезка равно единице.
Доказано, что положительное действительное число, являющееся мерой длины заданного отрезка, всегда существует и единственно. Доказано также, что для каждого положительного действительного числа существует отрезок, длина которого выражается этим числом.
Заметим, что часто, ради краткости речи, численное значение длины отрезка называют просто длиной. Например, в задании «Найдите длину данного отрезка» под словом «длина» подразумевается численное значение длины отрезка. Не менее часто допускают и другую вольность - говорят: «Измерь отрезок» вместо «Измерь длину отрезка».
Задача. Построить отрезок, длина которого 3,2Е. Каким будет численное значение длины этого отрезка, если единицу длины Е увеличить в 3 раза ?
Решение. Построим произвольный отрезок и будем считать его единичным. Затем построим прямую, отметим на ней точку А и отложим от нее 3 отрезка, длины которых равны Е. Получим отрезок АВ, длина которого 3Е (рис. 1).
Чтобы получить отрезок длиной 3,2Е, надо ввести новую единицу длины. Для этого единичный отрезок надо разбить либо на 10 равных частей, либо на 5, поскольку 0,2 = 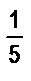 . Если от точки В отложить отрезок, равный
. Если от точки В отложить отрезок, равный 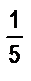 единичного, то длина отрезка АС будет равна 3,2Е.
единичного, то длина отрезка АС будет равна 3,2Е.
Чтобы выполнить второе требование задачи, воспользуемся свойством 3, согласно которому при увеличении единицы длины в 3 раза численное значение длины данного отрезка уменьшается в 3 раза. Разделим 3,2 на 3, получим:
3,2 : 3 == 3 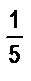 : 3 =
: 3 = 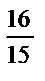 = 1
= 1 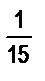 . Таким образом, при единице длины 3Е численное значение длины построенного отрезка АС будет равно 1
. Таким образом, при единице длины 3Е численное значение длины построенного отрезка АС будет равно 1 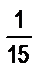 .
.
infopedia.su
 скачать работу скачать работу |
referat.resurs.kz
Длина отрезка и ее измерение.
Измерить отрезок – значит найти его длину. Длина отрезка – это расстояние между его концами.
Измерение отрезков производится путём сравнения данного отрезка с другим отрезком, принятым за единицу измерения. Отрезок, принятый за единицу измерения, называется единичным отрезком.
Если за единичный отрезок принят сантиметр, то для определения длины данного отрезка надо узнать, сколько раз в данном отрезке помещается сантиметр. В этом случае измерение удобно производить с помощью сантиметровой линейки.
Начертим отрезок AB и измерим его длину. Приложим шкалу сантиметровой линейки к отрезку AB так, чтобы её нулевая точка (0) совпала с точкой A:
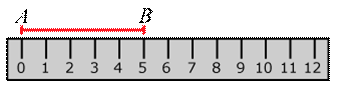
Если при этом окажется, что точка B совпадает с некоторым делением шкалы – например, 5, то говорят: длина отрезка AB равна 5 см, и пишут: AB = 5 см.
Свойства измерения отрезков
Когда точка делит отрезок на две части (на два отрезка), длина всего отрезка равна сумме длин этих двух отрезков.
Рассмотрим отрезок AB:
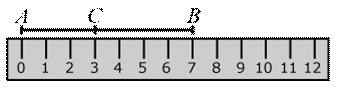
Точка C делит его на два отрезка: AC и CB. Мы видим, что AC = 3 см, CB = 4 см и AB = 7 см. Таким образом, AC + CB = AB.
Любой отрезок имеет определённую длину, большую нуля.

Величина угла и её измерение
Величиной угла называется положительная величина, определенная для каждого угла так, что: 1) равные углы имеют равные величины; 2) если угол состоит из двух углов, то его величина равна сумме величин его частей.
Эти свойства лежат в основе измерения величины угла. Оно аналогично измерению длины отрезка и состоит в сравнении измеряемой величины угла с величиной угла, принятой за единицу. Единичный угол, а если нужно и его доли, откладываются на угле, величина которого измеряется. В результате получается численное значение величины угла или мера величины угла при данной единице измерения.
Число, которое получается в результате измерения величины угла, должно удовлетворять ряду требований - они аналогичны требованиям, предъявляемым к числовому значению длины отрезка.
На практике за единицу величины угла принимают градус - 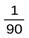 часть прямого угла. Один градус записывают так: 1°. Величина прямого угла равна 90°, величина развернутого - 180°.
часть прямого угла. Один градус записывают так: 1°. Величина прямого угла равна 90°, величина развернутого - 180°.
Градус делится на 60 минут, а минута на 60 секунд. Одну минуту обозначают 1', одну секунду – 1''. Так, если мера величины угла равна 5 градусам 3 минутам и 12 секундам, то пишут 5°3'12". Если нужна большая точность в измерении величин углов, используют и доли секунды. Заметим, что часто вместо «величина угла» говорят «угол». Например, вместо «величина угла равна 45 градусам» говорят, что «угол равен 45 градусам».
На практике величины углов измеряют с помощью транспортира. Для более точных измерений пользуются и другими приборами.
Площадь многоугольника.
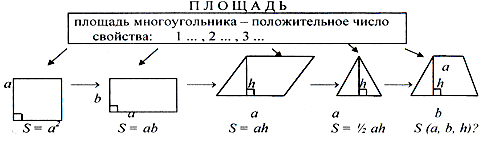
Площадь произвольной плоской фигуры и её измерение.
Формула Герона
S = √p(p - a)(p - b)(p - c)
3. Формула площади треугольника по двум сторонам и углу между ними Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.
4. Формула площади треугольника по трем сторонам и радиусу описанной окружности
5. Формула площади треугольника по трем сторонам и радиусу вписанной окружностиПлощадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.
Формулы площади квадрата
1. Формула площади квадрата по длине стороныПлощадь квадрата равна квадрату длины его стороны.
S = a2
2. Формула площади квадрата по длине диагоналиПлощадь квадрата равна половине квадрата длины его диагонали.
Формулы площади ромба
1. Формула площади ромба по длине стороны и высотеS = a · h
2. Формула площади ромба по длине стороны и углуS = a2 · sin α
3. Формула площади ромба по длинам его диагоналей
1. Формула Герона для трапеции
| S = | a + b | √(p - a)(p - b)(p - a - c)(p - a - d) |
| |a - b| |
2. Формула площади трапеции по длине основ и высоте Площадь трапеции равна произведению полусуммы ее оснований на высоту
| S = | (a + b) · h | ||||
Формулы площади круга
Формула площади круга через радиусS = π r2
Площадь круга
Длина отрезка и ее измерение.
Измерить отрезок – значит найти его длину. Длина отрезка – это расстояние между его концами.
Измерение отрезков производится путём сравнения данного отрезка с другим отрезком, принятым за единицу измерения. Отрезок, принятый за единицу измерения, называется единичным отрезком.
Если за единичный отрезок принят сантиметр, то для определения длины данного отрезка надо узнать, сколько раз в данном отрезке помещается сантиметр. В этом случае измерение удобно производить с помощью сантиметровой линейки.
Начертим отрезок AB и измерим его длину. Приложим шкалу сантиметровой линейки к отрезку AB так, чтобы её нулевая точка (0) совпала с точкой A:

Если при этом окажется, что точка B совпадает с некоторым делением шкалы – например, 5, то говорят: длина отрезка AB равна 5 см, и пишут: AB = 5 см.
Свойства измерения отрезков
Когда точка делит отрезок на две части (на два отрезка), длина всего отрезка равна сумме длин этих двух отрезков.
Рассмотрим отрезок AB:

Точка C делит его на два отрезка: AC и CB. Мы видим, что AC = 3 см, CB = 4 см и AB = 7 см. Таким образом, AC + CB = AB.
cyberpedia.su
Реферат на тему:
Отрезком может называться одно из двух близких понятий в геометрии и математическом анализе.
Отрезок прямой — это множество (часть прямой), состоящее из двух различных точек и всех точек, лежащих между ними. Отрезок прямой, соединяющий две точки и
(которые называются концами отрезка), обозначается следующим образом —
. Если в обозначении отрезка опускаются квадратные скобки, то пишут «отрезок
». Любая точка, лежащая между концами отрезка, называется его внутренней точкой. Расстояние между концами отрезка называют его длиной и обозначают как
.
Отрезок числовой (координатной) прямой (числовой отрезок, сегмент) — множество вещественных чисел , удовлетворяющих неравенству
, где заранее заданные вещественные числа
и
называются концами (граничными точками) отрезка. В противоположность им, остальные числа
, удовлетворяющие неравенству
, называются внутренними точками отрезка.[1]
Отрезок обычно обозначается [a,b]:
Любой отрезок заведомо включён в множество вещественных чисел. Отрезок является замкнутым промежутком.
Число называется длиной числового отрезка [a,b].
Система сегментов — это бесконечная последовательность элементов множества отрезков на числовой прямой .
Система сегментов обозначается . Подразумевается, что каждому натуральному числу
поставлен в соответствие отрезок
.
Система сегментов называется стягивающейся, если[2]
У любой стягивающейся системы сегментов существует единственная точка, принадлежащая всем сегментам этой системы.
Этот факт следует из свойств монотонной последовательности.
Обычно у отрезка прямой неважно, в каком порядке рассматриваются его концы: то есть отрезки AB и BA представляют собой один и тот же отрезок. Если у отрезка определить направление, то есть порядок перечисления его концов, то такой отрезок называется направленным. Например, выше указанные направленные отрезки не совпадают. Особого обозначения у направленных отрезков нет — то, что у отрезка важно его направление обычно указывается особо.
Дальнейшее обобщение приводит к понятию вектора — класса всех равных по длине и сонаправленных направленных отрезков.
wreferat.baza-referat.ru
Понятие длины отрезка и ее измерения были уже использованы неоднократно, в частности, когда рассматривали натуральное число как меру величины. В этом пункте мы только обобщим представления о длине отрезка как геометрической величине.
В геометрии длина - это величина, характеризующая протяженность отрезка, а также других линий (ломаной, кривой). В нашем курсе будет рассмотрено только понятие длины отрезка. При его определении будем использовать введенное в теме 18 понятие «отрезок состоит из отрезков».
Определение.Длиной отрезка называется положительная величина, обладающая следующими свойствами: 1) равные отрезки имеют равные длины; 2) если отрезок состоит из двух отрезков, то его длина равна сумме длин его частей.
Эти свойства длины отрезка используются при ее измерении. Чтобы измерить длину отрезка, нужно иметь единицу длины. В геометрии такой единицей является длина произвольного отрезка.
Как показано в теме 18, результатом измерения длины отрезка является положительное действительное число - его называют численным значением длины отрезка при выбранной единице длины или мерой длины данного отрезка. Если обозначить длину отрезка буквой X, единицу длины - Е, а получаемое при измерении действительное число - буквой а, то можно записать: а=mЕ (Х) или Х = а∙Е.
Получаемое при измерении длины отрезка положительное действительное число должно удовлетворять ряду требований:
1. Если два отрезка равны, то численные значения их длин тоже равны.
2. Если отрезок х состоит из отрезков х1 и х2, то численное значение его длины равно сумме численных значений длин отрезков х1 и х2.
3. При замене единицы длины численное значение длины данного отрезка увеличивается (уменьшается) во столько раз, во сколько новая единица меньше (больше) старой.
4. Численное значение длины единичного отрезка равно единице.
Доказано, что положительное действительное число, являющееся мерой длины заданного отрезка, всегда существует и единственно. Доказано также, что для каждого положительного действительного числа существует отрезок, длина которого выражается этим числом.
Заметим, что часто, ради краткости речи, численное значение длины отрезка называют просто длиной. Например, в задании «Найдите длину данного отрезка» под словом «длина» подразумевается численное значение длины отрезка. Не менее часто допускают и другую вольность - говорят: «Измерь отрезок» вместо «Измерь длину отрезка».
Задача. Построить отрезок, длина которого 3,2Е. Каким будет численное значение длины этого отрезка, если единицу длины Е увеличить в 3 раза ?
Решение. Построим произвольный отрезок и будем считать его единичным. Затем построим прямую, отметим на ней точку А и отложим от нее 3 отрезка, длины которых равны Е. Получим отрезок АВ, длина которого 3Е (рис. 1).
 |
Чтобы получить отрезок длиной 3,2Е, надо ввести новую единицу длины. Для этого единичный отрезок надо разбить либо на 10 равных частей, либо на 5, поскольку 0,2 = 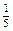 . Если от точки В отложить отрезок, равный
. Если от точки В отложить отрезок, равный 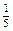 единичного, то длина отрезка АС будет равна 3,2Е.
единичного, то длина отрезка АС будет равна 3,2Е.
Чтобы выполнить второе требование задачи, воспользуемся свойством 3, согласно которому при увеличении единицы длины в 3 раза численное значение длины данного отрезка уменьшается в 3 раза. Разделим 3,2 на 3, получим:
3,2 : 3 == 3 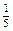 : 3 =
: 3 =  = 1
= 1 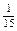 . Таким образом, при единице длины 3Е численное значение длины построенного отрезка АС будет равно 1
. Таким образом, при единице длины 3Е численное значение длины построенного отрезка АС будет равно 1 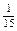 .
.
studopedya.ru