 .
.Лекция 10
Комплексные числа и действия над ними
Рассмотрим уравнение
 .
.
Среди действительных чисел решений данного уравнения нет. По этой причине, в частности, квадратные уравнения имеют решения только тогда, когда дискриминант такого уравнения неотрицателен. Расширим множество действительных чисел, формально добавив к ним число  (мнимую единицу), которая по определению удовлетворяет уравнению
(мнимую единицу), которая по определению удовлетворяет уравнению  . Поскольку мы желаем, чтобы элементы этого расширенного множества можно было бы умножать и складывать, то вместе с мнимой единицей мы автоматически присоединяем к вещественной прямой все возможные комбинации вида
. Поскольку мы желаем, чтобы элементы этого расширенного множества можно было бы умножать и складывать, то вместе с мнимой единицей мы автоматически присоединяем к вещественной прямой все возможные комбинации вида
 ,
,  ,
,  .
.
Совокупность всех чисел  называется множеством комплексных чисел. При этом число
называется множеством комплексных чисел. При этом число  называется вещественной частью комплексного числа
называется вещественной частью комплексного числа  и обозначается как
и обозначается как
 ,
,
а число  называется мнимой частью комплексного числа
называется мнимой частью комплексного числа  и обозначается как
и обозначается как
 .
.
Удобно изображать комплексные числа  в виде точек двумерной плоскости с декартовыми координатами
в виде точек двумерной плоскости с декартовыми координатами  . В этом случае соответствующая двумерная плоскость называется комплексной.
. В этом случае соответствующая двумерная плоскость называется комплексной.




Операции умножения и деления комплексных чисел.
При умножении комплексных чисел используется обычное соглашение о раскрытии скобок (дистрибутивность умножения):

Пример.
 .
.
При делении следует использовать операцию умножения на сопряженное выражение.
Пример.

Комплексному числу можно приписать понятие модуля и аргумента, используя полярные координаты на комплексной плоскости.
Модуль числа равен
равен  .
.
Аргументом числа  называется полярный угол
называется полярный угол  ,
,  (аргумент является многозначной функцией).
(аргумент является многозначной функцией).
Тригонометрическая форма записи комплексного числа:
 , где
, где  .
.
Теперь умножение комплексных чисел, записанных в тригонометрической форме, выполняется по формуле

(то есть при умножении комплексных чисел модули перемножаются, а аргументы складываются).
Следствием формулы умножения является следующая формула.
Формула возведения в степень (формула Муавра)
 .
.
Пример.
 ,
,  ,
,  ,
,

Формула извлечения корня  -й степени
-й степени
 ,
,  .
.
Пример. Вычислить  .
.
Запишем  в тригонометрической форме:
в тригонометрической форме:
 .
.
Тогда получаем
при 

при 

при 

Таким образом, всего имеется три комплексных кубических корня из числа  :
: ,
,  ,
,  .
.
Формула Эйлера
 .
.
Пример использования.
Вычислить  .
.
Воспользуемся формулой Эйлера для выражения функции  через показательную функцию. Имеем:
через показательную функцию. Имеем:

откуда
 Û
Û .
.
Следовательно,
 ,
,
откуда

 .
.
Первообразная является вещественной функцией, записанной в комплексной форме Чтобы получить вещественную запись этой функции, вновь воспользуемся формулой Эйлера.
 ,
,

Отсюда следует

Ответ:  .
.
Дифференциальные уравнения второго порядка с постоянными коэффициентами и специальной правой частью.
Рассмотрим уравнение

где  и
и  константы, а функция
константы, а функция  в правой части уравнения имеет один из следующих трех видов
в правой части уравнения имеет один из следующих трех видов
 ,
,  ,
,  ,
,
 - произвольный многочлен степени
- произвольный многочлен степени  . Решение такого уравнения может быть получено следующим образом. Квадратное уравнение
. Решение такого уравнения может быть получено следующим образом. Квадратное уравнение

назовем характеристическим уравнением для нашего уравнения. Пусть  ,
,  – корни этого квадратного уравнения. Общее решение однородного уравнения
– корни этого квадратного уравнения. Общее решение однородного уравнения

имеет вид
 ,
,
если  ,
,  - два различных вещественных числа; имеет вид
- два различных вещественных числа; имеет вид
 ,
,
если  и, наконец, решение имеет вид
и, наконец, решение имеет вид
 ,
,
если  ,
,  - комплексно-сопряженные корни характеристического уравнения.
- комплексно-сопряженные корни характеристического уравнения.
Общее решение неоднородного уравнения может быть получено как сумма общего решения однородного уравнения  и произвольного частного решения неоднородного уравнения
и произвольного частного решения неоднородного уравнения  . Это частное решение можно найти методом неопределенных коэффициентов по следующему правилу.
. Это частное решение можно найти методом неопределенных коэффициентов по следующему правилу.
Сопоставим функции  в правой части исходного уравнения число
в правой части исходного уравнения число  . Если
. Если  не является корнем характеристического уравнения, то частное решение
не является корнем характеристического уравнения, то частное решение  ищем в том же виде, в каком записана правая часть, то есть
ищем в том же виде, в каком записана правая часть, то есть

если  , и в виде
, и в виде

если  или
или  . Здесь
. Здесь  ,
,  многочлены степени
многочлены степени  , коэффициенты которых можно определить, подставив
, коэффициенты которых можно определить, подставив  в исходное уравнение и приравняв коэффициенты при одинаковых функциях. Если
в исходное уравнение и приравняв коэффициенты при одинаковых функциях. Если  является корнем характеристического уравнения (эта ситуация называется резонансом), то степень многочленов
является корнем характеристического уравнения (эта ситуация называется резонансом), то степень многочленов  ,
,  увеличивается на 1.
увеличивается на 1.
Пример. Найти решение задачи Коши для дифференциального уравнения.

Решение. Сначала найдем общее решение однородного уравнения. Выпишем характеристическое уравнение
 Û
Û
Следовательно, общее решение линейного однородного уравнения имеет вид
 .
.
Поскольку корни характеристического уравнения не совпадают с соответствующим показателем правой части  , частное решение неоднородного уравнения будем искать в виде
, частное решение неоднородного уравнения будем искать в виде
 .
.
Получаем:
 ,
,
 Подставляя
Подставляя  ,
,  ,
,  в исходное уравнение, получаем:
в исходное уравнение, получаем:

Сокращая на  и приводя подобные, получим
и приводя подобные, получим
 ,
,
 ,
,
откуда
 Û
Û
Общее решение неоднородного уравнения имеет, следовательно, вид
 .
.
Теперь найдем решение задачи Коши. Имеем:
 ,
,

Поскольку  , второе уравнение имеет вид
, второе уравнение имеет вид  . Решаем систему линейных уравнений на неизвестные
. Решаем систему линейных уравнений на неизвестные  и
и  :
:

Умножая первое уравнение системы на 2 и вычитая из него второе уравнение, получим:
 Û
Û .
.
Далее,
 .
.
Ответ:  .
.
Пример . Найти решение задачи Коши для дифференциального уравнения.

Решение. Характеристическое уравнение имеет вид:
 ,
,
откуда
 ,
,
где  - мнимая единица. Следовательно,
- мнимая единица. Следовательно,  ,
,  , и общее решение однородного уравнения есть
, и общее решение однородного уравнения есть
 .
.
Правая часть исходного неоднородного уравнения имеет то же собственное число, что и характеристическое уравнение, следовательно, мы имеем дело с резонансом. Поэтому частное решение неоднородного уравнения следует искать в виде
 .
.
Подставляя  в исходное уравнение, с учетом того, что
в исходное уравнение, с учетом того, что
 ,
,

получим:

откуда

и, следовательно,
 ,
,  .
.
Таким образом, частным решением неоднородного уравнения является функция
 .
.
Общее решение неоднородного уравнения может быть записано в виде
 .
.
Найдем константы  и
и  , при которых выполнены краевые условия
, при которых выполнены краевые условия
 ,
,  .
.
Так как
 ,
,
получаем систему линейных уравнений на  и
и  :
:

откуда  .
.
www.yurii.ru
Лекция 10
Комплексные числа и действия над ними
Рассмотрим уравнение
 .
.
Среди действительных чисел решений данного уравнения нет. По этой причине, в частности, квадратные уравнения имеют решения только тогда, когда дискриминант такого уравнения неотрицателен. Расширим множество действительных чисел, формально добавив к ним число (мнимую единицу), которая по определению удовлетворяет уравнению
(мнимую единицу), которая по определению удовлетворяет уравнению . Поскольку мы желаем, чтобы элементы этого расширенного множества можно было бы умножать и складывать, то вместе с мнимой единицей мы автоматически присоединяем к вещественной прямой все возможные комбинации вида
. Поскольку мы желаем, чтобы элементы этого расширенного множества можно было бы умножать и складывать, то вместе с мнимой единицей мы автоматически присоединяем к вещественной прямой все возможные комбинации вида
 ,
, ,
, .
.
Совокупность всех чисел называется множеством комплексных чисел. При этом число
называется множеством комплексных чисел. При этом число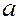 называется вещественной частью комплексного числа
называется вещественной частью комплексного числа и обозначается как
и обозначается как
 ,
,
а число называется мнимой частью комплексного числа
называется мнимой частью комплексного числа и обозначается как
и обозначается как
 .
.
Удобно изображать комплексные числа в виде точек двумерной плоскости с декартовыми координатами
в виде точек двумерной плоскости с декартовыми координатами . В этом случае соответствующая двумерная плоскость называется комплексной.
. В этом случае соответствующая двумерная плоскость называется комплексной.




Операции умножения и деления комплексных чисел.
При умножении комплексных чисел используется обычное соглашение о раскрытии скобок (дистрибутивность умножения):

Пример.
 .
.
При делении следует использовать операцию умножения на сопряженное выражение.
Пример.

Комплексному числу можно приписать понятиемодуляи аргумента, используя полярные координаты на комплексной плоскости.
Модуль числа равен
равен .
.
Аргументом числа называется полярный угол
называется полярный угол ,
, (аргумент является многозначной функцией).
(аргумент является многозначной функцией).
Тригонометрическая форма записи комплексного числа:
 , где
, где .
.
Теперь умножение комплексных чисел, записанных в тригонометрической форме, выполняется по формуле
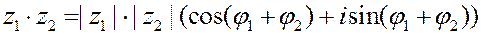
(то есть при умножении комплексных чисел модули перемножаются, а аргументы складываются).
Следствием формулы умножения является следующая формула.
Формула возведения в степень (формула Муавра)
 .
.
Пример.
 ,
, ,
, ,
,

Формула извлечения корня -й степени
-й степени
 ,
, .
.
Пример. Вычислить .
.
Запишем в тригонометрической форме:
в тригонометрической форме:
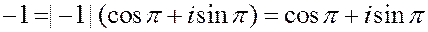 .
.
Тогда получаем
при

при

при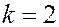

Таким образом, всего имеется три комплексных кубических корня из числа :
: ,
, ,
, .
.
Формула Эйлера
 .
.
Пример использования.
Вычислить .
.
Воспользуемся формулой Эйлера для выражения функции через показательную функцию. Имеем:
через показательную функцию. Имеем:

откуда
 Û
Û .
.
Следовательно,
 ,
,
откуда

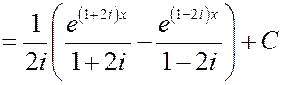 .
.
Первообразная является вещественной функцией, записанной в комплексной форме Чтобы получить вещественную запись этой функции, вновь воспользуемся формулой Эйлера.
 ,
,

Отсюда следует
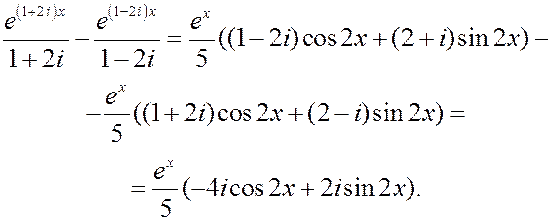
Ответ: .
.
Дифференциальные уравнения второго порядка с постоянными коэффициентами и специальной правой частью.
Рассмотрим уравнение

где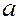 и
и константы, а функция
константы, а функция в правой части уравнения имеет один из следующих трех видов
в правой части уравнения имеет один из следующих трех видов
 ,
, ,
, ,
,
 - произвольный многочлен степени
- произвольный многочлен степени . Решение такого уравнения может быть получено следующим образом. Квадратное уравнение
. Решение такого уравнения может быть получено следующим образом. Квадратное уравнение

назовемхарактеристическим уравнениемдля нашего уравнения. Пусть ,
, – корни этого квадратного уравнения. Общее решение однородного уравнения
– корни этого квадратного уравнения. Общее решение однородного уравнения

имеет вид
 ,
,
если ,
, - два различных вещественных числа; имеет вид
- два различных вещественных числа; имеет вид
 ,
,
если и, наконец, решение имеет вид
и, наконец, решение имеет вид
 ,
,
если ,
, - комплексно-сопряженные корни характеристического уравнения.
- комплексно-сопряженные корни характеристического уравнения.
Общее решение неоднородного уравнения может быть получено как сумма общего решения однородного уравнения и произвольного частного решения неоднородного уравнения
и произвольного частного решения неоднородного уравнения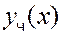 . Это частное решение можно найти методом неопределенных коэффициентов по следующему правилу.
. Это частное решение можно найти методом неопределенных коэффициентов по следующему правилу.
Сопоставим функции в правой части исходного уравнения число
в правой части исходного уравнения число . Если
. Если не является корнем характеристического уравнения, то частное решение
не является корнем характеристического уравнения, то частное решение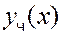 ищем в том же виде, в каком записана правая часть, то есть
ищем в том же виде, в каком записана правая часть, то есть

если , и в виде
, и в виде

если или
или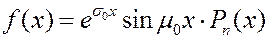 . Здесь
. Здесь ,
, многочлены степени
многочлены степени , коэффициенты которых можно определить, подставив
, коэффициенты которых можно определить, подставив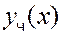 в исходное уравнение и приравняв коэффициенты при одинаковых функциях. Если
в исходное уравнение и приравняв коэффициенты при одинаковых функциях. Если является корнем характеристического уравнения (эта ситуация называется резонансом), то степень многочленов
является корнем характеристического уравнения (эта ситуация называется резонансом), то степень многочленов ,
, увеличивается на 1.
увеличивается на 1.
Пример.Найти решение задачи Коши для дифференциального уравнения.

Решение.Сначала найдем общее решение однородного уравнения. Выпишем характеристическое уравнение
 Û
Û
Следовательно, общее решение линейного однородного уравнения имеет вид
 .
.
Поскольку корни характеристического уравнения не совпадают с соответствующим показателем правой части , частное решение неоднородного уравнения будем искать в виде
, частное решение неоднородного уравнения будем искать в виде
 .
.
Получаем:
 ,
,
 Подставляя
Подставляя ,
, ,
, в исходное уравнение, получаем:
в исходное уравнение, получаем:

Сокращая на и приводя подобные, получим
и приводя подобные, получим
 ,
,
 ,
,
откуда
 Û
Û
Общее решение неоднородного уравнения имеет, следовательно, вид
 .
.
Теперь найдем решение задачи Коши. Имеем:
 ,
,

Поскольку , второе уравнение имеет вид
, второе уравнение имеет вид . Решаем систему линейных уравнений на неизвестные
. Решаем систему линейных уравнений на неизвестные и
и :
:

Умножая первое уравнение системы на 2 и вычитая из него второе уравнение, получим:
 Û
Û .
.
Далее,
 .
.
Ответ: .
.
Пример.Найти решение задачи Коши для дифференциального уравнения.

Решение.Характеристическое уравнение имеет вид:
 ,
,
откуда
 ,
,
где - мнимая единица. Следовательно,
- мнимая единица. Следовательно, ,
, , и общее решение однородного уравнения есть
, и общее решение однородного уравнения есть
 .
.
Правая часть исходного неоднородного уравнения имеет то же собственное число, что и характеристическое уравнение, следовательно, мы имеем дело с резонансом. Поэтому частное решение неоднородного уравнения следует искать в виде
 .
.
Подставляя в исходное уравнение, с учетом того, что
в исходное уравнение, с учетом того, что
 ,
,

получим:

откуда

и, следовательно,
 ,
, .
.
Таким образом, частным решением неоднородного уравнения является функция
 .
.
Общее решение неоднородного уравнения может быть записано в виде
 .
.
Найдем константы и
и , при которых выполнены краевые условия
, при которых выполнены краевые условия
 ,
, .
.
Так как
 ,
,
получаем систему линейных уравнений на и
и :
:

откуда .
.
superbotanik.net
Лекция 10
Комплексные числа и действия над ними
Рассмотрим уравнение
.
Среди действительных чисел решений данного уравнения нет. По этой причине, в частности, квадратные уравнения имеют решения только тогда, когда дискриминант такого уравнения неотрицателен. Расширим множество действительных чисел, формально добавив к ним число (мнимую единицу), которая по определению удовлетворяет уравнению
. Поскольку мы желаем, чтобы элементы этого расширенного множества можно было бы умножать и складывать, то вместе с мнимой единицей мы автоматически присоединяем к вещественной прямой все возможные комбинации вида
,
,
.
Совокупность всех чисел называется множеством комплексных чисел. При этом число
называется вещественной частью комплексного числа
и обозначается как
,
а число называется мнимой частью комплексного числа
и обозначается как
.Удобно изображать комплексные числа
в виде точек двумерной плоскости с декартовыми координатами
. В этом случае соответствующая двумерная плоскость называется комплексной.
Операции умножения и деления комплексных чисел.
При умножении комплексных чисел используется обычное соглашение о раскрытии скобок (дистрибутивность умножения):
Пример.
.При делении следует использовать операцию умножения на сопряженное выражение.
Пример.
Комплексному числу можно приписать понятие модуля и аргумента, используя полярные координаты на комплексной плоскости.
Модуль числа равен
.
Аргументом числа называется полярный угол
,
(аргумент является многозначной функцией). Тригонометрическая форма записи комплексного числа:
, где
.Теперь умножение комплексных чисел, записанных в тригонометрической форме, выполняется по формуле
(то есть при умножении комплексных чисел модули перемножаются, а аргументы складываются).
Следствием формулы умножения является следующая формула.
Формула возведения в степень (формула Муавра)
.
Пример.
,
,
,
Формула извлечения корня -й степени
,
.
Пример. Вычислить .
Запишем в тригонометрической форме:
.
Тогда получаем
при
при
при
Таким образом, всего имеется три комплексных кубических корня из числа :
,
,
.Формула Эйлера
.
Пример использования.
Вычислить .
Воспользуемся формулой Эйлера для выражения функции через показательную функцию. Имеем:
откуда
Û
.
Следовательно,
,
откуда
.
Первообразная является вещественной функцией, записанной в комплексной форме Чтобы получить вещественную запись этой функции, вновь воспользуемся формулой Эйлера.
,
Отсюда следует
Ответ: .Дифференциальные уравнения второго порядка с постоянными коэффициентами и специальной правой частью.Рассмотрим уравнение
где и
константы, а функция
в правой части уравнения имеет один из следующих трех видов
,
,
,
- произвольный многочлен степени
. Решение такого уравнения может быть получено следующим образом. Квадратное уравнение
назовем характеристическим уравнением для нашего уравнения. Пусть ,
– корни этого квадратного уравнения. Общее решение однородного уравнения
имеет вид
,
если ,
- два различных вещественных числа; имеет вид
,
если и, наконец, решение имеет вид
,
если ,
- комплексно-сопряженные корни характеристического уравнения.
Общее решение неоднородного уравнения может быть получено как сумма общего решения однородного уравнения и произвольного частного решения неоднородного уравнения
. Это частное решение можно найти методом неопределенных коэффициентов по следующему правилу.
Сопоставим функции в правой части исходного уравнения число
. Если
не является корнем характеристического уравнения, то частное решение
ищем в том же виде, в каком записана правая часть, то есть
если , и в виде
если или
. Здесь
,
многочлены степени
, коэффициенты которых можно определить, подставив
в исходное уравнение и приравняв коэффициенты при одинаковых функциях. Если
является корнем характеристического уравнения (эта ситуация называется резонансом), то степень многочленов
,
увеличивается на 1.Пример. Найти решение задачи Коши для дифференциального уравнения.
Решение. Сначала найдем общее решение однородного уравнения. Выпишем характеристическое уравнение
Û
Следовательно, общее решение линейного однородного уравнения имеет вид
.
Поскольку корни характеристического уравнения не совпадают с соответствующим показателем правой части , частное решение неоднородного уравнения будем искать в виде
.
Получаем:
,
Подставляя
,
,
в исходное уравнение, получаем:
Сокращая на и приводя подобные, получим
,
,
откуда
Û
Общее решение неоднородного уравнения имеет, следовательно, вид
.
Теперь найдем решение задачи Коши. Имеем:
,
Поскольку , второе уравнение имеет вид
. Решаем систему линейных уравнений на неизвестные
и
:
Умножая первое уравнение системы на 2 и вычитая из него второе уравнение, получим:
Û
.
Далее,
.
Ответ: .
Пример. Найти решение задачи Коши для дифференциального уравнения.
Решение. Характеристическое уравнение имеет вид:
,
откуда
,
где - мнимая единица. Следовательно,
,
, и общее решение однородного уравнения есть
.
Правая часть исходного неоднородного уравнения имеет то же собственное число, что и характеристическое уравнение, следовательно, мы имеем дело с резонансом. Поэтому частное решение неоднородного уравнения следует искать в виде
.
Подставляя в исходное уравнение, с учетом того, что
,
получим:
откуда
и, следовательно,
,
.
Таким образом, частным решением неоднородного уравнения является функция
.
Общее решение неоднородного уравнения может быть записано в виде
.
Найдем константы и
, при которых выполнены краевые условия
,
.
Так как
,
получаем систему линейных уравнений на и
:
откуда .
bukvasha.ru