Подготовил: Д.В. Объедков
преподаватель математики
«Рязанский технологический колледж»
г. Рязань 2016
Развернутый конспект открытого урока
Тема урока: «Тела вращения. Конус, цилиндр, шар и сфера».
Цели урока:
Обучающая: Изучение свойств геометрических тел в пространстве.
Развивающие: Развитие пространственных представлений учащихся, способов вычисления геометрических величин и дальнейшее развитие логического мышления.
Воспитательные: Воспитать сознательное отношение к учебе, усидчивость, аккуратность, эстетическое восприятие.
Студенты должны:
Знать:
основные понятия стереометрии и планиметрии;
взаимное расположение плоскостей;
признаки подобия фигур.
Уметь:
изображать пространственные геометрические тела, указанные в условиях задач и выделять известные тела на чертежах и моделях;
решать типичные задачи на вычисление и доказательство, опираясь на полученные теоретические сведения;
вычислять значения геометрических величин (длин, углов, площадей и объемов), применяя изученные в курсах планиметрии и стереометрии формулы и теоремы;
применять аппарат алгебры, начал анализа и тригонометрии в ходе решения геометрических задач.
Тип урока: комбинированный урок.
Оборудование:
учебник, конспект, пространственные фигуры, компьютер, мультимедийная доска, линейка, карандаш, резинка, циркуль.
Межпредметные связи: планиметрия, тригонометрия, программирование.
Ход урока
Откройте тетради и запишите тему сегодняшнего урока: «Тела вращения. Конус, цилиндр, шар и сфера».Целью нашего урока является изучение свойств пространственных фигур на примере конуса, цилиндра, шара и сферы.
Изучив тела вращения, вы сможете:
изображать те или иные геометрические тела;
строить сложные схемы, необходимые для оформления курсовой работы;
а также сможете нарисовать произвольный рисунок, с помощью которого оформите доклад или реферат.
Слушают, записывают.
II. Актуализация опорных знаний. (10 мин.)
Прежде чем мы перейдем к новой теме, давайте вспомним:
что такое параллельный перенос?
какие плоскости называются параллельными?
чем отличается круг от окружности?
по какой формуле вычисляется длина окружности, площадь круга?
какие формулы для вычисления площади треугольника вы знаете?
чему равен синус и косинус 30, 60, 90 градусов?
Отвечают на вопросы, делают записи в тетрадях.
III. Изучение нового материала (45 мин.)
Итак, класс был разбит на три группы, каждой из которой было поручено охарактеризовать одну из предложенных пространственных фигур: конус, цилиндр, шар и сферу и подготовить презентацию по данной фигуре.
Один студент из каждой группы дает краткую характеристику предложенной фигуры, второй студент из группы в это время показывает подготовленную группой презентацию (презентация2, презентация3, презентация4). Все остальные учащиеся внимательно слушают и конспектируют. После каждого выступления решают задачи.
IV. Закрепление нового материала (25 мин.)
1.Далее вам предлагается ответить на вопросы математического диктанта (презентация1).
Поменяйтесь тетрадями с соседом, проверьте правильность ответов друг друга, сравнив результаты с ответами на доске и выставьте друг другу отметки, опираясь на критерии оценок.
2.Заполните таблицу. Сравните свои ответы с ответами на доске.
3.Итак, обобщим материал сегодняшнего занятия, ответив устно на несколько вопросов Обобщающего опроса (презентация1).
1.Отвечают (письменно) на поставленные вопросы. Проводят взаимоконтроль, сверяя ответы соседа с ответами на доске. Выставляют друг другу отметки.
2.Заполняют таблицу. Проводят самоконтроль, сравнивая свои результаты с ответами на доске.
3. Закрепляют новый материал, отвечая (устно) на вопросы обобщающего опроса.
V. Итоги занятия (5 мин.)
Сейчас я объявлю оценки за работу на уроке…
Слушают, обсуждают, задают вопросы.
Спасибо за урок ребята!
Тела вращения— объёмные тела, возникающие при вращении замкнутой линии вокруг оси, лежащей в той же плоскости, что и вращающееся тело.
Шар — образован полукругом, вращающимся вокруг диаметра разреза.
Цилиндр — образован прямоугольником, вращающимся вокруг одной из сторон.
Конус — образован прямоугольным треугольником, вращающимся вокруг одного из катетов.
Тор — образован кругом, вращающимся вокруг прямой, не пересекающей его.
При вращении контуров фигур возникает поверхность вращения (например, сфера, образованная окружностью), в то время как при вращении заполненных контуров возникают тела (как шар, образованный кругом).
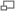
Правильный круглый цилиндр
Цили́ндр (греч. kýlindros, валик, каток) — геометрическое тело, которое состоит из двух кругов, не лежащих в одной плоскости и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов. Круги называются основаниями цилиндра, а отрезки, соединяющие соответствующие точки окружностей кругов, - образующими цилиндра.
Примеры тел, имеющих форму цилиндра:
Сквозное отверстие в стене, сделанное дрелью, является цилиндром: его основание – круг с диаметром, равным диаметру сверла, высота – толщина стены.
Ваши примеры:
Связанные определения.
Цилиндр называется прямым, если его образующие перпендикулярны плоскостям оснований.
Радиусом цилиндра называется радиус его основания.
Высотой цилиндра называется расстояние между его плоскостями.
Осью цилиндра называется прямая, проходящая через центр оснований. Она параллельна образующим.
Осевое сечение – сечение цилиндра плоскостью, проходящей через его ось.
Свойства
У цилиндра образующие параллельны и равны.
Поверхность цилиндра состоит из оснований и боковой поверхности. Боковая поверхность составлена из образующих.
Основные формулы
V = πr2h - объём прямого кругового цилиндра
S = 2πrh - Площадь боковой поверхности цилиндра
(где r — радиус основания, h — высота).
Площадь полной поверхности цилиндра складывается из площади боковой поверхности и площади оснований. Для прямого кругового цилиндра:
S = 2πrh + 2πr2.
Задачи по теме «Цилиндр»
1.Радиус основания цилиндра 2 см, высота 3 см. Найдите диагональ осевого сечения.
Дано: цилиндр,
r = 2 см,
h =3 см,
Найти: d – диагональ осевого сечения
Решение. Рассмотрим прямоугольный треугольник, катетами которого являются высота цилиндра и диаметр основания, а гипотенузой – диагональ осевого сечения. По теореме Пифагора получим:
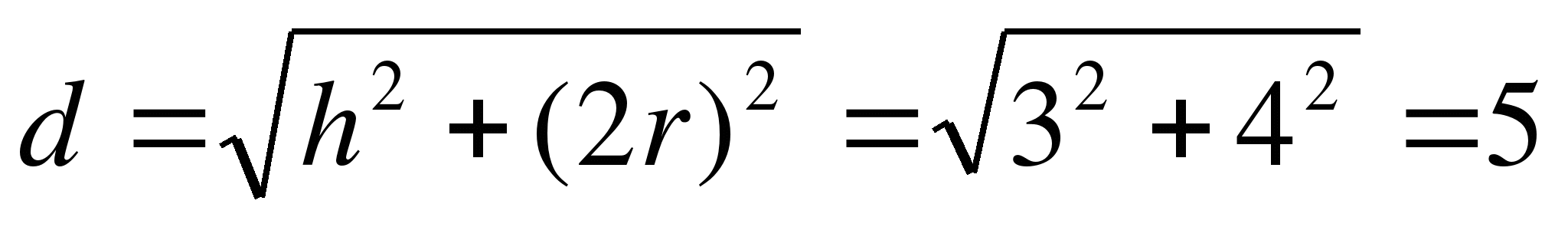см
Ответ: 5 см.
2 Радиус основания цилиндра равен 5 см, а его образующая – 9 см. Найдите площадь осевого сечения.
Дано: цилиндр,
ABCD – осевое сечение,
AO =5 см,
AB=9см.
Найти: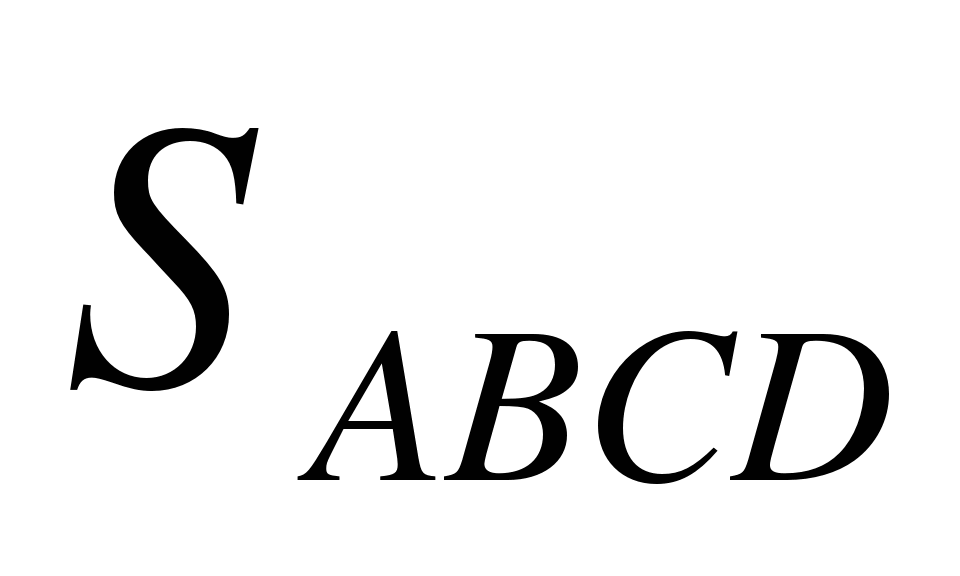 
Решение. Данное осевое сечение есть прямоугольник ABCD. Сторона прямоугольника AD=2*5 =10 (см). Поэтому площадь сечения
.
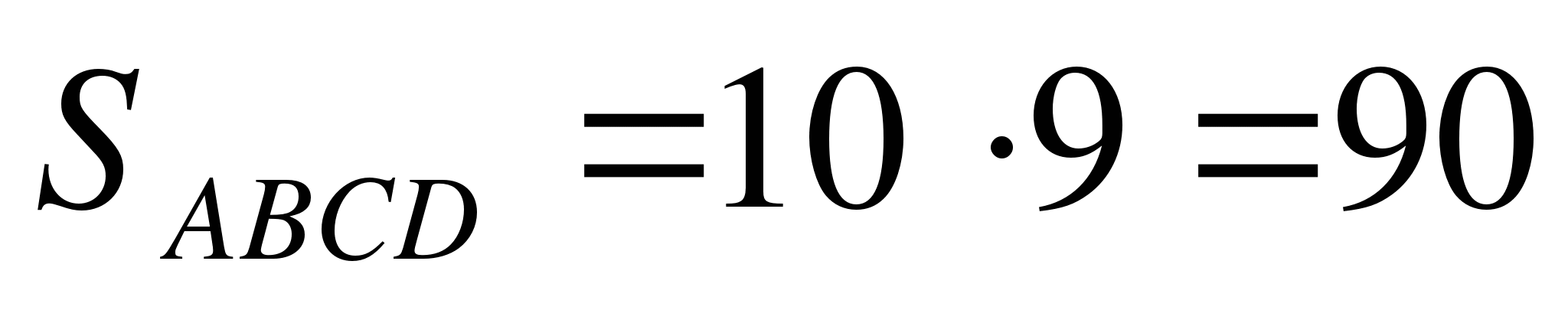
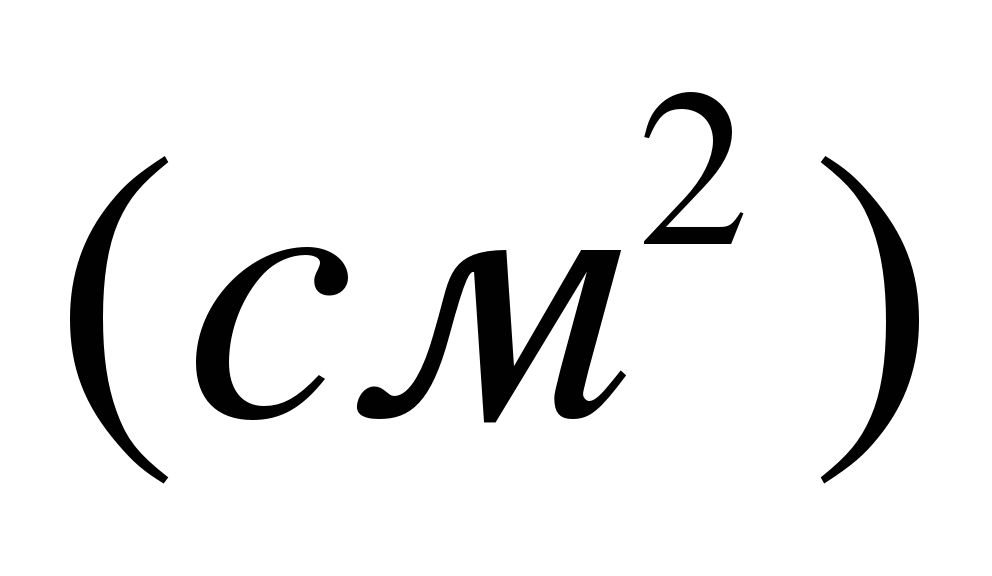Ответ: 90 .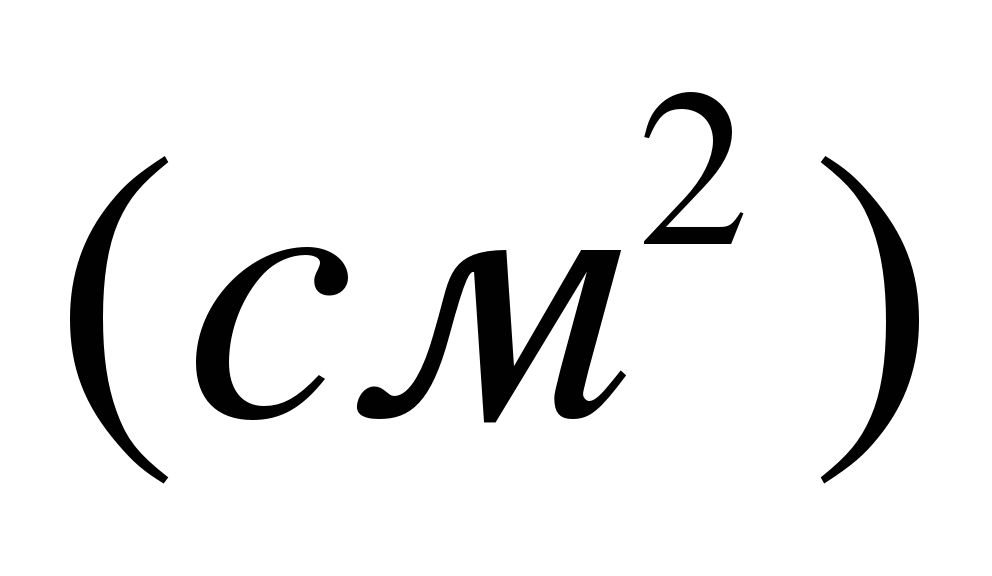
3.Прямоугольник, стороны которого равны 6 см и 4 см, вращается около меньшей стороны. Найдите площадь поверхности тела вращения.
Дано:
ABCD – прямоугольник,
AВ = 6 см,
BС = 4см,
ВC – ось вращения.
Найти: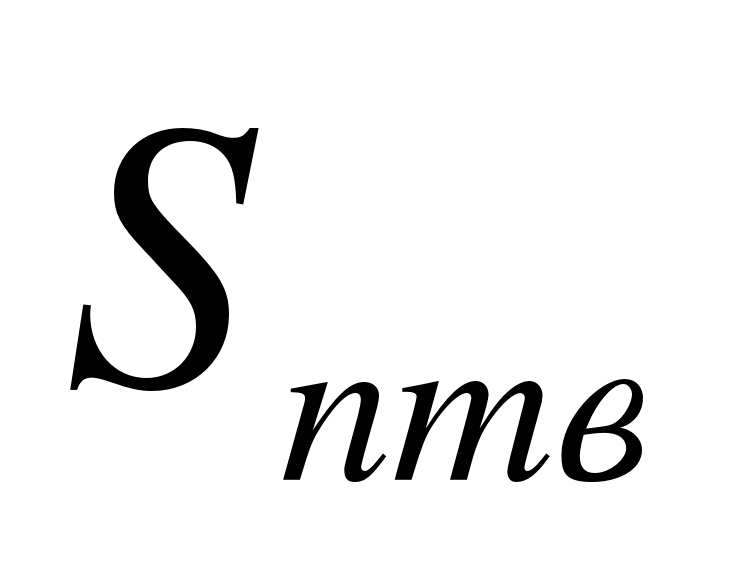 
Решение. Данное тело вращения – прямой круговой цилиндр с высотой BC = 4 см и радиусом основания АВ = 6 см.
Площадь боковой поверхности
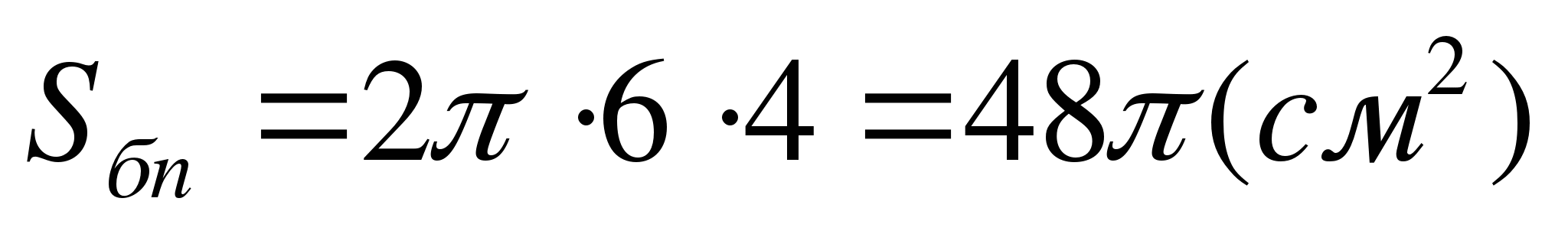
Площадь основания
Площадь полной поверхности
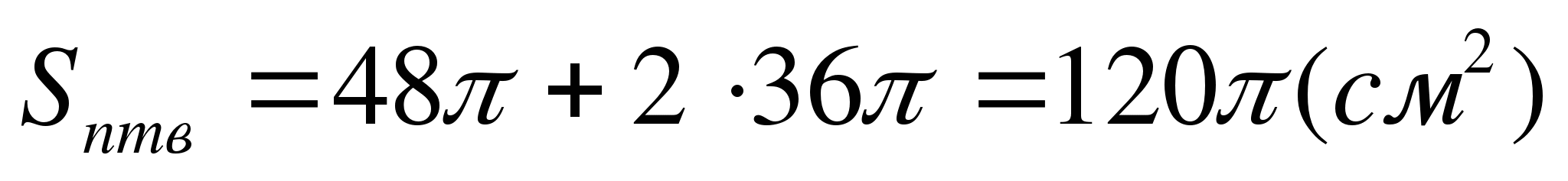
Ответ: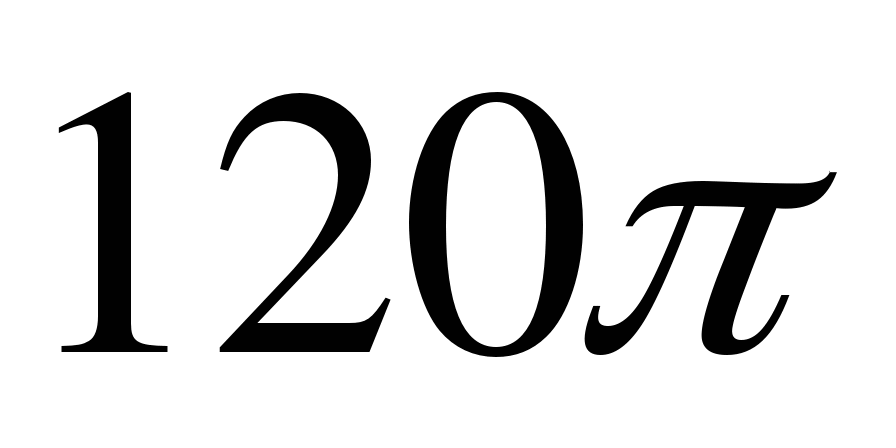 
.
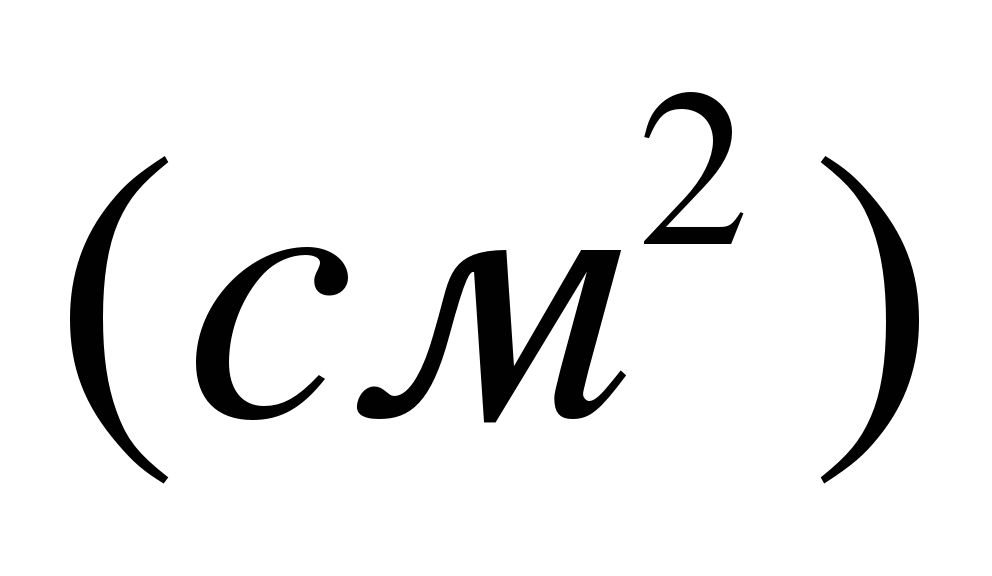4. Длина окружности основания прямого цилиндра С = 10 м, длина образующей l = 7 м. Чему равна площадь боковой поверхности цилиндра?
Дано: цилиндр,
C = 10 м,
l = 7 м.
Найти: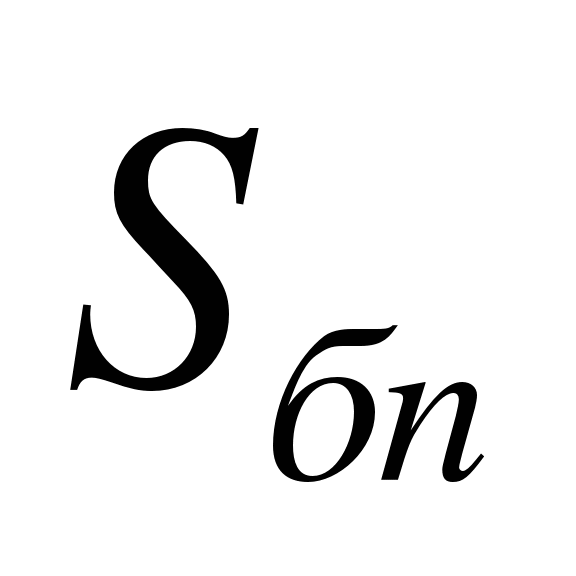 
Решение. Площадь боковой поверхности цилиндра равна произведению длины окружности его основания н высоту: S = CH. Высота цилиндра равна его образующей:
H = 10 м. Поэтому
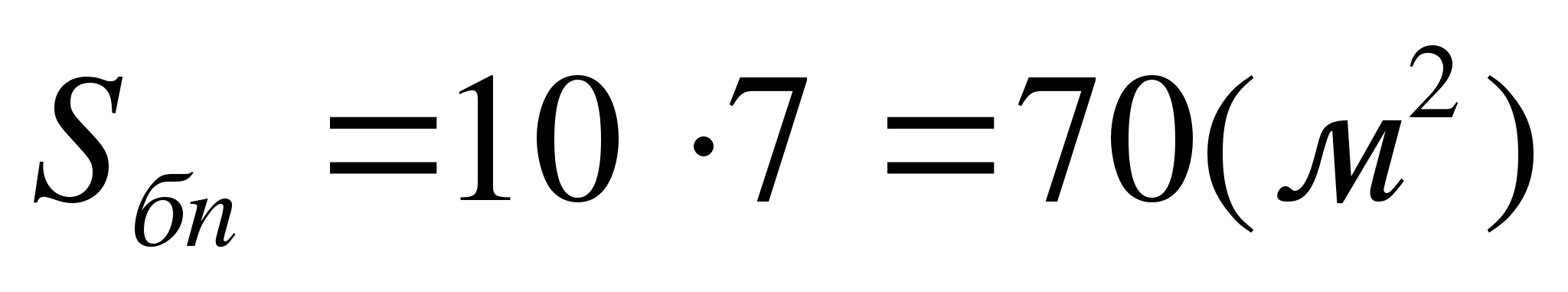
Ответ: 70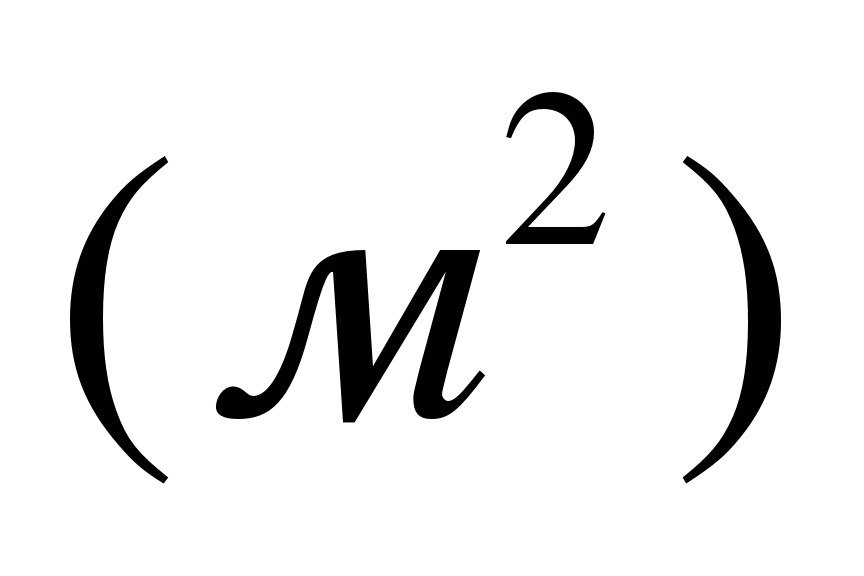
.
Вопросы по теме «Цилиндр»
Что такое цилиндр?
Что такое высота цилиндра?
Какой цилиндр называется прямым?
Осевое сечение цилиндр – квадрат, площадь которого Q. Чему равна площадь основания цилиндра?
Прямой круговой конус
Ко́нус — тело, которое состоит из круга – основания конуса, точки, не лежащей в плоскости этого круга, - вершины конуса и всех отрезков, соединяющих вершину конуса с точками основания. Если основание конуса представляет собой многоугольник, конус становится пирамидой.
Примеры тел, имеющих форму конуса:
Чум и яранга у северных народов, вигвам у индейцев Северной Америки имеют форму, близкую к форме конуса.
Ваши примеры из жизни и техники:
Отрезок, соединяющий вершину и границу основания, называется образующей конуса.
Объединение образующих конуса называется образующей (или боковой) поверхностью конуса. Образующая поверхность конуса является конической поверхностью.
Отрезок, опущенный перпендикулярно из вершины на плоскость основания (а также длина такого отрезка), называется высотой конуса.
Конус называется прямым, если прямая, соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания. При этом прямая, соединяющая вершину и центр основания, называется осью конуса.
Сечение конуса плоскостью, проходящей через его ось, называется осевым сечением.
Круговой конус — конус, основание которого является кругом.
Прямой круговой конус (часто его называют просто конусом) можно получить вращением прямоугольного треугольника вокруг прямой, содержащей катет (эта прямая представляет собой ось конуса).
Конус, опирающийся на эллипс, параболу или гиперболу, называют соответственно эллиптическим, параболическим и гиперболическим конусом (последние два имеют бесконечный объём).
Часть конуса, лежащая между основанием и плоскостью, параллельной основанию и находящейся между вершиной и основанием, называется усечённым конусом.
Плоскость, перпендикулярная оси конуса, пересекает конус по кругу, а боковую поверхность – по окружности с центром на оси конуса.
Сечение конуса плоскостью, параллельной основанию, отсекает от него конус, подобный данному.
Площадь полной поверхности конуса равна
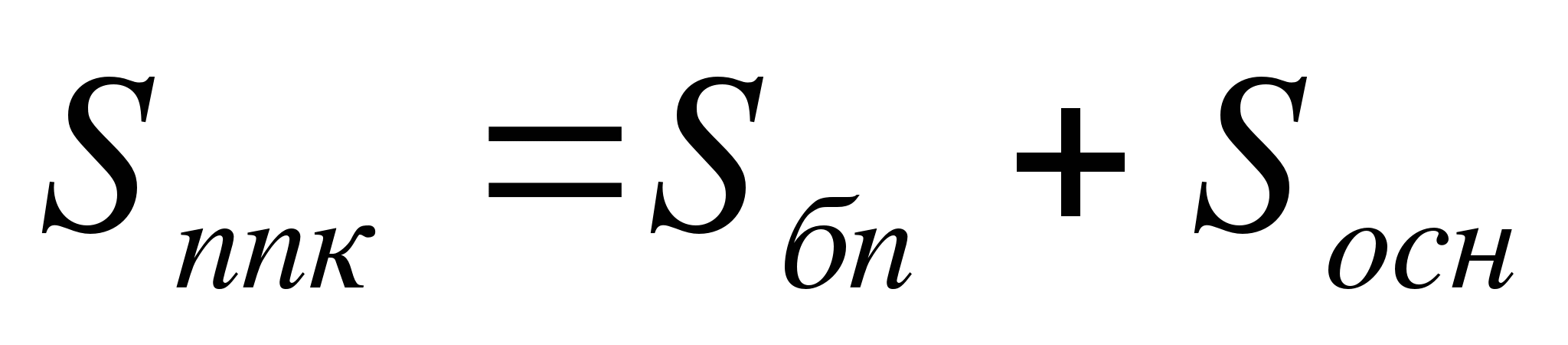
S = πRl
где R — радиус основания, l — длина образующей.
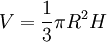
Задачи по теме «Конус»
1. Радиус основания конуса 3 м, высота 4 м. Найдите образующую l.
Дано: конус,
r = 3 м,
h =4 м,
Найти: l – образующая конуса
Решение. Рассмотрим прямоугольный треугольник, катетами которого являются высота конуса и радиус основания, а гипотенузой – образующая конуса. По теореме Пифагора получи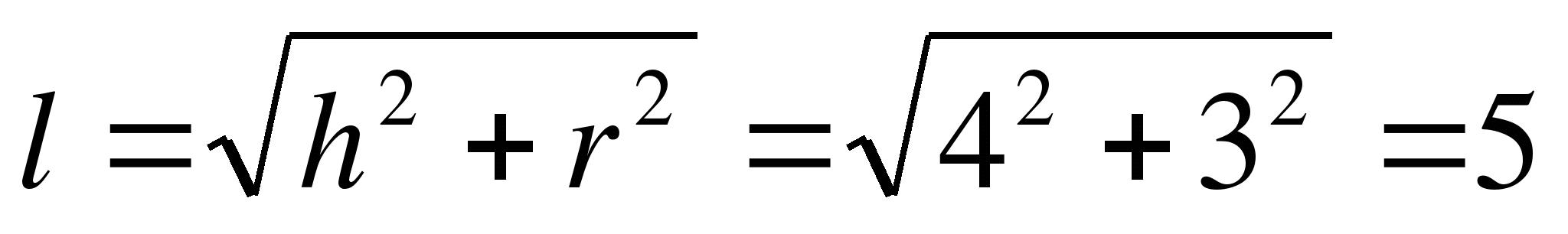м:
м
Ответ: 5 м.
2.Радиус основания конуса R.. Осевым сечением конуса является прямоугольный треугольник. Найдите его площадь.
Дано: конус,
R – радиус основания,
∆ABC – осевое сечение конуса,
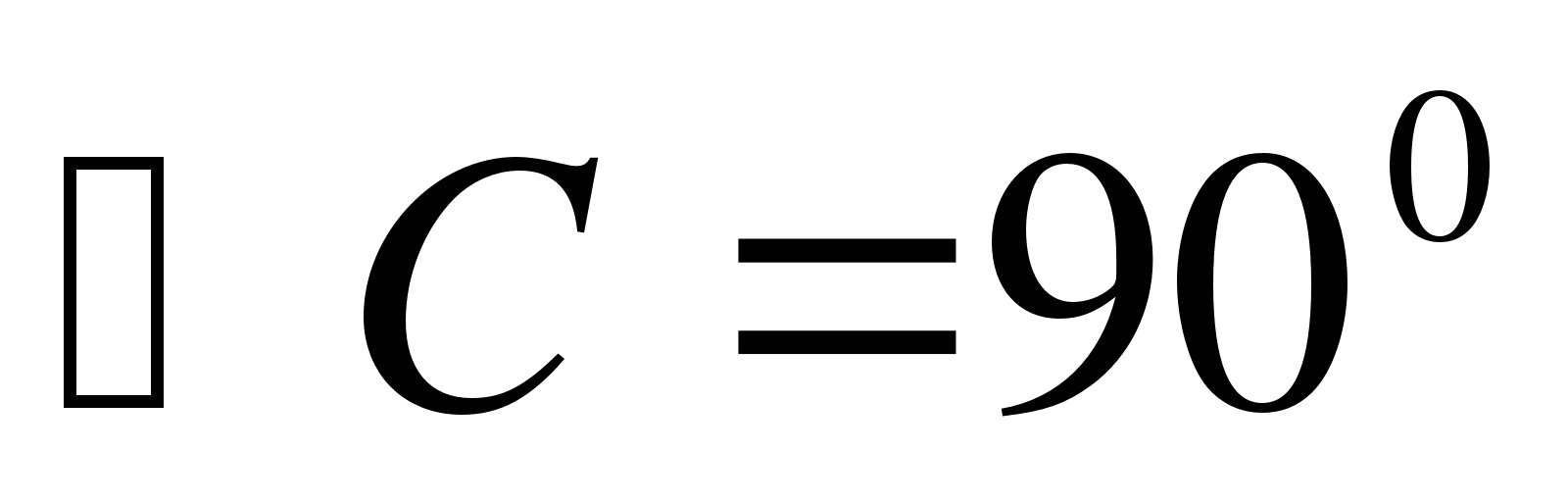
Найти: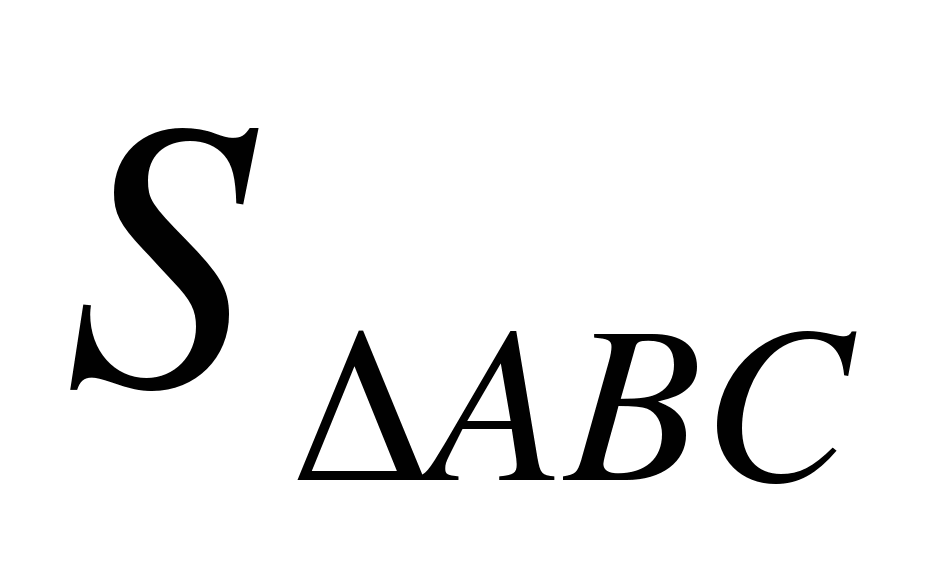 
Решение. Так как этот прямоугольный треугольник является еще и равнобедренным, то высота в нем, проведенная к основанию, является и медианой. Медиана, проведенная к гипотенузе равна половине гипотенузы, то есть, радиусу, так как гипотенуза равна диаметру.
Ответ: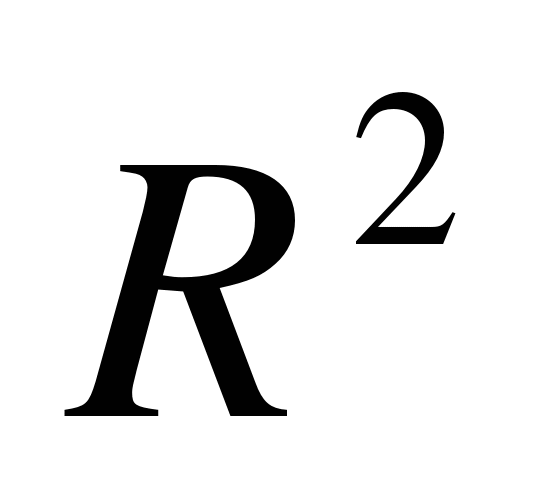 
.
3. В равностороннем конусе (осевое сечение – правильный треугольник) радиус основания R .Найдите площадь сечения, проведенного через две образующие, угол между которыми равен α.
Дано: конус,
R – радиус основания,
∆ABC – осевое сечение конуса,
MC, KC – образующие конуса,
Найти: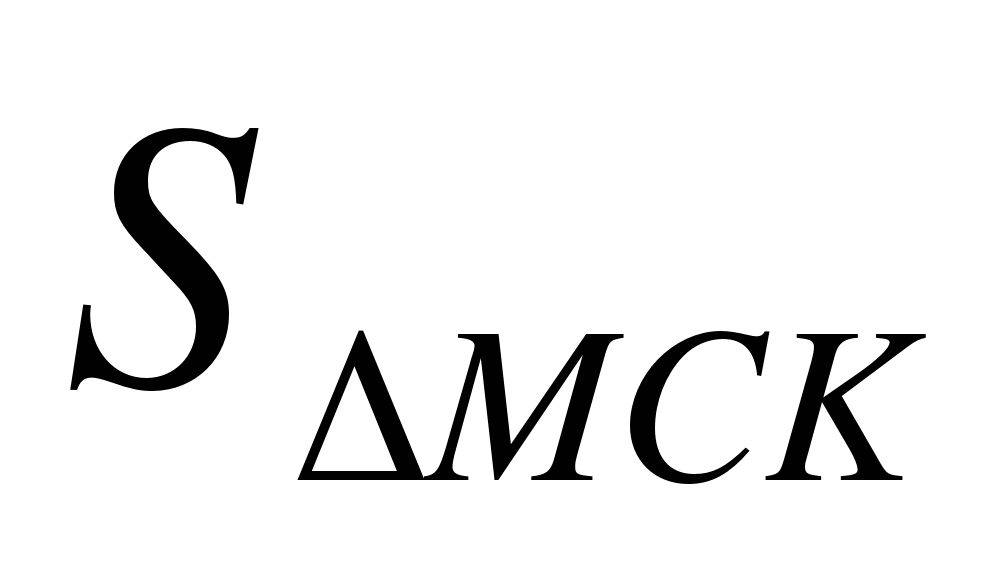 
Решение. Так как в осевом сечении ∆ABC – правильный, то образующая AC = AB = 2R. Площадь ∆MCK найдем по формуле
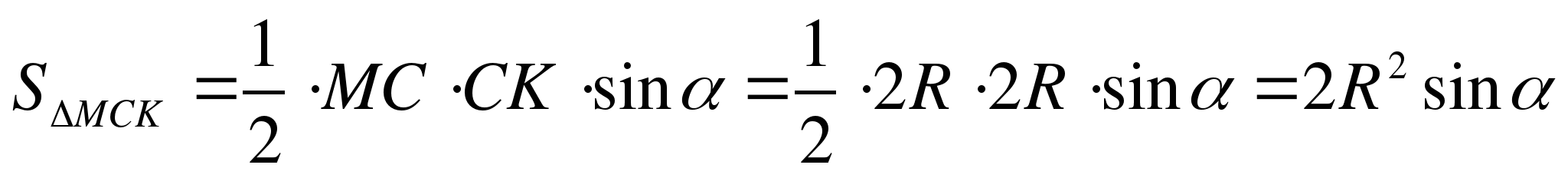
Ответ: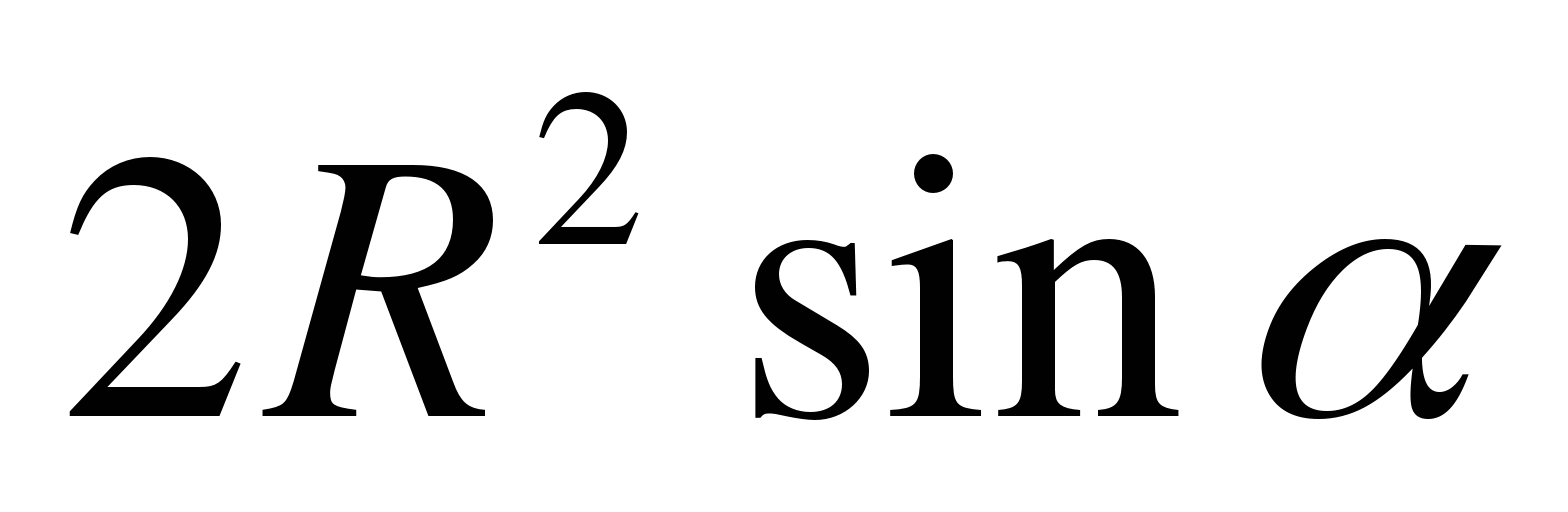 
.
4. Конус пересечен плоскостью, параллельной основанию, на расстоянии d от вершины. Найдите площадь сечения, если радиус основания конуса R, а высота H.
Дано: конус,
α – плоскость,
R – радиус основания,
СD = H,
С – вершина конуса,
СК = d
Найти: 
Решение.
Сечение конуса получается из основания конуса преобразованием гомотетии (гомотетия – преобразование подобия, то есть, преобразование фигуры F в фигуру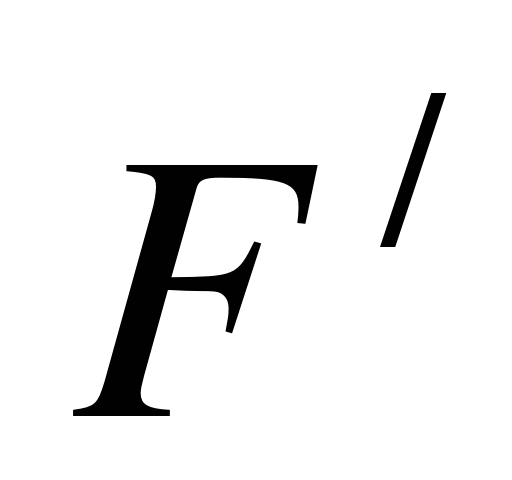 
, при котором расстояние между точками изменяются в одно и то же число раз) относительно вершины конуса с коэффициентом гомотетии 
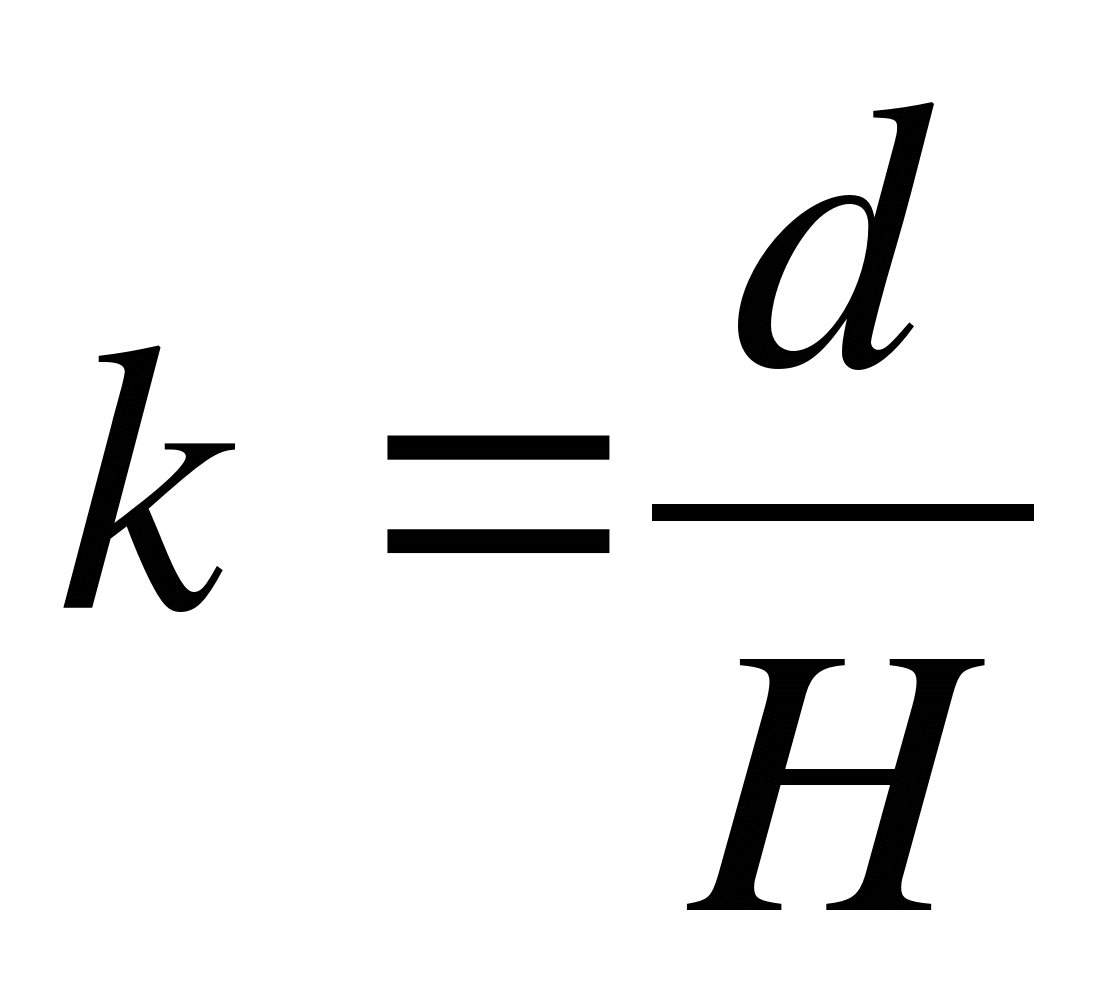. Поэтому 
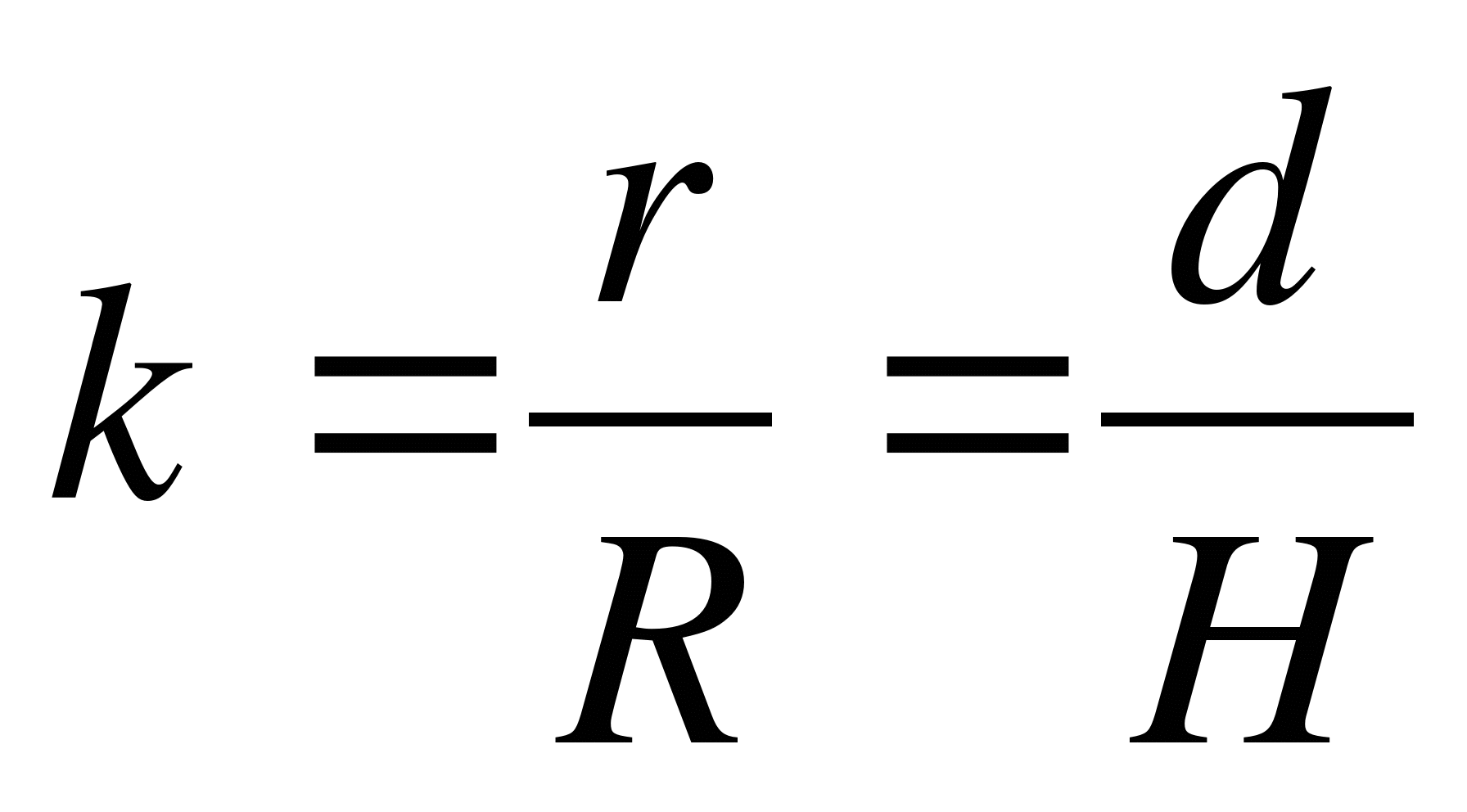и 
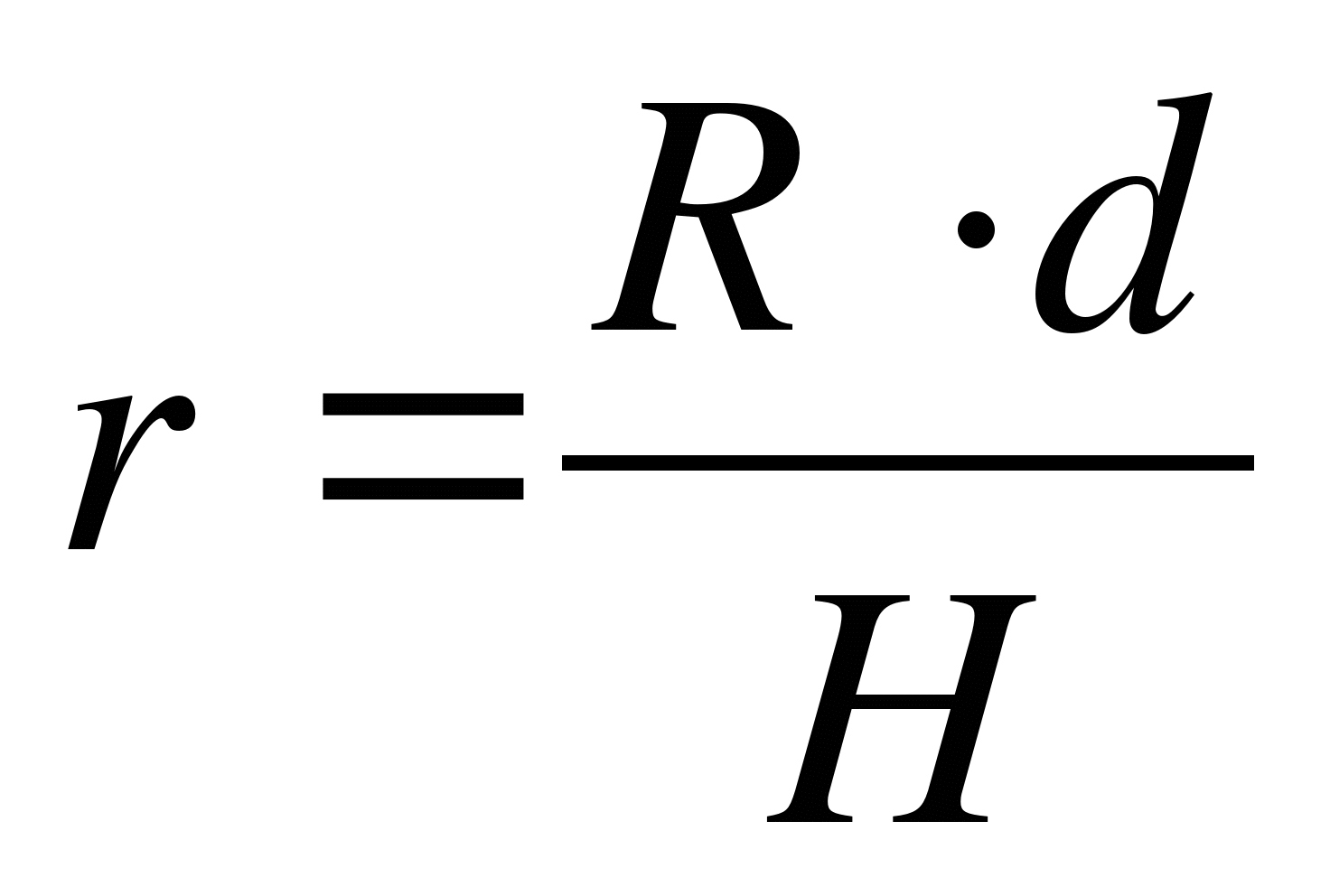. Следовательно, площадь сечения
.
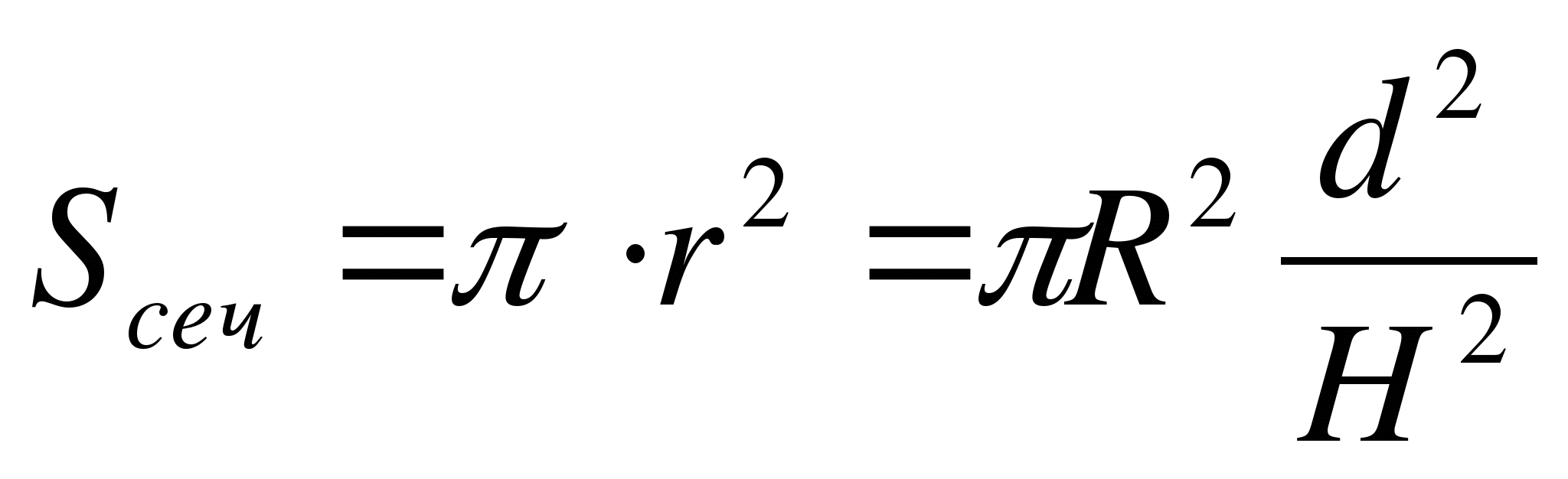Ответ: 
.
5. Высота конуса H. На каком расстоянии от вершины надо провести плоскость, параллельную основанию, чтобы площадь сечения была равна половине площади основания?
Дано: конус,
α – плоскость,
H - высота,
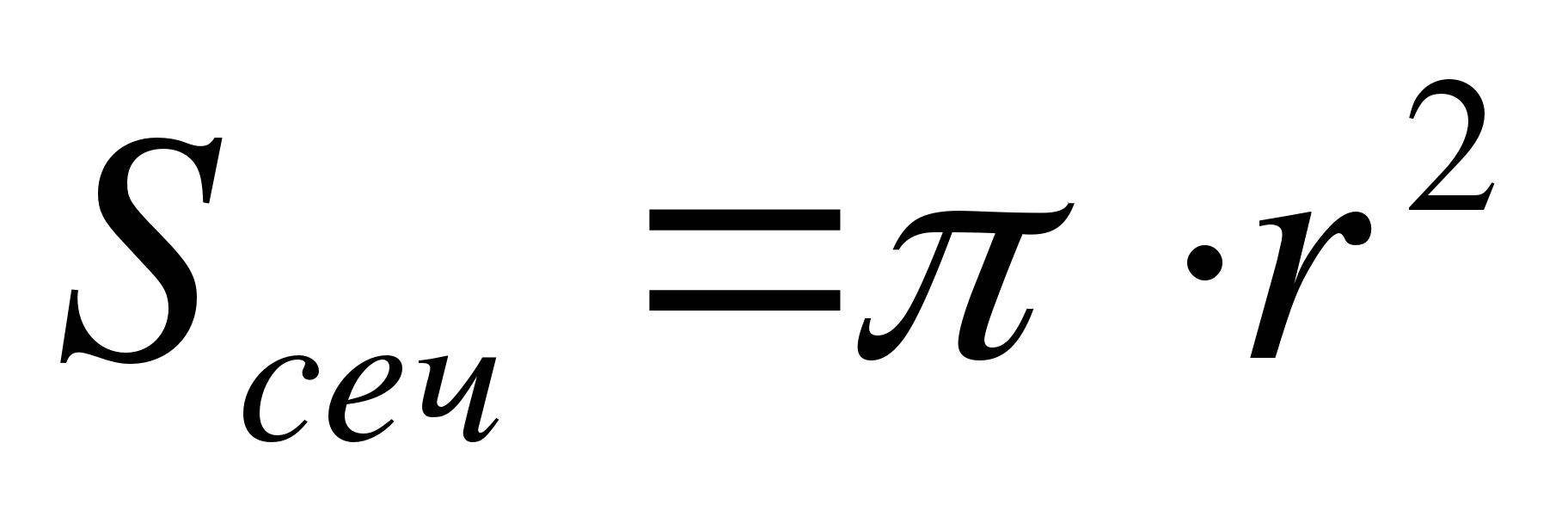
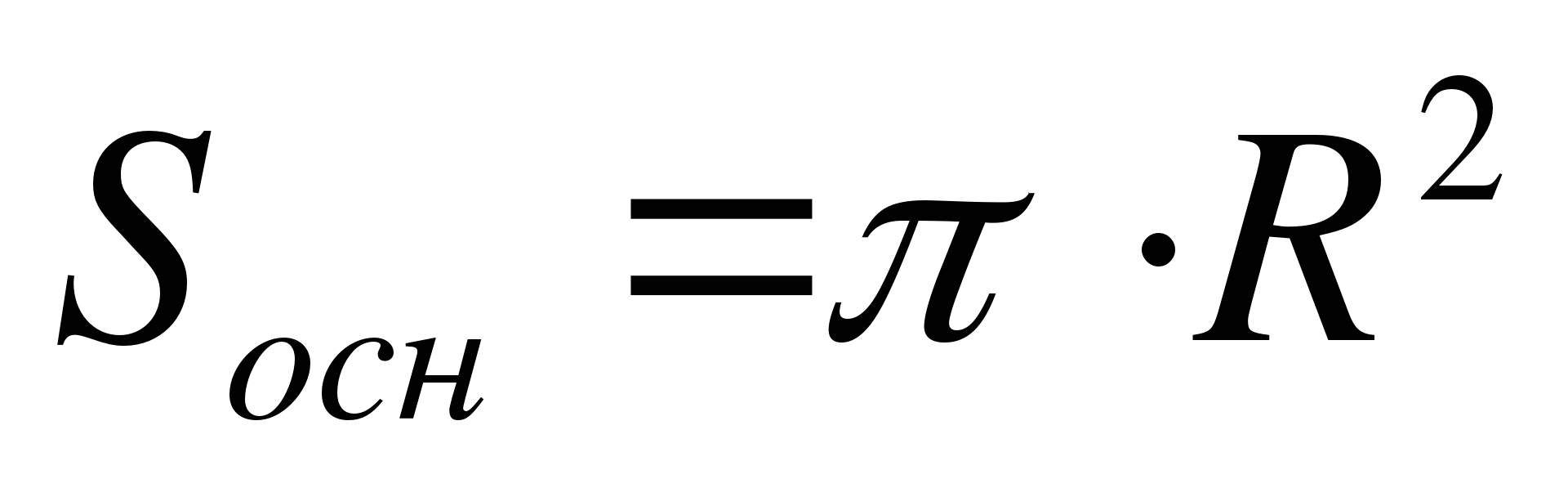
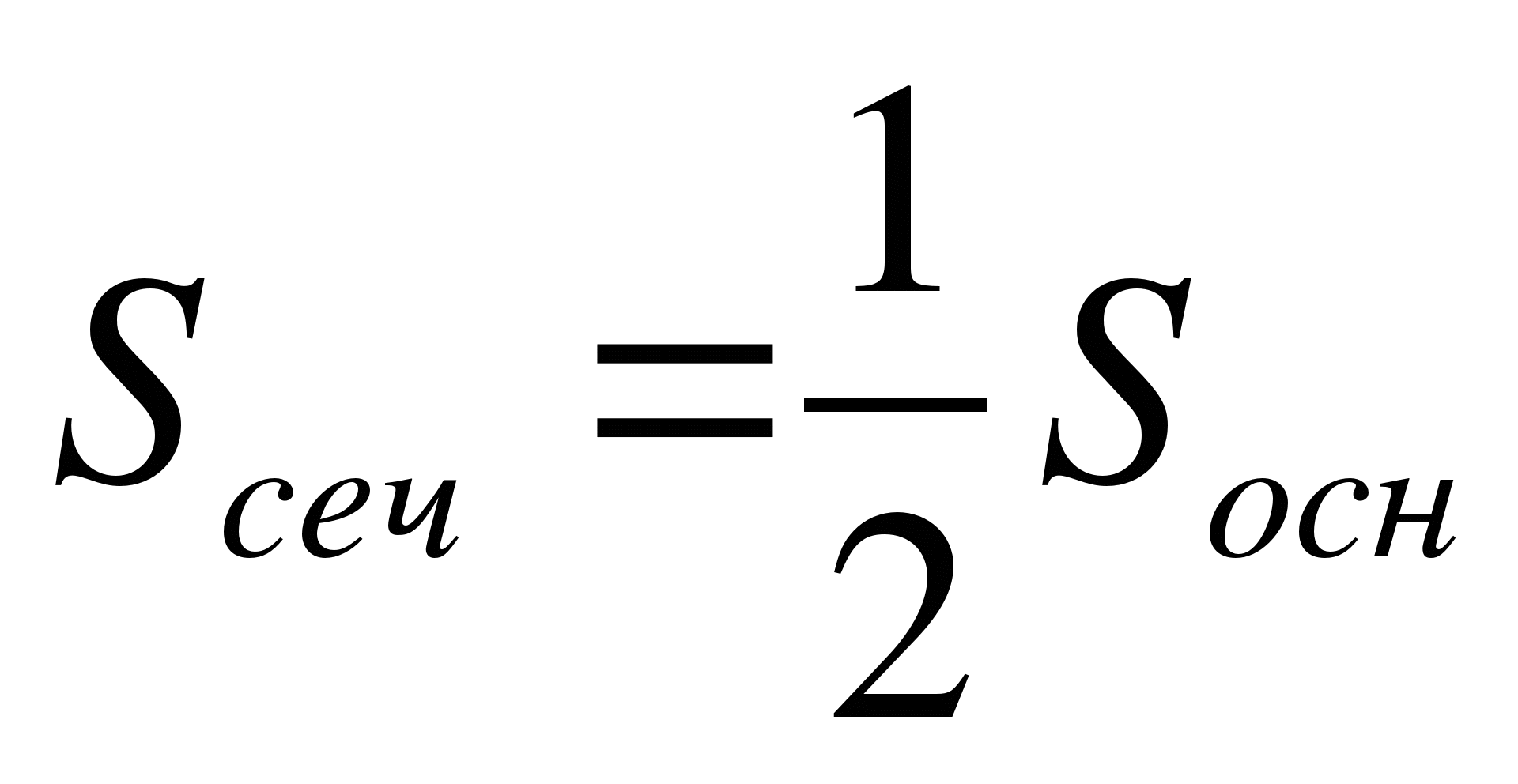
Найти: h
Решение.
Проведенная плоскость отсекает подобный конус. В подобных фигурах отношение линейных размеров равно коэффициенту подобия, а отношение соответствующих площадей – квадрату коэффициента подобия. Значит, 
. Отсюда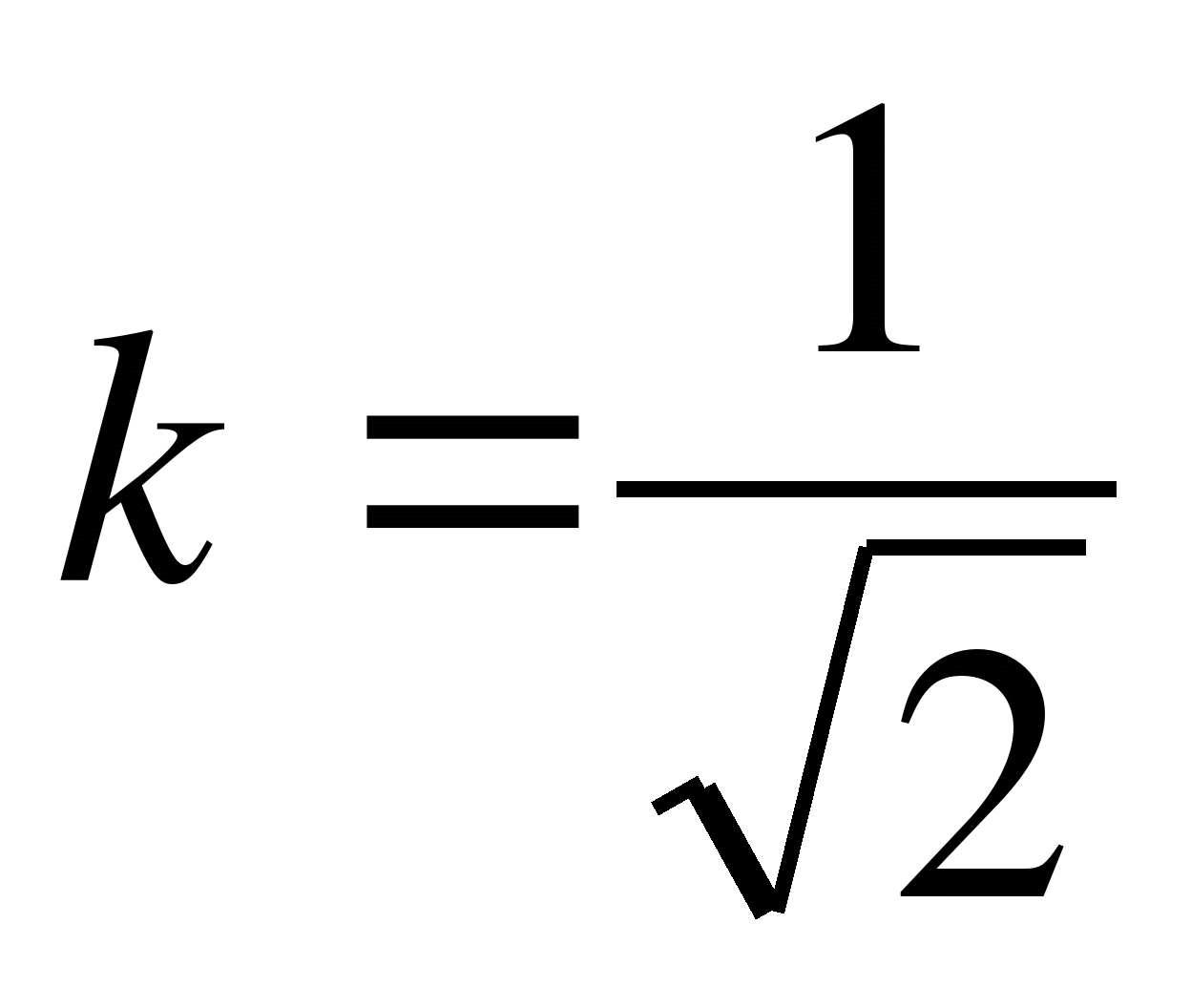 
. Тогда 
и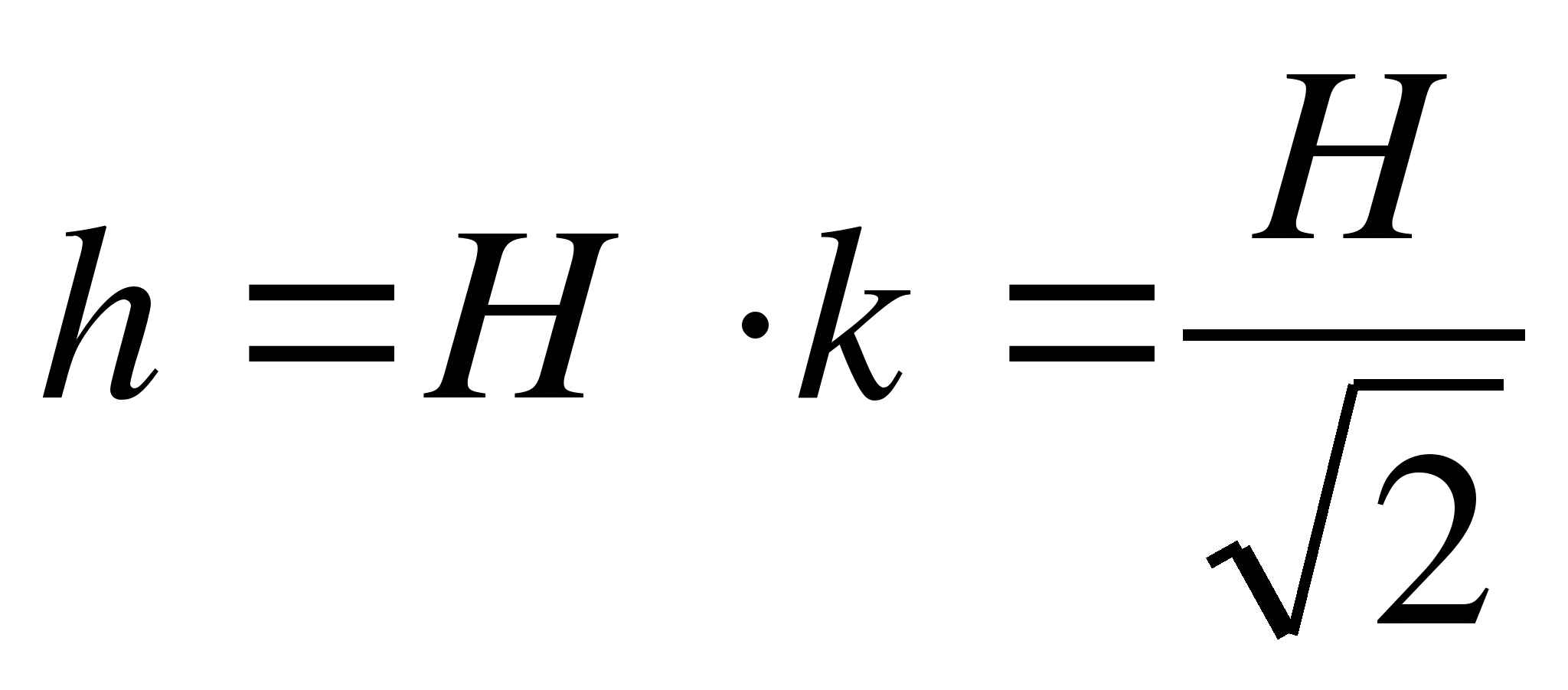 
Ответ: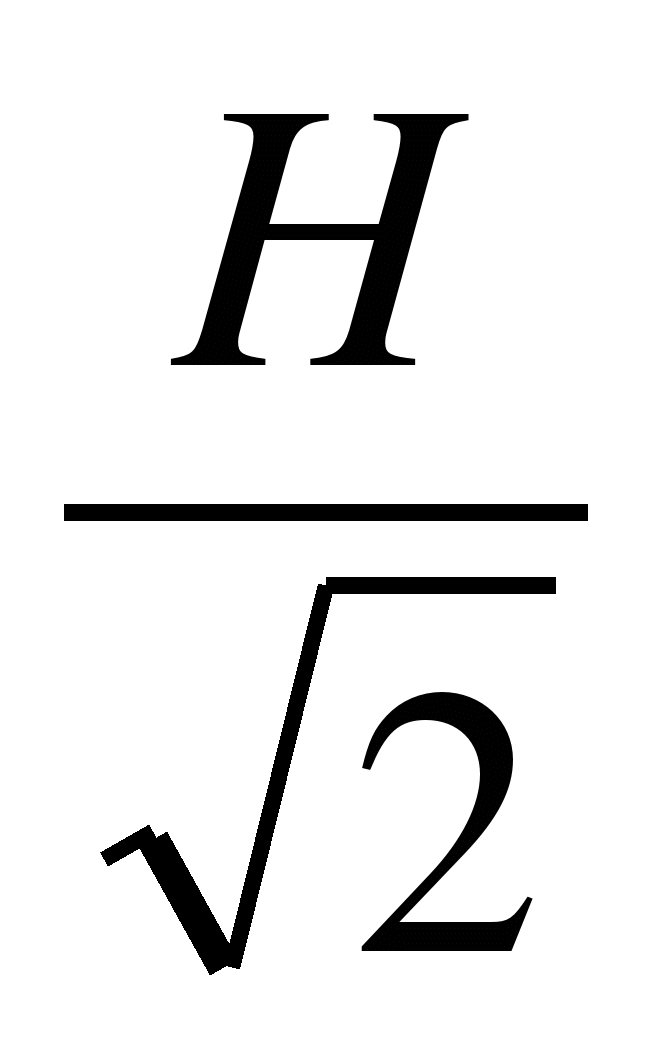 
.
Вопросы к теме «Конус»
Что такое конус?
Какой конус называется круговым?
Что такое образующая конуса?
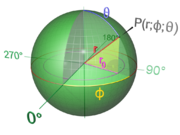
Шар — геометрическое тело, ограниченное поверхностью, все точки которой отстоят на равном расстоянии от центра. Это расстояние называется радиусом шара. Шар образуется вращением полукруга около его неподвижного диаметра. Этот диаметр называется осью шара, а его оба конца — полюсами шара. Поверхность шара называется сферой.
Примеры тел, имеющих форму шара или сферы:
Купол здания может иметь форму части сферы, отсеченной плоскостью.
Земля имеет форму, близкую к шару.
Мячи для игры в футбол, теннис имеют форму шара.
Ваши примеры:
Если секущая плоскость проходит через центр шара, то сечение шара называется большим кругом. Другие плоские сечения шара называются малыми кругами
Любой отрезок, соединяющий центр шара с точкой шаровой поверхности (сферы), называется радиусом.
Отрезок, соединяющий две точки шаровой поверхности и проходящей через центр шара, называется диаметром.
Концы любого диаметра называются диаметрально противоположными точками шара.
Плоскость, проходящая через центр шара, называется диаметральной плоскостью.
Плоскость, проходящая через точку А шаровой поверхности и перпендикулярная радиусу, проведенному в точку А, называется касательной плоскостью. Точка А называется точкой касания.
Свойства
Всякое сечение шара плоскостью есть круг. Центр этого круга есть основание перпендикуляра, опущенного из центра шара на секущую плоскость.
Любя диаметральная плоскость шара является его плоскостью симметрии. Центр шар является его центром симметрии.
Касательная плоскость имеет с шаром только одну общую точку – точку касания.
Линия пересечения двух сфер есть окружность.
Основные формулы
Площадь сферы радиуса R вычисляется по формуле
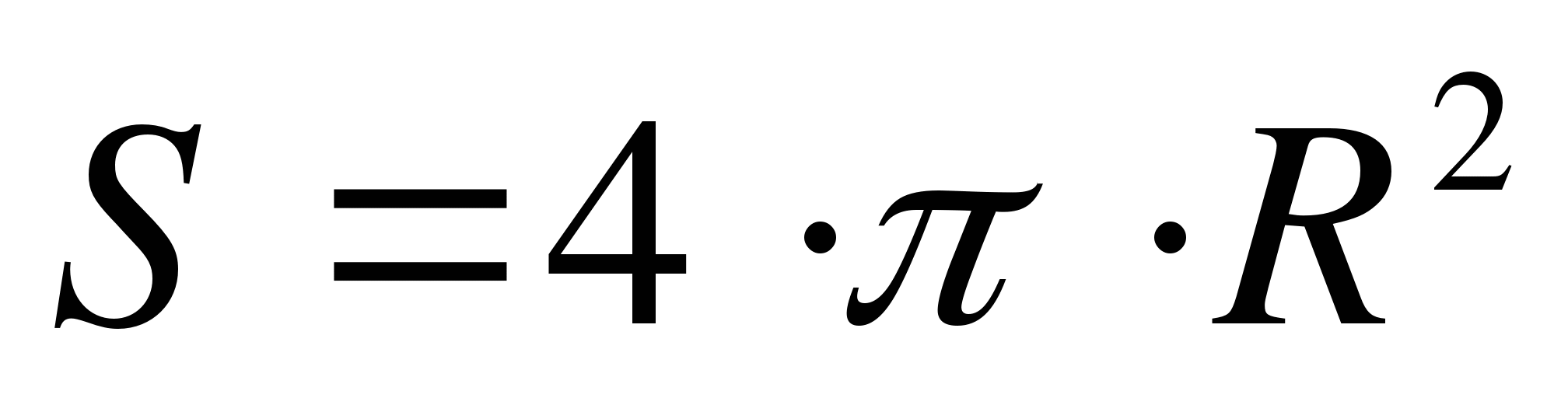
Задачи по теме «Шар и сфера»
1.Радиус сферы увеличили в 3 раза. Во сколько раз увеличится площадь сферы?
Дано: r – радиус исходной сферы,
R – радиус новой сферы,
R = 3r
Найти: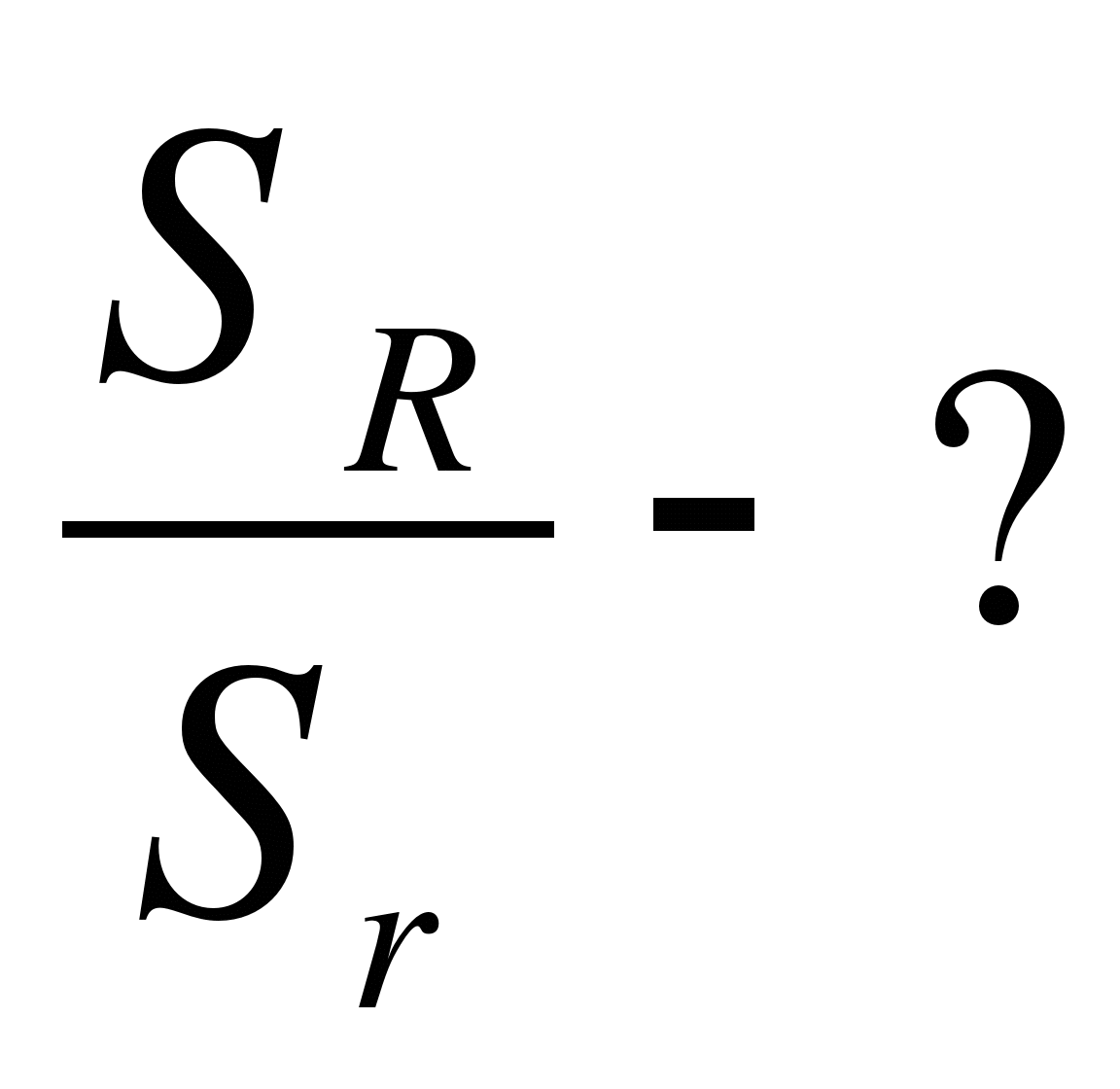 
Решение.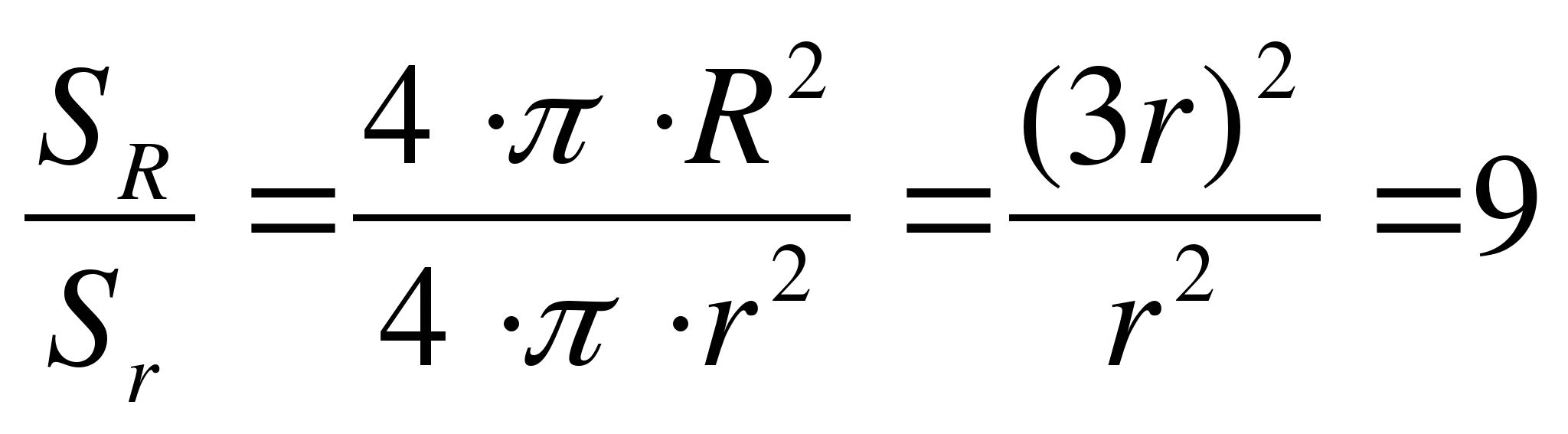 
Ответ: в 9 раз.
2. Шар, радиуса 41 дм, пересечен плоскостью на расстоянии 9 дм от центра
Найдите площадь сечения.
Дано: шар,
R = 41 дм,
ОА = 9 дм,
О – центр щара.
Найти:
Решение.
Из прямоугольного треугольника АВС: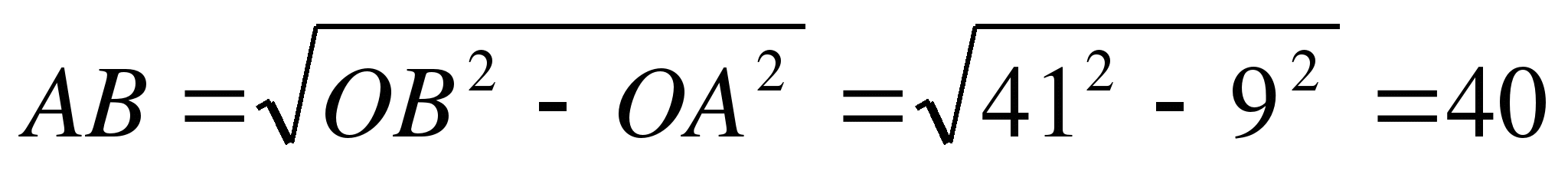 
дм.
Площадь сечения
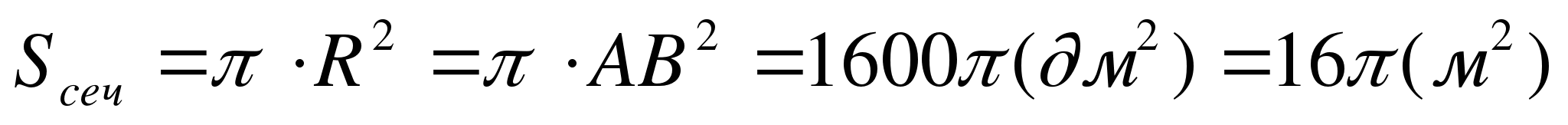
Ответ: 16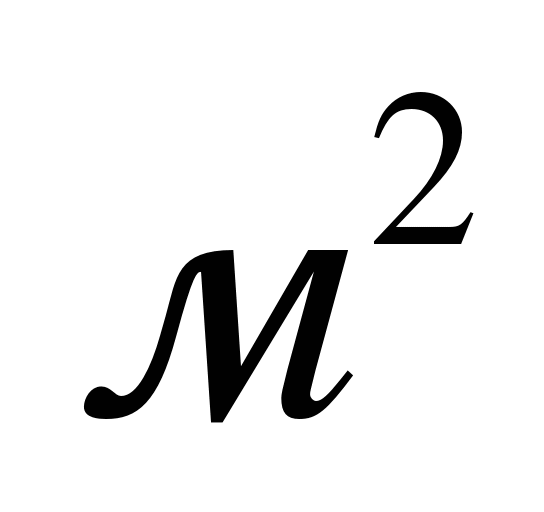 
.
3.Через середину радиуса шара проведена перпендикулярная ему плоскость. Как относится площадь полученного сечения к площади большого круга?
Дано: шар,
R – радиус шара,
α – плоскость,
ОА = 1/2R,
О – центр щара.
Найти: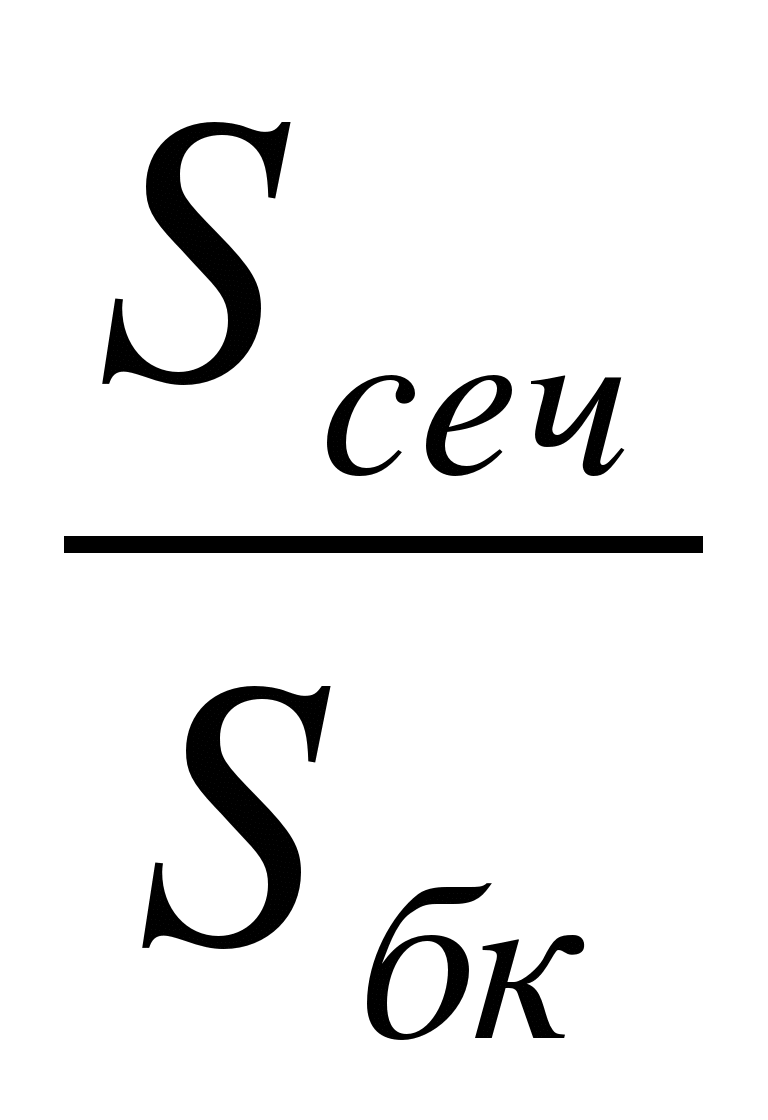 
Решение. Из прямоугольного треугольника АOВ: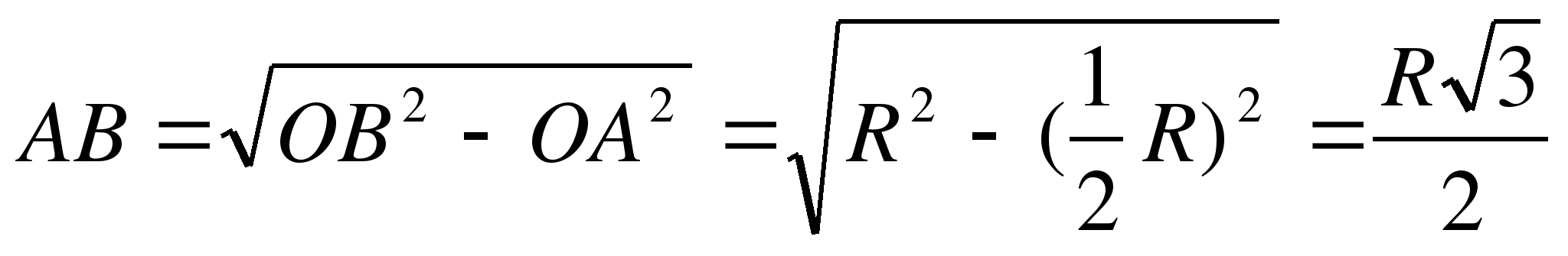 
.
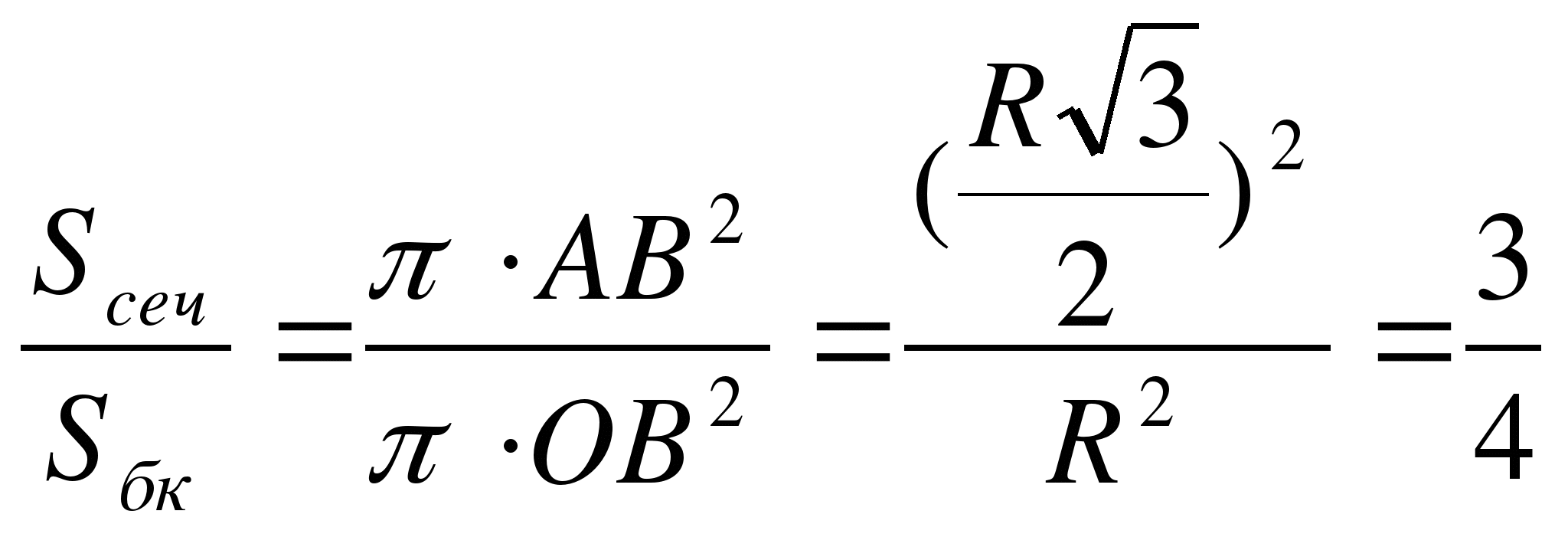
Ответ: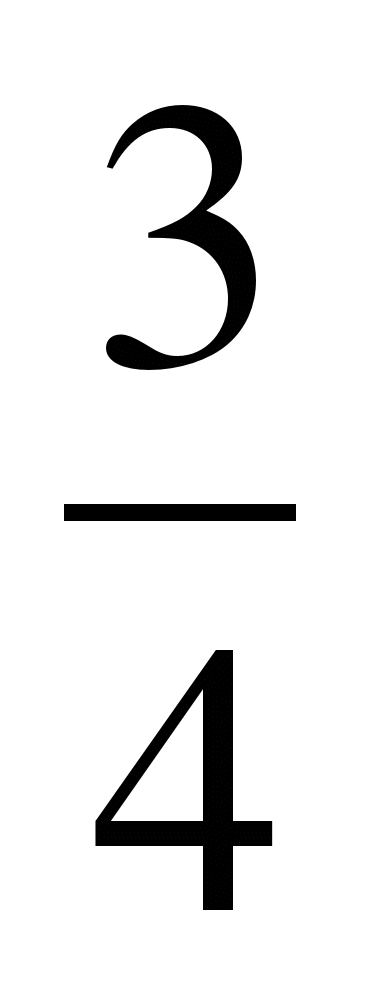 
.
4. Радиус шара R. Через конец радиуса проведена плоскость под углом 600 к нему. Найти площадь сечения.
Дано: шар,
R – радиус шара,
,
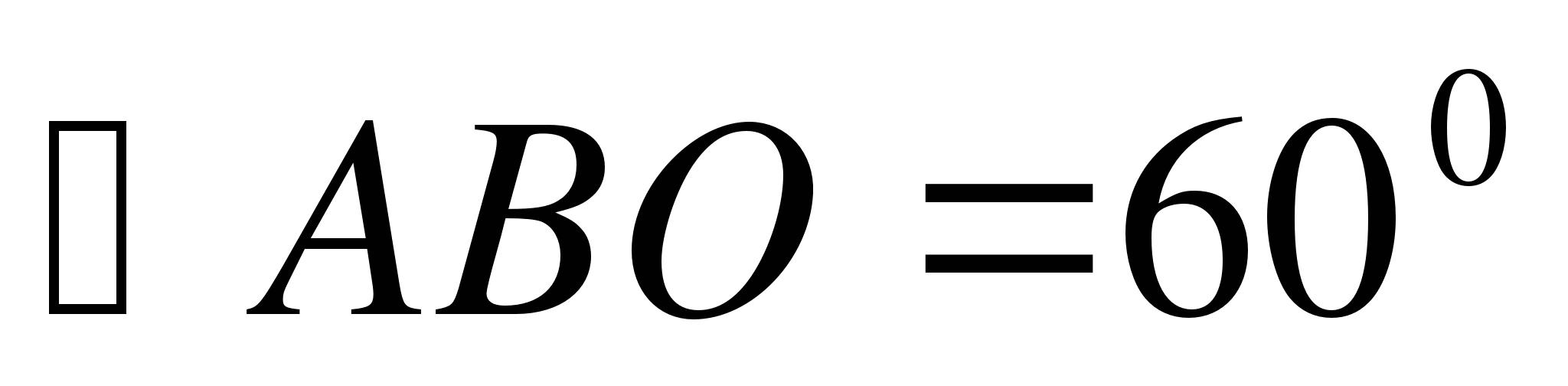О – центр щара.
Найти:
Решение. Из прямоугольного треугольника АОВ: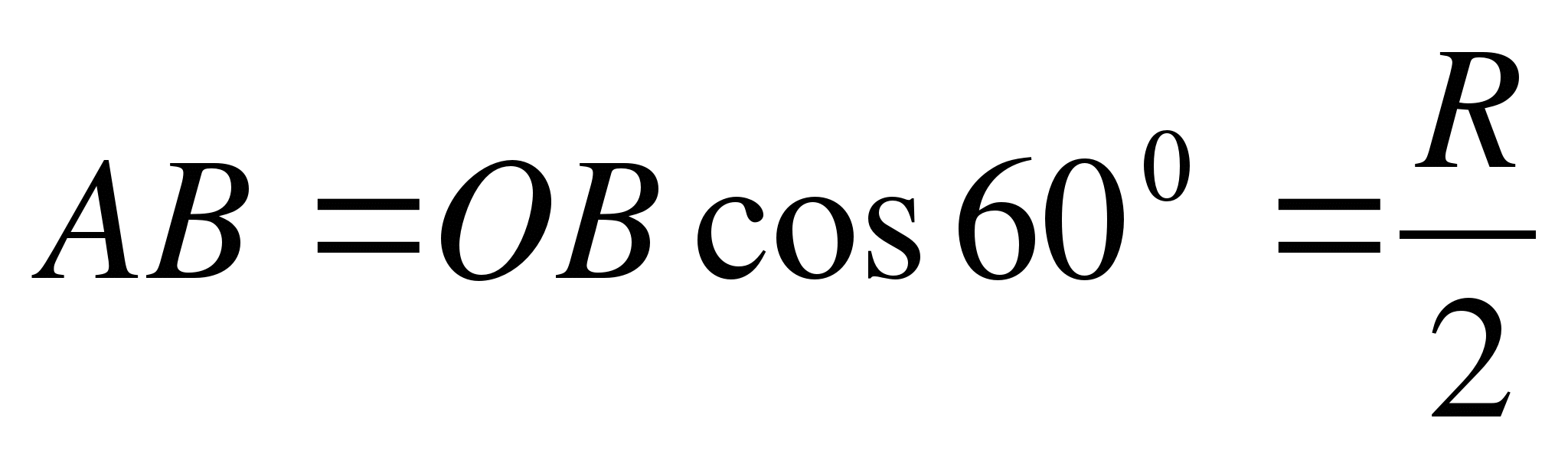 
.
Площадь сечения
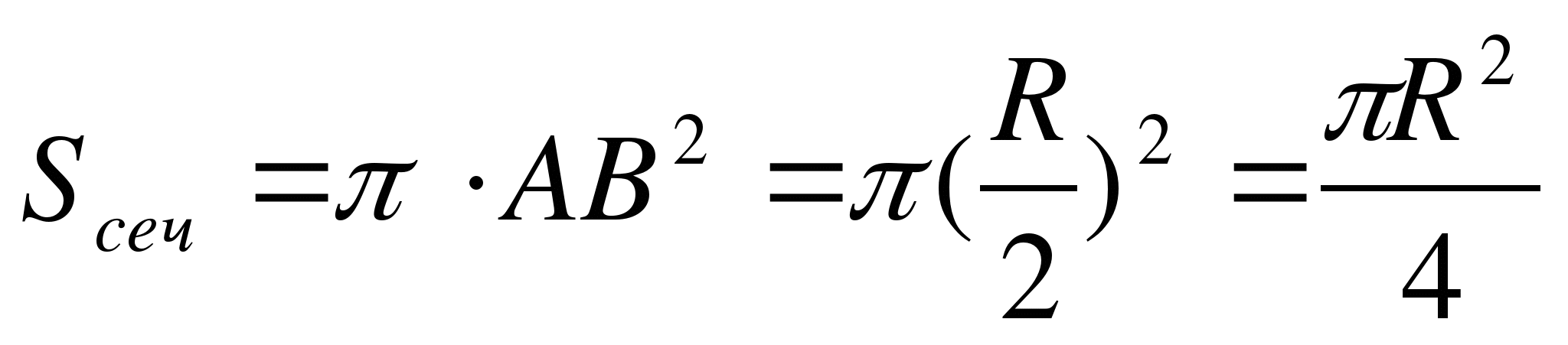
Ответ: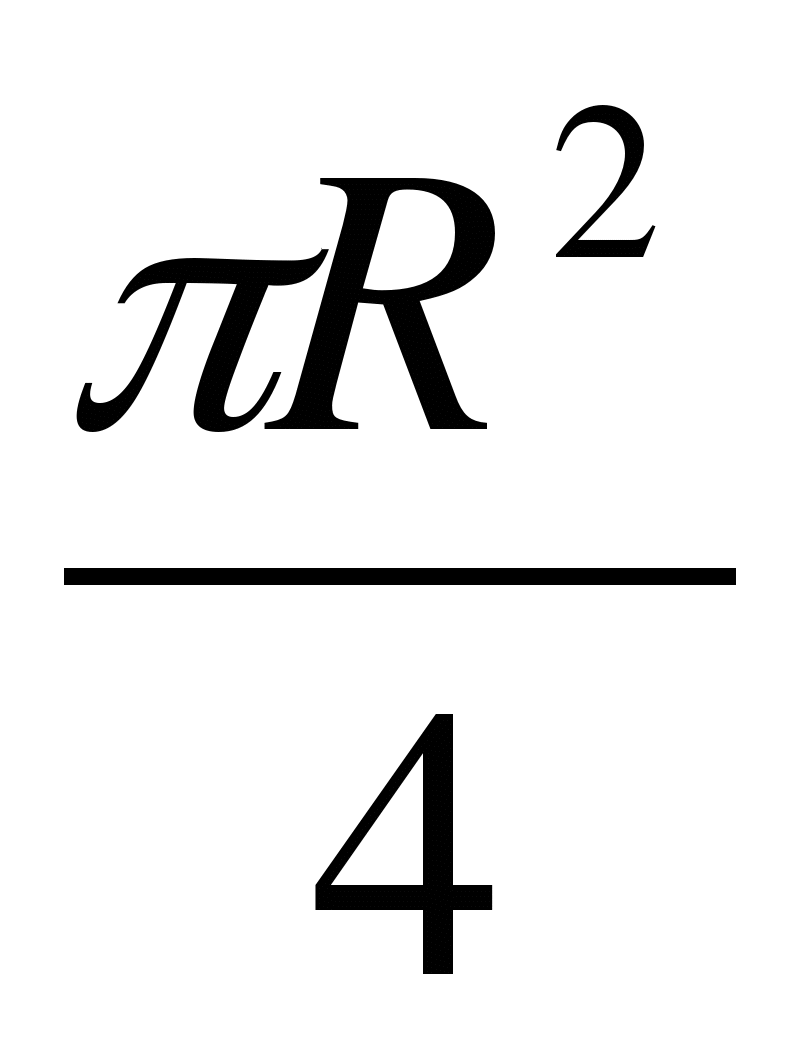 
5. Город N находится на 600 северной широты. Какой путь совершает этот пункт в течение 1 ч. Вследствие вращения Земли вокруг своей оси? Радиус Земли принять равным 6000 км.
Дано: шар,
R = 6000 км,
,
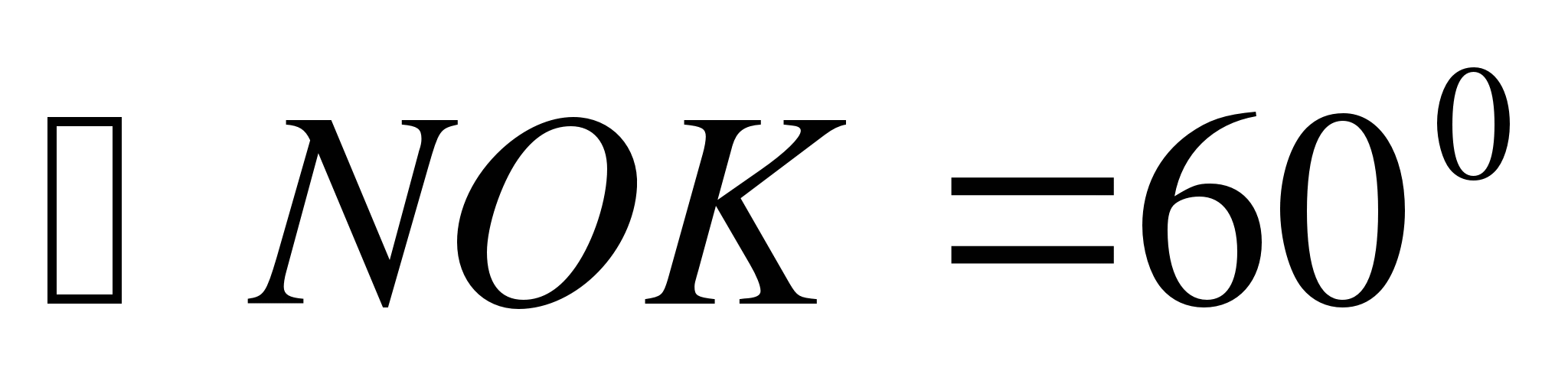О – центр щара.
Найти: S- путь
Решение.
В прямоугольном треугольнике АОN: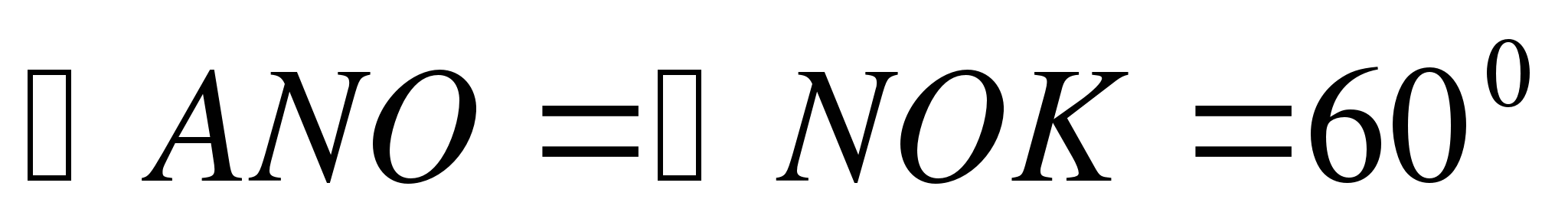 
(как внутренние накрест лежащие углы при параллельных прямых AB и OK). Тогда 
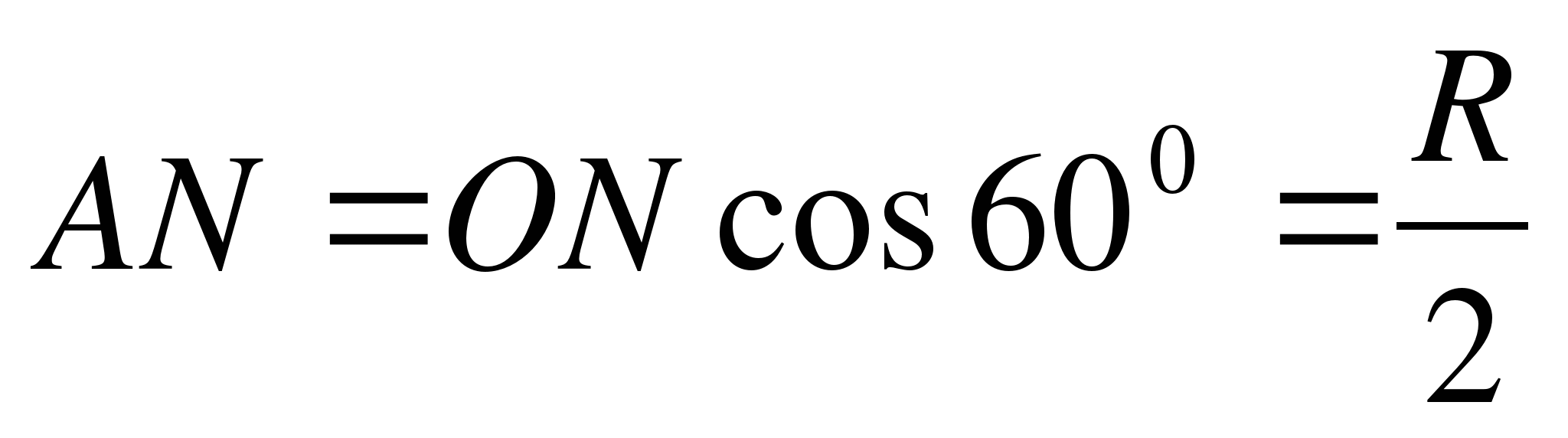. За один час город N опишет дугу, равную 1/24 части длины окружности с радиусом AN. Значит,
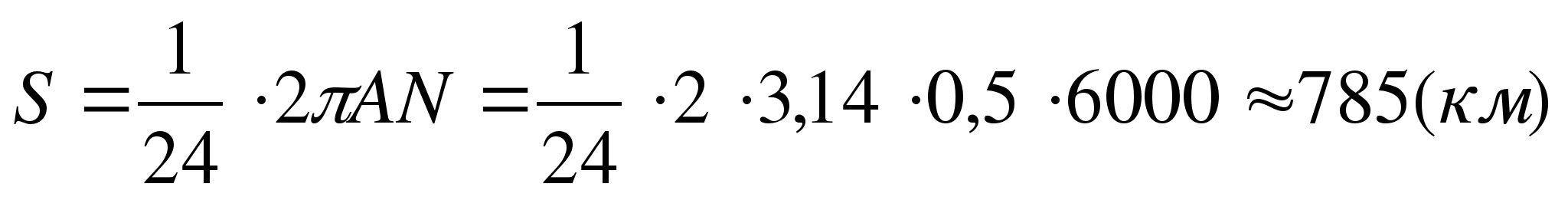
Ответ: 785 км.
Вопросы по теме «Шар и сфера»
Что такое шар?
Что такое радиус шара, диаметр шара? Какие точки шара называются диаметрально противоположными?
Что такое большой круг шара?
В каждой строке таблицы необходимо поставить один или несколько знаков «+», указывающих, какие из видов тел вращения обладают описанными свойствами.
цилиндр
конус
шар
Верно ли, что образующая конуса больше его высоты?
Может ли площадь боковой поверхности цилиндра равняться площади его осевого сечения?
Назовите плоскую фигуру, при вращении которой вокруг одной из сторон образуются два равных конуса с общим основанием.
Верно ли, что среди всех сечений цилиндра, проходящих через его образующую, наибольшую площадь имеет осевое сечение?
Может ли площадь боковой поверхности конуса равняться площади его основания?
Верно ли, что любое сечение сферы плоскостью является окружностью?
Может ли плоскость касаться сферы в двух точках?
Плоскость удалена от центра сферы радиуса R на расстояние d. Сравните R и d, если сфера и плоскость не имеют общих точек.
Верно ли, что расстояние между любыми двумя точками сферы не больше ее диаметра?
Верно ли, что сфера и прямая могут иметь не более двух общих точек?
Критерии оценок:
0 ошибок – «5»;
1-2 ошибки – «4»;
3 – 6 ошибок – «3»;
7 – и более – «2».
Ответы:
да
нет
равнобедренный треугольник
да
нет
да
нет
d>R
да
да
Задачи по теме «Цилиндр»
1.Радиус основания цилиндра 2 см, высота 3 см. Найдите диагональ осевого
сечения.
2 Радиус основания цилиндра равен 5 см, а его образующая – 9 см. Найдите
площадь осевого сечения.
3.Прямоугольник, стороны которого равны 6 см и 4 см, вращается около меньшей
стороны. Найдите площадь поверхности тела вращения.
4.Длина окружности основания прямого цилиндра С = 10 м, длина образующей l = 7 м. Чему равна площадь боковой поверхности цилиндра?
Задачи по теме «Конус»
1.Радиус основания конуса 3 м, высота 4 м. Найдите образующую l.
2.Радиус основания конуса R.. Осевым сечением конуса является прямоугольный треугольник. Найдите его площадь.
3.В равностороннем конусе (осевое сечение – правильный треугольник) радиус основания R. Найдите площадь сечения, проведенного через две образующие, угол между которыми равен α.
4.Конус пересечен плоскостью, параллельной основанию, на расстоянии d от вершины. Найдите площадь сечения, если радиус основания конуса R, а высота H.
5.Высота конуса H. На каком расстоянии от вершины надо провести плоскость, параллельную основанию, чтобы площадь сечения была равна половине площади основания?
Задачи по теме «Шар и сфера»
1.Радиус сферы увеличили в 3 раза. Во сколько раз увеличится площадь сферы?
2.Шар, радиуса 41 дм, пересечен плоскостью на расстоянии 9 дм от центра. Найдите площадь сечения.
3. Через середину радиуса шара проведена перпендикулярная ему плоскость. Как относится площадь полученного сечения к площади большого круга?
4.Радиус шара R. Через конец радиуса проведена плоскость под углом 600 к нему. Найти площадь сечения.
5.Город N находится на 600 северной широты. Какой путь совершает этот пункт в течение 1 ч. вследствие вращения Земли вокруг своей оси? Радиус Земли принять равным 6000 км.
Дайте определение цилиндра. Нарисуйте цилиндр, укажите его образующие и осевое сечение.
Дайте определение конуса, Нарисуйте конус, укажите его образующую и осевое сечение.
Назовите формулы площадей боковой и полной поверхностей конуса, цилиндра.
Дайте определение сферы и шара.
Верно ли, что все точки шара удалены от центра на расстояние, равное радиусу шара?
Может ли осевое сечение цилиндра быть трапецией?
Как относятся диаметр d и высота h цилиндра, если осевое сечение цилиндра квадрат?
по теме: «Геометрические тела и поверхности».
Тема урока: «Тела вращения. Конус, цилиндр, шар и сфера».
На данную тему «Геометрические тела и поверхности» выделено 18 часов. Данный урок №55 в этой теме.
Урок проводился с группой № 087 специальности 080110 «Экономика и бухгалтерский учет». (В группе 31 человек, студенты первого года обучения, группа эмоционально уравновешенная, уровень восприятия материала высокий).
С учетом возможностей восприятия учебного материала определены следующие цели урока:
Обучающая – изучение свойств геометрических тел в пространстве на примере конуса, цилиндра, шара и сферы.
Развивающая – развитие пространственных представлений учащихся, усвоение способов вычисления геометрических величин и дальнейшее развитие логического мышления.
Воспитывающая – воспитать сознательное отношение к учебе,
усидчивость, аккуратность, эстетическое восприятие окружающего мира.
Исходя из психолого-педагогической характеристики группы, для реализации учебной цели использовались следующие формы и методы работы на уроке
при актуализации опорных знаний:
фронтально повторили вопросы, связанные с понятием основных фигур на плоскости, вычислением значений геометрических величин.
при формировании умений и навыков:
в процессе изучения нового материала происходило многократное закрепление – это проявилось в решении нескольких типичных задач, проведении математического диктанта, заполнении контрольно – обобщающей таблицы, и фронтального опроса по изученной теме;
для реализации взаимоконтроля студентов был разработан слайд с вопросами (математический диктант) и для организации самоконтроля предложена контрольно – обобщающая таблица. Кроме того, студенты были разбиты на три группы, каждой из которых было поручено подготовить доклад и презентацию по одной из пространственных фигур, каждому учащемуся было предложено попытаться сделать эти фигуры из подручных материалов или принести предметы, имеющие форму тел вращения.
для усиления практической направленности:
Считаю, что учебная цель реализована. Группой было закреплено умение вычислять значения геометрических величин и изображать пространственные фигуры.
Неоднократное повторение основных моментов новой темы способствовало лучшему запоминанию и усвоению материала, а тем самым развитию мышления.
Отклонения от плана урока не было.
Считаю, что урок удался.
infourok.ru
Слайд 1
Тела вращения. Цилиндр, конус, шар Выполнил: Попоудин Кирилл 6 В классСлайд 2
Начало исследованию объемных тел положил древнегреческий математик Евклид. Главный труд Евклида – «Начала» (лат. Elementa) - посвящен построению геометрии и состоит из 13-ти книг, к которым присоединяют две книги о пяти правильных многогранниках.
Слайд 3
Шар Шар - это пространственная фигура. Поверхность шара называют сферой . Слово «Сфера» произошло от греческого слова «Сфайра» которое переводится как «Мяч». Сфера – это оболочка шара. Сфера обладает очень интересным свойством - все её точки одинаково удалены от центра шара. Отрезок, соединяющий любую точку сферы с центром шара, называется радиусом шара . Отрезок, соединяющий две точки сферы и проходящий через центр шара, называется диаметром шара . Диаметр шара равен двум радиусам. Шар – это тело, состоящее из всех точек пространства, которые находятся на расстоянии, не большем данного от данной точки. Эта точка называется центром шара , а данное расстояние – радиусом шара .
Слайд 4
Свойства шара Шар является телом вращения, так же как конус и цилиндр. Шар получается при вращении полукруга вокруг его диаметра как оси. Всякое сечение шара плоскостью есть круг. Радиус сечения тем больше, чем ближе секущая плоскости к центру шара. Наибольший радиус имеет сечение плоскостью, проходящей через центр шара. Радиус этого круга равен радиусу шара. Плоскость, проходящая через центр шара, называется диаметральной плоскостью. Сечение шара диаметральной плоскостью, называется большим кругом, а сечение сферы – большой окружностью. Площадь поверхности шара можно найти по формулам: S = 4 πr2 S = πd2, Объём шара находится по формуле: V = 4 / 3 πr3, где r – радиус шара, d – диаметр шара.
Слайд 5
Шар - это наиболее знакомая вам геометрическая фигура. Мяч, глобус- это сфера, а вот арбуз, апельсин. Солнце, Луна, Земля и остальные планеты имеют форму немного сплющенного шара. Примеры предметов имеющих форму шара.
Слайд 6
Цилиндр Цилиндр – является телом вращения, так же как конус и шар, это пространственная или объёмная фигура, которая получается при вращении прямоугольника вокруг его стороны. Полученная цилиндрическая поверхность называется боковой поверхностью цилиндра, а круги – основаниями цилиндра. Слово «Цилиндр» произошло от греческого слова «Кюлиндрос», означающего «Валик», «Каток». Высота цилиндра - это расстояние между основаниями, радиус цилиндра - радиус круга, является основанием цилиндра.
Слайд 7
Свойства цилиндра Сечение цилиндра плоскостью, проходящей через ось цилиндра, называется осевым сечением. Сечение цилиндра, параллельные его оси, являются прямоугольниками. Сечение цилиндра плоскостью, параллельной основаниям – круг, равный основаниям. Основания цилиндра равны и лежат в параллельных плоскостях. Образующие цилиндра равны и параллельны. Площадь поверхности цилиндра. Боковая поверхность цилиндра составлена из образующих. Полная поверхность цилиндра состоит из оснований и боковой поверхности. Sполн = 2Sосн + Sбок; Sосн = π ∙R2; Sбок = 2 π ∙R∙Н Sполн = 2 π R∙(R + Н)
Слайд 8
На рубеже 18-19 веков мужчины многих стран носили твёрдые шляпы с небольшими полями, которые так и назывались цилиндрами из-за большого сходства с геометрической фигурой цилиндром. Примеры предметов имеющих форму шара.
Слайд 9
Конус Круговой конус - это тело, состоящее из круга ( основание конуса ), точки, которая не лежит в плоскости этого круга ( вершина конуса) и всех отрезков, которые соединяют вершину конуса с точками основания. Конус, как шар и цилиндр, является пространственной фигурой. Конус, в отличие от цилиндра, имеет вершину. Слово «Конус» произошло от греческого слова «Конос» означающего сосновую шишку. Элементы конуса Виды конусов Прямой и косой круговой конусы с равным основанием и высотой. Эти конусы имеют равный объём.
Слайд 10
Свойства конуса Сечение конуса плоскостью, который проходит через вершину конуса – это равнобедренный треугольник , боковые стороны этого треугольника являются образующими конуса. Плоскость, которая параллельна основанию конуса и которая пересекает конус, отсекает от него конус меньшего размера. Оставшаяся часть является усеченным конусом . Когда основание конуса является многоугольником – это уже пирамида . Площадь боковой поверхности конуса определяют с помощью формулы: S= π R·l , Полная площадь поверхности конуса (то есть сумма площадей боковой поверхности и основания) определяют с помощью формулы: S= π R(l+R), где R - радиус основания конуса, l - длина образующей.
Слайд 11
Предметы имеющие форму конуса. Воронка Дорожные конусы Остриё иглы Суховская башня Абажур в виде усеченного конуса Коническая крыша
nsportal.ru
Разделы: Математика
Цели урока:
Образовательные: ввести понятия цилиндра, конуса и шара, познакомить учащихся с формулами нахождения площадей тел вращения, сформировать умения применять формулы (полученные знания) при решении задач на цилиндр, конус и шар;
Воспитательные: воспитание внимательности у учащихся.
Развивающие: развитие пространственного воображения, логического мышления, культуры устной математической речи.
План урока:
Оборудование: Компьютер, проектор, экран.
Ход урока
I. Организационный момент.
II. Объяснение нового материала.
- Сегодня на уроке мы познакомимся с новыми для вас понятиями: понятием цилиндра, конуса и сферы, площадями боковых поверхностей данных тел и рассмотрим сечения цилиндра и конуса различными плоскостями, а также взаимное расположение сферы и плоскости.
1. Начнем мы с понятия цилиндра.
Рассмотрим две параллельные плоскости 
и 
и окружность L с центром в точке O
радиуса r, расположенную в плоскости (слайд 2). Через каждую
точку окружности L проведем прямую,
перпендикулярную к плоскости .
Отрезки этих прямых, заключенные между
плоскостям и , образуют цилиндрическую
поверхность. Сами отрезки называются образующими
цилиндрической поверхности.
Тело, ограниченное цилиндрической поверхностью и двумя кругами с границами L и L1, называется цилиндром (слайд 2).
Цилиндрическая поверхность называется боковой поверхностью цилиндра, а круги – основаниями цилиндра.
Образующие цилиндрической поверхности называются образующими цилиндра, прямая OO1 – осью цилиндра.
Все образующие цилиндра параллельны и равны друг другу. Почему? (как отрезки параллельных прямых, заключенные между параллельными плоскостями).
Длина образующей называется высотой цилиндра, а радиус основания – радиусом цилиндра.
Ребята, давайте изобразим в своих тетрадях цилиндр и запишем его определение.
Цилиндр может быть получен вращением прямоугольника вокруг одной из его сторон (слайд 2).
Слайд 3. Ребята, посмотрите,
пожалуйста, на рисунок. Слева у нас изображен
цилиндр, а справа- развертка боковой поверхности
цилиндра. Оказывается, что за площадь боковой
поверхности цилиндра принимается площадь ее
развертки, т.е. площадь боковой поверхности
цилиндра радиуса r и высоты h равна произведению
длины окружности на высоту цилиндра. Запишем это
себе в тетрадь: 
. Как вы думаете, чему равна площадь
полной поверхности цилиндра? (
).
2. Понятие конуса.
Рассмотрим окружность L с центром O и прямую OP, перпендикулярную к плоскости этой окружности (слайд 4).Изображаем у себя в тетрадях. Каждую точку окружности соединим отрезком с точкой P. Делаем все вместе со мной. Поверхность, образованная этими отрезками, называется конической поверхностью, а сами отрезки – образующими конической поверхности.
Тело, ограниченное конической поверхностью и кругом с границей L, называется конусом (слайд 4). Записываем себе определение конуса под диктовку.
Коническая поверхность называется боковой поверхностью конуса, а круг – основанием конуса. Точка P называется вершиной конуса, а образующие конической поверхности – образующими конуса. Отрезок OP конуса называется высотой конуса.
Конус может быть получен вращением прямоугольного треугольника вокруг одного из его катетов (слайд 4).
Теперь давайте найдем площадь полной
поверхности конуса. Какие будут предложения?
(площадь полной поверхности конуса равна сумме
площадей боковой поверхности и основания) Чему
равна площадь основания конуса? (
) А площадь боковой
поверхности конуса равна произведению половины
длины окружности основания на образующую, т.е. 
(пояснить).
Тогда получаем, что 
.
Об усеченном конусе вы прочтете дома (стр.125) и сделаете конспект данного пункта.
3. Понятие сфера и шар.
- Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки (слайд 6).
Данная точка называется центром сферы, а данное расстояние – радиусом сферы. Отрезок, соединяющий две точки сферы и проходящей через ее центр, называется диаметром сферы.
Сфера может быть получена вращением полуокружности вокруг ее диаметра (слайд 6).
Тело, ограниченное сферой, называется шаром. Центр, радиус и диаметр сферы называются также центром, радиусом и сферой шара.
А теперь, ребята, давайте выведем уравнение сферы радиуса R с центром в точке C(x0, y0, z0). Изображаем в тетрадях рисунок такой же как у меня (слайд 7).
Расстояние от произвольной точки M (x, y, z) до
точки C вычисляется по формуле 
. Если точка M лежит на
данной сфере, то 
или
, т.е. координаты точки M удовлетворяют уравнению 
.
Если же точка M (x, y, z) не лежит на данной
сфере, то 
,
т.е. координаты точки M не удовлетворяют
уравнению. Следовательно, в прямоугольной
системе координат уравнение сферы радиуса R с
центром в точке C(x0, y0, z0)
имеет вид .
Запишем это себе в тетрадь. У кого есть вопросы?
- Рассмотрим сечения цилиндра различными плоскостями. Если секущая плоскость проходит через ось цилиндра, то сечение представляет собой прямоугольник, две стороны которого – образующие, а две другие – диаметры оснований цилиндра (слайд 8). Такое сечение называется осевым.
Если секущая плоскость перпендикулярна к оси цилиндра, то сечение является кругом (слайд 8). Изображаем у себя в тетрадях.
- Рассмотрим сечения конуса различными плоскостями. Если секущая плоскость проходит через ось конуса, то сечение представляет собой равнобедренный треугольник (почему?), основание которого – диаметр основания конуса, а боковые стороны – образующие конуса. Такое сечение называется осевым.
Если секущая плоскость перпендикулярна к оси конуса, то сечение представляет собой круг, расположенным на оси конуса. Изображаем у себя в тетрадях сечения конуса. Давайте сверим рисунки, посмотрите на экран (слайд 8).
- О взаимном расположении сферы и плоскости вы узнаете самостоятельно, сейчас поговорим о касательной плоскости к сфере.
Записываем определение: плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка называется точкой касания плоскости и сферы (слайд 10).
- Касательная плоскость к сфере обладает следующим свойством:
Теорема. Радиус сферы, проведенный в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.
Доказательство.
Вернемся к нашему рисунку. Докажем, что радиус 
перпендикулярен к плоскости 
.
Предположим, что это не так. Тогда радиус является
наклонной к плоскости , и, следовательно, расстояние от центра
сферы до плоскости меньше радиуса сферы. Поэтому сфера и
плоскость пересекаются по окружности. Но это
противоречит тому, что плоскость – касательная, т.е. сфера и
плоскость
имеют только одну общую точку. Полученное
противоречие доказывает, что радиус
перпендикулярен к плоскости . Теорема доказана.
Верна и обратная теорема. Давайте сформулируем ее вместе (если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащий на сфере, то эта плоскость является касательной к сфере)
Формула для вычисления площади сферы: 
.
III. Закрепление нового материала.
Решим задачу 539 (слайд 11, слайд 14).
Задача 539. Сколько понадобится краски, чтобы покрасить бак цилиндрической формы с диаметром основания 1,5 м и высотой 3 м, если на один квадратный метр расходуется 200 г краски?
| Вопросы учителя | Ответы учащихся |
| Что нужно найти? | Сколько понадобится краски, чтобы покрасить бак цилиндрической формы с диаметром основания 1,5 м и высотой 3 м, если на один квадратный метр расходуется 200 г краски? |
| Как будем находить? | Давайте сначала найдем площадь поверхности цилиндра. |
| Сразу условимся, что бак будет с крышкой. Тогда будем находить площадь полной поверхности цилиндра или боковой поверхности цилиндра? | Площадь полной поверхности цилиндра. |
| А что потом? | Полученную площадь умножим на 200 г. |
| Запишем ответ |
Сейчас проверим, как вы усвоили материал. (В зависимости от условий проведения урока тест может быть представлен учащимся в электронном варианте или в печатном.)
Решите тест (печатный вариант). Я вам сейчас выдам таблицу, в первой строке таблицы записаны номера заданий, во второй строке вы пишете номера правильных ответов.
Задания для теста.
IV. Постановка домашнего задания и подведение итогов урока.
Домашнее задание: учебник глава VI (выучить основные определения, теоремы), задача 541
Итоги: на данном занятии мы познакомились с такими понятиями как цилиндр, конус, шар и сферы (показать слайды 2, 4 и 6).
xn--i1abbnckbmcl9fb.xn--p1ai
