«Реферат по математике на тему «Число е»». Реферат на тему число е
Информационный доклад-сообщение в 10-м классе по теме: "Число е"
ПЕРВУШКИН БОРИС НИКОЛАЕВИЧ
ЧОУ «Санкт-Петербургская Школа «Тет-а-Тет»
Учитель Математики Высшей категории
Число e
Число  впервые появилось в математике как нечто незначительное. Это случилось в 1618 г. В приложении к работе Непера (Napier) по логарифмам была дана таблица натуральных логарифмов различных чисел. Однако никто не понял, что это логарифмы по основанию
впервые появилось в математике как нечто незначительное. Это случилось в 1618 г. В приложении к работе Непера (Napier) по логарифмам была дана таблица натуральных логарифмов различных чисел. Однако никто не понял, что это логарифмы по основанию  , так как в понятие логарифма того времени такая вещь как основание не входила. Это сейчас мы называем логарифмом степень, в которую нужно возвести основание, чтобы получить требуемое число. Мы еще вернемся к этому позже. Таблица в приложении скорее всего была сделана Отредом (Ougthred), хотя автор ее не был указан. Через несколько лет, в 1624 г., в математической литературе снова появляется
, так как в понятие логарифма того времени такая вещь как основание не входила. Это сейчас мы называем логарифмом степень, в которую нужно возвести основание, чтобы получить требуемое число. Мы еще вернемся к этому позже. Таблица в приложении скорее всего была сделана Отредом (Ougthred), хотя автор ее не был указан. Через несколько лет, в 1624 г., в математической литературе снова появляется  , но опять-таки завуалированно. В этом году Бриггс (Briggs) дал численное приближение десятичного логарифма
, но опять-таки завуалированно. В этом году Бриггс (Briggs) дал численное приближение десятичного логарифма  , но само число
, но само число  в его работе не упоминается.
в его работе не упоминается.
Следующее появление числа  снова cомнительно. В 1647 г. Сен-Винсент (Saint-Vincent) вычислил площадь сектора гиперболы. Понимал ли он связь с логарифмами, остается только догадываться, но даже если понимал, то вряд ли он мог прийти к самому числу
снова cомнительно. В 1647 г. Сен-Винсент (Saint-Vincent) вычислил площадь сектора гиперболы. Понимал ли он связь с логарифмами, остается только догадываться, но даже если понимал, то вряд ли он мог прийти к самому числу  . Только к 1661 г. Гюйгенс (Huygens) понял связь между равнобочной гиперболой и логарифмами. Он доказал, что площадь под графиком равнобочной гиперболы
. Только к 1661 г. Гюйгенс (Huygens) понял связь между равнобочной гиперболой и логарифмами. Он доказал, что площадь под графиком равнобочной гиперболы  равнобочной гиперболы на промежутке от 1 до
равнобочной гиперболы на промежутке от 1 до  равна 1. Это свойство делает
равна 1. Это свойство делает  основанием натуральных логарифмов, но это не понимали математики того времени, однако они медленно приближались к этому пониманию.
основанием натуральных логарифмов, но это не понимали математики того времени, однако они медленно приближались к этому пониманию.
Гюйгенс сделал следующий шаг в 1661 г. Он определил кривую, которую назвал логарифмической (в нашей терминологии мы будем называть ее экспоненциальной). Это кривая вида  . И снова появляется десятичный логарифм
. И снова появляется десятичный логарифм  , который Гюйгенс находит с точностью до 17 десятичных цифр. Однако он возник у Гюйгенса как некая константа и не был связан с логарифмом числа (итак, снова подошли вплотную к
, который Гюйгенс находит с точностью до 17 десятичных цифр. Однако он возник у Гюйгенса как некая константа и не был связан с логарифмом числа (итак, снова подошли вплотную к  , но само число
, но само число  остается неузнанным).
остается неузнанным).
В дальнейших работах по логарифмам опять-таки число  не появляется в явном виде. Однако изучение логарифмов продолжается. В 1668 г. Никола Меркатор (Nicolaus Mercator) опубликовал работуLogarithmotechnia, которая содержит разложение в ряд
не появляется в явном виде. Однако изучение логарифмов продолжается. В 1668 г. Никола Меркатор (Nicolaus Mercator) опубликовал работуLogarithmotechnia, которая содержит разложение в ряд  . В этой работе Меркатор впервые использует название “натуральный логарифм” для логарифма по основанию
. В этой работе Меркатор впервые использует название “натуральный логарифм” для логарифма по основанию  . Число
. Число  явно опять не появляется, а остается неуловимым где-то в стороне.
явно опять не появляется, а остается неуловимым где-то в стороне.
Удивительно, что число  в явном виде впервые возникает не в связи с логарифмами, а в связи с бесконечными произведениями. В 1683 г. Якоб Бернулли пытается найти
в явном виде впервые возникает не в связи с логарифмами, а в связи с бесконечными произведениями. В 1683 г. Якоб Бернулли пытается найти

Он использует биномиальную теорему для доказательства того, что этот предел находится между 2 и 3, и это мы можем рассматривать как первое приближение числа  . Хотя мы принимаем это за определение
. Хотя мы принимаем это за определение  , это первый случай, когда число определяется как предел. Бернулли, конечно, не понял связи между своей работой и работами по логарифмам.
, это первый случай, когда число определяется как предел. Бернулли, конечно, не понял связи между своей работой и работами по логарифмам.
Ранее упоминалось, что логарифмы в начале их изучения никак не связывались с экспонентами. Конечно, из уравнения  мы находим, что
мы находим, что  , но это гораздо более поздний способ восприятия. Здесь мы в самом деле подразумеваем под логарифмом функцию, тогда как сначала логарифм рассматривался только как число, которое помогало в вычислениях. Возможно, Якоб Бернулли первым понял, что логарифмическая функция является обратной показательной. С другой стороны, первым, кто связал логарифмы и степени, мог быть Джеймс Грегори (Games Gregory). В 1684 г. он определенно осознал связь между логарифмами и степенями, но, возможно, он был не первым.
, но это гораздо более поздний способ восприятия. Здесь мы в самом деле подразумеваем под логарифмом функцию, тогда как сначала логарифм рассматривался только как число, которое помогало в вычислениях. Возможно, Якоб Бернулли первым понял, что логарифмическая функция является обратной показательной. С другой стороны, первым, кто связал логарифмы и степени, мог быть Джеймс Грегори (Games Gregory). В 1684 г. он определенно осознал связь между логарифмами и степенями, но, возможно, он был не первым.
Мы знаем, что число  появилось в том виде, как сейчас, в 1690 г. Лейбниц в письме к Гюйгенсу использовал для него обозначение
появилось в том виде, как сейчас, в 1690 г. Лейбниц в письме к Гюйгенсу использовал для него обозначение  . Наконец у
. Наконец у  появилось обозначение (хотя оно не совпадало с современным), и это обозначение было признано.
появилось обозначение (хотя оно не совпадало с современным), и это обозначение было признано.
В 1697 г. Иоганн Бернулли начинает изучение показательной функции и публикует Principia calculi exponentialum seu percurrentium. В этой работе вычисляются суммы различных экспоненциальных рядов, и получены некоторые результаты их почленным интегрированием.
Эйлер (Euler) ввел так много математических обозначений, чтонеудивительно, что обозначение  также принадлежит ему. Кажется смешным утверждение, что он использовал букву
также принадлежит ему. Кажется смешным утверждение, что он использовал букву  из-за того, что это первая буква его имени. Вероятно, это даже не потому, что
из-за того, что это первая буква его имени. Вероятно, это даже не потому, что  взято от слова “exponential”, а просто это следующая гласная за “a”, а Эйлер уже использовал обозначение “a” в своей работе. Независимо от причины, обозначение
взято от слова “exponential”, а просто это следующая гласная за “a”, а Эйлер уже использовал обозначение “a” в своей работе. Независимо от причины, обозначение  впервые появляется в письме Эйлера Гольдбаху (Goldbach) в 1731 г. Он сделал много открытий, изучая
впервые появляется в письме Эйлера Гольдбаху (Goldbach) в 1731 г. Он сделал много открытий, изучая  в дальнейшем, но только в 1748 г. в Introductio in Analysin infinitorum он дал полное обоснование всем идеям, связанным с
в дальнейшем, но только в 1748 г. в Introductio in Analysin infinitorum он дал полное обоснование всем идеям, связанным с  . Он показал, что
. Он показал, что Эйлер также нашел первые 18 десятичных знаков числа
Эйлер также нашел первые 18 десятичных знаков числа  :
:

правда, не объясняя, как он их получил. Похоже, что он вычислил это значение сам. На самом деле, если взять около 20 членов ряда (1), то получится точность, которую получил Эйлер. Среди других интересных результатов в его работе приведена связь между функциями синус и косинус и комплексной показательной функцией, которую Эйлер вывел из формулы Муавра.
Интересно, что Эйлер нашел даже разложение числа  в непрерывные дроби и привел образцы такого разложения. В частности, он получил
в непрерывные дроби и привел образцы такого разложения. В частности, он получил Эйлер не привел доказательства, что эти дроби так же продолжаются, однако он знал, что если бы такое доказательство было, то оно доказывало бы иррациональность
Эйлер не привел доказательства, что эти дроби так же продолжаются, однако он знал, что если бы такое доказательство было, то оно доказывало бы иррациональность  . Действительно, если бы непрерывная дробь для
. Действительно, если бы непрерывная дробь для  , продолжалась так же, как в приведенном образце, 6,10,14,18,22,26,
, продолжалась так же, как в приведенном образце, 6,10,14,18,22,26, (каждый раз прибавляем по 4), то она никогда бы не прервалась, и
(каждый раз прибавляем по 4), то она никогда бы не прервалась, и  (а значит, и
(а значит, и  ) не могло бы быть рациональным. Очевидно, это первая попытка доказать иррациональность
) не могло бы быть рациональным. Очевидно, это первая попытка доказать иррациональность  .
.
Первым, кто вычислил довольно большое число десятичных знаков числа  , был Шенкс (Shanks) в 1854 г. Глейшер (Glaisher) показал, что первые 137 знаков, вычисленные Шенксом, были верными, однако далее нашел ошибку. Шенкс ее исправил, и было получено 205 десятичных знаков числа
, был Шенкс (Shanks) в 1854 г. Глейшер (Glaisher) показал, что первые 137 знаков, вычисленные Шенксом, были верными, однако далее нашел ошибку. Шенкс ее исправил, и было получено 205 десятичных знаков числа  . В действительности, нужно около120 членов разложения (1), чтобы получить 200 верных знаков числа
. В действительности, нужно около120 членов разложения (1), чтобы получить 200 верных знаков числа  .
.
В 1864 г. Бенджамен Пирс (Peirce) стоял у доски, на которой было написано

В своих лекциях он мог бы сказать своим студентам: “Джентльмены, мы не имеем ни малейшего представления, что бы это значило, но мы можем быть уверены, что это значит что-то очень важное”.
Большинство считает, что Эйлер доказал иррациональность числа  . Однако это сделал Эрмит (Hermite) в 1873 г. До сих пор остается открытым вопрос, является ли число
. Однако это сделал Эрмит (Hermite) в 1873 г. До сих пор остается открытым вопрос, является ли число  алгебраическим. Последний результат в этом направлении — это то, что по крайней мере одно из чисел
алгебраическим. Последний результат в этом направлении — это то, что по крайней мере одно из чисел  и
и  является трансцендентным.
является трансцендентным.
Далее вычисляли следующие десятичные знаки числа  . В 1884 г. Бурман (Boorman) вычислил 346 знаков числа
. В 1884 г. Бурман (Boorman) вычислил 346 знаков числа  , из которых первые 187 совпали со знаками Шенкса, но последующие различались. В 1887 г. Адамс (Adams) вычислил 272 цифры десятичного логарифма
, из которых первые 187 совпали со знаками Шенкса, но последующие различались. В 1887 г. Адамс (Adams) вычислил 272 цифры десятичного логарифма  .
.
kopilkaurokov.ru
Число e | Математика, которая мне нравится
Число  впервые появилось в математике как нечто незначительное. Это случилось в 1618 г. В приложении к работе Непера (Napier) по логарифмам была дана таблица натуральных логарифмов различных чисел. Однако никто не понял, что это логарифмы по основанию
впервые появилось в математике как нечто незначительное. Это случилось в 1618 г. В приложении к работе Непера (Napier) по логарифмам была дана таблица натуральных логарифмов различных чисел. Однако никто не понял, что это логарифмы по основанию  , так как в понятие логарифма того времени такая вещь как основание не входила. Это сейчас мы называем логарифмом степень, в которую нужно возвести основание, чтобы получить требуемое число. Мы еще вернемся к этому позже. Таблица в приложении скорее всего была сделана Отредом (Ougthred), хотя автор ее не был указан. Через несколько лет, в 1624 г., в математической литературе снова появляется
, так как в понятие логарифма того времени такая вещь как основание не входила. Это сейчас мы называем логарифмом степень, в которую нужно возвести основание, чтобы получить требуемое число. Мы еще вернемся к этому позже. Таблица в приложении скорее всего была сделана Отредом (Ougthred), хотя автор ее не был указан. Через несколько лет, в 1624 г., в математической литературе снова появляется  , но опять-таки завуалированно. В этом году Бриггс (Briggs) дал численное приближение десятичного логарифма
, но опять-таки завуалированно. В этом году Бриггс (Briggs) дал численное приближение десятичного логарифма  , но само число
, но само число  в его работе не упоминается.
в его работе не упоминается.
Следующее появление числа  снова cомнительно. В 1647 г. Сен-Винсент (Saint-Vincent) вычислил площадь сектора гиперболы. Понимал ли он связь с логарифмами, остается только догадываться, но даже если понимал, то вряд ли он мог прийти к самому числу
снова cомнительно. В 1647 г. Сен-Винсент (Saint-Vincent) вычислил площадь сектора гиперболы. Понимал ли он связь с логарифмами, остается только догадываться, но даже если понимал, то вряд ли он мог прийти к самому числу  . Только к 1661 г. Гюйгенс (Huygens) понял связь между равнобочной гиперболой и логарифмами. Он доказал, что площадь под графиком равнобочной гиперболы
. Только к 1661 г. Гюйгенс (Huygens) понял связь между равнобочной гиперболой и логарифмами. Он доказал, что площадь под графиком равнобочной гиперболы  равнобочной гиперболы на промежутке от
равнобочной гиперболы на промежутке от  до
до  равна
равна  . Это свойство делает
. Это свойство делает  основанием натуральных логарифмов, но это не понимали математики того времени, однако они медленно приближались к этому пониманию.
основанием натуральных логарифмов, но это не понимали математики того времени, однако они медленно приближались к этому пониманию.
Гюйгенс сделал следующий шаг в 1661 г. Он определил кривую, которую назвал логарифмической (в нашей терминологии мы будем называть ее экспоненциальной). Это кривая вида  . И снова появляется десятичный логарифм
. И снова появляется десятичный логарифм  , который Гюйгенс находит с точностью до 17 десятичных цифр. Однако он возник у Гюйгенса как некая константа и не был связан с логарифмом числа (итак, снова подошли вплотную к
, который Гюйгенс находит с точностью до 17 десятичных цифр. Однако он возник у Гюйгенса как некая константа и не был связан с логарифмом числа (итак, снова подошли вплотную к  , но само число
, но само число  остается неузнанным).
остается неузнанным).
В дальнейших работах по логарифмам опять-таки число  не появляется в явном виде. Однако изучение логарифмов продолжается. В 1668 г. Никола Меркатор (Nicolaus Mercator) опубликовал работу Logarithmotechnia, которая содержит разложение в ряд
не появляется в явном виде. Однако изучение логарифмов продолжается. В 1668 г. Никола Меркатор (Nicolaus Mercator) опубликовал работу Logarithmotechnia, которая содержит разложение в ряд  . В этой работе Меркатор впервые использует название “натуральный логарифм” для логарифма по основанию
. В этой работе Меркатор впервые использует название “натуральный логарифм” для логарифма по основанию  . Число
. Число  явно опять не появляется, а остается неуловимым где-то в стороне.
явно опять не появляется, а остается неуловимым где-то в стороне.
Удивительно, что число  в явном виде впервые возникает не в связи с логарифмами, а в связи с бесконечными произведениями. В 1683 г. Якоб Бернулли пытается найти
в явном виде впервые возникает не в связи с логарифмами, а в связи с бесконечными произведениями. В 1683 г. Якоб Бернулли пытается найти
![Rendered by QuickLaTeX.com \[\lim_{n\to\infty}\left(1+\frac{1}{n}\right)^n.\]](/800/600/http/hijos.ru//wp-content/ql-cache/quicklatex.com-f2c1c79898c92d1ab0bdb9157769768e_l3.png)
Он использует биномиальную теорему для доказательства того, что этот предел находится между  и
и  , и это мы можем рассматривать как первое приближение числа
, и это мы можем рассматривать как первое приближение числа  . Хотя мы принимаем это за определение
. Хотя мы принимаем это за определение  , это первый случай, когда число определяется как предел. Бернулли, конечно, не понял связи между своей работой и работами по логарифмам.
, это первый случай, когда число определяется как предел. Бернулли, конечно, не понял связи между своей работой и работами по логарифмам.
Ранее упоминалось, что логарифмы в начале их изучения никак не связывались с экспонентами. Конечно, из уравнения  мы находим, что
мы находим, что  , но это гораздо более поздний способ восприятия. Здесь мы в самом деле подразумеваем под логарифмом функцию, тогда как сначала логарифм рассматривался только как число, которое помогало в вычислениях. Возможно, Якоб Бернулли первым понял, что логарифмическая функция является обратной показательной. С другой стороны, первым, кто связал логарифмы и степени, мог быть Джеймс Грегори (Games Gregory). В 1684 г. он определенно осознал связь между логарифмами и степенями, но, возможно, он был не первым.
, но это гораздо более поздний способ восприятия. Здесь мы в самом деле подразумеваем под логарифмом функцию, тогда как сначала логарифм рассматривался только как число, которое помогало в вычислениях. Возможно, Якоб Бернулли первым понял, что логарифмическая функция является обратной показательной. С другой стороны, первым, кто связал логарифмы и степени, мог быть Джеймс Грегори (Games Gregory). В 1684 г. он определенно осознал связь между логарифмами и степенями, но, возможно, он был не первым.
Мы знаем, что число  появилось в том виде, как сейчас, в 1690 г. Лейбниц в письме к Гюйгенсу использовал для него обозначение
появилось в том виде, как сейчас, в 1690 г. Лейбниц в письме к Гюйгенсу использовал для него обозначение  . Наконец у
. Наконец у  появилось обозначение (хотя оно не совпадало с современным), и это обозначение было признано.
появилось обозначение (хотя оно не совпадало с современным), и это обозначение было признано.
В 1697 г. Иоганн Бернулли начинает изучение показательной функции и публикует Principia calculi exponentialum seu percurrentium. В этой работе вычисляются суммы различных экспоненциальных рядов, и получены некоторые результаты их почленным интегрированием.
Эйлер (Euler) ввел так много математических обозначений, чтонеудивительно, что обозначение  также принадлежит ему. Кажется смешным утверждение, что он использовал букву
также принадлежит ему. Кажется смешным утверждение, что он использовал букву  из-за того, что это первая буква его имени. Вероятно, это даже не потому, что
из-за того, что это первая буква его имени. Вероятно, это даже не потому, что  взято от слова “exponential”, а просто это следующая гласная за “a”, а Эйлер уже использовал обозначение “a” в своей работе. Независимо от причины, обозначение
взято от слова “exponential”, а просто это следующая гласная за “a”, а Эйлер уже использовал обозначение “a” в своей работе. Независимо от причины, обозначение  впервые появляется в письме Эйлера Гольдбаху (Goldbach) в 1731 г. Он сделал много открытий, изучая
впервые появляется в письме Эйлера Гольдбаху (Goldbach) в 1731 г. Он сделал много открытий, изучая  в дальнейшем, но только в 1748 г. в Introductio in Analysin infinitorum он дал полное обоснование всем идеям, связанным с
в дальнейшем, но только в 1748 г. в Introductio in Analysin infinitorum он дал полное обоснование всем идеям, связанным с  . Он показал, что
. Он показал, что
![Rendered by QuickLaTeX.com \[e=1+\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}+\ldots\mbox{ \rm и } e=\lim_{n\to\infty}\left(1+\frac{1}{n}\right)^n.\eqno(1)\]](/800/600/http/hijos.ru//wp-content/ql-cache/quicklatex.com-1aa5934667130ee9d9bdb5933f510358_l3.png)
Эйлер также нашел первые 18 десятичных знаков числа  :
:
![Rendered by QuickLaTeX.com \[e=2,718281828459045235\ldots,\]](/800/600/http/hijos.ru//wp-content/ql-cache/quicklatex.com-27cde3ed0b87c21801b7279bb364ae06_l3.png)
правда, не объясняя, как он их получил. Похоже, что он вычислил это значение сам. На самом деле, если взять около 20 членов ряда (1), то получится точность, которую получил Эйлер. Среди других интересных результатов в его работе приведена связь между функциями синус и косинус и комплексной показательной функцией, которую Эйлер вывел из формулы Муавра.
Интересно, что Эйлер нашел даже разложение числа  в непрерывные дроби и привел образцы такого разложения. В частности, он получил
в непрерывные дроби и привел образцы такого разложения. В частности, он получил и
и  Эйлер не привел доказательства, что эти дроби так же продолжаются, однако он знал, что если бы такое доказательство было, то оно доказывало бы иррациональность
Эйлер не привел доказательства, что эти дроби так же продолжаются, однако он знал, что если бы такое доказательство было, то оно доказывало бы иррациональность  . Действительно, если бы непрерывная дробь для
. Действительно, если бы непрерывная дробь для  продолжалась так же, как в приведенном образце,
продолжалась так же, как в приведенном образце,  (каждый раз прибавляем по
(каждый раз прибавляем по  ), то она никогда бы не прервалась, и
), то она никогда бы не прервалась, и  (а значит, и
(а значит, и  ) не могло бы быть рациональным. Очевидно, это первая попытка доказать иррациональность
) не могло бы быть рациональным. Очевидно, это первая попытка доказать иррациональность  .
.
Первым, кто вычислил довольно большое число десятичных знаков числа  , был Шенкс (Shanks) в 1854 г. Глейшер (Glaisher) показал, что первые 137 знаков, вычисленные Шенксом, были верными, однако далее нашел ошибку. Шенкс ее исправил, и было получено 205 десятичных знаков числа
, был Шенкс (Shanks) в 1854 г. Глейшер (Glaisher) показал, что первые 137 знаков, вычисленные Шенксом, были верными, однако далее нашел ошибку. Шенкс ее исправил, и было получено 205 десятичных знаков числа  . В действительности, нужно около120 членов разложения (1), чтобы получить 200 верных знаков числа
. В действительности, нужно около120 членов разложения (1), чтобы получить 200 верных знаков числа  .
.
В 1864 г. Бенджамен Пирс (Peirce) стоял у доски, на которой было написано
![Rendered by QuickLaTeX.com \[i^{-i}=\sqrt{e^{\pi}}.\]](/800/600/http/hijos.ru//wp-content/ql-cache/quicklatex.com-f7c2b55076b95685514f6e301e746120_l3.png)
В своих лекциях он мог бы сказать своим студентам: “Джентльмены, мы не имеем ни малейшего представления, что бы это значило, но мы можем быть уверены, что это значит что-то очень важное”.
Большинство считает, что Эйлер доказал иррациональность числа  . Однако это сделал Эрмит (Hermite) в 1873 г. До сих пор остается открытым вопрос, является ли число
. Однако это сделал Эрмит (Hermite) в 1873 г. До сих пор остается открытым вопрос, является ли число  алгебраическим. Последний результат в этом направлении — это то, что по крайней мере одно из чисел
алгебраическим. Последний результат в этом направлении — это то, что по крайней мере одно из чисел  и
и  является трансцендентным.
является трансцендентным.
Далее вычисляли следующие десятичные знаки числа  . В 1884 г. Бурман (Boorman) вычислил 346 знаков числа
. В 1884 г. Бурман (Boorman) вычислил 346 знаков числа  , из которых первые 187 совпали со знаками Шенкса, но последующие различались. В 1887 г. Адамс (Adams) вычислил 272 цифры десятичного логарифма
, из которых первые 187 совпали со знаками Шенкса, но последующие различались. В 1887 г. Адамс (Adams) вычислил 272 цифры десятичного логарифма  .
.
J.J.Connor, E.F.Robertson. The number e. Перевод статьи http://www-history.mcs.st-andrews.ac.uk/history/HistTopics/e.html
hijos.ru
Число е
ПЕРВУШКИН БОРИС НИКОЛАЕВИЧ
ЧОУ «Санкт-Петербургская Школа «Тет-а-Тет»
Учитель Математики Высшей категории
Число e
Число  впервые появилось в математике как нечто незначительное. Это случилось в 1618 г. В приложении к работе Непера (Napier) по логарифмам была дана таблица натуральных логарифмов различных чисел. Однако никто не понял, что это логарифмы по основанию
впервые появилось в математике как нечто незначительное. Это случилось в 1618 г. В приложении к работе Непера (Napier) по логарифмам была дана таблица натуральных логарифмов различных чисел. Однако никто не понял, что это логарифмы по основанию  , так как в понятие логарифма того времени такая вещь как основание не входила. Это сейчас мы называем логарифмом степень, в которую нужно возвести основание, чтобы получить требуемое число. Мы еще вернемся к этому позже. Таблица в приложении скорее всего была сделана Отредом (Ougthred), хотя автор ее не был указан. Через несколько лет, в 1624 г., в математической литературе снова появляется
, так как в понятие логарифма того времени такая вещь как основание не входила. Это сейчас мы называем логарифмом степень, в которую нужно возвести основание, чтобы получить требуемое число. Мы еще вернемся к этому позже. Таблица в приложении скорее всего была сделана Отредом (Ougthred), хотя автор ее не был указан. Через несколько лет, в 1624 г., в математической литературе снова появляется  , но опять-таки завуалированно. В этом году Бриггс (Briggs) дал численное приближение десятичного логарифма
, но опять-таки завуалированно. В этом году Бриггс (Briggs) дал численное приближение десятичного логарифма  , но само число
, но само число  в его работе не упоминается.
в его работе не упоминается.
Следующее появление числа  снова cомнительно. В 1647 г. Сен-Винсент (Saint-Vincent) вычислил площадь сектора гиперболы. Понимал ли он связь с логарифмами, остается только догадываться, но даже если понимал, то вряд ли он мог прийти к самому числу
снова cомнительно. В 1647 г. Сен-Винсент (Saint-Vincent) вычислил площадь сектора гиперболы. Понимал ли он связь с логарифмами, остается только догадываться, но даже если понимал, то вряд ли он мог прийти к самому числу  . Только к 1661 г. Гюйгенс (Huygens) понял связь между равнобочной гиперболой и логарифмами. Он доказал, что площадь под графиком равнобочной гиперболы
. Только к 1661 г. Гюйгенс (Huygens) понял связь между равнобочной гиперболой и логарифмами. Он доказал, что площадь под графиком равнобочной гиперболы  равнобочной гиперболы на промежутке от 1 до
равнобочной гиперболы на промежутке от 1 до  равна 1. Это свойство делает
равна 1. Это свойство делает  основанием натуральных логарифмов, но это не понимали математики того времени, однако они медленно приближались к этому пониманию.
основанием натуральных логарифмов, но это не понимали математики того времени, однако они медленно приближались к этому пониманию.
Гюйгенс сделал следующий шаг в 1661 г. Он определил кривую, которую назвал логарифмической (в нашей терминологии мы будем называть ее экспоненциальной). Это кривая вида  . И снова появляется десятичный логарифм
. И снова появляется десятичный логарифм  , который Гюйгенс находит с точностью до 17 десятичных цифр. Однако он возник у Гюйгенса как некая константа и не был связан с логарифмом числа (итак, снова подошли вплотную к
, который Гюйгенс находит с точностью до 17 десятичных цифр. Однако он возник у Гюйгенса как некая константа и не был связан с логарифмом числа (итак, снова подошли вплотную к  , но само число
, но само число  остается неузнанным).
остается неузнанным).
В дальнейших работах по логарифмам опять-таки число  не появляется в явном виде. Однако изучение логарифмов продолжается. В 1668 г. Никола Меркатор (Nicolaus Mercator) опубликовал работуLogarithmotechnia, которая содержит разложение в ряд
не появляется в явном виде. Однако изучение логарифмов продолжается. В 1668 г. Никола Меркатор (Nicolaus Mercator) опубликовал работуLogarithmotechnia, которая содержит разложение в ряд  . В этой работе Меркатор впервые использует название “натуральный логарифм” для логарифма по основанию
. В этой работе Меркатор впервые использует название “натуральный логарифм” для логарифма по основанию  . Число
. Число  явно опять не появляется, а остается неуловимым где-то в стороне.
явно опять не появляется, а остается неуловимым где-то в стороне.
Удивительно, что число  в явном виде впервые возникает не в связи с логарифмами, а в связи с бесконечными произведениями. В 1683 г. Якоб Бернулли пытается найти
в явном виде впервые возникает не в связи с логарифмами, а в связи с бесконечными произведениями. В 1683 г. Якоб Бернулли пытается найти

Он использует биномиальную теорему для доказательства того, что этот предел находится между 2 и 3, и это мы можем рассматривать как первое приближение числа  . Хотя мы принимаем это за определение
. Хотя мы принимаем это за определение  , это первый случай, когда число определяется как предел. Бернулли, конечно, не понял связи между своей работой и работами по логарифмам.
, это первый случай, когда число определяется как предел. Бернулли, конечно, не понял связи между своей работой и работами по логарифмам.
Ранее упоминалось, что логарифмы в начале их изучения никак не связывались с экспонентами. Конечно, из уравнения  мы находим, что
мы находим, что  , но это гораздо более поздний способ восприятия. Здесь мы в самом деле подразумеваем под логарифмом функцию, тогда как сначала логарифм рассматривался только как число, которое помогало в вычислениях. Возможно, Якоб Бернулли первым понял, что логарифмическая функция является обратной показательной. С другой стороны, первым, кто связал логарифмы и степени, мог быть Джеймс Грегори (Games Gregory). В 1684 г. он определенно осознал связь между логарифмами и степенями, но, возможно, он был не первым.
, но это гораздо более поздний способ восприятия. Здесь мы в самом деле подразумеваем под логарифмом функцию, тогда как сначала логарифм рассматривался только как число, которое помогало в вычислениях. Возможно, Якоб Бернулли первым понял, что логарифмическая функция является обратной показательной. С другой стороны, первым, кто связал логарифмы и степени, мог быть Джеймс Грегори (Games Gregory). В 1684 г. он определенно осознал связь между логарифмами и степенями, но, возможно, он был не первым.
Мы знаем, что число  появилось в том виде, как сейчас, в 1690 г. Лейбниц в письме к Гюйгенсу использовал для него обозначение
появилось в том виде, как сейчас, в 1690 г. Лейбниц в письме к Гюйгенсу использовал для него обозначение  . Наконец у
. Наконец у  появилось обозначение (хотя оно не совпадало с современным), и это обозначение было признано.
появилось обозначение (хотя оно не совпадало с современным), и это обозначение было признано.
В 1697 г. Иоганн Бернулли начинает изучение показательной функции и публикует Principia calculi exponentialum seu percurrentium. В этой работе вычисляются суммы различных экспоненциальных рядов, и получены некоторые результаты их почленным интегрированием.
Эйлер (Euler) ввел так много математических обозначений, чтонеудивительно, что обозначение  также принадлежит ему. Кажется смешным утверждение, что он использовал букву
также принадлежит ему. Кажется смешным утверждение, что он использовал букву  из-за того, что это первая буква его имени. Вероятно, это даже не потому, что
из-за того, что это первая буква его имени. Вероятно, это даже не потому, что  взято от слова “exponential”, а просто это следующая гласная за “a”, а Эйлер уже использовал обозначение “a” в своей работе. Независимо от причины, обозначение
взято от слова “exponential”, а просто это следующая гласная за “a”, а Эйлер уже использовал обозначение “a” в своей работе. Независимо от причины, обозначение  впервые появляется в письме Эйлера Гольдбаху (Goldbach) в 1731 г. Он сделал много открытий, изучая
впервые появляется в письме Эйлера Гольдбаху (Goldbach) в 1731 г. Он сделал много открытий, изучая  в дальнейшем, но только в 1748 г. в Introductio in Analysin infinitorum он дал полное обоснование всем идеям, связанным с
в дальнейшем, но только в 1748 г. в Introductio in Analysin infinitorum он дал полное обоснование всем идеям, связанным с  . Он показал, что
. Он показал, что Эйлер также нашел первые 18 десятичных знаков числа
Эйлер также нашел первые 18 десятичных знаков числа  :
:

правда, не объясняя, как он их получил. Похоже, что он вычислил это значение сам. На самом деле, если взять около 20 членов ряда (1), то получится точность, которую получил Эйлер. Среди других интересных результатов в его работе приведена связь между функциями синус и косинус и комплексной показательной функцией, которую Эйлер вывел из формулы Муавра.
Интересно, что Эйлер нашел даже разложение числа  в непрерывные дроби и привел образцы такого разложения. В частности, он получил
в непрерывные дроби и привел образцы такого разложения. В частности, он получил Эйлер не привел доказательства, что эти дроби так же продолжаются, однако он знал, что если бы такое доказательство было, то оно доказывало бы иррациональность
Эйлер не привел доказательства, что эти дроби так же продолжаются, однако он знал, что если бы такое доказательство было, то оно доказывало бы иррациональность  . Действительно, если бы непрерывная дробь для
. Действительно, если бы непрерывная дробь для  , продолжалась так же, как в приведенном образце, 6,10,14,18,22,26,
, продолжалась так же, как в приведенном образце, 6,10,14,18,22,26, (каждый раз прибавляем по 4), то она никогда бы не прервалась, и
(каждый раз прибавляем по 4), то она никогда бы не прервалась, и  (а значит, и
(а значит, и  ) не могло бы быть рациональным. Очевидно, это первая попытка доказать иррациональность
) не могло бы быть рациональным. Очевидно, это первая попытка доказать иррациональность  .
.
Первым, кто вычислил довольно большое число десятичных знаков числа  , был Шенкс (Shanks) в 1854 г. Глейшер (Glaisher) показал, что первые 137 знаков, вычисленные Шенксом, были верными, однако далее нашел ошибку. Шенкс ее исправил, и было получено 205 десятичных знаков числа
, был Шенкс (Shanks) в 1854 г. Глейшер (Glaisher) показал, что первые 137 знаков, вычисленные Шенксом, были верными, однако далее нашел ошибку. Шенкс ее исправил, и было получено 205 десятичных знаков числа  . В действительности, нужно около120 членов разложения (1), чтобы получить 200 верных знаков числа
. В действительности, нужно около120 членов разложения (1), чтобы получить 200 верных знаков числа  .
.
В 1864 г. Бенджамен Пирс (Peirce) стоял у доски, на которой было написано

В своих лекциях он мог бы сказать своим студентам: “Джентльмены, мы не имеем ни малейшего представления, что бы это значило, но мы можем быть уверены, что это значит что-то очень важное”.
Большинство считает, что Эйлер доказал иррациональность числа  . Однако это сделал Эрмит (Hermite) в 1873 г. До сих пор остается открытым вопрос, является ли число
. Однако это сделал Эрмит (Hermite) в 1873 г. До сих пор остается открытым вопрос, является ли число  алгебраическим. Последний результат в этом направлении — это то, что по крайней мере одно из чисел
алгебраическим. Последний результат в этом направлении — это то, что по крайней мере одно из чисел  и
и  является трансцендентным.
является трансцендентным.
Далее вычисляли следующие десятичные знаки числа  . В 1884 г. Бурман (Boorman) вычислил 346 знаков числа
. В 1884 г. Бурман (Boorman) вычислил 346 знаков числа  , из которых первые 187 совпали со знаками Шенкса, но последующие различались. В 1887 г. Адамс (Adams) вычислил 272 цифры десятичного логарифма
, из которых первые 187 совпали со знаками Шенкса, но последующие различались. В 1887 г. Адамс (Adams) вычислил 272 цифры десятичного логарифма  .
.
xn--j1ahfl.xn--p1ai
ЧИСЛО Е | Энциклопедия Кругосвет
ЧИСЛО e. Число, приближенно равное 2,718, которое часто встречается в математике и естественных науках. Например, при распаде радиоактивного вещества по истечении времени t от исходного количества вещества остается доля, равная e–kt, где k – число, характеризующее скорость распада данного вещества. Обратная величина 1/k называется средним временем жизни атома данного вещества, так как в среднем атом прежде, чем распасться, существует в течение времени 1/k. Величина 0,693/k называется периодом полураспада радиоактивного вещества, т.е. временем, за которое распадается половина исходного количества вещества; число 0,693 приближенно равно loge 2, т.е. логарифму числа 2 по основанию e. Аналогично, если бактерии в питательной среде размножаются со скоростью, пропорциональной их числу в настоящий момент, то по истечении времени t начальное количество бактерий N превращается в Nekt. Затухание электрического тока I в простом контуре с последовательным соединением, сопротивлением R и индуктивностью L происходит по закону I = I0e–kt, где k = R/L, I0 – сила тока в момент времени t = 0. Аналогичные формулы описывают релаксацию напряжений в вязкой жидкости и затухание магнитного поля. Число 1/k часто называют временем релаксации. В статистике величина e–kt встречается как вероятность того, что за время t не произошло событий, наступающих случайно со средней частотой k событий в единицу времени. Если S – сумма денег, вложенных под r процентов с непрерывным начислением вместо начисления через дискретные промежутки времени, то к моменту времени t первоначальная сумма возрастет до Setr/100.
Причина «вездесущности» числа e заключается в том, что формулы математического анализа, содержащие экспоненциальные функции или логарифмы, записываются проще, если логарифмы брать по основанию e, а не 10 или какому-либо другому основанию. Например, производная от log10 x равна (1/x)log10 e, тогда как производная от loge x равна просто 1/x. Аналогично, производная от 2x равна 2xloge 2, тогда как производная от eх равна просто ex. Это означает, что число e можно определить как основание b, при котором график функции y = logb x имеет в точке x = 1 касательную с угловым коэффициентом, равным 1, или при котором кривая y = bx имеет в x = 0 касательную с угловым коэффициентом, равным 1. Логарифмы по основанию e называются «натуральными» и обозначаются ln x. Иногда их также называют «неперовыми», что неверно, так как в действительности Дж.Непер (1550–1617) изобрел логарифмы с другим основанием: неперов логарифм числа x равен 107 log1/e (x/107) (см. также ЛОГАРИФМ).
Различные комбинации степеней e встречаются в математике так часто, что имеют специальные названия. Таковы, например, гиперболические функции
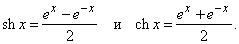
График функции y = ch x называется цепной линией; такую форму имеет подвешенная за концы тяжелая нерастяжимая нить или цепь. Формулы Эйлера

где i2 = –1, связывают число e с тригонометрией. Частный случай x = p приводит к знаменитому соотношению eip + 1 = 0, связывающему 5 наиболее известных в математике чисел.
При вычислении значения e могут быть использованы и некоторые другие формулы (чаще всего пользуются первой из них):

Значение e с 15 десятичными знаками равно 2,718281828459045. В 1953 было вычислено значение e с 3333 десятичными знаками. Символ e для обозначения этого числа был введен в 1731 Л.Эйлером (1707–1783).
Десятичное разложение числа e непериодично (e – иррациональное число). Кроме того, e, как и p, – трансцендентное число (оно не является корнем никакого алгебраического уравнения с рациональными коэффициентами). Это доказал в 1873 Ш.Эрмит. Впервые было показано, что столь естественным образом возникающее в математике число является трансцендентным.
Проверь себя!Ответь на вопросы викторины «Математика»
Как звали математика, который в 19 лет решил задачу, не поддававшуюся усилиям лучших геометров много столетий со времен Евклида?
www.krugosvet.ru
Число e
e— математическая константа, основание натурального логарифма, иррациональное и трансцендентное число.e= 2,718281828459045… Иногда числоeназываютчислом Эйлераилинеперовым числом. Играет важную роль в дифференциальном и интегральном исчислении.
Способы определения
Число e может быть определено несколькими способами.
Через предел:  (второй замечательный предел).
(второй замечательный предел).
Как сумма ряда: 
Как единственное число a, для которого выполняется
Как единственное положительное число a, для которого верно
Свойства
 Данное свойство играет важную роль в решении дифференциальных уравнений. Так, например, единственным решением дифференциального уравненияf'(x) =f(x) является функцияf(x) =cex, гдеc— произвольная константа.
Данное свойство играет важную роль в решении дифференциальных уравнений. Так, например, единственным решением дифференциального уравненияf'(x) =f(x) является функцияf(x) =cex, гдеc— произвольная константа.
Число eиррационально и даже трансцендентно. Это первое число, которое не было выведено как трансцендентное специально, его трансцендентность была доказана только в 1873 году Шарлем Эрмитом. Предполагается, чтоe— нормальное число, т. е. вероятность появления каждой из десяти его цифр одинакова.
eix=cos(x) +isin(x), см. формула Эйлера, в частности
Еще одна формула, связывающая числа еиπ, т.н. "интеграл Пуассона" или "интеграл Гаусса"

История
Данное число иногда называют неперовымв честь шотландского учёного Джона Непера, автора работы «Описание удивительной таблицы логарифмов» (1614 г.). Однако это название не совсем корректно, т. к. у него логарифм числаxбыл равен .
.
Впервые константа негласно присутствует в приложении к переводу на английский язык вышеупомянутой работы Непера, опубликованному в 1618 г. Негласно, потому что там содержится только таблица натуральных логарифмов, сама же константа не определена. Предполагается, что автором таблицы был английский математик Вильям Отред. Саму же константу впервые вывел швейцарский математик Якоб Бернулли при попытке вычислить значение следующего предела:

Первое известное использование этой константы, где она обозначалась буквой b, встречается в письмах Готфрида Лейбница Кристиану Гюйгенсу, 1690 и 1691 гг. Буквуeначал использовать Леонард Эйлер в 1727 г., а первой публикацией с этой буквой была его работа «Механика, или Наука о движении, изложенная аналитически» 1736 г. Соответственно,eиногда называютчислом Эйлера. Хотя впоследствии некоторые учёные использовали буквуc, букваeприменялась чаще и в наши дни является стандартным обозначением.
Почему была выбрана именно буква e, точно неизвестно. Возможно, это связано с тем, что с неё начинается словоexponential(«показательный», «экспоненциальный»). Другое предположение заключается в том, что буквыa,b,cиdуже довольно широко использовались в иных целях, иeбыла первой «свободной» буквой. Неправдоподобно предположение, что Эйлер выбралeкак первую букву в своей фамилии (нем.Euler), поскольку он был очень скромным человеком и всегда старался подчеркнуть значимость труда других людей.
Способы запоминания
Число eможно запомнить по следующему мнемоническому правилу: два и семь, далее два раза год рождения Льва Толстого (1828), затем углы равнобедренного прямоугольного треугольника (45,90и45градусов).
В другом варианте правила eсвязывается с президентом США Эндрю Джексоном: 2 — столько раз избирался, 7 — он был седьмым президентом США, 1828 — год его избрания, повторяется дважды, поскольку Джексон дважды избирался. Затем — опять-таки равнобедренный прямоугольный треугольник.
В ещё одном небезынтересном способе предлагается запомнить число eс точностью до трёх знаков после запятой через «число дьявола»: нужно разделить 666 на число, составленное из цифр 6 − 4, 6 − 2, 6 − 1 (три шестёрки, из которых в обратном порядке удаляются три первые степени двойки): .
.
В четвёртом способе предлагается запомнить eкак .
.
Грубое (с точностью до 0,001), но красивое приближение полагает eравным . Совсем грубое (с точностью 0,01) приближение даётся выражением
. Совсем грубое (с точностью 0,01) приближение даётся выражением .
.
«Правило Боинга»:  даёт неплохую точность 0,0005.
даёт неплохую точность 0,0005.
«Стих»: Мы порхали и блистали, но застряли в перевале; не признали наши крали авторалли.
e = 2.71828 18284 59045 23536 02874 71352 66249 77572 47093 69995 95749 66967 62772 40766 30353 54759 45713 82178 52516 64274 27466 39193 20030 59921 81741 35966 29043 57290 03342 95260 59563 07381 32328 62794 34907 63233 82988 07531 95251 01901 15738 34187 93070 21540 89149 93488 41675 09244 76146 06680 82264 80016 84774 11853 74234 54424 37107 53907 77449 92069 55170 27618 38606 26133 13845 83000 75204 49338 26560 29760 67371 13200 70932 87091 27443 74704 72306 96977 20931 01416 92836 81902 55151 08657 46377 21112 52389 78442 50569 53696 77078 54499 69967 94686 44549 05987 93163 68892 30098 79312 77361 78215 42499 92295 76351 48220 82698 95193 66803 31825 28869 39849 64651 05820 93923 98294 88793 32036 25094 43117 30123 81970 68416 14039 70198 37679 32068 32823 76464 80429 53118 02328 78250 98194 55815 30175 67173 61332 06981 12509 96181 88159 30416 90351 59888 85193 45807 27386 67385 89422 87922 84998 92086 80582 57492 79610 48419 84443 63463 24496 84875 60233 62482 70419 78623 20900 21609 90235 30436 99418 49146 31409 34317 38143 64054 62531 52096 18369 08887 07016 76839 64243 78140 59271 45635 49061 30310 72085 10383 75051 01157 47704 17189 86106 87396 96552 12671 54688 95703 50354 02123 40784 98193 34321 06817 01210 05627 88023 51920
studfiles.net
Исследовательская работа Число е | Образовательный портал EduContest.Net — библиотека учебно-методических материалов
ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА Число е Подготовила: Смирнова Кристина, учащаяся 11 класса МБОУ «Первомайская СОШ им. В.Митты» Научный руководитель: Киргизова Алина Геннадьевна, учитель математики МБОУ «Первомайская СОШ им. В.Митты» 2016 г. ВВЕДЕНИЕ
«Бессмысленное число «е» вновь предстает перед нами, начертанное на этот раз на паутине... Усеянные крохотными капельками, ее липкие нити провисают под тяжестью груза, образуя цепные линии...»
Жан Анри Фабр, книга «Жизнь паука».
Из курса математики мы знаем, числа делятся на натуральные, целые, рациональные, действительные, комплексные. Множество действительных чисел включает множество рациональных и иррациональных чисел. Иррациональные числа невозможно представить в виде обыкновенной дроби, они представляются бесконечными и непериодическими десятичными дробями. Они обозначаются особыми знаками (радикалами - √) или буквами (е, π). С иррациональным числом π мы встречались в 6 классе при изучении темы «Длина окружности и площадь круга». Истинное значение π ближе к 3,14159265358979323846, но и эта длинная десятичная дробь — не более чем приближение к истинному значению числа π. В действительности же, число π невозможно точно представить в виде десятичной дроби, так как десятичная дробь получается бесконечной.
С понятием числа е мы впервые встретились при изучении темы «Понятие предела последовательности» в 10 классе. Число е не так часто встречается в курсе математики и не столь знаменито, как число π, поэтому мы решили подробно изучить это число. Этой теме мы хотим посвятить исследовательскую работу, подробно изучить и обобщить материал о числе е.
Цель работы - исследовать историю числа е и расширить знания об иррациональном числе е.
Задачи:
- изучить литературу с целью получения информации об истории числа е;
- выяснить его приближенное значение;
- рассмотреть различные способы определения числа е;
- рассмотреть решение задачи практического содержания проявления числа е в реальной жизни.
Объект исследования: число е.
Предмет исследования: способы определения числа е, практическое применение числа е.
Гипотеза: При подробном изучении числа е возможно рассмотрение интересных фактов, связанных с этим числом.
Методы исследования: Изучение литературы, метод анализа, метод систематизации, опроса и обобщения.
Основная часть
история числа е
Число е иногда называют неперовым в честь шотландского учёного Непера, автора работы «Описание удивительной таблицы логарифмов» (1614 год). Однако это название не совсем корректно, так как у него логарифм числа x был равен .
Впервые константа негласно присутствует в приложении к переводу на английский язык вышеупомянутой работы Непера, опубликованному в 1618 году. Негласно, потому что там содержится только таблица натуральных логарифмов, определённых из кинематических соображений, сама же константа не присутствует.
Предполагается, что автором таблицы был английский математик HYPERLINK "http://ru.science.wikia.com/wiki/%D0%9E%D1%82%D1%80%D0%B5%D0%B4,_%D0%A3%D0%B8%D0%BB%D1%8C%D1%8F%D0%BC?action=edit&redlink=1" \o "Отред, Уильям (страница не существует)" Отред.
Саму же константу впервые вычислил швейцарский математик Бернулли при анализе следующего предела:
Первое известное использование этой константы, где она обозначалась буквой b, встречается в письмах Лейбница Гюйгенсу, 1690—1691 годы.
Букву e начал использовать Эйлер в 1727 году, а первой публикацией с этой буквой была его работа «Механика, или Наука о движении, изложенная аналитически» 1736 год. Соответственно, e обычно называют числом Эйлера. Хотя впоследствии некоторые учёные использовали букву c, буква e применялась чаще и в наши дни является стандартным обозначением.
Почему была выбрана именно буква e, точно неизвестно. Возможно, это связано с тем, что с неё начинается слово exponential («показательный», «экспоненциальный»). Другое предположение заключается в том, что буквы a, b, c и d уже довольно широко использовались в иных целях, и e была первой «свободной» буквой. Неправдоподобно предположение, что Эйлер выбрал e как первую букву в своей фамилии.
СПОСОБЫ ОПРЕДЕЛЕНИЯ ЧИСЛА е
Число е можно определить несколькими способами.
Рассмотрим числовую последовательность с общим членом
, где n=1, 2, 3, …
При n=1, u1=2;
При n=2, u2=
При n=3, u3=
При n=4, u4=
При n=5, u5= и т. д.
…
При ,
Можно сказать, что последовательность сходится, то есть существует предел. Предел этой последовательности обозначают латинской буквой е.
Этот предел называется вторым замечательным пределом.
Число е приблизительно равно 2,718281828459045…(приложение 1)
Эйлеру принадлежит много открытий, связанных с числом е, поэтому число е в конце концов стали называть «числом Эйлера». Число е является трансцендентным, т.е. оно не является корнем никакого алгебраического уравнения с рациональными коэффициентами.
Л. Эйлер открыл бесконечную цепную дробь для представления числа е:
e = 2 + 1
1 + 1
2 + 2
3 + 3
4 + …
Для быстрого вычисления большого числа знаков удобнее использовать другое разложение:
Число е можно записать в виде суммы ряда
Логарифмы с основанием е называются натуральными и обозначаются
Функцию ех называют экспонентой или экспоненциальной функцией, производная которой равна самой функции.
Таким образом, рассмотрев способы определения числа е, можно дать краткое определение этого числа. Число е - математическая константа, основание натурального логарифма, трансцендентное число.
ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ ЧИСЛА е
Число e играет огромную роль в математике, физике, астрономии и других науках. Вот некоторые вопросы, при математическом рассмотрении которых приходится пользоваться этим числом (список можно было бы увеличивать неограниченно):
Барометрическая формула (уменьшение давления с высотой)
Формула Эйлера
Закон охлаждения тел
Колебания маятника в воздухе
Формула Циолковского для скорости ракеты
Рост клеток Число Эйлера действительно имеет огромное значение как в математике, так и в жизни. Рассмотрим пример.
Задача о росте вклада. Предположим, что кто-то положил один рубль в банк, выплачивающий 4% годовых. Если проценты простые, то каждый год сумма вклада возрастает на 4% от первоначального капитала. Каждый рубль через двадцать пять лет «вырастет» и превратится в два рубля. Если же банк выплачивает сложный процент, то рубль будет расти быстрее, потому что после каждого начисления процентов капитал немного увеличивается и в следующий раз процент начисляется от большей суммы. Чем чаще производят перерасчет и прибавление прибыли к основному капиталу, тем быстрее растет вклад. При ежегодном начислении сложных процентов рубль за 25 лет превратится в , то есть в 2,66 рубля. При начислении сложных процентов каждые полгода (если банк выплачивает 4 (сложных) процента годовых, то прирост вклада за каждые шесть месяцев составляет 2 процента) рубль за 25 лет превратится в , или 2,69 рубля.
В рекламных проспектах банков их составители особо подчеркивают, сколько раз в год производится начисление прибыли. Непосвященному может показаться, что при достаточно частом начислении процентов (например, если производить пересчет миллион раз в год) за 25 лет рубль превратится в весьма ощутимую сумму. В действительности ничего подобного не произойдет. Через 25 лет один рубль вырос бы до величины , где п — число начислений прибыли. При п, стремящемся к бесконечности, это выражение стремится к пределу, равному 2,718 (e), что всего на 3 цента больше той суммы, которая получилась бы, если бы прибыль начислялась лишь раз в полгода. Этот предел и является числом е.
Однако не все величины возрастают так, как растет капитал в рассмотренных выше примерах. Тип роста, о котором шла речь, обладает одной весьма важной особенностью: в каждый момент времени скорость роста пропорциональна величине того, что возрастает.
Иначе, говоря, отношение приращения изменяющейся величины к ее текущему значению всегда одно и то же. Величины такого типа изменяются подобно снежному кому, несущемуся с вершины горы: чем больше становится ком, тем быстрее налипает на него снег. Этот тип роста свойствен многим процессам в живой и неживой природе. Все они описываются формулами, в которые входит экспоненциальная функция.
Заключение
В данной работе мы познакомились с числом е. Узнали, что число e — основание натурального логарифма, математическая константа, иррациональное и трансцендентное число. Приблизительно равно 2,71828. Иногда число e называют числом Эйлера или числом Непера. Узнали историю этого числа, рассмотрели способы его определения. Также узнали, что число e играет огромнейшую роль, как в математике, так и в других науках, и в жизни. На примере рассмотрели практическое применение числа е в жизни. И думаем, что достигли поставленной цели. Рассмотрев пример решения задачи о росте вклада, мы приходим к выводу, что число е является базовым соотношением роста для всех непрерывно растущих процессов.
Библиографический список
Кузьмин Е., Ширшов А. О числе е. // Квант, 1979 №8.
Болтянский В. Экспонента. // Квант, 1984 №3.
Никольский С.М. Алгебра и начала математического анализа. 10 класс, 2014г.
wikipedia.org
Приложение 1. Приближенное значение числа е
е = 2,7182818284 5904523536 0287471352 6624977572 4709369995 9574966967 6277240766 3035354759 4571382178 5251664274 2746639193 2003059921 8174135966 2904357290 0334295260 5956307381 3232862794 3490763233 8298807531 9525101901 1573834187 9307021540 8914993488 4167509244 7614606680 8226480016 8477411853 7423454424 3710753907 7744992069 5517027618 3860626133 1384583000 7520449338 2656029760 6737113200 7093287091 2744374704 7230696977 2093101416 9283681902 5515108657 4637721112 5238978442 5056953696 7707854499 6996794686 4454905987 9316368892 3009879312 7736178215 4249992295 7635148220 8269895193 6680331825 2886939849 6465105820 9392398294 8879332036 2509443117 3012381970 6841614039 7019837679 3206832823 7646480429 5311802328 7825098194 5581530175 6717361332 0698112509 9618188159 3041690351 5988885193 4580727386 6738589422 8792284998 9208680582 5749279610 4841984443 6346324496 8487560233 6248270419 7862320900 2160990235 3043699418 4914631409 3431738143 6405462531 5209618369 0888707016 7683964243 7814059271 4563549061 3031072085 1038375051 0115747704 1718986106 8739696552 1267154688 9570350354
educontest.net
«Реферат по математике на тему «Число е»»
«Число е»2016
Число е
e — основание натурального логарифма, математическая константа, иррациональное и трансцендентное число. Приблизительно равно 2,71828. Иногда число e называют числом Эйлера или числом Непера. Обозначается строчной латинской буквой «e».
Число e играет важную роль в дифференциальном и интегральном исчислении, а также во многих других разделах математики.
Поскольку функция экспоненты интегрируется и дифференцируется «в саму себя», логарифмы именно по основанию e принимаются как натуральные.
Иррациональные числаγ — ζ(3) — ρ — √2 — √3 — √5 — φ — δs — α — e — π — δСистема счисления Оценка числа
Двоичная10,101101111110000101010001011001…
Десятичная2,7182818284590452353602874713527…
Шестнадцатеричная2,B7E151628AED2A6A…
Шестидесятеричная2; 43 05 48 52 29 48 35 …
Рациональные приближения8/3; 11/4; 19/7; 87/32; 106/39; 193/71; 1264/465; 2721/1001; 23225/8544
(перечислено в порядке увеличения точности)
Непрерывная дробь[2; 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8, 1, 1, 10, 1, …]
(Эта непрерывная дробь не периодическая. Записана в линейной нотации)
2,7182818284 5904523536 0287471352 6624977572 4709369995 9574966967 6277240766 3035354759 4571382178 5251664274 2746639193 2003059921 8174135966 2904357290 0334295260 5956307381 3232862794 3490763233 8298807531 9525101901 1573834187 9307021540 8914993488 4167509244 7614606680 8226480016 8477411853 7423454424 3710753907 7744992069 5517027618 3860626133 1384583000 7520449338 2656029760 6737113200 7093287091 2744374704 7230696977 2093101416 9283681902 5515108657 4637721112 5238978442 5056953696 7707854499 6996794686 4454905987 9316368892 3009879312 7736178215 4249992295 7635148220 8269895193 6680331825 2886939849 6465105820 9392398294 8879332036 2509443117 3012381970 6841614039 7019837679 3206832823 7646480429 5311802328 7825098194 5581530175 6717361332 0698112509 9618188159 3041690351 5988885193 4580727386 6738589422 8792284998 9208680582 5749279610 4841984443 6346324496 8487560233 6248270419 7862320900 2160990235 3043699418 4914631409 3431738143 6405462531 5209618369 0888707016 7683964243 7814059271 4563549061 3031072085 1038375051 0115747704 1718986106 8739696552 1267154688 9570350354
Первые 1000 знаков после запятой числа e
(последовательность A001113 в OEIS)
Способы определения
Число e может быть определено несколькими способами.
Через предел:
(второй замечательный предел).
(формула Стирлинга).
Как сумма ряда:
или .
Как единственное число a, для которого выполняется
Как единственное положительное число a, для которого верно
Свойства
Данное свойство играет важную роль в решении дифференциальных уравнений. Так, например, единственным решением дифференциального уравнения является функция , где c — произвольная константа.
Число e иррационально и даже трансцендентно. Его трансцендентность была доказана только в 1873 году Шарлем Эрмитом. Предполагается, что e — нормальное число, то есть вероятность появления разных цифр в его записи одинакова.
Доказательство иррациональности
Предположим, что рационально. Тогда , где — целое, а — натуральное.
Следовательно
Умножая обе части уравнения на , получаем
Переносим в левую часть:
Все слагаемые правой части целые, следовательно, и сумма в левой части — целая. Но эта сумма и положительна, значит, она не меньше 1.
С другой стороны,
Суммируя геометрическую прогрессию в правой части, получаем:
Поскольку ,
Получаем противоречие.
Число e является вычислимым (а значит, и арифметическим) числом.
, см. формула Эйлера, в частности
Ещё формулы, связывающие числа e и π:
т. н. «интеграл Пуассона» или «интеграл Гаусса»
предел
Для любого комплексного числа z верны следующие равенства:
Число e разлагается в бесконечную цепную дробь следующим образом:
, то есть
Или эквивалентным ему:
Для быстрого вычисления большого числа знаков удобнее использовать другое разложение:
Представление Каталана:
Представление через произведение:
Через числа Белла
Мера иррациональности числа e равна 2 (что есть наименьшее возможное значение для иррациональных чисел).
История
Данное число иногда называют неперовым в честь шотландского учёного Непера, автора работы «Описание удивительной таблицы логарифмов» (1614 год). Однако это название не совсем корректно, так как у него логарифм числа x был равен .
Впервые константа негласно присутствует в приложении к переводу на английский язык вышеупомянутой работы Непера, опубликованному в 1618 году. Негласно, потому что там содержится только таблица натуральных логарифмов, определённых из кинематических соображений, сама же константа не присутствует.
Предполагается, что автором таблицы был английский математик Отред.
Саму же константу впервые вычислил швейцарский математик Бернулли в ходе решения задачи о предельной величине процентного дохода. Он обнаружил, что если исходная сумма $1 и начисляется 100 % годовых один раз в конце года, то итоговая сумма будет $2. Но если те же самые проценты начислять два раза в год, то $1 умножается на 1.5 дважды, получая $1.00×1.5² = $2.25. Начисления процентов раз в квартал приводит к $1.00×1.254 = $2.44140625, и так далее. Бернулли показал, что если частоту начисления процентов бесконечно увеличивать, то процентный доход в случае сложного процента имеет предел: и этот предел равен 2,71828…
$1.00×(1+1/12)12 = $2.613035…
$1.00×(1+1/365)365 = $2.714568…
Таким образом, константа e означает максимально возможную годовую прибыль при 100 % годовых и максимальной частоте капитализации процентов.
Первое известное использование этой константы, где она обозначалась буквой b, встречается в письмах Лейбница Гюйгенсу, 1690—1691 годы.
Букву e начал использовать Эйлер в 1727 году, впервые она встречается в письме Эйлера немецкому математику Гольдбаху от 25 ноября 1731 года, а первой публикацией с этой буквой была его работа «Механика, или Наука о движении, изложенная аналитически», 1736 год. Соответственно, e обычно называют числом Эйлера. Хотя впоследствии некоторые учёные использовали букву c, буква e применялась чаще и в наши дни является стандартным обозначением.
Почему была выбрана именно буква e, точно неизвестно. Возможно, это связано с тем, что с неё начинается слово exponential («показательный», «экспоненциальный»). Другое предположение заключается в том, что буквы a, b, c и d уже довольно широко использовались в иных целях, и e была первой «свободной» буквой. Также примечательно, что буква e является первой в фамилии Эйлер (Euler).
Приближения
Число можно запомнить как 2, 7 и повторяющиеся 18, 28, 18, 28.
Мнемоническое правило: два и семь, далее два раза год рождения Льва Толстого (1828), затем углы равнобедренного прямоугольного треугольника (45, 90 и 45 градусов). Стихотворная мнемофраза, иллюстрирующая часть этого правила: «Экспоненту помнить способ есть простой: два и семь десятых, дважды Лев Толстой»
Мнемоническое стихотворение, позволяющее запомнить первые 12 знаков после запятой (длины слов кодируют цифры числа e): Мы порхали и блистали, / Но застряли в перевале: / Не признали наши крали / Авторалли.
Правила e связывается с президентом США Эндрю Джексоном: 2 — столько раз избирался, 7 — он был седьмым президентом США, 1828 — год его избрания, повторяется дважды, поскольку Джексон дважды избирался. Затем — равнобедренный прямоугольный треугольник.
С точностью до трёх знаков после запятой через «число дьявола»: нужно разделить 666 на число, составленное из цифр 6−4, 6−2, 6−1 (три шестёрки, из которых в обратном порядке удаляются три первые степени двойки): .
Запоминание e как (с точностью менее 0.001).
Грубое (с точностью до 0,001) приближение полагает e равным . Совсем грубое (с точностью 0,01) приближение даётся выражением .
«Правило Боинга»: даёт точность 0,0005.
С точностью до : с точностью а с точностью
, с точностью 0.000001;
Число 19/7 превосходит число e менее чем на 0,004;
Число 87/32 превосходит число e менее чем на 0,0005;
Число 193/71 превосходит число e менее чем на 0,00003;
Число 1264/465 превосходит число e менее чем на 0,000003;
Число 2721/1001 превосходит число e менее чем на 0,0000002;
Число 23225/8544 превосходит число e менее чем на 0,00000001.
Открытые проблемы
Неизвестно, является ли число элементом кольца периодов.
Неизвестно, являются ли числа и алгебраически независимыми.
Неизвестна мера иррациональности ни для одного из следующих чисел: Ни для одного из них не известно даже, является ли оно рациональным числом, алгебраическим иррациональным или трансцендентным числом.
Неизвестно, является ли первое число Скьюза целым числом.
Интересные факты
В IPO компании Google в 2004 году было объявлено о намерении компании увеличить свою прибыль на 2 718 281 828 долл. Заявленное число представляет собой первые 10 цифр известной математической константы.
Теоретически считается, что наиболее производительные компьютеры должны иметь разрядность . Троичные ЭВМ ближе к данному значению, но из-за технических сложностей распространение получили двоичные компьютеры, в которых используются 1 и 0.
В языках программирования символу в экспоненциальной записи чисел соответствует число 10, а не Эйлерово число. Это связано с историей создания и использования языка FORTRAN для математических вычислений.
Ссылки
Число e — статья из энциклопедии «Кругосвет»Горобец Б. С. Мировые константы в основных законах физики и физиологии // Наука и жизнь. — 2004. — № 2. (статья с примерами физического смысла констант и )
J. J. O'Connor, E. F. Robertson. История числа e. MacTutor History of Mathematics archive. School of Mathematics and Statistics, University of St Andrews, Scotland (сентябрь 2001). (англ.)
e for 2.71828… (англ.) (история и правило Джексона)
«Экспонента и число е: просто и понятно» — перевод статьи An Intuitive Guide To Exponential Functions & Number e | BetterExplained (англ.)
schoolfiles.net
 впервые появилось в математике как нечто незначительное. Это случилось в 1618 г. В приложении к работе Непера (Napier) по логарифмам была дана таблица натуральных логарифмов различных чисел. Однако никто не понял, что это логарифмы по основанию
впервые появилось в математике как нечто незначительное. Это случилось в 1618 г. В приложении к работе Непера (Napier) по логарифмам была дана таблица натуральных логарифмов различных чисел. Однако никто не понял, что это логарифмы по основанию  , так как в понятие логарифма того времени такая вещь как основание не входила. Это сейчас мы называем логарифмом степень, в которую нужно возвести основание, чтобы получить требуемое число. Мы еще вернемся к этому позже. Таблица в приложении скорее всего была сделана Отредом (Ougthred), хотя автор ее не был указан. Через несколько лет, в 1624 г., в математической литературе снова появляется
, так как в понятие логарифма того времени такая вещь как основание не входила. Это сейчас мы называем логарифмом степень, в которую нужно возвести основание, чтобы получить требуемое число. Мы еще вернемся к этому позже. Таблица в приложении скорее всего была сделана Отредом (Ougthred), хотя автор ее не был указан. Через несколько лет, в 1624 г., в математической литературе снова появляется  , но опять-таки завуалированно. В этом году Бриггс (Briggs) дал численное приближение десятичного логарифма
, но опять-таки завуалированно. В этом году Бриггс (Briggs) дал численное приближение десятичного логарифма  , но само число
, но само число  в его работе не упоминается.
в его работе не упоминается. равнобочной гиперболы на промежутке от 1 до
равнобочной гиперболы на промежутке от 1 до  . И снова появляется десятичный логарифм
. И снова появляется десятичный логарифм  . В этой работе Меркатор впервые использует название “натуральный логарифм” для логарифма по основанию
. В этой работе Меркатор впервые использует название “натуральный логарифм” для логарифма по основанию 
 мы находим, что
мы находим, что  , но это гораздо более поздний способ восприятия. Здесь мы в самом деле подразумеваем под логарифмом функцию, тогда как сначала логарифм рассматривался только как число, которое помогало в вычислениях. Возможно, Якоб Бернулли первым понял, что логарифмическая функция является обратной показательной. С другой стороны, первым, кто связал логарифмы и степени, мог быть Джеймс Грегори (Games Gregory). В 1684 г. он определенно осознал связь между логарифмами и степенями, но, возможно, он был не первым.
, но это гораздо более поздний способ восприятия. Здесь мы в самом деле подразумеваем под логарифмом функцию, тогда как сначала логарифм рассматривался только как число, которое помогало в вычислениях. Возможно, Якоб Бернулли первым понял, что логарифмическая функция является обратной показательной. С другой стороны, первым, кто связал логарифмы и степени, мог быть Джеймс Грегори (Games Gregory). В 1684 г. он определенно осознал связь между логарифмами и степенями, но, возможно, он был не первым. . Наконец у
. Наконец у  Эйлер также нашел первые 18 десятичных знаков числа
Эйлер также нашел первые 18 десятичных знаков числа 
 Эйлер не привел доказательства, что эти дроби так же продолжаются, однако он знал, что если бы такое доказательство было, то оно доказывало бы иррациональность
Эйлер не привел доказательства, что эти дроби так же продолжаются, однако он знал, что если бы такое доказательство было, то оно доказывало бы иррациональность  , продолжалась так же, как в приведенном образце, 6,10,14,18,22,26,
, продолжалась так же, как в приведенном образце, 6,10,14,18,22,26, (каждый раз прибавляем по 4), то она никогда бы не прервалась, и
(каждый раз прибавляем по 4), то она никогда бы не прервалась, и 
 алгебраическим. Последний результат в этом направлении — это то, что по крайней мере одно из чисел
алгебраическим. Последний результат в этом направлении — это то, что по крайней мере одно из чисел  является трансцендентным.
является трансцендентным. впервые появилось в математике как нечто незначительное. Это случилось в 1618 г. В приложении к работе Непера (Napier) по логарифмам была дана таблица натуральных логарифмов различных чисел. Однако никто не понял, что это логарифмы по основанию
впервые появилось в математике как нечто незначительное. Это случилось в 1618 г. В приложении к работе Непера (Napier) по логарифмам была дана таблица натуральных логарифмов различных чисел. Однако никто не понял, что это логарифмы по основанию  равнобочной гиперболы на промежутке от
равнобочной гиперболы на промежутке от  до
до  . И снова появляется десятичный логарифм
. И снова появляется десятичный логарифм  . В этой работе Меркатор впервые использует название “натуральный логарифм” для логарифма по основанию
. В этой работе Меркатор впервые использует название “натуральный логарифм” для логарифма по основанию ![Rendered by QuickLaTeX.com \[\lim_{n\to\infty}\left(1+\frac{1}{n}\right)^n.\]](/800/600/http/hijos.ru//wp-content/ql-cache/quicklatex.com-f2c1c79898c92d1ab0bdb9157769768e_l3.png)
 и
и  , и это мы можем рассматривать как первое приближение числа
, и это мы можем рассматривать как первое приближение числа  мы находим, что
мы находим, что  , но это гораздо более поздний способ восприятия. Здесь мы в самом деле подразумеваем под логарифмом функцию, тогда как сначала логарифм рассматривался только как число, которое помогало в вычислениях. Возможно, Якоб Бернулли первым понял, что логарифмическая функция является обратной показательной. С другой стороны, первым, кто связал логарифмы и степени, мог быть Джеймс Грегори (Games Gregory). В 1684 г. он определенно осознал связь между логарифмами и степенями, но, возможно, он был не первым.
, но это гораздо более поздний способ восприятия. Здесь мы в самом деле подразумеваем под логарифмом функцию, тогда как сначала логарифм рассматривался только как число, которое помогало в вычислениях. Возможно, Якоб Бернулли первым понял, что логарифмическая функция является обратной показательной. С другой стороны, первым, кто связал логарифмы и степени, мог быть Джеймс Грегори (Games Gregory). В 1684 г. он определенно осознал связь между логарифмами и степенями, но, возможно, он был не первым. . Наконец у
. Наконец у ![Rendered by QuickLaTeX.com \[e=1+\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}+\ldots\mbox{ \rm и } e=\lim_{n\to\infty}\left(1+\frac{1}{n}\right)^n.\eqno(1)\]](/800/600/http/hijos.ru//wp-content/ql-cache/quicklatex.com-1aa5934667130ee9d9bdb5933f510358_l3.png)
![Rendered by QuickLaTeX.com \[e=2,718281828459045235\ldots,\]](/800/600/http/hijos.ru//wp-content/ql-cache/quicklatex.com-27cde3ed0b87c21801b7279bb364ae06_l3.png)
 и
и  Эйлер не привел доказательства, что эти дроби так же продолжаются, однако он знал, что если бы такое доказательство было, то оно доказывало бы иррациональность
Эйлер не привел доказательства, что эти дроби так же продолжаются, однако он знал, что если бы такое доказательство было, то оно доказывало бы иррациональность  продолжалась так же, как в приведенном образце,
продолжалась так же, как в приведенном образце,  (каждый раз прибавляем по
(каждый раз прибавляем по  ), то она никогда бы не прервалась, и
), то она никогда бы не прервалась, и  (а значит, и
(а значит, и ![Rendered by QuickLaTeX.com \[i^{-i}=\sqrt{e^{\pi}}.\]](/800/600/http/hijos.ru//wp-content/ql-cache/quicklatex.com-f7c2b55076b95685514f6e301e746120_l3.png)
 алгебраическим. Последний результат в этом направлении — это то, что по крайней мере одно из чисел
алгебраическим. Последний результат в этом направлении — это то, что по крайней мере одно из чисел  является трансцендентным.
является трансцендентным. впервые появилось в математике как нечто незначительное. Это случилось в 1618 г. В приложении к работе Непера (Napier) по логарифмам была дана таблица натуральных логарифмов различных чисел. Однако никто не понял, что это логарифмы по основанию
впервые появилось в математике как нечто незначительное. Это случилось в 1618 г. В приложении к работе Непера (Napier) по логарифмам была дана таблица натуральных логарифмов различных чисел. Однако никто не понял, что это логарифмы по основанию  равнобочной гиперболы на промежутке от 1 до
равнобочной гиперболы на промежутке от 1 до  . И снова появляется десятичный логарифм
. И снова появляется десятичный логарифм  . В этой работе Меркатор впервые использует название “натуральный логарифм” для логарифма по основанию
. В этой работе Меркатор впервые использует название “натуральный логарифм” для логарифма по основанию 
 мы находим, что
мы находим, что  , но это гораздо более поздний способ восприятия. Здесь мы в самом деле подразумеваем под логарифмом функцию, тогда как сначала логарифм рассматривался только как число, которое помогало в вычислениях. Возможно, Якоб Бернулли первым понял, что логарифмическая функция является обратной показательной. С другой стороны, первым, кто связал логарифмы и степени, мог быть Джеймс Грегори (Games Gregory). В 1684 г. он определенно осознал связь между логарифмами и степенями, но, возможно, он был не первым.
, но это гораздо более поздний способ восприятия. Здесь мы в самом деле подразумеваем под логарифмом функцию, тогда как сначала логарифм рассматривался только как число, которое помогало в вычислениях. Возможно, Якоб Бернулли первым понял, что логарифмическая функция является обратной показательной. С другой стороны, первым, кто связал логарифмы и степени, мог быть Джеймс Грегори (Games Gregory). В 1684 г. он определенно осознал связь между логарифмами и степенями, но, возможно, он был не первым. . Наконец у
. Наконец у  Эйлер также нашел первые 18 десятичных знаков числа
Эйлер также нашел первые 18 десятичных знаков числа 
 Эйлер не привел доказательства, что эти дроби так же продолжаются, однако он знал, что если бы такое доказательство было, то оно доказывало бы иррациональность
Эйлер не привел доказательства, что эти дроби так же продолжаются, однако он знал, что если бы такое доказательство было, то оно доказывало бы иррациональность  , продолжалась так же, как в приведенном образце, 6,10,14,18,22,26,
, продолжалась так же, как в приведенном образце, 6,10,14,18,22,26, (каждый раз прибавляем по 4), то она никогда бы не прервалась, и
(каждый раз прибавляем по 4), то она никогда бы не прервалась, и 
 алгебраическим. Последний результат в этом направлении — это то, что по крайней мере одно из чисел
алгебраическим. Последний результат в этом направлении — это то, что по крайней мере одно из чисел  является трансцендентным.
является трансцендентным.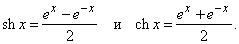


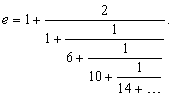
 (второй замечательный предел).
(второй замечательный предел).


 Данное свойство играет важную роль в решении дифференциальных уравнений. Так, например, единственным решением дифференциального уравненияf'(x) =f(x) является функцияf(x) =cex, гдеc— произвольная константа.
Данное свойство играет важную роль в решении дифференциальных уравнений. Так, например, единственным решением дифференциального уравненияf'(x) =f(x) является функцияf(x) =cex, гдеc— произвольная константа.

 .
.
 .
. .
. . Совсем грубое (с точностью 0,01) приближение даётся выражением
. Совсем грубое (с точностью 0,01) приближение даётся выражением .
. даёт неплохую точность 0,0005.
даёт неплохую точность 0,0005.