Главная » Реферат » Реферат мгновенная скорость

Ускорение. Реферат мгновенная скорость


Реферат Мгновенная скорость

скачать

Реферат на тему:

План:

Введение

Ско́рость (часто обозначается \vec v, от англ. velocity или фр. vitesse) — векторная физическая величина, характеризующая быстроту перемещения и направление движения материальной точки в пространстве относительно выбранной системы отсчёта (например, угловая скорость). Этим же словом может называться скалярная величина, точнее модуль производной радиус-вектора.

В науке используется также скорость в широком смысле, как быстрота изменения какой-либо величины (не обязательно радиус-вектора) в зависимости от другой (чаще изменения во времени, но также в пространстве или любой другой). Так, например, говорят о скорости изменения температуры, скорости химической реакции, групповой скорости, скорости соединения, угловой скорости и т. д. Математически характеризуется производной функции.

1. Скорость тела в механике

Вектор скорости материальной точки в каждый момент времени определяется производной по времени радиус-вектора {\vec r} этой точки:

\vec v = {d{\vec r} \over dt} = v {\vec \tau},

Здесь \ v  — модуль скорости, {\vec \tau}  — направленный вдоль скорости единичный вектор касательной к траектории в точке {\vec r} .

Скорость направлена вдоль касательной к траектории и равна по модулю производной дуговой координаты по времени.

Говорят, что тело совершает мгновенно-поступательное движение, если в данный момент времени скорости всех составляющих его точек равны. Так, например, равны скорости всех точек кабинки колеса обозрения (если, конечно, пренебречь колебаниями кабинки).

В общем случае, скорости точек, образующих твёрдое тело, не равны между собой. Так, например, для катящегося без проскальзывания колеса величина скорости точек на ободе относительно дороги принимает значения от нуля (в точке касания с дорогой) до удвоенного значения скорости автомобиля (в точке, диаметрально противоположной точке касания). Распределение скоростей в твёрдом теле определяется с помощью кинематической формулы Эйлера.

Если скорость тела (как векторная величина) не меняется во времени, то движение тела — равномерное (ускорение равно нулю) и тогда:

Скорость — характеристика движения точки, при равномерном движении численно равная отношению пройденного пути s к промежутку времени t, за который этот путь пройден.

1.1. Мгновенная и средняя скорость

Полезно отличать понятие средней скорости перемещения от понятия средней скорости пути, равной отношению пройденного точкой пути ко времени, за которое этот путь был пройден. В отличие от скорости перемещения, средняя скорость пути — скаляр.

Когда говорят о средней скорости , для различения, скорость согласно выше приведённому определению называют мгновенной скоростью. Так, хотя мгновенная скорость бегуна, кружащего по стадиону, в каждый момент времени отлична от нуля, его средняя скорость (перемещения) от старта до финиша оказывается равной нулю, если точки старта и финиша совпадают. Заметим, что при этом, средняя путевая скорость остаётся отличной от нуля.

1.2. В полярных координатах

См. радиальная скорость и поперечная скорость.

2. Преобразование скорости

В классической механике Ньютона скорости преобразуются при переходе из одной инерциальной системы отсчёта в другую согласно преобразованиям Галилея. Если скорость тела в системе отсчёта S была равна \vec v, а скорость системы отсчёта S' относительно системы отсчёта S равна \vec u, то скорость тела при переходе в систему отсчёта S' будет равна v' = \vec v - \vec u.

Для скоростей, близких к скорости света преобразования Галилея становятся несправедливы. При переходе из системы S в систему S' необходимо использовать преобразования Лоренца для скоростей:

v_x' = \frac{v_x - u}{1-(v_x u)/c^2}, v_y' = \frac{v_y \sqrt{1-\frac{u^2}{c^2}}}{1-(v_x u)/c^2}, v_z' = \frac{v_z \sqrt{1-\frac{u^2}{c^2}}}{1-(v_x u)/c^2},

в предположении, что скорость \vec u направлена вдоль оси х системы S. Легко убедиться, что в пределе нерелятивистских скоростей преобразования Лоренца сводятся к преобразованиям Галилея.

3. Единицы измерения скорости

Линейная скорость:

Угловая скорость:

3.1. Соотношения между единицами скорости

www.wreferat.baza-referat.ru

Вектор скорости. Средняя и мгновенная скорость., реферат — allRefers.ru

Вектор скорости. Средняя и мгновенная скорость. - раздел Физика, Несколько вводных замечаний о предмете физики

Движения различных тел различаются тем, что тела за одинаковые промежутки (равные) времени проходят различные по величине пути. Для характеристики такого движения вводят понятие скорости.

1) Введем понятие среднейскорости () – это величина, равная отношению перемещения 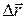к тому промежутку времени, в течение которого это перемещение произошло .

2) За малый промежуток времени Dt точка проходит путь DS, совершая перемещение 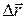(рис. 2.6). При Dt®0 отношения и практически перестают изменяться как по величине, так и по направлению и стремятся к определенному пределу

и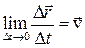

который будет выражать вектор мгновеннойскорости, т.е. скорости в данный момент времени.

В математике данный предел называется производной, следовательно, скорость можно определить как производную радиус-вектора движущейся точки по времени:

или по модулю .

При бесконечном уменьшении Dt различие между DS и будет уменьшаться и в пределе они совпадут, тогда можно записать, что модуль скорости

, (2.1)

т.е. мгновенная скорость при неравномерном движении численно равна первой производной пути по времени.

Итак, вектор мгновенной скорости в любой точке траектории направлен по касательной к траектории (и совпадает с направлением вектора перемещения) и численно равен первой производной пути по времени.

Единица измерения v: [v]=м/с.

Если рассматривать движение в пространстве, то величину и направление вектора скорости можно представить через проекции этого вектора на направления осей x, y, z (рис. 2.7).

;

где ,

– единичные вектора по осям x, y, z.

Тогда

Следовательно,

Все темы данного раздела:

Несколько вводных замечаний о предмете физики. Мир, окружающий нас материален: он состоит из вечно существующей и непрерывно движущейся материи. Мате

Механика Простейшим видом движения материи является механическое движение. ОПРЕДЕЛЕНИЕ: механическое движени

Кинематика движения материальной точки. Характеристики движения. Положение материальной точки M в пространстве в данный момент времени может быть задано радиус-вектором

Путь при неравномерном движении. За малый промежуток времени Dt перемещение графически изобра

Ускорение при криволинейном движении (тангенциальное и нормальное ускорение). Если траектория движения материальной точки представляет собой кривую линию, то такое движение мы будем на

Угловая скорость. ОПРЕДЕЛЕНИЕ: Вращательным движением будем называть такое движение, при котором все точки абсолютно тве

Угловое ускорение. Вектор угловой скорости может изменяться как за счет изменен

Связь между линейной и угловой скоростью. Пусть за малый промежуток времени Dt тело повернулось на угол Dj (рис. 2.17). Точка, находящаяся на рассто

Динамика Раздел механики, исследующий законы и причины, вызывающие движение тел, т.е. изучает движение материальных

II закон Ньютона. ОПРЕДЕЛЕНИЕ: Ускорение всякого тела прямо пропорционально действующей на него силе и обратно пропорционал

III закон Ньютона. Всякое действие тел друг на друга носит характер взаимодействия: если тело M1 действует на тело M2

Импульс. Закон сохранения импульса. В механической системе, состоящей из нескольких тел, существуют как силы взаимодействия между телами систе

Работа и энергия. Пусть тело, на которое действует сила , проходит, двигаясь по

Мощность. На практике имеет значение не только величина совершенной работы, но и время, в течение которого она соверш

Энергия. Из опыта известно, что тела часто оказываются в состоянии совершать работу над другими телами. ОПРЕДЕЛ

Кинетическая энергия тела. Рассмотрим простейшую систему, состоящую из одной частицы (материальной точки). Напишем уравнение дви

Потенциальное поле сил. Силы консервативные и неконсервативные. Если частица (тело) в каждой точке пространства подвержена воздействию других тел, то говорят, что эта части

Потенциальная энергия тела в поле сил тяжести (в поле тяготения Земли). Поле тяготения Земли есть силовое поле, поэтому любое движение тела в силовом поле сопровождается совершен

Потенциальная энергия в гравитационном поле (в поле всемирного тяготения). Установленный Ньютоном закон всемирного тяготения гласит: ОПРЕДЕЛЕНИЕ: Гравитационная сила или

Потенциальная энергия упруго деформированного тела. Потенциальной энергией может обладать не только система взаимодействующих тел, но и отдельно взятое упруг

Закон сохранения энергии. Без нарушения общности рассмотрим систему, состоящую из двух частиц массами m1 и m2. Пусть частиц

Поступательное движение твердого тела. ОПРЕДЕЛЕНИЕ: Абсолютно твердым телом будем называть такое тело, деформациями которого в условиях рассм

Вращательное движение твердого тела. ОПРЕДЕЛЕНИЕ: Вращательным движением твердого тела будем называть такое движение, при котором все точки

Момент импульса тела. Для описания вращательного движения потребуется ещё одна величина

Закон сохранения момента импульса. ФОРМУЛИРОВКА: Момент импульса замкнутой системы материальных точек остается постоянным. Отметим, что

Основное уравнение динамики вращательного движения. Рассмотрим систему материальных точек, каждая из которых может перемещаться, оставаясь в одной из плоскост

Кинетическая энергия вращающегося твердого тела. 1. Рассмотрим вращение тела вокруг неподвижной оси Z. Разо

Работа внешних сил при вращательном движении твердого тела. Найдем работу, которую совершают силы при вращении тела вокруг неподвижной оси Z. Пусть на массу

Линии и трубки тока. Гидродинамика изучает движение жидкостей, однако ее законы примени- мы и к движению газов. При стационарном

Уравнение Бернулли. Будем рассматривать идеальную несжимаемую жидкость, в котор

Силы внутреннего трения. Реальной жидкости присуща вязкость, которая проявляется в то

Ламинарное и турбулентное течения. При достаточно малой скорости движения жидкости наблюдается слоистое или ламинарное течение, ког

Течение жидкости в круглой трубе. При движении жидкости в круглой трубе ее скорость равна нулю

Движение тел в жидкостях и газах. При движении симметричных тел в жидкостях и газах возникает сила лобового сопротивления, направл

Законы Кеплера. К началу 17 столетия большинство ученых окончательно убедилось в справедливости гелиоцентрической системы

Опыт Кавендиша. Первой успешной попыткой определения «g» были измерения, осу

Напряженность гравитационного поля. Потенциал гравитационного поля. Гравитационное взаимодействие осуществляется через гравитационное поле. Это поле проявляет себя в том, по

Принцип относительности. В разд. 2.1. для механических систем был сформулирован следующий принцип относительности: во всех

Постулаты специальной (частной) теории относительности. Преобразования Лоренца Эйнштейн сформулировал два постулата, лежащие в основе специальной теории относительности: 1. Физиче

Следствия из преобразований Лоренца. Самым неожиданным следствием теории относительности является зависимость времени от системы отсчета.

Интервал между событиями. В теории относительности вводят понятие события, которое определяется местом, где оно произошло, и врем

Уравнение гармонического колебательного движения. Пусть на некоторое тело массы “m” действует квазиупругая сила

Графическое изображение гармонических колебаний. Векторная диаграмма. Сложение нескольких колебаний одинакового направления (или, что то же самое, сложение нескольких гармониче

Скорость, ускорение и энергия колеблющегося тела. Вернемся к формулам для смещения x, скорости v и ускорения a гармонического колебательного проце

Гармонический осциллятор. Систему, описываемую уравнением , где

Физический маятник. ОПРЕДЕЛЕНИЕ: Физическим маятником будем называть твердо

Затухающие колебания. При выводе уравнения гармонических колебаний считалось, что колеблющаяся точка находится под действием то

Вынужденные колебания. Резонанс. Для того чтобы система совершала незатухающие колебания, необходимо извне восполнять потери энергии колеб

Предмет и методы молекулярной физики. Молекулярная физика представляет собой раздел физики, изучающий строение и свойства вещества, исходя и так

Термодинамическая система. Параметры состояния системы. Равновесное и неравновесное состояние. ОПРЕДЕЛЕНИЕ: Термодинамической системой называется совокупность тел, обменивающихся энергией, как дру

Идеальный газ. Параметры состояния идеального газа. ОПРЕДЕЛЕНИЕ: Идеальным газом называется газ, при рассмотрении свойств которого соблюдаются следующие усло

Газовые законы. Если разрешить уравнение состояния идеального газа

Уравнение состояния идеального газа (уравнение Менделеева - Клапейрона). До этого рассматривались газовые процессы, при которых один

Физический смысл универсальной газовой постоянной. Универсальная газовая постоянная имеет размерность работы,

Основное уравнение кинетической теории газов Если в предыдущем разделе применялся термодинамический метод исследования, то в этом разделе будет исполь

Барометрическая формула. Распределение Больцмана Давно известно, что давление газа над поверхностью Земли уме

Максвелловское распределение молекул по скоростям В результате столкновений молекулы обмениваются скоростями, а в случае тройных и более сложных столкновен

Явления переноса. Длина свободного пробега молекул В предыдущих разделах мы рассматривали свойства тел, находящихся в тепловом равновесии. Данный раздел посв

Явление диффузии Диффузией называют процесс взаимного проникновения молекул соприкасающихся веществ, обусловле

Явление теплопроводности и вязкости Явление теплопроводности вещества определяет многие очень важные технические процессы и широко применяет

Термодинамика Термодинамика изучает физические явления с точки зрения тех превращений энергии, которыми эти явления соп

Внутренняя энергия идеального газа Важной величиной в термодинамике является внутренняя энергия тела. Любое тело кроме механической энергии

Работа и теплота. Первое начало термодинамики Внутренняя энергия газа (и другой термодинамической системы) может изменяться в основном за счет двух проц

Работа газовых изопроцессов Пусть газ заключен в цилиндрический сосуд, закрытый плотно п

Молекулярно-кинетическая теория теплоемкостей Теплоемкостью тела C называют физическую величину, численно равную количеству тепла, которое

Адиабатический процесс Наряду с изопроцессами существует адиабатический процесс, широко распространенный в природе. Адиабат

Круговые обратимые процессы. Цикл Карно Механические процессы обладают замечательным свойством обратимости. Например, брошенный камень, описав не

Понятие об энтропии. Энтропия идеального газа Для цикла Карно из формул (10.17) и (10.21) легко получить соотношение Q1 /T1 - Q2 /T2 = 0. (10.22

Второе начало термодинамики Понятие энтропии помогло строго математически сформулировать закономерности, позволяющие определить нап

Статистическое толкование второго начала термодинамики Состояние макроскопического тела (т.е. тела, образованного огромным числом молекул) может быть задано с пом

Уравнение Ван-дер-Ваальса Поведение реальных газов при их малых плотностях хорошо описывается уравнением Клапейрона:

Критическое состояние вещества   Важное значение уравнения Ван-дер-Ваальса заключается в том

Эффект Джоуля-Томсона В реальном газе между молекулами действуют силы притяжения и отталкивания. Силы притяжения обусловлены ди

allrefers.ru

Реферат Мгновенное ускорение

скачать

Реферат на тему:

План:

Введение

Ускоре́ние (обычно обозначается \vec a , в теоретической механике \vec w), производная скорости по времени — векторная величина, показывающая, насколько изменяется вектор скорости точки (тела) при её движении за единицу времени (т.е. ускорение учитывает не только изменение величины скорости, но и её направления).

Например, вблизи Земли падающее на Землю тело, в случае, когда можно пренебречь сопротивлением воздуха, увеличивает свою скорость примерно на 9,8 м/с каждую секунду, то есть, его ускорение равно 9,8 м/с².

Единицей ускорения служит метр в секунду за секунду (m/s2, м/с2), существует также внесистемная единица Гал (Gal), применяемая в гравиметрии и равная 1 см/с2.

Производная ускорения по времени, т.е. величина, характеризующая скорость изменения ускорения, называется рывок.

1. Кинематика точки

Вектор ускорения материальной точки в любой момент времени находится путём дифференцирования вектора скорости материальной точки по времени:

\vec a = {d\vec v \over dt} = {d^2\vec r \over dt^2}.

1.1. Ускорение точки при прямолинейном движении

Если вектор \vec a не меняется со временем, движение называют равноускоренным. При равноускоренном движении справедливы формулы:

\vec v(t) = \vec v_0 + (t - t_0)\vec a \vec r(t) = \vec r_0 + (t-t_0)\vec v_0 + {(t-t_0)^2\over 2}\vec a.

Частным случаем равноускоренного движения является случай, когда ускорение равно нулю в течение всего времени движения. В этом случае скорость постоянна, а движение происходит по прямолинейной траектории (если скорость тоже равна нулю, то тело покоится), поэтому такое движение называют прямолинейным и равномерным.

Равноускоренное движение точки всегда является плоским, а твёрдого тела — плоскопараллельным (поступательным). (Обратное, вообще говоря, не верно).

1.2. Ускорение точки при движении по окружности

Вектор ускорения

\mathbf a = \frac{d \mathbf v}{dt}

при движении точки по окружности можно разложить на два слагаемых (компоненты):

\mathbf a = \mathbf a_\tau + \mathbf a_n\

Тангенциальное ускорение — \mathbf a_\tau направлено по касательной к траектории (обозначается иногда \mathbf w_\tau, \mathbf u_\tau итд, в зависимости от того, какой буквой в данной книге принято обозначать ускорение). Является составляющей вектора ускорения a. Характеризует изменение скорости по модулю.

a_\tau = \frac{d |\mathbf v|}{dt}

Центростремительное или Нормальное ускорение \mathbf a_n — возникает (не равно нулю) всегда при движении точки по окружности (конечного радиуса) (также обозначается иногда \mathbf w_\tau, \mathbf u_\tau итд). Является составляющей вектора ускорения a, перпендикулярной вектору мгновенной скорости. Вектор нормального ускорения всегда направлен к центру окружности, а модуль равен:

|\vec a| = \omega ^2 r = {v^2 \over r}

Угловое ускорение — показывает, на сколько изменилась угловая скорость за единицу времени, и, по аналогии с линейным ускорением, равно:

\vec \varepsilon = {d\vec \omega \over dt}

Направление вектора здесь показывает, увеличивается или уменьшается модуль скорости. Если векторы углового ускорения и скорости сонаправлены, значение скорости растёт, и наоборот.

1.3. Ускорение точки при движении по кривой

Разложение ускорения по сопутствующему базису для движения в плоскости

Вектор ускорения \vec a можно разложить по сопутствующему базису \left\{\vec \tau, \vec{n}, \vec{b}\right\}:

\vec a = {a}_\tau {\vec \tau} + {a}_n {\vec n} + {a}_b {\vec b} = \frac{dv}{dt}{\vec \tau} + \frac{v^2}{R} {\vec n} + {a}_b {\vec b} ,

где

{a}_b{\vec b}, называемое бинормальным ускорением, всегда равно нулю. Это можно считать прямым следствием определения векторов \vec n, \vec b: можно сказать, что они выбираются именно так, чтобы первый всегда совпадал с нормальным ускорением, второй же ортогонально первому.

Векторы {a}_\tau{\vec \tau} и {a}_n{\vec n} называются касательным (тангенциальным) и нормальным ускорениями соответственно.

Итак, учитывая сказанное выше, вектор ускорения всегда можно записать как:

\vec a = {a}_\tau {\vec \tau} + {a}_n {\vec n} = \frac{dv}{dt}{\vec \tau} + \frac{v^2}{R} {\vec n},

2. Ускорения в твёрдом теле

Связь ускорений двух точек можно получить, продифференцировав формулу Эйлера для скоростей по времени:

\vec{w}_B = \vec{w}_A + \left[\vec{\omega}, \left[ \vec{\omega}, \vec{AB}\right] \right] + \left[ \varepsilon, \vec{AB} \right],

где \vec{\omega} — вектор угловой скорости тела, а \vec{\varepsilon} — вектор углового ускорения тела.

Второе слагаемое называется осестремительным ускорением.

3. Ускорение при сложном движении

Абсолютное ускорение равно сумме относительного, переносного и кориолисова:

\vec a_a=\vec {a}_r + \vec {a}_e + 2\left[\vec \omega \times \vec {v}_r \right].

4. Динамика точки

Первый закон Ньютона постулирует существование инерциальных систем отсчёта. В этих системах отсчёта равномерное прямолинейное движение имеет место в том случае, когда тело (материальная точка) не подвергается никаким внешним воздействиям в процессе своего движения. На основе этого закона возникает ключевое для механики понятие силы как такого внешнего воздействия на тело, которое выводит его из состояния покоя или влияет на скорость его движения. Таким образом, постулируется, что причиной возникновения ненулевого ускорения в инерциальной системе отсчёта всегда является некоторое внешнее силовое воздействие.

Второй закон Ньютона утверждает, что приложенная (к точке) сила и порождаемое ей ускорение точки всегда пропорциональны, причём коэффициент пропорциональности всегда один и тот же независимо от вида силового воздействия (он называется массой материальной точки):

\vec F = m\vec a.

5. Единицы измерения ускорения

wreferat.baza-referat.ru

Смотрите также