Понятие адсорбции. Автоадсорбция. Адсорбент и адсорбат. Абсолютная и Гиббсовская адсорбция. Единицы измерения адсорбции. Зависимость величины адсорбции от концентрации, давления и температуры. Изотерма, изобара, изопикна, изостера адсорбции
Адсорбция — процесс самопроизвольного перераспределения компонентов системы между поверхностным слоем и объемом фазы.
Адсорбция может наблюдаться в многокомпонентных системах и при перераспределении в поверхностный слой уходит тот компонент, который сильнее понижает поверхностное натяжение. В однокомпонентной системе при формировании поверхностного слоя происходит изменение его структуры — уплотнение, которое называется автоадсорбцией .
В общем случае адсорбция может происходить не только благодаря стремлению поверхностной энергии к уменьшению, но и за счет химической реакции компонентов с поверхностью вещества. В этом случае поверхностная энергия может даже увеличиваться на фоне снижения энергии всей системы.
Вещество, на поверхности которого происходит адсорбция, называется адсорбентом , а вещество, которое перераспределяется – адсорбатом .
Обратный процесс перехода вещества с поверхности в объем фазы — десорбция.
В зависимости от агрегатного состояния фаз различают адсорбцию газа на твердых адсорбентах, твердое тело – жидкость, жидкость — жидкость, жидкость — газ. Для количественного описания адсорбции применяют две величины: первая измеряется числом молей или граммами, приходящимися на единицу поверхности или массы адсорбента:
А = m 1 / m 2 — абсолютная адсорбция, А = ni / S .
Величина, определяемая избытком вещества в поверхностном слое, также отнесенным к единице площади поверхности или массы адсорбента, называется Гиббсовской или относительной адсорбцией (Г).
Адсорбция зависит от концентрации компонентов и температуры.
А = f ( c , T ) — жидкость;
А = f ( P , T ) — газ
Различают следующие виды зависимостей:
| 1. Изотерма (рис. 8) | 2. Изобара | 3. Изостера |
| А =fT (c) | А =fP (T) | c=fA (T) |
| A=fT (P) | A=fC (T) | P=fA (T) |
Считаем V поверхности раздела = 0.
dU = TdS + s dS + 
Проинтегрировав, получим: U = TS + sS + 
Полный дифференциал от этого уравнения:
dU = TdS + SdT + s dS + 
+ Sd s + 
.
Подставляя значение dU из (6) в (7) и сократив одинаковые члены правой и левой части, получим:
SdT + Sd s + 
= 0.
Предположим, что T = const: 
Разделив правую и левую часть на поверхность S, получим фундаментальное адсорбционное уравнение Гиббса:
; 
;
.
Определение зависимости поверхностного натяжения от адсорбции одного компонента, при постоянстве химических потенциалов других компонентов.
.
Известно, что 
, 
, (где 
, 
— равновесный и стандартный химический потенциал компонента i; lnai — логарифм активности i –го компонента). Тогда уравнение Гиббса будет выглядеть так
Активность связана с концентрацией: с = × а. Предположим, что = 1 (при с ® 0). Тогда
— для жидкости и газа
Обычно уравнение Гиббса применяют для растворов. Растворителем может быть не только индивидуальное вещество, но и смесь. В разбавленных растворах гиббсовская адсорбция очень мала, а его химический потенциал меняется очень мало с изменением концентрации растворенного вещества, т.е. d m= 0. Поэтому для разбавленного раствора фундаментальное уравнение Гиббса выглядит так:
Из этих уравнений следует, что зная зависимость 
= f (С) (где С — концентрация растворенного вещества), можно рассчитать изотерму адсорбции, пользуясь адсорбционным уравнением Гиббса. Схема графического расчета показана на рис. 2.2.2.1: Тангенс угла наклона соответствует значениям производных 
в этих точках.
Зная эти производныеуравнения Гиббса, можно рассчитать значение Г, что позволяет построить зависимость Г = f (С). Уравнение Гиббса показывает, что единица измерения гиббсовской адсорбции не зависит от единицы измерений концентрации, а зависит от размерности величины R. Так как величина R отнесена к молю вещества, а s - к единице площади, то Г = [моль/ единица площади]. Если s выразить в [Дж/м2 ], то R нужно подставлять: R = 8,314 Дж/моль×К.
В уравнении Гиббса влияние природы вещества на адсорбцию отражается производной
. Эта производная определяет и знак гиббсовской адсорбции, и может служить характеристикой вещества при адсорбции. Чтобы исключить влияние концентрации на производную берут ее предельные значения, т.е. при стремлении концентрации к нулю. Эту величину Ребиндер назвал поверхностной активностью .
;
g = [Дж×м/моль] = [Н×м2 /моль]; [эрг см/моль] = [Гиббс].
Уравнение показывает, что чем сильнее снижается 
= f ( c ) с увеличением концентрации, тем больше поверхностная активность этого вещества.
Физический смысл поверхностной активности состоит в том, что она представляет силу, удерживающую вещество на поверхности и отнесенную к единице гиббсовской адсорбции .
Поверхностную активность можно представить как отрицательный тангенс угла наклона к касательной, проведенной к кривой Г = f ( C ) в точке пересечения с осью ординат. Поверхностная активность может быть положительной и отрицательной. Значение и знак ее зависят от природы растворенного вещества и растворителя.
1. 
2 <
1, тогда 
<0 и Г>0: g >0 Þ с увеличением концентрации поверхностное натяжение на границе раздела фаз убывает и вещество поверхностно-активно .
1. 
2 <
1 , тоg <0 :Г <0 Þ вещество поверхностно-инактивно .
2. g = 0, Г = 0 — адсорбции нет, т.е. вещество индифферентно .
Поверхностно-активными веществами являются органические вещества, состоящие из углеводородного радикала и функциональной группы. Неорганические соли являются поверхностно-инактивными веществами. Ребиндер и Щукин в своих работах показали, что развитие микротрещин в твердых телах при деформации может происходить гораздо легче при адсорбции веществ из среды, в которой ведется деформирование: адсорбироваться могут как ионы электролитов, так и молекулы поверхностно-активного вещества (ПАВ), образуя на адсорбирующей поверхности их двумерный газ в результате нелокализованной адсорбции. Молекулы под давлением этого газа проникают в устье трещин и стремятся раздвинуть их, таким образом содействуя внешним силам, т.е. наблюдается адсорбционное понижение твердости твердого тела, что получило название эффекта Ребиндера. Поверхностная активность в гомологическом ряду поверхностно-активных веществ (ПАВ) повышается в среднем в 3,2 раза на каждую группу СН2 (в водных растворах) – правило Дюкло – Траубе .
Адсорбционное равновесие в системе «газ – жидкость». Закон Генри. Мономолекулярная адсорбция в системах «газ – жидкость», «жидкость – жидкость», «газ – твердое». Изотерма адсорбции Ленгмюра. Уравнение Фрейндлиха. Теория полимолекулярной адсорбции БЭТ. Уравнение БЭТ
Предположим, что имеются компоненты-неэлектролиты. Будем считать, что адсорбат образует на поверхности адсорбента мономолекулярный слой. Мономолекулярная адсорбция с точки зрения термодинамики процесса выражается химическим потенциалом в адсорбционном слое и объемной фазе:
;
;
,
где 
— химический потенциал вещества в адсорбционном слое;
— химический потенциал вещества в объемной фазе.
При равновесии потенциалы равны: 
.
Преобразуем:
; 
– адсорбция; а i = c .
,
, где D — коэффициент распределения.
Выражение 
— константа Генри. Она не зависит от концентрации, определяется при постоянной температуре, A / a = K г ,
А=а × Кг – закон Генри, т.е. при разбавлении системы коэффициент распределения стремится к постоянному значению, равному константе Генри. Если концентрация в сорбционном слое стремится к нулю, то а » с; а = × с; - 1. Поэтому на практике закон Генри используют в следующем виде: а=Кг с i. Если одна из фаз – газ, то имеем следующий вид: a = Кг Р i,
Кг = Кг/ RT .
Эти уравнения представляют собой уравнения изотермы адсорбции при малых концентрациях. В соответствии с этими уравнениями можно по другому сформулировать закон Генри: величина адсорбции при малых давлениях газа (малых концентрациях вещества в растворе) прямо пропорциональна давлению (концентрации). Эти зависимости показаны на рисунке 2.3.1.1. При адсорбции на твердых телах область действия закона мала из-за неоднородности поверхности, но даже на однородной поверхности при увеличении концентрации обнаруживается отклонение от закона. При малых концентрациях распределенного вещества отклонения обусловлены в основном соотношением между взаимодействием молекул друг с другом и с поверхностью адсорбента. Если когезионные взаимодействия адсорбата больше, то отклонение от закона отрицательно и <1, и коэффициент распределения увеличивается (кривая 1 на рис. 2.3.1.1). Если сильнее взаимодействие «адсорбат – адсорбент», то отклонение положительно и D уменьшается (кривая 2 на рис. 2.3.1.1). При дальнейшем увеличении концентрации происходит уменьшение свободной поверхности, снижается реакционная способность и кривые загибаются к оси абсцисс. Константу Генри получают экстраполяцией коэффициента распределения на нулевую концентрацию. В соответствии с правилом фаз Гиббса в гетерогенных системах равновесные параметры зависят от дисперсности или удельной поверхности. Для адсорбционных систем эта зависимость выражается в уменьшенных концентрациях вещества в объемной фазе с увеличением удельной поверхности адсорбента. Если в такой системе содержание распределяемого вещества постоянно, то
А mS уд + с V = const,
где m — масса адсорбента;
S уд — удельная поверхность адсорбента;
V — объем фазы, из которой извлекается вещество;
const – постоянное количество вещества в системе.
,
или
: разделим второй член на с ;
D — коэффициент распределения;
; 
.
Из соотношения следует, что с увеличением удельной поверхности при постоянной концентрации адсорбата концентрация уменьшается и тем сильнее, чем больше константа Генри и меньше объем фазы.
Теория Ленгмюра позволяет учесть наиболее сильные отклонения от закона Генри, что связано с ограничением адсорбционного объема или поверхности адсорбента. Ограниченность этого параметра приводит к адсорбционному насыщению поверхности адсорбента по мере увеличения концентрации распределяемого вещества. Это положение уточняется следующими утверждениями.
1. Адсорбция локализована на отдельных адсорбционных центрах, каждый из которых взаимодействует только с одной молекулой адсорбента — образуется мономолекулярный слой.
2. Адсорбционные центры энергетически эквивалентны — поверхность адсорбента эквипотенциальна.
3. Адсорбированные молекулы не взаимодействуют друг с другом.
Ленгмюр предположил, что при адсорбции происходит квазихимическая реакция между распределяемым компонентом и адсорбционными центрами поверхности:
,
где А — адсорбционые центры поверхности;
В — распределенное вещество;
АВ — образующийся комплекс на поверхности.
Константа равновесия процесса: 
,
где сав = А — величина адсорбции;
са = А0 = А ¥ — А,
где А ¥ — емкость адсорбционного монослоя или число адсорбционных центров, приходящихся на единицу поверхности или единицу массы адсорбента; А 0 — число оставшихся свободных адсорбционных центров, приходящихся на единицу площади или единицу массы адсорбента; с в – концентрация распределенного вещества.
Подставляя величину концентрации в уравнение константы, получим выражения
, св = с ,
А = А ¥ Кс – АКс, 
— для жидкостей;
— для газов.
Эти выражения – уравнения изотермы адсорбции Ленгмюра. К и Кр в уравнении характеризуют энергию взаимодействия адсорбента с адсорбатом. Адсорбционное уравнение часто представляют относительно степени заполнения поверхности, т.е. как отношение А/А ¥ :
,
.
Экспериментальные результаты по определению изотермы адсорбции обычно обрабатывают с помощью уравнения, записанного в линейной форме;
, т.е. уравнение типа y = b + ax .
Такая линейная зависимость позволяет графически определить А ¥ иК. Зная А ¥, можно определить удельную поверхность адсорбента (поверхность единицы массы адсорбента):
,
где А ¥ — предельная адсорбция, выражаемая числом молей адсорбата на единицу массы адсорбента;
NA – число Авогадро;
w0– площадь, занимаемая одной молекулой адсорбата.
1. Если с- 0, тогда уравнение примет вид:
А=А ¥ Кс ;
; А = Кг с, q =Кс ,
т.е. при с- 0 уравнение Ленгмюра переходит в уравнение Генри.
2. Если с-¥, тогда А = А ¥ , А/А ¥ = 1. Это случай предельной адсорбции.
3. Пусть адсорбция идет из смеси компонентов, в этом случае уравнение Ленгмюра записывается следующим образом:
.
Все рассмотренные выше уравнения справедливы для мономолекулярной адсорбции на адсорбенте с энергетически эквивалентными адсорбционными центрами. Однако реальные поверхности этим свойством не обладают. Приближенной к реальности является возможность распределения адсорбционных центров по энергии. Приняв линейное распределение, Темкин использовал формулу уравнения Ленгмюра и получил уравнение для средних степеней заполнения адсорбента.
,
где — константа, характеризующая линейное распределение;
К 0 — константа уравнения Ленгмюра, отвечающая максимальной теплоте адсорбции.
Из уравнения следует, что увеличение парциального давления (из-за увеличения концентрации) одного компонента подавляет адсорбцию другого и тем сильнее, чем больше его адсорбционная константа равновесия. Уравнение часто называют логарифмической изотермой адсорбции. Если принять экспоненциальное распределение центров по поверхности, то в области средних заполнений получается ранее найденное эмпирическим путем уравнение Фрейндлиха :
.
Прологарифмировав, получим 
,
где K , n – постоянные.
Использование уравнения Фрейндлиха в логарифмической форме позволяет определить константу уравнения.
Уравнение Ленгмюра можно использовать только при адсорбции в мономолекулярном слое. Это условие выполняется при хемосорбции, физической адсорбции газов при меньшем давлении и температуре выше критической. Однако в большинстве случаев мономолекулярный адсорбционный слой не компенсирует полностью избыточную поверхностную энергию и поэтому остается возможность влияния поверхностных сил на второй и т.д. адсорбционные слои. Это реализуется в том случае, когда газы и пары адсорбируются при температуре ниже критической, т.е. образуются полимолекулярные слои на поверхности адсорбента, что можно представить как вынужденную конденсацию (рис. 2.3.1.2 и 2.3.1.3).
В результате этих представлений была выведена следующая формула:
— уравнение полимолекулярной адсорбции БЭТ ,
где 
;
KL = a ж /ап – константа конденсации пара;
аж — активность вещества в жидкости;
ап — активность вещества в состоянии насыщенного пара;
ап = Р s .
Физический смысл С: характеризует разность энергии Гиббса в процессах чистой адсорбции и конденсации. Это уравнение получило название БЭТ (Бранауэр-Эммет- Теллер ).
При р/р s <<1, уравнение БЭТ превращается в уравнение Легмюра, которое при дальнейшем уменьшении давления (Р- 0) переходит в закон Генри:
.
При обработке экспериментальных данных уравнение БЭТ используют в линейной форме (рис. 2.3.1.4):
; 
,
таким образом графически находят обе константы уравнения А¥ и С.
www.ronl.ru
Понятие адсорбции. Автоадсорбция. Адсорбент и адсорбат. Абсолютная и Гиббсовская адсорбция. Единицы измерения адсорбции. Зависимость величины адсорбции от концентрации, давления и температуры. Изотерма, изобара, изопикна, изостера адсорбции
Адсорбция — процесс самопроизвольного перераспределения компонентов системы между поверхностным слоем и объемом фазы.
Адсорбция может наблюдаться в многокомпонентных системах и при перераспределении в поверхностный слой уходит тот компонент, который сильнее понижает поверхностное натяжение. В однокомпонентной системе при формировании поверхностного слоя происходит изменение его структуры — уплотнение, которое называется автоадсорбцией .
В общем случае адсорбция может происходить не только благодаря стремлению поверхностной энергии к уменьшению, но и за счет химической реакции компонентов с поверхностью вещества. В этом случае поверхностная энергия может даже увеличиваться на фоне снижения энергии всей системы.
Вещество, на поверхности которого происходит адсорбция, называется адсорбентом , а вещество, которое перераспределяется – адсорбатом .
Обратный процесс перехода вещества с поверхности в объем фазы — десорбция.
В зависимости от агрегатного состояния фаз различают адсорбцию газа на твердых адсорбентах, твердое тело – жидкость, жидкость — жидкость, жидкость — газ. Для количественного описания адсорбции применяют две величины: первая измеряется числом молей или граммами, приходящимися на единицу поверхности или массы адсорбента:
А = m 1 / m 2 — абсолютная адсорбция, А = ni / S .
Величина, определяемая избытком вещества в поверхностном слое, также отнесенным к единице площади поверхности или массы адсорбента, называется Гиббсовской или относительной адсорбцией (Г).
Адсорбция зависит от концентрации компонентов и температуры.
А = f ( c , T ) — жидкость;
А = f ( P , T ) — газ
Различают следующие виды зависимостей:
| 1. Изотерма (рис. 8) | 2. Изобара | 3. Изостера |
| А =fT (c) | А =fP (T) | c=fA (T) |
| A=fT (P) | A=fC (T) | P=fA (T) |
Считаем V поверхности раздела = 0.
dU = TdS + s dS +
Проинтегрировав, получим: U = TS + sS +
Полный дифференциал от этого уравнения:
dU = TdS + SdT + s dS + + Sd s + .
Подставляя значение dU из (6) в (7) и сократив одинаковые члены правой и левой части, получим:
SdT + Sd s + = 0.
Предположим, что T = const:
Разделив правую и левую часть на поверхность S, получим фундаментальное адсорбционное уравнение Гиббса:
; ;
.
Определение зависимости поверхностного натяжения от адсорбции одного компонента, при постоянстве химических потенциалов других компонентов.
.
Известно, что , , (где , — равновесный и стандартный химический потенциал компонента i; lnai — логарифм активности i –го компонента). Тогда уравнение Гиббса будет выглядеть так
Активность связана с концентрацией: с = × а. Предположим, что = 1 (при с ® 0). Тогда
— для жидкости и газа
Обычно уравнение Гиббса применяют для растворов. Растворителем может быть не только индивидуальное вещество, но и смесь. В разбавленных растворах гиббсовская адсорбция очень мала, а его химический потенциал меняется очень мало с изменением концентрации растворенного вещества, т.е. d m= 0. Поэтому для разбавленного раствора фундаментальное уравнение Гиббса выглядит так:
Из этих уравнений следует, что зная зависимость = f (С) (где С — концентрация растворенного вещества), можно рассчитать изотерму адсорбции, пользуясь адсорбционным уравнением Гиббса. Схема графического расчета показана на рис. 2.2.2.1: Тангенс угла наклона соответствует значениям производных в этих точках.
Зная эти производныеуравнения Гиббса, можно рассчитать значение Г, что позволяет построить зависимость Г = f (С). Уравнение Гиббса показывает, что единица измерения гиббсовской адсорбции не зависит от единицы измерений концентрации, а зависит от размерности величины R. Так как величина R отнесена к молю вещества, а s - к единице площади, то Г = [моль/ единица площади]. Если s выразить в [Дж/м2 ], то R нужно подставлять: R = 8,314 Дж/моль×К.
В уравнении Гиббса влияние природы вещества на адсорбцию отражается производной. Эта производная определяет и знак гиббсовской адсорбции, и может служить характеристикой вещества при адсорбции. Чтобы исключить влияние концентрации на производную берут ее предельные значения, т.е. при стремлении концентрации к нулю. Эту величину Ребиндер назвал поверхностной активностью .
;
g = [Дж×м/моль] = [Н×м2 /моль]; [эрг см/моль] = [Гиббс].
Уравнение показывает, что чем сильнее снижается = f ( c ) с увеличением концентрации, тем больше поверхностная активность этого вещества.
Физический смысл поверхностной активности состоит в том, что она представляет силу, удерживающую вещество на поверхности и отнесенную к единице гиббсовской адсорбции .
Поверхностную активность можно представить как отрицательный тангенс угла наклона к касательной, проведенной к кривой Г = f ( C ) в точке пересечения с осью ординат. Поверхностная активность может быть положительной и отрицательной. Значение и знак ее зависят от природы растворенного вещества и растворителя.
1. 2 <1, тогда <0 и Г>0: g >0 Þ с увеличением концентрации поверхностное натяжение на границе раздела фаз убывает и вещество поверхностно-активно .
1. 2 <1 , тоg <0 :Г <0 Þ вещество поверхностно-инактивно .
2. g = 0, Г = 0 — адсорбции нет, т.е. вещество индифферентно .
Поверхностно-активными веществами являются органические вещества, состоящие из углеводородного радикала и функциональной группы. Неорганические соли являются поверхностно-инактивными веществами. Ребиндер и Щукин в своих работах показали, что развитие микротрещин в твердых телах при деформации может происходить гораздо легче при адсорбции веществ из среды, в которой ведется деформирование: адсорбироваться могут как ионы электролитов, так и молекулы поверхностно-активного вещества (ПАВ), образуя на адсорбирующей поверхности их двумерный газ в результате нелокализованной адсорбции. Молекулы под давлением этого газа проникают в устье трещин и стремятся раздвинуть их, таким образом содействуя внешним силам, т.е. наблюдается адсорбционное понижение твердости твердого тела, что получило название эффекта Ребиндера. Поверхностная активность в гомологическом ряду поверхностно-активных веществ (ПАВ) повышается в среднем в 3,2 раза на каждую группу СН2 (в водных растворах) – правило Дюкло – Траубе .
Адсорбционное равновесие в системе «газ – жидкость». Закон Генри. Мономолекулярная адсорбция в системах «газ – жидкость», «жидкость – жидкость», «газ – твердое». Изотерма адсорбции Ленгмюра. Уравнение Фрейндлиха. Теория полимолекулярной адсорбции БЭТ. Уравнение БЭТ
Предположим, что имеются компоненты-неэлектролиты. Будем считать, что адсорбат образует на поверхности адсорбента мономолекулярный слой. Мономолекулярная адсорбция с точки зрения термодинамики процесса выражается химическим потенциалом в адсорбционном слое и объемной фазе:
;
;
,
где — химический потенциал вещества в адсорбционном слое;
— химический потенциал вещества в объемной фазе.
При равновесии потенциалы равны: .
Преобразуем:
; – адсорбция; а i = c .
,
, где D — коэффициент распределения.
Выражение — константа Генри. Она не зависит от концентрации, определяется при постоянной температуре, A / a = K г ,
А=а × Кг – закон Генри, т.е. при разбавлении системы коэффициент распределения стремится к постоянному значению, равному константе Генри. Если концентрация в сорбционном слое стремится к нулю, то а » с; а = × с; - 1. Поэтому на практике закон Генри используют в следующем виде: а=Кг с i. Если одна из фаз – газ, то имеем следующий вид: a = Кг Р i,
Кг = Кг/ RT .
Эти уравнения представляют собой уравнения изотермы адсорбции при малых концентрациях. В соответствии с этими уравнениями можно по другому сформулировать закон Генри: величина адсорбции при малых давлениях газа (малых концентрациях вещества в растворе) прямо пропорциональна давлению (концентрации). Эти зависимости показаны на рисунке 2.3.1.1. При адсорбции на твердых телах область действия закона мала из-за неоднородности поверхности, но даже на однородной поверхности при увеличении концентрации обнаруживается отклонение от закона. При малых концентрациях распределенного вещества отклонения обусловлены в основном соотношением между взаимодействием молекул друг с другом и с поверхностью адсорбента. Если когезионные взаимодействия адсорбата больше, то отклонение от закона отрицательно и <1, и коэффициент распределения увеличивается (кривая 1 на рис. 2.3.1.1). Если сильнее взаимодействие «адсорбат – адсорбент», то отклонение положительно и D уменьшается (кривая 2 на рис. 2.3.1.1). При дальнейшем увеличении концентрации происходит уменьшение свободной поверхности, снижается реакционная способность и кривые загибаются к оси абсцисс. Константу Генри получают экстраполяцией коэффициента распределения на нулевую концентрацию. В соответствии с правилом фаз Гиббса в гетерогенных системах равновесные параметры зависят от дисперсности или удельной поверхности. Для адсорбционных систем эта зависимость выражается в уменьшенных концентрациях вещества в объемной фазе с увеличением удельной поверхности адсорбента. Если в такой системе содержание распределяемого вещества постоянно, то
А mS уд + с V = const,
где m — масса адсорбента;
S уд — удельная поверхность адсорбента;
V — объем фазы, из которой извлекается вещество;
const – постоянное количество вещества в системе.
,
или: разделим второй член на с ;
D — коэффициент распределения;
; .
Из соотношения следует, что с увеличением удельной поверхности при постоянной концентрации адсорбата концентрация уменьшается и тем сильнее, чем больше константа Генри и меньше объем фазы.
Теория Ленгмюра позволяет учесть наиболее сильные отклонения от закона Генри, что связано с ограничением адсорбционного объема или поверхности адсорбента. Ограниченность этого параметра приводит к адсорбционному насыщению поверхности адсорбента по мере увеличения концентрации распределяемого вещества. Это положение уточняется следующими утверждениями.
1. Адсорбция локализована на отдельных адсорбционных центрах, каждый из которых взаимодействует только с одной молекулой адсорбента — образуется мономолекулярный слой.
2. Адсорбционные центры энергетически эквивалентны — поверхность адсорбента эквипотенциальна.
3. Адсорбированные молекулы не взаимодействуют друг с другом.
Ленгмюр предположил, что при адсорбции происходит квазихимическая реакция между распределяемым компонентом и адсорбционными центрами поверхности:
,
где А — адсорбционые центры поверхности;
В — распределенное вещество;
АВ — образующийся комплекс на поверхности.
Константа равновесия процесса: ,
где сав = А — величина адсорбции;
са = А0 = А ¥ — А,
где А ¥ — емкость адсорбционного монослоя или число адсорбционных центров, приходящихся на единицу поверхности или единицу массы адсорбента; А 0 — число оставшихся свободных адсорбционных центров, приходящихся на единицу площади или единицу массы адсорбента; с в – концентрация распределенного вещества.
Подставляя величину концентрации в уравнение константы, получим выражения
, св = с ,
А = А ¥ Кс – АКс, — для жидкостей;
— для газов.
Эти выражения – уравнения изотермы адсорбции Ленгмюра. К и Кр в уравнении характеризуют энергию взаимодействия адсорбента с адсорбатом. Адсорбционное уравнение часто представляют относительно степени заполнения поверхности, т.е. как отношение А/А ¥ :
,
.
Экспериментальные результаты по определению изотермы адсорбции обычно обрабатывают с помощью уравнения, записанного в линейной форме;
, т.е. уравнение типа y = b + ax .
Такая линейная зависимость позволяет графически определить А ¥ иК. Зная А ¥, можно определить удельную поверхность адсорбента (поверхность единицы массы адсорбента):
,
где А ¥ — предельная адсорбция, выражаемая числом молей адсорбата на единицу массы адсорбента;
NA – число Авогадро;
w0– площадь, занимаемая одной молекулой адсорбата.
1. Если с- 0, тогда уравнение примет вид:
А=А ¥ Кс ;; А = Кг с, q =Кс ,
т.е. при с- 0 уравнение Ленгмюра переходит в уравнение Генри.
2. Если с-¥, тогда А = А ¥ , А/А ¥ = 1. Это случай предельной адсорбции.
3. Пусть адсорбция идет из смеси компонентов, в этом случае уравнение Ленгмюра записывается следующим образом:
.
Все рассмотренные выше уравнения справедливы для мономолекулярной адсорбции на адсорбенте с энергетически эквивалентными адсорбционными центрами. Однако реальные поверхности этим свойством не обладают. Приближенной к реальности является возможность распределения адсорбционных центров по энергии. Приняв линейное распределение, Темкин использовал формулу уравнения Ленгмюра и получил уравнение для средних степеней заполнения адсорбента.
,
где — константа, характеризующая линейное распределение;
К 0 — константа уравнения Ленгмюра, отвечающая максимальной теплоте адсорбции.
Из уравнения следует, что увеличение парциального давления (из-за увеличения концентрации) одного компонента подавляет адсорбцию другого и тем сильнее, чем больше его адсорбционная константа равновесия. Уравнение часто называют логарифмической изотермой адсорбции. Если принять экспоненциальное распределение центров по поверхности, то в области средних заполнений получается ранее найденное эмпирическим путем уравнение Фрейндлиха :
.
Прологарифмировав, получим ,
где K , n – постоянные.
Использование уравнения Фрейндлиха в логарифмической форме позволяет определить константу уравнения.
Уравнение Ленгмюра можно использовать только при адсорбции в мономолекулярном слое. Это условие выполняется при хемосорбции, физической адсорбции газов при меньшем давлении и температуре выше критической. Однако в большинстве случаев мономолекулярный адсорбционный слой не компенсирует полностью избыточную поверхностную энергию и поэтому остается возможность влияния поверхностных сил на второй и т.д. адсорбционные слои. Это реализуется в том случае, когда газы и пары адсорбируются при температуре ниже критической, т.е. образуются полимолекулярные слои на поверхности адсорбента, что можно представить как вынужденную конденсацию (рис. 2.3.1.2 и 2.3.1.3).
В результате этих представлений была выведена следующая формула:
— уравнение полимолекулярной адсорбции БЭТ ,
где ;
KL = a ж /ап – константа конденсации пара;
аж — активность вещества в жидкости;
ап — активность вещества в состоянии насыщенного пара;
ап = Р s .
Физический смысл С: характеризует разность энергии Гиббса в процессах чистой адсорбции и конденсации. Это уравнение получило название БЭТ (Бранауэр-Эммет- Теллер ).
При р/р s <<1, уравнение БЭТ превращается в уравнение Легмюра, которое при дальнейшем уменьшении давления (Р- 0) переходит в закон Генри:
.
При обработке экспериментальных данных уравнение БЭТ используют в линейной форме (рис. 2.3.1.4):
; ,
таким образом графически находят обе константы уравнения А¥ и С.
www.ronl.ru
Реферат на тему:
Адсорбция (лат. ad — на, при; sorbeo — поглощаю) — это, в широком смысле, процесс изменения концентрации у поверхности раздела двух фаз, а в более узком и употребительном — это повышение концентрации одного вещества (газ, жидкость) у поверхности другого вещества (жидкость, твердое тело).
Поглощаемое вещество, ещё находящееся в объёме фазы, называют адсорбтив, поглощённое — адсорбат. В более узком смысле под адсорбцией часто понимают поглощение примеси из газа или жидкости твёрдым веществом (в случае газа и жидкости) или жидкостью (в случае газа) — адсорбентом. При этом, как и в общем случае адсорбции, происходит концентрирование примеси на границе раздела адсорбент-жидкость либо адсорбент-газ. Процесс, обратный адсорбции, то есть перенос вещества с поверхности раздела фаз в объём фазы, называется десорбция.
На поверхности раздела двух фаз помимо адсорбции, обусловленной в основном физическими взаимодействиями (главным образом это Ван-дер-Ваальсовы силы), может идти химическая реакция. Этот процесс называется хемосорбцией. Чёткое разделение на адсорбцию и хемосорбцию не всегда возможно. Одним из основных параметров по которым различаются эти явления является тепловой эффект: так, тепловой эффект физической адсорбции обычно близок к теплоте сжижения адсорбата, тепловой эффект хемосорбции значительно выше. Кроме того в отличае от адсорбции хемосорбция обычно является необратимой и локализованой. Примером промежуточных вариантов, сочетающих черты и адсорбции и хемосорбции является взаимодействие кислорода на металлах и водорода на никеле: при низких температурах они адсорбируются по законам физической адсорбции, но при повышении температуры начинает протекать хемосорбция.
В предыдущем разделе говорилось о случае протекания гетерогенной реакции на поверхности- хемосорбции. Однако бывают случаи гетерогенных реакций по всему объему, а не только на поверхности- это обычная гетерогенная реакция. Поглощение по всему объёму может проходить и под воздействием физических сил- этот случай называется абсорбцией.
| Физические | Адсорбция | Абсорбция |
| Химические | Хемосорбция | Гетерогенная реакция |
Причиной адсорбции являются неспецифические (то есть не зависящие от природы вещества) Ван-дер-Ваальсовы силы. Адсорбция, осложнённая химическим взаимодействием между адсорбентом и адсорбатом, является особым случаем. Явления такого рода называют хемосорбцией и химической адсорбцией. «Обычную» адсорбцию в случае, когда требуется подчеркнуть природу сил взаимодействия, называют физической адсорбцией.
Физическая адсорбция является обратимым процессом, условие равновесия определяется равными скоростями адсорбции молекул адсорбтива P на вакантных местах поверхности адсорбента S* и десорбции — освобождения адсорбата из связанного состояния S − P:
уравнение равновесияя в таком случае:
где K — константа равновесия, [S − P] и [S*] — доли поверхности адсорбента, занятые и незанятые адсорбатом, а [P] — концентрация адсорбтива.
Количественно процесс физической мономолекулярной адсорбции в случае, когда межмолекулярным взаимодействием адсорбата можно пренебречь, описывается уравнением Ленгмюра:
где θ — доля площади поверхности адсорбента, занятая адсорбатом, α — адсорбционный коэффициент Ленгмюра, а P — концентрация адсорбтива.
Поскольку [S − P] = θ и, соответственно, [S * ] = 1 − θ, уравнение адсорбционного равновесия может быть записано следующим образом:
Уравнение Ленгмюра является одной из форм уравнения изотермы адсорбции. Под уравнением изотермы адсорбции (чаще применяют сокращённый термин — изотерма адсорбции) понимают зависимость равновесной величины адсорбции от концентрации адсорбтива a=f(С) при постоянной температуре (T=const). Концентрация адсорбтива для случая адсорбции из жидкости выражается, как правило, в мольных либо массовых долях. Часто, особенно в случае адсорбции из растворов, пользуются относительной величиной: С/Сs, где С — концентрация, Сs — предельная концентрация (концентрация насыщения) адсорбтива при данной температуре. В случае адсорбции из газовой фазы концентрация может быть выражена в единицах абсолютного давления, либо, что особенно типично для адсорбции паров, в относительных единицах: P/Ps, где P — давление пара, Ps — давление насыщенных паров этого вещества. Саму величину адсорбции можно выразить также в единицах концентрации (отношение числа молекул адсорбата к общему числу молекул на границе раздела фаз). Для адсорбции на твёрдых адсорбентах, особенно при рассмотрении практических задач, используют отношение массы или количества поглощённого вещества к массе адсорбента, например мг/г или ммоль/г.
Адсорбция — всеобщее и повсеместное явление, имеющее место всегда и везде, где есть поверхность раздела между фазами. Наибольшее практическое значение имеет адсорбция поверхностно-активных веществ и адсорбция примесей из газа либо жидкости специальными высокоэффективными адсорбентами. В качестве адсорбентов могут выступать разнообразные материалы с высокой удельной поверхностью: пористый углерод (наиболее распространённая форма — активированный уголь), силикагели, цеолиты а также некоторые другие группы природных минералов и синтетических веществ.
Адсорбция (особенно хемосорбция) имеет также важное значение в гетерогенном катализе. Пример адсорбционных установок на азотные установки.
Установка для проведения адсорбции называется адсорбером.
wreferat.baza-referat.ru
Адсорбция — процесс самопроизвольного перераспределения компонентов системы между поверхностным слоем и объемом фазы.
Адсорбция может наблюдаться в многокомпонентных системах и при перераспределении в поверхностный слой уходит тот компонент, который сильнее понижает поверхностное натяжение. В однокомпонентной системе при формировании поверхностного слоя происходит изменение его структуры — уплотнение, которое называется автоадсорбцией .
В общем случае адсорбция может происходить не только благодаря стремлению поверхностной энергии к уменьшению, но и за счет химической реакции компонентов с поверхностью вещества. В этом случае поверхностная энергия может даже увеличиваться на фоне снижения энергии всей системы.
Вещество, на поверхности которого происходит адсорбция, называется адсорбентом , а вещество, которое перераспределяется – адсорбатом .
Обратный процесс перехода вещества с поверхности в объем фазы — десорбция.
В зависимости от агрегатного состояния фаз различают адсорбцию газа на твердых адсорбентах, твердое тело – жидкость, жидкость — жидкость, жидкость — газ. Для количественного описания адсорбции применяют две величины: первая измеряется числом молей или граммами, приходящимися на единицу поверхности или массы адсорбента:
А = m 1 / m 2 — абсолютная адсорбция, А = ni / S .
Величина, определяемая избытком вещества в поверхностном слое, также отнесенным к единице площади поверхности или массы адсорбента, называется Гиббсовской или относительной адсорбцией (Г).
Адсорбция зависит от концентрации компонентов и температуры.
А = f ( c , T ) — жидкость;
А = f ( P , T ) — газ
Различают следующие виды зависимостей:
| 1. Изотерма (рис. 8) | 2. Изобара | 3. Изостера |
| А =fT (c) | А =fP (T) | c=fA (T) |
| A=fT (P) | A=fC (T) | P=fA (T) |
Поскольку в качестве твердых адсорбентов используют пористые тела, рассмотрим некоторые методы получения твердых тел. Основных методов два.
1. Первый метод заключается в синтезе гидрозоля, который затем подвергают коагуляции до получения геля. Гель высушивают, частицы в результате этих операций срастаются с образованием твердого каркаса. Так как частицы золя высокодисперсны, то пористый материал получается с большой удельной поверхностью. Для удобства использования комки дробят, таблетируют, гранулируют. Обычно размер зерен адсорбента имеет предел от 0.1 до 7 микрон. Таким образом получают силикагель и другие адсорбенты.
2. Второй метод заключается в обработке крупнопористых материалов агрессивными газами или жидкостями. При такой обработке образуется губчатая структура. Этим методом получают активированный уголь из природных материалов, из которых сначала удаляют летучие вещества при нагревании без доступа воздуха. В результате образуется крупнопористая структура. Затем активируют уголь путем окисления газом кислорода или СО2, или водяным паром. Таким же образом получают никель Рэнея, т.е. берут сплав никеля и алюминия и его высушивают.
По классификации М.М. Дубинина за основу принят размер пор и механизм протекающих на них процессов.
1. Макропористые тела. Радиус пор от 100 — 200 нм, S уд = 0.5 — 2 м2 /г — Для этих же адсорбентов пригодна теория адсорбции Ленгмюра. В адсорбентах и катализаторах макропоры выступают в качестве транспортных каналов и адсорбцией в них можно пренебречь.
2. Переходно-пористые тела. Радиус пор более 2 — 100 нм, S уд = 100 — 500 м2 /г. Для них характерна полимолекулярная адсорбция, которая с увеличением давления заканчивается капиллярной конденсацией.
3. Микропористые тела. Радиус пор 0.5 — 2 нм, S уд = 500 — 1000 м2 /г. Отличительной особенностью этих тел является чрезвычайно близкое расположение противоположных стенок в порах. При этом их поля поверхностных сил перекрываются и они действуют во всем объеме микропор. К ним применима теория объемного заполнения микропор.
Реальные и промышленные адсорбенты имеют набор всех пор, но соотношение пор с разными радиусами различно. Каких пор больше, к такому классу их и относят.
Как уже отмечалось, влияние структуры пористого тела на адсорбцию заметно проявляется уже на переходно-пористых телах. Это обусловлено проявлением капиллярных сил. Появление этого связано со сродством адсорбата к адсорбенту. Основываясь на закономерностях капиллярных явлений, можно утверждать, что сродство должно быть достаточно для смачивания поверхности твердого тела жидкостью, появляющейся в результате конденсации в порах. Только в случае смачивания адсорбент будет втягивать в поры адсорбат, увеличивая тем самым адсорбцию. Чем меньше размер пор, тем сильнее капиллярное удерживание адсорбата. Если поверхность не смачивается, то наблюдается явление капиллярного выталкивания, адсорбция в этом случае минимальна и возможна только в крупных порах. Адсорбция в переходно-пористых телах происходит по механизму капиллярной конденсации. Капиллярная конденсация начинает проявляться при определенной степени заполнения адсорбента или при определенном давлении пара, характерном для данной системы. К этому моменту поверхностная энергия адсорбции практически полностью скомпенсирована в результате полимолекулярной адсорбции, а макропоры заполнены адсорбатом. В результате повышения давления пара заполняются конденсатом все крупные поры. Размеры радиусов менисков подчиняются уравнению капиллярной конденсации Томсона (Кельвина) .
,
где р — давление пара над искривленным мениском;
р s — давление насыщенного пара над плоской поверхностью;
s — поверхностное натяжение конденсированной жидкости;
r — радиус кривизны мениска.
Из уравнения видно, что при смачивании обеспечивается отрицательная кривизна мениска конденсата (вогнутый мениск), конденсация в порах наступает при давлении, которое меньше давления насыщенного пара, т.е. р/р s <1. Капиллярная конденсация не является следствием адсорбционных сил адсорбента и адсорбата в капилляре, но адсорбция является первым этапом капиллярной конденсации, если адсорбционные силы очень велики, а капилляры очень узкие, то конденсация идет до тех пор, пока не будет достигнуто давление насыщения над поверхностью.
Для адсорбентов переходной пористости характерна изотерма адсорбции с петлей капиллярно-конденсационного гистерезиса (рис. 2.3.2.1). При малых давлениях, когда конденсация не происходит, гистерезис не наблюдается. Начало его появления зависит от природы адсорбента и адсорбата.
Пористые структуры разнообразны, однако считается, что их можно смоделировать тремя видами:
1) конусообразные ;
2) цилиндрические с одним открытым концом ;
3) цилиндрические с двумя открытыми концами .
В реальных адсорбентах имеются все виды пор, которые заполняются при разных давлениях, поэтому реальные изотермы имеют вид, представленный на рис. 2.3.2.2:
В первой группе в конусообразных порах конденсация начинается со дна пор, где кривизна наибольшая. По мере заполнения поры радиус мениска увеличивается (уменьшается кривизна), поэтому для дальнейшего заполнения поры необходимо увеличить давление (рис. 2.3.2.2, а). Процесс десорбции идет в обратном направлении и описывается той же кривой.
Во второй группе конденсация также начинается со дна, где кривизна сферическая и поэтому наибольшая (см. рис. 2.3.2.2, б). Так как пора цилиндрическая, то она заполняется целиком при определенном радиусе мениска, что отвечает и определенному давлению пара. Капиллярная конденсация в этих порах также происходит обратимо. В третьей группе (в): конденсация начинается на стенках пор, имеющих кривизну, в 2 раза меньшую сферы того же радиуса. Поэтому заполнение происходит при больших давлениях пара. Конденсация на стенках приводит к уменьшению радиуса пор и ее мгновенному заполнению при давлении, отвечающем началу конденсации. На концах образуются сферические мениски жидкости. Десорбция может начаться при давлении, соответствующем радиусу кривизны этих менисков. Таким образом, опорожнение происходит при меньшем давлении, чем ее заполнение. Это и объясняет наличие гистерезиса на изотерме адсорбции. В некоторых случаях гистерезис вызывается кинетическими факторами (смачивание).
Капиллярная конденсация описывается уравнением Кельвина, в которое входит радиус кривизны мениска. Это позволяет рассчитывать функции распределения пор по размерам. В принципе количественная характеристика дисперсных систем по дисперсности может быть представлена распределением массы, объема, размером частиц по радиусу поверхности. Метод расчета функции распределения частиц (пор) по размерам заключается в построении интегральных и дифференциальных кривых распределения. Для простых тел наиболее типичными является распределение пор по радиусу. Поэтому интегральная кривая распределения выражает зависимость общего объема пор от их радиуса: Vn = f ( r ).
Из кривой (рис. 2.3.2.3, а) видно, что общий объем малых пор относительно небольшой. Однако доля поверхности, приходящаяся на эти поры, существенно велика. С увеличением размера пор объем увеличивается быстрее, чем поверхность. Построение разных кривых распределения позволяет более правильно представить структуру пористого тела.
Размеры микропор соизмеримы с размерами адсорбированных молекул. В отличие от Ленгмюровского микрослоя в микропорах молекулы расположены в основном вдоль поры и взаимодействуют друг с другом подобно взаимодействию с полимолекулярными слоями преобразования. Но в отличие от последнего большинство молекул находится в непосредственном контакте со стенками пор. Поэтому ни теория БЭТ, ни теория Ленгмюра для процесса адсорбции микропористыми телами неприемлемы. Закономерности заполнения микропор также нельзя описать теорией капиллярной конденсации. Это объясняется перекрыванием полей поверхностных сил в противоположных стенках, что значительно увеличивает энергию адсорбции. Гистерезис в микропорах обычно не наблюдается. Особенность адсорбции на микропористых телах проявляется в их избирательном действии. Это происходит благодаря тому, что большинство адсорбированных молекул взаимодействует непосредственно с поверхностью. Кроме этого у микропор наблюдается так называемый ситовый эффект. Суть его в том, что адсорбируются только те молекулы, размер которых меньше или равен радиусу пор. Поэтому микропористые адсорбенты часто называют молекулярными ситами. В основе количественных соотношений теории объемного заполнения пор лежит теория Поляни . Утверждается следующее.
1. В адсорбционном пространстве действуют только дисперсионные силы, которые аддитивны и не зависят от температуры. Т.е. при адсорбции характер взаимодействия между молекулами адсорбата не изменяется, а происходит только увеличение концентрации на поверхности адсорбента.
2. Активных центров нет, а есть непрерывное силовое поле.
3. Адсорбционные силы действуют на расстоянии большем, чем монослой адсорбата, поэтому говорят об абсорбционном объеме, который заполняется жидким адсорбатом.
4. Действие адсорбционных сил уменьшается по мере удаления от адсорбента и на каком-то расстоянии они равны нулю.
5. Притяжение данной молекулы поверхностного адсорбента не зависит от наличия в адсорбционнои пространстве других молекул, вследствие этого возможна полимолекулярная адсорбция.
6. Адсорбционные силы не зависят от температуры. И, следовательно, с изменением температуры адсорбционный объем не изменяется. Это не противоречит тому, что с увеличением температуры адсорбция уменьшается, а свидетельствует о том, что в результате нагревания и увеличения интенсивности теплового движения адсорбированных молекул увеличивается десорбция.
На рис. 2.3.2.4 показан разрез адсорбционного объема. Как во всяком поле, в них можно представить эквипотенциальные поверхности, т.е. поверхности, где адсорбционный потенциал постоянен — это пунктирные линии.
Под адсорбционным потенциалом e следует понимать работу, совершаемую против адсорбционных сил при перемещении одного моля газа с поверхности жидкого адсорбата (р s ) в газовую фазу (р ). В теории Поляни сделано допущение, что практически все адсорбированное вещество находится в жидком состоянии. Это позволяет заменить зависимость адсорбционного потенциала от расстояния (которое для пористого адсорбента определить невозможно) на функцию объемного жидкого адсорбента. Этот объем можно определить из экспериментально полученной изотермы адсорбции (рис. 2.3.2.5), дающей величину адсорбции:
V = AVm ,
где V — адсорбционный объем, заполненный жидкостью;
А — величина адсорбции, моль;
Vm — мольный объем адсорбата.
,
т.е. адсорбционный потенциал при постоянном объеме не зависит от температуры. Это так называемая температурная инвариантность. Для двух разных температур можно записать:
V = A 1V М 1= A 2V М 2 ;
.
Эти соотношения показывают, что, зная изотерму при одной температуре, можно рассчитать изотерму при другой температуре. В дальнейшем теорию Поляни разработал М.М. Дубинин. Так, им обнаружено важное свойство, характерное для потенциальных кривых адсорбции: характеристические кривые для одного и того же адсорбента и разных адсорбатов при всех значениях объемов адсорбата в поверхностном слое находятся в постоянном соотношении b, т.е.
( e / e 0) V = b — коэффициент аффинности, где e 0– адсорбционный потенциал для адсорбата, выбранного за стандарт.
Используя теорию Поляни и обобщив экспериментальный материал, Дубинин пришел к выводу о возможности применения функции распределения Вейбулла Q = f ( V ) в качестве функции распределения адсорбционного объема по значению потенциала для описания адсорбции на микропористых адсорбентах. Применительно к распределению степени заполнения по адсорбционному потенциалу функцию распределения Вейбулла представляют соотношением
q= f ( C ) .
Это выражается следующим образом:
,
где E , n — параметры, не зависящие от температуры;
e — адсорбционный потенциал;
Е – характеристическая энергия адсорбции.
Отношение характеристических энергий для двух адсорбатов также равно 
. Показатель степени n выражается целыми числами от 1 до 6 в зависимости от структуры адсорбента. Степень заполнения адсорбента можно представить как отношение А/А 0 (величины адсорбции к максимальной адсорбции) или как отношение заполненного объема V к предельному объему адсорбционного пространства V 0, тогда
A=A 0exp[-( e/E)n ] | — общие уравнения теории объемного заполнения микропор. |
В логарифмическом виде они имеют линейную форму:
.
Адсорбционное равновесие в системе «газ – жидкость». Закон Генри. Мономолекулярная адсорбция в системах «газ – жидкость», «жидкость – жидкость», «газ – твердое». Изотерма адсорбции Ленгмюра. Уравнение Фрейндлиха. Теория полимолекулярной адсорбции БЭТ. Уравнение БЭТ
Предположим, что имеются компоненты-неэлектролиты. Будем считать, что адсорбат образует на поверхности адсорбента мономолекулярный слой. Мономолекулярная адсорбция с точки зрения термодинамики процесса выражается химическим потенциалом в адсорбционном слое и объемной фазе:
;
;
,
где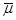 
— химический потенциал вещества в адсорбционном слое;
— химический потенциал вещества в объемной фазе.
При равновесии потенциалы равны: 
.
Преобразуем:
; 
– адсорбция; а i = c .
,
, где D — коэффициент распределения.
Выражение 
— константа Генри. Она не зависит от концентрации, определяется при постоянной температуре, A / a = K г ,
А=а × Кг – закон Генри, т.е. при разбавлении системы коэффициент распределения стремится к постоянному значению, равному константе Генри. Если концентрация в сорбционном слое стремится к нулю, то а » с; а = × с; - 1. Поэтому на практике закон Генри используют в следующем виде: а=Кг с i. Если одна из фаз – газ, то имеем следующий вид: a = Кг Р i,
Кг = Кг/ RT .
Эти уравнения представляют собой уравнения изотермы адсорбции при малых концентрациях. В соответствии с этими уравнениями можно по другому сформулировать закон Генри: величина адсорбции при малых давлениях газа (малых концентрациях вещества в растворе) прямо пропорциональна давлению (концентрации). Эти зависимости показаны на рисунке 2.3.1.1. При адсорбции на твердых телах область действия закона мала из-за неоднородности поверхности, но даже на однородной поверхности при увеличении концентрации обнаруживается отклонение от закона. При малых концентрациях распределенного вещества отклонения обусловлены в основном соотношением между взаимодействием молекул друг с другом и с поверхностью адсорбента. Если когезионные взаимодействия адсорбата больше, то отклонение от закона отрицательно и <1, и коэффициент распределения увеличивается (кривая 1 на рис. 2.3.1.1). Если сильнее взаимодействие «адсорбат – адсорбент», то отклонение положительно и D уменьшается (кривая 2 на рис. 2.3.1.1). При дальнейшем увеличении концентрации происходит уменьшение свободной поверхности, снижается реакционная способность и кривые загибаются к оси абсцисс. Константу Генри получают экстраполяцией коэффициента распределения на нулевую концентрацию. В соответствии с правилом фаз Гиббса в гетерогенных системах равновесные параметры зависят от дисперсности или удельной поверхности. Для адсорбционных систем эта зависимость выражается в уменьшенных концентрациях вещества в объемной фазе с увеличением удельной поверхности адсорбента. Если в такой системе содержание распределяемого вещества постоянно, то
А mS уд + с V = const,
где m — масса адсорбента;
S уд — удельная поверхность адсорбента;
V — объем фазы, из которой извлекается вещество;
const – постоянное количество вещества в системе.
,
или
: разделим второй член на с ;
D — коэффициент распределения;
; 
.
Из соотношения следует, что с увеличением удельной поверхности при постоянной концентрации адсорбата концентрация уменьшается и тем сильнее, чем больше константа Генри и меньше объем фазы.
Теория Ленгмюра позволяет учесть наиболее сильные отклонения от закона Генри, что связано с ограничением адсорбционного объема или поверхности адсорбента. Ограниченность этого параметра приводит к адсорбционному насыщению поверхности адсорбента по мере увеличения концентрации распределяемого вещества. Это положение уточняется следующими утверждениями.
1. Адсорбция локализована на отдельных адсорбционных центрах, каждый из которых взаимодействует только с одной молекулой адсорбента — образуется мономолекулярный слой.
2. Адсорбционные центры энергетически эквивалентны — поверхность адсорбента эквипотенциальна.
3. Адсорбированные молекулы не взаимодействуют друг с другом.
Ленгмюр предположил, что при адсорбции происходит квазихимическая реакция между распределяемым компонентом и адсорбционными центрами поверхности:
,
где А — адсорбционые центры поверхности;
В — распределенное вещество;
АВ — образующийся комплекс на поверхности.
Константа равновесия процесса: 
,
где сав = А — величина адсорбции;
са = А0 = А ¥ — А,
где А ¥ — емкость адсорбционного монослоя или число адсорбционных центров, приходящихся на единицу поверхности или единицу массы адсорбента; А 0 — число оставшихся свободных адсорбционных центров, приходящихся на единицу площади или единицу массы адсорбента; с в – концентрация распределенного вещества.
Подставляя величину концентрации в уравнение константы, получим выражения
, св = с ,
А = А ¥ Кс – АКс, 
— для жидкостей;
— для газов.
Эти выражения – уравнения изотермы адсорбции Ленгмюра. К и Кр в уравнении характеризуют энергию взаимодействия адсорбента с адсорбатом. Адсорбционное уравнение часто представляют относительно степени заполнения поверхности, т.е. как отношение А/А ¥ :
,
.
Экспериментальные результаты по определению изотермы адсорбции обычно обрабатывают с помощью уравнения, записанного в линейной форме;
, т.е. уравнение типа y = b + ax .
Такая линейная зависимость позволяет графически определить А ¥ иК. Зная А ¥, можно определить удельную поверхность адсорбента (поверхность единицы массы адсорбента):
,
где А ¥ — предельная адсорбция, выражаемая числом молей адсорбата на единицу массы адсорбента;
NA – число Авогадро;
w0– площадь, занимаемая одной молекулой адсорбата.
1. Если с- 0, тогда уравнение примет вид:
А=А ¥ Кс ;
; А = Кг с, q =Кс ,
т.е. при с- 0 уравнение Ленгмюра переходит в уравнение Генри.
2. Если с-¥, тогда А = А ¥ , А/А ¥ = 1. Это случай предельной адсорбции.
3. Пусть адсорбция идет из смеси компонентов, в этом случае уравнение Ленгмюра записывается следующим образом:
.
Все рассмотренные выше уравнения справедливы для мономолекулярной адсорбции на адсорбенте с энергетически эквивалентными адсорбционными центрами. Однако реальные поверхности этим свойством не обладают. Приближенной к реальности является возможность распределения адсорбционных центров по энергии. Приняв линейное распределение, Темкин использовал формулу уравнения Ленгмюра и получил уравнение для средних степеней заполнения адсорбента.
,
где — константа, характеризующая линейное распределение;
К 0 — константа уравнения Ленгмюра, отвечающая максимальной теплоте адсорбции.
Из уравнения следует, что увеличение парциального давления (из-за увеличения концентрации) одного компонента подавляет адсорбцию другого и тем сильнее, чем больше его адсорбционная константа равновесия. Уравнение часто называют логарифмической изотермой адсорбции. Если принять экспоненциальное распределение центров по поверхности, то в области средних заполнений получается ранее найденное эмпирическим путем уравнение Фрейндлиха :
.
Прологарифмировав, получим 
,
где K , n – постоянные.
Использование уравнения Фрейндлиха в логарифмической форме позволяет определить константу уравнения.
Уравнение Ленгмюра можно использовать только при адсорбции в мономолекулярном слое. Это условие выполняется при хемосорбции, физической адсорбции газов при меньшем давлении и температуре выше критической.
Однако в большинстве случаев мономолекулярный адсорбционный слой не компенсирует полностью избыточную поверхностную энергию и поэтому остается возможность влияния поверхностных сил на второй и т.д. адсорбционные слои. Это реализуется в том случае, когда газы и пары адсорбируются при температуре ниже критической, т.е. образуются полимолекулярные слои на поверхности адсорбента, что можно представить как вынужденную конденсацию (рис. 2.3.1.2 и 2.3.1.3).
В результате этих представлений была выведена следующая формула:
— уравнение полимолекулярной адсорбции БЭТ ,
где 
;
KL = a ж /ап – константа конденсации пара;
аж — активность вещества в жидкости;
ап — активность вещества в состоянии насыщенного пара;
ап = Р s .
Физический смысл С: характеризует разность энергии Гиббса в процессах чистой адсорбции и конденсации. Это уравнение получило название БЭТ (Бранауэр-Эммет- Теллер ).
При р/р s <<1, уравнение БЭТ превращается в уравнение Легмюра, которое при дальнейшем уменьшении давления (Р- 0) переходит в закон Генри:
.
При обработке экспериментальных данных уравнение БЭТ используют в линейной форме (рис. 2.3.1.4):
; 
,
таким образом графически находят обе константы уравнения А¥ и С.
www.ronl.ru
Курсовая работа
по дисциплине: Процессы и аппараты химической технологии
на тему: «Адсорбция»
Содержание
Введение
. Классификация процесса, основные определения
.1 Основные понятия процесса адсорбции
.2 Основные промышленные адсорбенты и их свойства
.3 Изотерма адсорбции
. Закономерности процесса адсорбции
.1 Теории адсорбции
.2 Адсорбция на границе раствор - пар
.3 Адсорбция на границе твердое тело - газ
.4 Адсорбция на границе твердое тело - раствор
.4.1 Молекулярная адсорбция из растворов
.4.2 Адсорбция из растворов электролитов
. Оборудование, реализующее процесс адсорбции
.1 Адсорбция с неподвижным слоем адсорбента
.2 Адсорбция силикагелем
.3 Гиперсорбция
.4 Адсорбция в кипящем (псевдоожиженном) слое
.5 Расчет адсорберов периодического действия
.6 Расчет адсорберов непрерывного действия
Заключение
Список использованной литературы
Введение
Адсорбцией называют процесс поглощения вещества из смеси газов, паров или растворов поверхностью или объемом пор твердого тела - адсорбента.
Явление адсорбции известно очень давно. Такие природные материалы, как песок и почва, использовали для очистки воды еще на заре человеческого общества. В конце XVIII века К. Шееле и одновременно Фонтана обнаружили способность свежепрокаленного древесного угля поглощать различные газы в объемах, в несколько раз превышающих его собственный объем. Вскоре выяснилось, что величина поглощенного объема зависит от типа угля и природы газа. Т.Е. Ловиц в 1785 году открыл явление адсорбции углем в жидкой среде, подробно исследовал его и предложил использовать уголь для очистки фармацевтических препаратов, спирта, вина, органических соединений. Ловиц показал, что древесный уголь способен быстро очищать испорченную воду и делать ее пригодной для питья. И сейчас основным действующим началом фильтров для воды служат углеродные материалы, конечно более современные, чем природные угли. Адсорбция отравляющих веществ из воздуха была использована Н.Д. Зелинским при создании противогаза во время первой мировой войны.
Адсорбция газов на твердых поверхностях используется в некоторых отраслях пищевой промышленности, а именно масложировой (например, в производстве маргарина) и в бродильной (например, в производстве дрожжей) для очистки технологических газовых потоков с целью предотвращения выбросов вредных веществ в атмосферу. Поглощение паров воды происходит на пористых веществах, которые выполняют роль твердого адсорбента. Подобные процессы наблюдаются в отношении сахара, соли и сухарей. Адсорбционный способ регулирования газового состава хранилищ скоропортящихся продуктов позволяет в несколько раз сократить потери и увеличить сроки хранения. Адсорбция различных пищевых кислот, лимонной в частности, снижает по сравнению с водой поверхностное натяжение большинства прохладительных напитков. Адсорбция веществ на поверхности раздела жидкость - газ способствует устойчивости пен. Подобный процесс имеет место в бродильной промышленности при производстве дрожжей и некоторых других полупродуктов. Усиление смачивания водой различных поверхностей широко используется в промышленности в качестве сопутствующего процесса при мойке оборудования, подготовке сырья, обработке полуфабрикатов и т.д. Адсорбция на границе твердое тело - жидкость широко применяется при очистке жидкостей (например, диффузионного сока при производстве сахара, растительных масел и соков) от примесей.
Развитие теории адсорбционных сил еще не достигло такой стадии, когда по известным физико-химическим свойствам газа и твердого тела можно было бы рассчитать изотерму адсорбции, не проводя экспериментальных исследований. Поэтому попыткам описать экспериментальные изотермы с помощью различных теоретических уравнений, которым соответствуют определенные модели адсорбции, посвящено огромное количество работ. Если теоретическое уравнение изотермы адсорбции хорошо воспроизводит экспериментальные данные, то можно рассчитать неизвестные величины адсорбции при разных условиях (р и Т) и определить различные геометрические параметры твердых тел. Рассмотрим лишь немногие, наиболее распространенные теоретические уравнения изотерм адсорбции.
1. Классификация процесса, основные определения
1.1 Основные понятия процесса адсорбции
Адсорбцией называется самопроизвольно протекающий диффузионный процесс взаимодействия двух фаз - твердого тела - адсорбента и газа, пара или растворенного вещества - адсорбтива, происходящий поглощением газа, пара или растворенного вещества поверхностью твердого тела.
Поглощение газов, паров и растворенных веществ твердыми телами обычно сопровождается процессами проникновения поглощаемого вещества в твердое тело (абсорбцией), капиллярной конденсацией и химическими реакциями (хемосорбцией), что весьма затрудняет изучение собственно адсорбции. Поэтому поглощение газов, паров и растворенных веществ твердыми телами обычно рассматривается как общий процесс сорбции.
Адсорбция всегда сопровождается выделением тепла. В большинстве случаев тепловой эффект адсорбции по своей величине приближается к теплоте конденсации поглощаемого газа или пара.
Адсорбцию подразделяют на два вида: физическую и химическую. Физическая адсорбция в основном обусловлена поверхностными вандервальсовыми силами, которые проявляются на расстояниях, значительно превышающих размеры адсорбируемых молекул, поэтому на поверхности адсорбента обычно удерживаются несколько слоев молекул адсорбата.
При химической адсорбции поглощаемое вещество вступает в химическое взаимодействие с адсорбентом с образованием на его поверхности обычных химических соединений.
Силы притяжения возникают на поверхности адсорбента благодаря тому, что силовое поле поверхностных атомов и молекул не уравновешено силами взаимодействия соседних частиц. По физической природе силы взаимодействия молекул поглощаемого вещества и адсорбента относятся в основном к дисперсионным, возникающим благодаря перемещению электронов в сближающихся молекулах. В ряде случаев адсорбции большое значение имеют электростатические и индукционные силы, а также водородные связи. Поэтому адсорбция является самопроизвольным процессом, течение которого сопровождается уменьшением свободной энергии и энтропии системы.
Процессы адсорбции избирательны и обратимы. Процесс, обратный адсорбции, называют десорбцией, которую используют для выделения поглощенных веществ и регенерации адсорбента.
Наиболее рационально применять адсорбцию для обработки смесей с низкой концентрацией извлекаемых веществ.
Статическая и динамическая активность адсорбентов.
Основной характеристикой адсорбента является его активность, определяемая весовым количеством вещества, поглощенного единицей объема или веса поглотителя.
Различают активность статическую и динамическую.
Статическая активность адсорбента характеризуется максимальным количеством вещества, адсорбированного к моменту достижения равновесия весовой или объемной единицей адсорбента при данной температуре и концентрации адсорбируемого вещества в газо-воздушной смеси.
Динамическая активность является характеристикой адсорбента при протекании паровоздушной смеси через слой адсорбента до момента проскока адсорбируемого газа.
Если газовая смесь проходит через слой адсорбента, то в начальный период процесса адсорбтив полностью извлекается из газовой смеси. По истечении определенного промежутка времени в газовой смеси, уходящей из поглотителя, начинают появляться заметные, все возрастающие количества адсорбтива (проскок), и к концу процесса концентрация уходящего газа становится равной начальной концентрации паровоздушной смеси.
В адсорберах промышленного типа с активированным углем динамическая активность составляет 85-95% от статической, а в случае применения силикагеля динамическая активность оказывается меньше статической на 60-70%.
Селективные свойства адсорбентов.
В процессах адсорбции, так же как и в процессах абсорбции, поглощающие вещества (адсорбенты обладают селективными свойствами по отношению к поглощаемым газам и парам. Иными словами, применение адсорбционных процессов в качестве метода разделения газовых смесей основано на том, что газовая смесь, приведенная в соприкосновение с адсорбентом, освобождается лишь от одного компонента, в то время как другие оказываются непоглощенными.
Если в процессах абсорбции селективные качества процесса определялись растворимостью или нерастворимостью газа в поглощающей жидкости, то в процессах адсорбции критерием селективных качеств является статическая активность адсорбента.
Из смеси газов, приведенных в соприкосновение с адсорбентом, в первую очередь и в значительно большем количестве поглощается газ или пар того вещества, которое имеет более высокую температуру кипения. В большинстве случаев температура кипения поглощаемого газа (например, паров бензола) сильно отличается от температуры кипения инертного газа (например, воздуха) и присутствие инертного газа почти не оказывает влияния на ход процесса. В данном случае поглощение бензола из паровоздушной смеси с парциальной упругостью паров бензола р протекает точно так же, как и поглощение чистых паров бензола, имеющих то же давление.
Разделение адсорбционным методом смеси газов, компоненты которой имеют близко лежащие температуры кипения, предоставляет большие трудности или практически невозможно.
1.2 Основные промышленные адсорбенты и их свойства
Основными промышленными адсорбентами являются пористые тела, обладающие большим объемом микропор. Свойства адсорбентов определяются природой материала, из которого они изготовлены, и пористой внутренней структурой.
В промышленных адсорбентах основное количество поглощенного вещества сорбируется на стенках микропор (r < 109 м). Роль переходных пор (10-9 < r < 10-7 м) и макропор (r < 10-7 м) в основном сводится к транспортированию адсорбируемого вещества к микропорам.
Адсорбенты характеризуются своей поглотительной, или адсорбционной способностью, определяемой максимально возможной концентрацией адсорбтива в единице массы или объема адсорбента, его пористой структуры, природы поглощаемого вещества, его концентрации, температуры, а для газов и паров - от их парциального давления. Максимально возможную при данных условиях поглотительную способность адсорбента условно называют равновесной активностью.
По химическому составу все адсорбенты можно разделить на углеродные и неуглеродные. К углеродным адсорбентам относятся активные (активированные угли), углеродные волокнистые материалы, а также некоторые виды твердого топлива. Неуглеродные адсорбенты включают в себя силикагели, активный оксид алюминия, алюмагели, цеолиты и глинистые породы.
Активные угли, состоящие из множества беспорядочно расположенных микрокристаллов графита, обычно используют для поглощения органических веществ в процессах очистки и разделения жидкостей и газов (паров). Эти адсорбенты получают сухой перегонкой ряда углеродсодержащих веществ (древесины, каменного угля, костей животных, косточек плодов и др.). После этого уголь активируют, например прокаливают его при температуре 850-900о С, что приводит к освобождению пор от смолистых веществ и образованию новых микропор. Активацию проводят также экстрагированием смол из пор органическими растворителями, окислением кислородом воздуха и др. Более однородная структура углей получается при их активации химическими методами: путем их обработки горячими растворами солей (сульфатами, нитратами и др.) или минеральными кислотами (серной, азотной и др.)
Качество активированных углей зависит от свойств исходных углеродсодержащих материалов и от условий активации. Характеристикой степени активации активированного угля является обгар, т. е. сгоревшая часть угля, выраженная в процентах от количества исходного материала.
Активированный уголь применяется при адсорбции либо в виде зерен величиной от 1 до 7 мм, либо в виде порошка. Зерна и порошок получают путем измельчения и классификации. Удельная активная поверхность активных углей выражается величиной от 600 до 1700 м2 на один грамм. Применяются активированные угли главным образом для поглощения паров органических жидкостей, находящихся в газовых смесях, и для очистки различных растворов от примесей.
Серьезным недостатком этих углей является горючесть, и применять их можно при температурах не выше 200°. Для уменьшения горючести к ним подмешивают силикагель, однако такая добавка приводит к понижению активности адсорбента, поэтому активированные угли с добавкой к ним силикагеля практически применяют сравнительно редко.
Силикагелем называют продукт обезвоживания геля кремневой кислоты, получаемого действием серной или соляной кислот или растворов кислых солей на раствор силиката натрия. Выпавший гель кремневой кислоты после промывки высушивается при температуре 115-130° до влажности 5-7%.
Силикагель отличается однородностью пор как по величине, так и распределению. Применяется силикагель в виде зерен диаметром от 0,2 до 7 мм главным образом для поглощения паров воды, т. е. для сушки газов. Удельная активная поверхность силикагеля выражается величиной порядка 600 м2 на один грамм.
К достоинствам силикагелей относятся их негорючесть и большая механическая прочность. Недостатком относится резкое снижение поглотительной способности по отношению к парам органических веществ в присутствии влаги.
По сорбционным свойствам к силикагелю близко примыкают алюмагели, получаемые термической обработкой гидроксида алюминия при температурах 600-1000оС. Поры полученного сорбента имеют диаметр 1-3 нм, удельную поверхность 2·10 5 - 4·10 5 м2/кг; насыпная плотность такого сорбента 1600 кг/м3. Алюмагели используют для осушки газов, очистки водных растворов и минеральных масел.
Цеолиты представляют собой природные или синтетические минералы, которые являются водными алюмосиликатами, содержащими оксиды щелочных щелочноземельных металлов. Эти адсорбенты отличаются регулярной структурой пор, размеры которых соизмеримы с размерами поглощаемых молекул. Особенность цеолитов состоит в том, что адсорбционные поверхности соединены между собой окнами определенного диаметра, через которые могут проникать только молекулы меньшего размера. На этом основано разделение смесей с разными по размеру молекулами, что послужило причиной называть цеолиты молекулярными ситами.
Для разделения газовых смесей применяют цеолиты в виде шариков или гранул размером от 1 до 5 мм, а для разделения жидких смесей - в виде мелкозернистого порошка.
referat911.ru
Курсовая работа
по дисциплине: Процессы и аппараты химической технологии
на тему: Адсорбция
Содержание
Введение
. Классификация процесса, основные определения
.1 Основные понятия процесса адсорбции
.2 Основные промышленные адсорбенты и их свойства
.3 Изотерма адсорбции
. Закономерности процесса адсорбции
.1 Теории адсорбции
.2 Адсорбция на границе раствор - пар
.3 Адсорбция на границе твердое тело - газ
.4 Адсорбция на границе твердое тело - раствор
.4.1 Молекулярная адсорбция из растворов
.4.2 Адсорбция из растворов электролитов
. Оборудование, реализующее процесс адсорбции
.1 Адсорбция с неподвижным слоем адсорбента
.2 Адсорбция силикагелем
.3 Гиперсорбция
.4 Адсорбция в кипящем (псевдоожиженном) слое
.5 Расчет адсорберов периодического действия
.6 Расчет адсорберов непрерывного действия
Заключение
Список использованной литературы
Введение
Адсорбцией называют процесс поглощения вещества из смеси газов, паров или растворов поверхностью или объемом пор твердого тела - адсорбента.
Явление адсорбции известно очень давно. Такие природные материалы, как песок и почва, использовали для очистки воды еще на заре человеческого общества. В конце XVIII века К. Шееле и одновременно Фонтана обнаружили способность свежепрокаленного древесного угля поглощать различные газы в объемах, в несколько раз превышающих его собственный объем. Вскоре выяснилось, что величина поглощенного объема зависит от типа угля и природы газа. Т.Е. Ловиц в 1785 году открыл явление адсорбции углем в жидкой среде, подробно исследовал его и предложил использовать уголь для очистки фармацевтических препаратов, спирта, вина, органических соединений. Ловиц показал, что древесный уголь способен быстро очищать испорченную воду и делать ее пригодной для питья. И сейчас основным действующим началом фильтров для воды служат углеродные материалы, конечно более современные, чем природные угли. Адсорбция отравляющих веществ из воздуха была использована Н.Д. Зелинским при создании противогаза во время первой мировой войны.
Адсорбция газов на твердых поверхностях используется в некоторых отраслях пищевой промышленности, а именно масложировой (например, в производстве маргарина) и в бродильной (например, в производстве дрожжей) для очистки технологических газовых потоков с целью предотвращения выбросов вредных веществ в атмосферу. Поглощение паров воды происходит на пористых веществах, которые выполняют роль твердого адсорбента. Подобные процессы наблюдаются в отношении сахара, соли и сухарей. Адсорбционный способ регулирования газового состава хранилищ скоропортящихся продуктов позволяет в несколько раз сократить потери и увеличить сроки хранения. Адсорбция различных пищевых кислот, лимонной в частности, снижает по сравнению с водой поверхностное натяжение большинства прохладительных напитков. Адсорбция веществ на поверхности раздела жидкость - газ способствует устойчивости пен. Подобный процесс имеет место в бродильной промышленности при производстве дрожжей и некоторых других полупродуктов. Усиление смачивания водой различных поверхностей широко используется в промышленности в качестве сопутствующего процесса при мойке оборудования, подготовке сырья, обработке полуфабрикатов и т.д. Адсорбция на границе твердое тело - жидкость широко применяется при очистке жидкостей (например, диффузионного сока при производстве сахара, растительных масел и соков) от примесей.
Развитие теории адсорбционных сил еще не достигло такой стадии, когда по известным физико-химическим свойствам газа и твердого тела можно было бы рассчитать изотерму адсорбции, не проводя экспериментальных исследований. Поэтому попыткам описать экспериментальные изотермы с помощью различных теоретических уравнений, которым соответствуют определенные модели адсорбции, посвящено огромное количество работ. Если теоретическое уравнение изотермы адсорбции хорошо воспроизводит экспериментальные данные, то можно рассчитать неизвестные величины адсорбции при разных условиях (р и Т) и определить различные геометрические параметры твердых тел. Рассмотрим лишь немногие, наиболее распространенные теоретические уравнения изотерм адсорбции.
1. Классификация процесса, основные определения
1.1 Основные понятия процесса адсорбции
Адсорбцией называется самопроизвольно протекающий диффузионный процесс взаимодействия двух фаз - твердого тела - адсорбента и газа, пара или растворенного вещества - адсорбтива, происходящий поглощением газа, пара или растворенного вещества поверхностью твердого тела.
Поглощение газов, паров и растворенных веществ твердыми телами обычно сопровождается процессами проникновения поглощаемого вещества в твердое тело (абсорбцией), капиллярной конденсацией и химическими реакциями (хемосорбцией), что весьма затрудняет изучение собственно адсорбции. Поэтому поглощение газов, паров и растворенных веществ твердыми телами обычно рассматривается как общий процесс сорбции.
Адсорбция всегда сопровождается выделением тепла. В большинстве случаев тепловой эффект адсорбции по своей величине приближается к теплоте конденсации поглощаемого газа или пара.
Адсорбцию подразделяют
www.studsell.com
Понятие адсорбции. Автоадсорбция. Адсорбент и адсорбат. Абсолютная и Гиббсовская адсорбция. Единицы измерения адсорбции. Зависимость величины адсорбции от концентрации, давления и температуры. Изотерма, изобара, изопикна, изостера адсорбции
Адсорбция — процесс самопроизвольного перераспределения компонентов системы между поверхностным слоем и объемом фазы.
Адсорбция может наблюдаться в многокомпонентных системах и при перераспределении в поверхностный слой уходит тот компонент, который сильнее понижает поверхностное натяжение. В однокомпонентной системе при формировании поверхностного слоя происходит изменение его структуры — уплотнение, которое называется автоадсорбцией .
В общем случае адсорбция может происходить не только благодаря стремлению поверхностной энергии к уменьшению, но и за счет химической реакции компонентов с поверхностью вещества. В этом случае поверхностная энергия может даже увеличиваться на фоне снижения энергии всей системы.
Вещество, на поверхности которого происходит адсорбция, называется адсорбентом , а вещество, которое перераспределяется – адсорбатом .
Обратный процесс перехода вещества с поверхности в объем фазы — десорбция.
В зависимости от агрегатного состояния фаз различают адсорбцию газа на твердых адсорбентах, твердое тело – жидкость, жидкость — жидкость, жидкость — газ. Для количественного описания адсорбции применяют две величины: первая измеряется числом молей или граммами, приходящимися на единицу поверхности или массы адсорбента:
А = m 1 / m 2 — абсолютная адсорбция, А = ni / S .
Величина, определяемая избытком вещества в поверхностном слое, также отнесенным к единице площади поверхности или массы адсорбента, называется Гиббсовской или относительной адсорбцией (Г).
Адсорбция зависит от концентрации компонентов и температуры.
А = f ( c , T ) — жидкость;
А = f ( P , T ) — газ
Различают следующие виды зависимостей:
| 1. Изотерма (рис. 8) | 2. Изобара | 3. Изостера |
| А =fT (c) | А =fP (T) | c=fA (T) |
| A=fT (P) | A=fC (T) | P=fA (T) |
Считаем V поверхности раздела = 0.
dU = TdS + s dS +
Проинтегрировав, получим: U = TS + sS +
Полный дифференциал от этого уравнения:
dU = TdS + SdT + s dS + + Sd s + .
Подставляя значение dU из (6) в (7) и сократив одинаковые члены правой и левой части, получим:
SdT + Sd s + = 0.
Предположим, что T = const:
Разделив правую и левую часть на поверхность S, получим фундаментальное адсорбционное уравнение Гиббса:
; ;
.
Определение зависимости поверхностного натяжения от адсорбции одного компонента, при постоянстве химических потенциалов других компонентов.
.
Известно, что , , (где , — равновесный и стандартный химический потенциал компонента i; lnai — логарифм активности i –го компонента). Тогда уравнение Гиббса будет выглядеть так
Активность связана с концентрацией: с = × а. Предположим, что = 1 (при с ® 0). Тогда
— для жидкости и газа
Обычно уравнение Гиббса применяют для растворов. Растворителем может быть не только индивидуальное вещество, но и смесь. В разбавленных растворах гиббсовская адсорбция очень мала, а его химический потенциал меняется очень мало с изменением концентрации растворенного вещества, т.е. d m= 0. Поэтому для разбавленного раствора фундаментальное уравнение Гиббса выглядит так:
Из этих уравнений следует, что зная зависимость = f (С) (где С — концентрация растворенного вещества), можно рассчитать изотерму адсорбции, пользуясь адсорбционным уравнением Гиббса. Схема графического расчета показана на рис. 2.2.2.1: Тангенс угла наклона соответствует значениям производных в этих точках.
Зная эти производныеуравнения Гиббса, можно рассчитать значение Г, что позволяет построить зависимость Г = f (С). Уравнение Гиббса показывает, что единица измерения гиббсовской адсорбции не зависит от единицы измерений концентрации, а зависит от размерности величины R. Так как величина R отнесена к молю вещества, а s - к единице площади, то Г = [моль/ единица площади]. Если s выразить в [Дж/м2 ], то R нужно подставлять: R = 8,314 Дж/моль×К.
В уравнении Гиббса влияние природы вещества на адсорбцию отражается производной. Эта производная определяет и знак гиббсовской адсорбции, и может служить характеристикой вещества при адсорбции. Чтобы исключить влияние концентрации на производную берут ее предельные значения, т.е. при стремлении концентрации к нулю. Эту величину Ребиндер назвал поверхностной активностью .
;
g = [Дж×м/моль] = [Н×м2 /моль]; [эрг см/моль] = [Гиббс].
Уравнение показывает, что чем сильнее снижается = f ( c ) с увеличением концентрации, тем больше поверхностная активность этого вещества.
Физический смысл поверхностной активности состоит в том, что она представляет силу, удерживающую вещество на поверхности и отнесенную к единице гиббсовской адсорбции .
Поверхностную активность можно представить как отрицательный тангенс угла наклона к касательной, проведенной к кривой Г = f ( C ) в точке пересечения с осью ординат. Поверхностная активность может быть положительной и отрицательной. Значение и знак ее зависят от природы растворенного вещества и растворителя.
1. 2 <1, тогда <0 и Г>0: g >0 Þ с увеличением концентрации поверхностное натяжение на границе раздела фаз убывает и вещество поверхностно-активно .
1. 2 <1 , тоg <0 :Г <0 Þ вещество поверхностно-инактивно .
2. g = 0, Г = 0 — адсорбции нет, т.е. вещество индифферентно .
Поверхностно-активными веществами являются органические вещества, состоящие из углеводородного радикала и функциональной группы. Неорганические соли являются поверхностно-инактивными веществами. Ребиндер и Щукин в своих работах показали, что развитие микротрещин в твердых телах при деформации может происходить гораздо легче при адсорбции веществ из среды, в которой ведется деформирование: адсорбироваться могут как ионы электролитов, так и молекулы поверхностно-активного вещества (ПАВ), образуя на адсорбирующей поверхности их двумерный газ в результате нелокализованной адсорбции. Молекулы под давлением этого газа проникают в устье трещин и стремятся раздвинуть их, таким образом содействуя внешним силам, т.е. наблюдается адсорбционное понижение твердости твердого тела, что получило название эффекта Ребиндера. Поверхностная активность в гомологическом ряду поверхностно-активных веществ (ПАВ) повышается в среднем в 3,2 раза на каждую группу СН2 (в водных растворах) – правило Дюкло – Траубе .
Адсорбционное равновесие в системе «газ – жидкость». Закон Генри. Мономолекулярная адсорбция в системах «газ – жидкость», «жидкость – жидкость», «газ – твердое». Изотерма адсорбции Ленгмюра. Уравнение Фрейндлиха. Теория полимолекулярной адсорбции БЭТ. Уравнение БЭТ
Предположим, что имеются компоненты-неэлектролиты. Будем считать, что адсорбат образует на поверхности адсорбента мономолекулярный слой. Мономолекулярная адсорбция с точки зрения термодинамики процесса выражается химическим потенциалом в адсорбционном слое и объемной фазе:
;
;
,
где — химический потенциал вещества в адсорбционном слое;
— химический потенциал вещества в объемной фазе.
При равновесии потенциалы равны: .
Преобразуем:
; – адсорбция; а i = c .
,
, где D — коэффициент распределения.
Выражение — константа Генри. Она не зависит от концентрации, определяется при постоянной температуре, A / a = K г ,
А=а × Кг – закон Генри, т.е. при разбавлении системы коэффициент распределения стремится к постоянному значению, равному константе Генри. Если концентрация в сорбционном слое стремится к нулю, то а » с; а = × с; - 1. Поэтому на практике закон Генри используют в следующем виде: а=Кг с i. Если одна из фаз – газ, то имеем следующий вид: a = Кг Р i,
Кг = Кг/ RT .
Эти уравнения представляют собой уравнения изотермы адсорбции при малых концентрациях. В соответствии с этими уравнениями можно по другому сформулировать закон Генри: величина адсорбции при малых давлениях газа (малых концентрациях вещества в растворе) прямо пропорциональна давлению (концентрации). Эти зависимости показаны на рисунке 2.3.1.1. При адсорбции на твердых телах область действия закона мала из-за неоднородности поверхности, но даже на однородной поверхности при увеличении концентрации обнаруживается отклонение от закона. При малых концентрациях распределенного вещества отклонения обусловлены в основном соотношением между взаимодействием молекул друг с другом и с поверхностью адсорбента. Если когезионные взаимодействия адсорбата больше, то отклонение от закона отрицательно и <1, и коэффициент распределения увеличивается (кривая 1 на рис. 2.3.1.1). Если сильнее взаимодействие «адсорбат – адсорбент», то отклонение положительно и D уменьшается (кривая 2 на рис. 2.3.1.1). При дальнейшем увеличении концентрации происходит уменьшение свободной поверхности, снижается реакционная способность и кривые загибаются к оси абсцисс. Константу Генри получают экстраполяцией коэффициента распределения на нулевую концентрацию. В соответствии с правилом фаз Гиббса в гетерогенных системах равновесные параметры зависят от дисперсности или удельной поверхности. Для адсорбционных систем эта зависимость выражается в уменьшенных концентрациях вещества в объемной фазе с увеличением удельной поверхности адсорбента. Если в такой системе содержание распределяемого вещества постоянно, то
А mS уд + с V = const,
где m — масса адсорбента;
S уд — удельная поверхность адсорбента;
V — объем фазы, из которой извлекается вещество;
const – постоянное количество вещества в системе.
,
или: разделим второй член на с ;
D — коэффициент распределения;
; .
Из соотношения следует, что с увеличением удельной поверхности при постоянной концентрации адсорбата концентрация уменьшается и тем сильнее, чем больше константа Генри и меньше объем фазы.
Теория Ленгмюра позволяет учесть наиболее сильные отклонения от закона Генри, что связано с ограничением адсорбционного объема или поверхности адсорбента. Ограниченность этого параметра приводит к адсорбционному насыщению поверхности адсорбента по мере увеличения концентрации распределяемого вещества. Это положение уточняется следующими утверждениями.
1. Адсорбция локализована на отдельных адсорбционных центрах, каждый из которых взаимодействует только с одной молекулой адсорбента — образуется мономолекулярный слой.
2. Адсорбционные центры энергетически эквивалентны — поверхность адсорбента эквипотенциальна.
3. Адсорбированные молекулы не взаимодействуют друг с другом.
Ленгмюр предположил, что при адсорбции происходит квазихимическая реакция между распределяемым компонентом и адсорбционными центрами поверхности:
,
где А — адсорбционые центры поверхности;
В — распределенное вещество;
АВ — образующийся комплекс на поверхности.
Константа равновесия процесса: ,
где сав = А — величина адсорбции;
са = А0 = А ¥ — А,
где А ¥ — емкость адсорбционного монослоя или число адсорбционных центров, приходящихся на единицу поверхности или единицу массы адсорбента; А 0 — число оставшихся свободных адсорбционных центров, приходящихся на единицу площади или единицу массы адсорбента; с в – концентрация распределенного вещества.
Подставляя величину концентрации в уравнение константы, получим выражения
, св = с ,
А = А ¥ Кс – АКс, — для жидкостей;
— для газов.
Эти выражения – уравнения изотермы адсорбции Ленгмюра. К и Кр в уравнении характеризуют энергию взаимодействия адсорбента с адсорбатом. Адсорбционное уравнение часто представляют относительно степени заполнения поверхности, т.е. как отношение А/А ¥ :
,
.
Экспериментальные результаты по определению изотермы адсорбции обычно обрабатывают с помощью уравнения, записанного в линейной форме;
, т.е. уравнение типа y = b + ax .
Такая линейная зависимость позволяет графически определить А ¥ иК. Зная А ¥, можно определить удельную поверхность адсорбента (поверхность единицы массы адсорбента):
,
где А ¥ — предельная адсорбция, выражаемая числом молей адсорбата на единицу массы адсорбента;
NA – число Авогадро;
w0– площадь, занимаемая одной молекулой адсорбата.
1. Если с- 0, тогда уравнение примет вид:
А=А ¥ Кс ;; А = Кг с, q =Кс ,
т.е. при с- 0 уравнение Ленгмюра переходит в уравнение Генри.
2. Если с-¥, тогда А = А ¥ , А/А ¥ = 1. Это случай предельной адсорбции.
3. Пусть адсорбция идет из смеси компонентов, в этом случае уравнение Ленгмюра записывается следующим образом:
.
Все рассмотренные выше уравнения справедливы для мономолекулярной адсорбции на адсорбенте с энергетически эквивалентными адсорбционными центрами. Однако реальные поверхности этим свойством не обладают. Приближенной к реальности является возможность распределения адсорбционных центров по энергии. Приняв линейное распределение, Темкин использовал формулу уравнения Ленгмюра и получил уравнение для средних степеней заполнения адсорбента.
,
где — константа, характеризующая линейное распределение;
К 0 — константа уравнения Ленгмюра, отвечающая максимальной теплоте адсорбции.
Из уравнения следует, что увеличение парциального давления (из-за увеличения концентрации) одного компонента подавляет адсорбцию другого и тем сильнее, чем больше его адсорбционная константа равновесия. Уравнение часто называют логарифмической изотермой адсорбции. Если принять экспоненциальное распределение центров по поверхности, то в области средних заполнений получается ранее найденное эмпирическим путем уравнение Фрейндлиха :
.
Прологарифмировав, получим ,
где K , n – постоянные.
Использование уравнения Фрейндлиха в логарифмической форме позволяет определить константу уравнения.
Уравнение Ленгмюра можно использовать только при адсорбции в мономолекулярном слое. Это условие выполняется при хемосорбции, физической адсорбции газов при меньшем давлении и температуре выше критической. Однако в большинстве случаев мономолекулярный адсорбционный слой не компенсирует полностью избыточную поверхностную энергию и поэтому остается возможность влияния поверхностных сил на второй и т.д. адсорбционные слои. Это реализуется в том случае, когда газы и пары адсорбируются при температуре ниже критической, т.е. образуются полимолекулярные слои на поверхности адсорбента, что можно представить как вынужденную конденсацию (рис. 2.3.1.2 и 2.3.1.3).
В результате этих представлений была выведена следующая формула:
— уравнение полимолекулярной адсорбции БЭТ ,
где ;
KL = a ж /ап – константа конденсации пара;
аж — активность вещества в жидкости;
ап — активность вещества в состоянии насыщенного пара;
ап = Р s .
Физический смысл С: характеризует разность энергии Гиббса в процессах чистой адсорбции и конденсации. Это уравнение получило название БЭТ (Бранауэр-Эммет- Теллер ).
При р/р s <<1, уравнение БЭТ превращается в уравнение Легмюра, которое при дальнейшем уменьшении давления (Р- 0) переходит в закон Генри:
.
При обработке экспериментальных данных уравнение БЭТ используют в линейной форме (рис. 2.3.1.4):
; ,
таким образом графически находят обе константы уравнения А¥ и С.
www.ronl.ru
V=V 0exp[-( e/E)n ] 