
(2часа - авто и эзс, 4 часа – арх)
1. Сходящиеся силы – силы, линии действия которых пересекаются в одной точке (построение силового многоугольника) – рис а,б

– по рис в.
1. Проектируем векторное равенство  +
+ +
+ =
= на оси координат
на оси координат
2. Получаем алгебраические равенства:

3. Отсюда определим значение равнодействующей всех сходящихся сил:

4. И направление вектора 
Cosα = Rx\R
Cosβ = Ry\R
1. При геометрическом способе сложения - равенство нулю равнодействующей  – т.е. силовой многоугольник должен быть замкнут
– т.е. силовой многоугольник должен быть замкнут
2. При аналитическом способе сложения – проекции равнодействующей силы на оси координат должны быть равны нулю (Rx= Ry = 0)
Отсюда для плоской системы сходящихся сил два уравнения равновесия этих сил:
∑Fix =0 ∑Fiу =0
Вывод: для равновесия системы сходящихся сил необходимо и достаточно, чтобы сумма проекций всех сил на каждую из осей координат была равна нулю.

- Тело находится в равновесии под действием двух сил  и
и  ( рис. 16в),
( рис. 16в),
- Следовательно, по аксиоме 1 они должны иметь общую линию действия,
- тогда  ,
, 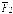 и
и  лежат в одной плоскости, их линии действия пересекаются в точке
лежат в одной плоскости, их линии действия пересекаются в точке 
1. При равновесии плоской системы сходящихся сил, приложенных к одному телу, число неизвестных величин не должно превышать двух (условие статической определимости):
А) неизвестна одна сила (модуль и направление)
Б) неизвестны направления двух сил системы
В) неизвестны: модуль одной силы и направление другой;
Г) неизвестны модули двух сил.
2. Методы решения задач на равновесие системы сходящихся сил:
А) графический - во всех четырех случаях можно построить замкнутый силовой многоугольник и найти в нем неизвестные величины.
Б) графо-аналитический – для равновесия трех сил: произвольном масштабе строится замкнутый треугольник, решается на основе геометрических либо тригонометрических соотношений.
В) аналитический (метод проекций) - для решения задач с числом сил больше трех.
Самостоятельная работа обучающихся по теме 1.2. – (эзс, арх - 3 часа)
1. Решить задачи на определение усилий в стержнях ферм по вариантам
2. Составить краткий алгоритм решения задач на равновесие плоской системы сходящихся сил
Авто – 2 часа
1. Выполнение расчётно-графической работы по определению реакций связей плоской системы сходящихся сил аналитически и графически
(1 час – все)
1. Сила действует на тело и может:
А) смещать его;
Б) поворачивать вокруг точки

2. Пусть сила  , приложенная в точке А, стремится повернуть тело вокруг точки О
, приложенная в точке А, стремится повернуть тело вокруг точки О
3. Вращательный моментэтой силы будетзависеть отрасстоянияh- от точки О до линии действия силы (ине зависеть от точки приложения силы– так как силу можно переносить по линии её действия)
4. Момент силы относительно точки (центра О) называется величина = сила ×на кратчайшее расстояние: от точки О до линии действия силы с соответствующим знаком.
5. Правило знаков:
А) знак «+» - момент (изгиб) силы, которая стремится повернуть тело вокруг точки О против хода часовой стрелки.
Б) знак «-» - по ходу часовой стрелки.
В) если линия действия силы проходит через точку, то момент силы относительно этой точки = нулю.
6. Плечо относительно центра О – перпендикуляр из точки О на линию действия силы 
studfiles.net
Количество просмотров публикации Система сходящихся сил - 755
Лекция 2
Системой сходящихся сил (ССС) принято называть такая система сил, линии действия которых пересекаются в одной точке.
ССС эквивалентна равнодействующей силе, которая равна векторной сумме слагаемых сил. Точка приложения равнодействующей силы совпадает с точкой пересечения линий действия сил.
Решение многих задач механики связано с операциями сложения сил.
Определение. Вектор, равный геометрической сумме системы сил, принято называть главным вектором системы сил.
Не путать с понятием равнодействующей!
Главный вектор определяется всегда для любой системы сил. Но существуют системы сил, которые нельзя заменить равнодействующей – пара сил, скрещивающиеся силы.
Операции сложения сил и разложение сил на составляющие
1. Сложение двух сил: .
Выполняется по правилу параллелограмма или путем построения силового треугольника.
Модуль силы находится с помощью теоремы косинусов или теоремы синусов:
R = ,
.
2.Сложение трех сил, не лежащих в одной плоскости: .
Операция сводится к нахождению диагонали параллелепипеда, построенного на этих силах. В простейшем случае параллелепипед прямоугольный (рис.1-9)
| | Модуль вектора находим по формуле:
|
3.Сложение системы сходящихся сил: .
Операция сложения выполняется либо последовательным применением к системе сил правила параллелограмма, либо путем построения силового многоугольника (рис.1-9).
4.Разложение силы на составляющие.
Операция, обратная сложению сил. Может быть выполнена неоднозначно. Необходимо задать направления составляющих сил. Наиболее часто встречаются два случая:
1) Разложение силы на две составляющие: .
Операция сводится к нахождению сторон параллелограмма, у которого известна диагональ R и углы, образованные с диагональю линиями действия составляющих сил. Ниже показаны три варианта разложения силы на составляющие: . Модули составляющих сил находятся по теореме синусов при известных значениях углов.
2) Разложение силы на три составляющие, не лежащие в одной плоскости:
.
Операция сводится к нахождению сторон параллелепипеда, у которого известной является диагональ.
Аналитический способ нахождения равнодействующей ССС
Аналитические методы решения задач механики основаны на методах проекций.
Аналитический способ задания силы.
В декартовых координатах приложенный в заданной точке А вектор можно задать двумя способами.
| 1) - задать координаты точки А (x,y,z), - задать модуль вектора F, - задать углы α, β, γ, образованные вектором с осями координат. | |
2) - задать координаты точки А (x,y,z),
- определить проекции вектора на оси координат: Fx, Fy, Fz.
- определить модуль вектора и направляющие косинусы:
F = ,
.
Аналитический способ нахождения равнодействующей
Используется теорема геометрии: Проекция вектора суммы на какую-либо ось равна алгебраической сумме проекций слагаемых сил на ту же ось.
Модуль равнодействующей и направляющие косинусы:
R =,
.
Главный вектор и равнодействующая ССС
Главный вектор и равнодействующая ССС находятся по правилу параллелограмма: , следовательно, эти два определения для ССС совпадают.
Необходимые и достаточные условия равновесия ССС
Формулируются в геометрической и аналитической форме.
1. Геометрическая форма. Для того, чтобы ССС находилась в равновесии крайне важно и достаточно, чтобы главный вектор (равнодействующая) равнялся нулю
= 0.
2.Аналитическая форма.
R == 0, в случае если выполняются три условия:
1) , 2)
3)
Для того, чтобы ССС находилась в равновесии крайне важно и достаточно, чтобы алгебраические суммы проекций всех сил на каждую их трех координатных осей равнялись нулю.
Каждое из условий соответственно означает, что тело под действием ССС не совершает линейные перемещения вдоль координатных осей x,y,z.
referatwork.ru
Количество просмотров публикации Система сходящихся сил - 1069
Плоской системы сил
Система сходящихся сил. Условия равновесия
Лекция 2.
Системой сходящихся сил (или пучком сил) принято называть такая система сил, линии действия которой пересекаются в одной точке – центре пучка.
Равнодействующая системы сходящихся сил равна векторной сумме слагаемых сил и определяется замыкающей стороной силового многоугольника, построенного на слагаемых силах как на составляющих. Точка приложения равнодействующей силы совпадает с точкой пересечения линий действия сил.
Проекции равнодействующей силы на оси координат равны алгебраической сумме проекций составляющих сил на эти оси.
Рис. 2.1
Условия равновесия системы сходящихся сил в векторной форме
Для равновесия сходящейся системы сил, приложенных к твердому телу, крайне важно и достаточно, чтобы равнодействующая сила была равна нулю.
Условия равновесия системы сходящихся сил в алгебраической форме
Для равновесия пространственной системы сходящихся сил, приложенных к твердому телу, крайне важно и достаточно, чтобы суммы проекций всех сил на каждую из трех прямоугольных осей координат были равны нулю.
Пример 2.1. Груз весом Q равномерно поднимается тросом лебедки, перекинутым через неподвижный блок, который подвешен на двух шарнирно закрепленных стержнях. Пренебрегая размерами блока, трением и весом каната͵ определить усилия Т1 и Т2 в стержнях (рис. 2.2. а).
Рис. 2.2
Применяя аксиому об освобождаемости от связей и считая, что натяжение каната на участке между лебедкой и блоком равно весу Q груза, составим расчетную схему (рис.2.2.б).
Учитывая условия равновесия для плоской системы сходящихся сил, запишем:
;
;
;
.
Как видно, получена система двух линейных уравнений с двумя неиз-вестными, решая которую определяем усилия Т1 и Т2 в стержнях.
В случае если в результате решения получается отрицательная реакция связи, то крайне важно старое направление этой реакции заменить на противоположное, отбросив минус.
Для проверки правильности решения крайне важно полученные значения реакций Т1 и Т2 подставить в систему уравнений и убедиться в их тождестве.
Системой сходящихся сил называют такую систему сил, линии действия которых пересекаются в одной точке – центре пучка. Сходящиеся системы сил могут быть пространственными и плоскими. Рассмотрим общий случай пространственной системы сходящихся сил. Применяя к... [читать подробнее].
Лекция 2 Системой сходящихся сил (ССС) называется такая система сил, линии действия которых пересекаются в одной точке. ССС эквивалентна равнодействующей силе, которая равна векторной сумме слагаемых сил. Точка приложения равнодействующей силы совпадает с точкой... [читать подробнее].
Системой сходящихся сил (или пучком сил) называется такая система сил, линии действия которой пересекаются в одной точке – центре пучка. Равнодействующая системы сходящихся сил равна векторной сумме слагаемых сил и определяется замыкающей стороной силового... [читать подробнее].
2.1. Система сходящихся сил и ее равнодействующая сила Система сил, линии действия которых пересекаются в одной точке, называется системой сходящихся сил. Точка, в которой пересекаются линии действия всех сил, называется точкой схода (рисунок 2.1). Следствие из 2-й аксиомы... [читать подробнее].
Сходящимися называются силы, линии действия которых пересекаются в одной точке. Равнодействующая сходящихся сил равна геометрической сумме этих сил и приложена в точке их пересечения . Равнодействующая может быть найдена геометрич. способом – построением силового... [читать подробнее].
referatwork.ru