ВВЕДЕНИЕ.
Целью моей работы было исследование и приминение свойств параллельного проектирования при изображениии фигур на плоскости и при построении сечений многогранников. Я выбрала данную тему потому что передо мной стояла задача научиться быстро и точно производить различные построения. Актуальность темы заключается в том, что построение сечение широко используется в строительном деле, архитектуре, машиностроении, геодезии, во многих других областях науки и техники, а в школьном курсе геометрии решение такого типа задач уделяется очень мало времени. В работе были использованы задачи, теоремы, аксиомы, свойства, которые являются методами и приемами изучения данной темы. Также были использованны научные пособия таких авторов как А.В. Бубенков, М.Я. Громов (Начертательная геометрия), С. А. Фролов (Начертательная геометрия), А.А. Беклемшнева (Сборник задач по аналитической геометрии и линейной алгебре).
Геометрические задачи традиционно делятся на три типа:
1. на вычисление;
2. на доказательство;
3. на построение.
Решение любых стереометрических задач требует не только вычислительных и логических умений и навыков, но и умений изображать пространственные фигуры на плоскости (например, на листке бумаги, классной доске), что по сути своей тесно связанно с темой Геометрические построения на плоскости. Стереометрические задачи на вычисления и доказательство легко можно решать, используя правильный рисунок пространственной фигуры. При изучении тем Параллельность прямых и плоскостей в пространстве, Перпендикулярность прямых и плоскостей, Углы между прямой и плоскостью, между двумя прямыми, между двумя плоскостями и других тем прекрасным иллюстрационным материалом является решение позиционных и метрических задач на построение пространственных фигур и сечений этих фигур плоскостями. [1].
ОСНОВНАЯ ЧАСТЬ
1. Основные понятия теории изображения фигур.
1.1. Параллельное проектирование и его свойства.
Параллельное (цилиндрическое) проецирование можно рассматривать как частный
случай центрального проецирования с несобственным центром. Здесь предмет
рассматривают с бесконечно удаленной точки зрения.
Чертежи геометрических образов в ортогональных проекциях широко применяются в
начертательной геометрии. Они просты в построениях, дают возможность легко
производить различные измерения геометрических образов и определять
взаимоположение отдельных элементов.
Пусть в евклидовом пространстве дана некоторая плоскость По и вектор р + По. Пусть М
- любая точка пространства, не принадлежащая плоскости По. Проведем прямую l || р
через М, тогда l ∩ По = (Мо). Мо называют проекцией точки М на плоскость По. Если р ┴ По, то Мо - ортогональная проекция точки М на По. Если М € По, то Мо=М. (рис. 1а и 16)
Множество Fо проекций точек данной фигуры F на плоскость По называется проекцией фигуры F на плоскость По.
Легко показать, что параллельное проецирование, как отображение множества точек пространства во множество точек плоскости По, обладает свойствами (рис. 2а, б, в)
1. Проекцией прямой l является прямая lо, если , если то проекцией прямой l является точка Lо, где (Lо) = l ∩ По.
2. Проекцией параллельных прямых являются параллельные прямые или совпавшие прямые, или две точки.
3. Коллинеарные точки А, В, С проектируются в коллинеарные точки Ао, Во, Со.
4. Неколлинеарные точки А, В, С, лежащие в плоскости П, не параллельной вектору р, проектируются в неколлинеарные точки Ао, Во, Со.
5. Сохраняется отношение лежать между для трех коллинеарных точек А, В, С, если
6. Сохраняется простое отношение трех точек А, В, С, если
7. Если отрезок (луч) АВ не параллелен вектору р, то проекцией АВ является отрезок (луч) АоВо (рис.3)
8. Проекцией пересекающихся прямых являются пересекающиеся прямые или совпадающие прямые.
9. Проекцией скрещивающихся прямых являются пересекающиеся прямые или параллельные прямые, или совокупность точки и прямой (рис. 4а, 46, 4в).
10. Проекцией угла АВС является угол АоВоСо в общем случае ему неравный. (плоскость АВС || р ).
11. Если две фигуры F и Ф - плоские и плоскости в которых они лежат
параллельны между собой, но не параллельные p, то отношение площадей проекций Fо и Фо равно отношению площадей самих фигур F и Ф
Если F - проектируемая фигура при параллельном проецировании, заданном вектором р на плоскость По, то F называют оригиналом, р , направлением проецирования, По - плоскостью проекции, Fо - проекция фигуры на плоскость По. Если некоторая фигура F плоскости П подобна фигуре Fо плоскости По, то F может быть принята за изображение фигуры, т.е. изображением фигуры может являться любая фигура F, подобная параллельной проекции Fо. [4]
1.2. Требования к чертежу
Я установила, что первым и важнейшим шагом решения геометрической задачи является построение чертежа, соответствующего условию. Если задача планиметрическая, то чертеж является либо копией оригинала, либо ему подобен. При изображении пространственных фигур возникают трудности, ибо не может плоская фигура быть подобной пространственной. Чертеж должен удовлетворять некоторым требованиям, способствующим наилучшему восприятию изображения пространственной фигуры.
Прежде всего, чертеж должен быть верен, т, е. представляет собой фигуру, подобную произволь
www.studsell.com
Учителю, работающему в начальных классах, часто приходится изображать различные фигуры. Для грамотного изображения фигур, выполнения несложных чертежей необходимо следовать определенным правилам. В математике изображение фигур основано на знании и использовании параллельного проектирования. Выясним, что понимают под словами «параллельное проектирование», «изображение фигуры».
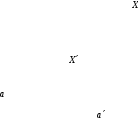
Пусть дана плоскость и пересекающая ее прямая a. Возьмем в пространстве произвольную точку X. Если точка X не лежит на , проведем через X прямую a´ || a. Прямая a´ пересекает плоскость в некоторой точке X´. Эта точка X´ является проекцией точки X на плоскость при проектировании параллельно прямой a.
Если точка X лежит на прямой a, то ее проекцией будет точка пересечения a с .
Если X, то X´ совпадает с X.
Прямая a задает направление проектирования.
Различают косоугольное параллельное проектирование и ортогональное параллельное проектирование. Если направление проектирования задает произвольная прямая, пересекающая плоскость , то имеем дело обычно с косоугольным проектированием. В случае, если прямая a, задающая направление проектирование, перпендикулярно плоскости , говорят об ортогональном проектировании.
Отображение, сопоставляющее каждой точке X фигуры F ее параллельную проекцию X´F´, называется параллельным проектированием фигуры F. Фигура F´ является проекцией фигуры F.
При параллельном проектировании выполняются следующие свойства:
проекция прямой есть прямая, проекция отрезка – отрезок;
проекции параллельных прямых параллельны или совпадают;
отношение длин проекций отрезков, лежащих на одной прямой или на параллельных прямых, равно отношению длин самих отрезков.
Эти свойства известны из школьного курса стереометрии, их легко проверить с помощью модели куба в лучах проектора или в солнечных лучах при условии, что лучи от источника света близки к параллельным.
Под изображением фигуры понимают ее параллельную проекцию на плоскость изображения или фигуру, подобную параллельной проекции.
Рассмотрим, какие требования предъявляются к изображению, используемому в школе на уроках математики, географии, биологии и т.д.
Изображение фигуры должно быть, прежде всего, верным. Это означает, что изображение должно представлять собой одну из проекций изображаемой фигуры или фигуру, подобную проекции. Средством достижения данного требования является использование параллельного проектирования.
Кроме того, изображение должно быть наглядным. Это требование означает, что изображение должно вызывать пространственное представление оригинала (изображаемой фигуры) наиболее точно и полно. Для достижения этого требования служат использование штриховых линий, цвета, особое расположение оригинала по отношению к плоскости изображения. Так, например, квадрат может быть верным изображением куба (проектирующая прямая совпадает с ребром куба, а плоскость, параллельная перпендикулярной ему грани куба- плоскость изображения), но вряд ли такое изображение можно признать наглядным.
Изображение не должно содержать каких-либо построений, не имеющих отношения к рассматриваемой задаче. На изображении, чертеже должно быть только самое необходимое, т.е. изображение должно быть простым. Понятно, что это отлично от того, что требуется на уроках черчения.
Построение изображения фигуры в педагогическом процессе отличается от тех требований, которые предъявляют к изображению, точнее к чертежу, в технических дисциплинах. Ясно, что при изготовлении какой либо детали требуется чтобы рабочий абсолютно точно воссоздал оригинал по его чертежу – изображению. Тогда схема построения изображения примерно выглядит так: Дан оригинал – деталь; выбирается определенный проектирующий аппарат, например известная из уроков черчения кабинетная проекция; этими данными изображение вполне определено. Это и означает, что рабочий может воссоздать оригинал.
В педагогическом процессе, напротив, дан не оригинал, а условия, которым он должен удовлетворять; проектирующий аппарат и положение оригинала относительно плоскости проекции остаются неопределенными; в результате и изображение является неопределенным. Но изображение отнюдь не произвольно!
Главный педагогический принцип: неопределенность не должна нарушить верности!
Какие теоретические положения лежат в основе построения изображений? Перечислим их. Прежде всего, как уже было сказано, это свойства параллельной проекции:
проекция прямой есть прямая, проекция отрезка – отрезок;
проекции параллельных прямых параллельны или совпадают;
отношение длин проекций отрезков, лежащих на одной прямой или на параллельных прямых, равно отношению длин самих отрезков.
Кроме того, важны следующие теоремы:
Теорема 1. Любой данный треугольник может быть изображен произвольным треугольником.
Это означает, что какой бы наперед заданный треугольник, равнобедренный, прямоугольный или какой-либо другой мы не взяли, его изображением может служить абсолютно произвольный треугольник. В истинности этой теоремы можно убедиться на опыте. Взяв треугольник определенной формы, вращая его в лучах проектора, увидим, что его тенью на экране, изображением в параллельной проекции может быть любой треугольник. (Помним, что лучи проекционного аппарата должны быть по возможности параллельными.)
Теорема 2. Если дано изображение треугольника, то однозначно определено изображение каждой точки, принадлежащей плоскости этого треугольника.
Данная теорема говорит о том, что как только получено изображение треугольника, произвол закончился. Рассмотрим это на примере. Пусть дан прямоугольный треугольник A´B´C´, в этом треугольнике из вершины прямого угла A´ проведен луч A´K´, делящий гипотенузу в отношении 1:2. На продолжении луча отложена точка M´ так, что отрезок K´M´ равный отрезку A´K´.
Изображением треугольника A´B´C´ служит произвольный треугольник ABC. Точка K делит сторону BC в том же отношении 1:2, считая от точки B. Этот факт вытекает из третьего свойства параллельной проекции. Следовательно, луч AK проводим на изображении не произвольно. Затем на его продолжении откладываем точку M вновь не произвольно, а так, чтобы отрезок KM был равен отрезку AK.
Теорема 3 (Польке-Шварца) Всякий невырожденный четырехугольник вместе с его диагоналями можно рассматривать как параллельную проекцию тетраэдра любой наперед заданной формы.
Невырожденный четырехугольник представляет собой любой плоский четырехугольник, т.е. замкнутую ломаную линию, составленную из четырех звеньев так, чтобы никакие два звена не лежали на одной прямой.
Тетраэдром в обще принятом смысле считают любую треугольную пирамиду. В противоположность этому иногда тетраэдром называют только правильную треугольную пирамиду. В данной теореме используется первое истолкование. Действительно, четырехугольник АВСД может быть рассмотрен как изображение пирамиды, основанием которой является треугольник АВД, а вершиной точка С. Конечно, требование наглядности здесь несколько нарушено. Отрезок ВД должен быть изображен пунктирной линией как невидимый. Хотя, если модель тетраэдра проволочная – то все линии будут видимыми.
На основании рассмотренных теорем можно начертить верное изображение любой пространственной фигуры, то есть решить прямую задачу: дан объект (оригинал) – изобрази его на плоскости!
Однако по полученному верному изображению не всегда можно судить о взаимном расположении элементов оригинала. Для решения обратной задачи - дано изображение, требуется выяснить, каким условиям отвечает оригинал, как расположены его элементы друг относительно друга – нужны дополнительные усилия.
studfiles.net
Лекция 1.Параллельное проектирование и его свойства. Изображение плоских фигур, многогранников и круглых тел при параллельном проектировании.
Литература:[1] §26 – 29, [2] §1 – 3.
Пусть в пространстве дана некоторая плоскость и вектор
, который ей не параллелен.
О
пределение 1.Под параллельной проекцией точки М на плоскость в направлении вектора 
понимается точка М, полученная при пересечении плоскости и прямой, параллельной 
и проходящей через М.
Ясно, что вместо вектора 
для определения параллельной проекции точки на плоскость можно взять прямую, не параллельную этой плоскости.
Е
сли в пространстве дана некоторая фигура, то, проектируя каждую ее точку, мы получимпараллельную проекцию этой фигуры на плоскость.
Будем предполагать в дальнейшем, что рассматриваемые в пространстве прямые, лучи и отрезки не параллельны направлению проектирования. При параллельном проектировании выполняются следующие свойства.
К
оллинеарные точки отображаются в коллинеарные и сохраняется их простое отношение.
Прямая проектируется в прямую, отрезок – в отрезок, луч – в луч.
Параллельные прямые отображаются либо в параллельные прямые, либо в одну прямую.
Сохраняется отношение длин отрезков, лежащих на одной прямой или на параллельных прямых.
Изображение плоских и пространственных фигур при параллельном проектировании
Пусть в пространстве дана некоторая плоскость , ее мы будем называть плоскостью изображения. Дано также некоторое направление проектирования на плоскость. Рассмотрим некоторую фигуруFв пространстве. Спроектируем ее на плоскость, получим фигуруF.
О
пределение.Фигура F1 плоскости изображения, подобная F, называется изображением фигуры F при параллельном проектировании.
Введем понятие аффинного отображения одной плоскости на другую.
Взаимно однозначное отображение плоскости на плоскостьназывается аффинным, если при этом отображении коллинеарные точки отображаются в коллинеарные и сохраняется простое отношение точек.
Аффинное отображение плоскости на себя представляет собой аффинное преобразование этой плоскости, которое было изучено ранее. Аффинные отображения обладают теми же свойствами, что и аффинные преобразования плоскости: неколлинеарные точки отображаются в неколлинеарные точки, репер плоскости – в репер плоскости, прямая линия – а прямую линию, отрезок – в отрезок, луч – в луч. Справедливо также основное свойство аффинных отображений, которое доказывается практически дословно, как и основное свойство аффинных преобразований плоскости.
Основное свойство аффинных отображений.Пусть на плоскости дан аффинный репер R, а на плоскости - аффинный репер R. Тогда существует единственное аффинное отображение плоскости на плоскость , при котором репер R отображается в репер R.
Будем считать, что фигура F плоскости аффинно эквивалентна фигуре F плоскости ,если существует аффинное отображениена, при котором образомFслужит фигураF.
Из основного свойства аффинных отображений следует, что два треугольника, один из которых принадлежит плоскости , а другой плоскости, аффинно эквивалентны.
Два четырехугольника АВСDиABCD, один из которых принадлежит плоскости, а другой плоскости, аффинно эквивалентны в том и только в том случае, когда (АС,О) =(AC,O), (BD,O) = (BD,O),где О иO' - соответственно точки пересечения их диагоналейACиBD,АСиВD.
Доказательства этого утверждения проводится дословно так же, как и в случае аффинных преобразований плоскости.
Справедлива следующая теорема.
Т
еорема.Фигура F1 плоскости служит изображением фигуры F плоскости в ом и только в том случае, когда они аффинно эквивалентны.
Треугольник изображается треугольником.
Четырехугольник – четырехугольником, точка пересечения диагоналей которого делит диагонали в том же отношении, что и у оригинала.
Поэтому прямоугольник, квадрат, ромб и параллелограмм изображаются параллелограммом.
Трапеция изображается трапецией, отношение оснований которой совпадает с отношением оснований оригинала.
Произвольный n– угольник изображаетсяn– угольником. Рассмотрим пятиугольникABCDEплоскости, который изображается пятиугольникомA1B1C1D1E1плоскости. ТреугольникABCизображается произвольным треугольникомA1B1C1, а точки D1E1с
троятся следующими образом: точки пересечения диагонали A1C1с диагоналями B1E1и B1D1делит их в том же отношении, что и у оригинала.
Т
ак как эллипс и окружности аффинно эквивалентны, то окружность изображается эллипсом, а ее перпендикулярные диаметры – сопряженными диаметрами эллипс, а центр - центром.
Теорема Польке – Шварца. Вершины любого четырехугольника A1B1C1D1плоскости, заданные в определенном порядке служат изображением аффинного репера, равного данномуR(A,B,C,D).
Изображение пространственных фигур при параллельном проектировании.
Из теоремы Польке – Шварца следует, что изображением тетраэдра, равного данному, при параллельном проектировании может служить произвольный четырехугольник (в частности и не выпуклый).
Изображением параллелепипеда, в том числе прямоугольного и куба, является фигура, состоящая из трех пар параллелепипедов, полученных друг из друга параллельным переносом.
П
ри этом строится вначале изображение тетраэдраABDA. И силу теоремы Польке – Шварца оно представляет собой четырехугольникA1B1D1A1плоскости изображения. Затем этот четырехугольник достраивается до трех пар указанных параллелограммов.
Построение изображения призмы. Изображением n– угольной призмы служит фигура, состоящая из двух равныхn– угольников – изображений оснований призмы, иnпараллелограммов – изображений ее боковых граней. При этом построение изображений оснований подчиняется правилу построения изображенияn– угольника.
Построение пирамиды. Основание n– угольной пирамиды изображаетсяn- угольником, построение которого подчиняется правилу построения изображенияn– угольника. Вершина пирамиды изображается точкой, а боковые грани – треугольниками.
При этом из теоремы Польке – Шварца следует, что в качестве изображения вершины пирамиды и трех вершин основания можно взять произвольный четырехугольник на плоскости.
Изображение цилиндра.
Д
ан прямой круговой цилиндр. Для наглядности будем считать, что плоскость изображенияпараллельна оси цилиндра, а направление проектирования, определенное вектором
не перпендикулярно. Проведем плоскости1и2, перпендикулярныеи касающиеся цилиндра. Основания цилиндра изобразятся эллипсами, а его образующие ААи ВВ- касательными к изображению оснований (контурные образующие).
Изображение конуса. Так же, как и в случае цилиндра, выберем плоскость изображения параллельно оси цилиндра, а вектор
, определяющий направление проектирования, не перпендикулярно плоскости изображения. Пусть- плоскость основания конуса. Проведем через его вершинуSпрямую, параллельную вектору
. Получим точкуSпересечения этой прямой и плоскости основания. Тогда конус проектируется в фигуру, полученную отрезками касательныхSAиSB, проведенных из точкиSк окружности основания, и самой окружностью. Поэтому при проекции конуса на плоскостьмы получим, что окружность основания изображается эллипсом, изображение вершиныSпринадлежит прямой, содержащей ее меньшую ось, а контурные образующие – отрезками касательных, проведенных из изображения вершины к изображению окружности основания.
Изображение сферы. При построении изображения сферы используется ортогональная проекция, иначе сфера будет изображена эллипсом. Поэтому изображением сферы служит окружность. Для наглядности на изображении сферы указывают окружность большого круга, не перпендикулярную и не параллельную плоскости изображения (экватор). Проведем прямую, перпендикулярную плоскости экватора. Изображения ее точек пересечения со с
ферой называются полюсами. Полюсы сферы не расположены на контурной окружности сферы, иначе экватор сферы представляет собой отрезок, а его плоскость – параллельна плоскости изображения. Укажем способ построения полюсов, соответствующих данному экватору.
Обозначим плоскость изображения через , а плоскость экватора через. АВ иCDоси эллипса экватора на изображении. Они принадлежат плоскости, Точки СиDпринадлежат большой окружности, полученной при пересечениии сферы. Эти точки проектируются в С иD. ПрямаяSNперпендикулярна плоскости, а сами эти точки служат пересечением прямой и сферы. Таким образом:
Величина угла между плоскостямииравна. Очевидно, этот угол совпадает по величине с углом СОСпрямоугольного треугольника СОС, а уголNONпрямоугольного треугольникаNONравен
. Отсюда следует, что
, а
.
С другой стороны, если СК – касательная к эллипсу экватора на изображении сферы, то треугольник СОК прямоугольный, 
, и, как было доказано ранее,
. Поэтому
. Отсюда следует, что
. Таким образом,
studfiles.net
