Презентация и доклад на тему "Математика в биологии". Математика в биологии реферат

Реферат - Математика в живых организмах

Кандидат биологических наук М. БЕРКИНБЛИТ,

кандидат педагогических наук Е. ГЛАГОЛЕВА

Живая природа сделала множество “изобретений”, которые люди поняли и смогли повторить лишь при соответствующем уровне развития науки и техники. Например, принцип эхолокации эффективно используют и дельфины, и летучие мыши, а в технике он появился только в XX веке; поиск добычи по инфракрасному излучению используют многие виды змей, в то время как очки для ночного видения созданы лишь недавно и т. д. До последнего времени бытовало убеждение, что природа не изобрела колеса, что здесь техника пошла своим оригинальным путем. Но оказалось, что жгутики бактерий вращаются в специальных “подшипниках” и, значит, колесо тоже “изобретено” природой еще на самых ранних этапах эволюции. Существует специальная наука — бионика, которая изучает “патенты природы”. Оказывается, что их можно иногда использовать и в “человеческой” технике.

Менее известно, что в живых организмах происходят явления, которые позволяют считать, что природе принадлежит “приоритет” и в создании своеобразных ЭВМ — устройств, производящих операции, весьма сходные с математическими операциями, которые мы склонны считать достижением человеческой науки. Похоже, что здесь повторяется история с изобретением колеса.

О некоторых таких операциях мы и расскажем в этой статье: о том как “считают” нервные клетки, как “логарифмирует” глаз (и зачем ему это понадобилось), как оперирует с векторами и тригонометрическими функциями мозг кошки и обезьяны (и наш с вами тоже). Может быть, кто-нибудь решит, что и изучать эти вещи не надо, раз это дано от природы. А, может быть, некоторые — мы надеемся, что таких будет больше,— захотят узнать о математической и биологической стороне дела.

Как считают нейроны

Первое знакомство с математикой — это счет: “Раз, два, три, четыре, пять, вышел зайчик погулять”. И самым простым кажется и считается натуральное число. Уже отрицательные числа очень медленно входили в математику. Появившись в раннем средневековье у математиков Индии, они лишь в XIII—XIV веках проникают в европейскую науку, встречая там поначалу весьма сдержанное, отношение. Их называют “ложными”, “абсурдными” числами. Но постепенно отрицательные числа доказали свое право на существование и стали привычными не только для специалистов — то, что было “на переднем крае науки” в средние века, сегодня спокойно воспринимают пятиклассники.

А вот в живых организмах, оказывается “все наоборот”: нервной клетке (нейрону) естественно и просто осуществлять операции с положительными и отрицательными действительными “числами”, а для того чтобы “считать” даже до двух, требуется система из нескольких нейронов — примитивный “мозг”.

Как же работает нейрон? Как всякая клетка, нейрон отделен от наружной межклеточной среды особой оболочкой — мембраной. Между внутренним содержимым клетки и наружной средой существует разность потенциалов. Если клетка находится в покое, разность потенциалов на ее мембране не меняется. Эту разность потенциалов в покое естественно принять за нулевой уровень (подобно тому, как приняли за нулевую температуру таяния льда).

На нейрон могут действовать другие нервные клетки — возбуждающие и тормозные. Сигналы, полученные от этих клеток, вызывают изменения разности потенциалов на мембране в двух противоположных направлениях. Когда разные сигналы приходят к нейрону одновременно, они складываются, причем, естественно, с учетом знака, т. е. нейрон суммирует приходящие к нему положительные и отрицательные сигналы; эта сумма может быть положительной или отрицательной.

Интересная особенность работы нейрона состоит в том, что в отличие от технических сумматоров — от древнего абака до ЭВМ — полученную сумму он “помнит” недолго: если внешние воздействия прекратились, то накопленная сумма начинает убывать по абсолютной величине, чтобы нейрон возвратился в состояние покоя (потенциал на мембране стремится к значению, которое мы приняли за нуль).

Такая вроде бы “ненадежность” нейрона связана с тем, что он предназначен не для хранения, а для передачи и преобразования информации: полученный сигнал нейрон передает другим клеткам нервной сети (клеткам-“мишеням” или “адресатам”). По способу передачи сигнала существуют два разных типа нейронов с разными принципами работы: “аналоговые” и “пороговые” нейроны.

Нейрон первого типа действует на клетки-мишени с силой, пропорциональной накопленной сумме, — но только в том случае, когда эта сумма положительна. Когда же сумма отрицательна, то она дальше не передается — нейрон заторможен. Правило преобразования сигналов аналоговыми нейронами описывается формулой, где х — накопленный потенциал, у — величина переданного сигнала, a k — коэффициент пропорциональности.

Нейроны второго типа работают иначе. Такой нейрон “молчит”, пока сумма воздействий не достигнет некоторой определенной положительной величины — “порога”. Тогда нейрон возбуждается и посылает по своему выходному отростку — аксону — электрический импульс (всегда одной и той же величины), который и действует на клетки-мишени. После возбуждения нейрон некоторое время “отдыхает” — молчит, независимо от того, действуют на него другие клетки или нет, а затем, если к концу отдыха накопленная сумма выше порога, посылает новый импульс. В результате в зависимости от величины входного сигнала, его длительности и в зависимости от характеристик нейрона на выходе получается сигнал в виде серии импульсов постоянной величины, но разной частоты. Таким образом, пороговые нейроны используют совершенно нетривиальный принцип кодирования информации частотой сигнала.

Однако, как и непрерывный выходной сигнал нейронов аналогового типа, изменение частоты несет информацию только о величине входного сигнала, меняющейся непрерывно. В то же время известно, что животные умеют считать (например, выдавать реакцию только на каждый третий стимул). Естественно предположить, что в нервной системе имеются устройства, которые по-разному реагируют, например, на двукратное воздействие и на однократное. То, что известно о принципах работы нейронов, позволяет утверждать: одиночной нервной клетке такая “простая” с человеческой точки зрения операция, как счет, не под силу. Недостаток места не позволяет нам описать устройство из нескольких нейронов, способное выдавать ответ, например, на каждый второй стимул.

Глаза и логарифмы

Зрительные рецепторы, так же, как и другие — слуховые, температурные и т. д., получают сигналы из внешнего мира; они должны передать зрительную информацию в мозг точно и своевременно. Передача сигналов от глаза к мозгу осуществляется нейронами “порогового” типа — аналоговый способ оказывается неприменимым при передаче сигналов на достаточно большие расстояния. А у пороговых нейронов, как уже говорилось, все импульсы совершенно одинаковы, и сведения о величине входного сигнала эти нейроны передают меняя частоту импульсации.

Тут возникает вот какая проблема. Освещенность в сумерках, когда предметы еле видны, отличается от освещенности при ярком солнечном свете примерно в миллиард (т. е. в 109 ) раз. Максимальная же частота, с которой может работать нейрон — 1000 импульсов в секунду. Легко сообразить, что нельзя передавать информацию, меняя частоту работы нейрона пропорционально освещенности: если при ярком свете частота импульсов будет максимальной (1000 имп/с), то при уменьшении освещенности в миллион раз сигнал будет поступать всего один раз в 15 минут. Но за это время он совершенно потеряет свою актуальность!

Но может быть, разумно такое устройство зрительной системы, когда разные ее элементы, разные нейроны работают каждый в своем диапазоне освещенности: одни в сумерки, другие в пасмурный день, третьи на ярком солнце. Простой подсчет показывает, что если принять за нижнюю границу частоты работы нейрона, необходимой для достаточно своевременной передачи информации, 1 имп/с, то для охвата диапазона изменения освещенности в миллиард раз потребуется миллион нейронов — и это без всякого “запаса” прочности, без дублирования их работы! Но главное вот что: в каждый момент будет работать только одна клетка из миллиона, а остальные 999 999 будут “даром есть хлеб”: ведь в отличие от технических, живые “механизмы” потребляют энергию (свой “бензин”) не только во время работы. А экономия энергии в живой природе — одно из главных условий выживания.

Итак, линейная зависимость между входными и выходными сигналами в случае глаза оказывается нецелесообразной. И действительно, в природе в этом случае используется другая функция, по школьным меркам довольно сложная.

Экспериментально это было установлено в 1932 году английским ученым X.Харлайном. На рисунке 1 приведены результаты его исследования. Он регистрировал нервные импульсы, идущие по одиночному нервному волокну от глаза к мозгу, у мечехвоста (морского членистоногого, похожего на вымерших трилобитов). На графике показана зависимость частоты импульсации от яркости света.

“Но позвольте! — скажете вы.— На графике прямая линия — значит, это линейная функция”. Не торопитесь, вглядитесь в шкалу на горизонтальной оси, она ведь неравномерна, нелинейна: при сдвиге на одно деление аргумент (яркость) меняется не на одну и ту же величину, а в одно и то же число раз.

При линейной зависимости равным приращениям аргумента соответствуют равные приращения функции, или, что то же самое, линейная зависимость переводит арифметическую прогрессию значений аргумента в арифметическую же прогрессию значений функции. Когда мы имеем дело с показательной функцией у=ах, то равным приращениям аргумента соответствует равномерный относительный прирост функции. Например, при постоянных условиях обитания и неограниченных ресурсах так растет численность какой-либо популяции: число особей за каждый год увеличивается на 10%, т. е. в 1,1 раза. Другими словами, показательная функция “переводит” арифметическую прогрессию в геометрическую. На нашем графике ситуация обратная: частота импульсации нейрона меняется на одну и ту же величину, когда воздействие меняется в одно и то же число раз. Значит, мы имеем дело с функцией, обратной к показательной, т.е. с логарифмической; иными словами, нейроны глаза мечехвоста превращают геометрическую прогрессию раздражений в арифметическую прогрессию сигналов.

Это свойство зрительных рецепторов, выработавшееся в ходе эволюции, позволяет глазу работать эффективно и экономно, обеспечивает возможность хорошо воспринимать контраст. Пусть светлый и темный предметы различаются по способности отражать свет в десять раз. Тогда и на ярком солнце, и в сумерках светлый предмет будет отражать в десять раз больше света, чем темный. Поэтому сравнительная яркость этих предметов не меняется; не меняется и расстояние между соответствующими точками на оси абсцисс. А это означает, что разница частот работы рецепторов, на которые падает свет от этих двух предметов, будет оставаться неизменной при разных освещенностях. Так что “умение логарифмировать” позволяет глазу не только работать в широком диапазоне освещенностей, но и при малой освещенности различать предметы, абсолютная разность освещенностей которых очень мала.

Интересно, что описанная зависимость между внешним сигналом (раздражением) и сигналом, воспринимаемым мозгом (ощущением), первоначально была обнаружена психологами. Сделал это французский ученый П. Бугер еще в XVIII веке. В начале XIX века немецкий физиолог и психолог Э. Вебер детально изучил связь между раздражением и ощущением. Он выяснял, как нужно изменить какой-то раздражитель, чтобы человек заметил это изменение. Оказалось, отношение изменения величины раздражителя к его первоначальному значению есть величина постоянная:

, где I — мера раздражителя,— прирост раздражителя, a k — константа Вебера.

Константа Вебера зависит от того, какой рецептор раздражается. Например, при восприятии веса k=1/30. Это значит, что, когда человек держит груз в 100 г, он замечает его изменение при увеличении веса на 3,4 г, а для груза в 200 г требуется прибавка в 6,7 г. Для высоты звука константа Вебера равна 0,003, для громкости звука — 0,09 и т. д.

Исходя из экспериментов Вебера, другой немецкий физиолог и психолог Г. Фехнер сформулировал знаменитый закон Вебера — Фехнера:

Ощущения растут в арифметической прогрессии, когда раздражение растет в геометрической прогрессии.

Этот закон был опубликован в книге Фехнера “Элементы психофизики” в 1859 году. Там же было приведено и математическое выражение закона:

,

где Е — мера ощущения, а и b — константы, I — мера раздражения.

Зачем кошке векторы?

Слово “вектор”, можно сказать, совсем “младенец” — по-видимому, оно появилось впервые в работе английского математика У. Гамильтона в 1845 году. Но соответствующее понятие использовалось в физике еще за несколько столетий до этого в связи с рассмотрением закона сложения сил (“правила параллелограмма”). Про векторы же в организме животных мы узнали только в самые последние годы.

Началось с кошек. В 1988 году канадский ученый Дж. Макферсон выполнила интересную работу. Она ставила кошку на специальную платформу, толкала эту платформу в каком-нибудь направлении и смотрела, каким образом кошка сохраняет равновесие. Допустим, она толкнула платформу вперед. Ноги кошки вместе с платформой стали уходить вперед, а тело остается на месте. Тогда кошка, чтобы возвратить центр тяжести в правильное положение над точками опоры активирует мышцы лап и, отталкиваясь от платформы, двигает тело вперед. Если платформу толкнуть вправо, центр тяжести отклонится влево по отношению к опоре и лапы должны создать силу, направленную вправо, и т.д.

Как же происходит эта работа лап при сохранении равновесия

Самое естественное — это предположить, что каждая из двух задних лап при толчке вперед создает силу, направленную вперед; сумма этих двух сил и восстанавливает правильное положение тела (рис. 2, а). Если платформу толкнули вправо, каждая лапа создает силу, направленную вправо, и т. д. Такая гипотеза согласуется с тем, что у кошки есть мощные мышцы, которые двигают лапу вперед или назад — они используются для ходьбы и прыжков, а также мышцы, отводящие лапу наружу или по направлению к оси тела. Однако, когда Макферсон стала выяснять, что происходит на самом деле, оказалось, что картина совершенно другая: при толчке платформы, независимо от направления движения, задние лапы кошки создают силы, направленные вдоль двух прямых (каждая лапа — вдоль своей), расположенных примерно под углом 45° к оси тела. Даже в простейшем случае, когда платформу толкают прямо вперед, силы, создаваемые лапами, направлены не вперед, а тоже под углом 45° к оси тела (снова см. рис. 2, а). И только их сумма имеет нужное направление и величину. На рисунке 2, б показано, как получается сила, направленная перпендикулярно телу, а на рисунке 2, в — сила, направленная под углом 30° к оси тела.

Значит, нервная система кошки решает следующую задачу. При толчке платформы по информации, полученной от разных рецепторов, определяется, какой вектор (силу) нужно получить, затем этот вектор раскладывается по фиксированным осям координат. При таком способе получается, что каждой из двух задних лап нужно передать всего одно число — координату вектора силы (положительную или отрицательную), которую должна создать эта лапа вдоль своей фиксированной оси.

Получается очень экономная схема. Но жизнь так полна неожиданностей! Разбираясь в том, какими мышцами создается это фиксированное направление (казалось бы, чего проще: использовать для единичного вектора одного направления мышцы, двигающие ногу вперед и внутрь, а для создания другого — назад и наружу, а дальше менять пропорционально силу, развиваемую этими мышцами,— “умножать на число”, и все в порядке), Макферсон получила еще один неожиданный результат. Оказалось, что в создании “единичного” вектора могут участвовать разные мышцы, их сочетание меняется в зависимости от направления толчка. В чем смысл такого, с нашей точки зрения, усложненного решения, еще выяснять и выяснять. Однако здесь проявляется общий принцип живого: избегать жестких схем, иметь всегда избыток “степеней свободы”, словом, плюрализм.

Векторы в мозгу обезьяны и человека

Трудности в выяснении вопроса о том, как на самом деле происходит решение той или иной задачи, связаны с тем, что заглянуть в “управляющий центр” — в мозг — очень трудно. В этом смысле мозг пока что во многом “черный ящик”: можно видеть, какая задача ему предложена, можно видеть, какой он выдает результат,— а вот что происходит внутри, об этом сведений еще очень и очень мало.

Тем более интересна и важна работа, которая позволила почти непосредственно увидеть, как идет работа мозговых нейронов при решении некоторых задач. Эту работу совсем недавно выполнил американский ученый А. Георгопулос. Он экспериментировал с дрессированными обезьянами. Лапа обезьяны помещалась в некоторой точке стола, а в различных точках стола помещались электрические лампочки. Обезьяну научили при вспышке какой-нибудь лампочки двигать лапу по направлению к этой лампочке. В это время экспериментатор регистрировал с помощью вживленных электродов активность (частоту импульсации) нервных клеток коры больших полушарий в той ее зоне, которая управляет движениями этой лапы.

Оказалось, что активность большинства клеток этой зоны мозга зависит от направления движения лапы; и эта зависимость достаточно четкая: для каждой из клеток существует такое направление движения, при котором активность максимальна; при других направлениях активность уменьшается примерно как косинус угла между данным направлением максимальной активности. Для тех направлений, для которых косинус отрицателен, клетка вообще перестаёт импульсировать.

Получается, что с каждой клеткой коры связан определенный вектор максимальной активности Аmax (рис. 3). Когда нужно двигать лапу по другому направлению, т. е. задан некоторый единичный вектор направления e, клетка находит проекцию Аmax на это направление, т. е. “вычисляет” скалярное произведение Аmax. е. Выяснив это, Георгопулос поставил обратную задачу: нельзя ли, регистрируя работу нервных клеток, определить направление движения лапы. Математически эта задача может быть сформулирована как вопрос о существовании функции, обратной к заданной. Ясно, что по активности одной клетки направление движения определить нельзя: во-первых, косинус — функция четная, и в том промежутке, который нас интересует, не имеет обратной. Действительно, если, например, направление максимальной активности — это прямо вперед, а активность нейрона составляет половину максимальной, то известно, что лапа движется под углом 60° к преимущественному направлению, но вправо или влево от него — определить невозможно. Во-вторых, у одной клетки слишком велика “мертвая зона” — зона, когда она вообще молчит. Но если регистрировать несколько клеток, то можно успешно определить направление, в котором движется лапа (и даже предсказать, в каком направлении она будет двигаться, так как клетки начинают работать за десятую долю секунды до того, как лапа начинает двигаться). Представляем читателю самостоятельно решить такую задачу: какое минимальное число клеток требуется для того, чтобы уверенно определять направление движения во всех случаях? (Конечно, мы даем эту задачу, так сказать, в математической формулировке, которая, как всегда, упрощает ситуацию — как и мы ее упрощаем в нашем рассказе.)

То, что по активности нейронов можно не только установить, куда движется лапа, но и предсказать, куда обезьяна еще только собирается двигать ее, т. е. как бы подсмотреть мысль о движении, позволило Георгопулосу сделать еще одну, очень красивую работу.

Еще в 1971 году американские психологи Р. Шепард и Дж. Метцлер обнаружили явление, которое они назвали “мысленным вращением”. В экспериментах испытуемым показывали две фигуры и спрашивали: это разные фигуры или одна и та же, но повернутая на некоторый угол? Время ответа оказалось линейной функцией величины угла поворота одной фигуры относительно другой.

В другом варианте эксперимента попеременно показывали букву R или ее зеркальное отражение — букву Я; надо быстро определить, какая это буква. При этом букву показывали в разных положениях. И здесь время ответа было пропорционально углу поворота буквы относительно “нормального” положения.

Ученые предположили, что человек в таком эксперименте мысленно вращает образ воспринимаемой фигуры (а по ряду психологических экспериментов, скорее, эталон фигуры, хранимый в памяти) с постоянной угловой скоростью и даже определили эту скорость. Получилось 450o /с. Однако такими экспериментами невозможно доказать гипотезу “мысленного вращения”, так как остается неизвестным, что же происходит в действительности в головах испытуемых.

Георгопулос, обретя возможность “подглядывать” за работой нейронов мозга обезьяны, получил в 1989 году данные, которые делают гипотезу о мысленном вращении более обоснованной.

Теперь обезьяну научили тянуть лапу не к той лампочке, которая горит, а к той, которая находится под углом 90° к ней. Экспериментаторы смогли узнать, что происходит в мозгу обезьяны от момента, когда зажглась лампа, до начала движения лапы. Оказалось, что после вспышки вектор направлен прямо на лампочку, затем начинает вращаться и, когда повернется на 90°, начинается движение лапы. Скорость вращения вектора оказалась равной примерно 730°/с, т. е. была того же порядка, что и в психологических опытах с человеком.

Таким образом, как показывают эти эксперименты, мозг может производить и геометрические преобразования (на самом деле, не только повороты, но, видимо, и многие другие, например преобразования подобия).

Сделаем еще один намек на математические способности мозга. Сейчас бурно развивается параллельное программирование. Но когда человек берет предмет, он одновременно управляет работой и плеча, и локтя, и пальцев, осуществляя самое настоящее параллельное программирование.

Заключение

Итак, в живых организмах идут процессы переработки, передачи информации и использование ее в целях управления. Эволюция постепенно находит удачные формы обработки информации, и эти формы имеют немалое сходство с математическими операциями. Такие ухищрения эволюции мы и назвали “математикой в живых организмах”.

Это действительно ЭВМ, так как действия этих устройств основаны на электрических явлениях в организме.

Как возникают эти сдвиги потенциала, вы можете прочитать в книге «Электричество в живых организмах» («Библиотечка „Квант“ выпуск 69).

Кстати, у мечехвоста нет зрачка, и, значит, нет диафрагмы. Впрочем, даже учёт эффекти диафрагмы не спасает положения, изменяя освещённость всего на 1-2 порядка.

Выяснилось, что при восстановлении положения центра тяжести у кошки передние лапы используются как пассивные подпорки. Активно работают именно задние лапы.

Пропорциональность частоты работы нервных клеток косинусу того или иного угла была известна и до работы Георгопулоса. Например, еще в 1981 году в стволе мозга были обнаружены нейроны, связанные со “скачками” глаз: их активность менялась в зависимости от направления скачка глаза по закону косинуса.

www.ronl.ru

Презентация и доклад на тему "Математика в биологии"

Иванушкина Ирина Геннадьевна

Семинар биологов. 20.02.2015 год

Математика в биологии.

Математика – царица всех наук. Как часто мы слышим эти слова, сказанные немецким математиком Карлом Гауссом (1777-1855) много лет назад. Эти слова можно подтвердить и высказываниями других ученых. Александров А.Д. говорил: «Значение математики сейчас непрерывно возрастает. В математике рождаются новые идеи и методы. Всё это расширяет сферу её приложения. Сейчас уже нельзя назвать такой области деятельности людей, где математика не играла бы существенной роли. Она стала незаменимым орудием во всех науках о природе, в технике, в обществоведении. Даже юристы и историки берут на своё вооружение математические методы» Слова Гнеденко Б.В, советского математика, подтверждают это высказывание: «В нашу современную жизнь вторгается математика с ее особым стилем мышления, становящимся сейчас обязательным и для инженера, и для биолога».

 Математика – царица всех наук.

Современный мир неожиданно обнаружил, что математика уверенно расположилась в самых разных его частях и уголках. Сейчас никого не удивишь словосочетаниями "математическая лингвистика", "математическая биология", "математическая экономика" и т.п. — какую дисциплину ни взять, вряд ли кому-нибудь покажется невозможным присоединение к ее наименованию эпитета "математический". Распространение математики вширь сопровождается се проникновением вглубь. Математика занимает сегодня видное место в жизни общества.

Сферу приложения математики мы можем увидеть из схемы:

Математика и биология.

В биологии так же широко используется показательная функция. Рост различных видов микроорганизмов и бактерий, дрожжей и ферментов подчиняются одному закону: N=N0ekt. По этому закону возрастает количество клеток гемоглобина в организме человека, который потерял много крови. Рассмотрим такие задачи:

1) Численность популяции составляет 5 тыс. особей. За последнее время в силу разных причин (браконьерство, сокращение ареалов обитания) она ежегодно сокращалась на 8%. Через сколько лет (если не будут предприняты меры по спасению данного вида и сохранятся темпы его сокращения) численность животных достигнет предела – 2 тыс. особей, за которым начнётся вымирание этого вида?

Решение: Применим для вычисления времени формулу сложных процентов: 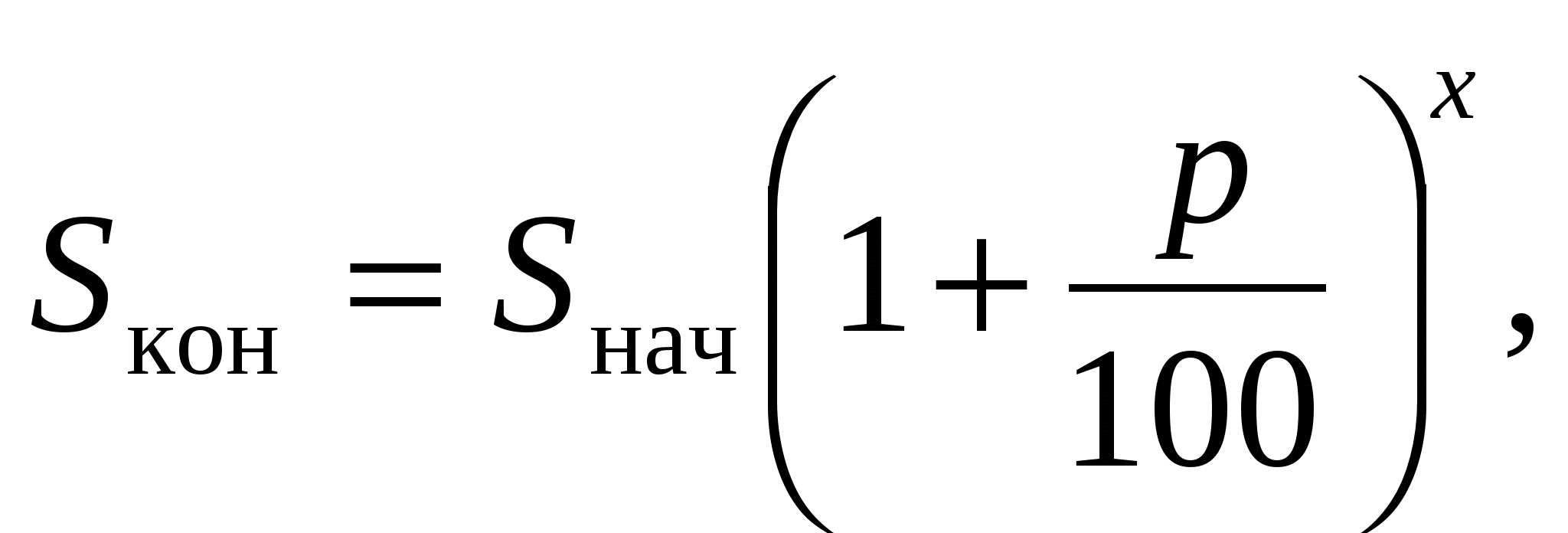 где

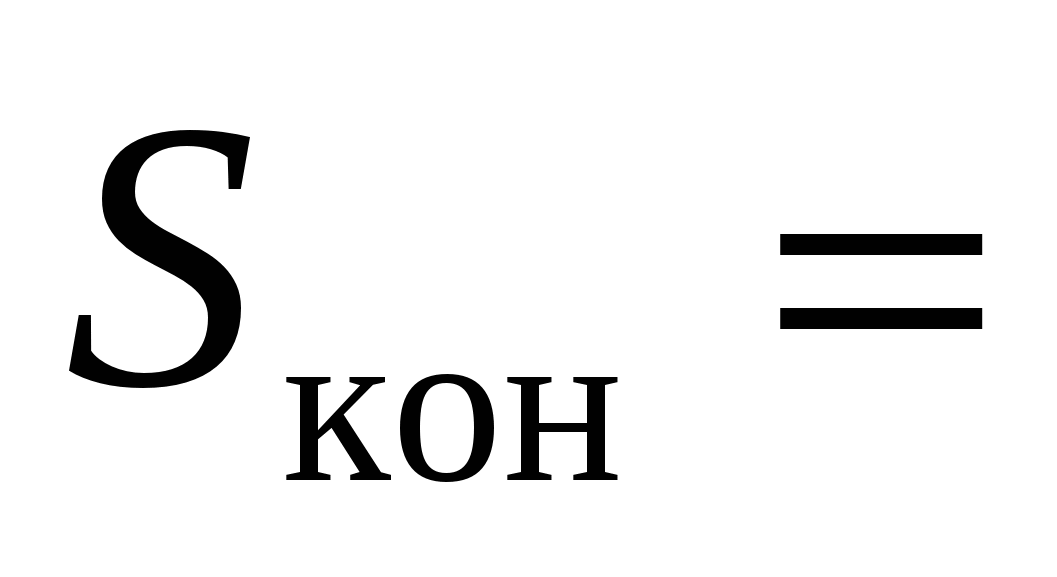2 тыс. – численность животных по истечению искомого времени;

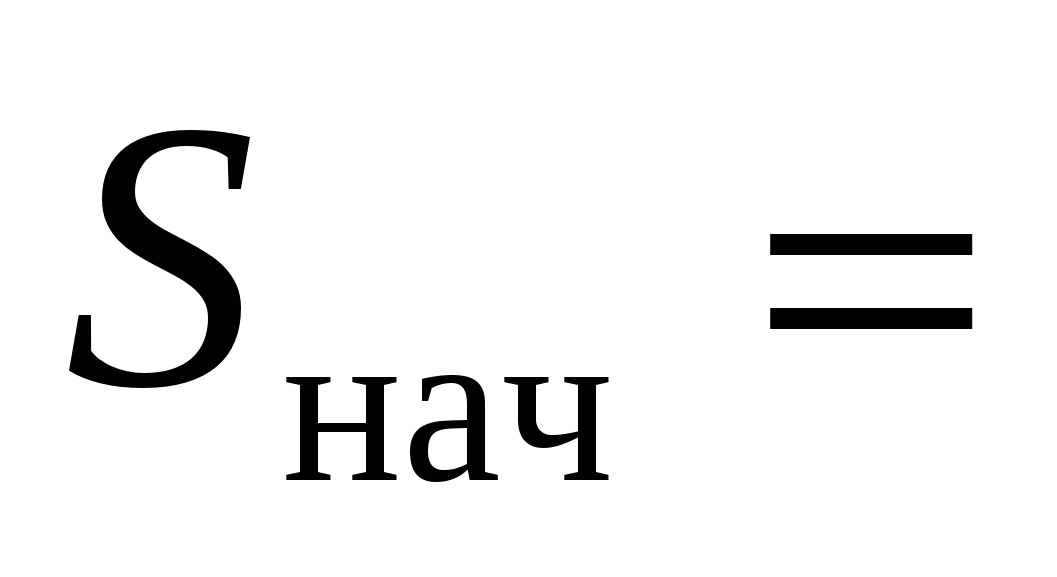5 тыс. – численность животных в начальный момент времени;

p = 8 - % сокращения численности животных.

Предварительно разделив обе части уравнения на 1000, получим:

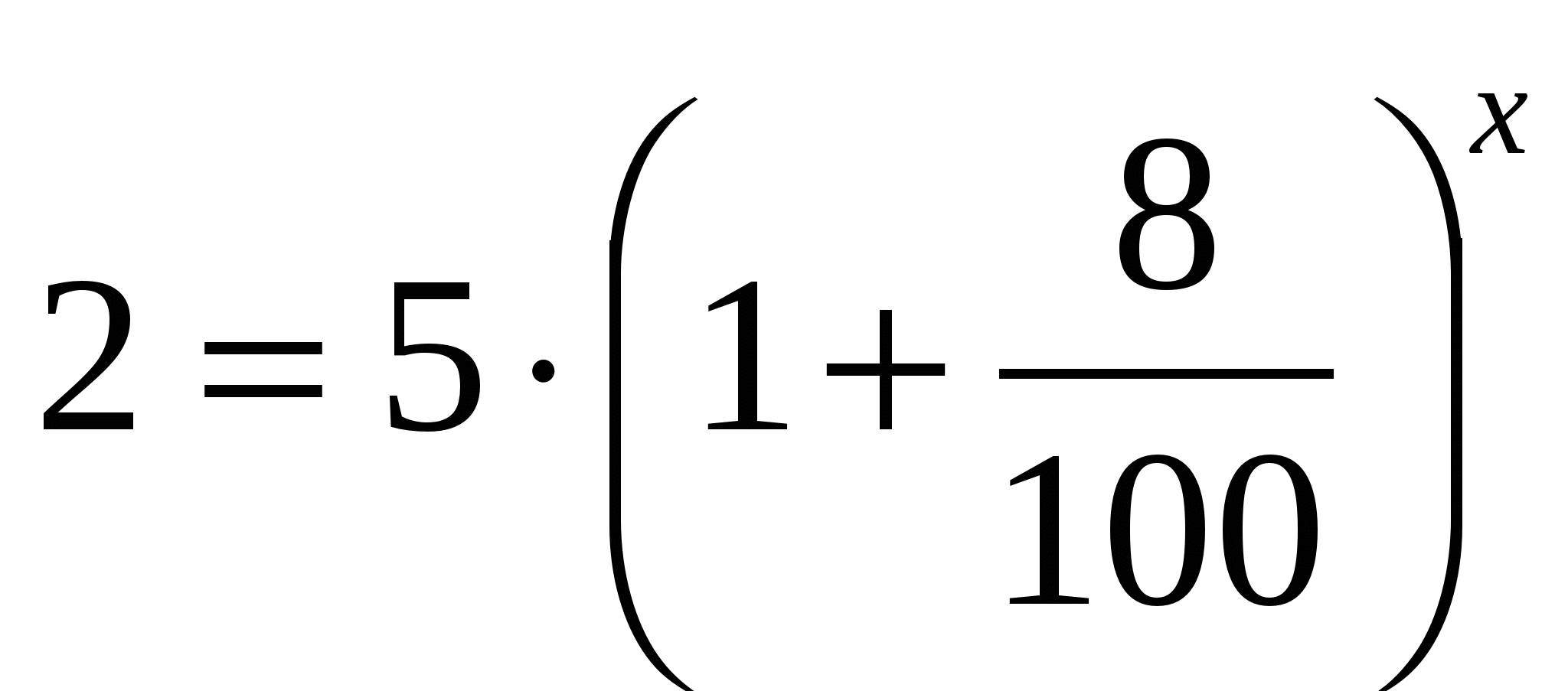
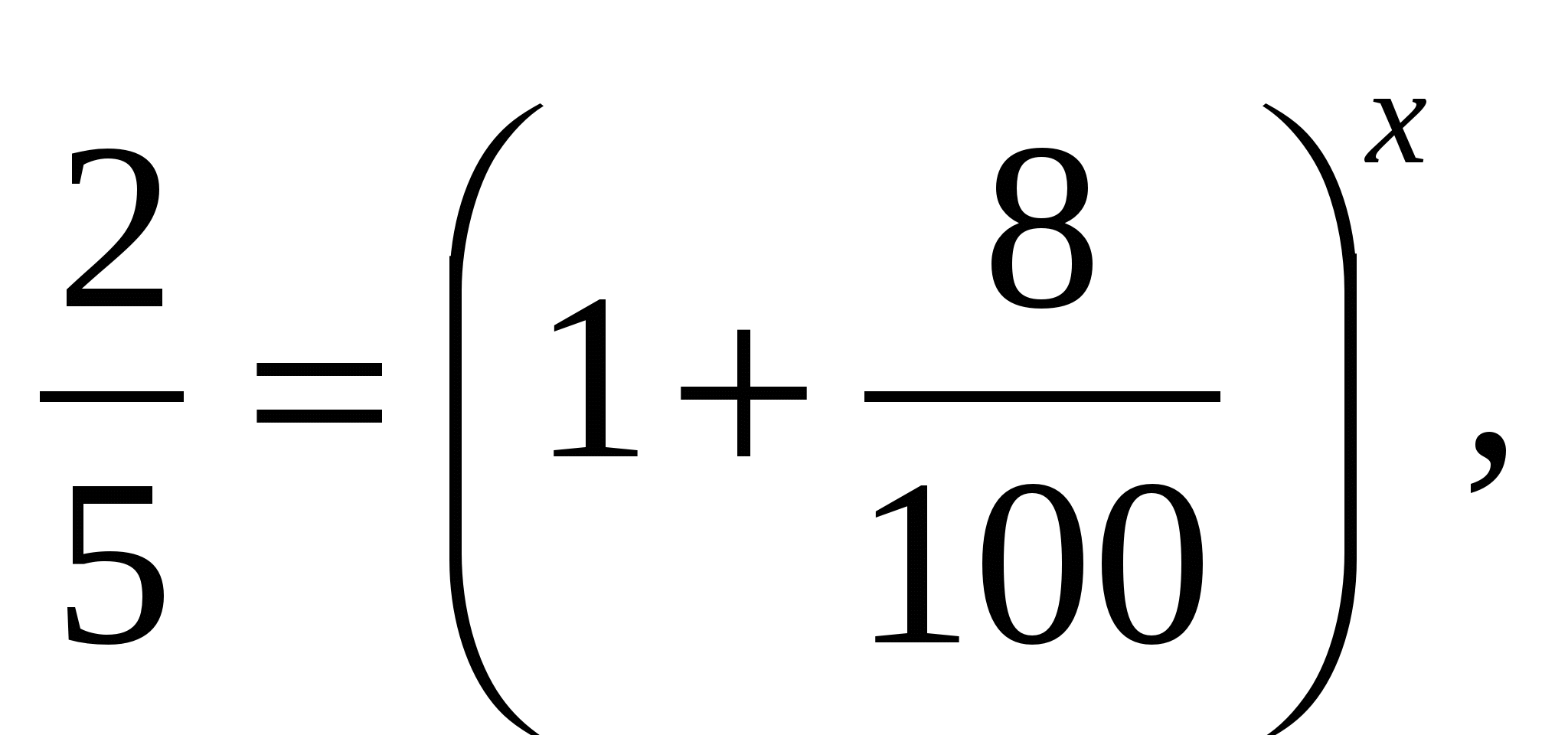
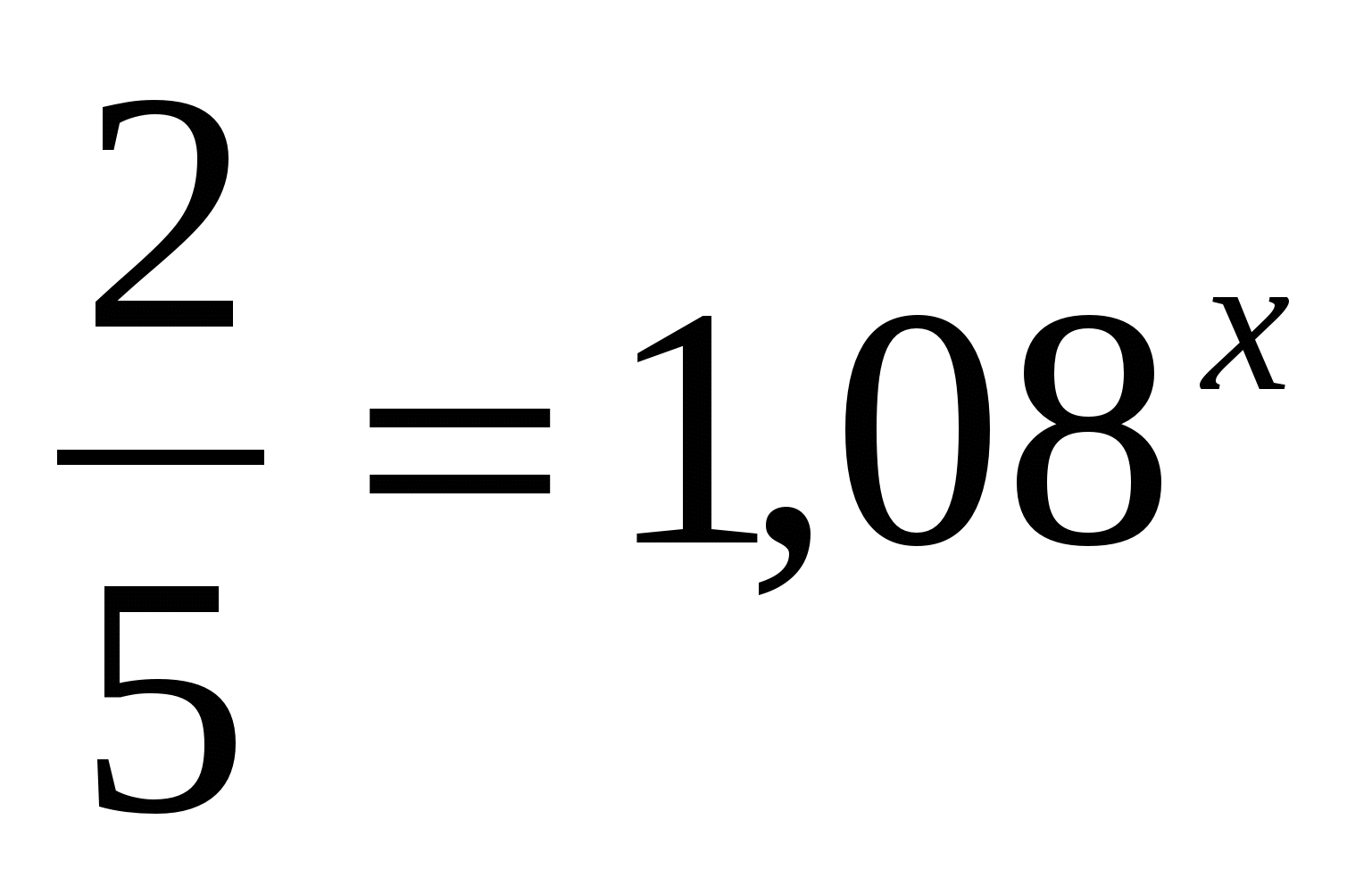
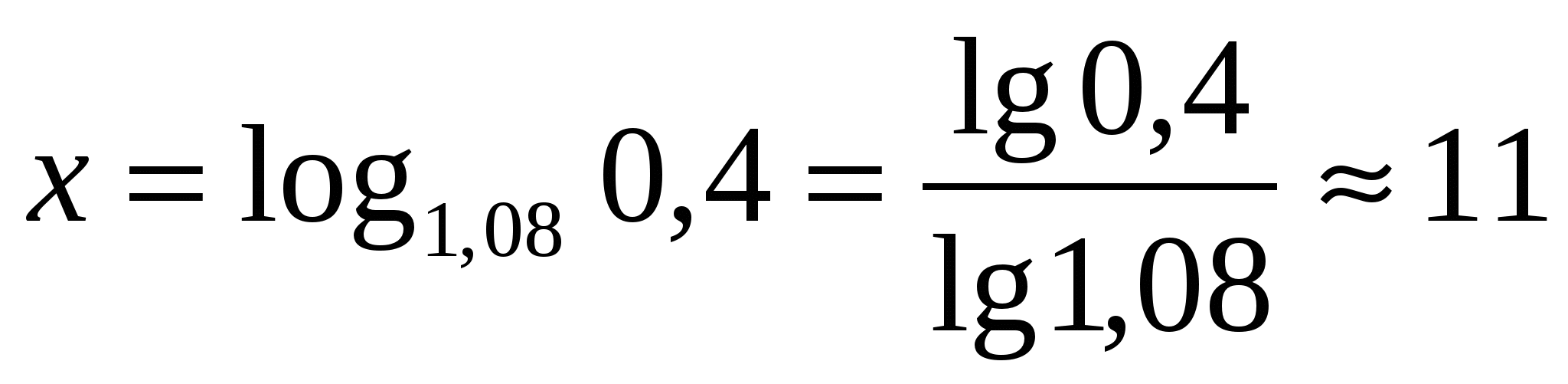 лет.

Ответ: Приблизительно через 11 лет.

2) Рассмотрим задачу об органическом росте в общем виде.

Пусть в начальный момент времени имелось q единиц некоторого компонента. В некоторый другой момент времени t имеющийся компонент изменился в p раз. Установите, через какой промежуток времени (начиная с начального момента) этот компонент достигнет заданного количества B единиц.

Решение: Для того чтобы это сделать, сначала напомним, что процессы, у которых происходит быстрый рост или быстрое затухание, описываются показательной функцией вида .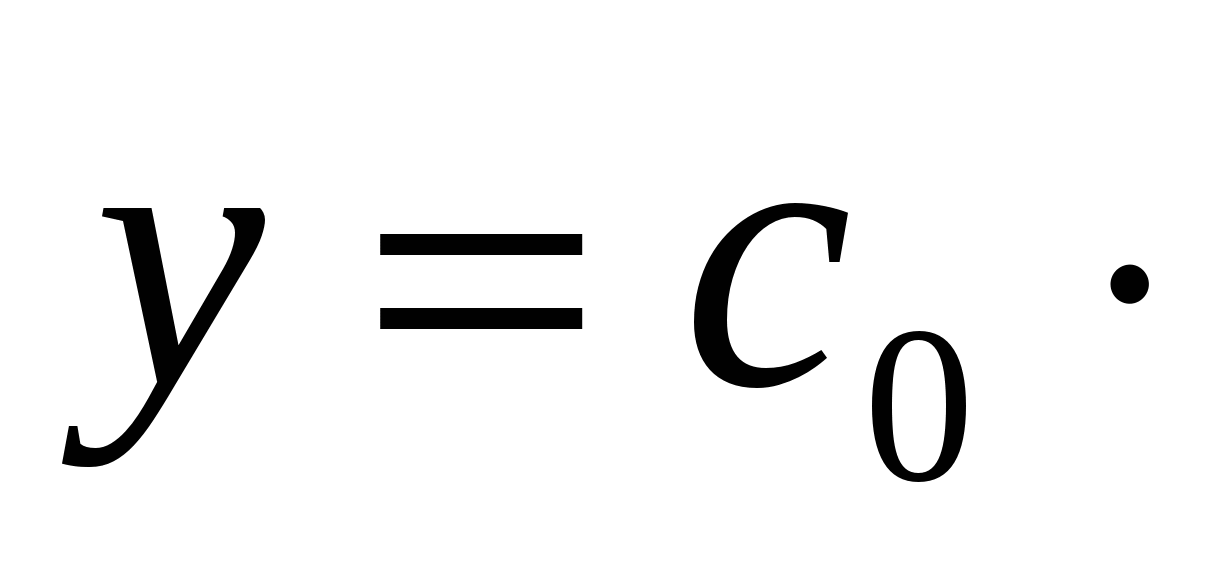

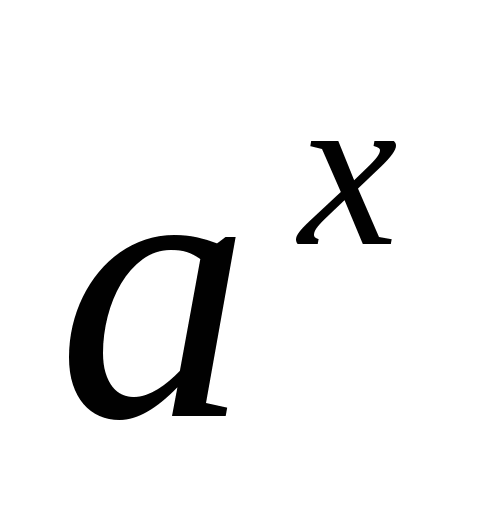В нашем случае будем считать, что начальный момент времени соответствует нулю, тогда 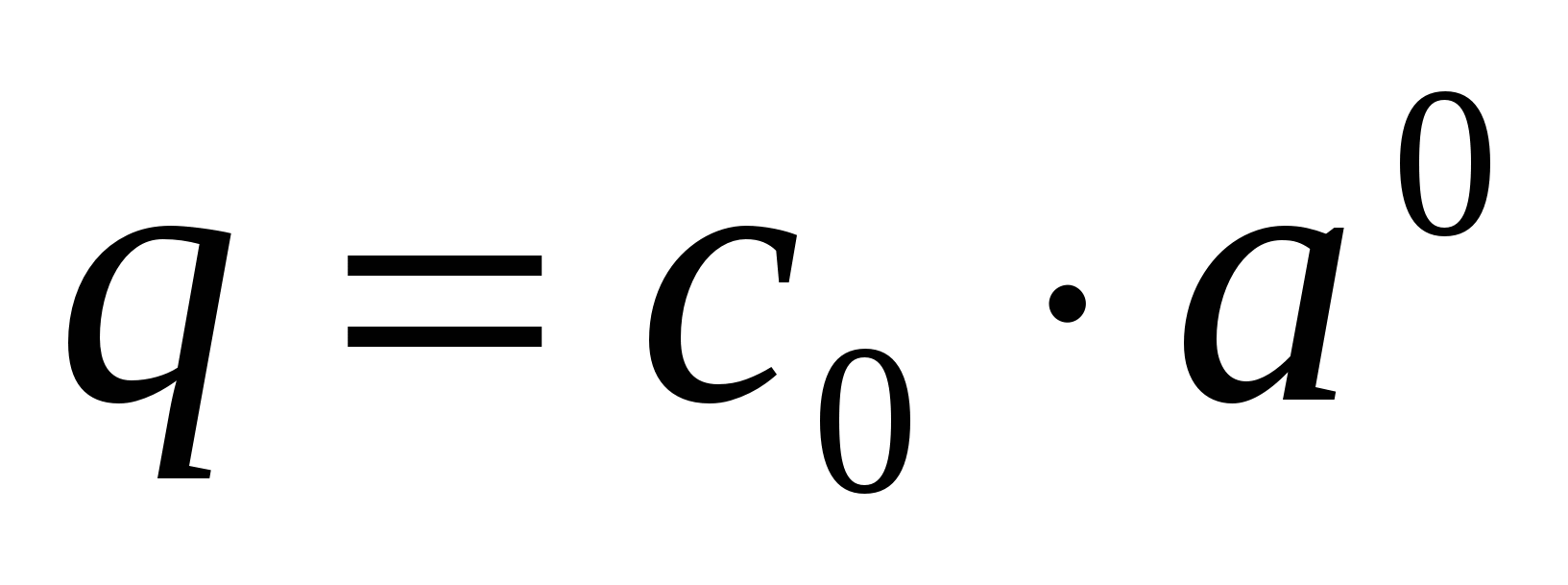, и значит, 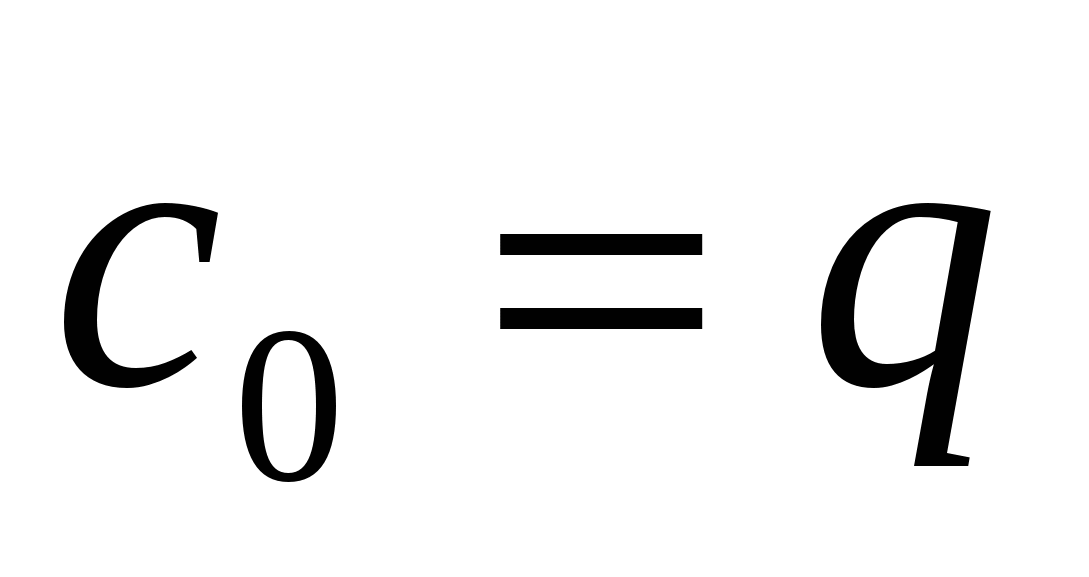, т.е. функция, описывающая этот процесс, имеет вид 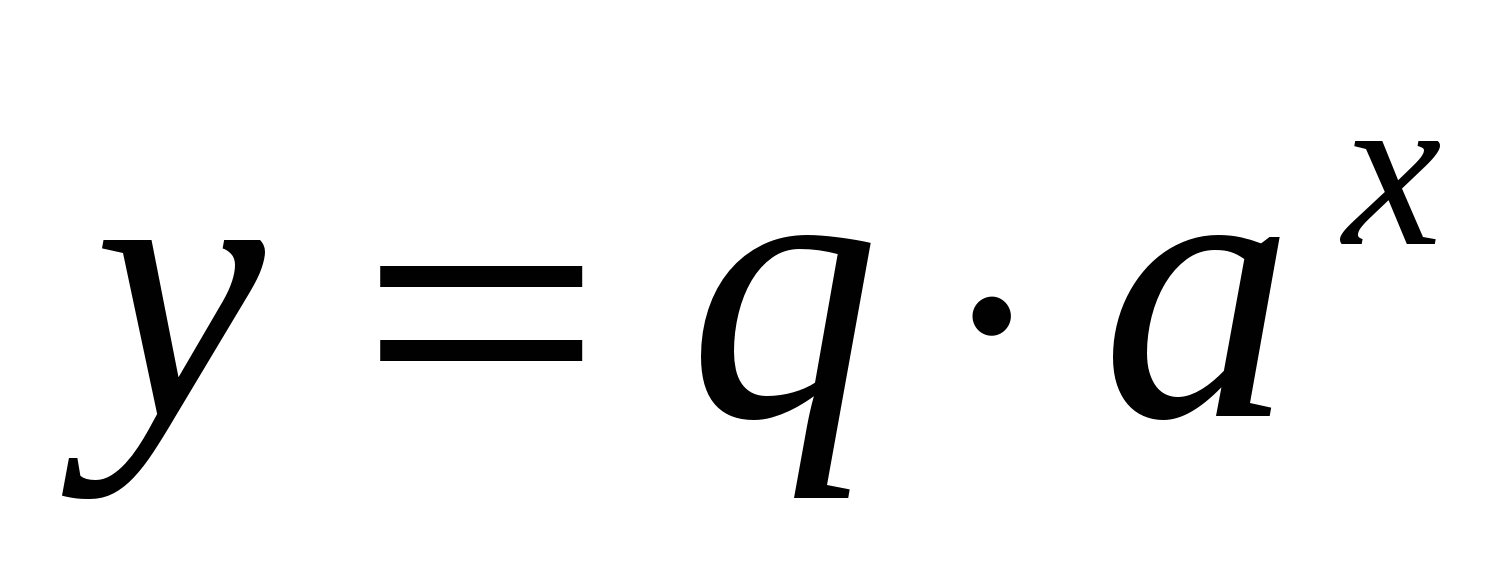. В следующий момент времени t у нас произошли изменения, описываемые уравнением 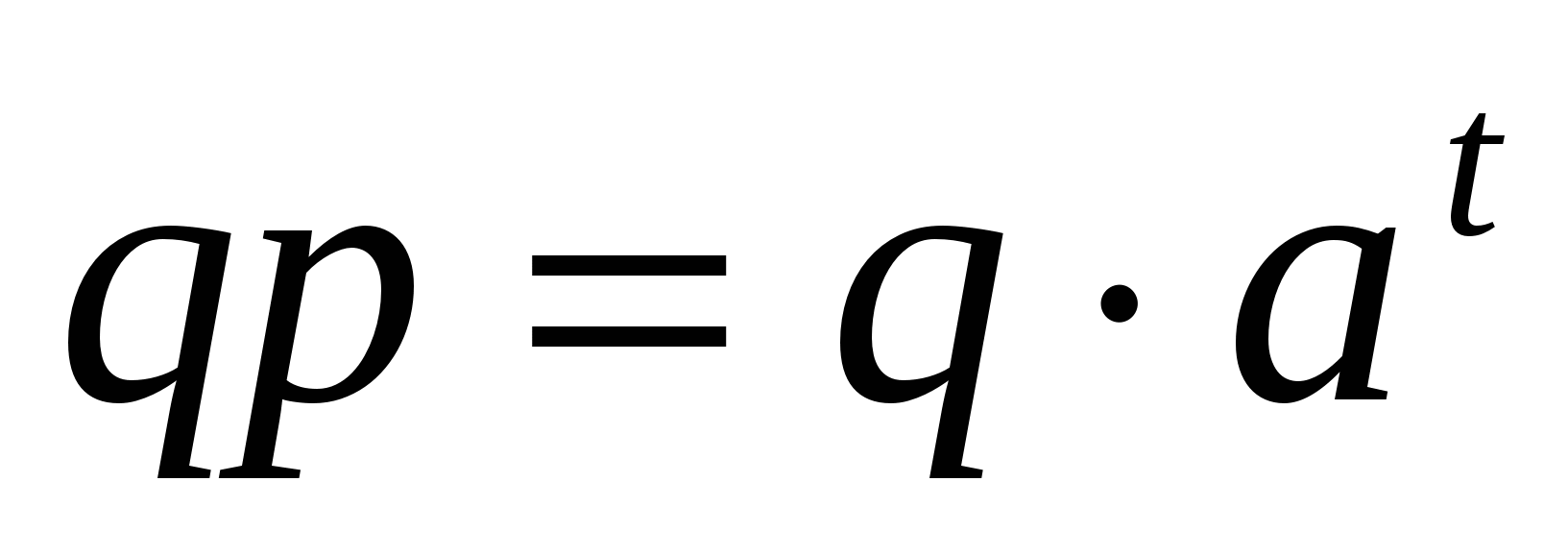, т.е. 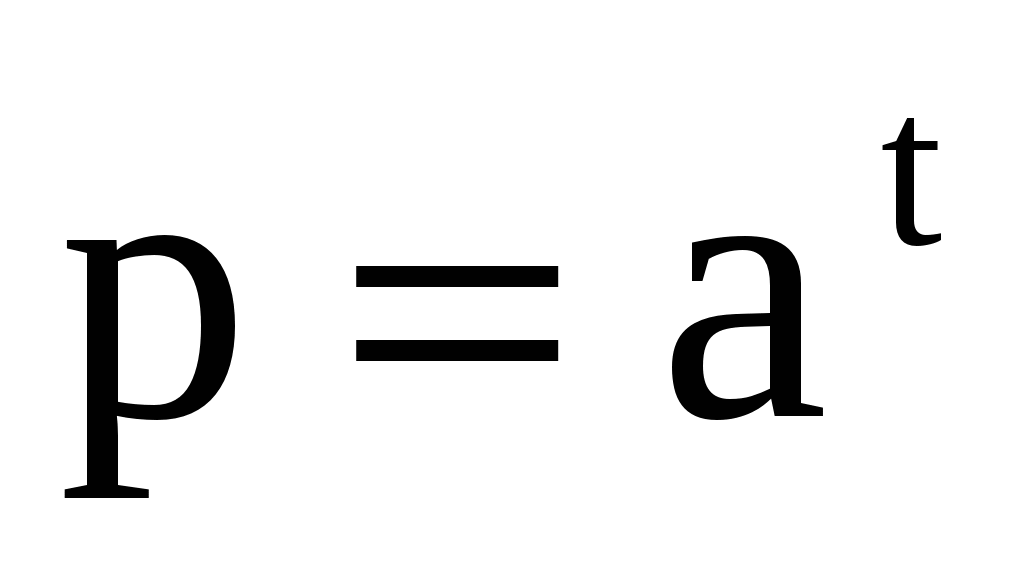, откуда 

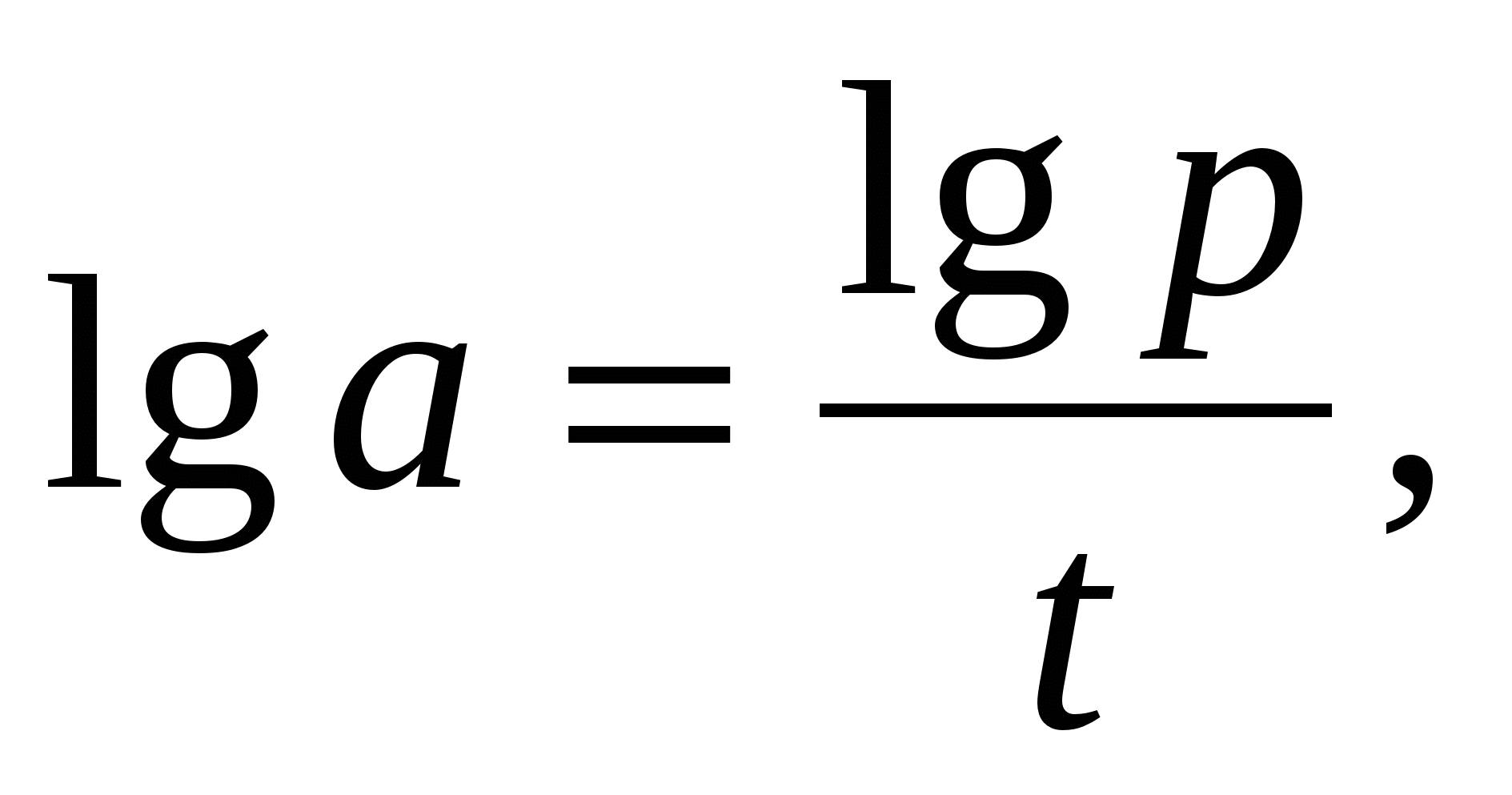
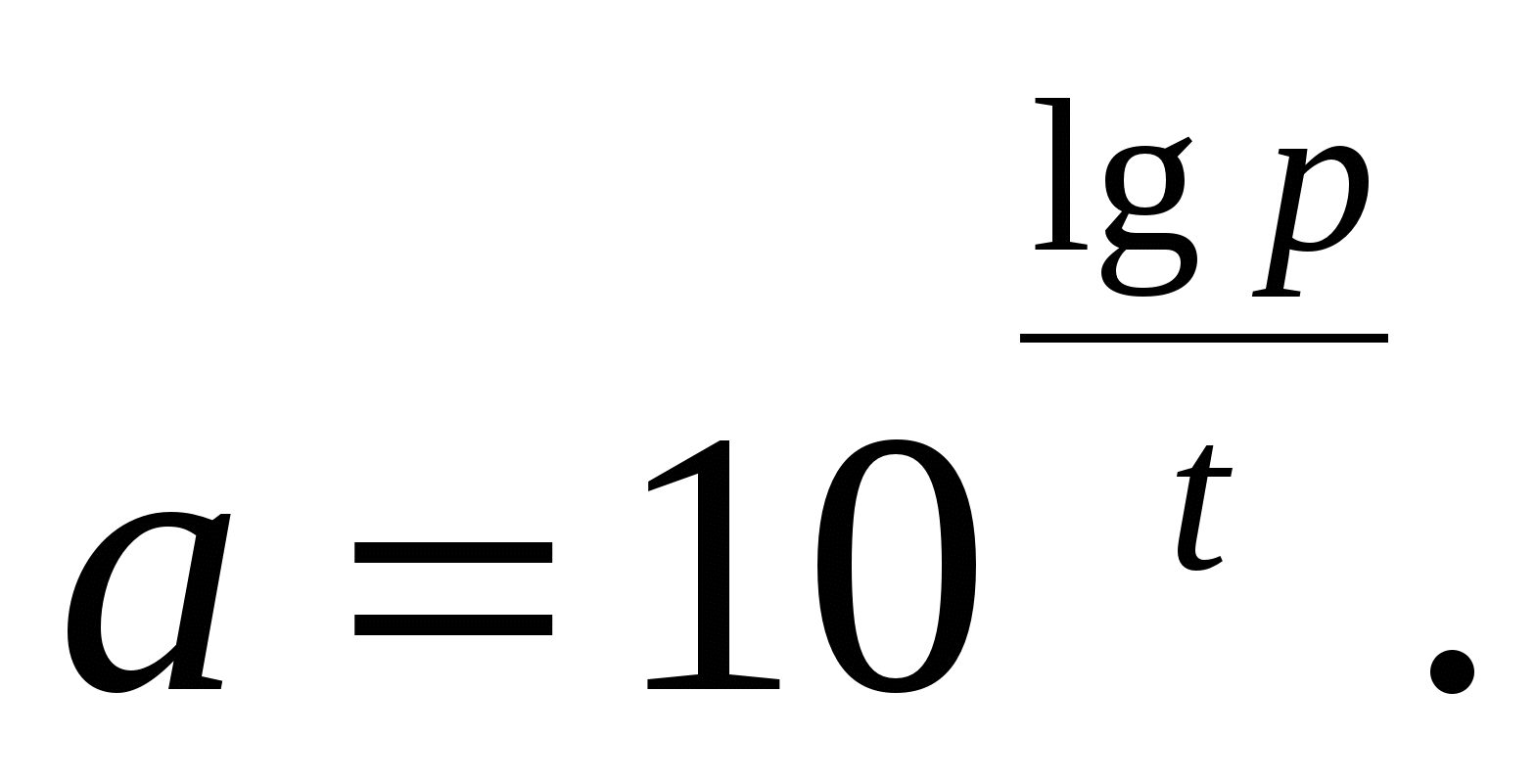  Таким образом, по данным условия мы получаем функцию 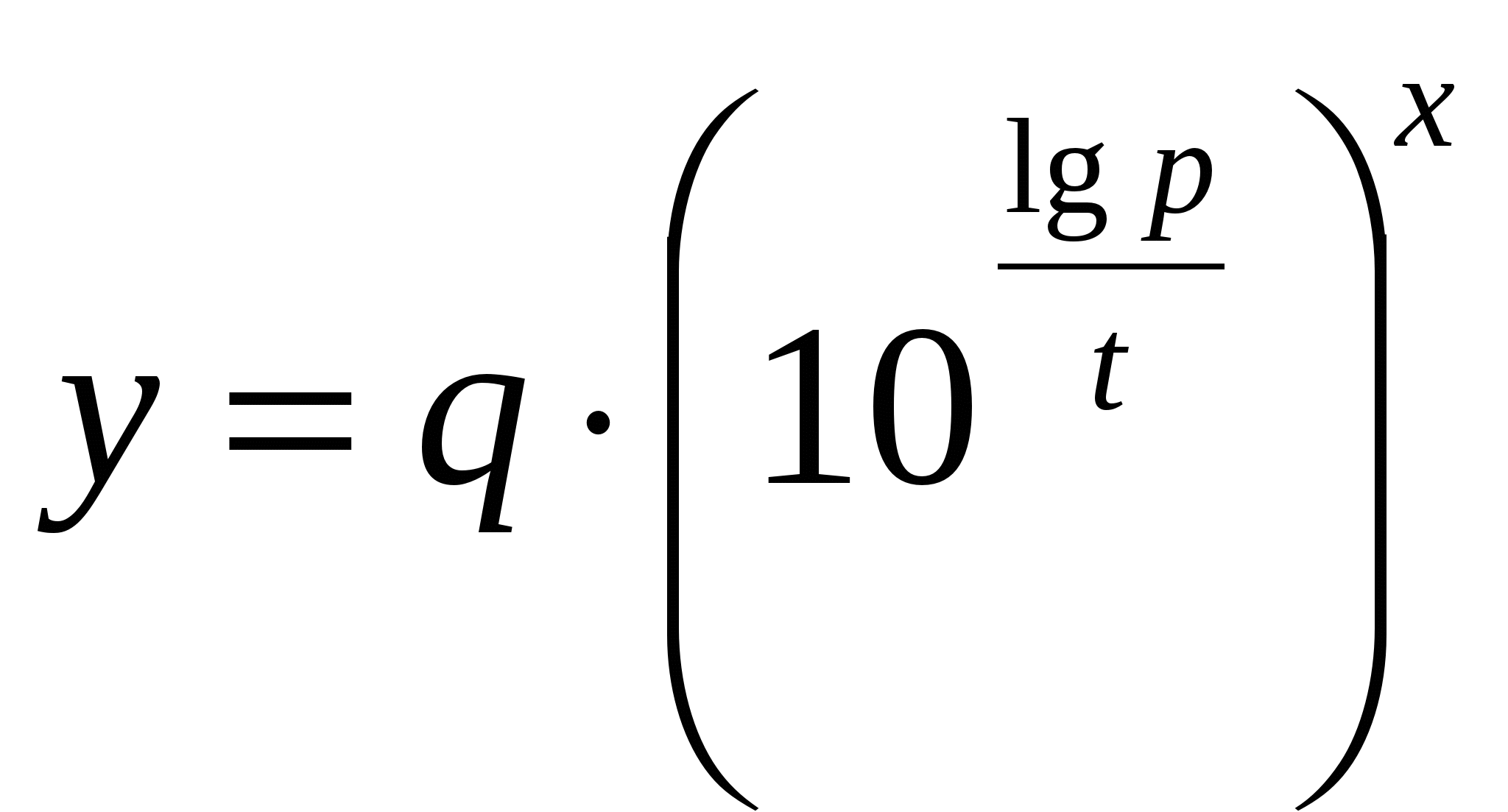. И теперь ясно, что мы ищем x, при котором 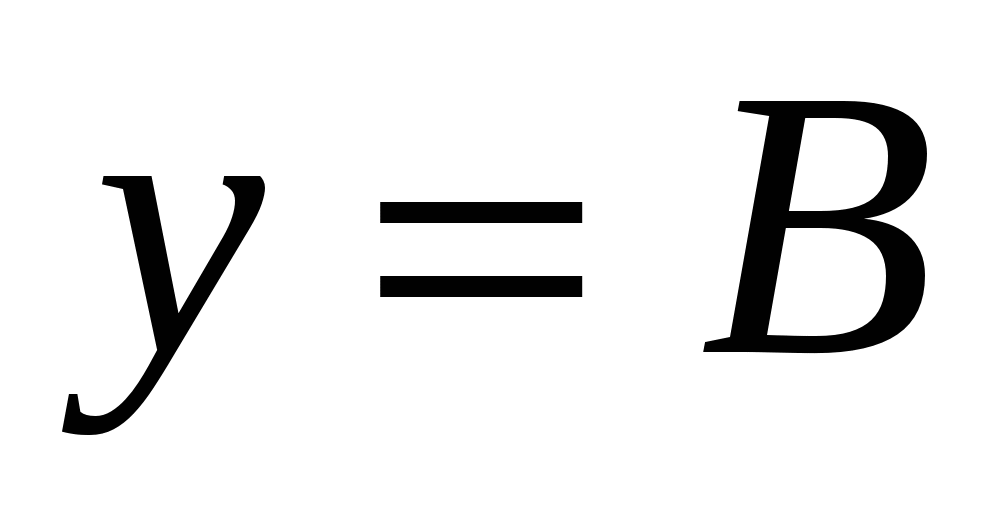, т.е. надо решить уравнение 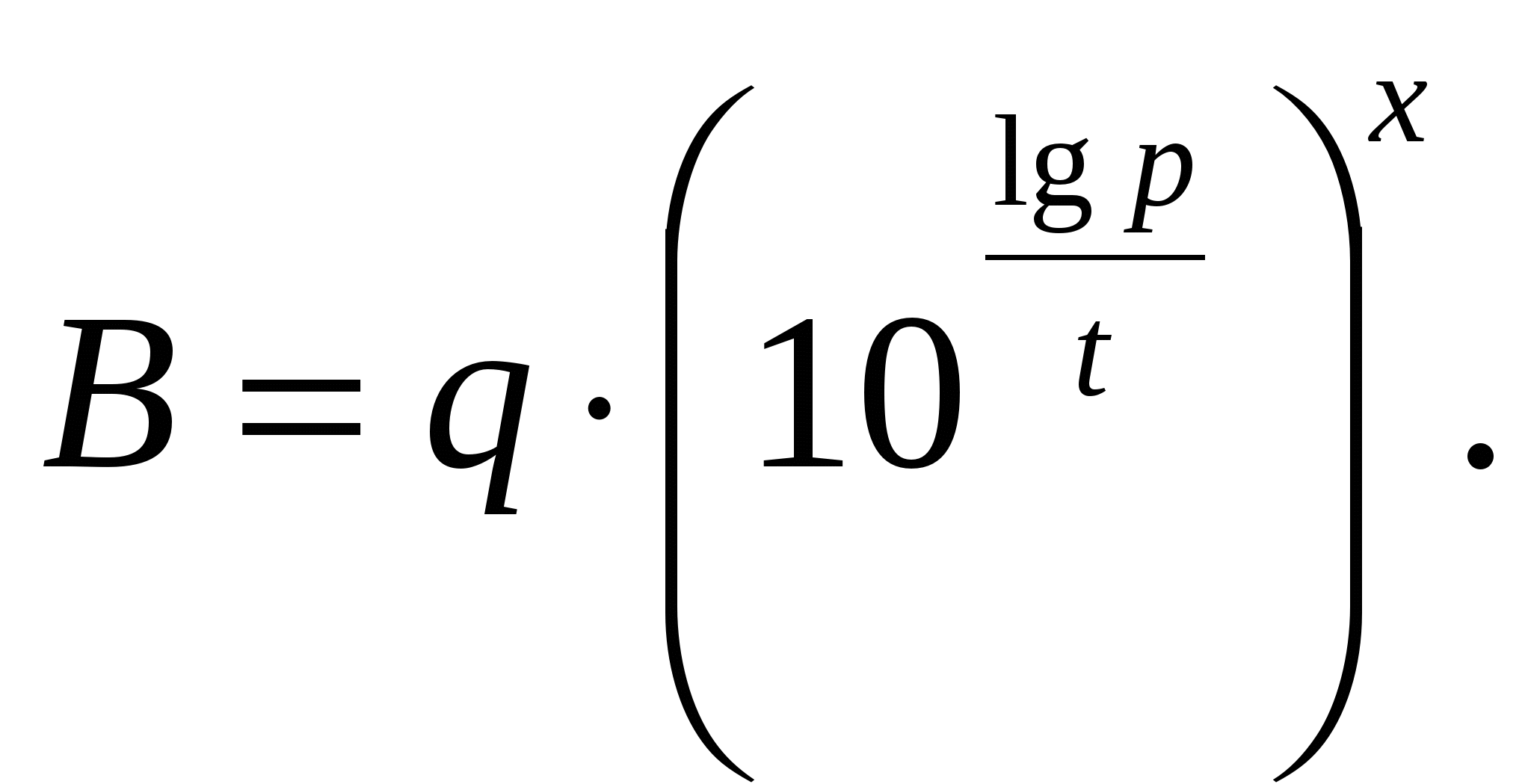Выполняя логарифмирование уравнения  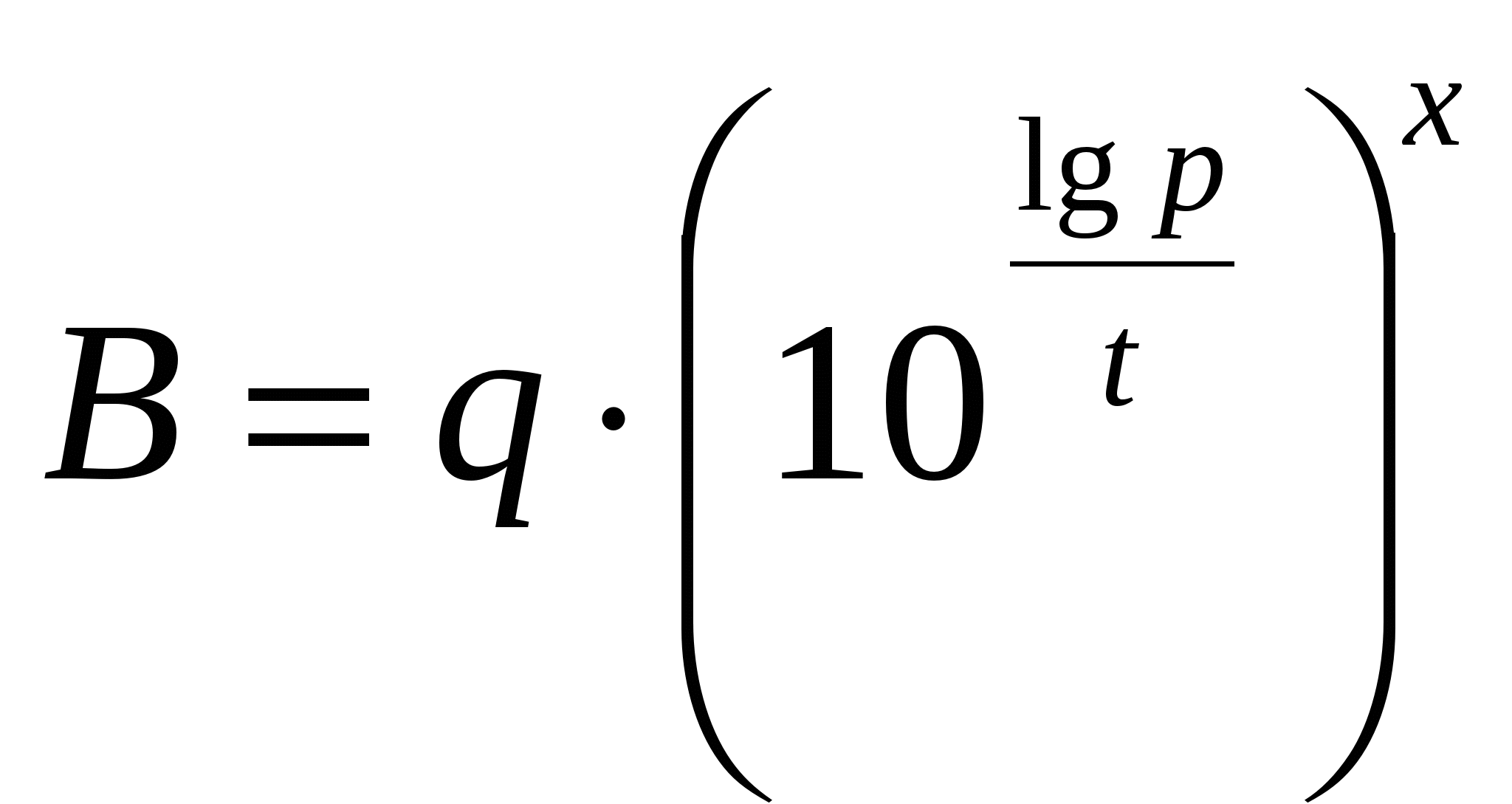по основанию 10, получим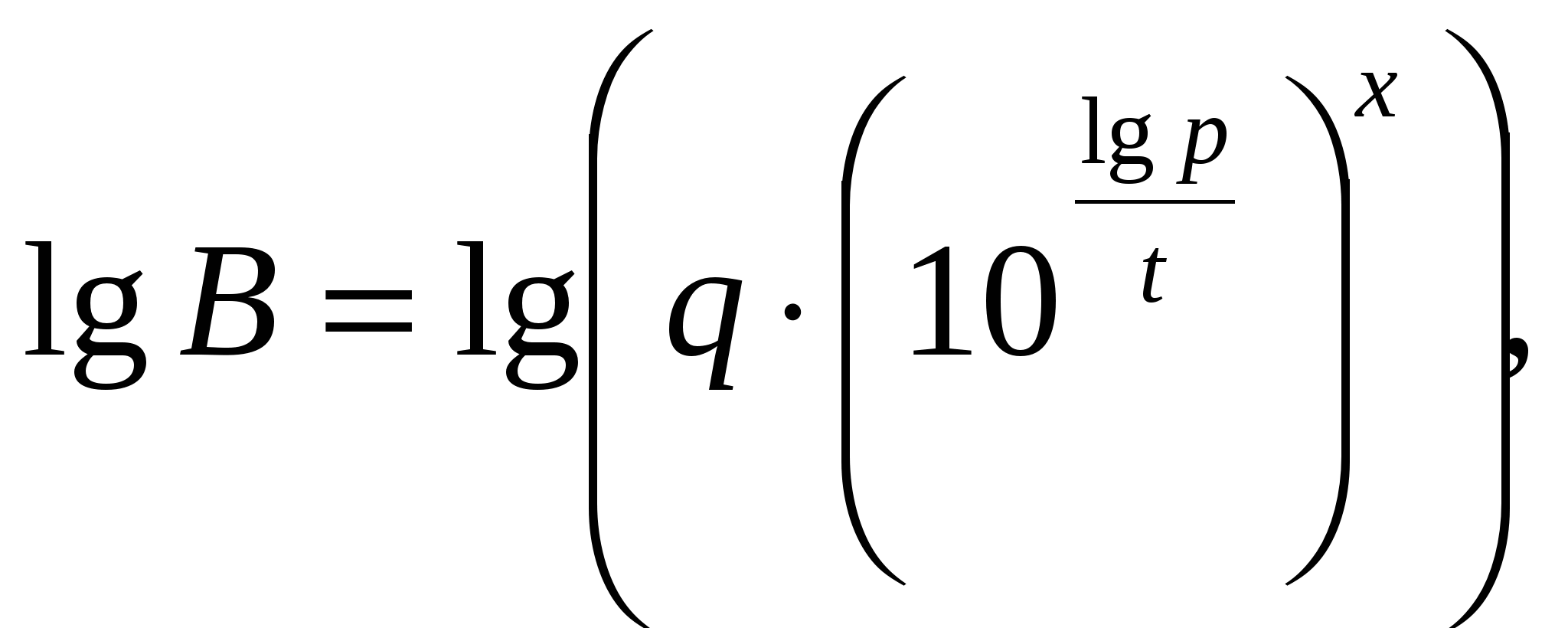  

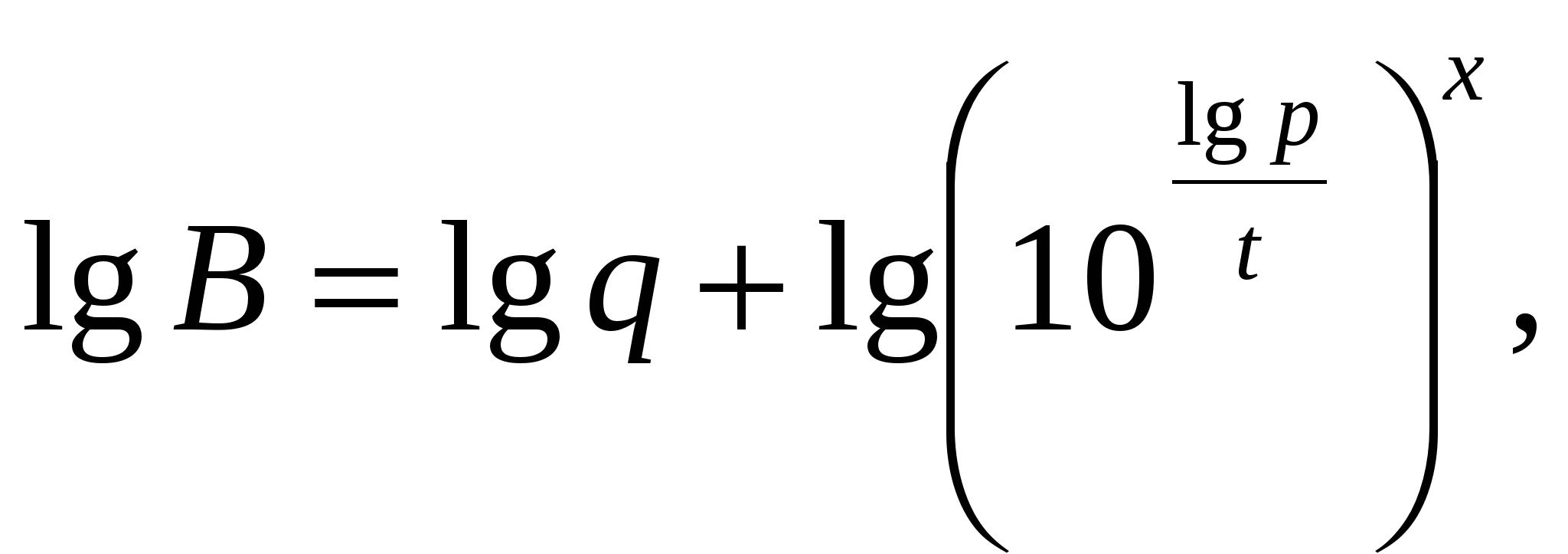
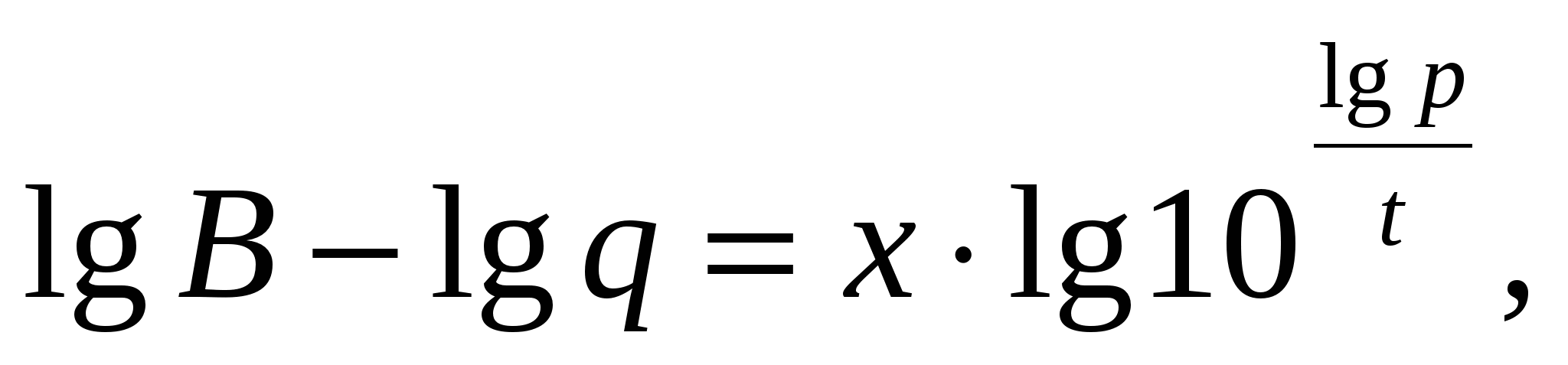
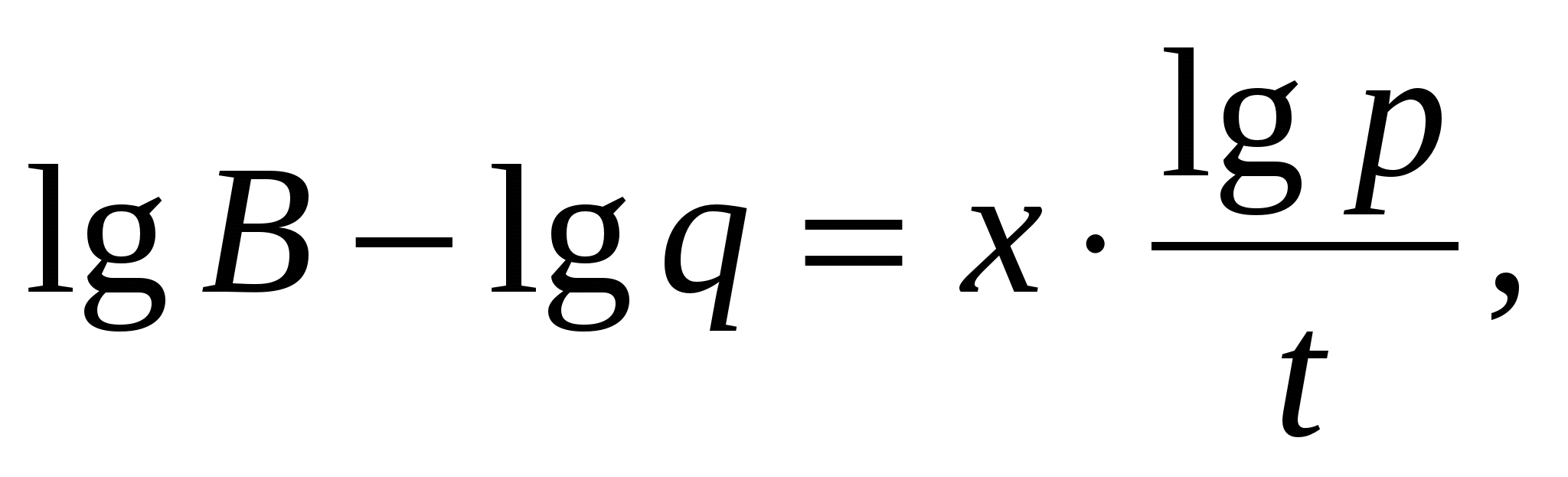
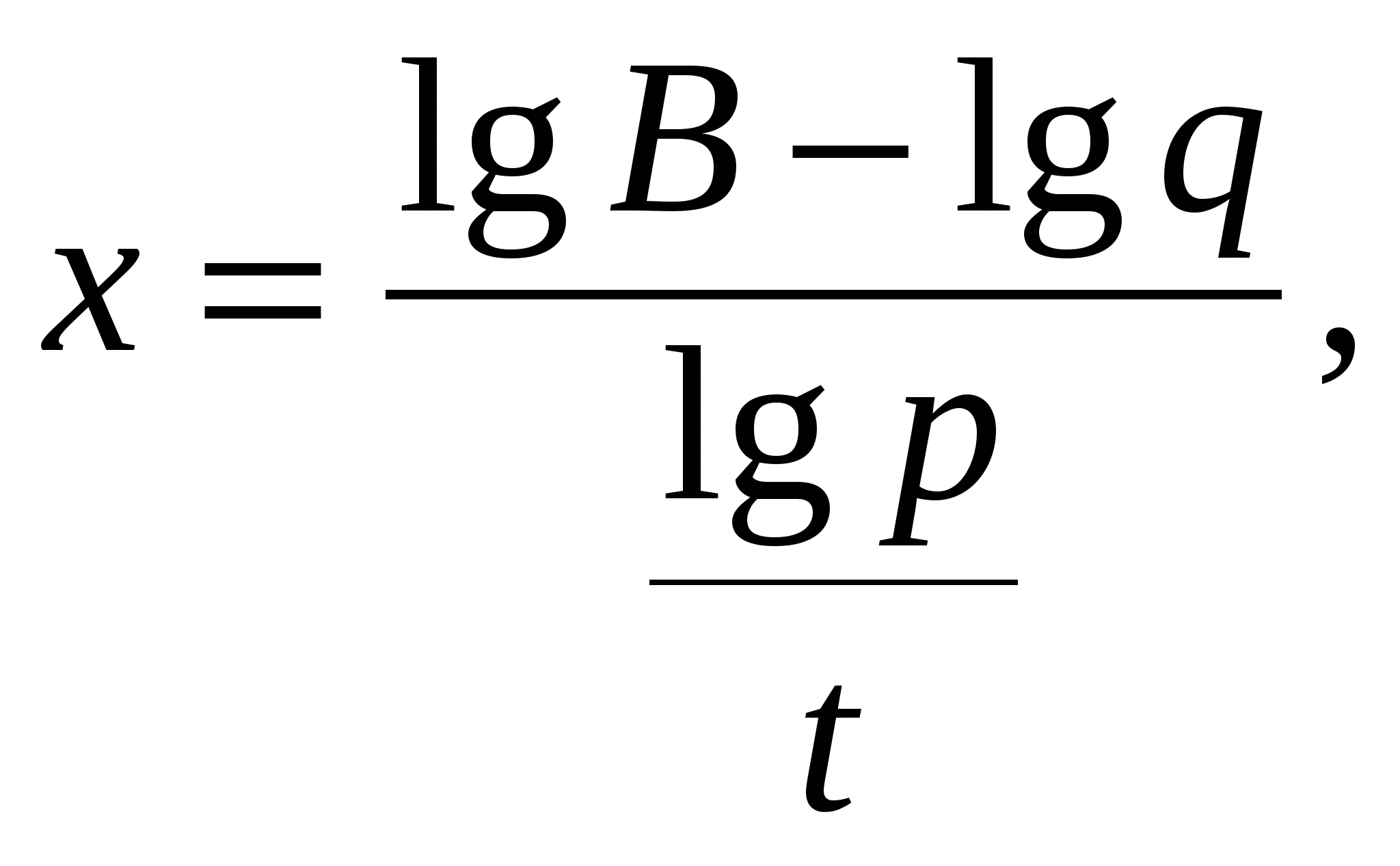
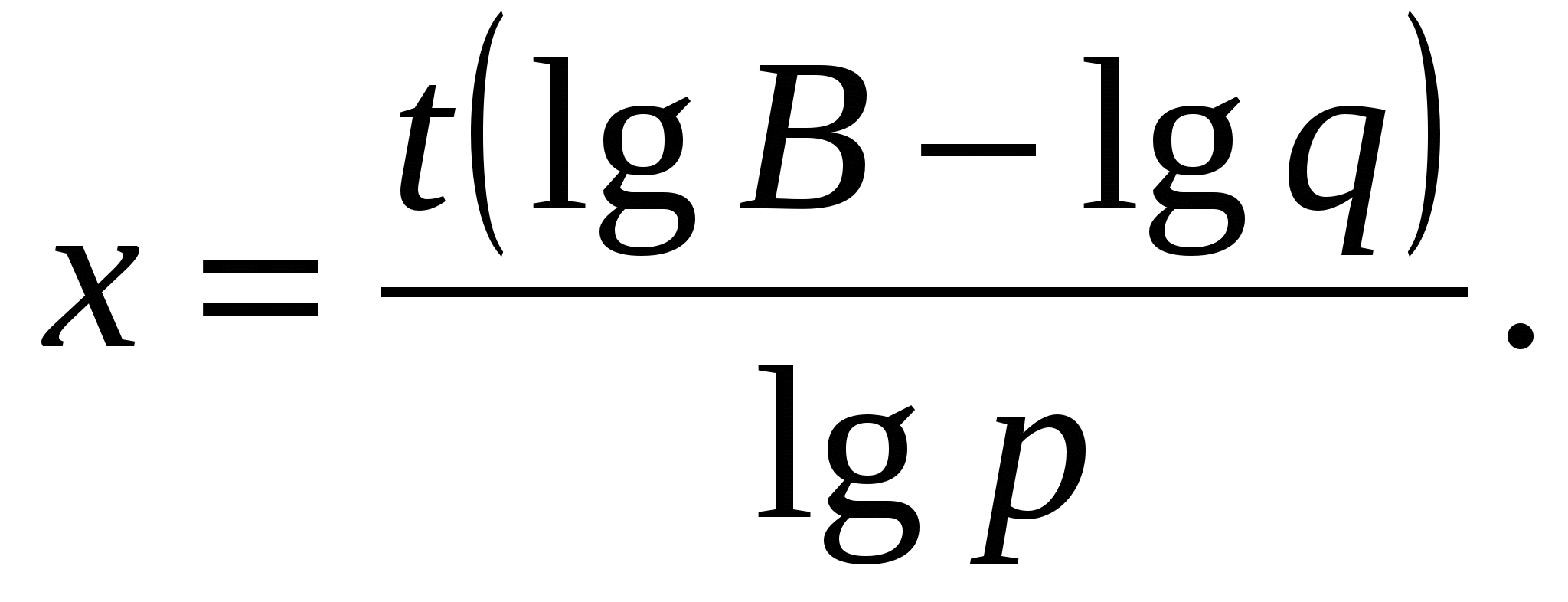
Ответ: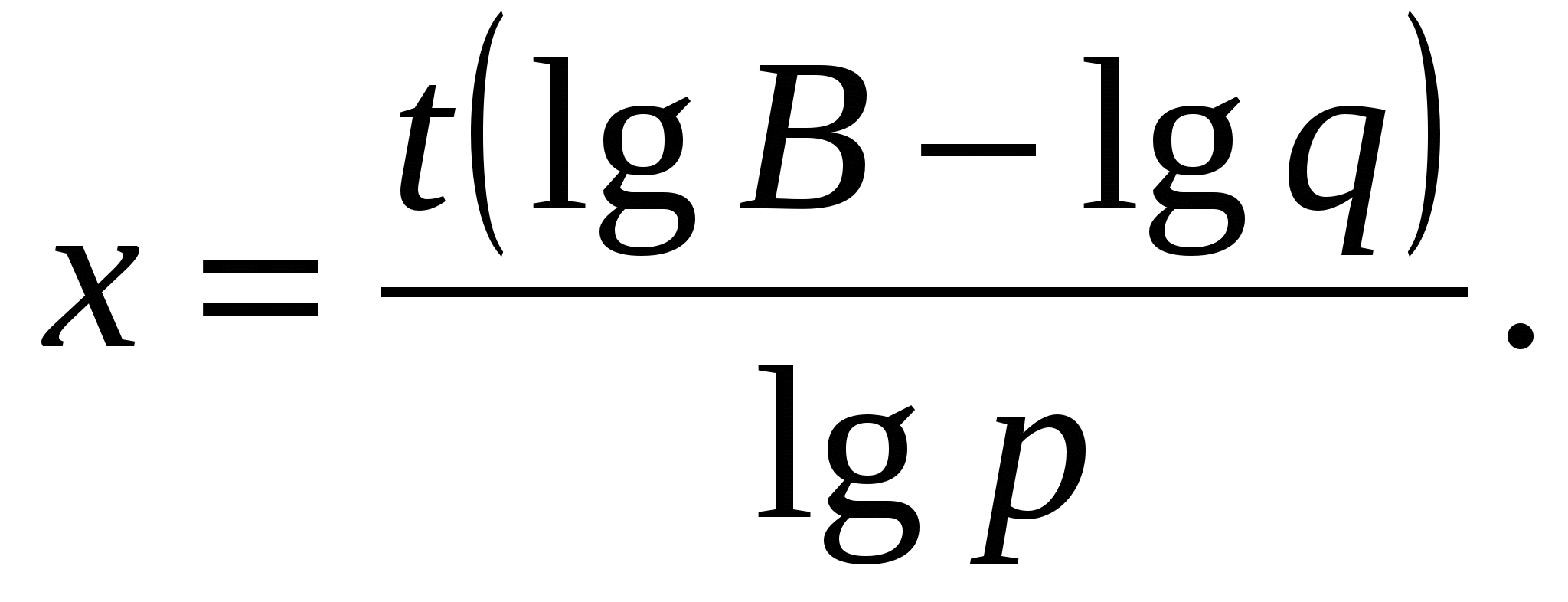 

infourok.ru

Доклад - Роль математики в современном естествознании 2

Содержание

Аннотация……………………………………………………………………….2

Ведение…………………………………………………………………………..4

1. Предмет и специфика математики…………………………………………..6

2. Математика – источник представлений и концепций в

естествознании………………………………………………………………..9

3. Математика – язык точного естествознания……………………………….13

Заключение……………………………………………………………………...19

Список использованной литературы…………………………………………..22

Введение

Вряд ли вызывает сомнение утверждение: математика нужна всем вне зависимости от рода занятий и профессии. Однако для разных людей необходима и различная математика: для продавца может быть достаточно знаний простейших арифметических операций, а для истинного естествоиспытателя обязательно требуются глубокие знания современной математики, поскольку только на их основе возможно открытие законов природы и познание ее гармонического развития. Иногда к познанию математики влекут и субъективные побуждения. Об одном из них Луций Анней Сенека ( 4 до н.э. – 65 н.э.), римский писатель и философ, писал: «Александр, царь Македонский, принялся изучать геометрию – несчастный! – только с тем, чтобы узнать, как мала земля, чью ничтожную часть он захватил. Несчастным я называю его потому, что он должен был понять ложность своего прозвища, ибо можно ли быть великим на ничтожном пространстве». [ 3, c.29].

Возникает вопрос: может ли серьезный естествоиспытатель обойтись без глубокого познания премудростей математики? Ответ несколько неожиданный: да, может. Однако к нему следует добавить: только в исключительном случае. И вот подтверждающий пример. Чарлз Дарвин, обобщая результаты собственных наблюдений и достижения современной ему биологии, вскрыл основные факторы эволюции органического мира. Причем он сделал это, не опираясь на хорошо разработанный к тому времени математический аппарат, хотя и высоко ценил математику: «… в последние годы я глубоко сожалел, что не успел ознакомиться с математикой, по крайней мере настолько, чтобы понимать в ее великих руководящих началах; так усвоившие их производят впечатление людей, обладающих одним органом чувств более, чем простые смертные».

Кто знает – может быть, обладание математическим чувством позволило бы Дарвину внести еще больший вклад в познание гармонии природы.

Известно, что еще в древние времена математике придавалось большое значение. Девиз первой академии – платоновской академии – «Не знающие математики сюда не входят» — ярко свидетельствует о том, насколько высоко ценили математику на заре науки, хотя в те времена основным предметом науки была философия.

Простейшие в современном понимании математические начала, включающие элементарный арифметический счет и простейшие геометрические измерения, служат отправной точкой естествознания.

«Тот, кто хочет решить вопросы естественных наук без помощи математики, ставит неразрешимую задачу. Следует измерять то, что измеримо, и делать измеримым то, что таковым не является», — утверждал выдающийся итальянский физик и астроном, один из основоположников естествознания Галилео Галилей (1564-1642).

1. Предмет и специфика математики

Математика имеет для естествознания непреходящее значение, а потому прежде чем обратиться непосредственно к анализу ее роли, целесообразно рассмотреть вопрос о ее достоинствах.

Самое лаконичное и притом довольно удачное определение математики дает Николай Бурбаки ( коллективное имя группы французских математиков). Он определяет современную математику как науку о структурах, «единственными математическими объектами становятся, собственно говоря, математические структуры». В данном случае под структурой имеется в виду определенным образом упорядоченное многообразие математических элементов (чисел, функций и т.п.). [ 2, c.27].

В основаниях любой математической дисциплины непременно обнаруживаются некоторые математические элементы и постилируемые различия между ними. При этом для построения математической системы используются, как правило, два метода: аксиоматический и конструктивистский.

При аксиоматическом методе исходят из аксиом ( исходных положений теории) и правил вывода ( дедукции) из них других положений. Широко используются символьные записи, а не громоздкие словесные выражения. Замена естественного языка математическими символами называется формализацией. Если формализация состоялась, то аксиоматическая система является формальной, а положения системы приобретают характер формул. Получаемые в результате вывода доказательства формулы называются теоремами. Таково описанное вкратце содержание аксиоматического метода.

В случае конструктивистского метода исходят из принимаемых интуитивно очевидными математических конструктов, на их основе строят более сложные, чем они, элементы ( а не выводят формулы), в процессе конструирования этих элементов используют подходящую для построения последовательность шагов.

Математик непременно оперирует конструктами, часть из которых принимается интуитивно, выражаясь точнее, на основе обобщения доступного ему математического опыта, а другие либо дедуцируются из аксиом, либо конструируются, чаще всего в форме последовательно осуществляемых символьных записей. Для математика важно задать отличие метематических конструктов друг от друга. В естествознании чувства, мысли, слова и предложения несут информацию об изучаемых природных явлениях, они обращены в сторону природы. В математике дело обстоит принципиально по –другому, здесь математические конструкты « не смотрят по сторонам », они соотносятся исключительно друг с другом. Поясним сказанное на примере задания натуральных чисел.

Натуральное число может быть задано на основе следующих аксиом ( правил):

1. 0 является натуральным числом.

2. Если n натуральное число, то и следующее за ним n′ — натуральное число.

3. Никаких натуральных чисел, кроме тех, которые получаются согласно 1 и 2, не существует.

4. Для любых натуральных чисел m и n из m′=n′ следует m=n.

5. Для любого натурального числа n, n′≠ 0.

Задать натуральное число – значит выразить операцию «′», читается «следующий за» столько раз, сколько это необходимо для задания числа. Так, задать натуральное число означает дважды применить операцию «′». Используя операцию «следующий за», «′», математик строит ряд натуральных чисел настолько далеко, насколько это возможно. Ему важно установить, какое число следует за каким, как соотносятся числа друг с другом ( так, 5 – 3 = 2, «5» — это число, которое на «2» больше, чем «3» ), то есть какова их упорядоченность. Вопрос о том, существуют ли числа в природе, математика не интересует ( природой пусть занимаются естествоиспытатели), ему важно изобрести систему упорядоченных конструктов, характер взаимосвязи которых невозможно установить без задания их отличительных признаков.

Характер математического знания таков, что его приверженцы, оправдывая свой статус, вынуждены, разумеется, это делается в силу их свободного волеизъявления, как можно более детально устанавливать характер упорядоченности тех совокупностей элементов, которые они изобретают и изучают. Именно в этой связи доказательство новой теоремы или построение ранее неизвестного конструкта расценивается как математический успех. Интерес математика заключен в изобретении многообразий упорядоченных математических конструктов.

Если многообразие математических конструктов не упорядочено, то есть невозможно их сопоставление друг с другом, то работа математика теряет всякий смысл. Дабы этого не случилось, математик внимательно следит за тем, чтобы математическая теория была непротиворечивой. Математическая теория называется непротиворечивой, если в ней не наличествуют два или больше взаимно исключающих предположения. Наличие противоречий «разваливает» математическую теорию. Простой пример: если бы согласно таблице умножения 3 × 3 = 9 и 3 × 3 = 8, то ее невозможно было бы продуктивно использовать.

Многовековое развитие математики показывает, что непротиворечивость – это ее основополагающий научный критерий.

2. Математика — источник представлений и концепций в естествознании

Назначение математики состоит в том, она вырабатывает для остальной науки, прежде всего для естествознания, структуры мысли, формулы, на основе которых можно решать проблемы специальных наук.

Это обусловлено особенностью математики описывать не свойства вещей, а свойства свойств, выделяя отношения, независимые от каких-либо конкретных свойств, то есть отношения отношений. Но поскольку и отношения, выводимые математикой, особые (будучи отношениями отношений), то ей удается проникать в самые глубокие характеристики мира и разговаривать на языке не просто отношений, а структур, определяемых как инварианты систем. Поэтому, кстати сказать, математики скорее говорят не о законах (раскрывающих общие, существенные, повторяющиеся и т.д. связи), а именно о структурах.

Эти глубинные проникновения в природу и позволяют математике исполнять роль методологии, выступая носителем плодотворных идей. Относительно сказанного современный американский исследователь Ф. Дайсон пишет: «Математика для физики — это не только инструмент, с помощью которого она может количественно описать явление, но и главный источник представлений и принципов, на основе которых зарождаются новые теории». Близкие мысли высказывает известный математик, академик Б. Гнеденко, также подчеркивая, что роль математики не ограничивается функцией аппарата вычисления, подчеркивал, что математика — определенная концепция природы. [ 7].

Поскольку привилегия математики — выделять чистые, безотносительные к какому-либо физическому (химическому или социально насыщенному содержанию), она тем самым вырабатывает модели возможных еще неизвестных науке состояний. Естествоиспытатель может выбирать из них и примеривать к своей области исследования. Это стимулирует научный поиск, пробуждая и будоража ученую мысль. В силу указанной особенности математику характеризуют как склад готовых костюмов, пошитых на все живые существа, мыслимые и немыслимые (Р. Фейнман), вообще на все возможные природные ситуации. То есть это своеобразный портной для разнообразных вещественных образований, которые могут быть вписаны в эти готовые одежды. Характеризуя рассматриваемую особенность отношений между математикой и физикой, американский физик-теоретик венгерского происхождения Е. Вигнер в режиме шутки произнес: «Физики — безответственные люди: они берут готовые математические уравнения и используют их, не зная, верны они или нет».

В свое время И. Кант метко определил: «Математика — наука, брошенная человеком на исследование мира в его возможных вариантах». Если физику или вообще естествоиспытателю позволено видеть мир таким, каков он есть, то математику дано видеть мир во всех его логических вариантах. Иначе сказать, физик не может строить мир, противоречивый физически (и уж тем более — логически), математику же разрешены построения, противоречивые физически, лишь бы они не страдали логическими противоречиями. Физики говорят, каков мир, математики исследуют, каким бы он мог быть в его потенциальных версиях. Это и придает стимул воображению. Как замечает австрийский математик и писатель нашего времени Р. Музиль, математика есть роскошь броситься вперед, очертя голову, потому математики предаются самому отважному и восхитительному авантюризму, какой доступен человеку. Стоит заметить лишь, что раскованность и рискованность — преимущество не только собственно математика, но и любого исследователя, если и поскольку он мыслит математически, то есть пытаясь дать, по выражению Г. Вейля, «теоретическое изображение бытия на фоне возможного».

Здесь не должно сложиться впечатления о возможности бескрайней фантазийной деятельности ученого. Истина состоит в том, что нематематические науки, сталкиваясь с запретами в проявлении какого-либо свойства, действия, не знают границ, до которых распространяется их компетенция. Это способна определить и узаконить лишь математика, владеющая искусством расчета на основе количественного описания явлений. Другие науки знают лишь, что нечто разрешено, но они не умеют знать той черты, до которой это разрешено, не умеют устанавливать пределов возможного — той количественной меры, определяющей вариантность изменений. Скажем, биолог не располагает сведениями пределов возможного для жизни и познает их в диапазоне лишь наблюдаемого.

Методологическое значение математики для других наук проявляется еще в одном аспекте. Поскольку ее абстракции отвлечены от конкретных свойств, она способна проводить аналогии между качественно различными объектами, переходить от одной области реальности к другой. Д. Пойа назвал это свойство математики умением «наводить мосты над пропастью». Там, где конкретная наука останавливается (кончается ее компетенция), математика в силу ее количественного подхода к явлениям, свободно переносит свои структуры на соседние, близкие и далекие, регионы природы.

Таковы некоторые методологические уроки, внушаемые математикой. Однако, сколь ни эффективна математическая наука, и на нее брошены некоторые тени, а лучше сказать: эти тени — есть продолжение ее достоинств (при неадекватном использовании последних).

Мы говорим: математический аппарат исследования применим там, где выявлена однородность, точнее сказать, математика и приводит природные образования к однородностям. Но тем самым она лишает мир многообразия и богатства качественных проявлений, ибо счет, по выражению отечественного математика современности И. Шафаревича, «убивает индивидуальность». Он пишет. Мы имеем, скажем, яблоко, цветок, кошку, дом, солдата, студента, луну. Можно сосчитать и объявить, что их 7. Но 7 чего? Единственный ответ: «7 предметов». Различия между солдатом, луной, яблоком и т.д. исчезают. Они все потеряли свою индивидуальность и превратились в лишенные признаков «предметы»69. То есть счет выравнивает вещи, убирая «персональные» характеристики. Как шутил В. Маяковский, математику все едино: он может складывать окурки и паровозы.

Описывая объект, процесс, математика выявляет какую-то лишь одну (существенную) характеристику и, прослеживая ее вариации, выводит закономерность. Все остальные характеристики уходят в тень, иначе они будут мешать исследованию. Конечно, эти другие также могут оказаться предметом изучения, но будучи взяты по тому же математическому сценарию: каждый раз только один единственный параметр, одно выделенное свойство в отвлечении от остального разнообразия. Напрашивается аналогия. Ее проводит Ю. Шрейдер, называя математику пародией на природу. И в самом деле. Пародия схватывает какую-то одну характеристическую черту пародируемого, за которой уже не видно других особенностей, просто они не важны.

Однако из этого обстоятельства не следуют лишь негативные выводы. Во-первых, математика по-иному работать не может, а во-вторых, в подобном подходе свое преимущество, оно сопряжено, так сказать, с «чистотой» описания: налицо четкая заданность исследования, когда необходимо проследить «поведение» объекта на основе определенного свойства, вычленить линию изменений, тенденцию развития и передать информацию в строгих графиках, схемах, уравнениях.

Используя математические методы исследования, вовлекая их в познавательный поиск, науки должны учитывать возможности математики, считаясь с границами ее применимости. Имеется в виду то, что сама по себе математическая обработка содержания, его перевод на язык количественных описаний не дает прироста информации.

Таким образом можно подчеркнуть важную роль этой математики как языка, арсенала особых методов исследования, источника представлений и концепций в естествознании.

3. Математика – язык точного естествознания

"… Все законы выводятся из опыта. Но для выражения их нужен специальный язык. Обиходный язык слишком беден, кроме того, он слишком неопределен для выражения столь богатых содержанием точных и тонких соотношений. Таково первое основание, по которому физик не может обойтись без математики; она дает ему единственный язык, на котором он в состоянии изъясняться". Математика — наука о количественных отношениях действительности. «Подлинно реалистическая математика, подобно физике, представляет собой фрагмент теоретической конструкции одного и того же реального мира.»(Г.Вейль) Она является междисциплинарной наукой. Результаты ее используются в естествознании и общественных науках. Роль математики в современном естествознании проявляется в том, что новая теоретическая интерпретация какого-либо явления считается полноценной, если удается создать математический аппарат, отражающий основные закономерности этого явления. Во многих случаях математика играет роль универсального языка естествознания, специально предназначенного для лаконичной точной записи различных утверждений.Точность есть выражение однозначности, исключающее вариантность, разброс значений, неопределенность. Этим и отличаются математические знаки — символы, обозначающие объекты и операции математики. Здесь символы жестко привязаны к значениям, не допуская разночтений, интерпретаций и объяснений, что имеет место относительно знаков других наук.[ 6].

Огромные успехи точных математических наук привели к появлению среди ученых, особенно среди физиков, веры в то, что все реально наблюдаемое в их опытах подчиняется законам математики вплоть до мельчайших деталей. Установление математических законов, которым подчиняется физическая реальность, было одним из самых поразительных чудесных открытий, сделанных человечеством. Ведь математика не основана на эксперименте, а порождена человеческим разумом. Когда физик использует свои знания для предсказаний и на основе нескольких экспериментов, проведенных в конкретное время и в конкретном месте, и подходящей теории пытается объяснить явления природы, происходящие в совершенно другом месте и в совершенно другое время, и такие предсказания сбываются, то это граничит с чудом. Физик при этом лишь с удовлетворением заключает, что, по-видимому, теория верна. Но почему, собственно говоря, реально существующий мир должен подчиняться теории, математической структуре? Кант дал на этот вопрос остроумный ответ: само наше восприятие выстраивает действительность, т. е. то, что отражается нашим разумом и воспринимается как реальность, подчиняется математическим законам. Другая мысль такова: в смирительную рубашку математики природу одевает вовсе не наша чувственная или познавательная деятельность, а сама природа в ходе своего эволюционного развития вкладывает математику в наш разум как реально существующую структуру, неотъемлемую от нее самой. Развитие наших способностей к абстрагированию и манипулированию логическими символами должно быть ориентировано на реально существующие структуры реального мира. «Вступая на проложенный древними путь, скажем вместе с ними, что если приступить к божественному нам дано только через символы, то всего удобнее воспользоваться математическими из-за их непреходящей достоверности» (Н.Кузанский).

Допустим, вы физик и в вашем распоряжении имеется уравнение, описывающее некоторые физические явления, например состояние движения. «Обрушив» на это уравнение всю мощь математического анализа, вы обнаружите множество регулярностей, упорядоченностей, о которых, возможно, и не подозревали. Предположим, речь идет о равноускоренном движении: S=Vt + at /2, где S– путь, V — начальная скорость, a — ускорение, t — время движения. Вам необходимо определить формулу скорости: V=dS/dt=V + at. Формула скорости найдена легко и не без изящества.

Совершенно очевидно, что наши геометрические и логические возможности простираются далеко за пределы окружающего мира. А это означает, что реальный мир подчиняется математическим законам в значительно большей степени, чем нам известно сейчас. Но даже если эти структурные (математические) принципы экстраполируются все более глубокими конструкциями и теоремами, то и в этом случае просто невероятно, чтобы действительность с исчерпывающей полнотой отражалась математическими конструкциями — от огромных космологических размеров и до микрочастиц. Открытыми остаются вопросы, как математика соотносится с миром и дает возможность познавать его; какой способ познания преобладает в математике — дискурсивный или интуитивный. По мнению В. Гейзенберга, «наиболее важными ему кажутся, прежде всего, математические законы природы, находящиеся за явлениями, а не сам многогранный мир явлений». Физику-теоретику нелегко с этим согласиться, но в эволюционной теории познания фактически неизбежно возникает предположение о том, что математические способности вида «хомо сапиенс» принципиально ограниченны, так как имеют биологическую основу и, следовательно, не могут полностью содержать все структуры, существующие в действительности. Иными словами, должны существовать пределы для математического описания природы. По мнению некоторых методологов, законы природы не сводятся к математическим соотношениям. Их надо понимать как любой вид организованности идеальных прообразов вещей, или пси-функций. Есть три вида организованности: простейший — числовые соотношения; более сложный — ритмика первого порядка, изучаемая математической теорией групп; ритмика второго порядка — «слово». Два первых вида организованности наполняют Вселенную мерой и гармонией, третий вид — смыслом. В рамках этого объяснения математика занимает свое особое место в познании. «Чисто логическое мышление не может принести нам никакого знания эмпирического мира. Все познание реальности отправляется от опыта и возвращается к нему. Предложения, полученные при помощи чисто логических средств, при сравнении с реальностью оказываются совершенно пустыми». (А.Эйнштейн).

Говоря о важности применения математики в естествознании, мы не должны абсолютизировать ее роль. Математические формулы сами по себе абстрактны и лишены конкретного содержания. Математика является лишь орудием, или средством, физического исследования. Только согласованные с научным наблюдением и экспериментом физические исследования наполняют математические формулы конкретным содержанием.

Ньютон обнаружил, что взаимное притяжение небесных тел можно описать законом обратных квадратов, который связывает силу тяготения (F) с расстоянием (r) от центра сферического тела. Закон всемирного тяготения И. Ньютона имеет вид:

F=Gm m /r .

Но так компактно и изящно закон выглядит лишь в формуле, а реально тяготеющие массы, например планеты Солнечной системы, движутся при наблюдении за ними сложно, с теми или иными отклонениями от той траектории, которая предписывается формулой. [ 4].

Построение различных формальных систем, моделей, алгоритмических схем — лишь одна из сторон научного познания. Научную интуицию и гениальные догадки формализовать не удается. Универсальной «логики открытий» нет. Кроме того, даже наиболее тщательно поставленный эксперимент никогда в конце концов не бывает полностью изолирован от влияния окружающей среды, а состояние системы ни в один момент времени не может быть известным точно. Абсолютная (математическая) точность физически недостижима — небольшие неточности будут всегда, и это принципиальный момент. Почти одинаковые причины будут давать почти одинаковые следствия, причем как в природе, так и в хорошо поставленном эксперименте. Это чаще всего именно так и происходит, особенно для коротких временных отрезков, в противном случае было бы невозможно установить какой-либо закон природы или же построить реально работающую машину. Но это весьма правдоподобное предположение оказывается справедливым не всегда, более того, оно неверно для больших промежутков времени даже в случае нормального (типичного) течения природных процессов. В этом смысл захватывающего прорыва, осуществленного при исследовании динамических систем. Существует раздел математики, посвященный анализу конфликтных ситуаций, где под компромиссом понимается коллективное решение, не нарушающее интересы всех сторон (устойчивой системы). Всякий компромисс достигается определенной последовательностью шагов и действий. Например, для разрешения экологических проблем необходимо учесть все ограничения, нарушения которых означало бы нарушение гомеостатического состояния. Это позволило составить формальную систему запретов или минимум условий, необходимых для обеспечения гомеостазиса. В 1944 г. в США опубликована книга Д. Неймана и О. Моргенштерна «Теория игр и экономическое поведение», в которой рассматривались вопросы математического описания способов принятия решений, типичных для конкурентной экономики. Впоследствии теория игр превратилась в общую математическую теорию конфликтов, описывающую военные, экономические и правовые коллизии, столкновения, связанные с биологической борьбой за существование, различные игровые стратегии. В случае игр с противоположными интересами (антагонистическая игра) оптимальной считается стратегия, направленная на достижение максимального выигрыша. Конкуренция здесь является разновидностью конфликта. Математический аппарат терии катастроф позволяет свести огромное многообразие сложных процессов к небольшому числу точно изученных схем. Для одной-двух переменных, характеризующих состояние системы, и не более пяти управляющих параметров существует семь типов элементарных катастроф. Теория катастроф широко используется в гидро- и аэродинамике, оптике, метеорологии, квантовой динамике для описания нелинейных систем, далеких от равновесия, подводя стандартную и эффективную базу под описание их качественных изменений.

Логическая стройность, строго дедуктивный характер построений, общеобязательность выводов математики создали ей славу образца научного знания. «Выгоды» естествознания от использования математики многообразны. Во многих случаях математика играет роль универсального языка естествознания, специально предназначенного для лаконичной точной записи различных утверждений. Точность есть выражение однозначности, исключающее вариантность, разброс значений, неопределенность. Этим и отличаются математические знаки — символы, обозначающие объекты и операции математики.

Огромные успехи точных математических наук привели к появлению среди ученых, особенно среди физиков, веры в то, что все реально наблюдаемое в их опытах подчиняется законам математики вплоть до мельчайших деталей. Установление математических законов, которым подчиняется физическая реальность, было одним из самых поразительных чудесных открытий, сделанных человечеством. Ведь математика не основана на эксперименте, а порождена человеческим разумом. Совершенно очевидно, что наши геометрические и логические возможности простираются далеко за пределы окружающего мира. А это означает, что реальный мир подчиняется математическим законам в значительно большей степени, чем нам известно сейчас. В эволюционной теории познания фактически неизбежно возникает предположение о том, что математические способности вида «хомо сапиенс» принципиально ограниченны, так как имеют биологическую основу и, следовательно, не могут полностью содержать все структуры, существующие в действительности. Иными словами, должны существовать пределы для математического описания природы.

Назначение математики состоит в том, она вырабатывает для остальной науки, прежде всего для естествознания, структуры мысли, формулы, на основе которых можно решать проблемы специальных наук.

Это обусловлено особенностью математики описывать не свойства вещей, а свойства свойств, выделяя отношения, независимые от каких-либо конкретных свойств, то есть отношения отношений.

Эти глубинные проникновения в природу и позволяют математике исполнять роль методологии, выступая носителем плодотворных идей.Поскольку привилегия математики — выделять чистые, безотносительные к какому-либо физическому (химическому или социально насыщенному содержанию), она тем самым вырабатывает модели возможных еще неизвестных науке состояний. Естествоиспытатель может выбирать из них и примеривать к своей области исследования. Это стимулирует научный поиск, пробуждая и будоража ученую мысль.

В свое время И. Кант метко определил: «Математика — наука, брошенная человеком на исследование мира в его возможных вариантах».

Если физику или вообще естествоиспытателю позволено видеть мир таким, каков он есть, то математику дано видеть мир во всех его логических вариантах.

Методологическое значение математики для других наук проявляется еще в одном аспекте. Поскольку ее абстракции отвлечены от конкретных свойств, она способна проводить аналогии между качественно различными объектами, переходить от одной области реальности к другой.

Используя математические методы исследования, вовлекая их в познавательный поиск, науки должны учитывать возможности математики, считаясь с границами ее применимости. Имеется в виду то, что сама по себе математическая обработка содержания, его перевод на язык количественных описаний не дает прироста информации.

Список использованной литературы:

1. Буслова М.К., Горалевич Т.А., Готт В.С. и др. Современное естествознание в системе науки и практики/ под ред. Сачкова Ю.В., Горолевич Т.А. – Мн.: Навука iтэхнiка, 1990.

2. Канке В.А. Концепции современного естествознания: Учебник для вузов. – М.: Логос, 2002.

3. Карпенков С.Х. Концепции современного естествознания. Краткий курс: Учебник. М.: Высш. шк., 2003.

4. Мотылева Л.С., Скоробогатов В.А., Судариков А.М. Концепции современного естествознания: Учебник для вузов/ под ред. Скоробогатова В.А. – Спб.: Союз,2002.

5. Соломантин В.А. История и концепций современного естествознания: Учебник для вузов. – М.: ПЕР СЭ, 2002.

6. www.domino.novsu.ac.ru.

7. www.ou.tsu.ru.

8. www.milogiya.narod.ru.

www.ronl.ru

Зачем биологу математика - математическая биология простыми словами

Законы эволюции хотя и основаны на фактах, но не имеют строгого математического обоснования. Это-то и позволяет ученым различных направлений трактовать их по-разному, а то и вовсе не признавать. Но все это до тех пор, пока до этих законов не добралась математика.

Первое по времени применение математики в биологии связано с обработкой результатов наблюдений. Так было установлено большинство экспериментальных закономерностей... Однако это в высшей степени полезное приложение математики к биологии не только не единственное, но даже и не самое важное.

Экспериментальные законы есть не только в биологии. Немало их в физике, технике, экономике и других областях человеческих знаний. Но какой бы науке ни принадлежал такой закон, у него всегда есть один серьезный изъян: он хотя и отвечает на вопрос "как", но не отвечает на вопрос "почему".

Еще алхимики знали, как растворяются вещества. Измеряя концентрацию раствора, легко начертить кривую, наглядно показывающую, что сначала вещество переходит в раствор большими дозами, затем эти дозы постепенно уменьшаются, пока наконец вещество совсем не перестанет растворяться.

Подобные кривые можно найти и в книгах по лесоводству. Они получены в результате сотен и тысяч обмеров и показывают, что дерево сначала растет быстро, затем рост замедляется и прекращается полностью.

Эти законы экспериментальные. Они довольно точно описывают явление — вполне достаточно для практики. Но вот прогнозировать, зная только их, трудно: можно сказать лишь, что данное вещество будет растворяться таким-то образом, если повторяются условия, при которых мы его изучали. Точно так же и с деревьями. Не зная, почему они растут так или иначе, нельзя предсказать, что случится с их ростом в иных условиях.

"Науки сильно различаются между собой по степени предсказуемости относящихся к ним фактов, и некоторые утверждают, что биология не наука. Поскольку биологические явления не всегда можно предсказать". Это грустное замечание ученого К. Вилли бьет прямо в цель. Чтобы получить ранг современной науки, биологии уже недостаточно располагать детальными сведениями о многочисленных и разрозненных фактах. Нужны законы, отвечающие на вопрос "почему". И именно тут заключена самая суть математической биологии.

Так же как в физике, изучая биологическое явление, стараются выявить его математические характеристики. Например, если обследуется больной, то для анализа его состояния требуются числовые данные — температура тела, давление и состав крови, частота пульса и т. д. и т. п.

Но ведь обычно изучают только одну какую-нибудь сторону, что-то является главным, а чем-то можно пренебречь. В астрономии, например, весь земной шар представляется как точка, лишенная размеров. Грубее, казалось бы, некуда. Тем не менее эти расчеты вот уже более 300 лет исправно служат при определении сроков затмений и в наши годы — при запуске спутников.

Но что считать главным, а что второстепенным? Здесь, на этой начальной стадии исследования, считаются и с интуицией, и с чутьем, и с мнением авторитета.

Часто, однако, биологи вообще отказываются делать какие-либо упрощения. На одном весьма представительном биологическом семинаре обсуждалась модель роста дерева. Докладчик, известный специалист своего дела, был принят аудиторией благожелательно. Все шло хорошо до тех пор, пока он не произнес фразу: "Так как энергия фотосинтеза пропорциональна площади листа, мы для простоты будем считать лист плоским, не имеющим толщины". Тут же посыпались недоуменные вопросы: "Как так? Ведь даже самый тонкий лист имеет толщину!". Вспомнили и о хвойных, у которых вообще трудно толщину отличить от ширины. С некоторым трудом удалось все же объяснить, что в задаче, которой, занимается докладчик, толщина листа не играет никакой роли и ею можно пренебречь. Зато вместо живого листа со всеми его бесконечными сложностями мы можем изучать простую модель.

Математическая модель изучается математическими средствами. Поэтому можно отвлечься на время от биологического содержания модели и сосредоточить свое внимание на ее математической сущности.

Разумеется, всю эту сложную работу, требующую специальных знаний, биолог проводит в тесном союзе с математиком, а некоторые моменты целиком препоручает математику-специалисту. В результате такой совместной работы получается биологический закон, записанный математически.

В отличие от экспериментального он отвечает на вопрос "почему", вскрывает внутренний механизм изучаемого процесса. Этот механизм описывается математическими соотношениями, входящими в модель. В модели роста дерева, например, таким механизмом является дифференциальное уравнение, выражающее закон сохранения энергий. Решив уравнение, получаем теоретическую кривую роста — она с поразительной точностью совпадает с экспериментальной.

Еще в 1931 году в Париже вышла в свет книга известного математика В. Вольтерра "Математическая теория борьбы за существование". В ней, в частности, была рассмотрена и проблема "хищник—жертва". Математик рассуждал так: "Прирост численности жертвы будет тем больше, чем больше родителей, то есть, чем больше численность жертвы в настоящий момент. Но, с другой стороны, чем больше численность жертвы, тем чаще она будет встречаться и уничтожаться хищниками. Таким образов, и убыль жертвы пропорциональна ее численности. Кроме того, эта убыль растет и с ростом численности хищников.

А от чего меняется численность хищников? Ее убыль происходит только из-за естественной смертности и поэтому пропорциональна количеству взрослых особей. А ее прибыль можно считать пропорциональной питанию, то есть пропорциональной количеству жертвы, уничтоженной хищниками".

Разумеется, система уравнений, составленная Вольтерра, упрощенно описывает ситуацию. Но он своей работой утвердил новый подход, новую методологию изучения биологических сообществ. Стало возможным строить математические теории таких сложных явлений, как симбиоз, паразитизм, распространение инфекционных заболеваний, искусственное подавление нежелательных видов и т. п.

Последняя из названных проблем очень интересна. Суть ее в том, что химические методы борьбы с вредными видами часто не удовлетворяют биологов. Некоторые химикалии настолько сильны, что вместе с вредными животными уничтожают и множество полезных. Бывает и наоборот: подавляемый вид очень быстро приспосабливается к химическим ядам и становится неуязвимым. Специалисты уверяют, например, что порошок ДДТ, один запах которого убивал клопов 30-х годов, нынешние клопы с успехом употребляют в пищу.

А вот еще один небольшой пример того, как математический подход прояснил запутанную биологическую ситуацию. В одном из экспериментов наблюдали удивительную вещь: стоило в колонию простейших микроорганизмов, обитающих в воде, поместить капельку сахарного сиропа, как все обитатели колонии, даже самые далекие, начинали продвигаться в направлении к капельке. Пораженные экспериментаторы готовы были утверждать, что у микроорганизмов есть специальный орган, который на большом расстоянии чувствует приманку и помогает двигаться к ней. Еще немного, и они бы бросились искать, этот никому не известный орган.

К счастью, один из биологов, знакомый с математикой, предложил другое объяснение феномена. Его версия состояла в том, что вдали от приманки движение микроорганизмов мало чем отличается от обычной диффузии, свойственной неживым частицам. Биологические особенности живых организмов проявляются только в непосредственной близости от приманки, когда они задерживаются около нее. Благодаря этой задержке следующий от капли слой становится менее насыщенным обитателями, чем обычно, и туда по законам диффузии устремляются микроорганизмы из соседнего слоя. В этот слой по тем же законам устремляются обитатели следующего, еще более удаленного слоя и т. д. и т. п. В результате получается тот поток микроорганизмов к капле, который и наблюдали экспериментаторы.

Эту гипотезу легко было проверить математически, и таинственный орган искать не пришлось.

Математические методы позволяли дать ответы на многие конкретные вопросы биологии. И эти ответы подчас поражают своей глубиной и изяществом. Однако говорить о математической биологии как о сложившейся науке еще рано.

distance-teacher.ru

Реферат - Математика и живые организмы

Содержание

<span Times New Roman"">      I.<span Times New Roman"">     

<span Times New Roman"">   II.<span Times New Roman"">     

1)<span Times New Roman"">   

2)<span Times New Roman"">   

3)<span Times New Roman"">   

4)<span Times New Roman"">   

5)<span Times New Roman"">   

6)<span Times New Roman"">   

7)<span Times New Roman"">   

8)<span Times New Roman"">   

9)<span Times New Roman"">   

10)Спиральные образования

<span Times New Roman""> III.<span Times New Roman"">     

IV.<span Times New Roman"">     

<span Times New Roman"">     I.<span Times New Roman"">     

Недавно мне попалась в руки увесистая монография, гдечуть ли не каждая страница была испещрена формулами. А речь шла всего лишь отом, как человек стоит. Что же произойдет, когда он сделает два- три шага?Какого размера должна быть страница, чтобы на ней уместилось хотя бы одно изалгебраических уравнений, описывающих движение? А разве менее сложна геометрияживых форм, начиная от амебы и кончая замысловатыми букетамиживотных-цветов—морских анемонов?

Живая природа сделала множество «изобретений», которыелюди поняли и смогли повторить лишь при соответствующем уровне развития науки итехники. Например, принцип эхолокации эффективно используют и дельфины, илетучие мыши, а в технике он появился только в XX веке; поиск добычи поинфракрасному излучению используют многие виды змей, в то время как очки дляночного видения созданы лишь недавно и т. д. До последнего времени бытовалоубеждение, что природа не изобрела колеса, что здесь техника пошла своиморигинальным путем. Но оказалось, что жгутики бактерий вращаются в специальных«подшипниках» и, значит, колесо тоже «изобретено» природой еще на самых раннихэтапах эволюции. Существует специальная наука — бионика, которая изучает«патенты природы». Оказывается, что их можно иногда использовать и в«человеческой» технике.

Менее известно, что в живых организмах происходятявления, которые позволяют считать, что природе принадлежит «приоритет» и в созданиисвоеобразных ЭВМ — устройств, производящих операции, весьма сходные сматематическими операциями, которые мы склонны считать достижением. Две руки,два глаза. Десять пальцев на руках — древнейший счетный прибор и основадесятичной системы счисления. Уже беглый взгляд на наше собственное телооткрывает то, что можно было бы назвать арифметикой живого. Прибавьте к этомуудивительную способность природы многократно копировать из поколения впоколение эти бесконечно прихотливые и, казалось бы, неповторимые комбинациилиний, фигур и поверхностей— и станет понятно, что математический расчетвнутренне присущ живой материи ничуть не меньше, чем миру «стальных машин, гдедышит интеграл». Попробуем уяснить себе, в чем именно проявляется присутствиематематики в биологическом организме.

Цель работы:исследовать связь математики с живой природой; доказать наличие упредставителей флоры и фауны тех признаков, которые позволяют создать ихматематическую модель; объяснить естественные процессы с точки зрения математики;рассказать о некоторых «изобретениях» природы, которые используются и будутиспользоваться в науке и технике; показать, как знания из области математикимогут помочь в биологии.

Задачи научной проблемы: научиться создавать технические объекты на основематематических моделей представителей флоры и фауны; решать вопросы, связанныес живыми организмами, используя математические законы; «перенять» у природы ее«изобретения».

<span Times New Roman"">  II.<span Times New Roman"">     

1)<span Times New Roman"">   

Первое знакомство с математикой — это счет: «Раз, два,три, четыре, пять, вышел зайчик погулять». И самым простым кажется и считаетсянатуральное число. Уже отрицательные числа очень медленно входили в математику.Появившись в раннем средневековье у математиков Индии, они лишь в XIII—XIVвеках проникают в европейскую науку, встречая там поначалу весьма сдержанноеотношение. Их называют «ложными», «абсурдными» числами. Но постепенноотрицательные числа доказали свое право на существование и стали привычными нетолько для специалистов — то, что было «на переднем крае науки» в средние века,сегодня спокойно воспринимают пятиклассники.

А вот в живых организмах, оказывается «все наоборот»:нервной клетке (нейрону) естественно и просто осуществлять операции сположительными и отрицательными действительными «числами», а для того чтобы«считать» даже до двух, требуется система из нескольких нейронов — примитивный«мозг».

Как же работает нейрон? Как всякая клетка, нейронотделен от наружной межклеточной среды особой оболочкой — мембраной. Междувнутренним содержимым клетки и наружной средой существует разность потенциалов.Если клетка находится в покое, разность потенциалов на ее мембране не меняется.Эту разность потенциалов в покое естественно принять за нулевой уровень(подобно тому, как приняли за нулевую температуру таяния льда).

На нейрон могут действовать другие нервные клетки —возбуждающие и тормозные. Сигналы, полученные от этих клеток, вызываютизменения разности потенциалов на мембране в двух противоположных направлениях.Когда разные сигналы приходят к нейрону одновременно, они складываются, причем,естественно, с учетом знака, т. е. нейрон суммирует приходящие к немуположительные и отрицательные сигналы; эта сумма может быть положительной илиотрицательной.

Интересная особенность работы нейрона состоит в том,что в отличие от технических сумматоров — от древнего абака до ЭВМ — полученнуюсумму он «помнит» недолго: если внешние воздействия прекратились, тонакопленная сумма начинает убывать по абсолютной величине, чтобы нейронвозвратился в состояние  покоя  (потенциал  на  мембране стремится к значению,которое мы приняли за нуль).

Такая вроде бы «ненадежность» нейрона связана с тем,что он предназначен не для хранения, а для передачи и преобразования информации:полученный сигнал нейрон передает другим клеткам нервной сети(клеткам-«мишеням» или «адресатам»). По способу передачи сигнала существуют дваразных типа нейронов с разными принципами работы: «аналоговые»    и   «пороговые»    нейроны.

Нейрон первого типа действует на клетки-мишени ссилой, пропорциональной накопленной сумме,— но только в том случае, когда этасумма положительна. Когда же сумма отрицательна, то она дальше не передается —нейрон заторможен. Правило преобразования сигналов аналоговыми нейронами описываетсяформулой y = k(x +|x|)/2, где х — накопленный потенциал, у — величина переданного сигнала, а k—коэффициент пропорциональности.

Нейроны второго типа работают иначе. Такой нейрон«молчит», пока сумма воздействий не достигнет некоторой определеннойположительной величины — «порога». Тогда нейрон возбуждается и посылает посвоему выходному отростку — аксону — электрический импульс (всегда одной и тойже величины), который и действует на клетки-мишени. После возбуждения нейроннекоторое время «отдыхает» — молчит, независимо от того, действуют на негодругие клетки или нет, а затем, если к концу отдыха накопленная сумма вышепорога, посылает новый импульс. В результате в зависимости от величины входногосигнала, его длительности и в зависимости от характеристик нейрона на выходеполучается сигнал в виде серии импульсов постоянной величины, но разнойчастоты. Таким образом, пороговые нейроны используют совершенно нетривиальныйпринцип кодирования информации частотой сигнала.

Однако, как и непрерывный выходной сигнал нейронованалогового типа, изменение частоты несет информацию только о величине входногосигнала, меняющейся непрерывно. В то же время известно, что животные умеютсчитать (например, выдавать реакцию только на каждый третий стимул).Естественно предположить, что в нервной системе имеются устройства, которыепо-разному реагируют, например, на двукратное воздействие и на однократное. То,что известно о принципах работы нейронов, позволяет утверждать: одиночнойнервной клетке такая «простая» с человеческой точки зрения операция, как счет,не под силу. Недостаток места не позволяет нам описать устройство из несколькихнейронов, способное выдавать ответ, например, на каждый второй стимул.

2)<span Times New Roman"">   

К одностороннему (гаплоидному) набору материнскиххромосом добавился такой же отцовский набор. Простейший пример па сложение:один плюс один. Но с него начинается возрастающая геометрическая прогрессия —цепная реакция делений клетки-прародительницы. Сумма ее потомков зависит, поизвестной формуле, от знаменателя прогрессии, а в переводе на биологическийязык — от темпа делений. Для того чтобы произошло очередное деление, клеткадолжна удвоить количество ядерной ДНК. Иначе говоря, скорость счета задаетсяконцентрацией ферментов, регулирующих скорость тиражирования (репликации) ДНК.

Попробуем представить себе работу воображаемоговычислительно программирующего    устройства,управляющего ростом зародыша. Сначала на стадии бластулы появляются отделы,которые условно можно обозначить как верхний и нижний, правый и левый. Они зеркальносимметричны. Бластулу сменяет гастула — образуется шар из клеток. И тутнаступает первая «катастрофа». Этот не слишком удачный, но уже прижившийсятермин обозначает нарушение симметрии. Внутренняя программа генетическогоразвития срабатывает таким образом, что дальнейшее разбухание шара — нарастаниемассы одинаковых клеток — приостанавливается. Но в отдельных участках делениепродолжается — оно становится ассиметричным. Прежде клетки зародыша были все наодно лицо. Теперь начинается их дифференцировка.

На этом стоит остановиться подробнее, потому что сутьпроцесса, по-видимому, одинакова, идет ли речь о закладке первичной трубки илиоб «отделочных работах», к которым можно отнести закладку боковыхпридатков.    В результате несколькихасимметричных делений накапливаются группы клеток с особым пространственнымрасположением и собственным темпом счета (размножения). Почему это происходит?Об этом можно высказываться лишь предположительно. Полагают, что гены сами посебе не предопределяют пространственное построение зародыша. То есть они задаютлишь общий план, замысел, « а не конкретный макет будущего здания. В самойобщей форме схема дифференцировки (возникновения катастроф) может бытьпредставлена так. Открытые (активированные) гены обеспечивают синтез несколькихактивных белков-организаторов. В свою очередь белки способны активизировать(открыть) гены, ответственные за последующие организаторы, и т. д. Предположим,что эти вещества-организаторы имеют различные коэффициенты диффузии (вполнеправдоподобное допущение). При достижении определенной концентрации такоговещества наступает критическое состояние, когда появляется    новая   асимметрия.

Другими словами — если вернуться к нашейвычислительной машине—мы получаем приблизительно такую программу: решениепервое (организатор № 1) дает 10 последовательных делений — образуется 210клеток. Они составляют «критическую массу». Катастрофа. Асимметричное деление вновом пространственном положении включает организатор № 2. Далее происходит,скажем, девять симметричных делений, дающих новую «критическую массу», изкоторой формируется гребень, уплотнение, тяж…

Например, на руке у человека пять пальцев. Какимобразом эмбрион считает до пяти? На самом деле он считает не до пяти, а додвух. Сначала два симметричных «рукава». Это так называемый креод, или каналразвития будущих рук.

Креод можно образно назвать судьбой        недифференцированной клетки: очутившисьв некоторой пространственной ситуации, клетка под действием организаторов почтинеотвратимо следует   своему   предназначению — кладет начало определенномуоргану. Происходит это вот как. В определенный момент своего развития креодплечевой кости терпит катастрофу — образуется гребень, который разграничиваетзачаток руки на два субкреода. Это зачатки будущих костей предплечья — локтевойи лучевой.

Если почему-либо процесс счета на этом оборвется,может родиться ребенок с врожденным дефектом — так называемой клешневиднойрукой. Нормальную работу «вычислительной машины» нарушает постороннеевмешательство — сюрприз вне программы. Его может преподнести попавшее извнемутагенное химическое вещество, искажающее генетическую программу, или,например, вирус краснухи — хорошо известная причина врожденных уродств. Внорме, однако, за первым счетом до двух следует второй, тоже до двух — новоеразделение субкреодов на два дочерних зачатка. После этого должна наступитькатастрофа — асимметричное деление в одном из зачатков; в итоге получитсяискомое число 5. Если же деление произойдет симметрично, то будет не пятьпальцев, а шесть. Известно, что шестипалость наследуется. То есть в некоторыхслучаях вычислительная машина дает систематическую и притом всегда двустороннюю(на обеих руках) ошибку.

Известны и другие варианты живой арифметики. Например,деление первичной нервной трубки на 32—35 сегментов — будущих позвонков. Притаких относительно больших числах возможна ошибка на две-три единицы за счеткопчика — рудиментарного хвоста. Фактически счет прерывается, когда иссякаюторганизаторы, т. е. с момента, когда генетический план оказывается полностьюреализованным. Словно некий прораб окидывает взглядом готовое здание, сверяетего с чертежом и убеждается, что все этажи на месте. А что будет, если ужевозведенную постройку частично разобрать? Эксперименты такого рода провел нанекоторых кольчатых червях Б. Момент. Он отсекал от червя несколько сегментов,и каждый раз регенерировало ровно столько сегментов, сколько их недоставало.Каждый раз восстанавливался стандарт — 22 сегмента. Значит, вычислительноеустройство функционирует и во взрослом организме.

3)<span Times New Roman"">   

Зрительные рецепторы, так же, как и другие — слуховые,температурные и т. д., получают сигналы из внешнего мира; они должны передатьзрительную информацию в мозг точно и своевременно. Передача сигналов от глаза кмозгу осуществляется нейронами «порогового» типа—аналоговый способ оказываетсянеприменимым при передаче сигналов на достаточно большие расстояния. А упороговых нейронов, как уже говорилось, все импульсы совершенно одинаковы, исведения о величине входного сигнала эти нейроны передают меняя частотуимпульсации.

Тут возникает вот какая проблема. Освещенность всумерках, когда предметы еле видны, отличается от освещенности при яркомсолнечном свете примерно в миллиард (т. е. в 109) раз. Максимальная же частота,с которой может работать нейрон — 1000 импульсов в секунду. Легко сообразить,что нельзя передавать информацию, меняя частоту работы нейрона пропорциональноосвещенности: если при ярком свете частота импульсов будет максимальной (1000имп/с), то при уменьшении освещенности в миллион раз сигнал будет поступатьвсего один раз в 15 минут. Но за это время он совершенно потеряет своюактуальность!

Но может быть, разумно такое устройство зрительнойсистемы, когда разные ее элементы, разные нейроны работают каждый в своемдиапазоне освещенности: одни в сумерки, другие в пасмурный день, третьи наярком солнце. Простой подсчет показывает, что если принять за нижнюю границучастоты работы нейрона, необходимой для достаточно своевременной передачиинформации, 1 имп/с, то для охвата диапазона изменения освещенности в миллиардраз потребуется миллион нейронов — и это без всякого «запаса» прочности, бездублирования их работы! Но главное вот что: в каждый момент будет работатьтолько одна клетка из миллиона, а остальные 999 999 будут «даром есть хлеб»:ведь в отличие от технических, живые «механизмы» потребляют энергию (свой«бензин») не только во время работы. А экономия энергии в живой природе — одноиз главных условий выживания.

Итак, линейная зависимость между входными и выходнымисигналами в случае глаза оказывается нецелесообразной. И действительно, вприроде в этом случае используется другая функция, по школьным меркам довольносложная.

Экспериментально это было установлено в 1932 годуанглийским ученым X. Харлайном. На рисунке 1приведены результаты его исследования. Он регистрировал нервные импульсы,идущие по одиночному нервному волокну от глаза к мозгу, у мечехвоста (морскогочленистоногого, похожего на вымерших трилобитов. На графике показана зависимостьчастоты импульсации от яркости света.

«Но позвольте! — скажете вы.— На графике прямая линия— значит, это линейная функция» Не торопитесь, вглядитесь в шкалу нагоризонтальной оси, она ведь неравномерна, нелинейна: при сдвиге на одноделение аргумент (яркость) меняется не на одну и ту же величину, а в одно и тоже число раз.

При линейной зависимости равным приращениям аргументасоответствуют равные приращения функции, или, что то же самое, линейнаязависимость переводит арифметическую прогрессию значений аргумента варифметическую же прогрессию значений функции. Когда мы имеем дело споказательной функцией у = ах,то равным приращениям аргумента соответствует равномерный относительный приростфункции. Например, при постоянных условиях обитания и неограниченных ресурсахтак растет численность какой-либо популяции: число особей за каждый годувеличивается на 10 %, т. е. в 1,1 раза. Другими словами, показательная функция«переводит» арифметическую прогрессию в геометрическую. На нашем графикеситуация обратная: частота импульсации нейрона меняется на одну и ту жевеличину, когда воздействие меняется в одно и то же число раз. Значит, мы имеемдело с функцией, обратной к показательной, т. е. с логарифмической; инымисловами, нейроны глаза мечехвоста превращают геометрическую прогрессиюраздражений в арифметическую прогрессию сигналов.

Это свойство зрительных рецепторов,    выработавшееся в ходе эволюции, позволяетглазу работать эффективно и экономно, обеспечивает возможность хорошовоспринимать контраст. Пусть светлый и темный предметы различаются поспособности отражать свет в десять раз. Тогда и на ярком солнце, и в сумеркахсветлый предмет будет отражать в десять раз больше света, чем темный. Поэтомусравнительная яркость этих предметов не меняется; не меняется и расстояниемежду соответствующими точками на оси абсцисс. А это означает, что разницачастот работы рецепторов, на которые падает свет от этих двух предметов, будетоставаться неизменной при разных освещенностях. Так что «умениелогарифмировать» позволяет глазу не только работать в широком диапазонеосвещенностей, но и при малой освещенности различать предметы, абсолютнаяразность освещенностей которых очень мала.

Интересно, что описанная зависимость между внешнимсигналом (раздражением) и сигналом, воспринимаемым мозгом (ощущением),первоначально была обнаружена психологами. Сделал это французский ученый П.Бугер еще в XVIII веке. В начале XIX века немецкий физиолог и психолог Э. Вебердетально изучил связь между раздражением и ощущением. Он выяснял, как нужноизменить какой-то раздражитель, чтобы человек заметил это изменение. Оказалось,отношение изменения величины раздражителя к его первоначальному значению   есть  величина    постоянная: <img src="/cache/referats/26832/image003.gif" v:shapes="_x0000_i1025"> I— мерараздражителя, ∆I— приростраздражителя,  k—константа Вебера.

Константа Вебера зависит от того, какой рецепторраздражается. Например, при восприятии веса й=1/30. Это значит, что, когдачеловек держит груз в <st1:metricconverter ProductID=«100 г» w:st=«on»>100 г</st1:metricconverter>,он замечает его изменение при увеличении веса на <st1:metricconverter ProductID=«3,4 г» w:st=«on»>3,4 г</st1:metricconverter>, а для груза в <st1:metricconverter ProductID=«200 г» w:st=«on»>200 г</st1:metricconverter> требуется прибавка в <st1:metricconverter ProductID=«6,7 г» w:st=«on»>6,7 г</st1:metricconverter>. Для высоты звукаконстанта Вебера равна 0,003, для громкости звука — 0,09 и т. д.

Исходя из экспериментов Вебера, другой немецкийфизиолог и психолог Г. Фехнер сформулировал знаменитый закон Вебера — Фехнера:ощущения растут в арифметической прогрессии, когда раздражение растет вгеометрической прогрессии.

Этот закон был опубликован в книге Фехнера «Элементыпсихофизики» в 1859 году. Там же было приведено и математическое выражениезакона:

E=alog I+ b

где  Е — мера ощущения,   а   и   Ь— константы,   I — мера    раздражения.

<img src="/cache/referats/26832/image005.gif" v:shapes="_x0000_i1026">

Рис. 1

4)<span Times New Roman"">   

Здесь уподобление мозга вычислительной машине сталонастолько тривиальным, что эти слова можно даже не брать в кавычки. Нотождественность результатов на «выходе» (задачку можно решить в голове, можно ина ЭВМ) еще не значит, что оба устройства работают одинаково. К тому же нас вданном случае интересует не столько способность мозга распутыватьматематические или какие-нибудь другие задачи как таковые, сколько его умениеуправлять телом. Точность движений роднит человека со всем животным миром, хотянадо признать, что в этой области он как раз не чемпион.

Предметы, окружающие нас, трехмерны. Однакоизображение их на сетчатке двухмерно. Формирование образа трехмерного объекта –процесс далеко не простой. В нем участвуют как бессознательные, так илогические операции.

Соотношение между зрительным ощущением перспективы итретьим измерением интересовало еще древних греков. Пифагорийцы выдвинули идеюоб особом флюиде, который испускается глазами и «ощупывает» предметы. Атомисты,например, были сторонниками испускания предметами «призраков», которые,…попадая в глаза, приносят ощущение формы и глубины.

Согласно Платону, от предметов исходит специальныйфлюид, который встречается со «светом дня», бьющим из наших глаз. Если обафлюида подобны друг другу, то, встречаясь, они «связываются» и газа получаютощущение глубины видимого. Если же «свет очей» встречается с несхожим флюидом,он гаснет и не дает ощущение.

Несмотря на наивность физической трактовки восприятия,древние греки достигли больших успехов в геометрической оптике. Евклид старалсяподчеркнуть геометрический характер оптических изображений. Великий астрономПтоломей не ограничился, как Евклид, рассмотрением геометрической оптики, онобсуждал физические процессы, лежавшие в основе зрения, и связанные с нимиоптические иллюзии.

Знаменитый французский монах Роджер Бэкон, живший в XIIIв., писал о том, что опыт не может основываться лишьна внешних ощущениях, потому что он не полностью говорит о духовных. Огромнуюроль в пространственной ориентации играет наше сознание.

В мозгу производиться синтез зрительного образа иизвлечение информации о его геометрической протяженности и пространственнойориентации из двух несовершенных, перевернутых и искривленных шарообразнойформой глазного яблока изображений. Чтобы получить информацию о глубине,необходимо иметь, по крайней мере, два плоских изображения, смещенных нанекоторый угол.

Глаза человека могут поворачиваться в глазных впадинахболее чем на 80˚ в вертикальном и горизонтальном направлениях. Мозгрегистрирует сигналы о натяжении мышц глаза, кроме того, существенная рольпринадлежит тремору – мелким движениям глазного яблока. Корректирующая работамозга при пространственном восприятии чрезвычайно велика. Именно этимобъясняется постоянство в восприятии размеров предметов в некотором диапазонерасстояний, когда изображения на сетчатке претерпевают изменения. Иногданаблюдается обратное явление, например не нашедшее еще объяснения кажущеесяувеличение размеров Солнца и Луны у Лии горизонта. Этот парадокс был известенеще Архимеду.

Сейчас нам довольно подробно известно, каким образомпроприоцептивные рецепторы, поставляющие информацию о взаимном расположениивсех частей нашего тела, создают в мозгу внутренний образ тела. Мы не тольковидим себя, но и ощущаем собственное тело как границу нашего Я в беспредельноммире. Эти ощущения привычны для нас, они дают нам реальную картину соотношенийвнутреннего и внешнего. Лишь в особых случаях — при некоторых заболеваниях — всознании возникают пространственные иллюзии: огромная рука, неимоверно длинныеноги, тяжелые пальцы… Известны и более причудливые искажения так называемойсхемы тела. Рассматривая эти и подобные им сбои в работе мозга каквычислительной машины, мы можем сказать, что в нервных центрах происходитсложнейшая интеграция постоянного потока разнородных импульсов, в результатечего на внутреннем экране возникает подвижное   изображение. Нарушение же настройки приводит к помехам, искажениям этогоизображения.

Конечно, аналогию с телевизором не следует толковатьбуквально. Нам пока недостаточно известно, как «видит» мозг. Есть основанияпредполагать, что уже в мозгу формируется трехмерное, т. е. объемноеизображение предметов. Но эксперименты, которые могли бы это подтвердить, едвалишь начаты. Нам важно понять и запомнить другое: в ходе развития живогоорганизма формируется аппарат самоуправления, который можно моделировать в видесамопрограммирующейся вычислительной машины. На ранних этапах эта машинасовпадает со всем развивающимся телом, но по мере его созревания функцииуправления сосредоточиваются в центральной нервной системе.

<img src="/cache/referats/26832/image007.jpg" v:shapes="_x0000_i1027">  <img src="/cache/referats/26832/image009.jpg" v:shapes="_x0000_i1028">

5)<span Times New Roman"">   

Слово «вектор», можно сказать, совсем «младенец» —по-видимому, оно появилось впервые в работе английского математика У.Гамильтона в 1845 году. Но соответствующее понятие использовалось в физике ещеза несколько столетий до этого в связи с рассмотрением закона сложения сил («правилапараллелограмма»). Про векторы же в организме животных мы узнали только в самыепоследние годы.

Началось с кошек. В 1988 году канадский ученый Дж.Макферсон выполнила интересную работу.  Она ставила кошку наспециальную платформу, толкала эту платформу в каком-нибудь направлении исмотрела, каким образом кошка сохраняет равновесие. Допустим, она толкнулаплатформу вперед. Ноги кошки вместе с платформой стали уходить вперед, а телоостается на месте. Тогда кошка, чтобы возвратить центр тяжести в правильноеположение над точками опоры активирует мышцы лап и, отталкиваясь от платформы,двигает тело вперед. Если платформу толкнуть вправо, центр тяжести отклонитсявлево по отношению к опоре и лапы должны создать силу, направленную вправо, ит. д.

Как же происходит эта работа лап при сохраненииравновесия?

Самое естественное — это предположить, что каждая издвух задних лап при толчке вперед создает силу, направленную вперед; сумма этихдвух сил и восстанавливает правильное положение тела (рис. 2, а). Еслиплатформу толкнули вправо, каждая лапа создает силу, направленную вправо, и т.д. Такая гипотеза согласуется с тем, что у кошки есть мощные мышцы, которыедвигают лапу вперед или назад — они используются для ходьбы и прыжков, а такжемышцы, отводящие лапу наружу или по направлению к оси тела. Однако когдаМакферсон стала выяснять, что происходит на самом деле, оказалось, что картинасовершенно другая: при толчке платформы, независимо от направления движения,задние лапы кошки создают силы, направленные вдоль двух прямых (каждая лапа —вдоль своей), расположенных примерно под углом 45° к оси тела. Даже впростейшем случае, когда платформу толкают прямо вперед, силы, создаваемыелапами, направлены не вперед, а тоже под углом 45° к оси тела (снова см. рис. 2,а). И только их сумма имеет нужное направление и величину.  На рисунке  2,  б показано, как получается сила, направленная перпендикулярно телу, а на рисунке 2,в — сила, направленная под углом 30 ° к оси тела.

Значит, нервная система кошки решает следующую задачу.При толчке платформы по информации, полученной от разных рецепторов,определяется, какой вектор (силу) нужно получить, затем этот векторраскладывается по фиксированным осям координат. При таком способе получается,что каждой из двух задних лап нужно передать всего одно число — координатувектора силы (положительную или отрицательную), которую должна создать эта лапавдоль своей фиксированной оси.

Получается очень экономная схема. Но жизнь так полнанеожиданностей! Разбираясь в том, какими мышцами создается это фиксированноенаправление (казалось бы, чего проще: использовать для единичного вектораодного направления мышцы, двигающие ногу вперед и внутрь, а для созданиядругого — назад и наружу, а дальше менять пропорционально силу, развиваемуюэтими мышцами,— умножать на число», и все в порядке), Макферсон получила ещеодин неожиданный результат. Оказалось, что в создании «единичного» векторамогут участвовать разные мышцы, их сочетание меняется в зависимости отнаправления толчка. В чем смысл такого, с нашей точки зрения, усложненногорешения, еще выяснять и выяснять. Однако здесь проявляется общий принципживого: избегать жестких схем, иметь всегда избыток «степеней свободы», словом,плюрализм.

<img src="/cache/referats/26832/image011.jpg" v:shapes="_x0000_i1029">

Рис. 2

6)<span Times New Roman"">   

Трудности в выяснении вопроса о том, как на самом делепроисходит решение той или иной задачи, связаны с тем, что заглянуть в«управляющий центр» — в мозг — очень трудно. В этом смысле мозг пока что вомногом «черный ящик»: можно видеть, какая задача ему предложена, можно видеть,какой он выдает результат,— а вот что происходит внутри, об этом сведений ещеочень и очень мало.

Тем более интересна и важна работа, которая позволилапочти непосредственно увидеть, как идет работа мозговых нейронов при решениинекоторых задач. Эту работу совсем недавно выполнил американский ученый А.Георгопулос. Он экспериментировал с дрессированными обезьянами. Лапа обезьяныпомещалась в некоторой точке стола, а в различных точках стола помещалисьэлектрические лампочки. Обезьяну научили при вспышке какой-нибудь лампочкидвигать лапу по направлению к этой лампочке. В это время экспериментаторрегистрировал с помощью вживленных электродов активность (частоту импульсации)нервных клеток коры больших полушарий в той ее зоне, которая управляетдвижениями этой лапы.

Оказалось, что активность большинства клеток этой зонымозга зависит от направления движения лапы; и эта зависимость достаточночеткая: для каждой из клеток существует такое направление движения, при которомактивность максимальна; при других направлениях активность уменьшается примернокак косинус   угла между даннымнаправлением и направлением максимальной активности. Для тех направлений, длякоторых косинус отрицателен, клетка вообще перестает импульсировать.

Получается, что с каждой клеткой коры связанопределенный вектор максимальной активности Amax(рис. 3). Когда нужно двигать лапу по другомунаправлению, т. е. задан некоторый единичный вектор направления е, клетканаходит проекцию Amaxна это направление, т. е. «вычисляет» скалярноепроизведение Amax∙e. Выяснив это, Георгопулос поставил обратную задачу:нельзя ли, регистрируя работу нервных клеток, определить направление движениялапы. Математически эта задача может быть сформулирована как вопрос осуществовании функции, обратной к заданной. Ясно, что по активности однойклетки направление движения определить нельзя: во-первых, косинус — функциячетная, и в том промежутке, который нас интересует, не имеет обратной.Действительно, если, например, направление максимальной активности — это прямовперед, а активность нейрона составляет половину максимальной, то известно, чтолапа движется под углом 60° к преимущественному направлению, но вправо иливлево от него — определить невозможно. Во-вторых, у одной клетки слишком велика«мертвая зона» — зона, когда она вообще молчит. Но если регистрироватьнесколько клеток, то можно успешно определить направление, в котором движетсялапа (и даже предсказать, в каком направлении она будет двигаться, так какклетки начинают работать за десятую долю секунды до того, как лапа начинает двигаться).Представляем читателю самостоятельно решить такую задачу: какое минимальноечисло клеток требуется для того, чтобы уверенно определять направление движенияво всех случаях? (Конечно, мы даем эту задачу, так сказать, в математическойформулировке, которая, как всегда, упрощает ситуацию — как и мы ее упрощаем внашем рассказе.)

То, что по активности нейронов можно не толькоустановить, куда движется лапа, но и предсказать, куда обезьяна еще толькособирается двигать ее, т. е. как бы подсмотреть мысль о движении, позволилоГеоргопулосу сделать еще одну, очень красивую работу.

Еще в 1971 году американские психологи Р. Шепард и Дж.Метцлер обнаружили явление, которое они назвали «мысленным вращением». Вэкспериментах испытуемым показывали две фигуры и спрашивали: это разные фигурыили одна и та же, но повернутая на некоторый угол? Время ответа оказалосьлинейной функцией величины угла поворота одной фигуры относительно другой.

В другом варианте эксперимента попеременно показывалибукву R или ее зеркальное отражение — букву Я; надо быстро определить, какаяэто буква. При этом букву показывали в разных положениях. И здесь время ответабыло пропорционально углу поворота буквы относительно «нормального» положения.

Ученые предположили,   что   человек в таком эксперименте мысленновращает образ воспринимаемой фиг

www.ronl.ru

Доклад - Математика в живых организмах

Кандидат биологических наук М. БЕРКИНБЛИТ,

кандидат педагогических наук Е. ГЛАГОЛЕВА

Живая природа сделала множество “изобретений”, которые люди поняли и смогли повторить лишь при соответствующем уровне развития науки и техники. Например, принцип эхолокации эффективно используют и дельфины, и летучие мыши, а в технике он появился только в XX веке; поиск добычи по инфракрасному излучению используют многие виды змей, в то время как очки для ночного видения созданы лишь недавно и т. д. До последнего времени бытовало убеждение, что природа не изобрела колеса, что здесь техника пошла своим оригинальным путем. Но оказалось, что жгутики бактерий вращаются в специальных “подшипниках” и, значит, колесо тоже “изобретено” природой еще на самых ранних этапах эволюции. Существует специальная наука — бионика, которая изучает “патенты природы”. Оказывается, что их можно иногда использовать и в “человеческой” технике.

Менее известно, что в живых организмах происходят явления, которые позволяют считать, что природе принадлежит “приоритет” и в создании своеобразных ЭВМ — устройств, производящих операции, весьма сходные с математическими операциями, которые мы склонны считать достижением человеческой науки. Похоже, что здесь повторяется история с изобретением колеса.

О некоторых таких операциях мы и расскажем в этой статье: о том как “считают” нервные клетки, как “логарифмирует” глаз (и зачем ему это понадобилось), как оперирует с векторами и тригонометрическими функциями мозг кошки и обезьяны (и наш с вами тоже). Может быть, кто-нибудь решит, что и изучать эти вещи не надо, раз это дано от природы. А, может быть, некоторые — мы надеемся, что таких будет больше,— захотят узнать о математической и биологической стороне дела.

Как считают нейроны

Первое знакомство с математикой — это счет: “Раз, два, три, четыре, пять, вышел зайчик погулять”. И самым простым кажется и считается натуральное число. Уже отрицательные числа очень медленно входили в математику. Появившись в раннем средневековье у математиков Индии, они лишь в XIII—XIV веках проникают в европейскую науку, встречая там поначалу весьма сдержанное, отношение. Их называют “ложными”, “абсурдными” числами. Но постепенно отрицательные числа доказали свое право на существование и стали привычными не только для специалистов — то, что было “на переднем крае науки” в средние века, сегодня спокойно воспринимают пятиклассники.

А вот в живых организмах, оказывается “все наоборот”: нервной клетке (нейрону) естественно и просто осуществлять операции с положительными и отрицательными действительными “числами”, а для того чтобы “считать” даже до двух, требуется система из нескольких нейронов — примитивный “мозг”.

Как же работает нейрон? Как всякая клетка, нейрон отделен от наружной межклеточной среды особой оболочкой — мембраной. Между внутренним содержимым клетки и наружной средой существует разность потенциалов. Если клетка находится в покое, разность потенциалов на ее мембране не меняется. Эту разность потенциалов в покое естественно принять за нулевой уровень (подобно тому, как приняли за нулевую температуру таяния льда).

На нейрон могут действовать другие нервные клетки — возбуждающие и тормозные. Сигналы, полученные от этих клеток, вызывают изменения разности потенциалов на мембране в двух противоположных направлениях. Когда разные сигналы приходят к нейрону одновременно, они складываются, причем, естественно, с учетом знака, т. е. нейрон суммирует приходящие к нему положительные и отрицательные сигналы; эта сумма может быть положительной или отрицательной.

Интересная особенность работы нейрона состоит в том, что в отличие от технических сумматоров — от древнего абака до ЭВМ — полученную сумму он “помнит” недолго: если внешние воздействия прекратились, то накопленная сумма начинает убывать по абсолютной величине, чтобы нейрон возвратился в состояние покоя (потенциал на мембране стремится к значению, которое мы приняли за нуль).

Такая вроде бы “ненадежность” нейрона связана с тем, что он предназначен не для хранения, а для передачи и преобразования информации: полученный сигнал нейрон передает другим клеткам нервной сети (клеткам-“мишеням” или “адресатам”). По способу передачи сигнала существуют два разных типа нейронов с разными принципами работы: “аналоговые” и “пороговые” нейроны.

Нейрон первого типа действует на клетки-мишени с силой, пропорциональной накопленной сумме, — но только в том случае, когда эта сумма положительна. Когда же сумма отрицательна, то она дальше не передается — нейрон заторможен. Правило преобразования сигналов аналоговыми нейронами описывается формулой, где х — накопленный потенциал, у — величина переданного сигнала, a k — коэффициент пропорциональности.

Нейроны второго типа работают иначе. Такой нейрон “молчит”, пока сумма воздействий не достигнет некоторой определенной положительной величины — “порога”. Тогда нейрон возбуждается и посылает по своему выходному отростку — аксону — электрический импульс (всегда одной и той же величины), который и действует на клетки-мишени. После возбуждения нейрон некоторое время “отдыхает” — молчит, независимо от того, действуют на него другие клетки или нет, а затем, если к концу отдыха накопленная сумма выше порога, посылает новый импульс. В результате в зависимости от величины входного сигнала, его длительности и в зависимости от характеристик нейрона на выходе получается сигнал в виде серии импульсов постоянной величины, но разной частоты. Таким образом, пороговые нейроны используют совершенно нетривиальный принцип кодирования информации частотой сигнала.

Однако, как и непрерывный выходной сигнал нейронов аналогового типа, изменение частоты несет информацию только о величине входного сигнала, меняющейся непрерывно. В то же время известно, что животные умеют считать (например, выдавать реакцию только на каждый третий стимул). Естественно предположить, что в нервной системе имеются устройства, которые по-разному реагируют, например, на двукратное воздействие и на однократное. То, что известно о принципах работы нейронов, позволяет утверждать: одиночной нервной клетке такая “простая” с человеческой точки зрения операция, как счет, не под силу. Недостаток места не позволяет нам описать устройство из нескольких нейронов, способное выдавать ответ, например, на каждый второй стимул.

Глаза и логарифмы

Зрительные рецепторы, так же, как и другие — слуховые, температурные и т. д., получают сигналы из внешнего мира; они должны передать зрительную информацию в мозг точно и своевременно. Передача сигналов от глаза к мозгу осуществляется нейронами “порогового” типа — аналоговый способ оказывается неприменимым при передаче сигналов на достаточно большие расстояния. А у пороговых нейронов, как уже говорилось, все импульсы совершенно одинаковы, и сведения о величине входного сигнала эти нейроны передают меняя частоту импульсации.

Тут возникает вот какая проблема. Освещенность в сумерках, когда предметы еле видны, отличается от освещенности при ярком солнечном свете примерно в миллиард (т. е. в 109 ) раз. Максимальная же частота, с которой может работать нейрон — 1000 импульсов в секунду. Легко сообразить, что нельзя передавать информацию, меняя частоту работы нейрона пропорционально освещенности: если при ярком свете частота импульсов будет максимальной (1000 имп/с), то при уменьшении освещенности в миллион раз сигнал будет поступать всего один раз в 15 минут. Но за это время он совершенно потеряет свою актуальность!

Но может быть, разумно такое устройство зрительной системы, когда разные ее элементы, разные нейроны работают каждый в своем диапазоне освещенности: одни в сумерки, другие в пасмурный день, третьи на ярком солнце. Простой подсчет показывает, что если принять за нижнюю границу частоты работы нейрона, необходимой для достаточно своевременной передачи информации, 1 имп/с, то для охвата диапазона изменения освещенности в миллиард раз потребуется миллион нейронов — и это без всякого “запаса” прочности, без дублирования их работы! Но главное вот что: в каждый момент будет работать только одна клетка из миллиона, а остальные 999 999 будут “даром есть хлеб”: ведь в отличие от технических, живые “механизмы” потребляют энергию (свой “бензин”) не только во время работы. А экономия энергии в живой природе — одно из главных условий выживания.

Итак, линейная зависимость между входными и выходными сигналами в случае глаза оказывается нецелесообразной. И действительно, в природе в этом случае используется другая функция, по школьным меркам довольно сложная.

Экспериментально это было установлено в 1932 году английским ученым X.Харлайном. На рисунке 1 приведены результаты его исследования. Он регистрировал нервные импульсы, идущие по одиночному нервному волокну от глаза к мозгу, у мечехвоста (морского членистоногого, похожего на вымерших трилобитов). На графике показана зависимость частоты импульсации от яркости света.

“Но позвольте! — скажете вы.— На графике прямая линия — значит, это линейная функция”. Не торопитесь, вглядитесь в шкалу на горизонтальной оси, она ведь неравномерна, нелинейна: при сдвиге на одно деление аргумент (яркость) меняется не на одну и ту же величину, а в одно и то же число раз.

При линейной зависимости равным приращениям аргумента соответствуют равные приращения функции, или, что то же самое, линейная зависимость переводит арифметическую прогрессию значений аргумента в арифметическую же прогрессию значений функции. Когда мы имеем дело с показательной функцией у=ах, то равным приращениям аргумента соответствует равномерный относительный прирост функции. Например, при постоянных условиях обитания и неограниченных ресурсах так растет численность какой-либо популяции: число особей за каждый год увеличивается на 10%, т. е. в 1,1 раза. Другими словами, показательная функция “переводит” арифметическую прогрессию в геометрическую. На нашем графике ситуация обратная: частота импульсации нейрона меняется на одну и ту же величину, когда воздействие меняется в одно и то же число раз. Значит, мы имеем дело с функцией, обратной к показательной, т.е. с логарифмической; иными словами, нейроны глаза мечехвоста превращают геометрическую прогрессию раздражений в арифметическую прогрессию сигналов.

Это свойство зрительных рецепторов, выработавшееся в ходе эволюции, позволяет глазу работать эффективно и экономно, обеспечивает возможность хорошо воспринимать контраст. Пусть светлый и темный предметы различаются по способности отражать свет в десять раз. Тогда и на ярком солнце, и в сумерках светлый предмет будет отражать в десять раз больше света, чем темный. Поэтому сравнительная яркость этих предметов не меняется; не меняется и расстояние между соответствующими точками на оси абсцисс. А это означает, что разница частот работы рецепторов, на которые падает свет от этих двух предметов, будет оставаться неизменной при разных освещенностях. Так что “умение логарифмировать” позволяет глазу не только работать в широком диапазоне освещенностей, но и при малой освещенности различать предметы, абсолютная разность освещенностей которых очень мала.

Интересно, что описанная зависимость между внешним сигналом (раздражением) и сигналом, воспринимаемым мозгом (ощущением), первоначально была обнаружена психологами. Сделал это французский ученый П. Бугер еще в XVIII веке. В начале XIX века немецкий физиолог и психолог Э. Вебер детально изучил связь между раздражением и ощущением. Он выяснял, как нужно изменить какой-то раздражитель, чтобы человек заметил это изменение. Оказалось, отношение изменения величины раздражителя к его первоначальному значению есть величина постоянная:

, где I — мера раздражителя,— прирост раздражителя, a k — константа Вебера.

Константа Вебера зависит от того, какой рецептор раздражается. Например, при восприятии веса k=1/30. Это значит, что, когда человек держит груз в 100 г, он замечает его изменение при увеличении веса на 3,4 г, а для груза в 200 г требуется прибавка в 6,7 г. Для высоты звука константа Вебера равна 0,003, для громкости звука — 0,09 и т. д.

Исходя из экспериментов Вебера, другой немецкий физиолог и психолог Г. Фехнер сформулировал знаменитый закон Вебера — Фехнера:

Ощущения растут в арифметической прогрессии, когда раздражение растет в геометрической прогрессии.

Этот закон был опубликован в книге Фехнера “Элементы психофизики” в 1859 году. Там же было приведено и математическое выражение закона:

,

где Е — мера ощущения, а и b — константы, I — мера раздражения.

Зачем кошке векторы?

Слово “вектор”, можно сказать, совсем “младенец” — по-видимому, оно появилось впервые в работе английского математика У. Гамильтона в 1845 году. Но соответствующее понятие использовалось в физике еще за несколько столетий до этого в связи с рассмотрением закона сложения сил (“правила параллелограмма”). Про векторы же в организме животных мы узнали только в самые последние годы.

Началось с кошек. В 1988 году канадский ученый Дж. Макферсон выполнила интересную работу. Она ставила кошку на специальную платформу, толкала эту платформу в каком-нибудь направлении и смотрела, каким образом кошка сохраняет равновесие. Допустим, она толкнула платформу вперед. Ноги кошки вместе с платформой стали уходить вперед, а тело остается на месте. Тогда кошка, чтобы возвратить центр тяжести в правильное положение над точками опоры активирует мышцы лап и, отталкиваясь от платформы, двигает тело вперед. Если платформу толкнуть вправо, центр тяжести отклонится влево по отношению к опоре и лапы должны создать силу, направленную вправо, и т.д.

Как же происходит эта работа лап при сохранении равновесия

Самое естественное — это предположить, что каждая из двух задних лап при толчке вперед создает силу, направленную вперед; сумма этих двух сил и восстанавливает правильное положение тела (рис. 2, а). Если платформу толкнули вправо, каждая лапа создает силу, направленную вправо, и т. д. Такая гипотеза согласуется с тем, что у кошки есть мощные мышцы, которые двигают лапу вперед или назад — они используются для ходьбы и прыжков, а также мышцы, отводящие лапу наружу или по направлению к оси тела. Однако, когда Макферсон стала выяснять, что происходит на самом деле, оказалось, что картина совершенно другая: при толчке платформы, независимо от направления движения, задние лапы кошки создают силы, направленные вдоль двух прямых (каждая лапа — вдоль своей), расположенных примерно под углом 45° к оси тела. Даже в простейшем случае, когда платформу толкают прямо вперед, силы, создаваемые лапами, направлены не вперед, а тоже под углом 45° к оси тела (снова см. рис. 2, а). И только их сумма имеет нужное направление и величину. На рисунке 2, б показано, как получается сила, направленная перпендикулярно телу, а на рисунке 2, в — сила, направленная под углом 30° к оси тела.

Значит, нервная система кошки решает следующую задачу. При толчке платформы по информации, полученной от разных рецепторов, определяется, какой вектор (силу) нужно получить, затем этот вектор раскладывается по фиксированным осям координат. При таком способе получается, что каждой из двух задних лап нужно передать всего одно число — координату вектора силы (положительную или отрицательную), которую должна создать эта лапа вдоль своей фиксированной оси.

Получается очень экономная схема. Но жизнь так полна неожиданностей! Разбираясь в том, какими мышцами создается это фиксированное направление (казалось бы, чего проще: использовать для единичного вектора одного направления мышцы, двигающие ногу вперед и внутрь, а для создания другого — назад и наружу, а дальше менять пропорционально силу, развиваемую этими мышцами,— “умножать на число”, и все в порядке), Макферсон получила еще один неожиданный результат. Оказалось, что в создании “единичного” вектора могут участвовать разные мышцы, их сочетание меняется в зависимости от направления толчка. В чем смысл такого, с нашей точки зрения, усложненного решения, еще выяснять и выяснять. Однако здесь проявляется общий принцип живого: избегать жестких схем, иметь всегда избыток “степеней свободы”, словом, плюрализм.

Векторы в мозгу обезьяны и человека

Трудности в выяснении вопроса о том, как на самом деле происходит решение той или иной задачи, связаны с тем, что заглянуть в “управляющий центр” — в мозг — очень трудно. В этом смысле мозг пока что во многом “черный ящик”: можно видеть, какая задача ему предложена, можно видеть, какой он выдает результат,— а вот что происходит внутри, об этом сведений еще очень и очень мало.

Тем более интересна и важна работа, которая позволила почти непосредственно увидеть, как идет работа мозговых нейронов при решении некоторых задач. Эту работу совсем недавно выполнил американский ученый А. Георгопулос. Он экспериментировал с дрессированными обезьянами. Лапа обезьяны помещалась в некоторой точке стола, а в различных точках стола помещались электрические лампочки. Обезьяну научили при вспышке какой-нибудь лампочки двигать лапу по направлению к этой лампочке. В это время экспериментатор регистрировал с помощью вживленных электродов активность (частоту импульсации) нервных клеток коры больших полушарий в той ее зоне, которая управляет движениями этой лапы.

Оказалось, что активность большинства клеток этой зоны мозга зависит от направления движения лапы; и эта зависимость достаточно четкая: для каждой из клеток существует такое направление движения, при котором активность максимальна; при других направлениях активность уменьшается примерно как косинус угла между данным направлением максимальной активности. Для тех направлений, для которых косинус отрицателен, клетка вообще перестаёт импульсировать.

Получается, что с каждой клеткой коры связан определенный вектор максимальной активности Аmax (рис. 3). Когда нужно двигать лапу по другому направлению, т. е. задан некоторый единичный вектор направления e, клетка находит проекцию Аmax на это направление, т. е. “вычисляет” скалярное произведение Аmax. е. Выяснив это, Георгопулос поставил обратную задачу: нельзя ли, регистрируя работу нервных клеток, определить направление движения лапы. Математически эта задача может быть сформулирована как вопрос о существовании функции, обратной к заданной. Ясно, что по активности одной клетки направление движения определить нельзя: во-первых, косинус — функция четная, и в том промежутке, который нас интересует, не имеет обратной. Действительно, если, например, направление максимальной активности — это прямо вперед, а активность нейрона составляет половину максимальной, то известно, что лапа движется под углом 60° к преимущественному направлению, но вправо или влево от него — определить невозможно. Во-вторых, у одной клетки слишком велика “мертвая зона” — зона, когда она вообще молчит. Но если регистрировать несколько клеток, то можно успешно определить направление, в котором движется лапа (и даже предсказать, в каком направлении она будет двигаться, так как клетки начинают работать за десятую долю секунды до того, как лапа начинает двигаться). Представляем читателю самостоятельно решить такую задачу: какое минимальное число клеток требуется для того, чтобы уверенно определять направление движения во всех случаях? (Конечно, мы даем эту задачу, так сказать, в математической формулировке, которая, как всегда, упрощает ситуацию — как и мы ее упрощаем в нашем рассказе.)

То, что по активности нейронов можно не только установить, куда движется лапа, но и предсказать, куда обезьяна еще только собирается двигать ее, т. е. как бы подсмотреть мысль о движении, позволило Георгопулосу сделать еще одну, очень красивую работу.

Еще в 1971 году американские психологи Р. Шепард и Дж. Метцлер обнаружили явление, которое они назвали “мысленным вращением”. В экспериментах испытуемым показывали две фигуры и спрашивали: это разные фигуры или одна и та же, но повернутая на некоторый угол? Время ответа оказалось линейной функцией величины угла поворота одной фигуры относительно другой.

В другом варианте эксперимента попеременно показывали букву R или ее зеркальное отражение — букву Я; надо быстро определить, какая это буква. При этом букву показывали в разных положениях. И здесь время ответа было пропорционально углу поворота буквы относительно “нормального” положения.

Ученые предположили, что человек в таком эксперименте мысленно вращает образ воспринимаемой фигуры (а по ряду психологических экспериментов, скорее, эталон фигуры, хранимый в памяти) с постоянной угловой скоростью и даже определили эту скорость. Получилось 450o /с. Однако такими экспериментами невозможно доказать гипотезу “мысленного вращения”, так как остается неизвестным, что же происходит в действительности в головах испытуемых.

Георгопулос, обретя возможность “подглядывать” за работой нейронов мозга обезьяны, получил в 1989 году данные, которые делают гипотезу о мысленном вращении более обоснованной.

Теперь обезьяну научили тянуть лапу не к той лампочке, которая горит, а к той, которая находится под углом 90° к ней. Экспериментаторы смогли узнать, что происходит в мозгу обезьяны от момента, когда зажглась лампа, до начала движения лапы. Оказалось, что после вспышки вектор направлен прямо на лампочку, затем начинает вращаться и, когда повернется на 90°, начинается движение лапы. Скорость вращения вектора оказалась равной примерно 730°/с, т. е. была того же порядка, что и в психологических опытах с человеком.

Таким образом, как показывают эти эксперименты, мозг может производить и геометрические преобразования (на самом деле, не только повороты, но, видимо, и многие другие, например преобразования подобия).

Сделаем еще один намек на математические способности мозга. Сейчас бурно развивается параллельное программирование. Но когда человек берет предмет, он одновременно управляет работой и плеча, и локтя, и пальцев, осуществляя самое настоящее параллельное программирование.

Заключение

Итак, в живых организмах идут процессы переработки, передачи информации и использование ее в целях управления. Эволюция постепенно находит удачные формы обработки информации, и эти формы имеют немалое сходство с математическими операциями. Такие ухищрения эволюции мы и назвали “математикой в живых организмах”.

Это действительно ЭВМ, так как действия этих устройств основаны на электрических явлениях в организме.

Как возникают эти сдвиги потенциала, вы можете прочитать в книге «Электричество в живых организмах» («Библиотечка „Квант“ выпуск 69).

Кстати, у мечехвоста нет зрачка, и, значит, нет диафрагмы. Впрочем, даже учёт эффекти диафрагмы не спасает положения, изменяя освещённость всего на 1-2 порядка.

Выяснилось, что при восстановлении положения центра тяжести у кошки передние лапы используются как пассивные подпорки. Активно работают именно задние лапы.

Пропорциональность частоты работы нервных клеток косинусу того или иного угла была известна и до работы Георгопулоса. Например, еще в 1981 году в стволе мозга были обнаружены нейроны, связанные со “скачками” глаз: их активность менялась в зависимости от направления скачка глаза по закону косинуса.

www.ronl.ru

Смотрите также

• 
  Марксизм в россии реферат
• 
  Космос и экология реферат
• 
  Женщина и карьера реферат
• 
  Реферат на тему наступление
• 
  Созвездия звездного неба реферат
• 
  Самооценка реферат по психологии
• 
  Ручные пожарные лестницы реферат
• 
  Реферат функции политической системы
• 
  Реферат стоматит у детей
• 
  Реферат по автомобильной подготовке
• 
  Реферат битва за кавказ