Наблюдать прецессию достаточно просто. Нужно запустить волчок и подождать, пока он начнёт замедляться. Первоначально ось вращения волчка вертикальна. Затем его верхняя точка постепенно опускается и движется по расходящейся спирали. Это и есть прецессия оси волчка.

Главное свойство прецессии — безынерционность: как только сила, вызывающая прецессию волчка, пропадёт, прецессия прекратится, а волчок займёт неподвижное положение в пространстве.

Можно получить эффект прецессии, не дожидаясь замедления вращения волчка: толкните его ось (приложите силу) — начнётся прецессия. С прецессией напрямую связан другой эффект, также показанный на иллюстрации — это нутация — колебательные движения оси прецессирующего тела. Скорость прецессии и амплитуда нутации связаны со скоростью вращения тела (изменяя параметры прецессии и нутации в случае, если есть возможность приложить силу к оси вращающегося тела, можно изменить скорость его вращения).

2. Прецессия небесных тел

Вращение (R, зелёный), прецессия (P, синий) и нутация (N, красный) планеты

Подобное движение совершает ось вращения Земли, что было отмечено Гиппархом как предварение равноденствий. По современным данным, полный цикл земной прецессии составляет около 25 765 лет.

Колебание оси вращения Земли влечёт изменение положения звёзд относительно экваториальной системы координат. В частности, через некоторое время Полярная звезда перестанет быть ближайшей к северному полюсу Мира яркой звездой.

Предположительно[1], с прецессией связано периодическое изменение климата Земли[2].

3. Физика явления

Рис.1 Прецессия велосипедного колеса

В основе объяснения явления прецессии лежит экспериментально подтверждаемый факт, что скорость изменения момента импульса вращающегося тела $\vec L$ прямо пропорциональна величине приложенного к телу момента силы $\vec M$ :

$\frac {d\vec L}{dt} = \vec M$

3.1. Пример

На рис. 1 изображено вращающееся велосипедное колесо, висящее на двух нитях «a» и «b». Вес колеса уравновешивается силами, вызванными деформациями нитей. Колесо обладает моментом импульса $\vec L$ , направленным по его оси и в том же направлении направлен вектор угловой скорости вращения колеса $\vec {\omega}$ .

Пусть в некоторый момент времени нить «b» будет разрезана. В таком случае, вопреки ожиданиям, вращающееся колесо не изменит горизонтального направления своей оси и, подобно маятнику, не будет качаться на нити «a» . Но его ось начнёт поворачиваться в горизонтальной плоскости благодаря действию на него момента силы $\vec M$ :

$\ \vec r\times\vec P= = \vec M$

Поскольку

$dL = {d \phi} {L(t)}$ и dL = Mdt , то $\frac {d\phi}{dt} = \frac{M}{L}$

и, так как угловая скорость прецессии :ωp равна: $\frac {d\phi}{dt} = \omega_p$ , получаем: $\omega_p =\frac {M}{L}$ или, с учётом того, что L = Iω, где I есть момент инерции колеса: $\omega_p =\frac {M}{I\omega}$ [3]

Формальное объяснение такого поведения вращающегося колеса заключается в том, что вектор приращения момента количества движения dL всегда перпендикулярен вектору $\vec L$ , кроме того, он всегда параллелен вектору момента силы $\vec M$ , всегда находящегося в плоскости горизонта (к которой перпендикулярен вектор веса тела $\vec P$ ).Поэтому ось колеса прецессирует в данном случае параллельно этой плоскости.

Приведённое объяснение показывает как происходит прецессия, но не даёт ответа почему, который состоит в том, что в начальный момент под действием силы тяжести ось колеса всё же наклоняется в плоскости чертежа и вектор количества движения меняет своё положение в пространстве: $\vec L^\prime$ . Однако сила тяжести не создаёт никакого момента в горизонтальной плоскости. И поэтому направление и величина момента количества движения должна оставаться прежними, что достигается появлением дополнительного момента $\delta\vec L$ в выражении:

$\vec L$ = $\vec L^\prime$ + $\delta\vec L$ .

Именно этот момент и вызывает прецессию.[4]

Примечания

«Элементы», Циклы Миланковича - elementy.ru/trefil/21168
Потепление. Ру. Сайт об изменении климата Земли. Терез Э. И. Устойчивое развитие и проблемы изменения глобального климата Земли - www.poteplenie.ru/doc/terez.htm
.Ulrich Leute Physik und ihre Anwendungen in Technik und Umwelt: Carl Hanser Verlag; München, Wien- 2004 ISBN 3-446-22884-5
Klaus Lüders, Gerhard von Oppen. Lehrbuch der Experimentalphysic. Band I. 12 völlig bearbeitete Auflage. Walter de Gruyter. Berlin. New York. 2008. ISBN 978-3-11-019311-4

wreferat.baza-referat.ru

14.Собственноедвижение звёзд.

Из сравнения экваториальных координат одних и тех же звезд, определенных через значительные промежутки времени, было обнаружено, что их прямые восхождения и склонения меняются с течением времени. Смещение звезды на небесной сфере за год называется собственным движением звезды m . Оно выражается в секундах дуги в год.

Собственные движения у разных звезд различны по величине и направлению. Только несколько десятков звезд имеют собственные движения больше 1" в год. Самое большое известное собственное движение m = 10”,27 (у “летящей” звезды Барнарда).

. Собственное движение каждой звезды происходит по дуге большого круга и с постоянной скоростью. Небольшие периодические отклонения от дуги большого круга в собственном движении замечены лишь у нескольких звезд.

Собственное же движение звезды m вычисляется по формуле

15.Лунно-солнечная и планетарная прецессия; нутация.

Прецессия и нутация земной оси

Если бы Земля имела форму однородного шара и была бы абсолютно твёрдым телом, то направление оси вращения Земли и период вращения были бы постоянными.

Однако Земля имеет форму, близкую к сфероиду (геоид). Притяжение сфероида складывается из притяжения шара (F) и двух выступов (F1 и F2). Т.к. F1 > F2, то притяжение тела L стремится повернуть ось вращения PNPS так, чтобы плоскость экватора сфероида совпала бы с направлением TL. В результате ось вращения будет перемещаться в пространстве.

Т.к. на экваториальные выступы Земли действуют силы притяжения Луны, Солнца и, в меньшей степени, планет, то ось вращения Земли совершает сложное движение.

Ось вращения Земли описывает конус вокруг оси эклиптики. Такая лунно-солнечная прецессия совершается с периодом 26 000 лет.

Ось вращения Земли совершает мелкие колебания около среднего положения, которые называются нутацией земной оси. Нутационные колебания возникают из-за того, что силы F1 и F2 всё время изменяют свою величину и направление. Воздействие этих сил на ось вращения Земли равно нулю, когда Луна и Солнце находятся в плоскости экватора Земли. Главное нутационное колебание земной оси совершается с периодом 18,6 года, и полюсы мира описывают на небесной сфере эллипсы, большие оси которых равны 18,42", а малые – 13,72".

Влияние планет слишком мало и сводится к воздействию на движение Земли вокруг Солнца, т.е. на положение в пространстве земной орбиты, т.е. плоскости эклиптики. Планетная прецессия смещает точку ¡ к востоку на 0,117" в год.

16. Неравномерность вращения Земли; движение полюсов Земли. Служба широты.

Неравномерность вращения Земли

В результате многочисленных исследований было установлено, что угловая скорость вращения Земли непостоянна, т.е. вращение Земли неравномерно.

Изменения скорости вращения Земли делятся на три типа:

Вековые, вызванные тормозящим действием лунных и солнечных приливов. В результате вековых изменений продолжительность одного оборота Земли увеличивалась за последние 2 000 лет в среднем на 0,0023s в столетие.

Нерегулярные (или скачкообразные) могут увеличивать или уменьшать продолжительность суток на тысячные доли секунды за время в несколько месяцев. Природа нерегулярных изменений пока достоверно не установлена (землетрясения и активизация вулканов?).

Сезонные (или периодические) изменения вызываются, по-видимому, сезонными перераспределениями воздушных и водных масс на поверхности Земли. В результате сезонных изменений скорости вращения Земли продолжительность суток в течение года может отличаться от средней за год на ±0,001s. Самые короткие сутки приходятся на июль-август, а самые длинные – на март.

Движение полюсов Земли, перемещение географических полюсов Земли по ее поверхности. Движение полюсов Земли происходит из-за того, что мгновенная ось вращения Земли не сохраняет в теле Земли неизменного направления. На возможность Движение полюсов Земли как одного из свойств вращения Земли впервые указал в 1687 И. Ньютон Движение полюсов Земли происходят непрерывные изменения координат точек поверхности Земли и азимутов земных предметов, что сказывается на результатах астрономических и геодезических измерений.

Служба широты, объединение научных учреждений, обеспечивающих регулярные астрономического определения географических широт ряда целесообразно выбранных пунктов земной поверхности с целью изучения движения полюсов географических. Международная Служба широты, позже преобразованная в службу движения полюса международную, была создана решением 12-й Международной геодезической конференции в 1898. Были построены и в 1899 начали работать пять широтных станций, Две из них были созданы в США, одна — в Италии, одна — в Японии и одна — в России. Впоследствии несколько станций были организованы в Южном полушарии.. Наблюдения всех международных широтных станций концентрируются в Центральном бюро Международной службы движения полюса в г. Мидзусава (Япония). В результате совместной обработки вычисляются координаты мгновенного полюса Земли, по которым может быть построена полодия. В изучении изменяемости широт и связанных с ней явлений участвуют многие астрономические обсерватории. В 1953 при Полтавской обсерватории создано Центральное бюро советской Служба широты.

studfiles.net

О лунно-солнечной прецессии. | Лаборатория космических исследований

Это сама природа наглядный дает урок

Крутится волчок…

В. Сауткин

Рис. 1. Системы координат.

Земля – волчок. Она «крутится» в гравитационном поле Солнца, вращается вокруг Солнца и увлекает за собой Луну. Все это отражается на поведении ее оси вращения. Но каким образом?

Говорят, что Солнце, Луна и планеты так воздействуют на земной сфероид, что пытаются поставить его наименьшую ось инерции перпендикулярно плоскости земной орбиты. Это, как мы знаем из опыта, приводит не к изменению наклона оси, а к особому виду движения – прецессии оси вращения.

Вклады возмущающих тел – Солнца, Луны и планет в поддержание прецессии земной оси аддитивны. Наибольший вклад дает Луна, существенно меньший Солнце и ничтожный – планеты солнечной системы.

Давайте посмотрим, какое действие на ось вращения Земли оказывает Солнце и тот факт, что Земля движется вокруг Солнца.

Это называется ограниченная постановка задачи движения твердого тела в центральном гравитационном поле.

Рассмотрим систему координат Ox'y'z' (Рис. 1), оси которой направлены по главным центральным осям инерции Земли (А=8.014х1037кг·м2, B=8.014х1037кг·м2, С=8.040х1037кг·м2). Орбитальная система координат Оxyz поворачивается относительно Солнца с постоянной угловой скоростью Ω=1.992x10-7рад/с. Ось x является продолжением радиус-вектора центра Земли. Земля движется по круговой орбите. Ось вращения Земли направлена по оси z'. Плоскость земной орбиты xOy, плоскость земного экватора x'Oy'. Линия их пересечения ON –линия узлов. Связь между координатам штрихованной и не штрихованной системы осуществляется матрицей направляющих косинусов (она же матрица поворота).

CodeCogsEqn (1).gif

(1)

А связь собственно такая:

(2)

Обозначим компоненты матрицы С буквами греческого алфавита:где v –произвольный вектор: скорость, угловая скорость, радиус-вектор, момент силы.

(3)

Уравнение движения в векторной форме можно найти в [1]. Перепишем его в соответствии с Рис.1 и обозначениями (3):

(4)

где J – тензор инерции Земли.

В учебниках в правой части (4) порой ставят ноль и обнаруживают трехсотдневный цикл колебания Земной оси, которого нет на самом деле, и не может быть понятно почему.

Распишем (4) по штрихованным осям, направленным по главным центральным осям инерции Земли:

(5)

где p, q, r – компоненты абсолютной угловой скорости вращения Земли.

Для полного описания движения Земли требуется еще три уравнения с одной оговоркой: поскольку речь идет об абсолютной угловой скорости, в уравнение угла прецессии введена угловая скорость переносного движения.

(6)

Уравнения (6) можно получить, если записать кинематические уравнения Эйлера с учетом орбитального движения Земли [1]:

CodeCogsEqn (11).gif (7)

Теперь начальные условия:

(8)

Мы не учитываем в начале прецессию земной оси. Она в принципе должна появиться в процессе.

Прецессия земной оси проявляется в движении проекции вектора абсолютной угловой скорости вращения Земли на плоскость эклиптики. Эта проекция определяется двумя составляющими : p(t) и q(t). Посчитаем среднее за Т=5 лет значение этой проекции:

CodeCogsEqn (13).gif (9)

Оно равно 1.299х10-12 рад/с, что составляет примерно 17% от принятой сегодня постоянной прецессии. Это означает, что вклад орбитального движения Земли вокруг Солнца вместе с неоднородностью гравитационного поля Солнца в теле Земли составляет 17% от общего эффекта, включающего действие Луны и планет. Если бы не было Луны прецессионный цикл длился бы более 153000 лет.

Действие Луны аналогично действию Солнца, за одним исключением: Луна заставляет центр Земли колебаться поперек плоскости земной орбиты. Возможно, такое движение приводит к более тонким, чем прецессия земной оси, эффектам, но это уже совсем другая история.

Источники информации.

1. Теоретическая механика: учебник для студ. Учреждений высш. Проф. Образования /С.В. Болотин, А.В.Карапетян, Е.И.Кугушев, Д.В. Трещев. – М.: Издательский центр «Академия», 2010.

www.spacephys.ru

это... Прецессия оси Земли: описание и интересные факты

У человечества за плечами почти четыре миллиона лет, и за это время мы достигли понимания движения тектонических плит, научились предсказывать погоду и освоили космическое пространство. Но наша планета таит в себе еще немало тайн и загадок. Одна из них, с которой связывают глобальное потепление климата и теорию катастроф, это прецессия оси планеты.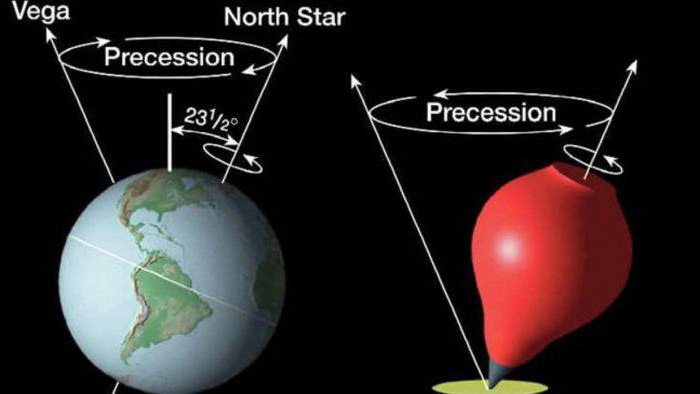 прецессия это

Исторический очерк

Движение точек равноденствия на фоне звезд заметил в III веке до нашей эры Аристарх Самосский. Но первым описал увеличение долготы звезд и различия между звездным и фактическим годом древнегреческий астроном Гиппарх во II веке до нашей эры. И это при том, что в тот период считали, что все звезды закреплены на неподвижной сфере, а движение небосвода – это движение этой сферы вокруг собственной оси. После были работы Птолемея, Теона Александрийского, Сабит ибн Курра, Николая Коперника, Тихо Браге и многих других. Причину прецессии оси Земли объяснил и описал Исаак Ньютон в своих «Началах» (1686). А формулу прецессии показал американский астроном Саймон Ньюком (1896). Именно его формула, уточненная в 1976 году Международным астрономическим союзом, описывает скорость прецессии в зависимости с временной привязкой.

Физика явления

В элементарной физике прецессия – это изменение момента импульса тела при изменении его направления движения в пространстве. Наблюдают этот процесс на примере волчка и его замедления. Первоначально вертикальная ось волчка при его замедлении начинает описывать конус – это и есть прецессия оси волчка. Главное физическое свойство прецессии – безинерционность. Это значит, что при прекращении действия силы, вызывающей прецессию, тело займет неподвижное положение. В отношении небесных тел – такой силой является гравитация. И так как она действует постоянно, то и движение, и прецессирование планет не прекратится никогда.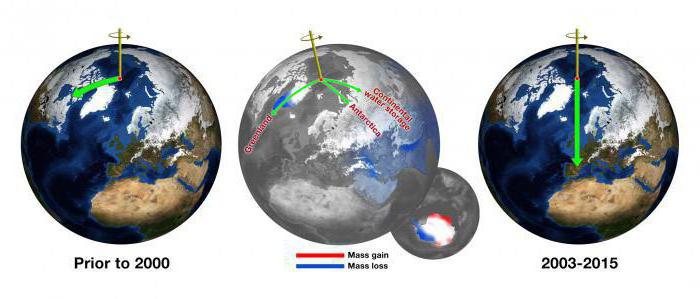 ось прецессии

Движение нашей неподвижной планеты

Каждому известно, что планета Земля вращается вокруг Солнца, совершает вращение по своей оси и меняет направление этой оси. Но это не все. Астрономия различает тринадцать видов движения нашего дома. Перечислим их вкратце:

Вращение вокруг собственной оси (смена дня и ночи).
Вращение вокруг Солнца (смена времен года).
«Хождение вперед» или предварение равноденствий – это прецессия.
Покачивание земной оси – нутация.
Изменение оси Земли к плоскости ее орбиты (наклон эклиптики).
Изменение эллипса земной орбиты (эксцентриситета).
Изменения перигелия (расстояние от наиболее отдаленной от солнца точки орбиты).
Параллактические неравенства Солнца (ежемесячные изменения расстояния между нашей планетой и светилом).
В момент парада планет (планеты расположены с одной стороны от Солнца) центр масс нашей системы выходит за границы солнечного шара.
Отклонения Земли (возмущения и пертурбации) под действием притяжения других планет.
Поступательное движение всей Солнечной системы к Веге.
Движение системы вокруг ядра Млечного пути.
Движение галактики Млечный путь вокруг центра скопления таких же галактик.

Все это сложно, но математически доказано. Мы остановимся на третьем движении нашей планеты - прецессии. лунно солнечная прецессия

Это юла?

Мы привыкли думать, что ось вращения планеты вокруг своей оси неизменна и северный ее конец направлен к точке полярной звезды. Но все не совсем так. Ось планеты описывает конус, также как детская игрушка юла или волчок, что вызвано притяжением нашего спутника и нашего светила. В результате полюсы планеты медленно перемещаются по отношению к звездам с радиусом дуги в 23 градуса и 26 минут.

Как это увидеть?

Наклон земной оси осуществляется вследствие взаимодействий в системе гравитации Солнце-Земля и Луна-другие планеты. Усилия гравитации так велики, что заставляют ось планеты совершать прецессию – медленное покачивание по ходу часовой стрелки в противоположном вращению планеты направлении. Увидеть явление лунно-солнечной прецессии в действии легко – достаточно посмотреть на заведенный волчок. Если отклонить его ручку от вертикали, то она начинает описывать круг в противоположном вращению направлении. Если представить, что ось планеты – ручка, а сама планета – юла, то это и будет пусть и грубым но примером прецессии оси Земли. Половину цикла прецессии наша планета проходит за 25776 лет. прецессия солнца

Последствия прецессий Солнца и комплекса Земля-Луна

Медленное перемещение точки весеннего равноденствия (пересечения небесного экватора и эклиптики), провоцируемое прецессией, приводит к двум последствиям:

Корректировке небесных координат.
Изменениям пребывания Солнца в зодиакальных созвездиях.

Изменения точки весеннего равноденствия привела к возникновению международной договоренности о координатах небесных тел с обязательным фиксированием на конкретную дату. Ведь из-за прецессии оси Земли в античные времена эта точка находилась в созвездии Овна, а сегодня она расположена в созвездии Рыб. По аналогии не существует и соответствия астрологических знаков зодиакальных созвездий. Например, знак Рыб говорит о том, что в период с 21 февраля по 21 марта светило располагается в созвездии Рыб. Так и было в античные времена. Но сегодня ввиду прецессии орбиты Земли в этот период времени Солнце находится в созвездии Водолея. прецессия орбиты

Вечной весны не будет

Прецессия - это предварение равноденствий, что означает смещение точек осеннего и весеннего равноденствия. Другими словами, весна на планете с каждым годом наступает раньше (на 20 минут и 24 секунды), а осень позже. К календарю это не имеет отношения – наш григорианский календарь учитывает длину тропического года (от равноденствия до равноденствия). Поэтому по факту уже включен в наш календарь эффект прецессии. Это смещение периодично, и его период, как уже было сказано ранее, составляет 25776 лет.

Когда наступит новый Ледниковый период?

Изменение направления оси Земли каждые примерно 26 тысяч лет (прецессия) – это изменение северного ее направления. Сегодня точка Северного полюса указывает на Полярную звезду, через 13 тысяч лет она укажет на Вегу. А через 50 тысяч лет планета пройдет два цикла прецессии и вернется в нынешнее состояние. Когда планета расположена «прямо» - количество получаемой солнечной энергии минимально и наступает ледниковый период – большую часть суши покрывает лед и снег. История планеты показывает, что ледниковый период длится порядка 100 тысяч лет, а межледниковый – 10 тысяч. Сегодня мы переживаем такое межледниковое время, а вот через 50 тысяч лет ледовая кора покроет планету до границ ниже Нью-Йорка. прецессия оси земли

Не только прецессия виновата

По данным Национального аэрокосмического агентства НАСА, географический Северный полюс планеты с 2000 года начал активно смещаться на восток. За 115 лет изучения климата на планете он отклонился на 12 метров. До 2000 года полюс со скоростью несколько сантиметров в год двигался в направлении Канады. Но после указанной даты он изменил и направление, и скорость. Сегодня он со скоростью до 17 сантиметров в год движется в сторону Британии. Причинами данного явления называют таяние Гренландских ледников, увеличение массы льда на востоке Антарктиды, засухи в бассейне Каспия и Индостана. А за этими явлениями стоит антропогенный фактор воздействия на Землю.

Почему зимы неодинаковые?

Кроме того, что наша планета прецессирует, она еще и совершает колебания при данном процессе. Это нутация – быстрые относительно прецессионного периода «покачивания полюсов». Именно она меняет погоду – то зима холоднее, то лето суше и жарче. В годы особенно сильной нутации ожидаются более суровые погодные условия.

fb.ru

О ТАК НАЗЫВАЕМОЙ ЛУННО-СОЛНЕЧНОЙ ПРЕЦЕССИИ ЗЕМНОЙ ОСИ

А.А.Гришаев, независимый исследователь

Известно, что ось вращения Земли, угол e наклона которой относительно нормали к эклиптике составляет примерно 23°.5, не сохраняет своё направление в пространстве. Земная ось, в частности, медленно поворачивается около нормали к эклиптике, совершая полный оборот по отношению к «неподвижным звёздам» за 25725 лет [1]. Поэтому моменты равноденствий от года к году наступают всё раньше – в угловой мере, приблизительно на 50² [2]. Это вековое вращение земной оси, приводящее к предварению равноденствий, называют лунно-солнечной прецессией.

Происхождение этого термина связано с тем, что вековое вращение земной оси считается прецессией Земли-гироскопа – из-за моментов опрокидывающих сил, обусловленных гравитационными воздействиями Луны и Солнца на экваториальную выпуклость Земли [2]. Если бы этот традиционный подход был верен, то один лишь феномен лунно-солнечной прецессии делал бы негодной нашу модель «унитарного» действия тяготения [3]. Согласно этой модели, действия на пробное тело солнечного и планетарных тяготений разграничены в пространстве: в пределах планетарной частотной воронки [4] солнечное тяготение «отключено», и пробное тело тяготеет там только к одному «притягивающему центру», а именно, к центру планетарной частотной воронки. При этом, в случае Земли, её экваториальная выпуклость не подвержена действию солнечного тяготения. Кроме того, имеются свидетельства о том, что лунное тяготение действует лишь в небольшой окололунной области [5,6], и тогда экваториальная выпуклость Земли не подвержена действию также и лунного тяготения. В предыдущих статьях мы постарались показать, что, в сравнении с концепцией всемирного тяготения, наша модель тяготения выглядит предпочтительнее, поскольку даёт, в частности, более адекватное объяснение фактической картины океанских приливов [7,8], аномальной кинематики пары Земля-Луна [5,7], феномена астероидов-Троянцев [9], признаков отсутствия собственного тяготения у поверхностных масс Земли [10,11] и у малых тел Солнечной системы [12], а также эффектов, сопровождающих пересечение границ планетарных частотных воронок автоматическими межпланетными станциями [4,3]. Теперь же мы постараемся показать, что и вековое вращение земной оси более адекватно объясняется с помощью нашей модели тяготения, согласно которой на экваториальную выпуклость Земли не действует тяготение ни Солнца, ни Луны.

Прежде всего, мы убедимся в том, что традиционный подход даёт лишь видимость объяснения векового вращения земной оси. Для этого сделаем оценку периода лунно-солнечной прецессии. Известно, что угловая скорость W прецессии гироскопа определяется выражением

W=Fl/(Jw), (1)

где Fl - момент опрокидывающей силы F, J – момент инерции гироскопа, w - его собственная угловая скорость вращения. В нашем случае w=7.3×10-5 рад/с и J=8.04×1037 кг×м2 [13]. Заметим, что моменты опрокидывающих сил, которые вызывались бы гравитационным воздействием Солнца и Луны на экваториальную выпуклость Земли, не были бы постоянными во времени: опрокидывающее действие того или иного светила уменьшалось бы до нуля, когда линия Земля-светило оказывалась бы ортогональна оси вращения Земли. Так, опрокидывающее действие Солнца было бы максимально в моменты солнцестояний и равно нулю в моменты равноденствий. Аналогично, и опрокидывающее действие Луны изменялось бы с периодом примерно в половину сидерического месяца. Результирующий, усреднённый по времени опрокидывающий момент из-за действия того или иного светила составлял бы половину от своего максимального значения, что компенсировало бы наличие пары одинаковых моментов – из-за действия светила на ближний и дальний участки экваториальной выпуклости. При оценке максимального значения лунного воздействия можно приближённо считать, что, как и для случая солнечного воздействия, плечо l равно произведению радиуса Земли на синус e, т.е. 2550 км. Массу m ближайшего к светилу участка экваториальной выпуклости Земли, действие на который давало бы основной вклад в опрокидывающий эффект (и, соответственно, массу противоположного участка экваториальной выпуклости), можно оценить как массу цилиндра с высотой 11 км, радиусом основания 1500 км, и средней плотностью 4000 кг/м3, т.е. m=3.1×1020 кг. Что касается опрокидывающей силы F, то она не являлась бы силой гравитационного притяжения к светилу соответствующего участка экваториальной выпуклости Земли. Действительно: светило действовало бы не только на экваториальную выпуклость, но и на остальные элементы объёма Земли, поэтому опрокидывающую силу следовало бы рассчитывать разностным, по отношению к центру Земли, способом – аналогично тому, как это обычно делается при расчётах приливных эффектов. Таким образом, сила F составляла бы величину ~2GMmrE/R3, где G – гравитационная постоянная, M – масса светила, rE – радиус Земли, R – расстояние между Землёй и светилом. Тогда угловая скорость чисто «лунной» прецессии составила бы WМ»1.5×10-13 рад/с, а чисто «солнечной» - WS»6.8×10-14 рад/с. Отношение угловой скорости WY»1.99×10-7 рад/с годичного обращения Земли к величине WМ или WS дало бы период, соответственно, «лунной» или «солнечной» прецессии, выраженный в годах. Как можно видеть, (WY/WМ)»1300000, а (WY/WS)»2900000, т.е. период комбинированной лунно-солнечной прецессии составлял бы примерно 900000 лет, будучи на порядок больше фактического значения периода векового вращения земной оси. Поэтому, на наш взгляд, традиционное объяснение этого вращения – в терминах лунно-солнечной прецессии – отнюдь не является корректным.

Напротив, вековое вращение земной оси находит весьма правдоподобное объяснение с помощью нашей модели тяготения. Для такого объяснения требуется вспомнить тезис о том, что земная частотная воронка, при своём орбитальном движении вокруг Солнца, испытывает также собственное вращение вокруг оси, ортогональной эклиптике, и с периодом в один год – таким образом, что она «обращена к Солнцу всё время одной и той же стороной» [5]. При этом участок «инерциального пространства», в котором находится вращающаяся Земля, и по отношению к которому следует отсчитывать локально-абсолютные скорости [14] элементов объёма вращающейся Земли, испытывает не только орбитальное годичное обращение, но и собственное годичное вращение по отношению к «неподвижным звёздам». Ключевым моментом здесь является то, что мы привыкли говорить о собственном вращении Земли по отношению как раз к «неподвижным звёздам», но дело в том, что локально-абсолютные скорости пробных тел, в том числе и линейные скорости различных элементов вращающейся Земли, следует отсчитывать по отношению к местному участку частотных склонов, т.е. к местному участку «инерциального пространства». И если собственное вращение Земли происходит в условиях, когда содержащий Землю участок «инерциального пространства» тоже имеет своё собственное вращение – причём, угол между векторами угловых скоростей этих двух собственных вращений составляет e=23°.5 – то комбинация этих собственных вращений приводит к дисбалансам линейных скоростей у пар элементов объёма, расположенных симметрично земной оси. Если эти дисбалансы линейных скоростей не были бы скомпенсированы каким-либо образом, то вращающаяся Земля должна была бы испытывать соответствующие механические напряжения и деформации. Но, как можно видеть, названные дисбалансы линейных скоростей могут быть скомпенсированы как раз с помощью обратного векового вращения вектора угловой скорости собственного вращения Земли (т.е., такого же вращения земной оси) около вектора угловой скорости собственного вращения местного «инерциального пространства». Для такой компенсации должно выполняться соотношение

rE×WY×cos e = RSE×W*, (2)

где rE – радиус Земли, WY – угловая скорость вращения с периодом в год, RSE – средний радиус орбиты Земли, W* - угловая скорость компенсирующего векового вращения земной оси. Едва ли может быть простым совпадением тот факт, что отношение WY/W*, выражающее в годах период компенсирующего векового вращения земной оси, оказывается равно

WY/W* = RSE/(rE×cos e) = 25647, (3)

т.е. что рассчитанный нами период отличается от фактического всего на 0.3% - причём, это небольшое рассогласование, на наш взгляд, не привнесено методом расчёта, а обусловлено погрешностями, с которыми известны фундаментальные астрономические постоянные. Поэтому можно считать, что, с большой вероятностью, вековое вращение земной оси является именно компенсатором дисбалансов линейных скоростей у элементов объёма Земли, которая вращается в «инерциальном пространстве», вращающемся по-своему.

Дополнительным свидетельством в пользу нашего подхода могло бы стать прояснение следующего вопроса. Если вековое вращение земной оси действительно является вышеописанным компенсатором, то угловая скорость W* этого векового вращения должна быть практически постоянной: угол поворота земной оси, увеличивающийся на »50² в год, должен быть линейной функцией от времени. Если же вековое вращение земной оси являлось бы лунно-солнечной прецессией, то, из-за упомянутой выше периодичности моментов опрокидывающих сил, угловая скорость прецессии имела бы полугодичную и полумесячную компоненты – поскольку отклик гироскопа на опрокидывающие воздействия, как известно, безынерционен. Результирующие максимумы и минимумы угловой скорости прецессии были бы вполне заметны с помощью астрооптических инструментов – не только современных, но и гораздо более ранних. Однако, нам не удалось найти сообщений о наблюдавшихся полугодичных и полумесячных вариациях угловой скорости векового вращения земной оси – что, по-видимому, говорит о том, что такие вариации действительно не существуют.

Суммируя вышеизложенное, можно сказать, что вековое вращение земной оси весьма проблематично объяснить с позиций закона всемирного тяготения, в рамках которого это вековое вращение считается лунно-солнечной прецессией. И, напротив, вековое вращение земной оси естественно объясняется на основе нашей модели тяготения, в которой это вековое вращение оказывается компенсатором дисбалансов линейных скоростей у элементов объёма Земли, которая вращается во вращающемся «инерциальном пространстве». Как можно видеть, по сравнению с подходом на основе закона всемирного тяготения, наш подход в очередной раз выглядит предпочтительнее.

Автор благодарит В.И.Беленко за полезное обсуждение.

Ссылки.

1. Справочное руководство по небесной механике и астродинамике. Г.Н.Дубошин, ред. «Наука», М., 1976.

2. К.А.Куликов. Фундаментальные постоянные астрономии. «Государственное издательство технико-теоретической литературы», М., 1956.

3. А.А.Гришаев. К реальной динамике пробных тел: локально-абсолютные ускорения. – Доступна на данном сайте.

4. А.А.Гришаев. Межпланетные полёты и концепция локально-абсолютных скоростей. – Доступна на данном сайте.

5. А.А.Гришаев. Синхронизатор орбитального движения Луны. – Доступна на данном сайте.

6. А.А.Гришаев. «Зыбкое пространство», порождающее собственное тяготение Луны. – Доступна на данном сайте.

7. А.А.Гришаев. Свидетельства об одномерности колебаний Земли в кинематике пары Земля-Луна. – Доступна на данном сайте.

8. А.А.Гришаев. Новый взгляд на природу приливообразующих сил. – Доступна на данном сайте.

9. А.А.Гришаев. Феномен астероидов-Троянцев и модель «унитарного» действия тяготения. – Доступна на данном сайте.

10. А.А.Гришаев. О всемирном тяготении: всё ли вещество оказывает притягивающее действие? – Доступна на данном сайте.

11. А.А.Гришаев. Форма геоида и опыт Кавендиша: как совместить несовместимое. – Доступна на данном сайте.

12. А.А.Гришаев. Имеют ли собственное тяготение малые тела Солнечной системы? – Доступна на данном сайте.

13. К.У.Аллен. Астрофизические величины. «Мир», М., 1977.

14. А.А.Гришаев. Эксперимент Майкельсона-Морли: детектирование локально-абсолютной скорости? – Доступна на данном сайте.

Источник: http://newfiz.narod.ru

Поступило на сайт: 05 февраля 2007.

newfiz.narod.ru

Прецессия

26 апреля Александру Александровичу Михайлову исполнится 90 лет. Труды академика А. А. Михайлова получили мировое признание. Поразительна многогранность его научных интересов. Это — практическая и теоретическая гравиметрия, теория затмений, звёздная астрономия и астрометрия. Велики заслуги академика А. А. Михайлова в становлении и развитии советской астрономии. Редакционная коллегия и читатели «Земли и Вселенной» сердечно поздравляют Александра Александровича с юбилеем и желают ему здоровья и новых творческих успехов.

«Прецессия» в переводе с латинского означает «хождение вперед». Что представляет собой прецессия и как определяется ее величина!

ГДЕ НАЧАЛО ОТСЧЕТА КООРДИНАТ?

Положение точки на поверхности Земли определяется двумя координатами — широтой и долготой. Экватор как начало отсчета широты дан самой природой. Это—линия, во всех точках которой отвес перпендикулярен оси вращения Земли. Начало же отсчета долгот приходится выбирать условно. Это может быть меридиан, проходящий через какую-нибудь точку, которая принимается за исходную. Поскольку вычисление долготы связано с измерением времени, то за такую точку принимают астрономическую обсерваторию, где время определяется наиболее точно. Так, во Франции в старину долготы исчислялись от Парижской обсерватории; в России после основания в 1839 году Пулковской обсерватории — от меридиана, проходящего через центр ее главного здания. Были попытки взять за исходную точку такую, чтобы на данной территории все долготы отсчитывались в одну сторону. Например, в XVII веке за начало была принята самая западная точка Старого света — Ферро, один из Канарских островов, к востоку от которого лежала вся Европа, Азия и Африка. В 1883 году по международному соглашению за начальный принят меридиан, проходящий через оптическую ось пассажного инструмента Гриничской обсерватории («Земля и Вселенная», № 5, 1975, с. 74—80.— Ред.).

Выбор начального меридиана для отсчета долгот не имеет принципиального значения и диктуется целесообразностью и удобством. Важно лишь, чтобы исходная точка была устойчива и не находилась бы в сейсмически неспокойном районе. Нужно также, чтобы она не располагалась слишком близко к полюсу, где положение меридиана определяется не очень уверенно. При соблюдении этих условий постоянство начального меридиана будет обеспечено на тысячи лет, так как смещение блоков земной коры не превышает нескольких миллиметров в год, что может вызвать изменение долготы на 0,1" лишь за тысячелетие.

На небесной сфере положение светил тоже определяется двумя сферическими координатами, аналогичными географическим координатам. Широта здесь заменена склонением, равным угловому расстоянию точки от небесного экватора — большого круга, плоскость которого перпендикулярна оси вращения Земли. Географической долготе соответствует прямое восхождение, которое отсчитывается с запада на восток — в сторону движения планет Солнечной системы. Однако выбор начальной точки на небесной сфере сложнее. Понятно, что такая точка должна быть неподвижной, но относительно чего? Нельзя брать за начало какую-нибудь звезду, ведь каждая звезда имеет собственное движение, и у некоторых оно превышает \" в год. Это в десятки тысяч раз больше, чем движение нуль-пункта географической долготы.

ПОЧЕМУ ИЗМЕНЯЕТСЯ СКЛОНЕНИЕ ЗВЕЗД?

Астрономия как наука возникла в глубокой древности отчасти вледст-вие потребности в измерении времени, связанного с видимым суточным и годичным движениями Солнца, которые вызывают смену дня и ночи и времен года. Отсюда сама собой появилась тесно связанная с Солнцем система астрономических координат. За нуль-пункт прямых восхождений была принята точка пересечения небесного экватора с эклиптикой, через которую Солнце проходит в момент весеннего равноденствия. Во времена древних астрономов эта точка находилась в зодиакальном созвездии Овна, знак которого Т похож на греческую букву гамма. Такое обозначение точки весеннего равноденствия сохранилось до сих пор. Она ничем не отмечена на небе и определить ее положение можно, лишь измеряя вблизи равноденствия склонения Солнца: в момент, когда при переходе из южного полушария в северное его склонение равно нулю, центр Солнца и будет находиться в точке весеннего равноденствия. Привязку ее к звездам астрономы умели делать более 2000 лет тому назад. В то время не было средств для наблюдения звезд днем наряду с Солнцем, так что приходится удивляться остроумию и умению древних наблюдателей.

Греческий астроном Клардий Пто-лемей в знаменитом сочинении, известном нам под искаженным арабским названием «Альмагест» (середина II века), писал, что живший за три столетия до него величайший греческий астроном Гиппарх определял широты звезд (угловые расстояния от эклиптики), а также их склонения (расстояния от экватора) и сравнивал их с аналогичными наблюдениями Тимохариса, произведенными на 100 лет раньше. Гиппарх нашел, что широты звезд остались неизмененными, а склонения заметно изменились. Это указывало на смещение экватора относительно эклиптики. Птолемей проверил выводы Гип-парха и получил следующие склонения звезд: а Тельца а Девы Альдебаран Спика + 8°45' +1°24' (Тимохарпс) + 9°45' +0°36' (Гиппарх) +11°0' —0°30' (Птолемей) Оказалось, что склонение Альде-барана со временем увеличилось, а Спики уменьшилось. Гиппарх истолковал это перемещением среди звезд точки весеннего равноденствия. Она движется навстречу Солнцу, поэтому Солнце возвращается к ней раньше, чем опишет полный оборот по эклиптике. Отсюда и произошел термин «предварение» равноденствия (по-латыни, ргаесезэеге). Перемещение точки весеннего равноденствия (Г) за период с III века до нашей эры по II век. Изменение склонений звезд Алъдебарана (А) и Спики (8) К. Птолемей связал со смещением экватора относительно эклиптики, а значит, и с движением точки их пересечения Г навстречу Солнцу (направление его движения указано стрелкой).

Изменилось и положение Северного полюса мира с Р на Р'

Скорость движения точки весеннего равноденствия по эклиптике весьма мала, Гиппарх оценил ее в 1° за 100 лет, или 36" в год. Птолемей получил большее значение—почти 60" в год. С тех пор эта фундаментальная для астрометрии величина уточнялась по мере накопления наблюдений, совершенствования техники и течения времени. Арабские ученые в Х—XI веках находили, что точка весеннего равноденствия смещается за год на 48—54", великий узбекский астроном Улугбек в 1437 году получил 51,4". Последний, кто проводил наблюдения невооруженным глазом, был Тихо Браге. В 1588 году он оценил эту величину в 51".

Год природы, то есть период повторения сезонов, называемый тропическим годом, определяется движением Солнца относительно точки весеннего равноденствия и равен 365,24220 средних солнечных суток. Полное обращение Солнца относительно неподвижной точки эклиптики, например звезды с исчезающе малым собственным движением, известно как звездный, или сидерический, год. Он равен 365,25636 суток, то есть на 0,01416 суток, или 20 минут 24 секунды, длиннее тропического года. Именно такой промежуток времени требуется Солнцу для прохождения отрезка эклиптики, на который отступила за год точка весеннего равноденствия.

ВСЕГДА ЛИ ПОЛЯРНАЯ ОСТАНЕТСЯ ПОЛЯРНОЙ

Итак, более 2000 лет назад было обнаружено явление прецессии, но объяснение его дал лишь в 1687 году Исаак Ньютон в своем бессмертном сочинении «Математические начала натуральной философии». Он правильно заключил, что вследствие суточного вращения вокруг оси Земля имеет форму слегка сплющенного у полюсов эллипсоида. Ее можно рассматривать как шар с добавочной массой, расположенной вдоль экваториального пояса. Притяжение Земли Луной и Солнцем в этом случае можно разделить на две части: притяжение земного шара силой, приложенной к его центру, и притяжение экваториального пояса. Когда Луна 2 раза в месяц, а Солнце 2 раза в год отходят от плоскости земкого экватора, их притяжение создает момент силы, стремящийся повернуть Землю так, чтобы ее экватор проходил через эти светила.

Силы притяжения Луны, действующие на центр нашей планеты и ее экваториальный пояс экватора, их притяжение создает момент силы, стремящийся повернуть Землю так, чтобы ее экватор проходил через эти светила. Если бы Земля не вращалась, то такой поворот действительно произошел бы, но быстрое вращение Земли (ведь точка ее экватора перемещается со скоростью 465 м/с) создает гироскопический эффект, как у вращающегося волчка. Сила тяжести стремится повалить волчок, но вращение удерживает от падения, и его ось начинает движение по конусу с вершиной в точке опоры. Подобно этому и земная ось описывает конус вокруг оси эклиптики, ежегодно отходя на 50,2" и совершая полный оборот почти за 26 000 лет. Это изменение направления земной оси в пространстве приводит к тому, что Северный полюс мира описывает вокруг Северного полюса эклиптики малый круг с радиусом около 23,5°, то же происходит и с Южным полюсом. Поскольку собственные движения звезд малы по сравнению с прецессионным движением, можно считать звезды практически неподвижными, а полюсы — перемещающимися среди них.

В настоящее время Северный полюс мира находится очень близко к яркой звезде 2-й величины к Малой Медведицы, которая поэтому называется Полярной. В 1978 году угловое расстояние полюса от этой звезды равно 50', а в 2103 году оно станет минимальным — всего 27'. Мы бы назвали такую близость полюса мира к яркой звезде удачной. Действительно, в практической астрономии и ее приложениях к географии, геодезии, навигации и авиации Полярная звезда используется для определения широты и азимута. К 3000 году Северный полюс удалится от нынешней Полярной звезды почти на 5°. Затем долгое время не будет близкой к полюсу яркой звезды. Около 4200 года полюс подойдет на расстояние 2° к звезде а Цефея 2-й величины. В 7600 году полюс окажется близ звезды б Лебедя 3-ей величины, а в 13800 году полярной, хотя и далекой от полюса (на 5°), будет наиболее яркая звезда северного полушария Вега в созвездии Лиры.

В южном полушарии, наоборот, полюс сейчас находится в области неба, крайне бедной яркими звездами. Ближайшая к полюсу звезда о Октанта имеет всего 5-ю величину и едва видна невооруженным глазом. Зато в будущем, хотя и далеком, в южном полушарии будет «урожай» на близполюсные звезды. Однако движение полюсов не строго равномерно, оно медленно изменяется вследствие векового уменьшения наклона экватора к эклиптике, а также уменьшения эксцентриситета земной орбиты. Кроме того, происходят более значительные периодические колебания в положении полюсов, вызванные изменениями склонений Луны и Солнца. Когда их склонения увеличиваются — светила удаляются от экватора,— возрастает их стремление повернуть Землю в свою сторону. Хотя Луна имеет массу в 27 млн. раз меньше массы Солнца, но она настолько ближе к Земле, что ее действие в 2,2 раза сильнее действия Солнца. Таким образом, почти 70% прецессионного движения вызывается Луной.Луна и Солнце периодически изменяют свое положение относительно экватора. Склонение Солнца регулярно меняется в пределах ±23,5° с годичным периодом, склонение Луны меняется более сложно, в зависимости от положения узлов лунной орбиты, которые совершают один оборот по эклиптике за 18,6 года. Наклон лунной орбиты к эклиптике составляет 5° и, когда восходящий узел близок к точке весеннего равноденствия, наклон орбиты складывается с наклоном эклиптиг.ч, так что склонение Луны в течение месяца колеблется между ±28,5°. Через 9,3 года, когда к точке весеннего равноденствия подходит нисходящий узел, наклоны вычитаются и склонение Луны меняется в пределах ±18,5°. Месячные изменения склонения Луны и годичные изменения склонения Солнца не успевают произвести значительного действия на прецессионное движение. Колебание же склонения Луны с периодом 18,6 года вызывает колебания земной оси с амплитудой 9,2", называемые нутацией. Это явление открыл английский астроном Джеймс Брад-лей в 1745 году.

Имеется еще одно обстоятельство, не влияющее на склонения звезд, но тем не менее вызывающее небольшое движение точки весеннего равноденствия. Это — притяжение планет Солнечной системы.Положения Северного (вверху) и Южного (внизу) полюсов мира среди, звезд. Положения полюсов отмечены цифрами через каждую тысячу лет, начиная с 2000 года до нашей эры (—2) и кончая 23000 годом (23). Планеты слишком далеки от Земли, чтобы их действие на экваториальный пояс Земли было ощутимым. Однако вследствие наклонов планетных орбит к эклиптике возникает некоторый, хотя и очень слабый момент сил, стремящийся повернуть плоскость земной орбиты до совпадения с плоскостью орбиты данной планеты. Суммарное действие всех больших планет слегка изменяет положение эклиптики, что сказывается и на положении точек пересечения ее с экватором, то есть на положении точки весеннего равноденствия. Это дополнительное смещение, равное примерно 0,1" в год, называется прецессией от планет, тогда как основное движение есть лунно-солнечная прецессия. Суммарное действие лунно-солнечной прецессии и прецессии от планет называется общей прецессией.

КАК ИЗМЕРИТЬ ПРЕЦЕССИЮ?

Зная массы планет и элементы их орбит, можно точно вычислить значение прецессии от планет, но лунно-солнечную прецессию приходится определять из наблюдений почти тем же способом, как это впервые сделал Гиппарх,— по изменениям планет Солнечной системы.

Прецессия и нутация земной оси (масштаб нутационных колебаний для наглядности увеличен)склонении звезд. Такой способ проще и надежнее, чем нахождение положений точки весеннего равноденствия среди звезд. Однако дело осложняется тем, что все звезды имеют собственные движения, также влияющие на их склонения, и приходится тщательно исследовать и исключать эти движения из наблюдавшихся склонений звезд. Особенно трудно исключить систематические движения звезд, вызванные перемещением Солнца в пространстве и вращением Галактики.

Большую работу по точному определению значения общей прецессии выполнил в конце прошлого века американский астроном Саймон Ньюком. Полученное им значение было утверждено в 1896 году международной комиссией, хотя теперь мы знаем, что определение этой важной постоянной, произведенное почти на полвека раньше пулковским астрономом, а впоследствии директором Пулковской обсерватории О. В. Струве, точнее. Значение общей прецессии, вычисленное Нью-комом для 1900 года, равно: 50,2564" + 0,000222" Т (второй член дает годичное изменение, Т—число лет, протекших с начала 1900 года). Постоянной прецессии Ньюкома пользовались все астрономы в течение 80 лет. Лишь в 1976 году XVI съезд Международного астрономического союза в Гренобле принял новое значение для 2000 года: 50,290966" + 0,0002222" Т. Старое значение для 2000 года (50,2786") на 0,0124" меньше нового. В заключение опишем способ определения постоянной прецессии, разработанный в последние десятилетия. Мы уже задавались вопросом, как найти на небесной сфере неподвижную точку для обоснования нуль-пункта прямых восхождений. Еще в 1806 году французский астроном и математик Пьер Лаплас высказал мысль, что наименьшими, исчезающе малыми собственными движениями обладают слабые и далекие туманные пятна, видимые в телескопы во многих местах неба. Лаплас считал их большими звездными системами, удаленными от нас на огромные расстояния. Впоследствии Лаплас, пытаясь обосновать свою космогоническую гипотезу, изменил мнение о природе туманностей. Он полагал, что это — планетные системы, находящиеся в стадии формирования, то есть образования, гораздо меньшие и более близкие к нам. Теперь мы знаем, что правильно первое мнение Лапласа, но на это предположение в свое время не обратили внимания, да и не было тогда для него обоснования. Практическое осуществление идеи Лапласа — определить нуль-пункт прямых восхождений относительно внегалактических туманностей — стало возможным только после усовершенствования астрофотографии.

Внегалактические туманности — галактики — нельзя считать абсолютно неподвижными. Как следует из теории расширяющейся Вселенной, галактики удаляются от нас со скоростями, пропорциональными их расстояниям. Если принять, что поперечные линейные скорости одного порядка со скоростями удаления, то они составляют примерно 75 км/с на 1 млн. парсек, или 3, 26 млн.'световых лет. Тогда получается, что смещения далеких галактик на небесной сфере станут заметными лишь через миллионы лет. Таким образом, галактики могут служить основой инерциальной системы координат — системы, которая не имеет вращения, а обладает только поступательным прямолинейным движением («Земля и Вселенная», № 5, 1967, с. 14—24.—Ред.). Строго говоря, движение должно быть и равномерным, но мы не располагаем способом обнаружения неравномерности и потому вынуждены с ней не считаться.

Лишь в 30-х годах текущего столетия пулковские и московские астрономы подняли вопрос о привязке системы звездных положений к далеким галактикам. Предложение советских астрономов подробно обсуждалось в 1952 году на VIII съезде Международного астрономического союза в Риме, и вскоре А. Н. Дейч в Пулкове и С. Василевские на Лик-ской обсерватории в США получили многочисленные фотографии галактик и слабых звезд. Эти снимки можно было использовать в качестве «первых эпох», дающих положения звезд для некоторых исходных моментов. Повторение таких снимков через 20 и более лет послужило для определения абсолютных собственных движений звезд относительно галактик. Эти работы выполнялись в Пулкове, Москве, Ташкенте и на нескольких зарубежных обсерваториях. Установление инерциальной системы с помощью далеких галактик осложняется тем, что галактики, которые имеют достаточно светлое и четкое ядро для уверенного измерения на фотонегативах, не ярче 15-й звездной величины. Такой же примерно величины бывают и «привязанные» к ним звезды. Для практики же интересны положения ярких звезд — от 1-й до 6-й или 7-й величины, блеск которых в десятки тысяч раз превосходит звезды 15-й величины. Поэтому приходится повторно фотографировать участки неба и производить необходимую привязку часто даже в две ступени, включая промежуточные звезды примерно 10-й величины.

С момента получения фотографий «первых эпох» прошло еще недостаточно времени, чтобы в полной мере использовать преимущества нового способа определения постоянной прецессии. В будущем этот метод даст уверенное и точное обоснование инерциальной системы координат. И тогда положение точки весеннего равноденствия — нуль-пункт прямых восхождений — будет «закреплено» на небесной сфере на многие тысячелетия.

www.moscowaleks.narod.ru

Планета Земля. Движения за большой промежуток времени. Прецессия,нутация.

Подробно:

Прецессия

Кроме вращения и обращения, Земля совершает множество других перемещений, которые происходят в течение более длительного времени. Самое заметное из них — прецессия. Прецессия была открыта Гиппархом во II веке до н.э. Она представляет собой очень медленное движение земной оси вращения, которая для поддержания постоянного наклона по отношению к плоскости эклиптики меняет свое направление в космосе, описывая при этом коническую поверхность. Причиной прецессии является гравитация, которую Солнце и Луна совместно оказывают на земной экватор. И действительно, наша планета не имеет идеальной сферической формы, она слегка приплюснута с полюсо́в. Поэтому Солнце и Луна, которые не лежат на плоскости небесного экватора, стремятся выровнять на своих орбитальных плоскостях земное экваториальное вздутие. А Земля, вращаясь вокруг своей оси, подвергается этому двойному гравитационному воздействию. Сумма этих сил такова, что ось земного вращения, которая перпендикулярна экваториальной плоскости, движется в космосе, как ось у детской юлы́. Ось вращения Земли, меняя во времени свое положение относительно Земли, Луны и Солнца, описывает двойную коническую поверхность, вершиной которой является центр Земли. Приблизительно раз в 26000 лет ось возвращается в свое первоначальное положение в космосе. Последствия этого движения проявляются не сразу, однако для астрономии они очень важны.

Из-за прецессии небесный Северный полюс смещается среди созвездий, описывая замкнутую окружность приблизительно за 26000 лет

И действительно, из-за прецессии происходит медленное смещение на небесной сфере основных астрономических точек отсчета: полюсо́в, точек равноденствия и солнцестояния. Поэтому Полярная звезда, по которой сегодня мы можем определить положение небесного Северного полюса, в будущем утратит эту функцию. Северный полюс и впрямь описывает на небосводе окружность и, например, в 14000 году н.э. он будет находиться рядом со звездой Вега созвездия Лира. Кроме того, так как ось вращения перпендикулярна небесному экватору, смещение направления оси приводит к смещению в космосе плоскости экватора, но он тем не менее составляет тот же угол склонения по отношению к эклиптике.

Последствия прецессии

Точка весеннего равноденствия, определяемая пересечением небесного экватора с эклиптикой, как уже говорилось, медленно смещается вследствие прецессии равноденствия. Изменение положения точки весеннего равноденствия имеет два последствия, одно из которых связано с небесными координатами, другое — с зодиака́льными созвездиями. И действительно, ведь точка весеннего равноденствия является точкой отсчёта прямого восхождения светил в экваториальной системе координат. Её перемещение по небесной сфере связано с тем, что координаты постоянно корректируются (прямое восхождение светила постоянно увеличивается), а именно — с международной договорённостью о координатах небесных тел на фиксированную дату, например 1950 или 2000 год. Когда в античные времена определяли положение объектов на небесной сфере, точка весеннего равноденствия находилась в созвездии О́вна. Сегодня же из-за прецессии точка весеннего равноденствия находится не в О́вне, а в созвездии Рыб. Аналогично не существует более соответствия между определенными в античные времена 12 зодиака́льными знаками и соответствующими созвездиями. Если мы, например, говорим о знаке Рыб, не надо думать, что между 21 февраля и 21 марта Солнце действительно находится в созвездии Рыб. Так было давно. А сегодня — нет, потому что из-за видимой с Земли прецессии Солнца этот период времени примерно приходится на пребывание Солнца в созвездии Водолея.

Нута́ции

Прецессия земной оси происходит из-за гравитационного воздействия на Землю Солнца и Луны (так называемая лунно-солнечная прецессия). Следует учитывать, что сила притяжения этих двух небесных тел находится в тесной зависимости от их удалённости от Земли. Этот факт оказывает влияние на коническое движение, при этом нельзя упускать из вида и небольшие колебания, так называемую нута́цию.

Нутации оси вращения

На коническое прецессионное движение, которое способствует перемещению полюса эклиптики (P), накладывается колебательное движение — нута́ция (N). В результате края́ конуса становятся «волнистыми». При нута́ции полюс мира описывает среди звёзд волнообра́зную кривую. Нута́ции имеют период 18,6 лет, их максимальная амплитуда (максимальный угол) составляет около 9 угловых секунд.

Полюса тоже двигаются

Кривые линии, представленные на рисунке, представляют передвижение Северного полюса Земли в течение нескольких лет. Это «путь полюса».

Движения Земли продолжительностью в тысячелетия

Не считая описанных, Земля медленно, на протяжении тысячелетий совершает и другие перемещения. Например, из-за притяжения других тел Солнечной системы с периодичностью примерно 92 тысячи лет меняется сама форма земной орбиты, которая становится то более, то менее вытянутой.

Со временем меняется и угол наклона земной оси́. Совсем чуть-чуть, и колеблется он от 21°55' до 24°20' с периодичностью приблизительно 41 тысячу лет. Сегодня, как говорилось выше, этот угол составляет 23°27'.

Прецессии, изменение эксцентрисите́та орбиты и угла наклона земной оси влияют на климат и смену времён года, потому что изменяется освещенность земных полушарий. Между прочим, весьма вероятно, что с этими незначительными смещениями связаны ледниковые периоды, потряса́вшие когда-то нашу планету. Но в любом случае количество солнечной энергии, достигающее земной поверхности, остается примерно одинаковым; меняется только её распределение.

znaniya-sila.narod.ru

Смотрите также

..:::Новинки:::..

Windows Commander 5.11 Свежая версия.

Новая версия
IrfanView 3.75 (рус)

Обновление текстового редактора TextEd, уже 1.75a

System mechanic 3.7f
Новая версия

Обновление плагинов для WC, смотрим :-)

Весь Winamp
Посетите новый сайт.

WinRaR 3.00
Релиз уже здесь

PowerDesk 4.0 free
Просто - напросто сильный upgrade проводника.

..:::Счетчики:::..