Основные элементарные функции, их свойства и графики. Графики и свойства элементарных функций реферат

Основные элементарные функции, их свойства и графики.

Основными элементарными функциями являются: постоянная функция (константа), корень n-ой степени, степенная функция, показательная, логарифмическая функция, тригонометрические и обратные тригонометрические функции.

Постоянная функция.

Постоянная функция задается на множестве всех действительных чисел формулой , гдеC – некоторое действительное число. Постоянная функция ставит в соответствие каждому действительному значению независимой переменной x одно и то же значение зависимой переменной y – значение С. Постоянную функцию также называют константой.

Графиком постоянной функции является прямая, параллельная оси абсцисс и проходящая через точку с координатами (0,C). Для примера покажем графики постоянных функций y=5,y=-2 и , которым на рисунке, приведенном ниже, отвечают черная, красная и синяя прямые соответственно.

Свойства постоянной функции.

Область определения: все множество действительных чисел.
Постоянная функция является четной.
Область значений: множество, состоящее из единственного числа С.
Постоянная функция невозрастающая и неубывающая (на то она и постоянная).
Говорить о выпуклости и вогнутости постоянной не имеет смысла.
Асимптот нет.
Функция проходит через точку (0,C) координатной плоскости.

Корень n-ой степени.

Рассмотрим основную элементарную функцию, которая задается формулой 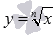, где n – натуральное число, большее единицы.

Корень n-ой степени, n - четное число.

Начнем с функции корень n-ой степени при четных значениях показателя корня n.

Для примера приведем рисунок с изображениями графиков функций и , им соответствуют черная, красная и синяя линии.

Аналогичный вид имеют графики функций корень четной степени при других значениях показателя.

Свойства функции корень n-ой степени при четных n.

Область определения: множество всех неотрицательных действительных чисел .
При x=0 функция принимает значение, равное нулю.
Эта функция общего вида (не является четной или нечетной).
Область значений функции: .
Функция при четных показателях корня возрастает на всей области определения.
Эта функция имеет выпуклость, направленную вверх, на всей области определения, точек перегиба нет.
Асимптот нет.
График функции корень n-ой степени при четных n проходит через точки (0,0) и(1,1).

Корень n-ой степени, n - нечетное число.

Функция корень n-ой степени с нечетным показателем корня n определена на всем множестве действительных чисел. Для примера приведем графики функций и , им соответствуют черная, красная и синяя кривые.

При других нечетных значениях показателя корня графики функции будут иметь схожий вид.

Свойства функции корень n-ой степени при нечетных n.

Область определения: множество всех действительных чисел.
Эта функция нечетная.
Область значений функции: множество всех действительных чисел.
Функция при нечетных показателях корня возрастает на всей области определения.
Эта функция вогнутая на промежутке и выпуклая на промежутке , точка с координатами (0,0) – точка перегиба.
Асимптот нет.
График функции корень n-ой степени при нечетных n проходит через точки (-1,-1),(0,0) и (1,1).

studfiles.net

Основные элементарные функции, их свойства и графики

Национальный научно-исследовательский университет

-ИрГТУ-

Кафедра прикладной геологии

Реферат по высшей математике

На тему: «Основные элементарные функции,

их свойства и графики»

Выполнил:

Проверил:

преподаватель

Коваленко Е.В.

Иркутск 2010

Содержание:

Показательные функции:- 3 -

Степенные функции:- 3 -

Логарифмические функции:- 3 -

Тригонометрические функции:- 3 -

Обратные тригонометрические функции:- 3 -

Список использованной литературы:- 3 -

Список рисунков:- 3 -

Показательные функции:

Определение. Функция, заданная формулой у=ах (где а>0, а≠1), называется показательной функцией с основанием а.

Сформулируем основные свойства показательной функции :

1. Область определения — множество (R) всех действительных чисел.

2. Область значений — множество (R+) всех положительных действительных чисел.

3. При а > 1 функция возрастает на всей числовой прямой; при 0<а<1 функция убывает.

4. Является функцией общего вида.

Рис. 1 График функции

, на интервале xÎ [-3;3]

Рис. 2 График функции

, на интервале xÎ [-3;3]

Степенные функции:

Функция вида у(х)=хn , где n – число ÎR, называется степенной функцией. Число n может принимать раличные значения: как целые, так и дробные, как четные, так и нечетные. В зависимости от этого, степенная функция будет иметь разный вид. Рассмотрим частные случаи, которые являются степенными функциями и отражают основные свойства данного вида кривых в следующем порядке: степенная функция у=х² (функция с четным показателем степени – парабола), степенная функция у=х³ (функция с нечетным показателем степени – кубическая парабола) и функция у=√х (х в степени ½) (функция с дробным показателем степени), функция с отрицательным целым показателем (гипербола).

Степенная функция у=х²

1. D(x)=R – функция определена на все числовой оси;

2. E(y)=[0;∞) - функция принимает положительные значения на всей области определения;

3. При х=0 у=0 - функция проходит через начало координат O(0;0).

4. Функция убывает на промежутке (-∞;0] и возрастает на промежутке [0;∞).

5. Функция является четной (симметрична относительно оси Оу).

В зависимости от числового множителя, стоящего перед х², функция может быть уже/шире и направлена вверх/вниз.

Рис. 3 График функции

, на интервале xÎ [-3;3]

Степенная функция у=х³

1. График функции у=х³ называется кубической параболой. Степенная функция у=х³ обладает следующими свойствами:

2. D(x)=R – функция определена на все числовой оси;

3. E(y)=(-∞;∞) – функция принимает все значения на своей области определения;

4. При х=0 у=0 – функция проходит через начало координат O(0;0).

5. Функция возрастает на всей области определения.

6. Функция является нечетной (симметрична относительно начала координат).

Рис. 4 График функции

, на интервале xÎ [-3;3]

В зависимости от числового множителя, стоящего перед х³, функция может быть крутой/пологой и возрастать/убывать.

Степенная функция с целым отрицательным показателем:

Если показатель степени n является нечетным, то график такой степенной функции называется гиперболой. Степенная функция с целым отрицательным показателем степени обладает следующими свойствами:

1. D(x)=(-∞;0)U(0;∞) для любого n;

2. E(y)=(-∞;0)U(0;∞), если n – нечетное число; E(y)=(0;∞), если n – четное число;

3. Функция убывает на всей области определения, если n – нечетное число; функция возрастает на промежутке (-∞;0) и убывает на промежутке (0;∞), если n – четное число.

4. Функция является нечетной (симметрична относительно начала координат), если n – нечетное число; функция является четной, если n – четное число.

5. Функция проходит через точки (1;1) и (-1;-1), если n – нечетное число и через точки (1;1) и (-1;1), если n – четное число.

Рис. 5 График функции

, на интервале xÎ [-3;3]

Степенная функция с дробным показателем

Степенная функция с дробным показателем вида (картинка) имеет график функции, изображенный на рисунке. Степенная функция с дробным показателем степени обладает следующими свойствами: (картинка)

1. D(x) ÎR, если n – нечетное число и D(x)=[0;∞), если n – четное число ;

2. E(y) Î (-∞;0)U(0;∞), если n – нечетное число; E(y)=[0;∞), если n – четное число;

3. Функция возрастает на всей области определения для любого числа n.

4. Функция проходит через начало координат в любом случае.

Рис. 6 График функции

, на интервале xÎ [0;3]

Рис. 7 График функции

, на интервале xÎ [0;5]

Рис. 8 График функции

, на интервале xÎ [-3;3]

Логарифмические функции:

Логарифмическая функция у = loga x обладает следующими свойствами :

1. Область определения D(x)Î (0; + ∞).

2. Область значений E(y) Î ( - ∞; + ∞)

3. Функция ни четная, ни нечетная (общего вида).

4. Функция возрастает на промежутке (0; + ∞) при a > 1, убывает на (0; + ∞) при 0 < а < 1.

График функции у = loga x может быть получен из графика функции у = ах с помощью преобразования симметрии относительно прямой у = х. На рисунке 9 построен график логарифмической функции для а > 1, а на рисунке 10 - для 0 < a < 1.

Рис. 9 График функции

; на интервале xÎ [0;5]

Рис. 10 График функции

; на интервале xÎ [0;5]

Тригонометрические функции:

Функции y = sin х, у = cos х, у = tg х, у = ctg х называют тригонометрическими функциями.

Функции у = sin х, у = tg х, у = ctg х нечетные, а функция у = соs х четная.

Функция y = sin (х).

1. Область определения D(x) ÎR.

2. Область значений E(y) Î [ - 1; 1].

3. Функция периодическая; основной период равен 2π.

4. Функция нечетная .

5. Функция возрастает на промежутках [ -π/2 + 2πn; π/2 + 2πn] и убывает на промежутках [ π/2 + 2πn; 3π/2 + 2πn], n Î Z.

График функции у = sin (х) изображен на рисунке 11.

Рис. 11 График функции

; на интервале xÎ [-2

]

Функция y = cos(х).

1. Область определения D(x) ÎR.

2. Область значений E(y) Î [ - 1; 1].

3. Функция периодическая с основным периодом 2π.

4. Функция четная.

5. Функция убывает на промежутках [2πn; π+ 2πn] и возрастает на промежутках [-π+ 2πn; 2πn], nπZ.

График функции у = соs (х) изображен на рисунке 12.

Рис. 12 График функции

; на интервале xÎ [-2

]

Функция y = tg х.

1. Область определения: D(x) Ï π/2 + πk, kÎZ.

2. Область значений E(y) Î (- ∞; + ∞)

3. π- основной период функции.

4. Функция нечетная.

5. Функция возрастает на промежутках ( -π/2 +πn;π/2 +πn).

График функции у = tg х изображен на рисунке 13.

Рис. 13 График функции

; на интервале xÎ (-

;

)

mirznanii.com

Реферат Элементарные функции

скачать

Реферат на тему:

План:

1 Элементарные функции по Лиувиллю
2 Дифференцирование элементарных функций
3 Интегрирование элементарных функций
- 3.1 Интегрирование функций вида p(x)eq(x)
- 3.2 Интегрирование алгебраических функций
4 Вычисление пределов

Введение

Элементарные функции — функции, которые можно получить с помощью конечного числа арифметических действий и композиций из следующих основных элементарных функций:

многочлен,
рациональная,
степенная,
показательная и логарифмическая,
тригонометрические и обратные тригонометрические.

Каждую элементарную функцию можно задать формулой, то есть набором конечного числа символов, соответствующих используемым операциям. Все элементарные функции непрерывны на своей области определения. Иногда к основным элементарным функциям относят также гиперболические и обратные гиперболические функции, хотя они могут быть выражены через перечисленные выше основные элементарные функции.

Элементарные функции разделяются на алгебраические и трансцендентные.

1. Элементарные функции по Лиувиллю

Рассматривая функции комплексного переменного, Лиувилль определил элементарные функции несколько шире. Элементарная функция y переменной x — аналитическая функция, которая может быть представлена как алгебраическая функция $y=\phi(x,z_1,\dots z_r)$ от x и функций $z_1(x), \dots z_r(x)$ , причём z1 является логарифмом или экспонентой от некоторой алгебраической функции g1 от x, z2 является логарифмом или экспонентой от некоторой алгебраической функции g2 от x и z1(x) и так далее.

Например, y = sin(x) — элементарная функция в этом смысле, поскольку она является алгебраической функцией eix. Функция $y=e^{e^x}$ тоже является элементарной, поскольку её можно представить в виде:

y = z2, где $z_2=e^{z_1}, \quad z_1=e^{x}$ .

Не ограничивая общности рассмотрения, можно считать функции $z_1, \dots, z_r$ алгебраически независимы, то есть если алгебраическое уравнение $\psi(x,z_1(x), \dots, z_r(x))=0$ выполняется для всех x, то все коэффициенты полинома $\psi(X,Z_1, \dots Z_r)$ равны нулю.

2. Дифференцирование элементарных функций

Элементарные функции бесконечно дифференцируемы всюду, где они определены. При этом производная элементарной функции всегда является элементарной функцией и может быть найдена за конечное число действий. Именно, по правилу дифференцирования сложной функции

$y'(x)=\frac{d}{dx}\phi(x,z_1, \dots, z_r)=\frac{\partial \phi}{\partial x} +\sum \limits_{i=1}^r\frac{\partial \phi}{\partial z_i}\frac{dz_i}{dx},$

где z1'(z) равно или g1' / g1 или z1g1' в зависимости от того, логарифм ли z1 или экспонента и т. д. На практике удобно использовать таблицу производных.

3. Интегрирование элементарных функций

Интеграл элементарной функции не всегда сам является элементарной функцией. Наиболее распространённые функции, интегралы которых найдены, собраны в таблице интегралов. В общем случае имеет место теорема:

Теорема Лиувилля. Если интеграл от элементарной функции $y=\phi(x,z_1, \dots z_r)$ сам является элементарной функцией, то он представим в виде

$\int \phi(x,z_1(x), \dots, z_r(x))\,dx= \sum \limits_i A_i \ln (\psi_i(x,z_1, \dots z_r)) + \psi_0(x,z_1, \dots, z_r) + C,$

где Ai — некоторые комплексные числа, а ψi — алгебраические функции своих аргументов.

Доказательство этой теоремы Лиувилль основал на следующем принципе. Если интеграл от y берётся в элементарных функциях, то верно

$\int \phi(x, z_1(x), \dots z_r(x))\,dx =\psi(x, z_1(x), \dots z_s(x)) + \operatorname{const}$

где ψ — алгебраическая функция, zr + 1 — логарифм или экспонента алгебраической функции $x,z_1, \dots z_r$ и т. д. Функции $z_1, \dots z_s$ являются алгебраически независимыми и удовлетворяют некоторой системе дифференциальных уравнений вида

$z_1'=\rho_1(x,z_1, \dots, z_s), \dots$

где ρi — алгебраические функции своих аргументов. Если $z_1=z_1(x,C), \dots$ — семейство решений этой системы, то

$\int \phi(x, z_1(x,C), \dots)\,dx = \psi(x, z_1(x, C), \dots z_s(x, C)) +\operatorname{const}$

откуда

$\psi(x, z_1(x), \dots) = \psi(x, z_1(x, C), \dots z_s(x, C)) +f(C)$

Для некоторых классов интегралов эта теорема позволяет весьма просто исследовать разрешимость в элементарных функциях задачи об интегрировании.

3.1. Интегрирование функций вида p(x)eq(x)

Следствие теоремы Лиувилля (См. Ритт, с. 47 и сл.). Если интеграл

$\int p(x)e^{q(x)}\,dx,$

где p,q — полиномы, берётся в элементарных функциях, то

$\int p(x)e^{q(x)}\,dx= r(x) e^{q(x)}$ ,

где r(x) — тоже некоторый полином, удовлетворяющий дифференциальному уравнению

r' + q'(x)r = p(x)

Пример. В частности, интеграл

$\int e^{x^2}\,dx$

не берётся, поскольку подстановка

$r=Ax^n+\dots \quad (A\not =0)$

в уравнение

r' + 2xr = 1

даёт A = 0. Интеграл же

$\int xe^{x^2}\,dx$

берётся, поскольку

r' + 2xr = x

имеет решение r = 1 / 2. При этом, конечно,

$\int xe^{x^2}\,dx=\frac{e^{x^2}}{2}+ \operatorname{const}$

Доказательство следствия. В силу теоремы Лиувилля

$\int p(x)e^{q(x)}\,dx= \psi_0(x, e^{q(x)}) + \sum A_i\ln \psi_i(x,e^{q(x)})+ \operatorname{const}$

Тогда в силу принципа Лиувилля при произвольной константе C верно

$\int p(x)C e^{q(x)}\,dx= \psi_0(x, Ce^{q(x)}) +\sum A_i\ln \psi_i(x,Ce^{q(x)})+ f(C)$

Дифференцируя по C и полагая C = 1, видим, что интеграл выражается алгебраически через x,eq(x), то есть

$\int p(x)e^{q(x)}\,dx= \psi(x,e^{q(x)}).$

Опять применяя принцип Лиувилля, имеем

Cψ(x,eq(x)) = ψ(x,Ceq(x)) + f(C).

Дифференцируя по C и полагая C = 1, имеем

$\psi(x,z) = z \frac{\partial \psi(x,z)}{\partial z} + B \quad (B=\operatorname{const})$

при z = eq(x), а следовательно, в силу алгебраической независимости x,eq(x), при всех x,z. Поэтому

ψ(x,z) = − B + zr(x),

где r — некоторая алгебраическая функция x. Таким образом,

$\int p(x)e^{q(x)}\,dx = r(x)e^{q(x)} + \operatorname{const},$

Коль скоро сам интеграл заведомо является целой функций x, то r — полином. Следствие доказано.

3.2. Интегрирование алгебраических функций

Наиболее сложным оказался вопрос об интегрировании в элементарных функциях функций алгебраических, то есть о взятии абелевых интегралов, которому посвящены обширные исследования Вейерштрасса, Пташицкого[1] и Риша[2].

Теорема Лиувилля является основой для создания алгоритмов символьного интегрирования элементарных функций, реализуемых, напр., в Maple.

См. также: Список интегралов элементарных функций

4. Вычисление пределов

Теория Лиувилля не распространяется на вычисление пределов. Неизвестно, существует ли алгоритм, который по заданной элементарной формулой последовательности даёт ответ, имеет ли она предел или нет. Например, открыт вопрос о том, сходится ли последовательность $\frac{1}{n^3 \sin n}$ .[3]

Примечания

Encyklopädie der mathematischen Wissenschaften mit Einschluss ihrer Anwendungen. Art. 2 B 2 (W. Wirtinger, 1901 г.)
Дэвенпорт Дж. Интегрирование алгебраических функций. Гл. 4. М., «Мир», 1985
Q&A - www.mccme.ru/ask/qa/pi_irr.html

Литература

J. Liouville. Mémoire sur l’intégration d’une classe de fonctions transcendantes - dz-srv1.sub.uni-goettingen.de/sub/digbib/loader?ht=VIEW&did=D267366 // J. Reine Angew. Math. Bd. 13, p. 93-118. (1835)
J.F. Ritt. Integration in Finite Terms. N.-Y., 1949// http://lib.homelinux.org - lib.homelinux.org
А. Г. Хованский. Топологическая теория Галуа: разрешимость и неразрешимость уравнений в конечном виде - www.mccme.ru/free-books/hov-galois/hov-galois.html Гл. 1. M, 2007

wreferat.baza-referat.ru

Основные элементарные функции, их свойства и графики

Национальный научно-исследовательский университет

-ИрГТУ-

Кафедра прикладной геологии

Реферат по высшей математике

На тему: «Основные элементарные функции,

их свойства и графики»

Выполнил:

Проверил:

преподаватель

Коваленко Е.В.

Иркутск 2010

Содержание:

Показательные функции:

Определение. Функция, заданная формулой у=ах (где а>0, а≠1), называется показательной функцией с основанием а.

Сформулируем основные свойства показательной функции :

Область определения — множество (R) всех действительных чисел.
Область значений — множество (R+) всех положительных действительных чисел.
При а > 1 функция возрастает на всей числовой прямой; при 0
Является функцией общего вида.

Рис. 1 График функции , на интервале x  [-3;3]

Рис. 2 График функции , на интервале x  [-3;3]

Степенные функции:

Функция вида у(х)=хn, где n – число  R, называется степенной функцией. Число n может принимать раличные значения: как целые, так и дробные, как четные, так и нечетные. В зависимости от этого, степенная функция будет иметь разный вид. Рассмотрим частные случаи, которые являются степенными функциями и отражают основные свойства данного вида кривых в следующем порядке: степенная функция у=х² (функция с четным показателем степени – парабола), степенная функция у=х³ (функция с нечетным показателем степени – кубическая парабола) и функция у=√х (х в степени ½) (функция с дробным показателем степени), функция с отрицательным целым показателем (гипербола).

Степенная функция у=х²

D(x)=R – функция определена на все числовой оси;
E(y)=[0;∞) - функция принимает положительные значения на всей области определения;
При х=0 у=0 - функция проходит через начало координат O(0;0).
Функция убывает на промежутке (-∞;0] и возрастает на промежутке [0;∞).
Функция является четной (симметрична относительно оси Оу).

В зависимости от числового множителя, стоящего перед х², функция может быть уже/шире и направлена вверх/вниз.

Рис. 3 График функции , на интервале x  [-3;3]

Степенная функция у=х³

График функции у=х³ называется кубической параболой. Степенная функция у=х³ обладает следующими свойствами:
D(x)=R – функция определена на все числовой оси;
E(y)=(-∞;∞) – функция принимает все значения на своей области определения;
При х=0 у=0 – функция проходит через начало координат O(0;0).
Функция возрастает на всей области определения.
Функция является нечетной (симметрична относительно начала координат).

Рис. 4 График функции , на интервале x  [-3;3]

Степенная функция с целым отрицательным показателем:

D(x)=(-∞;0)U(0;∞) для любого n;
E(y)=(-∞;0)U(0;∞), если n – нечетное число; E(y)=(0;∞), если n – четное число;
Функция убывает на всей области определения, если n – нечетное число; функция возрастает на промежутке (-∞;0) и убывает на промежутке (0;∞), если n – четное число.
Функция является нечетной (симметрична относительно начала координат), если n – нечетное число; функция является четной, если n – четное число.
Функция проходит через точки (1;1) и (-1;-1), если n – нечетное число и через точки (1;1) и (-1;1), если n – четное число.

Рис. 5 График функции , на интервале x  [-3;3]

Степенная функция с дробным показателем

D(x)  R, если n – нечетное число и D(x)=[0;∞), если n – четное число ;
E(y)  (-∞;0)U(0;∞), если n – нечетное число; E(y)=[0;∞), если n – четное число;
Функция возрастает на всей области определения для любого числа n.
Функция проходит через начало координат в любом случае.

Рис. 6 График функции , на интервале x  [0;3]

Рис. 7 График функции , на интервале x  [0;5]

Рис. 8 График функции , на интервале x  [-3;3]

Логарифмические функции:

Логарифмическая функция у = loga x обладает следующими свойствами :

Область определения D(x)  (0; + ∞).
Область значений E(y)  ( - ∞; + ∞)
Функция ни четная, ни нечетная (общего вида).
Функция возрастает на промежутке (0; + ∞) при a > 1, убывает на (0; + ∞) при 0

Рис. 9 График функции ; на интервале x  [0;5]

Рис. 10 График функции ; на интервале x  [0;5]

Тригонометрические функции:

Функции y = sin х, у = cos х, у = tg х, у = ctg х называют тригонометрическими функциями.

Функции у = sin х, у = tg х, у = ctg х нечетные, а функция у = соs х четная.

Функция y = sin (х).

Область определения D(x)  R.
Область значений E(y)  [ - 1; 1].
Функция периодическая; основной период равен 2π.
Функция нечетная .
Функция возрастает на промежутках [ -π/2 + 2πn; π/2 + 2πn] и убывает на промежутках [ π/2 + 2πn; 3π/2 + 2πn], n  Z.

График функции у = sin (х) изображен на рисунке 11.

Рис. 11 График функции ; на интервале x  [-2;2]

Функция y = cos(х).

Область определения D(x)  R.
Область значений E(y)  [ - 1; 1].
Функция периодическая с основным периодом 2π.
Функция четная.
Функция убывает на промежутках [2πn; π+ 2πn] и возрастает на промежутках [-π+ 2πn; 2πn], nπZ.

График функции у = соs (х) изображен на рисунке 12.

Рис. 12 График функции ; на интервале x  [-2;2]

Функция y = tg х.

Область определения: D(x)  π/2 + πk, kZ.
Область значений E(y)  (- ∞; + ∞)
π- основной период функции.
Функция нечетная.
Функция возрастает на промежутках ( -π/2 +πn;π/2 +πn).

График функции у = tg х изображен на рисунке 13.

Рис. 13 График функции ; на интервале x  (- ;)

Функция y = ctg х.

Область определения функции: D(x)  xπ/2 +πk, kZ.
Область значений функции E(y)  (- ∞; + ∞).
Функция периодическая с основным периодом π.
Функция нечетная.
Функция у = ctg х убывает на промежутках (πn;π+πn).

График функции у = ctg х изображен на рисунке 14.

Рис. 14 График функции ; на интервале x  (-;)

Обратные тригонометрические функции:

Функции y = arcsin (х), у = arccos (х), у = arctg (х), у = arcctg (х) называют обратными тригонометрическими функциями.

Функция y = arcsin (x):

Свойства функции y = arcsin (x):

1. Область определения D(x)[−1;1]

2. Область значения E(y) [−π/2;π/2]

3. y=arcsin(x)- непрерывная строговозрастающая функция на D

5. График y = arcsin(x) симметричен графику y = sin(x) относительно линии y=x

6. y=arcsin(x) нечетная функция т.е. ∀x∈[−1;1] arcsin(−x)=−arcsin(х)

График функции y = arcsin (x) изображен на рисунке 15.

Рис. 15 График функции ; на интервале x  [- ;]

Функция y = arccos (x):

Свойства функции y = arccos (x):

1. Область определения D(x)[−1;1]

2. Область значения E(y) [0;π]

3. y=arccos(x)- непрерывная строговозрастающая функция на D

5. График y = arccos(x) симметричен графику y = cos(x) относительно линии y=x

6. y=arccos(x) функция общего вида

График функции y = arccos (x) изображен на рисунке 16.

Рис. 16 График функции ; на интервале x  [- ;]

Функция y = arctg (x):

Свойства функции y = arctg (x):

Область определения D(x)(- ∞;+∞)
Область значения E(y) [−π/2;π/2]
y=arctg (x)- непрерывная строговозрастающая функция на D
График y = arctg(x) симметричен графику y = tg(x) относительно линии y=x
y=arctg (x) нечетная функция.

График функции y = arctg (x) изображен на рисунке 17.

Рис. 17 График функции ; на интервале x  [- 5; 5]

Функция y = arcсtg (x):

Свойства функции y = arcсtg (x):

Область определения D(x)(- ∞;+∞)
Область значения E(y) [0 ; π]
y=arctg (x)- непрерывная строгоубывающая функция на D
График y = arcсtg(x) симметричен графику y = сtg(x) относительно линии y=x
y=arcctg (x) функция общего вида.

График функции y = arcctg (x) изображен на рисунке 18.

Рис. 18 График функции .

Список использованной литературы:

Алгебра и начала анализа, учебник для 10 класса общеобразовательных учреждений ; С.М. Никольский; М. Просвещение, 2001
Конспект лекции по высшей математике.

Некоторые изображения взяты из сети Интернет, графики функции построены в программе Microsoft Office Exel.

Список рисунков:

globuss24.ru

Основные элементарные функции, их свойства и графики. Графики и свойства элементарных функций реферат

Основные элементарные функции, их свойства и графики.

Постоянная функция.

Корень n-ой степени.

Корень n-ой степени, n - четное число.

Корень n-ой степени, n - нечетное число.

Основные элементарные функции, их свойства и графики

Реферат Элементарные функции

План:

Введение

1. Элементарные функции по Лиувиллю

2. Дифференцирование элементарных функций

3. Интегрирование элементарных функций

3.1. Интегрирование функций вида p(x)eq(x)

3.2. Интегрирование алгебраических функций

4. Вычисление пределов

Примечания

Литература

Основные элементарные функции, их свойства и графики

Смотрите также