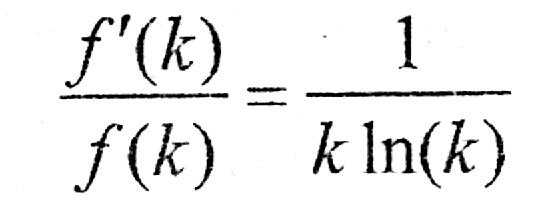
САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ имени Н.Г. Чернышевского
на тему: «Энтропия термодинамическая и информационная»
Выполнил: студент 521 группы физического факультета
Маляев Владимир Сергеевич
-САРАТОВ 2001-
План реферата:
Энтропия – энциклопедическое понятие 3
Термодинамическое описание энтропии 3
Энтропия и общество 5
Информационный аспект 7
Смысловая информация и бессмысленная 8
Краткий вывод 9
Список использованной литературы 10
Чтобы каким-либо образом описать упорядоченность любой системы, физикам необходимо было ввести величину, функцию состояния системы, которая бы описывала ее упорядоченность, степень и параметры порядка, самоорганизованность системы.
От греческого entropia — поворот, превращение. Понятие энтропии впервые было введено в термодинамике для определения меры необратимого рассеяния энергии. Энтропия широко применяется и в других областях науки: в статистической физике как мера вероятности осуществления какого — либо макроскопического состояния; в теории информации — мера неопределенности какого-либо опыта (испытания), который может иметь разные исходы. Все эти трактовки энтропии имеют глубокую внутреннюю связь.
Энтропия — это функция состояния, то есть любому состоянию можно сопоставить вполне определенное (с точность до константы — эта неопределенность убирается по договоренности, что при абсолютном нуле энтропия тоже равна нулю) значение энтропии.
Для обратимых (равновесных) процессов выполняется следующее математическое равенство (следствие так называемого равенства Клаузиуса)dQ — подведенная теплота,T — температура, A и B — состояния, SA и SB — энтропия, соответствующая этим состояниям (здесь рассматривается процесс перехода из состояния А в состояние В)
Для необратимых процессов выполняется неравенство, вытекающее из так называемого неравенства Клаузиуса
Поэтому энтропия адиабатически изолированной (нет подвода или отвода тепла) системы при необратимых процессах может только возрастать.Используя понятие энтропии Клаузиус (1876) дал наиболее общую формулировку 2-го начала термодинамики: при реальных (необратимых) адиабатических процессах энтропия возрастает, достигая максимального значения в состоянии равновесия (2-ое начало термодинамики не является абсолютным, оно нарушается при флуктуациях).
Значит функция состояния, дифференциалом которой является dQ/T, называется энтропией и обозначается обычно S.
.
Отметим, что справедливость этого выражения для полного дифференциала энтропии доказана выше лишь для обратимых процессов идеального газа.
Так же энтропия S определятся логарифмом числа микросостояний, посредством которых реализуется рассматриваемое макросостояние, т.е.
, (формула Больцмана)
где k – постоянная Больцмана, Г — число микросостояний.
Энтропия системы в каком-либо обратимом процессе изменяется под влиянием внешних условий, воздействующих на систему. Механизм воздействия внешних условий на энтропию состоит в следующем. Внешние условия определяют микросостояния, доступные системе, и их число. В пределах доступных для нее микросостояний система достигает равновесного состояния, а энтропия – соответствующего значения. В результате значение энтропии следует за изменением внешних условий, достигая максимального значения, совместимого с внешними условиями.
Чем более сильно упорядочена система, тем меньше число микросостояний, которыми осуществляется макросостояние.
Допустим, например, что все атомы закреплены в определенных местах. Тогда существует только одно микросостояние, а соответствующая ему энтропия равна нулю. Чем больше число микросостояний, тем больше разупорядочена система. Поэтому можно сказать, что энтропия является мерой упорядоченности системы. В состоянии равновесия энтропия достигает своего максимального значения, поскольку равновесие есть наиболее вероятное состояние, совместимое с фиксированными условиями и, следовательно, является макросостоянием, осуществляемым посредством максимального числа микросостояний. Очевидно, что система, предоставленная самой себе, движется в направлении равновесного состояния, т.е. энтропия должна возрастать в предоставленной самой себе системе.
Энтропия определяется логарифмом числа микросостояний, посредством которых реализуется макросостояние. В состоянии равновесия энтропия достигает максимального значения, поскольку в равновесном состоянии термодинамическая вероятность максимальна. Отсюда следует, что энтропия изолированной предоставленной самой себе системы должна возрастать до тех пор, пока не достигнет максимального значения, совместимого с условиями.
Следует заметить, что при адиабатическом обратимом процессе энтропия не изменяется, так как при адиабатическом расширении газа за счет увеличения объема энтропия увеличивается, однако за счет уменьшения температуры, которое при этом происходит, она уменьшается и эти две тенденции полностью компенсируют друг друга.
Неубывание энтропии в изолированной системе обусловливается в конечном счете равновероятностью всех ее микроскопических состояний, приводящей систему в наиболее вероятное макросостояние.
В процессах изолированной системы энтропия не убывает, в то время как в процессах неизолированных систем энтропия может и возрастать, и убывать, и оставаться неизменной в зависимости от характера процесса.
Так же отметим изменение энтропии в необратимых процессах. Вычисление основывается на том, что энтропия является функцией состояния. Если система перешла из одного состояния в другое посредством необратимого процесса, то логично мысленно перевести систему из первого состояния во второе с помощью некоторого обратимого процесса и рассчитать происходящее при этом изменение энтропии. Оно равно изменению энтропии при необратимом процессе.
Рассмотрим роль энтропии в производстве работы: принцип Кельвина запрещает циклический процесс, результатом которого было бы превращение нацело некоторого количества теплоты в работу в результате контакта с одним тепловым резервуаром. Формула для к.п.д. цикла Карно показывает, что взятое от нагревателя количество теплоты лишь частично может быть превращено в работу, причем часть теплоты, превращаемая в работу, тем больше, чем меньше температура холодильника. Физической причиной этого являются требования второго начала термодинамики. Поскольку энтропия при любых процессах в замкнутых системах не убывает, некоторое количество теплоты не может нацело превратиться в работу потому, что это означало бы исчезновение соответствующей энтропии, что противоречит второму началу термодинамики.
При совершении работы в холодильник должна быть передана по крайней мере такая же энтропия, какая была взята от нагревателя. Максимальный к.п.д. достигается в обратимой машине, поскольку в этом случае холодильнику передается минимально возможная энтропия.
Теперь рассмотрим другое приложение понятия энтропия:
Давно было замечено, что в одну и ту же реку дважды войти нельзя. Мир вокруг нас меняется, наше общество меняется, и мы сами, члены общества, только стареем. Изменения необратимы.
Энтропия первоначально была введена для объяснения закономерностей работы тепловой машины. В узком смысле энтропия характеризует равновесное состояние замкнутой системы из большого числа частиц.
В обычном понимании равновесие в системе означает просто хаос. Для человека максимум энтропии — это разрушение. Любое разрушение увеличивает энтропию.
Энтропия замкнутой системы необратима. Но в природе полностью замкнутых систем не существует. А для открытых неравновесных систем точного определения энтропии пока не известно. Измерить энтропию нельзя. Из строгих физических законов она не выводится. Энтропия вводится в термодинамике для характеристики необратимости протекающих в газах процессов.
Многие ученые не считают феноменологические законы термодинамики законами природы, а рассматривают их как частный случай при работе с газом с помощью тепловой машины. Поэтому не рекомендуются расширенная трактовка энтропии в физике.
С другой стороны необратимость протекающих физических процессов и самой нашей жизни – это факт. С этой позиции вполне оправдано использование понятия энтропии в нефизических дисциплинах для характеристики состояния системы.
Все природные системы, включая человеческий организм и человеческие сообщества, не являются замкнутыми. Открытость системы позволяет локальным образом уменьшать энтропию за счет обмена энергией с окружающей средой, что приводит к упорядочению и усложнению структуры системы.
Человеческие сообщества в любом виде, от племен и групп до народов и социальных обществ, также являются системами. Каждое человеческое сообщество имеет свои законы и структуру взаимодействий. Будем говорить об обществе в целом, ограничивая его рамками государств.
Любое общество как система старается сохранить себя в окружающем мире. Для этого существуют государственные, общественные, социальные и другие институты. Применение энтропии для характеристики общества позволяет установить некоторые приблизительные рамки, в пределах которых общество может успешно развиваться или, наоборот, деградировать.
В настоящее время существует множество параметров, характеризующих то или иное общество. Но большинство из этих параметров, в конечном счете, сводится к двум видам: параметры, характеризующие открытое демократическое общество, и параметры, описывающие тоталитарные системы.
Почему западные государства достигли такого впечатляющего прогресса в экономике и государственном устройстве и существенно опережают в своем развитии другие общественные системы? Западное общество характеризуется большей степенью открытости. Более открытая система, с одной стороны, впускает в себя больше энергии из внешнего мира и дает больше степеней свободы своим элементам, с другой стороны – позволяет увеличить отток «недоброкачественной» энергии. Таким образом, энтропия системы уменьшается. При этом усложняется структура системы, что в западном обществе мы и наблюдаем.
В более замкнутой общественной системе имеют место обратные процессы. Энтропия увеличивается. Структура общества упрощается. Ярким примером такой системы служит Северная Корея. Структура общества упростилась до трех основных элементов – партийная элита, армия и все остальные.
Таким образом, можно сделать вывод, что для успешного развития общества необходимо соблюдение некоторых условий. Главным из таких условий является степень свободы элементов общества, т.е. людей. Степень свободы человека можно определять в терминах прав человека, политических свобод, экономических возможностей. Суть от этого не меняется. Человек должен иметь право на свободу выбора целей и путей их достижения.
Если право выбора человека слишком ограничивается, то в обществе начинаются застойные процессы, и оно постепенно приходит в упадок. Как пример можно привести Советский Союз. Выбор человека ограничивался идеологическими установками и партийной принадлежностью. Добиться успеха, сделать карьеру вне партии было сложно. В конце концов, осталась одна возможность продвижения: школа, институт комсомол, партия. Партийная принадлежность была необходима для достижения успеха в любой сфере деятельности.
Такой вариант общественных отношений, в конечном счете, привел к упрощению структуры общества и последующему упадку. Открытость общества не является панацеей от всех бед, но создает предпосылки для дальнейшего прогресса.
Демократия — не лучшая система управления. Но, по — видимому, это одна из необходимых степеней свободы. При детальном исследовании можно вычислить необходимое для развития количество степеней свободы личности. Перебор также не желателен. В этом случае отдельные части общества получают слишком большую независимость, что может привести к распаду целого на отдельные независимые составляющие.
Поэтому на Западе наблюдается такое огромное количество норм и правил, регулирующих все сферы жизни человека. Большое количество норм и законов необходимо для регулирования сложной структуры общества и сохранения его целостности.
Не следует также путать экономическую и военную мощь государства с общественными институтами. Замкнутые общества могут иметь оболочку в виде мощных и сильных государств. Советский Союз тому пример. Государство является вторичным по отношению к обществу. Государства могут исчезать, но люди на территории остаются, и, следовательно, остается общество, которое в отсутствии государства может получить новый импульс к развитию. Если же распадается общество, то государство исчезает навсегда. В России государственное устройство неоднократно менялось, но общество, видоизменяясь, не распадалось.
При использовании понятия энтропии нельзя обойтись без закона сохранения. К сожалению, он гласит, что если энтропия где-то убывает, то где-то она прибывает. Прогресс человечества в целом, и общественных институтов — в частности, приводит к уменьшению энтропии системы. Значит, энтропия окружающей человека среды увеличивается. Это приводит к гибели природы и экологическим катастрофам.
На земле кроме человека есть и другая жизнь. Реакция живой природы на разрушающие действия человеческой системы может быть многообразной: от новых болезней и эпидемий до мутантов и планетарных катастроф.
Теперь можно разобрать энтропию в информационном аспекте.
При подходе к сложным системам используются законы статистической физики.
В этой области физики предпринимается, в частности, попытка вывести феноменологические макроскопические законы термодинамики из микроскопической теории. Такой микроскопической теорией может быть ньютоновская механика отдельных частиц газа или квантовая механика. Используя соответствующие статистические средние, мы получаем возможность вывести макроскопические величины из микроскопических законов. Центральным понятием и в этом случае является энтропия S. Согласно Больцману, она связана с числом W различных микроскопических состояний, порождающих одно и то же макроскопическое состояние системы соотношением
Решающее значение имеет так и не получивший убедительного ответа вопрос о том, почему макроскопические явления необратимы, хотя все фундаментальные законы обратимы. Например, если у нас есть сосуд с молекулами газа и мы откроем клапан, чтобы газ мог попасть во второй сосуд, то оба сосуда окажутся заполнены газом более или менее равномерно. Однако обратный процесс в природе никогда не наблюдается: никому не доводилось видеть, чтобы второй сосуд самопроизвольно опустел и все молекулы собрались в первом сосуде.
Несмотря на трудности, связанные со строгим обоснованием необратимости, статистическая физика позволяет нам объяснить ряд явлений неравновесной термодинамики, такие, как релаксационные процессы, теплопроводность, диффузия молекул и т.д.
Использование слова «информация» приводит ко многим недоразумениям. Это связано с тем, что оно имеет много различных значений. В обыденном языке это слово используется в смысле «сообщение» или «сведения». Письмо, телевизионная передача или телефонный разговор несут информацию. Начнем с понятия Шенноновской информации, согласно которому информация оценивается независимо от ее смысла. Средняя информация, приходящаяся например, на одну букву в книге определяется выражением
,
где pj – относительная частота j-ой буквы.
Шеннон использовал такое определение информации при изучении пропускной способности канала связи — способности передавать информацию даже при наличии помех. Шенноновская информация никак не связана со смыслом передаваемого сигнала. В его концепцию информации не входят такие аспекты, как осмысленность или бессмысленность, полезность или бесполезность и т.д. Шенноновская информация относится к замкнутым системам. Имеется ограниченный резервуар сигналов, число которых равно Z.
Одна из наиболее поразительных особенностей любой биологической системы — необычайная высокая степень координации между ее отдельными частями. В клетке одновременно и согласованно могут происходить тысячи метаболических процессов. У животных от нескольких миллионов до нескольких миллиардов нейронов и мышечных клеток своим согласованным действием обеспечивает координированные движения, сердцебиение, дыхание и кровообращение.
Распознавание образов — процесс в высшей степени кооперативный, равно как и речь и мышление у людей. Совершенно очевидно, что все эти высоко координированные, когерентные процессы становятся возможными только путем обмена информацией, которая должна быть произведена, передана, принята, обработана, преобразована в новые формы информации и должна участвовать в обмене информацией между различными частями системы и вместе с тем между различными иерархическими уровнями. Так мы приходим к непреложному выводу о том, что информация является решающим элементом существования самой жизни.
Понятие информации весьма тонкое. Как мы видим, она может так же обретать роль своего рода среды, существование которой поддерживается отдельными частями системы — среды, из которой эти части получают конкретную информацию относительно того, как им функционировать когерентно, кооперативно. И на этом уровне в дело вступает семантика.
Второе начало термодинамики говорит нам, что в замкнутых системах структуры распадаются и системы становятся всё более однородными – по крайней мере на макроскопическом уровне. На микроуровне может царить полный хаос. Именно по этим причинам информация не может порождаться системами в состоянии теплового равновесия; в замкнутых системах в конце концов устанавливается тепловое равновесие. Но система, находящаяся в состоянии теплового равновесия, не может и хранить информацию. Рассмотрим пример — книгу. На первый взгляд может показаться, что она находится в тепловом равновесии — ведь мы даже можем измерить ее температуру. Однако полного теплового равновесия книга достигнет лишь после того, как типографская краска продиффундирует и, расплываясь по каждой странице все больше и больше, распространится по ней, — но тогда текст исчезнет.
Таким образом мы видим многоликость понятия «информация». Я думаю, что будущее этого понятия разовьется именно в разделе самоорганизации сложных систем, так как синергетическое направление в наше время — одно из самых перспективных и малоисследованных.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ:
1. Г. Хакен, «Информация и самоорганизация».
2. А.Н. Матвеев, «Молекулярная физика»
3. Большая физическая энциклопедия
4. О. Наумов, газета «Монолог» 2000г, N4
www.ronl.ru
Энтропия и информация в системном анализе.
Современное понимание информации и ее роль в искусственных и естественных системах сложилось не сразу. Информация - это совокупность знаний, полученных разными науками: физикой, биологией, философией, теорией связи и т.д.
С другой стороны к этой проблеме пришла философская теория познания. Признав, что наше знание есть отражение реального мира, материалистическая теория познания установила, что отражение является всеобщим свойством материи. Сознание человека является специфической формой отражения.
Как только состояние одного объекта находится в соответствии с состояниями другого объекта, мы говорим, что один объект отражает другой, содержит информацию о другом.
В настоящее время информация рассматривается как фундаментальное свойство материи. Понятие информации столь же фундаментально для всей системологии как и понятие энергии для физики.
Исследуя информацию, кибернетика не открыла нового свойства материи: оно известно в философии под названием свойства отражения. Новое состоит в том, что информацию можно исследовать количественно.
Энтропия дискретного множества. Понятие неопределенности.
В системном анализе теоретическим ядром являются понятия энтропия и количество информации. Энтропия выступает как мера неопределенности. Характер неопределенности может быть самым различным, например:
- неопределенность типа незнания
- неопределенность типа расплывчатости
- неопределенность статистического типа
Неопределенность статистического типа можно свести к теории вероятности и измерить. Введем количественную меру для данного типа неопределенности.
Сосредоточим внимание по сущности неопределенности и рассмотрим несколько простейших опытов, которые обозначим А, Б и В.
Введем характеристики опыта:
k - число исходов опыта;
pi - вероятность г-го исхода опыта (i=1,k);
H - мера неопределенности результата опыта.
Опыт А будет заключаться в подбрасывании монеты. В этом опыте возможны два исхода (k=2). Монета упала гербом вверх, либо вниз. Вероятность каждого исхода pi =1/2 (i=1,2).
Опыт Б - подбрасывание игральной шестигранной кости. В этом опыте возможны шесть исходов (k=6). Вероятность каждою исхода pi =1/6(i=1,6).
Опыт В предполагает одновременное подбрасывание двух игральных костей. Для этого опыта k=36 и pi =1/36 (i=1,36).
Оценка неопределенности результатов этих опытов есть оценка трудности угадывания исходов опытов. Из всех описанных опытов опыт В имеет максимальную неопределенность, поскольку число исходов здесь самое большое и заранее предвидеть исход этого опыта труднее всего. Чтобы перейти к количественной оценке неопределенности, сформулируем основные требования к функции, которая должна выполнять роль меры неопределенности Н.
Так как любая теория строится па аксиоматике, постулируем.
1)Значение Н монотонно возрастающая функция при увеличении числа
исходов опыта, Н=f(k).
2) Значение H = 0, если опыт имеет единственный исход, (k=1 ). Это означает,
что никакой неопределенности не возникает и результат опыта очевиден.
3)Неопределенность двух опытов Б следует рассматривать как
неопределенность одного опыта В, т.е. суммарное значение энтропии двух
опытов Б равно энтропии опыта В. Нельзя утверждать, что это два опыта Б
или один опыт В, т.к. ситуация неразличима. Оценка неопределенности
обладает свойством аддитивности. Это положение следует из того, что эти
две ситуации физически неразличимы. По умолчанию мы принимаем, что
вероятность каждого исхода опыта одинакова.
2НБ = НВ
где H=f(k) - неопределенность опыта Б;
H=f(k2) - неопределенность опыта В;
k - число исходов опыта Б.
2f(k) = f(k2)
В общем виде для п простых опытов можно записать:
nf(k) = f(k2) (1)
Функциональное уравнение (1) можно решить относительно функции f(k). Дифференцируем уравнение (1) по k , используя свойство монотонности функции f(k).
(2)
Далее дифференцируем выражение (1 ) по п
(3)
Разделим уравнение (2) на (3)
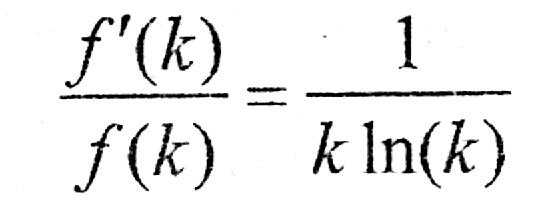

Интегрируя, находим:
где ln(С) - постоянная интегрирования. Из последнего выражения следует
Получено простое решение уравнения (1), но С определить нельзя, так как нет необходимой информации для отыскания постоянной интегрирования.
Так как с увеличением k энтропия растет, то С >0, и последнее выражение можно переписать в окончательном виде:
(4)
Из этого выражения видно, что оно удовлетворяет второму исходному постулату.
Итак, при k равновероятных исходах неопределенность опыта составляет:
(4*)
где p=1/k — вероятность исхода опыта.
Если учесть, что для равновероятных исходов
, то умножая (4*) на единицу в виде , получим
(5)
Каждый член правой части выражения (5) можно рассматривать как вклад отдельного исхода в общую неопределенность опыта. В случае равновероятных исходов вклад каждого исхода одинаков.
Выражение (5) можно записать в компактной форме:
(6)
Если число опытов N то в силу аддитивности энтропии
(7)
Функция (6) называется средняя энтропия опыта, энтропия выбора, а также информационная энтропия дискретного множества. Энтропия как мера неопределенности (7) была введена Шенноном при разработке математической теории связи.
Основные свойства энтропии.
Рассмотрим основные свойства энтропии дискретного множества. Прежде всего отметим, что энтропия дискретного множества не может принимать отрицательного значения. Так как 0 ≤ р ≤ 1 , то величина -plog(р) всегда положительна.
Если р 0 , то -р1og(р) 0 , если p1, то также - р1оg(p) 0 .
Так как -рlog(р) = 0 только при p=0 или р=1 , то энтропия опыта равна нулю только в том случае, когда одна из вероятностей равна единице, следовательно, все остальные равны нулю. Это хорошо согласуется со смыслом величины H как меры неопределенности: в этом случае опыт не содержит
никакой неопределенности, так как результат опыта можно предвидеть заранее. Рассмотрим пример: в ящике находятся белые и черные шары одного размера. Вынимаем наугад шар из ящика. Данный опыт имеет два исхода: мы можем вынуть из ящика только белый или черный тар.
Запишем формулу энтропии для двух исходов опыта:
где р1 - вероятность извлечения белого тара;
р2 — вероятность извлечения черного тара, р2=1-p1
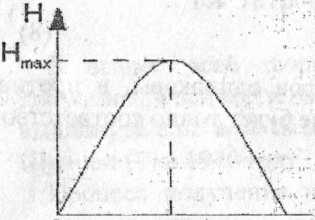
О 0.5 1 рис. 1.Энторопия для двух
На рис 1. изображен график функции H для двух исходов опыта. Из которого видно, как изменяется энтропия при изменении вероятности одного из исходов опыта от нуля до единицы. Из графика следует, что максимальное значение энтропии соответствует равновероятным событиям р1 = р2 = 0,5. При этом максимальное значение энтропии при выборе двоичного основания логарифма равно единице, т.е. H=log22=1. В общем случае для k исходов опыта максимальное значение энтропии соответствует H=log(k).
Максимум энтропии отвечает равновероятным событиям. В случае равновероятных событий нельзя отдать предпочтение ни одному из них и, таким образом, результат предвидеть труднее всего.
Понятие энтропии очень тесно связано с понятием количества информации.
Единица измерения энтропии.
Единицей неопределенности служит энтропия объекта с двумя равновероятными состояниями. Эта единица получила название 1 бит. Наряду с битом получила распространение более укрупненная единица - байт (1 байт = 8 бит).
Энтропия как мера разнообразия, неупорядоченности, хаоса.
До сих пор понятие энтропии мы связывали с неопределенностью. Энтропия допускает и другое толкование.
Представим себе систему, состоящую из камеры, в которой находятся N шаров разного сорта, например, отличающихся цветом. Предполагаем, что N достаточно большое число. Обозначим долю шаров i-го сорта (цвета) — хi, (i = 1,m). Проведем следующий опыт: наугад извлечем шар из камеры. Вероятность извлечения шара i-го сорта равна pi=xi .
Энтропия одного опыта составит:
(8)
При этом следует принять, что размеры шаров одинаковы, в противном случае вероятность извлечения шаров 1-го сорта не будет точно соответствовать их доле в камере.
Энтропия всех опытов над системой равна:
(9)
Правая часть выражений (8) и (9) включает параметры рассматриваемой системы. Первая из функций (8) характеризует степень неупорядоченности системы или степень разнообразия в ней с точки зрения выбранного признака для различения элементов системы (цвета шаров).
Вторая функция (9) измеряет неупорядоченность (разнообразие) в системе несколько иначе. Отличие этих двух функций можно иллюстрировать следующим примером. Если камеру разделить на две части, то при достаточно большом количестве шаров в ней доля шаров i-го сорта в каждой их двух частей , останется прежней, но число шаров уменьшится вдвое, вдвое уменьшится неупорядоченность, оцениваемая формулой (9). Однако степень неупорядоченности для каждой из двух частей останется прежней, равной степени неупорядоченности системы. Таким образом, функция (8) не зависит от количества элементов в системе. Такие характеристики в термодинамике называют интенсивными. Напротив, функция (9) зависит от числа элементов. Такие характеристики в термодинамике носят название экстенсивных. Неупорядоченность системы часто отождествляют с уровнем хаоса и неоднородности в ней. По аналогии с выше рассмотренным примером можно оценить неупорядоченность потока смеси каких-либо веществ:
(10)
где zi — концентрация i-го компонента в мольных долях (i=1,т );
N - расход потока или число молекул, проходящее через некоторое сечение в единицу времени;
т - количество компонентов в смеси.
Таким образом видно, что энтропия оценивает разнообразие элементов в системе по некоторому определенному признаку, который может нас интересовать в той или иной задаче.
Энтропия как мера количества информации.
В основе всей теории информации лежит открытие, что информация допускает количественную оценку.
Процесс получения информации можно интерпретировать как изменение неопределенности в результате опыта или сообщения.
Вернемся к простейшим опытам с монетой или костью. Перед проведением опыта существует некоторая неопределенность, связанная с незнанием результата опыта. После проведения опыта, т.е. после получения результата, эта неопределенность устраняется. В практике чаще всего встречаются случаи, когда после проведения опыта еще остается некоторая неопределенность.
Если неопределенность до опыта составляла H, а после опыта h2, то устраненная в ходе опыта неопределенность составляет:
(11)
Разность априорной (до опыта) энтропии H и апостериорной (после опыта) энтропии h2 носит название количества информации. Таким образом, количество информации замеряется количеством снятой неопределенности. В частном случае, когда неопределенность в результатеопыта снимается полностью, т.е. h2 = 0, получаем I=H. Хотя количество информации численно равно энтропии, следует иметь ввиду различный смысл количества информации и энтропии. Количество информации, как и энтропия измеряется в битах. Один бит информации — это количество информации, сообщающее о том, какое из двух равновероятных событий имело место, т.е. такое количество информации, которое уменьшает вдвое число возможных исходов (см. п. «Энтропия как мера разнообразия, неупорядоченности, хаоса»).
Энтропия непрерывного множества
На практике мы сталкиваемся с ситуацией, когда число исходов опыта может
быть сколь угодно велико, т.е. k ∞ . При этом вероятность каждого исхода стремится к нулю (p0), а искомый корень может принимать все возможные значения в заданном интервале (k ). Из теории вероятности известно, что в данном случае необходимо использовать плотность распределения вероятности Р(х).
Эта функция обладает тем свойством, что величина Р(х)dх есть вероятность того, что переменная x (значения корня в рассматриваемом примере) примет значения, заключенные в интервале от х до (х + dх).
Для оценки неопределенности опыта необходимо использовать энтропию непрерывного множества, которое по аналогии с энтропией дискретного множества (6) имеет вид:
(12)
При этом всегда
(аналогично случаю дискретного множества Σpi=1 ). Интегрирование осуществляется в интервале переменной х. Энтропия непрерывного множества (12) обладает большинством свойств энтропии дискретного множества.
Распределение Р(х), которое соответствует максимальному значению энтропии, имеет вид:
где x0, x1 - пределы интегрирования.
При этом, если обозначить l=x1-x0, то вероятность обнаружить корень уравнения на отрезке длиной l внутри интервала dх равна p=dx/l
По определению вероятности:
 (13)
(13)
Перепишем формулу (12) с учетом (13)
Итак, энтропия непрерывного множества запишется
(14)
Это выражение аналогично для энтропии дискретного множества (4).
Таким образом, если для дискретного множества энтропия измеряет неопределенность (неупорядоченность) абсолютным образом и энтропия дискретного множества всегда положительна, то в случае непрерывного множества под логарифмом формулы (14) может стоять величина меньше единицы и энтропия примет отрицательное значение.
Количество информации как критерий оценки степени организованности системы.
Как показано выше, энтропия является не только мерой неопределенности (7), но и мерой разнообразия, неупорядоченности, хаоса (9). Тогда вместо определения «устраненная неопределенность» можно употребить термин «блокированное разнообразие».
Термин «устраненная неопределенность» относится к энтропии, записанной через вероятность (7). Это определение ближе к теории информации (см. п. «Энтропия как мера количества информации»):
Если энтропия является мерой разнообразия (9), то употребляется термин «блокированное разнообразие». Это определение ближе к физике, термодинамике:
(15)
где I - блокированное разнообразие;
Нвх - энтропия, оценивающая неупорядоченность на входе системы; Нвых - энтропия, оценивающая неупорядоченность на выходе системы.
В кибернетике биологом Эшби был сформулирован закон «необходимого разнообразия». Согласно закону Эшби: каждая система, блокирующая разнообразие, должна иметь собственное разнообразие не менее блокированного, т.е. «только разнообразие может уменьшить другое разнообразие».
Критерии степени оценки организованности системы в общем виде записывается как отношение
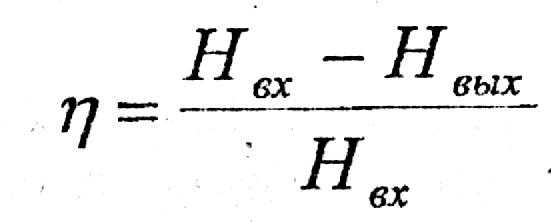 (16)
(16)
где η - критерий оценки степени организованности системы.
С помощью критерия η может оцениваться как разделительная способность колонны, так и многоколонной установки в целом.
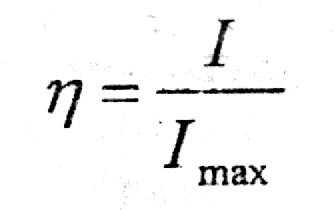
С точки зрения характера воздействия на организованность системы варьируемые параметры можно разбить на две группы: интенсивные и экстенсивные.
Интенсивные параметры в состоянии повысить организованность системы (качество разделения) при неизменных затратах работоспособной энергии и фиксированных энергетических затратах. Изменение этих параметров обязательно приводит к экстремальному значению критерия, качества разделения.
Экстенсивные параметры могут повысить организованность системы только за счет энергетических или неэнергетических затрат.
Двойственный характер энтропии и количества информации.
Энтропия является количественной мерой неопределенности случайного объекта. Неопределенность статистического типа можно измерить (7)
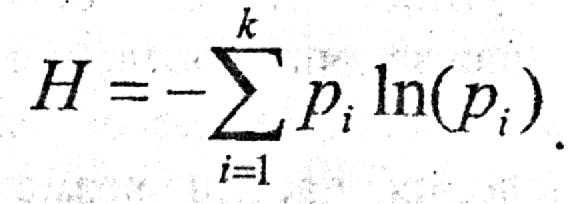
Количество информации определяется как мера снятой неопределенности (11)
В рассмотренном выше случае энтропия носит функциональный характер и применяется в теории информации.
Энтропия допускает и другое толкование (пример с шарами). В данном случае энтропия выступает как мера разнообразия, неупорядоченности, хаоса (9).
Энтропия как мера разнообразия ближе к физике, термодинамике и используется для оценки степени организованности системы. В данном случае энтропия носит атрибутивный характер.
Двойственный (функциональный и атрибутивный) характер энтропии и
информации.
| Характер энтропии и информации | Энтропия | Информация | Область применения |
| Функциональный | Мера неопределенности | Мера количества информации | Теория информации |
| Атрибутивный* | Мера разнообразия, неупорядоченности, хаоса | Мера степени организованности системы | Физика и техника |
* Атрибутивное - неотъемлемое, существенное свойство материи.
studfiles.net
САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ имени Н.Г. Чернышевского
на тему: «Энтропия термодинамическая и информационная»
Выполнил: студент 521 группы физического факультета
Маляев Владимир Сергеевич
-САРАТОВ 2001-
План реферата:
Энтропия – энциклопедическое понятие 3
Термодинамическое описание энтропии 3
Энтропия и общество 5
Информационный аспект 7
Смысловая информация и бессмысленная 8
Краткий вывод 9
Список использованной литературы 10
Чтобы каким-либо образом описать упорядоченность любой системы, физикам необходимо было ввести величину, функцию состояния системы, которая бы описывала ее упорядоченность, степень и параметры порядка, самоорганизованность системы.
От греческого entropia — поворот, превращение. Понятие энтропии впервые было введено в термодинамике для определения меры необратимого рассеяния энергии. Энтропия широко применяется и в других областях науки: в статистической физике как мера вероятности осуществления какого — либо макроскопического состояния; в теории информации — мера неопределенности какого-либо опыта (испытания), который может иметь разные исходы. Все эти трактовки энтропии имеют глубокую внутреннюю связь.
Энтропия — это функция состояния, то есть любому состоянию можно сопоставить вполне определенное (с точность до константы — эта неопределенность убирается по договоренности, что при абсолютном нуле энтропия тоже равна нулю) значение энтропии.
Для обратимых (равновесных) процессов выполняется следующее математическое равенство (следствие так называемого равенства Клаузиуса)dQ — подведенная теплота,T — температура, A и B — состояния, SA и SB — энтропия, соответствующая этим состояниям (здесь рассматривается процесс перехода из состояния А в состояние В)
Для необратимых процессов выполняется неравенство, вытекающее из так называемого неравенства Клаузиуса
Поэтому энтропия адиабатически изолированной (нет подвода или отвода тепла) системы при необратимых процессах может только возрастать.Используя понятие энтропии Клаузиус (1876) дал наиболее общую формулировку 2-го начала термодинамики: при реальных (необратимых) адиабатических процессах энтропия возрастает, достигая максимального значения в состоянии равновесия (2-ое начало термодинамики не является абсолютным, оно нарушается при флуктуациях).
Значит функция состояния, дифференциалом которой является dQ/T, называется энтропией и обозначается обычно S.
.
Отметим, что справедливость этого выражения для полного дифференциала энтропии доказана выше лишь для обратимых процессов идеального газа.
Так же энтропия S определятся логарифмом числа микросостояний, посредством которых реализуется рассматриваемое макросостояние, т.е.
, (формула Больцмана)
где k – постоянная Больцмана, Г — число микросостояний.
Энтропия системы в каком-либо обратимом процессе изменяется под влиянием внешних условий, воздействующих на систему. Механизм воздействия внешних условий на энтропию состоит в следующем. Внешние условия определяют микросостояния, доступные системе, и их число. В пределах доступных для нее микросостояний система достигает равновесного состояния, а энтропия – соответствующего значения. В результате значение энтропии следует за изменением внешних условий, достигая максимального значения, совместимого с внешними условиями.
Чем более сильно упорядочена система, тем меньше число микросостояний, которыми осуществляется макросостояние.
Допустим, например, что все атомы закреплены в определенных местах. Тогда существует только одно микросостояние, а соответствующая ему энтропия равна нулю. Чем больше число микросостояний, тем больше разупорядочена система. Поэтому можно сказать, что энтропия является мерой упорядоченности системы. В состоянии равновесия энтропия достигает своего максимального значения, поскольку равновесие есть наиболее вероятное состояние, совместимое с фиксированными условиями и, следовательно, является макросостоянием, осуществляемым посредством максимального числа микросостояний. Очевидно, что система, предоставленная самой себе, движется в направлении равновесного состояния, т.е. энтропия должна возрастать в предоставленной самой себе системе.
Энтропия определяется логарифмом числа микросостояний, посредством которых реализуется макросостояние. В состоянии равновесия энтропия достигает максимального значения, поскольку в равновесном состоянии термодинамическая вероятность максимальна. Отсюда следует, что энтропия изолированной предоставленной самой себе системы должна возрастать до тех пор, пока не достигнет максимального значения, совместимого с условиями.
Следует заметить, что при адиабатическом обратимом процессе энтропия не изменяется, так как при адиабатическом расширении газа за счет увеличения объема энтропия увеличивается, однако за счет уменьшения температуры, которое при этом происходит, она уменьшается и эти две тенденции полностью компенсируют друг друга.
Неубывание энтропии в изолированной системе обусловливается в конечном счете равновероятностью всех ее микроскопических состояний, приводящей систему в наиболее вероятное макросостояние.
В процессах изолированной системы энтропия не убывает, в то время как в процессах неизолированных систем энтропия может и возрастать, и убывать, и оставаться неизменной в зависимости от характера процесса.
Так же отметим изменение энтропии в необратимых процессах. Вычисление основывается на том, что энтропия является функцией состояния. Если система перешла из одного состояния в другое посредством необратимого процесса, то логично мысленно перевести систему из первого состояния во второе с помощью некоторого обратимого процесса и рассчитать происходящее при этом изменение энтропии. Оно равно изменению энтропии при необратимом процессе.
Рассмотрим роль энтропии в производстве работы: принцип Кельвина запрещает циклический процесс, результатом которого было бы превращение нацело некоторого количества теплоты в работу в результате контакта с одним тепловым резервуаром. Формула для к.п.д. цикла Карно показывает, что взятое от нагревателя количество теплоты лишь частично может быть превращено в работу, причем часть теплоты, превращаемая в работу, тем больше, чем меньше температура холодильника. Физической причиной этого являются требования второго начала термодинамики. Поскольку энтропия при любых процессах в замкнутых системах не убывает, некоторое количество теплоты не может нацело превратиться в работу потому, что это означало бы исчезновение соответствующей энтропии, что противоречит второму началу термодинамики.
При совершении работы в холодильник должна быть передана по крайней мере такая же энтропия, какая была взята от нагревателя. Максимальный к.п.д. достигается в обратимой машине, поскольку в этом случае холодильнику передается минимально возможная энтропия.
Теперь рассмотрим другое приложение понятия энтропия:
Давно было замечено, что в одну и ту же реку дважды войти нельзя. Мир вокруг нас меняется, наше общество меняется, и мы сами, члены общества, только стареем. Изменения необратимы.
Энтропия первоначально была введена для объяснения закономерностей работы тепловой машины. В узком смысле энтропия характеризует равновесное состояние замкнутой системы из большого числа частиц.
В обычном понимании равновесие в системе означает просто хаос. Для человека максимум энтропии — это разрушение. Любое разрушение увеличивает энтропию.
Энтропия замкнутой системы необратима. Но в природе полностью замкнутых систем не существует. А для открытых неравновесных систем точного определения энтропии пока не известно. Измерить энтропию нельзя. Из строгих физических законов она не выводится. Энтропия вводится в термодинамике для характеристики необратимости протекающих в газах процессов.
Многие ученые не считают феноменологические законы термодинамики законами природы, а рассматривают их как частный случай при работе с газом с помощью тепловой машины. Поэтому не рекомендуются расширенная трактовка энтропии в физике.
С другой стороны необратимость протекающих физических процессов и самой нашей жизни – это факт. С этой позиции вполне оправдано использование понятия энтропии в нефизических дисциплинах для характеристики состояния системы.
Все природные системы, включая человеческий организм и человеческие сообщества, не являются замкнутыми. Открытость системы позволяет локальным образом уменьшать энтропию за счет обмена энергией с окружающей средой, что приводит к упорядочению и усложнению структуры системы.
Человеческие сообщества в любом виде, от племен и групп до народов и социальных обществ, также являются системами. Каждое человеческое сообщество имеет свои законы и структуру взаимодействий. Будем говорить об обществе в целом, ограничивая его рамками государств.
Любое общество как система старается сохранить себя в окружающем мире. Для этого существуют государственные, общественные, социальные и другие институты. Применение энтропии для характеристики общества позволяет установить некоторые приблизительные рамки, в пределах которых общество может успешно развиваться или, наоборот, деградировать.
В настоящее время существует множество параметров, характеризующих то или иное общество. Но большинство из этих параметров, в конечном счете, сводится к двум видам: параметры, характеризующие открытое демократическое общество, и параметры, описывающие тоталитарные системы.
Почему западные государства достигли такого впечатляющего прогресса в экономике и государственном устройстве и существенно опережают в своем развитии другие общественные системы? Западное общество характеризуется большей степенью открытости. Более открытая система, с одной стороны, впускает в себя больше энергии из внешнего мира и дает больше степеней свободы своим элементам, с другой стороны – позволяет увеличить отток «недоброкачественной» энергии. Таким образом, энтропия системы уменьшается. При этом усложняется структура системы, что в западном обществе мы и наблюдаем.
В более замкнутой общественной системе имеют место обратные процессы. Энтропия увеличивается. Структура общества упрощается. Ярким примером такой системы служит Северная Корея. Структура общества упростилась до трех основных элементов – партийная элита, армия и все остальные.
Таким образом, можно сделать вывод, что для успешного развития общества необходимо соблюдение некоторых условий. Главным из таких условий является степень свободы элементов общества, т.е. людей. Степень свободы человека можно определять в терминах прав человека, политических свобод, экономических возможностей. Суть от этого не меняется. Человек должен иметь право на свободу выбора целей и путей их достижения.
Если право выбора человека слишком ограничивается, то в обществе начинаются застойные процессы, и оно постепенно приходит в упадок. Как пример можно привести Советский Союз. Выбор человека ограничивался идеологическими установками и партийной принадлежностью. Добиться успеха, сделать карьеру вне партии было сложно. В конце концов, осталась одна возможность продвижения: школа, институт комсомол, партия. Партийная принадлежность была необходима для достижения успеха в любой сфере деятельности.
Такой вариант общественных отношений, в конечном счете, привел к упрощению структуры общества и последующему упадку. Открытость общества не является панацеей от всех бед, но создает предпосылки для дальнейшего прогресса.
Демократия — не лучшая система управления. Но, по — видимому, это одна из необходимых степеней свободы. При детальном исследовании можно вычислить необходимое для развития количество степеней свободы личности. Перебор также не желателен. В этом случае отдельные части общества получают слишком большую независимость, что может привести к распаду целого на отдельные независимые составляющие.
Поэтому на Западе наблюдается такое огромное количество норм и правил, регулирующих все сферы жизни человека. Большое количество норм и законов необходимо для регулирования сложной структуры общества и сохранения его целостности.
Не следует также путать экономическую и военную мощь государства с общественными институтами. Замкнутые общества могут иметь оболочку в виде мощных и сильных государств. Советский Союз тому пример. Государство является вторичным по отношению к обществу. Государства могут исчезать, но люди на территории остаются, и, следовательно, остается общество, которое в отсутствии государства может получить новый импульс к развитию. Если же распадается общество, то государство исчезает навсегда. В России государственное устройство неоднократно менялось, но общество, видоизменяясь, не распадалось.
При использовании понятия энтропии нельзя обойтись без закона сохранения. К сожалению, он гласит, что если энтропия где-то убывает, то где-то она прибывает. Прогресс человечества в целом, и общественных институтов — в частности, приводит к уменьшению энтропии системы. Значит, энтропия окружающей человека среды увеличивается. Это приводит к гибели природы и экологическим катастрофам.
На земле кроме человека есть и другая жизнь. Реакция живой природы на разрушающие действия человеческой системы может быть многообразной: от новых болезней и эпидемий до мутантов и планетарных катастроф.
Теперь можно разобрать энтропию в информационном аспекте.
При подходе к сложным системам используются законы статистической физики.
В этой области физики предпринимается, в частности, попытка вывести феноменологические макроскопические законы термодинамики из микроскопической теории. Такой микроскопической теорией может быть ньютоновская механика отдельных частиц газа или квантовая механика. Используя соответствующие статистические средние, мы получаем возможность вывести макроскопические величины из микроскопических законов. Центральным понятием и в этом случае является энтропия S. Согласно Больцману, она связана с числом W различных микроскопических состояний, порождающих одно и то же макроскопическое состояние системы соотношением
Решающее значение имеет так и не получивший убедительного ответа вопрос о том, почему макроскопические явления необратимы, хотя все фундаментальные законы обратимы. Например, если у нас есть сосуд с молекулами газа и мы откроем клапан, чтобы газ мог попасть во второй сосуд, то оба сосуда окажутся заполнены газом более или менее равномерно. Однако обратный процесс в природе никогда не наблюдается: никому не доводилось видеть, чтобы второй сосуд самопроизвольно опустел и все молекулы собрались в первом сосуде.
Несмотря на трудности, связанные со строгим обоснованием необратимости, статистическая физика позволяет нам объяснить ряд явлений неравновесной термодинамики, такие, как релаксационные процессы, теплопроводность, диффузия молекул и т.д.
Использование слова «информация» приводит ко многим недоразумениям. Это связано с тем, что оно имеет много различных значений. В обыденном языке это слово используется в смысле «сообщение» или «сведения». Письмо, телевизионная передача или телефонный разговор несут информацию. Начнем с понятия Шенноновской информации, согласно которому информация оценивается независимо от ее смысла. Средняя информация, приходящаяся например, на одну букву в книге определяется выражением
,
где pj – относительная частота j-ой буквы.
Шеннон использовал такое определение информации при изучении пропускной способности канала связи — способности передавать информацию даже при наличии помех. Шенноновская информация никак не связана со смыслом передаваемого сигнала. В его концепцию информации не входят такие аспекты, как осмысленность или бессмысленность, полезность или бесполезность и т.д. Шенноновская информация относится к замкнутым системам. Имеется ограниченный резервуар сигналов, число которых равно Z.
Одна из наиболее поразительных особенностей любой биологической системы — необычайная высокая степень координации между ее отдельными частями. В клетке одновременно и согласованно могут происходить тысячи метаболических процессов. У животных от нескольких миллионов до нескольких миллиардов нейронов и мышечных клеток своим согласованным действием обеспечивает координированные движения, сердцебиение, дыхание и кровообращение.
Распознавание образов — процесс в высшей степени кооперативный, равно как и речь и мышление у людей. Совершенно очевидно, что все эти высоко координированные, когерентные процессы становятся возможными только путем обмена информацией, которая должна быть произведена, передана, принята, обработана, преобразована в новые формы информации и должна участвовать в обмене информацией между различными частями системы и вместе с тем между различными иерархическими уровнями. Так мы приходим к непреложному выводу о том, что информация является решающим элементом существования самой жизни.
Понятие информации весьма тонкое. Как мы видим, она может так же обретать роль своего рода среды, существование которой поддерживается отдельными частями системы — среды, из которой эти части получают конкретную информацию относительно того, как им функционировать когерентно, кооперативно. И на этом уровне в дело вступает семантика.
Второе начало термодинамики говорит нам, что в замкнутых системах структуры распадаются и системы становятся всё более однородными – по крайней мере на макроскопическом уровне. На микроуровне может царить полный хаос. Именно по этим причинам информация не может порождаться системами в состоянии теплового равновесия; в замкнутых системах в конце концов устанавливается тепловое равновесие. Но система, находящаяся в состоянии теплового равновесия, не может и хранить информацию. Рассмотрим пример — книгу. На первый взгляд может показаться, что она находится в тепловом равновесии — ведь мы даже можем измерить ее температуру. Однако полного теплового равновесия книга достигнет лишь после того, как типографская краска продиффундирует и, расплываясь по каждой странице все больше и больше, распространится по ней, — но тогда текст исчезнет.
Таким образом мы видим многоликость понятия «информация». Я думаю, что будущее этого понятия разовьется именно в разделе самоорганизации сложных систем, так как синергетическое направление в наше время — одно из самых перспективных и малоисследованных.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ:
1. Г. Хакен, «Информация и самоорганизация».
2. А.Н. Матвеев, «Молекулярная физика»
3. Большая физическая энциклопедия
4. О. Наумов, газета «Монолог» 2000г, N4
www.ronl.ru
Реферат на тему:
Энтропи́я (от греч. ἐντροπία — поворот, превращение) в естественных науках — мера беспорядка системы, состоящей из многих элементов. В частности, в статистической физике — мера вероятности осуществления какого-либо макроскопического состояния; в теории информации — мера неопределённости какого-либо опыта (испытания), который может иметь разные исходы, а значит и количество информации; в исторической науке, для экспликации феномена альтернативности истории (инвариантности и вариативности исторического процесса).
Понятие энтропии впервые было введено Клаузиусом в термодинамике в 1865 году для определения меры необратимого рассеивания энергии, меры отклонения реального процесса от идеального. Определённая как сумма приведённых теплот, она является функцией состояния и остаётся постоянной при обратимых процессах, тогда как в необратимых — её изменение всегда положительно.
,
где dS — приращение энтропии; δQ — минимальная теплота подведенная к системе; T — абсолютная температура процесса;
Энтропия — функция состояния системы, равная в равновесном процессе количеству теплоты сообщённой системе или отведённой от системы, отнесённому к термодинамической температуре системы.
Энтропия — связь между макро- и микро- состояниями, единственная функция в физике, которая показывает направленность процессов. Функция состояния системы, которая не зависит от перехода из одного состояния в другое, а зависит только от начального и конечного положения системы.
Категории: Физические величины, Термодинамика, Теория хаоса.
Текст доступен по лицензии Creative Commons Attribution-ShareAlike.wreferat.baza-referat.ru