Доклад: Движение тел переменной массы. Основы теоретической космонавтики. Движение тела переменной массы реферат

Доклад - Движение тел переменной массы. Основы теоретической космонавтики

.

Реферат подготовил судент: Перов Виталий Группа:1085/3

Санкт-Петербургский Государственный Политехнический Университет

Санкт-Петербург 2005г.

Зарождение космонавтики

Моментом зарождения космонавтики можно условно назвать первый полёт ракеты, продемонстрировавший возможность преодолевать силу земного притяжения. Первая ракета открыла перед человечеством огромные возможности. Много смелых проектов было предложено. Один из них — возможность полёта человека. Однако, этим проектам было суждено воплотится в реальность только спустя многие годы. Своё практическое применение ракета нашла только в сфере развлечений. Люди не раз любовались ракетными фейерверками, и, вряд ли кто-нибудь тогда мог представить себе её грандиозное будущее.

Рождение космонавтики, как науки, произошло в 1987 году. В этом году была опубликована магистерская диссертация И.В Мещерского, содержащая фундаментальное уравнение динамики тел переменной массы. Уравнение Мещерского дало космонавтике «вторую жизнь»: теперь в распоряжении ракетостроителей появились точные формулы, которые позволяли создавать ракеты основываясь не на опыте предыдущих наблюдении, а на точных математических расчетах.

Общие уравнения для точки переменной массы и некоторые частные случаи этих уравнений уже после их опубликования И. В. Мещерским «открывались» в XX веке многими учёными западной Европы и Америки (Годар, Оберт, Эсно-Пельтри, Леви-Чивита и др.).

Случаи движения тел, когда их масса меняется можно указать в самых различных областях промышленности.

Наибольшую известность в космонавтики получило не уравнение Мещерского, а уравнение Циолковского. Оно представляет собой частный случай уравнения Мещерского.

К. Э. Циолковского можно назвать отцом космонавтики. Он был первым, кто увидел в ракете средство для покорения человеком космоса. До Циолковского на ракету смотрели как на игрушку для развлечений или как на один из видов оружия. Заслуга К. Э. Циолковского состоит в том, что он теоретически обосновал возможность покорения космоса при помощи ракет, вывел формулу скорости движения ракеты, указал на критерии выбора топлива для ракет, дал первые схематические чертежи космических кораблей, привёл первые расчеты движения ракет в поле тяготения Земли и впервые указал на целесообразность создания на орбитах вокруг Земли промежуточных станций для полётов на другие тела Солнечной системы.

Уравнение Мещерского

Уравнения движения тел с переменной массой являются следствиями законов Ньютона. Тем не менее, они представляют большой интерес, главным образом, в связи с ракетной техникой.

Принцип действия ракеты очень прост. Ракета с большой скоростью выбрасывает вещество (газы), воздействуя на него с большой силой. Выбрасываемое вещество с той же, но противоположно направленной силой, в свою очередь, действует на ракету и сообщает ей ускорение в противоположном направлении. Если нет внешних сил, то ракета вместе с выброшенным веществом является замкнутой системой. Импульс такой системы не может меняться во времени. На этом положении и основана теория движения ракет.

Основное уравнение движения тела переменной массы при любом законе изменения массы и при любой относительной скорости выбрасываемых частиц было получено В. И. Мещерским в его диссертации 1897 г. Это уравнение имеет следующий вид:

где – вектор ускорения ракеты, –– вектор скорости истечения газов относительно ракеты, M- масса ракеты в данный момент времени, –– ежесекундный расход массы, — внешняя сила.

По форме это уравнение напоминает второй закон Ньютона, однако, масса тела m здесь меняется во времени из-за потери вещества. К внешней силе F добавляется дополнительный член, который называется реактивной силой.

Уравнение Циолковского

Если внешнюю силу F принять равной нулю, то, после преобразований, получим уравнение Циолковского:

V=u ln (m0/m)

Отношение m0/m называется числом Циолковского, и часто обозначается буквой z.

Скорость, рассчитанная по формуле Циолковского, носит название характеристической или идеальной скорости. Такую скорость теоретически имела бы ракета при запуске и реактивном разгоне, если бы другие тела не оказывали на неё никакого влияния.

Как видно из формулы, характеристическая скорость не зависит от времени разгона, а определяется на основе учёта только двух величин: числа Циолковского z и скорости истечения u. Для достижения больших скоростей необходимо повышать скорость истечения и увеличивать число Циолковского. Так как число z стоит под знаком логарифма, то увеличение u даёт более ощутимый результат, чем увеличение z в то же количество раз. К тому же большое число Циолковского означает, что конечной скорости достигает лишь небольшая часть первоначальной массы ракеты. Естественно, такой подход к проблеме увеличения конечной скорости не совсем рационален, ведь надо стремится выводить в космос большие массы, при помощи ракет с возможно меньшими массами. Поэтому конструкторы стремятся прежде всего к увеличению скоростей истечения продуктов сгорания из ракет.

Числовые характеристики одноступенчатой ракеты

При анализе формулы Циолковского было выяснено, что число z=m0/m является важнейшей характеристикой ракеты.

Разделим конечную массу ракеты на две составляющие: полезную массу Мпол, и массу конструкции Мконстр. К полезной относят только массу контейнера, который требуется запустить с помощью ракеты для выполнения заранее запланированной работы. Масса конструкции – вся остальная масса ракеты без топлива(корпус, двигатели, пустые баки, аппаратура). Таким образом M= Мпол + Мконстр; M0= Мпол + Мконстр + Мтопл

Обычно оценивают эффективность транспортировки груза при помощи коэффициента полезной нагрузки р. р= M0/ Мпол. Чем меньшим числом выражен этот коэффициент, тем большую часть от общей массы составляет масса полезного груза

Степень технического совершенства ракеты характеризуется конструктивной характеристикой s. . Чем большим числом выражается конструктивная характеристика, тем более высокий технический уровень у ракеты-носителя.

Можно показать, что все три характеристики s, z и p связаны между собой следующими уравнениями:

Многоступенчатые ракеты

Достижение очень больших характеристических скоростей одноступенчатой ракеты требует обеспечения больших чисел Циолковского и ещё больших по величине конструктивных характеристик (т.к всегда s>z). Так, например при скорости истечения продуктов сгорания u=5км/с для достижения характеристической скорости 20км/с требуется ракета с числом Циолковского 54,6. Создать такую ракету в настоящее время невозможно, но это не значит, что скорость 20км/с не может быть достигнута при помощи современных ракет. Такие скорости обычно достигаются при помощи одноступенчатых, т.е составных ракет.

Когда массивная первая ступень многоступенчатой ракеты исчерпывает при разгоне все запасы топлива, она отделяется. Дальнейший разгон продолжает другая, менее массивная ступень, и к ранее достигнутой скорости она добавляет ещё некоторую скорость, а затем отделяется. Третья ступень продолжает наращивание скорости, и т.д.

Согласно формуле Циолковского, первая ступень в конце разгона достигнет скорости , где . Вторая ступень увеличит скорость ещё на , где . Полная характеристическая скорость двухступенчатой ракеты будет равна сумме скоростей, сообщаемых каждой ступенью в отдельности:

. Если скорости истечения из ступеней одинаковы, то , где Z= — число Циолковского для двухступенчатой ракеты.

Нетрудно доказать, что в случае 3-x ступенчатой ракеты число Циолковского будет равно Z=.

Итак, предыдущая задача достичь скорости 20км/с легко решается с помощью 3-х ступенчатой ракеты. Для неё число Циолковского будет также равно 54,6, однако, числа Циолковского для каждой ступени (при условии их равенства между собой) будут равны 3.79, что является вполне достижимым для современной техники.

Список литературы

Основы космонавтики / А. Д. Марленский

Люди русской науки: Очерки о выдающихся деятелях естествознания и техники / под редакцией С. И. Вавилова.

www.ronl.ru

Реферат - Движение тел переменной массы. Основы теоретической космонавтики

Санкт-Петербургский ГосударственныйПолитехнический Университет

Факультет Технической Кибернетики

Реферат на тему:

Движение тел переменной массы. Основы теоретическойкосмонавтики.

Студент: Перов Виталий

Группа:1085/3

Преподаватель: Козловский В.В

Санкт-Петербург

2005г. Содержание:

История космонавтики                                                              3

Уравнение Мещерского                                                             3

Уравнение Циолковского                                                           4

Числовые характеристикиодноступенчатой ракеты               4

Многоступенчатые ракеты                                                        5

Списокиспользуемой литературы:                                          6

Зарождение космонавтики

Моментом зарождения космонавтики можно условноназвать первый полёт ракеты, продемонстрировавший возможность преодолевать силуземного притяжения. Первая ракета открыла перед человечеством огромныевозможности. Много смелых проектов было предложено. Один из них — возможностьполёта человека. Однако, этим проектам было суждено воплотится в реальностьтолько спустя многие годы. Своё практическое применение ракета нашла только всфере развлечений. Люди не раз любовались ракетными фейерверками, и, вряд ликто-нибудь тогда мог представить себе её грандиозное будущее.

Рождение космонавтики, как науки, произошло в1987 году. В этом году была опубликована магистерская диссертация  И.В Мещерского, содержащая фундаментальноеуравнение динамики тел переменной массы. Уравнение Мещерского дало космонавтике«вторую жизнь»: теперь в распоряжении ракетостроителей появились точныеформулы, которые позволяли создавать ракеты основываясь не на опыте предыдущихнаблюдении, а на точных математических расчетах.

Общие уравнения для точки переменной массы инекоторые частные случаи этих уравнений уже после их опубликования И. В.Мещерским «открывались» в XXвекемногими учёными западной Европы и Америки (Годар, Оберт, Эсно-Пельтри, Леви-Чивита и др.).

Случаи движения тел, когда их масса меняетсяможно указать в самых различных областях промышленности.

Наибольшую известность в космонавтики получилоне уравнение Мещерского, а уравнение Циолковского. Оно представляет собойчастный случай уравнения Мещерского.

К. Э. Циолковского можно назвать отцомкосмонавтики. Он был первым, кто увидел в ракете средство для покорениячеловеком космоса. До Циолковского на ракету смотрели как на игрушку дляразвлечений или как на один из видов оружия. Заслуга К. Э. Циолковского состоитв том, что он теоретически обосновал возможность покорения космоса при помощиракет, вывел формулу скорости движения ракеты, указал на критерии выборатоплива для ракет, дал первые схематические чертежи космических кораблей,привёл первые расчеты движения ракет в поле тяготения Земли и впервые указал нацелесообразность создания на орбитах вокруг Земли промежуточных станций дляполётов на другие тела Солнечной системы.

Уравнение Мещерского

Уравнения движения тел с переменной массойявляются следствиями законов Ньютона. Тем не менее, они представляют большойинтерес, главным образом, в связи с ракетной техникой.

Принцип действия ракеты очень прост. Ракета сбольшой скоростью выбрасывает вещество (газы), воздействуя на него с большойсилой. Выбрасываемое вещество с той же, но противоположно направленной силой, всвою очередь, действует на ракету и сообщает ей ускорение в противоположномнаправлении. Если нет внешних сил, то ракета вместе с выброшенным веществомявляется замкнутой системой. Импульс такой системы не может меняться вовремени. На этом положении и основана теория движения ракет.

Основное уравнение движения тела переменноймассы при любом законе изменения массы и при любой относительной скоростивыбрасываемых частиц было получено В. И. Мещерским в его диссертации 1897 г.Это уравнение имеет следующий вид:

<img src="/cache/referats/21345/image002.gif" v:shapes="_x0000_i1025"> 

где <img src="/cache/referats/21345/image004.gif" v:shapes="_x0000_i1026"><img src="/cache/referats/21345/image006.gif" v:shapes="_x0000_i1027">M — масса ракеты в данный момент времени, <img src="/cache/referats/21345/image008.gif" v:shapes="_x0000_i1028"><img src="/cache/referats/21345/image010.gif" v:shapes="_x0000_i1029">

По форме это уравнение напоминает второй законНьютона, однако, масса тела m здесь меняется вовремени из-за потери вещества. К внешней силе F добавляется дополнительныйчлен, который называется реактивной силой.

УравнениеЦиолковского

Если внешнюю силу Fпринять равной нулю, то, после преобразований,получим уравнение Циолковского:

V=uln(m0/m)

Отношение m0/mназывается числом Циолковского, и часто обозначается буквой z.

Скорость, рассчитанная по формуле Циолковского,носит название характеристической или идеальной скорости. Такую скоростьтеоретически имела бы ракета при запуске и реактивном разгоне, если бы другиетела не оказывали на неё никакого влияния.

Как видно из формулы, характеристическаяскорость не зависит от времени разгона, а определяется на основе учёта толькодвух величин: числа Циолковского zискорости истечения u. Длядостижения больших скоростей необходимо повышать скорость истечения иувеличивать число Циолковского. Так как число zстоит под знаком логарифма, то увеличение uдаёт более ощутимый результат, чем увеличение zв то же количество раз. К тому же большое числоЦиолковского означает, что конечной скорости достигает лишь небольшая частьпервоначальной массы ракеты. Естественно, такой подход к проблеме увеличения конечнойскорости  не совсем рационален, ведь надостремится  выводить в космос большиемассы, при помощи ракет с возможно меньшими массами. Поэтому конструкторыстремятся прежде всего к увеличению скоростей истечения продуктов сгорания изракет.

Числовые характеристики одноступенчатой ракеты

При анализе формулы Циолковского было выяснено,что число z=m0/mявляется важнейшейхарактеристикой ракеты.

Разделим конечную массу ракеты на двесоставляющие: полезную массу Мпол, и массуконструкции Мконстр. К полезной относяттолько массу контейнера, который требуется запустить с помощью ракеты длявыполнения заранее запланированной работы. Масса конструкции – вся остальнаямасса ракеты без топлива(корпус, двигатели, пустые баки, аппаратура). Такимобразом M=Мпол+ Мконстр;   M0=Мпол+ Мконстр+ Мтопл 

Обычно оценивают эффективность транспортировкигруза при помощи коэффициента полезной нагрузки р. р=M0/ Мпол. Чем меньшим числом выраженэтот коэффициент, тем большую часть от общей массы составляет масса полезногогруза

Степень технического совершенства ракетыхарактеризуется конструктивной характеристикой s. <img src="/cache/referats/21345/image012.gif" v:shapes="_x0000_i1030">

Можно показать, что все три характеристики s, zи pсвязаны между собой следующими уравнениями:

<img src="/cache/referats/21345/image014.gif" v:shapes="_x0000_i1031">          <img src="/cache/referats/21345/image016.gif" v:shapes="_x0000_i1032">

Многоступенчатые ракеты

Достижение очень больших характеристическихскоростей одноступенчатой ракеты требует обеспечения больших чисел Циолковскогои ещё больших по величине конструктивных характеристик (т.к всегда s>z).Так, например при скорости истечения продуктов сгорания u=5км/с для достижения характеристическойскорости 20км/с требуется ракета с числом Циолковского 54,6. Создать такуюракету в настоящее время невозможно, но это не значит, что скорость 20км/с неможет быть достигнута при помощи современных ракет. Такие скорости обычнодостигаются при помощи одноступенчатых, т.е составных ракет.

Когда массивная первая ступень многоступенчатойракеты исчерпывает при разгоне все запасы топлива, она отделяется. Дальнейшийразгон продолжает другая, менее массивная ступень, и к ранее достигнутойскорости она добавляет ещё некоторую скорость, а затем отделяется. Третьяступень продолжает наращивание скорости, и т.д.

Согласно формуле Циолковского, первая ступень вконце разгона достигнет скорости <img src="/cache/referats/21345/image018.gif" v:shapes="_x0000_i1033"><img src="/cache/referats/21345/image020.gif" v:shapes="_x0000_i1034"><img src="/cache/referats/21345/image022.gif" v:shapes="_x0000_i1035"><img src="/cache/referats/21345/image024.gif" v:shapes="_x0000_i1036">

<img src="/cache/referats/21345/image026.gif" v:shapes="_x0000_i1037"><img src="/cache/referats/21345/image028.gif" v:shapes="_x0000_i1038">Z=<img src="/cache/referats/21345/image030.gif" v:shapes="_x0000_i1039">  — число Циолковскогодля двухступенчатой ракеты.

Нетрудно доказать, что в случае 3-xступенчатой ракеты число Циолковского будетравно Z=<img src="/cache/referats/21345/image032.gif" v:shapes="_x0000_i1040">

Итак, предыдущая задача достичь скорости 20км/слегко решается с помощью 3-х ступенчатой ракеты. Для неё число Циолковскогобудет также равно 54,6, однако, числа Циолковского для каждой ступени (приусловии их равенства между собой) будут равны 3.79, что является вполнедостижимым для современной техники.

Список используемой литературы:

www.ronl.ru

Движение тел переменной массы | Рефераты KM.RU

Д. ф.-м. н. Б.Л.Воронов

Задача 1. Однородная неупругая цепь длиной L и массой М перекинута через блок. Часть цепи лежит на столе высотой h, а часть на полу. Найти скорость равномерного движения звеньев цепи (рис. 1).

Задача 2. Однородная нерастяжимая цепь подвешена на нити так, что нижний конец ее касается крышки стола. Нить пережигают. Найти силу давления цепочки на стол в тот момент, когда над ним находится часть цепи длиной h. Масса цепи – М, ее длина – L, удар каждого звена считать абсолютно неупругим (рис. 2).

Задача 3. С какой силой давит на землю кобра, когда она, готовясь к прыжку, поднимается вертикально вверх с постоянной скоростью v (рис. 3)? Масса змеи – M, ее длина – L.

Начнем с хорошо известной ситуации. Пусть тело можно считать материальной точкой (например, можно пренебречь его структурой и размерами или вести речь только о центре масс тела) либо все части протяженного тела имеют одну и ту же скорость v. Тогда 2-й закон Ньютона, в теоретической механике чаще говорят – уравнения движения, для такого тела имеет вид:

где m – неизменная масса тела, F – действующая на тело внешняя сила. В общем случае протяженных тел отдельные части тела движутся каждая со своей скоростью, и описание движения всех частей с учетом их взаимодействия резко усложняется.

Однако бывают случаи, когда движение некоторых частей составного тела можно описать сравнительно просто. Одним из таких случаев является случай движения тел переменной массы. Пусть имеется составная система и пусть в ней можно выделить некоторую часть, подсистему, движущуюся со скоростью v, причем состав ее меняется определенным образом. Будем называть эту подсистему телом переменной массы, если выполнены следующие условия. В каждый момент времени можно считать, что это тело либо является материальной точкой, либо все его части имеют одинаковую скорость v. С течением времени от тела непрерывно отделяются некоторые (бесконечно) малые его части, причем каждая со своей независимой скоростью v'; либо, наоборот, к телу непрерывно добавляются новые малые части, которые до «прилипания» имели свою скорость v' (возможно и то и другое). Таким образом, при движении тела меняется не только его скорость v = v(t), но и масса m = m(t), причем известна скорость изменения массы Случай <0 означает, что за промежуток времени t  t + dt от тела отделяются какие-то части массой –dm; случай Случай >0 означает, что за тот же промежуток времени к телу добавляются какие-то части массой dm. Примером первого случая являются ракета и поливальная машина, примером второго случая – снежная лавина. Мы ограничимся ситуациями, когда все отделяющиеся или добавляющиеся части имеют в каждый момент времени одну и ту же скорость v' = v'(t), следовательно, одну и ту же скорость u = v' – v относительно тела. Эту скорость u = u(t) называют относительной скоростью. Если она известна наряду с (например, в случае ракеты она определяется приготовлением, в случае снежной лавины v' = 0, стало быть, u = –v), то говорят о движении тела переменной массы.

2-й закон Ньютона для тел переменной массы имеет вид:

где F – суммарная внешняя сила, которая действует в данный момент времени как на тело (переменной массы m), так и на его отделяющиеся или добавляющиеся части (массы –dm или dm соответственно). Эту тонкость надо постоянно иметь в виду. Может случиться, что вся внешняя сила или конечная ее составляющая приложена именно к этим частям: под действием конечной внешней силы (бесконечно) малая масса (–dm или dm) за (бесконечно) малый промежуток времени t  t + dt меняет свою скорость на конечную величину, от v до v' или от v' до v, испытывая (бесконечно) большое ускорение. Именно этот случай реализуется в приводимых ниже задачах. Конечно, может случиться, что изменение скорости отделяющихся или добавляющихся частей обеспечивается внутренними силами. Так обстоит дело, например, в случае космической ракеты или снежной лавины.

2-й закон Ньютона для тел переменной массы можно переписать в эквивалентной форме (особенно удобной во втором случае):

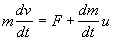
Отличие от привычного случая постоянной массы состоит в том, что m = m(t) является теперь известной функцией времени, а к внешней силе F добавляется реактивная сила

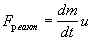
Дадим вывод 2-го закона Ньютона для тел переменной массы (при первом чтении этот абзац можно пропустить). Он следует из 2-го закона Ньютона для любой, в том числе составной системы, в следующей общей форме:

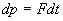
т.е. приращение dp полного импульса p системы за интервал времени t  t + dt равно импульсу Fdt действующей на систему внешней силы F. Системой в рассматриваемом интервале времени t  t + dt является тело переменной массы вместе с отделяющимися или добавляющимися частями. В любом случае (>0 или <0 ) изменение dp импульса p за промежуток времени t  t + dt дается формулой:

dp = p(t + dt) – p(t) = (m + dm)(v + dv) – dmv' – mv.

Вывод этой формулы предоставляем читателю в качестве упражнения. Укажем лишь, что первое слагаемое справа относится ко времени t + dt, третье слагаемое – ко времени t, а второе слагаемое (–dmv') относится к моменту t + dt в случае отделяющихся частей (массой –dm > 0, <0 ) и к моменту t в случае добавляющихся частей (массой dm, >0 ). Раскрывая правую часть

dp = mdv – dm (v' – v) + dmdv = mdv – dmu + dmdv

и приравнивая ее Fdt, имеем:

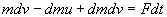
Деля обе части последнего равенства на dt, переходя к переделу dt  0 и отбрасывая стремящееся к нулю слагаемое 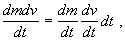 получаем окончательно:

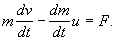
Из вывода следует указанное выше содержание понятия внешней силы F.

Теперь перейдем к решению задач.

Задача 1.Возьмем в качестве тела переменной массы лежащий на столе участок цепи. Цепь считается нерастяжимой, толщина цепи – пренебрежимо малой, поэтому можно считать, что весь этот участок занимает пренебрежимо малый объем (сосредоточен в точке) в основании левого вертикального участка цепи. Движение носит одномерный характер, вдоль вертикальной оси y (начало отсчета на полу), поэтому достаточно рассматривать только y-компоненту 2-го закона Ньютона (значок «y» для у-компонент векторов v, u, F в дальнейшем опускаем):

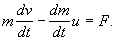
(прочие компоненты уравнений движения имеют вид 0 = 0). Именно это уравнение должно определить скорость равномерного движения вертикальных звеньев цепи, поскольку они отделяются от нашего тела.

В каждый момент времени все звенья рассматриваемого участка свободно, без натяжения, лежат на столе, v = 0, соответственно 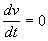, сила тяжести компенсируется силой реакции стола. Отделяющееся первое сверху звено, лежащее в основании вертикального участка, уходит вверх с постоянной во времени вертикальной скоростью v' > 0. Эта скорость и является искомой. Относительная скорость u = v' – v = v'. Масса тела m = l, где l – длина рассматриваемого участка, 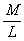 – линейная плотность цепи. Длина l, а значит, и масса m, уменьшаются за счет уходящих вверх звеньев; вследствие нерастяжимости цепи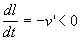

соответственно

Остается определить вертикальную компоненту F внешней силы F. Она равна натяжению Th левой вертикальной части цепи на нижнем ее конце, находящемся на высоте y = h. Приложена эта сила к отделяющемуся от тела первому сверху звену, тогда как все звенья тела лежат свободно (см. выше о внешней силе F). Th в свою очередь определяется условиями движения вертикальных участков цепи. Если они движутся равномерно, как это и принимается в условии задачи, и, кроме того, цепь справа ложится на пол свободно, т.е. натяжение T0 правого вертикального участка на нижнем его конце, у пола, на высоте y = 0, равно нулю (T0 = 0), то Th равно разности веса Pправ правого участка и веса Pлев левого вертикального участков цепи: Th = Pправ – Pлев.

Мы оставляем читателю соответствующие рассуждения, укажем лишь, что при равномерном движении любого вертикального участка цепи его вес компенсируется разностью натяжений на концах этого участка, кроме того, при безынерционном блоке (что неявно принимается), натяжение цепи справа и слева от блока одинаково. Разность весов определяется разностью масс, следовательно, разностью длин соответствующих участков:

Pправ – Pлев = hg,

так что

F = hg > 0.

С учетом сказанного 2-й закон Ньютона принимает вид:

– (–v')v' = hg,

или: v'2 = hg,

откуда находим искомую скорость: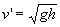

В качестве упражнения читателю предлагается решить задачу, взяв в качестве тела переменной массы некоторый участок вертикальной цепи. Видимо, проще всего выбрать некоторый нижний отрезок левого вертикального участка с фиксированным верхним звеном (но не высотой!). Тонкость будет в определении силы F: натяжение цепи Th на нижнем конце теперь, когда звено, лежащее в основании и имеющее скорость v', включается в состав тела переменной массы, равно нулю (Th = 0), а прежнее натяжение цепи Th = hg является теперь внутренней силой. Любопытно, что ответ не зависит от длины выбранного отрезка и его можно взять сколь угодно малым, достаточно рассматривать в каждый момент времени только звено, лежащее в основании цепи. Это же ясно и из предыдущего рассмотрения.

Задача 2. В качестве тела переменной массы возьмем вертикальный, падающий, участок цепи переменной длины l = h, h – высота цепи над столом. Как и в предыдущей задаче, движение одномерное, вдоль вертикальной оси y, поэтому вследствие нерастяжимости цепи все падающие звенья имеют одну и ту же скорость v, и 2-й закон Ньютона имеет прежний вид:

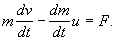
Оказывается, дополнительные соображения однозначно определяют закон движения, тем самым однозначно определяется левая часть последнего уравнения, что позволяет найти силу F, а затем и силу N давления цепочки на стол.

Рассмотрим эти соображения.

Во-первых, поскольку отделяющиеся от тела, упавшие на стол звенья имеют скорость v' = 0 (удар абсолютно неупругий), относительная скорость u = v' – v = –v, и 2-й закон Ньютона в данном частном случае принимает вид:

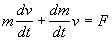
Во-вторых, как и в предыдущей задаче, m =  l =  h, 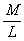=. Как следствие 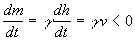, масса тела уменьшается вместе с высотой h, которая изменяется со скоростью v тела, v < 0. В третьих, как и в предыдущей задаче, последнее звено свободно ложится на стол, следовательно, натяжение T0 цепи на нижнем конце падающего участка равно нулю (T0 = 0). На верхнем его конце натяжение, очевидно, равно нулю, поэтому каждое звено вертикальной цепочки, за исключением упавшего последнего звена, падает свободно с ускорением . Как известно, при свободном падении с нулевой начальной скоростью текущая скорость v определяется пройденным путем s: 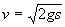. Для верхнего звена, а значит, и любого звена вертикального участка, при высоте h этот путь s = L – h, поэтому .

Полученные данные определяют силу F, действующую на вертикальный участок цепочки, включая последнее, покоящееся, звено:

Теперь силу F нужно связать с силой давления N всей цепи на стол. Сила F складывается из силы тяжести и силы реакции стола N > 0, действующей на вертикальный участок в точке падения звеньев. По 3-му закону Ньютона N равна силе давления вертикального участка на стол в этой точке (стандартно имеется в виду величина этой силы, направленной вниз):

F = N – mg.

Но N однозначно связана с полной силой давления N: N складывается из силы давления N вертикального участка и веса P = (M – m)g свободно лежащей на столе части цепочки:

N = N + p = N + (M – m)g,

откуда N = N – (M – m)g.

Стало быть, F = N – mg = N – Mg,

откуда, подставляя известное значение F:

Окончательно :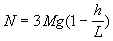

Кажется полезным прокомментировать как сам ответ, так и отдельные моменты решения. Ответ демонстрирует интересную разрывную зависимость силы давления N цепи на стол от времени. В начальный момент времени (t = 0), когда h = L, сила давления N = 0.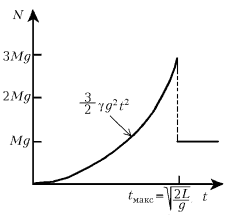

Затем, с уменьшением высоты h по закону свободного падения 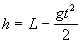она квадратично растет со временем по закону 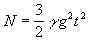. Наконец, в момент времени t=tмакс=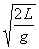, когда падает последнее звено цепи с максимальной скоростью  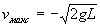и h = 0, сила давления достигает максимального значения Nмакс= 3Mg – тройной вес цепи. Но уже в следующий момент после падения и позднее, когда вся цепь свободно лежит на столе, сила давления равна просто весу цепочки: N = Mg при t > tмакс (см. рисунок).

Обратим внимание еще на одну тонкость. Когда мы делали заключение о свободном падении вертикального участка цепи, мы исключали из него нижнюю точку – последнее упавшее, отделившееся, звено, имеющее нулевую скорость. Сила, действующая на тело, была только силой тяжести, Fт = – mg. Когда же мы обсуждали силу F = N – mg, то это была внешняя сила, действующая на весь вертикальный участок, включая нижнюю точку, – последнее упавшее звено. Именно его останавливает сила N реакции стола (см. опять-таки обсуждение содержания внешней силы F при выводе 2-го закона Ньютона). Мы видим, что конечный вклад

в полную силу давления N связан с последним останавливающимся звеном, передающим свой импульс столу. (Сравните это явление с давлением молекулярного газа на стенку.)

И, наконец, последнее замечание. В качестве тела переменной массы можно взять участок цепи, лежащей на столе. При таком выборе будем иметь: скорость v = 0, масса m = (L – h) и увеличивается за счет падающих на стол звеньев, их скорость

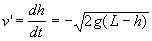
поэтому , относительная скорость u = v' – v = v', сила F = N – mg, 2-й закон Ньютона

принимает вид: -(-v')v'=N-mg, откуда, как и раньше,

На этот раз последнее упавшее, теперь добавляющееся, звено относится к лежащей на столе части цепи. Вот такие «хитрости». Их можно избежать, а решение задачи упростить, если рассмотреть целиком всю цепь и применить 2-й закон Ньютона к движению всей цепи.

Список литературы

Для подготовки данной работы были использованы материалы с сайта http://www.1september.ru/

Дата добавления: 17.05.2005

www.km.ru

Реферат Движение тел переменной массы

Д. ф.-м. н. Б.Л.Воронов

Задача 1. Однородная неупругая цепь длиной L и массой М перекинута через блок. Часть цепи лежит на столе высотой h, а часть на полу. Найти скорость равномерного движения звеньев цепи (рис. 1).

Задача 2. Однородная нерастяжимая цепь подвешена на нити так, что нижний конец ее касается крышки стола. Нить пережигают. Найти силу давления цепочки на стол в тот момент, когда над ним находится часть цепи длиной h. Масса цепи – М, ее длина – L, удар каждого звена считать абсолютно неупругим (рис. 2).

Задача 3. С какой силой давит на землю кобра, когда она, готовясь к прыжку, поднимается вертикально вверх с постоянной скоростью v (рис. 3)? Масса змеи – M, ее длина – L.

где m – неизменная масса тела, F – действующая на тело внешняя сила. В общем случае протяженных тел отдельные части тела движутся каждая со своей скоростью, и описание движения всех частей с учетом их взаимодействия резко усложняется.

Однако бывают случаи, когда движение некоторых частей составного тела можно описать сравнительно просто. Одним из таких случаев является случай движения тел переменной массы. Пусть имеется составная система и пусть в ней можно выделить некоторую часть, подсистему, движущуюся со скоростью v, причем состав ее меняется определенным образом. Будем называть эту подсистему телом переменной массы, если выполнены следующие условия. В каждый момент времени можно считать, что это тело либо является материальной точкой, либо все его части имеют одинаковую скорость v. С течением времени от тела непрерывно отделяются некоторые (бесконечно) малые его части, причем каждая со своей независимой скоростью v'; либо, наоборот, к телу непрерывно добавляются новые малые части, которые до «прилипания» имели свою скорость v' (возможно и то и другое). Таким образом, при движении тела меняется не только его скорость v = v(t), но и масса m = m(t), причем известна скорость изменения массы Случай <0 означает, что за промежуток времени t  t + dt от тела отделяются какие-то части массой –dm; случай Случай >0 означает, что за тот же промежуток времени к телу добавляются какие-то части массой dm. Примером первого случая являются ракета и поливальная машина, примером второго случая – снежная лавина. Мы ограничимся ситуациями, когда все отделяющиеся или добавляющиеся части имеют в каждый момент времени одну и ту же скорость v' = v'(t), следовательно, одну и ту же скорость u = v' – v относительно тела. Эту скорость u = u(t) называют относительной скоростью. Если она известна наряду с (например, в случае ракеты она определяется приготовлением, в случае снежной лавины v' = 0, стало быть, u = –v), то говорят о движении тела переменной массы.

2-й закон Ньютона для тел переменной массы имеет вид:

где F – суммарная внешняя сила, которая действует в данный момент времени как на тело (переменной массы m), так и на его отделяющиеся или добавляющиеся части (массы –dm или dm соответственно). Эту тонкость надо постоянно иметь в виду. Может случиться, что вся внешняя сила или конечная ее составляющая приложена именно к этим частям: под действием конечной внешней силы (бесконечно) малая масса (–dm или dm) за (бесконечно) малый промежуток времени t  t + dt меняет свою скорость на конечную величину, от v до v' или от v' до v, испытывая (бесконечно) большое ускорение. Именно этот случай реализуется в приводимых ниже задачах. Конечно, может случиться, что изменение скорости отделяющихся или добавляющихся частей обеспечивается внутренними силами. Так обстоит дело, например, в случае космической ракеты или снежной лавины.

2-й закон Ньютона для тел переменной массы можно переписать в эквивалентной форме (особенно удобной во втором случае):

Отличие от привычного случая постоянной массы состоит в том, что m = m(t) является теперь известной функцией времени, а к внешней силе F добавляется реактивная сила

Дадим вывод 2-го закона Ньютона для тел переменной массы (при первом чтении этот абзац можно пропустить). Он следует из 2-го закона Ньютона для любой, в том числе составной системы, в следующей общей форме:

т.е. приращение dp полного импульса p системы за интервал времени t  t + dt равно импульсу Fdt действующей на систему внешней силы F. Системой в рассматриваемом интервале времени t  t + dt является тело переменной массы вместе с отделяющимися или добавляющимися частями. В любом случае (>0 или <0 ) изменение dp импульса p за промежуток времени t  t + dt дается формулой:

dp = p(t + dt) – p(t) = (m + dm)(v + dv) – dmv' – mv.

Вывод этой формулы предоставляем читателю в качестве упражнения. Укажем лишь, что первое слагаемое справа относится ко времени t + dt, третье слагаемое – ко времени t, а второе слагаемое (–dmv') относится к моменту t + dt в случае отделяющихся частей (массой –dm > 0, <0 ) и к моменту t в случае добавляющихся частей (массой dm, >0 ). Раскрывая правую часть

dp = mdv – dm (v' – v) + dmdv = mdv – dmu + dmdv

и приравнивая ее Fdt, имеем:

Деля обе части последнего равенства на dt, переходя к переделу dt  0 и отбрасывая стремящееся к нулю слагаемое  получаем окончательно:

Из вывода следует указанное выше содержание понятия внешней силы F.

Теперь перейдем к решению задач.

Задача 1.Возьмем в качестве тела переменной массы лежащий на столе участок цепи. Цепь считается нерастяжимой, толщина цепи – пренебрежимо малой, поэтому можно считать, что весь этот участок занимает пренебрежимо малый объем (сосредоточен в точке) в основании левого вертикального участка цепи. Движение носит одномерный характер, вдоль вертикальной оси y (начало отсчета на полу), поэтому достаточно рассматривать только y-компоненту 2-го закона Ньютона (значок «y» для у-компонент векторов v, u, F в дальнейшем опускаем):

(прочие компоненты уравнений движения имеют вид 0 = 0). Именно это уравнение должно определить скорость равномерного движения вертикальных звеньев цепи, поскольку они отделяются от нашего тела.

В каждый момент времени все звенья рассматриваемого участка свободно, без натяжения, лежат на столе, v = 0, соответственно , сила тяжести компенсируется силой реакции стола. Отделяющееся первое сверху звено, лежащее в основании вертикального участка, уходит вверх с постоянной во времени вертикальной скоростью v' > 0. Эта скорость и является искомой. Относительная скорость u = v' – v = v'. Масса тела m = l, где l – длина рассматриваемого участка,  – линейная плотность цепи. Длина l, а значит, и масса m, уменьшаются за счет уходящих вверх звеньев; вследствие нерастяжимости цепи

соответственно

Остается определить вертикальную компоненту F внешней силы F. Она равна натяжению Th левой вертикальной части цепи на нижнем ее конце, находящемся на высоте y = h. Приложена эта сила к отделяющемуся от тела первому сверху звену, тогда как все звенья тела лежат свободно (см. выше о внешней силе F). Th в свою очередь определяется условиями движения вертикальных участков цепи. Если они движутся равномерно, как это и принимается в условии задачи, и, кроме того, цепь справа ложится на пол свободно, т.е. натяжение T0 правого вертикального участка на нижнем его конце, у пола, на высоте y = 0, равно нулю (T0 = 0), то Th равно разности веса Pправ правого участка и веса Pлев левого вертикального участков цепи: Th = Pправ – Pлев.

Мы оставляем читателю соответствующие рассуждения, укажем лишь, что при равномерном движении любого вертикального участка цепи его вес компенсируется разностью натяжений на концах этого участка, кроме того, при безынерционном блоке (что неявно принимается), натяжение цепи справа и слева от блока одинаково. Разность весов определяется разностью масс, следовательно, разностью длин соответствующих участков:

Pправ – Pлев = hg,

так что

F = hg > 0.

С учетом сказанного 2-й закон Ньютона принимает вид:

– (–v')v' = hg,

или: v'2 = hg,

откуда находим искомую скорость:

В качестве упражнения читателю предлагается решить задачу, взяв в качестве тела переменной массы некоторый участок вертикальной цепи. Видимо, проще всего выбрать некоторый нижний отрезок левого вертикального участка с фиксированным верхним звеном (но не высотой!). Тонкость будет в определении силы F: натяжение цепи Th на нижнем конце теперь, когда звено, лежащее в основании и имеющее скорость v', включается в состав тела переменной массы, равно нулю (Th = 0), а прежнее натяжение цепи Th = hg является теперь внутренней силой. Любопытно, что ответ не зависит от длины выбранного отрезка и его можно взять сколь угодно малым, достаточно рассматривать в каждый момент времени только звено, лежащее в основании цепи. Это же ясно и из предыдущего рассмотрения.

Задача 2. В качестве тела переменной массы возьмем вертикальный, падающий, участок цепи переменной длины l = h, h – высота цепи над столом. Как и в предыдущей задаче, движение одномерное, вдоль вертикальной оси y, поэтому вследствие нерастяжимости цепи все падающие звенья имеют одну и ту же скорость v, и 2-й закон Ньютона имеет прежний вид:

Оказывается, дополнительные соображения однозначно определяют закон движения, тем самым однозначно определяется левая часть последнего уравнения, что позволяет найти силу F, а затем и силу N давления цепочки на стол.

Рассмотрим эти соображения.

Во-первых, поскольку отделяющиеся от тела, упавшие на стол звенья имеют скорость v' = 0 (удар абсолютно неупругий), относительная скорость u = v' – v = –v, и 2-й закон Ньютона в данном частном случае принимает вид:

Во-вторых, как и в предыдущей задаче, m =  l =  h, =. Как следствие , масса тела уменьшается вместе с высотой h, которая изменяется со скоростью v тела, v < 0. В третьих, как и в предыдущей задаче, последнее звено свободно ложится на стол, следовательно, натяжение T0 цепи на нижнем конце падающего участка равно нулю (T0 = 0). На верхнем его конце натяжение, очевидно, равно нулю, поэтому каждое звено вертикальной цепочки, за исключением упавшего последнего звена, падает свободно с ускорением . Как известно, при свободном падении с нулевой начальной скоростью текущая скорость v определяется пройденным путем s: . Для верхнего звена, а значит, и любого звена вертикального участка, при высоте h этот путь s = L – h, поэтому .

Полученные данные определяют силу F, действующую на вертикальный участок цепочки, включая последнее, покоящееся, звено:

Теперь силу F нужно связать с силой давления N всей цепи на стол. Сила F складывается из силы тяжести и силы реакции стола N > 0, действующей на вертикальный участок в точке падения звеньев. По 3-му закону Ньютона N равна силе давления вертикального участка на стол в этой точке (стандартно имеется в виду величина этой силы, направленной вниз):

F = N – mg.

Но N однозначно связана с полной силой давления N: N складывается из силы давления N вертикального участка и веса P = (M – m)g свободно лежащей на столе части цепочки:

N = N + p = N + (M – m)g,

откуда N = N – (M – m)g.

Стало быть, F = N – mg = N – Mg,

откуда, подставляя известное значение F:

Окончательно :

Кажется полезным прокомментировать как сам ответ, так и отдельные моменты решения. Ответ демонстрирует интересную разрывную зависимость силы давления N цепи на стол от времени. В начальный момент времени (t = 0), когда h = L, сила давления N = 0.

Затем, с уменьшением высоты h по закону свободного падения она квадратично растет со временем по закону . Наконец, в момент времени t=tмакс=, когда падает последнее звено цепи с максимальной скоростью  и h = 0, сила давления достигает максимального значения Nмакс= 3Mg – тройной вес цепи. Но уже в следующий момент после падения и позднее, когда вся цепь свободно лежит на столе, сила давления равна просто весу цепочки: N = Mg при t > tмакс (см. рисунок).

Обратим внимание еще на одну тонкость. Когда мы делали заключение о свободном падении вертикального участка цепи, мы исключали из него нижнюю точку – последнее упавшее, отделившееся, звено, имеющее нулевую скорость. Сила, действующая на тело, была только силой тяжести, Fт = – mg. Когда же мы обсуждали силу F = N – mg, то это была внешняя сила, действующая на весь вертикальный участок, включая нижнюю точку, – последнее упавшее звено. Именно его останавливает сила N реакции стола (см. опять-таки обсуждение содержания внешней силы F при выводе 2-го закона Ньютона). Мы видим, что конечный вклад

в полную силу давления N связан с последним останавливающимся звеном, передающим свой импульс столу. (Сравните это явление с давлением молекулярного газа на стенку.)

И, наконец, последнее замечание. В качестве тела переменной массы можно взять участок цепи, лежащей на столе. При таком выборе будем иметь: скорость v = 0, масса m = (L – h) и увеличивается за счет падающих на стол звеньев, их скорость

поэтому , относительная скорость u = v' – v = v', сила F = N – mg, 2-й закон Ньютона

принимает вид: -(-v')v'=N-mg, откуда, как и раньше,

На этот раз последнее упавшее, теперь добавляющееся, звено относится к лежащей на столе части цепи. Вот такие «хитрости». Их можно избежать, а решение задачи упростить, если рассмотреть целиком всю цепь и применить 2-й закон Ньютона к движению всей цепи.

Список литературы

Для подготовки данной работы были использованы материалы с сайта http://www.1september.ru/

bukvasha.ru

Реферат : Движение тел переменной массы

Движение тел переменной массы

Д. ф.-м. н. Б.Л.Воронов

Задача 1. Однородная неупругая цепь длиной L и массой М перекинута через блок. Часть цепи лежит на столе высотой h, а часть на полу. Найти скорость равномерного движения звеньев цепи (рис. 1).

Задача 2. Однородная нерастяжимая цепь подвешена на нити так, что нижний конец ее касается крышки стола. Нить пережигают. Найти силу давления цепочки на стол в тот момент, когда над ним находится часть цепи длиной h. Масса цепи – М, ее длина – L, удар каждого звена считать абсолютно неупругим (рис. 2).

Задача 3. С какой силой давит на землю кобра, когда она, готовясь к прыжку, поднимается вертикально вверх с постоянной скоростью v (рис. 3)? Масса змеи – M, ее длина – L.

Начнем с хорошо известной ситуации. Пусть тело можно считать материальной точкой (например, можно пренебречь его структурой и размерами или вести речь только о центре масс тела) либо все части протяженного тела имеют одну и ту же скорость v. Тогда 2-й закон Ньютона, в теоретической механике чаще говорят – уравнения движения, для такого тела имеет вид:

где m – неизменная масса тела, F – действующая на тело внешняя сила. В общем случае протяженных тел отдельные части тела движутся каждая со своей скоростью, и описание движения всех частей с учетом их взаимодействия резко усложняется.

Однако бывают случаи, когда движение некоторых частей составного тела можно описать сравнительно просто. Одним из таких случаев является случай движения тел переменной массы. Пусть имеется составная система и пусть в ней можно выделить некоторую часть, подсистему, движущуюся со скоростью v, причем состав ее меняется определенным образом. Будем называть эту подсистему телом переменной массы, если выполнены следующие условия. В каждый момент времени можно считать, что это тело либо является материальной точкой, либо все его части имеют одинаковую скорость v. С течением времени от тела непрерывно отделяются некоторые (бесконечно) малые его части, причем каждая со своей независимой скоростью v'; либо, наоборот, к телу непрерывно добавляются новые малые части, которые до «прилипания» имели свою скорость v' (возможно и то и другое). Таким образом, при движении тела меняется не только его скорость v = v(t), но и масса m = m(t), причем известна скорость изменения массы Случай <0 означает, что за промежуток времени t  t + dt от тела отделяются какие-то части массой –dm; случай Случай >0 означает, что за тот же промежуток времени к телу добавляются какие-то части массой dm. Примером первого случая являются ракета и поливальная машина, примером второго случая – снежная лавина. Мы ограничимся ситуациями, когда все отделяющиеся или добавляющиеся части имеют в каждый момент времени одну и ту же скорость v' = v'(t), следовательно, одну и ту же скорость u = v' – v относительно тела. Эту скорость u = u(t) называют относительной скоростью. Если она известна наряду с (например, в случае ракеты она определяется приготовлением, в случае снежной лавины v' = 0, стало быть, u = –v), то говорят о движении тела переменной массы.

2-й закон Ньютона для тел переменной массы имеет вид:

где F – суммарная внешняя сила, которая действует в данный момент времени как на тело (переменной массы m), так и на его отделяющиеся или добавляющиеся части (массы –dm или dm соответственно). Эту тонкость надо постоянно иметь в виду. Может случиться, что вся внешняя сила или конечная ее составляющая приложена именно к этим частям: под действием конечной внешней силы (бесконечно) малая масса (–dm или dm) за (бесконечно) малый промежуток времени t  t + dt меняет свою скорость на конечную величину, от v до v' или от v' до v, испытывая (бесконечно) большое ускорение. Именно этот случай реализуется в приводимых ниже задачах. Конечно, может случиться, что изменение скорости отделяющихся или добавляющихся частей обеспечивается внутренними силами. Так обстоит дело, например, в случае космической ракеты или снежной лавины.

2-й закон Ньютона для тел переменной массы можно переписать в эквивалентной форме (особенно удобной во втором случае):

Отличие от привычного случая постоянной массы состоит в том, что m = m(t) является теперь известной функцией времени, а к внешней силе F добавляется реактивная сила

Дадим вывод 2-го закона Ньютона для тел переменной массы (при первом чтении этот абзац можно пропустить). Он следует из 2-го закона Ньютона для любой, в том числе составной системы, в следующей общей форме:

т.е. приращение dp полного импульса p системы за интервал времени t  t + dt равно импульсу Fdt действующей на систему внешней силы F. Системой в рассматриваемом интервале времени t  t + dt является тело переменной массы вместе с отделяющимися или добавляющимися частями. В любом случае (>0 или <0 ) изменение dp импульса p за промежуток времени t  t + dt дается формулой:

dp = p(t + dt) – p(t) = (m + dm)(v + dv) – dmv' – mv.

Вывод этой формулы предоставляем читателю в качестве упражнения. Укажем лишь, что первое слагаемое справа относится ко времени t + dt, третье слагаемое – ко времени t, а второе слагаемое (–dmv') относится к моменту t + dt в случае отделяющихся частей (массой –dm > 0, <0 ) и к моменту t в случае добавляющихся частей (массой dm, >0 ). Раскрывая правую часть

dp = mdv – dm (v' – v) + dmdv = mdv – dmu + dmdv

и приравнивая ее Fdt, имеем:

Деля обе части последнего равенства на dt, переходя к переделу dt  0 и отбрасывая стремящееся к нулю слагаемое получаем окончательно:

Из вывода следует указанное выше содержание понятия внешней силы F.

Теперь перейдем к решению задач.

Задача 1.Возьмем в качестве тела переменной массы лежащий на столе участок цепи. Цепь считается нерастяжимой, толщина цепи – пренебрежимо малой, поэтому можно считать, что весь этот участок занимает пренебрежимо малый объем (сосредоточен в точке) в основании левого вертикального участка цепи. Движение носит одномерный характер, вдоль вертикальной оси y (начало отсчета на полу), поэтому достаточно рассматривать только y-компоненту 2-го закона Ньютона (значок «y» для у-компонент векторов v, u, F в дальнейшем опускаем):

(прочие компоненты уравнений движения имеют вид 0 = 0). Именно это уравнение должно определить скорость равномерного движения вертикальных звеньев цепи, поскольку они отделяются от нашего тела.

В каждый момент времени все звенья рассматриваемого участка свободно, без натяжения, лежат на столе, v = 0, соответственно , сила тяжести компенсируется силой реакции стола. Отделяющееся первое сверху звено, лежащее в основании вертикального участка, уходит вверх с постоянной во времени вертикальной скоростью v' > 0. Эта скорость и является искомой. Относительная скорость u = v' – v = v'. Масса тела m = l, где l – длина рассматриваемого участка,  – линейная плотность цепи. Длина l, а значит, и масса m, уменьшаются за счет уходящих вверх звеньев; вследствие нерастяжимости цепи

соответственно

Остается определить вертикальную компоненту F внешней силы F. Она равна натяжению Th левой вертикальной части цепи на нижнем ее конце, находящемся на высоте y = h. Приложена эта сила к отделяющемуся от тела первому сверху звену, тогда как все звенья тела лежат свободно (см. выше о внешней силе F). Th в свою очередь определяется условиями движения вертикальных участков цепи. Если они движутся равномерно, как это и принимается в условии задачи, и, кроме того, цепь справа ложится на пол свободно, т.е. натяжение T0 правого вертикального участка на нижнем его конце, у пола, на высоте y = 0, равно нулю (T0 = 0), то Th равно разности веса Pправ правого участка и веса Pлев левого вертикального участков цепи: Th = Pправ – Pлев.

Мы оставляем читателю соответствующие рассуждения, укажем лишь, что при равномерном движении любого вертикального участка цепи его вес компенсируется разностью натяжений на концах этого участка, кроме того, при безынерционном блоке (что неявно принимается), натяжение цепи справа и слева от блока одинаково. Разность весов определяется разностью масс, следовательно, разностью длин соответствующих участков:

Pправ – Pлев = hg,

так что

F = hg > 0.

С учетом сказанного 2-й закон Ньютона принимает вид:

– (–v')v' = hg,

или: v'2 = hg,

откуда находим искомую скорость:

В качестве упражнения читателю предлагается решить задачу, взяв в качестве тела переменной массы некоторый участок вертикальной цепи. Видимо, проще всего выбрать некоторый нижний отрезок левого вертикального участка с фиксированным верхним звеном (но не высотой!). Тонкость будет в определении силы F: натяжение цепи Th на нижнем конце теперь, когда звено, лежащее в основании и имеющее скорость v', включается в состав тела переменной массы, равно нулю (Th = 0), а прежнее натяжение цепи Th = hg является теперь внутренней силой. Любопытно, что ответ не зависит от длины выбранного отрезка и его можно взять сколь угодно малым, достаточно рассматривать в каждый момент времени только звено, лежащее в основании цепи. Это же ясно и из предыдущего рассмотрения.

Задача 2. В качестве тела переменной массы возьмем вертикальный, падающий, участок цепи переменной длины l = h, h – высота цепи над столом. Как и в предыдущей задаче, движение одномерное, вдоль вертикальной оси y, поэтому вследствие нерастяжимости цепи все падающие звенья имеют одну и ту же скорость v, и 2-й закон Ньютона имеет прежний вид:

Оказывается, дополнительные соображения однозначно определяют закон движения, тем самым однозначно определяется левая часть последнего уравнения, что позволяет найти силу F, а затем и силу N давления цепочки на стол.

Рассмотрим эти соображения.

Во-первых, поскольку отделяющиеся от тела, упавшие на стол звенья имеют скорость v' = 0 (удар абсолютно неупругий), относительная скорость u = v' – v = –v, и 2-й закон Ньютона в данном частном случае принимает вид:

Во-вторых, как и в предыдущей задаче, m =  l =  h, =. Как следствие , масса тела уменьшается вместе с высотой h, которая изменяется со скоростью v тела, v < 0. В третьих, как и в предыдущей задаче, последнее звено свободно ложится на стол, следовательно, натяжение T0 цепи на нижнем конце падающего участка равно нулю (T0 = 0). На верхнем его конце натяжение, очевидно, равно нулю, поэтому каждое звено вертикальной цепочки, за исключением упавшего последнего звена, падает свободно с ускорением . Как известно, при свободном падении с нулевой начальной скоростью текущая скорость v определяется пройденным путем s: . Для верхнего звена, а значит, и любого звена вертикального участка, при высоте h этот путь s = L – h, поэтому .

Полученные данные определяют силу F, действующую на вертикальный участок цепочки, включая последнее, покоящееся, звено:

Теперь силу F нужно связать с силой давления N всей цепи на стол. Сила F складывается из силы тяжести и силы реакции стола N > 0, действующей на вертикальный участок в точке падения звеньев. По 3-му закону Ньютона N равна силе давления вертикального участка на стол в этой точке (стандартно имеется в виду величина этой силы, направленной вниз):

F = N – mg.

Но N однозначно связана с полной силой давления N: N складывается из силы давления N вертикального участка и веса P = (M – m)g свободно лежащей на столе части цепочки:

N = N + p = N + (M – m)g,

откуда N = N – (M – m)g.

Стало быть, F = N – mg = N – Mg,

откуда, подставляя известное значение F:

Окончательно :

Кажется полезным прокомментировать как сам ответ, так и отдельные моменты решения. Ответ демонстрирует интересную разрывную зависимость силы давления N цепи на стол от времени. В начальный момент времени (t = 0), когда h = L, сила давления N = 0.

Затем, с уменьшением высоты h по закону свободного падения она квадратично растет со временем по закону . Наконец, в момент времени t=tмакс=, когда падает последнее звено цепи с максимальной скоростью и h = 0, сила давления достигает максимального значения Nмакс= 3Mg – тройной вес цепи. Но уже в следующий момент после падения и позднее, когда вся цепь свободно лежит на столе, сила давления равна просто весу цепочки: N = Mg при t > tмакс (см. рисунок).

Обратим внимание еще на одну тонкость. Когда мы делали заключение о свободном падении вертикального участка цепи, мы исключали из него нижнюю точку – последнее упавшее, отделившееся, звено, имеющее нулевую скорость. Сила, действующая на тело, была только силой тяжести, Fт = – mg. Когда же мы обсуждали силу F = N – mg, то это была внешняя сила, действующая на весь вертикальный участок, включая нижнюю точку, – последнее упавшее звено. Именно его останавливает сила N реакции стола (см. опять-таки обсуждение содержания внешней силы F при выводе 2-го закона Ньютона). Мы видим, что конечный вклад

в полную силу давления N связан с последним останавливающимся звеном, передающим свой импульс столу. (Сравните это явление с давлением молекулярного газа на стенку.)

И, наконец, последнее замечание. В качестве тела переменной массы можно взять участок цепи, лежащей на столе. При таком выборе будем иметь: скорость v = 0, масса m = (L – h) и увеличивается за счет падающих на стол звеньев, их скорость

поэтому , относительная скорость u = v' – v = v', сила F = N – mg, 2-й закон Ньютона

принимает вид: -(-v')v'=N-mg, откуда, как и раньше,

На этот раз последнее упавшее, теперь добавляющееся, звено относится к лежащей на столе части цепи. Вот такие «хитрости». Их можно избежать, а решение задачи упростить, если рассмотреть целиком всю цепь и применить 2-й закон Ньютона к движению всей цепи.

Список литературы

Для подготовки данной работы были использованы материалы с сайта http://www.1september.ru/

topref.ru

Движение тел переменной массы — реферат

Движение тел переменной массы

Начнем с хорошо известной ситуации. Пусть тело можно считать материальной точкой (например, можно пренебречь его структурой и размерами или вести речь только о центре масс тела) либо все части протяженного тела имеют одну и ту же скорость v. Тогда 2-й закон Ньютона, в теоретической механике чаще говорят - уравнения движения, для такого тела имеет вид:

где m - неизменная масса тела, F - действующая на тело внешняя сила. В общем случае протяженных тел отдельные части тела движутся каждая со своей скоростью, и описание движения всех частей с учетом их взаимодействия резко усложняется.

Однако бывают случаи, когда движение некоторых частей составного тела можно описать сравнительно просто. Одним из таких случаев является случай движения тел переменной массы. Пусть имеется составная система и пусть в ней можно выделить некоторую часть, подсистему, движущуюся со скоростью v, причем состав ее меняется определенным образом. Будем называть эту подсистему телом переменной массы, если выполнены следующие условия. В каждый момент времени можно считать, что это тело либо является материальной точкой, либо все его части имеют одинаковую скорость v. С течением времени от тела непрерывно отделяются некоторые (бесконечно) малые его части, причем каждая со своей независимой скоростью v'; либо, наоборот, к телу непрерывно добавляются новые малые части, которые до «прилипания» имели свою скорость v' (возможно и то и другое). Таким образом, при движении тела меняется не только его скорость v = v(t), но и масса m = m(t), причем известна скорость изменения массы Случай <0 означает, что за промежуток времени t ¸ t + dt от тела отделяются какие-то части массой -dm; случай Случай >0 означает, что за тот же промежуток времени к телу добавляются какие-то части массой dm. Примером первого случая являются ракета и поливальная машина, примером второго случая - снежная лавина. Мы ограничимся ситуациями, когда все отделяющиеся или добавляющиеся части имеют в каждый момент времени одну и ту же скорость v' = v'(t), следовательно, одну и ту же скорость u = v' - v относительно тела. Эту скорость u = u(t) называют относительной скоростью. Если она известна наряду с (например, в случае ракеты она определяется приготовлением, в случае снежной лавины v' = 0, стало быть, u = -v), то говорят о движении тела переменной массы.

2-й закон Ньютона для тел переменной массы имеет вид:

где F - суммарная внешняя сила, которая действует в данный момент времени как на тело (переменной массы m), так и на его отделяющиеся или добавляющиеся части (массы -dm или dm соответственно). Эту тонкость надо постоянно иметь в виду. Может случиться, что вся внешняя сила или конечная ее составляющая приложена именно к этим частям: под действием конечной внешней силы (бесконечно) малая масса (-dm или dm) за (бесконечно) малый промежуток времени t ¸ t + dt меняет свою скорость на конечную величину, от v до v' или от v' до v, испытывая (бесконечно) большое ускорение. Именно этот случай реализуется в приводимых ниже задачах. Конечно, может случиться, что изменение скорости отделяющихся или добавляющихся частей обеспечивается внутренними силами. Так обстоит дело, например, в случае космической ракеты или снежной лавины.

2-й закон Ньютона для тел переменной массы можно переписать в эквивалентной форме (особенно удобной во втором случае):

Отличие от привычного случая постоянной массы состоит в том, что m = m(t) является теперь известной функцией времени, а к внешней силе F добавляется реактивная сила

Дадим вывод 2-го закона Ньютона для тел переменной массы (при первом чтении этот абзац можно пропустить). Он следует из 2-го закона Ньютона для любой, в том числе составной системы, в следующей общей форме:

т.е. приращение dp полного импульса p системы за интервал времени t ¸ t + dt равно импульсу Fdt действующей на систему внешней силы F. Системой в рассматриваемом интервале времени t ¸ t + dt является тело переменной массы вместе с отделяющимися или добавляющимися частями. В любом случае ( >0 или <0 ) изменение dp импульса p за промежуток времени t ¸ t + dt дается формулой:

dp = p(t + dt) - p(t) = (m + dm)(v + dv) - dmv' - mv.

Укажем лишь, что первое слагаемое справа относится ко времени t + dt, третье слагаемое - ко времени t, а второе слагаемое (-dmv') относится к моменту t + dt в случае отделяющихся частей (массой -dm > 0, <0 ) и к моменту t в случае добавляющихся частей (массой dm, >0 ). Раскрывая правую часть

dp = mdv - dm (v' - v) + dmdv = mdv - dmu + dmdv

и приравнивая ее Fdt, имеем:

Деля обе части последнего равенства на dt, переходя к переделу dt ® 0 и отбрасывая стремящееся к нулю слагаемое получаем окончательно:

Из вывода следует указанное выше содержание понятия внешней силы F.

myunivercity.ru

Реферат: Движение тел переменной массы

Д. ф.-м. н. Б.Л.Воронов

Задача 1. Однородная неупругая цепь длиной L и массой М перекинута через блок. Часть цепи лежит на столе высотой h, а часть на полу. Найти скорость равномерного движения звеньев цепи (рис. 1).

Задача 2. Однородная нерастяжимая цепь подвешена на нити так, что нижний конец ее касается крышки стола. Нить пережигают. Найти силу давления цепочки на стол в тот момент, когда над ним находится часть цепи длиной h. Масса цепи – М, ее длина – L, удар каждого звена считать абсолютно неупругим (рис. 2).

Задача 3. С какой силой давит на землю кобра, когда она, готовясь к прыжку, поднимается вертикально вверх с постоянной скоростью v (рис. 3)? Масса змеи – M, ее длина – L.

Начнем с хорошо известной ситуации. Пусть тело можно считать материальной точкой (например, можно пренебречь его структурой и размерами или вести речь только о центре масс тела) либо все части протяженного тела имеют одну и ту же скорость v. Тогда 2-й закон Ньютона, в теоретической механике чаще говорят – уравнения движения, для такого тела имеет вид:

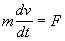
где m – неизменная масса тела, F – действующая на тело внешняя сила. В общем случае протяженных тел отдельные части тела движутся каждая со своей скоростью, и описание движения всех частей с учетом их взаимодействия резко усложняется.

Однако бывают случаи, когда движение некоторых частей составного тела можно описать сравнительно просто. Одним из таких случаев является случай движения тел переменной массы. Пусть имеется составная система и пусть в ней можно выделить некоторую часть, подсистему, движущуюся со скоростью v, причем состав ее меняется определенным образом. Будем называть эту подсистему телом переменной массы, если выполнены следующие условия. В каждый момент времени можно считать, что это тело либо является материальной точкой, либо все его части имеют одинаковую скорость v. С течением времени от тела непрерывно отделяются некоторые (бесконечно) малые его части, причем каждая со своей независимой скоростью v'; либо, наоборот, к телу непрерывно добавляются новые малые части, которые до «прилипания» имели свою скорость v' (возможно и то и другое). Таким образом, при движении тела меняется не только его скорость v = v(t), но и масса m = m(t), причем известна скорость изменения массы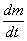Случай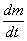<0 означает, что за промежуток времени t  t + dt от тела отделяются какие-то части массой –dm; случай Случай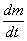>0 означает, что за тот же промежуток времени к телу добавляются какие-то части массой dm. Примером первого случая являются ракета и поливальная машина, примером второго случая – снежная лавина. Мы ограничимся ситуациями, когда все отделяющиеся или добавляющиеся части имеют в каждый момент времени одну и ту же скорость v' = v'(t), следовательно, одну и ту же скорость u = v' – v относительно тела. Эту скорость u = u(t) называют относительной скоростью. Если она известна наряду с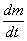(например, в случае ракеты она определяется приготовлением, в случае снежной лавины v' = 0, стало быть, u = –v), то говорят о движении тела переменной массы.

2-й закон Ньютона для тел переменной массы имеет вид:

где F – суммарная внешняя сила, которая действует в данный момент времени как на тело (переменной массы m), так и на его отделяющиеся или добавляющиеся части (массы –dm или dm соответственно). Эту тонкость надо постоянно иметь в виду. Может случиться, что вся внешняя сила или конечная ее составляющая приложена именно к этим частям: под действием конечной внешней силы (бесконечно) малая масса (–dm или dm) за (бесконечно) малый промежуток времени t  t + dt меняет свою скорость на конечную величину, от v до v' или от v' до v, испытывая (бесконечно) большое ускорение. Именно этот случай реализуется в приводимых ниже задачах. Конечно, может случиться, что изменение скорости отделяющихся или добавляющихся частей обеспечивается внутренними силами. Так обстоит дело, например, в случае космической ракеты или снежной лавины.

2-й закон Ньютона для тел переменной массы можно переписать в эквивалентной форме (особенно удобной во втором случае):

Отличие от привычного случая постоянной массы состоит в том, что m = m(t) является теперь известной функцией времени, а к внешней силе F добавляется реактивная сила

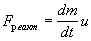
Дадим вывод 2-го закона Ньютона для тел переменной массы (при первом чтении этот абзац можно пропустить). Он следует из 2-го закона Ньютона для любой, в том числе составной системы, в следующей общей форме:

т.е. приращение dp полного импульса p системы за интервал времени t  t + dt равно импульсу Fdt действующей на систему внешней силы F. Системой в рассматриваемом интервале времени t  t + dt является тело переменной массы вместе с отделяющимися или добавляющимися частями. В любом случае (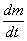>0 или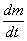<0 ) изменение dp импульса p за промежуток времени t  t + dt дается формулой:

dp = p(t + dt) – p(t) = (m + dm)(v + dv) – dmv' – mv.

Вывод этой формулы предоставляем читателю в качестве упражнения. Укажем лишь, что первое слагаемое справа относится ко времени t + dt, третье слагаемое – ко времени t, а второе слагаемое (–dmv') относится к моменту t + dt в случае отделяющихся частей (массой –dm > 0,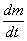<0 ) и к моменту t в случае добавляющихся частей (массой dm,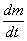>0 ). Раскрывая правую часть

dp = mdv – dm (v' – v) + dmdv = mdv – dmu + dmdv

и приравнивая ее Fdt, имеем:

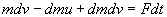
Деля обе части последнего равенства на dt, переходя к переделу dt  0 и отбрасывая стремящееся к нулю слагаемое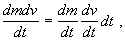получаем окончательно:

Из вывода следует указанное выше содержание понятия внешней силы F.

Теперь перейдем к решению задач.

Задача 1.Возьмем в качестве тела переменной массы лежащий на столе участок цепи. Цепь считается нерастяжимой, толщина цепи – пренебрежимо малой, поэтому можно считать, что весь этот участок занимает пренебрежимо малый объем (сосредоточен в точке) в основании левого вертикального участка цепи. Движение носит одномерный характер, вдоль вертикальной оси y (начало отсчета на полу), поэтому достаточно рассматривать только y-компоненту 2-го закона Ньютона (значок «y» для у-компонент векторов v, u, F в дальнейшем опускаем):

(прочие компоненты уравнений движения имеют вид 0 = 0). Именно это уравнение должно определить скорость равномерного движения вертикальных звеньев цепи, поскольку они отделяются от нашего тела.

В каждый момент времени все звенья рассматриваемого участка свободно, без натяжения, лежат на столе, v = 0, соответственно, сила тяжести компенсируется силой реакции стола. Отделяющееся первое сверху звено, лежащее в основании вертикального участка, уходит вверх с постоянной во времени вертикальной скоростью v' > 0. Эта скорость и является искомой. Относительная скорость u = v' – v = v'. Масса тела m = l, где l – длина рассматриваемого участка, – линейная плотность цепи. Длина l, а значит, и масса m, уменьшаются за счет уходящих вверх звеньев; вследствие нерастяжимости цепи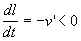

соответственно

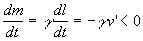
Остается определить вертикальную компоненту F внешней силы F. Она равна натяжению Th левой вертикальной части цепи на нижнем ее конце, находящемся на высоте y = h. Приложена эта сила к отделяющемуся от тела первому сверху звену, тогда как все звенья тела лежат свободно (см. выше о внешней силе F). Th в свою очередь определяется условиями движения вертикальных участков цепи. Если они движутся равномерно, как это и принимается в условии задачи, и, кроме того, цепь справа ложится на пол свободно, т.е. натяжение T0 правого вертикального участка на нижнем его конце, у пола, на высоте y = 0, равно нулю (T0 = 0), то Th равно разности веса Pправ правого участка и веса Pлев левого вертикального участков цепи: Th = Pправ – Pлев.

Мы оставляем читателю соответствующие рассуждения, укажем лишь, что при равномерном движении любого вертикального участка цепи его вес компенсируется разностью натяжений на концах этого участка, кроме того, при безынерционном блоке (что неявно принимается), натяжение цепи справа и слева от блока одинаково. Разность весов определяется разностью масс, следовательно, разностью длин соответствующих участков:

Pправ – Pлев = hg,

так что

F = hg > 0.

С учетом сказанного 2-й закон Ньютона принимает вид:

– (–v')v' = hg,

или: v'2 = hg,

откуда находим искомую скорость: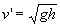

В качестве упражнения читателю предлагается решить задачу, взяв в качестве тела переменной массы некоторый участок вертикальной цепи. Видимо, проще всего выбрать некоторый нижний отрезок левого вертикального участка с фиксированным верхним звеном (но не высотой!). Тонкость будет в определении силы F: натяжение цепи Th на нижнем конце теперь, когда звено, лежащее в основании и имеющее скорость v', включается в состав тела переменной массы, равно нулю (Th = 0), а прежнее натяжение цепи Th = hg является теперь внутренней силой. Любопытно, что ответ не зависит от длины выбранного отрезка и его можно взять сколь угодно малым, достаточно рассматривать в каждый момент времени только звено, лежащее в основании цепи. Это же ясно и из предыдущего рассмотрения.

Задача 2. В качестве тела переменной массы возьмем вертикальный, падающий, участок цепи переменной длины l = h, h – высота цепи над столом. Как и в предыдущей задаче, движение одномерное, вдоль вертикальной оси y, поэтому вследствие нерастяжимости цепи все падающие звенья имеют одну и ту же скорость v, и 2-й закон Ньютона имеет прежний вид:

Оказывается, дополнительные соображения однозначно определяют закон движения, тем самым однозначно определяется левая часть последнего уравнения, что позволяет найти силу F, а затем и силу N давления цепочки на стол.

Рассмотрим эти соображения.

Во-первых, поскольку отделяющиеся от тела, упавшие на стол звенья имеют скорость v' = 0 (удар абсолютно неупругий), относительная скорость u = v' – v = –v, и 2-й закон Ньютона в данном частном случае принимает вид:

Во-вторых, как и в предыдущей задаче, m =  l =  h, =. Как следствие, масса тела уменьшается вместе с высотой h, которая изменяется со скоростью v тела, v < 0. В третьих, как и в предыдущей задаче, последнее звено свободно ложится на стол, следовательно, натяжение T0 цепи на нижнем конце падающего участка равно нулю (T0 = 0). На верхнем его конце натяжение, очевидно, равно нулю, поэтому каждое звено вертикальной цепочки, за исключением упавшего последнего звена, падает свободно с ускорением. Как известно, при свободном падении с нулевой начальной скоростью текущая скорость v определяется пройденным путем s: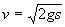. Для верхнего звена, а значит, и любого звена вертикального участка, при высоте h этот путь s = L – h, поэтому.

Полученные данные определяют силу F, действующую на вертикальный участок цепочки, включая последнее, покоящееся, звено:

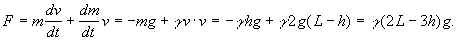
Теперь силу F нужно связать с силой давления N всей цепи на стол. Сила F складывается из силы тяжести и силы реакции стола N > 0, действующей на вертикальный участок в точке падения звеньев. По 3-му закону Ньютона N равна силе давления вертикального участка на стол в этой точке (стандартно имеется в виду величина этой силы, направленной вниз):

F = N – mg.

Но N однозначно связана с полной силой давления N: N складывается из силы давления N вертикального участка и веса P = (M – m)g свободно лежащей на столе части цепочки:

N = N + p = N + (M – m)g,

откуда N = N – (M – m)g.

Стало быть, F = N – mg = N – Mg,

откуда, подставляя известное значение F: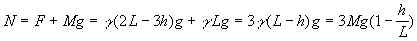

Окончательно :

Кажется полезным прокомментировать как сам ответ, так и отдельные моменты решения. Ответ демонстрирует интересную разрывную зависимость силы давления N цепи на стол от времени. В начальный момент времени (t = 0), когда h = L, сила давления N = 0.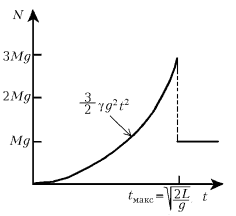

Затем, с уменьшением высоты h по закону свободного падения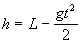она квадратично растет со временем по закону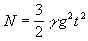. Наконец, в момент времени t=tмакс=, когда падает последнее звено цепи с максимальной скоростьюи h = 0, сила давления достигает максимального значения Nмакс= 3Mg – тройной вес цепи. Но уже в следующий момент после падения и позднее, когда вся цепь свободно лежит на столе, сила давления равна просто весу цепочки: N = Mg при t > tмакс (см. рисунок).

Обратим внимание еще на одну тонкость. Когда мы делали заключение о свободном падении вертикального участка цепи, мы исключали из него нижнюю точку – последнее упавшее, отделившееся, звено, имеющее нулевую скорость. Сила, действующая на тело, была только силой тяжести, Fт = – mg. Когда же мы обсуждали силу F = N – mg, то это была внешняя сила, действующая на весь вертикальный участок, включая нижнюю точку, – последнее упавшее звено. Именно его останавливает сила N реакции стола (см. опять-таки обсуждение содержания внешней силы F при выводе 2-го закона Ньютона). Мы видим, что конечный вклад

в полную силу давления N связан с последним останавливающимся звеном, передающим свой импульс столу. (Сравните это явление с давлением молекулярного газа на стенку.)

И, наконец, последнее замечание. В качестве тела переменной массы можно взять участок цепи, лежащей на столе. При таком выборе будем иметь: скорость v = 0, масса m = (L – h) и увеличивается за счет падающих на стол звеньев, их скорость

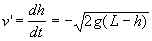
поэтому, относительная скорость u = v' – v = v', сила F = N – mg, 2-й закон Ньютона

принимает вид: -(-v')v'=N-mg, откуда, как и раньше,

На этот раз последнее упавшее, теперь добавляющееся, звено относится к лежащей на столе части цепи. Вот такие «хитрости». Их можно избежать, а решение задачи упростить, если рассмотреть целиком всю цепь и применить 2-й закон Ньютона к движению всей цепи.