|
|
|
|
 Far Far |
 WinNavigator WinNavigator |
 Frigate Frigate |
 Norton
Commander Norton
Commander |
 WinNC WinNC |
 Dos
Navigator Dos
Navigator |
 Servant
Salamander Servant
Salamander |
 Turbo
Browser Turbo
Browser |
|
|
 Winamp,
Skins, Plugins Winamp,
Skins, Plugins |
 Необходимые
Утилиты Необходимые
Утилиты |
 Текстовые
редакторы Текстовые
редакторы |
 Юмор Юмор |
|
|
|
File managers and best utilites |
/ Дробный факторный эксперимент_с46-49. Дробный факторный эксперимент реферат
2.3.2. Дробный факторный эксперимент (дфэ)
Полные факторные эксперименты обладают одним значительным недостатком – количество опытов стремительно растет с увеличением числа изучаемых параметров. Такие планы в той или иной степени могут ограничить исследования. Кроме того, количество опытов зачастую прямо пропорционально стоимости эксперимента.
Таблица ниже приводит данные о минимальном количестве опытов, необходимом для реализации экспериментов типа  в зависимости от количества параметров:
в зависимости от количества параметров:
| Количество параметров | Количество экспериментов |
| 2 | 4 |
| 3 | 8 |
| 4 | 16 |
| 5 | 32 |
| 6 | 64 |
| 7 | 128 |
| 8 | 256 |
| … | … |
| 15 | 32768 |
Чтобы сократить количество опытов применяют дробные факторные планы.
Дробным факторным экспериментом называется система экспериментов, представляющих собой часть ПФЭ, позволяющая рассчитывать коэффициенты уравнения регрессии и сократить объем экспериментальных данных. Такие эксперименты обладают меньшей информативностью, но позволяют значительно сократить количество опытов.
Метод построения дробных факторных планов легче продемонстрировать на конкретных примерах.
Запишем еще раз матрицу планирования ПФЭ (см. табл.2.3)
(см. табл.2.3)
Таблица 2.8
| № эксперимента | | | | | Отклик y |
| 1 | + | – | – | + | |
| 2 | + | + | – | – | |
| 3 | + | – | + | – | |
| 4 | + | + | + | + | |
Пользуясь таким планированием, можно вычислить четыре коэффициента и представить результаты эксперимента в виде неполного квадратного уравнения

Если имеются основания считать, что в выбранных интервалах варьирования процесс может быть описан линейной моделью, то достаточно определить три коэффициента:  и
и . Остается одна степень свободы. Употребим ее для минимизации числа опытов. При линейном приближении эффект взаимодействия стремиться к нулю
. Остается одна степень свободы. Употребим ее для минимизации числа опытов. При линейном приближении эффект взаимодействия стремиться к нулю  и вектор-столбец
и вектор-столбец можно использовать для нового фактора
можно использовать для нового фактора . Приравняем этот фактор взаимодействию
. Приравняем этот фактор взаимодействию . Матрица планирования запишется в виде табл.2.8.Полученный план содержит половину опытов ПФЭ и носит название полурепликой полного факторного эксперимента и обозначается
. Матрица планирования запишется в виде табл.2.8.Полученный план содержит половину опытов ПФЭ и носит название полурепликой полного факторного эксперимента и обозначается 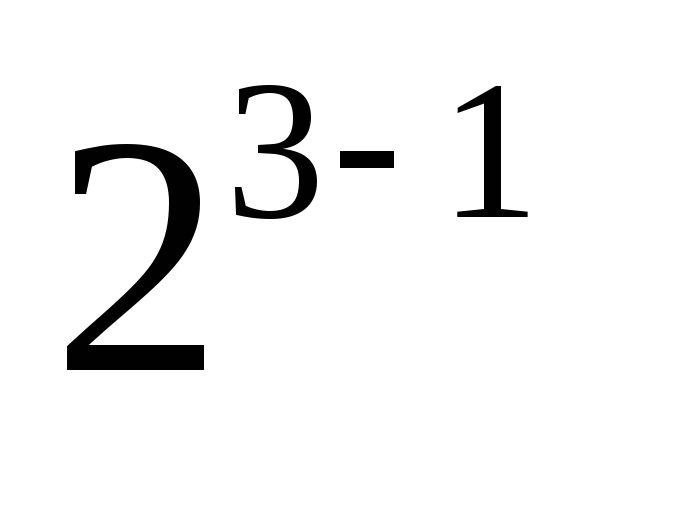 . Выбранное для дополнительного фактора произведение называетсягенератором плана (поскольку определяет для дополнительного фактора правило чередования уровней в ДФЭ).
. Выбранное для дополнительного фактора произведение называетсягенератором плана (поскольку определяет для дополнительного фактора правило чередования уровней в ДФЭ).
Графическое изображение планов ПФЭ 23 и ДФЭ 23-1 в факторном пространстве (для трех факторов - трехмерное пространство) представлено на рис. 2.11. План ПФЭ  представлен кубом с восемью узлами (точками плана), а возможные планы ДФЭ
представлен кубом с восемью узлами (точками плана), а возможные планы ДФЭ – проекциями этого куба на три плоскости. То есть из восьми узлов выбираются четыре. Из куба можно также выбрать четыре точки из восьми, не лежащие в одной плоскости, и сформировать план ДФЭ
– проекциями этого куба на три плоскости. То есть из восьми узлов выбираются четыре. Из куба можно также выбрать четыре точки из восьми, не лежащие в одной плоскости, и сформировать план ДФЭ .
.

По данному плану мы можем определить коэффициенты  . Однако коэффициенты
. Однако коэффициенты будут смешаны с парными взаимодействиями.
будут смешаны с парными взаимодействиями.
При значительном числе факторов определение смешанности в ДФЭ является трудоемким. Для нахождения, при каких факторах и взаимодействиях оценки коэффициентов будут смешанными, вводится понятие контраста. Контраст получают умножением обеих частей генератора плана вводимого дополнительного фактора  на этот фактор. Например, поскольку для ДФЭ (табл.2.8) генератор плана
на этот фактор. Например, поскольку для ДФЭ (табл.2.8) генератор плана , то для контраста получим
, то для контраста получим , т.к.
, т.к. , окончательно имеем
, окончательно имеем . Чтобы определить, с какими факторами и взаимодействиями смешана оценка
. Чтобы определить, с какими факторами и взаимодействиями смешана оценка , необходимо умножить обе части контраста на этот фактор. Например, для
, необходимо умножить обе части контраста на этот фактор. Например, для имеем:
имеем: , т.е.
, т.е. оценивается одновременно
оценивается одновременно и
и . Записывается это так
. Записывается это так 
Для  , имеем
, имеем  .
.
Для  , имеем
, имеем  ,
,
где  - действительные значения коэффициентов
- действительные значения коэффициентов .
.
В зависимости от числа факторов, входящих в контраст, говорят о разрешающей способности ДФЭ. Так, если для ДФЭ  в качестве генератора плана выбрано
в качестве генератора плана выбрано (контраст соответственно будет
(контраст соответственно будет ), то говорят, что у такого эксперимента разрешающая способность равна 4; если генератор
), то говорят, что у такого эксперимента разрешающая способность равна 4; если генератор и контраст
и контраст , то разрешающая способность равна 3. Генераторы плана с наибольшей разрешающей способностью называютглавными и отдают им предпочтение.
, то разрешающая способность равна 3. Генераторы плана с наибольшей разрешающей способностью называютглавными и отдают им предпочтение.
Аналогично могут быть построены полуреплики при более высокой размерности факторного пространства. Так, для четырех параметров  ПФЭ
ПФЭ возможны следующие взаимодействия:
возможны следующие взаимодействия:
 .
.
Полный факторный эксперимент, соответственно, потребует проведения 24 =16 экспериментов.
Составим матрицу для ДФЭ типа  . Эксперимент предполагает изучение 4 факторов, один из которых будет замещать взаимодействие между другими параметрами. Разрешение эксперимента составляет 3. Минимальное количество опытов рассчитываем как
. Эксперимент предполагает изучение 4 факторов, один из которых будет замещать взаимодействие между другими параметрами. Разрешение эксперимента составляет 3. Минимальное количество опытов рассчитываем как .
.
Ниже представлена матрица эксперимента 23:

Введем параметр  вместо взаимодействия
вместо взаимодействия . Значения фактора
. Значения фактора в каждом опыте будет вычисляться произведением факторов
в каждом опыте будет вычисляться произведением факторов и
и :
:

Так как параметр  приравнивается к взаимодействию трех других факторов, т.е. не считается самостоятельным параметром, все взаимодействия с его участием исключаются. Таким образом, взаимодействия
приравнивается к взаимодействию трех других факторов, т.е. не считается самостоятельным параметром, все взаимодействия с его участием исключаются. Таким образом, взаимодействия не изучаются в ходе эксперимента.
не изучаются в ходе эксперимента.
Можно было бы предположить, что подобное исключение членов матрицы значительно скажется на точности результатов эксперимента. В ряде случаев взаимодействия между параметрами действительно влияют на изучаемую систему и поэтому не могут быть исключены из эксперимента. Но, в остальном, пренебрежение взаимодействиями выше 2-го порядка, а иногда и взаимодействиями 2-го порядка, оправдано как минимум с точки зрения количества опытов и стоимости их проведения.
======
Очевидно, что ДФЭ типа  будет иметьp генераторов.
будет иметьp генераторов.
Планирование  позволяет наряду с линейными эффектами оценить и эффекты трех двойных взаимодействий
позволяет наряду с линейными эффектами оценить и эффекты трех двойных взаимодействий
Коэффициенты уравнения регрессии будут совместными оценками линейных эффектов и двойных взаимодействий

Объясняется это тем, что столбцы матрицы этих эффектов совпадают между собой и, следовательно, не могут быть разделены оценки этих эффектов.
Если бы мы положили 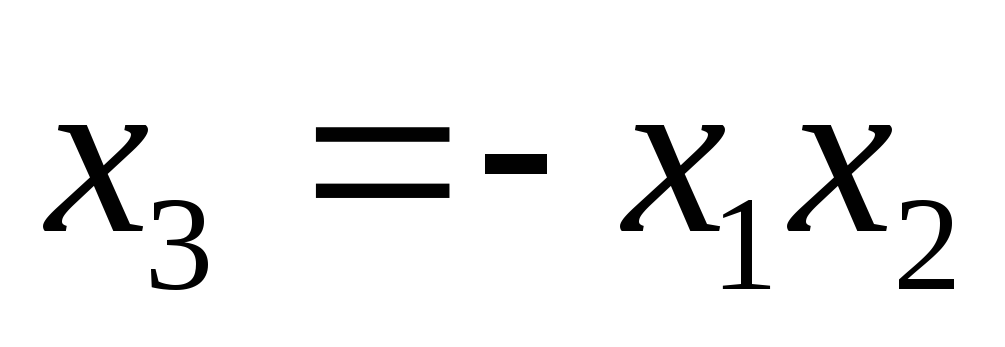 , то получили бы вторую половину матрицы
, то получили бы вторую половину матрицы 
| № эксперимента | | План | | Отклик y | |
| | | ||||
| 1 | + | – | – | – | |
| 2 | + | + | – | + | |
| 3 | + | – | + | + | |
| 4 | + | + | + | – | |
В этом случае совместные оценки имеют вид

При реализации обеих полуреплик можно получить раздельные оценки для линейных эффектов и эффектов взаимодействия, как и в полном факторном эксперименте . Объединение этих двух полуреплик и есть полный факторный эксперимент
. Объединение этих двух полуреплик и есть полный факторный эксперимент .
.
Аналогично могут быть построены полуреплики более высокой размерности факторного пространства. Так для оценки линейной модели четырех переменных  , содержащей пять членов, можно использовать полуреплики
, содержащей пять членов, можно использовать полуреплики  ПФЭ
ПФЭ (табл.2.5). Каждый план
(табл.2.5). Каждый план содержит 8 экспериментов, в то время как ПФЭ
содержит 8 экспериментов, в то время как ПФЭ содержит 16 экспериментов.
содержит 16 экспериментов.
| Номер эксперимента | | План | | | | | Реакция y | ||
| | | | |||||||
| 1 | + | - | - | - | - | + | + | + | y1 |
| 2 | + | + | - | - | + | - | - | + | y2 |
| 3 | + | - | + | - | + | - | + | - | y3 |
| 4 | + | + | + | - | - | + | - | - | y4 |
| 5 | + | - | - | + | + | + | - | - | y5 |
| 6 | + | + | - | + | - | - | + | - | y6 |
| 7 | + | - | + | + | - | - | - | + | y7 |
| 8 | + | + | + | + | + | + | + | + | y8 |
Генерирующие соотношения могут быть заданы в виде
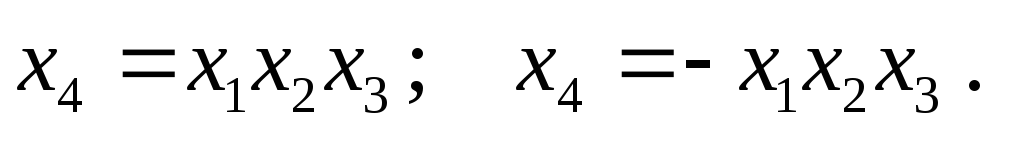
Дополнительные факторы  приравнены наиболее сложным (тройным) взаимодействиям, так как их влияние на модель в целом наименее существенно. Однако возможны и другие схемы построения полуреплик. Так можно было бы воспользоваться одной из следующих пар генерирующих соотношений
приравнены наиболее сложным (тройным) взаимодействиям, так как их влияние на модель в целом наименее существенно. Однако возможны и другие схемы построения полуреплик. Так можно было бы воспользоваться одной из следующих пар генерирующих соотношений
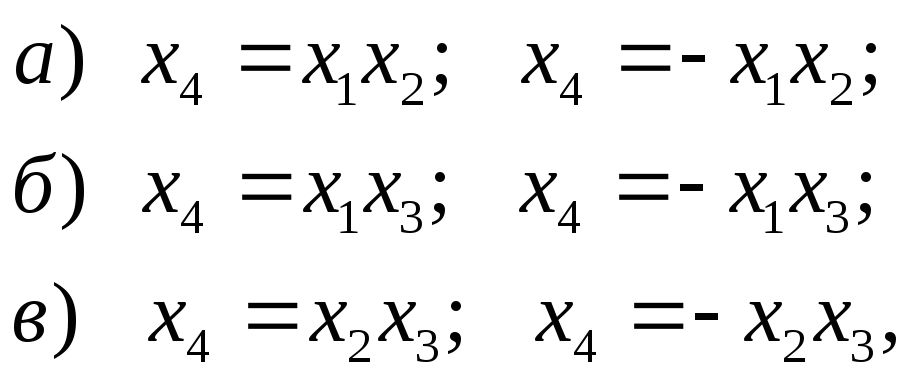
что привело бы к другим планам 
Если предполагается сохранить в модели кроме линейных членов какие-либо из взаимодействий, полезно провести предварительное статистическое исследование для выявления наиболее значимых из них. В этом случае выбор генерирующих соотношений осуществляется с учетом результатов такого исследования.
Поэтому, если после проведения экспериментов одной из полуреплик исследователь усомнился в правильности предположения о несущественности эффектов взаимодействий, он должен провести эксперименты второй полуреплики и разделить оценки по схеме

Возможность такого разделения очевидна, так как две полуреплики образуют полное факторное планирование 
studfiles.net
Дробный факторный эксперимент | Бесплатные курсовые, рефераты и дипломные работы
Во многих реальных процессах некоторые факторы взаимодействия могут отсутствовать. И тогда ПФЭ будет обладать избыточностью опытов.
Рассмотрим пути минимизации числа опытов.
Обратимся к уравнению (4.29). Если мы располагаем сведениями о том, что в выбранных интервалах варьирования процесс в статике может быть описан линейной моделью, то достаточно определить три коэффициента b0 ,b1 ,b2. В результате остается одна степень свободы, т.к. имеем четыре опыта, а количество констант три. Используем эту степень свободы для минимизации числа опытов. При линейном приближении b12 ®0 и тогда вектор -столбец х1х2 может быть использован для нового фактора х3.
Таблица 4.4
| Опыт | x0 | … x1 | x2 | x3 | y |
| 1 | +1 | +1 | +1 | +1 | y1 |
| 2 | +1 | -1 | +1 | -1 | y2 |
| 3 | +1 | +1 | -1 | -1 | y3 |
| 4 | +1 | -1 | -1 | +1 | y4 |
При этом эксперименте появляются смешанные оценки
 , (4.32)
, (4.32)
т.е. столбцы.
Пример. Допустим х1 и х2х3между собой неразличимы. Однако парные взаимодействия в линейной модели незначительны. Зато вместо восьми опытов для изучения влияния трех факторов можно поставить только четыре опыта, т.е. вместо ПФЭ 23 мы имеем 23-1. В теории эксперимента 23-1 называют полу- репликой. В общем случае имеют дело с дробной репликой. А факторный эксперимент называют дробным (ДФЭ).
Для уяснения принципа составления МПЭ ДФЭ введено понятие определяющего контраста. Он позволяет определить какие оценки смешаны друг с другом, не изучая МПЭ для выявления совпадающих столбцов. Для этого берут символичное обозначение произведения столбцов равного +1 или -1. Это и называют контрастом. Чтобы определить какой эффект смешан с данным, нужно помножить обе части определяющего контраста на столбец, соответствующий данному эффекту.
Пример. Пусть имеем три фактора х1 ,х2 ,х3 . При построении полуреплики 23-1 имеется только две возможности приравнять х3 либо к «+х1х2», либо к «-х1х2» (табл.4.5).
Таблица 4.5
| Опыт | x1 | x2 | x3 | x1x2x3 | Опыт | x1 | x2 | x3 | x1x2x3 |
| 1 | -1 | -1 | +1 | +1 | 1 | -1 | -1 | -1 | -1 |
| 2 | +1 | -1 | -1 | +1 | 2 | +1 | -1 | +1 | -1 |
| 3 | -1 | +1 | -1 | +1 | 3 | -1 | +1 | +1 | -1 |
| 4 | +1 | +1 | +1 | +1 | 4 | +1 | +1 | -1 | -1 |
Возьмем в качестве определяющего контраста  .Тогда
.Тогда  . Учитывая, что
. Учитывая, что  получаем
получаем  .
.
Теперь возьмем за определяющий контраст  . Получаем:
. Получаем:  . Эти выражения показывают, что коэффициенты линейного уравнения будут оценками (4.32).
. Эти выражения показывают, что коэффициенты линейного уравнения будут оценками (4.32).
Соотношение, показывающее с какими из эффектов смешан данный эффект, называется генерирующим соотношением.
При выборе полуреплики 24-1возможны восемь генерирующих соотношений:
Разрешающая способность этих полуреплик различна. Реплики 1-6 имеют по три фактора и носят название планов с расширяющей способностью III ( по наибольшему числу факторов в определяющем контрасте). Реплики 7-8 имеют по четыре фактора и обладают максимальной разрешающей способностью. Их называют главными репликами. Всегда стремятся выбрать реплику с наибольшей разрешающей способностью, т.к. чем больше эффектов взаимосвязано, тем точнее окажется полученная модель.
Однако, если имеется информация об эффектах взаимодействия, то реплики нужно выбирать с ее учетом.
Реализация МПЭ ДФЭ ничем не отличается от реализации МПЭ ПФЭ. Методика оценки значимости коэффициентов и проверка адекватности модели проводится также как и в ПФЭ.
refac.ru
Дробный факторный эксперимент_с46-49
Дробный факторный эксперимент (ДФЭ)
Полный факторный эксперимент позволяет оптимально использовать пространство независимых переменных:
- снизить погрешность определения коэффициентов
- получить элементарно простые формулы для их вычисления.
Однако число опытов, необходимое для реализации ПФЭ, в ряде случаев может все же оказаться неприемлемо большим. Так, если число факторов равно 10, то необходимое число опытов N = 210 = 1024. Поэтому желательно сократить число опытов, но так, чтобы матрица не потеряла своих оптимальных свойств.
Рассмотрим простейший случай — матрицу ПФЭ для двух факторов. Пользуясь ПФЭ, можно получить модель

Если есть основание предполагать, что а12 → 0, т. е. эффект взаимодействия мал, в матрицу ПФЭ вместо х1х2 можно включить третий фактор х3, который в опытах будет принимать значения, соответствующие столбцу х1х2. Запишем новую таблицу (табл. 4.2) и подсчитаем столбцы для всех взаимодействий.

Можно видеть, что в этой таблице совпадают столбцы для хо и х1х2х3, для х1 и х2х3, для х2 и х1х3, для х3 и х1х2, т. е. рассчитанные коэффициенты будут смешанными оценками
а0 → а0+а123 ; а1 → а1+а23 ; а2 → а2+а13 ; а3 → а3+а12 ;
Это значит, что найти истинное значение а0 , а1, а2 и а3 из такого эксперимента нельзя, но предполагая, что все эффекты взаимодействий стремятся к нулю, считаем, что

Иначе говоря, возможность сокращения числа опытов появляется при введении неко-торых допущений о свойствах функции отклика, а риск ошибочно оценить линейные эффек-ты за счет влияния взаимодействия является платой за это сокращение.
Факторный план может быть уменьшен в кратное двум количество раз без нарушения ортогональности. Матрица дробного факторного эксперимента представляет собой 1/2, 1/4, 1/8 и т. д. реплику, в которой столбец одного из эффектов получается перемножением столб-цов других эффектов. Это произведение, взятое со знаком + или —, называется генерирую-щим соотношением. В приведенном примере генерирующее соотношение для х3—х1х2.
Рассмотренный пример использования четырех опытов для трех факторов вместо вось-ми опытов, необходимых для ПФЭ, является дробным факторным экспериментом (ДФЭ) от ПФЭ 23–1 половиной ПФЭ (полуреплика).
Обозначим ДФЭ 2k–p, где k — общее число факторов, р — число эффектов взаимодей-ствия, замененных новыми факторами. Если полный факторный эксперимент для пяти факторов содержит 32 опыта, а желательно поставить лишь одну четвертую часть (четверть-реплику), то ДФЭ будет 25–2. Необходимо только, чтобы остающееся число опытов было больше числа факторов, иначе будут смешаны и линейные эффекты.
В общем случае определить, какие эффекты смешаны, можно, пользуясь определяю-щим контрастом, представляющим собою произведение генерирующего соотношения на генерируемый фактор. Определяющий контраст всегда равен +1 или —1. Для того чтобы определить, какой эффект смешан с данным, нужно умножить определяющий контраст на фактор. Так, если для трех факторов х1х2х3 = 1, то х1 будет смешанным с х2х3:

так как х1∙х1=1.
Для реплик большой дробности имеется лишь одна четкая рекомендация: если известно, что какое-либо взаимодействие существенно, его по возможности не следует заменять фактором и наиболее важный фактор следует ставить на место наиболее слабого взаимодействия. Пусть необходимо выбрать 1/8 реплики для ПФЭ 26 , т.е. 26–3 , причем известно, что сильным является взаимодействие х2х3 , а из вводимых факторов х4 , х5 и х6
наиболее сильный х4 . Тогда следует выбрать генерирующие соотношения
х4 = х1х2х3 ; х5 = х1х2 ; х6 = х1х3 .
Определяющие контрасты будут
1= х1х2х3х4 = х1х2х5 = х1х3х6 .
В табл. 4.3 приведена матрица планирования для этого случая. Чтобы исключить влияние систематических ошибок, рекомендуется случайная последовательность опытов матрицы, например 7, 6, 3, 8, 2, 5, 4, 1.
| N | x0 | x1 | x2 | x3 | x5 | x6 | x4 | N | x0 | x1 | x2 | x3 | x5 | x6 | x4 |
| x1x2 | x1x3 | x1x2x3 | x1x2 | x1x3 | x1x2x3 | ||||||||||
| 1 | + | + | + | + | + | + | + | 5 | + | + | + | – | + | – | – |
| 2 | + | – | + | + | – | – | – | 6 | + | – | + | – | – | + | + |
| 3 | + | + | – | + | – | + | – | 7 | + | + | – | – | – | – | + |
| 4 | + | – | – | + | + | – | + | 8 | + | – | – | – | + | + | – |
Анализ РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА
Определение ошибок эксперимента
Для оценки получаемых при планировании результатов эксперимента необходимо определить ошибку воспроизводимости опытов sв.
Ошибку опытов определяют по n специально поставленным параллельным опытам на основном уровне. Тогда дисперсия ошибку воспроизводимости будет равна

Анализ адекватности модели
Проведя эксперимент, можно воспользоваться отдельными результатами для выводов. Однако всегда представляют результаты в виде модели процесса. Опыты выполнены с ошиб-ками, и, как бы хорошо не были подобраны коэффициенты модели, всегда будут существо-вать μi, невязка — предсказанного по модели, и экспериментального результата

Полученное уравнение является наилучшим среди всех линейных уравнений в смысле минимума квадратов невязок. Хотя сумма квадратов невязок и минимальна, она существует и называется остаточной суммой квадратов.
Под адекватностью понимают пригодность модели. Смысл пригодности формулирует-
ся экспериментатором. Вычислим, например, остаточную дисперсию, равную остаточной сумме квадратов, деленной на число степеней свободы;

Число степеней свободы равно числу данных (опытов) за вычетом числа коэффициен-тов, которые уже вычислены по результатам этих опытов независимо друг от друга,
f = N–k–1
Здесь k соответствует числу коэффициентов в уравнении.
Параллельные реализации одного опыта соответствуют в этом случае одному опыту. Если поставлены пулевые опыты для оценки дисперсии воспроизводимости, но результат этих опытов не используется при подсчете коэффициентов модели, то нулевые опыты не участвуют и при расчете степеней свободы.
После определения s2ост и дисперсии воспроизводимости эксперимента s2В по крите-рию Фишера проверяют адекватность модели.
Проверка значимости коэффициентов
Дисперсия коэффициента регрессии aj определяется по формуле

Например, для ПФЭ двух факторов


Доверительный интервал для aj строится обычным образом с использованием
t-критерия.

Коэффициент значим, если его абсолютная величина больше доверительного
интервала.
49
studfiles.net
Курсовая работа: Дробный факторный эксперимент
Методы планирования многофакторных экспериментов и преимущества их использования. Математическое планирование эксперимента и его основные направления. Пример применения метода дробного факторного эксперимента. Расчет коэффициентов уравнения регрессии. Краткое сожержание материала:Размещено на
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«Московский государственный университет печати
имени Ивана Федорова»
Курсовая работа
по дисциплине: «Основы научных исследований, организация и планирование эксперимента»
Тема: Дробный факторный эксперимент
Подготовил:
студент группы ДТмом-1-1
Кушниренко Н.
Руководитель: Бобров В.И.
Москва-2012
Оглавление
Введение
1. Дробный факторный эксперимент
2. Пример использования ДФЭ
Список литературы
Введение
планирование эксперимент дробный
Решение большинства проблем, связанных с совершенствованием и разработкой новых полиграфических процессов и оборудования, требует проведение сложных и дорогостоящих исследований. Большинство объектов исследования представляют собой многофакторные системы, трудно поддающиеся аналитическому описанию. Поэтому оптимальному планирования и проведению экспериментальных исследований следует уделять большое внимание.
Долгое время порядок и методика проведения эксперимента целиком определялась личным опытом и интуицией исследователя. Для описания сложных многофакторных систем, как правило, использовалась одно- факторная методика, при которой исследовалось поведение объекта в зависимости от каждого фактора в отдельности, в то время как остальные фиксировались на определенных уровнях. Такой путь приводил к получению большого количества избыточной информации об объекте исследования, ккоторую очень трудно было перевести к компактной форме в виде единого уравнения. Информация представлялась в виде многочисленных графиков и таблиц и требовала длительного анализа и обработки.
Только в 20-е годы нашего столетия английским математиком статистиком Рональдом Фишером была впервые показана целесообразность одновременного варьирования всеми факторами в противовес широко распространенному однофакторному эксперименту.
Например, для проведения четырехфакторного эксперимента по однофакторной методике необходимо сделать 44 = 256 опытов, проводя опыты в четырех точках при фиксированных значениях трех факторов. В результате получается большое количество графических зависимостей или уравнений, в которых очень трудно ориентироваться.
Используя методику планируемого эксперимента, можно ограничиться 8, 16, 31 опытами, получить компактное уравнение, описывающее процесс, исследовать его на оптимальность и при желании построить сколько угодно графиков и диаграмм.
Методы планирования многофакторных экспериментов позволяют использовать математический аппарат не только на стадии обработки результатов измерений, как делалось раньше, но также при подготовке и проведении опытов. Проведение опытов по специальному плану позволяет значительно снизить трудоемкость определения коэффициентов уравнения исследуемого процесса и выполнить их с заранее запланированной статической точностью.
Применение планирования эксперимента делает поведение исследователя целенаправленным и организованным, существенно способствует повышению производительности его труда и надежности полученных результатов. Важным достоинством методов планирования эксперимента является их универсальность, пригодность в огромном большинстве областей исследований, интересующих современного человека.
В нашей стране планированием эксперимента начали заниматься в 50-х годах и к настоящему времени уже имеются сотня теоритических и прикладных работ в этой области. В некоторых вузах вопросы теория эксперимента в специально изучаемую дисциплину. В связи с этим можно говорить о появлении новой научной дисциплины - математической теории эксперимента.
Математическое планирование эксперимента - это процедура выбора числа и условий проведения опытов, необходимых и достаточных для решения поставленной задачи с требуемой точностью, методов математической обработки их результатов и принятия решений.
В приложении теории оптимального планирования эксперимента можно выделить два основных направления:
- изучения механизма процессов и свойств многофакторных систем;
- оптимизация параметров многофакторных технологических процессов и оборудования.
В технической литературе имеется ряд хорошо сформулированных критериев оптимального планирования для различных ситуаций, разработаны стандартные алгоритмы, используя которые, исследователь может легко выбрать наиболее эффективный путь решения конкретной задачи.
Все методы планирования эксперимента объединяют следующее:
- стремление к минимизации общего числа опытов;
- одновременное варьирование всеми параметрами, определяющими исследуемый процесс, по специальным правилам-алгоритмам;
- использование специального математического аппарата, формализующего многие действия экспериментатора;
- наличие четкой стратегии, позволяющей принимать обоснованные решения после каждой серии опытов.
С использованием четкой стратегии, позволяющей принимать обоснованные решения после каждой серии опытов.
1. Дробный факторный эксперимент
При количестве факторов K>4 эффективность использования ПФЭ резко уменьшается, так как количество опытов в плане значительно превышает число определяемых коэффициентов уравнения регрессии. Например, при К=5, для реализации ПФЭ необходимо поставить 32 опыта, а количество определяемых коэффициентов не превышает, как правило, 16, включая эффекты парного взаимодействия факторов «bJk»
На практике часто встречаются ситуации, когда некоторые эффекты взаимодействия факторов не являются существенными, т.е. мало отличаются друг от друга, что особенно относится к коэффициентам тройного взаимодействия и выше. Если влияние некоторого взаимодействия факторов признается ничтожно малым, возникает вопрос, имеет ли смысл находить его, и не лучше ли использовать соответствующий вектор-столбец матрицы планирования для оценки влияния дополнительного фактора?
Рассматриваемый метод заключается в том, что для нахождения коэффициентов математической модели изучаемого процесса используются не планы ПФЭ, а некоторые их части Ѕ, ј и т.д. эти системы опытов называются дробными репликами. В таблице 5.1 представлен план ПФЭ и его дробные реплики.
Рассмотрим метод ДФЭ на примере. Пусть необходимо найти математическое описание объекта исследования с тремя факторами в виде:
=b0+b1X1+b2X2+b3X3
Если использовать ПФЭ, то необходимо провести 8 опытов по плану, представленному в таблице 5.1. Однако эту же задачу можно решить и с помощью меньшего количества опытов. Например возьмем Ѕ дробную реплику ПФЭ при К=3 из таблицы 5.1, но третий вектор-столбец приравняем произвольно X1, X2. Такое преобразование возможно.
План ПФЭ и его дробные реплики
| № Опыта | Факторы | Дробные реплики | |||
| X1 | X2 | X3 | |||
| 1 2 3 4 5 6 7 8 | + - + - + - + - | + + - - + + - - | + + + + - - - - | 1/2 1/2 |
Если предположить, что эффект парного взаимодействия факторов «b12» ничтожно мал и стремится к нулю. В этом случае матрица планирования эксперимента имеет вид, представленный в таблице 5.2., а такой план будет считаться планов дробного факторного эксперимента (ДФЭ). Равенство X3 = X1X2 называется генерирующем соотношением. Планы ДФЭ обозначаются символом 2к-р, где р - число факторов., приравненных к произведениям.
Матрица планирования эксперимента
www.tnu.in.ua
Введение. Дробный факторный эксперимент - курсовая работа
Дробный факторный эксперимент
курсовая работапланирование эксперимент дробный
Решение большинства проблем, связанных с совершенствованием и разработкой новых полиграфических процессов и оборудования, требует проведение сложных и дорогостоящих исследований. Большинство объектов исследования представляют собой многофакторные системы, трудно поддающиеся аналитическому описанию. Поэтому оптимальному планирования и проведению экспериментальных исследований следует уделять большое внимание.
Долгое время порядок и методика проведения эксперимента целиком определялась личным опытом и интуицией исследователя. Для описания сложных многофакторных систем, как правило, использовалась одно- факторная методика, при которой исследовалось поведение объекта в зависимости от каждого фактора в отдельности, в то время как остальные фиксировались на определенных уровнях. Такой путь приводил к получению большого количества избыточной информации об объекте исследования, ккоторую очень трудно было перевести к компактной форме в виде единого уравнения. Информация представлялась в виде многочисленных графиков и таблиц и требовала длительного анализа и обработки.
Только в 20-е годы нашего столетия английским математиком статистиком Рональдом Фишером была впервые показана целесообразность одновременного варьирования всеми факторами в противовес широко распространенному однофакторному эксперименту.
Например, для проведения четырехфакторного эксперимента по однофакторной методике необходимо сделать 44 = 256 опытов, проводя опыты в четырех точках при фиксированных значениях трех факторов. В результате получается большое количество графических зависимостей или уравнений, в которых очень трудно ориентироваться.
Используя методику планируемого эксперимента, можно ограничиться 8, 16, 31 опытами, получить компактное уравнение, описывающее процесс, исследовать его на оптимальность и при желании построить сколько угодно графиков и диаграмм.
Методы планирования многофакторных экспериментов позволяют использовать математический аппарат не только на стадии обработки результатов измерений, как делалось раньше, но также при подготовке и проведении опытов. Проведение опытов по специальному плану позволяет значительно снизить трудоемкость определения коэффициентов уравнения исследуемого процесса и выполнить их с заранее запланированной статической точностью.
Применение планирования эксперимента делает поведение исследователя целенаправленным и организованным, существенно способствует повышению производительности его труда и надежности полученных результатов. Важным достоинством методов планирования эксперимента является их универсальность, пригодность в огромном большинстве областей исследований, интересующих современного человека.
В нашей стране планированием эксперимента начали заниматься в 50-х годах и к настоящему времени уже имеются сотня теоритических и прикладных работ в этой области. В некоторых вузах вопросы теория эксперимента в специально изучаемую дисциплину. В связи с этим можно говорить о появлении новой научной дисциплины - математической теории эксперимента.
Математическое планирование эксперимента - это процедура выбора числа и условий проведения опытов, необходимых и достаточных для решения поставленной задачи с требуемой точностью, методов математической обработки их результатов и принятия решений.
В приложении теории оптимального планирования эксперимента можно выделить два основных направления:
- изучения механизма процессов и свойств многофакторных систем;
- оптимизация параметров многофакторных технологических процессов и оборудования.
В технической литературе имеется ряд хорошо сформулированных критериев оптимального планирования для различных ситуаций, разработаны стандартные алгоритмы, используя которые, исследователь может легко выбрать наиболее эффективный путь решения конкретной задачи.
Все методы планирования эксперимента объединяют следующее:
- стремление к минимизации общего числа опытов;
- одновременное варьирование всеми параметрами, определяющими исследуемый процесс, по специальным правилам-алгоритмам;
- использование специального математического аппарата, формализующего многие действия экспериментатора;
- наличие четкой стратегии, позволяющей принимать обоснованные решения после каждой серии опытов.
С использованием четкой стратегии, позволяющей принимать обоснованные решения после каждой серии опытов.
math.bobrodobro.ru
Дробный факторный эксперимент. | Бесплатные курсовые, рефераты и дипломные работы
Во многих практических задачах идентификации влияние взаимодействий (произведений факторов) второго и высших порядков отсутствует или пренебрежимо мало. Кроме того, на первых •этапах исследования часто нужно получить в первом приближении лишь линейную аппроксимацию изучаемого уравнения связи при минимальном количестве опытов. Поэтому неэффективно использовать ПФЭ для оценивания коэффициентов лишь при линейных членах и некоторых парных произведениях из-за реализации большого числа вариантов варьирования (2n), в особенности при большом числе факторов n. При линейном росте числа независимых факторов число вариантов варьирования для ПФЭ растет по показательному закону; в результате чего на проверку гипотезы Об, адекватности остается излишне много степеней свободы.
Дробным факторным экспериментом (ДФЭ) называется эксперимент, реализующий часть (дробную реплику) полного факторного эксперимента. ДФЭ’ позволяет получить, например, … линейное приближение искомой функциональной зависимости  в некоторой небольшой окрестности точки базового режима при минимуме опытов.
в некоторой небольшой окрестности точки базового режима при минимуме опытов.
2.1 Планирование эксперимента. Для решения трехфакторной (п=3) задачи регрессии в линейном приближении можно ограничиться четырьмя вариантами варьирования, если в планировании ПФЭ типа 22 произведение z1z2 приравнять третьему независимому фактору z3. Такое планирование, представленное матрицей (табл. 3.3), позволяет найти свободный член bo и три оценки коэффициентов регрессии при линейных членах b1,b2,b3 (из четырех опытов нельзя получить более четырех оценок коэффициентов регрессии).
Таблица 3.3
| G | zo | z1 | z2 | z3 | z1z2 | z1z3 | z2z3 | z1z2z3 |
| +1 +1 +1 +1 | -1 +1 -1 +1 | -1 -1 +1 +1 | +1 -1 -1 +1 | +1 -1 -1 +1 | -1 -1 +1 +1 | -1 +1 -1 +1 | +1 +1 +1 +1 |
Применение ДФЭ всегда связано со смешиванием, т. е. с совместным оцениванием нескольких теоретических коэффициентов математической модели. В рассматриваемом случае, если коэффициенты регрессии bil при парных произведениях отличны от нуля, каждый из найденных коэффициентов bi служит оценкой двух теоретических коэффициентов регрессии:
bo®bo+b123; b1®b1+b23; b2®b2+b13; b3=b3+b12
Действительно, указанные теоретические коэффициенты в таком планировании не могут быть оценены раздельно, поскольку столбцы МП для линейных членов и парных произведений совпадают (полностью коррелированы). Рассмотренный план ДФЭ представляет половину плана ПФЭ типа 23 и называется полурепликой от ПФЭ типа 23 или планированием типа N ==23-1 (см. табл. 3.3).
Для правильного планирования ДФЭ необходимо использовать все полученные ранее сведения теоретического и интуитивного характера об объекте и выделить те факторы и произведения факторов, влияние которых на отклик существенно. При этом смешивание нужно производить так, чтобы линейные коэффициенты bo, b1, …, bn были смешаны с коэффициентами при взаимодействиях самого высокого порядка (так как обычно они в модели отсутствуют), или при тех взаимодействиях, о которых априори известно, что они не оказывают влияния на отклик. Следовательно, недопустимо произвольное разбиение плана ПФЭ типа 23 на две части для выделения полуреплики типа 23-1.
При большом числе п факторов для получения линейного приближения можно построить дробные реплики высокой степени дробности. Так, при п =7 можно составить дробную реплику на основе ПФЭ типа 23, приравняв четыре из семи факторов к взаимодействиям трех других факторов: парным и тройному. Будем обозначать тип дробней реплики записью 2n-p, если р факторов приравнены к произведениям остальных n—р факторов.
План ДФЭ можно построить, приравнивая факторы различным взаимодействиям (парным, тройным и т. д.), разумеется, при этом меняется система совместных оценок теоретических коэффициентов. Для получения системы совместных оценок и анализа разрешающей способности дробных реплик удобно пользоваться понятиями генерирующего и определяющего соотношений.
Генерирующее соотношение служит для построения дробной реплики. Так, в рассмотренном планировании мы задавали полуреплику плана ПФЭ типа 23 с помощью генерирующего соотношения z3=z1z2.
Определяющим соотношением называется соотношение, задающее элементы первого столбца матрицы планирования для фиктивной переменной (все они всегда равны 1). Выражение определяющего соотношения в рассматриваемом случае получается умножением левой и правой частей приведенного генерирующего соотношения на z3, т. е. 1=z1z2z3, так как всегда  =1.
=1.
Знание определяющего соотношения позволяет найти, всю систему совместных оценок без изучения матрицы планирования ДФЭ. Соотношения, задающие эти оценки, можно найти, последовательно перемножив независимые факторы на определяющее соотношение:
загрузка…
zo=z1z2z3; z1=z2z3; z2=z1z2; z3=z1z2;
отсюда легко находятся; смешиваемые теоретические коэффициенты регрессии и их оценки:
bo®bo+b123; b1®b1+b23; b2®b2+b13; b3®b3+b12
Если априори „можно принять, что коэффициенты при всех парных и тройном взаимодействии равны нулю, то реализация этой полуреплики позволит получить раздельные оценки для всех четырех линейных коэффициентов регрессии. Разрешающая способность полуреплик определяется их генерирующими соотношениями. Разрешающая способность тем выше, чем более высок порядок взаимодействий, с коэффициентами которых смешаны линейные коэффициенты. Она увеличивается для главных полуреплик с ростом числа независимых факторов.
2.2 Проведение эксперимента на объекте исследования. Реализация плана ДФЭ ничем не отличается от реализации плана ПФЭ.
2.3 Проверка воспроизводимости эксперимента. Проверку однородности оценок дисперсии отклика в различных точках факторного пространства проводят в полном соответствии с методикой, изложенной для ПФЭ, различие состоит лишь в числе точек плана.
2.4 Получение математической модели объекта. Процедура определения оценок коэффициентов регрессии и проверки их значимости полностью совпадает с процедурой, применяемой при исследовании объекта методом ПФЭ.
Проверка адекватности математического описания. Адекватность математического описания функции отклика проверяют теми же методами, что и для ПФЭ.
refac.ru
|
|
..:::Счетчики:::.. |
|
|
|
|
|
|
|
|




























