|
|
|
|
 Far |
| WinNavigator |
| Frigate |
| Norton
Commander |
| WinNC |
| Dos
Navigator |
| Servant
Salamander |
| Turbo
Browser |
|
|
| Winamp,
Skins, Plugins |
| Необходимые
Утилиты |
| Текстовые
редакторы |
| Юмор |
|
|
|
File managers and best utilites |
Приложение 1 Конспекты занятий Урок №1 «Числовая окружность». Числовая окружность реферат
Приложение 1 Конспекты занятий Урок №1 «Числовая окружность»
- С числовой окружностью вы до сих пор не встречались, зато хорошо знакомы с числовой прямой. Скажите мне, пожалуйста, что такое числовая прямая?
- Совершенно верно, это прямая, на которой задана начальная точка О, масштаб (единичный отрезок) и положительное направление (слайд 7) .
На числовой прямой мы можем двигаться как в положительном направление, так и в отрицательном направление.
- Так и у числовой окружности, есть начальная точка О, масштаб. На ней так же отмечаются точки, как в положительном направлении, против часовой стрелки, так и в отрицательном направлении, по часовой стрелки (слайд 8).
- Числовая окружность разбита на 4 четверти (слайд 8). Длина окружности, как нам известно, С=2
R. Мы для удобства обозначим наш радиус равный 1, то есть мы будем рассматривать единичную окружность С=2
(слайд 8).
- Как я уже говорила, на этой единичной числовой окружности мы можем отмечать точки. Нарисуем окружность. Отмечаем начальную точку О и будем отмечать точки, как в положительном направлении, так и в отрицательном направлении. Для начала отметим следующие точки
0, 
, (слайд 9)
- Нарисуем еще одну окружность и отметим следующие точки 
- Причем точки расположены симметрично друг другу (слайд 10).
- Когда мы отмечали данные точки на числовой окружности, что вы заметили?
- Молодцы, правильно. Нарисуем еще одну окружность и отметим следующие точки
, (слайд 11)
- Молодцы. Нарисуем еще одну окружность и отметим следующие точки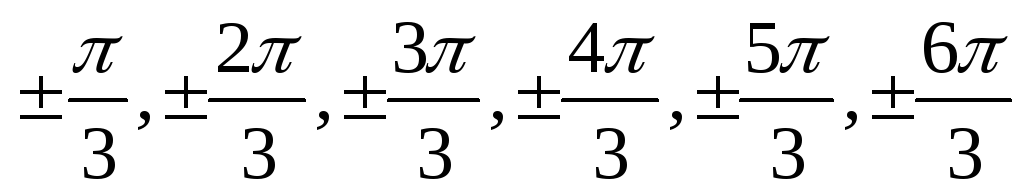 
, (слайд 12)
- Молодцы. Теперь все эти значения мы нанесем на одну числовую окружность (Учащиеся наносит значения на одну окружность), (слайд 14).
- это прямая, на которой задана начальная точка О, масштаб (единичный отрезок) и положительное направление.
На числовой прямой мы можем двигаться как в положительном направление, так и в отрицательном направление.
( учащиеся рисуют окружность, и отмечают на ней все, что показывается на слайде)
(учащиеся у себя в тетрадях рисуют окружность).
(Учащиеся отмечают эти точки, причем со знаком минус, они отмечают самостоятельно)
(Учащиеся отмечают эти точки, причем со знаком минус, они отмечают самостоятельно).
- мы заметили, что значение 
совпадает с
,
совпадает с
,
совпадает с
, а
с 2
(Учащиеся отмечают эти точки. Учащиеся так же замещают, что некоторые значения совпадают),
(Учащиеся отмечают эти точки. Учащиеся так же замещают, что некоторые значения совпадают),
(Учащиеся наносят значения на одну числовую окружность)
studfiles.net
10 класс. Алгебра. Тригонометрические функции. Числовая окружность. - Числовая окружность. Числовая окружность на координатной плоскости.
Комментарии преподавателя
Для любой функции независимый аргумент откладывается либо на числовой прямой, либо на окружности. Охарактеризуем и числовую прямую, и числовую окружность.
Прямая становится числовой (координатной) прямой, если отмечено начало координат, выбраны направление и масштаб (рис. 1).
Числовая прямая устанавливает взаимно-однозначное соответствие между всеми точками прямой и всеми действительными числами.
Например, берем число 
откладываем на координатной оси, получаем точку 
Возьмем число 
откладываем на оси, получаем точку 
(рис. 2).
И наоборот, если мы взяли любую точку 
на координатной прямой, то найдется единственное соответствующее ей действительное число (рис. 2).
К такому соответствию люди пришли не сразу. Чтобы понять это, вспомним основные числовые множества.
Сначала ввели множество натуральных чисел 
Затем множество целых чисел 
Множество рациональных чисел 
Предполагалось, что этих множеств будет достаточно, и существует взаимно-однозначное соответствие между всеми рациональными числами и точками прямой. Но оказалось, что на числовой прямой есть бесчисленное множество точек, которые нельзя описать числами вида 
Пример – гипотенуза прямоугольного треугольника с катетами 1 и 1. Она равна 
(рис. 3).
Найдется ли среди множества рациональных чисел число, в точности равное 
Нет, не найдется. Докажем этот факт.
Докажем методом от противного. Предположим, что существует дробь, равная 
т.е. 
Тогда 
Возведем обе части в квадрат, 
Очевидно, что правая часть равенства делится на 2, 
. Значит и 
Тогда 
Но тогда и 
А значит, 
Тогда получается, что дробь 
сократимая. Это противоречит условию, значит 
Число 
иррациональное. Множество рациональных и иррациональных чисел образуют множество действительных чисел 
Если мы возьмем любую точку на прямой, ей будет соответствовать какое-либо действительное число. И если мы возьмем любое действительное число, ему будет соответствовать единственная точка на координатной прямой.
Уточним, что такое числовая окружность и каковы взаимоотношения между множеством точек окружности и множеством действительных чисел.
Начало отсчета – точка A. Направление отсчета – против часовой стрелки – положительное, по часовой стрелке – отрицательное. Масштаб – длина окружности 
(рис. 4).
Вводя эти три положения, мы имеем числовую окружность. Укажем, каким образом каждому числу 
поставить в соответствие точку на окружности и наоборот.
Задав число 
получаем точку на окружности 
(рис. 4).
Каждому действительному числу соответствует точка на окружности. А наоборот?
Точка 
соответствует числу . А если взять числа 
Все эти числа своим образом на окружности имеют только одну точку
Например, 
соответствует точке B (рис. 4).
Возьмем все числа 
Все они соответствуют точке B. Нет взаимно-однозначного соответствия между всеми действительными числами и точками окружности.
Если есть фиксированное число то ему соответствует только одна точка окружности
Если есть точка окружности, то ей соответствует множество чисел
В отличии от прямой, координатная окружность не обладает взаимно-однозначным соответствием между точками и числами. Каждому числу соответствует только одна точка, но каждой точке соответствует бесчисленное множество чисел, и мы можем их записать.
Рассмотрим основные точки на окружности.
Задано число 
Найти, какой точке на окружности оно соответствует.
Разделив дугу 
пополам, получаем точку 
(рис. 5).
Обратная задача – дана точка 
середина дуги 
Найти все действительные числа, которые ей соответствуют.
Отметим на числовой окружности все дуги, кратные 
(рис. 6).
Важны также дуги, кратные 
Дано число 
Нужно найти соответствующую точку.
Обратная задача – дана точка, нужно найти каким числам она соответствует.
(рис. 7).
Мы рассмотрели две стандартные задачи на двух важнейших точках.
Пример 1.
a) Найти на числовой окружности точку с координатой 
Решение:
Откладываем от точки A
это два целых оборота и еще половина, и 
Получаем точку M – это середина третьей четверти (рис. 8).
Ответ. Точка M – середина третьей четверти.
b) Найти на числовой окружности точку с координатой 
Решение:
Откладываем от точки A полный оборот и еще 
получаем точку N (рис. 9).
Ответ: Точка N находится в первой четверти.
Мы рассмотрели числовую прямую и числовую окружность, вспомнили их особенности. Особенностью числовой прямой является взаимно-однозначное соответствие между точками этой прямой и множеством действительных чисел. Такого взаимно-однозначного соответствия нет на окружности. Каждому действительному числу на окружности соответствует единственная точка, но каждой точке числовой окружности соответствует бесчисленное множество действительных чисел.
Ранее мы изучили числовую окружность и выяснили её свойства (рис. 1).
Рис. 1
Каждому действительному числу 
соответствует единственная точка 
на окружности.
Каждой точке 
на числовой окружности соответствует не только число 
но и все числа вида 
Поместим окружность в координатную плоскость. По прежнему, каждому числу соответствует точка на окружности. Теперь этой точке на окружности соответствуют две координаты, как и любой точке координатной плоскости.
(рис. 2).
Рис. 2
Наша задача – по данному числу найти не только точку, но и её координаты, и наоборот, по координатам найти одно или несколько соответствующих чисел.
Пример 1.Дана точка 
– середина дуги 
Точке соответствуют числа вида 
Найти координаты точки (рис. 3).
Рис. 3
Решение:
Координаты можно найти двумя разными способами, рассмотрим их по очереди.
1. Точка лежит на окружности, R=1, значит, она удовлетворяет уравнению окружности 
по условию. Мы помним, что величина центрального угла численно равна длине дуги в радианах, значит, угол 
Это значит также, что прямая 
делит первую четверть ровно пополам, значит, это прямая 
Точка лежит на прямой 
поэтому удовлетворяет уравнению этой прямой.
Составим систему из двух уравнений.
Решив систему, получим искомые координаты.
2. Рассмотрим 
прямоугольный (рис. 4).
Рис. 4
Итак, мы задали число нашли точку и её координаты. Определим также координаты симметричных ей точек (рис. 5).
Рис. 5
Следующая задача – таким же образом определить координаты точек, кратных 
Окружность радиуса R=1 помещена в координатную плоскость, 
Найти точку на окружности и её координаты (рис. 6).
Рис. 6
Решение:
Рассмотрим 
– прямоугольный.
т. е. угол 
Найдем координаты симметричных точек (рис. 7).
Рис. 7
Мы задали число 
нашли точку на окружности, эта точка единственная, и нашли её координаты.
Самостоятельно рекомендуется найти координаты точки, соответствующей числу 
Пример 1. Дана точка 
Найти её прямоугольные координаты.
Решение:
Точка 
середина третьей четверти (рис. 8).
Рис. 8
Мы поместили числовую окружность в координатную плоскость, научились находить по числу точку на окружности и её координаты. Эта техника лежит в основе определения синуса и косинуса, которые будут рассмотрены далее.
ИСТОЧНИК
http://interneturok.ru/ru/school/algebra/10-klass/trigonometricheskie-funkcii/chislovaya-okruzhnost-2
http://interneturok.ru/ru/school/algebra/10-klass/trigonometricheskie-funkcii/chislovaya-okruzhnost-na-koordinatnoy-ploskosti
https://www.youtube.com/watch?v=NTqNXLwAaKo
https://www.youtube.com/watch?v=k6UPDd--yGo
https://www.youtube.com/watch?v=8aUlWR5zNis
http://mathematics-tests.com/10-klass-chislovaya-okruzhnost
http://www.kmrz.ru/catimg/40/400239.jpg
http://shkolnie.ru/pars_docs/refs/18/17881/17881_html_m73662372.jpg
www.kursoteka.ru
Урок по теме "Числовая окружность". 10-й класс
Разделы: Математика
Цели урока:
- Повторение алгебраических функций, изучаемых в 7-9 классах, единиц измерения угловых величин, формул для нахождения длины окружности, геометрического смысла числа П и его значения.
- Формирование понятия “числовая окружность”, длина дуги окружности.
- Развитие логического мышления.
- Воспитание ответственного отношения к учебе.
Оборудование: компьютер, проектор, презентация “Числовая окружность” (Microsoft Office PowerPoint 2007), рабочие карты учащихся, бланки для самостоятельной работы (Microsoft Office Word 2007).
Ход урока
1) Повторение (повторяются основные функции 7–9 класса их отличительные особенности, уравнения, основные свойства функций – подготовка к изучению тригонометрических функций).
• График какой из функций изображен на рисунке?
• Дайте характеристику каждой прямой, составьте ее уравнение.
• Укажите свойства данной функции?
2) Решение задач (повторение градусной, радианной меры и перевода из одной меры в другую).
№ 1. Найдите радианную меру неизвестного угла и градусную меру всех углов треугольника.
№ 2. Найдите радианную меру углов треугольника, если их величины относятся как 2:3:4. (задача решается в рабочей карте учащегося с последующей проверкой на слайде)
№ 3. Переведите из градусной меры в радианную следующие углы 1°, 180°, 45°, 60° (задача решается в рабочей карте учащегося, 1 угол совместно, остальные самостоятельно с последующей проверкой на слайде)
3) Изучение нового материала (беседа с учащимися по тексту §1 учебника, формирование понятия “Числовая окружность”, умения определять длины основных и произвольных дуг окружности, все основные сведения и решение задач фиксируются в рабочей карте)
1. Найдите на числовой окружности точку, которая
соответствует заданному числу 
2. Вторая четверть единичной окружности разделена пополам точкой М, а четвертая четверть разделена на 3 равных части точками К и Р. Чему равны длины дуг АМ, АК, АР, РВ, МК, КМ?
4) Закрепление изученного (используется бланк для самостоятельной проверки, работа оценивается по желанию учащихся, слабые учащиеся могут пользоваться помощью или поэтапным контролем со стороны учителя).
1. Изобразите на числовой окружности точку,
которая соответствует числу 
.
2. Первая четверть единичной окружности разделена пополам точкой М, а третья четверть разделена на 3 равных части точками К и Р. Чему равны длины дуг АМ, BD, CK, MР, DM, МК, СР?
5) Домашнее задание §1 (до построения макетов), № 3, 10, 19.
Литература
- Мордкович А.Г. Алгебра и начала математического анализа. 10-11 классы. В 2 ч. Учебник и задачник для учащихся общеобразовательных учреждений (базовый уровень). М.: Мнемозина, 2008 г.
- http://www.virtualcard.ru/postcard.php?image=images04/pic3311.jpg
Приложение 1
Приложение 2
Приложение 3
Поделиться страницей:xn--i1abbnckbmcl9fb.xn--p1ai
|
|
..:::Счетчики:::.. |
|
|
|
|
|
|
|
|